Simulating solid electrolyte interphase formation spanning 10⁸ time scales with an atomically informed phase-field model

Abstract

The solid electrolyte interphase (SEI) governs the reversibility of advanced electrochemical devices such as batteries, but  the role of cations in its formation remains poorly understood. Here, the thickness and compositional evolution of the SEI are tracked over time scales from nanoseconds to seconds with a newly developed atomically informed phase-field multiscale model. We deconvolve the complex interplay among electron tunneling, species diffusion, and chemical/electrochemical reactions by probing different controlling factors separately and jointly to determine the rate-limiting steps. We show that the SEI growth begins with the formation of organic products, followed by the conversion of these organic products into inorganic ones, and in the end the inorganic products fully cover the lithium metal surface to form a passivation layer. While electron tunneling determines the thickness of these layers, the growth rates of the organic and inorganic SEI layers are controlled by the rates of Li-ion diffusion and electrochemical reactions, respectively. This predictive model is universally applicable to multiphase and multicomponent electrochemical systems and represents a significant advancement in simulating complex reaction processes.

---

Broader context

The solid-electrolyte interphase (SEI) plays a critical role in battery performance and longevity, yet its formation process remains one of the most ambiguous issues in battery science due to the complex, spatially and temporally dynamic nature of this interfacial layer. To capture the rapid SEI formation process across various scales, an atomically informed phase-field model (AI-PFM), capable of handling complex reaction networks with multiple species, is developed. This model enables the investigation of SEI formation and initial growth from nanoseconds to seconds in time and angstroms to 100 nm in length. By tracking the evolution of SEI products and electrolyte species up to surface passivation, the interplay among reaction kinetics, species transport, and electron tunneling during SEI formation is successfully deconvoluted with the identification of the governing factors. For the first time, this study reveals that the competition between Li-ion diffusion and reaction kinetics is a key determinant of the growth rates of different SEI products. Such deconvolution is difficult to achieve with current modelling and experimental techniques, which underscores the major advancement and benefits of this AI-PFM framework. It offers a unique approach to evaluate the competing complex mechanistic pathways and understand the formation mechanism of the SEI.

Introduction

The solid electrolyte interphase (SEI) plays a vital role in enabling advanced batteries where electrode materials operate beyond the electrochemical stability limits of electrolytes. Its chemical building blocks come from the sacrificial decomposition of electrolytes, which remains conductive to the working ions but prevents electron tunneling that drives the parasitic reactions.^1–5 The SEI governs the reversibility and power density of the battery system. Given such importance, extensive efforts have been devoted to understanding its formation process, but a thorough mechanistic knowledge at a fine timescale is still absent. Recently, it was found that the SEI in Li-ion batteries formed at high charging current during the first cycle extends the battery cycle life by an average of 50%,⁶ revealing that the properties and chemistry of the SEI also rely on the rate of formation. Experiments indicated that the initial SEI formation on a bare Li metal surface completes in less than 1 second.⁷ This rate is comparable to the rate of lithium metal deposition, where a typical 1 mA cm⁻² rate means depositing 8 Li (001) layers or 1.4 nm thick Li atoms in 1 second. Therefore, it is logical to infer that SEI formation and lithium growth compete at the same timescale, resulting in various deposition morphologies.^8,9 However, experimental limitations in temporal and spatial resolutions often make it challenging to characterize fast in situ SEI formation processes and deconvolute the intricate physical and chemical processes across multiple length and time scales.

At microscopic and mesoscopic timescales, atomic-scale theoretical approaches, such as density functional theory (DFT) calculations and ab initio molecular dynamics (AIMD) simulations, offer insights into the reaction energy profiles,^10–12 species transport properties^13,14 and electrolyte reduction pathway within a system¹¹ that are otherwise unavailable from experiments. However, their simulation time is typically limited to scales of 10–100 picoseconds (10⁻¹¹–10⁻¹⁰ s) for a system of hundreds of atoms,^15,16 thus offering only limited information on SEI formation, which typically occurs over timescales approaching 1 s. A Monte Carlo-molecular dynamics (MC-MD) method can predict the time evolution of SEI species over 10 ns (10⁻⁸ s).¹⁵ Using classical reactive force fields, MD simulations can extend the process further up to 100 nanoseconds (10⁻⁷ s).¹⁷

At a macroscopic scale, continuum models have been developed to study the long-term SEI growth over hours and even months.^18–23 Despite the widespread acceptance and observation of a two-layer structured SEI in many experimental works, the reaction networks and SEI compositions are simplified so that only a single SEI product is included in most continuum-level models.^20,24,25 For example, Christensen and Newman²⁰ proposed a mathematical model to estimate the growth rate of inorganic Li₂CO₃ and determined that the SEI grows around 20 nm in 15 h on graphite, which is limited by the electron transport via a Li interstitial diffusion mechanism. The continuum model in the study by Horstmann et al.²³ predicted that the capacity fade shifts from a square-root-of-time dependence to a linear time dependence as the charging current density increased, suggesting a shift from diffusion-controlled to electron-migration-controlled SEI growth. Their simulations concluded that it would take several months for an SEI layer a few nanometers in thickness to form. While these models have been effective in predicting the battery lifetime^25,26 at a macroscale, they overlooked several critical kinetic processes involved in SEI growth, which prevents them from accurately predicting the precise composition and morphology of the SEI. For instance, the detailed electrolyte reduction reaction networks and the competitive interactions between the various reaction products are neglected. Furthermore, these continuum models fail to account for the electron transport mechanisms, which is crucial for understanding the SEI formation and growth processes.

Since single-scale atomistic simulations are insufficient to capture the complex interfacial reactions and phase transformations involved in SEI formation, multiscale computational frameworks have therefore become indispensable for describing the growth, composition, and dynamic evolution of the SEI and its impact on battery performance. Among these, DFT and MD integrated kinetic Monte Carlo (kMC) methods have been used to track the stochastic reaction nature of electrolyte decomposition. For instance, Gerasimov et al.²⁷ tracked EC decomposition and SEI formation on the Li metal for 100 ns, revealing an inorganic-rich inner layer (LiF/Li₂CO₃) and a porous organic-rich outer layer (Li₂EDC) together forming a structure ∼11 nm thick. U. Krewer et al.²⁸ constructed a DFT-kMC-continuum electroneutrality model that predicted a 7-nm-thick inorganic SEI layer within 1 μs (10⁻⁶ s), while the resulting bilayer architecture (porous Li₂CO₃ beneath dense LiF) deviates from experimental observations.^29,30 Recently, chemical reaction networks (CRNs) have been developed to automatically identify the reaction pathways for over 80 million reactions among over 5000 species, in which DFT calculations are combined with kMC simulations to simulate the competition between SEI products within 10 μs (10⁻⁵ s), revealing the formation of distinct inorganic and organic layers in the SEI.³¹ While these kMC-based models have demonstrated success in capturing reaction mechanisms and compositional diversity at the molecular level, they remain limited in temporal and spatial scalability. Their inherently discrete spatial nature restricts the ability to simulate mesoscale structural evolution, such as growth, coarsening, polycrystallinity, and crack formation. Additionally, coupling external physical fields (e.g., mechanical stress relaxation, thermal transport, etc.) with kMC frameworks is generally indirect through modifications of reaction rates.

The phase-field (PF) method offers a continuum framework well-suited for modeling multicomponent, multiphase systems with intrinsic flexibility to incorporate physical fields. By introducing multiple concentrations or order parameter fields governed by free energy functionals, PF models can capture the spatiotemporal evolution of competing SEI phases, while naturally incorporating additional physical phenomena such as ion/electron transport, electrochemical reactions, elastic deformation, thermal transport, and other physical effects. Previously, phase-field modeling has been successfully applied to the investigation of Li electrodeposition^32–38 and the interaction between Li dendrites and artificial SEIs.^39,40 However, only a limited number of phase field investigations have been applied to the study of SEI formation and growth,^29,41–43 with several important thermodynamic/kinetic parameters associated with SEI formation still absent. Compared with kMC-based models, previous PF models have simplified the SEI as a single homogeneous phase and thus failed to account for the chemical diversity observed experimentally.^40,41 This is because PF simulations face numerical challenges in simulating multiple moving interfaces with distinct kinetics when tracking the evolution of reaction intermediates, which requires careful parameter calibration and efficient algorithms to ensure numerical stability and convergence.

In this work, we demonstrate that an atomically informed phase-field model (AI-PFM), which incorporates multiple electrochemical reactions, species transport and electron tunneling process, can track the temporal and spatial evolution of SEI formation from nanoseconds to seconds until it passivates the Li metal surface. The AI-PFM here incorporates these parameters obtained from DFT and MD calculations through simplification and parameterization. We apply this model to a 1-D prototypical battery system with a Li metal anode and a liquid electrolyte consisting of 1 M LiPF₆ in ethylene carbonate (EC) and simulate the evolution of two common SEI products, i.e., organic component dilithium butylene dicarbonate (Li₂BDC) and inorganic component lithium carbonate (Li₂CO₃). By tracking the temporal evolution of the spatial distribution of these products and electrolyte species, we analyze the effect of electron tunneling on SEI thickness, examine the competition between the reactive and diffusive processes during the growth of different SEI products, and identify the governing mechanism behind the formation of different SEI products. Our findings pinpoint the Li⁺ diffusion as the key limiting factor of the formation of organic Li₂BDC during the initial 10⁻⁵ s scale, whereas Li₂CO₃ directly formed by two-electron reduction of EC is limited by its slow reaction kinetics within around 10⁻² s. This multiscale approach, for the first time, provides profound insights into the SEI formation across time scales spanning 8 orders of magnitudes (from nanoseconds to seconds) and length scales spanning 3 orders of magnitudes (from angstroms to 100 nm). Furthermore, the ability of AI-PFM to simulate complex reaction networks that encompass multiphases and multicomponent systems has been demonstrated.

Results and discussion

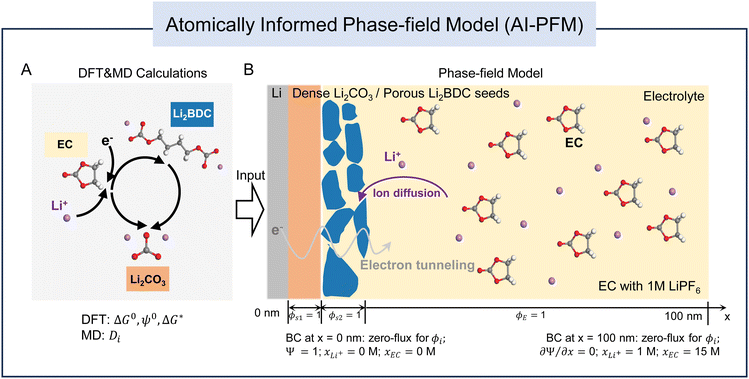
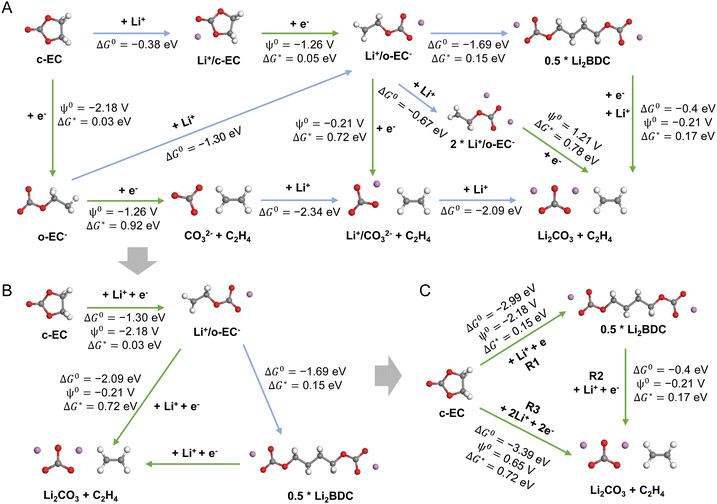
Fig. 1 shows the overall framework for modeling the SEI growth integrating multiple electrochemical reactions, species transport, and electron tunneling. DFT calculations are utilized to determine the reaction pathways and their corresponding energy profiles, while MD simulations are employed to obtain the diffusivity of species. Next, phase-field simulations are performed to study the temporal and spatial evolution of SEI products, incorporating parameters derived from atomic-scale calculations. Details of all sub-models can be found in the Experimental section.

Fig. 1 Schematic modeling framework of SEI formation on a lithium metal. (A) Reaction networks and corresponding energy profiles (Gibbs free energy change ΔG⁰, reduction potential ψ⁰, and kinetic barrier ΔG* obtained from DFT calculations) of the considered reactions. MD simulations provide the diffusivity of species D_i. (B) Phase-field model and boundary conditions (BC) for three coupled processes: electrochemical reactions, ion diffusion and electron tunneling. The simulation domain ranges from the surface of the Li metal electrode at x = 0 nm to the bulk liquid electrolyte region (the other boundary is at x = 100 nm). The initial concentrations of EC and LiPF₆ in the electrolyte are 15 M and 1 M, respectively. Unless otherwise specified, the initial SEI nucleus on the Li metal surface consists of two layers: a 0.5 nm dense Li₂CO₃ layer adjacent to the Li metal and a 6 nm Li₂BDC layer with a porosity of 50% adjacent to the electrolyte. A set of evolving non-conserved order parameters (ϕ_E, ϕ_S1, and ϕ_S2) represent the electrolyte, inorganic Li₂CO₃, and organic Li₂BDC phases, respectively.

To obtain the atomic-scale input parameters, we perform an extensive DFT study to establish the predefined reaction network that contains both electrochemical reactions (magenta arrows) and purely chemical reactions (green arrows) (Fig. 2). For each reaction, we calculate its standard Gibbs free energy change ΔG⁰ (for purely chemical reactions) or reduction potential ψ⁰ (for electrochemical reactions), as well as the electron transfer kinetic barrier ΔG* according to Marcus theory.^44,45 Fig. 2A shows all the reactions considered in our atomistic simulations, involving multiple reactants (Li⁺, c-EC, and e⁻), intermediate species (o-EC⁻, Li⁺/c-EC, Li⁺/o-EC⁻, Li⁺/CO₃²⁻, and 2Li⁺/o-EC⁻), and SEI products (Li₂BDC, Li₂CO₃, and C₂H₄). Here, c-EC represents the neutral cyclic EC molecule, and o-EC⁻ represents the reduced ring-opened EC.

Fig. 2 Illustration of the reaction pathways. (A) All the reaction products and pathways considered in atomistic simulations. The reduction potentials ψ⁰ (vs. SHE), the electron transfer kinetic barrier ΔG* for electrochemical reactions (green arrows), and Gibbs free energy change (ΔG⁰) for chemical reactions (blue arrows) are included. (B) and (C) Simplified reaction pathways and their corresponding thermodynamic and kinetic parameters. The reaction steps, R1, R2, and R3, along with the parameters in (C), are adopted for the phase-field simulations.

While it is possible to develop a comprehensive phase-field model that incorporates all these reactions, such simulations would not efficiently bridge the length and time scales. Thus, we simplify the reaction paths and focus on the primary SEI products: the organic Li₂BDC and inorganic Li₂CO₃ (Fig. 2B and C), based on DFT computed thermodynamics driving forces, consistent with extensive theoretical and experimental studies.^15,28,46 We note that Li₂BDC is thermodynamically more favorable than Li₂EDC, in agreement with other computational studies,^3,47 and both products have been experimentally observed to coexist within the SEI.⁴⁶ Therefore, we consider Li₂BDC as the representative organic product in our model. The impact of Li ions on EC reduction is considered, but the anions are not, as recent molecular dynamics simulations showed that the typical PF₆⁻ anions do not enter the electric double layer (EDL) in strong carbonate-based solvents.⁴⁸ The simplification treatment involves two procedures: (1) for two or more parallel reactions, we select the smallest reaction barrier as the simplified reaction barrier and record the Gibbs free energy change (parallel reactions have the same Gibbs free energy change); (2) for series reactions, we select the largest reaction barrier as the simplified reaction barrier and record the sum of Gibbs free energies for these series reactions.

In the phase-field simulations, we focus on the formation kinetics of organic Li₂BDC and inorganic Li₂CO₃ via simplified reactions (R1, R2, and R3 in Fig. 2C) at a constant voltage of −3.04 V with respect to the standard hydrogen electrode potential, SHE (or 0 V versus Li⁺/Li⁰). As illustrated in Fig. 1, we employ a 1-D system representing a half-cell, and the simulation domain spans from the Li metal electrode surface at x = 0 nm into the bulk liquid electrolyte comprising EC and 1 M LiPF₆ at x = 100 nm. A set of non-conserved order parameters (ϕ_E, ϕ_S1, and ϕ_S2) represent the electrolyte (E), inorganic Li₂CO₃ (S1), and organic Li₂BDC (S2) phases, respectively. The phase evolution is governed by the Allen–Cahn equations (eqn (3)–(5) in the Experimental section). The total Gibbs free energy change ΔG^r_m and the linearized reaction rate R_m for each reaction (m is the reaction index for R1, R2, and R3) are related to its standard Gibbs free energy change ΔG⁰, reduction potential ψ⁰, and the activation energy ΔG* from DFT, as well as the local activities of species including electrons, Li⁺ and EC molecules, as shown in eqn (6) and (7) in the Experimental section. Electron tunneling is a key short-term electron transport mechanism for SEI formation, which is governed by the tunneling barrier of SEIs. Therefore, we numerically solve the steady-state Schrödinger electron tunneling equation by formulating a phase-dependent tunneling barrier to calculate the probability of electrons in the SEI, so that the SEI/electrolyte interface positions do not need to be explicitly tracked, taking advantage of phase-field modeling. The local electron activity can then be defined as the probability of electrons in the SEI, i.e., a_e⁻ = |Ψ*Ψ|, where Ψ is the electron wave function (see “Electron tunneling” in the Experimental section for details). At the Li metal surface, a_e⁻ is presumed to be 1 and decays exponentially through the SEI and the electrolyte. The time-dependent evolution of the concentration distribution of Li⁺ and EC is dominated by the reaction-diffusion equation (eqn (9) in the Experimental section), and the diffusivities of species are obtained from MD calculations (see the “Species transport” section in the Experimental section for details). We assume that the concentration of both Li⁺ and EC at the Li/SEI interface is 0 M. At the right electrolyte boundary, their concentrations are fixed at 1 M for Li⁺ and 15 M for EC, corresponding to their initial bulk concentration. The activities of species are given by a_i = x_i/x⁰_i, where x_i is the concentration of species Li⁺ and EC, and the standard concentrations of Li⁺ and EC (x⁰_EC) are 1 M and 15 M, respectively. Therefore, the initial activity of both a_Li⁺ and a_EC is 1.

Electron tunneling effect on SEI thickness

SEI formation is initiated with the electrolyte reduction at the electrode surface, where electrons are transferred from the electrode via tunneling through the growing SEI layer. The electrolyte reduction products are precipitated on the electrode surface, serving as a protective layer against further electrolyte decomposition, and the thickness of the SEI is determined by the electron tunneling range. Therefore, in this section, we first investigate the effect of electron tunneling on the growth of both organic Li₂BDC and inorganic Li₂CO₃ via R1 and R3, respectively. We consider a 1-D system with different single SEI nuclei representing the initial dense organic Li₂BDC and inorganic Li₂CO₃ seeds, as illustrated in Fig. 3A and B. To focus on investigating the electron tunneling behavior, we temporally disregarded the transport of Li⁺ and EC during SEI growth by assuming that the activities of Li⁺ and EC remain constant at their initial value (a_Li⁺ = a_EC = 1), mimicking a semi-infinite system with sufficient supplies of these species from the electrolyte. Thus, the Gibbs free energy changes of organic Li₂BDC (ΔG^r_R1) and inorganic Li₂CO₃ formation (ΔG^r_R3) from eqn (6) in the Experimental section are modified as follows:

ΔG^r_R1 = ΔG⁰_R1 + F(ψ_e − ψ_sol − ψ⁰_R1) − RT ln a_e⁻ (1)

ΔG^r_R3 = ΔG⁰_R3 + F(ψ_e − ψ_sol − ψ⁰_R3) − 2RT ln a_e⁻ (2)

where F is the Faraday constant, R is the gas constant and T is the temperature.

Fig. 3 The effect of electron tunneling on the growth of the organic Li₂BDC based on R1 and inorganic Li₂CO₃ based on R3. (A) and (B) Illustrations of reactions R1 and R3 considered and the 1D system, respectively, (C) comparison of organic Li₂BDC growth behaviors between assuming a_e⁻ = 1 and electron tunneling, and (D) comparison of inorganic Li₂CO₃ growth behaviors assuming a_e⁻ = 1 and electron tunneling.

To highlight the electron tunneling effect, we compare two cases: one assuming the electron activity a_e⁻ = 1 throughout the system (i.e., assuming that the SEI behaves like a metal) and the other with electron activity a_e⁻ obtained from the steady-state Schrödinger electron tunneling equation. As shown in Fig. 3C and D, starting with an initial thickness of 6 nm, the SEI will continuously grow when a_e⁻ = 1 until the electrolyte is fully consumed. However, when considering the electron tunneling effect, both organic and inorganic SEIs exhibit self-limiting growth behavior. They stop the initial quick growth after reaching a specific thickness. This occurs because the Gibbs free energy changes of reactions R1 and R3 (from eqn (1) and (2)) remain consistently negative, allowing the reactions to proceed indefinitely; but with electron tunneling, the electron activity decays exponentially as the SEI grows (Fig. S1, ESI†). Once the electron activity reduces to a certain level (i.e., when ΔG^r_R1 = 0 and ΔG^r_R3 = 0 in eqn (1) and (2)), reactions R1 and R3 reach equilibrium, where the SEI reaches a tunneling-limited thickness and stops further growth. In our model, the tunneling barrier for Li₂CO₃ (ΔE_Li2CO3 = 1.78 eV) is derived from the DFT calculation.⁴⁹ The tunneling barrier for Li₂BDC is estimated to be a lower bound of ΔE_Li2BDC = 0.24 eV due to porosity⁵⁰ and the fact that the organic Li₂DEC, structurally close to Li₂BDC, has been experimentally measured to exhibit a tunneling barrier of ∼1 eV lower than that of inorganic SEI components.⁵¹ It aligns with the general trend that the inorganic component in the SEI blocks electron tunneling more effectively than the organic species. Using these values, our model predicts tunneling-limited SEI thicknesses of ∼29.4 nm and ∼11 nm for Li₂BDC and Li₂CO₃, respectively, which are close to the experimentally reported values^29,30 during SEI formation. These can be referred to as the “tunneling-limited thickness”, which leads to a good estimation of the first cycle capacity loss, corresponding to the Li consumed to form the SEI up to the tunneling-limited thickness, agreeing well with experiments.^49,52

Fig. 3 also shows the time scales to grow the Li₂BDC and Li₂CO₃ layers to reach a stable thickness. They are 66 ps and 20 ms for Li₂BDC and Li₂CO₃ layers, respectively, under the assumption of no concentration variation of Li⁺ and EC during SEI growth. The electron tunneling generally occurs within a few attoseconds.⁵³ Consequently, this discrepancy in timescales is primarily attributed to the kinetic barrier of the single-electron reduction reaction (R1), substantially lower than that of the two-electron reduction reaction (R3), despite the overall Gibbs free energy of R3 being much greater than that of R1.

Effect of Li⁺ and EC molecules on SEI formation rates

In addition to the electronic tunneling effect on the SEI thickness, the evolution of the concentration of Li⁺ and EC in the system is also critical to the growth dynamics of SEI products. To further investigate the governing factors for both organic and inorganic SEI growth kinetics, we performed a series of simulations by turning on/off the diffusivities of Li⁺ and EC. By assuming the activity of species, we can compare four different cases: (1) not evolving both Li⁺ and EC (a_Li⁺ = 1 and a_EC = 1) means that the concentrations of Li⁺ and EC remain constant at their initial values during SEI growth. Under this idealized condition, the reaction rate is governed mainly by charge-transfer kinetics. (2) Only evolving EC (a_Li⁺ = 1, and a_EC ≠ 1 calculated using eqn (9)) represents the scenario where only the consumption of EC is considered while the Li⁺ concentration remains at its initial value. The reaction rate is affected by both charge-transfer kinetics and the local activity of EC. (3) Only evolving Li⁺ (a_Li⁺ ≠ 1 calculated using eqn (9), and a_EC = 1) represents the scenario where only the consumption of Li⁺ is considered while the EC concentration remains at its initial value. The rate is thus governed by charge-transfer kinetics and the local activity of Li⁺. (4) Evolving both Li⁺ and EC (a_Li⁺ ≠ 1 and a_EC ≠ 1 calculated using eqn (9)) indicates that both Li⁺ and EC are consumed according to their stoichiometric ratio during SEI growth, and their concentration distributions over time are determined using the diffusion equation. Reaction rates in this case reflect a coupled control by charge-transfer kinetics and the activities of all species. The simulation system is the same as those presented in Fig. 3A and B.

In case (1) shown in Fig. 4A, the organic SEI layer growth via R1 will reach their tunneling-limited thickness within around 66 ps (solid blue line), and its rate is purely governed by the reaction kinetics. Furthermore, we find that the EC diffusion has no significant effect on the Li₂BDC growth (the solid and dotted blue lines overlap) by comparing cases (1) and (2), as the EC concentration in the electrolyte closely matches that in Li₂BDC, suggesting that EC molecules could be reduced on-site without requiring additional EC supplied by the electrolyte. Considering the Li⁺ consumption and diffusion by comparing cases (3) and (4), it is found that the predicted Li₂BDC growth time in Fig. 4A increased from 36 ns to ∼57 μs (solid and dotted purple lines). This is consistent with the time scale (∼29 μs) for Li⁺ to diffuse from the right boundary of the electrolyte region to the Li₂BDC surface. It is estimated by using , where L = 100 nm is the diffusion length and 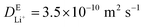is the diffusivity of Li⁺ in the electrolyte obtained from MD simulations. The simulated Li₂BDC growth time (∼57 μs) is close to the 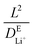estimation, indicating the Li⁺ diffusion-controlled growth nature. This is because, in contrast to EC, the Li site density inside Li₂BDC (∼13.5 M) is significantly higher than the initial concentration of Li⁺ in the electrolyte (1 M) and the reaction rate of R1 is much faster than that of the Li⁺ diffusion, which means that a large amount of Li⁺ needs to be consumed to grow the SEI, necessitating Li⁺ diffusion from the electrolyte to the SEI/electrolyte interface to sustain Li₂BDC growth, as shown in Fig. S2A (ESI†).

Fig. 4 1-D phase-field simulation of the growth of the organic and inorganic SEI products, considering reactions R1 and R3 in Fig. 2C. Parameter study for the governing kinetic factors for organic Li₂BDC growth (A) and inorganic Li₂CO₃ growth (B). Four cases: (1) not evolving both Li⁺ and EC (a_Li⁺ = 1 and a_EC = 1): the concentrations of Li⁺ and EC remain constant at their initial values during SEI growth; (2) only evolving EC (a_Li⁺ = 1, and a_EC ≠ 1 calculated using eqn (9)): only the consumption of EC is considered while the Li⁺ concentration remains at its initial value; (3) only evolving Li⁺ (a_Li⁺ ≠ 1 calculated using eqn (9), and a_EC = 1): only the consumption of Li⁺ is considered, while the EC concentration remains at its initial value; (4) evolving both Li⁺ and EC (a_Li⁺ ≠ 1 and a_EC ≠ 1 calculated using eqn (9)): both Li⁺ and EC are consumed according to their stoichiometric ratio during SEI growth.

Regarding the inorganic Li₂CO₃ growth via R3, the Li₂CO₃ layer grows to its tunneling-limited thickness of about 11 nm under ∼20 ms, which is much slower than the diffusion time of both Li⁺ (∼29 μs) and EC, and thus their diffusion does not influence the inorganic Li₂CO₃ SEI layer growth behavior (Fig. 4B and Fig. S2B, ESI†). In contrast to the organic Li₂BDC, the growth rate of Li₂CO₃ is much (∼10³ times) slower due to the significantly larger kinetic barrier of R3 than for R1. We further show that by increasing the Li⁺ concentration from 1 M to 4 M, the time required for Li₂BDC to reach its stable thickness decreases from 57 μs to 1 μs, while the growth rate of dense Li₂CO₃ remains unchanged (Fig. S3, ESI†). Consequently, the growth rate of Li₂BDC is determined by Li⁺ diffusion, whereas the growth of Li₂CO₃ is controlled by the reaction rate.

Spatial, chemical, and temporal evolution of the SEI

In the previous section, we separately investigate the effects of electron tunneling and species diffusion on the growth kinetics of single-layered dense organic Li₂BDC or inorganic Li₂CO₃ products. However, experimental studies indicate that the formed SEI often consists of a two-layer structure, with an inner inorganic layer and an outer organic layer that usually exhibits a porous structure.^29,30 Therefore, it is crucial to study the spatial, chemical, and temporal evolution of the SEI layer, as well as the competition between products, to gain an in-depth understanding of the limiting processes, their interactions, and the final SEI composition and thickness. To this end, we analyze the temporal SEI formation via R1 to R3 based on Fig. 2C. Initially, we assume that there is a two-layer structured SEI nucleus within the simulation system, comprising a 0.5 nm dense Li₂CO₃ layer adjacent to the Li metal and a 6 nm thick layer of Li₂BDC at the outer layer with a constant porosity of 50%, as shown in Fig. S4 (ESI†). Subsequently, we calculate the SEI formation from nanoseconds to seconds. Fig. 5A illustrates the general trends of SEI thickness over time. Initially, from nanoseconds to microseconds, the porous Li₂BDC will grow to its stable thickness (∼27.2 nm) via R1. After 21.7 μs, Li₂BDC near the Li metal side transforms into porous Li₂CO₃ via R2, growing to its stable thickness (∼11 nm). After 1 ms, the pores in the porous Li₂CO₃ are filled via R3. The eventual SEI consists of a porous outer organic layer (∼16.2 nm thick) and a thinner dense inner inorganic layer (∼11 nm) covering the anode surface. This aligns well with experimental finding of a two-layered structure.^2,5,29

Fig. 5 Temporal evolution of SEI growth in the Li/(EC + 1 M LiPF₆) model system. (A) Temporal evolution of the SEI thickness. The dashed and solid lines represent the porous and dense products, respectively. Temporal evolution of the order parameters (B) indicating the products and the concentration distribution of Li⁺ (C) at 6 selected times. The position (0–100 nm) signifies the distance from the Li anode surface to the electrolyte region. (D) Schematic depiction of SEI growth in the Li/(EC + 1 M LiPF₆) model system from nanoseconds to seconds. Color scheme: gray for the Li anode, blue for Li₂BDC, orange for Li₂CO₃, light yellow for EC, and purple for Li⁺.

To understand the underlying processes governing SEI formation, we conduct a detailed analysis of the temporal evolution in the distribution of chemical reaction species and SEI products, as shown in Fig. 5B and C. The corresponding SEI morphologies at 6 selected time frames are displayed in Fig. 5D. The diffusion rate of Li⁺ is slower than that of EC decomposition via R1 as the porous Li₂BDC products gradually grow. As a result, Li⁺ ions are immediately consumed when they arrive at the SEI/electrolyte interface, leading to a concentration gradient in the electrolyte zone from 1 μs to 21.7 μs (stages I to II). This indicates that Li₂BDC production is a Li⁺ diffusion-limited process. Despite the charge-transfer rate for the R2 pathway being slightly slower than that of R1, the formation of Li₂CO₃ via R2 does not occur in this stage due to limited Li⁺ availability as Li⁺ is preferentially consumed by the faster-growing R1 process. After 21.7 μs, when Li₂BDC reaches its tunneling-limited thickness, additional Li⁺ begins to diffuse into this porous layer (stages II to III), enabling Li₂BDC to react with Li⁺ and electrons to form Li₂CO₃ via R2, and the overall process still remains diffusion-limited. After ∼0.02 s, Li₂CO₃ can be generated inside the pores. Since direct two-electron reduction of EC to Li₂CO₃ via R3 has a much slower charge-transfer rate, the Li⁺ diffusion from the electrolyte rapidly compensates for the consumption of Li⁺ during the two-electron reduction of EC, which is a reaction-controlled process (stages IV to VI), as shown in Fig. 5C. In contrast to the Li⁺ concentration profiles, no EC-concentration gradient develops during the entire process, as shown in Fig. S5 (ESI†). From this, we conclude that the first two steps of one-electron reduction process including the electrolyte degradation to organic Li₂BDC and transformation to Li₂CO₃ are Li⁺ diffusion-limited processes (stages I to III); then, the two-electron reduction reaction that directly formed dense Li₂CO₃ is a reaction-controlled process (stages IV to VI).

Furthermore, after 0.02 s, the Li metal surface is fully covered with SEI products and the EC can no longer be reduced due to the blocking of electron tunneling. This indicates that the initial SEI formation is completed within this short time frame, which agrees with the experimental results.^7,54 Direct in situ measurements of the initial SEI formation are rather challenging, as these reactions occur very fast,⁵⁵ as pointed out by Odziemkowski and Irish,⁷ who tracked the corrosion potential time transients of the Li-metal electrode in various electrolyte systems and indicated that the passivating reactions, which lead to SEI formation, are often completed in less than 1 second. The two-layered SEI model, with the inorganic species (LiF, Li₂CO₃, and Li₂O) close to the electrode surface and the porous organic layer (e.g. LEDC) closer to the electrolyte, obtained from postmortem analysis, does not reveal the formation sequence and timelines of these species.⁵⁶ Notably, the absence of operando tools with nanosecond-to-second temporal resolution and nanoscale chemical specificity is a well-recognized gap.³ Recently, the formation sequence obtained from gas evolution combined with other spectroscopy analysis revealed LEDC as the major product with little Li₂CO₃ during initial SEI formation, and LEDC eventually evolved into Li₂CO₃.^57–60 Using isotope exchange along with in situ time-of-flight secondary ion mass spectroscopy (TOF-SIM) measurements, a bottom-up SEI growth mechanism was proposed, suggesting that the SEI components formed in the early stage (organic species) are on the outer side (electrolyte side), while those formed in the latter stage (inorganic species) are on the inner side (electrode side).⁶¹ These experimental results on the temporal and spatial evolution of SEI formation collectively support the prediction from our atomically informed phase-field model (AI-PFM). This sequence, LEDC forms first and converts into Li₂CO₃ near the electrode surface, is different from the CRN-kMC, which predicted that LEDC continues to grow even after Li₂CO₃ stops growing.³¹

Influence of key parameters on the SEI growth dynamic

Having elucidated the growth dynamics and governing mechanisms of SEI formation on the Li metal in EC with LiPF₆, we further employ our model to explore how key parameters, including electron tunneling barriers (ΔE), species diffusivities, and reaction kinetic barriers (ΔG*), affect SEI evolution.

The relative tunneling barriers play an important role in determining the SEI morphology. Higher electron-tunneling barriers led to a thinner Li₂BDC layer via R1 and a Li₂CO₃ layer via R3 and a shorter time to reach the tunneling-limited thickness (Fig. S6A–C, ESI†). Since the tunneling barrier of the organic phase (Li₂BDC) is more susceptible to factors such as porosity and electrolyte composition,⁵⁰ while only varying ΔE_Li2BDC from 0.24 to 1.8 eV, the overall SEI formation sequence remained the same: rapid porous Li₂BDC deposition via R1, partial conversion to Li₂CO₃ via R2, and final pore filling by Li₂CO₃ via two-electron EC reduction in R3. However, the bilayer morphology was only formed when ΔE_Li2BDC < ΔE_Li2CO3. Conversely, when ΔE_Li2BDC ≥ ΔE_Li2CO3, a thinner initial Li₂BDC layer is ultimately fully consumed and converted to a thicker dense Li₂CO₃ layer, yielding a predominantly single inorganic SEI layer (Fig. S8, ESI†). These results underscore the critical role of relative tunneling barriers in determining the SEI morphology.

The effect of Li⁺ diffusivity on SEI growth has also been systematically examined. Increasing Li⁺ diffusivity in the liquid electrolyte from 10⁻¹¹ m² s⁻¹ to 10⁻⁸ m² s⁻¹ significantly accelerates Li₂BDC growth via R1, reducing the growth timescale from ∼10⁻⁴ s to ∼10⁻⁷ s (Fig. S9A, ESI†), with no impact on the Li₂CO₃ growth via R3, as it is governed by the reaction kinetics rather than diffusion (Fig. S9C, ESI†). Notably, variations in Li⁺ diffusivity within both solid phases have a negligible influence on both Li₂BDC and Li₂CO₃ growth (Fig. S9B and D, ESI†), further underscoring that liquid-phase Li⁺ transport is the rate-limiting step for initial organic SEI formation. Additionally, Li⁺ diffusivity has a minimal influence on the SEI growth sequence and the resulting bilayer architecture (Fig. S10, ESI†).

We further evaluated the impact of the charge-transfer kinetic barrier (ΔG*) on SEI growth by sweeping ΔG* from 0.15 to 0.75 eV for both Li₂BDC (R1) and Li₂CO₃ (R3). This range corresponds to a decrease in the intrinsic electron-transfer rate constant k⁰_m from 2.08 × 10¹⁰ s⁻¹ to 1.736 s⁻¹. As shown in Fig. S11 (ESI†), two kinetic regimes emerge: (i) Li⁺-diffusion-limited region: for lower ΔG*, both SEI products reach their tunneling-limited thickness around the same time and remain largely insensitive to ΔG* and (ii) charge-transfer kinetic-limited: for higher ΔG*, the growth rates of both Li₂BDC and Li₂CO₃ decrease exponentially with increasing ΔG*. The transition occurs at ΔG* ≈ 0.49 eV, where the calculated charge-transfer reaction rate equals the Li⁺ diffusion rate, delineating the shift between Li⁺-diffusion and electron-transfer-controlled regimes (Fig. S11C, ESI†). These results highlight variations in kinetic barriers for each reaction, and their relative relationship to Li⁺ diffusion rates can lead to multiple rate hierarchies among R1–R3, ultimately altering the overall SEI growth sequence and one-layer or two-layer SEI structures.

It should be clarified that our simulations focus on the initial formation of the SEI, occurring on the timescale of seconds. Although our phase-field model can simulate and demonstrate the SEI evolution from nanoseconds to seconds, this self-limiting behavior is featured only during the initial short-term growth of SEIs. Ideally, the SEI would stabilize after initial formation, preventing further Li⁺ consumption and electrolyte degradation, since it is electronic insulating. However, the SEI layer thickness can change during cycling and calendar aging.³ Electron leakage mechanisms through hole polaron migration,⁶² the formation and transport of Li-atom interstitials,⁶³ radical species shuttling,⁵⁰ as well as grain boundaries,^64,65 may dominate the SEI evolution over longer timescales. Shi et al.⁶⁶ reported that Li atoms can diffuse through the SEI via interstitial mechanisms, forming positive-charged Li interstitials and electrons. A continuum model²⁰ predicted that the SEI can continue to grow to 1400 nm in 1000 days, where the neutral Li atoms carrying electrons facilitate this long-term SEI growth. Moreover, defects such as grain boundaries and heterogeneous interfaces,⁶⁴ cracks, and pores⁶⁷ can serve as short-circuit transport paths for electrons and other reacting species. These mechanisms lead to continuous “growth” of the SEI as the battery degrades. We intend to thoroughly investigate these possibilities in our forthcoming study with a 2-D model.

The major strength demonstrated by this model framework is its ability to resolve the spatial and temporal evolution of the SEI composition and thickness that span from nanoseconds to seconds and deconvolute the interplay among multiple physical phenomena (reactions, species transport, and electron tunneling), as well as reveal the governing factors for each electrolyte degradation process. Although this deconvolution provides insights into the governing mechanisms of electrolyte decomposition that are currently inaccessible to experimental microscopy or spectroscopy techniques, the predictions from our simulations, such as the initial SEI formation and thickness of the SEI within milliseconds and the preferential formation of inorganic vs. organic products near the Li surface, serve as testable hypotheses for future experimental studies and can guide experimentalists by identifying key mechanistic signatures to be probed indirectly through ex situ quenching or rapid-interruption experiments followed by surface analysis.

The modeling framework developed in this study is broadly extensible to other electrochemical systems beyond lithium-based batteries, owing to two central features. First, it is explicitly informed by DFT calculations, which capture the chemical changes at the electrode/electrolyte interface. Second, the model is formulated as a general multiphase, multicomponent phase-field framework capable of capturing complex couplings among interfacial reactions, species transport, and microstructural evolution. To adapt this framework to other electrochemical systems, such as sodium-ion, lithium–sulfur, or solid-state batteries, the key steps involve determining the reaction networks and corresponding parameters via DFT calculations, redefining the phase-field variables to reflect the relevant phases, and modifying the free energy functional to include new phases and reaction intermediates. Transport parameters (e.g., diffusivities and electron tunneling barriers) can be similarly updated to reflect system-specific physical properties. For instance, the same model structure can simulate Na SEI formation by introducing Na-containing decomposition reactions and products (e.g., Na₂CO₃ and Na₂O⁶⁸) and recalibrating the thermodynamic driving force and reduction kinetics accordingly. In solid-state systems, the framework can be further extended to include coupled electrochemical-mechanical effects by incorporating additional mechanical energy terms or coupling coefficients in the free energy functional, thereby enabling the simulation of multiplephase evolution at the solid–solid interface. By extending to higher dimensional simulations, it can potentially capture the detailed SEI morphology and its competition with Li stripping/plating. Combining this model with high-throughput calculations and virtual screening for materials discovery would provide data-based design guidance.

Conclusions

In summary, we present an atomically informed phase-field framework that reveals SEI evolution across unprecedented time scales (from nanoseconds to seconds) and lengths (from angstroms to 100 nm). Initially, porous Li₂BDC grows to ∼27.2 nm via one-electron reduction within microseconds. After 21.7 μs, part of the Li₂BDC near the Li metal converts into porous Li₂CO₃ (∼11 nm). By 1 ms, the pores are filled with Li₂CO₃ directly via two-electron reduction, forming a final SEI with a porous organic outer layer (∼16.2 nm) and a dense inorganic inner layer (∼11 nm). Li₂BDC formation and its transformation into Li₂CO₃ are limited by Li⁺ diffusion, while the final two-electron reduction of EC to form Li₂CO₃ is reaction-controlled. Electron tunneling determines the thickness of both layers. This study enhances the understanding of SEI formation and demonstrates potential for simulating complex reaction networks across broad time and length scales.

Experimental

Phase-field model

We formulate the phase-field model by considering the simplified reaction networks as well as the reacting species Li⁺, e⁻ and EC, based on our recently developed phase-field model of stoichiometric compounds and solution phases.⁶⁹ With this approach, the phase-field governing equations can be directly derived via the variational derivatives of the free energies without any approximation or arbitrary treatments. The thermodynamic and kinetic parameters of the simplified reactions are shown in Fig. 2C and Table S2 (ESI†). We also consider the following assumptions/simplifications:

• The SEI products are considered stoichiometric compounds whose free energy only exists at their stoichiometric composition points rather than being a continuous function of composition, as shown in Fig. S12 (ESI†). Meanwhile, the electrolyte is assumed to be an ideal solution, whose realistic interaction behavior will be investigated in our future work using MD simulations or Debye–Hückel approximations. The Li metal anode is assumed to be at the left boundary of the simulation region and not explicitly simulated.

• The electric potential is assumed to be uniform within the electrolyte and the SEI. Therefore, the applied voltage is imposed, and the Poisson equation is not solved, which significantly improves numerical efficiency and stability. The electron transport within the system is assumed to be dominated by tunneling.

• To improve numerical convergence, we use linear kinetics for most of the simulations involving SEI products in this work.

• The organic Li₂BDC is inherently micro-porous due to molecular disorder and low packing density. In our 1D model, porosity is represented by a fixed value rather than explicitly evolving pore structures, which is a common simplification in 1-D SEI simulations.^18,22 Thus, the porous SEI layer is considered as a mixture of electrolyte and solid products. While the current framework does not incorporate dynamic porosity, it retains the ability to resolve the competitive formation, spatial distribution, and temporal evolution of major inorganic and organic SEI species.

• The evolution of the gas phase (e.g., C₂H₄) is neglected because it escapes from the SEI or system and does not contribute to further reactions and the SEI film.³¹ Their formation energies and reaction barriers are still accounted for when selecting the dominant solid-phase pathways, influencing the free energy landscape and kinetics of the phase-field model. Thus, neglecting explicit gas-phase evolution has a minimal impact on the predicted solid-state SEI growth kinetics.

• The decomposition of both lithium hexafluorophosphate (LiPF₆) and the formed SEI products (i.e., Li₂O) is not considered in this model. We assume that the diffusion and dissolution of primary electrolyte reduction products (Li₂CO₃ and Li₂BDC) formed during SEI formation are ignored due to relatively low solubility.^70,71

Three phases are distinguished by a set of non-conserved order parameters, in which (ϕ_E,ϕ_S1,ϕ_S2) = (1,0,0), (0,1,0), and (0,0,1) represent the liquid electrolyte (E), Li₂CO₃ (S1) and Li₂BDC (S2) phases, respectively. The kinetic evolution of the primary order parameters ξ is governed by the following Allen–Cahn equations:⁶⁹

where g_well is a multi-well function to ensure that the local minima are at the above-mentioned order parameter values, k_i represents the gradient coefficients which are related to the interfacial energies and thicknesses, h(ϕ) = 6ϕ⁵ − 15ϕ⁴ + 10ϕ³ is an interpolation function, and L_j is the interface mobility coefficient. The detailed derivation can be found in Supplementary note 1 (ESI†).

The total Gibbs free energy change ΔG^r_m and the linearized reaction rate R_m of reactions R1 to R3 can be written as follows:

where is the electron transfer kinetic with the unit of (s⁻¹), is the kinetic barrier of the electron transfer, m is the reaction index from R1 to R3, F is the Faraday constant, ψ_e is the electric potential in the electrode, ψ_sol is the electric potential in the electrolyte, and ψ⁰_m is the reduction potential vs. SHE; ΔG⁰_m is the standard Gibbs free energy change, R is the ideal gas constant, T = 298 K is the temperature, a_k and a_l are the activities of the reactants and products of a given reaction, and ν^m_k is the stoichiometric coefficient for species k in reaction m, which is positive for the reactants and negative for the products. In this work, we simulate the SEI formation at a constant voltage of −3.04 V vs. SHE (i.e., 0 V versus Li⁺/Li⁰). At this voltage, the overpotential of reaction Li⁺ + e⁻ = Li is 0, which means ψ_e − ψ_sol − ψ_Li⁺/Li⁰ (vs. SHE) = 0 V. The interfacial potential difference at the Li metal and electrolyte interface is thus ψ_e − ψ_sol = −3.04 V.

Electron transport

To describe the electron tunneling from the Li metal through the SEIs and electrolyte behavior, we develop a diffuse-interface description of the steady-state Schrödinger equation with a phase-dependent tunneling barrier,where Ψ is the electron wave function, m_e is the electron mass, ℏ is the reduced Planck constant, and is the phase-dependent tunneling barrier, with ΔE⁰_tj being the electron tunneling barrier for each phase. The electron tunneling barrier for the porous structure is assumed to be a constant, without explicitly accounting for the local variations introduced by solvent-filled pores.^50,72 As the 1D model does not resolve the pore geometry, the uniform electron tunneling barrier is a reasonable assumption.⁷³ As such, the Schrödinger electron tunneling equation is numerically solved for the entire system without the need to distinguish the different phase regions and phase interfaces. The local electron activity can then be defined as the probability of electrons in the SEI, i.e., a_e⁻ = |Ψ*Ψ|. This numerical solution to the Schrödinger equation indicates an exponential decay of the electron concentration at the SEI/electrolyte interface with the increase of the SEI thickness, which would lead to extremely low electron concentrations when the SEI becomes thicker than its tunneling-limited thickness d_lim and cause the SEI to shrink. However, the electron concentration is lower bounded by the intrinsic electron concentration of the SEI and electrolyte. Therefore, in the phase-field simulations, we use a_e⁻ = |Ψ*Ψ| with a lower cut-off of 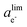that ensures ΔG^r_m = 0 and an equilibrium SEI thickness of d_lim to avoid the SEI shrinkage.

Species transport

The time-dependent evolution of the concentration distribution of Li⁺ and EC is dominated by diffusion. We directly evaluate the reduced concentration x_i = c_i/c₀ in the electrolyte rather than the total concentration, which follows the reaction–diffusion equation below:where i = [Li⁺,EC] is the concentration of species, c₀ = 1 M is the bulk concentration of Li⁺, and c^j_i is the site density in phase j. D^eff_i is the effective diffusion coefficient of species i, which is given by D^eff_i = h(ϕ_S1)D^S1_i + h(ϕ_S2)D^S2_i + h(ϕ_E)D^E_i. The diffusion coefficient of species (Li⁺ and EC) in the porous structure is calculated using the relationship D^S2_i = P^1.5D^E_i based on the Bruggeman relation.⁷⁴ However, it is difficult to obtain a specific porosity of the outer organic layer, since the morphology and the porosity vary during the SEI formation.^29,30,75,76 In this work, we assume that the porosity (P) of the formed porous organic SEI layer is a constant of 50%. The self-diffusion coefficients of independent species can be found in Table S3 in the ESI.†

Atomistic simulations

Density functional theory (DFT) calculations for ΔG⁰ and ψ⁰

All DFT calculations were conducted using the Gaussian 09 code.⁷⁷ The double hybrid functional M06-2X^78–81 and the basis set 6-31+G(d,p) together with the D3 dispersion correction⁸² were used. The SMD solvation model⁸³ was used to account for the solvation environment with the dielectric constant set to ε = 20.5 for the carbonate-based electrolyte.^84,85 The standard Gibbs free energy change (ΔG⁰) of the Li⁺ coordination reaction (the only chemical reaction considered in this work) is calculated as the Gibbs free energy difference between the product and the reactants. The Li⁺ coordination reaction was considered barrierless.³¹ The reduction potential of an electrochemical reaction with respect to the standard hydrogen electrode (SHE) was calculated via ψ⁰ = −ΔG⁰/F − 4.44. The calculation results of all reactions in Fig. 2A are presented in Table S1 (ESI†).

Kinetic barrier ΔG* for electron transfer

Marcus theory^44,45 was used to calculate the kinetics of reduction reactions. Specifically, it is assumed that all reduction reactions occur heterogeneously, with electrons transferred from the electrode.⁸⁶ The energy barrier ΔG* for a reduction reaction iswhere λ is the reorganization energy, which can be decomposed into the inner-shell reorganization energy λ_in and a bulk outer-shell reorganization energy λ_out (λ = λ_in + λ_out). The four-point method in the study by Nelsen⁸⁷ is used to approximate the inner-shell electron reorganization energy, while Marcus's expression is used for the outer-shell term:^31,86where Δe is the transferred electron (that is e for each one-electron reduction reaction), ε₀ is the vacuum permittivity (8.85 × 10⁻¹² F m⁻¹), r is the radius of the reacting molecule and its first solvation shell (all assumed to be 5.0 Å for simplicity³¹), D is the molecule-electrode distance (set to 5.0 Å for calculating λ_out), ε is the optical dielectric constant (∼2.0)³¹ and ε_s is the static dielectric constant (taken to be 20.5).^84,85 The calculation results of all the reactions are shown in Fig. 2A.

Molecular dynamics simulations of diffusion coefficients

MD simulations were conducted to calculate the diffusion coefficients of Li⁺ and EC in the bulk electrolyte following our recent work.⁴⁸ To be more specific, MD simulations were carried out using the Forcite module as implemented in the Materials Studio (MS) 2020⁸⁸ with the COMPASS III force field⁸⁹ and a charge scale of 0.7 applied to the salt ions.⁴⁸ The atomistic model for the carbonate-based electrolyte was constructed to be ∼1.0 M LiPF₆ salt dissolved in the mixed solvent composed of 30 vol% EC and 70 vol % EMC. The MD simulations were first conducted under the constant particle number, volume, and temperature (NPT) ensemble for 2.0 ns at room temperature (20 °C). Then production runs under the NPT ensemble were conducted for 4.0 ns for statistical analyses to obtain the diffusion coefficients of Li⁺ and EC following the approach proposed in a recent work.⁹⁰ The calculation results are presented in Table S2 (ESI†).

Model implementation

The simulations are performed using COMSOL Multiphysics based on the finite element method. A one-dimensional model with a size of 100 nm is built in this work, and the simulation domain is discretized by a grid spacing of 0.5 nm. Zero-flux boundary conditions are applied for order parameters (ϕ_E, ϕ_S1, and ϕ_S2) at the left and right boundaries. The Li⁺ concentration in the electrolyte drops during SEI formation due to the consumption of large amounts of Li⁺ ions, and a new equilibrium needs to be established by stripping some Li⁺ into the electrolyte. The equilibrium Li-plating/stripping potential will shift due to the Li⁺ activity. However, the stripping of Li⁺ during initial SEI formation at potentiostatic voltages can be safely ignored, as the reaction rate of lithium deposition and stripping is much lower than that of SEI formation.³⁵ Hence, we assume that the concentration of both Li⁺ and EC at the Li metal surface is 0 M. The concentrations of Li⁺ and EC at the right electrolyte boundary are 1 M and 15 M, respectively, corresponding to their initial bulk concentrations. The activity coefficients of Li⁺ and EC are 1 and 15, respectively. The boundary condition for solving the steady-state Schrödinger equation is maintained at Ψ = 1 (to mimic the pure Li metal) at the left boundary of our 1-D simulation region and at the right boundary. These boundary conditions are shown in Fig. 1. The phase-field parameters are summarized in Table S3 in the ESI.†

Author contributions

K. N. Z.: methodology, investigation, data curation, writing – original draft, and visualization; Y. Z. J.: conceptualization, methodology, investigation, writing – review & editing, and supervision; Q. S. W.: methodology, investigation, data curation, and writing – review & editing; S. A. N.: methodology; L. Q. C. and Y. Q.: conceptualization, methodology, resources, writing – review & editing, supervision, project administration, and funding acquisition.

Conflicts of interest

The work was performed when Dr Yanzhou Ji was at Penn State. His current affiliation is Ohio State University, Columbus, OH, USA. The work was performed when Dr Seyed Amin Nabavizadeh was at Penn State. His current affiliation is GE Power, Greenville, SC, USA. The work was performed when Dr Qisheng Wu was at Brown. His current affiliation is Suzhou Laboratory, Jiangsu, China.

Data availability

The first-principles computational results on the structure of reaction products and the COMSOL input file for this model are available in the NOMAD repository at https://nomad-lab.eu/prod/v1/gui/user/uploads/upload/id/I6rPnwjtTAOafwYpwN_qPQ.

Acknowledgements

We thank Dr John Lawson, Dr Mehta, and Dr Joakim H. Stenlid from NASA, as well as Dr Kang Xu from the SES AI Corp for stimulating discussions and reviewing the manuscript. The authors acknowledge financial support from NASA under grant number 80NSSC21M0107. K. N. Z. and L. Q. C. also appreciate the generous support from the Donald W. Hamer Foundation through a Hamer Professorship at Penn State. The computations were performed on the Roar supercomputers at Penn State and the Center for Computation and Visualization (CCV) at Brown.

References

1. X. B. Cheng, R. Zhang, C. Z. Zhao, F. Wei, J. G. Zhang and Q. Zhang, Adv. Sci., 2016, 3, 1500213.
2. P. Verma, P. Maire and P. Novák, Electrochim. Acta, 2010, 55, 6332–6341.
3. A. Wang, S. Kadam, H. Li, S. Shi and Y. Qi, npj Comput. Mater., 2018, 4, 15.
4. H. Wu, H. Jia, C. Wang, J. G. Zhang and W. Xu, Adv. Energy Mater., 2021, 11, 2003092.
5. K. Xu, Chem. Rev., 2014, 114, 11503–11618.
6. X. Cui, S. D. Kang, S. Wang, J. A. Rose, H. Lian, A. Geslin, S. B. Torrisi, M. Z. Bazant, S. Sun and W. C. Chueh, Joule, 2024, 8(11), 3072–3087.
7. M. Odziemkowski and D. E. Irish, J. Electrochem. Soc., 1992, 139, 3063–3074.
8. A. Yulaev, V. Oleshko, P. Haney, J. Liu, Y. Qi, A. A. Talin, M. S. Leite and A. Kolmakov, Nano Lett., 2018, 18, 1644–1650.
9. D. T. Boyle, Y. Li, A. Pei, R. A. Vila, Z. Zhang, P. Sayavong, M. S. Kim, W. Huang, H. Wang, Y. Liu, R. Xu, R. Sinclair, J. Qin, Z. Bao and Y. Cui, Nano Lett., 2022, 22, 8224–8232.
10. T. Li and P. B. Balbuena, Chem. Phys. Lett., 2000, 317, 421–429.
11. Y. Wang, S. Nakamura, M. Ue and P. B. Balbuena, J. Am. Chem. Soc., 2001, 123, 11708–11718.
12. J. Halldin Stenlid, P. Žguns, D. Vivona, A. Aggarwal, K. Gordiz, Y. Zhang, S. Pathak, M. Z. Bazant, Y. Shao-Horn, A. Baskin and J. W. Lawson, ACS Energy Lett., 2024, 9, 3608–3617.
13. O. Borodin and G. D. Smith, J. Phys. Chem. B, 2009, 113, 1763–1776.
14. K. Tasaki, J. Phys. Chem. B, 2005, 109, 2920–2933.
15. J. W. Abbott and F. Hanke, J. Chem. Theory Comput., 2022, 18, 925–934.
16. Y. Liu, P. Yu, Y. Wu, H. Yang, M. Xie, L. Huai, W. A. Goddard, 3rd and T. Cheng, J. Phys. Chem. Lett., 2021, 12, 1300–1306.
17. F. Ospina-Acevedo, N. Guo and P. B. Balbuena, J. Mater. Chem. A, 2020, 8, 17036–17055.
18. P. J. Weddle, E. W. C. Spotte-Smith, A. Verma, H. D. Patel, K. Fink, B. J. Tremolet de Villers, M. C. Schulze, S. M. Blau, K. A. Smith, K. A. Persson and A. M. Colclasure, Electrochim. Acta, 2023, 468, 143121.
19. D. Li, D. Danilov, Z. Zhang, H. Chen, Y. Yang and P. H. L. Notten, J. Electrochem. Soc., 2015, 162, A858–A869.
20. J. Christensen and J. Newman, J. Electrochem. Soc., 2004, 151, A1977–A1988.
21. B. Horstmann, F. Single and A. Latz, Curr. Opin. Electrochem., 2019, 13, 61–69.
22. F. Single, B. Horstmann and A. Latz, J. Electrochem. Soc., 2017, 164, E3132–E3145.
23. L. von Kolzenberg, A. Latz and B. Horstmann, ChemSusChem, 2020, 13, 3901–3910.
24. M. Uppaluri, K. Shah, V. Viswanathan and V. R. Subramanian, J. Electrochem. Soc., 2022, 169, 040548.
25. M. Safari, M. Morcrette, A. Teyssot and C. Delacourt, J. Electrochem. Soc., 2009, 156, A145–A153.
26. R. Li, S. O’Kane, M. Marinescu and G. J. Offer, J. Electrochem. Soc., 2022, 169, 060516.
27. M. Gerasimov, F. A. Soto, J. Wagner, F. Baakes, N. Guo, F. Ospina-Acevedo, F. Röder, P. B. Balbuena and U. Krewer, J. Phys. Chem. C, 2023, 127, 4872–4886.
28. J. Wagner-Henke, D. Kuai, M. Gerasimov, F. Roder, P. B. Balbuena and U. Krewer, Nat. Commun., 2023, 14, 6823.
29. P. Guan, L. Liu and X. Lin, J. Electrochem. Soc., 2015, 162, A1798–A1808.
30. S.-H. Lee, H.-G. You, K.-S. Han, J. Kim, I.-H. Jung and J.-H. Song, J. Power Sources, 2014, 247, 307–313.
31. E. W. C. Spotte-Smith, R. L. Kam, D. Barter, X. Xie, T. Hou, S. Dwaraknath, S. M. Blau and K. A. Persson, ACS Energy Lett., 2022, 7, 1446–1453.
32. L. Chen, H. W. Zhang, L. Y. Liang, Z. Liu, Y. Qi, P. Lu, J. Chen and L.-Q. Chen, J. Power Sources, 2015, 300, 376–385.
33. L. Liang and L.-Q. Chen, Appl. Phys. Lett., 2014,(105), 263903.
34. L. Liang, Y. Qi, F. Xue, S. Bhattacharya, S. J. Harris and L.-Q. Chen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 051609.
35. Z. Liu, Y. Li, Y. Ji, Q. Zhang, X. Xiao, Y. Yao, L.-Q. Chen and Y. Qi, Cell Rep. Phys. Sci., 2021, 2, 100294.
36. H. K. Tian, Z. Liu, Y. Ji, L.-Q. Chen and Y. Qi, Chem. Mater., 2019, 31, 7351–7359.
37. Q. Wang, G. Zhang, Y. Li, Z. Hong, D. Wang and S. Shi, npj Comput. Mater., 2020, 6, 176.
38. D. Cao, K. Zhang, W. Li, Y. Zhang, T. Ji, X. Zhao, E. Cakmak, J. Zhu, Y. Cao and H. Zhu, Adv. Funct. Mater., 2023, 33, 2307998.
39. W. Mu, X. Liu, Z. Wen and L. Liu, J. Energy Storage, 2019, 26, 100921.
40. V. Yurkiv, T. Foroozan, A. Ramasubramanian, R. Shahbazian-Yassar and F. Mashayek, Electrochim. Acta, 2018, 265, 609–619.
41. J. Deng, G. J. Wagner and R. P. Muller, J. Electrochem. Soc., 2013, 160, A487–A496.
42. P. Guan, X. Lin and L. Liu, ECS Trans., 2014, 61, 29–41.
43. Z. Gao, Y. Bai, H. Fu, J. Yang, T. Ferber, J. Feng, W. Jaegermann and Y. Huang, Adv. Funct. Mater., 2022, 32, 2112113.
44. R. A. Marcus, Rev. Mod. Phys., 1993, 65, 599–610.
45. T. P. Silverstein, J. Chem. Educ., 2012, 89, 1159–1167.
46. A. L. Michan, M. Leskes and C. P. Grey, Chem. Mater., 2016, 28, 385–398.
47. D. Bedrov, O. Borodin and J. B. Hooper, J. Phys. Chem. C, 2017, 121, 16098–16109.
48. Q. Wu, M. T. McDowell and Y. Qi, J. Am. Chem. Soc., 2023, 145, 2473–2484.
49. Y. X. Lin, Z. Liu, K. Leung, L.-Q. Chen, P. Lu and Y. Qi, J. Power Sources, 2016, 309, 221–230.
50. F. A. Soto, Y. Ma, J. M. Martinez de la Hoz, J. M. Seminario and P. B. Balbuena, Chem. Mater., 2015, 27, 7990–8000.
51. L. Dong, H. J. Yan, Q. X. Liu, J. Y. Liang, J. Yue, M. Niu, X. Chen, E. Wang, S. Xin, X. Zhang, C. Yang and Y. G. Guo, Angew. Chem., Int. Ed., 2024, 63, e202411029.
52. F. Joho, B. Rykart, A. Blome, P. Novák, H. Wilhelm and M. E. Spahr, J. Power Sources, 2001, 97–98, 78–82.
53. M. Yu, K. Liu, M. Li, J. Yan, C. Cao, J. Tan, J. Liang, K. Guo, W. Cao, P. Lan, Q. Zhang, Y. Zhou and P. Lu, Light: Sci. Appl., 2022, 11, 215.
54. S. Menkin, C. A. O'Keefe, A. B. Gunnarsdottir, S. Dey, F. M. Pesci, Z. Shen, A. Aguadero and C. P. Grey, J. Phys. Chem. C, 2021, 125, 16719–16732.
55. X. He, D. Bresser, S. Passerini, F. Baakes, U. Krewer, J. Lopez, C. T. Mallia, Y. Shao-Horn, I. Cekic-Laskovic, S. Wiemers-Meyer, F. A. Soto, V. Ponce, J. M. Seminario, P. B. Balbuena, H. Jia, W. Xu, Y. Xu, C. Wang, B. Horstmann, R. Amine, C.-C. Su, J. Shi, K. Amine, M. Winter, A. Latz and R. Kostecki, Nat. Rev. Mater., 2021, 6, 1036–1052.
56. D. Aurbach, J. Power Sources, 2000, 89, 206–218.
57. D. M. Seo, D. Chalasani, B. S. Parimalam, R. Kadam, M. Nie and B. L. Lucht, ECS Electrochem. Lett., 2014, 3, A91–A93.
58. S. K. Heiskanen, J. Kim and B. L. Lucht, Joule, 2019, 3, 2322–2333.
59. G. M. Hobold, A. Khurram and B. M. Gallant, Chem. Mater., 2020, 32, 2341–2352.
60. B. von Holtum, C. Peschel, U. Rodehorst, D. Wang, Y. Shao-Horn, M. Winter, S. Nowak and S. Wiemers-Meyer, J. Electrochem. Soc., 2025, 172, 050511.
61. Z. Liu, P. Lu, Q. Zhang, X. Xiao, Y. Qi and L.-Q. Chen, J. Phys. Chem. Lett., 2018, 9, 5508–5514.
62. J. M. Garcia-Lastra, J. S. G. Myrdal, R. Christensen, K. S. Thygesen and T. Vegge, J. Phys. Chem. C, 2013, 117, 5568–5577.
63. S. Shi, Y. Qi, H. Li and L. G. Hector, J. Phys. Chem. C, 2013, 117, 8579–8593.
64. M. Feng, J. Pan and Y. Qi, J. Phys. Chem. C, 2021, 125, 15821–15829.
65. M. Smeu and K. Leung, Phys. Chem. Chem. Phys., 2021, 23, 3214–3218.
66. S. Shi, P. Lu, Z. Liu, Y. Qi, L. G. Hector, H. Li and S. J. Harris, J. Am. Chem. Soc., 2012, 134, 15476–15487.
67. J. Heine, P. Hilbig, X. Qi, P. Niehoff, M. Winter and P. Bieker, J. Electrochem. Soc., 2015, 162, A1094–A1101.
68. S. Singsen, F. Ospina-Acevedo, S. Suthirakun, P. Hirunsit and P. B. Balbuena, Phys. Chem. Chem. Phys., 2023, 25, 26316–26326.
69. Y. Ji and L. Q. Chen, Acta Mater., 2022, 234, 118007.
70. K. Tasaki, Z. A. Goldberg, J.-J. Lian, M. Walker, A. Timmons and S. J. Harrisc, J. Electrochem. Soc., 2009, 156, A1019–A1027.
71. K. Tasaki and S. J. Harris, J. Phys. Chem. C, 2010, 114, 8076–8083.
72. H. B. Akkerman, R. C. Naber, B. Jongbloed, P. A. van Hal, P. W. Blom, D. M. de Leeuw and B. de Boer, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 11161–11166.
73. Z. Wang, D. L. Danilov, R. A. Eichel and P. H. L. Notten, J. Power Sources Adv., 2024, 29, 100157.
74. B. Tjaden, D. J. L. Brett and P. R. Shearing, Int. Mater. Rev., 2018, 63, 47–67.
75. S. J. An, J. Li, C. Daniel, D. Mohanty, S. Nagpure and D. L. Wood, Carbon, 2016, 105, 52–76.
76. M. Esmaeilpour, S. Jana, H. Li, M. Soleymanibrojeni and W. Wenzel, Adv. Energy Mater., 2023, 13, 2203966.
77. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ort and D. J. Fox, Gaussian 09, 2016.
78. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
79. S. Debnath, V. A. Neufeld, L. D. Jacobson, B. Rudshteyn, J. L. Weber, T. C. Berkelbach and R. A. Friesner, J. Phys. Chem. A, 2023, 127, 9178–9184.
80. H. Neugebauer, F. Bohle, M. Bursch, A. Hansen and S. Grimme, J. Phys. Chem. A, 2020, 124, 7166–7176.
81. D. Coskun, S. V. Jerome and R. A. Friesner, J. Chem. Theory Comput., 2016, 12, 1121–1128.
82. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
83. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396.
84. O. Borodin, W. Behl and T. R. Jow, J. Phys. Chem. C, 2013, 117, 8661–8682.
85. D. S. Hall, J. Self and J. R. Dahn, J. Phys. Chem. C, 2015, 119, 22322–22330.
86. R. A. Marcus, J. Chem. Phys., 1965, 43, 679–701.
87. S. F. Nelsen, S. C. Blackstock and Y. Kim, J. Am. Chem. Soc., 1987, 109, 677–682.
88. M. Nie, D. Chalasani, D. P. Abraham, Y. Chen, A. Bose and B. L. Lucht, J. Phys. Chem. C, 2013, 117, 1257–1267.
89. R. L. C. Akkermans, N. A. Spenley and S. H. Robertson, Mol. Simul., 2021, 47, 540–551.
90. X. He, Y. Zhu, A. Epstein and Y. Mo, npj Comput. Mater., 2018, 4, 18.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ee01030f

‡ Kena Zhang and Yanzhou Ji contributed equally.

---