 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Water electrolysis technologies: the importance of new cell designs and fundamental modelling to guide industrial-scale development†
Muhammad Adil
Riaz
a,
Panagiotis
Trogadas
 *ad,
David
Aymé-Perrot
b,
Christoph
Sachs
b,
Nicolas
Dubouis
b,
Hubert
Girault
*ad,
David
Aymé-Perrot
b,
Christoph
Sachs
b,
Nicolas
Dubouis
b,
Hubert
Girault
 c and
Marc-Olivier
Coppens
c and
Marc-Olivier
Coppens
 *a
*a
aCentre for Nature Inspired Engineering & Department of Chemical Engineering, University College London, London, WC1E 7JE, UK. E-mail: p.trogadas@ucl.ac.uk; m.coppens@ucl.ac.uk
bTotalEnergies SE, OneTech, 2 Place Jean Millier, La Défense 6, 92078 Paris, France
cInstitute of Chemistry and Chemical Engineering, Station 6, Ecole Polytechnique Fédérale de Lausanne, CH-1015 Lausanne, Switzerland
dDepartment of Chemistry, Aristotle University of Thessaloniki, 54124 Thessaloniki, Greece
First published on 30th April 2025
Abstract
Large-scale, sustainable, low-cost production of hydrogen can reduce the negative effects of climate change by decarbonising energy infrastructure. Low-carbon hydrogen can be synthesised via water electrolysis. Today, however, this only constitutes a minor proportion of global hydrogen production, as fossil fuel-based processes are used predominantly with large amounts of carbon emissions. Low-temperature electrolysis (<100 °C) has garnered significant attention, due to lower capital cost and operational complexity than high-temperature electrolysis (>700 °C). In this review, the latest advancements in low-temperature water electrolysers are provided from the classical membrane-based designs to new potential designs such as membrane-less designs. The coverage of electrodes by gas bubbles can cause a drastic loss in their activity and, hence, the hydrogen production efficiency of the device. To alleviate this issue, aerophobic and aerophilic electrodes are being developed. Their advantageous properties are discussed. Furthermore, models of water electrolysers are reviewed to provide critical understanding of the different parameters affecting the electrochemical performance of these devices. Finally, an industrial perspective is given to discuss the challenges in large-scale Gigawatt-level deployment of these devices in coming decades to meet future green hydrogen demand.
Broader impactExcessive usage of fossil fuels in the last century to meet the energy demands of a rapidly growing population has caused global warming by drastically increasing CO2 emissions. Hydrogen gas can play a key role in decarbonising the energy infrastructure. However, current hydrogen production is dominated by natural gas reforming and coal gasification, generating “grey” hydrogen with large CO2 emissions. “Green” hydrogen with net-zero emissions could be produced through water electrolysis using renewable electricity, however, its high cost and low production efficiency are limiting its widespread utilisation. To meet the United Nations’ climate goal of net-zero carbon emissions by 2050 (following the Paris Agreement), large-scale deployment of water electrolysers is required at the gigawatt level, which is a massive ramp-up from current deployment at the megawatt level. Several challenges, such as low current density, gas bubble accumulation and non-uniform water distribution exist in the electrolyser components (electrodes, gas diffusion layers and flow channels) of current cell designs. This review aims to provide a comprehensive overview of current and next-generation cell designs along with fundamental modelling studies of cell components to guide future designs that are more suitable for large-scale deployment at the industrial level. |
1. Introduction
With rapid technological developments after the industrial revolution, urbanisation and population growth, demand for electricity has grown tremendously this past century, reaching ∼33![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 TW h in 2024, which is expected to rise further by ∼3% annually through 2026.1 Fossil fuels, such as oil, natural gas or coal, have been the main source of energy for various sectors, however, their excessive usage has caused a significant increase of carbon dioxide emissions to the atmosphere, resulting in the greenhouse effect and global warming.2 In this context, the development of renewable alternatives with limited or no negative impact on the environment is necessary. The past decade has seen considerable efforts on a global scale with countries committing to achieve net zero emissions by 2050 (Paris Agreement 2015) via renewable energy technologies.3,4 Among various options explored, hydrogen obtained via low carbon emission processes is a promising route towards decarbonisation.5
000 TW h in 2024, which is expected to rise further by ∼3% annually through 2026.1 Fossil fuels, such as oil, natural gas or coal, have been the main source of energy for various sectors, however, their excessive usage has caused a significant increase of carbon dioxide emissions to the atmosphere, resulting in the greenhouse effect and global warming.2 In this context, the development of renewable alternatives with limited or no negative impact on the environment is necessary. The past decade has seen considerable efforts on a global scale with countries committing to achieve net zero emissions by 2050 (Paris Agreement 2015) via renewable energy technologies.3,4 Among various options explored, hydrogen obtained via low carbon emission processes is a promising route towards decarbonisation.5
Hydrogen, traditionally used as chemical feedstock for, e.g., ammonia production, is mainly produced by high carbon emissive processes, such as steam reforming of methane and gasification of coal or oil.6,7 Interest has grown in pushing the research and development of hydrogen production by clean processes with limited or no CO2 emission, such as the European Union (EU) 2020 “Hydrogen Strategy for Climate-Neutral Europe” and “European Clean Hydrogen Alliance”.8,9 Among several technologies, water electrolysis is a strong contender, since it utilises electricity to split water into hydrogen and oxygen.10,11 Green production of hydrogen with net zero carbon emissions can be achieved through water electrolysis using electricity produced by renewable energy sources, such as wind or solar power.12,13 Large-scale deployment of green hydrogen (also called renewable hydrogen) can mitigate the effects of climate change by decarbonisation of energy infrastructure and hard-to-abate sectors, such as aviation, shipping, steel, chemicals, and petrochemicals.14 However, the current high cost of green hydrogen (∼5 to 10 € per kgH2)15,16 limits its market share to only 4% of total hydrogen production and many other challenges, such as production efficiency, scalability and durability need to be addressed to increase its demand.17 Amid the global hydrogen demand of ∼90 Mt in 2021, water electrolysers produce only a negligible amount (∼40 kt) of green hydrogen.6 The demand for renewable hydrogen is expected to grow drastically within the coming years and decades, requiring ∼100 Mt per year by 2030 and 500 Mt per year by 2050, according to the International Renewable Energy Agency (IRENA) to decarbonise carbon-intensive sectors.18 The European Commission announced in its REPowerEU plan a projected domestic production of 10 Mt of renewable hydrogen in Europe by 2030, importing the same quantity from abroad.19 The European Clean Hydrogen Alliance has set the target to install electrolysers at a Gigawatt-scale (∼40 GW) by 2030 for green hydrogen production, a significant increase in its decarbonisation effort from the current installed capacity at a Megawatt-scale (∼250 MW) in the EU.9,20 To meet these ambitions, the global green hydrogen industry must be developed at a fast pace as IRENA's Transforming Energy Scenario for 2050 estimates deployment of electrolysers at the capacity of Terawatt-scale (at least 1.7 TW with further increase in case of deep decarbonisation scenarios).18
Water splitting (H2O → H2 + ½O2) via electrolysis proceeds through two electrochemical reactions: the hydrogen evolution reaction (HER) at the cathode, involving a reduction reaction, and the oxygen evolution reaction (OER) at the anode, involving an oxidation reaction. These reactions follow different mechanisms in acidic and basic electrolytes.21 Devices in which these electrochemical reactions take place are called electrolysers, which consist of electrodes coated with catalysts, a separator, bipolar plates, and flow channels. Low-temperature water electrolysis operating below 100 °C offers the advantages of a wide choice of compatible materials making operation simple, low-cost and durable, in contrast to high-temperature electrolysis, which offers better H2 production efficiency but operates above 700 °C.22,23 The current electrolyser technologies with their high cost of hydrogen production face several challenges at the cell level, e.g., energy losses due to high overpotentials, bubble accumulation, inefficient catalyst utilisation, etc.24–27 Therefore, novel electrolyser cell designs are urgently needed with improved efficiency, durability, cost competitiveness, and scalability to meet the rapid increase in demand for green hydrogen to achieve the net-zero targets of 2050.
This review presents the latest advancements of low-temperature electrolysers from current-generation, membrane-based (proton exchange or alkaline) electrolysers to the development of the next generation of electrolysers, using, for instance, a membrane-less design. Emphasis is given to various electrode designs for effective bubble management, as hydrogen and oxygen bubbles generated during the electrochemical reactions of water splitting cover the electrode surface, resulting in a drastic loss in hydrogen production efficiency of the device.28–30 To further improve the design of these electrodes and accelerate their development, modelling should be used prior to their manufacturing, as it is a powerful tool that can reveal the relationship between their electrocatalytic as well as geometric characteristics and the efficiency of the device.31 However, remarkably, there are only limited modelling reports in the literature on water electrolysers, indicating that this fundamentally guided approach is still at an early stage. Herein, a critical review of the reported models, either focusing on the electrode or the whole device, is presented to showcase the crucial parameters affecting the efficiency of water electrolysers and improve their design. An industrial perspective is added to discuss the potential and challenges in large Gigawatt-scale deployment of these devices needed to meet massive increase of green hydrogen demand in coming decades. We note that this perspective is missing in many papers, as most articles only discuss challenges at the lab scale, such as catalyst development.
2. Electrolyser technologies
2.1. Membrane-based designs
The current generation of industrial electrolysers utilise membranes to separate the produced hydrogen and oxygen gases from each other, which can form an explosive mixture (lower flammability limit: 4% of H2 in O2).32,33 Various designs have been explored for these membrane-based water electrolysers, such as simple diaphragms for alkaline electrolysis,34,35 proton exchange membranes (PEMs),36,37 anion exchange membranes (AEMs),38,39 and solid oxide ceramics.40,41 PEM technology emerged in the 1960s during NASA's space programs, where lab-scale PEM cells provided high-purity hydrogen with compact designs.42 Early laboratory versions struggled with membrane stability and high catalyst costs, limiting their industrial adaptation. Advances in these components (1980–2000) led to commercial PEM stacks (1–10 MW), which are now widely used in renewable green hydrogen projects.A PEM electrolyser cell (Fig. 1A) comprises of two electrodes separated by a PEM (usually perfluorosulfonic acid, such as Nafion®) as a solid electrolyte in contrast to a liquid electrolyte present in an alkaline electrolyser. The most active catalysts for HER and OER reactions are platinum (Pt) and iridium oxide (IrO2).43–45 Therefore, two half-cell electrochemical reactions of the PEM electrolyser proceed on the catalytic materials, IrO2 and Pt, which are coated on the anode and cathode, respectively.46 A schematic diagram of different components of the PEM electrolyser is shown in Fig. 1A. Water is typically fed to the anode, producing oxygen, protons (H+) and electrons (e−) through an oxidation reaction (OER):
| 2H2O → O2 + 4H+ + 4e− | (1) |
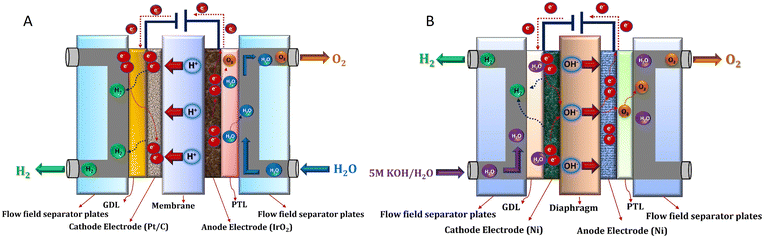 | ||
| Fig. 1 Membrane-based electrolyser designs: (A) proton exchange membrane (PEM) and (B) alkaline exchange membrane (AEM). Reproduced with permission.47 Copyright 2022, Elsevier. | ||
It should be remembered that writing H+, is just a simplified notation to describe a dynamic positively charged aqueous species, and not necessarily a lone proton. As electrons pass through the external circuit, protons selectively pass through the membrane and combine with electrons at the cathode to produce hydrogen through a reduction reaction (HER):
| 2H+ + 2e− → 2H2 | (2) |
The main advantages of PEM electrolysers include high current density (>1 A cm−2) and energy efficiency (∼80%), production of hydrogen with high purity (≥99.9%), as well as a robust design, even when powered by intermittent energy sources.17 However, the utilisation of expensive and scarce noble metal catalysts remains a big challenge from a high ramping-up perspective.48 Being a subproduct of platinum mining, the availability of iridium is limited, with an annual production of around 8–9 tons per year. Given that a 1 GW PEM plant would require between 5 to 10% of this iridium amount, large-scale industrial deployment seems very complicated to conceive. Therefore, novel electrodes with reduced metal loadings while maintaining high intrinsic catalytic activity are necessary for future large-scale deployment of PEM electrolysis.49,50 Moreover, the degradation of fluorine-based membranes, potentially generating toxic polyfluoroalkyl substances (PFAS), remains a major topic to address.51
On the contrary, alkaline water electrolysis (AWE) is a mature, commercialised technology, which has been in use for almost a century.6 Initially, AWE was utilised for industrial hydrogen production for use in fertiliser manufacturing (ammonia synthesis via the Haber–Bosch process) and petroleum refining.42 Early systems used asbestos diaphragms and nickel electrodes, operating at low current densities. However, with improvements of these components and pressurised operation, it saw widespread adoption in the 1950s–1970s with MW-sized electrolysers, and, today, AWE remains dominant in large-scale hydrogen plants around the world.
An alkaline electrolyser cell (Fig. 1B) consists of two electrodes immersed in a liquid electrolyte (30–40% potassium hydroxide KOH). Water in a cathodic chamber undergoes an electrochemical reduction reaction on the electrode surface to form hydrogen and hydroxide (OH−) ions:
| 2H2O + 2e− → H2 + 2OH− | (3) |
OH− ions pass through a diaphragm to the anodic compartment and undergo an oxidation reaction at the electrode surface generating oxygen and water:
| 4OH− → O2 + 2H2O + 4e− | (4) |
The diaphragm generally consists of a porous zirconium oxide ceramic deposited on an open mesh polyphenylene sulfide fabric (Agfa's Zirfon®, 500 μm thick), whereas catalyst materials are classically RANEY® Ni and/or pure Ni mesh and potentially metallic alloys based on transition metal compounds, such as Ni, Co, Mn, and Fe oxides.34 Alkaline electrolysers are less expensive than PEM (capital cost for a large >1 MW stack is ∼270$ per kW), due to the employed low-cost metals and electrocatalysts (Ni-based)52 and can be easily scaled up (cell size ∼3 m2) making them suitable for hydrogen production at industrial level.17 However, alkaline electrolysers suffer from low current densities (∼500 mA cm−2), high energy consumption (∼50–65 kW h per kgH2), corrosion of stainless steel elements of the balance of plant exposed to the alkaline electrolyte, and a long startup time, making them less suitable for use with intermittent electricity sources.6,17,18
2.2. New generation of designs
The major disadvantage of the design of electrolysers presented in the above section is the membrane itself, as it increases the electrical resistance and hence the cell overpotential (≥0.2 V). The polymeric membrane undergoes irreversible degradation at high temperatures, resulting in a limited operating range (50–90 °C) and low voltage efficiency (∼50–60%) of these electrolysers.17 Hence, in recent years, various innovative new designs have been proposed, some of which are illustrated in Fig. 2.53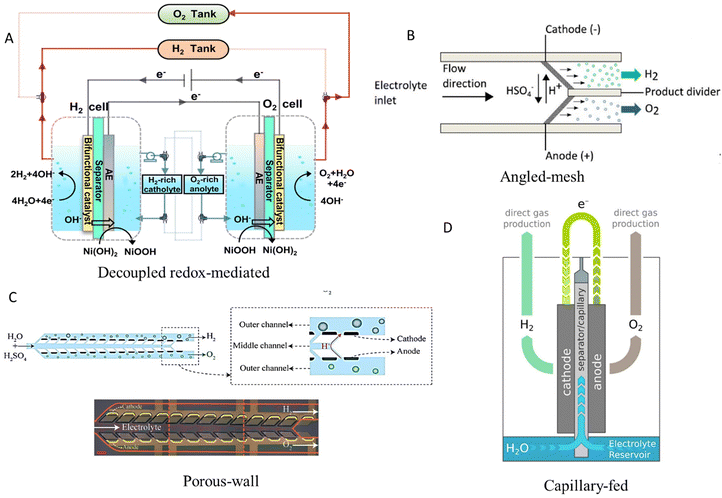 | ||
| Fig. 2 Membrane-less electrolyser designs. (A) Decoupled electrolysis operation of oxygen and hydrogen evolution in two separate compartments mediated by an auxiliary electrode (AE) coated with a redox couple of NiOOH/Ni(OH)2 electrocatalyst. Reproduced with permission.54 Copyright 2021, Springer Nature. (B) 3D printed porous electrodes placed at an angle to each other, enabling product gases to accumulate in separate channels. Reproduced with permission.55 Copyright 2016, The Electrochemical Society and IOP Publishing. (C) Microfluidic porous wall electrolyser, utilising permeable solid barriers instead of fluidic forces to keep gases separate. Reproduced with permission.56 Copyright 2021, The Royal Society of Chemistry. (D) Capillary-fed operation where electrodes receive a continuous flow of electrolyte through natural capillary action within an intermediate separator whose lower end is immersed in an electrolyte. Reproduced with permission.57 Copyright 2022, Springer Nature. | ||
Mesh flow-through electrodes employing RuO2/IrO2 and Pt as anode and cathode, respectively, with a ∼0.8 mm gap interelectrode distance and electrolyte velocity >0.1 m s−1 cause the formation of gas bubbles on the surface of the electrodes, which then move through their porous structure towards the back chamber.59 As a result, high-purity hydrogen (∼99.83%) is generated, while operating at a current density of ∼3500 mA cm−2. A similar design to the above exhibits similar results, in which the mesh electrodes (Fig. 2B) are placed at an angle instead of parallel to each other.55 This architecture allows the flow of acidic or alkaline electrolyte into two separate effluent channels where the produced gases are separated from each other by a thin barrier. Electrolyser operation with ∼72.5% efficiency and ∼2.8% H2 crossover is achieved at ∼100 mA cm−2 and ∼26.5 cm s−1 fluid flow.55 This Y-shaped cell design demonstrates improved gas separation and uniform current distribution compared to conventional I- and T-shaped membrane-less designs. Stable operation at a current density up to 250 mA cm−2 is achieved with an efficient bubble removal rate from the surface of the electrode.60
Another successful design of a membrane-less electrolyser relies on permeable solid barriers to keep produced gas bubbles separate instead of leveraging the Segré–Silberberg effect.56 It comprises three separate channels where the electrolyte is introduced into the central channel and subsequently diffuses into the outer channels through the porous walls (Fig. 2C). Electrodes are positioned on the exterior of these porous walls. As a result, product gas bubbles of hydrogen and oxygen are formed only in the separate outer channels and do not enter the central channel, as the continuous flow of the electrolyte prevents them from mixing. This results in a very low gas crossover of ∼0.14% at ∼300 mA cm−2 and electrolyte flowrate of ∼80 ml h−1 which is ∼58 times lower than the gas crossover for a membrane-less electrolyser with electrodes parallel to each other under similar operating conditions.56 Electrolyser scaling is possible without increasing interelectrode distance due to the absence of bubble flow, even though the fabrication of inclined pores as well as selective catalyst deposition remains challenging, whereas additive manufacturing can potentially provide some solution to these issues with the customisation of the porous network of the electrode.
3. Electrodes and bubble management for water electrolysis
The electrodes are key components of a water electrolyser. Their design significantly influences the H2 production efficiency.48,63,64 The choice of electrocatalyst in the electrode plays a crucial role in determining the electrochemical performance of the cell, which is often dependent on its nanostructure and material type. High current density in HER and OER electrochemical reactions is often achieved by either increasing the intrinsic activity of the catalyst or the number of its active sites.65 Various strategies are utilised for the synthesis of highly efficient electrocatalysts, including alloying,66–68 doping,69,70 morphology engineering,71,72 porous nano-structuring,73,74 loading on high surface area supports,49,75,76 and reducing the particle size to ultra-small,77,78 or single atoms.74,79 Several recent reviews80–85 discuss in detail the design of the electrocatalysts for water splitting reactions and aspects of electrode engineering48,63,86,87 for current generation membrane-based electrolysers. Interested readers are referred to these articles for further information. As redox reactions of water splitting occur on the electrocatalysts coated on these electrodes, hydrogen and oxygen bubbles are generated from product gases. When these bubbles cover the electrode surface this results in lower production efficiency of the device due to an increase of activation and Ohmic overpotentials.88,89 These bubbles-induced overpotentials for water electrolysis are substantial, ranging from ∼80 mV at 10 mA cm−2 in the case of nanobubbles to ∼308 mV at above 500 mA cm−2.28 The development of novel electrodes for effective bubble management is crucial for next-generation devices, e.g., in membrane-less designs, where product gases could mix, posing a safety risk.90–92Bubble coverage on gas-evolving electrodes generally increases with current density, whereas an increase of temperature and pressure decreases it.93 Bubble break-off radius (Rr) and volume (Vr) immediately prior to its detachment can also impact the amount of electrode bubble coverage.93 Moreover, higher flow velocity in electrolyser microchannels is favourable, as it reduces bubble detachment diameter and time.94
Electrocatalytic gas evolution is governed by the Marangoni effect, which refers to a flow driven by variations in surface tension along the gas–liquid interface caused by temperature (thermo-capillary force) or concentration gradients (solute-capillary flow).95–97 The non-uniform coverage of the electrode by gas bubbles produced during the electrochemical reactions results in the appearance of a solutal Marangoni force.98 Such force causes the gas bubbles to oscillate along the surface of the electrode, leading to a self-pinning effect preventing the gas bubbles from leaving the surface. When instead, these bubbles are relocated to the bubble-free side of the electrode, it exposes the previously covered electrode surface to ensure the production and growth of gas bubbles.96 The understanding of Marangoni effects on gas bubble dynamics at the nanoscale remains elusive, due to the limitations in current technology, which cannot provide detailed information on the morphology and growth of gas bubbles.99 These limitations could be overcome via molecular dynamics simulations,96 or dark field microscopy100 providing valuable insights on the nucleation and growth of nanobubbles.
Bubbles covering the electrode are typically micrometre sized (10–800 μm) during continuous water electrolysis.101,102 Transient nanobubbles, which appear for a very short time (1–100 μs) as a result of gas supersaturation, dissolve rapidly in electrolyte during water electrolysis.103 However, highly stable surface nanobubbles on an electrode are observed by atomic force microscopy.104 These nanobubbles, characterised by long lifetime and low contact angle, require location gas supersaturation and contact line pinning for their stability.105 Moreover, molecular dynamic simulations of single electrolytic nanobubbles reveal that a threshold current density (or a threshold gas flux ∼10–12 kg m−2 s−1) exists. Below this threshold, the nanobubbles are stable, whereas the nanobubbles grow indefinitely and detach from the surface of the electrode by buoyancy for a gas flux higher than its threshold value.106
Bubble management in water electrolysers can be achieved by electrode surface engineering or alteration of the operating conditions, such as pressure or electrolyte composition.28,107 Superwetting electrodes with superaerophobic or superaerophilic properties have gathered significant attention for electrochemical reactions involving gases.108 The next section discusses various superwetting electrode designs utilised for effective bubble management.
3.1. Aerophobic electrodes
Morphology tuning and chemical surface modification of electrodes have been explored in the literature to make them bubble-repellent and achieve better electrochemical performance in water electrolysis.109–111 Nano-structuring the catalyst layer to make a porous electrode can improve its surface utilisation as well as multiphase transport.65,112 For example, honeycomb (HC) nanostructured electrodes have unique porous morphology and high surface area, which provides efficient ion transport, improved conductivity and mechanical stability.113 An HC-structured iridium (Ir) catalyst layer (Fig. 3A) has a large electrochemically active surface area (outer charge Q ∼71.4 mC cm−2 for HC Ir and ∼32.9 mC cm−2 for dense Ir, respectively) with much lower Ir loading of ∼0.27 mg cm−2 on the anode (compared to 3 mg cm−2 for typical anode catalyst).101 As a result, a ∼2.2 times improvement in OER performance is achieved compared to a dense Ir-coated electrode due to its higher mass activity of 4.16 A mg−1. The HC design favours the formation of smaller bubbles (∼100 μm) with the majority of bubbles detaching within the 10–20 μm range and it achieves a low cell voltage of 1.8 V at 2 A cm−2 current density in electrolyser operation.101 Instead of Ir, a nickel/gold (Ni/Au) honeycomb structured electrode, prepared via hard templating employing ∼100–300 nm polystyrene beads, is a feasible alternative.114 Compared to a flat Ni/Au electrode, much improved HER activity with 115 mV reduction of overpotential is observed for a HC Ni/Au electrode containing a uniform distribution of holes with ∼31 nm diameter.114 This is attributed to the change in surface wettability as the average bubble diameter decreases from ∼519 μm for a flat Ni/Au electrode to ∼128 μm for this modified electrode. | ||
| Fig. 3 Aerophobic electrode designs: (A) honeycomb structured Ir catalyst layer. Reproduced with permission.101 Copyright 2023, American Chemical Society. (B) Oblique angles deposited nickel nanorod arrays-based Ni films. Reproduced with permission.115 Copyright 2023, Wiley-VCH. (C) Electrodeposited nickel nanocones-based Ni electrodes. Reproduced with permission.116 Copyright 2023, Wiley-VCH. (D) Bubble-repellent fibrous polyallylamine hydrogels coated Pt/Ni foils. Reproduced with permission.102 Copyright 2023, Wiley-VCH. | ||
Depositing nanomaterials on the surface of the electrocatalyst can alter its wetting properties for favourable bubble detachment by reducing their contact area and adhesion. To elucidate the effect of surface morphology of catalyst thin films, nickel nanorod arrays have been deposited at oblique angles from 60 to 80° on a flat Ni-film (Fig. 3B) using an electron beam evaporator.115 Ni arrays deposited at 80° angle (Ni-80) have the highest porosity of 52% and an air contact angle of 156°. As a result, Ni-80 produced an ∼2.4 times smaller bubble radius and released bubbles ∼3.8 times faster than a flat Ni-film, resulting in much reduced overpotentials at a current density of 100 mA cm−2 for HER. Further investigation by chronopotentiometry reveals a nearly mass transfer-free reaction for Ni-80, as the potential remained stable from 100 to 1600 RPM, whereas noticeable fluctuations in voltage are seen for a flat Ni-film below 400 RPM.115 Nickel nanocones (NC) with base sizes ranging from 300 to 700 nm have been electrodeposited on various types of nickel electrodes (foil, foam and 3D printed lattices) to increase their aerophobicity, retaining >95% of electrolyser performance over 100 h of operation at ∼900 mA cm−2 (Fig. 3C).116 Visualisation of hundreds of bubbles generated at different locations on the electrode, via high-speed camera measurements, confirms the smaller size of the bubbles (∼97 μm vs. ∼379 μm) and their shorter residence time (∼3 s vs. ∼56 s) on NC-modified electrodes compared to pristine nickel foil for both HER and OER. This is because the adhesion force exerted on bubbles by a NC-modified electrode surface creates an angle instead of being perpendicular to the flat electrode surface, thereby reducing its effect on the opposite, upward buoyancy force on bubbles and promoting their easier detachment.116 Transition metal layered double hydroxide (LDH) has been deposited on a Ni foam (NF) electrode by hydrothermal treatment with metal precursors for 12 h.117 This results in the vertical growth of hierarchical nanoarrays with 2D nanosheets (∼58–105 nm thickness) and 1D nanowires (∼1.7 μm length), intersecting at 75° angle and forming a knitted structured surface with superaerophobicity (contact angle (CA) ∼151°). This modified electrode exhibits excellent OER performance in alkaline seawater with a low overpotential of ∼320 mV at 400 mA cm−2, and negligible reduction (∼19 mV) in overpotential occurs after 300 h of operation at 100 mA cm−2.117
Apart from surface structural engineering to create an aerophobic electrode, chemical coating of the surface can also modulate the bubble adhesion force to facilitate its early detachment.102,111,118 Layer-by-layer deposition is employed on a NF electrode by conjugate reaction between acrylate and amine groups of polymeric chemical modifiers to achieve a very low adhesion force of ∼4.6 μN for H2 bubbles.111 Apart from superior HER activity at a high current density of 500 mA cm−2 with ∼512 mV overpotential compared to ∼748 mV for bare NF electrode, it also shows low overpotential (∼250 mV) at a lower current density of 100 mA cm−2 where smaller gas bubbles tend to attach more firmly to the unmodified electrode due to smaller buoyancy forces. Physical coating of the catalyst surface also provides an alternative route to fabricate aerophobic surfaces with lower cost and easy scale-up.102,118 Large area superaerophobic electrodes up to 100 cm2 in size can be fabricated by spin coating of fibrous polyallylamine hydrogels on Pt-coated Ni foils (Fig. 3D).102 The porous network of this hydrogel provides removal pathways for bubbles resulting in better HER and OER activity in a three-electrode system and an improved polarisation curve in a two-electrode cell compared to a pristine Pt electrode. Polyethylenimine (PEI) hydrogel coating on platinum-coated FTO and NF electrodes has also been deposited via condensation reaction of precursors and freeze-drying.118 Hydrogels with optimum 2 wt% PEI concentration have the highest porosity of ∼10.94% with an average pore size of ∼20.18 μm creating a superaerophobic electrode surface with an air contact angle above 150°. As a result, lower HER overpotential (∼608 mV vs. ∼774 mV of bare NF electrode) at 500 mA cm−2 and stable voltage for 20 h of operation in an alkaline medium is achieved.
Superaerophobic designs can effectively remove bubbles from an electrode surface in membrane-based electrolysers and enhance their electrochemical performance. To implement such technical solutions in industrially relevant systems, the challenge remains of transferring such preparation methods to large-scale production. Furthermore, in the case of the development of membrane-less electrolysers, such superaerophobic design may not be a suitable choice, as hydrogen and oxygen gas bubbles repelled from the electrode surfaces can then mix in the main chamber. Hence, there are no literature reports so far on using superaerophobic electrodes in membrane-less electrolysers. However, the modification of the surface of the electrode to moderate bubble adhesion via alteration of its orientation has been utilised to increase the efficiency of a membrane-less water electrolyser.90 This tilted micro-cone array (TMCA) electrode fabricated by electrochemical etching of Cu foil with an optimised tilting angle of 50° provides facile, unidirectional bubble transport, preventing bubble accumulation and gas crossover. At a current density of 240 mA cm−2, the TMCA electrode achieves 99.99% pure hydrogen separation with an interelectrode distance of just 1.5 mm, compared to conventional designs with superaerophobic electrodes, which only achieve 88.3% H2 purity.90 This issue of gas mixing in membraneless electrolysers can be resolved using aerophilic electrodes, providing an effective strategy for bubble management and prevention of gas crossover for these electrolysers.119
3.2. Aerophilic electrodes
Aerophilic electrodes have been explored for directional bubble transportation by utilising a hydrophobic membrane coating or structural modifications of electrodes.91,120 A breathable anode electrode (Fig. 4A) has been prepared by sputter deposition of ∼30–40 nm sized platinum nanoparticles on hydrophobic polytetrafluoroethylene (PTFE) membrane (Gore-Tex), with well-defined pores and narrow size distribution of 1–10 μm.119 This electrode rapidly removes oxygen bubbles (∼92%) from its surface, reducing the need for a separator to prevent gas crossover. Another porous electrode is fabricated by incorporating an inactive hydrophobic layer of polyethylene on the catalyst layer to direct formed bubbles to the gas chamber at the back of the electrode.91 This concept enables the fabrication of a bubble-less alkaline electrolyser using NiCo2O4 and Ni as anode and cathode catalysts, respectively, without any membrane between electrodes. It achieves a very low onset potential of ∼1.28 V due to the significantly reduced electrode overpotentials (∼0.11 V at anode) at 10 mA cm−2.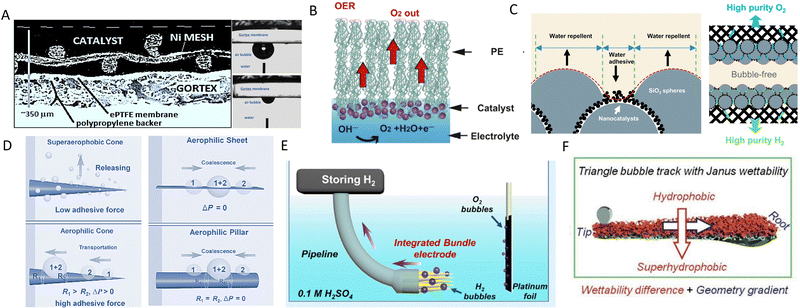 | ||
| Fig. 4 Aerophilic electrode designs (A) Porous electrode prepared by coating Ni-based catalysts on hydrophobic PTFE membrane. Reproduced with permission.91 Copyright 2019, Elsevier. (B) Alveolus-like oxygen electrode with Au/NiFeOx catalyst layer of 50–100 nm thickness on hydrophobic nanoporous polyethylene substrate. Reproduced with permission.121 Copyright 2018, Elsevier. (C) Rose-petal-effect mimicking electrode. Reproduced with permission.92 Copyright 2023, Elsevier. (D) Hydrophobic cone electrode by electroetching of copper wire and silica nanoparticle coating. Reproduced with permission.122 Copyright 2016, Wiley-VCH. (E) Integrated copper cones array electrode with wettability gradient due to concentration variation of aerophilic silica nanoparticle from tip to base. Reproduced with permission.123 Copyright 2021, American Chemical Society. (F) Conical nickel foam electrode with asymmetric wettability for dual self-propelled bubble transport. Reproduced with permission.124 Copyright 2020, Wiley-VCH. | ||
Apart from utilising hydrophobic membranes for bubble removal from the surface of the electrodes in water electrolysers, nanostructured electrodes with geometry gradients are also explored as an alternative for effective bubble removal.122,123 A hydrophobic cone-shaped electrode (Fig. 4D) is fabricated by electroetching of a copper wire (∼0.8 mm diameter) and immersion in 1-dodecanethiol solution for 12 h.122 Its conical structure creates a Laplace pressure difference for gas bubbles, which, coupled with the hydrophobic surface (contact angle ∼102.3°) and high adhesive force of ∼167 μN, results in efficient movement of bubbles from the tip to the base of the electrode in the HER reaction. The wettability of this hydrophobic cone-shaped electrode can be further improved by coating superhydrophobic nano-silica particles. This enables the facile transportation of produced hydrogen during HER at the base of an integrated bundle electrode consisting of an array of copper cones (Fig. 4E) and its continuous removal from the reaction chamber.123 Combined concepts of geometry gradient and wettability difference, seen in Janus materials with opposite wetting properties,125,126 can be used to design an electrode with dual self-propelled bubble transport interface, enabling more efficient bubble removal. Such an example is a Janus nickel foam electrode (Fig. 4F), consisting of a hydrophobic (CA ∼ 125°) and superhydrophobic (CA ∼ 158°) surface on opposite sides of its hierarchical structure, resulting in the directional self-transport of generated gas bubbles.124
Study of gas bubble manipulation by biological organisms found in nature (such as, super-aerophilic lotus leaf, super-aerophobic fish scale, or asymmetric pitcher plant peristome) has provided an effective strategy to address gas bubble issues of electrochemical reactions.127 The mammalian lung is one of the most efficient gas exchange systems in nature for breathing. It utilises tiny sacs called alveoli at the end of bronchioli for two-way gas diffusion.128 Air inhaled into lungs and CO2 in blood capillaries are exchanged through a micron-thick alveolus membrane, whose asymmetric wetting properties facilitate rapid gas diffusion. Inspired by this sophisticated design, an alveolus-imitating oxygen electrode has been fabricated, mimicking the breathing mechanism of mammals by coating an Au/NiFeOx catalyst layer of ∼50–100 nm thickness on a nanoporous polyethylene (PE) membrane of 12 μm thickness.121 O2 molecules formed on the hydrophilic catalyst surface undergo rapid diffusion into the gas phase through the hydrophobic PE membrane, which is impenetrable for water. This electrode achieves a low onset potential of 1.42 V (vs. RHE) at 10 mA cm−2 in the alkaline OER with bubble-free operation due to a reduced overpotential to only 0.19 V. A rose petal surface displays a wetting regime with high water contact angle, which prevents a water droplet from leaving its surface, unlike a lotus leaf, where a water droplet rolls over and leaves the surface.129 This originates from multiscale surface roughness with alternate blocks of superhydrophobic (nanoscale folds on micro papillae) and water adhesive (grooves between micro papillae) patches. As these features are useful for efficient contact of electrolyte and catalyst to minimise overpotentials and remove gas quickly, an electrode design was proposed (Fig. 4C) for bubble-less electrolysis imitating the rose petal effect having multiscale roughness with adhesive superhydrophobicity (∼161°).92 Alternate water adhesion and repelling blocks are created by filling hydrophilic Pt/C nanoparticles to the void spaces of closely packed hydrophobic silica (SiO2) microspheres through mixing and loading on carbon paper substrate. This allows the quick release of formed bubbles by spreading and moving away from the catalyst surface compared to a conventional aerophilic electrode,119 where gas bubbles need to diffuse through the membrane electrode assembly (MEA) of high diffusion resistance for their removal. As a result, a high current density of ∼4.2 A cm−2 is achieved for this rose petal mimetic electrode in bubble-less HER reaction with ∼61.5% H2 production efficiency and negligible gas crossover (∼0.003% at 1 mm interelectrode distance) occurs for membrane-less electrolyser operation.92
Instead of designing an electrode with bubble repelling or attracting property alone, electrodes with localised aerophobic and aerophilic patches have been designed for directional movement and removal of gas bubbles.130–133 A novel electrode incorporating a pattern of stripes of superaerophobic (SAB) electrocatalytic Pt and superaerophilic (SAL) SiO2 nanoparticles (Fig. 5A) has been fabricated for HER.132 As H2 bubbles are formed on a Pt surface in the SAB stripe with an optimal width of 250 μm, they are quickly moved into adjacent regions of SAL stripes with an optimal width of 500 μm, working as gas channels transporting hydrogen out of the reaction system. This design keeps the electrocatalyst surface clean from any blockage by bubble adhesion and enhances the H+ diffusion from the bulk acid electrolyte. Finite element simulations reveal that the H2 concentration at the electrode reduced from 0.66 M to 0.29 M by the introduction of adjacent SAL stripes, which reduce the H2 diffusion distance owing to the presence of a gas cushion, resulting in much reduced overpotentials of −80 mV compared to −511 mV for a flat Pt electrode.132 Another electrode design (Fig. 5B) employs microporous stainless-steel mesh (1 × 1 cm), which is spray-coated with PTFE on one side and contains the Pt/C electrocatalyst on the other side.133 This enables directional bubble movement from the aerophobic catalyst side to the aerophobic PTFE side through the pores of a mesh, leading to a ∼15 times enhancement of HER current density.
 | ||
| Fig. 5 Electrode designs with aerophilic/aerophobic patches for directional removal of bubbles: (A) electrode with alternative stripes of micrometre width of superaerophobic (SAB) electrocatalytic Pt and superaerophilic (SAL) SiO2 nanoparticles for HER reaction. Reproduced with permission.132 Copyright 2023, American Association for the Advancement of Science. (B) stainless-steel mesh electrode, with aerophilic (AI) coating of polytetrafluoroethylene (PTFE) on one side and aerophobic (AO) Pt/C catalyst on the other side. Reproduced with permission.133 Copyright 2020, American Chemical Society. | ||
In summary, electrode wettability in water electrolysis is dynamic, influenced by surface properties, applied potential, and gas evolution. When a voltage is applied, the distribution of ions at the electrode–electrolyte interface changes, causing a shift in surface charge. This phenomenon, known as the electrocapillary effect,134 can modify the wettability of the electrode, while gas films increase local hydrophobicity, hindering electrolyte contact. To counter this, nanostructuring, coatings, and chemical treatments enhance wetting,102,111,114,115 while surfactants and pH adjustments can optimise electrode-liquid interactions.135–137 To ensure efficient gas removal and maintain electrode wettability, understanding these factors is essential for the optimised electrochemical performance of water electrolysers.
4. Electrolyser models
For the development of advanced water electrolysis devices, data are often needed under various operating conditions and using various materials.21,138,139 Modelling of water electrolysers can aid towards this goal, since it is a powerful tool for understanding the relationship between structure/property and electrochemical performance, which can accelerate the technology development by saving time and cost of experiments.31 Electrolyser models can be grouped into two categories: the first one investigates the integral behaviour of the complete cell (e.g. polarisation curve) as a function of the operating conditions, while the second category focuses on individual functional layers of the electrolyser device (electrode, gas diffusion layer (GDL), flow field) to obtain a mechanistic understanding of the underlying phenomena (e.g. gas and water transport).140Most of the electrolyser models utilise a continuum approach, which applies principles of classical fluid dynamics and electrochemistry, treating the electrode, GDL and electrolyte as continuous media.141,142 With the advancement of computational power and the realisation that the microstructure of the electrode and the GDL significantly impact transport phenomena, pore-scale models have been developed recently for electrolysers.143,144 With the development of artificial intelligence in the past decade, machine learning based predictive models are developed as well, which can analyse much larger and more complex datasets with high accuracy. These tools could accelerate the development and optimisation of key components of water electrolysers, such as electrocatalysts and the membrane electrode assembly (MEA).145,146
Models developed thus far for water electrolysers face several challenges, such as computational resources, complexity, data requirements, and validation.31 However, literature on modelling water electrolysers is scant,147–149 and a review summarising the state-of-the-art and problems in model development is lacking. Therefore, a comprehensive overview of models with various levels of detail (complete cell models to layer-specific models) is provided here, that can serve as a tool for their further advancement.
4.1. Layer specific models
 | (5) |
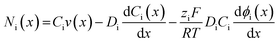 | (6) |
Each term on the right-hand side of eqn (6) represents convection, diffusion (concentration gradient) and migration contributions, respectively, where Ni(x) is the flux of species i (mol s−1 cm−2) at a distance x (cm) from the electrode surface, Di is the diffusion coefficient (cm2 s−1), ziis the charge (unitless), Ci is the concentration (mol cm−3), v(x) is the velocity (cm s−1) with which a volume element in solution moves along the axis, 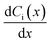 is the concentration gradient and
is the concentration gradient and  is the potential gradient at distance x, neglecting any pressure or temperature gradient, and electro-osmosis.
is the potential gradient at distance x, neglecting any pressure or temperature gradient, and electro-osmosis.
Several equations have been developed to capture the kinetics of electrochemical reactions at the electrolyte-electrode interface, the most notable of which is the Butler–Volmer equation, which computes electrode current density i as a function of the activation overpotential η:152
 | (7) |
At higher overpotentials (>50 mV), the Tafel equation can be used to describe electrode kinetics, which links applied overpotential η to the current i passing through the electrode:152
 | (8) |
η = a + b × ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) i i | (9) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) i, also known as the Tafel plot, providing important information about the electrochemical activity of an electrode for a specific reaction.153
i, also known as the Tafel plot, providing important information about the electrochemical activity of an electrode for a specific reaction.153
Modelling of the gas bubbles formed during electrochemical reactions in an electrolyser is of significant interest, as their coverage of the electrode surface has a detrimental effect on cell overpotential.154 Gas bubbles undergo nucleation first on the electrode surface, after which their growth and detachment take place.155 The geometry of the electrode surface and its wettability are the two most influential parameters affecting the gas bubble behaviour. Hence, the tuning of these properties provides an important strategy for effective bubble management and improved electrochemical performance.150,156
Bubbles formed in water electrolysis are modelled using Lagrangian or Eulerian approaches.155,157 The Lagrangian approach allows the monitoring of individual gas bubbles at the gas–liquid interface.155 For example, a gas–liquid two-phase model is developed to simulate the flow, as well as the growth and detachment of gas bubbles from the surface of the electrode (Fig. 6A).156 The model provides detailed information on bubble detachment and coalescence from the electrode surface and in bulk electrolyte, considering the wettability of the electrode surface as well as the size of the bubbles, via Cahn–Hilliard (C–H) eqn (10) and (11):
 | (10) |
| ψ = −∇·(εpf2∇ϕ) − (ϕ2 − 1)ϕ | (11) |
![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) is the velocity field (m s−1), γ is the mobility (m3 s kg−1) and λ is the mixing energy density (N). It is revealed that the coalescence of smaller bubbles on the surface of the electrode is the main mechanism for the detachment of gas bubbles.156 The hydrophilic surface of the electrode with a sufficiently small contact angle (∼π/5) shrinks bubbles to a round shape that are less attached to the solid surface. Further decrease of the contact angle detaches and repels this round bubble from the surface of the electrode into the bulk electrolyte. The smaller the contact angle (from π/5 to π/9) of the bubble, the further the bubble is repelled.156
is the velocity field (m s−1), γ is the mobility (m3 s kg−1) and λ is the mixing energy density (N). It is revealed that the coalescence of smaller bubbles on the surface of the electrode is the main mechanism for the detachment of gas bubbles.156 The hydrophilic surface of the electrode with a sufficiently small contact angle (∼π/5) shrinks bubbles to a round shape that are less attached to the solid surface. Further decrease of the contact angle detaches and repels this round bubble from the surface of the electrode into the bulk electrolyte. The smaller the contact angle (from π/5 to π/9) of the bubble, the further the bubble is repelled.156
 | ||
| Fig. 6 Electrode models for gas bubble management. (A) Model of bubble coalescence on and detachment off a vertical gas-evolving electrode; reproduced with permission.156 Copyright 2020, The Electrochemical Society and IOP Publishing. (B) Model of growth of single gas bubble of hydrogen at the cathode side of an alkaline electrolyser. Reproduced with permission.158 Copyright 2019, Elsevier. (C) Effect of electrode morphology on bubble hydrodynamics. Reproduced with permission.150 Copyright 2023, Elsevier. (D) Hydrogen bubble nucleation study on electrode surface in alkaline solution; reproduced with permission.159 Copyright 2020, American Chemical Society. | ||
In another Lagrangian model, the growth of a hydrogen bubble on a vertical electrode is simulated in a cathodic half-cell compartment (30% KOH solution) (Fig. 6B) using equations of fluid flow, mass transfer, and tertiary current distribution.158 The effect of flow rate and pressure on the growth of a single stagnant gas bubble is evaluated; an increase of both parameters (∼1.2 to ∼40 mm s−1 and 1 to 40 bar for velocity and pressure, respectively) decreases the radius of the gas bubble by ∼20% and ∼82% (from ∼40 to ∼32 and ∼7 μm), respectively. CFD simulations are also employed to study the effect of electrolyte flow velocity and morphology of the nanostructured electrode on bubble dynamics (Fig. 6C).150 The surface of the electrode contains hematite arrays with hydrophilic properties; these arrays have a large electrochemically active surface area and attract liquid into their structure via capillary action, creating a reactive liquid film favouring electrochemical reactions. As a result, the removal of formed gas bubbles is accelerated, and electrochemical reaction sites become mostly available due to minimal bubble adhesion, resulting in an increase in current density. A ∼4.3 mA cm−2 current density at 2 V (vs. RHE) is obtained for this modified electrode at ∼0.1 m s−1 flow compared to ∼3.5 mA cm−2 at no electrolyte flow.150
The second modelling approach of multiphase flow, namely the Eulerian approach, treats both dispersed (gas bubbles) and continuous phases (liquid electrolyte) as interpenetrating continua. It is based on averaging the Navier–Stokes equations (eqn (S1) and (S2) in ESI†) for each phase present.160 Even though it does not allow the monitoring of individual bubble growth at the microscale, it requires a much lower computational cost than the E–L approach for simulating bubble dynamics at the macroscopic scale in water electrolysers.161 It can provide an estimate of the bubble coverage of the electrode surface (an important parameter increasing cell overpotential) by measuring gas plume thickness.162 A 2D two-fluid Euler–Euler model is developed for a water electrolysis cell of 12 cm length and 3 cm width.163 Two 4 cm long vertical planar electrodes for the HER and OER are placed parallel to each other at a 3 mm gap and 40 mm distance from the bottom of the cell with an alkaline electrolyte in the channel. As the current is applied, gas bubbles evolve over the electrodes and form a diphasic boundary layer, which becomes thicker along the height of the electrodes. Increasing current density from 500 A m−2 to 2000 A m−2 results in an increase of the bubble void fraction (ε) and boundary layer thickness (δ) of both anode (εan from ∼0.23 to ∼0.33 and δan from ∼515 μm to ∼690 μm) and cathode (εcath from ∼0.13 to ∼0.19 and δcath from ∼600 μm to ∼800 μm). As electrolyte resistance increases with bubble void fraction, this model provides an important tool to optimise the operating conditions and cell design for effective bubble management.163
A 2D Euler–Euler model of multiphase flow has been developed for a porous HER electrode in alkaline electrolyte using the Euler–Euler model to investigate the impact of electrode surface properties on gas fraction.164 In a stagnant electrolyte, an electrode with a superaerophobic surface facilitates bubble detachment and increases gas fraction; a decrease of electrode CA from 161.3° to 29.4° raises gas fraction from ∼0.9% to ∼1.4% at ∼125 mA cm−2. Furthermore, forced electrolyte flow can improve diffusive ion transport into the porous electrode by lowering the gas fraction near its surface; it is observed that an increase of flow velocity from ∼1 to ∼15 cm s−1 reduces the gas fraction from ∼2.7% to ∼1.3%.164 Another Eulerian model of a parallel plate membrane-less electrolyser highlights the potential trade-offs between current density, efficiency, and product gas purity.165 High-speed camera imaging is used to estimate the width of the generated downstream H2 bubble plume in the cathode as an indicator of gas crossover. Exploration of various flowrates (from low Re ∼ 131 to high Re ∼ 1419) reveals that the smallest width of the bubble plume is achieved at Re ∼ 796 for this electrolyser operating at 200 mA cm−2 in a 0.5 M H2SO4 electrolyte solution. A 1D model is used to estimate the required channel width for specific voltage efficiency (∼45–85%) and current density (up to ∼1000 mA cm−2) for the safe operation (H2 crossover <4%) of this device. The required channel width to achieve electrolyser efficiency >65% at ∼400 mA cm−2 in an acidic solution (0.5 M H2SO4) should be less than 1.8 mm. For a more conductive alkaline electrolyte (30% KOH), the channel width can be increased to larger values (<2.6 mm) to achieve the same efficiency and current density. To reach >85% electrolyser efficiency while maintaining H2 crossover below 4%, its channel width should be <0.5 mm and operated at a small current density (<25 mA cm−2), demonstrating the structural and performance limitations of this design.165
 | ||
| Fig. 7 Gas diffusion layer models: (A) 2D model of porous GDL of PEMEC to investigate the impact of its thickness on liquid saturation of the anode catalyst layer. Reproduced with permission.167 Copyright 2020, Elsevier. (B) Model studying the effect of GDL wettability and pore size on oxygen bubble transport and overpotential. Reproduced with permission.170 Copyright 2017, Elsevier. | ||
Gas bubble dynamics in a PTL are highly dependent on the operating conditions of the electrolyser.171 Modelling and high-speed camera visualisation of micropores of a PTL show that both current density and temperature increase bubble growth rate, whereas flowrate has no impact on bubble behaviour. Surface properties of a PTL can also significantly impact multi-phase transport and gas bubble dynamics of water electrolysers. The impact of the wettability of the PTL and anode catalyst layer (ACL) on the growth and stability of three types of bubbles has been investigated (Fig. 7B): nucleation-driven, buoyancy-driven, and drag-driven.170 While nucleation driven bubbles flowing inside the pores of PTL show an overpotential of ∼28 mV, buoyancy- and drag-driven bubbles formed at the interface of the PTL and flow channel block the water transport to the PTL pores located underneath, resulting in larger overpotentials (∼43 and 35 mV for buoyancy-driven and drag-driven bubbles, respectively). The wettability of the ACL and PTL affect significantly the bubble overpotential and their lifetime; the more hydrophilic they are (contact angle ∼140°–175°), the smaller the bubble overpotential (∼40 to 5 mV for drag-driven bubbles located on a hydrophilic ACL and ∼55 to ∼35 mV located on a hydrophilic PTL) and their lifetime (∼3.4 to 2.6 s).170
 | ||
| Fig. 8 Flow field models (A) effect of flow field designs (parallel, serpentine or interdigitate) on PEMEC cell performance. Reproduced with permission.174 Copyright 2023, MDPI. (B) Effect of circular flow field design on the distribution of oxygen volume fraction in a PEMEC. Reproduced with permission.175 Copyright 2023, Elsevier. | ||
As design parameters of channels have a significant impact on multiphase flow and device performance, 3D simulations were performed to investigate the influence of various characteristics (height, wettability, upper wall geometry) of the microchannels of a PEMEC on bubble dynamics to optimise its design for favourable bubble detachment.176 Visualisation by high-speed camera using transparent flow channels was employed to qualitatively show the four stages of bubble detachment based on the interplay of surface tension and forces of fluid flow: initial phase, instability, deformation, and detachment. The required power for the detachment of a ∼100 μm bubble from a flow channel with 1 mm height and CA ∼60° is ∼60.8 μW; it was demonstrated that a reduction in CA (∼30°) and height (∼0.6 mm) of the flow-field can significantly decrease the parasitic losses, as the power required is significantly reduced to ∼7 and ∼33 μW, respectively. However, a reduction in height of the flow channel will obstruct the flow of the electrolyte and, hence, the H2 production efficiency of the electrolyser; to circumvent this issue, while maintaining the same low height of the flow channel, a waveform design (such as, sinusoidal and rectangular) can be employed for the engineering of the flow cell, minimising the power requirement for bubble detachment.176 A 3D cell model has been developed using coupling of heat transfer, two-phase flow and electrochemistry to study the temperature evolution in alkaline electrolyser flow channels with zero-gap cell design configuration.177 This showed is a non-uniform temperature distribution along the flow channels of the electrolyser and formation of local hot spots in the regions where gas bubbles are accumulated due to inadequate flow of the electrolyte. At higher current density (∼4242 mA cm−2) temperature uniformity deteriorates with maximum temperature variation along the x-axis reaching up to 5.1 K. A high flow rate (∼2.1 vs. ∼0.9 ml min−1 cm−2) can reduce the temperature difference in a cathode channel significantly (0.4 K vs. 3.6 K), whereas a higher inlet temperature (351.35 K vs. 303.15 K) can also aid in the reduction of the temperature variation (1.4 K vs. 2.2 K).
To study the effect of pore diameter (dpore) on two-phase transport properties, the pore network of a titanium-based PTL in a PEM electrolyser is numerically generated by stochastic modelling, possessing spherical pores connected through cylindrical throats.143 The larger pores of the PTL show higher permeation for liquid water; at 36% oxygen coverage, a PTL with dpore ∼ 33.5 μm has a two-phase water permeability of ∼5.5 × 10−13 m2, which is higher than the ∼1 × 10−13 m2 for a PTL with dpore ∼ 26.5 μm. The effect of the porosity gradient between the PTL-catalyst coated membrane (CCM) interface and PTL-flow-field interface is examined by employing two PTLs with specific structural properties obtained from micro-tomography (25–65% gentle gradient, GG-PTL and 8–85% steep gradient, SG-PTL). SG-PTL shows lower ∼15% gas saturation than GG-PTL at its centre, causing higher water permeation (3 × 10−13 m2), and suggesting that a lower porosity at the PTL-CCM interface can further improve reactant transport through PTLs.143 The design parameters of these PTLs can be optimised by investigating the impact of particle diameter (dP) of precursor titanium powder and PTL porosity (ε) on reactant transport.144 As dP increases from ∼25 μm to ∼75 μm, the two-phase water permeability increases significantly from ∼6.37 × 10−14 m2 to ∼76.9 × 10−14 m2. Although higher porosity yields improved water permeation, it also increases the surface roughness and contact resistance of the PTL. This effect is more prominent at porosity values above 40% leading to severe PTL roughness of ∼80 μm and, thus, to performance losses. To overcome this issue, a PTL with dP ∼ 25 μm and ε ∼ 0.265 is suggested for electrolyser operation at intermediate current density, while a PTL with dP ∼ 25 μm and ε ∼ 0.405 is suggested for electrolyser operation at high current density.144
A current–voltage and gas crossover model has been developed for a zero-gap alkaline electrolyser with ∼20 N m3 h−1 hydrogen generation capacity. The impact of the thickness of the diaphragm (100–500 μm), temperature (60–100 °C) and pressure (1–50 bar) on electrolyser performance with minimum gas crossover has been investigated. Simulation results show that a current density up to 1.6 A cm−2 is achievable for a zero-gap cell design vs. 0.4–0.6 A cm−2 for a conventional alkaline cell design by reducing the thickness of the diaphragm up to 0.1 mm and using the higher temperature of 100 °C. However, such alterations cause high gas crossover, which must be decreased below 10% via operation below 8 bar.191 A 1D numerical model of an MEA has been developed for investigating the effect of temperature on the membrane degradation in a PEMWE (25 cm2).192 The production of fluoride ions is increased as temperature climbs from 333 K to 353 K, while the thickness of the membrane is reduced by half after ∼380–500 h of operation at 333 K and ∼80–700 h at 353 K, emphasising the need for optimised operating conditions to extend electrolyser lifespan.192
4.2. Complete cell models
There are several reports in the literature of complete cell models to study the effect of the operating conditions and design parameters on electrolyser performance.193,194 Apart from standard equations of charge transfer and kinetics, which are used to model electrode layers in such models, the overall cell voltage (Vcell) is composed of several components: open-circuit voltage (Vocv), the activation overvoltage (Vact), the ohmic overvoltage (Vohm) and the mass transport or diffusion overvoltage (Vdiff), which are described by eqn (S3)–(S11) in the ESI.† Complete cell models are usually three-dimensional (3D) to investigate coupled physicochemical phenomena encompassing electrochemical reactions, mass transport, and capillary flow of multiple phases within cathodic/anodic channels and porous gas diffusion layers (Fig. 9A and B).195,196 For a PEM electrolyser, an increase in the porosity of the GDL from ∼0.2 to ∼0.6 results in lower water saturation in the cathode diffusion layer (CDL), i.e. ∼0.21 and ∼0.19 for the previously mentioned porosity values of the GDL.195 The opposite effect is observed at the anode diffusion layer (ADL), as the water saturation increases with porosity (∼0.55 and ∼0.61 at ∼0.2 and ∼0.6 porosity, respectively). This is due to the enhancement of capillary flow as the porosity of the GDL increases, transporting water rapidly from the cathode to the anode.195 A similar result is obtained with the alteration of the hydrophobicity of the GDL, since any increase decreases the capillary pressure and, hence, capillary flow, leading to water transport from CDL to ADL.196 However, to avoid water starvation or flooding of the catalyst layer, the hydrophobicity of the GDL should be higher than the ACL's. Under such conditions, the direction of capillary pressure from the ACL to GDL promotes the detachment of the generated gas bubbles from the ACL, resulting in an increase in H2 production efficiency (∼13%).196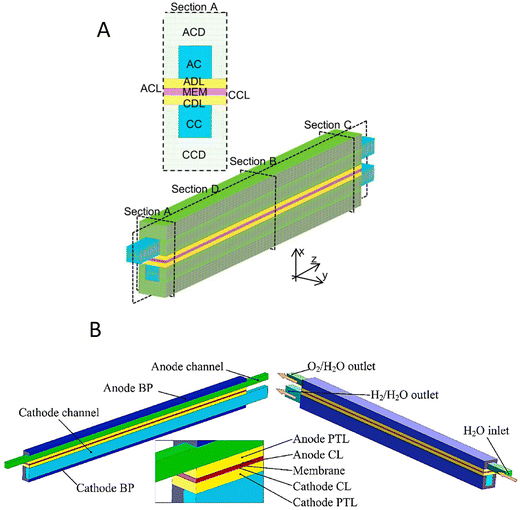 | ||
| Fig. 9 Geometries for various cell models of water electrolysers: (A) 3D model of PEM design. Reproduced with permission.195 Copyright 2022, Elsevier. (B) 3D model of PEM design with single channel and multiphase flow. Reproduced with permission.196 Copyright 2022, Elsevier. | ||
The impact of thermal limitations on electrolyser performance at high current density is investigated via a 1D thermal model and validated with experimental measurements in a 5 cm2 cell.177 At high current densities up to 25 A cm−2, significant heat (up to 35.5 W cm−2 compared to ∼1 W cm−2 for today's PEMWE typical current density range of 1–2 A cm−2) is generated due to ohmic and activation losses, leading to increased MEA temperatures (∼90 °C). This excessive heating without proper cooling management accelerates membrane and catalyst degradation. To avoid this, high water flow rates (∼25 ml min−1 cm−2 at 10 A cm−2) are essential for effective dissipation of the heat produced (∼5.7 W cm−2) and stable operation. The possibility to use such higher current densities can result in a significant reduction in material usage and device cost, ultimately paving the way to meet the future goal of their large-scale application.177
The integration of electrolyser technologies with renewable power is often required in practical conditions. This is investigated in Multiphysics modelling to optimise the design of industrial alkaline water electrolysis (AWE) stacks under varying load conditions when coupled with renewable energy sources.197 Small cell (SC) design has a higher number of smaller cells, resulting in a reduction of bubble coverage (∼12.5% lower volume fraction near the electrode) and an increase of hydrogen production (∼6.7% higher at 2.3 V) under heavy loads (on-grid scenario). However, under light and dynamic load conditions, SC suffers from high shunt currents, leading to lower efficiency. For off-grid scenarios, such as the use of wind power, large cell (LC) design, which has fewer but larger cells, is more suitable as it minimises shunt currents and improves current efficiency (∼20% higher at 1.7 V). However, the longer flow channels in LC design result in a larger bubble curtain, which can negatively impact the contact between electrolyte and catalyst.197 Integration with renewable power sources is further explored in system-level models, encompassing the entire electrolysis stack, balance of plant (BOP) and power supply.198,199
Thus far, there are limited reports on numerical models for membrane-less electrolysers.60,165,200 An analytical multiphase flow model has been developed for a parallel-plate electrolyser without a separator, focusing on gas–liquid flow dynamics.200 By quantifying the gas fraction profile of bubble plumes along the vertical electrodes, it estimated the maximum height of the membrane-less electrolyser required for safe operation at specific interelectrode distance and flow velocity. At 1000 mA cm−2, a buoyancy-driven membrane-less electrolyser with a 3 mm interelectrode distance can achieve a maximum height of ∼7.6 cm while maintaining 98% product purity at atmospheric pressure. However, by introducing forced flow at Re = 1000, the same electrolyser can be scaled up to ∼17.6 cm.200 Increasing the operating pressure can allow a further increase in its height, as the bubble size is reduced, enhancing gas dissolution.200 The effect of cell geometry on the efficiency of membrane-less electrolysers is also investigated via numerical simulations and experimental validation.60 A Y-shaped cell geometry is introduced as an optimised design compared to a flow-through T-shape or straight I-shape cell design. The Y-shaped cell design provides more uniform current distribution and increased efficiency, whereas T- and I-shaped cell designs suffer from non-uniform bubble accumulation, leading to increased local resistance and higher voltage losses. The cell voltage can be reduced further by ∼0.17 V for Y-shaped electrolyser at a current density of 250 mA cm−2 by increasing the flow rate (Re ∼ 1500).60
Overall, electrolyser numerical models offer critical insights from fundamental microscale phenomena to system-level optimisation. Although current models can describe electrode kinetics, bubble dynamics, mass transport and fluid flow, challenges lie in Multiphysics complexity and scalability. Addressing this gap will require the refinement of current electrolyser models and the development of multiscale models through integrated computational approaches.
5. Development of water electrolyser technologies from an industrial perspective
5.1. Technoeconomic context
PEM and alkaline electrolysers (AWE) remain the most mature technologies with several large-scale manufacturers in the USA (Plug Power and Proton onsite), Europe (ITM Power, NEL Hydrogen, ThyssenKrupp) and China (LongGi, PERIC Hydrogen and Tianjin Mainland).201 Among alkaline electrolysers, atmospheric technology remains much more mature than pressurised technologies where there remain many questions about the operational limits. Besides, several challenges need to be addressed by 2050 in the development of very large-scale electrolyser plants. This includes enhancement of current densities (>2 A cm−2 for alkaline from current ∼0.2–0.8 A cm−2 and up to 4–6 A cm−2 for PEM from current ∼1–2 A cm−2) to increase the hydrogen production rates and improve the energy efficiency (<45 kW h per kgH2 from current ∼50–70 kW h per kgH2) to reduce power consumption.18 Other 2050 targets include operation possibly at higher pressure (>70 bar vs. current <30 bar) and increasing the stack unit size to 10 MW from 1 MW along with doubling its lifetime to ∼100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 h and above.18 An important challenge for such a massive scale-up is to bring down the current high cost of electrolytic hydrogen to a much lower level (<2 $ per kg) to make it competitive enough with other hydrogen production technologies on the market, notably steam methane reforming, which had a 45% market share in 2020.202 This will require reduction of both capital expenditure (CAPEX) and operational expenditure (OPEX).
000 h and above.18 An important challenge for such a massive scale-up is to bring down the current high cost of electrolytic hydrogen to a much lower level (<2 $ per kg) to make it competitive enough with other hydrogen production technologies on the market, notably steam methane reforming, which had a 45% market share in 2020.202 This will require reduction of both capital expenditure (CAPEX) and operational expenditure (OPEX).
The high production cost (OPEX) of electrolytic hydrogen is mainly because of the high cost of electricity. The electricity costs represent the largest share of the renewable H2 production technical cost from 50% up to 80% depending on the geographical zone. Moreover, grid electricity cannot meet the total demand of electricity consumption while scaling up the electrolysers to GW scale. For example, if all of today's hydrogen demand is to be met by water electrolysers with 60% assumed efficiency, it will require 3600 TW h of electricity consumption, which exceeds the total grid electricity generated in Europe annually.20 Electricity from renewable sources, such as solar or wind, can bring down its cost to make it more affordable.203 That is why large GW-scale plant projects are envisaged in regions with the highest load factors of wind or sun to benefit from the lowest possible levelised cost of electricity (LCOE). In this context, it is essential to maximise the conversion rate from the produced electrons to hydrogen. As an illustration, if one considers an islanded plant delivering 75 kt per year of green H2 (powered roughly by 1 GW of renewables): the increase of the energy efficiency of the electrolysis plant by 10% may reduce the global electricity expenditure by more than 400 M$ with a 55 $ per MW h electricity price over the project life. In addition to the reduction of the electricity OPEX, substantial efforts are required to decrease at the same time the installation cost of electrolysers (CAPEX). This should be achieved by automating the manufacturing processes and the use of affordable materials. For a minimum 10 MW electrolyser plant, total installed system CAPEX for alkaline (∼500–1000 $ per kW) and PEM (∼700–1400 $ per kW) electrolysers reported in 2020 – numbers that are even higher if one consider the full installation costs – are far away from the 2030 CAPEX target (<200 $ per kW).18 Stack cost, which is a major component of CAPEX, is expected to decrease significantly by 2030 to 52–79 € per kW for alkaline and 63–234 € per kW for PEM electrolysers respectively, while ramping up their stack power densities from 0.5 W cm−2 to 2.3 W cm−2 and 4.75 W cm−2 to 6.3 W cm−2, respectively.204
5.2. Technological status and development
Electrocatalyst development with advanced architectures and manufacturing techniques will play a critical role in GW-scale electrolyser deployment.205 Current catalysts are not only expensive materials (Pt, Ir) but have limited supplies. For example, finding an alternative to Ir and/or being able to recycle it fully is crucial, because of its very limited availability worldwide. As of today, the iridium requirement in a PEM stack is around 0.75 kg per MW, while the annual global iridium production ranges from 8 to 9 tonnes. One can reasonably consider that around 20% of today's iridium supply could be allocated to electrolyser production, which would allow the construction of only 2 or 3 GW of PEM electrolysers.206 Those figures must be put in comparison to electrolyser production forecasts. IRENA estimates an average of 160 GW annually installed electrolyser capacity over the next 25 years to meet the demand objective of renewable H2.207 By combining such a capacity with IEA's predictions of a 90% alkaline to 10% PEM ratio, the future stress on iridium is not negotiable. Technological breakthroughs are required in current electrode catalysts to significantly reduce the amount utilised of these rare and expensive noble metals; it is expected to decrease iridium loading on the anode to 0.2 mg cm−2 and platinum loading on the cathode to 0.05 mg cm−2 by 2030.18 Nanostructured electrocatalyst design strategies, e.g. alloying, doping, size reduction to small nanoparticles or single atoms and loading on advanced nanocarbon supports can assist in achieving these targets.208
 | ||
| Fig. 10 Cost breakdown for PEM and AWE technologies from a single cell (membrane electrode assembly) to a complete stack (1 MW electrolysers), reproduced from the International Renewable Energy Agency Report: Green Hydrogen Cost Reduction.18 Copyright 2020, IRENA. | ||
The stability of a PEM electrolyser is highly dependent on the durability of MEA components and operating conditions, including temperature, current density, and water flow rate. To translate any lab scale PEM electrolyser to a commercial product, accelerated stress tests (ASTs) of MEA components are essential. These tests are extensively discussed in recent reviews209–211 for evaluating the feasibility of PEM electrolysers for industrial deployment in long-term operation. With a long PEM electrolyser operational lifetime of ∼50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 h, high electrocatalyst stability is needed to maintain the stack performance. Many phenomena, such as morphology change, metal dissolution and surface passivation, can lead to voltage deterioration during the industrial operation of an electrolyser.212 This opens the question of the duration of stability tests of catalysts in the literature: roughly limited to 100 h, such results are insufficient to be able to anticipate the catalyst's behaviour in an industrial context and potentially transfer the technology. Electrocatalyst durability testing is often neglected in laboratory studies where performance degradation testing of an MEA for an initial few thousand hours (∼4000 h) can even provide some insights into catalyst stability.213 As the Ir catalyst in the anode is more prone to degradation at high potentials (>1.8 V), its stability can be better evaluated in shorter time by various ASTs such as potential cycling between 1.45 to 2 V at 80 °C and a square-wave current cycling between 0.1–1 A cm−2 for 100 h.209 From a CAPEX point of view, bipolar plates represent a major portion (∼50%) of the stack cost. They are based on titanium coated with noble metal: platinum-coated titanium at the anode and gold-coated titanium at the cathode. Research on alternative materials like carbon-based bipolar plates is an interesting route for cost optimisation of the stack.214 Chemical, thermal or mechanical degradation of the membrane can occur under various stressors; membrane degradation occurs due to radical attack at the weak links (end groups) of the perfluorosulfonic membrane, which is accelerated at high current densities (>2 A cm−2). As the membrane backbone is attacked by oxidative species, fluorine and sulphur are released.209,210 The porous transport layer (PTL) at the anode side is more prone to chemical degradation due to higher voltage and oxygen-rich environment compared to the cathode side. The anode PTL, which is typically titanium-based, experiences passivation, hydrogen embrittlement, and conductivity loss over time.209 An AST for PTL stability involves constant current operation (2 A cm−2 for 1000 h) demonstrating that Ti passivation increases ohmic resistance, which can be reduced by 89% with Pt-coating.210 Carbon corrosion can occur at the gas diffusion layer (GDL) at the cathode side. An AST for GDL involves its immersion in 35% H2O2 at 90 °C for 12 h, resulting in loss of its hydrophobicity and increased water flooding. Furthermore, an AST for evaluating GDL mechanical stability involves cyclic compression (1.4–3.4 MPa, ∼5 cycles), resulting in structural changes in the GDL, such as cracks and reduced porosity.210
000 h, high electrocatalyst stability is needed to maintain the stack performance. Many phenomena, such as morphology change, metal dissolution and surface passivation, can lead to voltage deterioration during the industrial operation of an electrolyser.212 This opens the question of the duration of stability tests of catalysts in the literature: roughly limited to 100 h, such results are insufficient to be able to anticipate the catalyst's behaviour in an industrial context and potentially transfer the technology. Electrocatalyst durability testing is often neglected in laboratory studies where performance degradation testing of an MEA for an initial few thousand hours (∼4000 h) can even provide some insights into catalyst stability.213 As the Ir catalyst in the anode is more prone to degradation at high potentials (>1.8 V), its stability can be better evaluated in shorter time by various ASTs such as potential cycling between 1.45 to 2 V at 80 °C and a square-wave current cycling between 0.1–1 A cm−2 for 100 h.209 From a CAPEX point of view, bipolar plates represent a major portion (∼50%) of the stack cost. They are based on titanium coated with noble metal: platinum-coated titanium at the anode and gold-coated titanium at the cathode. Research on alternative materials like carbon-based bipolar plates is an interesting route for cost optimisation of the stack.214 Chemical, thermal or mechanical degradation of the membrane can occur under various stressors; membrane degradation occurs due to radical attack at the weak links (end groups) of the perfluorosulfonic membrane, which is accelerated at high current densities (>2 A cm−2). As the membrane backbone is attacked by oxidative species, fluorine and sulphur are released.209,210 The porous transport layer (PTL) at the anode side is more prone to chemical degradation due to higher voltage and oxygen-rich environment compared to the cathode side. The anode PTL, which is typically titanium-based, experiences passivation, hydrogen embrittlement, and conductivity loss over time.209 An AST for PTL stability involves constant current operation (2 A cm−2 for 1000 h) demonstrating that Ti passivation increases ohmic resistance, which can be reduced by 89% with Pt-coating.210 Carbon corrosion can occur at the gas diffusion layer (GDL) at the cathode side. An AST for GDL involves its immersion in 35% H2O2 at 90 °C for 12 h, resulting in loss of its hydrophobicity and increased water flooding. Furthermore, an AST for evaluating GDL mechanical stability involves cyclic compression (1.4–3.4 MPa, ∼5 cycles), resulting in structural changes in the GDL, such as cracks and reduced porosity.210
Alkaline electrolyser stacks are indeed 2 to 3 times less expensive than PEM stacks as they use non-noble catalysts, typically nickel, coupled with nickel bipolar plates, making the technology more attractive in terms of CAPEX compared with PEM electrolysis. The reduction in costs of materials in alkaline electrolysers is not trivial, especially since the price of nickel could rise if a context of strong demand emerges. However, the tendency regarding the development of new catalysts is less driven by cost reduction than by an increase in catalytic activity to promote the cells’ current density. This improved performance must persist over the long term with low degradation rates, as, in practice, the operating voltage of current electrolyser stacks degrades by ∼0.4–5 μV h−1, leading to a 10% lower performance after ∼40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 h of operation compared to the startup.20 Therefore, it is important to develop longer-lasting tests and relevant accelerated stress tests that could better extrapolate to real operational conditions of alkaline electrolysers.215 Moreover, electrocatalyst testing at industrially relevant harsher conditions such as a high temperature (70 °C vs. 25 °C in the laboratory) and using more concentrated electrolytes (6.9 M vs. 1 or 0.1 M KOH in the laboratory) is required.216 For alkaline electrolysers, an intermittent rather than continuous operation puts stress on electrodes, causing irreversible changes by catalyst dissolution and performance degradation. Therefore, the development of catalysts is needed that are more robust to reverse currents to handle dynamic load changes of renewable energy sources.216 Scaling up electrocatalyst synthesis from laboratory milligram scale to industrial kilogram scale requires the development of high-throughput production methods such as a roll-to-roll method demonstrated for manufacturing catalyst thin films of 5 m length and 0.25 m width for alkaline water electrolysis.217 The development of alternative diaphragms that are stable at high temperatures while maintaining conductivity could be relevant, as a reduction in overpotential by increasing temperature can be achieved (∼2.3 to 3.6 mV °C−1 for the temperature range of 50–200 °C, while operating at a current density of 1 A cm−2).216 However, the current state-of-the-art Zirfon diaphragm limits the electrolysis operation below 100 °C. Utilising zero-gap designs and thinning diaphragms down to 150 μm should lead to a major increase in efficiency of these devices in the future.
000 h of operation compared to the startup.20 Therefore, it is important to develop longer-lasting tests and relevant accelerated stress tests that could better extrapolate to real operational conditions of alkaline electrolysers.215 Moreover, electrocatalyst testing at industrially relevant harsher conditions such as a high temperature (70 °C vs. 25 °C in the laboratory) and using more concentrated electrolytes (6.9 M vs. 1 or 0.1 M KOH in the laboratory) is required.216 For alkaline electrolysers, an intermittent rather than continuous operation puts stress on electrodes, causing irreversible changes by catalyst dissolution and performance degradation. Therefore, the development of catalysts is needed that are more robust to reverse currents to handle dynamic load changes of renewable energy sources.216 Scaling up electrocatalyst synthesis from laboratory milligram scale to industrial kilogram scale requires the development of high-throughput production methods such as a roll-to-roll method demonstrated for manufacturing catalyst thin films of 5 m length and 0.25 m width for alkaline water electrolysis.217 The development of alternative diaphragms that are stable at high temperatures while maintaining conductivity could be relevant, as a reduction in overpotential by increasing temperature can be achieved (∼2.3 to 3.6 mV °C−1 for the temperature range of 50–200 °C, while operating at a current density of 1 A cm−2).216 However, the current state-of-the-art Zirfon diaphragm limits the electrolysis operation below 100 °C. Utilising zero-gap designs and thinning diaphragms down to 150 μm should lead to a major increase in efficiency of these devices in the future.
Moreover, corrosion of stainless-steel equipment of the balance of stack (BoS) can take place during pressurised alkaline electrolyser operation, releasing some impurities that can impact the electrode quality. Exogenous and endogenous impurities from various sources can impact the electrolytic performance of the cell by catalyst poisoning, lowering membrane conductivity, etc.218 but it is seldomly studied in literature. For example, iron oxide impurities are released in alkaline electrolysers due to the corrosion of stainless-steel equipment exposed to KOH in 30 wt% lye. Some of those iron particles are trapped by the mechanic and/or magnetic filters that can be present in the lye circulation loop of the BoS, but soluble impurities and fine particles can go through it, causing some deposition on and/or insertion in the electrodes. Demnitz et al. showed recently the growth of iron dendrites on the Ni cathodes of alkaline electrolyser in presence of iron dissolved in the lye.219 That being said, we must question the stability of new catalysts (which generally contain a fraction of noble metals) under aged electrolyte conditions, since they could be more sensitive to metallic impurities or traces, which would impact their expected performance over time.
Typically, membrane-less or capillary-fed electrolyser cell/stack designs discussed in Section 2.2 are attractive, since, via potentially relevant choices of materials and simplification of designs, they could fulfil the requirements mentioned above in terms of material stability to corrosion or operating temperature range. This would allow a reduction in CAPEX and potentially OPEX in case of increased energy efficiency of the system. Nevertheless, at that stage, the real impact of such cell designs on gas separation via the control of flux of the electrolyte or gas in the vicinity of the electrodes remains to be demonstrated at a larger scale (MW system).53 All those new approaches in cell (Section 2.2) and electrode design (Section 3) are still at an early stage and far from large deployment, but this opens the route to potential breakthroughs in the long term.
From a shorter-term perspective, the anion exchange membrane (AEM) or solvating membrane (like PBI) appears as a promising route for optimising alkaline-based systems. AEM can be much thinner than traditional diaphragms with better gas tightness, significantly reducing ohmic losses and optimising the energy efficiency of the cells when paired with non-noble catalysts.220 For AEM water electrolysis, membrane degradation is a major concern due to its chemical instability in an alkaline environment, while the noble metal-free electrocatalysts are susceptible to corrosion over extended operation (≥300 h).221 Despite advances in AEM membrane chemistries enhancing stability, additional fundamental research is needed to optimise this technology. Specifically, developing tailored ionomers and catalysts for low-concentration electrolytes or pure water and a better understanding of the catalyst/ionomer/membrane interactions are crucial to compete with traditional technologies in performance and lifespan for industrial-scale deployment.222
5.3. Operation perspective
From an operational point of view, beyond safety aspects, the efficiency and reliability of the production plants are compulsory. Accordingly, the question of the real stack efficiency and performance decay over time is of paramount importance, since the repeated unexpected change of stacks would have a drastic impact on the maintenance costs. Typically, the operational lifespan of an electrolyser stack is expected to be between 8 to 10 years. This limitation of replacement OPEX costs is necessary to ensure the economic viability of any projects for large production of green H2.That is why R&D on new designs of materials, cells (Section 2) and stacks are still necessary to optimise performance and/or reduce costs. For example, new electrode designs mentioned in Section 3, based on hydrophilic or hydrophobic material solutions28,108 for gas removal are attractive, since the management of bubbles and dissolved gas is of paramount importance to reduce the gas crossover. A reduction of the latter is particularly interesting to optimise the operational range of the electrolyser system.
The modelling of the different elements of the cells/stacks will help to promote future optimised architectures of cells and stack designs. Modelling is also very useful at a system level to optimise industrial operations. At that stage, acquiring operational data on real stacks remains the Holy Grail to feed and refine models. Building stack models integrating the ageing aspect would be extremely beneficial for supporting operations by developing predictive maintenance tools.
6. Conclusions
Green hydrogen production by water electrolysis can help to fight climate change, which has arisen mainly due to the enormous increase in energy produced from fossil fuels in the past century, raising it from ∼23 to ∼548 EJ.223 However, to meet the United Nations' goal of net zero carbon emissions by 2050, widespread GW-scale hydrogen production is required, which is a significant increase from the current installed capacity at the MW-scale, dominated by PEM and alkaline electrolyser technologies. Several challenges need to be addressed to achieve this target of developing very-large-scale electrolyser plants, such as reduction of cost of electrolytic hydrogen (<2 $ per kg), enhancement of current densities (>2 A cm−2 for alkaline and 4–6 A cm−2 for PEM) and improvement of the energy efficiency (<45 kW h per kgH2). Bubbles (10–800 μm) generated in water electrolysis cover the electrode, blocking its surface and degrading the cell performance substantially (overpotential of ∼308 mV at current density above 500 mA cm−2). Therefore, the latest electrode designs reported in the literature have been comprehensively reviewed for effective bubble management of the water electrolysis reactions (HER and OER), based on either bubble mitigation strategy (aerophobic electrode) or transportation strategy (aerophilic electrode). As models can aid experiments and accelerate technological development, the latest advancements in the modelling of water electrolysers have been reviewed, from complete cell models to more specific layer models. Membranes used in water electrolysers for separation of product gases pose challenges of high electrical resistance (≥0.2 Ω cm2) and thermal degradation above 90 °C. As a result, a new generation of membrane-less electrolysers has emerged within the last decade whose cell designs and electrochemical performance have been reviewed here. Despite various promising new designs of membrane-less electrolysers, several challenges remain to be addressed for achieving their commercial viability. Future research should focus on developing scalable and robust designs, improving gas separation and safety, and ensuring their long-term stability. Efficiency at the stack and system level needs to be evaluated for any proposed new cell design, along with techno-economic analysis and integration with renewable energy sources, to compete with existing electrolysis technologies.Nomenclature
| 1D | One-dimensional |
| 2D | Two-dimensional |
| 3D | Three-dimensional |
| ACL | Anode catalyst layer |
| ADL | Anode diffusion layer |
| AE | Auxiliary electrode |
| AEM | Anion exchange membrane |
| AI | Aerophilic |
| AO | Aerophobic |
| AWE | Alkaline water electrolysis |
| CA | Contact angle |
| CAPEX | Capital expenditure |
| CCM | Catalyst coated membrane |
| CDL | Cathode diffusion layer |
| CL | Catalyst layer |
| EU | European Union |
| FC | Fuel cell |
| GDL | Gas diffusion layer |
| HC | Honeycomb |
| HER | Hydrogen evolution reaction |
| LDH | Layered double hydroxide |
| MEA | Membrane electrode assembly |
| NC | Nanocone |
| NF | Nickel foam |
| OER | Oxygen evolution reaction |
| OPEX | Operational expenditure |
| PEM | Proton exchange membrane |
| PEMEC | Proton exchange membrane electrolysis cell |
| PEMWE | Proton exchange membrane water electrolyser |
| PFAS | Polyfluoroalkyl substances |
| PNMs | Pore network models |
| PEI | Polyethylenimine |
| PE | Polyethylene |
| PS | Polystyrene |
| PSD | Pore size distribution |
| PTFE | Polytetrafluoroethylene |
| PTL | Porous transport layer |
| RDE | Rotating disk electrode |
| RHE | Reversible hydrogen electrode |
| RPM | Revolutions per minute |
| SAB | Superaerophobic |
| SAL | Superaerophilic |
| SHE | Standard hydrogen electrode |
| WE | Water electrolyser |
Data availability
No primary research results, software or code have been included and no new data were generated or analysed as part of this review.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge funding from TotalEnergies and EPSRC through an EPSRC “Frontier Engineering: Progression” Grant (EP/S03305X/1), supporting nature-inspired electrochemical research in the UCL Centre for Nature-Inspired Engineering (CNIE).References
- IEA (2024), Electricity 2024: Analysis and forecast to 2026, International Energy Agency, Paris. https://www.iea.org/reports/electricity-2024.
- R. J. Andres, D. J. Fielding, G. Marland, T. A. Boden, N. Kumar and A. T. Kearney, Tellus B, 1999, 51, 759–765 CrossRef.
- J. Delbeke, A. Runge-Metzger, Y. Slingenberg and J. Werksman, Towards a climate-neutral Europe, Routledge, 2019, pp. 24–45 Search PubMed.
- S. Baruch-Mordo, J. M. Kiesecker, C. M. Kennedy, J. R. Oakleaf and J. J. Opperman, Environ. Res. Lett., 2019, 14, 1–8 Search PubMed.
- W. Lubitz and W. Tumas, Chem. Rev., 2007, 107, 3900–3903 CrossRef CAS.
- N. Dubouis, D. Aymé-Perrot, D. Degoulange, A. Grimaud and H. Girault, Joule, 2024, 8, 883–898 CrossRef CAS.
- P. Nikolaidis and A. Poullikkas, Renewable Sustainable Energy Rev., 2017, 67, 597–611 CrossRef CAS.
- B. Vivanco-Martín and A. Iranzo, Energies, 2023, 16, 3866 CrossRef.
- E. Gregor and J. Liselotte, EU hydrogen policy: Hydrogen as an energy carrier for a climate-neutral economy, European Parliamentary Research Service, 2021 Search PubMed.
- K. Scott, in Electrochemical Methods for Hydrogen Production, ed. K. Scott, The Royal Society of Chemistry, 2019, ch. 1, pp. 1–25 Search PubMed.
- E. Amores, M. Sánchez, N. Rojas and M. Sánchez-Molina, Sustainable Fuel Technologies Handbook, 2021, ch. 9, pp. 271–313 Search PubMed.
- H. Zhao and Z. Y. Yuan, Adv. Energy Mater., 2023, 13, 2300254 CrossRef CAS.
- H. Shin, D. Jang, S. Lee, H.-S. Cho, K.-H. Kim and S. Kang, Energy Convers. Manage., 2023, 286, 117083 CrossRef CAS.
- IRENA, Decarbonising hard-to-abate sectors with renewables: Perspectives for the G7, International Renewable Energy Agency, Abu Dhabi, 2024 Search PubMed.
- F. Frieden and J. Leker, Sustainable Energy Fuels, 2024, 8, 1806–1822 RSC.
- The European hydrogen market landscape: A report by European Hydrogen Observatory, 2023. https://observatory.clean-hydrogen.europa.eu/tools-reports/observatory-reports, 2023.
- M. Chatenet, B. G. Pollet, D. R. Dekel, F. Dionigi, J. Deseure, P. Millet, R. D. Braatz, M. Z. Bazant, M. Eikerling, I. Staffell, P. Balcombe, Y. Shao-Horn and H. Schafer, Chem. Soc. Rev., 2022, 51, 4583–4762 RSC.
- E. Taibi, H. Blanco, R. Miranda and M. Carmo, IRENA (2020), Green Hydrogen Cost Reduction: Scaling up Electrolysers to Meet the 1.5 °C Climate Goal, International Renewable Energy Agency, Abu Dhabi.
- RePowerEU Plan: Joint European action on renewable energy and energy efficiency, https://www.iea.org/policies/15691-repowereu-plan-joint-european-action-on-renewable-energy-and-energy-efficiency.
- M. Yue, H. Lambert, E. Pahon, R. Roche, S. Jemei and D. Hissel, Renewable Sustainable Energy Rev., 2021, 146, 111180 CrossRef.
- A. J. Shih, M. C. O. Monteiro, F. Dattila, D. Pavesi, M. Philips, A. H. M. da Silva, R. E. Vos, K. Ojha, S. Park, O. van der Heijden, G. Marcandalli, A. Goyal, M. Villalba, X. Chen, G. T. K. K. Gunasooriya, I. McCrum, R. Mom, N. López and M. T. M. Koper, Nat. Rev. Methods Primers, 2022, 2, 84 CrossRef CAS.
- K. Ayers, N. Danilovic, R. Ouimet, M. Carmo, B. Pivovar and M. Bornstein, Annu. Rev. Chem. Biomol. Eng., 2019, 10, 219–239 CrossRef CAS.
- K. O. Obodo, C. N. M. Ouma and D. Bessarabov, Power to Fuel, Academic Press, 2021, ch. 2, pp. 17–50 Search PubMed.
- J. W. Haverkort and H. Rajaei, J. Power Sources, 2021, 497, 229864 CrossRef CAS.
- R. Wu, Z. Hu, H. Zhang, J. Wang, C. Qin and Y. Zhou, Langmuir, 2024, 40, 721–733 CrossRef CAS.
- C. V. M. Inocêncio, Y. Holade, C. Morais, K. B. Kokoh and T. W. Napporn, Electrochem. Sci. Adv, 2022, 3, 1–52 Search PubMed.
- M. Bernt, A. Hartig-Weiß, M. F. Tovini, H. A. El-Sayed, C. Schramm, J. Schröter, C. Gebauer and H. A. Gasteiger, Chem. Ing. Tech., 2019, 92, 31–39 CrossRef.
- G. F. Swiegers, R. N. L. Terrett, G. Tsekouras, T. Tsuzuki, R. J. Pace and R. Stranger, Sustainable Energy Fuels, 2021, 5, 1280–1310 RSC.
- D. Zhang and K. Zeng, Ind. Eng. Chem. Res., 2012, 51, 13825–13832 CrossRef CAS.
- S. Yuan, C. Zhao, X. Cai, L. An, S. Shen, X. Yan and J. Zhang, Prog. Energy Combust. Sci., 2023, 96, 101075 CrossRef.
- B. Bensmann, A. Rex and R. Hanke-Rauschenbach, Curr. Opin. Chem. Eng., 2022, 36, 100829 CrossRef.
- S. A. Grigoriev, P. Millet, S. V. Korobtsev, V. I. Porembskiy, M. Pepic, C. Etievant, C. Puyenchet and V. N. Fateev, Int. J. Hydrogen Energy, 2009, 34, 5986–5991 CrossRef CAS.
- P. Trinke, P. Haug, J. Brauns, B. Bensmann, R. Hanke-Rauschenbach and T. Turek, J. Electrochem. Soc., 2018, 165, F502–F513 CrossRef CAS.
- A. S. Emam, M. O. Hamdan, B. A. Abu-Nabah and E. Elnajjar, Int. J. Hydrogen Energy, 2024, 64, 599–625 CrossRef CAS.
- N. Guillet and P. Millet, Hydrogen Production, 2015, ch. 4, pp. 117–166 Search PubMed.
- S. S. Kumar and H. Lim, Sustainable Energy Fuels, 2023, 7, 3560–3583 RSC.
- M. S. Thomassen, A. H. Reksten, A. O. Barnett, T. Khoza and K. Ayers, Electrochemical Power Sources: Fundamentals, Systems, and Applications, 2022, pp. 199–228 Search PubMed.
- N. Du, C. Roy, R. Peach, M. Turnbull, S. Thiele and C. Bock, Chem. Rev., 2022, 122, 11830–11895 CrossRef CAS PubMed.
- H. A. Miller, Curr. Opin. Electrochem, 2022, 36, 101122 CrossRef CAS.
- S. E. Wolf, F. E. Winterhalder, V. Vibhu, L. G. J. de Haart, O. Guillon, R.-A. Eichel and N. H. Menzler, J. Mater. Chem. A, 2023, 11, 17977–18028 RSC.
- A. Hauch, R. Kungas, P. Blennow, A. B. Hansen, J. B. Hansen, B. V. Mathiesen and M. B. Mogensen, Science, 2020, 370, eaba6118 CrossRef CAS.
- T. Smolinka, H. Bergmann, J. Garche and M. Kusnezoff, in Electrochemical Power Sources: Fundamentals, Systems, and Applications, ed. T. Smolinka and J. Garche, Elsevier, 2022, pp. 83–164 Search PubMed.
- R. Solanki, I. Patra, N. Ahmad, N. B. Kumar, R. M. R. Parra, M. Zaidi, G. Yasin, T. C. Anil Kumar, H. A. Hussein, R. Sivaraman, H. S. Majdi, O. K. A. Alkadir and R. Yaghobi, J. Environ. Chem. Eng., 2022, 10, 108207 CrossRef CAS.
- C. Li and J. B. Baek, ACS Omega, 2020, 5, 31–40 CrossRef CAS PubMed.
- T. Naito, T. Shinagawa, T. Nishimoto and K. Takanabe, Inorg. Chem. Front., 2021, 8, 2900–2917 RSC.
- M. El-Shafie, Results Eng., 2023, 20, 101426 CrossRef CAS.
- S. Shiva Kumar and H. Lim, Energy Rep., 2022, 8, 13793–13813 CrossRef.
- C. V. Pham, D. Escalera-López, K. Mayrhofer, S. Cherevko and S. Thiele, Adv. Energy Mater., 2021, 11, 2101998 CrossRef CAS.
- L. A. King, M. A. Hubert, C. Capuano, J. Manco, N. Danilovic, E. Valle, T. R. Hellstern, K. Ayers and T. F. Jaramillo, Nat. Nanotechnol., 2019, 14, 1071–1074 CrossRef CAS PubMed.
- M. A. Hubert, L. A. King and T. F. Jaramillo, ACS Energy Lett., 2021, 7, 17–23 CrossRef.
- Z. Rui, K. Hua, Z. Dou, A. Tan, C. Zhang, X. Shi, R. Ding, X. Li, X. Duan, Y. Wu, Y. Zhang, X. Wang, J. Li and J. Liu, J. Mater. Chem. A, 2024, 12, 9563–9573 RSC.
- N. Wang, S. Song, W. Wu, Z. Deng and C. Tang, Adv. Energy Mater., 2024, 14, 2303451 CrossRef CAS.
- G. F. Swiegers, A. L. Hoang, A. Hodges, G. Tsekouras, C.-Y. Lee, K. Wagner and G. Wallace, Curr. Opin. Electrochem, 2022, 32, 100881 CrossRef CAS.
- X. Yan, J. Biemolt, K. Zhao, Y. Zhao, X. Cao, Y. Yang, X. Wu, G. Rothenberg and N. Yan, Nat. Commun., 2021, 12, 4143 CrossRef CAS PubMed.
- G. D. O'Neil, C. D. Christian, D. E. Brown and D. V. Esposito, J. Electrochem. Soc., 2016, 163, F3012–F3019 CrossRef.
- P. Hadikhani, S. M. H. Hashemi, S. A. Schenk and D. Psaltis, Sustainable Energy Fuels, 2021, 5, 2419–2432 RSC.
- A. Hodges, A. L. Hoang, G. Tsekouras, K. Wagner, C. Y. Lee, G. F. Swiegers and G. G. Wallace, Nat. Commun., 2022, 13, 1304 CrossRef CAS PubMed.
- S. M. H. Hashemi, M. A. Modestino and D. Psaltis, Energy Environ. Sci., 2015, 8, 2003–2009 RSC.
- M. I. Gillespie, F. van der Merwe and R. J. Kriek, J. Power Sources, 2015, 293, 228–235 CrossRef CAS.
- K. Schoppmann, H. Rox, E. Frense, F. Rüdiger, X. Yang, K. Eckert and J. Fröhlich, Chem. Eng. J., 2025, 507, 160040 CrossRef CAS.
- S. Liang, Y. Ma, H. Luo, K. Wu, J. Chen and J. Yang, Chem. – Eur. J., 2023, 29, e202302160 CrossRef CAS.
- Capillary-fed electrolysis technology © Hysata, 2024, (https://hysata.com/our-technology/).
- L. Wan, Z. Xu, Q. Xu, M. Pang, D. Lin, J. Liu and B. Wang, Energy Environ. Sci., 2023, 16, 1384–1430 RSC.
- Q. Xu, L. Zhang, J. Zhang, J. Wang, Y. Hu, H. Jiang and C. Li, EnergyChem, 2022, 4, 100087 CrossRef CAS.
- Z. W. Seh, J. Kibsgaard, C. F. Dickens, I. Chorkendorff, J. K. Norskov and T. F. Jaramillo, Science, 2017, 355, eaad4998 CrossRef.
- H. Shi, Y. T. Zhou, R. Q. Yao, W. B. Wan, X. Ge, W. Zhang, Z. Wen, X. Y. Lang, W. T. Zheng and Q. Jiang, Nat. Commun., 2020, 11, 2940 CrossRef CAS PubMed.
- X. Wang, R. Su, H. Aslan, J. Kibsgaard, S. Wendt, L. Meng, M. Dong, Y. Huang and F. Besenbacher, Nano Energy, 2015, 12, 9–18 CrossRef CAS.
- S. Saha and A. K. Ganguli, ChemistrySelect, 2017, 2, 1630–1636 CrossRef CAS.
- K. Qu, Y. Zheng, X. Zhang, K. Davey, S. Dai and S. Z. Qiao, ACS Nano, 2017, 11, 7293–7300 CrossRef CAS.
- X. Yue, S. Huang, J. Cai, Y. Jin and P. K. Shen, J. Mater. Chem. A, 2017, 5, 7784–7790 RSC.
- A. Sivanantham, P. Ganesan, L. Estevez, B. P. McGrail, R. K. Motkuri and S. Shanmugam, Adv. Energy Mater., 2018, 8, 1702838 CrossRef.
- Y. Luo, L. Tang, U. Khan, Q. Yu, H. M. Cheng, X. Zou and B. Liu, Nat. Commun., 2019, 10, 269 CrossRef.
- L. Wei, K. Goh, O. Birer, H. E. Karahan, J. Chang, S. Zhai, X. Chen and Y. Chen, Nanoscale, 2017, 9, 4401–4408 RSC.
- T. Ami, K. Oka, H. Kasai and T. Kimura, Chem. Commun., 2025, 61, 1533–1558 RSC.
- S. Zaman, M. Khalid and S. Shahgaldi, ACS Energy Lett., 2024, 9, 2922–2935 CrossRef CAS.
- Y. Yang, H. Yao, Z. Yu, S. M. Islam, H. He, M. Yuan, Y. Yue, K. Xu, W. Hao, G. Sun, H. Li, S. Ma, P. Zapol and M. G. Kanatzidis, JACS, 2019, 141, 10417–10430 CrossRef CAS.
- Q. Gong, Y. Wang, Q. Hu, J. Zhou, R. Feng, P. N. Duchesne, P. Zhang, F. Chen, N. Han, Y. Li, C. Jin, Y. Li and S. T. Lee, Nat. Commun., 2016, 7, 13216 CrossRef CAS PubMed.
- S. Pattaweepaiboon, P. Samarungkasut, P. Iamprasertkun, P. Arkasalerks, K. Nueangnoraj, A. Boonchun, A. Pumsantier, W. Hirunpinyopas and W. Sirisaksoontorn, ACS Appl. Nano Mater., 2024, 8, 438–448 CrossRef.
- C. Tsounis, B. Subhash, P. V. Kumar, N. M. Bedford, Y. Zhao, J. Shenoy, Z. Ma, D. Zhang, C. Y. Toe, S. Cheong, R. D. Tilley, X. Lu, L. Dai, Z. Han and R. Amal, Adv. Funct. Mater., 2022, 32, 2203067 CrossRef CAS.
- L. Quan, H. Jiang, G. Mei, Y. Sun and B. You, Chem. Rev., 2024, 124, 3694–3812 CrossRef CAS PubMed.
- Y. Luo, Z. Zhang, M. Chhowalla and B. Liu, Adv. Mater., 2022, 34, e2108133 CrossRef PubMed.
- H. Wu, Q. Huang, Y. Shi, J. Chang and S. Lu, Nano Res., 2023, 16, 9142–9157 CrossRef.
- R. Wan, T. Yuan, L. Wang, B. Li, M. Liu and B. Zhao, Nat. Catal, 2024, 7, 1288–1304 CrossRef CAS.
- F. Liu, C. Shi, X. Guo, Z. He, L. Pan, Z. F. Huang, X. Zhang and J. J. Zou, Adv. Sci., 2022, 9, e2200307 CrossRef.
- J. Shi, Y. Bao, R. Ye, J. Zhong, L. Zhou, Z. Zhao, W. Kang and S. B. Aidarova, Catal. Sci. Technol., 2025, 2104–2131 RSC.
- W. Zheng, L. Y. S. Lee and K. Y. Wong, Nanoscale, 2021, 13, 15177–15187 RSC.
- J. Tang, C. Su and Z. Shao, Exploration, 2024, 4, 20220112 CrossRef CAS PubMed.
- X. Zhao, H. Ren and L. Luo, Langmuir, 2019, 35, 5392–5408 CrossRef CAS.
- A. Angulo, P. van der Linde, H. Gardeniers, M. Modestino and D. Fernández Rivas, Joule, 2020, 4, 555–579 CrossRef CAS.
- L. Yu, Y. Yang, P. Xie, Q. Xu, A. Kumar, L. Luo, H. Li, H. Xu, H. Duan and X. Sun, EES Catal., 2025, 3, 152–160 RSC.
- P. Tiwari, G. Tsekouras, K. Wagner, G. F. Swiegers and G. G. Wallace, Int. J. Hydrogen Energy, 2019, 44, 23568–23579 CrossRef CAS.
- K. Deng, H. Feng, Y. Zhang, D. Liu and Q. Li, Joule, 2023, 7, 1852–1866 CrossRef CAS.
- H. Vogt, Electrochim. Acta, 2017, 235, 495–499 CrossRef CAS.
- Y. Li, G. Yang, S. Yu, Z. Kang, J. Mo, B. Han, D. A. Talley and F.-Y. Zhang, Int. J. Hydrogen Energy, 2019, 44, 28283–28293 CrossRef CAS.
- A. M. Meulenbroek, A. W. Vreman and N. G. Deen, Electrochim. Acta, 2021, 385, 138298 CrossRef CAS.
- H. Zhang, Y. Ma, M. Huang, G. Mutschke and X. Zhang, Soft Matter, 2024, 20, 3097–3106 RSC.
- X. Yang, D. Baczyzmalski, C. Cierpka, G. Mutschke and K. Eckert, Phys. Chem. Chem. Phys., 2018, 20, 11542–11548 RSC.
- S. Park, L. Liu, C. Demirkir, O. van der Heijden, D. Lohse, D. Krug and M. T. M. Koper, Nat. Chem., 2023, 15, 1532–1540 CrossRef CAS PubMed.
- Q. Chen, J. Zhao, X. Deng, Y. Shan and Y. Peng, J. Phys. Chem. Lett., 2022, 13, 6153–6163 CrossRef CAS PubMed.
- M. Suvira, A. Ahuja, P. Lovre, M. Singh, G. W. Draher and B. Zhang, Anal. Chem., 2023, 95, 15893–15899 CrossRef CAS.
- L. Ding, W. Wang, Z. Xie, K. Li, S. Yu, C. B. Capuano, A. Keane, K. Ayers and F. Y. Zhang, ACS Appl. Mater. Interfaces, 2023, 15, 24284–24295 CrossRef CAS.
- Y. Kang, S. Lee, S. Han, D. Jeon, M. Bae, Y. Choi, D. W. Lee and J. Ryu, Adv. Funct. Mater., 2024, 34, 2308827 CrossRef CAS.
- V. B. Svetovoy, R. G. Sanders and M. C. Elwenspoek, J. Phys.: Condens. Matter, 2013, 25, 184002 CrossRef PubMed.
- M. Mita, H. Matsushima, M. Ueda and H. Ito, J. Colloid Interface Sci., 2022, 614, 389–395 CrossRef CAS PubMed.
- D. Lohse and X. Zhang, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 031003 CrossRef.
- Y. Zhang, X. Zhu, J. A. Wood and D. Lohse, Proc. Natl. Acad. Sci. U. S. A., 2024, 121, e2321958121 CrossRef CAS PubMed.
- H. Wang, Z. Xu, W. Lin, X. Yang, X. Gu, W. Zhu and Z. Zhuang, Nano Res., 2022, 16, 420–426 CrossRef.
- W. Xu, Z. Lu, X. Sun, L. Jiang and X. Duan, Acc. Chem. Res., 2018, 51, 1590–1598 CrossRef CAS.
- L. Wan, Z. Xu, Q. Xu, P. Wang and B. Wang, Energy Environ. Sci., 2022, 15, 1882–1892 RSC.
- T. Kou, S. Wang, R. Shi, T. Zhang, S. Chiovoloni, J. Q. Lu, W. Chen, M. A. Worsley, B. C. Wood, S. E. Baker, E. B. Duoss, R. Wu, C. Zhu and Y. Li, Adv. Energy Mater., 2020, 10, 2002955 CrossRef.
- J. Das, S. Mandal, A. Borbora, S. Rani, M. Tenjimbayashi and U. Manna, Adv. Funct. Mater., 2023, 2311648 Search PubMed.
- R. Xu, L. Du, D. Adekoya, G. Zhang, S. Zhang, S. Sun and Y. Lei, Adv. Energy Mater., 2020, 11, 2001537 CrossRef.
- H. Fan, S. Zhou, Q. Wei and X. Hu, Renewable Sustainable Energy Rev., 2022, 165, 112585 CrossRef CAS.
- H. H. Lin, C. H. Lin and S. C. Luo, ACS Appl. Mater. Interfaces, 2023, 15, 29214–29223 CrossRef CAS PubMed.
- J. Kim, S. M. Jung, N. Lee, K. S. Kim, Y. T. Kim and J. K. Kim, Adv. Mater., 2023, 35, 2305844 CrossRef CAS.
- Q. Ren, L. Feng, C. Ye, X. Xue, D. Lin, S. Eisenberg, T. Kou, E. B. Duoss, C. Zhu and Y. Li, Adv. Energy Mater., 2023, 13, 2302073 CrossRef CAS.
- D. Wang, L. Liu, Y. Liu, W. Luo, Y. Xie, T. Xiao, Y. Wang, Z. Song, H. Zhang and X. Wang, ACS Sustainable Chem. Eng., 2023, 11, 16479–16490 CrossRef CAS.
- M. Bae, Y. Kang, D. W. Lee, D. Jeon and J. Ryu, Adv. Energy Mater., 2022, 12, 2201452 CrossRef CAS.
- O. Winther-Jensen, K. Chatjaroenporn, B. Winther-Jensen and D. R. MacFarlane, Int. J. Hydrogen Energy, 2012, 37, 8185–8189 CrossRef CAS.
- X. Dai, W. Si, Y. Liu, W. Zhang and Z. Guo, ACS Appl. Mater. Interfaces, 2024, 16, 11984–11996 CrossRef CAS.
- J. Li, Y. Zhu, W. Chen, Z. Lu, J. Xu, A. Pei, Y. Peng, X. Zheng, Z. Zhang, S. Chu and Y. Cui, Joule, 2019, 3, 557–569 CrossRef CAS.
- C. Yu, M. Cao, Z. Dong, K. Li, C. Yu, J. Wang and L. Jiang, Adv. Funct. Mater., 2016, 26, 6830–6835 CrossRef CAS.
- J. Zhang, F. Dong, C. Wang, J. Wang, L. Jiang and C. Yu, ACS Appl. Mater. Interfaces, 2021, 13, 32435–32441 CrossRef CAS.
- Z. Long, Y. Zhao, C. Zhang, Y. Zhang, C. Yu, Y. Wu, J. Ma, M. Cao and L. Jiang, Adv. Mater., 2020, 32, 1908099 CrossRef CAS PubMed.
- S. Roy, U. Qamar, A. A. Sasikala Devi and S. Das, APL Energy, 2024, 2, 011504 CrossRef CAS.
- Y. Li, H. Zhang, N. Han, Y. Kuang, J. Liu, W. Liu, H. Duan and X. Sun, Nano Res., 2018, 12, 177–182 CrossRef.
- Z. Long, C. Yu, M. Cao, J. Ma and L. Jiang, Adv. Mater., 2024, 36, e2312179 CrossRef.
- P. Trogadas and M. O. Coppens, Chem. Soc. Rev., 2020, 49, 3107–3141 RSC.
- M. N. MacGregor-Ramiasa and K. Vasilev, Adv. Mater. Interfaces, 2017, 4, 1700381 CrossRef.
- C. Zhang, C. Teng, S. Guo, Y. Sun, C. Yu, X. Jin, K. Liu and L. Jiang, Nano Lett., 2024, 24, 1959–1966 CrossRef CAS.
- Y. Dong, H. Wang, X. Wang, H. Wang, Q. Dong, W. Wang, X. Wei, J. Ren, J. Liu and R. Wang, Chem. Eng. J., 2024, 488, 150953 CrossRef CAS.
- C. Zhang, Z. Xu, N. Han, Y. Tian, T. Kallio, C. Yu and L. Jiang, Sci. Adv., 2023, 9, eadd6978 CrossRef.
- S. Sheng, B. Shi, C. Wang, L. Luo, X. Lin, P. Li, F. Chen, Z. Shang, H. Meng, Y. Kuang, W. F. Lin and X. Sun, ACS Appl. Mater. Interfaces, 2020, 12, 23627–23634 CrossRef CAS.
- I. Morcos, J. Electroanal. Chem. Interfacial Electrochem., 1975, 62, 313–340 CrossRef CAS.
- H. Qiu, K. Obata, Z. Yuan, T. Nishimoto, Y. Lee, K. Nagato, I. Kinefuchi, J. Shiomi and K. Takanabe, Langmuir, 2023, 39, 4993–5001 CrossRef CAS PubMed.
- J. da Silva, E. Nobrega, F. Staciaki, F. R. Almeida, G. Wosiak, A. Gutierrez, O. Bruno, M. C. Lopes and E. Pereira, Chem. Eng. J., 2024, 494, 152943 CrossRef CAS.
- X. Lu, D. Yadav, B. Ma, L. Ma and D. Jing, J. Power Sources, 2024, 599, 234217 CrossRef CAS.
- A. F. M. Mahrous, I. M. Sakr, A. Balabel and K. Ibrahim, Int. J. Ther. Environ. Eng., 2010, 2, 113–116 CrossRef.
- S. J. Hendel and E. R. Young, J. Chem. Educ., 2016, 93, 1951–1956 CrossRef CAS.
- B. Bensmann and R. Hanke-Rauschenbach, ECS Trans., 2016, 75, 1065 CrossRef CAS.
- G. Schmidt, M. Suermann, B. Bensmann, R. Hanke-Rauschenbach and I. Neuweiler, J. Electrochem. Soc., 2020, 167, 114511 CrossRef CAS.
- D. Grondin, J. Deseure, P. Ozil, J. P. Chabriat, B. Grondin-Perez and A. Brisse, J. Power Sources, 2011, 196, 9561–9567 CrossRef CAS.
- J. K. Lee, C. H. Lee and A. Bazylak, J. Power Sources, 2019, 437, 226910 CrossRef CAS.
- J. K. Lee and A. Bazylak, J. Electrochem. Soc., 2020, 167, 013541 CrossRef.
- R. Ding, Y. Chen, Z. Rui, K. Hua, Y. Wu, X. Li, X. Duan, J. Li, X. Wang and J. Liu, J. Power Sources, 2023, 556, 232389 CrossRef CAS.
- X. Chen, A. Rex, J. Woelke, C. Eckert, B. Bensmann, R. Hanke-Rauschenbach and P. Geyer, Appl. Energy, 2024, 371, 123550 CrossRef CAS.
- S. Hu, B. Guo, S. Ding, F. Yang, J. Dang, B. Liu, J. Gu, J. Ma and M. Ouyang, Appl. Energy, 2022, 327, 120099 CrossRef CAS.
- D. S. Falcão and A. M. F. R. Pinto, J. Cleaner Prod., 2020, 261, 121184 CrossRef.
- C. Daoudi and T. Bounahmidi, Int. J. Hydrogen Energy, 2024, 49, 646–667 CrossRef CAS.
- S. K. Sarma, A. Singh, R. Mohan and A. Shukla, Int. J. Hydrogen Energy, 2023, 48, 17769–17782 CrossRef CAS.
- H. H. Girault, Analytical and physical electrochemistry, EPFL Press, 2004 Search PubMed.
- C. G. Zoski, Handbook of electrochemistry, Elsevier, 2006 Search PubMed.
- O. van der Heijden, S. Park, R. E. Vos, J. J. J. Eggebeen and M. T. M. Koper, ACS Energy Lett., 2024, 9, 1871–1879 CrossRef CAS PubMed.
- A. Taqieddin, R. Nazari, L. Rajic and A. Alshawabkeh, J. Electrochem. Soc., 2017, 164, E448–E459 CrossRef CAS.
- A. Taqieddin, M. R. Allshouse and A. N. Alshawabkeh, J. Electrochem. Soc., 2018, 165, E694–E711 CrossRef CAS PubMed.
- Z. Zhang, W. Liu and M. L. Free, J. Electrochem. Soc., 2019, 167, 013532 CrossRef.
- F. F. Rivera, T. Pérez, L. F. Castañeda and J. L. Nava, Chem. Eng. Sci., 2021, 239, 116622 CrossRef CAS.
- F. Khalighi, N. G. Deen, Y. Tang and A. W. Vreman, Chem. Eng. Sci., 2023, 267, 118280 CrossRef CAS.
- Z. Lu, L. Zhang, R. Iwata, E. N. Wang and J. C. Grossman, Langmuir, 2020, 36, 15112–15118 CrossRef CAS PubMed.
- N. Varallo, G. Besagni and R. Mereu, Chem. Eng. Sci., 2023, 280, 119090 CrossRef CAS.
- S. Subramaniam, Prog. Energy Combust. Sci., 2013, 39, 215–245 CrossRef.
- J. Schillings, O. Doche and J. Deseure, Int. J. Heat Mass Transfer, 2015, 85, 292–299 CrossRef CAS.
- D. Le Bideau, P. Mandin, M. Benbouzid, M. Kim, M. Sellier, F. Ganci and R. Inguanta, Energies, 2020, 13, 3394 CrossRef CAS.
- W. Yang, L. Sun, J. Tang, Z. Mo, H. Liu, M. Du and J. Bao, Ind. Eng. Chem. Res., 2022, 61, 8323–8332 CrossRef CAS.
- X. Pang, J. T. Davis, A. D. Harvey and D. V. Esposito, Energy Environ. Sci., 2020, 13, 3663–3678 RSC.
- T. L. Doan, H. E. Lee, S. S. H. Shah, M. Kim, C. H. Kim, H. S. Cho and T. Kim, Int. J. Energy Res., 2021, 45, 14207–14220 CrossRef CAS.
- Q. Chen, Y. Wang, F. Yang and H. Xu, Int. J. Hydrogen Energy, 2020, 45, 32984–32994 CrossRef CAS.
- J. A. Wrubel, Z. Kang, L. Witteman, F.-Y. Zhang, Z. Ma and G. Bender, Int. J. Hydrogen Energy, 2021, 46, 25341–25354 CrossRef CAS.
- C. C. Weber, T. Schuler, R. De Bruycker, L. Gubler, F. N. Büchi and S. De Angelis, J. Power Sources Adv., 2022, 15, 100095 CrossRef CAS.
- A. Nouri-Khorasani, E. Tabu Ojong, T. Smolinka and D. P. Wilkinson, Int. J. Hydrogen Energy, 2017, 42, 28665–28680 CrossRef CAS.
- Y. Li, Z. Kang, J. Mo, G. Yang, S. Yu, D. A. Talley, B. Han and F.-Y. Zhang, Int. J. Hydrogen Energy, 2018, 43, 11223–11233 Search PubMed.
- M. Maier, K. Smith, J. Dodwell, G. Hinds, P. R. Shearing and D. J. L. Brett, Int. J. Hydrogen Energy, 2022, 47, 30–56 CrossRef CAS.
- J. Nie and Y. Chen, Int. J. Hydrogen Energy, 2010, 35, 3183–3197 CrossRef CAS.
- J. Zheng, Z. Kang, B. Han and J. Mo, Materials, 2023, 16, 1310 CrossRef CAS PubMed.
- A. Ni, M. Upadhyay, S. S. Kumar, H. Uwitonze and H. Lim, Int. J. Hydrogen Energy, 2023, 48, 16176–16183 CrossRef CAS.
- W. Wang, B. Han, B. Cao and J. Mo, Int. J. Hydrogen Energy, 2023, 48, 36240–36253 CrossRef CAS.
- M. Zhang, L. Gao, L. Yang, G. Shan, Y. Wang, X. Huo, W. Li and J. Zhang, Fuel, 2024, 367, 131418 CrossRef CAS.
- P. Dyson, R. Ransing, P. H. Williams and R. Williams, Fluid properties at nano/meso scale: a numerical treatment, John Wiley & Sons, 2008 Search PubMed.
- L. Chen, A. He, J. Zhao, Q. Kang, Z.-Y. Li, J. Carmeliet, N. Shikazono and W.-Q. Tao, Prog. Energy Combust. Sci., 2022, 88, 100968 CrossRef.
- L. Chen, R. Zhang, Q. Kang and W.-Q. Tao, Chem. Eng. J., 2020, 391, 123590 CrossRef CAS.
- M. El Hannach, M. Prat and J. Pauchet, Int. J. Hydrogen Energy, 2012, 37, 18996–19006 CrossRef CAS.
- L. Chen, Q. Kang and W. Tao, Int. J. Hydrogen Energy, 2021, 46, 13283–13297 CrossRef CAS.
- M. Shahraeeni and M. Hoorfar, Int. J. Hydrogen Energy, 2014, 39, 10697–10709 CrossRef CAS.
- H. Nakajima, S. Iwasaki and T. Kitahara, J. Power Sources, 2023, 560, 232677 CrossRef CAS.
- T. Seip, N. Shaigan, M. Dinu, K. Fatih and A. Bazylak, J. Power Sources, 2023, 559, 232654 CrossRef CAS.
- B. Tjaden, S. J. Cooper, D. J. L. Brett, D. Kramer and P. R. Shearing, Curr. Opin. Chem. Eng., 2016, 12, 44–51 CrossRef.
- M. Ebner and V. Wood, J. Electrochem. Soc., 2015, 162, A3064–A3070 CrossRef CAS.
- B. Tjaden, D. J. L. Brett and P. R. Shearing, Int. Mater. Rev., 2016, 63, 47–67 CrossRef.
- G. Li, M. Xu, Y. Qin, Y. Zhang, Y. Wang, X. Yu and J. Li, Fuel, 2024, 368, 131444 CrossRef CAS.
- M. F. Kaya and N. Demir, Fuel Cells, 2017, 17, 37–47 CrossRef CAS.
- M. T. de Groot, J. Kraakman and R. L. Garcia Barros, Int. J. Hydrogen Energy, 2022, 47, 34773–34783 CrossRef CAS.
- M. Chandesris, V. Médeau, N. Guillet, S. Chelghoum, D. Thoby and F. Fouda-Onana, Int. J. Hydrogen Energy, 2015, 40, 1353–1366 CrossRef CAS.
- B. Han, S. M. Steen, J. Mo and F.-Y. Zhang, Int. J. Hydrogen Energy, 2015, 40, 7006–7016 CrossRef CAS.
- V. Liso, G. Savoia, S. S. Araya, G. Cinti and S. K. Kær, Energies, 2018, 11, 3273 CrossRef CAS.
- X. Qian, K. Kim and S. Jung, Energy Convers. Manage., 2022, 268, 116070 CrossRef CAS.
- Y. Jiang, Y. Li, Y. Ding, S. Hu, J. Dang, F. Yang and M. Ouyang, J. Power Sources, 2023, 553, 232303 CrossRef CAS.
- D. Huang, Z. Zhong, X. Ai, K. Hu, B. Xiong, Q. Wen, J. Fang and S. Cheng, Energy Convers. Manage., 2024, 300, 117955 CrossRef CAS.
- M. Espinosa-López, C. Darras, P. Poggi, R. Glises, P. Baucour, A. Rakotondrainibe, S. Besse and P. Serre-Combe, Renewable Energy, 2018, 119, 160–173 CrossRef.
- Z. Ren, J. Wang, Z. Yu, C. Zhang, S. Gao and P. Wang, J. Power Sources, 2022, 544, 231886 CrossRef CAS.
- A. Rajora and J. W. Haverkort, J. Power Sources, 2022, 260, 117823 CAS.
- X. Guo, H. Zhu and S. Zhang, Int. J. Hydrogen Energy, 2024, 49, 1048–1059 CrossRef.
- M. G. Rasul, M. A. Hazrat, M. A. Sattar, M. I. Jahirul and M. J. Shearer, Energy Convers. Manage., 2022, 272, 116326 CrossRef CAS.
- D. Tonelli, L. Rosa, P. Gabrielli, K. Caldeira, A. Parente and F. Contino, Nat. Commun., 2023, 14, 5532 CrossRef CAS PubMed.
- S. Krishnan, V. Koning, M. Theodorus de Groot, A. de Groot, P. G. Mendoza, M. Junginger and G. J. Kramer, Int. J. Hydrogen Energy, 2023, 48, 32313–32330 CrossRef CAS.
- R. J. Ouimet, J. R. Glenn, D. De Porcellinis, A. R. Motz, M. Carmo and K. E. Ayers, ACS Catal., 2022, 12, 6159–6171 CrossRef CAS.
- M. Clapp, C. M. Zalitis and M. Ryan, Catal. Today, 2023, 420, 114140 CrossRef CAS.
- IRENA, World Energy Transitions Outlook 2022: 1.5 °C Pathway, International Renewable Energy Agency, Abu Dhabi, 2022 Search PubMed.
- X. Fu, R. Shi, S. Jiao, M. Li and Q. Li, J. Energy Chem., 2022, 70, 129–153 CrossRef CAS.
- E. Urbano, E. Pahon, N. Yousfi-Steiner and M. Guillou, J. Power Sources, 2024, 623, 235451 CrossRef CAS.
- E. Kuhnert, V. Hacker, M. Bodner and P. Subramanian, Int. J. Energy Res., 2023, 2023, 1–23 CrossRef.
- F. N. Khatib, T. Wilberforce, O. Ijaodola, E. Ogungbemi, Z. El-Hassan, A. Durrant, J. Thompson and A. G. Olabi, Renewable Sustainable Energy Rev., 2019, 111, 1–14 CrossRef CAS.
- F. Meharban, C. Lin, X. Wu, L. Tan, H. Wang, W. Hu, D. Zhou, X. Li and W. Luo, Adv. Energy Mater., 2024, 2402886 CrossRef CAS.
- M. Möckl, M. F. Ernst, M. Kornherr, F. Allebrod, M. Bernt, J. Byrknes, C. Eickes, C. Gebauer, A. Moskovtseva and H. A. Gasteiger, J. Electrochem. Soc., 2022, 169, 064505 CrossRef.
- L. Messing, K. Pellumbi, L. Hoof, N. Imming, S. Wilbers, L. Kopietz, M. Joemann, A. Grevé, K. Junge Puring and U. P. Apfel, Adv. Energy Mater., 2024, 2402308 CrossRef CAS.
- R. A. Marquez, M. Espinosa, E. Kalokowski, Y. J. Son, K. Kawashima, T. V. Le, C. E. Chukwuneke and C. B. Mullins, ACS Energy Lett., 2024, 9, 547–555 CrossRef CAS.
- J. C. Ehlers, A. A. Feidenhans’l, K. T. Therkildsen and G. O. Larrazábal, ACS Energy Lett., 2023, 8, 1502–1509 CrossRef CAS.
- Y. Devi, P. J. Huang, W. T. Chen, R. H. Jhang and C. H. Chen, ACS Appl. Energy Mater., 2023, 15, 9231–9239 CrossRef CAS.
- H. Becker, J. Murawski, D. V. Shinde, I. E. L. Stephens, G. Hinds and G. Smith, Sustainable Energy Fuels, 2023, 7, 1565–1603 RSC.
- M. Demnitz, Y. M. Lamas, R. L. Garcia Barros, A. de Leeuw den Bouter, J. van der Schaaf and M. Theodorus de Groot, iScience, 2024, 27, 108695 CrossRef CAS PubMed.
- L. Liu, H. Ma, M. Khan and B. S. Hsiao, Membranes, 2024, 14, 85 CrossRef CAS PubMed.
- Z. Tang, B. Wu, K. Yan, J. Luo, M. U. Haq and L. Zeng, Future Batteries, 2025, 5, 100024 CrossRef.
- U. K. Ghorui, G. Sivaguru, U. B. Teja, A. M, S. Ramakrishna, S. Ghosh, G. K. Dalapati and S. Chakrabortty, ACS Appl. Energy Mater., 2024, 7, 7649–7676 CrossRef CAS.
- G. A. Jones and K. J. Warner, Energy Policy, 2016, 93, 206–212 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ee05559d |
| This journal is © The Royal Society of Chemistry 2025 |
