 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The nature of nanoclusters in aqueous zinc sulfate electrolytes†
Emma N.
Antonio‡
 *ab,
Luis
Kitsu Iglesias‡
*ab,
Luis
Kitsu Iglesias‡
 cd,
Thomas P.
Chaney
cd,
Thomas P.
Chaney
 a,
Yinke
Jiang
e,
Mrinal K.
Bera
f,
Julian
Mars
c,
Kee Sung
Han
a,
Yinke
Jiang
e,
Mrinal K.
Bera
f,
Julian
Mars
c,
Kee Sung
Han
 g,
Nathan T.
Hahn
g,
Nathan T.
Hahn
 h,
Sanja
Tepavcevic
h,
Sanja
Tepavcevic
 i,
Edward
Maginn
i,
Edward
Maginn
 e,
Yong
Zhang
e,
Yong
Zhang
 e and
Michael F.
Toney
e and
Michael F.
Toney
 *acj
*acj
aMaterials Science and Engineering, University of Colorado at Boulder, Boulder, CO 80303, USA. E-mail: Michael.Toney@colorado.edu; emma.antonio12@imperial.ac.uk
bDepartment of Chemical Engineering, Imperial College London, London, SW7 2AZ, UK
cDepartment of Chemical and Biological Engineering, University of Colorado Boulder, Boulder, CO 80303, USA
dElectrochemical Energy Systems Laboratory, Department of Mechanical and Process Engineering, ETH Zurich, 8092 Zurich, Switzerland
eDepartment of Chemical and Biomolecular Engineering, University of Notre Dame, Notre Dame, Indiana 46556, USA
fNSF's ChemMatCARS, Pritzker School of Molecular Engineering, University of Chicago, Chicago, Illinois 60637, USA
gJoint Center for Energy Storage Research, Pacific Northwest National Laboratory, Richland, WA 99354, USA
hMaterial, Physical and Chemical Sciences Center, Sandia National Laboratories, Albuquerque, NM 87185, USA
iMaterials Science Division, Argonne National Laboratory, Lemont, Illinois 60439, USA
jRenewable and Sustainable Energy Institute (RASEI), University of Colorado at Boulder, Boulder, CO 80303, USA
First published on 30th June 2025
Abstract
The presence of ion nanoclusters or aggregates in electrolytes strongly impacts the electrolyte physical and chemical properties. Herein, we investigate the nature of ion nanoclusters in aqueous zinc sulfate electrolytes for zinc-ion batteries, specifically their size distribution, composition and lifetime, and subsequent influence on transport properties. Using a combination of X-ray scattering, molecular dynamics (MD) simulations and forward scattering calculations, we reveal the presence of free ions and a distribution of nanoclusters composed of solvent-separated ion pairs, whose size distributions are concentration-independent. Transient interactions between sulfate ions and long-lived hydrated zinc ions produce nanoclusters with varying sizes, compositions and geometries. Pair distribution functions calculated from MD simulations show strong agreement with experimental X-ray total scattering measurements. Nanoclusters were identified from MD simulations and used to forward simulate small-angle X-ray scattering (SAXS) of these nanoclusters. By fitting our measured SAXS using these forward simulations, we determine the distribution of nanocluster sizes in the electrolyte. Transport calculations from MD simulations and experimental measurements show that while nanoclusters hinder ion transport, their short-lived and dynamic nature enables efficient ion diffusion. Determining the nature of these nanoclusters is essential for understanding their impact on transport, solvation, and interfacial chemistry, and guiding the rational design of electrolytes for energy storage, chemical separations and environmental science.
Broader contextElectrolytes are essential to batteries, fuel cells, electrochemical separations, and environmental remediation technologies, where their solvation structure and nanoscale organization dictate key properties such as ion mobility and interfacial reactivity. While traditional models describe electrolytes as collections of free ions or simple ion pairs, recent studies suggest the presence of nanoclusters—ion aggregates that play a significant role in electrolyte behavior. Understanding these structures is critical for designing next-generation electrolytes with enhanced performance across energy and environmental remediation. In this work, we investigate nanocluster formation in aqueous ZnSO4 electrolytes, which are relevant for aqueous zinc batteries, a sustainable, low-cost, and safe alternative to lithium-ion batteries. Using a new multi-modal approach that integrates X-ray scattering, molecular dynamics simulations, forward scattering calculations, and transport measurements, we provide a quantitative understanding of nanocluster size, composition, and structure and their influence on ion transport. Our findings reveal a highly polydisperse system of nanoclusters with diverse sizes, compositions, and structures, introducing short-range correlations that reduce ionic conductivity. Yet, their transient and dynamic nature enables continuous reorganization, enabling facile transport. These insights introduce a new framework for electrolyte design, offering a pathway to improved energy storage systems and electrochemical technologies critical for clean energy and sustainability. |
Introduction
Electrolytes play a crucial role in energy storage, catalysis, separation, and environmental remediation, influencing properties such as ionic transport and interfacial reactions. The design of electrolytes with specific properties is vital for numerous applications, including electrochemical energy storage in batteries,1–4 water treatment,5,6 electrocatalysis,7,8 electroplating,9,10 and extraction processes, such as electrowinning/electroextraction.11,12 The intricate balance between solute–solute and solvent–solute interactions—including electrostatic, hydrogen bonding and solvophobic interactions as well as steric exclusion—dictates much of the properties of electrolytes. Our ability to design better electrolytes relies on a deeper understanding of these interactions. Electrolyte properties have been related to thermodynamic principles using activities as well as nanoscale interactions using ion pairing models.13 Ion pairs, including solvent-separated ion pairs (SSIPs) and contact ion pairs (CIPs), are based on electrostatic interactions, in contrast to complexes which form via covalent interactions. Ion pair formation is proposed to depend on the nature of the electrolyte, the charge of ionic species, the salt concentration, the dielectric constant, chelating properties of the solvent, and the temperature.14 Recently, larger ion aggregates with sizes greater than 1 nm were predicted in some electrolytes.1,14 Despite advances in simulations and experimental techniques, a detailed understanding of the solution structures resulting from ion interactions, as well as their effect on electrolyte properties, such as transport and stability, remains elusive.Metal sulfate electrolytes are crucial in a range of fields, including energy storage, electroplating, and water treatment. Here we focus on the local solvation in aqueous ZnSO4 electrolytes, which are a low cost and safe option for zinc-based batteries with zinc metal anodes.15,16 Zinc-ion batteries have high volumetric capacity (5851 mAh cm−3), low redox potential (−0.76 V vs. SHE) and use widely available materials, making them attractive for grid-scale energy storage.17–19 Understanding nanoclusters in battery electrolytes is important due to their proposed effect on electronic properties, and thus redox properties; transport (deviations from transport predictions due to strong ionic correlations); and/or surface interactions including the electrical double layer, desolvation processes and interfacial reactions.1,14 These phenomena are particularly relevant for multivalent-ion-based electrolytes, including other battery chemistries such as calcium and magnesium.20–22
Gaining a comprehensive understanding of ion pairs and nanoclusters is challenging due to limitations in experimental and computational techniques. Experimental methods that probe ion pairs and nm-scale structures and chemistries include total scattering (or X-ray pair distribution function (XPDF)), Fourier-transform infrared spectroscopy (FTIR), Raman spectroscopy, X-ray absorption spectroscopy (XAS), nuclear magnetic resonance (NMR), and dielectric relaxation spectroscopy (DRS). Small-angle neutron and X-ray scattering (SANS/SAXS) probe more extended >1 nm sizes. Computational studies, mainly based on molecular dynamics (MD) simulations and density functional theory (DFT), have provided structural information and insight into the driving forces for cluster and ion pair formation. While the limitations of each of these methods are outside the scope of this work; here we only note that the time scales probed will impact the results.
Nanometric clusters in aqueous ZnSO4 have been hypothesized based on self-diffusion and conductance measurements showing positive cation–cation and anion–anion correlations, even at low concentrations (0.05 M).23 More recently, an experimental study using DRS revealed the presence of CIPs and SSIP,24 with both free ions and ion pairs being strongly hydrated (>1 hydration shells).24 The mean activity coefficient of 1 M ZnSO4 was reported to be 0.042 (where the mean activity coefficient for each component in an ideal solution = 1), demonstrating deviations from ideal solution behavior, due to significant molecular interactions.25 There are several studies suggesting the presence of nanometric clusters for sulfate anions and other divalent metals including magnesium26–30 and calcium.31 However, further studies are required to understand the extent of nanocluster formation, the nature of nanoclusters (including their composition, size, polydispersity, charge, geometry and lifetimes) and their impact on ion transport within these electrolytes.
In this study, as summarized in Fig. 1, we synergistically integrate experimental measurements with computational modeling to unravel the nature of nanoclusters in aqueous ZnSO4 electrolytes. Utilizing SAXS and XPDF analyses alongside MD calculations and forward scattering simulations, we achieve detailed characterization of the size, structure, composition, and distribution of nanoclusters. We then determine the transport from MD and compare it to diffusivity and conductivity measurements, using pulse-field gradient nuclear magnetic resonance spectroscopy (PFG-NMR) and electrochemical impedance spectroscopy (EIS), respectively. We relate the transport measurements to the cluster size distributions determined by X-ray scattering techniques. Our findings reveal a highly polydisperse system of transient nanoclusters composed of hydrated zinc ions and sulfate ions that reduces the ionic conductivity. This combined approach provides a novel method of interrogating electrolyte properties and yields valuable insights for the rational design of electrolytes for sustainable energy storage and other complex liquid systems.
Results & discussion
Characterizing nanoclusters composed of Zn(H2O)6 and SO4
The presence of nanoclusters in aqueous ZnSO4 electrolytes was measured using SAXS, as shown in Fig. 2a by the shoulder position (gray arrow), which approximately corresponds to electron density variations (nanoclusters in this work) with a size of π/qshoulder where qshoulder is the scattering vector value at the shoulder. Historically these data are fitted to an analytical model to obtain a single size or size distribution based on a series of assumptions such as the shape (form factor). The similarity in shoulder position between the concentrations measured (0.1–1 M) indicates that the average sizes of the nanoclusters are unchanged by concentration. Qualitatively, these measurements are consistent with previous SAXS measurements of calcium sulfate salts (0.05–0.15 M) which revealed clusters of a similar size.31,32 To understand these clusters, Benning and coworkers fit these data to an analytical expression for a cylindrical form factor,31 and later a surface fractal structure factor and a shape-independent Guiner approximation to capture the radius of gyration for primary cylindrical particles.32 However, more advanced and nuanced approaches are needed to accurately interpret cluster size distributions and relate them to specific chemistry and local structure (e.g., solvation shells, ion pairs) and the resulting electrolyte properties. Furthermore, for a wide range of electrolytes, a distribution of cluster sizes and cluster net charges is expected; for example, DFT calculations of MgSO4 predict the formation of a variety of linear clusters, or ‘contact ion chains’, containing up to 8 ions.33Herein, we use the term nanocluster to describe the measured microheterogeneities in electron density observed by SAXS. These microheterogeneities represent deviations from ideal solution behavior and have historically been referred to as ‘ion pairing’. These microheterogeneities encompass various forms of ion associations, including SSIPs, where cations and anions are connected by solvent molecules; CIPs, where cations and anions are directly connected without intervening solvent; and larger ion clusters (also referred to as nanometric aggregates) that form more complicated structures involving cations, anions, and solvent molecules. As discussed below, we find clusters to be composed of sulfate ions (SO42−) and zinc ions hydrated by 6 water molecules (Zn(H2O)6); a coordination number of six is widely accepted in the literature.26,34–38 For clarity, here we define nanocluster ‘size’ as the ion count which is the number of ions within a nanocluster (as opposed to dimension which is dependent on the geometry) with the expression (Zn(H2O)6)x(SO4)y used to describe a cluster containing x hydrated zinc units and y sulfate ions (cluster size = x + y ions). For simplicity, we do not include sulfate's flexible hydration shell.39–46
To understand the local structure of these nanoclusters, we performed XPDF and MD simulations, obtaining the reduced pair distribution function, G(r), which are shown in Fig. 2b and c. We observe good agreement between the experimental G(r) with MD simulations, shown in Fig. 2b for 0.5 M ZnSO4, where the MD simulations capture the main peak positions and relative intensities found in the measurement, validating the short-range correlations from the MD model. Slight differences in the relative intensities and peak positions may be attributed to the MD force field not perfectly representing the interatomic potentials and/or experimental error for intensities. A clearer understanding of the local structural changes with concentration can be obtained from the differential pair distribution function (dG(r)), shown in Fig. 2d, where the G(r) of a lower concentration solution is subtracted from a higher concentration ZnSO4 solution. The dG(r) highlights changes in the local structure with increasing concentration and is valuable for assessing local cluster structure. Fig. 2d shows good agreement between the differential XPDF for the experimental measurements and MD simulations for 0.5–0.1 M. Correlations identified by the MD simulations are given in more detail in Table S1.†
As expected, the correlations associated with sulfate ion and hydrated zinc increase with increased salt concentration (Fig. 2c and d); specifically the intensity of the correlations associated with the sulfur–oxygen bond within the sulfate ion at approximately 1.54 Å (S–O(SO4)) and zinc–oxygen interaction at 2.1 Å (Zn–O(H2O)), where the subscript refers to the molecule/ion where the element is located. The Zn–O(H2O) correlation distance (position) does not change with increasing salt concentration (Fig. 2c); six water molecules were found in the first solvation shell by MD at all concentrations (0.1–1 M) consistent with the literature where zinc is widely accepted to have six water molecules tightly bound in its first solvation shell in an octahedral geometry.26,34–38 With increasing concentration, the peak at 2.8 Å, related to the hydrogen bonding network in pure water (O–O bond), decreases (Fig. 2c).47 Based on MD simulations, the broad but well-defined peak between 4 and 5 Å (Fig. 2b and c) is due to the second solvation shell of Zn2+ cations which has contributions from both H2O and SO42− anions. In Fig. 2d, the dG(r) shows peaks around 4.2, 5 (black arrow) and 5.8 Å. Using the MD to understand these data, we find that the peak at 4.2 Å primarily arises from correlations between oxygen atoms of water molecules solvating Zn2+ (O(H2O)–Zn–O(H2O)). The correlations around 4.2 and 5.0 Å are attributed to Zn–SO4 solvent-separated ion pairs, both as isolated pairs and within larger nanoclusters. The broad correlations around 5.8 Å and subtle correlations above 7 Å are attributed to the ordering of water, perhaps enhanced by the polarizing nature of zinc (Fig. S1 and S2†).36,38 Although Zn–SO4, Zn–water, and SO4–water correlations extend to distances beyond ∼5.5 Å, these nanocluster correlations are relatively weak; MD simulations show that for distances above ∼5.5 Å the G(r) is dominated by water–water interactions (Fig. S1†). Aside from a larger mean S–O bond distance measured by XPDF compared to the MD (Fig. 2b and d), we observed excellent agreement between MD and experiment. Comparison to the SAXS data, which is unchanged with concentration, suggests that more nanoclusters form as opposed to larger nanoclusters at higher concentrations.
The agreement between experimental and simulated G(r) and dG(r) demonstrates that the MD simulations effectively capture the short-range (here up to ∼8 Å) structural features of (Zn(H2O)6)x(SO4)y nanoclusters and water ordering. As seen in Fig. 2, above 8 Å there are no observable correlations in G(r). Building on this very good agreement between the simulations and measurements, we employ this understanding to investigate the longer-range correlations (above 8 Å) probed by SAXS and gain insights that were previously inaccessible.
Nanocluster composition from molecular dynamics
As the short-range correlations measured by XPDF and calculated using MD show good agreement, we can use the MD to quantitatively investigate the composition and size distribution of these nanoclusters. Some examples of 2–4 ion clusters present in the MD simulations are shown in Fig. 3a–c. These clusters were identified using our algorithm which statistically analyzes the MD simulations (explained below in detail). Despite variations in their spatial arrangements and sizes, these clusters share common structural features: the formation of solvent-separated ion pairs (SSIPs), where the hydrogens in the water molecules within the zinc solvation shell interact with oxygen on the sulfate, as shown by the dashed lines in Fig. 3a–c. | ||
| Fig. 3 Schematic showing a few examples of (a) 2-ion Zn(H2O)6SO4, (b) 3-ion (Zn(H2O)6)2SO4, (c) 4-ion (Zn(H2O)6)2(SO4)2 clusters. Dark gray spheres represent zinc ions, orange spheres represent sulfur ions, red spheres represent oxygen atoms, and light pink spheres represent hydrogen atoms. Dashed lines show interactions of oxygen on the sulfate with hydrogens in water molecules in the zinc solvation shell. (d) Statistical analysis of simulated clusters in 1 M ZnSO4 solution using our clustering algorithm based on distance thresholds. The x-axis is the cluster size (number of ions in each cluster) while the y-axis represents the normalized probability of finding a Zn or SO4 ions in each cluster size. This normalization is calculated by dividing the number of ions in clusters of a specific size by the total number of ions in all clusters, thereby reflecting the relative abundance of each cluster size. Gray, orange, and purple bars indicate the fraction of ions that belong to clusters rich in Zn2+, rich in SO42−, and charge-balanced, respectively. Another representation of these data is given in Fig. S9.† (e) Small-angle X-ray scattering data of 1 M ZnSO4 in water compared with the forward simulated SAXS profile calculated from the sum of all nanoclusters from the MD simulations (d) with a scaling factor accounted for the total number of scatters in the probed volume. This poor agreement motivated the method described below. | ||
To gain a quantitative understanding of ZnSO4 nanoclusters, we developed a clustering algorithm that identifies ion nanoclusters based only on distance thresholds within each MD snapshot. To ensure that our statistical analysis is representative, we analyzed 1400 snapshots over a 14 ns trajectory from the 1 M ZnSO4 MD simulation (each containing 70 Zn and 70 SO4 ions). The size distribution and composition of these nanoclusters determined by this algorithm are shown in Fig. 3d. The analysis reveals a highly polydisperse distribution of nanoclusters from isolated ions up to 22-ion nanoclusters. In Fig. 3d, the number fraction of ions with a particular cluster size (isolated ions are defined as cluster size of 1), with the ratio of ions that belong to Zn-rich, SO4-rich and balanced nanoclusters shown by the colors. The average charge per cluster size are shown in Fig. S8,† assuming a formal charge of +2e for the Zn and −2e for SO4 ions. There is a higher number of free Zn ions compared to SO4 ions (Fig. 3d). Even-numbered clusters generally exhibit a balanced ratio of Zn to SO4 ions, tending towards charge neutrality. Odd-numbered clusters and larger clusters tend to be SO4-rich with an increasingly average negative charge. Sulfate-rich nanoclusters are anticipated from the literature due to sulfate's flexible solvation shell and its ability to form clusters through different mechanisms, such as the equilibrium between bisulfate and sulfate.39–46
The clustering algorithm begins by selecting a zinc ion or the central sulfur atom of a sulfate ion as the starting point and identifying all neighboring zinc and sulfur within the specified distance thresholds (vide infra). These ions are grouped to form the initial cluster. For each ion added to the cluster, the algorithm searches for the newly added ion's neighbors within the distance threshold and incorporates these into the cluster. This process is repeated iteratively for each newly added ion, expanding the cluster to include all connected ions, and the algorithm terminates when no additional neighbors are within the distance thresholds. After defining the cluster with the zinc ions and sulfur atoms from SO42− ions, solvating water molecules surrounding the zinc ions and the oxygen atoms bonded to the sulfur atoms are incorporated into the cluster. The distance thresholds are Zn–S (6.4 Å), S–S (7.5 Å), Zn–Zn (6.6 Å), Zn–O(H2O) (3.1 Å) and S–O (1.51 Å) and were chosen as the first minimum between the first two peaks of their partial pair distribution functions of the MD simulations (Fig. S3–S7†).48 The use of the first solvation shell as the distance threshold is rooted in capturing the most significant and relevant atomic correlations without overestimating cluster connectivity, which might lead to unrealistic cluster sizes. Importantly, variations (±0.3 Å) in these thresholds do not significantly affect the results, demonstrating the robustness of the algorithm. Note that for Zn–S the first peak (CIPs) is not used for distance threshold as the coordination number (0.01) is very small, indicative of negligible CIPs. Using the first solvation shell as the distance threshold ensures that all correlations within the range of significant atomic proximity are included, even those that are transient or less enthalpically favorable. We note this algorithm includes transient clusters formed either through electrostatic or stochastic fluctuations. Despite repulsive forces, the probability of finding a zinc-to-zinc or sulfate-to-sulfate correlation within the defined distance threshold is non-zero, highlighting the role of entropy in forming short-lived ion clusters.
While our work concludes that the majority of ions are in clusters, previous studies using DRS found the majority of ions were free; a comparison is provided in Table S2.† Interestingly, these authors also reported CIPs, however, they stated that the CIP fraction was an unresolved mixture of CIPs and dynamically-retarded (‘slow’) water.24 The difference between our conclusions and those of the DRS likely arise because of differences in time scales probed. Dielectric spectroscopy probes ion dynamics in the 0.1–100 GHz regime, corresponding to ∼10 ps to 10 ns timescales, while SAXS and XPDF probes near-instantaneous (fs) structure, time- and space-averaged over the measurement time and probed volume. The nanoclusters observed with SAXS and characterized in our MD simulations have lifetimes much shorter than ns, therefore DRS is insensitive to the nanoclusters described here. Furthermore, even if these nanoclusters are long-lived, they could rotate too slowly and/or have a net dipole that is too small to be detected by DRS.
Forward-simulating SAXS from clusters identified in MD
Compared with methods to interpret SAXS data that rely on simple form factor models (shapes), here we used the atomic positions within the nanoclusters identified from the MD simulations to forward simulate the SAXS data. Initially we forward simulated the SAXS profiles for isolated ions and each nanocluster identified in the MD simulations (Fig. S10†). We then compared the sum of the SAXS profiles calculated for all ions/clusters in the MD simulations with the experimental data, however we did not obtain a good agreement as shown in Fig. 3e. The MD-derived nanocluster size distribution overestimated the cluster sizes resulting in a shoulder at lower q values in the SAXS profiles (Fig. 3e). Possible causes for this discrepancy are the accuracy of the force field used in the MD simulations or limitations in the nanoclustering algorithm.As the experimental XPDF results (Fig. 2) align well with the MD results, we are confident of the reliability of the nanocluster's short-range structure. Therefore, the MD nanocluster configurations provide an exciting opportunity to interpret the SAXS data without the need of a model requiring assumptions regarding the shape, polydispersity or atomic positions of atoms within nanoclusters. To better understand how clusters of each size contribute to the SAXS data, we created average scattering curves for nanoclusters of the same ion count. We note that a wide range of nanocluster sizes are present, which could be defined by a variety of parameters such as correlation length, volume, geometry or radius of gyration; therefore, we define nanoclusters by their ion count for simplicity. Note, we report the size range (electron weighted radius of gyration) for different cluster ion counts based on the atomic positions determined by the MD in Table S3.†
Here we first forward-simulate the SAXS for each unique nanocluster configuration obtained from the MD simulation from the nanocluster's specific arrangement of atoms. Then, these individual SAXS profiles were averaged for nanoclusters with the same ion count to generate an ensemble SAXS pattern for that ion count (Fig. S10†). Examples of the calculated SAXS profiles are given in Fig. 4, where the intensity of these simulations has been scaled to the experimental SAXS data. This qualitative analysis reveals that smaller nanoclusters, specifically those with three ions, model the high-q region (corresponding to small cluster sizes) reasonably well but inadequately model the low-q region (corresponding to larger cluster sizes) of the experimental SAXS profile. Similarly, larger nanoclusters agree with the low-q region but do not adequately represent the high-q region. Nanoclusters containing four ions exhibit excellent agreement with the experimental data across a broader q range, with some deviation at higher q. Whilst nanoclusters with an ion count of 4 can adequately fit the experimental data, this overlooks the broader complexity inherent in the system. This simplification can lead to incomplete conclusions about the nature of the interactions and structures present, which in turn can inhibit our ability to understand and thus predict behavior.
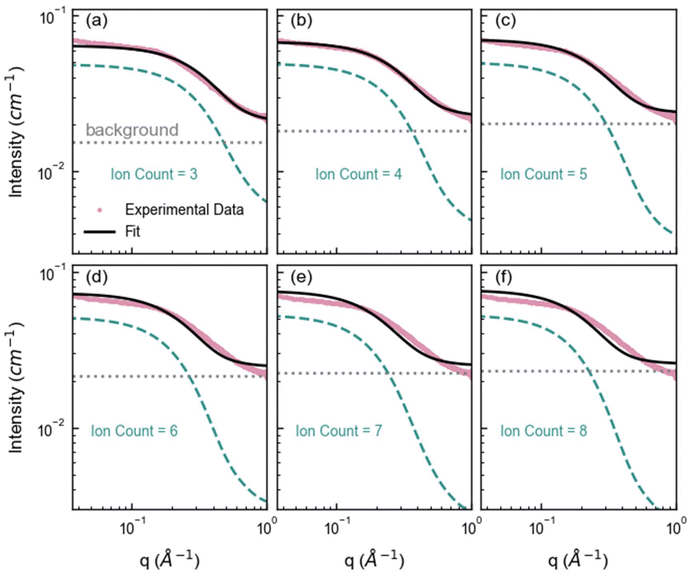 | ||
| Fig. 4 Average SAXS forward simulations from the SAXS profiles of each cluster configuration identified in the MD containing (a) 3, (b) 4, (c) 5, (d) 6, (e) 7, and (f) 8 ions. The pink markers represent the experimental SAXS profile for 1 M ZnSO4 solution, the green dashed line represents the forward simulated average SAXS profile for each cluster ion count, the gray dotted line represents the fitted constant background and the black line represents the overall fit (cluster + background). Note that small clusters, such as clusters with ion count of 3 fit the high q region well, and larger clusters with ion count more or equal to 5 fit the low q region well, highlighting that a distribution of cluster sizes is necessary to capture the experimental data. (As q is roughly inversely proportional to the cluster size, the low and high q region correspond to large and small clusters respectively.) The radius of gyration for each cluster ion count as well as the standard deviation is given in Table S3.† | ||
To best relate the experimental SAXS to the cluster size distribution, we fitted the experimental data using a weighted sum of these average SAXS profiles for each cluster size (Fig. S10†). In SAXS, the intensity of a scattering curve is proportional to the number density of scatterers. Thus, the fitted weight of each SAXS profile is proportional to the number density of nanoclusters of the corresponding size within the experimental ZnSO4 solution. At first, the distribution of weights was constrained in the fit to a predetermined Schulz-Zimm distribution (Fig. S11†). However, a variety of nanocluster distributions may result in good fits. To better explore the parameter space and account for many possible fits, we employed a Monte Carlo Markov Chain (MCMC) method implemented via the Differential Evolution Adaptive Metropolis (DREAM) algorithm. This MCMC method enabled us to sample from a variety of cluster size distributions that may fit the experimental SAXS data.49,50 In this MCMC method, the weight of each cluster size's average scattering profile was allowed to independently vary, and the MD-derived cluster size distribution served as an initial distribution of weights to initialize each Markov chain. This approach produced a well-converged posterior distribution with excellent agreement with the experimental SAXS data, as shown in Fig. 5a. Note that the MCMC forward simulation was done with 120 MD snapshots rather than with 1400 snapshots for efficiency. However, the distribution of the 120 snapshots is representative of the 1400 snapshots (Fig. S12†).
 | ||
Fig. 5 (a) Small angle X-ray scattering data of 1 M ZnSO4 in water (shown in pink), overlaid with the fitted SAXS profile (black line). The fit was generated through a weighted sum of averaged simulated SAXS curves for each cluster size. Weights were fitted using a Monte Carlo Markov-chain algorithm (25 chains, 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps). (b) Comparison of the cluster size distribution (number of zinc and sulfate ions in each cluster) obtained from MD simulations and most probable cluster size distribution from fitting the SAXS data using the Monte Carlo Markov-chain algorithm. The shaded region indicates the range of the posterior distribution of probable fits. Here, we do not show clusters with ion counts above 10; the full distribution is shown in Fig. S13.† 000 steps). (b) Comparison of the cluster size distribution (number of zinc and sulfate ions in each cluster) obtained from MD simulations and most probable cluster size distribution from fitting the SAXS data using the Monte Carlo Markov-chain algorithm. The shaded region indicates the range of the posterior distribution of probable fits. Here, we do not show clusters with ion counts above 10; the full distribution is shown in Fig. S13.† | ||
As seen in Fig. 5 and Fig. S11,† we consistently observed a wide distribution of nanoclusters and the absence of large nanoclusters (>10-ion clusters), irrespective of the approach used to fit the SAXS data. In Fig. S11,† we explored different fitting methods, including Levenberg-Marquardt optimization with weights derived from a Schulz-Zimm distribution model,51–53 and a direct fitting approach based on a modified MD cluster size distribution. While these approaches provided excellent fits, the MCMC method demonstrated greater flexibility by accounting for a broader range of possibilities, offering a statistically robust distribution of solutions. Based on this, we consider the MCMC method implemented through DREAM to be a reliable approach for exploring potential fits to SAXS data that may not be uniquely described by a single model such as directly using the MD or a Schulz-Zimm distribution. We encourage the independent validation of our methodology on other systems.
The shaded region in Fig. 5b indicates the posterior distribution of probable fits, illustrating that multiple ion cluster distributions can adequately fit the SAXS data, especially for nanoclusters smaller than 6 ions where the possibilities/error bars are relatively wide. Despite variations between the MD and the resulting distribution of fitted weights from the DREAM analysis (Fig. 5b and Fig. S13†), the distribution determined by MD generally falls within the posterior distribution for nanocluster sizes up to 6 (Fig. 5b). While MD simulations predict the presence of large nanoclusters, the experimental SAXS data (low q region) show that these nanoclusters are unlikely to form in significant quantities, shown in Fig. 5b. Meanwhile, nanoclusters with ion counts of 3 and 4 are the most common nanocluster size, as evidenced by their larger probabilities in the posterior distribution (Fig. 5b), suggesting that these configurations may be energetically favorable. Further investigation into the thermodynamics of nanocluster formation is needed to fully understand the preferential formation of certain nanocluster sizes.
In addition, we forward-simulated the G(r) for both the MCMC and MD cluster size distributions. As shown in Fig. S14,†G(r) is not sensitive to differences in these two different cluster size distributions. This insensitivity explains why determining cluster size distributions solely based on MD and experimental G(r) is challenging. The variety of size distributions that adequately fit the experimental data highlights the inherent complexity in modeling solutions with polydisperse nanoclusters—dynamic arrangements exhibiting a wide range of sizes, geometries, and compositions. This polydispersity arises from thermodynamic and kinetic factors driving the formation of diverse nanocluster populations, emphasizing the inadequacy of simplistic models that assume uniformity in nanocluster characteristics. Importantly, based in the MD these nanoclusters are short-lived, existing transiently on ∼picosecond timescales, further underscoring the dynamic nature of these systems.
(Zn(H2O)6)x(SO4)y ion clusters modify the transport properties
Nanoclusters have a direct effect on the liquid's properties, especially ionic conductivity.1 In a previous study, we found that local ion pair interactions in ionic systems can be quantitatively correlated to macroscopic properties such as ionic conductivity and self-diffusion coefficient.54 To understand the effect of ion correlations on transport, we calculated the ionic conductivity, diffusivity, and inverse Haven ratio from the MD simulations. The ionic conductivity of a 1 M solution was calculated using both the Nernst-Einstein (sNE) and Einstein (sE) relations: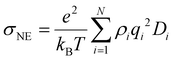 | (1) |
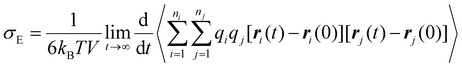 | (2) |
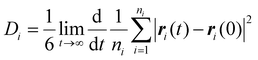 | (3) |
Based on MD simulations, the diffusivity was found to be 6.4 × 10−10 and 9.1 × 10−10 m2 s−1 for Zn and SO4 ions, respectively. The system size correction was applied using the Yeh and Hummer method55,56 with the calculated viscosity. Using these values, sNE was found to be 23.2 S m−1. When the Einstein relation is used, which includes ion correlations, the sE was found to be 18.7 S m−1, lower than sNE by about 20%. These values are higher than the experimental conductivity of 4.42 S m−1, obtained using EIS (Fig. S15†). The experimental conductivity is consistent with previously reported values in the literature.57,58 This discrepancy between MD and experimental results is similar to our prior studies, where the diffusivity (probed experimentally over smaller length scales) shows good agreement but the conductivity (probed experimentally over larger length scales) was found to be overestimated in simulations.59 Further studies to validate the force field with experimental transport measurements, such as viscosity and NMR diffusion studies, will shed further light on whether this discrepancy is a physical effect, such as solvation drag effects. The ratio sE/sNE is called inverse Haven ratio (or ‘degree of uncorrelated ion motion’), which is a measure of the ionicity of the electrolyte. For an ideal electrolyte without any ion correlation the inverse Haven ratio equals one, while for the 1 M ZnSO4 solution the inverse Haven number was found to be 0.81, indicating that ion correlations decrease conductivity but not dramatically. Furthermore, the apparent transference numbers were determined from the MD to be 0.41 for Zn2+ and 0.59 for SO42−, reflecting their relative contributions to ionic transport in the electrolyte.
Experimentally, the diffusivity of Zn2+ measured using PFG-NMR was slightly lower, at 4.24 × 10−10 m2 s−1, compared to the MD-calculated value (6.4 × 10−10 m2 s−1). This difference may be due to more clusters or longer-lived transient clusters in the real system, therefore restricting ion mobility. This interpretation could be connected to higher probability of smaller clusters observed experimentally via SAXS compared to calculated in the MD simulations (Fig. 3e). The difference in diffusivity between experiment and simulations, combined with the difference between calculated sNE and sE, suggests that the ions are weakly correlated, and the clusters are relatively short-lived. Rather than a purely hopping mechanism, ion transport in zinc sulfate electrolytes involves a combination of vehicular and hopping motion. While zinc ions move with their hydration shell (first solvation shell containing 6 water molecules) via vehicular motion, the interactions between zinc and it's second solvation shell are transient, similar to the hopping mechanism proposed for sulfate ions. This interplay allows for efficient ion migration, where ions dynamically migrate between transient clusters, preserving high conductivity.
As shown in our previous studies, sE can be divided into contributions from different correlations.60,61 The same analyses were carried out in the current study and the results are shown in Table 1. As indicated by the Einstein relation and illustrated in Fig. 6a to aid interpretation, for ions with like charges, an overall negative or positive contribution to the Einstein relation corresponds to the motions of these ions being anticorrelated or correlated, respectively. Here we find a negative contribution for the zinc ions (Zn–Zn); this may be due to coulombic repulsion of like ions. Meanwhile we hypothesize that the small positive contribution to the Einstein relation observed for the sulfate ions (SO4–SO4) may be due to the lower coulombic repulsion between sulfate ions due to their delocalized charge and therefore weaker interactions and less specific correlations and/or sulfate's ability to form transient clusters with protons. We observe a negative contribution to the Einstein relation for ions with opposing charges (Zn–SO4).
 | ||
Fig. 6 (a) Illustration to aid the interpretation of negative or positive contributions to the ionic conductivity determined by the Einstein relation (sE) given in Table 1, which depends on the ion's charge (where stripped and clear are used to represent different charges) and direction of travel (denoted by the arrow). This schematic depicts the overall average contribution of ions in the simulation box, not individual atom pairs. (b) Normalized probability of finding isolated or clustered zinc or sulfate ions. The normalization is calculated by dividing the number of zinc or sulfate ions in each state by the total number of zinc and sulfate ions in the system. (c) Illustration showing the coordination number (CN), residence time (τ) and expected motion calculated from the MD simulations and given in Table 2 for [ion]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [first solvation shell] [first solvation shell]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [second solvation shell] for [zinc] [second solvation shell] for [zinc]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [water] [water]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [water] (left), [zinc] [water] (left), [zinc]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [water] [water]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [sulfate] (center) and [sulfate] [sulfate] (center) and [sulfate]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [water] [water]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [water] (right). Zinc ions, sulfate ions and water molecules are represented by gray circles, orange circles and black arrowheads (> with the apex representing the oxygen) respectively, with the water molecules oriented within the solvation shell to represent their bonding. The turquoise gradient color represents the lifetime of interactions within the first and second solvation shells based on the (discontinuous) scale bar. Darker turquoise corresponds to long residence times (and thus signifies strong solvation and a tendency for vehicular motion) meanwhile lighter turquoise corresponds to short residence times (and weak solvation and a tendency for hopping motion). The associated values are provided in Table 2. [water] (right). Zinc ions, sulfate ions and water molecules are represented by gray circles, orange circles and black arrowheads (> with the apex representing the oxygen) respectively, with the water molecules oriented within the solvation shell to represent their bonding. The turquoise gradient color represents the lifetime of interactions within the first and second solvation shells based on the (discontinuous) scale bar. Darker turquoise corresponds to long residence times (and thus signifies strong solvation and a tendency for vehicular motion) meanwhile lighter turquoise corresponds to short residence times (and weak solvation and a tendency for hopping motion). The associated values are provided in Table 2. | ||
| Contribution to σE (S m−1) | Motion type | |
|---|---|---|
| Zn | 9.573 | |
| SO4 | 13.573 | |
| Zn–Zn | −3.227 | Anticorrelated |
| Zn–SO4 | −1.673 | Correlated |
| SO4–SO4 | 0.490 | Correlated |
As shown in Fig. 3d and 6b, the results of our transport measurements and calculations can be explained by our observation of the formation of nanoclusters which on average tend to be sulfate-rich together with some isolated zinc ions. Overall, the negative contributions to the ionic conductivity suggest that the Zn–Zn and Zn–SO4 correlations reduce the number of free, independently moving charge carriers, thereby lowering the overall ionic conductivity.
The residence times of ions/molecules in the first and second solvation shell of zinc and sulfate ions provide insights into overall transport processes. The results are summarized in Table 2 and illustrated in Fig. 6c. Consistent with our model of hydrated zinc and sulfate units forming nanoclusters, we observe long residence times for zinc's first solvation shell containing water as well as zinc's second solvation shell containing sulfate ions. For water molecules in zinc's first solvation shell, the residence time correlation function almost does not decay during the simulation time scale, indicative of a strong and stable hydration shell around Zn2+ containing 6 water molecules; this structure has been widely reported.26,34–38 Furthermore, the 2nd shell Zn–SO4 solvation shows significant long lifetimes (∼0.2 ns) with a coordination number of 2.4. Note, whilst the Zn–O(SO4) interaction in the first solvation shell also shows a relatively long lifetime (∼1 ns) compared to other interactions, the coordination number is very small (0.01).
| Solvation shell | Cutoff (Å) | CN | τ RT (ns) | Travel distance (Å) | Motion type | |
|---|---|---|---|---|---|---|
Zn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O(SO4) O(SO4) |
1st | 3.1 | 0.01 | 0.989 | 17.74 | Vehicular |
| 2nd | 5.5 | 2.39 | 0.212 | 8.22 | Hopping | |
Zn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O(H2O) O(H2O) |
1st | 3.1 | 5.99 | ≫14 | ≫3.1 | Vehicular |
| 2nd | 5.2 | 15.50 | 0.041 | 3.62 | Hopping | |
O(SO4)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H(H2O) H(H2O) |
1st | 2.7 | 3.79 | 0.007 | 1.84 | Hopping |
| 2nd | 4.7 | 24.61 | 0.034 | 4.01 | Hopping |
Using the measured diffusivity and the calculated residence times, the distance an ion can travel during the period of the residence time was calculated and included in Table 2. It is clear that Zn2+ and its first hydration shell can travel a distance much longer than the cluster size indicated by the corresponding cutoff distance before the cluster breaks, suggesting a vehicular transport mechanism, where the ion and its solvation shell move together through the electrolyte.60,62 On the contrary, other interactions are more likely to transport through a ‘hopping’ mechanism, involving frequent breaking and reforming of interactions. We note that the SAXS reveals these nanoclusters are present but provides no insight into their lifetimes.
The presence of some of the ions within nanoclusters (Fig. 6b) leads to a 20% reduction in Einstein conductivity compared to the Nernst-Einstein conductivity, indicating that extensive and varied nanoclusters (Fig. 5) modestly hinder ion transport. Their transient nature prevents a significant decline in overall conductivity. These findings further reinforce the role of transient ion clusters in mediating ionic transport. While the strong zinc–water interaction stabilizes the ion's local environment, the dynamic exchange of both hydrated zinc and sulfates between solvation shells contributes to the continuous evolution of clusters and enables efficient ion transport.
Overall, this analysis reveals that the complicated clustering structure of the ZnSO4 electrolyte introduces significant heterogeneity into the dynamics and transport behavior. While transient ion clusters reduce diffusivity and ionic conductivity compared to ideal systems, their short-lived and dynamic nature ensures that ions retain significant mobility, enabling effective charge transport.
Conclusions
By integrating X-ray scattering measurements (SAXS, XPDF), MD simulations, forward scattering simulations and diffusivity measurements, we achieve a holistic understanding of the size, charge, composition and transport behavior of ion nanoclusters in zinc sulfate electrolytes. We find that zinc maintains its hydration shell and forms a distribution of nanoclusters with sulfate, which appears to be independent of concentration. These nanoclusters have a variety of sizes, compositions and geometries. The transient nature of these nanoclusters allows efficient transport mechanism through the breaking and forming of nanoclusters (‘hopping’ mechanism). Our synergistic approach using measurements, simulations and analysis enables superior insights to be obtained from the measurements, compared to typical SAXS studies.We envision that the approach established here will serve as a foundation for future studies to experimentally investigate nanocluster properties, such as dynamics or ion pairing. By using our methodology to interrogate how the nanocluster's properties vary with conditions (such as concentration, temperature or pH), and strategies to improve performance, such as the use of additives, we can meaningfully understand how the presence of nanoclusters affects battery performance, such as cycling stability and overpotentials. In addition, our methodology is applicable to other systems where nanometric aggregates are formed, for example other electrolytes or perovskite solutions. A deeper understanding of the nature of nanoclusters in electrolytes will facilitate more comprehensive studies on ion transport, electronic structures, solvation processes and interfacial mechanisms; all of which are essential for the rational design of superior electrolytes for a wide range of applications.
Experimental procedures
Solution preparation
Aqueous zinc sulfate solutions were prepared from dried zinc sulfate heptahydrate (ZnSO4·7H2O, 99% and ≥99.95% metals basis) and water (MilliporeSigma Milli-Q Direct purification) by mass. The zinc salt was dried overnight under vacuum at 80 °C.Small angle X-ray scattering (SAXS)
SAXS measurements of the electrolyte solutions were performed at the ASWAXS facility (15ID-D) of NSF's ChemMatCARS (Sector 15) at the Advanced Photon Source, Argonne National Laboratory. Five measurements (exposure time 1 s) were taken at an X-ray energy of 9.16 keV using a Pilatus 3X 300k detector at a sample-detector-distance of 0.54 m. The electrolyte solutions were measured in 1 mm quartz capillaries. For the background subtraction and absolute scale normalization, measurements were performed of an empty capillary tube and glassy carbon, respectively. For transmission corrections, transmission values were determined using photodiode mounted to the beamstop. The data were corrected for transmission, sample thickness, and normalized to give absolute intensities.X-ray pair distribution function
X-ray total scattering of the electrolyte solutions was measured at the Advanced Photon Source, Argonne National Laboratory at beamline 11-ID-B. These measurements were performed at an X-ray energy of 58.6 keV (0.2116 Å) with a PerkinElmer XRD1620 amorphous silicon detector placed 30.1 cm from the sample. The electrolyte solutions were measured in sealed 2 mm quartz or glass capillaries for a total exposure time of 1800 s per sample under ambient temperature and pressure. A diode mounted on the beamstop was used to measure the X-ray transmission, which was corrected for dark current. Samples were monitored for beam damage by alternating measurement positions and exposure times. Polarization and geometric corrections were applied to the raw data, which was reduced using the pyFAI package.63 The scattering from the empty capillary was subtracted from the sample measurements. PDFGetX264 was used to obtain the S(q) and pair distribution function in G(r) space, with corrections for sample self-absorption, detector oblique incidence, and Compton and Laue scattering.SAXS forward simulation
Forward scattering simulations of isolated clusters was carried out using the IsoScatter code available on github (https://github.com/tchaney97/IsoScatter). This code uses the Debye equation to calculate scattering intensity:65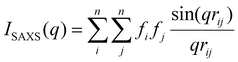 | (4) |
X-ray pair distribution function forward simulation
XPDF simulations of isolated clusters was also carried out using the IsoScatter code. We again calculate the scattering intensity I(q) using the Debye equation up to 30 Å−1. Then we normalize the I(q) by the Laue scattering to obtain the structure function S(q): | (5) |
To calculate the reduced pair distribution function G(r), we do the sine Fourier transform of the reduced structure function:
 | (6) |
Here qmax is the maximum q value and we used 30 Å−1, and L(q) is the Lorch function to account for termination effects:
 | (7) |
Fitting of SAXS data with Monte Carlo Markov Chain (MCMC) method
In order to explore the full parameter space of cluster size distributions that could produce the observed SAXS data, we employed an MCMC approach using the DREAM (Differential Evolution Adaptive Metropolis) algorithm implemented in the pyDREAM package.49,50 Weights for each cluster size were initialized as independent variables with a prior distribution defined by a log–normal centered about the number of clusters found in the MD simulations. Additionally, a constant background offset was included as a free parameter. The likelihood function was defined as the probability of each I(q) point produced by the weighted sum of simulated SAXS curves falling within a normal distribution of intensity with sigma = 1 × 10−4 cm−1 about each experimental I(q) point. The DREAM algorithm was run with 25 chains taking 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps. All chains showed excellent convergence, as indicated by a Gelman-Rubin statistic of 1.001. A burn-in period defined as the first 20% of steps was discarded and the remaining posterior distribution was then used for analysis.
000 steps. All chains showed excellent convergence, as indicated by a Gelman-Rubin statistic of 1.001. A burn-in period defined as the first 20% of steps was discarded and the remaining posterior distribution was then used for analysis.
Pulsed-field gradient nuclear magnetic resonance (PFG-NMR) diffusion measurements
The 1H and 67Zn PFG-NMR was performed at 25 °C on a 600 MHz NMR spectrometer equipped with a 5 mm liquid-NMR probe (Doty Scientific, USA) at Larmor frequencies of 2π × 599.782 and 2π × 37.527 rad MHz, respectively, with a bipolar gradient stimulated echo sequence (Dbppste sequence in VNMRJ, Agilent, USA). The gradient length (δ) was fixed 4 ms for all measurements and the diffusion delay (Δ) for 1H was 50 ms while it was 5 ms for 67Zn due to the fast nuclear relaxation of 67Zn nucleus. Diffusion coefficient (D) was determined by fitting the PFG-echo profile obtained with 16 equal steps as a function of gradient strength with the Stejskal-Tanner equation | (8) |
Electrochemical impedance spectroscopy
Ionic conductivity was measured at room temperature using electrochemical impedance spectroscopy (EIS) within a custom glass cell containing two Pt electrodes. The cell constant was measured using 0.1 M and 0.01 M KCl solutions. EIS was measured from 100 kHz to 10 Hz, and the solution resistance was extracted from high-frequency intercept of the Nyquist plot.Modeling
All the MD simulation in this work was performed using the package LAMMPS.68 Three species are included in the simulation system: zinc (Zn2+), sulfate (SO42−) and water. The force field of Zn2+ were taken from the literature which were optimized for aqueous solution simulation.69 The force field of sulfate ions are based on Sadra Kashefolgheta's work.70 Its Lennard-Jones potential parameters are optimized against experimental hydration free energies. Electronic structure calculations at the B3LYP/aug-cc-pvdz level were carried out using Gaussian software71 on an isolated SO42−. The electrostatic potential surface of the optimized structure from quantum mechanics was fitted using the restrained electrostatic potential (RESP) method72 and the atomic partial charges were derived for MD simulation. The SPC/Fw water model73 was applied for water molecules. These force field models were validated in our previous publications on the same or similar systems.74,75Three salt concentrations, 0.1 M, 0.5 M and 1 M, respectively, were studied. The box compositions are shown in Table 3. Periodic boundary conditions were applied in all three dimensions. The long-range electrostatic interactions, with a real space cutoff of 12 Å, were calculated based on the particle–particle particle–mesh (PPPM) method.76 The same cutoff was used for van der Waals interactions and a tail correction was applied.77 The systems were first simulated for 2 ns in the isothermal-isobaric (NPT) ensemble at 1 atm pressure (isotropic volume fluctuations) and 298 K. The equilibrated simulation boxes were simulated for 14 ns as the production simulation in the canonical (NVT) ensemble at the same temperature. The Nose–Hoover thermostat78 and the extended Lagrangian approach79 were applied to control the temperature and pressure, respectively. Five independent trajectories were generated using different initial atomic velocities. The time step for all the simulation was 1 fs and snapshots were saved every 1000 steps.
| ZnSO4 concentration (M) | Number of ZnSO4 | Number of water |
|---|---|---|
| 0.1 | 7 | 3866 |
| 0.5 | 30 | 3320 |
| 1.0 | 70 | 3866 |
Author contributions
E. N. A. and L. K. I. contributed equally to this work. E. N. A., S. T. and M. F. T. conceived the research and designed the experiments. E. N. A. and M. B. conducted the SAXS experiment, while J. M. performed the XPDF experiment. L. K. I., and Y. Z. analyzed the XPDF data. L. K. I., and T. P. C. developed the clustering algorithm and analyzed the SAXS data. K. S. H. conducted the PFG-NMR experiment, and N. T. H. performed the EIS experiment. Y. J., E. M., and Y. Z. performed the MD simulations. The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Data availability
The data supporting this article have been included as part of the ESI.†Acknowledgements
This work was partly supported by Joint Center for Energy Storage Research (JCESR), an Energy Innovation Hub funded by the U.S. Department of Energy (DOE), Office of Science, Basic Energy Sciences. T. P. C. received support for this research from the National Science Foundation Graduate Research Fellowship Program under Grant No. (DGE 2040434). Sandia National Laboratories is a multi-mission laboratory managed and operated by National Technology & Engineering Solutions of Sandia, LLC, a wholly owned subsidiary of Honeywell International Inc., for the U.S. Department of Energy's National Nuclear Security Administration under contract DE-NA0003525. This paper describes objective technical results and analysis. Any subjective views or opinions that might be expressed in the paper do not necessarily represent the views of the U.S. Department of Energy or the United States Government. Y. Z. and E. M. thank the Center for Research Computing (CRC) at the University of Notre Dame for providing computational resources. NSF's ChemMatCARS, Sector 15 at the Advanced Photon Source (APS), Argonne National Laboratory (ANL) is supported by the Divisions of Chemistry (CHE) and Materials Research (DMR), National Science Foundation, under grant number NSF/CHE-2335833. This research used resources of the Advanced Photon Source, a U.S. Department of Energy (DOE) Office of Science user facility operated for the DOE Office of Science by Argonne National Laboratory under Contract No. DE-AC02-06CH11357. Electrochemical measurements were performed at the Electrochemical Discovery Laboratory, a JCESR facility at Argonne National Laboratory.References
- Z. Yu, N. P. Balsara, O. Borodin, A. A. Gewirth, N. T. Hahn, E. J. Maginn, K. A. Persson, V. Srinivasan, M. F. Toney, K. Xu, K. R. Zavadil, L. A. Curtiss and L. Cheng, ACS Energy Lett., 2022, 7(1), 461–470 CrossRef CAS.
- Z. Tian, Y. Zou, G. Liu, Y. Wang, J. Yin, J. Ming and H. N. Alshareef, Adv. Sci., 2022, 9(22), 2201207 CrossRef CAS.
- D. Hubble, D. Emory Brown, Y. Zhao, C. Fang, J. Lau, B. D. McCloskey and G. Liu, Energy Environ. Sci., 2022, 15(2), 550–578 RSC.
- H. Cheng, Q. Sun, L. Li, Y. Zou, Y. Wang, T. Cai, F. Zhao, G. Liu, Z. Ma, W. Wahyudi, Q. Li and J. Ming, ACS Energy Lett., 2022, 7(1), 490–513 CrossRef CAS.
- T. R. Nickerson, E. N. Antonio, D. P. McNally, M. F. Toney, C. Ban and A. P. Straub, Chem. Sci., 2023, 14(4), 751–770 RSC.
- R. Fu, P.-S. Zhang, Y.-X. Jiang, L. Sun and X.-H. Sun, Chemosphere, 2023, 311, 136993 CrossRef CAS.
- B. Deng, M. Huang, X. Zhao, S. Mou and F. Dong, ACS Catal., 2022, 12(1), 331–362 CrossRef CAS.
- X. Lu, W. Tu, Y. Zhou and Z. Zou, Adv. Energy Mater., 2023, 13(27), 2300628 CrossRef CAS.
- N. Çakmakçı, M. Shin, H. Jung, J. Lee and Y. Jeong, Carbon Lett., 2023, 33(4), 1035–1043 CrossRef.
- E. C. Gugua, C. O. Ujah, C. O. Asadu, D. V. Von Kallon and B. N. Ekwueme, Hybrid Adv., 2024, 7, 100286 CrossRef.
- M. Zhang, V. Kamavaram and R. G. Reddy, Min. Metall. Explor., 2006, 23(4), 177–186 CAS.
- W. Zhang and C. Y. Cheng, Hydrometallurgy, 2007, 89(3), 178–188 CrossRef CAS.
- L. O. S. Colbin, Y. Shao and R. Younesi, Batteries Supercaps, 2025, e202400160 CrossRef.
- N. N. Rajput, T. J. Seguin, B. M. Wood, X. Qu and K. A. Persson, Elucidating Solvation Structures for Rational Design of Multivalent Electrolytes—A Review, Springer International Publishing, Cham, 2018, pp. 79–124 Search PubMed.
- F. Wan, X. Zhou, Y. Lu, Z. Niu and J. Chen, ACS Energy Lett., 2020, 5(11), 3569–3590 CrossRef CAS.
- J. Ming, J. Guo, C. Xia, W. Wang and H. N. Alshareef, Mater. Sci. Eng., R, 2019, 135, 58–84 CrossRef.
- M. Song, H. Tan, D. Chao and H. J. Fan, Adv. Funct. Mater., 2018, 28(41), 1802564 CrossRef.
- Q. Zhang, J. Luan, Y. Tang, X. Ji and H. Wang, Angew. Chem., Int. Ed., 2020, 59(32), 13180–13191 CrossRef CAS.
- J.-Q. Huang, X. Lin, H. Tan, X. Du and B. Zhang, J. Energy Chem., 2020, 43, 1–7 CrossRef.
- Y. Liang, H. Dong, D. Aurbach and Y. Yao, Nat. Energy, 2020, 5(9), 646–656 CrossRef CAS.
- A. Ponrouch, J. Bitenc, R. Dominko, N. Lindahl, P. Johansson and M. R. Palacin, Energy Storage Mater., 2019, 20, 253–262 CrossRef.
- M. R. Palacin, P. Johansson, R. Dominko, B. Dlugatch, D. Aurbach, Z. Li, M. Fichtner, O. Lužanin, J. Bitenc, Z. Wei, C. Glaser, J. Janek, A. Fernández-Barquín, A. R. Mainar, O. Leonet, I. Urdampilleta, J. A. Blázquez, D. S. Tchitchekova, A. Ponrouch, P. Canepa, G. S. Gautam, R. S. R. G. Casilda, C. S. Martinez-Cisneros, N. U. Torres, A. Varez, J.-Y. Sanchez, K. V. Kravchyk, M. V. Kovalenko, A. A. Teck, H. Shiel, I. E. L. Stephens, M. P. Ryan, E. Zemlyanushin, S. Dsoke, R. Grieco, N. Patil, R. Marcilla, X. Gao, C. J. Carmalt, G. He and M.-M. Titirici, J. Phys.: Energy, 2024, 6(3), 031501 CAS.
- W. E. Price and H. Weingaertner, J. Phys. Chem., 1991, 95(22), 8933–8938 CrossRef CAS.
- R. Buchner and G. Hefter, J. Mol. Liq., 2023, 383, 122146 CrossRef CAS.
- J. G. Albright, J. A. Rard, S. Serna, E. E. Summers and M. C. Yang, J. Chem. Thermodyn., 2000, 32(11), 1447–1487 CrossRef CAS.
- W. W. Rudolph, M. H. Brooker and P. Tremaine, Z. Phys. Chem., 1999, 209(2), 181–207 CrossRef CAS.
- A. R. Davis and B. G. Oliver, J. Phys. Chem., 1973, 77(10), 1315–1316 CrossRef CAS.
- W. Rudolph and G. Irmer, J. Solution Chem., 1994, 23(6), 663–684 CrossRef CAS.
- W. W. Rudolph, Ber. Bunsenges. Phys. Chem., 1998, 102(2), 183–196 CrossRef CAS.
- H. Zhang, Y.-H. Zhang and F. Wang, J. Comput. Chem., 2009, 30(3), 493–503 CrossRef CAS.
- T. M. Stawski, A. E. S. van Driessche, M. Ossorio, J. Diego Rodriguez-Blanco, R. Besselink and L. G. Benning, Nat. Commun., 2016, 7(1), 11177 CrossRef CAS.
- R. Besselink, T. M. Stawski, A. E. S. Van Driessche and L. G. Benning, J. Chem. Phys., 2016, 145(21), 211908 CrossRef CAS.
- X. Zhang, Y. Zhang and Q. Li, J. Mol. Struct.: THEOCHEM, 2002, 594(1), 19–30 CrossRef CAS.
- Y. Marcus, Ion Properties, Springer, New York, NY, 2014, pp. 1101–1106 Search PubMed.
- Y. Marcus, J. Chem. Soc., Faraday Trans., 1991, 87(18), 2995–2999 RSC.
- H. Ohtaki and T. Radnai, Chem. Rev., 1993, 93(3), 1157–1204 CrossRef CAS.
- F. Stellato, M. Calandra, F. D'Acapito, E. D. Santis, G. L. Penna, G. Rossi and S. Morante, Phys. Chem. Chem. Phys., 2018, 20(38), 24775–24782 RSC.
- M. Xu, T. Zhu and J. Z. H. Zhang, J. Phys. Chem. A, 2019, 123(30), 6587–6595 CrossRef CAS.
- J. D. Bazak, A. R. Wong, K. Duanmu, K. S. Han, D. Reed and V. Murugesan, J. Phys. Chem. B, 2021, 125(19), 5089–5099 CrossRef CAS.
- A. Kundu, S. I. Mamatkulov, F. N. Brünig, D. J. Bonthuis, R. R. Netz, T. Elsaesser and B. P. Fingerhut, ACS Phys. Chem. Au, 2022, 2(6), 506–514 CrossRef CAS.
- H.-J. Li, D. Yan, H.-Q. Cai, H.-B. Yi, X.-B. Min and F.-F. Xia, Phys. Chem. Chem. Phys., 2017, 19(18), 11390–11403 RSC.
- N. B.-M. Kalish, E. Shandalov, V. Kharlanov, D. Pines and E. Pines, J. Phys. Chem. A, 2011, 115(16), 4063–4075 CrossRef CAS.
- T. F. Young and G. E. Walrafen, Trans. Faraday Soc., 1961, 57(0), 34–39 RSC.
- A. M. Margarella, K. A. Perrine, T. Lewis, M. Faubel, B. Winter and J. C. Hemminger, J. Phys. Chem. C, 2013, 117(16), 8131–8137 CrossRef CAS.
- S. Espinosa, E. Bosch and M. Rosés, Anal. Chim. Acta, 2002, 454(1), 157–166 CrossRef CAS.
- W. Wang and D. B. Breisinger, Metall. Mater. Trans. B, 1998, 29(6), 1157–1166 CrossRef.
- A. H. Narten, W. E. Thiessen and L. Blum, Science, 1982, 217(4564), 1033–1034 CrossRef CAS.
- K. D. Fong, J. Self, B. D. McCloskey and K. A. Persson, Macromolecules, 2021, 54(6), 2575–2591 CrossRef CAS.
- E. M. Shockley, J. A. Vrugt and C. F. Lopez, Bioinformatics, 2018, 34(4), 695–697 CrossRef CAS.
- J. A. Vrugt, C. J. F. ter Braak, C. G. H. Diks, B. A. Robinson, J. M. Hyman and D. Higdon, Int. J. Nonlinear Sci. Numer. Simul., 2009, 10(3), 273–290 Search PubMed.
- J. J. Moré, in Numerical Analysis, ed. G. A. Watson, Springer, Berlin, Heidelberg, 1978, pp. 105–116 Search PubMed.
- G. V. Schulz, A. Dinglinger and E. Husemann VII, Z. Phys. Chem., Abt. B, 1939, 43(1), 385–408 Search PubMed.
- B. H. Zimm, J. Chem. Phys., 1948, 16(12), 1093–1099 Search PubMed.
- Y. Zhang and E. J. Maginn, J. Phys. Chem. Lett., 2015, 6(4), 700–705 CrossRef CAS.
- I.-C. Yeh and G. Hummer, J. Phys. Chem. B, 2004, 108(40), 15873–15879 Search PubMed.
- O. A. Moultos, Y. Zhang, I. N. Tsimpanogiannis, I. G. Economou and E. J. Maginn, J. Chem. Phys., 2016, 145(7), 074109 CrossRef.
- Z. Xu, Y. Zhang, W. Gou, M. Liu, Y. Sun, X. Han, W. Sun and C. Li, Chem. Commun., 2022, 58(58), 8145–8148 RSC.
- J. Yang, M. A. Bissett and R. A. W. Dryfe, ChemSusChem, 2021, 14(7), 1700–1709 Search PubMed.
- Y. Zhang and E. J. Maginn, J. Phys. Chem. B, 2021, 125(48), 13246–13254 CrossRef CAS.
- I. Alfurayj, C. C. Fraenza, Y. Zhang, R. Pandian, S. Spittle, B. Hansen, W. Dean, B. Gurkan, R. Savinell, S. Greenbaum, E. Maginn, J. Sangoro and C. Burda, J. Phys. Chem. B, 2021, 125(31), 8888–8901 CrossRef CAS.
- Y. Zhang, E. Carino, N. T. Hahn, N. Becknell, J. Mars, K. S. Han, K. T. Mueller, M. Toney, E. J. Maginn and S. Tepavcevic, J. Phys. Chem. Lett., 2023, 14(50), 11393–11399 CrossRef CAS.
- O. Borodin, G. D. Smith and W. Henderson, J. Phys. Chem. B, 2006, 110(34), 16879–16886 CrossRef CAS.
- J. Kieffer and D. Karkoulis, J. Phys.: Conf. Ser., 2013, 425(20), 202012 CrossRef.
- X. Qiu, J. W. Thompson and S. J. L. Billinge, J. Appl. Crystallogr., 2004, 37(4), 678–678 CrossRef CAS.
- P. Debye, Ann. Phys., 1915, 351(6), 809–823 CrossRef.
- P. J. Brown, A. G. Fox, E. N. Maslen, M. A. O'Keefe and B. T. M. Willis, Int. Tables Crystallogr., 2006, C, 554–595 Search PubMed.
- C. L. Farrow and S. J. L. Billinge, Acta Crystallogr., Sect. A: Found. Crystallogr., 2009, 65(3), 232–239 CrossRef CAS.
- S. Plimpton, J. Comput. Phys., 1995, 117(1), 1–19 CrossRef CAS.
- C. S. Babu and C. Lim, J. Phys. Chem. A, 2006, 110(2), 691–699 CrossRef CAS.
- S. Kashefolgheta and A. V. Verde, Phys. Chem. Chem. Phys., 2017, 19(31), 20593–20607 RSC.
- M. J. E. A. Frisch, G. W. Trucks, H. Bernhard Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman and G. Scalmani, et al., Gaussian 09 G09 | Gaussian.com, Inc., Wallingford CT, 2009, 121, 150–166 Search PubMed.
- C. I. Bayly, P. Cieplak, W. Cornell and P. A. Kollman, J. Phys. Chem., 1993, 97(40), 10269–10280 CrossRef CAS.
- Y. Wu, H. L. Tepper and G. A. Voth, J. Chem. Phys., 2006, 124(2), 024503 CrossRef.
- Y. Zhang, G. Wan, N. H. C. Lewis, J. Mars, S. E. Bone, H.-G. Steinrück, M. R. Lukatskaya, N. J. Weadock, M. Bajdich, O. Borodin, A. Tokmakoff, M. F. Toney and E. J. Maginn, ACS Energy Lett., 2021, 6(10), 3458–3463 CrossRef CAS.
- G. Bergman, N. Bruchiel-Spanier, O. Bluman, N. Levi, S. Harpaz, F. Malchick, L. Wu, M. Sonoo, M. S. Chae, G. Wang, D. Mandler, D. Aurbach, Y. Zhang, N. Shpigel and D. Sharon, J. Mater. Chem. A, 2024, 12, 14456–14466 RSC.
- R. W. Hockney and J. W. Eastwood, Computer Simulation Using Particles, CRC Press, Boca Raton, 2021 Search PubMed.
- H. Sun, J. Phys. Chem. B, 1998, 102(38), 7338–7364 CrossRef CAS.
- W. G. Hoover, Phys. Rev. A, 1985, 31(3), 1695–1697 CrossRef.
- W. Shinoda, M. Shiga and M. Mikami, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69(13), 134103 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5eb00119f |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2025 |


