Macrocyclic transition-metal parashift complexes for MRI at clinical and pre-clinical magnetic fields

Abstract

A series of macrocyclic transition-metal complexes, including Fe(II), Co(II), Ni(II), and Cu(II) complexes, have been evaluated for parashift MRI imaging applications, by assessing their paramagnetic NMR properties, including proton chemical shifts, nuclear relaxation rates, and any exchange dynamics in solution, at magnetic fields strengths relevant to clinical and pre-clinical imaging. Among the complexes studied, Fe(II) and Co(II) systems demonstrated significant paramagnetic shifts with desirable relaxation properties, making them potential candidates for lanthanide-free parashift molecular probes for MRI. Field-dependent nuclear relaxation rate analyses provided insights into electronic relaxation times, confirming the suitability of certain complexes for parashift imaging at lower magnetic fields. Phantom imaging experiments at 9.4 T further validated the feasibility of molecular imaging using a cyclen-based macrocyclic Fe(II) complex, making a significant advance toward developing transition metal-based MRI probes using biogenic metal ions, and offer promise for future responsive imaging due to the direct signal detection.

---

1. Introduction

Contrast enhanced MRI has revolutionised radiology and diagnostics over the last four decades, particularly for imaging tumour tissue and vascular diseases.^1–3 More recently there has been a drive towards molecular imaging agents to complement current progress towards personalised medicine. Whilst conventional MRI contrast agents enable visualisation of pathologies, usually due to residing in blood pools and highlighting vascular structures, parashift probes (i.e. metal complexes that can be detected directly due to a paramagnetically-shifted proton resonance that is shifted outside of the diamagnetic window of the endogenous signal) have great potential as molecular probes.

Using magnetic resonance spectroscopy (MRS) imaging, parashift agents offer scope to monitor molecular processes in the body and encode molecular-level information i.e. a calibrated response to specific biomolecules or physiological conditions, and to map and quantify biochemical changes associated with disease. The speciation of the molecular probe is reported by a signature chemical shift that is independent of probe concentration.

Lanthanide-containing ¹H NMR parashift agents have been developed previously,^4–9 with limits of detection possible in the 10 micromolar range, and acquisition times of just 1 minute per image.⁷ Despite reducing the lanthanide dose for the direct-detection method down to 0.04 mmol kg⁻¹ (compared with 0.1 mmol kg⁻¹ dosing for standard indirect gadolinium MRI contrast agents), it is desirable to replace the xenobiotic lanthanide ions altogether. Transition metal complexes with magnetic anisotropy offer attractive biogenic alternatives for parashift agents¹⁰ because essential ‘trace’ metals including cobalt can be metabolised, and hence better long-term toxicity profiles are envisaged.

First row transition metal ions have a long history of being used as shift agents (e.g. in metalloprotein work¹¹), and whilst they have comparatively smaller magnetic moments than Ln(III) ions, shifts of up to 400 ppm have been observed, as well as significant relaxation enhancement effects.¹² Transition metal complexes have been developed for paraCEST (paramagnetic chemical exchange saturation transfer) imaging in order to shift the exchangeable proton signal far from the exchanging pool of water protons to access CEST signals from protons with more rapid exchange, and enable the design of responsive systems.^10,13–16 Paramagnetic transition metal complexes with low-lying excited states (ΔE ∼ k_BT) are required for parashift probes, where magnetic susceptibility anisotropies can be quite large (giving large pseudocontact shifts) and Orbach electronic relaxation mechanisms can operate efficiently (otherwise long electronic relaxation times will shorten T₁ and T₂ too much for imaging).¹²

To optimise the detection sensitivity of a parashift agent, a large, sharp NMR signal is desired (i.e. several isochronous protons) that is shifted outside of the physiological diamagnetic NMR window for direct detection. The overall rigidity and symmetry of a parashift agent is therefore an important design criterion, as a single NMR environment is desired for the reporting protons, not a range of conformational isomers, as exchange broadening can arise from dynamic interconversions between conformers on the NMR timescale.

Fast longitudinal relaxation (short T₁) of the NMR reporter group is also a sensitivity requirement (i.e. that the proton signal returns to thermal equilibrium quickly) so that fast imaging pulses can be used to enhance sensitivity;¹⁷ similar strategies are also used to enhance the sensitivity of ¹⁹F contrast agents.^18–20 Fast imaging sequences require wide spectral bandwidths (>10 kHz),⁷ however, and therefore highly shifted signals (±40 ppm at 3 T) are also a sensitivity requirement to avoid signal overlap with endogenous protons.^7,21 The sensitivity of a parashift probe is also determined by the transverse signal decay (T₂), which reduces the overall signal-to-noise (SNR) due to line broadening, and hence a T₂/T₁ ratio close to unity is desired.^7,21

Metal ions with a relatively short electronic relaxation time (i.e. <10 ps) are required to avoid significant T₂-broadening, such as high-spin pseudo-octahedral Fe(II) and Co(II) complexes.^12,22 The contact contributions (which are quite reasonably ignored for Ln(III) systems) can be significant in d-block complexes, even for nuclei several bonds away from the metal centre.²³ In addition, some Co(II) complexes exhibit slightly longer electronic relaxation times (T_1E = 1–10 ps) than most of the Ln(III) shift ions, which influences the dipolar relaxation mechanism that is important at the lower (clinically relevant) magnetic fields.¹²

In pursuit of lanthanide-free parashift agents for imaging at clinical (i.e. 1.5–3 T) and pre-clinical (i.e. 7–9.4 T) imaging fields, we have studied a set of transition metal complexes (Scheme 1). We evaluate the paramagnetic shifts and nuclear relaxation rates of protons within each complex at variable magnetic field strengths to aid future probe design.

Scheme 1 Schematic of model transition metal parashift complexes.

2. Results and discussion

A series of water-soluble complexes [using Fe(II), Co(II), Ni(II), and Cu(II) chloride salts] has been prepared to evaluate their paramagnetic NMR properties at a range of magnetic fields (Fig. 1). Macrocyclic ligands bearing picolyl coordinating pendants were synthesised by alkylation of 1,4,7-triazacyclononane (TACN) or 1,4,7,10-tetraazacyclododecane (cyclen) with either 2-bromomethyl-6-methylpyridine,²⁴ or (5-tert-butylpyridin-2-yl)methyl methanesulfonate.⁵ Divalent transition metal complexes were formed using the respective dichloride salt, and for comparison the diamagnetic Zn(II) analogues ([ZnL^1a](ClO₄)₂ and [ZnL^2a](ClO₄)₂) were synthesised using the perchlorate salt, as confirmed by high-resolution mass spectrometry (ESI). Macrocyclic ligands were chosen to impart thermodynamic stability and kinetic inertness with these labile first-row transition metal ions, and nitrogen donors were incorporated to favour the divalent high-spin states. Morrow and co-workers have previously reported the Fe(II) and Co(II) complexes of L^1a and L^2a, and found that the 6-methyl group on the picolyl unit is important for imparting rigidity into these structures; sharp signals were observed in the NMR spectra at 11.7 T.²⁴ The 6-methyl group also facilitates the stabilisation of the 2+ oxidation states with L^1a and the high spin states required for the desired paramagnetic shift and relaxation properties, due to the steric demand of the three intertwined methyl groups inducing M–N^py elongation, in the M–N bond lengths determined by X-ray crystallography vs. unsubstituted tripicolyl-TACN.^24,25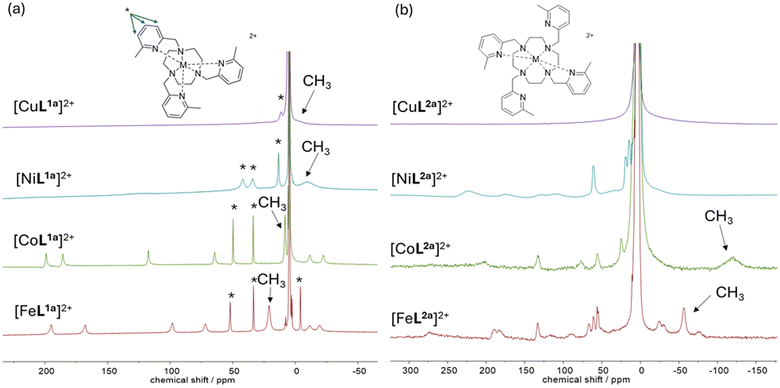

Fig. 1 ¹H NMR spectra of [ML^1a]²⁺ (a) and [ML^2a]²⁺ (b) where (M = Fe(II), Co(II), Ni(II), Cu(II)) at 60 MHz (1.4 T, 299 K) in D₂O. Pyridyl proton resonances indicated by *.

In this study, we have expanded the series to include Ni(II) and Cu(II), and assessed paramagnetic NMR properties and the conformational dynamics of the complexes in solution, at clinically relevant magnetic fields. We have also synthesised ligand frameworks with tert-butyl groups in the 5-position on the pyridyl unit (L^1b and L^2b) to assess whether the steric bulk at the 5-position could impart rigidity, and whether the protons of the tert-butyl could experience an enhanced paramagnetic shift at this distance (ca. 6.5 Å)⁵ from the metal centre.

2.1 Solution-state NMR and solid-state structures

Complexes of L^1a and L^2a. The effective magnetic susceptibilities of the water soluble L^1a and L^2a complexes of Fe(II) and Co(II) were estimated using the Evans NMR method. However, the Co(II) values seemed higher than expected; for complexes ‘[CoL^1a]Cl₂’ and ‘[CoL^2a]Cl₂’ we measured μ_eff = 5.9 ± 0.3μ_B, and 5.7 ± 0.6μ_B respectively, assuming the molecular weight based on dichloride salts of the cations (similar to previously reported values of 5.8 ± 0.2μ_B, and 6.0 ± 0.3μ_B).²⁴ The spin-only μ_eff = 3.9μ_B for an S = 3/2 high spin system, and the experimental values tend to fall in the range 4.3–5.2μ_B due to spin–orbit coupling. We observe that the solid powder of the cobalt complexes is a different colour to the aqueous solutions (e.g. ‘[CoL^2a]Cl₂’ is a pale blue powder and forms a pale pink solution when dissolved in water) and the single crystal X-ray data showed that [CoL^2b]²⁺ crystallised with a [CoCl₄]²⁻ counterion when synthesised using CoCl₂ as the cobalt source (vide infra). ICPMS analysis of the powders reveal that the complexes contain 20 wt% more Co(II) than expected for [CoL^1a]Cl₂ and [CoL^2a]Cl₂ (even without solvent molecules of crystallisation), consistent with some presence of CoCl₄²⁻ anions, hence the discrepancies in the measured effective magnetic moments, whilst the Fe concentrations were within error of the expected values for ‘[FeL^1a]Cl₂’ and ‘[FeL^2a]Cl₂’. We therefore synthesised [CoL^2a]²⁺ from Co(II)nitrate, and in this case the solid powder is pink like the solution, ICPMS analysis shows that the powder contains 6.9 ± 0.7 wt% cobalt ([CoL^2a](NO₃)₂ = 7.6 wt% Co) and the effective magnetic moment of [CoL^2a](NO₃)₂ = 5.1 ± 0.3μ_B by Evans method. The ¹H NMR spectra of the two samples, however, are indistinguishable (Fig. S50, ESI†). We suggest using Co(II)nitrate as the cobalt source for water soluble complexes in the future to circumvent this problem, and to avoid unwanted possible toxicity effects of uncoordinated metal ions for imaging. Similarly, the Ni(II) complexes may contain [NiCl₄]²⁻ anions, (we note that ‘[NiL^2a]Cl₂’ is a turquoise powder whilst the aqueous solution is orange and the magnetic moment measured by Evans method assuming the ‘[NiL^2a]Cl₂’ molecular weight is again higher than expected at 4.3 ± 0.2μ_B), and the Cu(II) complexes may contain CuCl₄²⁻ anions (‘[CuL^1a]Cl₂’ is a lime green powder whilst the aqueous solution is turquoise/green, and the magnetic moment measured by Evans method assuming ‘[CuL^2a]Cl₂’ is again higher than expected at 2.3 ± 0.2μ_B).

The ¹H NMR spectra of complexes of L^1a and L^2a were recorded at 1.4 T in D₂O for M = Fe(II), Co(II), Ni(II), and Cu(II) (Fig. 1) and 9.4 T (see ESI, Fig. S83†), i.e. typical clinical and pre-clinical imaging fields respectively. The spectra were recorded using a large sweep width and short acquisition time as the paramagnetic complexes contain resonances that extend well beyond the conventional diamagnetic range and relax back to thermal equilibrium quickly. The ¹H NMR spectra contain ten discernible resonances for compounds [FeL^1a]²⁺and [CoL^1a]²⁺, indicative of a single diastereomer in solution in each case, with high-spin dicationic metal centres, rigid structures, and three-fold symmetry. The ¹H NMR spectrum of [NiL^1a]²⁺ contains broad resonances (observable in the +220 to −20 ppm range), and that of [CuL^1a]²⁺ contains further broadened resonances evident in the range +40 to −20 ppm. For [CoL^1a]²⁺ and [FeL^1a]²⁺ the pyridyl protons in the ¹H NMR spectra were assigned in accordance with Morrow et al.²⁴ (see * Fig. 1); if we assume that the relaxation rates follow pseudocontact Bloch–Redfield–Wangsness theory, such that R₁ rates decrease steeply with the distance, r, from the paramagnetic centre (i.e. R₁ is proportional to r⁻⁶) the three pyridyl protons are expected to be the sharpest signals in all complexes, with the slowest longitudinal relaxation rates, as they are furthest from the paramagnetic metal centre. The methyl peak was identified by its relative signal intensity.

The methyl resonance appears most shifted from the diamagnetic region for FeL^1a (at +22 ppm, 299 K), with R₁ = 290 ± 5 Hz and R₂ = 440 ± 40 Hz at 1.4 T, and R₁ = 356 ± 1 Hz and R₂ = 600 ± 30 Hz at 9.4 T.

The manganese complex, [MnL^1a]Cl₂ was also synthesised but its NMR spectra were broad and featureless (see ESI, Fig. S15†) owing to the long electronic relaxation times associated with Mn(II).²² The sample also appeared to oxidise in solution (D₂O) within the NMR tube (formation of brown precipitate – presumably MnO₂ – was observed at 24 h), suggesting that the complex is not kinetically stable in water to oxidation, owing to the lack of crystal field stabilisation of a d⁵ metal ion.

Crystallography data of the L^1a complexes, including the previously reported structures of [FeL^1a](CF₃SO₃)₂ and [CoL^1a](NO₃)₂,²⁴ revealed six-coordinate metal centres with approximate C₃-symmetry, containing an ‘N₃^TACN’ plane of coordinated nitrogen atoms of the macrocycle and an ‘N₃^Py’ plane of the three coordinated picolyl nitrogen atoms (Fig. 2). The pendant arms twist around the metal centre in a helical array (Δ or Λ configuration), whilst the macrocyclic chelate rings adopt cooperative helicity (either λλλ or δδδ).‡

Fig. 2 Structure of the Λ(δδδ) cationic complexes [ML^1a]²⁺ both side-on and top-down (with ‘N₃^TACN’ plane highlighted in light blue spheres, ‘N₃^py’ plane highlighted with dark blue spheres) for (a) M = Zn²⁺, (b) M = Ni²⁺, and (c) M = Cu²⁺ (elongated axial Cu–N bonds are highlighted with spheres in the side-on view). H atoms and counterions removed for clarity.

The diamagnetic [ZnL^1a](ClO₄)₂ complex was also synthesised, and crystallised in the P2₁/c space group, with Δ(λλλ) and Λ(δδδ) enantiomers within the unit cell, and all Zn–N bond distances were 2.16–2.25 Å [Fig. 2(a)]. The complex geometry is best described as distorted octahedral, with average apical twist angles§ of 44.2(6)°. The [FeL^1a]²⁺ and [CoL^1a]²⁺ unit cells also contain analogous diastereomers with average twist angles of 43.6(8)° and 45.4(3)° respectively,²⁴ although there are also two other conformations present in the [FeL^1a]²⁺ structure, i.e. Δ(λλλ) with twist angle = 30.1(9)° and Λ(λλλ) with twist angle = 43.6(5)°, perhaps due to the crystal packing effects of neighbouring [Na(CF₃SO₃)₄]³⁻ anions.

Compounds [NiL^1a](ClO₄)₂ and [CuL^1a](ClO₄)₂ also crystallised in the P2₁/c space group, again with Δ(λλλ)and Λ(δδδ) enantiomers in the unit cell [Fig. 2(b) and (c)]. In the former case, the complex has distorted octahedral geometry with an average apical twist angle of 46.5(9)° and the Ni–N bonds were in the 2.10–2.21 Å range, whilst for the latter we observed distinct elongation in one axis, ascribed to Jahn–Teller distortion; four of the Cu–N bonds are in the 2.06–2.14 Å range, with two axially-related bonds at 2.24(1) Å and 2.47(1) Å and three apical twist angles of 41.5°, 44.3°, and 49.1°. The twist angles increase from Fe(II) to Ni(II) as the metal ion radius decreases across the period and varies to accommodate the tetragonal distortion for Cu(II).

The ¹H NMR spectra of [FeL^2a]²⁺ and [CoL^2a]²⁺ contain 20 resonances, consistent with a single diastereomer of the previously reported C₂-symmetry of the complexes in the solid state, in which the metal centres are six-coordinate with two trans-coordinated pyridine groups on the same face of the macrocycle and two uncoordinated pendant arms pointing away from the metal centre.²⁴ The six-coordinate system is best described as a slightly distorted trigonal prism (unlike the distorted octahedra with L^1a) and Λ(λλλλ)/Δ(δδδδ) helicity.²⁴ The ¹H NMR spectrum of [NiL^2a]²⁺ is also consistent with a single diastereomer with average two-fold symmetry, whilst the ¹H NMR spectra of [CuL^2a]²⁺ is broadened significantly (like that of [CuL^1a]²⁺). For the Fe(II) and Co(II) complexes, the CH₃ resonances (from the coordinated picolyl unit) have greater linewidths for L^2a complexes than L^1a, whilst in general the resonances appear sharper in the spectra of [NiL^2a]²⁺ than [NiL^1a]²⁺. We were unsuccessful in growing crystals of [NiL^2a]²⁺ suitable for crystallography, whilst a crystal structure of the protonated species [CuL^2aH₂](ClO₄)₄ (see ESI Fig. S6†) was obtained from the addition of Zn(ClO₄)₂ to [CuL^2a]Cl₂ in water, revealing a five-coordinate Cu(II) centre, in contrast to [FeL^2a]²⁺ and [CoL^2a]²⁺, although like the Fe(II) and Co(II) complexes two pyridines coordinate and two do not.

Complexes of L^1b and L^2b. We also synthesised the 5-tert-butyl-appended picolyl complexes L^1b and L^2b, analogous to the design of previous lanthanide parashift molecular probes,^5,26 incorporating a nine-fold NMR-equivalent tert-butyl resonance for signal enhancement. For the TACN macrocycle (in the absence of the 6-methyl groups on the pyridine ring) the ligand L^1b provides a six coordination sites with a smaller cavity size cf.L^1a, and upon complexation with CoCl₂ we observe the formation of the diamagnetic Co(III) complex [CoL^1b]Cl₃; the ¹H NMR contains resonances in the diamagnetic region, whilst X-ray crystallography confirms that each complex has three anions, with an average Co–N bond length of 1.95(1) Å (see ESI, Fig. S71 and S76†). Complexation with FeCl₂ led to the diamagnetic low spin Fe(II) complex [FeL^1b]Cl₂, as confirmed by solution NMR spectroscopy and X-ray crystallography (see ESI, Fig. S67 and S70†), akin to the previously reported analogue of [FeL^1a]²⁺ that lacks a methyl substituent in the pendant group.²⁴ The ¹H NMR spectra of both [CoL^1b]Cl₃ and [FeL^1b]Cl₂ revealed predominantly one diastereomer in solution at room temperature.

In the solid state we observe Δ(λλλ) and Λ(δδδ) enantiomers of [FeL^1b]²⁺ in the crystal structure (Fig. S70, ESI†), with a larger twist angle of 47.9(5)° [cf. 43.6(8)°] and shorter Fe–N bonds of 1.98(2) Å [cf. 2.21–2.32 Å] than the [FeL^1a]²⁺ complexes. The tert-butyl protons are ca. 6.5 Å from the metal centre but do not create enough steric bulk at the 5-position to favour high-spin Fe(II) or Co(II), even with the fac-oriented crowding of the three tert-butyl groups within the octahedral-type geometry of L^1a.

For complex [CoL^2b]²⁺, unlike with the L^1b ligand, the ¹H NMR spectrum spans a +200 to −20 ppm range (Fig. 3a) and is indicative of a paramagnetic Co(II) metal centre, hence the larger cyclen ring favours Co²⁺ over the smaller Co³⁺ ion, as it cannot easily form the small-cavity octahedral donor environment that stabilised Co(III). However, the NMR spectral resonances are relatively broad with only half the number of signals as the L^2a complex, consistent with a fluxional structure in solution with averaged four-fold symmetry on the NMR time scale, even at high field (500 MHz, 296 K), and a single tert-butyl resonance at −1 ppm. Variable temperature ¹H NMR revealed signal sharpening with increased temperature (see ESI, Fig. S78†), as expected for a further increase in the exchange rates.

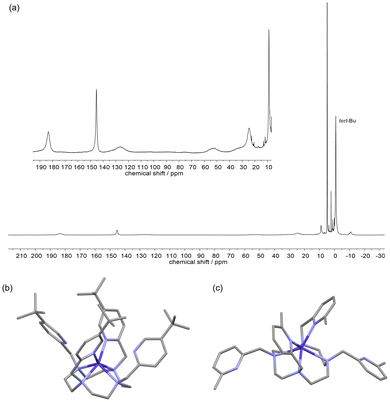Fig. 3 Solution and solid-state structures of [CoL^2b]²⁺. (a) ¹H NMR (500 MHz, D₂O, 296 K) of [CoL^2b]Cl₂ (inset showing zoomed in resonances in the +190 to +0 ppm region). (b) X-ray crystal structure of (b) [CoL^2b]²⁺ and (c) [CoL^2a]²⁺ for comparison (taken from ref. 24), H atoms and counterions removed for clarity.

Vapour deposition of ethyl acetate into a methanolic solution of [CoL^2b]Cl₂ led to complex crystallisation in the P2₁/n space group with [CoCl₄]²⁻ counterions, as shown in Fig. 3(b). Unlike the crystal structure of CoL^2a,²⁴ [Fig. 3(c)] the four picolyl groups all point towards the Co(II) metal centre, with two sets of Co–N_py bond lengths of 2.18(1) and 3.2(1) Å. The unit cell contains Δ(δδδδ) and Λ(λλλλ) isomers, similar to [CoL^2a]²⁺,²⁴ but with a smaller twist angle around the C₂ axis of 22.0(1)°, cf. 33.0(1)° for [CoL^2a]²⁺. The six-coordinate system can be described as a distorted trigonal prism, similar to [CoL^2a]²⁺, whereby the ‘pseudo-C₃’-axis is perpendicular to the C₂-symmetry axis of the molecule; apical twist angles of 28.2, 8.3, and 8.6° around the ‘pseudo-C₃’-axis are similar to [CoL^2a]²⁺ (cf. 18.6, 4.2, and 4.2°) but more distorted particularly at the two coordinated N^py atoms (i.e. the 28.2° twist angle).

2.2 Complex rigidity in solution

The diamagnetic analogues [ZnL^1a](ClO₄)₂ and [ZnL^2a](ClO₄)₂ were prepared in order to compare the conformational dynamics in solution by ¹H NMR spectroscopy. The ¹H NMR spectrum of [ZnL^1a](ClO₄)₂ revealed narrow resonances at 9.4 T with clear J-coupling evident for the macrocycle ring protons (Fig. S35, ESI†), consistent with a rigid complex structure in (acetonitrile) solution, and formation of a single diastereomer; variable temperature ¹H NMR (9.4 T) revealed no further species at 253 K, whilst slight broadening of the TACN ring and methylene protons was observed at 313 K and above, indicative of the ring and/or pendant arms wobbling at these elevated temperatures (see ESI, Fig. S37†).

The ¹H NMR spectrum of [ZnL^2a](ClO₄)₂ shows exchange-broadening at room temperature at 9.4 T (see ESI, Fig. S61†), indicating less rigidity in the cyclen-based structures.

Although it is very common to observe exchange between the Δ(λλλλ)/Λ(δδδδ) and Λ(λλλλ)/Δ(δδδδ) diastereomeric configurations in lanthanide complexes based on cyclen macrocyclic frameworks,²⁷ (due to ring inversion between δδδδ and λλλλ configurations as well as arm rotation that converts between Δ and Λ helicities) we do not observe major/minor conformational isomers in the ¹H NMR spectra for the paramagnetic Fe(II)/Co(II) complexes of L^1a; this exchange process would have to be incredibly fast to give rise to an average species in solution, rather than two sets of resonances at e.g. 9.4 T, with such large Δω differences expected between diastereomer proton pairs with the paramagnetic complexes.

Variable temperature ¹H NMR spectra of [ZnL^2a](ClO₄)₂ (at 9.4 T, see ESI, Fig. S63†) revealed one set of cyclen and pendent arm methylene protons at 253 K, and two types of pyridyl protons (one sharp and one broadened), consistent with a single structure with two-fold symmetry. Upon heating, the resonances broaden and coalesce to give a spectrum consistent with a four-fold-symmetric complex at 333 K, whilst at 1.4 T the NMR spectrum of [ZnL^2a](ClO₄)₂ contains a single set of sharpened pyridyl signals at room temperature. Thus, we conclude that the L^2a complexes exist with ‘on’–‘off’ dancing pendant arms, such that they are on average six-coordinate at all times at room temperature, whilst the complexes remain in their Δ(λλλλ) or Λ(δδδδ) preferred helicities, as a racemic mixture.

In the case of [CoL^2b]²⁺ the tert-butyl groups are at the 5-position of the coordinating picolyl units (trans- to the methylene group that attaches to the macrocycle) and do not introduce steric hindrance to the pendent arm rotation as effectively as the methyl groups in the 6-position, and hence fast exchange dynamics are observed to give average four-fold symmetry in the paramagnetic ¹H NMR; it is thus crucial that the picolyl pendants have substituents in the 6-position for these cyclen-based complexes, to render them sufficiently rigid in solution to give distinct NMR spectral resonances for use in parashift applications.

2.3 Evaluating the nuclear relaxation rates for MRI

The ideal transition metal parashift probe will contain reporting protons that appear as a single NMR-equivalent peak that is shifted significantly (ca. 50 ppm) so that the probe can be detected free of endogenous background proton signals. The relaxation rates of the reporter protons are key to optimising the SNR for detection of a parashift agent by MRI, by exploiting paramagnetic relaxation enhancement effects;^7,21 fast longitudinal relaxation rates, R₁ (i.e. T₁⁻¹) allow rapid pulsing when at the order of 100 Hz, such that the SNR can be increased by a factor of √R₁ in a given scan duration. The sensitivity of a parashift probe is also influenced by the transverse relaxation rate, R₂ (i.e. T₂⁻¹), which reduces the overall SNR due to line broadening (T₂-losses during the echo time), and hence an R₁/R₂ ratio close to unity is desired. The rate at which the imaging can be performed is limited by the minimum possible repetition time (predominantly determined by the spectral width) and is also limited in vivo by the specific absorption rate of tissue, to prevent heating.²⁸ Previously reported parashift imaging in vivo (preclinical murine imaging at 7 T) used image sequences with repetition times of approximately 8 ms range (with a 90° excitation pulse and a spectral width of 20 kHz), and echo times of ca. 1 ms.⁷ The limit at which increasing R₁ enhances the SNR per unit time is ca. 400 Hz under similar experimental conditions (assuming the repetition time needs to be three times R₁ for signal recovery); signals with R₁ > 400 Hz will fully recover within the 3 ms repetition time but cannot be imaged any faster at the same spectral width and matrix size, whilst a greater proportion of signal loss in the 1 ms echo time scales with increasing R₂. Faster repetition times are possible with larger spectral widths, but this is determined by the water/fat-parashift frequency difference (approximately 20 kHz for the signal 60 ppm away from the endogenous signals at 7 T), and risks tissue damage from heating. At a clinical field of 3 T, 60 ppm is only 8 kHz, therefore the minimum repetition time will approximately double with a similar setup and R₁ > 200 Hz cannot be imaged any faster to improve SNR.

To assess the L^1a and L^2a complexes for parashift imaging, relaxation measurements (see Table 1) were performed at 1.4 T (60 MHz) and 9.4 T (400 MHz) using an inversion recovery sequence to measure R₁ and spectral linewidths to estimate R₂, as any contributions to the linewidths from magnetic field inhomogeneity is small compared to the fast intrinsic R₂ rates measured here (however, R₂ estimates assume there are no chemical exchange processes leading to line broadening). The table displays values highlighted in bold where the relaxation properties or shifts are favourable for parashift imaging, i.e. R₁ > 100 Hz, R₁/R₁ > 0.5, and |δ| > 50 ppm.

Table 1 Measured internuclear M–H distance, r, and relaxation rates measured at 1.4 T and 9.4 T

Complex	Proton	r /Å	δ /ppm	1.4 T	1.4 T	R 1/R2 (1.4 T)	9.4 T	9.4 T	R 1/R2 (9.4 T)
				Est. R2 ^c/Hz	R 1 ^c/Hz		Est. R2 ^d/Hz	R 1 ^d/Hz
a δ at 299 K. b Taken from crystal structure data. c T = 299 K. d T = 296 ± 1 K. e R 1 measurement not possible due to broad resonance and very fast R1 relaxation. f Difficult to measure due to overlapping resonances. R1 > 100 Hz, R1/R2 > 0.5, and |δ| > 50 ppm highlighted in bold.
FeL^1a	CH3	3.75	+22	440 ± 40	290 ± 5	0.66	600 ± 30	356 ± 1	0.59
	py-H^5	5.36	+53	110 ± 10	24 ± 2	0.22	230 ± 20	34 ± 2	0.15
	py-H^3	5.00	+34	70 ± 5	34 ± 4	0.49	220 ± 20	48 ± 1	0.22
	py-H^4	5.90	−4	75 ± 5	16 ± 4	0.21	40 ± 5	20 ± 1	0.50
CoL^1a	CH3	3.78	+8.5	180 ± 10	160 ± 5	0.89	200 ± 10	140 ± 4	0.70
	py-H^5	5.30	+50	65 ± 5	19 ± 2	0.29	65 ± 5	18 ± 1	0.28
	py-H^3	4.98	+34	60 ± 5	23 ± 2	0.38	65 ± 5	22 ± 1	0.34
	py-H^4	5.91	+6	45 ± 5	11 ± 1	0.24	50 ± 10	7 ± 1	0.14
NiL^1a	CH3	3.83	−10	ca. 2000	—^e	—	ca. 4000	—^e	—
	py-H^5/3	4.94/5.27	+42	630 ± 60	420 ± 40	0.67	1400 ± 100	477 ± 4	0.34
	py-H^5/3	4.94/5.27	+34	530 ± 50	380 ± 40	0.72	1400 ± 100	641 ± 9	0.49
	py-H^4	5.88	+13	180 ± 20	130 ± 10	0.72	290 ± 30	219 ± 4	0.76
CuL^1a	CH3	3.83	−3	ca. 1000	—^e	—	ca. 3000	—^e	—
	py-H^4	5.90	+11	225 ± 15	90 ± 20	0.40	250 ± 20	133 ± 6	0.53
FeL^2a	CH3	3.66	−57	750 ± 150	760 ± 180	ca. 1	1700 ± 200	875 ± 3	0.51
	—	—	+62	340 ± 30	305 ± 15	0.90	390 ± 10	229 ± 3	0.59
	—	—	+57	120 ± 20	105 ± 5	0.88	170 ± 10	100 ± 2	0.59
CoL^2a	CH3	3.69	−122	ca. 3000	—^e	—	ca. 3000	—^e	—
	—	—	+56	570 ± 80	530 ± 10	0.93	505 ± 25	440 ± 10	0.87
	—	—	+25	410 ± 60	330 ± 30	0.80	370 ± 10	275 ± 10	0.74
	—	—	+134	720 ± 70	—^e	—	1290 ± 100	396 ± 2	0.45
NiL^2a	—	—	+63	ca. 330 ± 30	—^f	—	ca. 1800 ± 200	—^f	—

---

The methyl resonance of [CoL^1a]²⁺ has a promising ratio of R₁/R₂ rates (at r = 3.75 Å), of 0.70 at 9.4 T (and 0.89 at 1.4 T), whilst the R₁ of 160 Hz at low field would allow repetition times of 20 ms for imaging. Unfortunately, the resonance is not shifted very far from the diamagnetic window, however similar complexes with r = 3.75 Å have potential for imaging if the contact and/or pseudocontact shifts can be modulated, perhaps by functionalisation of the pyridine ring. In comparison, the R₁/R₂ ratio for [FeL^1a]²⁺ is slightly lower at both fields, but the R₁ rates are faster, allowing repetition times of 10 ms at low field (8 ms at 9.4 T). Again, the moderately shifted resonance at +22 ppm will only allow 5 kHz bandwidth at 7 T (2 kHz at 3 T), reducing the possible repetition times to ca. 30 ms for a similar imaging experiment to that previously described above,⁷ and 70 ms at 3 T. The pyridyl protons of [CoL^1a]²⁺and [FeL^1a]²⁺ have inferior R₁/R₂ ratios than the methyl resonances, and the R₁ relaxation rates are much slower (ca. 20 Hz), limiting the minimum repetition times used to increase SNR in imaging experiments to ca. 150 ms; they are too slow for fast imaging sequences and are thus too far away from the paramagnetic centre.

The methyl proton resonances are much broader (FWHM ca. 1000 Hz) for [NiL^1a]²⁺ and [CuL^1a]²⁺, consistent with expected longer electronic relaxation rates that enhance dipolar relaxation mechanisms; long electronic relaxation times are expected as these metal complexes do not have low-lying electronic levels to facilitate efficient Orbach-type electronic relaxation mechanisms, due to an A_1g electronic ground state in the case of octahedral Ni(II) and the lifted degeneracy of the E_g ground state [CuL^1a]²⁺ due to Jahn–Teller distortion (see crystal structure, Fig. 2(c)). [NiL^1a]²⁺ and [CuL^1a]²⁺ contain resonances (at +13 and +11 ppm respectively) with appropriate relaxation properties for imaging, and we assume that these are the furthest pyridyl-H⁴ protons from the metal centres (ca. 5.9 Å away) as they are the sharpest peaks in each spectrum. There are only three equivalent protons per complex, however, and the chemical shifts are still not far enough from endogenous water for distinct imaging. In general, it will be difficult to enhance the hyperfine shift for Ni/Cu(II) complexes based on L^1a, as the reporter group needs to be at these longer distances to reduce signal broadening, where the contact shift term diminishes.

In the case of both [FeL^2a]²⁺ and [CoL^2a]²⁺, the R₁ and R₂ rates of the methyl group on the coordinated picolyl unit are faster than their L^1a analogues, significantly so in the case of Co(II) where resonances are so broad and the R₁ is so fast that it could not be determined. The resonances observed at +62 ppm and +57 ppm for [FeL^2a]²⁺ have ideal relaxation rates for imaging at both fields, as well as hyperfine shifts far enough from water for large spectral widths but only represent two equivalent protons per molecule in each case. In contrast, the resonances generally appear sharper for the [NiL^2a]²⁺ than [NiL^1a]²⁺, i.e. the resonances out at +50 to +300 ppm are readily observable for the former.

We have previously observed significant decreases in the relaxation rates at low field with many lanthanide parashift complexes (particularly Tm(III), Dy(III), and Tb(III) complexes)²⁹ due to the substantial Curie terms and fast electronic relaxation rates, but with these transition metal complexes, particularly the Co(II) complexes, the Curie term does not dominate as much due to their comparatively moderate magnetic susceptibilities, as demonstrated in Fig. 4 (see also Table S1, ESI†).

Fig. 4 Variation of R₁ with magnetic field in the range 1.4–16.4 T for (a) [FeL^1a]²⁺ (red filled circles), [CoL^1a]²⁺ (blue filled circles), [NiL^1a]²⁺ (green filled circles), [FeL^2a]²⁺ (red open circles), [CoL^2a]²⁺ (blue open circles). (b) Zoomed in section of [FeL^1a]²⁺ (red filled circles) and [CoL^1a]²⁺ (blue filled circles). Multiparameter fitting of ¹H R₁ data (298 ± 3 K, D₂O) to Bloch–Redfield–Wangsness theory, using the measured fixed values of μ_eff (lines).

In the case of [FeL^2a]²⁺, the R₁ relaxation rate of the coordinated picolyl methyl protons only vary by 25% over the 1.4–16.4 T magnetic field range, and for [CoL^2a]²⁺R₁ in fact decreases at high field, with the dipolar term dominating the relaxation mechanism. This is particularly important when considering parashift probe development for imaging at clinical fields.

Fitting the field-dependent R₁ relaxation rates to Bloch–Redfield–Wangsness theory (Fig. 4) using multiparameter fitting for r, τ_r and T_1e and the experimental values of μ_eff, gives T_1e values of 0.3 and 0.6 ps for [FeL^1a]²⁺ and [FeL^2a]²⁺ respectively, and 0.3 and 1.2 ps for [CoL^1a]²⁺ and [CoL^2a]²⁺ (Table 2). We also fitted the data for [NiL^1a]²⁺, which estimates a much larger T_1e of 40 ps, as expected for an A_1g electronic ground state,²² hence the much broader NMR resonances cf. the Fe(II) and Co(II) analogues (Fig. 1). We acknowledge that Bloch–Redfield–Wangsness theory assumes a point dipole approximation, and neglects to account for contact effects and the relaxation effects of the magnetic anisotropy. The model assumes that the Zeeman interactions are much larger than the zero field splitting (ZFS) effects,²² which is not the case for transition metal complexes. Even with lanthanide complexes, previous studies have demonstrated an angular-dependence of the paramagnetic relaxation enhancement effects.³⁰ It has also been shown recently that ZFS rhombicity can significantly slow down nuclear relaxation at low field.³¹ That being said, fitting the longitudinal relaxation data (Fig. 4 and Table 2) using the Bloch–Redfield–Wangsness theory returns r values similar to those determined experimentally (except for [CoL^2a]²⁺where r is not known). The resulting rotational correlation times also appear reasonable when compared to literature values for macrocyclic lanthanide complexes³² as well as with approximations derived from the hydrodynamic diameters of the L^1a and L^2a complexes estimated from the crystal structures.¶

Table 2 Measured internuclear M–H distance, r, effective magnetic susceptibility, μ_eff, and corresponding values calculated by fitting the field-dependent proton relaxation data [see ESI eqn (1)] using the fixed experimental value of μ_eff, and minimising the fit of three variables: r, τ_r, and T_1e at 298 K. Errors estimated from errors in R₁ and temperature

Compound	Experimental data		Calculated values (using exp. μeff)
	r /Å	μ eff/μB	r/Å	τ r/ps	T 1e/ps
a From crystal structure. b Estimated using Evans method. c μ eff assumed to be similar to that measured by Evans method of [CoL^2a](NO3)2. d Assignment unknown. e μ eff measured by Evans method of [CoL^2a](NO3)2.
[FeL^1a]^2+ (pyH^5)	5.36	5.4 ± 0.3^b	5.7 ± 0.1	200 ± 20	0.34 ± 0.02
[CoL^1a]^2+ (pyH^5)	5.30	5.1^c	5.6 ± 0.2	80 ± 20	0.27 ± 0.08
[NiL^1a]^2+ (pyH^3/5)	5–5.3	3.4 ± 0.1^b	5.3 ± 0.1	280 ± 15	39 ± 3
[FeL^2a]^2+ (pyCH3)	3.66	5.8 ± 0.7^b	3.6 ± 0.1	380 ± 60	0.59 ± 0.16
[CoL^2a]^2+	—^d	5.1 ± 0.7^e	4.2 ± 0.1	450 ± 25	1.16 ± 0.24

---

The simple point-dipole approximation correlates the faster low-field proton relaxation rates of the L^2a complexes cf. their L^1a analogues with slower T_1e rates. When there are electronic energy levels within ca. 1000 cm⁻¹ from the ground state vibrational-orbital couplings (Orbach mechanism) via phonons in the 50–1000 cm⁻¹ energy range (at 300 K) can occur,¹² which induces spin-changes and fast electronic relaxation times due to the spin–orbit coupling. It is plausible that the pseudo-octahedral L^1a complexes have faster electronic relaxation rates with respect to the more trigonal-prismatic L^2a analogues complexes due to greater orbital degeneracy in the ground state and therefore a higher density of low-lying energy levels to facilitate Orbach relaxation.

The six-fold methyl resonance at −57 ppm of [FeL^2a]²⁺ presents the best option for imaging in the table, certainly at preclinical fields; at 7 T a 20 kHz spectral width is possible, thus for imaging with 8 ms repetition times R₁ up to 400 Hz can enhance signal, although R₂ is faster than desired.

2.4 Phantom MR imaging

Phantom imaging studies of [FeL^2a]²⁺ were undertaken at 400 MHz (9.4 T) to assess the feasibility of imaging the resonance at −57 ppm at preclinical fields (Fig. 5, for unprocessed data see ESI, Fig. S84†). A 10 mM solution of [FeL^2a]²⁺ (right hand side, Fig. 4) was prepared in D₂O, in a 5 mm NMR tube, alongside a tube containing H₂O (left hand side, Fig. 4), and the two phantoms were placed inside a 30 mm ¹H imaging coil (Bruker, Germany). Imaging was performed by simultaneous signal acquisition of the diamagnetic water signal and the parashift reporter resonance of [FeL^2a]²⁺ (i.e. the methyl group) achieved by exciting the signal at −57 ppm using a Gaussian pulse, followed by 2D gradient echo using localising gradients with amplitudes to achieve the field of view (FOV) shown in Fig. 5. Simultaneous acquisition of the water signal (excited by the sufficient excitation within the bandwidth of the −57 ppm pulse) was collected by sampling across a wide MRI FOV to generate a ‘double image’ with two independent imaging channels for water (bottom) and the [FeL^2a]²⁺ complex (top) in Fig. 5. The water phantom (ca. 50 M) appears as a very intense image in the water (lower) channel, whilst the [FeL^2a]²⁺ phantom is visible in both channels due to the residual protonated solvent in the D₂O, as well as the resonance at −57 ppm.

Fig. 5 Non-slice selective 2D gradient echo MRI of two 5 mm tubes (cross-section) containing water (left) and 10 mM [FeL^2a]²⁺ dissolved in D₂O (right) at 9.4 T. TR = 40 ms, TE = 1.48 ms, NS = 512, SW = 249 ppm (100 kHz) matrix size = 256 × 32. Raw data processed using ROI mapping to remove noise. Frequency-resolved image in the vertical direction, showing the shifted image for [FeL^2a]²⁺ (arrow) due to the resonance at −57 ppm. Image acquired in 12 min.

3. Conclusions

This study presents the development of lanthanide-free macrocyclic transition-metal parashift complexes, evaluating their potential as MRI molecular probes at clinical and pre-clinical magnetic field strengths. The findings underscore the significance of molecular rigidity and strategic ligand design in optimizing nuclear relaxation rates and minimizing resonance broadening.

The ¹H NMR spectra of Fe(II) and Co(II) complexes of L^1a and L^2a displayed sharp resonances with significant hyperfine shifts, whilst those of the analogous Ni(II) and Cu(II) complexes contained much broader resonances, almost indiscernible in the case of Cu(II). In the solid state, the [ML^1a]²⁺ complexes were pseudo-octahedral for M = Zn(II), Fe(II), Co(II), and Ni(II), whilst Jahn–Teller distortion was observed for Cu(II). The [ML^2a]²⁺ complexes crystallise as six-coordinate trigonal prismatic systems for M = Fe(II), Co(II), whilst a five-coordinate complex was observed in the case of Cu(II).

In both the TACN and cyclen complexes studied the methyl group is required at the 6-position on the coordinating pyridines (complexes of L^1a or L^2a) to produce potential parashift complexes, but for different reasons; for the TACN complexes it is needed to extend the M–N^py bond length and prevent the formation of LS Fe(II) or LS Co(III) complexes (e.g. in the case of the L^1b complexes), whereas in the trigonal prismatic cyclen complexes (where HS Co(II) is stabilised regardless, e.g. in the case of [CoL^2b]²⁺), the bulky group serves to limit exchange broadening. We synthesised analogues of L^1a and L^2a with a tert-butyl group in the 5-position of the coordinating pyridines (rather than the 6-methyl group) but found that the steric bulk from the 5-pyridyl position cannot impart rigidity in the cyclen system (i.e. [CoL^2b]²⁺) or influence the M–N^py distance in the L^1b systems. It is not possible to put the tert-butyl at the 6-position, as this prevents metal coordination.

The nuclear relaxation rates (R₁ and R₂) of proton resonances within the L^1a and L^2a complexes were measured at a range of magnetic fields, to assess their suitability for imaging. Among the complexes studied, [FeL^1a]²⁺ and [CoL^1a]²⁺ have potential for imaging (based on the relaxation properties of the picolyl methyl group) if the contact shift can be modulated via functionalisation of the pyridine ring, such that the hyperfine shift is in the <−50 ppm or >+50 ppm range.

The electronic relaxation time (T_1e) of [FeL^1a]²⁺, [CoL^1a]²⁺, [NiL^1a]²⁺, [FeL^2a]²⁺, and [CoL^2a]²⁺ were estimated by fitting field-dependent nuclear relaxation rates of a given proton in each complex; T_1e is a function of both the transition metal ion and the local ligand field and is an important parameter for the design of parashift agents for low field imaging, where the dipolar term tends to dominate the relaxation rates according to Bloch–Redfield–Wangsness theory. For the Fe(II) and Co(II) complexes investigated, the T_1e values are slower in the trigonal prismatic L^2a complexes than their pseudo-octahedral L^1a analogues, likely due to the reduction in symmetry lifting orbital degeneracy of the ground states, reducing the density of low-lying states that facilitate Orbach relaxation mechanisms.

[FeL^2a]²⁺ demonstrates promising imaging capability due to its highly shifted methyl resonance at −57 ppm, fast longitudinal relaxation rates, and sufficient complex stability over 24 hours. To our knowledge this is the first example of imaging a parashift complex that incorporates a biogenic metal centre, which could exploit the body's natural metal metabolism for clearance if trace metal leaches into the system. We have successfully imaged the parashift probe selectively, in the presence of phantom tubes containing both strong (control tube) and weak (parashift tune) water signals, even though the resonance is rather broad (FWHM is ca. 500 Hz at 9.4 T). The signal is distinct from even a high background of water within the same image. Future systems with slower relaxation rates (R₁ and R₂ca. 400 Hz) would reduce T₂-losses whilst allowing fast imaging sequences with greater sensitivity.

Author contributions

Project conceptualisation and management was performed by N. J. R. Data collection was carried out by N. J. R., C. A. K., C. A., D. B., G. C., G. P., and P. H. Data curation, analyses, project supervision, and article writing was performed by N. R.

Conflicts of interest

There are no conflicts to declare.

Data availability

The data supporting this article have been included as part of the ESI.† Crystallographic data for [[CoL^1b]³⁺, [CoL^2b]²⁺, [CuL^1a]²⁺, [CuL^2a]²⁺, [FeL^1b]²⁺, [NiL^1a]²⁺, [ZnL^1a]²⁺] have been deposited at the CCDC under deposition numbers 2446484–2446490.†

Acknowledgements

NJR thanks HKBU, the Hong Kong Jockey Club Charities Trust, and the University of Warwick for support. CAK and CA thank the Hong Kong Jockey Club for support under the Global JC STEM Professorship scheme. PH was supported by a URKI Future Leaders Fellowship [MR/X034046/1]. We acknowledge Dr Andrew Coy and Dr Bertram Manz at Magritek and Dr Alan Kenwright for assistance with NMR, Dr Guy Clarkson for support with X-ray crystallography, and Professor David Parker and Professor Thomas Meersmann for useful discussions.

References

1. J. H. Duyn and A. P. Koretsky, Novel frontiers in ultra-structural and molecular MRI of the brain, Curr. Opin. Neurol., 2011, 24, 386–393.
2. J. C. Ferré, M. S. Shiroishi and M. Law, Advanced techniques using contrast media in neuroimaging, Magn. Reson. Imaging Clin. N. Am., 2012, 20, 699–713.
3. C. S. Restrepo, S. Tavakoli and A. Marmol-Velez, Contrast-enhanced cardiac magnetic resonance imaging, Magn. Reson. Imaging Clin. N. Am., 2012, 20, 739–760.
4. S. Aime, M. Botta, M. Fasano, E. Terreno, P. Kinchesh, L. Calabi and L. Paleari, A new ytterbium chelate as contrast agent in chemical shift imaging and temperature sensitive probe for MR spectroscopy, Magn. Reson. Med., 1996, 35, 648–651.
5. P. Harvey, A. M. Blamire, J. I. Wilson, K.-L. N. A. Finney, A. M. Funk, P. K. Senanayake and D. Parker, Moving the goal posts: enhancing the sensitivity of PARASHIFT proton magnetic resonance imaging and spectroscopy, Chem. Sci., 2013, 4, 4251–4258.
6. D. Coman, R. A. de Graaf, D. L. Rothman and F. Hyder, In vivo three-dimensional molecular imaging with Biosensor Imaging of Redundant Deviation in Shifts (BIRDS) at high spatiotemporal resolution, NMR Biomed., 2013, 26, 1589–1595.
7. P. K. Senanayake, N. J. Rogers, K.-L. N. A. Finney, P. Harvey, A. M. Funk, J. I. Wilson, D. O'Hogain, R. Maxwell, D. Parker and A. M. Blamire, A new paramagnetically shifted imaging probe for MRI, Magn. Reson. Med., 2017, 77, 1307–1317.
8. R. Schmidt, N. Nippe, K. Strobel, M. Masthoff, O. Reifschneider, D. D. Castelli, C. Höltke, S. Aime, U. Karst, C. Sunderkötter, C. Bremer and C. Faber, Highly Shifted Proton MR Imaging: Cell Tracking by Using Direct Detection of Paramagnetic Compounds, Radiology, 2014, 272, 785–795.
9. C. Harriswangler, F. Lucio-Martínez, L. Godec, L. K. Soro, S. Fernández-Fariña, L. Valencia, A. Rodríguez-Rodríguez, D. Esteban-Gómez, L. J. Charbonnière and C. Platas-Iglesias, Effect of Magnetic Anisotropy on the ¹H NMR Paramagnetic Shifts and Relaxation Rates of Small Dysprosium(III) Complexes, Inorg. Chem., 2023, 62, 14326–14338.
10. F. Slade, J. F. Collingwood and N. J. Rogers, Transition metal Parashift and ParaCEST MRI agents: Current progress and challenges, Coord. Chem. Rev., 2024, 516, 215940.
11. I. Bertini, P. Turano and A. J. Vila, Nuclear magnetic resonance of paramagnetic metalloproteins, Chem. Rev., 1993, 93, 2833–2932.
12. I. Bertini, C. Luchinat, G. Parigi and E. Ravera, in NMR of Paramagnetic Molecules, ed. I. Bertini, C. Luchinat, G. Parigi and E. Ravera, Elsevier, Boston, 2nd edn, 2017, pp. 175–253,  DOI:10.1016/B978-0-444-63436-8.00008-9.
13. S. K. Panda, A. Rai and A. K. Singh, Study of paraCEST response on six-coordinated Co(ii) and Ni(ii) complexes of a pyridine-tetraamide-based ligand, Dalton Trans., 2023, 52, 18407–18415.
14. P. Pérez-Lourido, E. Madarasi, F. Antal, D. Esteban-Gómez, G. Wang, G. Angelovski, C. Platas-Iglesias, G. Tircsó and L. Valencia, Stable and inert macrocyclic cobalt(II) and nickel(II) complexes with paraCEST response, Dalton Trans., 2022, 51, 1580–1593.
15. S. J. Dorazio, A. O. Olatunde, P. B. Tsitovich and J. R. Morrow, Comparison of divalent transition metal ion paraCEST MRI contrast agents, JBIC, J. Biol. Inorg. Chem., 2014, 19, 191–205.
16. R. Uzal-Varela, A. Rodríguez-Rodríguez, D. Lalli, L. Valencia, M. Maneiro, M. Botta, E. Iglesias, D. Esteban-Gómez, G. Angelovski and C. Platas-Iglesias, Endeavor toward Redox-Responsive Transition Metal Contrast Agents Based on the Cross-Bridge Cyclam Platform, Inorg. Chem., 2024, 63, 1575–1588.
17. F. Schmid, C. Höltke, D. Parker and C. Faber, Boosting 19F MRI—SNR efficient detection of paramagnetic contrast agents using ultrafast sequences, Magn. Reson. Med., 2013, 69, 1056–1062.
18. J. Blahut, L. Benda, J. Kotek, G. Pintacuda and P. Hermann, Paramagnetic Cobalt(II) Complexes with Cyclam Derivatives: Toward 19F MRI Contrast Agents, Inorg. Chem., 2020, 59, 10071–10082.
19. V. Herynek, M. Martinisková, Y. Bobrova, A. Gálisová, J. Kotek, P. Hermann, F. Koucký, D. Jirák and M. Hájek, Low-molecular-weight paramagnetic 19F contrast agents for fluorine magnetic resonance imaging, Magn. Reson. Mater. Phys., Biol. Med., 2019, 32, 115–122.
20. Z. Garda, F. Szeremeta, O. Quin, E. Molnár, B. Váradi, R. Clémençon, S. Même, C. Pichon, G. Tircsó and É. Tóth, Small, Fluorinated Mn2+ Chelate as an Efficient 1H and 19F MRI Probe, Angew. Chem., Int. Ed., 2024, 63, e202410998.
21. K. H. Chalmers, A. M. Kenwright, D. Parker and A. M. Blamire, 19F-lanthanide complexes with increased sensitivity for 19F-MRI: Optimization of the MR acquisition, Magn. Reson. Med., 2011, 66, 931–936.
22. E. Ravera, L. Gigli, L. Fiorucci, C. Luchinat and G. Parigi, The evolution of paramagnetic NMR as a tool in structural biology, Phys. Chem. Chem. Phys., 2022, 24, 17397–17416.
23. B. Martin and J. Autschbach, Kohn–Sham calculations of NMR shifts for paramagnetic 3d metal complexes: protocols, delocalization error, and the curious amide proton shifts of a high-spin iron(II) macrocycle complex, Phys. Chem. Chem. Phys., 2016, 18, 21051–21068.
24. P. B. Tsitovich, J. M. Cox, J. B. Benedict and J. R. Morrow, Six-coordinate Iron(II) and Cobalt(II) paraSHIFT Agents for Measuring Temperature by Magnetic Resonance Spectroscopy, Inorg. Chem., 2016, 55, 700–716.
25. L. Christiansen, D. N. Hendrickson, H. Toftlund, S. R. Wilson and C. L. Xie, Synthesis and structure of metal complexes of triaza macrocycles with three pendant pyridylmethyl arms, Inorg. Chem., 1986, 25, 2813–2818.
26. Antimicrobial Peptide Database. Journal.
27. J. Blahut, P. Hermann, Z. Tošner and C. Platas-Iglesias, A combined NMR and DFT study of conformational dynamics in lanthanide complexes of macrocyclic DOTA-like ligands, Phys. Chem. Chem. Phys., 2017, 19, 26662–26671.
28. S. Oh, A. G. Webb, T. Neuberger, B. Park and C. M. Collins, Experimental and numerical assessment of MRI-induced temperature change and SAR distributions in phantoms and in vivo, Magn. Reson. Med, 2010, 63, 218–223.
29. A. M. Funk, P. Harvey, K.-L. N. A. Finney, M. A. Fox, A. M. Kenwright, N. J. Rogers, P. K. Senanayake and D. Parker, Challenging lanthanide relaxation theory: erbium and thulium complexes that show NMR relaxation rates faster than dysprosium and terbium analogues, Phys. Chem. Chem. Phys., 2015, 17, 16507–16511.
30. E. A. Suturina, K. Mason, C. F. G. C. Geraldes, N. F. Chilton, D. Parker and I. Kuprov, Lanthanide-induced relaxation anisotropy, Phys. Chem. Chem. Phys., 2018, 20, 17676–17686.
31. J. C. Ott, E. A. Suturina, I. Kuprov, J. Nehrkorn, A. Schnegg, M. Enders and L. H. Gade, Observability of Paramagnetic NMR Signals at over 10 000 ppm Chemical Shifts, Angew. Chem., Int. Ed., 2021, 60, 22856–22864.
32. A. M. Funk, P. H. Fries, P. Harvey, A. M. Kenwright and D. Parker, Experimental Measurement and Theoretical Assessment of Fast Lanthanide Electronic Relaxation in Solution with Four Series of Isostructural Complexes, J. Phys. Chem. A, 2013, 117, 905–917.

---

Footnotes

† Electronic supplementary information (ESI) available. CCDC 2446484–2446490. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d5dt01149c

‡ Λ/Δ denote pendant arm helicity with respect to the pseudo-C₃ axis, λλλ/δδδ denote the configuration in each NCCN chelate ring.

§ Apical twist angles measured from the crystal structure data, using the torsion angle between the nitrogen atom of a pyridine and its connected TACN nitrogen, around the axis comprising the centroids of the “N3-py” and “N3-TACN”.

¶ Estimated hydrodynamic diameters of L^1a and L^2a complexes (10 and 15 Å respectively) from the crystal structures correspond to rotational correlation times of 100 and 400 ps at 298 K, using Stokes–Einstein law.

---