Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Copper(II) complex with a redox-noninnocent Schiff base bearing a tetraphenyldisiloxane unit: synthesis, structure and catalytic oxidation of cyclohexane†
Christopher
Wittmann
a,
Oleg
Palamarciuc
bc,
Mihaela
Dascalu
b,
Maria
Cazacu
 b,
Dmytro S.
Nesterov
b,
Dmytro S.
Nesterov
 *de,
Armando J. L.
Pombeiro
*de,
Armando J. L.
Pombeiro
 *e,
Peter
Rapta
*e,
Peter
Rapta
 *f and
Vladimir B.
Arion
*f and
Vladimir B.
Arion
 *ab
*ab
aUniversity of Vienna, Institute of Inorganic Chemistry, Währinger Strasse 42, 1090 Vienna, Austria
bInorganic Polymers Department, “Petru Poni” Institute of Macromolecular Chemistry, Aleea Gr. Ghica Voda 41 A, Iasi 700487, Romania. E-mail: vladimir.arion@univie.ac.at
cPhysics of Semiconductors and Devices Laboratory, Faculty of Physics and Engineering and Institute of Applied Physics, Moldova State University, MD-2009, Chişinău, Republic of Moldova
dCentro de Estudos de Engenharia Química, Instituto Superior de Engenharia de Lisboa, Instituto Politécnico de Lisboa, R. Conselheiro Emídio Navarro, 1, 1959-007 Lisboa, Portugal
eCentro de Química Estrutural, Institute of Molecular Sciences, Instituto Superior Técnico, Universidade de Lisboa, Av. Rovisco Pais, 1049-001 Lisboa, Portugal. E-mail: dmytro.nesterov@vis.isel.pt; dmytro.nesterov@tecnico.ulisboa.pt; pombeiro@tecnico.ulisboa.pt
fInstitute of Physical Chemistry and Chemical Physics, Faculty of Chemical and Food Technology, Slovak University of Technology in Bratislava, Radlinského 9, SK-81237 Bratislava, Slovak Republic. E-mail: peter.rapta@stuba.sk
First published on 17th June 2025
Abstract
An organic–inorganic diamine, 1,3-bis(aminopropyl)tetraphenyldisiloxane, was prepared and introduced as a flexible spacer into the structure of a salen-type Schiff base (H2L7) extending the available small library of similar compounds derived from 1,3-bis(aminopropyl)tetramethyldisiloxane and substituted 2-hydroxybenzaldehydes (H2L1–H2L6). Like the previously reported mononuclear copper(II) complexes [CuL1]–[CuL6], the new copper(II) complex [CuL7], obtained by reaction of Cu(OAc)2·H2O with H2L7 in a mixture of organic solvents, has a tetrahedrally distorted square-planar (N2O2) coordination geometry. X-ray crystallography has shown that compared to [CuL1]–[CuL6] the Si–O–Si angle in [CuL7] is even closer to linear due to stronger intramolecular interactions between Ph groups than between Me groups in the central–R2Si–O–SiR2– fragment (R = Ph and Me, respectively). [CuL7] can be electrochemically reversibly oxidised by two successive one-electron processes, generating stable phenoxyl mono- and diradicals. Both oxidations are ligand-centred, leading to the formation of coordinated phenoxyl radicals. The UV spectrum of [CuL7] consists of π → π* and LMCT σ → d transitions. The low-energy d–d absorption is well described by AILFT CAS(9,5)/NEVPT2 calculations. The one-electron oxidised compound [CuL7]+ should exist in the triplet ground state as 3[CuL7]+ with one unpaired electron located on the dx2−y2 orbital of copper(II) (d9, SCu = ½) and another electron on the molecular orbital (MO) comprising pz oxygen and carbon atoms of the phenoxyl radical (Srad = ½). The broad absorption in the vis-NIR region of the optical spectrum of the one-electron oxidised complex is due to intervalence charge transfer in the triplet species 3[CuL7]+, but not in the [CuL7]2+ one. The doubly oxidised [CuL7] species shows very close doublet and quartet states, where the doublet state has an unpaired electron located on the Cu(II) d-orbital, while the quartet state has one unpaired electron on the Cu(II) d-orbital and two unpaired electrons on π-bonding orbitals. In all state-averaged CASSCF cases, the occupation of the Cu(II) d-orbital is nearly 1.0, indicating its limited involvement in the excited states. Catalytic studies showed that [CuL7] acts as a catalyst for the oxidation of alkanes with peroxides under very unusual solvent-free conditions, converting cyclohexane into cyclohexanol and cyclohexanone (with hydrogen peroxide or tert-butyl hydroperoxide as the oxidant) or into cyclohexanol and ε-caprolactone (with m-chloroperoxybenzoic acid as the oxidant). Theoretical investigations of the catalytic reaction mechanisms disclosed the principal intermediates.
Introduction
Recently, we reported that 2-hydroxybenzaldehyde and related derivatives react with 1,3-bis(3-aminopropyl)tetramethyldisiloxane in the presence of Ni(II), Cu(II) or Zn(II) in a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio with the formation of tetrahedrally distorted square-planar metal(II) complexes of tetradentate Schiff bases with a trans-arrangement of N2O2 donor atoms.1–6 The most interesting feature is the formation of a 12-membered central chelate ring including the tetramethyldisiloxane unit, which separates the aliphatic chains, significantly diminishing the mechanical strain in the emerging chelate ring. This was called a “shoulder yoke effect”.
1 molar ratio with the formation of tetrahedrally distorted square-planar metal(II) complexes of tetradentate Schiff bases with a trans-arrangement of N2O2 donor atoms.1–6 The most interesting feature is the formation of a 12-membered central chelate ring including the tetramethyldisiloxane unit, which separates the aliphatic chains, significantly diminishing the mechanical strain in the emerging chelate ring. This was called a “shoulder yoke effect”.
In addition to basic research interest, the reported metal complexes with open-chain and macrocyclic Schiff bases have found application in catalysis. Some of the potential candidates for such catalysts are polynuclear or mononuclear Cu(II) complexes with tetramethyldisiloxane-spaced hexadentate macrocyclic ligands or potentially tridentate or tetradentate Schiff bases bearing trimethylsilane units, as shown in Chart 1. Oxidation of cyclohexane with H2O2 in acetonitrile/water (ACN/H2O) in the presence of tetranuclear copper(II) complexes with macrocyclic (I) and open-chain (II) disiloxane-spaced ligands afforded 8% total product yield after ca. 30 min.7 Addition of trifluoroacetic acid (TFA) improved the catalytic performance of the complexes by increasing the total product yield to 14% after ca. 1 h. Cu(II) complexes of type III, especially those with electron-withdrawing substituents, such as chloro, bromo and nitro on the aromatic ring, showed high catalytic activity in the aerobic oxidation of benzyl alcohol to benzaldehyde, mediated by the TEMPO radical, under mild conditions in the presence of K2CO3 as a base with overall yields and TONs up to 99% and 990, respectively.2 A tetranuclear Zn(II) complex with four Schiff base entities built on an oligomeric silsesquioxane (known as POSS) core was reported recently to act as an effective catalyst in the cycloaddition reactions of CO2 with terminal alkyl and aryl epoxides under mild conditions, while tolerating different functionalities including halide and ether groups.8
The flexible siloxane unit confers specific features to these Schiff bases, such as low intermolecular forces, low surface free energy, large free volume, good thermal, oxidative and UV–vis stability, good environmental compatibility and biocompatibility. One critical issue is associated with the requirement for efficient catalyst recycling. Recycling of the catalysts is essential for a practical and cost-effective implementation. A possible approach to resolve this problem is the application of a heterogeneous catalyst (a MOF or coordination polymer resistant to the operating conditions) that is totally insoluble in the reaction mixture (usually, an ACN or ACN/H2O mixture).
Another strategy suggests the use of a hydrophobic catalyst, which is predicted to be selectively soluble in apolar alkane substrates (e.g., cyclohexane), but insoluble in the liquid polar oxidation products of alkanes (e.g. cyclohexanol and cyclohexanone). In this case, no solvent is required (that is very attractive from the ecological point of view), and the catalyst might be precipitated and easily separated for recycling after the formation of the reaction products. In this context, we aimed (i) to replace the tetramethyldisiloxane unit by a more lipophilic disiloxane unit, (ii) to prepare a Schiff base and a copper(II) complex, (iii) to study the influence of this new unit on complex formation, and its structure, stability, lipophilicity and solubility in apolar solvents, (iv) to investigate whether the complex exhibits noninnocent behaviour9–14 and (v) to evaluate its potential to act as a catalyst in the oxidation of cyclohexane in the absence of other solvents. While the aerobic solvent-free oxidation of cyclohexane is a common subject of investigation, the respective solvent-free oxidations with organic peroxides are much less studied and, moreover, there is a lack of knowledge about the behaviour and catalytic decomposition of organic oxidants under such conditions.
Herein, we report on the multistep synthesis and the spectroscopic and structural characterisation of the Schiff base, H2L7, derived from 3,5-di-tert-butyl-2-hydroxybenzaldehyde and 1,3-bis-(3-aminopropyl)tetraphenyldisiloxane, as well as its Cu(II) complex [CuL7] (see Scheme 1). The noninnocent behaviour of [CuL7] was disclosed by electrochemical and spectroelectrochemical measurements and supported by DFT and CASSCF calculations. The application of the complex with a redox-active ligand as a catalyst in the oxidation of cyclohexane in the very unusual absence of any other solvent (by taking advantage of the solubility of the complex in the alkane substrate) was disclosed. The effect of the oxidant on the degree of cyclohexane oxidation and thus on the types of obtained oxidised products was also investigated. The key intermediates of the catalytic reactions were studied using DFT calculations.
Results and discussion
Synthesis of H2L7 and [CuL7]
The synthesis of H2L7 was performed in seven chemical steps, as shown in Scheme 1. The synthesis of H2L7 started from diphenyldichlorosilane (A) by reaction with 3-chloropropan-1-ol in the presence of N,N-diisopropylethylamine (DIPEA) as a base in dry toluene to afford 3-chloropropoxydiphenylsilyl chloride (B) in 88% yield. Further reaction of species B with Na0 in dry boiling toluene resulted in the formation of 1,1-diphenyl-1-sila-2-oxacyclopentane (C) in 27% yield. In the next step, species C was hydrolysed in boiling dioxane by addition of water and a small amount of 1 M HCl to give the crude diol D in 90% yield. The structure of the diol was confirmed by X-ray crystallography and is shown in Fig. S1 in the ESI.†Species D was then converted into dimesylate E in 72% yield by reaction with mesyl chloride in DCM, in the presence of triethylamine. Thereafter, the quantitative reaction of species E with sodium azide in DMF upon heating led to the formation of diazido species F, which was then catalytically reduced with H2 in the presence of Pd/C to a diamine and isolated as a crude lyophilisate of diammonium formate salt G. Purification of this species on reverse-phase HPLC was required to give a white cloudy solid in 31% yield. The condensation reaction of the pure product G with 3,5-di-tert-butyl-2-hydroxybenzaldehyde in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 molar ratio in methanol in the presence of triethylamine afforded the Schiff base H2L7 (Scheme 1) in 83% yield. The number of resonances in the 1H, 13C, and 29Si NMR spectra of species G and Schiff base H2L7 in DMSO-d6 (see Fig. S2–S7†) was in accordance with the two-fold symmetry of the molecule in solution. The ESI mass spectra of species C, D, E and G are shown in Fig. S8–S12.† The positive-ion ESI mass spectrum of H2L7 showed a strong peak with m/z 929.62 (Fig. S13†) attributed to the [M + H+]+ ion. The reaction of H2L7 with Cu(OAc)2·H2O in chloroform/methanol 1
2 molar ratio in methanol in the presence of triethylamine afforded the Schiff base H2L7 (Scheme 1) in 83% yield. The number of resonances in the 1H, 13C, and 29Si NMR spectra of species G and Schiff base H2L7 in DMSO-d6 (see Fig. S2–S7†) was in accordance with the two-fold symmetry of the molecule in solution. The ESI mass spectra of species C, D, E and G are shown in Fig. S8–S12.† The positive-ion ESI mass spectrum of H2L7 showed a strong peak with m/z 929.62 (Fig. S13†) attributed to the [M + H+]+ ion. The reaction of H2L7 with Cu(OAc)2·H2O in chloroform/methanol 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.3 produced green crystals suitable for single-crystal X-ray diffraction (SC-XRD) upon cooling the solution to room temperature. The positive-ion high-resolution ESI mass spectrum of the complex showed a peak with m/z 990.4615, which could be assigned to [CuL7 + H+]+ and a peak with m/z 495.7338 attributed to the doubly charged ion [CuL7 + 2H+]2+ (Fig. S14 and S15†). Both experimental isotopic patterns were in good agreement with theoretical isotopic distributions. The formation of the complex and its coordination geometry, as well as other peculiarities of the molecular structure of [CuL7] were established by SC-XRD.
1.3 produced green crystals suitable for single-crystal X-ray diffraction (SC-XRD) upon cooling the solution to room temperature. The positive-ion high-resolution ESI mass spectrum of the complex showed a peak with m/z 990.4615, which could be assigned to [CuL7 + H+]+ and a peak with m/z 495.7338 attributed to the doubly charged ion [CuL7 + 2H+]2+ (Fig. S14 and S15†). Both experimental isotopic patterns were in good agreement with theoretical isotopic distributions. The formation of the complex and its coordination geometry, as well as other peculiarities of the molecular structure of [CuL7] were established by SC-XRD.
X-ray crystallography
The result of the crystallographic study of [CuL7]·0.875CHCl3·0.375CH3OH is shown in Fig. 1. The complex crystallized in a noncentrosymmetric monoclinic space group P21. There are two crystallographically independent molecules in the asymmetric unit. The crystal contains interstitial solvent (CHCl3 and MeOH). In the following discussion, the co-crystallised solvent will not be included in the formula. Selected metric parameters, quite similar for both crystallographically independent molecules, are summarized in Table 1 and compared to those in related complexes [CuL1] and [CuL6] (see Chart 1, structure III). The tetradentate Schiff base is coordinated to Cu(II) via two phenolato oxygen donors O1 and O2 and two azomethine nitrogen atoms N1 and N2 (for the one crystallographically independent molecule of [CuL7] shown in Fig. 1). Upon coordination of the tetradentate ligand to Cu(II), two six-membered rings and one central 12-membered ring were formed as reported previously for other 3d metal complexes with analogous type III Schiff bases bearing a tetramethyldisiloxane unit (Chart 1, structure III).2,3 The bond lengths from Cu(II) to N and O donor atoms are well-comparable with those in [CuL6] (Table 1). The Cu(II) ion has a strongly tetrahedrally distorted square-planar (N2O2) coordination geometry. The degree of tetrahedral distortion of coordination geometry in four-coordinate complexes characterised by three descriptors (τ4,15τδ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 16 and
16 and  17) yields values very close to 0.4 when applied to [CuL7] and comparable with those observed previously in [CuL1] and [CuL6] (see Table 1). The value of τ4 in four-coordinate metal complexes varies from 0 for an ideal square-planar geometry to 1 for a perfect tetrahedral geometry. The values of τ4, τδ and
17) yields values very close to 0.4 when applied to [CuL7] and comparable with those observed previously in [CuL1] and [CuL6] (see Table 1). The value of τ4 in four-coordinate metal complexes varies from 0 for an ideal square-planar geometry to 1 for a perfect tetrahedral geometry. The values of τ4, τδ and  close to 0.4 are indicative of a see-saw or sawhorse coordination geometry in all these complexes.18
close to 0.4 are indicative of a see-saw or sawhorse coordination geometry in all these complexes.18
| Bond length, Å | [CuL7] | [CuL1] | [CuL6] |
|---|---|---|---|
a
τ
4 = 360 − (α + β)/141, where α and β are the two largest angles at the Cu atom.
b
τ
δ = τ4 × (α/β), where α and β are the two largest angles at the Cu atom.
c
 = (β − α)/(360 − θ) + (180 − β/180 − θ), where α and β(β > α) are the two largest angles at the Cu atom and the θ value is cos−1(−1/3) ≈ 109.5°.
d Second crystallographically independent molecule in the asymmetric unit.
e The actual formula is [CuL7]·0.875CHCl3·0.375CH3OH. = (β − α)/(360 − θ) + (180 − β/180 − θ), where α and β(β > α) are the two largest angles at the Cu atom and the θ value is cos−1(−1/3) ≈ 109.5°.
d Second crystallographically independent molecule in the asymmetric unit.
e The actual formula is [CuL7]·0.875CHCl3·0.375CH3OH.
|
|||
| Cu1–N1 [Cu2–N3]d | 1.958(4) [1.953(4)] | 1.960(2) | 1.963(3) |
| Cu1–N2 [Cu2–N4]d | 1.962(5) [1.974(5)] | 1.963(2) | 1.965(3) |
| Cu1–O1 [Cu2–O4]d | 1.903(4) [1.897(4)] | 1.882(1) | 1.913(2) |
| Cu1–O2 [Cu2–O5]d | 1.892(4) [1.899(4)] | 1.886(1) | 1.899(2) |
| Si1–O3 [Si3–O6]d | 1.623(4) [1.629(4)] | 1.629(4) | 1.610(4) |
| Si2–O3 [Si4–O6]d | 1.626(4) [1.618(4)] | 1.614(2) | 1.616(3) |
| Bond angles (°) | |||
| O1–Cu1–O2 [O4–Cu2–O5]d | 150.86(18) [153.27(17)] | 147.77(7) | 154.2(1) |
| O1–Cu1–N1 [O4–Cu2–N3]d | 93.7(2) [92.52(18)] | 94.52(7) | 92.7(1) |
| O2–Cu1–N1 [O5–Cu2–N3]d | 93.46(19) [93.50(19)] | 95.65(7) | 92.5(1) |
| O1–Cu1–N2 [O4–Cu2–N4]d | 93.33(18) [92.84(18)] | 93.48(6) | 94.3(1) |
| O2–Cu1–N2 [O5–Cu2–N4]d | 94.50(18) [93.41(18)] | 94.26(7) | 92.5(1) |
| N1–Cu1–N2 [N3–Cu2–N4]d | 149.9(2) [153.22(19)] | 147.28(7) | 153.1(2) |
| Si1–O3–Si2 [Si3–O6–Si4]d | 172.1(3) [173.8(3)] | 169.75(2) | 161.1(3) |
τ
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
0.420 [0.380] | 0.460 | 0.374 |
τ
δ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
0.417 [0.380] | 0.458 | 0.371 |
 ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c |
0.417 [0.379] | 0.459 | 0.370 |
The Si–O–Si bond angle in [CuL7] with a tetraphenyldisiloxane unit is close to linear and larger by 11.5–12.5° than in the analogous complex [CuL6] with a tetramethyldisiloxane moiety (see Table 1). This is likely due to stronger repulsions between phenyl groups in [CuL7] than between the methyl groups attached to Si atoms in [CuL6], while the tetrahedral distortion of the square-planar coordination geometry is substantial and close in both complexes (see Table 1). Wide variability of the Si–O–Si bond angle is reported in the literature. Specifically, in dioxadisilethane, it is 93.5°,19 and in quartz, it is 143.7°,20 while in hexaphenyldisiloxane, this angle is linear.21,22 In contrast to the linear Si–O–Si angle in Ph3Si–O–SiPh3, the C–O–C angles in Ph3C–O–CPh3 and Ph2CH–O–CHPh2 are 127.8 and 113.3°, respectively.23–25 The close to linear Si–O–Si angle is not only the result of minimisation of the effects of steric repulsion of the phenyl groups and optimisation of the delocalisation of the electron density between the oxygen and silicon atoms, but also due to the predominantly ionic character of the Si–O bonds and the highly polarised covalent Si–C bonds.2 This was evidenced by both charge density and DFT calculations, which disclosed that the second derivative of electron density at the bond critical points (BCPs) ∇2ρ (rBCP) for the two Si–O bonds in [CuL1] is positive, as was also the case for difluorobis[N-(dimethylamino)phenylacetimidato-N,O]silicon26 with a predominantly ionic character of the Si–O bond and NaCl.2
The crystal structure consists of neutral molecules [CuL7] which form channels along the a-axis of the unit cell, in which interstitial chloroform and methanol molecules are localised. The volume of the voids per unit cell is 666.9 Å3 (see Fig. S16 in the ESI†).
Cyclic voltammetry and spectroelectrochemistry
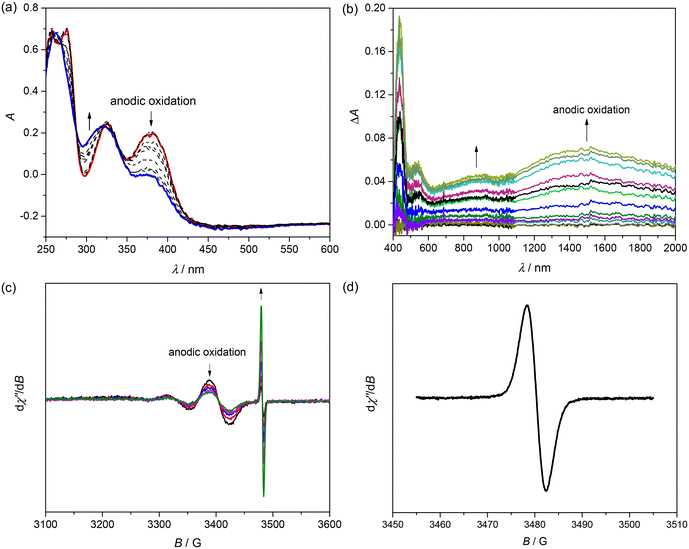
The cyclic voltammogram (CV) of [CuL7] in dichloromethane (DCM) in the presence of 0.1 M tetrabutylammonium hexafluorophosphate (nBu4NPF6) as a supporting electrolyte shows two reversible oxidations in the anodic region at 0.55 and 0.85 V vs. the ferricenium/ferrocene couple as shown in Fig. 2a.The optical spectrum of [CuL7] in DCM shows three strong absorptions with maxima at 275, 327 and 380 nm and one weak and broad absorption between 550 and 750 nm (Fig. 2b, blue trace). The detailed characterisation of the observed transitions will be provided in the theoretical part below. The broad-line EPR spectrum of [CuL7] in 0.2 M nBu4NPF6 in DCM at room temperature (inset in Fig. 2b) is characteristic of paramagnetic Cu(II) (d9, SCu = ½).
Upon anodic oxidation of [CuL7] in 0.2 M nBu4NPF6 in DCM at the first oxidation peak, the optical bands at 275, 327 and 380 nm decrease and a new UV band at 304 nm emerges (Fig. 3a). Simultaneously, several weak optical bands appear in the vis–NIR region at 530, 880 and 1500 nm (Fig. 3b), which are typical of phenoxyl radicals (difference spectra were measured during the experiment due to the low-intensity transitions in the vis–NIR region).27 A decrease in the intensity of the room-temperature Cu(II) (d9, SCu = ½) EPR signal was also observed after anodic oxidation of [CuL7] in 0.2 M nBu4NPF6 in DCM when using a large Pt mesh working electrode (Fig. 3c). Additionally, a new EPR spectrum characteristic of an organic radical (g factor ∼2.002) appears at more positive potentials (see the details in Fig. 3d).
Upon progressing to the region of the second oxidation peak, the optical band at 304 nm steadily increases, as shown in Fig. 4a. All oxidation processes seem to be chemically reversible as illustrated by the 3D plots of the spectroelectrochemical responses in Fig. 4c and d.
We also studied the optical absorption properties of the chemically oxidised complex [CuL7] using tris(4-bromophenyl)ammoniumyl hexachloroantimonate (Magic Blue, MB) as a single-electron oxidising agent. The vis–NIR absorption spectra resulting from the chemical oxidation of the initial [CuL7] (black trace) in DCM using MB (red trace: 0.8 equiv.; blue trace: 1.1 equiv.) are shown in Fig. 5a. The corresponding spectrum measured after one-electron anodic oxidation of [CuL7] in DCM/0.2 M nBu4NPF6 (Fig. 5b) is well-defined and almost identical to those recorded upon chemical oxidation (Fig. 5a).
Considering a quite recent comprehensive review describing the properties and reactivities of a variety of Cu(II)-phenolato and Cu(II)-phenoxyl radical complexes,28 we compared the experimentally measured vis–NIR spectra of the mono-oxidised species [CuL7]+ with the well-documented examples of one-electron oxidised Schiff base complexes with substituted phenolato moieties.29–32 These Cu(II)-salen-type complexes were oxidised to form mainly the Cu(II)-phenoxyl radical species with the localised unpaired electron on one of the two phenolic moieties both in the solid state and in solution. Note that our vis–NIR spectra are very similar to those reported for Cu(II)-phenoxyl radical species. The X-ray diffraction structures clearly suggested that the unpaired electron is mainly localised on one of the two phenolic moieties.29–31 Therefore, based on these literature data and on the Robin and Day classification of mixed-valence systems, the NIR band at 6490 cm−1 (1540 nm) can be well described as the intervalence charge transfer (IVCT) band of Class II with a Cu(II)-localised phenoxyl radical.
Thus, [CuL7] can be reversibly oxidised by two successive one-electron processes with the generation of stable phenoxyl mono- and diradicals as also reported previously for other systems.27,33 In other words, both oxidations are ligand-centred and lead to the formation of coordinated phenoxyl radicals [CuL7]˙+ and [CuL7]2˙2+. Copper(II)-phenoxyl mono-radical species are known to undergo intramolecular magnetic exchange interactions between the unpaired electron on the Cu(II) d-orbital (d9, S = ½) and the phenoxyl radical (Srad = ½) leading to either the diamagnetic ground state (ST = 0) via antiferromagnetic spin coupling or the triplet ST = 1 ground state via ferromagnetic spin–spin interaction. In both cases, full or nearly full disappearance of the EPR signal is observed. The nearly silent triplet ground state is difficult to observe because of its closeness to the X-band energy quantum (0.35 cm−1) zero-field splitting parameters documented for Cu(II) phenoxyl radical salen-type complexes.34–36 This intramolecular magnetic spin interaction will be discussed in more detail below.
Theoretical calculations
| No solv. | CH2Cl2 | CyH | MeCyH | cis-1,2-DMCH | MeCN | MeOH | |
|---|---|---|---|---|---|---|---|
| Angle | −21.39 | −23.97 | −23.24 | −23.23 | −23.19 | −23.79 | −24.24 |
The compound [CuL7c] was subjected to TDDFT calculations at the PBE0/aug-cc-pVDZ-DK/aug-cc-pVTZ-DK (for Cu) level. The presence of diffuse functions in the basis set is known to be essential for accurate prediction of the energies of excited states.37 The numerical results of the TDDFT calculations strongly depend on the DFT functional; thus a careful choice of the latter is crucial for obtaining relevant spectra. The PBE0 functional was earlier demonstrated to have a balanced accuracy for TDDFT calculations of metal complexes, and hence, it was used in the present case.38,39 The theoretical UV–vis spectrum in the range of 200–1000 nm is shown in Fig. 6b.
The four lowest-energy excited states S1–S4 originate from d–d transitions, while the others are mostly due to the aromatic fragments of the ligands. The overall view of the TDDFT spectrum follows the experimental one. The most prominent bands of the spectrum are due to the strong transitions to the S12, S21 and S31 excited states (340.3, 300.5 and 254.2 nm, respectively). While the S12 and S31 states are of the typical π → π* nature and originate from the transitions within the aromatic fragments of the ligands, the S21 state has the LMCT σ → d character involving the dx2−y2 orbital of Cu(II).
Despite the efficiency of the TDDFT method for the prediction of the π → π* transitions, it lacks accuracy in the description of the lower-energy transitions within the d-shell of the metal centres. The presence of a single metal ion in [CuL7c] enabled the possibility of Ab Initio Ligand Field Theory (AILFT) calculations based on the CAS(9,5) active space with the NEVPT2 correction. Here and further, the CASSCF studies were performed employing the def2-TZVP basis set for Cu(II), its N,O-donor coordination environment and the carbon atoms of the aromatic rings and Schiff base groups, keeping all other atoms at the def2-SVP level. The fully occupied orbitals of Cu(II) in the [CuL7c] group in two degenerate levels dxz/dxy and dz2/dyz, while the singly occupied dx2−y2 one has significantly higher energy (Fig. 6c). The CAS(9,5) space allows for four possible transitions to the S1–S4 states, from which the excitation S0 → S4 (dz2 → dx2−y2) is the strongest one. The broad line has a maximum at 547.0 nm (Fig. 6d) which matches well with the experimentally observed shoulder at 600 nm (see Fig. 2b).
The interaction of the five d-orbitals and all pz orbitals of the aromatic rings results in the huge CAS(21,17) active space which, unfortunately, under our conditions could not be handled in a reasonable time even with ICE or DMRG approximations. Another obstacle is the limited participation of the lower-lying Cu(II) d-orbitals in the excited states, which results in their occupations close to 2 with the subsequent tendency of these orbitals to run out from the active space. Therefore, for further studies, we have limited the active space by involving only one Cu(II) d-orbital (the half-occupied dx2−y2 one) leading to a reasonable CAS(13,13) state-averaged calculation with 6 roots. The respective active space natural orbitals are depicted in Fig. S17.† They can be grouped into π-bonding and π-antibonding orbitals as well as the Cu(II) dx2−y2 orbital. As for AILFT calculations, the ground state of [CuL7c] in terms of the CAS(13,13) space features an unpaired electron located on the dx2−y2 orbital, while the π-bonding ones are doubly occupied.
The absorption spectrum reconstructed from the CAS(13,13) study of [CuL7c] is shown in Fig. S18,† right. Only the S0 → S5 transition shows a notable oscillator strength with a wavelength of 288.1 nm. This transition is of the π → π* type and involves several excitations, from which one is dominant (57%). The corresponding excitation S31 from the TDDFT calculation has a close wavelength of 254.2 nm (Fig. 6b). The excited states of [CuL7c] were also evaluated using the MC-RPA model with the CAS(1,2) state-specific starting configuration and 14 roots. Although the overall shape of the MC-RPA-generated spectrum (Fig. S19†) does not fit well with the experimental one, it correctly predicts the grouping of the transitions into the weak d → d and strong π → π* ones. The singly oxidised forms of [CuL7] were optimised and truncated in the same manner as the non-oxidised form produces 3[CuL7c]+, 2[CuL7c]2+ and 4[CuL7c]2+ model fragments. The vertical and adiabatic first ionisation energies of [CuL7] were estimated to be 5.4 and 5.2 eV, respectively (PBE0/def2-TZVPP single-point energies after PBE0/def2-TZVP optimisation in DCM medium). The small difference in these values originates from the close geometries of the natural ([CuL7]) and oxidised (3[CuL7]+) forms. The dihedral θ(O–N–O–N) for 3[CuL7]+ is −25.56°. Remarkably, an attempt to optimise the oxidised form in a singlet state failed, producing an unrealistic geometry with “twisted” ligands. The spin densities obtained at the various levels of theory are shown in Fig. 7a.
Both DFT and state-specific CASSCF predict the unpaired electrons to be localised on the dx2−y2 copper(II) orbital and the ligand-centred molecular orbital that involves pz carbon and oxygen atomic orbitals. The DFT broken-symmetry calculation of 3[CuL7c]+ predicts the ferromagnetic ground state with J = 252.08 cm−1 (for Ĥ = –2JŜ1Ŝ2 Hamiltonian), confirming the triplet spin state to be energetically favorable. The calculations performed for the whole 3[CuL7]+ molecule resulted in a very close value of J = 251.83 cm−1. These observations indicate that the influence of the siloxane moiety on the electronic structure of the Cu(II) chromophore is negligible, in agreement with the above TDDFT studies (Fig. 6a). The unrestricted corresponding (“magnetic”) orbital of the broken-symmetry solution shows an overlap value S = 0.0023, where the α and β operators indicate the interacting electrons to be localised in the same manner as for SS-CASSCF and DFT (Fig. 7b). The inability to see the S = 1 EPR signal after the one-electron oxidation step in our experiments even at low temperatures might be due to the properties of the triplet being unsuitable for observation by conventional X-band EPR spectroscopy and by the temperature limit (100 K) in our laboratory.
The state-averaged CAS(12,13) solution resulted in the triplet ground spin state after the SC-NEVPT2 correction, with the first singlet state lying 112 cm−1 above. The absorption spectrum reconstructed from the CAS(12,13)/NEVPT2 calculated excitation energies and oscillator strengths is shown in Fig. 7c, left. The three lowest excitations are of π → π* nature, where the acceptor π-bonding orbital is singly occupied, stipulating the low energy of these transitions. No transitions involving the Cu(II) dx2−y2 orbital were observed. The excited states S4 and S5 of low intensity are based on the π → π* transitions.
The TDDFT calculations of 3[CuL7c]+ confirm the presence of a strong absorption band in the vis–NIR region (Fig. 8a). As for CASSCF studies, the first excited state involves the singly occupied π-orbital as an acceptor. The following series of transitions to the S2–S5 states is in the low-energy visible region and comprises π → π* and π → d transitions. The structure of the UV region is only slightly affected by the oxidation of the molecule. The MC-RPA model applied for 3[CuL7c]+ starting from the CAS(2,2) state-specific solution also showed an increase in low-energy absorbance, showing the transitions of similar nature (Fig. 8b).
From the DFT single-point and broken-symmetry calculations, as well as the CASSCF ones, all indicating the triplet ground spin state, the existence of 3[CuL7c]+ with a formal Cu(I) or Cu(III) oxidation state is not likely. To further correlate these results with the experimental data, we calculated the adiabatic ionisation energies of a series of related copper(II) complexes with salen-type ligands, for which the redox potentials have been determined under similar conditions.28 After optimisation of the respective non-oxidised doublet and oxidised triplet forms and calculation of the single-point energies at the higher DFT level (ωB97M-V/def2-QZVPP), a clear dependence of the redox potential vs. ionisation energy appeared (Fig. S20, Tables S2 and S3†). Within this dependence, the position of the complex [CuL7] stands far from that of compound f (Fig. S20†) for which the formal Cu(III) oxidation state was proposed upon (electro)chemical oxidation in solution,40 providing further evidence of the Cu(II) oxidation state in the one-electron oxidised [CuL7].
DFT geometry optimisations of the doubly oxidised complex [CuL7] were performed for both doublet and quartet spin states, 2[CuL7c]2+ and 4[4CuL7c]2+, resulting in indistinguishable geometries (Fig. 9a). Hence, both these structures can be used for calculations of both ground spin states. The DFT single-point calculations at the ωB97M-V/def2-QZVPP level indicated ΔE = 401.9 cm−1 between 4[CuL7c]2+ and 2[CuL7c]2+ with the prevalence of the quartet state. The TDDFT predicts that the spectra of 2[CuL7c]2+ and 4[CuL7c]2+ are almost equal with the lowest transition located around 800 nm (Fig. 9b). The DFT-calculated spin densities of the quartet state show an expected plot with the three unpaired electrons distributed over the π ligand and Cu(II) dx2−y2 orbitals (Fig. 9b, right), while in the doublet model, the single unpaired electron is located on the broad molecular orbital that involves both aromatic ligands (Fig. 9b, left). Hence, the CASSCF studies were invoked to understand the physical nature of these states.
The SA-CAS(11,13) calculations with the SC-NEVPT2 ones on top of that suggested the quartet ground spin state of doubly oxidised [CuL7c]2+. However, in contrast to the [CuL7c]+ species, the first state of different multiplicity is practically of the same energy as the ground state ΔE = 11.7 cm−1 and the next doublet state is 145.4 cm−1 above the ground quartet state. The electron configuration of the lowest doublet state is of multideterminant character where the two π-bonding orbitals of the ligand have almost equal [20] and [02] configurations, while the Cu(II) dx2−y2 orbital remains singly occupied. The 4S0 → 4S1 excitation is located at 780 nm and constitutes π → π* transitions (Fig. S21†). No excitations in the NIR region were found. The MC-RPA calculations based on the SS-CAS(3,3) ground state also confirm the absence of NIR-located transitions (Fig. S22†).
 | ||
| Scheme 2 Solvent-free oxidation of cyclohexane with H2O2, tert-butyl hydroperoxide (TBHP) and m-chloroperoxybenzoic acid (mCPBA) catalyzed by [CuL7]. | ||
Replacement of H2O2 as an oxidant with tert-butyl hydroperoxide (TBHP) under similar solvent-free conditions (1 M of the oxidant) resulted in a large amount of CyOOH (Fig. S24 and S25†). The peak of CyOOH (Fig. S25†) underwent gradual disappearance upon the addition of PPh3 due to its quantitative reduction to cyclohexanol, leading to a high alcohol/ketone ratio of 3.7 (Fig. S24†). The final total yield of cyclohexanol and cyclohexanone was 9.0% relative to TBHP. A notable amount of di-tert-butylperoxide, DTBP, was detected as a reaction product, indicating the participation of long-lived tBuO˙ radicals in the catalytic cycle (Fig. S26†).
Solvent-free oxidation of cyclohexane with m-chloroperoxybenzoic acid (mCPBA) was performed by using a lower concentration of the oxidant (0.1 M) due to the limited solubility of mCPBA in hydrocarbons and due to the production of a large amount of poorly soluble m-chlorobenzoic acid (mCBA). As mCPBA can produce a range of radical species (ArC(O)OO˙, ArC(O)O˙ and Ar˙) as well as oxidise substrates via a concerted mechanism (Scheme 3),48,49 identification of the exact mechanism of mCPBA action is often a challenging task. The main products obtained after 24 h of the solvent-free reaction of mCPBA with cyclohexane catalysed by [CuL7] (1 mM) are cyclohexanol, ε-caprolactone and cyclohexene oxide (Fig. S27†), while only traces of cyclohexanone were detected. The latter fact can be explained by the efficient Baeyer–Villiger reaction of cyclohexanone with mCPBA catalysed by [CuL7] (Scheme 2). Hence, the formation of ε-caprolactone requires 2 equiv. of mCPBA, which should be taken into account when calculating the yields. The overall yield of products is 62.4% relative to mCPBA, of which 29.1% corresponds to cyclohexanol, 3.0% to cyclohexene oxide and 29.8% to ε-caprolactone. The yield of cyclohexanone does not exceed 0.5%. A blank test in the absence of the catalyst gave cyclohexanol as a single product with 3.0% yield after 24 h.
Oxidation of methylcyclohexane revealed a normalised 3°![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2° selectivity of 15
2° selectivity of 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
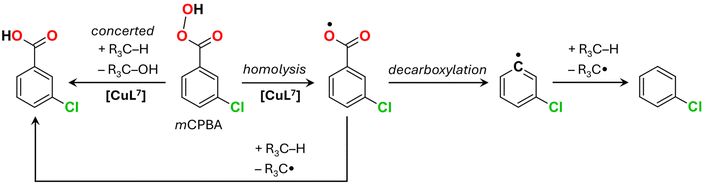
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 which is consistent with the participation of ArC(O)O˙ as an H-abstracting radical.50,51 The absence of stereoselectivity in the oxidation of cis-1,2-dimethylcyclohexane (ESI and Fig. S28–S31† there) agrees with the above assumption, confirming the existence of long-lived alkyl radicals in accordance with the homolytic O–O mCPBA bond splitting route (Scheme 3). However, the amount of chlorobenzene as a side product generated by the [CuL7]/mCPBA catalytic system upon the oxidation of cyclohexane is surprisingly low, only 2.5%. This result contradicts the common observation of large amounts of chlorobenzene in Cu(II) or Ni(II)-catalysed oxidations of alkanes in ACN or DCM media.50,52 Chlorobenzene is formed through the decarboxylation of the ArC(O)O˙ radical with the subsequent abstraction of the H-atom by the Ar˙ radical (Scheme 3). In turn, the ArC(O)O˙ radical is generated via the homolytic splitting of the O–O bond of mCPBA.48,49 The low amount of the chlorobenzene by-product in the case of the [CuL7]/mCPBA system indicates either the reaction of the ArC(O)O˙ radical with the substrate prior to its decarboxylation or heterolytic splitting of the oxidant. Since the latter pathway is not favourable for Cu(II) complexes which do not form stable high-valent copper-oxo species, fast consumption of the ArC(O)O˙ radical upon reaction with the alkane could be an explanation. Other details including the evolution of the optical spectra of [CuL7] in the presence of mCPBA and different substrates and the GC chromatograms of different substrates can be seen in Fig. S32–S35.†
1 which is consistent with the participation of ArC(O)O˙ as an H-abstracting radical.50,51 The absence of stereoselectivity in the oxidation of cis-1,2-dimethylcyclohexane (ESI and Fig. S28–S31† there) agrees with the above assumption, confirming the existence of long-lived alkyl radicals in accordance with the homolytic O–O mCPBA bond splitting route (Scheme 3). However, the amount of chlorobenzene as a side product generated by the [CuL7]/mCPBA catalytic system upon the oxidation of cyclohexane is surprisingly low, only 2.5%. This result contradicts the common observation of large amounts of chlorobenzene in Cu(II) or Ni(II)-catalysed oxidations of alkanes in ACN or DCM media.50,52 Chlorobenzene is formed through the decarboxylation of the ArC(O)O˙ radical with the subsequent abstraction of the H-atom by the Ar˙ radical (Scheme 3). In turn, the ArC(O)O˙ radical is generated via the homolytic splitting of the O–O bond of mCPBA.48,49 The low amount of the chlorobenzene by-product in the case of the [CuL7]/mCPBA system indicates either the reaction of the ArC(O)O˙ radical with the substrate prior to its decarboxylation or heterolytic splitting of the oxidant. Since the latter pathway is not favourable for Cu(II) complexes which do not form stable high-valent copper-oxo species, fast consumption of the ArC(O)O˙ radical upon reaction with the alkane could be an explanation. Other details including the evolution of the optical spectra of [CuL7] in the presence of mCPBA and different substrates and the GC chromatograms of different substrates can be seen in Fig. S32–S35.†
The large size of the molecule of [CuL7], augmented with the oxidant and/or substrate binding, excluded the possibility of the use of a PBE0/def2-TZVP level of theory for the calculation of the vibrational energy. Hence, the composite DFT method B97-3c was applied,53 which is among the lightest methods producing reliable geometries and frequencies.54 The electronic energies of the optimised structures were recalculated at the PBE0/def2-TZVPP level. It should however be stressed that even at this level, the search for the transition states was not computationally feasible. Therefore, the current study is focused on the stable intermediates (IMs) only. The interaction of TBHP (tBuOOH) with a Cu(II) or Cu(I) catalyst under aerobic conditions is known to proceed through the following general steps (1)–(4). The experimental observation of di-tert-butylhydroperoxide (Fig. S26†) agrees with reaction (3), while its direct formation from the coupling of two tBuO˙ radicals is not likely due to the large excess of the substrate (cyclohexane), which quickly consumes these radicals.
| tBuOOH + CuII → tBuOO˙ + CuI + H+ | (1) |
| tBuOOH + CuI + H+ → tBuO˙ + CuII + H2O | (2) |
| tBuOO˙ + ˙OOtBu → tBuOOtBu | (3) |
| tBuOO˙ + ˙OOtBu → 2 tBuO˙ + O2 | (4) |
Optimisation of the {[CuL7]·TBHP} intermediate 2IM1 with the TBHP molecule docked close to the apical position of copper(II) led to several possible configurations. The high flexibility of the [CuL7] molecule as well as of its assemblies with the oxidant explains the significant discrepancies in the obtained Gibbs energies, as a small change in geometry results in several units of Gibbs energy change. The selected {[CuL7]·tBuOOH} intermediate structure (2IM2) has a free Gibbs energy of 5.0 kcal mol−1 above the sum of the separated components ([CuL7] + tBuOOH) and shows weak Cu⋯O interaction as evidenced by the long Cu⋯O distance of 2.877 Å with the electron density ρ(rBCP) at the respective bond critical point of 0.014 a.u. (Fig. S36†).
Given that the reaction proceeds in an aprotic medium (cyclohexane), the proton released in reaction (1) was presumed to remain in the catalyst structure. The respective reduced and protonated complex 1[CuHL7] has several possible configurations, 1IM2a, 1IM2b, and 1IM2c (Fig. S37†). The intermediates 1IM2a and 1IM2b showed distorted tetrahedral geometries around the Cu(I) centre with Cu–OH bond lengths of 2.406 and 2.494 Å, respectively. The principal difference between 1IM2a and 1IM2b is in the ligand geometry which has a “twisted” form in the case of 1IM2b. The ΔΔG difference between these two molecules is negligible (1IM2b is 0.7 kcal mol−1 more stable). In contrast, the 1IM2c structure features a dissociated hydroxyl group with d(Cu⋯O) = 3.105 Å, where the H-atom forms a hydrogen bond with one of the N-atoms (Fig. S37†). The Cu(I) atom adopts a trigonal-planar coordination geometry. The free Gibbs energy of 1IM2c is 6.7 kcal mol−1 higher than that of 1IM2b. Since the topologies of 1IM2a and 1IM2b are equal and the energies are close, one can presume fast interconversion of these two forms in solution.
As reaction (1) assumes the elimination of the tBuOO˙ radical, the search for the respective {1[CuHL7]·tBuOO˙} intermediate was performed. The interaction of the tBuOO˙ radical with 1IM2a results in the oxidation of copper(I), H-transfer, and subsequent return to the starting 2IM1 assembly {[CuL7]·tBuOOH}, revealing the insufficient resistance of 1IM2a towards such an attack. The “twisted” intermediate 1IM2b (Fig. S37†) forms a stable assembly {1[CuHL7]·tBuOO˙} where the tBuOO· radical is docked between the ligand groups (intermediate 2IM3b, Fig. S38†) and the copper ion maintains its +1 oxidation state. The ΔΔG(2IM3b–2IM1) difference of 32.5 kcal mol−1 (37.5 kcal mol−1 relative to the starting components tBuOOH + 1[CuHL7]) indicates that this pathway of H-abstraction from tBuOOH is possible, but not a favourable one. As the reduced catalyst should then interact with a second tBuOOH molecule (reaction (2)), the respective intermediate {1[CuHL7]·tBuOOH} was modelled (1IM4b, Fig. S38†). However, it was found to have a high ΔG of 41.9 kcal mol−1 relative to the starting components. Hence, the favourable pathway implies that the “twisted” form 1IM2b is converted first to 1IM2a, in which copper(I) is less sterically hindered (Fig. S37†). The participation of 1IM2a could be possible if one considers the reaction of a second molecule of tBuOOH with the starting assembly 2IM2a, {[CuL7]·tBuOOH}, at the moment of release of the tBuOO˙ radical from it. In this way, the intermediate 1IM3a is generated (Fig. 10), in which the tBuOOH molecule forms a bifurcated H-bond with the phenolato oxygen atoms of the Cu(I) catalyst species. This kind of oxidant substitution results in a ΔG change of −1.0 kcal mol−1 (Fig. 10). The final reoxidation of Cu(I) and decomposition of 1IM3a into 2IM1, H2O and tBuO˙ lead to a final ΔG of −10.3 kcal mol−1.
 | ||
| Fig. 10 Molecular structures and relative free Gibbs energies (kcal mol−1) of the reaction between [CuL7] and the tBuOOH oxidant. | ||
Modelling of the interaction of tBuOO˙ with the intermediate 1IM2c (Fig. S37†) showed the formation of a species where the tBuOO˙ radical is coordinated to copper (intermediate 2IM3c, Fig. S39†). Löwdin analysis reveals a 0.5708 spin population on the copper atom, which suggests its formal +2 oxidation state. The spin density of 2IM3c is clearly distributed over the Cu(II) as well as the oxygen atoms of the coordinated peroxide (Fig. S39†). Remarkably, the free Gibbs energy of 2IM3c is considerably smaller than that of 2IM3b, with ΔΔG(2IM3c–2IM1) = 19.7 kcal mol−1 (Fig. S40†). The disassembly of 2IM3c into the reduced complex 1[CuHL7] (intermediate 1IM2c) and the free tBuOO˙ radical shows a further increase in free Gibbs energy by 13.0 kcal mol−1 (overall ΔΔG of 37.7 kcal mol−1 relative to the sum of the starting components). This increase in the energy can be avoided if one considers the reaction of tBuOOH with the 2IM3c intermediate and replacement of the tBuOO˙ radical with the tBuOOH molecule (intermediate 1IM4c, Fig. S38†), which has ΔΔG(1IM4c–2IM3c) = 6.8 kcal mol−1 and ΔΔG(1IM4c–2IM1) = 25.9 kcal mol−1.
Since the ligand in [CuL7] was shown to participate in the redox processes, the possibility of ligand oxidation during the catalytic process was assessed. Modelling of the direct homolytic splitting of the O–O bond of tBuOOH in 2IM1 resulted in the configuration 4IM2d with the Cu–OH entity (Fig. S41†) and interatomic separation d(Cu–O) = 1.999 Å. The analysis of the spin density revealed that the eliminated species is a tBuO˙ radical, and most of the other spin densities concentrated on both the phenoxyl group and one of the phenolic rings of the coordinated ligand. The overall ΔG of 4IM2d is too high (41.4 kcal mol−1 relative to the starting components) for this pathway to be considered as a likely one.
In contrast to the [CuL7]/TBHP catalytic system, the UV–vis spectra of [CuL7]/mCPBA solutions in cyclohexane reveal fast degradation of the complex as evidenced by the disappearance of the characteristic absorption bands at 327 and 382 nm (Fig. S32 and S33†). This result is associated with mCPBA only, since the treatment of [CuL7] with m-chlorobenzoic acid (mCBA) in cyclohexane at 50 °C does not afford degradation of the compound.
The non-catalytic decomposition of mCPBA is known to be rather complex49 and may involve numerous organic radicals, from which the most principal ones are Ar˙, ArC(O)O˙ and ArC(O)OO˙. The calculated energy barriers of H-abstraction from cyclohexane at 50 °C are 10.9, 9.8 and 21.2 kcal mol−1, respectively (Table S5†), indicating that aryl and aroyloxyl radicals readily react with cyclohexane, while the aroylperoxyl one is less active. The energy barrier of the decarboxylation of ArC(O)O˙ was estimated to be 8.6 kcal mol−1 (Table S5†). The experimental catalytic selectivity data agree with the involvement of aroyloxyl radicals. Since the latter can be formed through the direct decomposition of mCPBA, the energy of its O–O bond splitting was studied. The respective MECP point is approximately 39.1 kcal mol−1 higher than the energy of a singlet state of mCPBA (Table S6†), suggesting that the catalyst-free decomposition of mCPBA should be negligible, in agreement with the experimental data.
Similarly to TBPH, the interaction between complex [CuL7] and mCPBA produced several plausible configurations, where the mCPBA molecule is located parallel to one of the phenyl groups of the ligand or coordinated to the Cu(II) atom. The kind of the starting configuration determines the further reaction pathway. The intermediate 2IM1e formed by the non-covalent interaction of [CuL7] and mCPBA has a free Gibbs energy by 8.0 kcal mol−1 higher than the sum of the energies of the starting components (Fig. 11). It is commonly assumed that the homolytic splitting of the O–O bond of mCPBA required for the elimination of the ArC(O)O˙ radical coordinated to a metal centre Mn results either in the increase of its oxidation state (Mn+1) or in the formation of the oxyl species Mn![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O˙.50 In the present case, splitting of the O–O bond produced a stable intermediate 4IM2e featuring a Cu–OH entity with d(Cu–O) = 1.980 Å and the ArC(O)O˙ radical located in close proximity (Fig. 11). Analysis of the spin density clearly indicates the oxidation of one of the phenolato groups of the coordinated ligand to a phenoxyl radical (Fig. S42†). Remarkably, the relative energy of the intermediate 4IM2e of ΔΔG(4IM2e–2IM1e) = 19.2 kcal mol−1 suggests that this step is possible. Further decomposition of the intermediate 4IM2e into the oxidised species 3[Cu(OH)L7] (intermediate 3IM3e) and release of the ArC(O)O˙ radical afforded a slight increase in the energy by 6.6 kcal mol−1. Replacement of the ArC(O)O˙ radical in 4IM2e by an mCPBA molecule produced the intermediate 3IM4e, whose energy is 4.3 kcal mol−1 higher than that of 4IM2e (Fig. 11). Note that H-transfer of the proton from mCPBA to the coordinated OH group proceeded with a huge −40.1 kcal mol−1 drop of the free Gibbs energy down to −8.6 kcal mol−1 relative to the starting energy sum of [CuL7] and 2 mCPBA molecules (intermediate 3IM5e).
O˙.50 In the present case, splitting of the O–O bond produced a stable intermediate 4IM2e featuring a Cu–OH entity with d(Cu–O) = 1.980 Å and the ArC(O)O˙ radical located in close proximity (Fig. 11). Analysis of the spin density clearly indicates the oxidation of one of the phenolato groups of the coordinated ligand to a phenoxyl radical (Fig. S42†). Remarkably, the relative energy of the intermediate 4IM2e of ΔΔG(4IM2e–2IM1e) = 19.2 kcal mol−1 suggests that this step is possible. Further decomposition of the intermediate 4IM2e into the oxidised species 3[Cu(OH)L7] (intermediate 3IM3e) and release of the ArC(O)O˙ radical afforded a slight increase in the energy by 6.6 kcal mol−1. Replacement of the ArC(O)O˙ radical in 4IM2e by an mCPBA molecule produced the intermediate 3IM4e, whose energy is 4.3 kcal mol−1 higher than that of 4IM2e (Fig. 11). Note that H-transfer of the proton from mCPBA to the coordinated OH group proceeded with a huge −40.1 kcal mol−1 drop of the free Gibbs energy down to −8.6 kcal mol−1 relative to the starting energy sum of [CuL7] and 2 mCPBA molecules (intermediate 3IM5e).
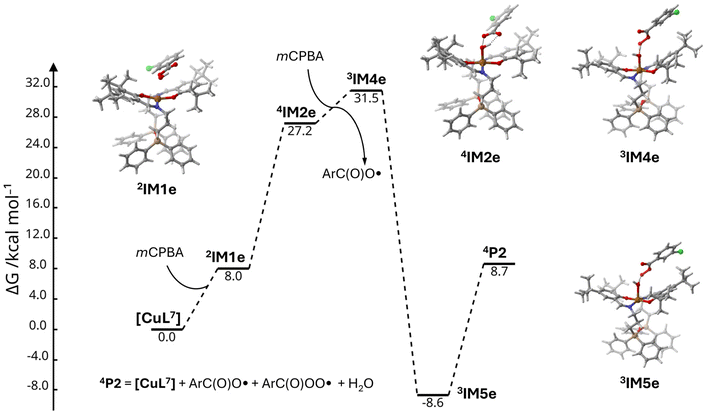 | ||
| Fig. 11 Molecular structures and relative free Gibbs energies (kcal mol−1) of the reaction between [CuL7] and the mCPBA oxidant, route (e). | ||
Optimisation of the complex [CuL7] with an approaching water molecule led to the decoordination of the latter from the copper centre. Hence, the release of the ArC(O)OO˙ radical from the intermediate 3IM5e should regenerate the initial [CuL7] structure and release a free water molecule. The overall energies of the intermediates (Fig. 11) suggest that this pathway is feasible.
The search for an intermediate with mCPBA coordinated to the Cu(II) centre in [CuL7] gave rise to the structure 2IM1f, where the phenolato group is protonated and dissociated, while the deprotonated mCPBA acts as a bidentate chelating co-ligand (Fig. 12). Splitting of the O–O bond in the intermediate 2IM1f is followed by the complete dissociation of one N,O-donor Schiff base chelating group (intermediate 4IM2f). Surprisingly, the analysis of the spin density indicated a doubly oxidised ligand, while the coordinated m-chlorobenzoate holds no unpaired electrons (Fig. S42†). The energy of 4IM2f is rather low (18.3 kcal mol−1 relative to the starting components). If no O–O bond splitting is assumed, the intermediate 2IM1f converts into the 2IM3f species, where the protonated half of the Schiff base ligand is decoordinated moving further apart, while the mCPBA peroxycarboxylate replaces the dissociated part of the ligand in the coordination sphere (Fig. 12). Finally, the peroxycarboxylate residue shifts to form a square-planar intermediate 2IM4f. All the intermediates 4IM2f, 2IM3f and 2IM4f stipulate degradation of the starting catalyst [CuL7] because decoordination of m-chlorobenzoate in 4IM2f seems to be not likely in the presence of excess mCPBA and mCBA which should react with the oxidised ligand and further replace it in the coordination sphere of copper. The fate of the intermediates 2IM3f and 2IM4f is expected to be a step-by-step formation of the [Cu(mCBA)2] species, achieved through the protonation and replacement of the second Schiff base group. One can presume that [Cu(mCBA)2] undergoes dimerisation to form a quite stable paddlewheel carboxylate complex [Cu2(mCBA)4], which is responsible for further catalytic activity. Moreover, the UV–vis spectrum of the adduct of [Cu2(mCBA)4] with acetonitrile is reported55 to be similar to that observed after degradation of the [CuL7]/mCPBA catalytic system (Fig. S32†) and after dissolving metallic copper in a cyclohexane solution of mCPBA (Fig. S34†).
 | ||
| Fig. 12 Molecular structures and relative free Gibbs energies (kcal mol−1) of the reaction between [CuL7] and the mCPBA oxidant, route (f). | ||
The stability of [CuL7] in the presence of m-chlorobenzoic acid (mCBA), in contrast to mCPBA, can be rationalised in terms of the absence of numerous intermediate states (2IM1f, 2IM3f and 2IM4f). Optimisation of the {[CuL7]·mCBA} assemblies does not afford monodentate coordination of m-chlorobenzoate but shows the starting approach of mCBA (2IM1g) and complete dissociation of the protonated bidentate Schiff base ligand (2IM2g, Fig. S43†). Thus, although the overall process is energetically favourable, it may have sufficiently high barriers to prevent the rapid decomposition of [CuL7] by mCBA.
Conclusion
In this work, we aimed at the synthesis of a Cu(II) complex soluble in non-polar solvents and studied its potential to act as a catalyst in the oxidation of cyclohexane used both as the substrate and the solvent. Our previous studies on the synthesis and catalytic activity of copper(II) complexes with quite unusual Schiff bases derived from substituted 2-hydroxybenzaldehydes and 1,3-bis(3-aminopropyl)tetramethyldisiloxane (H2L1–H2L6) prompted us to develop the synthesis of a similar Schiff base, in which the central tetramethyldisiloxane unit is replaced by a more lipophilic tetraphenyldisiloxane moiety. We performed a seven-step synthesis of a new Schiff base H2L7 resulting finally from the condensation reaction of the commercially unavailable 1,3-bis(3-aminopropyl)tetraphenyldisiloxane as a diformate salt and 3,5-di-tert-butyl-2-hydroxybenzaldehyde in the presence of a base. The Cu(II) complex [CuL7] obtained by the reaction of H2L7 with Cu(OAc)2 has a see-saw or sawhorse coordination geometry, as established by SC-XRD. This was also the case for [CuL1]–[CuL6] reported previously, with comparable τ4-parameters of 0.420 and 0.372 for the two crystallographically independent molecules of [CuL7]. The optical spectrum of [CuL7] showed three intense absorption bands at 275, 327 and 380 nm due to π–π* and LMCT σ–d transitions according to TDDFT calculations and weak absorption bands between 550 and 750 nm due to d–d transitions. Two consecutive one-electron reversible electrochemical oxidations were accompanied by a decrease in absorptions in the UV region of the optical spectrum of [CuL7] and the simultaneous appearance and further development of a band at 304 nm due to the formation of phenoxyl mono- and di-radicals, respectively. Three new absorption bands appeared in the vis–NIR region of the optical spectrum at 530, 880 and 1500 nm. The DFT calculations have shown that the one-electron oxidised Cu(II) complex should exist in the triplet ground state as 3[CuL7]+ with one unpaired electron located on the dx2−y2 orbital of Cu(II) (d9, S = ½) and another unpaired electron located on the MO including pz orbitals of oxygen and carbon atoms of the phenoxyl moiety. Strong ferromagnetic interaction with coupling constant J = 251.83 cm−1 is predicted, even though the ferromagnetic ground state S = 1 remains to be confirmed experimentally. In turn, the doubly oxidised species [CuL7]2+ showed very close doublet and quartet states. The doublet state has an unpaired electron on the Cu(II) d-orbital, whereas the quartet state accommodates one unpaired electron on the Cu(II) d-orbital and two unpaired electrons on the ligand. Thus, spectroscopic and theoretical data clearly demonstrated the noninnocent behaviour of the coordinated Schiff base bearing the tetraphenyldisiloxane unit. Finally, [CuL7] was found to act as a catalyst for the oxidation of cyclohexane to cyclohexanol and cyclohexanone under solvent-free conditions with hydrogen peroxide and tert-butyl hydroperoxide. Oxidation of cyclohexane with m-chloroperoxybenzoic acid in the presence of the Cu(II) complex resulted in cyclohexanol (29.1%), cyclohexene oxide (3.0%) and ε-caprolactone (29.8%) relative to mCPBA. DFT theoretical investigations of the reaction mechanism disclosed principal intermediates formed upon the reaction of [CuL7] with organic peroxides, where participation of the noninnocent ligand in the redox processes is among the possible reaction pathways.Experimental section
The multistep synthesis of the diammonium formate salt G is described in the ESI.†Synthesis of the Schiff base and Cu(II) complex
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ethylacetate 9
ethylacetate 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 as an eluent to give a yellow solid after drying at 50 °C in vacuo overnight. Yield: 394.2 mg, 83%. 1H NMR (600 MHz, DMSO-d6), δ, ppm: 14.10 (s, 1H, H20), 8.35 (s, 1H, H13), 7.46 (dd, J = 7.9, 1.3 Hz, 4H, H2, H6), 7.37–7.33 (m, 2H, H4, H8), 7.29 (dd, J = 12.7, 4.9 Hz, 5H, H17, H3, H7), 7.19 (d, J = 2.4 Hz, 1H, H19), 3.42 (t, J = 6.4 Hz, 2H, H11), 1.60–1.53 (m, 2H, H10), 1.37 (s, 9H, H22), 1.25 (s, 9H, H24), 1.15–1.10 (m, 2H, H9). 13C NMR (151 MHz, DMSO-d6) δ, ppm: 166.78 (CH, C13), 157.85 (Cq, C15), 139.29 (Cq, C18), 135.71 (Cq, C1, C5), 135.59 (Cq, C16), 133.72 (CH, C2, C6), 129.84 (CH, C4, C8), 127.88 (CH, C3, C7), 126.13 (CH, C19), 126.00 (CH, C17), 117.57 (Cq, C14), 60.62 (CH2, C11), 34.55 (Cq, C21), 33.80 (Cq, C23), 31.26 (CH3, C24), 29.15 (CH3, C22), 24.41 (CH2, C10), 12.29 (CH2, C9). 29Si NMR (119 MHz, DMSO-d6) δ, ppm: −10.35 (s). ESI-MS (acetonitrile/methanol + 1% water), positive: m/z 929.62 [M + H+]+ (calcd m/z for [C60H77N2O3Si2]+ 929.55). Anal. calcd for C60H76N3O3Si2·0.75H2O (Mr = 942.94), %: C, 76.43; H, 8.28; N, 2.97. Found, %: C, 76.33; H, 8.13; N, 3.06.
1 as an eluent to give a yellow solid after drying at 50 °C in vacuo overnight. Yield: 394.2 mg, 83%. 1H NMR (600 MHz, DMSO-d6), δ, ppm: 14.10 (s, 1H, H20), 8.35 (s, 1H, H13), 7.46 (dd, J = 7.9, 1.3 Hz, 4H, H2, H6), 7.37–7.33 (m, 2H, H4, H8), 7.29 (dd, J = 12.7, 4.9 Hz, 5H, H17, H3, H7), 7.19 (d, J = 2.4 Hz, 1H, H19), 3.42 (t, J = 6.4 Hz, 2H, H11), 1.60–1.53 (m, 2H, H10), 1.37 (s, 9H, H22), 1.25 (s, 9H, H24), 1.15–1.10 (m, 2H, H9). 13C NMR (151 MHz, DMSO-d6) δ, ppm: 166.78 (CH, C13), 157.85 (Cq, C15), 139.29 (Cq, C18), 135.71 (Cq, C1, C5), 135.59 (Cq, C16), 133.72 (CH, C2, C6), 129.84 (CH, C4, C8), 127.88 (CH, C3, C7), 126.13 (CH, C19), 126.00 (CH, C17), 117.57 (Cq, C14), 60.62 (CH2, C11), 34.55 (Cq, C21), 33.80 (Cq, C23), 31.26 (CH3, C24), 29.15 (CH3, C22), 24.41 (CH2, C10), 12.29 (CH2, C9). 29Si NMR (119 MHz, DMSO-d6) δ, ppm: −10.35 (s). ESI-MS (acetonitrile/methanol + 1% water), positive: m/z 929.62 [M + H+]+ (calcd m/z for [C60H77N2O3Si2]+ 929.55). Anal. calcd for C60H76N3O3Si2·0.75H2O (Mr = 942.94), %: C, 76.43; H, 8.28; N, 2.97. Found, %: C, 76.33; H, 8.13; N, 3.06.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) V0m where E is the single-point energy. The last term (2.1 kcal mol−1) is a correction69 for the standard state to 1 M and 323.15 K. The search for minimum energy crossing points (MECP) was performed using the BHandLYP functional70 and the def2-TZVP basis set, along with the D4 dispersion correction. To reduce the numerical noise and increase the stability, the integration grid of high density was used (Defgrid3 keyword) along with the ExtremeSCF convergence criteria. Also, all the RI approximations were switched off by the NORI and NoSplit-RI-J keywords. The maximum step in the optimisation was limited by the “Maxstep 0.01” command. Finally, the starting guess for every SCF cycle was switched from the default “MORead” to “PModel” (command “OptGuess = PModel”). All these parameters were essential for achieving the MECP structures and avoiding spin contamination of the low-spin S = 0 state.
V0m where E is the single-point energy. The last term (2.1 kcal mol−1) is a correction69 for the standard state to 1 M and 323.15 K. The search for minimum energy crossing points (MECP) was performed using the BHandLYP functional70 and the def2-TZVP basis set, along with the D4 dispersion correction. To reduce the numerical noise and increase the stability, the integration grid of high density was used (Defgrid3 keyword) along with the ExtremeSCF convergence criteria. Also, all the RI approximations were switched off by the NORI and NoSplit-RI-J keywords. The maximum step in the optimisation was limited by the “Maxstep 0.01” command. Finally, the starting guess for every SCF cycle was switched from the default “MORead” to “PModel” (command “OptGuess = PModel”). All these parameters were essential for achieving the MECP structures and avoiding spin contamination of the low-spin S = 0 state.
The broken symmetry calculations were done using the PBE0 functional and the def2-TZVPP basis set64 for all atoms. The TDDFT excited-state calculations, unless stated otherwise, were performed using the PBE0 functional and the DKH relativistic approximation,71,72 employing the aug-cc-pVTZ-DK basis set for the copper atom and aug-cc-pVDZ-DK for all other atoms,73,74 along with the SARC/J auxiliary basis set.75,76 The Tamm–Dancoff approximation (TDA)77 and Gaussian finite nucleus model78 were applied for all TDDFT calculations, as well as the SMD implicit solvation model. In certain cases, the TDDFT calculations involved the ma-def2-SVP79 or 6-311G*80 basis sets and the B3LYP hybrid functional.81–83 Natural transition orbitals84 were used for visualisation of electronic transitions. The CASSCF/SC-NEVPT2 studies85,86 were performed using the def2-TZVP basis set for copper and the N,O,C-atoms of the Schiff base ligands (excluding tBu groups) and def2-SVP64 for all other atoms, employing VeryTightSCF convergence criteria and considering the SMD implicit solvation model. In certain cases, the Ab Initio Ligand Field Theory (AILFT) calculations87 were involved in the CASSCF studies. The MC-RPA calculations88 were performed using the same basis set combination as for the CASSCF studies. All calculations involved RIJ-COSX89–91 (for DFT and MC-RPA) or RI92 (for CASSCF) speed-up approximations. Visualisation of the molecular structures of intermediates, orbitals and spin densities was drawn using the CYLview2093 and Avogadro 1.2 programs.94 Free energy profile diagrams were drawn using the mechaSVG 0.1.1 program.95 Unless stated otherwise, the isosurfaces of the molecular orbitals are shown at the 0.03 a.u. level and isosurfaces of spin densities at the 0.005 a.u. level. Selected ORCA inputs and outputs used for the calculations are provided in Listings S1–S8. The Cartesian xyz files provided in the ESI† contain the DFT-optimised structures.
Author contributions
Christopher Wittmann – formal analysis; investigation; and writing – original draft. Oleg Palamarciuc – investigation. Mihaela Dascalu – data curation and investigation. Maria Cazacu – writing – original draft; formal analysis; and methodology. Dmytro Nesterov – investigation; methodology; software; validation; and writing – review. Armando J. L. Pombeiro – conceptualisation and writing – review and editing. Peter Rapta – investigation; methodology; and writing – original draft. Vladimir B. Arion – conceptualisation; funding acquisition; investigation; project administration; and writing – review and editing.Conflicts of interest
There are no conflicts to declare.Data availability
The data supporting this article have been included as part of the ESI.†Crystallographic data for compounds diol D and CuL7 have been deposited at the CCDC under accession numbers 2413535 and 2413536† and can be obtained from CCDC e-mail: deposit@ccdc.cam.ac.uk.
Acknowledgements
This work was funded by a grant from the Ministry of Research, Innovation and Digitalization, project no. PNRR-III-C9-2023-I8-99/31.07.2023 within the National Recovery and Resilience Plan (Romania), as well as by the Slovak Research and Development Agency under contract no. APVV-19-0024 and APVV-23-0195 (P. R.) and the grant agency VEGA (contract no. 1/0392/24). The authors acknowledge the Fundação para a Ciência e a Tecnologia (FCT), Portugal, through the projects UIDB/00100/2020 (https://doi.org/10.54499/UIDB/00100/2020), UIDP/00100/2020 (https://doi.org/10.54499/UIDP/00100/2020), LA/P/0056/2020 (https://doi.org/10.54499/LA/P/0056/2020) of Centro de Química Estrutural. We thank Mr Alexander Prado-Roller for X-ray diffraction measurements.References
- M. Damoc, A.-C. Stoica, M. Dascalu, M. Asandulesa, S. Shova and M. Cazacu, Dalton Trans., 2021, 50, 13841–13858 RSC.
- A. Soroceanu, M. Cazacu, S. Shova, C. Turta, J. Kožíšek, M. Gall, M. Breza, P. Rapta, T. C. O. Mac Leod, A. J. L. Pombeiro, J. Telser, A. A. Dobrov and V. B. Arion, Eur. J. Inorg. Chem., 2013, 1458–1474 CrossRef.
- M. Cazacu, S. Shova, A. Soroceanu, P. Machata, L. Bucinsky, M. Breza, P. Rapta, J. Telser, J. Krzystek and V. B. Arion, Inorg. Chem., 2015, 54, 5691–5706 CrossRef.
- A. Vlad, M.-F. Zaltariov, S. Shova, M. Cazacu, M. Avadanei, A. Soroceanu and P. Samoila, Polyhedron, 2016, 115, 76–85 CrossRef.
- A. Vlad, M. Avadanei, S. Shova, M. Cazacu and M.-F. Zaltariov, Polyhedron, 2018, 146, 129–135 CrossRef.
- S. Shova, A. Vlad, M. Cazacu, J. Krzystek, L. Bucinsky, M. Breza, D. Darvasiová, P. Rapta, J. Cano, J. Telser and V. B. Arion, Dalton Trans., 2017, 46, 11817–11829 RSC.
- M. Zaltariov, M. Alexandru, M. Cazacu, S. Shova, G. Novitchi, C. Train, A. Dobrov, M. V. Kirillova, E. C. B. A. Alegria, A. J. L. Pombeiro and V. B. Arion, Eur. J. Inorg. Chem., 2014, 4946–4956 CrossRef CAS.
- M. Janeta, T. Lis and S. Szafert, Chem. – Eur. J., 2020, 26, 13686–13697 CrossRef PubMed.
- B. A. Jazdzewski and W. B. Tolman, Coord. Chem. Rev., 2000, 200–202, 633–685 CrossRef.
- S. Itoh, M. Taki and S. Fukuzumi, Coord. Chem. Rev., 2000, 198, 3–20 CrossRef.
- C. T. Lyons and T. D. P. Stack, Coord. Chem. Rev., 2013, 257, 528–540 CrossRef.
- E. Saint-Aman, S. Ménage, J.-L. Pierre, E. Defrancq and G. Gellon, New J. Chem., 1998, 22, 393–394 RSC.
- A. K. Nairn, S. J. Archibald, R. Bhalla, B. C. Gilbert, E. J. MacLean, S. J. Teat and P. H. Walton, Dalton Trans., 2006, 172–176 RSC.
- K. Bernardo, S. Leppard, A. Robert, G. Commenges, F. Dahan and B. Meunier, Inorg. Chem., 1996, 35, 387–396 CrossRef PubMed.
- L. Yang, D. R. Powell and R. P. Houser, Dalton Trans., 2007, 955–964 RSC.
- M. H. Reineke, M. D. Sampson, A. L. Rheingold and C. P. Kubiak, Inorg. Chem., 2015, 54, 3211–3217 CrossRef PubMed.
- A. Okuniewski, D. Rosiak, J. Chojnacki and B. Becker, Polyhedron, 2015, 90, 47–57 CrossRef.
- T. Guchhait, M. Giri and S. P. Mishra, J. Coord. Chem., 2024, 77, 49–68 CrossRef.
- T. Iwamoto, H. Masuda, S. Ishida, C. Kabuto and M. Kira, J. Am. Chem. Soc., 2003, 125, 9300–9301 CrossRef PubMed.
- K. Kihara, Eur. J. Mineral., 1990, 2, 63–78 CrossRef.
- C. Glidewell and D. C. Liles, J. Chem. Soc., Chem. Commun., 1977, 632–633 RSC.
- K. Suwińska, G. J. Palenik and R. Gerdil, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1986, 42, 615–620 CrossRef.
- C. Glidewell and D. C. Liles, Acta Crystallogr., Sect. B, 1978, 34, 696–698 CrossRef.
- M. A. Mazid and R. A. Palmer, J. Cryst. Mol. Struct., 1975, 5, 35–46 CrossRef.
- P. K. Sahoo, S. S. Gawali and C. Gunanathan, ACS Omega, 2018, 3, 124–136 CrossRef PubMed.
- N. Kocher, J. Henn, B. Gostevskii, D. Kost, I. Kalikhman, B. Engels and D. Stalke, J. Am. Chem. Soc., 2004, 126, 5563–5568 CrossRef.
- E. Bill, J. Müller, T. Weyhermüller and K. Wieghardt, Inorg. Chem., 1999, 38, 5795–5802 CrossRef.
- T. Takeyama and Y. Shimazaki, Dalton Trans., 2024, 53, 3911–3929 RSC.
- H. Kanso, R. M. Clarke, A. Kochem, H. Arora, C. Philouze, O. Jarjayes, T. Storr and F. Thomas, Inorg. Chem., 2020, 59, 5133–5148 CrossRef.
- T. Takeyama, T. Suzuki, M. Kikuchi, M. Kobayashi, H. Oshita, K. Kawashima, S. Mori, H. Abe, N. Hoshino, S. Iwatsuki and Y. Shimazaki, Eur. J. Inorg. Chem., 2021, 4133–4145 CrossRef.
- T. Takeyama, M. Kobayashi, M. Kikuchi, T. Ogura, Y. Shimazaki and S. Iwatsuki, Inorg. Chim. Acta, 2020, 511, 119848 CrossRef.
- T. Storr, P. Verma, R. C. Pratt, E. C. Wasinger, Y. Shimazaki and T. D. P. Stack, J. Am. Chem. Soc., 2008, 130, 15448–15459 CrossRef PubMed.
- P. Chaudhuri and K. Wieghardt, in Progress in Inorganic Chemistry, ed. K. D. Karlin, Wiley, 1st edn, 2001, vol. 50, pp. 151–216 Search PubMed.
- K. Asami, K. Tsukidate, S. Iwatsuki, F. Tani, S. Karasawa, L. Chiang, T. Storr, F. Thomas and Y. Shimazaki, Inorg. Chem., 2012, 51, 12450–12461 CrossRef PubMed.
- D. De Bellefeuille, M. Orio, A.-L. Barra, A. Aukauloo, Y. Journaux, C. Philouze, X. Ottenwaelder and F. Thomas, Inorg. Chem., 2015, 54, 9013–9026 CrossRef.
- M. Orio, O. Jarjayes, H. Kanso, C. Philouze, F. Neese and F. Thomas, Angew. Chem., Int. Ed., 2010, 49, 4989–4992 CrossRef PubMed.
- J. Liang, X. Feng, D. Hait and M. Head-Gordon, J. Chem. Theory Comput., 2022, 18, 3460–3473 CrossRef.
- O. V. Nesterova, O. Yu. Vassilyeva, B. W. Skelton, A. Bieńko, A. J. L. Pombeiro and D. S. Nesterov, Dalton Trans., 2021, 50, 14782–14796 RSC.
- A. D. Laurent and D. Jacquemin, Int. J. Quantum Chem., 2013, 113, 2019–2039 CrossRef.
- L. Chiang, K. Herasymchuk, F. Thomas and T. Storr, Inorg. Chem., 2015, 54, 5970–5980 CrossRef PubMed.
- D. S. Nesterov, O. V. Nesterova and A. J. L. Pombeiro, Coord. Chem. Rev., 2018, 355, 199–222 CrossRef.
- I. Gryca, K. Czerwińska, B. Machura, A. Chrobok, L. S. Shul'pina, M. L. Kuznetsov, D. S. Nesterov, Y. N. Kozlov, A. J. L. Pombeiro, I. A. Varyan and G. B. Shul'pin, Inorg. Chem., 2018, 57, 1824–1839 CrossRef CAS.
- O. V. Nesterova, D. S. Nesterov, A. Krogul-Sobczak, M. F. C. Guedes Da Silva and A. J. L. Pombeiro, J. Mol. Catal. Chem., 2017, 426, 506–515 CrossRef CAS.
- P. T. Wierzchowski and L. W. Zatorski, Chromatographia, 2000, 51, 83–86 CrossRef CAS.
- Y. N. Kozlov, G. V. Nizova and G. B. Shul'pin, Russ. J. Phys. Chem., 2001, 75, 770–774 Search PubMed.
- G. B. Shul'pin, Dalton Trans., 2013, 42, 12794 RSC.
- G. B. Shul'pin, J. Mol. Catal. Chem., 2002, 189, 39–66 CrossRef.
- O. V. Nesterova, M. L. Kuznetsov, A. J. L. Pombeiro, G. B. Shul'pin and D. S. Nesterov, Catal. Sci. Technol., 2022, 12, 282–299 RSC.
- A. Bravo, H.-R. Bjorsvik, F. Fontana, F. Minisci and A. Serri, J. Org. Chem., 1996, 61, 9409–9416 CrossRef CAS.
- D. S. Nesterov and O. V. Nesterova, Catalysts, 2021, 11, 1148 CrossRef CAS.
- Y. Qiu and J. F. Hartwig, J. Am. Chem. Soc., 2020, 142, 19239–19248 CrossRef CAS.
- G. S. Astakhov, A. N. Bilyachenko, A. A. Korlyukov, M. M. Levitsky, L. S. Shul'pina, X. Bantreil, F. Lamaty, A. V. Vologzhanina, E. S. Shubina, P. V. Dorovatovskii, D. S. Nesterov, A. J. L. Pombeiro and G. B. Shul'pin, Inorg. Chem., 2018, 57, 11524–11529 CrossRef CAS PubMed.
- J. G. Brandenburg, C. Bannwarth, A. Hansen and S. Grimme, J. Chem. Phys., 2018, 148, 064104 CrossRef.
- S. A. Katsyuba, E. E. Zvereva and S. Grimme, J. Phys. Chem. A, 2019, 123, 3802–3808 CrossRef CAS.
- R. Kumar, A. Maji, B. Biswas and A. Draksharapu, Dalton Trans., 2024, 53, 5401–5406 RSC.
- A. L. Spek, J. Appl. Crystallogr., 2003, 36, 7–13 CrossRef CAS.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112–122 CrossRef CAS.
- M. N. Burnett and C. K. Johnson, ORTEP-III: Oak Ridge Thermal Ellipsoid Plot Program for crystal structure illustrations, 1996 Search PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2025, 15, e70019 Search PubMed.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed.
- F. Neese, J. Comput. Chem., 2023, 44, 381–396 CrossRef CAS.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- M. Ernzerhof and G. E. Scuseria, J. Chem. Phys., 1999, 110, 5029–5036 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- E. Caldeweyher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2017, 147, 034112 CrossRef PubMed.
- G. L. Stoychev, A. A. Auer and F. Neese, J. Chem. Theory Comput., 2017, 13, 554–562 CrossRef CAS PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS.
- N. Mardirossian and M. Head-Gordon, J. Chem. Phys., 2016, 144, 214110 CrossRef.
- J. N. Harvey, F. Himo, F. Maseras and L. Perrin, ACS Catal., 2019, 9, 6803–6813 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS.
- B. A. Hess, Phys. Rev. A, 1985, 32, 756–763 CrossRef CAS.
- M. Douglas and N. M. Kroll, Ann. Phys., 1974, 82, 89–155 CAS.
- N. B. Balabanov and K. A. Peterson, J. Chem. Phys., 2005, 123, 064107 CrossRef.
- K. A. Peterson and C. Puzzarini, Theor. Chem. Acc., 2005, 114, 283–296 Search PubMed.
- D. A. Pantazis and F. Neese, Theor. Chem. Acc., 2012, 131, 1292 Search PubMed.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- S. Hirata and M. Head-Gordon, Chem. Phys. Lett., 1999, 314, 291–299 CrossRef CAS.
- L. Visscher and K. G. Dyall, At. Data Nucl. Data Tables, 1997, 67, 207–224 CrossRef CAS.
- J. Zheng, X. Xu and D. G. Truhlar, Theor. Chem. Acc., 2011, 128, 295–305 Search PubMed.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS.
- R. H. Hertwig and W. Koch, Chem. Phys. Lett., 1997, 268, 345–351 CrossRef CAS.
- R. L. Martin, J. Chem. Phys., 2003, 118, 4775–4777 CrossRef CAS.
- C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J.-P. Malrieu, J. Chem. Phys., 2001, 114, 10252–10264 CrossRef CAS.
- Y. Guo, K. Sivalingam and F. Neese, J. Chem. Phys., 2021, 154, 214111 CrossRef CAS.
- S. K. Singh, J. Eng, M. Atanasov and F. Neese, Coord. Chem. Rev., 2017, 344, 2–25 CrossRef CAS.
- B. Helmich-Paris, J. Chem. Phys., 2019, 150, 174121 CrossRef.
- B. Helmich-Paris, B. De Souza, F. Neese and R. Izsák, J. Chem. Phys., 2021, 155, 104109 CrossRef CAS PubMed.
- F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98–109 CrossRef CAS.
- F. Neese, J. Comput. Chem., 2003, 24, 1740–1747 CrossRef CAS PubMed.
- F. Neese and G. Olbrich, Chem. Phys. Lett., 2002, 362, 170–178 CrossRef CAS.
- C. Y. Legault, CYLview20, Université de Sherbrooke, 2020 Search PubMed.
- M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminf., 2012, 4, 17 CAS.
- R. A. Angnes, ricalmang/mechaSVG v.0.0.8 (version v.0.0.8), Zenodo, 2020 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental details; synthesis of 1,3-bis(aminopropyl)tetraphenyldisiloxane; tables and figures with structural, spectroscopic (NMR and UV–vis) and mass spectrometry details; theoretical calculations; and catalytic data. CCDC 2413535 and 2413536. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d5dt01028d |
| This journal is © The Royal Society of Chemistry 2025 |