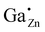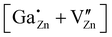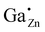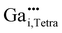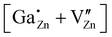Structural changes induced by the promoter Ga in nanocrystalline ZnO support used in methanol catalysis

Abstract

Ga has an ionic radius fitting the radius of Zn much better than Al, which makes it an interesting candidate for doping of ZnO, which is relevant in context with Cu/ZnO-catalysts and with transparent conductive oxides. Here, the structural changes of Ga-doping of nano-scale ZnO, which is obtained via thermal decomposition of hydrozincite, are studied by a combination of X-ray diffraction, ⁷¹Ga/¹H MAS NMR, quantum-chemical calculations and electron microscopy techniques. By quantum chemical calculations the NMR fingerprint of different Ga point defects is predicted, the calculations are validated against experimental data for different crystalline compounds. The relevant point defect in ZnO could be identified by the point symmetry of the isolated defect and comparison to the calculated values. The kinetic solubility limit for Ga in ZnO is determined by X-ray diffraction and NMR. It is shifted to higher values as compared to the Al variant. Finally, the distribution of Ga and H atoms within the nano-scale material is studied by “paramagnetically assisted surface peak assignment” (PASPA) NMR, REDOR and electron microscopy which shows that for Ga substitution ratios above the solubility limit the excess of Ga is incorporated into a heavily disordered or amorphous, hydrogen-rich surface-layer.

---

1. Introduction

Cu/ZnO is an industrial catalyst known for its efficiency in converting mixtures of CO/CO₂ and H₂ into methanol, which can also be used, with lower selectivity though, in converting pure streams of the greenhouse gas CO₂ and H₂ into methanol,¹ which triggered the interest to find ways to further reduce costs for the catalyst² and improve its catalytic activity.³ It has been observed that the substitution/doping of ZnO with other ions can improve the catalytic activity of the catalyst Cu/ZnO explaining the electronic promoter ion effect by Al³⁺ in the industrial catalyst.^4,5 To the list of dopants which have been observed to promote the catalytic activity belong Al³⁺,^6,7 Cr³⁺,⁸ Zr⁴⁺,⁹ Mg²⁺,¹⁰ Si⁴⁺ (ref. 11) and Ga³⁺.^12,13 The doping induced defects of the host-structure are known to change the electronic band gap,¹⁴ the surface area of the particle¹⁵ and the catalytic selectivity.¹⁶ With the introduction of the Cu/ZnO:Al catalyst the temperature and pressure requirements for the catalytic process could be reduced to values of 490–560 K and 60–100 bar.¹⁷ In 2022 over 111 Mtons of methanol were produced by this method.¹⁸ A convenient way to introduce the promoter is by doping the ZnO support by co-precipitation with Al₂O₃, which is the technically employed method of catalyst manufacture.^19,20

Similar to Al₂O₃, Ga₂O₃ also promotes the performance of the binary Cu/Zn (CZ) catalyst (see Fig. 1), as previously demonstrated under industrially relevant conditions.⁵ Compared to the unpromoted Cu/Zn catalyst, the Ga-promoted Cu/Zn:Ga (CZG) catalyst exhibited enhanced activity (Fig. 1a) not only in CO hydrogenation but also in syngas mixtures containing both CO and CO₂. The high methanol activity was attributed to the synergistic interaction between Cu and ZnO, with the Ga dopant improving ZnO reducibility. Moreover, the catalyst demonstrated stability for over 800 hours on stream (TOS), which was attributed to the structural robustness imparted by the coprecipitation synthesis method (see Fig. 1b).⁵

Fig. 1 Illustration of the effect of Ga promotion on the performance of a Cu/ZnO catalyst in methanol synthesis: (a) enhanced activity in both CO hydrogenation and syngas (CO + CO₂) conversion of Ga³⁺-promoted catalyst (CZG) compared with a binary unpromoted one (CZ), and (b) long-term stability of both catalysts in CO hydrogenation (TOS = time-on-stream). The reactions were carried out at 235 °C, 30 bar, with a gas hourly space velocity (GHSV) of 1700 h⁻¹ and a CO_x : H₂ ratio of 2. This data was previously reported in ref. 5 and further experimental details can be found therein.

It was recently shown that Al³⁺ can be replaced by Ga³⁺ and both showed a marked promoting effect compared to a binary unpromoted Cu/ZnO catalyst (CZ in Fig. 1) under industrially relevant conditions.⁵ A Ga³⁺-promoted Cu/ZnO:Ga (CZG in Fig. 1) exhibited enhanced activity (Fig. 1a) not only in CO hydrogenation but also in syngas mixtures containing both CO and CO₂. The high methanol activity was attributed to the synergistic interaction between Cu and ZnO, while Ga was present as a dopant to ZnO improving its reducibility. In addition to its higher activity, the CZG catalyst demonstrated an interesting stability for over 800 hours on stream (TOS), which was higher than that of the unpromoted CZ catalyst (Fig. 1b). In the light of these promising catalytic properties, this present work now addresses fundamental questions such as the structural changes to coprecipitated zinc oxide supports induced by Ga³⁺ doping or the solubility limit.

Gallium also is in the focus of recent research by other groups and it was also reported to have a positive effect on the selectivity of Cu during methanol synthesis from CO₂ if applied with proper loading.²¹ For incorporation into the ZnO component of Cu catalysts, Ga has an ionic radius better matching that of the host cation compared to Al (r_Al³⁺ = 0.53 Å < r_Ga³⁺ = 0.61 Å < r_Zn²⁺ = 0.74 Å),²² potentially allowing a higher substitution ratio. It remains important to understand for the catalysts ZnO component is modified by the incorporation of promoter ions on different length scales. XANES measurements indicate, that Ga³⁺ occupies a fourfold coordinated position in ZnO in the Cu/ZnO:Ga catalyst and that it is not incorporated into metallic copper phase.^4,5,23 This behavior is different from that of Al,²¹ which is also not expected to be incorporated into Cu, but not only exclusively found inside the ZnO phase and rather forms disordered and complex highly dispersed phases.⁴

Another aspect regarding the incorporation of promoter ions is the question up to which concentration ZnO takes up Ga³⁺.^24,25 By the application of different techniques, solubility limits were determined ranging from 0.5 mol% by XRD and RAMAN,²⁶ 2 mol% by static solid-state NMR,²⁷ 2 mol% by resistivity,²⁸ to 4 mol% by conductivity measurements.²⁹ A reason for the difference in the reported solubility limits is that depending on sample synthesis the limit, that is set by thermodynamics, can be overcome by kinetic control for example by low-temperature decomposition reactions.³⁰ The thermodynamic solubility limit is difficult to determine precisely, however, results from samples quenched from different temperatures can serve as a reference and show the thermodynamic limit at 1500 °C is below 0.1 (mol/mol)%.²⁴ As for the case of ZnO:Al, the thermodynamic solubility limit is also lower than the solubility limit that can be achieved under kinetic control.^31,32

Different low-temperature routes to nano-scale ZnO:Ga have been reported to achieve a high substitution ratio: nano-scale ZnO:Ga has been obtained similar to the industrially known low-temperature synthesis by decomposition of a hydroxycarbonate precursor.³³ Other methods include sol–gel synthesis,³⁴ Pecchini method,²⁴ radio frequency magnetron sputtering³⁵ or a solid-state reaction.²⁹ Depending on the synthesis temperatures mixtures of ZnO and ZnGa₂O₄ spinel instead of ZnO:Ga are obtained.^36,37 In case of Al, the spinel is not considered a promoting species for Cu/ZnO catalysts and its formation was associated to deactivation.³⁸ For a catalyst in addition to the present phases also the morphology is relevant. So far films,³⁹ platelets⁴⁰ and rods⁴¹ of ZnO:Ga could be obtained, while the synthesis route via co-precipitated hydroxy carbonates usually leads to porous aggregates of doped ZnO nanoparticles that inherit their morphology from the crystalline precursor phases.³¹

For the optical and electrical materials properties, it matters how the Ga is incorporated into the host crystal structure of ZnO. To obtain site specific information about the Ga environments, solid-state NMR is a powerful method as gallium atoms have two NMR active nuclei with spin 3/2, namely ⁶⁹Ga and ⁷¹Ga.⁴² Ga and Al are both group 13 elements and besides have good quadrupolar nuclei (²⁷Al and ^71/69Ga) suitable for NMR. Given the similarity in their chemistry, it is not surprising that correlations between the NMR observables of isostructural crystal structures have been reported for ²⁷Al and ⁷¹Ga.^43,44 Nano-scale ZnO:Ga did not get studied in detail by Ga NMR yet. What has been studied is a material synthesized at 1200 °C, most likely resulting in a composite of ZnO and ZnGa₂O₄ spinel instead of ZnO:Ga²⁷ and in a different study static NMR experiments have been performed, which suffer from limited spectral resolution.¹³ Missing are NMR studies trying to identify the surface signals as in case of nano-scale ZnO:Al by ¹H and ²⁷Al NMR, using DNP-SENS⁴⁵ or a combination of REDOR and “paramagnetically assisted surface peak assignment”.⁴⁶ Also missing is the spectroscopic NMR finger-print for ^69/71Ga defects by quantum chemical calculations similar to what is available for ²⁷Al in ZnO:Al.⁴⁷

The purpose of this contribution is to study how Ga³⁺ is incorporated into nano-scale ZnO at different substitution levels on the example of a material which was obtained under kinetic control using a synthetic protocol adopted from Cu/ZnO catalyst synthesis.

2. Experimental part

2.1 Precursor synthesis

The precursor of the zinc oxide sample was synthesized by co-precipitation (reagents Table S1†). The precipitation was carried out in an automated stirred tank reactor (OptiMax, Mettler Toledo) from 1 M metal salt nitrate solution at a temperature of 65 °C and at a constant pH of 6.5. As precipitating agent, 1.6 M sodium carbonate solution was used. Before starting precipitation, 200 ml deionized water was filled into the reactor, followed by pH-adjustment. The dosing rate of metal solution was adjusted to 4.2 g min⁻¹. The setting of the synthesis parameter were taken from typical conditions of Cu/ZnO catalyst manufacture²⁰ under the omission of Cu. After precipitation, the precipitate was aged for 10 minutes without further pH control in the mother liquor. The precursor was washed with deionized water 10 times, to reach a conductivity of the filtrate lower than 100 μS cm⁻¹ and dried at 80 °C for 14 h in a heating cabinet.

2.2 Zinc oxide synthesis

The zinc oxide was synthesized by calcination of the ground hydrozincite from co-precipitation. The calcination was performed at 320 °C with a heating ramp of 2 °C min⁻¹ for 4 h in a Nabertherm (LE 6/11/B150) muffle furnace in static air (without any volume flow), which again resembles the typical conditions of catalyst synthesis.

2.3 Sample labeling

The samples are labeled according to their nominal gallium content relative to the total amount of metal atoms either as molar percentage or as a value x_Ga representing the nominal metal-based ratio of gallium atoms calculated as shown in eqn (1).

Here, n_i is the molar amount of element i (i = Zn, Ga). It should be noted that the Ga content in reality is a bit lower as indicated by an analysis by atomic absorption spectroscopy (Fig. S10†). Those values in the following are referred to as x_Ga(AAS). Nevertheless the nominal values have been used throughout to be consistent with a previous study on ZnO:Al.

2.4 Characterization methods

Powder X-ray diffraction (PXRD). X-ray analysis was performed on a Bruker D8 advance with copper Kα radiation and a LYNXEYE XE-T detector. The diffractograms were recorded in reflection in a Bragg–Brentano geometry at room temperature between 5° and 90° of the angle 2θ. Phase analysis was performed by comparing the recorded with structural data from ICSD and COD databases. Structure refinements were carried out using TOPAS academic Version 6.0.⁴⁸ Instrumental line broadening was accounted for by fitting a Thompson–Cox–Hastings pseudo-Voigt profile⁴⁹ to a measurement of the line shape standard LaB₆ (NIST SRM 660 b). Line broadening of the sample was modeled by anisotropic size broadening, which is justified by the small crystallite size evidenced by TEM and SEM imaging.

Nuclear magnetic resonance (NMR). ¹H and ⁷¹Ga solid-state NMR experiments were performed at 14.1 T on a Bruker Avance Neo NMR spectrometer equipped with a commercial 3.2 mm MAS probe head at a frequency of 600.2 and 183.0 MHz for ¹H and ⁷¹Ga, respectively. The chemical shift values of ⁷¹Ga are reported on a deshielding scale, relative to a solution of 1.1 M Ga(NO₃)₃ in D₂O.^50,51 The ¹H resonance of 1% TMS in CDCl₃ served as an external secondary reference using the Ξ values for ⁷¹Ga as reported by IUPAC. The peak areas were determined by deconvolution into mixed Gaussian/Lorentzian profile functions with the program deconv2Dxy.⁵² For the ⁷¹Ga and ¹H paramagnetically assisted surface peak assignment (PASPA) NMR measurements the ZnO:Ga with x_Ga = 0.03 and 0.1 was treated according to the procedure described in ref. 46. The organic solvent was degased by bubbling Ar through it and all solutions and samples were handled under a protective gas atmosphere to prevent from REDOX reactions.

Quantum-chemical calculations. The atomic positions were relaxed under periodic boundary conditions using the Quantum ESPRESSO v.6.6 software.^53,54 The input file for Pwscf featured the usage of an energy cutoff of 120 Ry (1633 eV) and a Monkhorst–Pack⁵⁵ like k-point mesh of 4 × 4 × 4 over the Brillouin zone. All fractional atomic coordinates were allowed to relax in P1 symmetry. Norm-conserving Troullier–Martins type⁵⁶ pseudopotentials with PAW reconstruction⁵⁷ were chosen. The convergence threshold for self-consistency of the electronic wave function was set to 10⁻¹⁴ a.u., while the thresholds for the total energy and the atomic forces were set to 10⁻¹³ a.u. and 10⁻¹⁰ a.u., respectively. For the generation of the calculated supercells the program supercell was used.⁵⁸ The cif2cell program was used to assist in the input file generation.⁵⁹ To obtain NMR parameters, GIPAW calculations^60,61 with standard setup (job = nmr, q_gipaw = 0.01 and spline_ps = .true.) were performed. For the calculation of the isotropic chemical shifts, gallium containing compounds with known isotropic chemical shifts were used to generate a conversion formula from the isotropic chemical shielding parameter σ_iso. The quadrupolar coupling C_Q and the quadrupolar asymmetry parameter η_Q were calculated based on the electric field tensor eigenvalues V_ii and the nuclear quadrupole moment eQ.

Brunauer–Emmett–Teller (BET) analysis. The specific surface areas were measured by nitrogen physisorption at 77 K in a Nova 3200e sorption station from Quantachrome. Before recording the isotherms, 500 mg sample material was degassed under vacuum at 100 °C (hydrozincite) and 250 °C (zinc oxide) for 5 h. Afterwards, the isothermal profiles between p/p₀ = 0.0 and 1 referred to a reference cell were recorded. The multipoint BET surface area was determined by applying the Brunauer–Emmett–Teller equation in a sample specific range determined by the Micropore-Assistant of the NovaWin software by only considering the increasing volume.

Scanning electron microscopy (SEM). The SEM analysis of the doped ZnO samples were taken on a Zeiss Gemini Ultra Plus with an Oxford EDX detector. A spatula tip of the sample was dispersed on a carbon covered stainless steel pin mount sample holder.

Transmission electron microscopy (TEM). TEM analyses were performed on a FEI Tecnai F30 G2 STwin (300 kV, FEG) equipped with an EDX detector (Si/Li, EDAX). The TEM samples were ground and dispersed in n-butanol (spatula tip sample in few drops of n-butanol) and prepared on Cu lacey TEM grids.

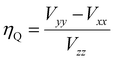3. Results and discussion

First the materials synthesis of nano-scale ZnO:Ga is presented which is achieved via thermal decomposition of nano-scale Ga-doped precursors. The products are characterized for surface area, morphology and crystallinity. In the second part solid-state nuclear magnetic resonance (NMR) is used to obtain insight into the defect structure of ZnO. NMR fingerprint for various possible Ga site defects is predicted and the NMR resonances are localized in bulk or particle surface.

3.2 Nano-scale gallium substituted precursors for ZnO

The precursor phase obtained under the co-precipitation conditions applied in this study is hydrozincite Zn₅[(OH)₆|(CO₃)₂]. In our previous study on Al,³¹ this phase was shown to be able to incorporate certain amounts of trivalent cations. We made an attempt to incorporate Ga³⁺ in hydrozincite, a compound structurally related to hydrotalcite or layered double hydroxides (LDH). As the latter ones are able to incorporate di- and trivalent cations, Powder X-ray diffraction (PXRD) reveals a similar behavior in the sense, that the samples up to a gallium to zinc substitution ratio x_Ga = 0.04 are crystalline and free of crystalline side phases (Fig. 2). The hydrozincite reflections become broader as the gallium content in the starting solution was increased, indicating that our attempt to incorporate Ga³⁺ in this phase was successful and that gallium doping leads to a reduction of the crystallite size. For a gallium content x_Ga > 0.04 an additional reflection of a side phase at around 2θ = 12° evolved, which is assigned to a hydrotalcite-type crystalline phase. The mineral of the analogous aluminum-rich hydrotalcite-type side-phase is called zaccagnaite with the composition: Zn₄Al₂(OH)₁₂(CO₃)·3H₂O. This side phase was also found in a study about Al incorporation into hydrozincites and zinc oxides.³¹ Here, instead of aluminum gallium cations were incorporated, resulting in a Zn,Ga layered double hydroxide (Zn,Ga LDH) side-phase similar to zaccagnaite. With further increase of x_Ga further line broadening is observed. Additionally, new reflections at angles of 2θ = 6.45° and 19.49° evolved for x_Ga > 0.06. No matching entries could be found for these reflections in the ICSD and COD databases. The additional reflection at 2θ = 19.49° was also observed in a previous investigation with aluminum as trivalent cation and presumably corresponds to a defect enriched hydrozincite with broken symmetry.³¹ Interestingly for x_Ga = 0.15 all observed reflections aside the ones assigned to the gallium-containing zaccagnaite become sharper again, including both the additional ones as well as those assigned to hydrozincite. This further corroborates that all belong to a common phase.

Fig. 2 PXRD pattern of the co-precipitated gallium-doped hydrozincite precursors and a gallium containing zaccagnaite (b). In (a) is a higher resolution of the range up to 2θ = 15° shown, to demonstrate the evolution of the zaccagnaite-like Zn,Ga LDH phase (“Ga Zaccagnaite”). The reference pattern was taken from ICSD, hydrozincite (ICSD-16583) and the zaccagnaite (ICSD-190041, marked with *). The new and unassigned reflections at 2θ = 6.45°, 2θ = 19.45° and 2θ = 27.03° are marked with a triangle. x_Ga denotes the metal-based fraction of gallium atoms.

Further temperature resolved PXRD was carried out (Fig. S1†). Analogous to the Al-substituted hydrozincite,³¹ the gallium-doped precursor decomposes at around 220 °C to ZnO, which is in line with the results from thermogravimetric analysis (compare Fig. S2†). Contrarily, the zaccagnaite-like side phase reflections disappeared at a temperature of around 120 °C. The additional reflections at 2θ = 6.45° and 2θ = 19.49° vanish at virtually identical temperatures, further corroborating that these belong to a common hydrozincite phase modified by x_Ga > 0.06. The Ga-containing zaccagnaite side phase reflections disappear already at a temperature of around 120 °C, a much lower temperature despite the chemical and structural relationship to hydrozincite. In order to obtain further insight about the gallium incorporation into the hydrozincite host lattice ⁷¹Ga magic-angle spinning (MAS) NMR measurements were performed (Fig. 3).

Fig. 3 Scaled ¹H decoupled ⁷¹Ga MAS NMR stackplot of gallium doped hydrozincite and a zaccagnaite-like Zn,Ga LDH phase (“Ga Zaccagnaite”). The gallium content for the hydrozincites is given by x_Ga. All spectra were recorded with a spinning frequency of 20 kHz.

In the hydrozincite crystal structure there are three different Zn sites, two of which show a six-fold coordination and one being four-fold coordinated, which can in principle all be substituted by Ga. Through ⁷¹Ga MAS NMR the presence of six-fold coordinated gallium cations in a potential gallium substituted hydrozincite Zn_5−5xGa_10/3·x(CO₃)₂(OH)₆ could be confirmed (δ^exp_obs = 37 ppm), indicating a preferred substitution of atoms on the six-fold coordinated Zn sites by Ga atoms. A similar preferred substitution of the atoms on the six-fold coordinated Zn sites has also been observed for Al-doped hydrozincite.³¹ The chemical shift and the quadrupolar lineshape differ slightly from the one observed for the octahedrally coordinated gallium atoms in a Ga-containing zaccagnaite. This peculiar lineshape was not observed in the spectra of the doped hydrozincite samples, indicating that the formation of zaccagnaite as observed by PXRD at x_Ga > 0.06 is only a minor impurity, while most gallium atoms are incorporated into the hydrozincite.

With the incorporation of Ga³⁺ ions in the hydrozincite precursor and the formation of potential side-phases at high concentrations characterized, the next subchapter focuses on the ZnO:Ga decomposition products. A deeper investigation of the precursors defect chemistry will be subject of a forthcoming study.

3.3 Formation and characterization of nano-scale ZnO:Ga

Nano-scale ZnO:Ga was formed by calcination of the Ga-doped hydrozincite at a temperature of 320 °C in static air, involving the elimination of H₂O and CO₂. PXRD analysis (Fig. 4) exhibits reflections of ZnO. Potential side phases like the spinel phase ZnGa₂O₄ ⁶² or homologous phases of Ga₂O₃(ZnO)_x ^63,64 could not be observed, which also indicates that both hydrozincite and the zaccagnaite-like side phase have decomposed, which is also in agreement with the temperature-resolved PXRD investigation (Fig. S1†). The exclusive formation of ZnO is also supported by electron diffraction performed during the transmission electron microscopy (TEM) analysis (Fig. S3†). Herein samples with a Ga content of x_Ga = 0.4, and x_Ga = 0.15 were analyzed in the TEM with electron diffraction (ED) and energy dispersive X-Ray spectroscopy (EDX) with regard to phases and chemical composition. Electron diffraction of the ZnO:Ga sample with x_Ga = 0.04 (Fig. S3a and b†) exhibits a for ZnO typical d-spacing and a polycrystalline diffraction pattern. Fig. S3c† shows an overview image of the heavily doped ZnO (x_Ga = 0.15) sample with a big platelet having a diameter of about 200 nm, as well as an agglomeration comparable to that shown in Fig. S3a† with lower Ga concentration. The larger platelet shows a single-crystalline electron diffraction pattern (zone axis [001], Fig. S3d†) with a d-spacing slightly bigger than the one typical for ZnO (010 reflection 2.864 Å instead of 2.8145 Å; −120 reflection 1.669 Å instead of 1.6249 Å). Larger platelets are assumed to be a zaccagnaite-like side phase, as it was observed for the Al doped series, as well. Even, in case of Al as dopant, the decomposition of the side phase resulted in a highly defective ZnO. The main difference is, that in case of Ga as dopant, the side phase only evolved at higher doping levels in the precursor phase (x_Ga > 0.04). These results are also supported by EDX point measurements on the platelet and on the agglomerate shown in Fig. S3c.† As a result, the platelet has an amount of 33.3 (mol/mol) % Ga in contrast to the agglomerate where the amount of Ga is only slightly increased in comparison to the average composition (x_Ga = 0.15). The higher amount of Ga, as seen by EDX, in the big platelets can be explained by the high concentration of Ga in the zaccagnaite-like side phase which leads to a higher amount of amorphous/disordered side-phase covering the ZnO-platelets than in the rest of the sample.

Fig. 4 (a) PXRD pattern of the gallium doped zinc oxides after calcination of the hydrozincite precursors. The reflection positions are indicated by tickmarks and were taken from COD entry for zinc oxide (COD-2107059). x_Ga is the metal-based fraction of gallium atoms and is indicated in (a) on the right hand side. In (b) the lattice parameters are presented, the purple line is an extrapolated fit to the range of to the range of x_Ga = 0.01–0.04. In (c) crystallite sizes for two distinct directions of the crystallites are shown.

The visual inspection of the powder patterns in Fig. 4a shows that for all compositions studied, ZnO is observed as the only crystalline phase. The lattice parameters (Fig. 4b) a and c show for x_Ga = 0.01–0.04 a linear trend, which is corroborated by the fitted line. For a this trend appears to continue up to x_Ga = 0.1, while for c already at x_Ga = 0.06 a clear deviation from linearity is observed. Over the entire range of Ga-contents under study the reflections become broader. Further, the line broadening is anisotropic, i.e. more pronounced for specific crystallographic directions. The resulting crystallite sizes for h00 and 00l reflections are shown in Fig. 4c. A steady decline from above 10 nm down to 4–5 nm evolves. Further, the aspect ratio is inverted, which would correspond to a change in shape from slightly needle-like to platelets with increasing x_Ga. It must be mentioned that the line shape analysis is here limited to the assumption of pure size contribution for the sake of simplicity, neglecting possible strain broadening. Inclusion of strain contributions did not improve the fit significantly, but ZnO is well-known for its tendency to form stacking faults,^65,66 which have an anisotropic line broadening effect as well (note the pronounced broadening of cross plane reflections like 102 and 103), but this analysis is beyond the scope of this work. The steady decrease of the crystallite size is in line with a continuous increase of the BET surface area (Fig. 4) with increasing x_Ga.

Regarding the question of the solubility limit of Ga³⁺ in ZnO the results are somewhat contradictory: a linear dependence of the lattice parameter on chemical composition may be stated for a up to x_Ga = 0.1, while c is only linear up to x_Ga = 0.04. The determination of the lattice parameters becomes increasingly unreliable due to the broad reflections and correlations with the specimen displacement. The crystallite size declines rather quickly up to x_Ga = 0.06 beyond which it rather converges. From these results a solubility limit of x_Ga = 0.06 or even lower may be inferred, requiring combination with results from complementary methods.

Further a brief comparison to the case of ZnO:Al from our previous study³¹ shall be drawn: the dependence of the crystallite size on the chemical composition was less pronounced, but still extended when exceeding the solubility limit determined by ²⁷Al MAS NMR (∼1.3 mol%). Further the crystallite shape was needle-like as inferred from the aspect ratio of the anisotropic crystallite sizes. For ZnO:Ga this inverts around an nominal substitution ratio of x_Ga = 0.03 corresponding to a real value of x_Ga(AAS) = 0.023. This change in aspect ratio may be seen as further evidence for a substitution limit beyond x_Ga = 0.03 in ZnO:Ga.

Qualitatively, the increase in the surface area for ZnO:Ga with rising gallium concentration is associated with a change in the morphology as seen in SEM micrographs (Fig. 6).

While the overall platelet-like morphology from the hydrozincite is maintained during thermal decomposition (see Fig. S4†), with increasing Ga content a reduction in size of the ZnO:Ga aggregates is observed. Simultaneously, a reduction in the pore size and a rise of the numbers of pores occurs (see Fig. S5†), which is consistent with the increase in the surface area observed by BET (Fig. 5). Especially for the ZnO doped with x_Ga = 0.15 the pore size is reduced to the nano-scale. Furthermore, for this sample, additional platelets on top of the typical ZnO agglomerates are observed (marked with arrows in Fig. 6). Due to the typical shape for layered double hydroxide (LDH) crystallites and because of the observed side phase reflections of a zaccagnaite-like Zn,Ga LDH phase in PXRD in the precursor characterization, the platelets are expected to be the zaccagnaite-like side phase. This is in alignment with the earlier reported study of Al doped ZnO.³¹

Fig. 5 Evolution of the BET-surface for the gallium doped hydrozincites (white columns; HZ) and their corresponding zinc oxides (black filled columns; ZnO) after calcination at 320 °C for 4 h in static air.

Fig. 6 SEM micrographs of selected ZnO:Ga samples with x_Ga = 0.01 (left), 0.04 (center) and 0.15 (right). Larger platelets observed in the sample with x_Ga = 0.15 are marked with arrows.

3.4 Ga-defects in ZnO

In order to study the incorporation of the Ga³⁺ ions into the ZnO crystal lattice ⁷¹Ga MAS NMR measurements were performed (Fig. 7) on a series of samples with different degree of substitution.

Fig. 7 ¹H decoupled ⁷¹Ga MAS NMR stackplot of doped zinc oxide, annealed at 320 °C for 4 h, with different cation-based molar gallium fractions, x_Ga. All spectra were recorded with a spinning frequency of 20 kHz.

In ⁷¹Ga MAS NMR spectra several gallium environments can be resolved: two peaks which can be assigned to 4-fold coordinated Ga atoms (δ^exp_obs = 213 and ∼200 ppm) and one broad resonance corresponding to 5- and/or 6-fold coordinated gallium atoms (δ^exp_obs ≈ 50 ppm) for samples with a high gallium concentration, x_Ga > 0.03. The overlap of peaks in ⁷¹Ga MAS NMR spectra is stronger than that in the corresponding ²⁷Al MAS NMR spectra of ZnO:Al, which makes the distinction of different environments more difficult.³¹ Importantly, at low Ga-content only a single tetrahedrally coordinated gallium environment at δ^exp_obs = 213 ppm could be observed. This ⁷¹Ga MAS NMR signal features a narrow linewidth, which indicates, that the Ga atom has a well-ordered environment and a small quadrupolar coupling because no second-order quadrupolar lineshape is observed, so that the observed chemical shift δ^exp_obs equals the isotropic chemical shift δ^exp_iso within error limits. This peak is assigned to Ga cations on a Zn-site in ZnO, i.e., which needs to be confirmed by quantum-chemical calculations presented in the following.

3.5 NMR finger-print of different possible Ga defects

In principle, a number of different defects has been suggested previously for ZnO,^24,29,47 besides the already mentioned defect. To obtain NMR fingerprint for the different point defects (see below), quantum chemical calculations can be applied. By comparison of chemical shift values and quadrupolar parameters to experimental values on known crystal structures, scales to translate calculated values on the experimental scale can empirically be determined and it is possible to estimate the error of prediction. To this end literature values were collected on 14 compounds yielding 18 individual, unambiguously assigned Ga peaks (Table S2†). Deliberately only non-metallic compounds were considered, which are chemically similar to the investigated system.

Shielding calculations which are determined via density functional theory need to be converted from a shielding scale to a deshielding scale against a different standard which is required by the experimentalist. This not only requires a sign change and calculation of a reference compound but also needs a scaling of the shielding parameter, which is due to the imperfections of the theoretical method. Here, density functional theory under periodic boundary conditions using Kresse Joubert projector augmented wave (kjpaw) pseudopotentials,⁶⁷ the Perdew–Burke–Ernzerhof (pbe) functional type and a cutoff energy of 120 Ry was applied. The shielding values were estimated using “Gauge Including Projector Augmented Waves” (GIPAW) as implemented in quantum espresso. The conversion formula to obtain from calculated isotropic shielding σ^calc_iso predicted isotropic chemical shift values δ^pred_iso for ^69/71Ga.

δ^pred_iso = A·σ^calc_iso + B

The parameters A = −0.930 ± 0.014 and B = (1600 ± 22) ppm were obtained by a linear regression of experimental deshielding values δ^pred_iso against calculated shielding values σ^calc_iso (Fig. 8a, Table S2†). The average error of prediction of shielding values δ^pred_iso amounts to roughly 6 ppm over a range from −98 to 333 ppm, which provides a good basis for predicting the hypothetical shift values for different defects.

Fig. 8 (a) Correlation plot of the experimentally determined isotropic chemical shifts δ^exp_iso to the calculated isotropic chemical shielding values σ^calc_iso for ⁷¹Ga. The gray line represents a linear regression with the δ^pred_iso = A·σ^calc_iso + B conversion formula with A = −0.930 ± 0.014 and B = 1600 ± 22 ppm (R² = 0.9965). The corresponding values were taken from Table S2.† (b) Correlation plot between the experimentally determined quadrupolar coupling C^exp_Q and the calculated quadrupolar coupling C^calc_Q. The dotted line represents a linear regression with the C^pred_Q = C·C^calc_Q prediction formula with C = 1.20 ± 0.07 (R² = 0.9764).

For the quadrupole interaction, quantum chemical calculations were used to get the electric field gradient tensor, whose eigenvalues V_xx, V_yy and V_zz are required to calculate the quadrupolar coupling C_Q and the asymmetry parameter η_Q. The quadrupolar coupling C^calc_Q in principle was obtained by a simple multiplication with the nuclear quadrupole moment Q for ⁷¹Ga as tabulated and the eigenvalue V^calc_zz.⁶⁸ The GIPAW method at this level of theory introduces an apparent scaling of the electric field gradients, which can be seen from the deviation of the slope parameter C from unity. The latter being determined via linear regression of the experimental quadrupole coupling C^exp_Q against calculated quadrupole couplings C^calc_Q for of 16 individual Ga sites (Fig. 8b, and Table S2†), which leads to the conversion formula

C^pred_Q = C·C^calc_Q

and a C parameter C = 1.20 ± 0.07.

The calculated electric quadrupole couplings C^calc_Q underestimate the experimental values C^exp_Q by about 20%. This discrepancy is partially related to the difference in temperatures between simulation and experiment but also to limitations of the theoretical method, for example using a pseudopotential for a nuclear property instead of an all-electron treatment.

The average error of prediction for the predicted quadrupolar couplings C^pred_Q is 6% in a range from 0 to 15 MHz. An especially drastic error in prediction was observed for ZnGa₂O₄, which could be a consequence of disorder and defects in the spinel structure.⁶⁹ Nevertheless, the calculations in general provide a reliable basis to distinguish big from small quadrupolar couplings which is what is required for the identification of Ga defects.

For the following calculations different defect models were generated following literature and a similar study on ZnO:Al.^24,29,47 The considered defect models are (a) the 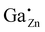defect, in which a zinc atom is substituted by a gallium atom, (b) the defect, in which a gallium atom is positioned on a tetrahedrally coordinated interstitial position, (c) the defect, in which a gallium atom is positioned on an octahedrally coordinated interstitial position and (d) a coupled defect of a gallium atom substituting a zinc atom neighboring to a zinc vacancy (Table 1). The defects are illustrated in Fig. 9. It should be noted that all models carry a non-zero formal charge.

Fig. 9 Gallium defect models (a) , (b) , (c) and (d) . The defect structures were calculated embedding them in a supercell with a background charge and relaxing the atomic positions. The atoms in the relaxed (Ga: red, O: dark blue, Zn: dark gray) and the original structure (Ga: red, O: light blue, Zn: light gray) are shown in comparison. The empty circles label zinc vacancies either caused by relaxation (c) or by the investigated defect itself (d).

Table 1 Predicted NMR fingerprint for various different point defects in ZnO:Ga including the site symmetry in Hermann–Mauguin notation, predicted isotropic chemical shift δ^pred_iso, ⁷¹Ga quadrupolar coupling and quadrupolar asymmetry parameter C^pred_Q. The ⁷¹Ga quadrupolar coupling and quadrupolar asymmetry parameter were calculated from the electric field gradient eigenvalues using a 4 × 4 × 2 ZnO supercell and converted using the conversion factor C. The necessary nuclear quadrupole moment for ⁷¹Ga was taken from ref. 68. The isotropic chemical shift δ^pred_iso for the , , and 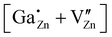defects was obtained by conversion of the supercell size converged isotropic chemical shielding values σ^calc_iso (see Fig. 10, S6, S7 and S8†)

Defect	Site symmetry	δ iso ^pred /ppm	C ^predQ/MHz	η ^predQ
	3m	200(4)	2.0	0.0
	3m	92(4)	6.5	0.0
	m	220(4)	−22.3	0.74(6)
	m	204(3)	−15.1	0.36(5)

---

To calculate charged point-defects, an opposite jellium background charge is required.⁷⁰ The interaction of charged defects in neighboring unit cells will influence the results, unlike when applying for example embedded point charge models, which allow to calculate defects at infinite dilution.⁷¹ To study the convergence behavior of the NMR parameters, the size of the supercells hosting a single defect were changed from 2 × 1 × 1 to 4 × 4 × 2, where the basic cell refers to the conventional unit cell of ZnO. In each case the structures were relaxed while keeping the cell parameters fixed. The values at infinite dilution were estimated by plotting the shielding values σ^calc_iso as a function of shortest distance found between the charged defects in neighboring unit cells. In this way, results from a number of supercell combinations yield a plot which is dense enough to evaluate the convergence behavior. The converged value was estimated by fitting a decaying exponential function into the obtained curve (Fig. 10, S6–S8†). In all cases it was possible to obtain converged values with an additional estimated error of about 4 ppm for the predicted chemical shift δ^pred_iso. These values could then be converted using the above mentioned conversion formulas (Fig. 8, and Table S3†).

Fig. 10 Isotropic chemical shielding σ^calc_iso convergence plot for the defect, resulting in an isotropic chemical shielding value of 1503.1 ± 3.9 ppm extrapolated to an infinitely large supercell. Plotted are the isotropic chemical shielding σ^calc_iso values against the shortest Ga–Ga distance in the different supercell d_Ga–Ga. The d_Ga–Ga distance is illustrated on the example of a 2 × 1 × 2 supercell. The isotropic chemical shielding σ^calc_iso values for the different sized supercells (points are labeled with the corresponding supercell) are shown in Table S3.†

For all defect models the energy of the model was minimized by optimizing the positions of the atoms in a quantum-chemical calculation, which hereinafter is referred to as “relaxation”. By relaxation the structure of the defect in (a) the Ga–O bonds become shorter, forming an almost ideal tetrahedron, while the distances to the next environmental sphere increase.²⁴ The relaxation conserves the point group symmetry C_3v of the site. Based on the pseudo symmetry T_d, a small quadrupolar coupling C_Q is expected, while an asymmetry parameter η^pred_Q of zero is the consequence of the C_3v symmetry of the defect.

In (b) the gallium atom is originally located in a coordination with an O_h pseudosymmetry.⁴⁷ By relaxation the gallium atom shifts along the c-axis, resulting in the formation of three shorter and three longer Ga–O bonds. The point group symmetry of this defect is C_3v. The symmetry is consistent with a low quadrupolar coupling C^pred_Q and an asymmetry parameter η^pred_Q of zero (Table 1).

The defect in (c) exhibits a tetrahedral coordination in its unrelaxed state. During relaxation, due to electrostatic repulsion between the cations, the Zn²⁺ ion of the edge-sharing ZnO₄ tetrahedron, is shifted onto an octahedrally coordinated interstitial position, similar to the one previously discussed for the 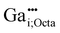defect. Taking these changes into consideration, the relaxed defect would need to be assessed as a defect. Relaxation causes a reduction in the point group symmetry to C_s. Therefore, a high quadrupolar coupling C^pred_Q and an asymmetry parameter η^pred_Q unequals zero are expected. This behavior differs from the one previously reported for the similar aluminium defect, in which no zinc vacancy is generated.⁴⁷

The coupled defect 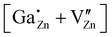in (d) consists of a defect and a defect, located in the first coordination sphere of the defect²⁴ along the c-axis. During the relaxation process no significant change in the atomic coordinates occurred, resulting in a point group symmetry of C_s, giving rise to a considerable quadrupolar coupling C^pred_Q and an asymmetry parameter η^pred_Q unequals zero.

3.6 Point defects in nano-scale ZnO:Ga

In this subchapter the predicted finger-print for different point defects is compared with the experimental results. Experimentally, a ⁷¹Ga MAS NMR resonance with a chemical shift δ^exp_iso of 213 ppm, a quadrupolar coupling with a magnitude |C^exp_Q| of roughly 3 MHz and a low quadrupolar asymmetry parameter η^exp_Q could be determined for the signal occurring at low substitution ratios x_Ga. By exclusion principle it will be discussed which defects in principle are consistent with the experimental observations.

Defects in (c) and (d) exhibit a large quadrupolar coupling C^pred_Q as well as a non-zero quadrupolar asymmetry parameter η^pred_Q, which clearly rules out the defects 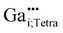and , because of the mismatch between expected and experimentally observed lineshape in ⁷¹Ga NMR (see Fig. S9†).

The remaining two defects (a) and (b) both would result in a relatively narrow lineshape matching the ones of the experimental spectra. However, the difference in coordination number of the and the defect is expected to produce a significant change in isotropic chemical shift, which is consistent with predicted values from quantum chemical calculations. This results in an unambiguous assignment of the ⁷¹Ga signal at δ^exp_iso = 213 ppm to the defect (see Fig. S9†). We note in passing, that the signal assignment is consistent with the shift of the 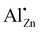defect in ZnO of δ^exp_iso = 82 ppm applying a correlation found between ²⁷Al and ⁷¹Ga shift data established for isostructural solids, which suggests an isotropic chemical shift value of 227 ppm.^43,44

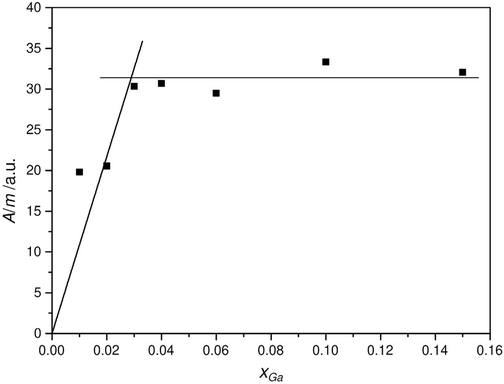
In order to access the solubility limit of the species in ZnO by ⁷¹Ga MAS NMR, the peak area per mass was quantified as a function of the substitution ratio x_Ga. To this end the lineshape parameters, which were used to deconvolute of different resonances, are determined by fitting of the signals of the extreme substitution ratios. Then only the peak areas for the individual peaks were fitted which removes ambiguity in the fitting process introduced by the observed strong signal overlap (Fig. 11).

Fig. 11 Ratio of the ⁷¹Ga MAS NMR signal area per mass A/m for the signal at δ^exp_iso = 213 ppm of ZnO:Ga, annealed with 320 °C for 4 h with different cation-based molar gallium fractions x_Ga. The NMR spectra were excited with a selective π/2 pulse. The lines to interpolate the substitution limit were obtained by fitting linear functions into the corresponding data points.

An increase of the signal area per mass of the resonance at δ^exp_iso = 213 ppm up to around x_Ga = 0.03 gallium concentration can be observed which then levels off to an almost constant value (Fig. 11). The solubility limit is estimated by fitting to linear functions into the rising part and the plateau, respectively and by determining their crossing point, which indicates a solubility limit for the species of about nominal substitution ratio x_Ga = 0.029 (x_Ga(AAS) = 0.022). From PXRD the lattice parameter c showed marked deviations from a Vegard-like behavior for x_Ga > 0.04, which would roughly coincide with the limit found by ⁷¹Ga MAS NMR. Apparently, other factors influence the further evolution of lattice parameters and crystallite size beyond this limit. One may speculate that this could be the hindrance of crystallite growth by an amorphous, Ga-containing matrix or Ga³⁺ being attached to specific crystallite surfaces, giving rise to the observed change in the apparent crystallite shape.

3.7 Surface characterization of nano-scale ZnO:Ga by NMR

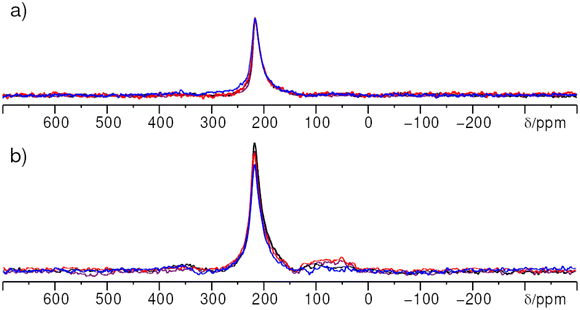
A remaining question is if the different ⁷¹Ga resonances can be associated with the bulk of the ZnO particles or the surface. To this end two different experiments were applied: surface characterization of the nanoparticles by paramagnetic impregnation (PASPA) and ⁷¹Ga{¹H} rotational-echo double resonance (REDOR) experiments.

In order to distinguish the gallium signals arising from the inside of the ZnO:Ga particles from those from the particle surface, the surface of ZnO:Ga was impregnated with manganese(II)-acetylacetonate according to the procedure described in reference.⁴⁶⁷¹Ga paramagnetically assisted surface peak assignment (PASPA) NMR measurements were performed on ZnO:Ga samples with x_Ga = 0.03 and x_Ga = 0.1 (Fig. 12). The condition, that the particles must be smaller than 20 nm for PASPA to cause big enough peak changes, is met (see results from PXRD above).

Fig. 12 ¹H decoupled ⁷¹Ga PASPA MAS NMR of ZnO:Ga with x_Ga = 0.03 (a) and x_Ga = 0.1 (b) recorded at 20 kHz rotation frequency, comparing the as-made sample (purple spectrum) to the reference sample (black spectrum), the acetonitrile blind test sample (red spectrum) and the paramagnetically impregnated sample (blue spectrum).

Acetonitrile was selected as solvent for the paramagnetic agent, as it has been shown to keep the surface of doped ZnO nanoparticles intact.⁴⁶

Only a single ⁷¹Ga resonance at δ^exp_iso = 213 ppm is observed corresponding to the 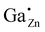defect in case of ZnO:Ga with a gallium content of x_Ga = 0.03. By ⁷¹Ga PASPA a suppression ratio R_sup close to zero is determined for this species, as there is no significant change present between peak of the reference and the paramagnetically impregnated sample. This indicates that the species is located in the particle bulk of the ZnO nanoparticles.

A suppression ratio R_sup of 0.23 is determined for the resonance at δ^exp_iso = 213 ppm for the sample with a gallium content of x_Ga = 0.1 by ⁷¹Ga PASPA. This can be explained by an overlap of the NMR resonance of the 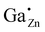defect in ZnO with a second resonance of a fourfold coordinated Ga atom (“GaO₄”) in an amorphous/disordered side phase, which is close to the particle surface (see Fig. 7). Additionally, a sixfold coordinated Ga species “GaO₆” could be resolved for the sample with a gallium content of x_Ga = 0.1. This species also shows a high suppression ratio in ⁷¹Ga PASPA, which means that both species can be attributed to the surface. The presence of fivefold coordinate Ga atoms “GaO₅” can neither be confirmed nor rejected because of the limited resolution in direct excitation ⁷¹Ga NMR. A MQMAS was impossible because of the limitations in signal to noise ratio at the given substitution ratios.

Because hydrogen atoms played an important role for surface defects of ZnO:Al,⁴⁶ it was necessary to evaluate if this is also the case for the ZnO:Ga surface. To this end ¹H PASPA experiments were performed (Fig. 13).

Fig. 13 ¹H PASPA MAS NMR of ZnO:Ga with x_Ga = 0.03 recorded at 20 kHz rotation frequency, comparing the as-made sample (purple) to the reference sample (black), the acetonitrile blind test sample (red) and the paramagnetically impregnated sample (blue).

The as-made ZnO:Ga exhibits two different H environments similar to ZnO:Al,⁴⁶ corresponding to a resonance at δ^exp_iso = 2 ppm and one at δ^exp_iso = 4.3 ppm, respectively. The latter signal can be assigned to H₂O molecules on the particle surface, which are removed under vacuum. The other resonance is assigned to hydroxyl functions. Their peak shows a high suppression ratio in ¹H PASPA, giving strong evidence for the claim that hydroxyl functions are located close-to or on the particle surface. The high suppression ratios observed in ¹H PASPA indicate that the amount of hydrogen in the bulk of the ZnO particles is negligible.

This scenario can further be corroborated by ⁷¹Ga {¹H} REDOR experiments (Fig. 14). In contrast to the signal of in ZnO, the GaO₆ signal exhibits a fast and complete dephasing, proving the presence of ¹H in close proximity to all of the GaO₆ groups. As the ¹H species could be assigned to the particle surface, it can be concluded, GaO₆ species can only be found at the surface of the nanoparticles.

Fig. 14 ⁷¹Ga {¹H} REDOR NMR curves using the universal dephasing scale τ_uds ^72,73 of the ⁷¹Ga MAS NMR signals at δ^exp_iso = 213 ppm (left; 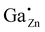) and δ^exp_obs = 50 ppm (right; GaO₆), of as-made ZnO:Ga with x_Ga = 0.03 for the defect and x_Ga = 0.15 for the GaO₆ defect. The upper dotted line corresponds to the heterogeneous error and the lower dashed line corresponds to the homogeneous error.⁷⁴ The measurements were performed at 20 kHz spinning frequency.

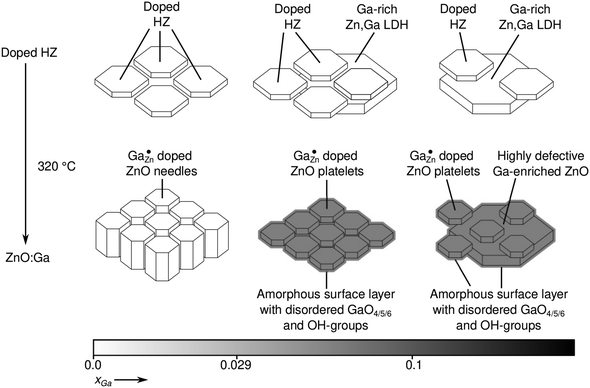
On the basis of the previous findings a model for the ZnO:Ga nanoparticle is suggested which is in agreement with all presented observations (Fig. 15). For low Ga substitution ratios x_Ga, Zn atoms in the crystalline particle core (δ^exp_iso = 213 ppm) are substituted by gallium cations up to a solubility limit of about x_Ga = 0.029 (x_Ga(AAS) = 0.022). Additional gallium cations, exceeding this limit, are not incorporated into the crystal bulk anymore, but into an amorphous/disordered surface layer surrounding the crystalline ZnO core. GaO₄, GaO₆ and potentially GaO₅ species are present in this surface shell. The amorphous shell further contains hydrogen atom containing defects in the form of water and hydroxyl functions. Given that the particles did not show a Knight-shift of ⁷¹Ga resonance, it can be concluded that the additional electrons introduced through Ga as an n-dopant are compensated for example by the formation of –O⁻ groups in the surface of the particles or by color center in ZnO.⁴⁷

Fig. 15 Model for the structural and compositional changes in hydrozincite and ZnO with increasing gallium content. For samples below the solubility limit of x_Ga = 0.029 (x_Ga(AAS) = 0.022), solely doped hydrozincite platelets are present, which result in ZnO:Ga needles after calcination. In the concentration region 0.029 < x_Ga < 0.1 aside from the doped HZ also first larger platelets corresponding to a Zn,Ga LDH are potentially forming. The corresponding ZnO:Ga after calcination exhibits a smaller crystallite size and resulting in a more platelet-like morphology compared to lower gallium concentrations. The excess is deposited along the OH-groups in an amorphous surface layer with an unknown composition including Ga, H, O and potentially Zn. Above x_Ga = 0.1 (x_Ga(AAS) = 0.087) the formation of the Zn,Ga LDH becomes more dominant, giving rise to bigger highly-defective Ga-enriched ZnO platelets after calcination.

4. Conclusions

The incorporation of Ga into nanocrystalline ZnO synthesized via the low-temperature decomposition of hydrozincite has been studied by PXRD, electron microscopy, gas adsorption and NMR. As expected from the ionic radii, a higher solubility limit of Ga in ZnO as compared to Al in ZnO could be achieved. The experiments provide evidence for a detailed model with a disordered/amorphous surface and a crystalline ZnO core of the nano-scale high-surface materials, which follows the example of ZnO:Al synthesized via the same route. The structural insight will help to improve the catalytic activity of ZnO support materials with different promoter ions.

Besides conversion formula for computed shielding parameters and quadrupole parameters are provided, which could be applied in NMR studies of other gallium oxides.

Conflicts of interest

There are no conflicts to declare.

Data availability

All experimental and computed data are made available if required.

References

1. E. Kunkes and M. Behrens, in Chemical Energy Storage, ed. R. Schlögl, De Gruyter, 2013, pp. 413–442.  DOI:10.1515/9783110266320.413.
2. D. Sheldon, Methanol Production - A Technical History, Johnson Matthey Technol. Rev., 2017, 61, 172–182,  DOI:10.1595/205651317x695622.
3. R. Guil-Lopez, N. Mota, J. Llorente, E. Millan, B. Pawelec, J. L. G. Fierro and R. M. Navarro, Methanol synthesis from CO₂: a review of the latest developments in heterogeneous catalysis, Mater., 2019, 12, 3902,  DOI:10.3390/ma12233902.
4. M. Behrens, S. Zander, P. Kurr, N. Jacobsen, J. Senker, G. Koch, T. Ressler, R. W. Fischer and R. Schlögl, Performance Improvement of Nanocatalysts by Promoter-Induced Defects in the Support Material: Methanol Synthesis over Cu/ZnO:Al, J. Am. Chem. Soc., 2013, 135, 6061–6068,  DOI:10.1021/ja310456f.
5. B. Mockenhaupt, J. Gieser, S. Najafishirtari, L. Baumgarten, J. Jelic, T. Lunkenbein, E.-J. Ras, J.-D. Grunwaldt, F. Studt and M. Behrens, On the secondary promotion effect of Al and Ga on Cu/ZnO methanol synthesis catalysts, J. Catal., 2024, 439, 115785,  DOI:10.1016/j.jcat.2024.115785.
6. K. Hagedorn, W. Li, Q. Liang, S. Dilger, M. Noebels, M. R. Wagner, J. S. Reparaz, A. Dollinger, J. Schmedt auf der Günne, T. Dekorsy, L. Schmidt-Mende and S. Polarz, Catalytically Doped Semiconductors for Chemical Gas Sensing: Aerogel-Like Aluminum-Containing Zinc Oxide Materials Prepared in the Gas Phase, Adv. Funct. Mater., 2016, 26, 3424–3437,  DOI:10.1002/adfm.201505355.
7. T. Tsubota, M. Ohtaki, K. Eguchi and H. Arai, Thermoelectric properties of Al-doped ZnO as a promising oxide material for high-temperature thermoelectric conversion, J. Mater. Chem., 1997, 7, 85–90,  10.1039/a602506d.
8. K.-D. Jung and O.-S. Joo, Preparation of Cu/ZnO/M₂O₃ (M = Al, Cr) catalyst to stabilize Cu/ZnO catalyst in methanol dehydrogenation, Catal. Lett., 2002, 84, 21–25.
9. G. Wang, D. Mao, X. Guo and J. Yu, Methanol synthesis from CO₂ hydrogenation over CuO-ZnO-ZrO₂-M_xO_y catalysts (M=Cr, Mo and W), Int. J. Hydrogen Energy, 2019, 44, 4197–4207,  DOI:10.1016/j.ijhydene.2018.12.131.
10. J. Schumann, M. Eichelbaum, T. Lunkenbein, N. Thomas, M. C. Álvarez Galván, R. Schlögl and M. Behrens, Promoting Strong Metal Support Interaction: Doping ZnO for Enhanced Activity of Cu/ZnO:M (M = Al, Ga, Mg) Catalysts, ACS Catal., 2015, 5, 3260–3270,  DOI:10.1021/acscatal.5b00188.
11. N. Barrow, J. Bradley, B. Corrie, Y. Cui, T. D. Tran, T. E. Erden, A. Fish, M. Garcia, P. Glen, N. Mistry, M. Nicholson, S. Roloff-Standring, D. Sheldon, T. Smith, A. Summer, K. U. Din and N. Macleod, Doubling the life of Cu/ZnO methanol synthesis catalysts via use of Si as a structural promoter to inhibit sintering, Sci. Adv., 2024, 10, eadk2081,  DOI:10.1126/sciadv.adk2081.
12. J. Toyir, P. R. De la Piscina, J. L. G. Fierro and N. Homs, Highly effective conversion of CO₂ to methanol over supported and promoted copper-based catalysts: influence of support and promoter, Appl. Catal., B, 2001, 29, 207–215,  DOI:10.1016/s0926-3373(00)00205-8.
13. N. Roberts, R.-P. Wang, A. W. Sleight and W. W. Warren Jr., ²⁷Al and ⁶⁹Ga impurity nuclear magnetic resonance in ZnO:Al and ZnO:Ga., Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 5734–5741,  DOI:10.1103/PhysRevB.57.5734.
14. B. E. Sernelius, K. F. Berggren, Z. C. Jin, I. Hamberg and C. G. Granqvist, Band-gap tailoring of zinc oxide by means of heavy aluminum doping, Phys. Rev. B: Condens. Matter, 1988, 37, 10244.
15. S. Miao, R. N. d'Alnoncourt, T. Reinecke, I. Kasatkin, M. Behrens, R. Schlögl and M. Muhler, A study of the influence of composition on the microstructural properties of ZnO/Al₂O₃ mixed oxides, Eur. J. Inorg. Chem., 2009, 910–921,  DOI:10.1002/ejic.200800987.
16. C. S. Santana, L. F. Rasteiro, F. C. F. Marcos, E. M. Assaf, J. F. Gomes and J. M. Assaf, Influence of Al, Cr, Ga, or Zr as promoters on the performance of Cu/ZnO catalyst for CO₂ hydrogenation to methanol, Mol. Catal., 2022, 528, 112512,  DOI:10.1016/j.mcat.2022.112512.
17. A. Beck, M. A. Newton, L. G. A. van de Water and J. A. van Bokhoven, The Enigma of Methanol Synthesis by Cu/ZnO/Al₂O₃-Based Catalysts, Chem. Rev., 2024, 124, 4543–4678,  DOI:10.1021/acs.chemrev.3c00148.
18. G. Pacchioni, From CO₂ to Methanol on Cu/ZnO/Al₂O₃ Industrial Catalyst. What Do We Know about the Active Phase and the Reaction Mechanism?, ACS Catal., 2024, 14, 2730–2745,  DOI:10.1021/acscatal.3c05669.
19. M. Behrens, G. Lolli, N. Muratova, I. Kasatkin, M. Hävecker, R. N. d'Alnoncourt, O. Storcheva, K. Köhler, M. Muhler and R. Schlögl, The effect of Al-doping on ZnO nanoparticles applied as catalyst support, Phys. Chem. Chem. Phys., 2013, 15, 1374–1381,  10.1039/c2cp41680h.
20. M. Behrens and R. Schlögl, How to Prepare a Good Cu/ZnO Catalyst or the Role of Solid State Chemistry for the Synthesis of Nanostructured Catalysts, Z. Anorg. Allg. Chem., 2013, 639, 2683–2695,  DOI:10.1002/zaac.201300356.
21. J. L. Alfke, M. Tejeda-Serrano, S. Phadke, A. Tereshchenko, T. Z. H. Gani, L. Rochlitz, S. B. X. Y. Zhang, L. Lin, C. Copéret and O. V. Safonova, Boundary Conditions for Promotion versus Poisoning in Copper–Gallium-Based CO₂-to-Methanol Hydrogenation Catalysts, ACS Catal., 2024, 14, 9166–9175,  DOI:10.1021/acscatal.4c01985.
22. R. D. Shannon and C. T. Prewitt, Effective ionic radii in oxide and fluorides, Acta Crystallogr., Sect. B, 1969, 25, 925,  DOI:10.1107/s0567740869003220.
23. L. Zhong-Lin, Z. Wen-Qin, X. Ming-Xiang, Z. Feng-Ming and D. You-Wei, Structural and Electrical Properties of Single Crystalline Ga-Doped ZnO Thin Films Grown by Molecular Beam Epitaxy, Chin. Phys. Lett., 2009, 26, 116102,  DOI:10.1088/0256-307X/26/11/116102.
24. H. Serier, A. Demourgues and M. Gaudon, Investigation of Ga Substitution in ZnO Powder and Opto-Electronic Properties, Inorg. Chem., 2010, 49, 6853–6858,  DOI:10.1021/ic1000733.
25. V. J. Norman, Diffusion of aluminum and gallium in zinc oxide, Aust. J. Chem., 1969, 22, 325,  DOI:10.1071/ch9690325.
26. M. H. Yoon, S. H. Lee, H. L. Park, H. K. Kim and M. S. Jang, Solid solubility limits of Ga and Al in ZnO, J. Mater. Sci. Lett., 2002, 21, 1703–1704,  DOI:10.1023/A:1020841213266.
27. W. W. Warren Jr., N. Roberts, R. P. Wang and A. W. Sleight, NMR study of carrier states and trapping complexes in the transparent conductor ZnO:MIII., Mater. Sci. Forum, 1997, 258–263, 1365–1370,  DOI:10.4028/www.scientific.net/MSF.258-263.1365.
28. G. K. Paul and S. K. Sen, Sol–gel preparation, characterization and studies on electrical and thermoelectrical properties of gallium doped zinc oxide films, Mater. Lett., 2002, 57, 742–746,  DOI:10.1016/S0167-577X(02)00865-0.
29. R. Wang, A. W. Sleight and D. Cleary, High Conductivity in Gallium-Doped Zinc Oxide Powders, Chem. Mater., 1996, 8, 433,  DOI:10.1021/cm950372k.
30. S. Lany and A. Zunger, Dopability, Intrinsic Conductivity, and Nonstoichiometry of Transparent Conducting Oxides, Phys. Rev. Lett., 2007, 98, 045501,  DOI:10.1103/PhysRevLett.98.045501.
31. B. Mockenhaupt, J. K. Wied, S. Mangelsen, U. Schürmann, L. Kienle, J. Schmedt auf der Günne and M. Behrens, Phase evolution, speciation and solubility limit of aluminium doping in zinc oxide catalyst supports synthesized via co-precipitated hydrozincite precursors, Dalton Trans., 2023, 52, 5321–5335,  10.1039/d3dt00253e.
32. A. Walsh and A. Zunger, Instilling defect tolerance in new compounds, Nat. Mater., 2017, 16, 964–967,  DOI:10.1038/nmat4973.
33. D. Waller, D. Stirling, F. S. Stone and M. S. Spencer, Copper-zinc oxide catalysts: activity in relation to precursor structure and morphology, Faraday Discuss. Chem. Soc., 1989, 87, 107,  10.1039/dc9898700107.
34. M. Hjiri, R. Dhahri, L. E. Mir, A. Bonavita, N. Donato, S. G. Leonardi and G. Neri, CO sensing properties of Ga-doped ZnO prepared by sol-gel route, J. Alloys Compd., 2015, 634, 187–192,  DOI:10.1016/j.jallcom.2015.02.083.
35. X. Yu, J. Ma, F. Ji, Y. Wang, X. Zhang, C. Cheng and H. Ma, Effects of sputtering power on the properties of ZnO:Ga films deposited by r.f. magnetron sputtering at low temperature, J. Cryst. Growth, 2005, 274, 474–479,  DOI:10.1016/j.jcrysgro.2004.10.037.
36. G. R. Patzke, S. Locmelis, R. Wartchow and M. Binnewies, Chemical transport phenomena in the ZnO–Ga₂O₃ system, J. Cryst. Growth, 1999, 203, 141–148,  DOI:10.1016/S0022-0248(99)00083-4.
37. G. B. Palmer and K. R. Poeppelmeier, Phase relations, transparency and conductivity in Ga₂O₃-SnO₂-ZnO, Solid State Sci., 2002, 4, 317–322,  DOI:10.1016/S1293-2558(01)01258-4.
38. T. Lunkenbein, F. Girgsdies, T. Kandemir, N. Thomas, M. Behrens, R. Schlögl and E. Frei, Bridging the Time Gap: A Copper/Zinc Oxide/Aluminum Oxide Catalyst for Methanol Synthesis Studied under Industrially Relevant Conditions and Time Scales, Angew. Chem., Int. Ed., 2016, 55, 12708–12712,  DOI:10.1002/anie.201603368.
39. C.-Y. Tsay, K.-S. Fan and C.-M. Lei, Synthesis and characterization of sol-gel derived gallium-doped zinc oxide thin films, J. Alloys Compd., 2012, 512, 216–222,  DOI:10.1016/j.jallcom.2011.09.066.
40. M. S. Bernardo, P. G. Villanueva, T. Jardiel, D. G. Calatayud, M. Peiteado and A. C. Caballero, Ga-doped ZnO self-assembled nanostructures obtained by microwave-assisted hydrothermal synthesis: Effect on morphology and optical properties, J. Alloys Compd., 2017, 722, 920–927,  DOI:10.1016/j.jallcom.2017.06.160.
41. M. Yan, H. T. Zhang, E. J. Widjaja and R. P. H. Chang, Self-assembly of well-aligned gallium-doped zinc oxide nanorods, J. Appl. Phys., 2003, 94, 5240–5246,  DOI:10.1063/1.1608473.
42. K. J. D. MacKenzie and M. E. Smith, Multinuclear Solid-State Nuclear Magnetic Resonance of Inorganic Materials, Pergamon, 2002.
43. S. M. Bradley, R. F. Howe and R. A. Kydd, Correlation between aluminum-27 and gallium-71 NMR chemical shifts, Magn, Reson. Chem., 1993, 31, 883,  DOI:10.1002/mrc.1260311002.
44. D. Massiot, T. Vosegaard, N. Magneron, D. Trumeau, V. Montouillout, P. Berthet, T. Loiseau and B. Bujoli, ⁷¹Ga NMR of reference Ga_IV, Ga_V, and Ga_VI compounds by MAS and QPASS, extension of gallium/aluminum NMR parameter correlation, Solid State Nucl. Magn. Reson., 1999, 15, 159–169,  DOI:10.1016/s0926-2040(99)00053-3.
45. H. Nagashima, J. Trébosc, Y. Kon, K. Sato, O. Lafon and J.-P. Amoureux, Observation of Low-γ Quadrupolar Nuclei by Surface-Enhanced NMR Spectroscopy, J. Am. Chem. Soc., 2020, 142, 10659–10672,  DOI:10.1021/jacs.9b13838.
46. J. K. Wied, B. Mockenhaupt, U. Schürmann, L. Kienle, S. Mangelsen, J. Glänzer, V. R. Celinski, M. Behrens and J. Schmedt auf der Günne, Method for Surface Characterization Using Solid-State Nuclear Magnetic Resonance Spectroscopy Demonstrated on Nanocrystalline ZnO:Al, Anal. Chem., 2024, 96, 11290–11298,  DOI:10.1021/acs.analchem.4c01170.
47. Y. S. Avadhut, J. Weber, E. Hammarberg, C. Feldmann and J. Schmedt auf der Günne, Structural investigation of aluminium doped ZnO nanoparticles by solid-state NMR spectroscopy, Phys. Chem. Chem. Phys., 2012, 14, 11610–11625,  10.1039/c2cp41139c.
48. A. A. Coelho, TOPAS and TOPAS-Academic: an optimization program integrating computer algebra and crystallographic objects written in C++, J. Appl. Crystallogr., 2018, 51, 210–218,  DOI:10.1107/s1600576718000183.
49. P. Thompson, D. E. Cox and J. B. Hastings, Rietveld refinement of Debye-Scherrer synchrotron X-ray data from alumina, J. Appl. Crystallogr., 1987, 20, 79–83,  DOI:10.1107/s0021889887087090.
50. R. K. Harris and E. D. Becker, NMR nomenclature: nuclear spin properties and conventions for chemical shifts - IUPAC recommendations, J. Magn. Reson., 2002, 156, 323–326,  DOI:10.1006/jmre.2002.2554.
51. R. K. Harris, E. D. Becker, S. M. Cabral De Menezes, P. Granger, R. E. Hoffman and K. W. Zilm, Further conventions for NMR shielding and chemical shifts: (IUPAC recommendations 2008), Pure Appl. Chem., 2008, 80, 59–84,  DOI:10.1351/pac200880010059.
52. D. Jardón-Álvarez and J. Schmedt auf der Günne, Reduction of the temperature gradients in laser assisted high temperature MAS NMR., Solid State Nucl. Magn. Reson., 2018, 94, 26–30,  DOI:10.1016/j.ssnmr.2018.08.002.
53. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials, J. Phys.: Condens. Matter, 2009, 21, 395502,  DOI:10.1088/0953-8984/21/39/395502.
54. P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. Buongiorno Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. Dal Corso, S. de Gironcoli, P. Delugas, R. A. Di Stasio Jr., A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H.-Y. Ko, A. Kokalj, E. Kucukbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H.-V. Nguyen, A. Otero-de-la-Roza, L. Paulatto, S. Ponce, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, Advanced capabilities for materials modelling with QUANTUM ESPRESSO, J. Phys.: Condens. Matter, 2017, 29, 465901,  DOI:10.1088/1361-648x/aa8f79.
55. H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B:Condens. Matter Mater. Phys., 1976, 13, 5188–5192,  DOI:10.1103/PhysRevB.13.5188.
56. N. Troullier and J. L. Martins, Efficient pseudopotentials for plane-wave calculations, Phys. Rev. B:Condens. Matter Mater. Phys., 1991, 43, 1993–2006,  DOI:10.1103/PhysRevB.43.1993.
57. P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B:Condens. Matter Mater. Phys., 1994, 50, 17953–17979,  DOI:10.1103/PhysRevB.50.17953.
58. K. Okhotnikov, T. Charpentier and S. Cadars, Supercell program: a combinatorial structure-generation approach for the local-level modeling of atomic substitutions and partial occupancies in crystals, J. Cheminf., 2016, 8, 17,  DOI:10.1186/s13321-016-0129-3.
59. T. Björkman, CIF2Cell: Generating geometries for electronic structure programs, Comput. Phys. Commun., 2011, 182, 1183–1186,  DOI:10.1016/j.cpc.2011.01.013.
60. C. J. Pickard and F. Mauri, All-electron magnetic response with pseudopotentials: NMR chemical shifts, Phys. Rev. B:Condens. Matter Mater. Phys., 2001, 63, 245101,  DOI:10.1103/PhysRevB.63.245101.
61. C. Gervais, L. Bonhomme-Coury, F. Mauri, F. Babonneau and C. Bonhomme, GIPAW (gauge including projected augmented wave) and local dynamics in ¹³C and ²⁹Si solid state NMR: the study case of silsesquioxanes (RSiO_1.5)₈, Phys. Chem. Chem. Phys., 2009, 11, 6953–6961,  10.1039/B907450C.
62. A. d. S. Goncalves, S. A. Marques de Lima, M. R. Davolos, S. G. Antonio and C. d. O. Paiva-Santos, The effects of ZnGa₂O₄ formation on structural and optical properties of ZnO:Ga powders, J. Solid State Chem., 2006, 179, 1330–1334,  DOI:10.1016/j.jssc.2006.01.046.
63. N. Kimizuka, M. Isobe and M. Nakamura, Syntheses and Single-Crystal Data of Homologous Compounds, In₂O₃(ZnO)_m (m = 3, 4, and 5), InGaO₃(ZnO)₃, and Ga₂O₃(ZnO)_m (m = 7, 8, 9, and 16) in the In₂O₃-ZnGa₂O₄-ZnO System, J. Solid State Chem., 1995, 116, 170–178,  DOI:10.1006/jssc.1995.1198.
64. M. Nakamura, N. Kimizuka and T. Mohri, The phase relations in the In₂O₃·Ga₂ZnO₄·ZnO system at 1350 °C, J. Solid State Chem., 1991, 93, 298–315,  DOI:10.1016/0022-4596(91)90304-Z.
65. J. P. Cline, M. Leoni, D. Black, A. Henins, J. E. Bonevich, P. S. Whitfield and P. Scardi, Crystalline domain size and faulting in the new NIST SRM 1979 zinc oxide, Powder Diffr., 2013, 28, S22,  DOI:10.1017/s0885715613001188.
66. J. I. Langford, A. Boultif, J. P. Auffrédic and D. Louër, The use of pattern decomposition to study the combined X-ray diffraction effects of crystallite size and stacking faults in ex-oxalate zinc oxide, J. Appl. Crystallogr., 1993, 26, 22–33,  DOI:10.1107/S0021889892007684.
67. G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B:Condens. Matter Mater. Phys., 1999, 59, 1758–1775,  DOI:10.1103/PhysRevB.59.1758.
68. P. Pyykkö, Year-2008 nuclear quadrupole moments, Mol. Phys., 2008, 106, 1965–1974,  DOI:10.1080/00268970802018367.
69. M. Allix, S. Chenu, E. Veron, T. Poumeyrol, E. A. Kouadri-Boudjelthia, S. Alahrache, F. Porcher, D. Massiot and F. Fayon, Considerable Improvement of Long-Persistent Luminescence in Germanium and Tin Substituted ZnGa₂O₄, Chem. Mater., 2013, 25, 1600–1606,  DOI:10.1021/cm304101n.
70. N. D. Lang and W. Kohn, Theory of Metal Surfaces: Charge Density and Surface Energy, Phys. Rev. B, 1970, 1, 4555–4568,  DOI:10.1103/PhysRevB.1.4555.
71. J. Weber and J. Schmedt auf der Günne, Calculation of NMR parameters in ionic solids by an improved self-consistent embedded cluster method, Phys. Chem. Chem. Phys., 2010, 12, 583–603,  10.1039/b909870d.
72. T. Gullion and J. Schaefer, Rotational-echo double-resonance NMR, J. Magn. Reson., 1989, 81, 196–200,  DOI:10.1016/0022-2364(89)90280-1.
73. M. Roming, C. Feldmann, Y. S. Avadhut and J. Schmedt auf der Günne, Characterization of Noncrystalline Nanomaterials: NMR of Zinc Phosphate as a Case Study, Chem. Mater., 2008, 20, 5787–5795,  DOI:10.1021/cm800805f.
74. V. R. Celinski, J. Weber and J. Schmedt auf der Günne, C-REDOR curves of extended spin systems, Solid State Nucl. Magn. Reson., 2013, 49–50, 12–22,  DOI:10.1016/j.ssnmr.2012.10.001.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5dt00928f

‡ These authors contributed equally.

---