Open Access Article
Open Access ArticlePrecipitation of morphology-controlled uranium(VI) peroxide in nitric acid media†
Lucas
Muller
 ab,
Paul
Estevenon
ab,
Paul
Estevenon
 *a,
Christelle
Tamain
*a,
Christelle
Tamain
 a,
Nicolas
Dacheux
a,
Nicolas
Dacheux
 b and
Nicolas
Clavier
b and
Nicolas
Clavier
 b
b
aCEA, DES, ISEC, DMRC, Univ Montpellier, Marcoule, France. E-mail: paul.estevenon@cea.fr; Tel: +33 4 66 79 65 66
bICSM, Univ Montpellier, CEA, CNRS, ENSCM, Marcoule, France
First published on 19th March 2025
Abstract
The precipitation of U(VI) peroxide (UO2(O2)·4H2O, known as studtite) has been extensively studied in mildly acidic media (i.e. pH > 1). However, only a few studies have investigated the influence of highly acidic conditions (i.e. pH < 1) on the precipitation of studtite, particularly regarding the morphology of the final powder. Therefore, the influence of high acidity (0.1 M < C(H+)ini < 2.0 M) and the C(H2O2)ini/C(U)ini molar ratio (ranging from 10 to 70) on the precipitation kinetics, as well as the morphological and crystallographic properties of U(VI) peroxide, was investigated in this study. Decreasing the acidity and increasing the C(H2O2)ini/C(U)ini molar ratio have significantly enhanced both the final precipitation yield and the reaction kinetics. Furthermore, a correlation was found between the initial saturation index of the reaction mixture and the final morphology and crystallite size of the precipitated U(VI) peroxide, independent of the initial precipitation conditions. These results demonstrate that in highly acidic nitric media, it is possible to control the morphology of the precipitated U(VI) peroxide by simply adjusting the initial saturation index. This correlation opens up interesting perspectives for the synthesis of powders with specific morphologies, in particular uranium peroxide or corresponding oxide powders obtained after thermal treatment. This morphology control is of great interest in the field of nuclear fuel fabrication, as the characteristics of oxide powder, such as flowability or sintering reactivity, have a strong impact on the manufacturing process and the properties of the final ceramic.
1. Introduction
Uranium(VI) peroxide tetrahydrate, UO2(O2)(H2O)2·2H2O, commonly called “studtite”, from the name of the natural mineral form of this compound,1 is ubiquitous in the industrial uranium chemical treatment process. In the initial steps of the nuclear fuel cycle, particularly during the uranium extraction process, uranium(VI) peroxide can be precipitated and then calcined at low temperature to recover uranium from the in situ leaching of uranium ore:2,3 it is usually precipitated in sulfuric media at low acidity (pH 3–4).4 Peroxide precipitation can also be a purification step prior to isotopic enrichment.5 Downstream, in advanced reprocessing of spent nuclear fuel, uranium can be recovered by peroxide precipitation.6 In addition, in the context of the direct long-term repository of spent nuclear fuel, the interactions between dissolved uranium and H2O2 produced by water radiolysis7 likely lead to the formation of UO2(O2)·4H2O that can passivate the dissolving surface.8–12There have been many studies on the precipitation of uranium(VI) peroxide. Some phenomenological ones have demonstrated quantitative precipitation of studtite at low acidity (pH 2–3),13,14 and then its conversion to pure U3O8 after calcination in air.15 Several reactors technologies have also been studied to precipitate uranium(VI) peroxide, such as continuous reactors16 or fluidized beds.17 Nevertheless, only a few studies have dealt with a fundamental approach. For example, Planteur et al. have addressed the crystal growth of uranium(VI) peroxide at pH = 3 in sulfuric acid18,19 while Kim et al.20 and Schwerdt et al.21 have established a relationship between the particle size and initial conditions of precipitation.
Only two papers have measured precipitation yields in acidic media. Kornilov et al.22 assessed the precipitation yield after 24 hours in 1 to 3 M HNO3 solutions and for different peroxide ion concentrations. The higher the acidity, the lower the yield was for a given initial peroxide concentration. Hibert et al. studied the precipitation of U(VI) and demonstrated the co-precipitation of U(VI) and Pu(IV) (potential production of MOx fuel directly from U–Pu flow) working between 0.8 M and 2.0 M HNO3.23
Still, there is very little data on the morphology adopted by U(VI) peroxide, especially in very acidic media (0.1 to 2.0 M), despite the fact that UO2(O2)·4H2O precipitation is a way of conversion and fabrication of nuclear fuel24 with the preservation of the peroxide morphology during the calcination step. With this objective, the shape of the particles is of great importance, as it is the main parameter that impacts the powder flowability25 and sinterability.26
In this work, the precipitation of uranium(VI) peroxide has been studied in nitric acid concentrations between 0.1 M and 2.0 M. To this end, several precipitation reactions were performed with a fixed uranium concentration (0.07 M) over a wide acidity range from 0.1 to 2.0 M H+ and molar ratios of C(H2O2)ini/C(U)ini ranging from 10 to 70. The precipitated U(VI) peroxide was characterized by X-ray diffraction and observed using scanning electron microscopy. The evolution of the precipitation yield was also measured under specific conditions.
2. Materials and methods
2.1. Precipitation of uranium(VI) peroxide
Caution! 238 U is an α-emitter and is considered a health risk. Experiments involving actinides require appropriate facilities and persons trained in the handling of radioactive materials.Commercial powdered uranyl nitrate, UO2(NO3)2·6H2O (Prolabo, purity 99%), was used as the uranium source for all the experiments. Acidity was fixed using concentrated analytical grade nitric acid solution at 70 wt% from CARLO ERBA. The hydrogen peroxide used was an analytical grade commercial solution at 30 wt%, supplied by CARLO ERBA (the concentration was determined to be C(H2O2) = 10.05 M by potentiometric titration with Ce(IV)).
1.00 mL of uranium(VI) solution with a uranyl concentration of 0.46 M was prepared in nitric media by dissolving around 235 mg of uranyl nitrate hydrate in diluted nitric acid solution with acidity ranging from 0.1 to 2.0 M. 5.80 mL of hydrogen peroxide solution was prepared by diluting concentrated H2O2 in nitric acid media with the same acidity as the uranium solution. A uranyl concentration of 0.46 M was arbitrarily set so that the final uranyl concentration after mixing these two solutions was 0.07 M. The concentration of hydrogen peroxide was determined so that the C(H2O2)ini/C(U)ini molar ratio was between 10 and 70 (Table ESI 1†) after the mixing of the two solutions.
Uranyl peroxide precipitation was achieved by adding the uranyl solution dropwise to the corresponding hydrogen peroxide solution in 10 mL glass beakers with a diameter of 2.5 cm and stirring with a 1.2 cm magnetic stirring rod at 500 rpm. The resulting mixture was stirred for a few hours, resulting in the formation of a yellow precipitate, with kinetics varying significantly depending on the chemical conditions considered. The progress of the reaction at the end of the experiment was calculated from the ratio of the effective yield to the theoretical yield at equilibrium. The reaction was arbitrarily considered to be at equilibrium when its progress reached 95%.
At the end of the precipitation, the suspension was collected and centrifuged at 4500 rpm (i.e. 3260× g) for 5 min in 15 mL tubes. The powder and the supernatant were then separated. A washing step was carried out twice with 2 mL of a 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 (vol
50 (vol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) vol) water/ethanol mixture. The solid was isolated from the supernatant by centrifugation and finally dried overnight at room temperature.
vol) water/ethanol mixture. The solid was isolated from the supernatant by centrifugation and finally dried overnight at room temperature.
It is worth noting that under the experimental conditions considered, although nitrous acid (HNO2) was autocatalytically generated in the nitric medium27 and can catalyze the decomposition of hydrogen peroxide, this reaction remains negligible for HNO2 concentrations below 8 M.28 In addition, since the reactions were carried out at room temperature, the decomposition rate of H2O2 was further limited. Additionally, the reaction durations are relatively short compared to the characteristic decomposition kinetics of H2O2. Consequently, the amount of H2O2 added can be considered nearly constant throughout the experiment.
2.2. Determination of uranium concentrations
Uranium concentration measurements were performed using an ICP-OES (inductively coupled plasma optical emission spectroscopy) Spectro Arcos apparatus. λ = 367.007 nm, λ = 385.958 nm, λ = 263.553 nm and λ = 393.203 nm wavelengths were considered to determine the uranium concentration. Calibration was performed using a series of standard uranium solutions (0.5 to 20 ppm), prepared by dilution of a 1000 ppm standard solution supplied by SCP Science. Uranium concentration was also determined by photon electron rejecting alpha liquid scintillation (PERALS) considering the protocol developed by Dacheux et al.29 The extraction was performed by contacting 6 mL of analyzed aqueous solutions with 1.5 mL of Alphaex™ scintillating cocktail purchased from ORDELA Inc. (Oak Ridge, USA). Alphaex™ is an organic cocktail containing HDEHP (bis-(2-ethylhexyl)phosphoric acid) as the extractant, PBBO (2-(4′-biphenylyl)-6-phenylbenzoxazole), PPO (2,5-diphenyloxazole) and NPO (2-(1-naphthyl)-5-phenyloxazole) as scintillators, naphthalene as the energy transfer agent and toluene as the solvent. The mixture was shaken for approximately 2–3 minutes and then centrifuged at 2000 rpm (i.e. 643× g) for 5 minutes. 1.3 mL of the organic phase was then collected and the 238U + 234U activity was measured, leading to uranium concentration in the leachate.2.3. Characterization of the prepared solids
Solids were analyzed using a Bruker D8 diffractometer equipped with a Lynxeye detector adopting the reflection geometry with a Göbel mirror and using Cu Kα1,2 radiation (λKα1 = 1.540593 Å; λKα2 = 1.544427 Å). For each acquisition, the PXRD (powder X-ray diffraction) pattern was recorded in the 10° < 2θ < 60° range with a step size of 0.027° (2θ) and a counting time of 1 s per step. Powders were prepared on flat sample holders with top-loading, placed in a dome-shaped specimen holder aiming to avoid radioactive contamination (Bruker airtight specimen holder with a knife edge, acting as an anti-scattering blade). Note that this PMMA (poly(methyl methacrylate)) dome can be the source of a large diffusion peak in the range of 10° < 2θ < 20°. Le Bail refinements30 of these patterns were performed using the FullProf Suite program31 with the Cox–Hastings pseudo-Voigt profile function.32 The instrumental function was obtained by refinement of a LaB6 reference. The backgrounds were manually selected.For SEM characterization, the samples were deposited on carbon adhesive tape and measured directly without any metal coating step. An FEI Quanta 200 scanning electron microscope, equipped with an Everhart–Thornley detector (ETD) and a backscattered electron detector (BSED), was used to record images at an acceleration voltage of 15 kV under high-vacuum conditions (10−6 Pa).
Specific surface areas (SSA) were measured on a Micrometric ASAP 2020 apparatus with the BET method (nitrogen adsorption at 77 K).
2.4. Determination of precipitation yield, saturation index and progress of the reaction
The precipitation yield at time t was calculated from the initial and final uranium concentrations in the supernatant, by using eqn (1). The final uranium concentrations were measured either by ICP-OES or PERALS (depending on experimental availability), after a 100-fold dilution to avoid any precipitation in the analysis tube. The initial uranium concentration was calculated from the mass of uranyl nitrate added. | (1) |
The initial saturation index (SIini) was calculated from the U(VI) peroxide precipitation reaction (eqn (2)) according to eqn (3), i.e. from the logarithm of the ratio between the reaction quotient out of equilibrium, Qini (eqn (4)), and the solubility constant, K (eqn (5)). The saturation index is useful here, as it expresses the driving force of the precipitation reaction. Indeed, when SI > 0, the solution is supersaturated with respect to the precipitated phase, whereas it remains undersaturated for SI < 0. In the latter case, no phase precipitation is expected in the solution. For the solubility constant of studtite (eqn (5)), the recommendations of the Nuclear Energy Agency were followed33 and the value from Kubatko et al.34 was selected, i.e. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (K) = −2.87.
(K) = −2.87.
 | (2) |
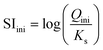 | (3) |
 | (4) |
 | (5) |
To simplify the calculations, the reaction progress has been calculated by taking into account only the U(VI) peroxide precipitation reaction (eqn (2)). The first step is to calculate the reaction quotient Qt for a time t(eqn 6).
 | (6) |
Taking into account the initial reactant concentration and the progress ε, Qt can be expressed as follows (eqn 7):
 | (7) |
The reaction reaches equilibrium when Qt equals K. The progress of the reaction is thus (eqn 8):
 | (8) |
It is then possible to calculate the theoretical yield of precipitation, which would correspond to (eqn 9):
 | (9) |
And then to access the rate of progress of the reaction by comparison with the final experimental yield (eqn 10):
 | (10) |
3. Results
3.1. Kinetic study associated with the precipitation of studtite
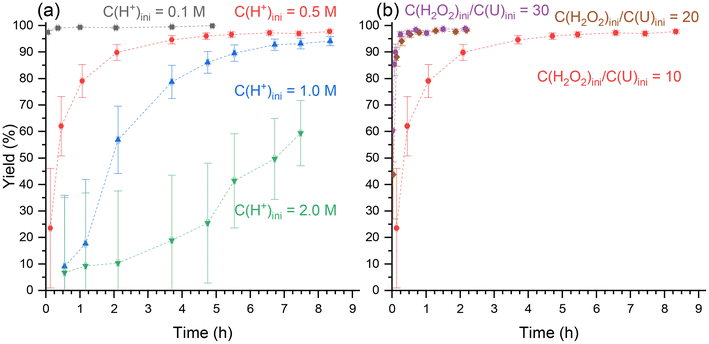
Two sets of precipitation experiments were carried out. For the first one, the initial nitric acid concentration was varied from 0.1 to 2.0 M and the C(H2O2)ini/C(U)ini molar ratio was set to 10 (Fig. 1a). In contrast, for the second set, C(H2O2)ini/C(U)ini was varied from 10 to 30, while the initial nitric acid concentration was set to 0.5 M. For both sets, the evolution of the precipitation yield (eqn (1)) was monitored (Fig. 1b), since it is clear from eqn (2) that the initial concentrations of both nitric acid and peroxide have an effect on the precipitation of UO2(O2)·4H2O.Simulations were performed using Phreeqc software and the Thermochimie v12 database35 to determine the uranium speciation under these conditions (Fig ESI 1 and Table ESI 3†). These simulations exclusively relied on thermodynamic constants validated by the latest NEA (Nuclear Energy Agency) review.33 In addition to the various species included in the Thermochimie database, H2O2, HO2−, and the complexes [(UO2)(O2)(OH)]− and [(UO2)2(O2)2(OH)]− were added.
However, these simulations do not match the experimental data, as the precipitation of U(VI) peroxide is significantly overestimated. This discrepancy is most likely due to the omission of higher-order uranyl nitrate complexes, for which no constants have been validated by the NEA, except for the mono-nitrate species.
Nevertheless, it remains possible to qualitatively estimate that the only expected solid phase under these conditions is U(VI) peroxide, while the predominant species in solution are uranyl nitrate and the U(VI) hydroxide complex. Regarding peroxo complexes, they only form under highly basic conditions and are therefore not expected in our system.
For both sets of experiments, a plateau seems to be reached more or less quickly depending on the initial conditions. The maximum precipitation yield is different for each precipitation and depends on the acidity or the C(H2O2)ini/C(U)ini molar ratio. The higher the initial acidity, the lower the plateau value. From the mass action law, it is clear that the precipitation reaction is favored by increasing the initial uranium or peroxide concentrations and disfavored by increasing the initial acidity. This explains why the plateau reached at the end of the precipitation reaction increases as the initial nitric acid concentration decreases (Fig. 1a) and as the C(H2O2)ini/C(U)ini molar ratio increases (Fig. 1b), which agrees well with Le Chatelier's principle. Kornilov et al. obtained similar results for similar initial acidities of 0.5 and 1.0 M, a molar ratio C(H2O2)ini/C(U)ini of 10, and an initial uranium concentration of 0.1 M after 24 hours.22 In 2.0 M H+, a yield of 90% was measured after 24 h, while in this work it did not exceed 60% after 7 hours, without reaching equilibrium. This means that the precipitation in 2.0 M H+ had not reached equilibrium after 7 hours.
In terms of kinetics, the precipitation rate can be written considering eqn (11), where k1 and k−1 represent the straightforward and the indirect kinetic constants, respectively. α, β, and γ stand for the partial orders related to uranium, hydrogen peroxide and proton concentrations, respectively, and s is the surface of the particles. From this equation, it can be confirmed that the precipitation rate increases with the initial uranium or peroxide concentration (i.e. C(H2O2)ini/C(U)ini molar ratio for a given uranium concentration) (Fig. 1b) and decreases with increasing initial proton concentration (Fig. 1a).
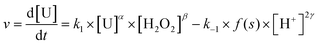 | (11) |
3.2. Morphological characterization of the studtite precipitates
The influence of the initial nitric acid concentration (i.e. 0.1, 0.5, 1.0 and 2.0 M) and the C(H2O2)ini/C(U)ini molar ratio (i.e. 10, 20, 40, and 68) on the powder morphology was also studied. SEM images are shown in Fig. 2. It is clear that larger particles are formed when the initial nitric acid concentration is increased for a given C(H2O2)ini/C(U)ini molar ratio. A similar effect is also observed when the C(H2O2)ini/C(U)ini molar ratio is decreased for a given initial nitric acid concentration.As it has already been described for other systems, the morphology of the precipitate can also be correlated with saturation conditions in the solution.36,37 For each sample, the initial saturation index associated with the corresponding precipitation conditions was calculated. A correlation is clearly evidenced, as the particle size decreases with increasing starting SI value. Furthermore, three different types of particle morphologies were observed depending on the initial SI values. For an initial SIini < 2.9, the powder is composed of needle-like crystals less than 1 μm wide and a few micrometers long, which become longer for lower SIini (around 10 μm for SI = 0.9). These needles are agglomerated to form pseudo-spheres for 2.4 < SIini < 2.9 (from a few micrometers for SI = 2.4 and less than 1 μm for SI = 2.9). It should be noted that, to our knowledge, these particular shapes have never been observed for UO2(O2)·4H2O. Nanoparticles are obtained for SIini > 2.9.
The influence of the saturation index on the morphology can be explained by the impact of saturation on the nucleation phenomenon. The higher the saturation index, the more primary nucleation is promoted and the less uranium in solution is available for crystal growth. Consequently, as SIini increases, the crystal size formed at equilibrium decreases.
With respect to the spherical agglomerates, the morphology of the particles was followed during precipitation with C(H+)ini = 0.5 M and C(H2O2)ini/C(U)ini = 20 by regularly sampling the powder throughout the process (Fig. 3). SEM images show that at the very beginning of the reaction, when only about 20% of the uranium has precipitated, needles of 1–2 μm are formed. They quickly agglomerate into a parallelepiped shape with nearly aligned needles. The needles and agglomerates stop growing when the yield exceeds 80%. This could mean that the number of agglomerated particles is likely to increase.
3.3. Structural characterization of the studtite precipitates
PXRD patterns were recorded for all the samples prepared. All powders correspond to studtite, UO2(O)2·4H2O (monoclinic, space group C2/c38). For C(H2O2)ini/C(U)ini = 10, UO2(O)2·4H2O precipitates obtained at different acidities are compared in Fig. 4a. While there is no obvious difference between 0.5, 1.0 and 2.0 M H+, the lower acidity studied (0.1 M) clearly resulted in much larger diffraction peaks. Similarly, the effect of the C(H2O2)ini/C(U)ini molar ratio was investigated in 0.5 M H+ (Fig. 4b). Here, the studtite synthesized with a molar ratio of 10 has sharper peaks than the other samples. | ||
| Fig. 4 PXRD patterns of studtite precipitates obtained for various H+ concentrations (0.1 M in black, 0.5 M in red, 1.0 M in blue, and 2.0 M in green), with C(H2O2)ini/C(U)ini = 10 and C(U)ini = 0.07 M (a) and for different initial C(H2O2)ini/C(U)ini molar ratios (10 in red, 20 in brown and 30 in purple) with C(H+)ini = 0.5 M and C(U)ini = 0.07 M (b); PXRD lines in red correspond to uranium(VI) peroxide from Burns et al.38 | ||
The difference in PXRD line widths reflects a difference in crystallite size. Crystallite size and unit cell volume were determined by Le Bail refinement from the PXRD patterns (Fig. 5). The data confirm that the crystallite size increases as the initial acidity increases. This crystallite size also decreases as the C(H2O2)ini/C(U)ini molar ratio increases.
Except for the uranium(VI) peroxide synthesized at 0.1 M H+, no changes in the volume of the unit cell (681 Å3) are observed. The volume of 684 Å3 observed for the uranium(VI) peroxide synthesized in 0.1 M H+ can be explained by nanocrystalline particles. This lattice parameter expansion for nanocrystallites is commonly reported39,40 and can be attributed to (i) the accumulation of sorbed species on the nanoparticle surfaces, which has a tensile effect on the crystal lattice41 and/or (ii) the accumulation of defects such as vacancies at the boundaries of nanocrystals, which locally increases the lattice parameters.42
Le Bail refinements were also performed on the other precipitates (Table ESI 2†). From these data, the crystallite size and lattice parameters of the studtite crystals can then be expressed as a function of the SIini value (Fig. 6). First of all, regarding the lattice parameters, b and c do not seem to vary with SIini. In contrast, a and β increase with SIini above 2.2, i.e. for conditions where spherical agglomerates are obtained. A plateau seems to be reached for SIini > 2.7, i.e. under conditions where nanoparticles are formed. The cell volume logically follows this tendency. The evolution of these parameters is probably related to the three morphologies obtained. For nanoparticles, the effect of the particle surface is isotropic and greater than for the other two morphologies. In contrast, for the needle-like morphologies, the effect of the surface on the lattice parameter is more likely to be anisotropic. This could then explain the variation of a and β as a function of particle morphology.
 | ||
| Fig. 6 Lattice parameters (a, b, c and β), unit cell volume and crystallite size of studtite crystals as a function of initial saturation index. Grey points are U(VI) peroxide samples from precipitation that have not reached equilibrium. Refinement results are available in Table ESI 2.† | ||
Finally, there is a good correlation between the SIini value and crystallite size. Indeed, as the SIini increases, the crystallite size decreases from about 150–200 nm to about 10–50 nm. For SIini < 2.7, which corresponds to the formation of studtite needle-like crystals, the crystallite sizes are about 150 nm, which is smaller than the size of the crystals observed in the SEM images for these SIini values (Fig. 2). This implies that the needle crystals are composed of multiple crystallites. In contrast, it is likely that the crystallite sizes obtained for SIini < 2.7 correspond to the nanoparticles observed in the SEM images.
4. Discussion
In the context of the high importance of powder morphology for fuel fabrication, the saturation index seems to be the key parameter controlling the morphology and the microstructure of the precipitate. The higher the SIini, the smaller the crystallite and the crystal size of the agglomerates. These observations suggest that neither the initial concentration of nitric acid nor that of peroxide ions, considered individually and for the same initial SI, influences the morphology of the precipitate. Instead, the morphology appears to be primarily influenced by the value of the saturation index in the solution. Indeed, it appears to be identical for a given saturation index value (images within frames of matching colors in Fig. 2), even though the initial acidity and peroxide concentration are different. The relative lack of effect of the initial acidity and C(H2O2)ini/C(U)ini ratio on the particle characteristics compared to the saturation index is somewhat surprising, since the kinetics of precipitation would be expected to differ under different initial chemical conditions. Therefore, the nucleation processes should be different and thus the final powder morphology should be distinct. Two additional precipitation experiments with kinetic monitoring were performed with the same initial saturation index (i.e. 1.7) but different initial reactant concentrations (i.e. C(U)ini = 0.07 M, C(H+)ini = 1.0 M and 2.0 M, and C(H2O2)ini/C(U)ini = 14.7 and 59.4) to confirm the predominant influence of the initial saturation on the final morphology (Fig. 7).First, the morphologies at the end of the precipitation are indeed identical (Fig. 7). However, the evolution of the yield does not follow the same curve, although the plateau reached by the two precipitation processes is almost the same. For the precipitation in 1.0 M H+ (Fig. 7, red squares), a first plateau seems to be formed at the beginning of the experiment, unlike under other conditions where precipitation occurs faster. This difference is probably explained by a different evolution of the saturation index during precipitation. The precipitation in 2.0 M H+, with more peroxide and no plateau at the beginning, exhibits a higher saturation index that is maintained in the reacting system during the precipitation compared to the first experiment. This agreement of the morphologies but not of the kinetics for the same SIini could be explained by the fact that the evolution of these two precipitation processes is not sufficiently different to form different morphologies or that the difference between the particles is not visible at the SEM scale. Nevertheless, it seems that in very acidic media, particle morphologies are controlled only by supersaturation. A wide variety of particle morphologies from nanoparticles to needles or spherical agglomerates can then be synthesized on demand.
Finally, given that thermal treatment preserves the morphology of U(VI) peroxides,21 oxides with corresponding morphologies can be produced. However, it remains difficult to determine whether a specific morphology is optimal for nuclear fuel fabrication. As mentioned above, the two key parameters to consider are powder flowability and sinterability.
In terms of flowability, and based on the correlations established by Cayla Arianer et al.,25 the most influential morphological factor appears to be the particle size distribution for particle size below 75 μm. While spherical morphologies (such as those observed for SIini values between 2.4 and 2.9) are generally expected to improve flowability, this advantage is offset by the strong cohesion induced by small particle sizes.
From a reactivity standpoint, which directly influences sinterability, the nanometric powder obtained at SIini values above 2.9 appears to be the most favorable. Specifically, the specific surface areas (SSA) of four representative morphologies from this study (Table 1) were determined via the BET method, revealing that the nanometric powder synthesized at SIini = 3.5 exhibits the highest SSA. In general, a higher specific surface area translates into lower required pressing pressure and sintering temperature, which ultimately leads to a higher final pellet density.43
| ISini | 3.5 | 2.4 | 2.1 | 1.8 |
|---|---|---|---|---|
| C(H+)ini (M) | 0.1 | 0.5 | 1.0 | 2.0 |
| C(H2O2)ini/C(U)ini | 10 | 20 | 40 | 68 |
| SSA (m2 g−1) | 21 ± 1 | 7 ± 1 | 5 ± 1 | 5 ± 1 |
5. Conclusion
The effect of initial chemical conditions on the precipitation of studtite in acidic media has been studied. Initial acidity and peroxide concentration (expressed as the molar ratio of initial peroxide concentration to uranium concentration at constant initial C(U)) both affect the kinetics of precipitation. Increasing acidity and decreasing peroxide concentration both slow down the precipitation of studtite.Secondly, a correlation was found between the initial saturation index and the final morphology and crystallite size of the powder. The higher the SIini value, the smaller the particles and the smaller the crystallite size. Conversely, low SIini values promote the formation of larger crystals with larger crystallite sizes. An intermediate morphology consisting of spherical needle clusters is also observed for 2.4 < SIini < 2.9. This correlation is explained by the fact that a high saturation index favors the nucleation phenomenon over crystal growth, which increases the formation of small particles. At low values of SIini, larger crystals are formed because the crystal growth phenomenon is promoted. Under the conditions studied, the saturation conditions seem to be the only parameter controlling the morphology. In fact, for the same SIini value, but different initial concentrations of the reactants, the final morphologies were found to be similar. Although the obtained morphologies cannot be considered as optimal for fuel fabrication at this stage, these results show that the morphology of U(VI) peroxide powder precipitated from an acidic uranyl solution can be controlled by adding an appropriate amount of peroxide ions, corresponding to the correct initial saturation index.
Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
The authors are grateful to Stéphanie Szenknect for her help with Phreeqc simulations and Renaud Podor and Joseph Lautru for SEM micrographs. The authors would like to thank the CEA for funding the PhD work of Lucas Muller.References
- K. Walenta, On Studtite and Its Composition, Am. Mineral., 1974, 59(1–2), 166–171 CAS.
- D. Lunt, P. Boshoff, M. Boylett and Z. El-Ansary, Uranium Extraction: The Key Process Drivers, J. South. Afr. Inst. Min. Metall., 2007, 107(7), 419–426 CAS.
- J. Dugua, Uranium Peroxide in the Form of Spherical Particles Having Good Flowability and Processes for Preparing Same, US4530823A, 1985 Search PubMed.
- F. E. Caropreso and D. F. Kreuz, Production of Uranium Peroxide, US4024215A, 1977 Search PubMed.
- B. Morel, D. Amaraggi, M. Arab, R. Thomas, M. Rivenet and F. Abraham, Process for Converting UO3 or U3O8 to Hydrated UO4, FR2969659B1, 2013 Search PubMed.
- H. Lagrave, C. Beretti and P. Bros, Treatment of Uranium and Plutonium Solutions Generated in Atalante by R and D Activities, 2008 Search PubMed.
- B. Pastina and J. A. LaVerne, Hydrogen Peroxide Production in the Radiolysis of Water with Heavy Ions, J. Phys. Chem. A, 1999, 103(11), 1592–1597 CrossRef CAS.
- B. D. Hanson, B. McNamara, E. C. Buck, J. I. Friese, E. Jenson, K. Krupka and B. W. Arey, Corrosion of Commercial Spent Nuclear Fuel. 1. Formation of Studtite and Metastudtite, Radiochim. Acta, 2005, 93(3), 159–168 CAS.
- B. McNamara, B. D. Hanson, E. C. Buck and C. Soderquist, Corrosion of Commercial Spent Nuclear Fuel. 2. Radiochemical Analyses of Metastudtite and Leachates, Radiochim. Acta, 2005, 93(3), 169–175 CrossRef CAS.
- C. Jégou, R. Caraballo, J. De Bonfils, V. Broudic, S. Peuget, T. Vercouter and D. Roudil, Oxidizing Dissolution of Spent MOX47 Fuel Subjected to Water Radiolysis: Solution Chemistry and Surface Characterization by Raman Spectroscopy, J. Nucl. Mater., 2010, 399, (1), 68–80 Search PubMed.
- A. Perrot, A. Canizares, S. Miro, L. Claparede, R. Podor, T. Sauvage, S. Peuget, C. Jegou and N. Dacheux, In Situ Raman Monitoring of Studtite Formation under Alpha Radiolysis in 18O-Labeled Water, J. Nucl. Mater., 2024, 600, 155267 CAS.
- M. L. Schlegel and C. Jegou, Uraninite Alteration by H2O2 Solutions and Formation of Secondary Phases: An, in Situ MicroRaman Spectroscopy and Synchrotron X-Ray Diffraction Study, J. Nucl. Mater., 2022, 572, 154056 CAS.
- J. S. Hopkins, J. A. Golding and G. M. Ritcey, The Critical Factors Influencing Uranium Precipitation by Hydrogen Peroxide: The Use of Experimental Design Techniques, Hydrometallurgy, 1987, 17(3), 315–334 CAS.
- M. Shabbir and K. E. Tame, Hydrogen Peroxide Precipitation of Uranium; Report of investigations RI7931, U.S, Department of the Interior, Bureau of Mines, 1974.
- R. Gupta, V. M. Pandey, S. R. Pranesh and A. B. Chakravarty, Study of an Improved Technique for Precipitation of Uranium from Eluted Solution, Hydrometallurgy, 2004, 71(3–4), 429–434 CrossRef CAS.
- A. E. Cahill and L. E. Burkhart, Continuous Precipitation of Uranium with Hydrogen Peroxide, Metall. Trans. B, 1990, 21(5), 819–826 Search PubMed.
- L. Mojica-Rodríguez, M. Bertrand, J. Gaillard, H. Muhr, E. Plasari, F. Auger and E. Brackx, Study on Uranium Peroxide Precipitation in a Continuous Fluidized-Bed Reactor with Mechanical Stirring, Nucl. Eng. Des., 2015, 293, 150–158 Search PubMed.
- S. Planteur, M. Bertrand, E. Plasari, B. Courtaud and J.-P. Gaillard, Thermodynamic and Crystal Growth Kinetic Study of Uranium Peroxide, CrystEngComm, 2013, 15(12), 2305 RSC.
- S. Planteur, M. Bertrand, E. Plasari, B. Courtaud and J. P. Gaillard, Crystal Growth Kinetics of the Uranium Peroxide, Procedia Chem., 2012, 7, 725–730 CrossRef CAS.
- K.-W. Kim, J.-T. Hyun, K.-Y. Lee, E.-H. Lee, K.-W. Lee, K.-C. Song and J.-K. Moon, Effects of the Different Conditions of Uranyl and Hydrogen Peroxide Solutions on the Behavior of the Uranium Peroxide Precipitation, J. Hazard. Mater., 2011, 193, 52–58 CrossRef CAS PubMed.
- I. J. Schwerdt, A. Olsen, R. Lusk, S. Heffernan, M. Klosterman, B. Collins, S. Martinson, T. Kirkham and L. W. McDonald, Nuclear Forensics Investigation of Morphological Signatures in the Thermal Decomposition of Uranyl Peroxide, Talanta, 2018, 176, 284–292 CrossRef CAS PubMed.
- A. S. Kornilov, E. V. Piterkina, K. O. Shcherbakova, A. O. Makarov and O. S. Dmitrieva, Specific Features of Peroxide Precipitation of Uranium from Acid Water–Ethanol Solutions, Radiochemistry, 2020, 62(2), 173–176 CrossRef CAS.
- N. Hibert, B. Arab-Chapelet, M. Rivenet, L. Venault, C. Tamain and O. Tougait, Dalton Trans., 2022, 51(34), 12928–12942 RSC.
- A. L. Tamasi, L. J. Cash, W. Tyler Mullen, A. R. Ross, C. E. Ruggiero, B. L. Scott, G. L. Wagner, J. R. Walensky, S. A. Zerkle and M. P. Wilkerson, Comparison of Morphologies of a Uranyl Peroxide Precursor and Calcination Products, J. Radioanal. Nucl. Chem., 2016, 309(2), 827–832 CrossRef CAS.
- L. Cayla Arianer, M. Leturia, A.-C. Robisson, C. Ablitzer, E. Daouk and K. Saleh, Assessment of the Influence of Model Powder Characteristics on Their Flowability Using Correlation Matrices, Powder Technol., 2025, 453, 120636 CrossRef CAS.
- Powder Technology Handbook, ed. H. Masuda, K. Higashitani and H. Yoshida, CRC Press, Boca Raton, 3rd edn, 2006 Search PubMed.
- D. Sicsic, F. Balbaud-Célérier and B. Tribollet, Mechanism of Nitric Acid Reduction and Kinetic Modelling, Eur. J. Inorg. Chem., 2014, 6174–6184 CrossRef CAS.
- R. E. Elson, Lawrence Radiation Laboratory, in The Homogenous Decomposition of Hydrogen Peroxide by Plutonium(IV), UCRL; 6536; Lawrence Radiation Laboratory, Livermore, CA, 1961 Search PubMed.
- N. Dacheux and J. Aupiais, Determination of Uranium, Thorium, Plutonium, Americium, and Curium Ultratraces by Photon Electron Rejecting α Liquid Scintillation, Anal. Chem., 1997, 6(13), 2275–2282 CrossRef PubMed.
- A. Le Bail and D. Louër, Smoothing and Validity of Crystallite-Size Distributions from X-Ray Line-Profile Analysis, J. Appl. Crystallogr., 1978, 11(1), 50–55 CrossRef CAS.
- C. Frontera and J. Rodríguez-Carvajal, FullProf as a New Tool for Flipping Ratio Analysis, Physica B: Condens. Matter, 2003, 335(1), 219–222 CAS.
- P. Thompson, D. E. Cox and J. B. Hastings, Rietveld Refinement of Debye–Scherrer Synchrotron X-Ray Data from Al2O3, J. Appl. Crystallogr., 1987, 20(2), 79–83 CAS.
- OECD, Second update on the Chemical Thermodynamics of Uranium, Neptunium, Plutonium, Americium And Technetium, Organisation for Economic Co-operation and Development, Paris, 2021, vol. 14 Search PubMed.
- K.-A. H. Kubatko, K. B. Helean, A. Navrotsky and P. C. Burns, Stability of Peroxide-Containing Uranyl Minerals, Science, 2003, 302(5648), 1191–1193 Search PubMed.
- B. Madé, W. Bower, S. Brassinnes, E. Colàs, L. Duro, P. Blanc, A. Lassin, L. Harvey and J. D. Begg, Recent Developments in ThermoChimie – A Thermodynamic Database Used in Radioactive Waste Management, Appl. Geochem., 2025, 180, 106273 Search PubMed.
- S. Shaddel, S. Ucar, J.-P. Andreassen and S. W. Østerhus, Engineering of Struvite Crystals by Regulating Supersaturation – Correlation with Phosphorus Recovery, Crystal Morphology and Process Efficiency, J. Environ. Chem. Eng., 2019, 7(1), 102918 CAS.
- L. Wang, J.-P. Andreassen and S. Ucar, Precipitation of Silver Particles with Controlled Morphologies from Aqueous Solutions, CrystEngComm, 2020, 22(3), 478–486 CAS.
- P. C. Burns and K.-A. Hughes, Studtite, [(UO2)(O2)(H2O)2](H2O)2: The First Structure of a Peroxide Mineral., Am. Mineral., 2003, 88(7), 1165–1168 CAS.
- K. Lu and Y. H. Zhao, Experimental Evidences of Lattice Distortion in Nanocrystalline Materials, Nanostruct. Mater., 1999, 12(1–4), 559–562 CrossRef.
- X. D. Liu, H. Y. Zhang, K. Lu and Z. Q. Hu, The Lattice Expansion in Nanometre-Sized Ni Polycrystals, J. Phys.: Condens. Matter, 1994, 6(34), L497 CAS.
- T. V. Plakhova, A. Y. Romanchuk, D. V. Likhosherstova, A. E. Baranchikov, P. V. Dorovatovskii, R. D. Svetogorov, T. B. Shatalova, T. B. Egorova, A. L. Trigub, K. O. Kvashnina, V. K. Ivanov and S. N. Kalmykov, Size Effects in Nanocrystalline Thoria, J. Phys. Chem. C, 2019, 123(37), 23167–23176 CAS.
- W. Qin, T. Nagase, Y. Umakoshi and J. A. Szpunar, Relationship between Microstrain and Lattice Parameter Change in Nanocrystalline Materials, Philos. Mag. Lett., 2008, 88(3), 169–179 CAS.
- I. R. Gibson, S. Ke, S. M. Best and W. Bonfield, Effect of Powder Characteristics on the Sinterability of Hydroxyapatite Powders, J. Mater. Sci.:Mater. Med., 2001, 12(2), 163–171 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dt03467h |
| This journal is © The Royal Society of Chemistry 2025 |