Open Access Article
Open Access ArticleFluor-tools: an integrated platform for dye property prediction and structure optimization
Wenxiang
Song
a,
Yuyang
Zhang
bc,
Le
Xiong
a,
Xinmin
Li
a,
Jingwei
Zhang
a,
Guixia
Liu
 a,
Weihua
Li
a,
Weihua
Li
 a,
Youjun
Yang
a,
Youjun
Yang
 *bc and
Yun
Tang
*bc and
Yun
Tang
 *a
*a
aShanghai Frontiers Science Center of Optogenetic Techniques for Cell Metabolism, Shanghai Key Laboratory of New Drug Design, School of Pharmacy, East China University of Science and Technology, Shanghai 200237, China
bState Key Laboratory of Bioreactor Engineering, East China University of Science and Technology, 130 Meilong Road, Shanghai 200237, China
cShanghai Key Laboratory of Chemical Biology, Shanghai Frontiers Science Center of Optogenetic Techniques for Cell Metabolism, School of Pharmacy, East China University of Science and Technology, 130 Meilong Road, Shanghai 200237, China
First published on 10th November 2025
Abstract
With the rapid advancement of fluorescent dye research, there is an urgent need for tools capable of accurately predicting dye optical properties while facilitating structural modification. However, the field currently lacks reliable and user-friendly tools for this purpose. To address this gap, we have developed Fluor-tools—an integrated platform for dye property prediction and structural optimization. The platform comprises two core modules: (1) Fluor-pred, a dye property prediction model that integrates domain-specific knowledge of fluorophores with a label distribution smoothing (LDS) reweighting strategy and an advanced residual lightweight attention (RLAT) architecture. This model achieves state-of-the-art performance in predicting four key photophysical properties of dyes. (2) Fluor-opt, a structural optimization module that employs a matched molecular pair analysis (MMPA) method enhanced with symmetry-aware and environment-adaptive modifications. This module derives 1579 structural transformation rules, enabling the directional optimization of non-NIR (non-near-infrared) dyes to NIR properties. In summary, Fluor-tools provides robust computational support for research in biomedical imaging and optical materials. The platform is freely accessible at https://lmmd.ecust.edu.cn/Fluor-tools/.
1 Introduction
Fluorescent materials are compounds that absorb light and re-emit it as fluorescence. A defining feature of these materials is their conjugated π-electron systems, which enable fine-tuning of optical properties. They play pivotal roles across diverse applications, including pharmaceuticals, dyes and pigments, optoelectronics, organic light-emitting diodes, environmental monitoring, light-harvesting antennas, organic photovoltaics, information encryption, bioimaging, and high-throughput material discovery.1–7 Notably, the near-infrared (NIR) region serves as an optimal optical imaging window, characterized by minimal tissue absorption and reduced light scattering.8,9 This spectral range offers distinct advantages: low phototoxicity, deep tissue penetration, minimal autofluorescence interference, high signal-to-noise ratios, and low false-positive rates—all of which enable high-quality in vivo deep-tissue imaging.10–16However, the development of fluorophores currently relies heavily on empirical knowledge and extensive trial-and-error experimentation, creating substantial barriers to designing high-performance dyes.12 While existing empirical rules (e.g., the Woodward–Fieser rules) can estimate the maximum absorption wavelength of dyes,17 and time-dependent density functional theory (TD-DFT) allows calculation of absorption and emission spectral parameters,18ab initio calculations remain often time-consuming and cost-prohibitive, restricting their widespread application.
Recently, with the rapid advancement of artificial intelligence (AI), AI-based approaches have significantly transformed dye design by offering greater computational efficiency and predictive accuracy than traditional methods. These approaches are primarily applied in two domains: (1) dye property prediction, and (2) dye structure optimization. Property prediction represents the most widely studied application, where regression models are built to forecast key optical characteristics—including absorption wavelength (λabs), emission wavelength (λem), fluorescence quantum yield (ΦPL), and molar absorption coefficient (εmax).19–23 For example, Joung et al. developed a multi-property prediction model using graph convolutional networks (GCNs), trained on an experimental dataset of 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 094 dye–solvent pairs; this model enabled accurate predictions of multiple optical properties.20 Similarly, Wang et al. proposed NIRFluor, a multimodal prediction model trained on 5179 NIR fluorescent molecules, which achieved high accuracy in predicting four critical properties of NIR dyes.23 In the field of dye structure optimization, conventional approaches typically involve generating a large number of derivatives based on target molecular scaffold, followed by screening using property prediction models to identify candidate molecules with desired characteristics.24 Recently, Zhu et al. integrated the Reinvent4 to successfully synthesize a novel fluorescent compound exhibiting exceptional brightness.25,26 Additionally, Han et al. developed DeepMoleculeGen, a generative deep learning (DL) model trained on a comprehensive experimental database containing 71
094 dye–solvent pairs; this model enabled accurate predictions of multiple optical properties.20 Similarly, Wang et al. proposed NIRFluor, a multimodal prediction model trained on 5179 NIR fluorescent molecules, which achieved high accuracy in predicting four critical properties of NIR dyes.23 In the field of dye structure optimization, conventional approaches typically involve generating a large number of derivatives based on target molecular scaffold, followed by screening using property prediction models to identify candidate molecules with desired characteristics.24 Recently, Zhu et al. integrated the Reinvent4 to successfully synthesize a novel fluorescent compound exhibiting exceptional brightness.25,26 Additionally, Han et al. developed DeepMoleculeGen, a generative deep learning (DL) model trained on a comprehensive experimental database containing 71![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 424 molecule–solvent pairs.27
424 molecule–solvent pairs.27
However, current methodologies still suffer from notable limitations, which are elaborated as follows: (1) in terms of dye property prediction: existing models rely exclusively on molecular structures to forecast properties. They merely adopt generic molecular representations—such as molecular graphs or molecular fingerprints—while lacking the integration of dye-specific knowledge. Moreover, the imbalanced distribution of dye-related data leads to particularly poor prediction accuracy in spectral regions where data is sparse. (2) In the field of structural optimization: the currently prevalent “undirected random generation and subsequent screening” strategy suffers from certain accuracy limitations, primarily due to its reliance on the aforementioned property prediction models. Additionally, Reinvent4 is not specifically developed for dyes, making it difficult to generate structurally reasonable dye molecules. (3) Finally, previous models have not yet been truly delivered to end-users. Most previous studies failed to deploy their models, leaving these models unable to provide tangible support for the dye industry.
To address the aforementioned challenges, we have developed Fluor-tools—an innovative computational platform for the rational design of dyes. The platform architecture integrates two synergistic modules:
(1) Fluor-pred: a multimodal property prediction model that incorporates domain-specific knowledge of fluorophores. In terms of architectural design, we innovatively designed a residual lightweight attention (RLAT) architecture, coupled with a label distribution smoothing (LDS) reweighting strategy. These design elements collectively enhance model performance—particularly improving prediction accuracy in data-sparse regions. For dye representation, we integrated domain-specific knowledge of dyes, such as HOMO–LUMO gaps and custom-developed MMP fingerprints. Ultimately, Fluor-pred achieved state-of-the-art performance in predicting four core photophysical properties of dyes.
(2) Fluor-opt: this module enables the directed modification of non-NIR dyes to achieve NIR properties. It adopts an optimized quantitative structure–activity relationship-molecular matching pair (QSAR-MMP) algorithm, into which we have integrated symmetry modification methods and the applicability context of MMP transformation rules. This approach comprehensively captures the differences in structural transformation and structure–activity relationships (SARs) between non-NIR and NIR dyes. It supports the automated structural optimization of non-NIR dyes into NIR dyes and has been successfully applied in multiple cases.
Finally, we have integrated all the aforementioned research into the website (https://lmmd.ecust.edu.cn/Fluor-tools/)), ensuring convenient access and utilization for researchers.
2 Results
2.1 Overall of Fluor-tools
Fluor-tools incorporates an accurate dye property prediction model, Fluor-pred. The model architecture of Fluor-pred is shown in Fig. 1a–c. This model was developed based on FluoDB,26 the largest publicly available dye database to date, and employs a comprehensive set of effective molecular representations, as detailed in Fig. 1b. (1) First, we utilize the Attentive FP architecture to encode dye molecular graphs, effectively capturing structural information.42 (2) To account for the distinct property distributions exhibited by different scaffold types, we incorporate scaffold-specific annotations as additional input features. (3) Building on the experimentally validated transformation rules extracted from Fluor-opt (which significantly alter dye properties), we identify 136 high-frequency substructures to construct dye-specific MMP fingerprints. (4) Recognizing the well-established correlation between dye properties and HOMO–LUMO gaps (where smaller gaps correspond to longer absorption wavelengths),45–48 we integrate HOMO–LUMO gap predictions from the advanced quantum property prediction model Uni-mol+.43 (5) Incorporates several RDKit-calculated molecular properties along with Morgan fingerprints—features that have been extensively adopted in previous studies.19–23 For solvent representation, we employ Morgan fingerprints combined with solvent-type annotations. | ||
Fig. 1 Overview of Fluor-tools platform, integrating two core models: Fluor-pred (a–c) and Fluor-opt (d–g). The development process of Fluor-pred includes: (a) data collection and preprocessing: Fluor-pred is built upon the FluoDB database,26 which, after preprocessing, contains 49![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 831 dye–solvent pairs; (b) molecular and solvent representations: Fluor-pred incorporates multiple representations, including molecular graphs, dye category labels, custom-designed MMP fingerprints, and HOMO–LUMO gap computed by Uni-mol+, and so on; (c) model architecture: Fluor-pred employs an optimized RLAT architecture for efficient feature extraction. The workflow of Fluor-opt includes: (d) data collection and preprocessing: data were obtained from multiple databases and literature mining. After processing, a total of 1096 NIR dye molecules and 16 831 dye–solvent pairs; (b) molecular and solvent representations: Fluor-pred incorporates multiple representations, including molecular graphs, dye category labels, custom-designed MMP fingerprints, and HOMO–LUMO gap computed by Uni-mol+, and so on; (c) model architecture: Fluor-pred employs an optimized RLAT architecture for efficient feature extraction. The workflow of Fluor-opt includes: (d) data collection and preprocessing: data were obtained from multiple databases and literature mining. After processing, a total of 1096 NIR dye molecules and 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 144 non-NIR dye molecules were collected; (e) construction of NIR classification models: building a set of binary classifiers to distinguish between NIR and non-NIR dyes; (f) MMPA-based transformation rule extraction: deriving structural transformation rules for converting non-NIR dyes into NIR dyes; (g) structure optimization and candidate screening: applying appropriate transformation rules to target molecules to generate candidate compounds, which are then filtered by the binary classifiers. The molecules predicted as NIR dyes are retained as optimized outputs. 144 non-NIR dye molecules were collected; (e) construction of NIR classification models: building a set of binary classifiers to distinguish between NIR and non-NIR dyes; (f) MMPA-based transformation rule extraction: deriving structural transformation rules for converting non-NIR dyes into NIR dyes; (g) structure optimization and candidate screening: applying appropriate transformation rules to target molecules to generate candidate compounds, which are then filtered by the binary classifiers. The molecules predicted as NIR dyes are retained as optimized outputs. | ||
Regarding the model architecture of Fluor-pred (Fig. 1c), we designed a RLAT framework for small molecule information extraction—a framework originally developed for protein sequence information extraction.49,50 In Fluor-pred, the AttentionCNN module processes concatenated sequential information from dye molecules, which is then integrated with graph features and solvent representations. Compared to conventional deep attention models, RLAT maintains robust representational capacity while significantly reducing both parameter size and computational overhead, making it particularly suitable for dye molecular feature extraction. Notably, the four properties show severe distribution skewness (Fig. S1), causing significant accuracy drops in sparse-data regions. To address this, we introduced LDS to reweight the loss function based on estimated data density.44 This method assigns higher weights to samples in low-density regions and lower weights to those in high-density regions, and fine-tunes the reweighting intensity via the hyperparameter α to achieve an optimal balance.
In addition, Fluor-tools also incorporates a module called Fluor-opt, which enables the directed transformation of non-NIR dyes into NIR dyes. Fluor-opt employs an optimized QSAR-MMP algorithm, where we incorporate symmetry modifications and the applicability context of transformation rules. This approach comprehensively captures the differences in structural transformations and SARs between non-NIR and NIR dyes, ultimately enabling the automated structural optimization of non-NIR dyes into NIR dyes. Compared with molecular generation methods, the MMPA approach implements minimal yet critical molecular modifications, which significantly enhances the synthetic feasibility of optimized dye molecules. The general development process of Fluor-opt includes: (1) building the largest open-source NIR dye database through literature mining and database integration (Fig. 1d); (2) creating a binary classification model with defined applicability domains to evaluate transformation rules and filter modified molecules (Fig. 1e); (3) developing an enhanced MMP method incorporating dye symmetry features, yielding 1579 transformation rules (Fig. 1f); (4) validating rules with transformation context to establish an iterative optimization cycle for NIR dye data enhancement (Fig. 1g).
2.2 Data analysis
In the Fluor-pred study, we utilized the original dataset from FluoDB database,26 comprising 49![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 831 validated dye–solvent pairs. Fig. S1 illustrates the dataset characteristics and distributions for the four prediction tasks.
831 validated dye–solvent pairs. Fig. S1 illustrates the dataset characteristics and distributions for the four prediction tasks.
For the Fluor-opt model, as illustrated in Fig. 2, we constructed a comprehensive dye database by integrating multiple data sources, which was used for extracting transformation rules via the MMPA method. Furthermore, due to the limited number of NIR dyes in existing databases, we conducted systematic literature mining using the keywords “near-infrared” and “dye”—screening for valid information from approximately 500 retrieved articles. After data processing, the final dataset comprises 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 240 experimentally validated dye structures, including 1096 NIR dyes and 16
240 experimentally validated dye structures, including 1096 NIR dyes and 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 144 non-NIR dyes.
144 non-NIR dyes.
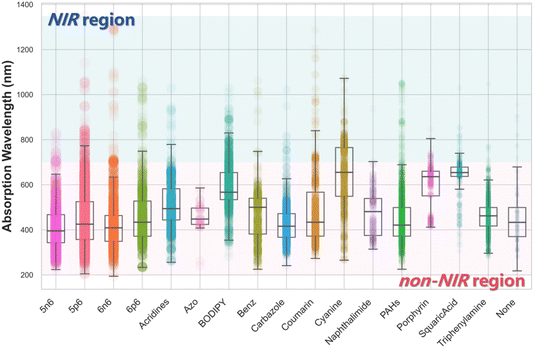
In this study, we conducted systematic statistical analyses of the structural and property differences between NIR and non-NIR dyes within the Fluor-opt dataset. Fig. 2b demonstrates the relationship between dye properties and their classification as NIR or non-NIR dyes. NIR dyes tend to exhibit slightly higher molecular weights, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P values, ring counts, and degrees of unsaturation compared to non-NIR counterparts. This trend can be attributed to characteristic structural motifs of NIR dyes, such as: extended conjugated systems, as seen in porphyrins and cyanine dyes; and fused ring frameworks (e.g., pentacene, perylene derivatives) or rigid bridging cores (e.g., BODIPY scaffold). Collectively, these features account for the increased molecular weight and lipophilicity observed in NIR dyes. Based on the structural classification framework established by Zhu et al., all dyes were categorized into 17 distinct scaffold types (Fig. 2c).26 Among these, cyanine scaffolds contain the highest proportion of NIR dyes, followed by BODIPY derivatives. Notably, certain scaffold classes such as carbazole and triphenylamine show a significant skew toward non-NIR dyes. This scaffold-dependent variation underscores the pivotal influence of molecular scaffolds on the photophysical behavior of dyes. We provide detailed statistical data in Fig. S2.
P values, ring counts, and degrees of unsaturation compared to non-NIR counterparts. This trend can be attributed to characteristic structural motifs of NIR dyes, such as: extended conjugated systems, as seen in porphyrins and cyanine dyes; and fused ring frameworks (e.g., pentacene, perylene derivatives) or rigid bridging cores (e.g., BODIPY scaffold). Collectively, these features account for the increased molecular weight and lipophilicity observed in NIR dyes. Based on the structural classification framework established by Zhu et al., all dyes were categorized into 17 distinct scaffold types (Fig. 2c).26 Among these, cyanine scaffolds contain the highest proportion of NIR dyes, followed by BODIPY derivatives. Notably, certain scaffold classes such as carbazole and triphenylamine show a significant skew toward non-NIR dyes. This scaffold-dependent variation underscores the pivotal influence of molecular scaffolds on the photophysical behavior of dyes. We provide detailed statistical data in Fig. S2.
To further elucidate the relationship between dye scaffolds and the characteristics of NIR dyes, we performed a statistical analysis of the λabs distributions across different scaffold types in the Fluor-opt dataset, as shown in Fig. 3. The results show that cyanine derivatives most frequently exhibit high λabs, followed by squaric acid, porphyrin, and BODIPY scaffolds. Notably, some scaffold types, such as triphenylamine, naphthalimide, and azo derivatives, exhibit a near-complete absence of NIR dyes, indicating that their structures impose substantial constraints on photophysical properties. Nonetheless, most scaffold types exhibit broad absorption wavelength ranges, demonstrating that rational structural optimization can effectively modulate their photophysical properties for the majority of scaffolds.
2.3 Results of fluor-pred
Furthermore, to demonstrate the extrapolation capability of our model, we re-partitioned the entire dataset using scaffold-based split. Specifically, dye molecules were divided according to their Murcko scaffolds into training, validation, and test sets at a 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ratio, ensuring that molecules sharing the same scaffold appeared in only one subset. We compared the results of random partitioning and scaffold partitioning, as shown in Fig. S3. It can be observed that the stricter scaffold split led to a moderate decline in model performance, yet the predictions remained robust, particularly for λabs and λem. However, the prediction of photoluminescence ΦPL still showed similar limitations as in the random split, with performance noticeably lower than for the other three properties.
2 ratio, ensuring that molecules sharing the same scaffold appeared in only one subset. We compared the results of random partitioning and scaffold partitioning, as shown in Fig. S3. It can be observed that the stricter scaffold split led to a moderate decline in model performance, yet the predictions remained robust, particularly for λabs and λem. However, the prediction of photoluminescence ΦPL still showed similar limitations as in the random split, with performance noticeably lower than for the other three properties.
First, the binned MAE analysis reveals the variation of errors with respect to the true ΦPL values (Fig. S4a): in the low-ΦPL range, the prediction errors are relatively small, whereas in the high-ΦPL range, the errors increase markedly, with the MAE in the highest bin approaching 0.18. This indicates that predicting samples with high quantum yields is considerably more challenging. Second, the residual histogram shows that the overall residuals approximately follow a normal distribution, with the peak centered around zero, suggesting no severe systematic bias in the model (Fig. S4b). However, the distribution exhibits a slight negative skew and extended tails, indicating that a small number of samples still suffer from large prediction deviations. Such long-tail errors may arise from experimental measurement uncertainties or outliers present in the dataset. Finally, the residual versus predicted values scatter plot demonstrates that the residuals are not entirely random (Fig. S4c): in the low-prediction region, the model tends to slightly underestimate, while in the high-prediction region, it tends to overestimate. Moreover, the magnitude of residual fluctuations increases with larger predicted values, reflecting evident heteroscedasticity.
Therefore, the relatively low R2 in ΦPL prediction does not simply result from insufficient model performance. The primary contributing factors include imbalanced data distribution, the limited number of high-ΦPL samples, and greater experimental noise in the high-ΦPL region.
To evaluate the importance of the LDS reweighting mechanism, as shown in Fig. 4c, removing the LDS reweighting led to a decrease in performance across all prediction tasks, with the most pronounced drop observed in the εmax task. To further assess whether LDS reweighting genuinely improves prediction accuracy in low-density regions, we analyzed λabs as a representative property with a skewed distribution. The dataset was divided into three intervals: ≤300 nm, 300–700 nm, and ≥700 nm. The middle interval contains the majority of the data, while the lower and upper ends account for only 2.22% and 3.27%, respectively. As shown in Fig. S6, LDS improved accuracy across all intervals, with the most significant reduction in error observed in the NIR region (≥700 nm). Interestingly, in the data-rich 300–700 nm high-density region, the MAE also decreased. This may be due to the varying internal density within the 300–700 nm range, where certain subregions benefit more than others. Overall, LDS effectively improved the overall prediction accuracy of Fluor-pred, particularly enhancing the model's performance in sparse regions. Finally, we visualized the latent feature space from the final layer of the model using dimensionality reduction techniques. In Fig. 4d, smooth color gradients show each target property's variation trends and exhibit clear distinguishability, indicating the model has effectively distinguished and learned different properties.
| Algorithms | MAEa | RMSEb | R 2 | |
|---|---|---|---|---|
| a MAE: mean absolute error. b RMSE: root mean square error. c R 2: Coefficient of determination. All models were trained and tested using the same data split from the FluoDB dataset, with some results directly taken from FLSF. The bolded numbers indicate the optimal results for the corresponding tasks. | ||||
| λ abs | GBRT | 13.67 | 28.71 | 0.93 |
| SMFluo | 21.19 | 35.44 | 0.89 | |
| SchNet | 22.17 | 41.05 | 0.63 | |
| ABT-MPNN | 12.66 | 26.23 | 0.94 | |
| Fluor-predictor | 14.70 | 28.07 | 0.92 | |
| FLSF | 12.56 | 25.99 | 0.94 | |
| Fluor-RLAT | 12.44 | 25.68 | 0.94 | |
| λ em | GBRT | 14.56 | 25.91 | 0.92 |
| SMFluo | 27.82 | 38.31 | 0.83 | |
| SchNet | 38.26 | 51.91 | 0.43 | |
| ABT-MPNN | 13.30 | 22.84 | 0.94 | |
| Fluor-predictor | 15.65 | 25.92 | 0.92 | |
| FLSF | 13.27 | 23.35 | 0.94 | |
| Fluor-RLAT | 13.04 | 22.34 | 0.94 | |
| Φ PL | GBRT | 0.12 | 0.18 | 0.68 |
| SMFluo | 0.13 | 0.21 | 0.57 | |
| SchNet | 0.15 | 0.20 | 0.39 | |
| ABT-MPNN | 0.12 | 0.19 | 0.65 | |
| Fluor-predictor | 0.13 | 0.19 | 0.62 | |
| FLSF | 0.12 | 0.19 | 0.66 | |
| Fluor-RLAT | 0.11 | 0.18 | 0.66 | |
| ε max | GBRT | 0.20 | 0.31 | 0.66 |
| SMFluo | 0.22 | 0.37 | 0.53 | |
| SchNet | 0.51 | 0.71 | −2.01 | |
| ABT-MPNN | 0.32 | 0.45 | 0.31 | |
| Fluor-predictor | 0.17 | 0.34 | 0.70 | |
| FLSF | 0.23 | 0.34 | 0.59 | |
| Fluor-RLAT | 0.15 | 0.29 | 0.78 | |
However, in the fluorescence ΦPL prediction task, none of the models achieved an R2 value above 0.7, which is significantly lower than the performance observed in the other three tasks. The limitations in ΦPL prediction primarily stem from two key factors: (1) the ΦPL dataset is the most limited among the four tasks and exhibits a highly skewed distribution, with experimental values heavily clustered at one extreme of the range; (2) ΦPL is influenced by molecular structure and solvent effects, and it is also highly sensitive to experimental conditions—including temperature, light source characteristics, filter selection, detector sensitivity, and sample-to-solvent ratios. These inherent complexities make ΦPL prediction fundamentally more challenging than other optical properties. Despite these challenges in ΦPL prediction, Fluor-pred maintains superior performance compared to existing models.
2.4 Results of Fluor-opt
To further ensure prediction reliability, we conducted an applicability domain (AD) analysis. Based on the test set, the average Tanimoto similarity (γ) between test and training molecules was 0.3772 (σ = 0.1274). After jointly optimizing chemical space coverage and model performance, the optimal parameters (k = 20, Z = 2) yielded a similarity threshold of 0.632, which successfully captured 90% of the test set (Fig. 5b). For compounds within the applicability domain, the model maintained strong predictive power (PRAUC = 0.9077, MCC = 0.9789, F1-score = 0.8378).
Ultimately, we applied the model to the previously collected set of 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 194 dye molecules lacking experimental absorption wavelength data, successfully identifying 78 high-confidence NIR candidates (i.e., AD-compliant compounds with prediction probabilities > 0.8) for MMP dataset augmentation. Due to the limited number of NIR dyes in the dataset, these molecules help further alleviate the shortage of NIR dyes and facilitate the extraction of more comprehensive structural transformation rules in MMPA analysis.
194 dye molecules lacking experimental absorption wavelength data, successfully identifying 78 high-confidence NIR candidates (i.e., AD-compliant compounds with prediction probabilities > 0.8) for MMP dataset augmentation. Due to the limited number of NIR dyes in the dataset, these molecules help further alleviate the shortage of NIR dyes and facilitate the extraction of more comprehensive structural transformation rules in MMPA analysis.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 287 dye molecules, including 1149 NIR dyes and 16
287 dye molecules, including 1149 NIR dyes and 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 138 non-NIR dyes. Traditional MMP approaches overlook the contextual environment of structural transformations.33 They often apply extracted transformation rules indiscriminately to all molecular structures. This practice is clearly inappropriate in the field of dyes. As shown in Fig. 3, dye molecules with different scaffolds exhibit significant differences in their properties; therefore, transformation rules derived from one scaffold, such as squaraine, may not be applicable to other types like cyanine dyes. We addressed these limitations by defining the shared scaffold fragments as the applicability context for each rule. During the optimization process, we introduced a hyperparameter, similarity_value, to identify the most compatible transformation rule for a given target molecule. This parameter quantifies how well a rule matches the target molecule; higher similarity implies stronger compatibility and a higher chance of valid NIR transformation. Furthermore, traditional MMP analysis is typically limited to single-site modifications. However, dye molecules are often subjected to symmetric modifications. To account for this, we extended the traditional MMP framework by incorporating symmetry-aware transformation rules, treating molecule pairs with consistent dual-site substitutions as valid matched molecular pairs. Detailed steps of the MMPA are provided in Section 4.2.4.
138 non-NIR dyes. Traditional MMP approaches overlook the contextual environment of structural transformations.33 They often apply extracted transformation rules indiscriminately to all molecular structures. This practice is clearly inappropriate in the field of dyes. As shown in Fig. 3, dye molecules with different scaffolds exhibit significant differences in their properties; therefore, transformation rules derived from one scaffold, such as squaraine, may not be applicable to other types like cyanine dyes. We addressed these limitations by defining the shared scaffold fragments as the applicability context for each rule. During the optimization process, we introduced a hyperparameter, similarity_value, to identify the most compatible transformation rule for a given target molecule. This parameter quantifies how well a rule matches the target molecule; higher similarity implies stronger compatibility and a higher chance of valid NIR transformation. Furthermore, traditional MMP analysis is typically limited to single-site modifications. However, dye molecules are often subjected to symmetric modifications. To account for this, we extended the traditional MMP framework by incorporating symmetry-aware transformation rules, treating molecule pairs with consistent dual-site substitutions as valid matched molecular pairs. Detailed steps of the MMPA are provided in Section 4.2.4.
The first step in the MMP process is molecular fragmentation. To achieve comprehensive fragmentation coverage, we applied bond disconnection strategies involving one to three disconnection points. As shown in Table 2, three-point cuts resulted in significantly more fragments, and consequently, more MMPs. This outcome is primarily due to the inherent structural complexity of dye molecules, which often feature extended conjugated systems and polycyclic frameworks. These characteristics make simple single- or double-bond cuts insufficient for effective decomposition. Using this strategy, we generated a total of 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 436
436![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 377 unique fragments and identified 8
377 unique fragments and identified 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 462
462![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 578 matched molecular pairs.
578 matched molecular pairs.
| Cutting strategy | Number of fragments | MMPs |
|---|---|---|
| Single cut | 150![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 318 (2.76%) 318 (2.76%) |
168![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 030 (0.21%) 030 (0.21%) |
| Double cut | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 149 149![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 542 (21.14%) 542 (21.14%) |
818![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 033 (1.05%) 033 (1.05%) |
| Triple cut | 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 136 136![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 517 (76.1%) 517 (76.1%) |
7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 476 476![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 515 (98.74%) 515 (98.74%) |
| Total | 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 436 436![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 377 377 |
77![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 263 263![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 789 789 |
To identify rules that favor the conversion of non-NIR dyes into NIR dyes, we analyzed the transformation frequency of each rule between non-NIR and NIR molecules and introduced an evaluation metric, label_value. As defined in eqn (1), N(0 → 1) indicates the number of times the rule converts non-NIR dyes into NIR dyes; N(1 → 0) indicates the number of times it converts NIR dyes into non-NIR dyes; indicates the total number of occurrences of the rule. Therefore, a label_value greater than 0 indicates that the transformation rule tends to promote the conversion from non-NIR to NIR dyes. After removing duplicate entries, we identified 1579 transformation rules that favor the non-NIR to NIR conversion (with label_value greater than 0) and extracted a total of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 354 distinct transformation contexts.
354 distinct transformation contexts.
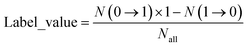 | (1) |
Table S6 presents several transformation rule examples, where frequency denotes the occurrence frequency of a given rule in converting non-NIR dyes into NIR dyes within the dataset, and label_value quantifies its effectiveness in promoting such conversions. For example, transformation rule 6 has a label_value of 1, indicating that all instances of its application resulted in forward transformations. Statistically, the majority of these forward rules (61.1%) appeared only once, while a smaller subset (10.7%) appeared more than 20 times. This imbalance is primarily attributed to the limited number of available NIR dye samples.
 | ||
| Fig. 6 (a) Line plot showing the total number of generated molecules and the corresponding proportion of NIR-classified compounds at different similarity thresholds. Higher similarity thresholds reduce the number of generated molecules but increase the success rate of conversion to NIR dyes. (b) Case studies: the compounds on the left side of the arrow represent the original input molecules, while the compounds on the right side correspond to the optimized molecules generated by Fluor-opt. Fluorescent markers highlight the transformed substructures, with all λabs values obtained from experimental measurements. m1 and m2 represent the original and modified dye molecules by Pascal et al.;51m3 and m4 denote the dye variants before and after modification by Li et al.;52m5, m6, m9, and m10 correspond to Zhang et al.'s original and engineered dye molecules;53m7 and m8 indicate the pre- and post-modified dyes developed by Cosco et al.;54,55m11 and m12 refer to Zhou et al.'s molecular designs before and after optimization.56 | ||
Fluor-opt performs structural modifications including functional group substitution, functional group addition, and linker extension while preserving the core scaffold of the molecule. To validate its effectiveness, we conducted multiple case studies. As shown in Fig. 6b, the molecules on the left represent the original non-NIR dyes, while the molecules on the right correspond to their optimized structures. After optimization, the target dyes generally exhibited significant absorption redshift, typically ranging from 50 to 200 nm. For instance, when m1 was used as the target molecule, optimization via Fluor-opt yielded the optimized molecule m2—a structure previously reported by Pascal et al.—with an absorption wavelength increase of nearly 150 nm.51 Additionally, we optimized m7, a molecule developed by Cosco et al. in 2017, and the resulting optimized structure was identified as m8—a high-performance NIR dye first reported in 2021, which exhibited an absorption wavelength enhancement of over 200 nm.52,53
Remarkably, Fluor-opt achieves highly effective optimization through minor modifications, primarily by substituting a single key functional group. Compared to molecular generation methods, this strategy offers significant advantages in terms of synthetic accessibility. This tool provides valuable guidance for dye chemists, significantly expanding both the application scope and translational potential of fluorescent dyes in NIR-related technologies.
2.5 Website setup and services
As shown in Fig. 7, to establish a user-friendly and integrated platform for dye design and analysis, we integrated Fluor-opt and Fluor-pred into a unified tool—Fluor-tools, which has been deployed as a publicly accessible web application. Fluor-tools is freely accessible at https://lmmd.ecust.edu.cn/Fluor-tools/.These modules form a synergistic closed-loop system through bidirectional knowledge transfer: the MMP fingerprints constructed from transformation rules extracted by Fluor-opt provide Fluor-pred with critical structural features, while Fluor-pred's high-accuracy predictions enable reliable evaluation of Fluor-opt's optimization results (Fig. 7d). Through this synergistic mechanism, researchers can first generate NIR candidate molecules via Fluor-opt, then efficiently screen them using Fluor-pred's predictive capabilities, enabling multi-parameter optimization that dramatically accelerates the development of high-performance fluorescent dyes.
3 Discussion and conclusions
This paper presents Fluor-tools, an integrated computational platform designed to address key challenges in the design and property prediction of fluorescent dyes. The platform comprises two core, synergistically working components: Fluor-pred and Fluor-opt. (1) Fluor-pred incorporates multimodal domain-specific knowledge of dyes, and by combining a specially designed RLAT architecture with a LDS reweighting strategy, it achieves state-of-the-art performance across all four critical photophysical property prediction tasks. Moreover, although the multimodal architecture of Fluor-pred is tailored for dye, its use of the RLAT architecture and LDS reweighting strategy can also be explored in other molecular property prediction tasks. (2) Fluor-opt, on the other hand, leverages QSAR-enhanced MMPA and integrates dye-specific characteristics. Ultimately, it captures 1579 key structural transformations, enabling automated and targeted modification of dyes from non-NIR to NIR. Multiple case studies have validated its reliability.However, Fluor-tools still has certain limitations. For example, due to the limited amount of training data for fluorescence quantum yield and inherent experimental measurement errors, the prediction accuracy of Fluor-pred for quantum yield remains relatively low. In addition, Fluor-opt currently focuses only on the directed optimization of absorption wavelength and has not yet undergone experimental validation. In future research, we will conduct in-depth investigations into the key factors influencing quantum yield and develop more rational methods to improve the prediction accuracy of ΦPL For the structure optimization model Fluor-opt, we plan to explore incorporating target properties as constraints to establish a multi-objective generation framework and carry out corresponding experimental validations. In summary, Fluor-tools provides a reliable computational framework for the property prediction and rational optimization of dyes, and is well-positioned to play a significant role in biomedical imaging, materials science, and related fields.
4 Methods
4.1 Methods of Fluor-pred
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 861 fluorophore-solvent pairs with experimental data on four optical properties: λabs, λem, ΦPL, and εmax.
861 fluorophore-solvent pairs with experimental data on four optical properties: λabs, λem, ΦPL, and εmax.
On this basis, after further excluding molecules incompatible with Uni-mol+ calculations, the final dataset used in Fluor-pred contained 49![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 831 valid dye–solvent pairs. To ensure fairness in model comparison, we retained FluoDB's original 7
831 valid dye–solvent pairs. To ensure fairness in model comparison, we retained FluoDB's original 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 random partitioning scheme, resulting in 34
2 random partitioning scheme, resulting in 34![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 881 samples for training, 4982 for validation, and 9968 for testing, which were used for model training, hyperparameter optimization, and performance evaluation, respectively. In addition, to address the strong skew in the distribution of εmax and improve model performance, a logarithmic transformation was applied to εmax values prior to training.
881 samples for training, 4982 for validation, and 9968 for testing, which were used for model training, hyperparameter optimization, and performance evaluation, respectively. In addition, to address the strong skew in the distribution of εmax and improve model performance, a logarithmic transformation was applied to εmax values prior to training.
The physicochemical properties of the dyes—namely molecular weight, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P, average Gasteiger charge, ring count, double bond count, and topological polar surface area (TPSA)—were all calculated using RDKit and custom scripts. For dye scaffold classification, we used the script provided by Zhu et al., which defines 728 fluorescent dye scaffolds and categorizes the dyes into 17 scaffold types.26 Detailed definitions of these scaffold categories can be found in Fig. S7.
P, average Gasteiger charge, ring count, double bond count, and topological polar surface area (TPSA)—were all calculated using RDKit and custom scripts. For dye scaffold classification, we used the script provided by Zhu et al., which defines 728 fluorescent dye scaffolds and categorizes the dyes into 17 scaffold types.26 Detailed definitions of these scaffold categories can be found in Fig. S7.
The construction of MMP fingerprints in Fluor-pred was carried out as follows: among the 1579 key structural transformations extracted in Fluor-opt, we retained transformation rules that occurred more than 20 times and identified 136 associated substructures. These substructures were then used to build dye-specific, substructure-aware MMP fingerprints. The complete list of 136 substructures, along with the code for generating the MMP fingerprints, is freely available at https://lmmd.ecust.edu.cn/Fluor-tools/.
In this study, we employed Uni-mol+, a deep learning model that uses 3D molecular conformations for accurate HOMO–LUMO gap prediction. The Uni-mol + framework starts by generating an initial 3D conformation using RDKit, then iteratively refines this conformation to the DFT equilibrium state through neural network-based optimization. The final optimized conformation is then used to predict the HOMO–LUMO gap. Since our ablation studies showed that the HOMO–LUMO gap contributes minimally to the improvement in model performance, we chose to use the average HOMO–LUMO gap values in the web service to save computational time.
Hyperparameter optimization was performed using a grid search strategy, encompassing both general parameters (learning rate, weight decay, batch size) and architecture-specific parameters (number of network layers, dropout rate, graph feature dimension). To prevent overfitting and optimize computational efficiency, we implemented an early stopping strategy that terminated training if no improvement in validation metrics was observed for 20 consecutive epochs. For the four regression tasks predicted by Fluor-pred, we primarily used MAE, RMSE, and R2 as evaluation metrics. The definitions and formulas for all metrics are summarized in Table S8.
To mitigate this issue, we introduce the label distribution smoothing with inverse density strategy. The core idea of this approach is to estimate the smoothed label density distribution via kernel density estimation (KDE) and assign higher importance to samples located in low-density regions, thereby encouraging the model to learn more effectively from underrepresented targets. The detailed procedure is as follows:
(1) Label discretization and density estimation: for each task, the labels in the training set are uniformly discretized into a fixed number of bins (e.g., 100), and Gaussian kernels are applied to smooth the label distribution. The smoothed density ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) (yi) for a given label yi is computed as follows:
(yi) for a given label yi is computed as follows:
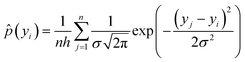 | (2) |
(2) Weight assignment: based on the smoothed density ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) (yi), each sample is assigned a weight inversely proportional to its estimated density, encouraging higher importance for rare labels:
(yi), each sample is assigned a weight inversely proportional to its estimated density, encouraging higher importance for rare labels:
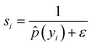 | (3) |
(3) Weight normalization: to avoid gradient instability due to large variance in sample weights, all weights are normalized by their mean:
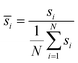 | (4) |
(4) Reweighted loss function: the final loss used during training is a reweighted Mean Squared Error (MSE), incorporating the normalized weights. To further stabilize training and make the loss more interpretable, we take the square root of the weighted average:
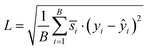 | (5) |
By incorporating LDS-Inverse, the model can better learn features from low-frequency sample regions, thereby improving its performance on edge cases, especially for dye molecules with extreme spectral properties or uncommon photophysical behaviors.
4.2 Methods of Fluor-opt
| Data source | Number of entries |
|---|---|
| ChemFluor | 4386 |
| Deep4Chem | 30094 |
| SMFluo | 1181 |
| ChemDataExtractor | 1915 |
| Dye aggregation | 3626 |
| DSSCDB | 2438 |
| Fluor-predictor | 36756 |
| Ksenofontov's data | 20608 |
| Literature retrieval | 1583 |
(1) Standardization: all datasets were unified in terms of format and units. Furthermore, dye and solvent molecules were converted into standardized SMILES representations using RDKit.
(2) Data Cleaning: since Fluor-opt focuses exclusively on optimizing λabs, we retained only λabs data from the above sources. In addition, identical dye–solvent pairs may exhibit conflicts across different datasets; therefore, we identified and removed entries with abnormal discrepancies (λabs > 5 nm). For entries within the acceptable range of variation, the average value was taken as a substitute.
(3) Removal of solvent conditions: as MMPA is a structure-based analytical method that does not account for solvent effects on dye properties, we averaged the λabs values of each dye molecule across different solvent conditions and adopted λabs ≥ 700 nm as the classification threshold for near-infrared dyes.
The final curated dataset consists of 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 240 experimentally validated dye structures, including 1096 NIR dyes and 16
240 experimentally validated dye structures, including 1096 NIR dyes and 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 144 non-NIR dyes. This dataset was initially used to build a binary classification model for NIR dye identification. Additionally, we retained 17
144 non-NIR dyes. This dataset was initially used to build a binary classification model for NIR dye identification. Additionally, we retained 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 194 dye molecules without experimentally measured λabs. These molecules were predicted using the trained binary classification model, and those predicted as NIR dyes with high confidence and falling within the model's applicability domain were selected as supplementary data for subsequent MMPA analysis. For data analysis, we used RDKit and custom scripts to compute six physicochemical properties for both types of dyes, including molecular weight, log
194 dye molecules without experimentally measured λabs. These molecules were predicted using the trained binary classification model, and those predicted as NIR dyes with high confidence and falling within the model's applicability domain were selected as supplementary data for subsequent MMPA analysis. For data analysis, we used RDKit and custom scripts to compute six physicochemical properties for both types of dyes, including molecular weight, log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P, number of rings, number of double bonds, average Gasteiger charge, and TPSA. Dye scaffold classification was based on the structural classification framework established by Zhu et al., which categorizes dyes into 17 distinct scaffold types.26
P, number of rings, number of double bonds, average Gasteiger charge, and TPSA. Dye scaffold classification was based on the structural classification framework established by Zhu et al., which categorizes dyes into 17 distinct scaffold types.26
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 240 experimentally validated dye compounds. The dataset was randomly split into training (13
240 experimentally validated dye compounds. The dataset was randomly split into training (13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 792 compounds), validation (1724 compounds), and test sets (1724 compounds) with an 8
792 compounds), validation (1724 compounds), and test sets (1724 compounds) with an 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio. We employed five ML models (LGBM, GBRT, XGBoost, RF, and SVM) and five DL models (GraphTransformer, GIN, GCN, GAT, and Attentive FP), applying both undersampling and oversampling strategies. ML models used Morgan fingerprints to represent molecules, while DL models used various GNN algorithms for molecular representation. The ensemble model was constructed by integrating individual models with PRAUC scores greater than 0.9, where the predicted probabilities from each individual model were used as inputs for logistic regression integration.
1 ratio. We employed five ML models (LGBM, GBRT, XGBoost, RF, and SVM) and five DL models (GraphTransformer, GIN, GCN, GAT, and Attentive FP), applying both undersampling and oversampling strategies. ML models used Morgan fingerprints to represent molecules, while DL models used various GNN algorithms for molecular representation. The ensemble model was constructed by integrating individual models with PRAUC scores greater than 0.9, where the predicted probabilities from each individual model were used as inputs for logistic regression integration.
In the training of our binary classification model, we considered the severe imbalance between the two classes (with non-NIR dyes outnumbering NIR dyes). To address this issue, we employed both over-sampling and under-sampling strategies to balance the training set. (1) Over-sampling: we applied random over-sampling to the minority class (NIR dyes) by sampling with replacement, expanding its size to match that of the majority class. This ensured that the model was exposed to sufficient minority-class examples during training, thereby mitigating the risk of bias toward the majority class. (2) Under-sampling: conversely, we also performed random under-sampling of the majority class (non-NIR dyes), by randomly selecting a subset equal in size to the minority class. This yielded a smaller but balanced training set, which reduces the risk of overfitting introduced by over-sampling, though at the expense of potentially discarding part of the majority-class information.
Hyperparameter optimization was performed using a grid search strategy, encompassing both general parameters (learning rate, weight decay, batch size, dropout rate) and GNN-specific parameters (number of network layers, graph feature dimension). To prevent overfitting and optimize computational resource utilization, we implemented an early stopping strategy that terminated training if no improvement in validation set performance metrics was observed for 20 consecutive epochs. Detailed model parameters are provided in Table S5. For model evaluation, we used several metrics, including ACC (accuracy), MCC (Matthews correlation coefficient), F1 Score, recall, precision, SP (specificity), BA (balanced accuracy), AUC, and PRAUC. The definitions and formulas for all metrics are summarized in Table S8.
δ = ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) + Zσ + Zσ | (6) |
d is the mean Euclidean distance between each compound in the training set and its nearest neighbor (also within the training set); σ is the standard deviation of these distances; Z is a user-defined parameter (typically between 0.5 and 1.0) that adjusts the significance level or strictness of the boundary. To evaluate whether a compound in the test set falls within the model's AD, we proceed as follows: for each compound in the test set, calculate the Euclidean distances to all compounds in the training set. Retain the k nearest neighbors and compute their average distance. If any of the k distances exceed the threshold δ, the compound is classified as outside domain; otherwise, it is inside domain.41 This approach allows us to systematically assess the reliability of predictions based on structural proximity to known training data and prevents overinterpretation of extrapolated results.
(1) Molecular fragmentation: for molecular fragmentation, we implemented the algorithm proposed by Hussain and Rea automatically.35,36 To comprehensively capture the property differences caused by structural changes, we performed extensive fragmentation of the molecules, including single-cut, double-cut, and triple-cut strategies, while preserving chirality during bond disconnection. As shown in Fig. 8a, the same molecule can be fragmented into different combinations of fragments, which are classified as either side chains or scaffolds.
(2) Identification of matched molecular pairs: two molecules are considered a matched molecular pair if they differ by only a single structural change. We identified the relevant MMPs by comparing the substructure fragments obtained in the previous step. If there is only one fragment difference between two fragment sequences, the corresponding molecules are considered a MMP. Additionally, since symmetric modifications are commonly used in dye modifications, we introduced molecular symmetry changes as an additional criterion for MMPs. As shown in Fig. 8b, if two molecules undergo symmetric modifications at the same position, they are also considered a MMP. The MMP extraction process was carried out using custom scripts, which was time-consuming and took approximately 10 days to complete.
(3) Extracting transformation rules: as shown in Fig. 8c, after obtaining the matched molecular pairs, the next step is to extract the transformation rules from these pairs. We first quantified the label changes corresponding to each transformation rule. As described in Section 2.4.2, we introduced label_value to evaluate the transformation rules. If label_value is greater than 0, it indicates a positive rule that favors the conversion of non-NIR dyes to NIR dyes. The calculation method for label_value is shown in eqn (1). Ultimately, we obtained 1579 positive transformation rules, which were used for structural optimization in Fluor-opt. Traditional MMPA do not account for the transformation context, which could result in low conversion success rates. To address this issue, we retained the usage context for all positive transformation rules, meaning we preserved all molecules that successfully underwent transformation using the rule. These molecules then served as the context for applying the rule.
(4) Molecular optimization: as shown in Fig. 8d, during the optimization of the target molecule using transformation rules, we first introduced the hyperparameter similarity_value to select the most suitable transformation rules for the target molecule. similarity_value calculates the Tanimoto similarity between the target molecule and the environment molecules associated with each positive transformation rule, with the similarity computed based on Morgan fingerprints. The utility of similarity_value is described in Section 2.4.2, where it is shown that as similarity increases, the success rate of optimizing the molecule into an NIR dye also increases. Upon determining the transformation rules, Fluor-opt automatically substitutes the substructures of target molecules to achieve optimization, and evaluates the optimized molecules using the NIR dye prediction model, retaining only those predicted as NIR dyes. Finally, Fluor-pred performs detailed predictions of four key photophysical properties for the identified NIR dyes.
Author contributions
Y. T. and Y. Y. conceived and directed the work. W. S., Y. Z., L. X., X. L., J. Z., G. L., W. L., Y. Y., and Y. T. designed the study. W. S. collected and prepared the data and constructed the model. W. S., Y. Y., and Y. T. interpreted the results and wrote the manuscript.Conflicts of interest
There are no conflicts to declare.Data availability
Fluor-tools is freely available for access and use at https://lmmd.ecust.edu.cn/Fluor-tools/. All data and related codes, as well as user instructions, are freely available at: https://github.com/wenxiang-Song/fluor_tools or https://zenodo.org/records/17489518 (DOI: https://doi.org/10.5281/zenodo.17489518). The FluoDB and dye scaffold classification scripts are available for free at https://github.com/ChemloverYuchen/FLAME (DOI: https://doi.org/10.1038/s41467-025-58881-5). Uni-mol + can be freely installed and used viahttps://github.com/deepmodeling/Uni-Mol (DOI: https://doi.org/10.48550/arXiv.2303.16982). ChemFluor's DOI: https://doi.org/10.1021/acs.jcim.0c01203. Deep4Chem's DOI: https://doi.org/10.1021/jacsau.1c00035. SMFluo's DOI: https://doi.org/10.1021/acs.jcim.1c01449. ChemDataExtractor's DOI: https://doi.org/10.1038/s41597-019-0306-0. Dye Aggregation's DOI: https://doi.org/10.3390/data5020045. DSSCDB's DOI: https://doi.org/10.1186/s13321-018-0272-0. Fluor-predictor's DOI: https://doi.org/10.1021/acs.jcim.5c00127. Experimental data from Ksenofontov et al. is a publicly available fluorescent dye database, sourced from DOI: https://doi.org/10.1016/j.saa.2022.121442.Supplementary information is available. See DOI: https://doi.org/10.1039/d5dd00402k.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant U23A20530) and Shanghai Frontiers Science Center of Optogenetic Techniques for Cell Metabolism (Shanghai Municipal Education Commission).Notes and references
- Y. Cai, W. Si, W. Huang, P. Chen, J. Shao and X. Dong, Small, 2018, 14, 1704247 CrossRef.
- W. Cheng, H. Chen, C. Liu, C. Ji, G. Ma and M. Yin, VIEW, 2020, 1, 20200055 CrossRef.
- C. Ji, L. Lai, P. Li, Z. Wu, W. Cheng and M. Yin, Aggregate, 2021, 2, e39 CrossRef.
- M. Kapil Dev and K. Uday, Mini-Rev. Org. Chem., 2023, 20, 655–674 CrossRef.
- K. D. Mahato and U. Kumar, Methods Appl. Fluoresc., 2023, 11, 035003 CrossRef.
- A. Tkaczyk, K. Mitrowska and A. Posyniak, Sci. Total Environ., 2020, 717, 137222 CrossRef CAS.
- N. Tomar, G. Rani, V. S. Dhaka and P. K. Surolia, Int. J. Energy Res., 2022, 46, 11556–11573 CrossRef CAS.
- M. Yang, J. Huang, J. Fan, J. Du, K. Pu and X. Peng, Chem. Soc. Rev., 2020, 49, 6800–6815 RSC.
- R. Wang, J. Chen, J. Gao, J. A. Chen, G. Xu, T. Zhu, X. Gu, Z. Guo, W. H. Zhu and C. Zhao, Chem. Sci., 2019, 10, 7222–7227 RSC.
- F. Salehpour, P. Cassano, N. Rouhi, M. R. Hamblin, L. De Taboada, F. Farajdokht and J. Mahmoudi, Photobiomodulation, Photomed., Laser Surg., 2019, 37, 581–595 CrossRef PubMed.
- M. Wolf, M. Ferrari and V. Quaresima, J. Biomed. Opt., 2007, 12, 062104 CrossRef.
- H. Li, H. Kim, F. Xu, J. Han, Q. Yao, J. Wang, K. Pu, X. Peng and J. Yoon, Chem. Soc. Rev., 2022, 51, 1795–1835 RSC.
- H. Chen, B. Dong, Y. Tang and W. Lin, Acc. Chem. Res., 2017, 50, 1410–1422 CrossRef CAS PubMed.
- Y. Wang, H. Yu, Y. Zhang, C. Jia and M. Ji, Dyes Pigm., 2021, 190, 109284 CrossRef CAS.
- J. I. Scott, Q. Deng and M. Vendrell, ACS Chem. Biol., 2021, 16, 1304–1317 CrossRef CAS PubMed.
- Z. Lei and F. Zhang, Angew Chem. Int. Ed. Engl., 2021, 60, 16294–16308 CrossRef CAS PubMed.
- J. F. Joung, M. Han, M. Jeong and S. Park, J. Chem. Inf. Model., 2022, 62, 2933–2942 CrossRef CAS.
- C. Adamo and D. Jacquemin, Chem. Soc. Rev., 2013, 42, 845–856 RSC.
- C.-W. Ju, H. Bai, B. Li and R. Liu, J. Chem. Inf. Model., 2021, 61, 1053–1065 CrossRef CAS PubMed.
- J. F. Joung, M. Han, J. Hwang, M. Jeong, D. H. Choi and S. Park, JACS Au, 2021, 1, 427–438 CrossRef PubMed.
- K. P. Greenman, W. H. Green and R. Gómez-Bombarelli, Chem. Sci., 2022, 13, 1152–1162 RSC.
- S. G. Jung, G. Jung and J. M. Cole, J. Chem. Inf. Model., 2024, 64, 1486–1501 CrossRef PubMed.
- X. Wang, H. Wu, T. Wang, Y. Chen, B. Jia, H. Fang, X. Yin, Y. Zhao and R. Yu, Anal. Chem., 2025, 97, 1992–2002 CrossRef PubMed.
- A. D. Gorse, Curr. Top. Med. Chem., 2006, 6, 3–18 CrossRef PubMed.
- H. H. Loeffler, J. He, A. Tibo, J. P. Janet, A. Voronov, L. H. Mervin and O. Engkvist, J. Cheminf., 2024, 16, 20 Search PubMed.
- Y. Zhu, J. Fang, S. A. H. Ahmed, T. Zhang, S. Zeng, J.-Y. Liao, Z. Ma and L. Qian, Nat. Commun., 2025, 16, 3598 CrossRef PubMed.
- M. Han, J. F. Joung, M. Jeong, D. H. Choi and S. Park, ACS Cent. Sci., 2025, 11, 219–227 CrossRef PubMed.
- J. Shao, Y. Liu, J. Yan, Z.-Y. Yan, Y. Wu, Z. Ru, J.-Y. Liao, X. Miao and L. Qian, J. Chem. Inf. Model., 2022, 62, 1368–1375 CrossRef PubMed.
- V. Venkatraman and L. Kallidanthiyil Chellappan, Data, 2020, 5, 45 CrossRef.
- V. Venkatraman, R. Raju, S. P. Oikonomopoulos and B. K. Alsberg, J. Cheminf., 2018, 10, 18 Search PubMed.
- E. J. Beard, G. Sivaraman, Á. Vázquez-Mayagoitia, V. Vishwanath and J. M. Cole, Sci. Data, 2019, 6, 307 CrossRef PubMed.
- A. A. Ksenofontov, M. M. Lukanov and P. S. Bocharov, Spectrochim. Acta Mol. Biomol. Spectrosc., 2022, 279, 121442 CrossRef PubMed.
- D. Gurvic, A. G. Leach and U. Zachariae, J. Med. Chem., 2022, 65, 6088–6099 CrossRef PubMed.
- S. Bhatia, T. Schultz, D. Roberts, J. Shen, L. Kromidas and A. Marie Api, Regul. Toxicol. Pharmacol., 2015, 71, 52–62 CrossRef CAS PubMed.
- J. Hussain and C. Rea, J. Chem. Inf. Model., 2010, 50, 339–348 CrossRef CAS PubMed.
- A. Dalke, J. Hert and C. Kramer, J. Chem. Inf. Model., 2018, 58, 902–910 CrossRef CAS.
- J. Shao, Y. Liu, J. Yan, Z.-Y. Yan, Y. Wu, Z. Ru, J.-Y. Liao, X. Miao and L. Qian, J. Chem. Inf. Model., 2022, 62, 1368–1375 CrossRef CAS.
- S.-H. Hung, Z.-R. Ye, C.-F. Cheng, B. Chen and M.-K. Tsai, J. Chem. Theory Comput., 2023, 19, 4559–4567 CrossRef CAS.
- C. Liu, Y. Sun, R. Davis, S. T. Cardona and P. Hu, J. Cheminf., 2023, 15, 29 Search PubMed.
- W. Song, L. Xiong, X. Li, Y. Zhang, B. Wang, G. Liu, W. Li, Y. Yang and Y. Tang, J. Chem. Inf. Model., 2025, 65, 2854–2867 CrossRef CAS PubMed.
- T. Alexander and G. Alexander, Curr. Pharm. Des., 2007, 13, 3494–3504 CrossRef.
- Z. Xiong, D. Wang, X. Liu, F. Zhong, X. Wan, X. Li, Z. Li, X. Luo, K. Chen, H. Jiang and M. Zheng, J. Med. Chem., 2020, 63, 8749–8760 CrossRef CAS.
- S. Lu, Z. Gao, D. He, L. Zhang and G. Ke, Nat. Commun., 2024, 15, 7104 CrossRef CAS PubMed.
- M. Steininger, K. Kobs, P. Davidson, A. Krause and A. Hotho, Mach. Learn., 2021, 110, 2187–2211 CrossRef.
- D. Jacquemin, V. Wathelet, E. A. Perpète and C. Adamo, J. Chem. Theory Comput., 2009, 5, 2420–2435 CrossRef CAS.
- A. Dreuw and M. Head-Gordon, Chem. Rev., 2005, 105, 4009–4037 CrossRef CAS.
- J. R. De Lile, S. G. Kang, Y.-A. Son and S. G. Lee, ACS Omega, 2020, 5, 15052–15062 CrossRef CAS.
- H. Luo and M. Mohammadnia, Inorg. Chem. Commun., 2022, 141, 109522 CrossRef.
- J. E. Gado, M. Knotts, A. Y. Shaw, D. Marks, N. P. Gauthier, C. Sander and G. T. Beckham, Nat. Mach. Intell., 2025, 7, 716–729 CrossRef.
- S. Qiu, B. Hu, J. Zhao, W. Xu and A. Yang, Briefings Bioinf., 2025, 26(2) DOI:10.1093/bib/bbaf114.
- S. Pascal, A. Haefele, C. Monnereau, A. Charaf-Eddin, D. Jacquemin, B. Le Guennic, C. Andraud and O. Maury, J. Phys. Chem., 2014, 118, 4038–4047 CrossRef CAS.
- N. Li, T. Wang, N. Wang, M. Fan and X. Cui, Angew. Chem., Int. Ed., 2023, 62, e202217326 CrossRef PubMed.
- J. Zhang, M. Moemeni, C. Yang, F. Liang, W.-T. Peng, B. G. Levine, R. R. Lunt and B. Borhan, J. Mater. Chem. C, 2020, 8, 16769–16773 RSC.
- E. D. Cosco, J. R. Caram, O. T. Bruns, D. Franke, R. A. Day, E. P. Farr, M. G. Bawendi and E. M. Sletten, Angew. Chem., Int. Ed., 2017, 56, 13126–13129 CrossRef.
- E. D. Cosco, B. A. Arús, A. L. Spearman, T. L. Atallah, I. Lim, O. S. Leland, J. R. Caram, T. S. Bischof, O. T. Bruns and E. M. Sletten, J. Am. Chem. Soc., 2021, 143, 6836–6846 CrossRef PubMed.
- H. Zhou, X. Zeng, A. Li, W. Zhou, L. Tang, W. Hu, Q. Fan, X. Meng, H. Deng, L. Duan, Y. Li, Z. Deng, X. Hong and Y. Xiao, Nat. Commun., 2020, 11, 6183 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2025 |