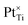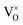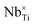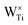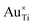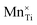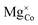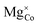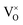Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Machine learning generalised DFT+U projectors in a numerical atom-centred orbital framework
Amit
Chaudhari
 ,
Kushagra
Agrawal
,
Kushagra
Agrawal
 and
Andrew J.
Logsdail
and
Andrew J.
Logsdail
 *
*
Cardiff Catalysis Institute, School of Chemistry, Cardiff University, Translational Research Hub, Maindy Road, Cardiff, CF24 4HF, UK. E-mail: LogsdailA@cardiff.ac.uk
First published on 30th October 2025
Abstract
Accurate electronic structure simulations of strongly correlated metal oxides are crucial for the atomic level understanding of heterogeneous catalysts, batteries and photovoltaics, but remain challenging to perform in a computationally tractable manner. Hubbard corrected density functional theory (DFT+U) in a numerical atom-centred orbital framework has been shown to address this challenge but is susceptible to numerical instability when simulating common transition metal oxides (TMOs), e.g., TiO2 and rare-earth metal oxides (REOs), e.g., CeO2, necessitating the development of advanced DFT+U parameterisation strategies. In this work, the numerical instabilities of DFT+U are traced to the default atomic Hubbard projector, which we refine for Ti 3d orbitals in TiO2 using Bayesian optimisation, with a cost function and constraints defined using symbolic regression (SR) and support vector machines, respectively. The optimised Ti 3d Hubbard projector enables the numerically stable simulation of electron polarons at intrinsic and extrinsic defects in both anatase and rutile TiO2, with comparable accuracy to hybrid-DFT at several orders of magnitude lower computational cost. We extend the method by defining a general first-principles approach for optimising Hubbard projectors, based on reproducing orbital occupancies calculated using hybrid-DFT. Using a hierarchical SR-defined cost function that depends on DFT-predicted orbital occupancies, basis set parameters and atomic material descriptors, a generalised workflow for the one-shot computation of Hubbard U values and projectors is presented. The method transferability is shown for 10 prototypical TMOs and REOs, with demonstrable accuracy for unseen materials that extends to complex battery cathode materials like LiCo1−xMgxO2−x. The work highlights the integration of advanced machine learning algorithms to develop cost-effective and transferable workflows for DFT+U parameterisation, enabling more accurate and efficient simulations of strongly correlated metal oxides.
1 Introduction
A knowledge of the electronic structure of transition metal oxides (TMOs) and rare-earth metal oxides (REOs) is essential for the development of energy materials for net zero. For example, TMOs and REOs are widely used as support materials in heterogeneous catalysis to enhance the reactivity of metal nanoparticles via the formation of catalytically active electron traps (i.e., electron polarons) at interfacial and defect sites. By controlling the formation of electron polarons, catalytic activity and selectivity can be tuned to achieve controllable CO2 conversion using CeO2-based catalysts,1 H2 production using MoO3-based catalysts2 and the production of sustainable aviation fuel via the Fischer Tropsch process using TiO2-based catalysts.3 TMOs and REOs are also widely applicable for technologies in the generation and storage of electricity, due to the ability to tune the mobility of electrons and ions. Tuneable charge carrier mobility can be exploited for the development of photovoltaics and lithium ion battery cathodes using dopants such as Nb and Mg to optimise the electrical performance of TiO2 and LiCoO2, respectively.4,5Despite extensive experimental research across a broad range of TMO- and REO-based energy materials, realising a step change in their design and optimisation requires first-principles simulation methods, such as density functional theory (DFT),6,7 to bridge theory and experiment; however, accurate DFT simulations of the ground state electronic structures of TMOs and REOs can be very challenging. The self-interaction error (SIE), which arises when using local and semi-local exchange–correlation density functionals to describe the correlation between electrons occupying localised d or f orbitals, results in electronic repulsion that causes systematic errors in predicted material properties, e.g., underestimated insulator band gaps, inaccurate lattice parameters and inaccurate formation energies of point defects and electron polarons.8–10 To overcome the limitations of DFT for strongly correlated materials, “beyond-DFT” methods can be applied that add corrective schemes to combat the SIE. Hubbard corrected density functional theory (DFT+U) is a suitable and popular beyond-DFT method, involving a tuneable on-site Coulomb repulsion, i.e., an energy penalty against electron delocalisation that is applied selectively to correlated orbitals in the system.11 DFT+U is popular because it adds minimal computational cost compared to standalone DFT,12 whilst achieving the accuracy of higher levels of theory such as hybrid-DFT if parameterised carefully.13
To accurately parameterise DFT+U, one must account for both the magnitude and basis of the Hubbard correction, which are defined using the Hubbard U value and the Hubbard projector function (or Hubbard projector) respectively. These parameters are used to correct the DFT-predicted total energy (EDFT) with a corrective Hubbard term that treats localised states only (E0U) and a double counting correction (EdcU) that prevents the double counting of localised states in both EDFT and E0U:
| EDFT+U[ρ(r), nI,mσ] = EDFT[ρ(r)] + E0U[nI,mσ] − EdcU[nI,mσ] | (1) |
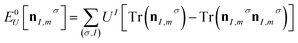 | (2) |
The occupation matrix is calculated by projecting all DFT-predicted Kohn–Sham states onto reference orbitals defined by the Hubbard projector, i.e., calculating the overlap between Kohn–Sham states and spatially localised orbitals, before an overlap-dependent assignment of the occupancy of each Kohn–Sham state to the localised orbitals.15 After evaluating E0U, the corresponding Hubbard potential, i.e., the added correction to the standard Kohn–Sham effective potential, is then obtained by taking the functional derivative of the corrective Hubbard energy with respect to the occupation matrix, yielding an orbital-dependent potential that acts only on the subspace defined by the chosen projector.14 The Hubbard correction therefore acts as an occupancy-based bias potential that corrects the total energy using the Hubbard U value and the occupation matrix, which necessitates careful choice of both the Hubbard U value and the projector. Choosing an appropriate Hubbard projector is particularly important for accurate simulations of materials with strong covalent character,15–18 and their specific representation prevents the transferability of Hubbard parameters across electronic structure codes that employ different types of Hubbard projector, e.g., atomic orbitals,15 Wannier functions,19–21 projector augmented wave (PAW) projectors22 and muffin-tin orbitals (MTOs).16
Typically, the Hubbard U value is parameterised in DFT+U calculations with no consideration of the Hubbard projector, using semi-empirical benchmarking of DFT+U-predicted electronic, geometric and energetic properties against reference data from experiments or higher levels of theory.23,24 These semi-empirical approaches are reliant on accurate and available reference data, which prevents the high-throughput optimisation of Hubbard U values for vast numbers of materials. Several first-principles approaches for computing Hubbard U values have also been developed, including the linear response approach based on constrained DFT (LR-cDFT),25 density functional perturbation theory (DFPT),26 constrained random phase approximation (cRPA)27 and Hartree Fock based approaches (e.g., UHF and ACBN0).28,29 Of these methods, LR-cDFT is most popular and has been applied in a planewave basis for the high-throughput optimisation of Hubbard U values for over 1000 transition metal oxides.30 However, LR-cDFT can yield unphysical U values, suffers from numerical instability for closed-shell systems31,32 and is computationally expensive due to the requirement of calculations using large supercells.18 In addition, Hubbard U values computed using LR-cDFT are site-specific and therefore not transferable from stoichiometric systems with symmetry-equivalent sites to defective systems with broken symmetry.33 The lack of transferability can prevent the simulation of experimentally observed electrical conductivities of defective TMOs, including the Li-ion battery cathode material LiCo1−xMgxO2, where deep defect states are predicted using Hubbard U values from LR-cDFT in a planewave basis, thus incorrectly suggesting material resistivity.5
To minimise the cost and instability of first-principles methods for computing Hubbard U values, active learning methods have been combined with global optimisation algorithms, such as Bayesian optimisation (BO) and Monte Carlo sampling, to minimise a cost function based on reproducing geometric and electronic properties predicted using higher levels of theory.34–36 In active learning, the cost function is refined by comparison with the output of successive DFT+U calculations, which means there is no a priori knowledge of the DFT+U potential energy surface and the entire approach must be repeated for different systems. Supervised machine and deep learning approaches have been used to improve the transferability of active learning methods for computing Hubbard U values, by attempting to learn the DFT+U potential energy surface for different materials. For example, BO and Random Forest Regression have been used to determine the structure-dependence of the Mn 3d Hubbard U value required to reproduce the electronic band structures of various MnOx polymorphs computed using hybrid-DFT.37 Similarly, equivariant neural networks have been used to estimate DFPT-predicted Hubbard U values using ground state atomic occupation matrices and interatomic distances for a range of materials, including LixFePO4 and MnO2.38 However, none of these methods address the parameterisation of Hubbard projectors, as well as differences in the numerical stability of DFT+U calculations with different Hubbard parameters.
The aforementioned challenges in DFT+U parameterisation (accuracy, numerical instability, computational cost and transferability across materials) are considered in this work in the context of simulations of stoichiometric and defective TMOs and REOs in a numerical atom-centred orbital (NAO) framework. In a NAO framework, there is a strong dependence of the accuracy and numerical stability of DFT+U calculations on both the Hubbard U value and the projector. Relying on semi-empirically derived Hubbard U values and the default atomic Hubbard projector can result in inaccurate, unphysical (calculations terminate due to excessive polaron localisation) and unstable (SCF cycle does not converge) simulations of common TMOs, e.g., TiO2 and REOs, e.g., CeO2. Thus, we demonstrate simultaneous optimisation of the Hubbard U value and the projector for Ti 3d orbitals in anatase TiO2 using BO with a cost function defined using symbolic regression (SR), to minimise the errors of target properties relative to experimental references. BO is also subject to constraints on the DFT+U-predicted covalency, to ensure the numerical stability of point defect calculations, as determined using support vector machines (SVMs). Combining SR, SVMs and BO in this manner avoids the need for multiple successive DFT+U calculations, which significantly reduces the overall computational cost for Hubbard parameter optimisation compared to the existing first-principles and active learning approaches. We then extend the method across different materials by expanding the primary feature space for SR to include DFT-predicted orbital occupancies, basis set parameters and atomic material descriptors for a diverse training set of TMOs and REOs; application of hierarchical SR39 allows us to optimise Hubbard U values and projectors from first-principles, by targeting orbital occupancies calculated using hybrid-DFT. The outcome is a transferable approach for the one-shot computation of Hubbard U values and projectors, with good accuracy that is also achieved for unseen materials. Overall, the work demonstrates the development of cost-effective and transferable machine learning-based workflows for more complete DFT+U parameterisation, enabling more accurate and efficient simulations of complex energy materials.
2 Methodology
2.1 Electronic structure calculations
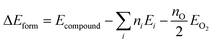 | (3) |
 | (4) |
Where presented, modified atomic-like Hubbard projectors were therefore constructed as a linear combination of atomic and hydrogenic auxiliary basis functions, given the available basis functions in the light basis set (SI Section S1.3, Table S2). With this definition of the Hubbard projector, the use of basis sets with multiple radial functions for the same localised orbital can reportedly lead to erroneous ground state predictions due to the occupation of electronic states outside the correlated subspace;15,57 therefore, we restrict our study to the unmodified light basis set, which contains at most one auxiliary basis function per localised orbital as listed in the SI Section S1.3, Table S2. The Hubbard projector is therefore defined using the linear expansion coefficients c1 and c2, which correspond to the atomic and auxiliary basis functions, respectively. Positive values of c2 were avoided to prevent the mixing of the metal d or f auxiliary basis functions with O 2p states in an unphysical manner, as determined by Kick et al. from comparisons with hybrid-DFT.15 Before constructing modified projectors, the auxiliary basis functions are subject to a Gram–Schmidt orthogonalisation with respect to the corresponding atomic functions, which avoids double counting of the Hubbard correction from the overlap of basis functions with long tails of radial decay.15,58
 | ||
| Fig. 1 Simulating an electron polaron in W-doped TiO2 at a nearest neighbour Ti atom, denoted Ti3+ by setting the 3dz2 orbital occupation number to 1. The electron polaron can be fixed using the occupation matrix control (OMC) method or initialised using the occupation matrix release (OMR) method. The diagonal elements of the occupation matrix correspond to orbital occupancies for a given magnetic quantum number (3dm) in the order (from top left to bottom right) 3d−2, 3d−1, 3d0, 3d1 and 3d2 corresponding to the 3dxy, 3dyz, 3dz2, 3dxz and 3dx2−y2 orbitals, respectively.60 Off-diagonals elements in the occupation matrix reflect orbital hybridisation. In this work, the diagonal elements of the occupation matrix are used as a quantitative measure of local chemical bonding environments and to construct workflows for Hubbard parameter optimisation by assessing how the occupation matrix varies with the chosen simulation method (i.e., DFT, DFT+U or hybrid-DFT, detailed in the SI Section S1.3), Hubbard parameters and atomic properties of different materials. | ||
In Section 3.2, self-consistent DFT+U calculations are performed for TiO2 using a modified atomic-like Ti 3d Hubbard projector, determined using the semi-empirical machine learning approach detailed in Section 2.2. This is expanded in Section 3.3, where self-consistent DFT+U calculations are performed for all materials in Table S2 in the SI Section S1.3, using modified atomic-like Hubbard projectors that were determined using the first-principles machine learning approach detailed in Section 2.3. Self-consistent defect calculations were performed using the “occupation matrix release” (OMR) method to initialise polaron(s); the DFT+U-predicted total energy (E) is then pre-converged using OMC until ΔE ≤ 0.001 eV, at which point the OMC constraint is relaxed and the orbital occupancies are calculated self-consistently.15 All point defect calculations in this work were performed in a 3 × 3 × 3 supercell, which avoids spurious long-range defect–defect interactions between periodic images. The oxygen vacancy formation energy (ΔEOV) and the defect energies (ΔEdefect) following substitution of a host metal atom (Ti in TiO2 and Co in LiCoO2) with a Nb, W, Co, Mn, Pt, Au, Pd or Mg atom, are calculated as:
| ΔEOV = Eoxygen deficient bulk + µO − Estoichiometric bulk | (5) |
| ΔEdefect = Edoped bulk + µhost − Estoichiometric bulk − µdopant | (6) |
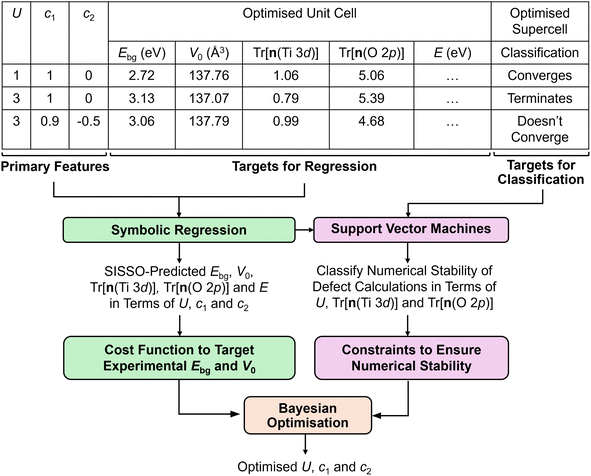
2.2 Semi-empirical machine learning approach
A semi-empirical approach was adopted to optimise the Ti 3d Hubbard U value and projector to enable accurate and numerically stable simulations of anatase TiO2 using DFT+U-calculated properties of the TiO2 unit cell (targets for regression) and the classified outcome of point defect calculations in a TiO2 supercell using the OMR method (targets for classification), as illustrated in Fig. 2. , before using sparse regression techniques to select a minimal set of secondary features and linear regression to optimise the coefficients of the final expression. Empirical correlations were fitted with up to three terms, using a recursive depth of three, yielding a linear combination of non-linear terms, e.g., F1, F2 and F3 using the constants a0, a1, a2 and a3 for a three term correlation:
, before using sparse regression techniques to select a minimal set of secondary features and linear regression to optimise the coefficients of the final expression. Empirical correlations were fitted with up to three terms, using a recursive depth of three, yielding a linear combination of non-linear terms, e.g., F1, F2 and F3 using the constants a0, a1, a2 and a3 for a three term correlation:| Target = a0 + a1 × F1 + a1 × F2 + a3 × F3 | (7) |
Empirical correlations were constructed to estimate the DFT+U-predicted band gap (Ebg), V0 and traces of the Ti 3d (Tr[n(Ti 3d)]) and O 2p (Tr[n(O 2p)]) occupation matrices, with the accuracy of each correlation evaluated using the Pearson's coefficient of determination (R2) and root mean squared error (RMSE). The SISSO correlations were then used to evaluate a unitless, regularised cost function (JSE), which is defined as the Euclidean norm of two terms JSE1 and JSE2. JSE1 is itself the Euclidean norm of the percentage errors of the DFT+U-predicted Ebg and V0 of bulk anatase TiO2versus experimental references from the literature (EExpbg and VExp0, respectively).64,65JSE2 is an additional regularisation term to bias JSE towards larger values of U and c1, which favours stronger polaron localisation at point defects that is consistent with the experimentally observed formation of mid-gap states within the TiO2 band gap.15,66,67JSE therefore takes the form:
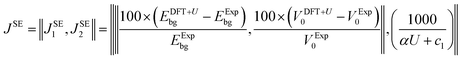 | (8) |
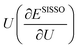 ,
, 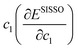 and
and 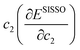 were calculated using the forward finite difference method with a step size of 0.01. Both SR and SVM classification were performed using a training set of ≤60 geometry optimised unit cells and bulk oxygen vacancy calculations, where all computational settings are kept constant except the Ti 3d Hubbard parameters. Feature scaling was performed for all primary features and target properties (denoted using
were calculated using the forward finite difference method with a step size of 0.01. Both SR and SVM classification were performed using a training set of ≤60 geometry optimised unit cells and bulk oxygen vacancy calculations, where all computational settings are kept constant except the Ti 3d Hubbard parameters. Feature scaling was performed for all primary features and target properties (denoted using ![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) ) for the SISSO correlation for V0 and SVM boundaries S1 and S2. The normalisation constants are listed with the non-linear terms, constants and accuracy metrics for all SISSO correlations and SVM boundaries in the SI Section S2.1.
) for the SISSO correlation for V0 and SVM boundaries S1 and S2. The normalisation constants are listed with the non-linear terms, constants and accuracy metrics for all SISSO correlations and SVM boundaries in the SI Section S2.1.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 iterations.
000 iterations.
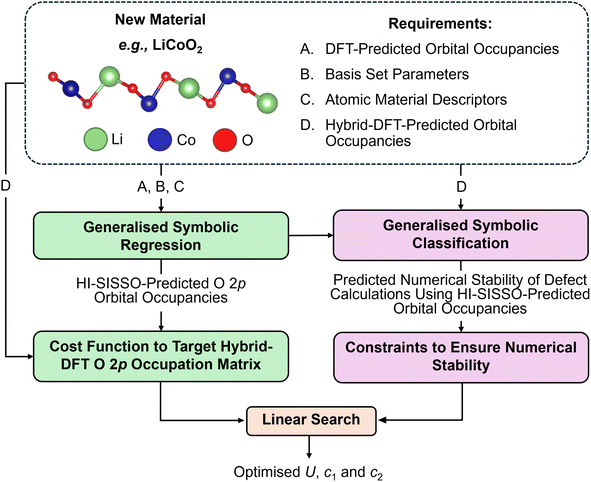
2.3 First-principles machine learning approach
To extend the semi-empirical approach across different materials, a first-principles approach was adopted to parameterise Hubbard U values and projectors by targeting the O 2p orbital occupancies calculated using hybrid-DFT, which was identified as crucial to enable self-consistency of DFT+U simulations of intrinsic and extrinsic defects in TiO2 using the OMR method. The first-principles approach was similar to the semi-empirical approach outlined in Section 2.2, by aiming to ensure the accuracy and numerical stability of DFT+U simulations of stoichiometric and defective TMOs and REOs using generalised symbolic regression and classification, as illustrated in Fig. 3.The expanded set of 20 primary features makes the SISSO method computationally intractable due to the attempted exhaustive search of the secondary feature space, which scales exponentially with the number of primary features, therefore, a two-step hierarchical SISSO (HI-SISSO)39 approach was adopted where the output from a first step using SISSO, with 13/20 of all primary features (Hubbard parameters and DFT-predicted orbital occupancies), was used as an input for a second step using HI-SISSO where the remaining primary features are included as inputs. HI-SISSO was used to fit ten empirical correlations to estimate DFT+U-predicted orbital occupancies across the full range of magnetic quantum numbers (m), with seven correlations for m = −3 to +3 (grouping together d and f orbitals) and three correlations for m = −1 to 1 for O 2p orbitals. The training set contained 197 sets of DFT+U-calculated orbital occupancies from optimised unit cells of anatase and rutile TiO2 (46%), CeO2 (13%), Cu2O (11%), Y2O3 (11%), ZrO2 (11%), WO3 (7%) and MoO3 (1%), where the percentages correspond to the proportion of each material in the dataset. LiCoO2 and LiFePO4 were used as blind test cases with no training data. The constants, accuracy metrics and non-linear terms F1, F2 and F3 for all HI-SISSO correlations are listed in the SI Section S2.2.1. As illustrated by the parity plots in Fig. 4 for O 2p orbitals, the HI-SISSO approach (including basis set parameters and atomic descriptors) improved the predictive accuracy of all three correlations compared to the single step SISSO approach, which is equivalent to Δ-machine learning with respect to DFT-predicted orbital occupancies.73
The HI-SISSO-predicted O 2p occupancies were then used to construct a cost function for optimising Hubbard U values and projectors from first-principles, JFP, by targeting O 2p orbital occupancies calculated using hybrid-DFT, as outlined in Section 3.3.1.
 | (9) |
 | (10) |
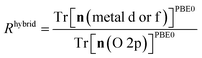 | (11) |
Generalised constraints on the Hubbard parameter space were determined using two linear SVMs to determine the equations of the boundaries S4 and S5 that separated regions in the primary feature space leading to the termination and non-convergence of bulk oxygen vacancy calculations using the OMR method. The training set consisted of 86 DFT+U simulations across anatase and rutile TiO2 (76%), CeO2 (6%), ZrO2 (6%), MoO3 (6%), WO3 (5%) and Cu2O (2%), where the percentages correspond to the proportion of each material in the dataset. To reduce the number of misclassified data points associated with S4 and S5, classification was performed symbolically using the SISSO algorithm to recursively combine the primary features using the same algebraic operators as in SR, but with the objective of minimising the number of data points in the overlap region of a two-dimensional convex hull.63 The secondary features generated from SISSO were then used as inputs for two linear SVMs, which identified simple boundaries to perform binary classifications in a highly non-linear feature space. The associated constants and accuracy metrics for S4 and S5 are listed in the SI Section S2.2.1.
 | (12) |
The relationship between the accuracy of the one-shot approach for minimising JFPpredicted and the training set size for each material was investigated using the Mahalanobis distance (DM)75 to quantify the distance of the primary feature vector for each material (x), in a reduced two dimensional feature space determined using principal component analysis (PCA) with the Scikit-learn Python library,68 from the mean vector of the training data (κ), using the inverse covariance matrix of the training data (C−1):
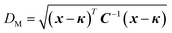 | (13) |
An integrated one-shot approach for optimising Hubbard U values and projectors from first-principles was tested for computing the Co 3d Hubbard U value and projector for the simulation of stoichiometric, Mg-doped and oxygen defective LiCoO2 (i.e., LiCo1−xMgxO2−x), which is unseen by any of the trained regression or classification models. Here, the three HI-SISSO correlations to estimate the DFT+U-predicted O 2p orbital occupancies (for m = −1, 0 and 1) were used to screen the landscape of JFPpredicted for stoichiometric LiCoO2, before all Hubbard parameters that violate the generalised constraints S4 and S5, which are evaluated using all ten HI-SISSO correlations, are removed from the landscape. The remaining Hubbard parameters were reduced to a smaller set of candidates with K-means clustering, using the Scikit-learn Python library,68 which uses unsupervised learning to partition the landscape of JFPpredicted into smaller clusters by minimising intra-cluster variance. The centroids of these clusters were then used as screened Hubbard parameters for the simulation of stoichiometric and defective LiCoO2, using the OMR method.
3 Results and discussion
3.1 Projector sensitivities in DFT+U simulations
In a NAO framework, similar observations are made when modelling stoichiometric REOs using the default atomic Hubbard projector. For example, applying a Hubbard correction to Ce 4f electrons in stoichiometric CeO2, using the atomic Ce 4f Hubbard projector, results in an insulator-metal transition (IMT) in the predicted ground state. Upon increasing the Ce 4f Hubbard U value, there is a monotonic change in the DFT+U-predicted Ebg in Fig. 5(a) and ΔEform in Fig. 5(b) between U values of 0 eV to 9 eV. Beyond U = 9 eV, which would be required if adopting the standard approach of benchmarking against the experimental Ebg of 3.2 eV,82 there is a sudden deviation in these trends and DFT+U predicts strong electron localisation in the Ce 4f m = −2 orbital, corresponding to metallic behaviour with no band gap. To trace the root cause of the observed IMT at U = 9.5 eV, constrained DFT+U calculations were performed using the ground state Ce 4f occupation matrix calculated using U = 9.5 eV, but with the m = −2 and m = −3 orbital occupancies systematically varied and all other occupancies fixed. As illustrated in Fig. 5(c), there is a metallic global energy minimum and an insulating low-lying metastable state in the potential energy surface, therefore the observed IMT is caused by the small energy differences between these energy minima, which decreases as the Hubbard U value increases. For U = 9.5 eV, self-consistent determination of the Ce 4f occupation matrix leads to a metallic solution, irrespective of the initial occupation matrix; therefore, we conclude that there are no other insulating solutions with lower energy than the metallic solution and that this represents an IMT in the potential energy surface.
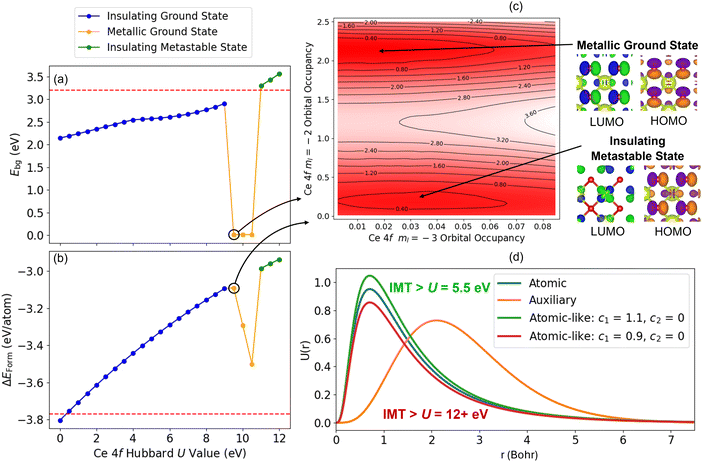 | ||
| Fig. 5 Overview of errors when modelling stoichiometric CeO2 using the default Ce 4f atomic Hubbard projector, including the variation in the DFT+U-predicted (a) band gap and (b) formation energy with respect to the Ce 4f Hubbard U value, relative to experimental references denoted by the red dashed lines.82,83 Blue markers correspond to insulating ground states, yellow markers correspond to metallic ground states and green markers correspond to insulating metastable states. (c) Contour plot of the constrained DFT+U-predicted total energy relative to the ground state energy at U = 9.5 eV, after constraining the m = −2 and m = −3 orbital occupancies. The two regions in dark red correspond to global and low-lying local minima in the potential energy surface with respect to Ce 4f orbital occupancies. The metallic global minimum is 0.273 eV more stable than the insulating local minimum. (d) The radial functions corresponding to the atomic Ce 4f (blue) and hydrogenic auxiliary (orange) basis functions available for constructing a modified atomic-like Hubbard projector. The green and red radial functions correspond to modified projectors that do not include any contribution from the hydrogenic auxiliary function (i.e., c2 = 0) and are noted with the corresponding shift of the observed IMT. | ||
Beyond U = 11 eV, the insulating ground state character is seemingly restored in Fig. 5(a) and (b); however, these were found to be metastable states as confirmed using OMR with a modified initial Ce 4f occupation matrix, which enabled convergence to the true metallic ground state that exists at all U values beyond the IMT at U = 9.5 eV. The IMT was also found to vary with the definition of the Hubbard projector, as shown in Fig. 5(d), where the more localised projector in green brings the IMT forward to U > 5.5 eV and the more diffuse projector defers the IMT beyond U = 12 eV. The results exemplify the importance of developing new strategies for parameterising the Hubbard U value and projector to enable the accurate simulation of insulating ground states of REOs like CeO2, whilst avoiding erroneous IMTs and metastable states; this goal cannot be achieved using the standard approach of semi-empirical benchmarking of the Hubbard U value to reproduce the experimental Ebg.
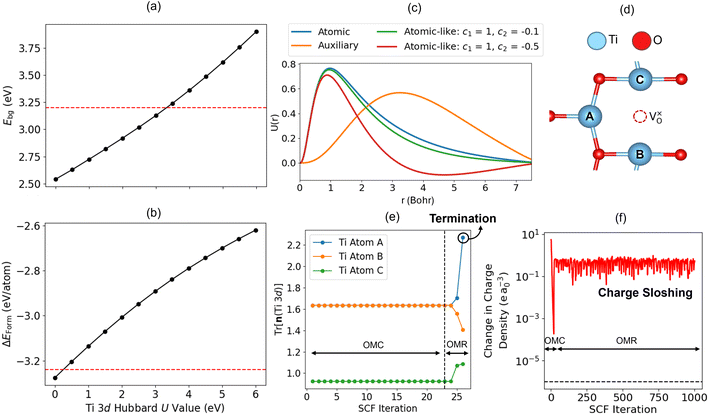 | ||
| Fig. 6 Overview of errors when modelling stoichiometric and defective TiO2, including the variation of the DFT+U-predicted (a) band gap and (b) formation energy with respect to the Ti 3d Hubbard U value, using the default atomic Ti 3d Hubbard projector, relative to experimental references denoted by the red dashed lines.64,87 (c) The radial functions corresponding to the atomic Ti 3d (blue) and hydrogenic auxiliary (orange) basis functions available for constructing a modified atomic-like Hubbard projector. The green and red radial functions correspond to modified projectors that incorporate a contribution from hydrogenic auxiliary function given by the linear expansion coefficient c2. (d) The nearest neighbour Ti atoms surrounding a bulk oxygen vacancy in anatase TiO2. (e) The evolution of Tr[n(Ti 3d)] for Ti atoms A, B and C in (d) during an oxygen vacancy calculation using U = 3 eV, c1 = 1, c2 = −0.1, which leads to calculation termination due to excessive polaron localisation at atom A, after 3 SCF iterations of OMR (which begins after 23 SCF iterations of OMC). (f) The evolution of the change in charge density during SCF optimisation, during the 1st geometry optimisation step for an oxygen vacancy calculation using U = 3 eV, c1 = 1, c2 = −0.5. The calculation does not achieve the convergence criteria of changes in charge density below 1 × 10−6 e a0−3, denoted by the black dashed line, due to charge sloshing. | ||
We note three approaches that are observed to overcome the numerical instabilities when simulating point defects using DFT+U in a NAO framework. Kick et al. overcame SCF non-convergence when simulating Ti3+ polarons at oxygen vacancies in a rutile (110) TiO2 surface by increasing the effective core charge (Zval) of the Tier 1 hydrogenic auxiliary basis function from 2.7e to 4.4e, before using an atomic Ti 3d Hubbard projector to define the basis for the Hubbard correction.15 Using very small Hubbard U values, or employing constrained DFT+U using the OMC method, can also overcome the observed numerical instability; however, we have previously shown that this comes at the expense of accuracy when modelling polarons in Nb- and W-doped bulk anatase and rutile TiO2.67 For these systems, self-consistent resolution of the system occupation matrices was achieved using a modified Ti 3d Hubbard projector, defined as a linear combination of the atomic and Tier 1 hydrogenic basis functions with the expansion coefficients c1 = 0.828 and c2 = −0.561 determined by Jakob and Oberhofer using a first-principles generalised LR-cDFT method in FHI-aims.57 With a modified Ti 3d Hubbard projector, DFT+U successfully simulated the polymorph-dependent formation of Nb4+ and W5+ polarons as observed in electron paramagnetic resonance (EPR) spectroscopy, which cannot be rationalised by the current planewave DFT+U studies in the literature.67 It is therefore essential to understand how to define an appropriate Hubbard projector to enable DFT+U simulations with appreciable Hubbard U values without sacrificing self-consistency and remaining robust with respect to the default basis sets, and we investigate this challenge herein for TiO2 before establishing a generalised understanding for a broader range of TMOs and REOs.
3.2 Bayesian optimisation of the Ti 3d Hubbard projector
![[V with combining macron]](https://www.rsc.org/images/entities/i_char_0056_0304.gif) 0, Tr[n(Ti 3d)] and Tr[n(O 2p)] in terms of the primary features U, c1 and c2, as listed in the SI Section S2.1. Three constraints for sampling the Hubbard parameter space were also defined to ensure physicality of the model and avoid numerical instability during point defect calculations using OMR, which result in either termination or non-convergence in Fig. 6. Hubbard parameters that are predicted by the SISSO models to give a negative occupation matrix trace for Ti 3d or O 2p orbitals, or occupation matrix traces that deviate from the respective hybrid-DFT-predicted occupation matrix trace by over 50%, were excluded. The third constraint was applied using two linear SVMs that classify the validity of a bulk oxygen vacancy calculation in terms of the normalised Ū,
0, Tr[n(Ti 3d)] and Tr[n(O 2p)] in terms of the primary features U, c1 and c2, as listed in the SI Section S2.1. Three constraints for sampling the Hubbard parameter space were also defined to ensure physicality of the model and avoid numerical instability during point defect calculations using OMR, which result in either termination or non-convergence in Fig. 6. Hubbard parameters that are predicted by the SISSO models to give a negative occupation matrix trace for Ti 3d or O 2p orbitals, or occupation matrix traces that deviate from the respective hybrid-DFT-predicted occupation matrix trace by over 50%, were excluded. The third constraint was applied using two linear SVMs that classify the validity of a bulk oxygen vacancy calculation in terms of the normalised Ū, 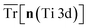 and
and 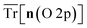 , as illustrated in Fig. 7, which shows the boundaries S1 and S2 that separate regions in the Hubbard parameter space that lead to unphysical (termination), charge sloshing (preventing SCF convergence) and ground state (stable convergence) calculation outcomes.
, as illustrated in Fig. 7, which shows the boundaries S1 and S2 that separate regions in the Hubbard parameter space that lead to unphysical (termination), charge sloshing (preventing SCF convergence) and ground state (stable convergence) calculation outcomes.
 | ||
| Fig. 7 Illustration of the linear boundaries used to classify simulations of a bulk oxygen vacancy in anatase TiO2. The boundaries separate successful convergence (green markers), termination due to an unphysical ground state (red markers) and charge sloshing preventing SCF convergence (orange markers). The convex hull associated with each binary classification S1 and S2 is shown to illustrate the basis for constructing the constraint in eqn (14). | ||
Fig. 7 illustrates how the numerical stability of defect calculations in TiO2 is sensitive to the DFT+U-predicted covalency, with calculation termination occurring at high covalency, i.e.,  and charge sloshing occurring at high metallicity, i.e.,
and charge sloshing occurring at high metallicity, i.e., 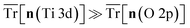 . To ensure the successful convergence of point defect calculations whilst mitigating the effects of the changing DFT+U-predicted covalency, the equations of the decision boundaries S1 and S2 (trained on DFT+U data, with all constants listed in the SI Section S2.1) were used as constraints on the sampled Hubbard parameter space, based on the SISSO-computed cost function JSE, with the critical values for S1 and S2 chosen based on the convex hull plots in Fig. 7:
. To ensure the successful convergence of point defect calculations whilst mitigating the effects of the changing DFT+U-predicted covalency, the equations of the decision boundaries S1 and S2 (trained on DFT+U data, with all constants listed in the SI Section S2.1) were used as constraints on the sampled Hubbard parameter space, based on the SISSO-computed cost function JSE, with the critical values for S1 and S2 chosen based on the convex hull plots in Fig. 7:
| S1 > −9.84 ∧ S2 > −9.16 | (14) |
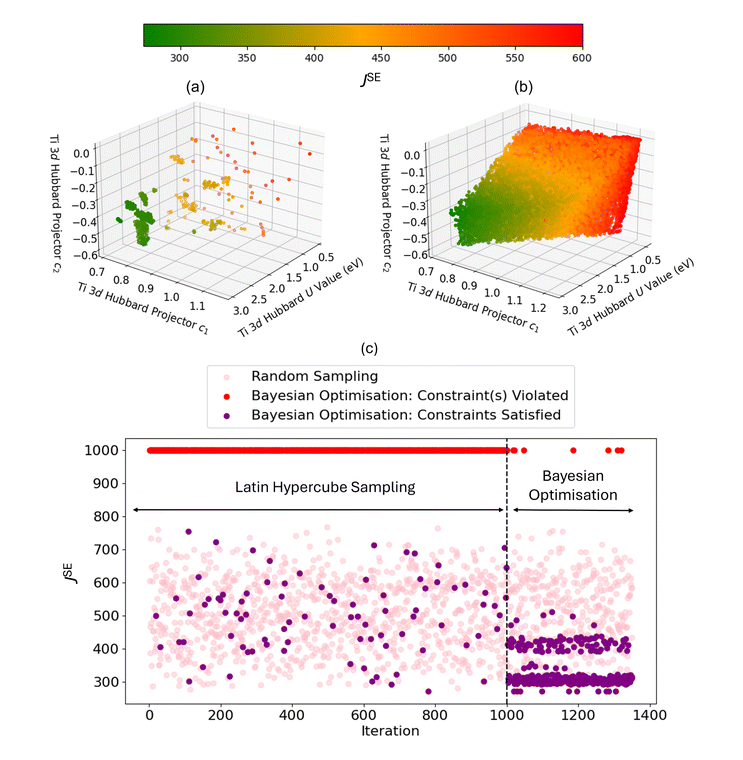
Fig. 8(a) and (b) show the results of BO and random sampling, respectively, where BO is able to efficiently optimise U, c1 and c2, yielding an almost equivalent set of optimised Hubbard parameters, to those obtained using random sampling, with minimal values of JSE. This is further supported by Fig. 8(c), which shows the values of JSE corresponding to the sampled Hubbard parameters. The markers in pink show the first 1350 randomly sampled Hubbard parameters, where constraint violations do not inform subsequent sampling, making the approach highly inefficient. The markers in purple correspond to BO, where the 1000 randomly sampled points selected using Latin Hypercube Sampling are used to train the BO prior and enable efficient optimisation of U, c1 and c2. The Hubbard parameters U = 2.749 eV, c1 = 0.758 and c2 = −0.354, from the region of lowest JSE in Fig. 8(a) and (b), were tested for the simulation of both anatase and rutile TiO2 polymorphs. With the refined atomic-like Ti 3d Hubbard projector, oxygen vacancies and the substitutional dopants Nb, W, Co, Mn, Pt, Au and Pd all successfully converged to the ground state, whilst 11 of these 16 calculations failed when using the same Hubbard U value with the default atomic Ti 3d Hubbard projector (listed in Section 3.2.3, Table 2).
Refining the Ti 3d Hubbard projector therefore enables numerically stable self-consistent defect calculations; however, the predictions for anatase TiO2 have unphysical defect energies, ranging from −11.59 eV and −1.28 eV; the same is not observed for defective rutile TiO2, with defect energies ranging from −0.97 eV to 8.22 eV. These unphysical defect energies for anatase TiO2 necessitate further study into how tuning the Ti 3d Hubbard projector affects the DFT+U-predicted total energy (E). As discussed in the SI Section S2.1.2, we construct an additional SVM constraint S3 to classify whether a particular combination of U, c1, and c2 leads to “physical” (4 eV ≤ ΔEOV ≤ 6 eV) or “unphysical” (ΔEOV < 4 eV or ΔEOV > 6 eV) oxygen vacancy formation energies. Filtering out the data points in Fig. 8(b) that do not satisfy S3 yields the optimal Hubbard parameters U = 2.575 eV, c1 = 0.752 and c2 = −0.486. The approximate similarity is noted of our optimised Ti 3d Hubbard projector with that determined by Jakob and Oberhofer for bulk rutile TiO2, defined by c1 = 0.828 and c2 = −0.561, using a first-principles generalised LR-cDFT method in FHI-aims.57
| TiO2 polymorph | Method | E bg (eV) | V 0 (Å3) | ΔEform (eV per atom) | Tr[n(Ti 3d)] | Tr[n(O 2p)] |
|---|---|---|---|---|---|---|
| Anatase | DFT | 2.54 | 137.26 | −3.28 | 1.18 | 4.91 |
| Anatase | DFT+U | 2.75 | 137.09 | −3.02 | 0.69 | 4.64 |
| Anatase | Hybrid-DFT | 4.29 | 135.49 | −3.21 | 1.25 | 4.66 |
| Anatase | Experiment | 3.20 (ref. 64) | 136.28 (ref. 65) | −3.24 (ref. 87) | N/A | N/A |
| Rutile | DFT | 2.21 | 63.50 | −3.26 | 1.17 | 4.95 |
| Rutile | DFT+U | 2.42 | 62.51 | −3.01 | 0.68 | 4.63 |
| Rutile | Hybrid-DFT | 4.05 | 62.39 | −3.20 | 1.23 | 4.69 |
| Rutile | Experiment | 3.00 (ref. 64) | 62.44 (ref. 65) | −3.26 (ref. 87) | N/A | N/A |
The hybrid-DFT-predicted V0 is closest to the experimental value, although hybrid-DFT significantly overestimates Ebg. DFT+U predicts a smaller ΔEform than DFT, hybrid-DFT and experiment, although all computational methods maintain a similar relative difference between ΔEform for anatase and rutile TiO2, with ΔEanataseform − ΔErutileform values of −0.02 eV, −0.01 eV and −0.01 eV for DFT, DFT+U and hybrid-DFT, respectively. The DFT+U-predicted covalency of TiO2 is also suppressed compared to hybrid-DFT, as evidenced by the reduced total Ti 3d orbital occupancy, i.e., Tr[n(Ti 3d)], whilst the DFT+U-predicted total O 2p orbital occupancy, given by Tr[n(O 2p)], remains close to that of hybrid-DFT.
Next, self-consistent DFT+U simulations were performed for anatase and rutile TiO2 containing an oxygen vacancy and the substitutional dopants Nb, W, Au, Pd, Pt, Co and Mn. Table 2 summarises the success or failure of these simulations, both with or without a refined Ti 3d Hubbard projector and with or without the Hubbard parameters satisfying the error correction constraint derived from S3 in the SI Section S2.1.2.
| Polymorph | U (eV) | c 1 | c 2 | Satisfied constraints | Point defect | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Anatase | 2.749 | 1 | 0 | None | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ | ✗ |
| Anatase | 2.575 | 1 | 0 | None | ✗ | ✗ | ✗ | ✗ | ✓ | ✓ | ✓ | ✓ |
| Anatase | 2.749 | 0.758 | −0.354 | S 1, S2 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Anatase | 2.575 | 0.752 | −0.486 | S 1, S2, S3 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Rutile | 2.749 | 1 | 0 | None | ✗ | ✗ | ✗ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Rutile | 2.575 | 1 | 0 | None | ✗ | ✗ | ✗ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Rutile | 2.749 | 0.758 | −0.354 | S 1, S2 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Rutile | 2.575 | 0.752 | −0.486 | S 1, S2, S3 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
Comparing the rows in Table 2 that use the same Ti 3d Hubbard U value but a different Ti 3d Hubbard projector shows that refining the Hubbard projector has a direct effect on enabling self-consistent defect simulations. All calculation failures were due to unphysical ground states causing the termination of calculations due to excessive polaron localisation as seen in Fig. 6(e). Refining the Ti 3d Hubbard parameters further from U = 2.749 eV, c1 = 0.758 and c2 = −0.354 to U = 2.575 eV, c1 = 0.752 and c2 = −0.486, using the constraint derived from the SVM boundary S3, gave physical defect energies for all studied defects in anatase and rutile TiO2, as illustrated in Fig. 9(a). Comparing the DFT-, DFT+U- (U = 2.575 eV, c1 = 0.752 and c2 = −0.486) and hybrid-DFT predicted defect energies, the DFT+U-predicted ΔEOV in anatase (5.42 eV) and rutile (5.48 eV) are both much closer to the corresponding values computed using hybrid-DFT (5.29 and 5.76 eV, respectively) than those computed using DFT (4.44 and 4.43 eV, respectively). Without the application of a Hubbard correction to the dopant atom d orbitals, there was no obvious trend in the raw DFT+U-predicted substitutional defect energies when compared to hybrid-DFT. However, when normalised with respect to ΔEOV in the same TiO2 polymorph, the DFT+U-predicted values of ΔEdefect were closer to the corresponding hybrid-DFT-predicted values then DFT, as illustrated in Fig. 9(b), which shows the relative defect energies for Pt- and Pd-doped anatase and rutile TiO2 computed using DFT, DFT+U and hybrid-DFT (single point calculations using the DFT+U geometry). The blue columns in Fig. 9(c) plot the cost of the hybrid-DFT single-point calculation in core-hours per atom, relative to the cost of the DFT+U geometry optimisation. For the four systems presented in Fig. 9(b), DFT+U with geometry optimisation is between 79–189× faster than the hybrid-DFT single-point calculations.
The degree of defect state localisation in W-doped rutile TiO2, given by the energy gap between the localised state and the TiO2 conduction band minimum, is predicted as 0.46 eV using DFT+U and 1.76 eV using hybrid-DFT. As illustrated by the charge density isosurfaces of the highest occupied molecular orbital (HOMO) predicted by DFT in Fig. 10(d) and DFT+U in Fig. 10(e), DFT predicts both W 5d and Ti 3d states to be delocalised, i.e., predicting W6+ formation, whilst DFT+U predicts a hybridised defect state of W 5d and Ti 3d character, indicating the predicted formation of W5+. Similarly, DFT+U simulations of Nb-doped rutile TiO2 predict a Nb 4d signature at the Fermi level that is 5.5× larger than that in Nb-doped anatase TiO2. The results support previous work using EPR spectroscopy to characterise the formation of paramagnetic Nb4+ and W5+ in doped rutile TiO2, which is recoverable using self-consistent DFT+U as opposed to standalone DFT or constrained DFT+U using OMC.67
More generally, the DFT+U simulations reveal clear differences in the electronic structures of substitutionally doped anatase and rutile TiO2, particularly in the occupancies of the dopant atom d orbitals, as illustrated in Fig. 11(a). In rutile TiO2, there are greater occupancies of the dopant atom eg orbitals (m = 0 and 2)60 than in anatase, indicating a structural and electronic environment that favours the filling of orbitals aligned along the metal–oxygen bonds. Conversely, substitutionally doped anatase TiO2 shows increased occupancies of the dopant atom t2g orbitals (m = −2, −1 and 1)60 reflecting a local electronic environment that favours the filling of orbitals aligned between the metal–oxygen bonds. The formation of localised vs. delocalised defects states is directly affected by the filling of the eg and t2g orbitals, respectively, leading to polymorph-sensitivity in the electrical conductivity and chemical reactivity of TiO2-based materials.67 Localised defect states within the TiO2 band gap (or present at the valence or conduction band edges), as observed for Nb- and W-doped rutile in Fig. 11(c) and (d), respectively, and both TiO2 polymorphs containing an oxygen vacancy and Au, Pd, Pt, Co and Mn dopants in Fig. 11(b), (e)–(i), respectively, give rise to electronic conduction via thermally activated polaron hopping (conductivity increases with temperature) and provide readily available sites for activating reactant molecules.92,93 Conversely, delocalised defect states located deeper in the valence or conduction bands, as observed for Nb- and W-doped anatase in Fig. 11(c) and (d), respectively, give rise to improved electronic conductivity according to a band-like model and can both reduce the degrading recombination of electrons and holes in solar cells and lower the rate determining step of the oxygen evolution reaction on rutile TiO2 surfaces.94,95
3.3 Optimising Hubbard U values and projectors from first-principles
To investigate how best to construct a first-principles cost function (JFP), the DFT+U-predicted Ti 3d and O 2p orbital occupancies in anatase and rutile TiO2, using a refined and atomic Ti 3d Hubbard projector, were compared with the occupancies calculated using hybrid-DFT, as illustrated in Fig. 12. Fig. 12(a) and (c) show that DFT+U using an atomic Ti 3d Hubbard projector predicts Ti 3d orbital occupancies closer to those calculated using hybrid-DFT, although this is expected as the hybrid-DFT-calculated occupancies are derived from the atomic Ti 3d Hubbard projector and so cannot be compared in a like-for-like manner to those derived from a modified Hubbard projector (detailed in the SI Section S1.3). Fig. 12(b) and (d) show that DFT+U using the refined Ti 3d Hubbard projector predicts O 2p orbital occupancies closer to those predict using hybrid-DFT, with errors <5% for all values of m, which is a like-for-like comparison as the O 2p orbital occupancies are derived from the atomic O 2p Hubbard projector across all methods (detailed in the SI Section S1.3). The first-principles cost function was therefore defined as the average error in the DFT+U-predicted O 2p orbital occupancies vs. hybrid-DFT (defined in Section 2.3.1), which is obtained from a single reference calculation of a geometry optimised unit cell. To investigate the requirement for SVM constraints in a first-principles approach for optimising Hubbard U values and projectors, the dataset for classifying the validity of bulk oxygen vacancy calculations in anatase TiO2 (Fig. 12(e)) was considered again in terms of percentage errors of Tr[n(Ti 3d)] and Tr[n(O 2p)] vs. hybrid-DFT (Fig. 12(f)). Fig. 12(f) shows that minimising JFP towards zero is necessary but not a sufficient condition to ensure the numerical stability of point defect calculations in anatase TiO2, highlighting the requirement of satisfying SVM-derived constraints as well as minimising JFP for accurate Hubbard parameter optimisation.
 | ||
| Fig. 12 Comparing the percentage errors of the DFT+U-predicted Ti 3d and O 2p orbital occupancies in anatase and rutile TiO2vs. hybrid-DFT (PBE0 density functional); (a) Ti 3d in anatase TiO2, (b) O 2p in anatase TiO2, (c) Ti 3d in rutile TiO2 and (d) O 2p in rutile TiO2. Blue bars correspond to DFT+U using the mBEEF density functional, U = 2.575, c1 = 0.752 and c2 = −0.486. Red bars correspond to DFT+U using the mBEEF density functional, U = 2.575, c1 = 1 and c2 = 0. The same outcomes of bulk oxygen vacancy calculations plotted in Fig. 7 are plot in (e) and (f), where (e) is plotted in terms of the raw U, Tr[n(Ti 3d)] and Tr[n(O 2p)] values, whilst (f) is plotted in terms of U and the percentage errors of Tr[n(Ti 3d)] and Tr[n(O 2p)] vs. hybrid-DFT. | ||
In the following sections, we outline the generalisation of both the regression and classification methods adopted in Section 3.2, extending them towards the development of a single unified model that can automatically parameterise Hubbard U values and projectors from material-dependent inputs, i.e., in the spirit of a foundation model for DFT+U parameterisation. This serves as a test of how well the insights gained from TiO2 transfer across chemical space, with the ultimate goal of enabling accurate, self-consistent simulations of defects and polarons across a broad range of TMOs and REOs. We note that such a framework could equally be formulated as an iterative active learning scheme for systems that are difficult to incorporate within a single unified model, as outlined in Section 4.2.
To investigate the relationship between the residuals in Fig. 13(a) and the size of the training set per material, the MAE was compared with DM (both averaged per material) to quantify whether Hubbard projector optimisation is interpolative or extrapolative. As illustrated in Fig. 13(b), the generalised approach is more interpolative for anatase TiO2, rutile TiO2 and ZrO2, which have the three smallest values of DM. Large values of DM, as seen for CeO2, Cu2O and LiCoO2, indicate the generalised approach is comparatively extrapolative for these materials. As there is no correlation between the MAE and DM, the larger residuals in Fig. 13(a) for ZrO2 and MoO3 do not appear to be related to the training set size and are likely due to the choice of primary features used in HI-SISSO, such as the lack of structure-dependent features, and requires further study to enhance the method transferability.
| S4 ≥ 0 ∧ S5 ≥ 0 | (15) |
Literature reported DFT+U studies, in a planewave basis, have yet to provide an unambiguous rationale for the increased electrical conductivity of Mg-doped LiCoO2, with significant sensitivity of the DFT+U-predicted localisation of Co4+ holes with respect to the choice of Hubbard parameters. For example, DFT+U using a Co 3d Hubbard U value determined from first-principles using LR-cDFT (between 4.91 eV to 5.62 eV) predicts deep Co 3d defect states within the LiCoO2 band gap, which is inconsistent with the experimentally observed high electrical conductivity of LiCo1−xMgxO2, whilst DFT+U using smaller Hubbard U values predicts shallow defect states, supporting the experimental observations.5,104 Whilst no explanation for the sensitivity of DFT+U simulations of LiCo1−xMgxO2 was given, Hoang and Johannes used DFT+U to simulate the self-trapping of Ni4+ holes in LiNiO2, where the DFT+U-predicted instability of Ni4+ was attributed to the predicted O 2p character of the LiNiO2 valence band edge, highlighting the importance of considering band edge effects when choosing appropriate Hubbard parameters.105
To test the DFT+U-predicted localisation of hole polarons in LiCo1−xMgxO2 in a NAO framework, the one-shot approach was first applied to determine an appropriate Co 3d Hubbard U value and projector for stoichiometric LiCoO2. The parameters were determined using a linear search of the HI-SISSO-predicted cost function (JFPpredicted) for U between 0 eV and 5 eV, c1 between 0.5 and 1 and c2 between 0 and -0.6, before all Hubbard parameters that violate eqn (15) were discarded. The output of this initial screening is a region of the Hubbard parameter space (U, c1 and c2) that minimises JFPpredicted and satisfies eqn (15) but contains multiple possible solutions. We therefore narrow this region down to three candidate Hubbard parameters for validation using K-means clustering of a reduced subset of the screened Hubbard parameter space that corresponds to the lowest 10% of JFPpredicted (illustrated in the SI Section S2.2.2).
From the three candidate Hubbard parameters determined using K-means clustering, DFT+U using U = 3.342 eV, c1 = 0.792 and c2 = −0.506, which is henceforth referred to as “refined-DFT+U”, provided the best accuracy in the predicted Ebg (4.18 eV), V0 (97.38 Å3) and ΔEform (−2.40 eV per atom) after validating against experimental references (listed in the SI Section S2.2.2). Comparing the DFT+U-predicted electronic structure of stoichiometric LiCoO2 using refined-DFT+U and U = 3.342 eV, c1 = 1 and c2 = 0 (i.e., the same Co 3d Hubbard U value with an atomic projector, which is henceforth referred to as “atomic-DFT+U”), projector refinement was found to be essential to predict the mixed Co 3d and O 2p valence band edge character of LiCoO2 in Fig. 15(a), which is also predicted using hybrid-DFT and reported experimentally.106 Conversely, DFT+U using atomic-DFT+U, or a much larger Hubbard U value than in Fig. 15(a), both predict the LiCoO2 valence band edge to be dominated by O 2p states, as illustrated in Fig. 15(b).
The defective LiCoO2 bulk containing 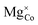 was simulated using both refined-DFT+U and atomic-DFT+U, using the OMR method with the 3dz2 orbital occupancy of the Co atom nearest the Mg dopant reduced by 1 to initialise Co4+. In both simulations, SCF convergence and geometry optimisation completed successfully without termination or charge sloshing. Both simulations also predict the formation of shallow defect states at the top of the valence band in Fig. 16(b), corresponding to a delocalised hole polaron that exists hybridised between Co 3d and O 2p states using refined-DFT+U in Fig. 16(d), compared to non-hybridised across only O atoms using atomic-DFT+U in Fig. 16(e). These differences in the DFT+U-predicted character of the hole polaron also directly affect their stability, with ΔEdefect = 1.48 eV using refined-DFT+U and ΔEdefect = 10.89 eV using atomic-DFT+U. Given that compositions with a 1
was simulated using both refined-DFT+U and atomic-DFT+U, using the OMR method with the 3dz2 orbital occupancy of the Co atom nearest the Mg dopant reduced by 1 to initialise Co4+. In both simulations, SCF convergence and geometry optimisation completed successfully without termination or charge sloshing. Both simulations also predict the formation of shallow defect states at the top of the valence band in Fig. 16(b), corresponding to a delocalised hole polaron that exists hybridised between Co 3d and O 2p states using refined-DFT+U in Fig. 16(d), compared to non-hybridised across only O atoms using atomic-DFT+U in Fig. 16(e). These differences in the DFT+U-predicted character of the hole polaron also directly affect their stability, with ΔEdefect = 1.48 eV using refined-DFT+U and ΔEdefect = 10.89 eV using atomic-DFT+U. Given that compositions with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio of Co and Mg, i.e., LiCo0.5Mg0.5O2, have been synthesised experimentally,107 DFT+U with the default atomic Co 3d Hubbard projector therefore incorrectly predicts the total insolubility of Mg in LiCoO2.
1 ratio of Co and Mg, i.e., LiCo0.5Mg0.5O2, have been synthesised experimentally,107 DFT+U with the default atomic Co 3d Hubbard projector therefore incorrectly predicts the total insolubility of Mg in LiCoO2.
Both refined- and atomic-DFT+U were further used to simulate a bulk oxygen vacancy in Mg-doped LiCoO2 using the OMR method. Here, the nearest O atom to the Mg dopant was removed and the two nearest Co atoms to the vacancy were initialised as Co2+ by increasing their 3dyz orbital occupancies by 1. With the atomic Co 3d Hubbard projector, the simulation did not converge due to charge sloshing, i.e., oscillations in the charge density illustrated in the SI Section S2.2.2, similar to TiO2 in Section 3.1.2. Conversely, DFT+U using the refined Co 3d Hubbard projector successfully converged without termination or charge sloshing, predicting a deep defect state of 3dx2−y2 character and an associated oxygen vacancy formation energy of ΔEOV = 3.61 eV. These results suggest that both Mg-doping and oxygen vacancy formation could enhance the electrical conductivity of LiCoO2via the transport of delocalised hole and localised electron polarons, respectively, whilst the generalised approach for optimising the Co 3d Hubbard U value and projector is robust with respect to numerical instability that is often observed when using the default atomic Hubbard projector. These results give promise to the development of the first-principles approach by extending the size and diversity of the training set used for generalised regression and classification.
4 Future work
Whilst we have demonstrated how supervised machine learning can be applied to simultaneously optimise Hubbard U values and projectors to improve the accuracy and numerical stability of DFT+U in a NAO framework, we note clear avenues for further research that are not accounted for in the current work.4.1 Extension to challenging open-shell systems
The methods and results presented generally hold well for closed-shell systems or those with ions in a low-spin state. In contrast, we encountered significant challenges applying DFT+U to open-shell systems containing ions in a high spin state, e.g., Co2+ in CoO, Mn4+ in MnO2, Fe3+ in Fe2O3 and Cr3+ in Cr2O3. For these materials, DFT+U was found to consistently suffer from SCF non-convergence as a result of charge sloshing, i.e., excessive oscillations in the charge density, which even occurred during single point calculations of small unit cells, irrespective of the chosen Hubbard U values and projectors. Upon analysing the DFT-predicted ground state electronic structures for these materials, all cases are incorrectly predicted to be metallic with zero band gap, therefore we hypothesise that the starting electronic structure from DFT makes SCF convergence for DFT+U very challenging in a NAO framework. After further testing, we find that switching to spin polarisation in combination with meta-GGA exchange–correlation density functionals and carefully selected SCF mixing parameters can improve the DFT-predicted electronic structure to restore a bandgap (albeit which is underestimated compared to experiment). These changes make the convergence of DFT+U with refined Hubbard projectors feasible and will be the focus of a future study translating this work to defects in magnetic TMOs and REOs. Whilst this remains an unresolved challenge at the moment, we note that the restoration of semiconducting or insulating ground states from an initial DFT-predicted metallic state is routinely achievable in planewave implementations of DFT+U,108 therefore a more detailed investigation into exact differences between implementations may help.4.2 Universal models vs. active learning
In Section 3.3, we outline the development of a single universal model for parameterising Hubbard U values and projectors across materials. This approach served as a test for how well the insights gained from TiO2 transfer across chemical space, with the ultimate goal of enabling accurate, self-consistent simulations of defects and polarons across a broad range of TMOs and REOs. A valid alternative approach could be an iterative active learning scheme, where U, c1 and c2 are progressively refined so that the DFT+U-predicted electronic structure resembles that from hybrid-DFT, e.g., via comparison of orbital occupation numbers or band structures. This active learning approach may work well for systems that are not accurately incorporated within a single universal model, but would require repeating for different materials and incur a potentially significant cost for the total number of DFT+U calculations required. We have shown that Bayesian optimisation can efficiently sample a SISSO-derived semi-empirical cost function in Section 3.2.2, therefore this could be repurposed to iteratively perform DFT+U geometry optimisation calculations for a small unit cell, sampling Hubbard parameters and targeting orbital occupancies calculated using hybrid-DFT. If the cost function landscape is very difficult to optimise with an iterative approach, both the universal and active learning schemes could be combined, i.e., the outputs from the one-shot approach used as initial positions for active learning, which may improve convergence to good solutions whilst requiring fewer DFT+U iterations.4.3 Compatibility with high-throughput simulations
The current framework outputs several combinations of Hubbard U values and projectors, which serve as optimised candidate parameters for validation with the aim of enabling self-consistent defect simulations. Further development into a high-throughput optimisation requires an improvement in accuracy of the generalised symbolic regression model on out-of-training data, which should be feasible since this work considers a very small training set of 197 sets of DFT+U-calculated orbital occupancies from geometry optimised unit cells, of which nearly half correspond to TiO2. With a better extrapolative accuracy, the generalised approach could be used to output a single Hubbard parameter, rather than relying on K-means clustering to output several candidate parameters for further validation. The reliance on small unit cells further reduces the computational overhead associated with generating corresponding hybrid-DFT reference data.4.4 Choice of high-level reference and extension to other codes
In the current work, we chose hybrid-DFT as the high-level reference method to obtain target orbital occupancies for metal d or f and O 2p states. This choice was made in order to establish a consistent and computationally tractable benchmark against which machine learning-optimised U values and projectors could be compared. While this introduces a dependency on the choice of reference, it is entirely possible within our framework to select another level of theory depending on the target material and available computational resources. The framework could equally be extended to optimise against alternative physics-informed quantities, e.g., minimising errors in band structure plots, enforcing piecewise linearity of the total energy with respect to fractional occupancy of the correlated subspace, or maximising occupation matrix idempotency. In the case of magnetic systems, for which identifying the true ground state is complicated by the presence of metastable states in the potential energy surface, one could instead target experimentally observed magnetic orderings as the optimisation criteria.The methods presented could also be extended to other electronic structure codes, for which there already exist several schemes that require simultaneous parameter optimisation, e.g., DFT+U+V and orbital resolved DFT+U.32,109 In such frameworks, rather than tuning linear expansion coefficients as in our NAO-based approach, one would instead adjust the definition of the Hubbard projector via the projector augmented wave (PAW) augmentation radius in a planewave basis,17 or the muffin-tin radius in a linear augmented planewave (LAPW) basis, both of which have been reported to significantly influence the predicted geometric, energetic and electronic properties of complex oxides.16,110 Direct adaptation of the framework for other electronic structure codes will be essential, as Hubbard parameters are generally not transferable across codes with different basis sets and definitions of the Hubbard projector. As discussed by Kick et al., DFT+U in a NAO framework typically requires U values ∼1–2 eV smaller than other formalisms to achieve comparable charge localisation.15 The observation agrees with the results of this work concerning Ti 3d Hubbard parameters for simulating TiO2 (U = ∼ 2.5–3 eV) vs. literature reported values computed in a real-space formalism (U = ∼ 5–6 eV).111
5 Conclusions
To navigate the numerical instability of self-consistent DFT+U simulations of TMOs and REOs, including the prediction of erroneous metallic ground states and the termination or non-convergence of point defect calculations, it is essential to carefully define an appropriate Hubbard projector. Simultaneous optimisation of the Hubbard U value and projector has been demonstrated semi-empirically using SR and SVMs, before using BO to minimise the errors of target properties relative to experimental references. The Ti 3d Hubbard U value and projector have been semi-empirically refined to enable self-consistent DFT+U simulations of intrinsic and extrinsic defects in both anatase and rutile TiO2. The outcome is DFT+U simulations with comparable accuracy to hybrid-DFT in terms of the relative stabilities of point defects and the formation of localised Holstein polarons, but at orders of magnitude lower cost. The DFT+U-predicted occupation matrices reproduce the hybrid-DFT O 2p occupation matrix, which can be an effective cost function for a first-principles strategy for Hubbard U value and projector optimisation.The semi-empirical approach was therefore defined as a first-principles approach and generalised across materials using hierarchical SR to screen the Hubbard parameter space using empirical correlations to learn the DFT+U potential energy surface in terms of orbital occupancies. Predictions of metal d or f orbital and O 2p orbital occupancies were made in terms of Hubbard parameters, basis set parameters, DFT-predicted orbital occupancies and atomic material descriptors. The first-principles approach enables the development of a generalised workflow for the one-shot computation of Hubbard U values and projectors for different materials that requires no successive DFT+U calculations, as in active learning schemes. The method transferability is demonstrated for 10 prototypical TMOs and REOs (anatase and rutile TiO2, Cu2O, MoO3, WO3, Y2O3, ZrO2, CeO2, LiCoO2 and LiFePO4), which each require one reference DFT and hybrid-DFT calculation as inputs, whilst generating families of solutions for each material, i.e., optimised Hubbard projectors for a given Hubbard U value. Upon validating a subset of these solutions, a MAE of 5.02% for the DFT+U-predicted O 2p orbital occupancies was achieved, with demonstrated accuracy for materials unseen from model training (LiCoO2 and LiFePO4).
Predicting the numerical stability of point defect calculations can also be generalised across materials using symbolic classification, using Hubbard U values and material-dependent descriptors of covalency, enabling the determination of Hubbard U values and projectors that are robust against numerical instability. The validity of Hubbard U values and projectors determined from first-principles has been investigated for the self-consistent simulation of Mg-doped and oxygen deficient LiCoO2, where refining the Co 3d Hubbard projector enables the numerically stable simulation of experimentally reported charge compensation mechanisms driving the material's high electrical conductivity. The same results were not possible using an atomic Co 3d Hubbard projector and did not require any prior testing of suitable Co 3d Hubbard U values or projectors, which gives promise for the development of a foundational tool for simultaneously determining multiple Hubbard parameters in a NAO framework and beyond. The work demonstrates how advanced machine learning algorithms can aid the development of inexpensive and transferable workflows for DFT+U parameterisation, achieving extrapolative accuracy beyond the limits of small training sets, for more accurate and efficient simulations of complex energy materials.
Author contributions
All authors contributed to the conceptualisation of the project and to software choices and method development in this work. AC performed the electronic structure calculations presented in this work and performed the analysis of results. All authors contributed to the preparation of the manuscript.Conflicts of interest
There are no conflicts to declare.Data availability
All Python scripts for global optimisation, datasets for regression/classification and input/output files for electronic structure calculations have been uploaded to the GitHub repository https://github.com/amitmc1/Hubbardprojectors, with an archived version accessible at the DOI: https://doi.org/10.5281/zenodo.17454878.Supplementary information: information on the determination of DFT and DFT+U parameters, settings and outputs for machine learning methods, and combined application in a first-principles screening approach for the DFT+U parameters. See DOI: https://doi.org/10.1039/d5dd00292c.
Acknowledgements
We thank Harald Oberhofer, Matthias Kick, and Maximilian Brand for valuable scientific discussions regarding the implementation of DFT+U in FHI-aims. We also acknowledge funding by the Prosperity Partnership project Sustainable Catalysis for Clean Growth, funded by the UK Engineering and Physical Sciences Research Council (EPSRC), bp through the bp International Centre for Advanced Materials (bp-ICAM) and Johnson Matthey plc in collaboration with Cardiff University and The University of Manchester (EPSRC grant number EP/V056565/1). A. J. L. acknowledges funding by the UKRI Future Leaders Fellowship program (MR/T018372/1 and MR/Y034279/1). We acknowledge computational resources and support from the Supercomputing Wales project, which is part-funded by the European Regional Development Fund (ERDF) via the Welsh Government; and the UK National Supercomputing Services ARCHER and ARCHER2, accessed via membership of the Materials Chemistry Consortium, which is funded by Engineering and Physical Sciences Research Council (EP/L000202/1, EP/R029431/1 and EP/T022213/1).Notes and references
- K. Chang, H. Zhang, M.-j. Cheng and Q. Lu, Application of Ceria in CO2 Conversion Catalysis, ACS Catal., 2020, 10, 613–631 CrossRef.
- A. Avani and E. Anila, Recent advances of MoO3 based materials in energy catalysis: Applications in hydrogen evolution and oxygen evolution reactions, Int. J. Hydrogen Energy, 2022, 47, 20475–20493 CrossRef.
- M. Lindley, P. Stishenko, J. W. M. Crawley, F. Tinkamanyire, M. Smith, J. Paterson, M. Peacock, Z. Xu, C. Hardacre, A. S. Walton, A. J. Logsdail and S. J. Haigh, Tuning the Size of TiO2-Supported Co Nanoparticle Fischer–Tropsch Catalysts Using Mn Additions, ACS Catal., 2024, 14, 10648–10657 CrossRef.
- A. Folli, J. Z. Bloh, A. Lecaplain, R. Walker and D. E. Macphee, Properties and photochemistry of valence-induced-Ti3+ enriched (Nb,N)-codoped anatase TiO2 semiconductors, Phys. Chem. Chem. Phys., 2015, 17, 4849–4853 RSC.
- J. A. Santana, J. Kim, P. R. C. Kent and F. A. Reboredo, Successes and failures of Hubbard-corrected density functional theory: The case of Mg doped LiCoO2, J. Chem. Phys., 2014, 141, 164706 CrossRef.
- W. Kohn and L. J. Sham, Self-Consistent Equations Including Exchange and Correlation Effects, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- W. Kohn, A. D. Becke and R. G. Parr, Density Functional Theory of Electronic Structure, J. Phys. Chem., 1996, 100, 12974–12980 CrossRef CAS.
- N. L. Nguyen, N. Colonna, A. Ferretti and N. Marzari, Koopmans-Compliant Spectral Functionals for Extended Systems, Phys. Rev. X, 2018, 8, 021051 Search PubMed.
- J. P. Perdew and A. Zunger, Self-interaction correction to density-functional approximations for many-electron systems, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 5048–5079 CrossRef CAS.
- M. Reticcioli, U. Diebold and C. Franchini, Modeling polarons in density functional theory: lessons learned from TiO2, J. Condens. Matter Phys., 2022, 34, 204006 CrossRef CAS.
- H. J. Kulik, Perspective: Treating electron over-delocalization with the DFT+U method, J. Chem. Phys., 2015, 142, 240901 CrossRef PubMed.
- M. Capdevila-Cortada, Z. Łodziana and N. López, Performance of DFT+U Approaches in the Study of Catalytic Materials, ACS Catal., 2016, 6, 8370–8379 CrossRef CAS.
- D. S. Lambert and D. D. O'Regan, Use of DFT + U + J with linear response parameters to predict non-magnetic oxide band gaps with hybrid-functional accuracy, Phys. Rev. Res., 2023, 5, 013160 CrossRef CAS.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+U study, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509 CrossRef CAS.
- M. Kick, K. Reuter and H. Oberhofer, Intricacies of DFT+U, Not Only in a Numeric Atom Centered Orbital Framework, J. Chem. Theory Comput., 2019, 15, 1705–1718 CrossRef CAS.
- K. Park, M. Raman, A.-J. Olatunbosun and J. Pohlmann, Revisiting DFT+U calculations of TiO2 and the effect of the local-projection size, AIP Adv., 2024, 14, 065114 CrossRef CAS.
- Z. Wang, C. Brock, A. Matt and K. H. Bevan, Implications of the DFT + U method on polaron properties in energy materials, Phys. Rev. B, 2017, 96, 125150 CrossRef.
- I. Timrov, N. Marzari and M. Cococcioni, Self-consistent Hubbard parameters from density-functional perturbation theory in the ultrasoft and projector-augmented wave formulations, Phys. Rev. B, 2021, 103, 045141 CrossRef CAS.
- D. D. O'Regan, N. D. M. Hine, M. C. Payne and A. A. Mostofi, Projector self-consistent DFT + U using nonorthogonal generalized Wannier functions, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 081102 CrossRef.
- Y.-Y. Ting and P. M. Kowalski, Refined DFT+U method for computation of layered oxide cathode materials, Electrochim. Acta, 2023, 443, 141912 CrossRef.
- G. L. Murphy, Z. Zhang, R. Tesch, P. M. Kowalski, M. Avdeev, E. Y. Kuo, D. J. Gregg, P. Kegler, E. V. Alekseev and B. J. Kennedy, Tilting and Distortion in Rutile-Related Mixed Metal Ternary Uranium Oxides: A Structural, Spectroscopic, and Theoretical Investigation, Inorg. Chem., 2021, 60, 2246–2260 CrossRef.
- I. Timrov, F. Aquilante, L. Binci, M. Cococcioni and N. Marzari, Pulay forces in density-functional theory with extended Hubbard functionals: From nonorthogonalized to orthogonalized manifolds, Phys. Rev. B, 2020, 102, 235159 CrossRef.
- O. Y. Long, G. Sai Gautam and E. A. Carter, Evaluating optimal U for 3d transition-metal oxides within the SCAN+U framework, Phys. Rev. Mater., 2020, 4, 045401 CrossRef.
- L. Wang, T. Maxisch and G. Ceder, Oxidation energies of transition metal oxides within the GGA + U framework, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 195107 CrossRef.
- M. Cococcioni and S. de Gironcoli, Linear response approach to the calculation of the effective interaction parameters in the LDA + U method, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035105 CrossRef.
- I. Timrov, N. Marzari and M. Cococcioni, Hubbard parameters from density-functional perturbation theory, Phys. Rev. B, 2018, 98, 085127 CrossRef.
- M. Springer and F. Aryasetiawan, Frequency-dependent screened interaction in Ni within the random-phase approximation, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 4364–4368 CrossRef.
- N. J. Mosey, P. Liao and E. A. Carter, Rotationally invariant ab initio evaluation of Coulomb and exchange parameters for DFT+U calculations, J. Chem. Phys., 2008, 129, 014103 CrossRef.
- L. A. Agapito, S. Curtarolo and M. Buongiorno Nardelli, Reformulation of DFT + U as a Pseudohybrid Hubbard Density Functional for Accelerated Materials Discovery, Phys. Rev. X, 2015, 5, 011006 Search PubMed.
- G. C. Moore, M. K. Horton, E. Linscott, A. M. Ganose, M. Siron, D. D. O'Regan and K. A. Persson, High-throughput determination of Hubbard U and Hund J values for transition metal oxides via the linear response formalism, Phys. Rev. Mater., 2024, 8, 014409 CrossRef.
- K. Yu and E. A. Carter, Communication: Comparing ab initio methods of obtaining effective U parameters for closed-shell materials, J. Chem. Phys., 2014, 140, 121105 CrossRef PubMed.
- E. Macke, I. Timrov, N. Marzari and L. C. Ciacchi, Orbital-Resolved DFT+U for Molecules and Solids, J. Chem. Theory Comput., 2024, 20, 4824–4843 CrossRef PubMed.
- C. Ricca, I. Timrov, M. Cococcioni, N. Marzari and U. Aschauer, Self-consistent site-dependent DFT+U study of stoichiometric and defective SrMnO3, Phys. Rev. B, 2019, 99, 094102 CrossRef.
- M. Yu, S. Yang, C. Wu and N. Marom, Machine learning the Hubbard U parameter in DFT+ U using Bayesian optimization, npj Comput. Mater., 2020, 6, 180 CrossRef CAS.
- W. Yu, Z. Zhang, X. Wan, H. Guo, Q. Gui, Y. Peng, Y. Li, W. Fu, D. Lu, Y. Ye and Y. Guo, Active Learning the High-Dimensional Transferable Hubbard U and V Parameters in the DFT+U+V Scheme, J. Chem. Theory Comput., 2023, 19, 6425–6433 CrossRef CAS PubMed.
- P. Tavadze, R. Boucher, G. Avendaño-Franco, K. X. Kocan, S. Singh, V. Dovale-Farelo, W. Ibarra-Hernández, M. B. Johnson, D. S. Mebane and A. H. Romero, Exploring DFT+U parameter space with a Bayesian calibration assisted by Markov chain Monte Carlo sampling, npj Comput. Mater., 2021, 7, 182 CrossRef CAS.
- G. Cai, Z. Cao, F. Xie, H. Jia, W. Liu, Y. Wang, F. Liu, X. Ren, S. Meng and M. Liu, Predicting structure-dependent Hubbard U parameters via machine learning, Mater. Futures, 2024, 3, 025601 CrossRef.
- M. Uhrin, A. Zadoks, L. Binci, N. Marzari and I. Timrov, Machine learning Hubbard parameters with equivariant neural networks, npj Comput. Mater., 2025, 11, 19 CrossRef PubMed.
- L. Foppa, T. A. R. Purcell, S. V. Levchenko, M. Scheffler and L. M. Ghiringhelli, Hierarchical Symbolic Regression for Identifying Key Physical Parameters Correlated with Bulk Properties of Perovskites, Phys. Rev. Lett., 2022, 129, 055301 CrossRef CAS PubMed.
- V. Blum, R. Gehrke, F. Hanke, P. Havu, V. Havu, X. Ren, K. Reuter and M. Scheffler, Ab initio molecular simulations with numeric atom-centered orbitals, Comput. Phys. Commun., 2009, 180, 2175–2196 CrossRef CAS.
- A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. B. Jensen, J. Kermode, J. R. Kitchin, E. L. Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. B. Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, The atomic simulation environment—a Python library for working with atoms, J. Phys.: Condens. Matter, 2017, 29, 273002 CrossRef.
- O. Lamiel-Garcia, K. C. Ko, J. Y. Lee, S. T. Bromley and F. Illas, When Anatase Nanoparticles Become Bulklike: Properties of Realistic TiO2 Nanoparticles in the 1–6 nm Size Range from All Electron Relativistic Density Functional Theory Based Calculations, J. Chem. Theory Comput., 2017, 13, 1785–1793 CrossRef CAS PubMed.
- J. Wellendorff, K. T. Lundgaard, K. W. Jacobsen and T. Bligaard, mBEEF: An accurate semi-local Bayesian error estimation density functional, J. Chem. Phys., 2014, 140, 144107 CrossRef.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- S. Lehtola, C. Steigemann, M. J. Oliveira and M. A. Marques, Recent developments in libxc — A comprehensive library of functionals for density functional theory, SoftwareX, 2018, 7, 1–5 CrossRef.
- C. Adamo and V. Barone, Toward reliable density functional methods without adjustable parameters: The PBE0 model, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- X. Ren, P. Rinke, V. Blum, J. Wieferink, A. Tkatchenko, A. Sanfilippo, K. Reuter and M. Scheffler, Resolution-of-identity approach to Hartree–Fock, hybrid density functionals, RPA, MP2 and GW with numeric atom-centered orbital basis functions, New J. Phys., 2012, 14, 053020 CrossRef.
- C. G. Broyden, The Convergence of a Class of Double-rank Minimization Algorithms 1. General Considerations, IMA J. Appl., 1970, 6, 76–90 CrossRef.
- R. Fletcher, A new approach to variable metric algorithms, Comput. J., 1970, 13, 317–322 CrossRef.
- D. F. Shanno, Conditioning of Quasi-Newton Methods for Function Minimization, Math. Comput., 1970, 24, 647–656 CrossRef.
- D. Goldfarb, A Family of Variable-Metric Methods Derived by Variational Means, Math. Comput., 1970, 24, 23–26 CrossRef.
- F. Birch, Finite Elastic Strain of Cubic Crystals, Phys. Rev., 1947, 71, 809–824 CrossRef CAS.
- G. L. Murphy, Z. Zhang, R. Tesch, P. M. Kowalski, M. Avdeev, E. Y. Kuo, D. J. Gregg, P. Kegler, E. V. Alekseev and B. J. Kennedy, Tilting and distortion in rutile-related mixed metal ternary uranium oxides: a structural, spectroscopic, and theoretical investigation, Inorg. Chem., 2021, 60, 2246–2260 CrossRef CAS.
- K. O. Kvashnina, P. M. Kowalski, S. M. Butorin, G. Leinders, J. Pakarinen, R. Bès, H. Li and M. Verwerft, Trends in the valence band electronic structures of mixed uranium oxides, Chem. Commun., 2018, 54, 9757–9760 RSC.
- P. M. Kowalski, Z. He and O. Cheong, Electrode and electrolyte materials from atomistic simulations: properties of LixFePO4 electrode and zircon-based ionic conductors, Front. Energy Res., 2021, 9, 653542 CrossRef.
- Y.-Y. Ting and P. M. Kowalski, Refined DFT+U method for computation of layered oxide cathode materials, Electrochim. Acta, 2023, 443, 141912 CrossRef.
- K. Jakob and H. Oberhofer, Master's thesis: Self-Consistency in the Hubbard-Corrected DFT+U Method, Faculty of Chemistry, Technical University of Munich, 2021 Search PubMed.
- W. B. Begna, G. S. Gurmesa and C. A. Geffe, Ortho-atomic projector assisted DFT+U study of room temperature Ferro- and antiferromagnetic Mn-doped TiO2 diluted magnetic semiconductor, Mater. Res. Express, 2022, 9, 076102 CrossRef CAS.
- B. Dorado, B. Amadon, M. Freyss and M. Bertolus, DFT + U calculations of the ground state and metastable states of uranium dioxide, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 235125 CrossRef.
- J. P. Allen and G. W. Watson, Occupation matrix control of d- and f-electron localisations using DFT+U, Phys. Chem. Chem. Phys., 2014, 16, 21016–21031 RSC.
- R. Ouyang, S. Curtarolo, E. Ahmetcik, M. Scheffler and L. M. Ghiringhelli, SISSO: A compressed-sensing method for identifying the best low-dimensional descriptor in an immensity of offered candidates, Phys. Rev. Mater., 2018, 2, 083802 CrossRef.
- T. A. R. Purcell, M. Scheffler, C. Carbogno and L. M. Ghiringhelli, SISSO++: A C++ Implementation of the Sure-Independence Screening and Sparsifying Operator Approach, J. Open Source Softw., 2022, 7, 3960 CrossRef.
- T. A. R. Purcell, M. Scheffler and L. M. Ghiringhelli, Recent advances in the SISSO method and their implementation in the SISSO++ code, J. Chem. Phys., 2023, 159, 114110 CrossRef PubMed.
- Y. Zhang, J. W. Furness, B. Xiao and J. Sun, Subtlety of TiO2 phase stability: Reliability of the density functional theory predictions and persistence of the self-interaction error, J. Chem. Phys., 2019, 150, 014105 CrossRef.
- T. Arlt, M. Bermejo, M. A. Blanco, L. Gerward, J. Z. Jiang, J. Staun Olsen and J. M. Recio, High-pressure polymorphs of anatase TiO2, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 14414–14419 CrossRef.
- M. Setvin, C. Franchini, X. Hao, M. Schmid, A. Janotti, M. Kaltak, C. G. Van de Walle, G. Kresse and U. Diebold, Direct View at Excess Electrons in TiO2 Rutile and Anatase, Phys. Rev. Lett., 2014, 113, 086402 CrossRef.
- A. Chaudhari, A. J. Logsdail and A. Folli, Polymorph-Induced Reducibility and Electron Trapping Energetics of Nb and W Dopants in TiO2, J. Phys. Chem. C, 2025, 129, 15453–15461 CrossRef PubMed.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and E. Duchesnay, Scikit-learn: Machine Learning in Python, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- The GPyOpt authors, GPyOpt: A Bayesian Optimization framework in Python, http://github.com/SheffieldML/GPyOpt, 2016, Accessed June 2024.
- D. R. Jones, M. Schonlau and W. J. Welch, Efficient Global Optimization of Expensive Black-Box Functions, J. Glob. Optim., 1998, 13, 455–492 CrossRef.
- M. D. Mckay, R. J. Beckman and W. J. Conover, A Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output From a Computer Code, Technometrics, 2000, 42, 55–61 CrossRef.
- S. Dalton and D. Richardson, pyDOE: The experimental design package for Python, https://pythonhosted.org/pyDOE/, 2014, Accessed June 2024.
- R. Ramakrishnan, P. O. Dral, M. Rupp and O. A. von Lilienfeld, Big Data Meets Quantum Chemistry Approximations: The -Machine Learning Approach, J. Chem. Theory Comput., 2015, 11, 2087–2096 CrossRef PubMed.
- D.-H. Seo, A. Urban and G. Ceder, Calibrating transition-metal energy levels and oxygen bands in first-principles calculations: Accurate prediction of redox potentials and charge transfer in lithium transition-metal oxides, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 115118 CrossRef.
- P. Mahalanobis, On the Generalised Distance in Statistics, Sankhya, Ser. A, 1936, 80, 1–7 Search PubMed.
- V. I. Anisimov, F. Aryasetiawan and A. I. Lichtenstein, First-principles calculations of the electronic structure and spectra of strongly correlated systems: the LDA+U method, J. Phys.: Condens. Matter, 1997, 9, 767–808 CrossRef.
- B. Himmetoglu, A. Floris, S. de Gironcoli and M. Cococcioni, Hubbard-corrected DFT energy functionals: The LDA+U description of correlated systems, Int. J. Quantum Chem., 2014, 114, 14–49 CrossRef.
- T. Schäfer, N. Daelman and N. López, Cerium Oxides without U: The Role of Many-Electron Correlation, J. Phys. Chem. Lett., 2021, 12, 6277–6283 CrossRef.
- R. song Li, D. qiang Xin, S. qi Huang, Z. jian Wang, L. Huang and X. hua Zhou, A full potential all-electron calculation on electronic structure of NiO, Chin. J. Phys., 2018, 56, 2829–2836 CrossRef.
- G. Gebreyesus, L. Bastonero, M. Kotiuga, N. Marzari and I. Timrov, Understanding the role of Hubbard corrections in the rhombohedral phase of BaTiO3, Phys. Rev. B, 2023, 108, 235171 CrossRef.
- T.-c. Liu, D. Gaines, H. Kim, A. Salgado-Casanova, S. B. Torrisi and C. Wolverton, Anomalous reversal of stability in Mo-containing oxides: A difficult case exhibiting sensitivity to DFT + U and distortion, Phys. Rev. Mater., 2025, 9, 055402 CrossRef.
- S. Phoka, P. Laokul, E. Swatsitang, V. Promarak, S. Seraphin and S. Maensiri, Synthesis, structural and optical properties of CeO2 nanoparticles synthesized by a simple polyvinyl pyrrolidone (PVP) solution route, Mater. Chem. Phys., 2009, 115, 423–428 CrossRef.
- F. B. Baker, E. J. Huber, C. E. Holley and N. Krikorian, Enthalpies of formation of cerium dioxide, cerium sesquicarbide, and cerium dicarbide, J. Chem. Thermodyn., 1971, 3, 77–83 CrossRef.
- M. Kick, C. Grosu, M. Schuderer, C. Scheurer and H. Oberhofer, Mobile Small Polarons Qualitatively Explain Conductivity in Lithium Titanium Oxide Battery Electrodes, J. Phys. Chem. Lett., 2020, 11, 2535–2540 CrossRef.
- M. Kick, C. Scheurer and H. Oberhofer, Formation and stability of small polarons at the lithium-terminated Li4Ti5O12 (LTO) (111) surface, J. Chem. Phys., 2020, 153, 144701 CrossRef.
- J. Aarons, M. Sarwar, D. Thompsett and C.-K. Skylaris, Perspective: Methods for large-scale density functional calculations on metallic systems, J. Chem. Phys., 2016, 145, 220901 CrossRef.
- M. Arrigoni and G. K. H. Madsen, A comparative first-principles investigation on the defect chemistry of TiO2 anatase, J. Chem. Phys., 2020, 152, 044110 CrossRef.
- T. D. Pham and N. A. Deskins, Efficient Method for Modeling Polarons Using Electronic Structure Methods, J. Chem. Theory Comput., 2020, 16, 5264–5278 CrossRef.
- R. Zhang, A. Chutia, A. A. Sokol, D. Chadwick and C. R. A. Catlow, A computational investigation of the adsorption of small copper clusters on the CeO2(110) surface, Phys. Chem. Chem. Phys., 2021, 23, 19329–19342 RSC.
- G. P. Kerker, Efficient iteration scheme for self-consistent pseudopotential calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 3082–3084 CrossRef.
- K. Warda, E. Macke, I. Timrov, L. C. Ciacchi and P. M. Kowalski, Getting the manifold right: The crucial role of orbital resolution in DFT+ U for mixed df electron compounds, arXiv, 2025, preprint, arXiv:2508.16435, DOI:10.48550/arXiv.2508.16435.
- C. Spreafico and J. VandeVondele, The nature of excess electrons in anatase and rutile from hybrid DFT and RPA, Phys. Chem. Chem. Phys., 2014, 16, 26144–26152 RSC.
- C. Bigi, Z. Tang, G. M. Pierantozzi, P. Orgiani, P. K. Das, J. Fujii, I. Vobornik, T. Pincelli, A. Troglia, T.-L. Lee, R. Ciancio, G. Drazic, A. Verdini, A. Regoutz, P. D. C. King, D. Biswas, G. Rossi, G. Panaccione and A. Selloni, Distinct behavior of localized and delocalized carriers in anatase TiO2 (001) during reaction with O2, Phys. Rev. Mater., 2020, 4, 025801 CrossRef.
- P. Nandi, S. Shin, H. Park, Y. In, U. Amornkitbamrung, H. J. Jeong, S. J. Kwon and H. Shin, Large and Small Polarons in Highly Efficient and Stable Organic-Inorganic Lead Halide Perovskite Solar Cells: A Review, Sol. RRL, 2024, 8, 2400364 CrossRef.
- P. Gono, J. Wiktor, F. Ambrosio and A. Pasquarello, Surface Polarons Reducing Overpotentials in the Oxygen Evolution Reaction, ACS Catal., 2018, 8, 5847–5851 CrossRef.
- Y. Huang, Y. Zhu, H. Fu, M. Ou, C. Hu, S. Yu, Z. Hu, C.-T. Chen, G. Jiang, H. Gu, H. Lin, W. Luo and Y. Huang, Mg-Pillared LiCoO2: Towards Stable Cycling at 4.6V, Angew. Chem., Int. Ed., 2021, 60, 4682–4688 CrossRef PubMed.
- J. Xia, N. Zhang, D. Yi, F. Lu, Y. Yang, X. Wang and Y. Wang, Stabilizing 4.6 V LiCoO2 via Er and Mg Trace Doping at Li-Site and Co-Site Respectively, Small, 2024, 20, 2311578 CrossRef.
- M. Mladenov, R. Stoyanova, E. Zhecheva and S. Vassilev, Effect of Mg doping and MgO-surface modification on the cycling stability of LiCoO2 electrodes, Electrochem. Commun., 2001, 3, 410–416 CrossRef.
- S. Levasseur, M. Ménétrier and C. Delmas, On the Dual Effect of Mg Doping in LiCoO2 and Li1+δCoO2: Structural, Electronic Properties, and 7Li MAS NMR Studies, Chem. Mater., 2002, 14, 3584–3590 CrossRef.
- S. Shi, C. Ouyang, M. Lei and W. Tang, Effect of Mg-doping on the structural and electronic properties of LiCoO2: A first-principles investigation, J. Power Sources, 2007, 171, 908–912 CrossRef.
- X. G. Xu, C. Li, J. X. Li, U. Kolb, F. Wu and G. Chen, Electronic Structure of Li(Co, Mg)O2 Studied by Electron Energy-Loss Spectrometry and First-Principles Calculation, J. Phys. Chem. B, 2003, 107, 11648–11651 CrossRef.
- H. Tukamoto and A. R. West, Electronic Conductivity of LiCoO2 and Its Enhancement by Magnesium Doping, J. Electrochem. Soc., 1997, 144, 3164 CrossRef.
- W. Luo, X. Li and J. R. Dahn, Synthesis and Characterization of Mg Substituted LiCoO2, J. Electrochem. Soc., 2010, 157, A782 CrossRef.
- F. Zhou, M. Cococcioni, C. A. Marianetti, D. Morgan and G. Ceder, First-principles prediction of redox potentials in transition-metal compounds with LDA + U, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 235121 CrossRef.
- K. Hoang and M. D. Johannes, Defect chemistry in layered transition-metal oxides from screened hybrid density functional calculations, J. Mater. Chem. A, 2014, 2, 5224–5235 RSC.
- L. Dahéron, H. Martinez, R. Dedryvère, I. Baraille, M. Ménétrier, C. Denage, C. Delmas and D. Gonbeau, Surface Properties of LiCoO2 Investigated by XPS Analyses and Theoretical Calculations, J. Phys. Chem. C, 2009, 113, 5843–5852 CrossRef.
- R. Sathiyamoorthi, P. Shakkthivel, R. Gangadharan and T. Vasudevan, Layered LiCo1-xMgxO2 (x = 0.0, 0.1, 0.2, 0.3 and 0.5) cathode materials for lithium-ion rechargeable batteries, Ionics, 2007, 13, 25–33 CrossRef CAS.
- N. E. Kirchner-Hall, W. Zhao, Y. Xiong, I. Timrov and I. Dabo, Extensive benchmarking of DFT+U calculations for predicting band gaps, Appl. Sci., 2021, 11, 2395 CrossRef CAS.
- I. Timrov, F. Aquilante, M. Cococcioni and N. Marzari, Accurate Electronic Properties and Intercalation Voltages of Olivine-Type Li-Ion Cathode Materials from Extended Hubbard Functionals, Phys. Rev. X, 2022, 1, 033003 Search PubMed.
- Y.-C. Wang, Z.-H. Chen and H. Jiang, The local projection in the density functional theory plus U approach: A critical assessment, J. Chem. Phys., 2016, 144, 144106 CrossRef PubMed.
- S. Bhowmik, A. J. Medford and P. Suryanarayana, Real-space Hubbard-corrected density functional theory, arXiv, 2025, preprint, arXiv:2507.23612, DOI:10.48550/arXiv.2507.23612.
| This journal is © The Royal Society of Chemistry 2025 |