Open Access Article
Open Access ArticlePIL-Net: a physics-informed graph convolutional network for predicting atomic multipoles†
Caitlin
Whitter
 *a,
Alex
Pothen
*a,
Alex
Pothen
 a and
Aurora
Clark
a and
Aurora
Clark
 b
b
aDepartment of Computer Science, Purdue University, 305 N University St., West Lafayette, IN 47907, USA. E-mail: cwhitter@purdue.edu; apothen@purdue.edu
bDepartment of Chemistry, The University of Utah, 315 1400 E, Salt Lake City, UT 84112, USA. E-mail: Aurora.Clark@utah.edu
First published on 16th July 2025
Abstract
We introduce PIL-Net, a physics-informed graph convolutional network capable of predicting molecular properties quickly and with low error, using only basic information about each molecule's atoms and bonds. The PIL-Net model combines the representational power of graph neural networks with domain knowledge to predefine a set of constraints that force the network to make physically consistent predictions; this leads to faster model convergence. We apply PIL-Net to the task of predicting atomic multipoles, which describe the charge distribution within an atom. Atomic multipoles have several applications, including their incorporation into force fields for molecular dynamics simulations. We emphasize our model's ability to predict atomic octupoles, a higher-order atomic multipole property, with a mean absolute error of only 0.0013 eÅ3, more than an order of magnitude less than results reported in the literature. Moreover, our framework can approximate molecular multipole moments post-training with little additional cost. Finally, we elaborate on how our network can be used for greater model interpretability, reconstruction of the molecular electrostatic surface potential, and prediction on out-of-domain datasets.
1 Introduction
Prediction of the properties of atoms in molecules has experienced much interest (and success) within the realm of machine learning. Many atomic and molecular properties are well understood to be influenced by local bonding environments, not the least of which are those associated with the distribution of electrons or charge. The multipole expansion describes the electrostatic potential due to a charge distribution and is expressed as a series of increasingly higher-order charge contributions (i.e., monopoles, dipoles, quadrupoles, octupoles, etc.),1 termed multipole moments. Collectively, multipole moments characterize the long-range interaction between a charge distribution and a reference point.2 As a description of the distribution of electric charge within molecules, multipole moments are essential for describing a number of physicochemical and response properties, e.g., the response to external perturbations such as electromagnetic fields3 and intermolecular interactions (as in the development of force fields).Here we report PIL-Net (Physics-Informed Loss Network), a physics-informed graph convolutional network capable of predicting atomic multipoles within a molecule quickly and with high accuracy, using only basic information about the molecule's atoms and bonds. In particular, we emphasize PIL-Net's ability to predict atomic octupoles, a more rarely predicted higher-order atomic multipole property. The charge distributions of atomic octupoles exhibit complex angular dependencies. As such, reducing the error in atomic octupole predictions can result in more finely-tuned calibrations for computational methods such as force fields. In short, less error in the atomic octupole moment predictions can lead to less error in downstream applications.
The electrostatic potential V at point P(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) due to charge distribution ρ(
) due to charge distribution ρ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ′) is defined as1,4,5
′) is defined as1,4,5
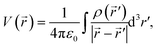 | (1) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ′) denotes the charge distribution at a point P(
′) denotes the charge distribution at a point P(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ′) in the distribution and
′) in the distribution and ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) corresponds to the position vector of a point at a large distance from the charge distribution. The prefactor corresponds to Coulomb's constant, where ε0 is the vacuum permittivity constant. This equation leads to the multipole expansion in spherical coordinates4
corresponds to the position vector of a point at a large distance from the charge distribution. The prefactor corresponds to Coulomb's constant, where ε0 is the vacuum permittivity constant. This equation leads to the multipole expansion in spherical coordinates4 | (2) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ), Vdip(
), Vdip(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ), Vquad(
), Vquad(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ), and Voct(
), and Voct(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) describe the contribution of the monopole, dipole, quadrupole, and octupole terms, respectively, to the electrostatic potential. The variable r corresponds to the distance between the point P(
) describe the contribution of the monopole, dipole, quadrupole, and octupole terms, respectively, to the electrostatic potential. The variable r corresponds to the distance between the point P(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ) and the origin, and θ corresponds to the angle between the
) and the origin, and θ corresponds to the angle between the ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) and
and ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ′ position vectors.
′ position vectors.
The monopole, dipole, quadrupole, and octupole moments associated with an individual atom are termed atomic multipoles, whereas the moments associated with a molecule are termed molecular multipoles. The monopole term represents the total charge of the molecular system, while the dipole describes the separation of positive and negative charge in the system. The quadrupole and octupole, the higher-order terms of the expansion, reveal more complex angular dependencies of the charge distribution.6 While a dipole is formed by placing two monopoles with opposite charges near each other, a quadrupole requires two dipoles with opposite charges, and the octupole follows the same pattern and is constructed from two oppositely-charged quadrupoles.6
Ab initio methods such as Density Functional Theory (DFT) have been commonly used for computing multipole moments and other molecular properties for many decades. They have been shown to accurately calculate atomic and molecular dipoles7 and have been used in the construction of many databases to support machine learning of electron densities and the electrostatic properties of atoms in molecules.5,8–11 Empirical data are increasingly being used to check the validity of calculations and refine calculated potentials, as opposed to being the main source of data for them.2 Following that trend, machine learning has become a popular computational method for fast assignment of properties to molecules. There have been several benchmark datasets constructed for the purpose of molecular property prediction across a broad range of properties.12–22 Researchers have also applied machine learning to a number of other domains, including bioinformatics,23 materials science,24 image classification,25 natural language processing,26 meteorology,27 agriculture,28 and astronomy.29 Most relevant to our PIL-Net model, in order to reduce the cost of computationally expensive ab initio methods, a wide variety of machine learning based approaches have been employed for the prediction of electrostatic properties.30–41 More specifically, prior machine learning models for predicting atomic multipole moments include EGNN5 (graph neural network), DynamPol8 (standard neural network), AIMNet10 (neural network potential), CMPNN9 (message passing neural network), and Δ-ML-85 (ref. 11) (kernel ridge regression). The model architecture used for PIL-Net is based on the graph convolutional network42 construction. Section S1 in the ESI† contains an overview of neural networks and graph convolutional networks. The physics-informed neural network (PINN) employed in this work is a neural network in which biases are introduced to guide the learning process toward a physically consistent configuration.43 Physics-informed neural networks have several scientific applications, including drug discovery,44 stiff chemical kinetic systems,45 and thermo-chemical systems in astrophysical contexts.46 Moreover, in their survey, Willard et al. reference several other methods for incorporating physics-based modeling into machine learning to solve problems in chemistry.47 PIL-Net employs four physics-informed constraints that narrow the search space and accelerate the convergence of the network to a low-error solution. Since PIL-Net's physics-informed constraints are incorporated directly into the model architecture, as opposed to indirectly in the form of loss function penalties, their presence contributes significantly to the interpretability of the model. These constraints are the last computations performed on the model, as well as the last transformations applied to the model predictions prior to applying the loss function. As a result, once a constraint is incorporated, all model predictions are forced to adhere to that constraint, regardless of any model weight optimization procedure. Therefore, given a low-error (or high-error) model, one can assess the relative influence of a particular constraint on model performance by re-training the model and monitoring the impact of adding or removing the constraint on the model's predictive error. PIL-Net's weighted loss function and post-training molecular multipole moment approximations also differentiate PIL-Net from prior methods. We include a comparison between PIL-Net's physics-informed components and those of other machine learning methods for predicting atomic multipoles in Methods subsection 2.4.
In the Results section, we show that the PIL-Net model architecture leads to highly accurate atomic multipole moment predictions, achieving 0.0013 eÅ3 error for the atomic octupole moment property in the QM Dataset for Atomic Multipoles5 (QMDFAM). To demonstrate the transferability of the PIL-Net model to other datasets, we also performed inference on the out-of-domain dataset ANI-1x10,20,48,49 using our PIL-Net models trained on the QMDFAM. Even when making predictions on an unknown dataset, our model's predictive error was up to 1.4× less than that of the Δ-ML-85 (ref. 11) method. Finally, to further demonstrate the utility of using the PIL-Net model for predicting atomic multipole moments, we applied the model to two downstream tasks. We show that the PIL-Net atomic multipole moment predictions can be leveraged to predict corresponding molecular multipole moments post-training with minimal additional cost. The PIL-Net atomic multipole moment predictions can also be used for highly accurate reconstruction of the electrostatic potential on a molecular surface, with an error as small as 0.80 kcal mol−1.
2 Methods
We begin by describing the QM Dataset for Atomic Multipoles (QMDFAM) employed in this work (Subsection 2.1). In Subsection 2.2, we describe the PIL-Net training architecture in detail. QMDFAM informs the particulars behind some PIL-Net architectural decisions, including the physics-informed constraints and the weighted loss function. We next discuss the PIL-Net post-training molecular dipole moment approximation equation (Subsection 2.3). Finally, in Subsection 2.4, we compare the PIL-Net model architecture to that of prior machine learning atomic multipole prediction architectures.2.1 QM Dataset for Atomic Multipoles (QMDFAM)
QMDFAM5 is a molecular dataset consisting of elements H, C, N, O, F, S, and Cl with 1m molecular conformations with up to 20 heavy (non-hydrogen) atoms. The dataset includes atomic number/nuclear charge and Cartesian coordinate information for each atom, as well as corresponding SMILES strings for the molecules. Fig. S1 in the ESI† displays a rendering of a molecule from QMDFAM. The dataset contains several target properties, including atomic monopoles (e), atomic dipoles (eÅ), atomic quadrupoles (eÅ2), and atomic octupoles (eÅ3), as well as molecular dipole moments (eÅ). The e unit refers to the elementary charge (charge on a proton). The atomic multipole moments and molecular dipole moments were derived via the minimal basis iterative Stockholder (MBIS) method at the PBE0-D3BJ/def2-TZVP level of theory. One of many models for atomic multipole assignment, MBIS50 is an atoms-in-molecule method that endeavors to partition the total electron density into atomic contributions. We removed 58 molecular conformations from the dataset that were missing atomic multipole, element, coordinate, and/or SMILES string data.In the QMDFAM, the dimension of each atomic monopole moment vector is 1, atomic dipole moment vector is 3, atomic quadrupole moment vector is 6, atomic octupole moment vector is 10, and molecular dipole moment vector is 3. Prior to model training, the atomic quadrupole and octupole moment vectors are transformed so that their corresponding full tensor representations are traceless. This detracing procedure is described in ESI Section S2†. Additional distribution information about the dataset is displayed in Table S1, Fig. S2 and S3 in the ESI.† As shown in ESI Fig. S2,† the atomic monopoles have the widest distribution of all the atomic multipole moments in the dataset, followed by the dipoles, quadrupoles, and octupoles. ESI Fig. S3† indicates that the dataset molecules are neutral, as the sum of their monopoles is approximately zero for all.
2.2 PIL-Net training architecture
 | ||
| Fig. 2 Detailed view of a PIL-Net module, where k corresponds to the original length of the corresponding feature vector. For example, this value is 3 for the Cartesian coordinate feature. | ||
E(3)-Equivariance. Maintaining E(3)-equivariance in multipole moment prediction is important because moving a single molecule in 3D space should impact its multipole moments in a predictable manner. An E(3)-equivariant model generates representations that preserve the relationship between the function inputs and outputs under translations and rotations in three-dimensional space. For models that belong to the E(3)-equivariant group, if the input (a graph) to the function (a trained model) is translated and/or rotated, then the output (the predictions) must translate and/or rotate in the same manner. PIL-Net is an E(3)-equivariant model because its predictions are derived from the relative distances between the atomic positions, not the atomic positions themselves. As a consequence, the PIL-Net model learns representations that preserve symmetries under translations and rotations. Further detail is provided under the Graph convolution heading within Subsection 2.2.3.
 | (3) |
 is set to one. A smaller interatomic distance will result in a larger kernel value, and a larger interatomic distance will result in a smaller kernel value. This feature can be particularly beneficial for model training when there is an inverse relationship between distance and the target predictive property.
is set to one. A smaller interatomic distance will result in a larger kernel value, and a larger interatomic distance will result in a smaller kernel value. This feature can be particularly beneficial for model training when there is an inverse relationship between distance and the target predictive property.
Beyond nuclear charges and atomic coordinates, we use the dataset SMILES information in tandem with the RDKit software package51 to obtain additional node features and edge features for the molecules in the dataset. These features include atom hybridization state, bond type, bond aromaticity, bond conjugacy, and bond ring membership. The Cartesian coordinates are treated separately from the other node features in the network, and they form their own coordinate features. This brings our total number of features to eight: two node features, five edge features, and one coordinate feature. Using this feature information, one can embed the dataset molecules into a low-dimensional space, providing each molecule with a representation suitable for input into the neural network.
Prior to training, we apply a one-hot encoding to the nuclear charge, hybridization state, and bond type features, since these features are categorical, and we do not want the network to use their magnitude to infer information about each atom's relative importance. We also normalize the training set interatomic distance features to have a mean of zero and a standard deviation of one, so the edge features are not assigned greater importance relative to the other features. We apply this normalization to the validation and test sets as well, using the training set mean and standard deviation. We do not apply further transformations to the three remaining edge features, as they are binary.
Altogether, each molecule has a node feature matrix of size (n × 16), an edge feature matrix of size (m × 26), and a coordinate feature matrix of size (n × 3) associated with it, where n corresponds to the number of atoms in the molecule and m corresponds to the number of bonds. Since the interatomic distance edge feature is a function of the coordinate feature, there may be some redundancies between the two features. In the future, removing the interatomic distance feature might result in a slight speedup in model training, while having minimal effect on model accuracy.
Feature expansions. The input node, edge, and coordinate features [colored gray in Fig. 2] are expanded independently through the application of a fully-connected linear layer with 256 hidden neurons [colored green]. Section 3, the Results section, includes a discussion on PIL-Net hyperparameter selection. This linear layer application is followed by the CELU non-linear activation function [same green-colored blocks]. CELU stands for Continuously Differentiable Exponential Linear Units,52 and is defined as:
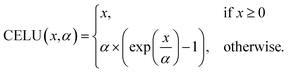 | (4) |
In PIL-Net, α is set to 1.0. CELU is used to enable faster network convergence, since the function has a mean activation near zero and its gradients do not vanish. Additionally, CELU has the benefit of being continuously differentiable for all x.
Graph convolution. Following the transformations from the feature expansion blocks, the node, edge, and coordinate feature representations have the same dimension, 256. Now, in the graph convolution block, the goal is to combine these data so that each atom's updated node feature representation is a function of its neighbors' feature representations. PIL-Net achieves this outcome via a graph convolution [colored pink in Fig. 2] operation. The equation for computing the resulting feature matrix F for a given graph is:
 | (5) |
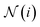 refers to the neighboring nodes of node i (nodes that share an edge with node i). Row index k is given by the function g(i,j), which returns the edge index of the edge incident on nodes i and j.
refers to the neighboring nodes of node i (nodes that share an edge with node i). Row index k is given by the function g(i,j), which returns the edge index of the edge incident on nodes i and j.
Through computing distances and not using absolute coordinates, PIL-Net is invariant with respect to translation and rotation of the input data. If a model is invariant with respect to a certain transformation, the model's output (the predictions) will remain unchanged under the application of that transformation to the model's input (a graph). PIL-Net is also equivariant with respect to the permutation of node indices. If a transformation is applied that permutes the nodes of the input graph, then the output predictions will be permuted in the same manner. It should be noted that invariant operations are also equivariant.
Combined feature expansion and compression. The output from the graph convolution block is an updated node representation. To this new node representation, PIL-Net applies two sets of linear and CELU functions [colored green in Fig. 2]. The first linear layer has 256 neurons and the second has k neurons, which corresponds to the dimension of the original node feature vector. This transformation is to enable combination with the input node feature representation in the next block. PIL-Net applies one set of linear and CELU functions [colored green] each to the edge and coordinate feature representations, which are output directly from their corresponding feature expansion blocks. The rationale for applying an additional set of functions to the node feature representation as compared to the edge and coordinate feature representations is due to the updated node features containing more complex information because of the graph convolution step.
Skip connections. In this block [colored yellow in Fig. 2], PIL-Net adds the output from each combined feature expansion and compression block to the input node, edge, and coordinate features. Skip connections help to stabilize network convergence by providing an alternative pathway for the gradient during backpropagation. They also help preserve initial feature information as the features are propagated through the network.
Module output. Following the skip connection blocks, the updated node, edge, and coordinate feature representations [colored gray in Fig. 2] are output from the module. From there, they are either used as input to the next module, or the updated node representations are fed into the fully-connected linear layer to obtain the initial multipole predictions, as depicted in Fig. 1.
(1) Monopole total charge constraint. The sum of the atomic monopoles within each molecule should equal the net charge of the molecule. As the molecules are neutral, the absolute sum of the atomic monopoles within a molecule should equal zero. If this sum exceeds 10−2e, PIL-Net redistributes the charges to sum to zero by subtracting the mean charge.
(2) Monopole hydrogen constraint. Since the molecules are composed of H, C, N, O, F, S, and Cl atoms, all the atomic monopoles corresponding to the hydrogen atoms (the least electronegative dataset element) must be positive. PIL-Net enforces this constraint by setting the hydrogen atomic monopole predictions equal to their absolute values.
(3) Quadrupole trace constraint. Since the dataset atomic quadrupoles are traceless quantities, PIL-Net ensures that its quadrupole predictions are similarly traceless by redistributing the charges as in eqn (S4).†
(4) Octupole trace constraint. Since the dataset atomic octupoles are traceless quantities, PIL-Net ensures that its octupole predictions are similarly traceless by redistributing the charges as in eqn (S5).†
Due to rounding errors in floating point representations and computations, not all monopole sums may equal the net charge of the molecule exactly, so PIL-Net only redistributes the charges if their sum exceeds the cutoff 10−2e. This soft constraint does not preclude PIL-Net from learning model parameters that assign charges to molecules such that their total charge sums to zero. This constraint instead ensures that for molecules in which the total charge does not exactly equal the true net charge (due to errors in the computation of the reference values), the architecture does not force charge redistribution. Section 3, the Results section, includes further information on how the monopole sum cutoff was decided. There were no cutoffs for the atomic quadrupole and octupole constraints because we could verify that all their traces are sufficiently near zero in the training set. Similarly, for the monopole hydrogen constraint, the error is sufficiently small.
The physical motivation behind the monopole hydrogen constraint is that all the organic molecules in the QMDFAM dataset are composed of H, C, N, O, F, S, and/or Cl atoms. As such, the hydrogen atoms (electronegativity 2.20) are the least electronegative and therefore will always have a positive atomic monopole moment. This is the reason the monopole hydrogen constraint enforces all monopoles associated with hydrogen atoms to be positive. If the dataset contained atoms with lesser electronegativity, then this constraint would need to be modified to reflect that change. It is also important to be aware that the model applies the monopole hydrogen constraint prior to the monopole total charge constraint. As a result, some atomic monopoles corresponding to hydrogen may not be positive in the final model predictions. Nevertheless, such instances are few, as indicated by the low error displayed in Fig. 5. Moreover, the absolute value function is used when applying the monopole hydrogen constraint. This function, like the popular ReLU function, is not differentiable at input x = 0. In these cases, machine learning libraries such as PyTorch53 often compute the gradients during backward propagation in a piecewise fashion, setting the gradient at x = 0 to zero. However, this implementation could eventually lead to vanishing gradients. In the future, we could replace the absolute value function with a smooth approximation to the ReLU function, such as the softplus function.
Regarding the quadrupole and octupole trace constraints, an alternative method for enforcing tracelessness in the atomic quadrupole and octupole predictions could be to design the earlier layers of the model to produce irreducible representations54,55 so that the trace is removed prior to redistributing the charges. It is also worth noting that an additional possible physics-informed constraint for this dataset is a monopole fluorine constraint, where the network forces all atomic monopole fluorine predictions to be negative. In practice, we found that PIL-Net learned this constraint within the first couple of epochs of training, so it was an unnecessary computation. Furthermore, PIL-Net does not have a dipole moment constraint, which would be a good addition to a future iteration of the PIL-Net model.
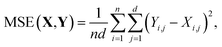 | (6) |
During training, the MSE loss is computed for each multipole moment property. Then, each loss is scaled according to multipole property-specific weights. Finally, these losses are summed to form the overall loss score for the mini-batch as
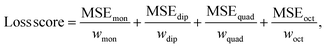 | (7) |
The rationale behind including these weights is that each atomic multipole type comes from a different distribution of values. If the network combined these errors without taking the different distributions into account, the error of a multipole type from a wider distribution (i.e., atomic monopoles, as displayed in Fig. S2 in the ESI†) might dominate the loss score. This could lead the network to prioritize reducing the loss of the simpler but larger error atomic monopole property at the expense of the other properties. To prevent this, the network scales the error arising from each multipole type by w. The scalar w is precomputed as the average interquartile range (to exclude outliers) of each component of the reference atomic multipole values from the training set. This value is then normalized with respect to the other multipole types' computed scalar weights.
An additional approach for implementing a physics-informed neural network is by augmenting the loss function with the errors computed from the physics-informed constraints (as a form of regularization), instead of modifying the predictions directly on the model. We opted for PIL-Net's more explicit way of correcting model predictions, as we found it resulted in better model performance during early testing.
2.3 Molecular moment approximation
PIL-Net can also approximate molecular dipole moments [not pictured in Fig. 1] without explicitly training over the molecular property. Instead, incorporating our domain knowledge, PIL-Net can compute each molecular dipole moment as a function of its atomic monopole and dipole predictions, as well as the corresponding atomic Cartesian coordinates, post-training.It is well-known that one can approximate the molecular dipole moment via the simple point charge model:2
 | (8) |
 | (9) |
Eqn (9) combines local atomic dipole information (which describes the separation of charge in each atom) and knowledge about the spatial arrangement of the corresponding atomic charges, through a summation over all atoms in the molecule. In the Results section, Table 6 reveals that the addition of the atomic dipole term to the molecular dipole moment approximation equation reduces the error from eqn (8). Moreover, in Section S9 of the ESI,† we describe two equations for approximating the molecular quadrupole moment and the molecular octupole moment. We assess the quality of the approximations through quantitative comparison with reference calculations. Recently, new equations for approximating molecular dipole moments post-training have emerged (under the assumption of model equivariance), including those that directly incorporate information about the chemical bonds of the molecule and the oxidation state of the atoms.56
2.4 PIL-Net architecture comparison with prior work
There are many aspects of a machine learning pipeline that can contribute to it being “physics-informed”. For example, the input features can be chosen to maximize the amount of information relevant to the target properties. Additionally, the architecture can be designed so that each atom's property prediction is dependent on that of its neighboring atoms, incorporating local atomistic information. Both of these factors assist in increasing the accuracy of a model's predictions through the use of outside knowledge about what influences each atom's local properties.PIL-Net implements both through our choice of node, edge, and coordinate features, as well as the model's graph convolutions, but this is not unique to PIL-Net. For example, PIL-Net uses most of the same features as EGNN.5 It is also common for machine learning models to take the local atomistic neighborhood into account when predicting an atomic property. What sets PIL-Net apart as a physics-informed neural network is the specific implementation of our physics-informed constraints, weighted loss function, and post-training molecular moment approximation equations. In Table 1, we have included a comparison between these PIL-Net components and those from prior work for predicting atomic multipoles using machine learning. As displayed in Table 1, EGNN,5 AIMNet,10 and CMPNN9 are the only methods that implement some version of PIL-Net's listed physics-informed components in their architectures. Collectively, these methods implement a monopole total charge constraint, quadrupole trace constraint, and physics-informed weighted loss function. Of these prior work methods, CMPNN has the most overlap with PIL-Net, incorporating three out of seven of PIL-Net's physics-informed components. Therefore, the majority of the physics-informed components implemented in PIL-Net's architecture are unique in the literature for atomic multipole prediction using machine learning. In the following paragraphs, we detail the similarities and differences between PIL-Net's implementation of these components and the prior works' implementations.
Ensuring charge conservation through redistributing charges within a molecule (i.e., with some form of a monopole total charge constraint) is common in the literature for predicting atomic monopoles. However, EGNN5 and CMPNN9 apply these corrections to all molecules, regardless of whether the sum of the charges indicates the need for redistribution. Since neural networks operate on floating point numbers, which cannot represent real numbers exactly, the sum of the atomic monopoles may not equal the net charge of the molecule exactly. As such, we designed the PIL-Net total charge enforcement scheme to allow for some flexibility regarding the exact value of the monopole sum. Therefore, we only apply the correction when the absolute difference between the monopole sum and net charge is sufficiently large. EGNN5 and CMPNN9 also describe the process of enforcing traceless quadrupole tensors. Here, PIL-Net does enforce this constraint for all molecules, since we could verify prior to training that the trace of the quadrupoles in the training set is sufficiently small.
PIL-Net's weighted loss function combines the individual loss scores of each multipole type, scaled by the width of each multipole's distribution. The PIL-Net weighting scheme is to prevent multipoles coming from wider distributions (and consequently resulting in errors of larger magnitude) from dominating the loss function, biasing the network towards prioritizing its loss at the expense of the other properties. CMPNN9 identifies that it weights its loss function in accordance with the relative importance of each multipole type, but it does not mention this weighting scheme being a function of the distribution of the atomic multipole properties. AIMNet10 uses a weighting scheme for its loss function, where it scales the contribution of the different target properties to enforce their equal contribution to the loss function. However, the AIMNet loss function combines loss scores from charges, energies, and volumes, each having a different associated weight. In AIMNet, all charge properties have the same weight, whereas PIL-Net associates each atomic multipole charge type with a different weight.
3 Results
In this section, we begin by describing the software libraries and hardware employed to implement and run our experiments using the PIL-Net framework. Then we detail our PIL-Net hyperparameter selection process. Finally, we describe the PIL-Net training procedure and present our main experimental results. Our out-of-domain experimental results can be found in ESI Section S12.†3.1 Libraries and hardware
We employed the machine learning libraries PyTorch53 and Deep Graph Library57 to implement the PIL-Net framework. Our code was run on a single NVIDIA A100 GPU58 on the Gilbreth community cluster59 at Purdue University.3.2 Hyperparameters
Through the hyperparameter tuning procedure described in ESI Section S4,† we decided to use a PIL-Net model with a depth of five convolutional layers and a width of 256 hidden neurons per layer in the following experiments. The bound of 10−2e for the monopole total charge physics-informed constraint was decided via inspection. We computed a sum over the atomic monopole vectors for each molecule in the training set. The absolute value of all the sums exists in the range [0, 10−2] e for the atomic monopole property, as shown in Fig. S3 of the ESI.† There is some room to further tighten this bound, but we did not want to be too stringent in case the validation or test set's distribution differed slightly.3.3 Training procedure
We now turn to describing the remaining components of our PIL-Net experimental set-up. In each experiment, 900k, 100k, and 13k molecular conformations were included in the training, validation, and test sets, respectively, in accordance with the splits identified in the HDF5 files of the QM Dataset for Atomic Multipoles.5 In our experiments, we trained three separate PIL-Net models for 200 epochs each. Additional information regarding the PIL-Net training procedure can be found in ESI Section S4.† All results reported in this work are averaged across three PIL-Net models unless stated otherwise.3.4 Model evaluation metrics
The evaluation metrics used in these experiments are Mean Absolute Error (MAE), coefficient of determination (R2), Root Mean Squared Deviation (RMSD), and Pearson Correlation Coefficient (PCC). Their corresponding equations can be found in ESI Section S5.†3.5 Chemical accuracy
The chemical accuracy of a molecular property is the accuracy to which it needs to be computed to make useful predictions, matching or exceeding experimental accuracy. In the context of multipole moments, this is the accuracy needed for practical purposes, such as in molecular modeling. Partial charge, a similar property to the atomic monopole moment, has a chemical accuracy of 0.01 e.10 The chemical accuracy for the dipole moment property is 0.01 D, or approximately 0.0021 eÅ.60 For the higher-order multipole moments, quadrupole and octupole, the experimental data are not very accurate and different measurements often disagree.2 Therefore, it is difficult to assign a desired chemical accuracy to these properties.3.6 Atomic multipole prediction results
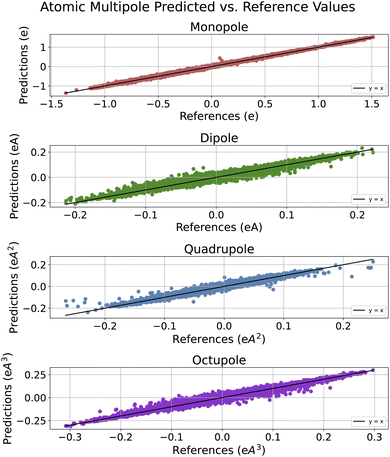
We now report the PIL-Net atomic multipole moment prediction results. In addition to using chemical accuracy as a metric, we demonstrate PIL-Net's effectiveness in predicting atomic multipole moments through comparison with other computational methods, in Tables 2, 3 and 5. Section S11 of the ESI† provides insight into how the PIL-Net predictive error changes as a function of training set size.In Table 2, we compare PIL-Net's MAE results for the atomic monopole, dipole, quadrupole, and octupole properties with those from other machine learning models. PIL-Net exceeds the chemical accuracy for the atomic monopole and dipole properties with mean absolute errors of 0.0074 e and 0.0020 eÅ, respectively. Comparing PIL-Net's atomic multipole results to those of other methods, PIL-Net has lower error compared to Δ-ML-85 (ref. 11) for all recorded properties and is within an order of magnitude of the error for all EGNN5 and CMPNN9 properties.
| Method | Train + valid | Test | Elements | MAE q (e) | MAE μ (eÅ) | MAE θ (eÅ2) | MAE Ω (eÅ3) | Train time (hours) |
|---|---|---|---|---|---|---|---|---|
| PIL-Net | 1m | 13k | C, H, O, N, F, S, Cl | 7.4 × 10− 3 | 2.0 × 10− 3 | 1.2 × 10− 3 | 1.3 × 10− 3 | 17 |
| EGNN5 | 850k | 13k | C, H, O, N, F, S, Cl | 2.19 × 10−3 | 6.4 × 10−4 | 6.3 × 10−4 | — | — |
| CMPNN9 | 42k | 5k | C, H, O, N, F, S, Cl, P, Br | 3 × 10−3 | 2 × 10−3 | 3 × 10−3 | — | 132 |
| Δ-ML-85 (ref. 11) | 2.7k | 500 | C, H, O, N, F, S, Cl | 4 × 10−2 | 6 × 10−2 | 1.3 × 10−2 | — | — |
In terms of training time, PIL-Net took approximately 17 hours and CMPNN9 took 132 hours. The other machine learning methods did not report training time. Both PIL-Net and CMPNN trained on small molecules. CMPNN had a greater diversity of elements in its dataset, but PIL-Net's training set size is over 23 times larger. Both PIL-Net and CMPNN trained on the atomic monopole, dipole, and quadrupole properties, but PIL-Net also trained on the atomic octupole property. In terms of hardware, PIL-Net ran on a single NVIDIA A100 GPU58 with a FP32 (single-precision floating-point format) performance of 19.5 teraflops, while the CMPNN model was run on a single NVIDIA P100 GPU.61 The CMPNN paper did not report the precision used, but the NVIDIA P100 GPU has a FP32 performance of 9.3 teraflops. PIL-Net's hardware is newer with 2.1 times greater performance than that of CMPNN. Nevertheless, PIL-Net trained over seven times faster than CMPNN, so PIL-Net's training time appears to be superior.
To our knowledge, the AIMNet paper10 contains the only machine learning-derived atomic octupole predictive results reported in the literature, but AIMNet does not report MAE or R2 for its atomic multipole results. The most similar evaluation metric to MAE that the AIMNet paper reported is root mean squared deviation (RMSD). As a result, we compute the RMSD of our PIL-Net atomic octupole results and compare it with that of AIMNet in Table 3, separate from our other reported results. We also include a comparison with AIMNet's atomic dipole and quadrupole results in Table S2 of the ESI.† The AIMNet paper does not report atomic monopole results.
| Method | Train + valid | Test | Elements | RMSD Ω (eÅ3) | Train time (hours) |
|---|---|---|---|---|---|
| PIL-Net | 1m | 13k | C, H, O, N, F, S, Cl | 2.4 × 10− 3 | 17 |
| *AIMNet10 | 9m | 156k | C, H, O, N, F, S, Cl | 2.98 × 10−2 | 270 |
At RMSD 0.0024 eÅ3, PIL-Net's error is 12.4× smaller than that of AIMNet, which is more than one order of magnitude less than that of AIMNet, making this a state-of-the-art result. Besides that, AIMNet trained on a dataset that provided the norms of atomic octupole vectors, as opposed to the atomic octupole vectors themselves. This difference makes PIL-Net's performance even more impressive, as predicting a vector of ten values is more challenging than predicting a single scalar value. A contributing factor to PIL-Net's superior performance could be the four physics-informed constraints that PIL-Net incorporates, but AIMNet does not, as shown in Table 1. The two best performing models (excluding PIL-Net), EGNN and CMPNN, were the only models that incorporated some of the PIL-Net model constraints and not only a weighted loss function.
In terms of hardware, PIL-Net ran on a single NVIDIA A100 GPU58 with a FP32 (single-precision floating-point format) performance of 19.5 teraflops. AIMNet used four GPUs in parallel for model training, including dual NVIDIA GTX 1080 GPUs,62 each GPU with 8.87 teraflop FP32 performance. In terms of training time, PIL-Net took approximately 17 hours and AIMNet10 took 270 hours, nearly 16× longer. Both PIL-Net and AIMNet trained on small molecules, composed of the same elements, but AIMNet's training set size was more than 9× the size of PIL-Net's training set. However, AIMNet trained on energies, volumes, and forces in addition to charge properties, likely increasing the training time further. Given the differences in the experimental setups, it is difficult to compare the training time for these two models, but taking all this into account, PIL-Net and AIMNet seem to be about on par in training time.
Fig. S4 in the ESI† provides additional insight into PIL-Net's training time. This figure depicts the PIL-Net validation loss over the full course of training for each of the atomic multipoles. Most progress in terms of reduction in validation loss is made within the first 100 epochs of training. As a result, if one were time-constrained, an option would be to end training early (50% through), resulting in a mostly converged model, while cutting training time in half.
Perhaps counter-intuitively, in Table 2, the predictions for the higher-order properties (e.g., atomic quadrupoles) appear more accurate than those of the lower-order properties (e.g., atomic monopoles), when one would expect the higher-order properties to be more difficult to predict. This disparity in error is due to the disparity in the width of the distributions of the properties (i.e., the atomic monopoles come from a wider distribution than that of the atomic quadrupoles, as displayed in Fig. S2 of the ESI†). As a result, the absolute errors for the atomic monopoles, for example, are larger than those of the atomic quadrupoles. This is why, during training, as described in eqn (7), the PIL-Net framework scales the loss contribution of each multipole type by the width of its distribution.
In Table 4, we display the unweighted vs. weighted training loss for each atomic multipole during an example PIL-Net training epoch. Looking at the unweighted column in Table 4, the loss associated with the atomic monopoles is more than 10 times greater than that of each of the other properties. Yet, following re-weighting, one can see that in actuality, the atomic monopole is the easiest property to train on (smallest weighted loss), followed by the atomic dipole, quadrupole, and octupole, as expected. Without this loss function weighting scheme, PIL-Net training might have become overly biased towards reducing the atomic monopole loss at the expense of the other properties.
| Atomic multipole | Unweighted | Weighted |
|---|---|---|
| Monopole (e) | 1.06 × 10−4 | 1.18 × 10−4 |
| Dipole (eÅ) | 9.10 × 10−6 | 1.29 × 10−4 |
| Quadrupole (eÅ2) | 3.91 × 10−6 | 2.24 × 10−4 |
| Octupole (eÅ3) | 5.22 × 10−6 | 4.82 × 10−4 |
| Total | 1.25 × 10−4 | 9.53 × 10−4 |
In Fig. 3, we display the PIL-Net mean absolute error results, grouped by element. There is a similar trend amongst the four multipole types, where sulfur has a large error relative to the other elements while hydrogen's error is low. One reason for this phenomenon might be that multipoles are more difficult to model for more complex elements such as sulfur. Moreover, many more hydrogen atoms exist in the training set compared to sulfur, as displayed in Table S1 in the ESI.† However, while these two reasons may be factors in the error discrepancies amongst the elements, there must be additional factors since chlorine also has great complexity relative to the other elements, but exhibits less error than sulfur. Additionally, fluorine has less representation in the dataset than sulfur, but also exhibits smaller error. An additional explanation could be that the QMDFAM dataset was calculated at the PBE0-D3BJ/def2-TZVP level of theory, meaning that diffuse functions were not included in the basis set. Diffuse functions aid in describing the portion of the atom's electron density that is distant from the nucleus. Out of the H, C, N, O, F, S, and Cl elements, sulfur has the largest atomic radius and therefore the largest electron cloud. As a result, the density functional theory calculations likely produce worse representations of the sulfur atoms compared to the other atoms, leading to larger predictive errors when attempting to model their behavior. A good direction for future work may be to train PIL-Net using reference atomic multipole moments originating from a more descriptive level of theory and/or develop physics-informed constraints to target the higher error elements more directly.
Next, in Table 5, we compare PIL-Net's coefficient of determination results with those of other machine learning models that report the R2 metric. Section S11 of the ESI† provides insight into how this correlation changes as a function of training set size. Table 5 indicates that, across all the atomic multipole results, PIL-Net demonstrates very high correlation between the PIL-Net predicted values and the dataset reference values, with all results exceeding 97% in R2 value. PIL-Net outperforms two of the three models that report this metric: Δ-ML-85 (ref. 11) and DynamPol.8 As expected, the results indicate that the atomic monopole was the easiest property to learn, followed by the increasingly higher-order properties: atomic dipole, quadrupole, and octupole.
| Method | Train + valid | Test | Elements | R 2 q (e) | R 2 μ (eÅ) | R 2 θ (eÅ2) | R 2 Ω (eÅ3) | Train time (hours) |
|---|---|---|---|---|---|---|---|---|
| PIL-Net | 1m | 13k | C, H, O, N, F, S, Cl | 0.9988 | 0.9839 | 0.9794 | 0.9777 | 17 |
| *Δ-ML-85 (ref. 11) | 2.7k | 500 | C, H, O, N, F, S, Cl | 0.97 | 0.50 | 0.65 | — | — |
| DynamPol8 | 1.3k | 1.3k | C, H, O, N | 0.983 | 0.931 | 0.867 | — | — |
| CMPNN9 | 42k | 5k | C, H, O, N, F, S, Cl, P, Br | 1.000 | 0.997 | 0.993 | — | 132 |
In Fig. 4, we include an additional view of how well correlated PIL-Net's predicted values are with the dataset reference values. Since the R2 standard deviation was very low across PIL-Net models, we chose one model's predictions to be representative of the other two PIL-Net models. As such, this plot depicts the predicted values from one trained PIL-Net model, as opposed to an average of the predictions across the three models. Since these predictions are near zero, averaging could lead to cancellation errors from positive and negative predictions. As displayed in Fig. 4, the atomic monopole predictions have the best fit, as expected for the lowest-order property. The higher-order properties have excellent fits as well. The majority of the data in the scatter plots follow the target y = x line. Where there is error, its bulk is primarily distributed at the center of each plot. This is because the majority of the reference target data are centered around zero, as shown in Fig. S2 of the ESI.†
3.7 Molecular dipole moment approximation results
As defined in eqn (9), the PIL-Net framework approximates the test set molecular dipole moments post-training as a function of the predicted atomic monopoles and dipoles, as well as atomic position information.Table 6 displays the resulting PIL-Net MAE and R2 results for the molecular dipole moment property. Table 6 reveals that incorporating PIL-Net's atomic dipole predictions into the approximation equation (eqn (9)) resulted in a 29% decrease in MAE and a 2.27% increase in R2 over using the standard point charge model for approximating molecular dipole moments (eqn (8)). Moreover, the improved R2 value, at 97%, nearly matches that of the predicted atomic monopoles and dipoles, indicating excellent correlation between the PIL-Net molecular dipole moment approximations and the reference values. Although training on the molecular dipole moments directly would yield more accurate results, since PIL-Net uses separate model weights for different target properties, this would increase training time by a non-insignificant amount. Instead, the PIL-Net framework can perform these post-training computations to obtain molecular dipole moment predictions over all the molecules in the test set in a fraction of a second.
| MAE (eÅ) | R 2 | |
|---|---|---|
| Dipole moment approx. with μ | 6.59 × 10−2 (±6 × 10−4) | 0.9697 (±3 × 10−4) |
| Dipole moment approx. without μ | 9.28 × 10−2 (±5 × 10−4) | 0.9482 (±5 × 10−4) |
Since the PIL-Net model implements the monopole total charge constraint as a soft constraint, only forcing redistribution of charge if the total charge within a molecule exceeds 10−2e, one might question the impact this has on approximating the molecular dipole moment. We tested this empirically by training an additional PIL-Net model on the QM Dataset for Atomic Multipoles5 that employed a hard monopole total charge constraint, redistributing the charge so that the sum of the atomic monopole predictions equaled exactly zero for all molecules in the training set. The results from this experiment demonstrated that using a soft constraint led to molecular dipole moments with less error than using a hard constraint. Section S7 in the ESI† contains details about the set-up of this experiment and the implications of its results.
The MAE in the molecular dipole moments computed from eqn (9), relative to the values given in the dataset, is due to a number of factors. Since the atomic monopole and dipole inputs to the equation are predictions and not ground truth values, they have associated uncertainty. Additionally, since this approximation equation is a model and not an exact equation, there is also uncertainty in the equation itself. In ESI Section S8,† we bound and analyze these uncertainties. Our conclusion is that there is little uncertainty in the model itself, so using eqn (9) to approximate molecular dipole moments is a good option if training time is a limiting factor. Furthermore, in the ESI Section S9,† we define equations for approximating both the molecular quadrupole moment and the molecular octupole moment. We also record their respective MAE and R2 metrics when compared to PSI4 (ref. 63) reference calculations.
3.8 Ablation study: PINN vs. non-PINN
In the following set of experiments, we sought to evaluate the effect of the PIL-Net physics-informed constraints and weighted loss function on the PIL-Net model's predictive performance. In this manner, we can investigate to what extent these components assist the model in producing accurate atomic multipole moment predictions. To that end, we trained three PIL-Net models (denoted non-PINN) without the physics-informed model constraints or weighted loss function, averaged their results, and compared them to the original physics-informed PIL-Net models (denoted PINN). Fig. 5 displays how the mean absolute error from each constraint changes throughout training for both the PINN and non-PINN models. To form the subplot for the monopole total charge constraint, for example, we computed the sum of the atomic monopole predictions associated with each molecule and calculated the mean absolute error with respect to the sum of the reference atomic monopole predictions for each molecule. Fig. 5 indicates that the monopole total charge, quadrupole trace, and octupole trace constraints included in the PINN model were very effective in reducing the constraint error, relative to the non-PINN model learning the constraints implicitly.While the PINN errors from the monopole hydrogen (MH) constraint are very small, retaining their value around order 1 × 10−5, the reason the PINN error is similar to that of non-PINN is because PIL-Net applies the monopole total charge (MTC) constraint following the application of the MH constraint. Since the MTC constraint subtracts the mean atomic monopole value from the atomic monopole predictions, this redistribution of charge can cause some of the atomic monopole predictions associated with the hydrogen atoms to become negative. When implementing the two atomic monopole constraints, it was decided that the MTC constraint was more important to optimize in PIL-Net because the MTC constraint involves all the atoms in the molecule as opposed to only the hydrogen atoms. An additional deciding factor was that the MTC error for non-PINN is two orders of magnitude larger than the MH error for non-PINN, so the former had more room for error minimization.
Regarding the fluctuations for PINN and non-PINN in the MH constraint subplot, these are more apparent compared to the other constraints' subplots because the range of error the MH constraint subplot covers is much smaller (within one order of magnitude). This limited range of y-values results in a zoomed-in subplot that makes the oscillations more apparent compared to the other subplots. In the future, the MTC constraint charge redistribution procedure could be modified to guarantee that none of the atomic monopole predictions for hydrogen are made negative. Introducing this change should cause the MH constraint error for PINN to decrease beyond the non-PINN error, which would also reduce the appearance of fluctuations in the MH constraint subplot. However, modifying the MTC constraint procedure may also worsen the results for the MTC constraint, so there would likely need to be a tradeoff between the two constraints to ensure that neither is too negatively affected.
Fig. 6 displays the effects on the PIL-Net validation loss of including the physics-informed constraints versus removing them. Although we used the weighted loss function to train the PINN model, we plot the corresponding unweighted loss for both the PINN and non-PINN models for a more equal validation loss comparison. According to Fig. 6, all the physics-informed constraints improved their corresponding atomic multipole property predictions at the beginning of training. The constraints allowed the PIL-Net model with physics-informed constraints (PINN) to converge faster than the PIL-Net model without the constraints (non-PINN). Fig. 6 also shows that the PINN and non-PINN performance for the atomic dipole moment was very similar. This is expected because the PINN model does not contain a dipole moment constraint. For the dipole moment property, the PINN and non-PINN architectures are effectively the same, except for the weighted loss function. As such, the figure also reveals that the weighted loss function does not appear to have much impact on the atomic dipole moment property during the early stages of training.
For the other atomic multipole properties, as shown in Fig. 6, the PINN model outperforms the non-PINN model in validation loss during the first 25 epochs, or 12.5%, of training. Around the 25-epoch mark, the losses from the two model frameworks begin to meet. In subsequent epochs, the validation loss of the two frameworks becomes approximately equal when training has proceeded long enough for the non-PINN model to match the PINN performance. Yet, as shown in Fig. 5, at epoch 25, the non-PINN model's constraint error is still several orders of magnitude larger than that of PINN for all constraints except monopole hydrogen. As such, completely eliminating the error for these constraints does not appear to be a requirement for obtaining low loss, once the constraint error is small enough and the model has been trained for sufficiently long. As future work, it would be interesting to identify a constraint for which the constraint error must approach zero for the loss to continue reducing.
This ablation study also demonstrates that incorporating the physics-informed constraints in the model has a minimal impact on the training time. Applying the four PINN model constraints resulted in an additional cost of 4.4 seconds per epoch, accounting for only 1.5% of overall training time. Additionally, the PINN model only incurred an additional cost of 0.2 seconds per epoch from multiplying the loss function components by the pre-computed weights, amounting to near-negligible additional training time. Consequently, the PIL-Net model with physics-informed constraints contributes very little additional cost, making it excellent to use, even in time-constrained scenarios.
Finally, beyond improving model performance, these constraints can serve as a framework for greater model interpretability. Broadly, our PIL-Net framework is a testbed for what one presumes to know about the laws that govern the physical world. If the physical assumptions (and therefore the physics-informed model constraints) were incorrect, this gap in knowledge would reveal itself in these results. For example, if the sum of the atomic monopoles of a molecule did not equal the net charge of the molecule, PIL-Net's explicit redistribution of the charges to enforce this constraint would result in elevated error. The non-PINN models would instead outperform PINN in validation loss. As such, one can use PIL-Net as a general framework to confirm or reject hypotheses relating to the molecules that exist in any dataset. Furthermore, one can apply these physics-informed constraints in isolation to discover the influence a particular constraint has on the overall loss.
3.9 Application: electrostatic potential reconstruction
In the final set of experiments, the PIL-Net predicted atomic multipole moments were applied to the downstream task of accurately reconstructing the electrostatic potential (ESP) on the van der Waals (vdW) surface of the test set molecules. The ESP is an important molecular property because it provides a complete picture of the electrostatic environment at different spatial points on the surface of a molecule. Details about the ESP dataset reference values and the equations used for ESP reconstruction can be found in ESI Section S13.†Table 7 displays the mean absolute error (MAE) and coefficient of determination (R2) results from using increasingly higher-order multipole moments to reconstruct the electrostatic potential on each molecular surface. As indicated by the table, the error decreased with the addition of each higher-order atomic multipole moment type. In particular, the addition of the atomic quadrupole moment predictions and then the atomic octupole moment predictions placed the ESP reconstructive error within the chemical accuracy for the property (1 kcal mol−1). The R2 correlation increased with the addition of each higher-order atomic multipole moment contribution, with the exception of the atomic octupole moment. While the ESP reconstruction up to the octupole moment is still well-correlated at 90%, the correlation is worse than that of only using the atomic monopoles in the reconstruction. This distinction might be due to the octupoles improving the representation of the asymmetries in local areas of the ESP, resulting in smaller MAE, but not generalizing as well to the full ESP.
| Multipole type | MAE (kcal mol−1) | R 2 |
|---|---|---|
| Up to monopoles | 1.29 (±5 × 10−3) | 0.9248 (±3 × 10−4) |
| Up to dipoles | 1.03 (±3 × 10−3) | 0.9417 (±4 × 10−5) |
| Up to quadrupoles | 0.82 (±4 × 10−3) | 0.9538 (±2 × 10−4) |
| Up to octupoles | 0.80 (±5 × 10−3) | 0.9015 (±2 × 10−2) |
Fig. 7 displays the ESP of a test set molecule from the QM Dataset for Atomic Multipoles5 (QMDFAM), reconstructed using atomic multipole moment predictions up to and including atomic octupoles from one trained PIL-Net model. The figure also displays the error in this ESP reconstruction with respect to the reference ESP values available in the QMDFAM. Fig. 7 depicts visually that there is very little error in the ESP reconstruction, providing an additional view of the strength of reconstructing the ESP as a function of the PIL-Net predicted atomic multipole moments.
 | ||
| Fig. 7 The electrostatic potential (ESP) on the vdW surface of molecule 1 from the QMDFAM test set, approximated as a function of PIL-Net atomic multipole predictions up to and including the atomic octupole moments (top). Molecule 1 has CID 10778246.64 The difference between the QMDFAM reference ESP calculations and the reconstructed ESP values (ESPref − ESPrec) for this molecule (bottom). The mean absolute error in the ESP reconstruction is 0.56 kcal mol−1 and the maximum absolute error is 2.24 kcal mol−1. | ||
4 Discussion and conclusion
In this paper, we have introduced PIL-Net, a physics-informed graph convolutional neural network, capable of predicting atomic multipole moments quickly and with low error. The PIL-Net predictions for the atomic octupole property are state-of-the-art, and the error in the predictions for the lower-order atomic multipole properties is within chemical accuracy and/or within an order of magnitude of what is reported in the literature. Moreover, following training on the atomic multipole moments, we showed that PIL-Net can approximate molecular multipole moments in a fraction of a second, as a function of PIL-Net's predicted atomic multipoles. We also demonstrated how the PIL-Net physics-informed constraints and scaled loss function contribute to the PIL-Net model performance, as well as described how PIL-Net can be used as a testbed for validating hypotheses about the physical world. Beyond that, we applied the PIL-Net atomic multipole moment predictions to the downstream task of accurate electrostatic potential reconstruction. Furthermore, we showed that the PIL-Net model can perform well in an out-of-domain setting, indicating its transferability to other molecular datasets.In the future, we would like to expand our physics-informed constraints to incorporate coverage for additional molecular properties, such as those related to energies, structures, and forces. An additional avenue to explore is applying transfer learning to train a PIL-Net model on a higher-order property, such as atomic octupoles, and then fine-tuning the model on the lower-order atomic multipole properties. Using transfer learning in such a way may result in predictions that approach the accuracy of the original predictions, but obtained in even less time.
Data availability
The software for the PIL-Net framework can be found at https://doi.org/10.5281/zenodo.15683278. The QM Dataset for Atomic Multipoles5 is publicly accessible at https://doi.org/10.3929/ethz-b-000509052. The dataset authors have made related software available at https://github.com/rinikerlab/EquivariantMultipoleGNN. The ANI-1x dataset10,20,48,49 is available at https://doi.org/10.6084/m9.figshare.c.4712477.v1. The dataset authors have made related software available at https://github.com/aiqm/ANI1x_datasets.Author contributions
C. W., A. P., and A. C. designed the project. C. W. carried out the implementation, performed the analysis, and wrote the initial draft of the manuscript. A. P. and A. C. edited the manuscript. All authors participated in meaningful discussions related to the project throughout its development.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
C. W. was supported by the U.S. Department of Energy through a Computational Science Graduate Fellowship under Award Number DE-SC0019323. Both C. W. and A. P. were supported by U.S. Department of Energy grant DE-SC0022260. The authors would like to thank Siddhartha Shankar Das at Purdue University for his comments on this manuscript. This research is an offshoot from the work C. W. performed at Lawrence Berkeley National Laboratory with Dr Yu-Hang Tang and Dr Aydın Buluç. This material is based upon work supported by the U.S. Department of Energy, Office of Science, Office of Advanced Scientific Computing Research, Department of Energy Computational Science Graduate Fellowship under Award Number DE-SC0019323. This report was prepared as an account of work sponsored by an agency of the United States Government. Neither the United States Government nor any agency thereof, nor any of their employees, makes any warranty, express or implied, or assumes any legal liability or responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed, or represents that its use would not infringe privately owned rights. Reference herein to any specific commercial product, process, or service by trade name, trademark, manufacturer, or otherwise does not necessarily constitute or imply its endorsement, recommendation, or favoring by the United States Government or any agency thereof. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof.Notes and references
- D. J. Griffiths, Introduction to Electrodynamics, Cambridge University Press, 2023, pp. 85, 151–154 Search PubMed.
- A. J. Stone, The Theory of Intermolecular Forces, Oxford University Press, USA, 2013, pp. 4–5, 13, 17, 136 Search PubMed.
- D. Harrison, The Multipole Expansion, https://phys.libretexts.org/Bookshelves/Mathematical_Physics_and_Pedagogy/Mathematical_Methods/The_Multipole_Expansion, viewed on 05/03/24 Search PubMed.
- D. Ghosh, Electrostatics-VI: Multipole Expansion of Potential, Dipole and Quadrupole Potential, http://www.dipanghosh.com/electricity-and-magnetism, viewed on 05/03/24 Search PubMed.
- M. Thürlemann, L. Böselt and S. Riniker, J. Chem. Theory Comput., 2022, 18, 1701–1710 CrossRef PubMed.
- E. M. Purcell and D. J. Morin, Electricity and Magnetism, Cambridge University Press, 2013 Search PubMed.
- D. Hait and M. Head-Gordon, J. Chem. Theory Comput., 2018, 14, 1969–1981 CrossRef CAS PubMed.
- M. G. Darley, C. M. Handley and P. L. Popelier, J. Chem. Theory Comput., 2008, 4, 1435–1448 CrossRef CAS PubMed.
- Z. L. Glick, A. Koutsoukas, D. L. Cheney and C. D. Sherrill, J. Chem. Phys., 2021, 154, 224103 CrossRef CAS PubMed.
- R. Zubatyuk, J. S. Smith, J. Leszczynski and O. Isayev, Sci. Adv., 2019, 5, eaav6490 CrossRef CAS PubMed.
- T. Bereau, D. Andrienko and O. A. Von Lilienfeld, J. Chem. Theory Comput., 2015, 11, 3225–3233 CrossRef CAS PubMed.
- J. S. Delaney, J. Chem. Inf. Comput. Sci., 2004, 44, 1000–1005 CrossRef CAS PubMed.
- L. C. Blum and J.-L. Reymond, J. Am. Chem. Soc., 2009, 131, 8732–8733 CrossRef CAS PubMed.
- L. Ruddigkeit, R. Van Deursen, L. C. Blum and J.-L. Reymond, J. Chem. Inf. Model., 2012, 52, 2864–2875 CrossRef CAS PubMed.
- J. J. Irwin, T. Sterling, M. M. Mysinger, E. S. Bolstad and R. G. Coleman, J. Chem. Inf. Model., 2012, 52, 1757–1768 CrossRef CAS PubMed.
- R. Ramakrishnan, P. O. Dral, M. Rupp and O. A. Von Lilienfeld, Sci. Data, 2014, 1, 1–7 Search PubMed.
- D. L. Mobley and J. P. Guthrie, J. Comput.-Aided Mol. Des., 2014, 28, 711–720 CrossRef CAS PubMed.
- M. Kuhn, I. Letunic, L. J. Jensen and P. Bork, Nucleic Acids Res., 2016, 44, D1075–D1079 CrossRef CAS PubMed.
- J. S. Smith, O. Isayev and A. E. Roitberg, Sci. Data, 2017, 4, 1–8 Search PubMed.
- J. S. Smith, R. Zubatyuk, B. Nebgen, N. Lubbers, K. Barros, A. E. Roitberg, O. Isayev and S. Tretiak, Sci. Data, 2020, 7, 1–10 CrossRef PubMed.
- D. Balcells and B. B. Skjelstad, J. Chem. Inf. Model., 2020, 60, 6135–6146 CrossRef CAS PubMed.
- A. M. Richard, R. Huang, S. Waidyanatha, P. Shinn, B. J. Collins, I. Thillainadarajah, C. M. Grulke, A. J. Williams, R. R. Lougee and R. S. Judson, et al. , Chem. Res. Toxicol., 2020, 34, 189–216 Search PubMed.
- J. Jumper, R. Evans, A. Pritzel, T. Green, M. Figurnov, O. Ronneberger, K. Tunyasuvunakool, R. Bates, A. Žídek and A. Potapenko, et al. , Nature, 2021, 596, 583–589 CrossRef CAS PubMed.
- A. Khajeh, X. Lei, W. Ye, Z. Yang, L. Hung, D. Schweigert and H.-K. Kwon, Digital Discovery, 2025, 4, 11–20 RSC.
- A. Krizhevsky, I. Sutskever and G. E. Hinton, Adv. Neural Inf. Process. Syst., 2012, 25, 1097–1105 Search PubMed.
- T. Mikolov, I. Sutskever, K. Chen, G. S. Corrado and J. Dean, Adv. Neural Inf. Process. Syst., 2013, 26, 3111–3119 Search PubMed.
- A. G. Salman, B. Kanigoro and Y. Heryadi, 2015 International Conference on Advanced Computer Science and Information Systems (ICACSIS), 2015, pp. 281–285 Search PubMed.
- X. E. Pantazi, D. Moshou, T. Alexandridis, R. L. Whetton and A. M. Mouazen, Comput. Electron. Agric., 2016, 121, 57–65 CrossRef.
- P. Graff, F. Feroz, M. P. Hobson and A. Lasenby, Mon. Not. R. Astron. Soc., 2014, 441, 1741–1759 CrossRef.
- K. T. Schütt, F. Arbabzadah, S. Chmiela, K. R. Müller and A. Tkatchenko, Nat. Commun., 2017, 8, 1–8 CrossRef PubMed.
- J. Gilmer, S. S. Schoenholz, P. F. Riley, O. Vinyals and G. E. Dahl, International Conference on Machine Learning, 2017, pp. 1263–1272 Search PubMed.
- K. Schütt, P. Kindermans, H. E. S. Felix, S. Chmiela, A. Tkatchenko and K. Müller, Advances in Neural Information Processing Systems 30: Annual Conference on Neural Information Processing Systems 2017, December 4-9, 2017, Long Beach, CA, USA, 2017, pp. 991–1001 Search PubMed.
- P. Bleiziffer, K. Schaller and S. Riniker, J. Chem. Inf. Model., 2018, 58, 579–590 CrossRef CAS PubMed.
- N. Lubbers, J. S. Smith and K. Barros, J. Chem. Phys., 2018, 148, 241715 CrossRef PubMed.
- O. T. Unke and M. Meuwly, J. Chem. Theory Comput., 2019, 15, 3678–3693 CrossRef CAS PubMed.
- B. Anderson, T. S. Hy and R. Kondor, Adv. Neural Inf. Process. Syst., 2019, 32, 14537–14546 Search PubMed.
- J. Gasteiger, J. Groß and S. Günnemann, arXiv, 2020, preprint, arXiv:2003.03123, 1–13, DOI:10.48550/arXiv.2003.03123.
- B. K. Miller, M. Geiger, T. E. Smidt and F. Noé, arXiv, 2020, preprint, arXiv:2008.08461, 1–12, DOI:10.48550/arXiv.2008.08461.
- V. G. Satorras, E. Hoogeboom and M. Welling, International Conference on Machine Learning, 2021, pp. 9323–9332 Search PubMed.
- K. Schütt, O. Unke and M. Gastegger, International Conference on Machine Learning, 2021, pp. 9377–9388 Search PubMed.
- Z. Zhang, 2024 7th International Conference on Computer Information Science and Application Technology (CISAT), 2024, pp. 919–922 Search PubMed.
- T. N. Kipf and M. Welling, 5th International Conference on Learning Representations, ICLR 2017, Toulon, France, April 24-26, 2017, Conference Track Proceedings, 2017 Search PubMed.
- G. E. Karniadakis, I. G. Kevrekidis, L. Lu, P. Perdikaris, S. Wang and L. Yang, Nat. Rev. Phys., 2021, 3, 422–440 CrossRef.
- S. Moon, W. Zhung, S. Yang, J. Lim and W. Y. Kim, Chem. Sci., 2022, 13, 3661–3673 RSC.
- W. Ji, W. Qiu, Z. Shi, S. Pan and S. Deng, J. Phys. Chem. A, 2021, 125, 8098–8106 CrossRef CAS PubMed.
- L. Branca and A. Pallottini, Monthly Notices of the Royal Astronomical Society, 2023, vol. 518, pp. 5718–5733 Search PubMed.
- J. Willard, X. Jia, S. Xu, M. Steinbach and V. Kumar, Integrating Physics-Based Modeling with Machine Learning: A Survey, arXiv, 2020, preprint, arXiv:2003.04919, DOI:10.48550/arXiv.2003.04919.
- J. S. Smith, B. Nebgen, N. Lubbers, O. Isayev and A. E. Roitberg, J. Chem. Phys., 2018, 148, 241733 CrossRef PubMed.
- J. S. Smith, B. T. Nebgen, R. Zubatyuk, N. Lubbers, C. Devereux, K. Barros, S. Tretiak, O. Isayev and A. E. Roitberg, Nat. Commun., 2019, 10, 1–8 CrossRef PubMed.
- T. Verstraelen, S. Vandenbrande, F. Heidar-Zadeh, L. Vanduyfhuys, V. Van Speybroeck, M. Waroquier and P. W. Ayers, J. Chem. Theory Comput., 2016, 12, 3894–3912 CrossRef CAS PubMed.
- RDKit: Open-source Cheminformatics, https://www.rdkit.org, Version 2022.9.4 Search PubMed.
- J. T. Barron, Continuously Differentiable Exponential Linear Units, arXiv, 2017, preprint, arXiv:1704.07483, DOI:10.48550/arXiv.1704.07483.
- A. Paszke, S. Gross, F. Massa, A. Lerer, J. Bradbury, G. Chanan, T. Killeen, Z. Lin, N. Gimelshein, L. Antiga, A. Desmaison, A. Kopf, E. Yang, Z. DeVito, M. Raison, A. Tejani, S. Chilamkurthy, B. Steiner, L. Fang, J. Bai and S. Chintala, Adv. Neural Inf. Process. Syst., 2019, 32, 8024–8035 Search PubMed.
- M. Geiger and T. Smidt, arXiv, 2022, preprint, arXiv:2207.09453, 1–22, DOI:10.48550/arXiv.2207.09453.
- S. Batzner, A. Musaelian, L. Sun, M. Geiger, J. P. Mailoa, M. Kornbluth, N. Molinari, T. E. Smidt and B. Kozinsky, Nat. Commun., 2022, 13, 2453 CrossRef CAS PubMed.
- J. Li, L. Knijff, Z.-Y. Zhang, L. Andersson and C. Zhang, J. Chem. Theory Comput., 2025, 21, 1382–1395 CrossRef CAS PubMed.
- M. Wang, D. Zheng, Z. Ye, Q. Gan, M. Li, X. Song, J. Zhou, C. Ma, L. Yu, Y. Gai, T. Xiao, T. He, G. Karypis, J. Li and Z. Zhang, Deep Graph Library: A Graph-centric, Highly-performant Package for Graph Neural Networks, arXiv, 2019, preprint, arXiv:1909.01315, DOI:10.48550/arXiv.1909.01315.
- NVIDIA Corporation, NVIDIA A100 Datasheet, 2022 Search PubMed.
- ITaP Research Computing, Gilbreth User Guide, Purdue University, 2022 Search PubMed.
- S. R. Jensen, S. Saha, J. A. Flores-Livas, W. Huhn, V. Blum, S. Goedecker and L. Frediani, J. Phys. Chem. Lett., 2017, 8, 1449–1457 CrossRef CAS PubMed.
- NVIDIA Corporation, NVIDIA Tesla P100 Datasheet, 2016 Search PubMed.
- Tech Powerup, NVIDIA GeForce GTX 1080 Specifications, 2016, https://www.techpowerup.com/gpu-specs/geforce-gtx-1080.c2839, viewed on 05/03/24 Search PubMed.
- D. G. Smith, L. A. Burns, A. C. Simmonett, R. M. Parrish, M. C. Schieber, R. Galvelis, P. Kraus, H. Kruse, R. Di Remigio and A. Alenaizan, et al. , J. Chem. Phys., 2020, 152, 184108 CrossRef CAS PubMed.
- National Center for Biotechnology Information, PubChem Compound Summary for CID 10778246, 2025, https://pubchem.ncbi.nlm.nih.gov/compound/10778246, accessed 05/23/2025 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5dd00228a |
| This journal is © The Royal Society of Chemistry 2025 |