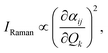Open Access Article
Open Access ArticleMol2Raman: a graph neural network model for predicting Raman spectra from SMILES representations
Salvatore Sorrentino†
 *abc,
Alessandro Gussoni
*abc,
Alessandro Gussoni d,
Francesco Calcagno
d,
Francesco Calcagno ef,
Gioele Pasotti
ef,
Gioele Pasotti a,
Davide Avagliano
a,
Davide Avagliano g,
Ivan Rivalta
g,
Ivan Rivalta ef,
Marco Garavelli
ef,
Marco Garavelli e and
Dario Polli
e and
Dario Polli *ah
*ah
aDepartment of Physics, Politecnico di Milano, Piazza Leonardo da Vinci, 32, 20133 Milan, Italy. E-mail: salvatore.sorrentino@polimi.it; dario.polli@polimi.it
bLaser Biomedical Research Center, G. R. Harrison Spectroscopy Laboratory, Massachusetts Institute of Technology, Cambridge, MA, USA
cCutaneous Biology Research Center, Massachusetts General Hospital, Harvard Medical School, Boston, MA, USA
dCitizen Scientist, Italy
eDepartment of Industrial Chemistry “Toso Montanari”, Universitá degli Studi di Bologna, Via Piero Gobetti, 85, I-40129 Bologna, Italy
fCenter for Chemical Catalysis – C3, Alma Mater Studiorum University of Bologna, via Piero Gobetti 85, 40129 Bologna, Italy
gChimie ParisTech, PSL University, CNRS, Institute of Chemistry for Life and Health Sciences (iCLeHS UMR 8060), 75005 Paris, France
hCNR-Institute for Photonics and Nanotechnologies (CNR-IFN), Milan, Italy
First published on 25th November 2025
Abstract
Raman spectroscopy is a powerful technique for probing molecular vibrations, yet the computational prediction of Raman spectra remains challenging due to the high cost of quantum chemical methods and the complexity of structure–spectrum relationships. Here, we introduce Mol2Raman, a deep-learning framework that predicts spontaneous Raman spectra directly from SMILES representations of molecules. The model leverages Graph Isomorphism Networks with edge features (GINE) to encode molecular topology and bond characteristics, enabling accurate prediction of both peak positions and intensities across diverse chemical structures. Trained on a novel dataset of over 31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules with state-of-the-art Density Functional Theory (DFT)-calculated Raman spectra, Mol2Raman outperforms both fingerprint-based similarity models and Chemprop-based neural networks. It achieves a high fidelity in reproducing spectral features, including for molecules with low structural similarity to the training set and for enantiomeric inversion. The model offers fast inference times (22 ms per molecule), making it suitable for high-throughput molecular screening. We further deploy Mol2Raman as an open-access web application, enabling real-time predictions without specialized hardware. This work establishes a scalable, accurate, and interpretable platform for Raman spectral prediction, opening new opportunities in molecular design, materials discovery, and spectroscopic diagnostics.
000 molecules with state-of-the-art Density Functional Theory (DFT)-calculated Raman spectra, Mol2Raman outperforms both fingerprint-based similarity models and Chemprop-based neural networks. It achieves a high fidelity in reproducing spectral features, including for molecules with low structural similarity to the training set and for enantiomeric inversion. The model offers fast inference times (22 ms per molecule), making it suitable for high-throughput molecular screening. We further deploy Mol2Raman as an open-access web application, enabling real-time predictions without specialized hardware. This work establishes a scalable, accurate, and interpretable platform for Raman spectral prediction, opening new opportunities in molecular design, materials discovery, and spectroscopic diagnostics.
1 Introduction
Raman spectroscopy is a versatile, label-free analytical technique widely applied in chemistry, materials science, and pharmaceuticals, offering molecular structure and bonding information through vibrational modes.1,2 Its applications include compound identification,3 material characterization,4 and non-invasive medical diagnostics.5 However, acquiring experimental high-quality Raman spectra is expensive and time-consuming, limiting their use in large-scale molecular screening.6Computational methods, particularly Density Functional Theory (DFT), provide an alternative for calculating Raman-active vibrational frequencies.7,8 While highly accurate, DFT-based approaches scale poorly with molecular size due to their high computational cost, making them impractical for high-throughput applications.9,10 Similarly, universal machine learning models, such as the Artificial Intelligence-Quantum Mechanical (AIQM) approach, have been successfully applied to infrared (IR) spectrum prediction, offering accuracy comparable to DFT with significantly reduced inference times.11,12 However, these models still face scalability challenges in the context of large-scale screening, where sub-second predictions are often required. Fast and accurate computational predictions of spectroscopic properties are particularly crucial in fields such as molecular identification and molecular design, where Raman-active molecules are used in applications such as biomedical imaging, environmental sensing, and anti-counterfeiting technologies.13,14 Other predictive models, such as heuristic fingerprint-based approaches, often fail to capture the nuanced relationships between molecular structure and vibrational properties.15 Descriptor-based methods, such as polarizability tensor predictions, introduce propagation errors and transferability limitations, leading to misalignment between predicted and actual Raman peak localization.16–19 In addition, recent advances in machine learning for vibrational spectroscopy have also demonstrated the significant potential of neural network architectures in predicting vibrational density of states and phonon band structures,20,21 though these methods have not been specifically optimized for the unique challenges of Raman spectroscopy.
To address these limitations, we introduce Mol2Raman, a Graph Neural Network (GNN)-based framework that directly predicts spontaneous Raman spectra from SMILES (Simplified Molecular Input Line Entry System) molecular representations.22–24 GNNs have demonstrated significant impact across various scientific fields, particularly in drug discovery, where they have enabled accurate prediction of molecular interactions, drug-target binding affinities, and de novo molecular design, accelerating pharmaceutical research.25–27 Unlike descriptor-based approaches, Mol2Raman learns from graph-based molecular representations, where atoms and bonds are modeled as nodes and edges, aligning naturally with the underlying physics of molecular vibrations.28–30 By leveraging Graph Isomorphism Networks with Edge (GINE) convolutions,31 Mol2Raman effectively captures both local atomic interactions and global molecular structure, improving predictive accuracy over conventional ML models.30 In addition, we integrate traditional chemical descriptors such as Daylight and Morgan fingerprints into the GINE molecular representation.32,33 This combination provides a more comprehensive molecular description, improving the model's ability to predict Raman spectral properties, such as differences in enantiomeric Raman modes. By leveraging this hybrid approach, Mol2Raman benefits from both detailed molecular graph learning and the chemical insights encoded in established descriptors. One of the key contributions of this work is the development of a large-scale, high-fidelity dataset comprising over 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 organic molecules taken from the QM9 database,34 each paired with DFT-calculated Raman spectra using the academic-free ORCA software,8,35 used to train the Mol2Raman model. This study focuses on training the model on high-quality DFT-generated spectra, given the challenges of assembling sufficiently large and standardized experimental Raman spectral datasets available online,36 representing also a foundation model for possible future fine-tuning with experimental data.
000 organic molecules taken from the QM9 database,34 each paired with DFT-calculated Raman spectra using the academic-free ORCA software,8,35 used to train the Mol2Raman model. This study focuses on training the model on high-quality DFT-generated spectra, given the challenges of assembling sufficiently large and standardized experimental Raman spectral datasets available online,36 representing also a foundation model for possible future fine-tuning with experimental data.
Additionally, we introduce a custom loss function specifically designed for Raman spectrum prediction. This function balances global spectral similarity with precise peak-position constraints. Unlike conventional loss functions that prioritize only overall spectral shape, our hybrid approach enhances Raman-active peak localization, leading to significantly improved predictive accuracy.
While not a perfect match to DFT calculations, our model provides highly accurate predictions with an inference time of less than a second per molecule, compared to the hours required for DFT calculations. This balance of speed and accuracy makes Mol2Raman particularly valuable for preliminary molecular design studies, where researchers need to rapidly screen thousands of candidate molecules to identify those with desirable spectroscopic properties. By enabling efficient pre-selection, Mol2Raman significantly accelerates high-throughput screening workflows. Once an initial shortlist is identified, more precise DFT calculations or experimental measurements can be performed to refine the selection and obtain final optimized molecular candidates.
Finally, we developed a free web-based platform for Mol2Raman, enabling real-time Raman spectrum predictions directly from SMILES input. By combining a novel dataset, an advanced GNN architecture, and an accessible web application, Mol2Raman provides a fast, scalable, and high-accuracy alternative to first-principles Raman spectrum calculations. To the best of our knowledge, this work represents the first deep-learning framework specifically designed for Raman spectral predictions,37 with broad implications for materials discovery, molecular design, and high-throughput chemical screening.
2 Methods
2.1 Dataset preparation
The Mol2Raman model is trained using a novel dataset of Raman spectra for 31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 776 molecules. These molecules are extracted from the dataset provided by Ramakrishnan et al.,34 which contains the elements C, H, O, N, and F with up to nine heavy atoms. This dataset comprises 134
776 molecules. These molecules are extracted from the dataset provided by Ramakrishnan et al.,34 which contains the elements C, H, O, N, and F with up to nine heavy atoms. This dataset comprises 134![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules and provides a chemical space with diverse molecular and stoichiometric properties.
000 molecules and provides a chemical space with diverse molecular and stoichiometric properties.
The molecular geometries in the QM9 dataset were optimized using DFT at the B3LYP/6-31G(2df,p) level of theory,38,39 which balances computational efficiency with predictive accuracy for organic compounds.34 The dataset contains a wide range of quantum chemical properties, such as dipole moments, isotropic polarizabilities, frontier orbital eigenvalues, harmonic vibrational frequencies, and thermodynamic properties like atomization energies, enthalpies, and free energies at 298.15 K.
Starting from these optimised geometries in Cartesian coordinates, we calculate the Raman spectral activities using ORCA software8 and a high-performance computing (HPC) cluster provided by CINECA,40 using the BP86/DEF2-SVP level of theory as suggested in ORCA.41,42 This calculation allows us to obtain molecular Raman spectral information in the region from 500 cm−1 to 3500 cm−1. We retain only molecules whose numerical frequency calculations are completed without any error or missing displaced geometry, and discard all incomplete runs. The final curated dataset, after excluding 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 782 molecules that report SCF/NUMCALC failures in finite-difference frequency calculations, contains 31
782 molecules that report SCF/NUMCALC failures in finite-difference frequency calculations, contains 31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 776 molecules used for training, validation, and testing of the model. No additional filtering of DFT activities is applied. The ORCA software package provides advanced tools for calculating vibrational spectra using DFT,43 including Raman activities and IR spectra, which are essential for understanding molecular interactions with light. Raman activity is a distinct concept from Raman intensity. The former is an intrinsic molecular property derived from quantum chemical calculations, while the latter depends on experimental conditions, such as the wavelength of incident light and the temperature of the system.44 Raman activities are determined using the derivatives of the molecular polarizability tensor with respect to the vibrational normal coordinates as given by:43
776 molecules used for training, validation, and testing of the model. No additional filtering of DFT activities is applied. The ORCA software package provides advanced tools for calculating vibrational spectra using DFT,43 including Raman activities and IR spectra, which are essential for understanding molecular interactions with light. Raman activity is a distinct concept from Raman intensity. The former is an intrinsic molecular property derived from quantum chemical calculations, while the latter depends on experimental conditions, such as the wavelength of incident light and the temperature of the system.44 Raman activities are determined using the derivatives of the molecular polarizability tensor with respect to the vibrational normal coordinates as given by:43
To encode the chemical information of each molecule, we use its SMILES representation as input to the neural network. SMILES is a widely used notation to represent the structure of chemical molecules in a compact and machine-processable format,22–24 encoding the molecular structure as a linear string of ASCII characters, where atoms are represented by their atomic symbols, and bonds are described (implicitly or explicitly) by specific characters. The simplicity and expressiveness of SMILES made it one of the standards for molecular representation in cheminformatics and computational chemistry. However, it should be noted that while SMILES encodes connectivity, it does not inherently capture all the three-dimensional geometric information of molecules, which may be necessary for certain property predictions.45
2.2 Dataset preprocessing
Spontaneous Raman spectra exhibit two distinct spectral regions: the fingerprint region and the C–H stretching region.46 The former (500–1800 cm−1) is characterized by complex vibrational modes arising from bending and stretching of functional groups47 and is widely used for molecular identification and structural elucidation. The latter (2800–3300 cm−1) corresponds to stretching vibrations of carbon–hydrogen bonds,47 providing insights into aliphatic and aromatic structures and aiding in conformational analysis and intermolecular interaction studies.48Given the distinct physical mechanisms governing Raman modes in these spectral regions, we divided the global spectrum (500–3500 cm−1) into two subregions: the fingerprint region between 500 cm−1 and 2100 cm−1 and the C–H stretching region between 1900 cm−1 and 3500 cm−1. To ensure a smooth transition between spectral subregions, we introduce an overlapping window (1900–2100 cm−1), facilitating seamless integration of predictions across both regions.
Moreover, because DFT calculations yield discrete Raman-active vibrational frequencies, they lack natural peak broadening effects,8 resulting in sparse spectra with numerous zero-intensity points. This sparsity introduces challenges during neural network training by adding unnecessary complexity. To address this, we employ a two-stage max pooling strategy,49 commonly used in computer vision, to downsample spectra. Max pooling involves selecting the maximum value within a defined window, helping to reduce the dimensionality of the data while retaining important features. First, we apply max pooling with a resolution of 2 cm−1 to the raw DFT-calculated Raman activities. The resulting 800-point spectra are used as the reference spectra, namely these are considered the “true” Raman spectra of each molecule and are used for evaluation throughout the paper. Second, for the training phase of the Mol2Raman model, we further apply max pooling with a 6 cm−1 resolution to reduce the 800-point spectra to 267 points. This coarser representation simplifies the learning task by reducing sparsity and dimensionality, while retaining the key vibrational features. The resulting training spectra retain spectral integrity, with Raman-active frequencies still well-aligned and a maximum deviation of only 3 cm−1 from the reference.
In addition to these graph-based local descriptors, we also employ two other sets of features to enhance the input descriptive power of molecules, the Daylight fingerprint32 and the Morgan fingerprint.33 Briefly, the Daylight fingerprint encodes the global molecular structures into a binary vector where each bit represents the presence or absence of a specific substructure or molecular pattern. The fingerprint is generated by systematically decomposing the molecule into all possible linear substructures up to a certain length. Each substructure is then converted into a numerical representation that activates one or more specific positions within a fixed-length binary vector, encoding the presence of that feature, in a process called hashing. This method is particularly effective in similarity searching, where the Tanimoto similarity is often used to compare fingerprints.51 Alongside this, the Morgan fingerprint is an advanced and widely used fingerprinting method, particularly in modern machine learning applications. It is based on the Extended Connectivity Fingerprints algorithm.33 Unlike the Daylight fingerprint, which relies on linear paths, the Morgan fingerprint captures local circular environments around each atom, making it more effective at encoding molecular topology and chemical context. The algorithm iteratively expands around each atom up to a specified radius, generating unique identifiers (hash codes) for the substructures at each step. These identifiers are then mapped to a fixed-length binary or integer vector.
The combination of Daylight and Morgan fingerprints as input to a neural network allows the model to learn from the complementary strengths of linear path-based substructure detection and circular neighbourhood encoding. These complementary descriptors encode long-range molecular interactions and structural patterns, refining the ability of the model to capture both local and global spectroscopic variations.
2.3 Mol2Raman architecture
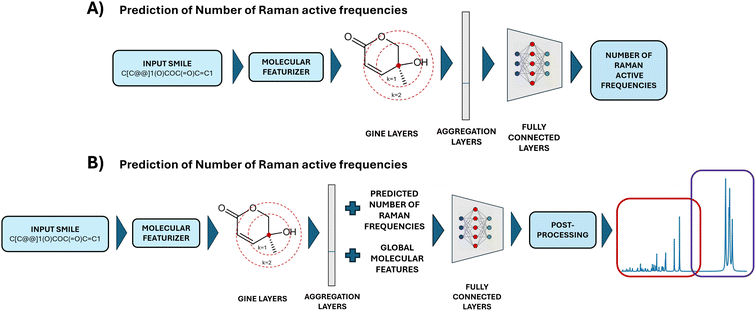
The model architecture employed in this work relies on two graph neural networks: one for predicting the number of Raman-active frequencies for a given SMILES and one for predicting the corresponding Raman activities. Both networks are trained twice: once for predicting Raman spectra in the fingerprint region and once in the C–H stretching region, therefore resulting in four training runs in total. These two networks share the same core architecture, but are differentiated in terms of which features they take in input and on which target variable they are trained.As illustrated in Fig. 1A, the network follows a graph-based deep learning architecture. The input SMILES undergoes transformation through the molecular featurizer, converting the molecular structure into a graph representation that captures atomic and bond-level information. This featurization enables the model to extract meaningful structural features directly from the molecular graph.
At its core, the network consists of four GINEConv layers,31 which allow the atomic features to be influenced by neighboring atoms up to four hops away. This hierarchical aggregation captures complex interatomic relationships and molecular topologies that are essential for predicting vibrational frequencies. Each GINEConv layer incorporates a linear transformation of the node features, followed by batch normalization to stabilize learning and improve convergence,52 and a ReLU activation function is applied after each linear transformation to introduce non-linearity.53 These steps ensure robust feature extraction, preserving both local atomic environments and global molecular connectivity.54
Following the GINEConv layers, a global pooling operation is applied to aggregate node-embedding information across the entire molecular graph54 through a sum pooling function. This step allows the network to produce a fixed-size embedding, irrespective of the number of atoms in the molecule. The pooled representation is then passed through two fully-connected linear layers. The first linear layer expands the dimensionality of the pooled features by a factor of 4 to enhance expressiveness before making the final predictions. The second linear layer maps these features to the final output, which corresponds to the predicted number of peaks in the spectrum and it is obtained via a Softplus function.55 Between the two layers, a dropout of a factor 0.25 is used.
The output from the aggregation layers goes in input to three fully connected layers, with two dropout layers having a dropout parameter of 0.4 between them. The last layer is represented by a Softplus layer having a dimension equal to the training spectra (267 points, see Dataset Preprocessing), which generates the network output, namely the Raman spectrum. The final output of the network is obtained after a Monte Carlo dropout step with 10 rounds of predictions.56 Fixed hyperparameters are selected on the validation set to balance model complexity and computational efficiency, following a 20-trial random search over the architecture's layers, dropout rate, and loss weights, and targeted manual adjustments informed by validation curves.
Like the previous one, also this architecture works both in the fingerprint and C–H regions, providing in output two vectors of size 267 representing the predicted Raman activities for the two spectral regions. Moreover, an overlap of 33 points between the fingerprint and C–H regions is included in these 267-sized vectors, which is given by the overlap in the range between 1900–2100 cm−1 discussed above.
2.4 Model training
The training process is designed to independently optimize models for the fingerprint and C–H stretching regions, allowing each network to specialize in the distinct spectral characteristics of its respective domain. This approach improves generalization and predictive accuracy by ensuring that the model effectively captures the molecular vibrational modes relevant to each spectral region. Every molecule in the dataset contains at least one carbon and one hydrogen atom. Additionally, 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 129 molecules include oxygen, 19
129 molecules include oxygen, 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 416 contain nitrogen, and 484 feature fluorine. More details on the molecular properties of the dataset are reported in SI Table 1. The dataset is randomly split into 80% (25
416 contain nitrogen, and 484 feature fluorine. More details on the molecular properties of the dataset are reported in SI Table 1. The dataset is randomly split into 80% (25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 440 molecules) for training, 10% (3
440 molecules) for training, 10% (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 168 molecules) for validation, and 10% (3
168 molecules) for validation, and 10% (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 168 molecules) for testing. SI Fig. S1 shows the distribution of training and test molecules in the space of the first two Principal Components (PC1 and PC2) calculated over the Morgan fingerprint representation of each SMILES, which proves the random sampling of the test molecules from the entire dataset population. The training and validation datasets are used to iteratively refine model parameters, while the independent test set is reserved for final performance evaluation.
168 molecules) for testing. SI Fig. S1 shows the distribution of training and test molecules in the space of the first two Principal Components (PC1 and PC2) calculated over the Morgan fingerprint representation of each SMILES, which proves the random sampling of the test molecules from the entire dataset population. The training and validation datasets are used to iteratively refine model parameters, while the independent test set is reserved for final performance evaluation.
The two networks discussed above are trained using different loss functions. The network predicting the number of Raman-active frequencies is optimized using the Root Mean Squared Error (RMSE), whereas the network predicting Raman intensities is trained with a custom peak-weighted RMSE loss function. This loss function enhances the model's ability to correctly identify Raman peaks by assigning different weights to true positives (TP), true negatives (TN), false positives (FP), and false negatives (FN).57 The function is formally defined as:
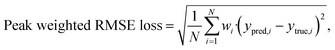 | (1) |
Model parameters are optimized using Stochastic Gradient Descent (SGD) with momentum.58 The learning rate is set to an initial fixed value and gradually reduced throughout training to ensure stable convergence. Momentum is included to accelerate updates in the correct direction while mitigating oscillations, and weight decay is applied to prevent overfitting by penalizing excessively large parameter values. Training is conducted for a maximum of 1500 epochs under an early-stopping framework, where every two epochs the validation loss is computed, and the model parameters corresponding to the lowest loss value are retained.59 The computational time for the prediction of Raman spectra is on average 22 milliseconds per molecule, representing a substantial improvement over DFT calculations, which require hours. More details on the hardware and computational time for training are reported in SI Note 1.
The number of trainable parameters differs significantly between the two models due to architectural variations. The network predicting the number of Raman-active frequencies consists of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 530
530![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 193 parameters per spectral region, while the network predicting Raman activity has 77
193 parameters per spectral region, while the network predicting Raman activity has 77![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 091
091![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 419 parameters per spectral region. The larger parameter count in the latter model results from the inclusion of both global molecular features and the predicted number of Raman-active frequencies before the fully connected network. This additional information increases the dimensionality of the first layer, leading to a more complex multi-layer architecture.
419 parameters per spectral region. The larger parameter count in the latter model results from the inclusion of both global molecular features and the predicted number of Raman-active frequencies before the fully connected network. This additional information increases the dimensionality of the first layer, leading to a more complex multi-layer architecture.
2.5 Prediction post-processing
Predictions generated from the second network undergo a post-processing step to fully use the information learnt by the network predicting the number of Raman modes and to join the fingerprint and C–H spectral regions on a final spectral window between 500 cm−1 and 3500 cm−1 with a spectral step of 2 cm−1.In detail, the initial post-processing step involves upscaling the 267-dimensional vectors (obtained from max pooling) corresponding to the fingerprint and C–H predictions back to 800-dimensional vectors. This is accomplished through linear interpolation, ensuring a continuous and coherent spectral representation across the entire frequency range.
After the upscaling process, we perform a filtering step on the predictions of Raman activities. This is done using the prediction on the number of Raman-active modes using prominence as a parameter.60 In this context, prominence measures how much a Raman peak rises above its neighboring valleys. This metric assures that only peaks that are distinctly higher than their immediate surroundings are detected, filtering out minor fluctuations or noise. Specifically, using the information on the predicted number of Raman peaks for the fingerprint and C–H regions, we retain in the prediction of Raman activities only the points corresponding to the most significant peaks. To achieve this, the predicted peaks are first ranked in descending order based on their prominence. We then select only the top peaks, matching the number predicted by the first network, ensuring that the most prominent spectral features are preserved while less significant fluctuations are discarded. Here, prominence is computed with the signal.peak_prominences method in the Scipy library, which measures how much a peak rises above its surrounding valleys and it is used solely for ranking predicted peaks and does not alter the peak definition. This approach effectively refines the predicted spectrum by focusing on the most relevant Raman signals.
We then concatenate the predictions from the two distinct spectral regions, performing an averaging operation within the overlapping window between 1900 and 2100 cm−1. This averaging step ensures a smooth and continuous transition between the two spectral domains, facilitated by the few Raman activities that generally occur in this region.46 Eventually, the final spectrum accurately represents the complete Raman profile (from 500 cm−1 to 3500 cm−1 Raman shift with a step of 2 cm−1), essential for downstream analyses and comparison with experimental spectra.
Subsequently, since the model output consists of discrete peak predictions, we apply a convolution with a Lorentzian function defined by a full width at half maximum (FWHM) of 10 cm−1.61 This specific FWHM value ensures that each predicted peak is broadened to realistically reproduce the natural line shape typically observed in experimental Raman spectra.62 This convolution process broadens the predicted peaks, generating a continuous and smooth spectrum that more accurately resembles an experimentally measured Raman spectrum.
After that, we normalize the resulting spectrum dividing it by the sum of its vector representation, such that the sum of the entire spectrum equals 1. These smoothing and normalization processes facilitate a continuous and coherent representation across the entire spectrum of the Raman predictions and are important for accurate performance evaluation and comparisons with other models.
3 Results and discussion
3.1 Evaluation metrics
To evaluate the performance of the Mol2Raman network and compare it against other models, we employ a novel evaluation metric, the F1 score with tolerance as described below. In addition to this, we assess model performance also using well-established metrics like Spectral Information Similarity (SIS)63 and cosine similarity.64![[small nu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e1dd.gif) 1,
1, ![[small nu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e1dd.gif) 2 ,…,
2 ,…, ![[small nu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e1dd.gif) n}, the set of True Positives (TP) is defined as:
n}, the set of True Positives (TP) is defined as:
TP = {![[small nu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e1dd.gif) j|∃νi such that | j|∃νi such that |![[small nu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e1dd.gif) j − νi| ≤ δ & | j − νi| ≤ δ & |![[small nu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e1dd.gif) k − νi| > δ∀k < j}. k − νi| > δ∀k < j}.
| (2) |
This formulation ensures that each true peak is matched only once within the defined tolerance, preventing multiple assignments and maintaining evaluation integrity. We adopt three tolerance values—δ = 10, 15, and 20 cm−1—to benchmark model flexibility and accuracy.
Based on this framework, we compute the F1 score, defined as the harmonic mean of precision (the fraction of predicted peaks that are correct) and recall (the fraction of true peaks that were identified):
 | (3) |
Extending from the concept of F1 score with tolerance, seamlessly also a Precision with Tolerance and a Recall with Tolerance can be defined.
3.2 Model performance for the number of Raman-active frequencies
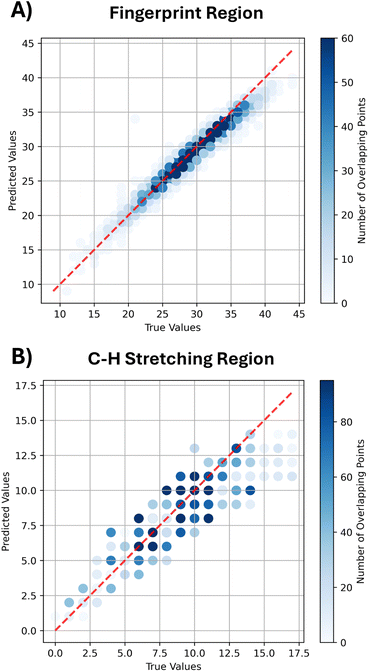
An essential component of the Mol2Raman architecture is the accurate prediction of the number of Raman-active frequencies for a given molecule. This step plays a dual role: it serves as an input feature for predicting Raman activities and acts as a filtering criterion in the post-processing of spectral data.Fig. 2A and B illustrate the model's predictive performance by comparing predicted and actual Raman-active peaks on the test set of 3,168 molecules. The density of points in these scatterplots highlights the frequency distribution of prediction outcomes.
To quantitatively assess model performance, standard regression metrics, including the coefficient of determination (R2), root mean squared error (RMSE) and accuracy, are computed. Here, accuracy is defined as the ratio between the number of molecules for which the predicted number of Raman-active modes exactly matches the DFT-calculated value, and the total number of molecules. The results, summarized in Table 1, confirm the model's strong predictive capability.
| Metric | Fingerprint region | C–H region |
|---|---|---|
| R2 | 0.937 | 0.844 |
| RMSE | 1.282 | 1.089 |
| Accuracy | 0.349 | 0.458 |
The high R2 values (0.937 for the fingerprint region and 0.844 for the C–H region) indicate that the model successfully captures the correlation between molecular structure and Raman activity. Notably, the observed accuracy values for fingerprint (0.349) and C–H (0.458) regions are meaningful considering the difficulty of predicting exact counts across a wide range of possible peak values in the two regions, as shown in SI Fig. S2 and S3. Additionally, the low RMSE values suggest minimal deviation from actual peak counts, ensuring reliable performance. The few mispredictions observed are primarily limited to differences of one or two peaks, demonstrating the robustness of the model. An analysis of different performances for the prediction of the number of Raman-active frequencies in the C–H and fingerprint regions is reported in SI Note 2 and Fig. S2, S3.
This predictive accuracy is critical for the overall Mol2Raman pipeline. First, the estimated number of Raman-active peaks guides the subsequent network in predicting Raman activities, helping it focus on the correct number of peaks as an initial molecular feature. Second, it enhances the post-processing step by refining the final spectral output, ensuring that only the most chemically relevant peaks are retained. This filtering improves the interpretability of the predicted spectra and their alignment with experimental data. The strong performance of this model establishes a reliable foundation for subsequent stages in the Mol2Raman framework.
3.3 Model performance for Raman activities
The evaluation of the model for the predictions of Raman activities within the global Mol2Raman framework is performed by calculating metrics on the test dataset composed of 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 168 molecules. This model is responsible for generating Raman spectra, which are subsequently refined through the post-processing pipeline. The primary metric used to assess the model performance is the F1 score with tolerance. This choice is motivated by the central role of peak positions in defining Raman spectral specificity,3 ensuring both selectivity and completeness in spectral peak identification, a key requirement in molecular vibrational analysis.
168 molecules. This model is responsible for generating Raman spectra, which are subsequently refined through the post-processing pipeline. The primary metric used to assess the model performance is the F1 score with tolerance. This choice is motivated by the central role of peak positions in defining Raman spectral specificity,3 ensuring both selectivity and completeness in spectral peak identification, a key requirement in molecular vibrational analysis.
Results in terms of F1 score, precision and recall for different tolerance levels are shown in Table 2. These outcomes highlight the robustness of the Mol2Raman model in accurately predicting Raman activities in both the fingerprint and C–H stretching regions, respectively achieving F1 scores of 0.631 and 0.680, with a tolerance window of 15 cm−1. This performance aligns well with standard experimental practices in Raman spectroscopy, acknowledging that experimental Raman peaks often exhibit shifts of up to 10–15 cm−1 due to thermal broadening, matrix effects, and instrumental resolution, thus a ±15 cm−1 tolerance window provides a chemically realistic and spectroscopically grounded evaluation criterion.67,68
| Metric (tolerance) | Fingerprint region | CH region |
|---|---|---|
| F1 score (10 cm−1) | 0.551 | 0.617 |
| F1 score (15 cm−1) | 0.631 | 0.680 |
| F1 score (20 cm−1) | 0.705 | 0.739 |
| Precision (10 cm−1) | 0.549 | 0.614 |
| Precision (15 cm−1) | 0.629 | 0.677 |
| Precision (20 cm−1) | 0.703 | 0.736 |
| Recall (10 cm−1) | 0.553 | 0.624 |
| Recall (15 cm−1) | 0.634 | 0.688 |
| Recall (20 cm−1) | 0.708 | 0.748 |
To better evaluate the model, we also calculate the spectral similarity between predicted and calculated Raman spectra using Spectral Information Similarity (SIS) and Cosine Similarity,63,64 as shown in Table 3. These metrics assess the overall spectral shape and intensity distribution, complementing the peak-based evaluation. For this purpose, both the predicted and calculated spectra are convolved with Lorentzian functions to simulate natural peak broadening, as discussed previously.
| Metric | Fingerprint region | C–H region |
|---|---|---|
| SIS | 0.604 | 0.698 |
| Cosine similarity | 0.689 | 0.737 |
The results in Table 3 reveal differences in model performance between the two spectral regions. Higher average SIS and cosine similarity scores in the C–H region (0.698 and 0.737, respectively) indicate superior performance in predicting C–H stretching vibrations compared to the fingerprint region (0.604 and 0.689). This discrepancy is likely due to the simpler vibrational modes in the C–H region, which are predominantly influenced by localized molecular bonds. On the other hand, the fingerprint region reflects the complex global 3D molecular geometry, which is more challenging to model from SMILES representations.69,70
After evaluating the two separated spectral windows, we also assess the full spectral range between 500 and 3500 cm−1 consequent to the concatenation of the two regions as discussed previously.
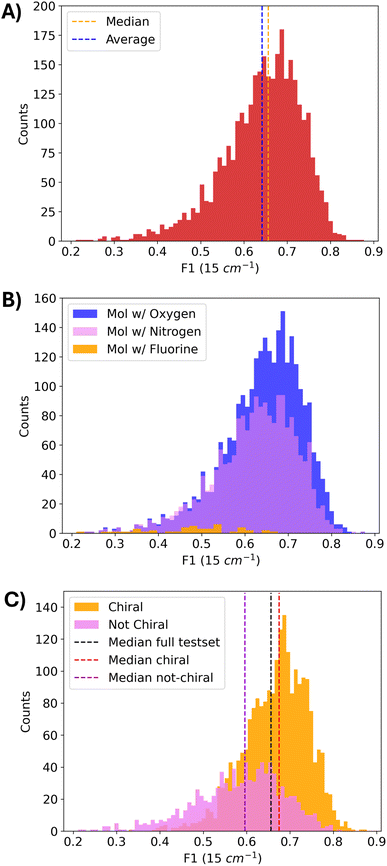
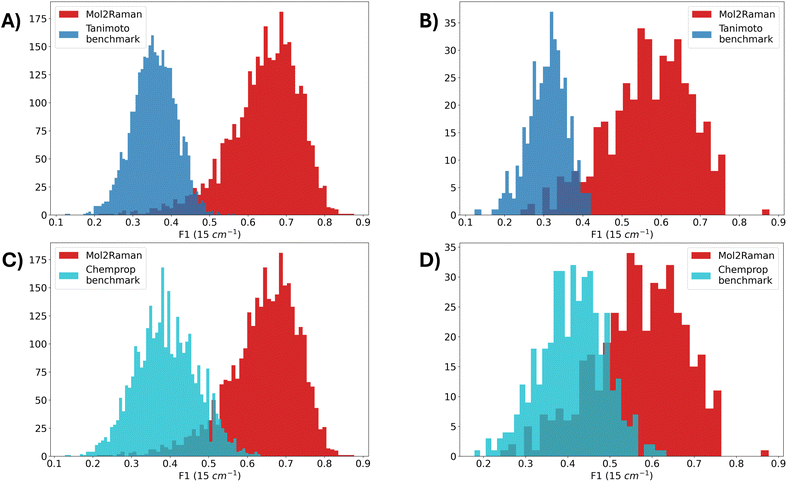
As shown in Table 4, the model demonstrates consistent performance across the entire Raman spectrum, in terms of both distribution mean and median. The model achieves a mean F1 score of 0.642, with corresponding precision and recall values of 0.640 and 0.645. Additionally, the F1 score distribution across the entire test dataset, shown in Fig. 3A, further highlights the model's reliability and generalizability, with the majority of predictions achieving high F1 scores, reflecting consistent performance across diverse molecular structures.
| Metric | Full spectrum mean (15 cm−1 tolerance) | Full spectrum median (15 cm−1 tolerance) |
|---|---|---|
| F1 score | 0.642 | 0.656 |
| Precision | 0.640 | 0.651 |
| Recall | 0.645 | 0.658 |
Furthermore, the SIS score of 0.669 and cosine similarity of 0.735 (Table 5) reflect the ability of Mol2Raman to integrate predictions from both spectral regions into a coherent and accurate full-spectrum representation reproducing DFT calculated spectra at a very high degree. The combined analysis benefits from the complementary information in the fingerprint and C–H regions, enhancing the overall spectral prediction. In SI Table 2 we also show that combining the predicted number of Raman-active modes with Daylight and Morgan fingerprints yields the best performance across metrics, outperforming all other combinations of these three global molecular descriptors.
| Metric | Full spectrum |
|---|---|
| SIS | 0.669 |
| Cosine similarity | 0.735 |
Moreover, Fig. 3B shows the distribution of F1 scores at 15 cm−1 tolerance for different molecules of the test dataset, namely molecules with at least one oxygen atom (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 703 molecules), at least one nitrogen atom (1
703 molecules), at least one nitrogen atom (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 940 molecules) and at least one fluorine atom (44 molecules), whose results are provided in Table 6. We see that molecules with at least one fluorine atom are strongly underrepresented in both the training and test datasets (SI Table 1); however, they still present a fairly good F1 score of 0.481. Instead, molecules with at least one nitrogen (mean F1 score of 0.622) or one oxygen atom (mean F1 score of 0.641) more closely resemble the global F1 score distribution of Fig. 3A, as expected due to the larger representativeness in the training dataset.
940 molecules) and at least one fluorine atom (44 molecules), whose results are provided in Table 6. We see that molecules with at least one fluorine atom are strongly underrepresented in both the training and test datasets (SI Table 1); however, they still present a fairly good F1 score of 0.481. Instead, molecules with at least one nitrogen (mean F1 score of 0.622) or one oxygen atom (mean F1 score of 0.641) more closely resemble the global F1 score distribution of Fig. 3A, as expected due to the larger representativeness in the training dataset.
| Typology | Mean | Median | St. dev. |
|---|---|---|---|
| Atomic species | |||
| Oxygen | 0.641 | 0.655 | 0.093 |
| Nitrogen | 0.622 | 0.633 | 0.096 |
| Fluorine | 0.481 | 0.488 | 0.108 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Chirality | |||
| Chiral | 0.667 | 0.675 | 0.074 |
| Not chiral | 0.584 | 0.596 | 0.103 |
We further examine the distribution of F1 scores for chiral and achiral molecules in the test dataset, as presented in Fig. 3C and summarized in Table 6. Notably, the model exhibits stronger predictive performance on chiral molecules compared to not-chiral ones. This trend is partially attributed to the underrepresentation of non-chiral compounds in the training set (see the SI), but also to the fact that chirality is explicitly included as a molecular input feature. Moreover, the model successfully captures the influence of the enantiomeric inversion on Raman spectra, reproducing the differences between enantiomers' Raman modes, as illustrated in SI Fig. S9 and S10. We mainly attribute this result to the comprehensive set of descriptors used to represent molecules, combining both local features through GINE layers and global features through Morgan and Daylight fingerprints. Thus, this combination allows the model to learn the subtle structural relations which produce spectral differences under enantiomeric inversion.
Additional analyses of model performance concerning other molecular properties are provided in SI Fig. S4–S10.
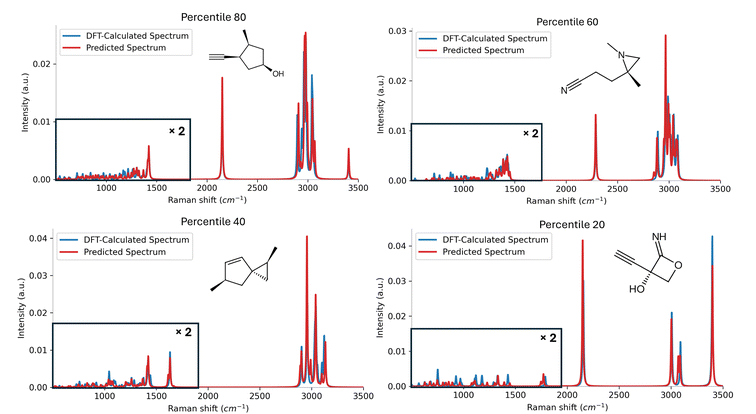
To qualitatively assess the predictive performance of the model, Fig. 4 displays the comparison between the DFT-calculated and Mol2Raman-predicted spectra for four representative molecules across the 80th, 60th, 40th and 20th percentiles in the distribution of F1 scores with 15 cm−1 tolerance. As shown in Fig. 4, the predicted spectra in the 80th and 60th percentiles closely match the DFT-calculated spectra, demonstrating excellent agreement in both the fingerprint and CH stretching regions. Even in the 40th and 20th percentiles, where performance slightly drops, the model still successfully predicts most of the significant peaks, with only a few missed or shifted peak-positions above the 15 cm−1 threshold. This consistency across various performance levels highlights the robustness and reliability of the Mol2Raman model in capturing both prominent and subtle spectral characteristics, showing strong predictive capability for both peak localization and spectral shape. Additional comparisons between DFT-calculated and Mol2Raman-predicted spectra for these percentile thresholds are shown in SI Fig. S11–S14.
To probe how Mol2Raman arrives at its predictions, we performed peak-conditioned Integrated Gradients (IG) on the graph inputs and visualized atom- and bond-level relevance maps.71 For a target peak j (chosen as the largest peak in either the fingerprint or the C–H region), we integrated the gradient of the scalar output ŷj from a zero baseline to the true input; atom scores are obtained by summing absolute attributions over node-feature channels, and bond scores by averaging the scores of their two incident atoms. Scores are normalised per molecule and reported on a scale of 0 to 1. Fig. 5 illustrates this analysis for the shown molecule: panel (A) reports the Mol2Raman prediction and the DFT-calculated spectrum, whereas panels (B) and (C) display the relative attributions from the peak–conditioned IG analysis, respectively, for the C–H and the fingerprint regions. As shown in Fig. 5B, in the C–H stretching region the most intense peak is captured almost entirely by the local C–H environment: attributions concentrate on carbon atoms and their adjacent C–H/C–C bonds, consistent with CH2/CH3 stretching. In contrast, Fig. 5C shows attributions distributed across the entire molecular scaffold, indicating that the model relies on global, molecule-wide patterns typical of fingerprint vibrations. Full methods and an additional example are provided in SI Note 3 and Fig. S15.
 | ||
| Fig. 5 Peak-conditioned integrated gradient attributions for the most intense C–H and fingerprint peaks. (A) Mol2Raman- and DFT-calculated spectra for the molecule shown in (B) (C–H region) and (C) (fingerprint region); atom and bond colors denote relative attribution (scaled to [0, 1]) from the peak-conditioned IG analysis. The localized attributions on C–H bonds in (B) corroborate the well-known prominence of C–H vibrations for Raman activity near 3000 cm−1,72 whereas the broadly elevated attribution across the molecule in (C) supports a delocalized, concerted vibration consistent with fingerprint-region modes.66 | ||
3.4 Comparison with a tanimoto benchmark
To further evaluate the performance of the Mol2Raman model, we compare it against a benchmark model based on molecular similarity using the Tanimoto coefficient.51,73 This baseline model predicts the Raman spectrum of a test molecule by taking the weighted average of the DFT-calculated spectra of its 10 most structurally similar molecules in the training set, where similarity is measured by the Tanimoto coefficient computed on Daylight molecular fingerprints. The resulting averaged spectrum is then used as a benchmark to evaluate the performance of Mol2Raman. The weights are thus calculated using the Tanimoto similarity itself. The metric used for comparison is the F1 score with a 15 cm−1 tolerance.As shown in Fig. 6A and Table 7, the Mol2Raman model significantly outperforms the Tanimoto-based benchmark. The mean F1 score for Mol2Raman is 0.642, which is 81% higher than the F1 score calculated with the weighted Tanimoto model. A Mann–Whitney test also shows that the F1-score distribution of Mol2Raman is statistically larger than the Tanimoto model distribution with a p-value lower than 10−8.74 This first comparison is motivated by the intuitive idea that the Raman spectrum of a molecule could be fairly approximated by the average of the most similar molecules. However, this analysis proves that this intuition leads to unreliable predictions. Raman modes do not just easily follow chemical similarity but are generated by more subtle and complex structure–spectral relationships that Mol2Raman can capture better than this benchmark model.75 The results in Table 7 emphasize the advantage of the Mol2Raman model over the Tanimoto-based benchmark also across all the other tolerance windows, underlining how the difference in F1 score increases enlarging the tolerance window.
| Metric | F1 tol. 10 cm−1 | F1 tol. 15 cm−1 | F1 tol. 20 cm−1 |
|---|---|---|---|
| Mol2Raman | |||
| Mean | 0.565 | 0.642 | 0.713 |
| Median | 0.576 | 0.656 | 0.727 |
| St. dev. | 0.094 | 0.092 | 0.088 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Tanimoto benchmark | |||
| Mean | 0.353 | 0.355 | 0.356 |
| Median | 0.353 | 0.355 | 0.356 |
| St. dev. | 0.057 | 0.056 | 0.056 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Chemprop benchmark | |||
| Mean | 0.347 | 0.391 | 0.428 |
| Median | 0.346 | 0.386 | 0.426 |
| St. dev. | 0.076 | 0.079 | 0.085 |
To further examine model generalization capabilities on structurally novel compounds, we evaluated both models on a subset of the test dataset, which consists of 425 structurally diverse molecules with a Tanimoto similarity of less than 0.6 to any molecule in the entire training dataset. Fig. 6B illustrates that Mol2Raman is again consistently better than the benchmark even on structurally novel compounds, achieving an F1 score of 0.568 compared to 0.392 of the benchmark. The performance gap between Mol2Raman and the Tanimoto-based model further widens on the low-similarity dataset. This result underlines the inherent limitation of relying solely on molecular similarity for spectral prediction. In contrast, Mol2Raman effectively captures complex molecular interactions, making it a more robust and scalable solution for Raman spectra prediction.
3.5 Comparison with a chemprop benchmark model
We furthermore compare our model against a Message Passing Neural Network (MPNN) model developed by McGill et al. for IR spectral prediction, known as Chemprop-IR.76 This is a more sophisticated and reliable benchmark on which to assess the performance and the goodness of Mol2Raman. To perform this comparison, we retrained the Chemprop-IR architecture on our Raman training dataset of 25440 molecules and evaluated it on the same test dataset of 3168 molecules used to assess Mol2Raman performance. Since Chemprop was originally designed for dense IR spectra, we adapted it for Raman spectra by convolving the sparse Raman activity data extracted from DFT with a Lorentzian function (full width at half maximum, FWHM = 10 cm−1). This preprocessing step is necessary to transform the sparse Raman data into continuous spectra suitable for Chemprop's input pipeline.The comparison is performed using the F1 score with a tolerance of 15 cm−1, evaluating both models on the entire test set and on the subset consisting of molecules with a Tanimoto similarity lower than 0.6, as done against the Tanimoto benchmark. As shown in Fig. 6C, the Mol2Raman model outperforms Chemprop across the full test dataset. The mean F1 score for Mol2Raman is 0.642, compared to Chemprop's 0.391, providing a 64% improvement. The F1 score for the Chemprop models is calculated using a prominence of 0.05 not to include peaks originated by noise in its calculation. A Mann–Whitney U test confirms that this difference is statistically significant (p < 10−6), highlighting Mol2Raman's superior capability in identifying Raman-active frequencies. The F1 score distribution of Mol2Raman is skewed towards higher values, indicating its superior ability to predict Raman-active frequencies accurately. This better performance can be explained by the Mol2Raman specialized architecture, designed to handle the spectral sparsity and peak-specific information inherent in Raman spectra. Table 7 reports a comprehensive comparison of Mol2Raman and Chemprop performance in terms of different F1 score tolerances, showing how Mol2Raman outperforms Chemprop for each considered tolerance window.
The comparison on the low similarity dataset is reported in Fig. 6D and Table 8. Fig. 6D demonstrates that Mol2Raman maintains its advantage on unseen molecular structures, with an F1 score of 0.568 compared to Chemprop's 0.412. This 38% improvement underlines Mol2Raman's high robustness in generalizing to novel chemical spaces. Table 8 presents the comparison of both models on this low-similarity dataset. Interestingly, the Chemprop model shows slightly better performance on the low-similarity subset (Tanimoto similarity <0.6) compared to its predictions on the full test dataset. This counterintuitive result can be attributed to several factors. Firstly, Chemprop may exhibit overfitting tendencies towards molecular structures prevalent in the training dataset, limiting its ability to generalize effectively within structurally similar groups in the full test dataset. In contrast, the more structurally diverse molecules in the filtered dataset could reduce this bias, enabling the model to generalize better. However, even with this modest improvement, Mol2Raman consistently outperforms Chemprop across both datasets, highlighting its superior capability to model Raman spectra and generalize across varying chemical spaces.
| Metric | F1 tol. 10 cm−1 | F1 tol. 15 cm−1 | F1 tol. 20 cm−1 |
|---|---|---|---|
| Mol2Raman | |||
| Mean | 0.491 | 0.568 | 0.639 |
| Median | 0.500 | 0.576 | 0.655 |
| St. dev. | 0.107 | 0.107 | 0.105 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Tanimoto benchmark | |||
| Mean | 0.306 | 0.309 | 0.311 |
| Median | 0.311 | 0.314 | 0.316 |
| St. dev. | 0.050 | 0.050 | 0.049 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Chemprop benchmark | |||
| Mean | 0.353 | 0.412 | 0.468 |
| Median | 0.356 | 0.415 | 0.467 |
| St. dev. | 0.082 | 0.077 | 0.079 |
The observed performance gap between Mol2Raman and Chemprop can be explained by the differing design philosophies of the two models. Chemprop was originally optimized for IR spectra, which are inherently denser and smoother than Raman spectra. In contrast, Mol2Raman was specifically engineered to model the sparse and peak-oriented nature of Raman spectra, effectively capturing both peak localization and relative intensities. Mol2Raman's GINE layers, combined with traditional chemical descriptors, allow for a richer encoding of molecular properties, enabling more accurate peak prediction. In contrast, Chemprop's standard MPNN architecture struggles to capture the nuanced spectral features inherent in Raman spectroscopy, particularly in the fingerprint region where structural complexity is more pronounced.
3.6 Mol2Raman open web application
To bridge the gap between advanced computational models and practical usability, the Mol2Raman algorithm has been further developed into a user-friendly open web application, accessible at https://mol2raman.streamlit.app and deployed using the Streamlit library.77,78 This platform allows users to interact with the model's predictions in a seamless manner, eliminating the need for extensive computational resources or specialized technical expertise. By integrating machine learning-based Raman spectral prediction into a web-accessible tool, Mol2Raman extends its applicability beyond computational chemistry experts to a wider scientific community. Users can use the input box to write molecular structures in SMILES format, which are automatically preprocessed and analyzed using the Mol2Raman model. The system performs all inference steps and post-processing in real-time, generating high-quality Raman spectra that can be visualized and downloaded for further analysis.A key advantage of this web-based platform is its integration of visualization tools that allow users to explore and interpret the predicted spectra effectively. This enhances the interpretability of computational predictions, facilitating their adoption in experimental workflows. The model is optimized to provide fast and accurate spectral predictions, making it suitable for both small-scale academic research and high-throughput industrial applications.79 This democratization of access is particularly relevant for researchers working in disciplines such as drug discovery, materials science, and process chemistry, where rapid molecular analysis is essential for decision-making.1,25
The development of this web-based interface exemplifies how cutting-edge machine learning models can be translated into practical, accessible tools that enhance scientific discovery. Beyond its immediate application, this platform lays the foundation for future expansions, including the integration of additional spectroscopic techniques and more sophisticated analytical capabilities. By providing an intuitive and interactive framework, Mol2Raman not only demonstrates the feasibility of deep learning-based Raman spectrum prediction but also highlights the broader potential of artificial intelligence in transforming computational chemistry into a more accessible and impactful discipline.
4 Conclusions
In this work, we introduce Mol2Raman, a novel GNN model designed to predict spontaneous Raman spectra directly from molecular structures. By combining our tailored peak-aware loss function with our GNN-based molecular representation, leveraging on GINE layers and traditional chemical descriptors, along with a spectral-filtering procedure informed by the predicted number of Raman modes, Mol2Raman achieves an F1-score exceeding 64% for peak prediction within a 15 cm−1 window and a cosine similarity above 0.7. This approach enables the model to capture also intricate and subtle molecular properties, like Raman spectral differences arising from enantiomeric inversion. By utilizing a large dataset of over 31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecules with DFT-calculated Raman spectra, Mol2Raman demonstrates a significant step forward in integrating deep learning approaches into molecular spectroscopy.
000 molecules with DFT-calculated Raman spectra, Mol2Raman demonstrates a significant step forward in integrating deep learning approaches into molecular spectroscopy.
The performance of Mol2Raman is rigorously evaluated against two benchmarks: a Chemprop-based model adapted for Raman spectral prediction and a Tanimoto similarity-based model. Across the F1 score with various tolerance windows (10, 15, and 20 cm−1), Mol2Raman consistently outperforms both benchmarks. Notably, the model achieves a mean F1 score of 0.642 with a 15 cm−1 tolerance, substantially surpassing the Chemprop model (0.391) and the Tanimoto benchmark (0.355). This consistent outperformance is observed not only on the full test set but also on more challenging subsets composed of structurally novel molecules (Tanimoto similarity <0.6), highlighting the model's robust generalization capabilities.
One of the most impressive aspects of Mol2Raman is its ability to generalize beyond structurally similar compounds. The model's superior performance on the low-similarity subset emphasizes its capacity to capture complex structure–spectrum relationships that cannot be adequately modeled by simpler similarity-based approaches. This capability is particularly important for real-world applications, where new or previously unseen molecules are frequently encountered.
Despite its larger number of parameters (157 million), comprising the two models and the two spectral windows for each model, Mol2Raman demonstrated fast inference time (22 ms). This efficiency enables large-scale molecular screening in drug discovery, materials optimization, or spectroscopic probe design, where rapid pre-selection of candidates based on predicted vibrational fingerprints is essential, as shown by Stokes et al.25 Our model goes exactly in this direction, facilitating and speeding up this first screening. Then, starting from this shortlist, more detailed DFT calculations or experimental measurements can be performed to reach the final optimal molecules. This efficiency stems from the model's architecture, which effectively uses its higher capacity to learn and generalize complex molecular features without introducing significant computational overhead.
The development of a user-friendly web application further extends the impact of this work. By deploying Mol2Raman through an accessible web interface, it is possible to easily generate high-quality Raman spectra predictions without the need for specialized hardware or advanced computational skills, enhancing the model's practical utility.
While Mol2Raman presents a significant advancement in Raman spectrum prediction, some limitations remain. The current model is trained exclusively on DFT-calculated spectra, which, while accurate, may not fully capture experimental complexities such as instrumental noise and environmental effects. However, this DFT-based training may also be seen as a strong pretraining stage that can be adapted to experimental data through transfer learning. Fine-tuning on curated experimental Raman spectra should help close the gap between simulation and measurement by accounting for baseline backgrounds, instrument response, and temperature effects, as also shown in Chemprop-IR.76 In practice, this can be achieved by freezing the early GINE layers and updating only the final blocks and readout with a small learning rate, thereby preserving the information learned from DFT while aligning predictions to experimental variability. We therefore expect that incorporating experimental spectra into the training process could further improve the model's robustness and real-world applicability. Additionally, although the model shows excellent performance in predicting peak positions and intensities, expanding its capabilities to predict other spectroscopic properties or extending its application to molecular datasets composed of more atomic species could further enhance its utility. Exploring hybrid models that combine data-driven approaches with physical constraints could also offer new avenues for improving spectral predictions.
In summary, Mol2Raman represents a significant advancement in applying machine learning to spectroscopic analysis. By combining an innovative GNN-based architecture with strong predictive performance and computational efficiency, the model provides a practical and scalable solution for molecular spectroscopy. The additional deployment as a web application further broadens its accessibility, enabling seamless integration into research and industrial workflows. Beyond its immediate applications, this work lays the foundation for future developments aimed at expanding the model's capabilities. Incorporating experimental spectra into training could enhance robustness, while extending its framework to other spectroscopic techniques would further increase its utility. With continued open-source refinement of the model, Mol2Raman has the potential to accelerate discoveries across materials science, pharmaceuticals, and chemical engineering, contributing to molecular design and diagnostics in an increasingly data-driven era.
Author contributions
Conceptualization: S. S., D. P., I. R., M. G.; data curation: S. S., D. A.; methodology: S. S., A. G, F. C, D. A.; software: S. S., A. G., G. P.; formal analysis: S. S., A. G., F. C., G. P., D. A., I. R.; writing – original draft preparation: S. S; writing – review and editing: S. S., A. G., F. C., G. P., D. A., I. R., M. G., D. P.; visualization: S. S., F. C.; supervision: D. P., M. G.; funding acquisition, D. P, M. G., I. R. All authors have read and agreed to the published version of the manuscript.Conflicts of interest
There are no conflicts to declare.Data availability
The dataset used for the training of Mol2Raman presented in this article is available on Zenodo at https://doi.org/10.5281/zenodo.15391264. This dataset contains the DFT calculations on 31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 776 molecules performed using the ORCA software, including the Raman and IR active modes, and the actual dataset used to train the model. The code for the architecture and training of Mol2Raman can be found at https://doi.org/10.5281/zenodo.17654620 for the version used in this work, and at https://github.com/salvasorrentino/Mol2Raman.git for any future updates. In addition, the code for the webapp is available at https://doi.org/10.5281/zenodo.17654690 and at https://github.com/vibralab/mol2raman_webapp.git.
776 molecules performed using the ORCA software, including the Raman and IR active modes, and the actual dataset used to train the model. The code for the architecture and training of Mol2Raman can be found at https://doi.org/10.5281/zenodo.17654620 for the version used in this work, and at https://github.com/salvasorrentino/Mol2Raman.git for any future updates. In addition, the code for the webapp is available at https://doi.org/10.5281/zenodo.17654690 and at https://github.com/vibralab/mol2raman_webapp.git.
Supplementary information is available. See DOI: https://doi.org/10.1039/d5dd00210a.
Acknowledgements
The authors acknowledge financial support by the following funders: European Union's NextGenerationEU Program with the I-PHOQS Infrastructure (IR0000016, ID D2B8D520, CUP B53C22001750006) “Integrated infrastructure initiative in Photonic and Quantum Sciences”; the National Institutes of Health (UH3CA275687); the National Cancer Center, Korea (NCC-24H1170); and the EIC under grant agreement no. 101187508 (SpectraBREAST).Notes and references
- H. J. Butler, L. Ashton, B. Bird, G. Cinque, K. Curtis, J. Dorney, K. Esmonde-White, N. J. Fullwood, B. Gardner, P. L. Martin-Hirsch, M. J. Walsh, M. R. McAinsh, N. Stone and F. L. Martin, Nat. Protoc., 2016, 11, 664–687 CrossRef CAS PubMed.
- R. Vanna, A. De la Cadena, B. Talone, C. Manzoni, M. Marangoni, D. Polli and G. Cerullo, Riv. Nuovo Cimento., 2022, 45, 107–187 CrossRef CAS.
- X. Fan, W. Ming, H. Zeng, Z. Zhang and H. Lu, Analyst, 2019, 144, 1789–1798 RSC.
- A. Stoll and P. Benner, GAMM-Mitteilungen, 2021, 44, e202100003 CrossRef.
- Q. Liang, S. Dwaraknath and K. A. Persson, Sci. Data, 2019, 6, 135 CrossRef PubMed.
- G. Cutshaw, S. Uthaman, N. Hassan, S. Kothadiya, X. Wen and R. Bardhan, Chem. Rev., 2023, 123, 8297–8346 CrossRef CAS PubMed.
- E. Runge, Phys. Rev. Lett., 1984, 52, 997–1000 CrossRef CAS.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed.
- S. Y. Willow, A. Hajibabaei, M. Ha, D. C. Yang, C. W. Myung, S. K. Min, G. Lee and K. S. Kim, Chem. Phys. Rev., 2024, 5, 041307 CrossRef CAS.
- M. Gastegger, J. Behler and P. Marquetand, Chem. Sci., 2017, 8, 6924–6935 RSC.
- Y.-F. Hou, C. Wang and P. O. Dral, J. Phys. Chem. A., 2025, 129(16), 3613–3623 CrossRef CAS PubMed.
- C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671 CrossRef CAS PubMed.
- Z. Movasaghi, S. Rehman and I. U. Rehman, Appl. Spectrosc. Rev., 2007, 42, 493–541 CrossRef CAS.
- L. Wei, F. Hu, Y. Shen, Z. Chen, Y. Yu, C.-C. Lin, M. C. Wang and W. Min, Nat. Methods, 2014, 11, 410–412 CrossRef CAS.
- S. Kearnes, K. McCloskey, M. Berndl, V. Pande and P. Riley, J. Comput.-Aided Mol. Des., 2016, 30, 595–608 CrossRef CAS PubMed.
- M. Fang, S. Tang, Z. Fan, Y. Shi, N. Xu and Y. He, J. Phys. Chem. A., 2024, 128, 2286–2294 CrossRef CAS.
- M. Miotto and L. Monacelli, npj Comput. Mater., 2024, 10, 1–9 CrossRef.
- J. Andraos, J. Chem. Educ., 1996, 73, 150 CrossRef CAS.
- X. Yang, X. Zhang, Y. Zhang, J. Jiang and W. Hu, J. Phys. Chem. Lett., 2025, 2023–2028 CrossRef CAS.
- S. Kong, F. Ricci, D. Guevarra, J. B. Neaton, C. P. Gomes and J. M. Gregoire, Nat. Commun., 2022, 13, 949 CrossRef CAS PubMed.
- R. Okabe, A. Chotrattanapituk, A. Boonkird, N. Andrejevic, X. Fu, T. S. Jaakkola, Q. Song, T. Nguyen, N. Drucker, S. Mu, Y. Wang, B. Liao, Y. Cheng and M. Li, Nat. Comput. Sci., 2024, 4, 522–531 CrossRef PubMed.
- D. Weininger, J. Chem. Inf. Comput. Sci., 1988, 28, 31–36 CrossRef CAS.
- D. Weininger, A. Weininger and J. L. Weininger, J. Chem. Inf. Comput. Sci., 1989, 29, 97–101 CrossRef CAS.
- D. Weininger, J. Chem. Inf. Comput. Sci., 1990, 30, 237–243 CrossRef CAS.
- J. M. Stokes, K. Yang, K. Swanson, W. Jin, A. Cubillos-Ruiz, N. M. Donghia, C. R. MacNair, S. French, L. A. Carfrae, Z. Bloom-Ackermann, V. M. Tran, A. Chiappino-Pepe, A. H. Badran, I. W. Andrews, E. J. Chory, G. M. Church, E. D. Brown, T. S. Jaakkola, R. Barzilay and J. J. Collins, Cell, 2020, 180, 688–702 CrossRef CAS PubMed.
- D. Buterez, J. P. Janet, S. J. Kiddle, D. Oglic and P. Lió, Nat. Commun., 2024, 15, 1517 CrossRef CAS PubMed.
- S. Shilpa, G. Kashyap and R. B. Sunoj, J. Phys. Chem. A., 2023, 127, 8253–8271 CrossRef CAS PubMed.
- F. Wong, E. J. Zheng, J. A. Valeri, N. M. Donghia, M. N. Anahtar, S. Omori, A. Li, A. Cubillos-Ruiz, A. Krishnan, W. Jin, A. L. Manson, J. Friedrichs, R. Helbig, B. Hajian, D. K. Fiejtek, F. F. Wagner, H. H. Soutter, A. M. Earl, J. M. Stokes, L. D. Renner and J. J. Collins, Nature, 2024, 626, 177–185 CrossRef CAS PubMed.
- Z. Wu, J. Wang, H. Du, D. Jiang, Y. Kang, D. Li, P. Pan, Y. Deng, D. Cao, C.-Y. Hsieh and T. Hou, Nat. Commun., 2023, 14, 2585 CrossRef CAS PubMed.
- K. Xu, W. Hu, J. Leskovec and S. Jegelka, How Powerful are Graph Neural Networks?, arXiv, 2019, preprint, arXiv:1810.00826cs, DOI:10.48550/arXiv:1810.00826,.
- W. Hu, B. Liu, J. Gomes, M. Zitnik, P. Liang, V. Pande and J. Leskovec, Strategies for Pre-training Graph Neural Networks, arXiv, 2020, preprint, arXiv:1905.12265cs, DOI:10.48550/arXiv:1905.12265.
- D. Butina, J. Chem. Inf. Comput. Sci., 1999, 39, 747–750 CrossRef CAS.
- D. Rogers and M. Hahn, J. Chem. Inf. Model., 2010, 50, 742–754 CrossRef CAS PubMed.
- R. Ramakrishnan, P. O. Dral, M. Rupp and O. A. von Lilienfeld, Sci. Data, 2014, 1, 140022 CrossRef CAS PubMed.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- R. Luo, J. Popp and T. Bocklitz, Analytica, 2022, 3, 287–301 CrossRef.
- C. M. K. Stienstra, T. van Wieringen, L. Hebert, P. Thomas, K. J. Houthuijs, G. Berden, J. Oomens, J. Martens and W. S. Hopkins, J. Chem. Inf. Model., 2025, 65, 2385–2394 CrossRef CAS PubMed.
- M. J. Frisch, J. A. Pople and J. S. Binkley, J. Chem. Phys., 1984, 80, 3265–3269 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- M. Turisini, M. Cestari and G. Amati, JLSRF., 2024, 9, 1–16 Search PubMed.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100 CrossRef CAS PubMed.
- A. Hellweg and D. Rappoport, Phys. Chem. Chem. Phys., 2015, 17, 1010–1017 RSC.
- E. K. U. Gross and W. Kohn, Advances in Quantum Chemistry, Academic Press, 1990, vol. 21, pp. 255–291 Search PubMed.
- J. Neugebauer, M. Reiher, C. Kind and B. A. Hess, J. Comput. Chem., 2002, 23, 895–910 CrossRef CAS PubMed.
- J. Wang, H. Luo, R. Qin, M. Wang, X. Wan, M. Fang, O. Zhang, Q. Gou, Q. Su, C. Shen, Z. You, L. Liu, C.-Y. Hsieh, T. Hou and Y. Kang, Chem. Sci., 2025, 16, 637–648 RSC.
- M. Z. Vardaki, V. G. Gregoriou and C. L. Chochos, RSC Chem. Biol., 2024, 5, 273–292 RSC.
- E. Smith and G. Dent, Modern Raman Spectroscopy: A Practical Approach, Wiley, 2005 Search PubMed.
- S. Nie and S. R. Emory, Science, 1997, 275, 1102–1106 CrossRef CAS PubMed.
- Y. Cui, F. Zhou, J. Wang, X. Liu, Y. Lin and S. Belongie, 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2017, pp. 3049–3058 Search PubMed.
- RDKit: Open-source cheminformatics, https://www.rdkit.org.
- D. Bajusz, A. Rácz and K. Héberger, J. Cheminf., 2015, 7, 20 Search PubMed.
- S. Ioffe and C. Szegedy, Proceedings of the 32nd International Conference on Machine Learning, 2015, pp. 448–456 Search PubMed.
- A. F. Agarap, Deep Learning using Rectified Linear Units (ReLU), arXiv, 2019, preprint, arXiv:1803.08375cs, DOI:10.48550/arXiv:1803.08375.
- J. Gilmer, S. S. Schoenholz, P. F. Riley, O. Vinyals and G. E. Dahl, Neural Message Passing for Quantum Chemistry, arXiv, 2017, preprint, arXiv:1704.01212cs, DOI:10.48550/arXiv:1704.01212.
- H. Zheng, Z. Yang, W. Liu, J. Liang and Y. Li, 2015 International Joint Conference on Neural Networks (IJCNN), 2015, pp. 1–4 Search PubMed.
- Y. Gal and Z. Ghahramani, Dropout as a Bayesian Approximation: Representing Model Uncertainty in Deep Learning, arXiv, 2016, preprint, arXiv:1506.02142stat, DOI:10.48550/arXiv:1506.02142.
- J. Lever, M. Krzywinski and N. Altman, Nat. Methods, 2016, 13, 603–604 CrossRef CAS.
- S. Ruder, An overview of gradient descent optimization algorithms, arXiv, 2017, preprint, arXiv:1609.04747cs, DOI:10.48550/arXiv:1609.04747.
- L. Prechelt, Early Stopping – But When?, inNeural Networks: Tricks of the Trade, ed. G. B. Orr and K. R. Müller, Springer, Berlin, Heidelberg, 1998, vol. 1524, DOI:10.1007/3-540-49430-8_3.
- J. Griffié, L. Boelen, G. Burn, A. P. Cope and D. M. Owen, J. Biophot., 2015, 8, 925–934 CrossRef PubMed.
- X. Yuan and R. A. Mayanovic, Appl. Spectrosc., 2017, 71, 2325–2338 CrossRef CAS PubMed.
- Y. Shen, F. Hu and W. Min, Annu. Rev. Biophys., 2019, 48, 347–369 CrossRef CAS PubMed.
- C.-I. Chang, IEEE Trans. Inf. Theor., 2000, 46, 1927–1932 CrossRef.
- A. Singhal, IEEE Data Eng. Bull., 2001, 24, 1–9 Search PubMed.
- P. Christen, D. J. Hand and N. Kirielle, ACM Comput. Surv., 2023, 56(73), 1–73 Search PubMed.
- G. Pezzotti, J. Raman Spectrosc., 2021, 52, 2348–2443 CrossRef CAS.
- D. J. Gardiner, G. Turrell, D. L. Gerrard, J. D. Louden, H. J. Bowley and P. R. Graves, Practical Raman Spectroscopy publisher - Springer, Springer, Berlin, Heidelberg, 1989, DOI:10.1007/978-3-642-74040-4, ISBN 978-3-540-50254-8.
- A. C. Ferrari, Solid State Commun., 2007, 143, 47–57 CrossRef CAS.
- G. Zerbi, P. Roncone, G. Longhi and S. L. Wunder, J. Chem. Phys., 1988, 89, 166–173 CrossRef CAS.
- B. Handzo, J. Peters and R. Kalyanaraman, A fingerprint in a fingerprint: A Raman spectral analysis of pharmaceutical ingredients, Spectroscopy, 2022, 37, 24–30 CAS.
- K. McCloskey, A. Taly, F. Monti, M. P. Brenner and L. J. Colwell, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 11624–11629 CrossRef CAS PubMed.
- N. K. Howell, G. Arteaga, S. Nakai and E. C. Y. Li-Chan, J. Agric. Food Chem., 1999, 47, 924–933 CrossRef CAS PubMed.
- D. C. Anastasiu and G. Karypis, Int J Data Sci Anal., 2017, 4, 153–172 CrossRef.
- H. B. Mann and D. R. Whitney, Ann. Math. Stat., 1947, 18, 50–60 CrossRef.
- J. R. T. Chen, E. X. Tan, J. Tang, S. X. Leong, S. K. X. Hue, C. S. Pun, I. Y. Phang and X. Y. Ling, J. Am. Chem. Soc., 2025, 147, 6654–6664 CrossRef CAS PubMed.
- C. McGill, M. Forsuelo, Y. Guan and W. H. Green, J. Chem. Inf. Model., 2021, 61, 2594–2609 CrossRef CAS PubMed.
- Mol2Raman, 2024, https://mol2raman.streamlit.app.
- D. Avagliano, M. Skreta, S. Arellano-Rubach and A. Aspuru-Guzik, Chem. Sci., 2024, 15, 4489–4503 RSC.
- P. Schwaller, T. Laino, T. Gaudin, P. Bolgar, C. A. Hunter, C. Bekas and A. A. Lee, ACS Cent. Sci., 2019, 5, 1572–1583 CrossRef CAS PubMed.
Footnote |
| † Current address: Laser Biomedical Research Center, G. R. Harrison Spectroscopy Laboratory, Massachusetts Institute of Technology, Cambridge, Massachusetts, 02139, USA; E-mail address: E-mail: ssorrent@mit.edu. |
| This journal is © The Royal Society of Chemistry 2025 |