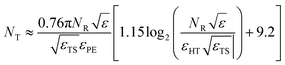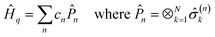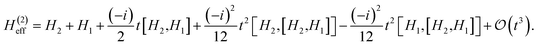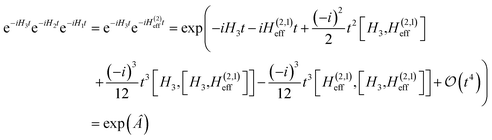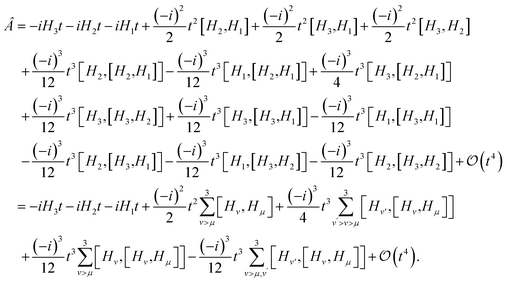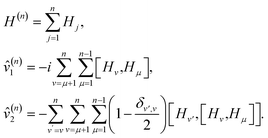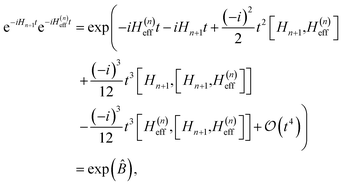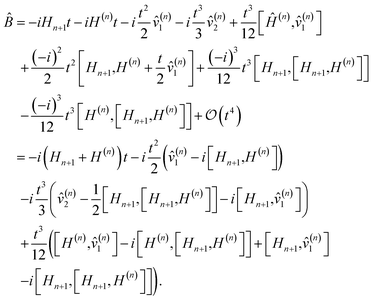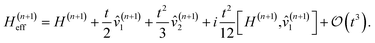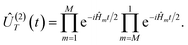Estimating Trotter approximation errors to optimize Hamiltonian partitioning for lower eigenvalue errors
Received
7th May 2025
, Accepted 20th October 2025
First published on 28th October 2025
Abstract
Trotter approximation in conjunction with quantum phase estimation can be used to extract eigen-energies of a many-body Hamiltonian on a quantum computer. There were several ways proposed to assess the quality of this approximation based on estimating the norm of the difference between the exact and approximate evolution operators. Here, we explore how different error estimators for various partitionings correlate with the true error in the ground state energy due to Trotter approximation. For a set of small molecules we calculate these exact error in ground-state electronic energies due to the second-order Trotter approximation. Comparison of these errors with previously used upper bounds show correlation less than 0.5 across various Hamiltonian partitionings. On the other hand, building the Trotter approximation error estimation based on perturbation theory up to a second order in the time-step for eigenvalues provides estimates with very good correlations with the exact Trotter approximation errors. These findings highlight the non-faithful character of norm-based estimations for prediction of best Hamiltonian partitionings and the need for perturbative estimates.
I. Introduction
Solving the electronic structure problem is one of the anticipated uses of quantum computing. As an eigenvalue problem with a Hamiltonian operator that can be expressed compactly, this problem is convenient for quantum computing because classical-quantum data transfer is usually a bottleneck.1 Obtaining electronic wavefunctions and energies is one of the key procedures in first principles modeling of molecular physics since molecular energy scale is dominated by the electronic part. Yet, solving this problem scales exponentially with the size unless some approximations are made.
Fault-tolerant quantum computers offer potential advantages for efficient estimation of energy eigenvalues through exponential speedup with respect to classical methods, by means of the Quantum Phase Estimation (QPE) algorithm.2 The QPE framework contains three main parts: (1) initial state preparation, (2) procedure for an evolution or a walker operator that involves the Hamiltonian encoding, and (3) the eigenvalue extraction. Here, we focus on the second part, two main approaches for the Hamiltonian encoding are representing the Hamiltonian exponential function via the Trotter approximation3 and embedding the Hamiltonian as a block of a larger unitary via decomposing the Hamiltonian as a Linear Combination of Unitaries (LCU).4
Qubitization can prepare exp(−i![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos−1(Ĥ/λ)) when given access to an LCU decomposition of a Hamiltonian, where λ is the induced 1-norm of the LCU.5 Unlike the Trotter approximation, Qubitization can encode the Hamiltonian exactly. This allows a straightforward cost analysis with tight bounds on T-gate counts in terms of target accuracy. The downside, however, is the significant number of ancillas required, which are not needed in the Trotter approximation. In the early fault-tolerant era, when the number of logical qubits is expected to be limited, this trade-off is crucial. Hence, in this work we focus on the Trotter approximation for Hamiltonian simulation.
cos−1(Ĥ/λ)) when given access to an LCU decomposition of a Hamiltonian, where λ is the induced 1-norm of the LCU.5 Unlike the Trotter approximation, Qubitization can encode the Hamiltonian exactly. This allows a straightforward cost analysis with tight bounds on T-gate counts in terms of target accuracy. The downside, however, is the significant number of ancillas required, which are not needed in the Trotter approximation. In the early fault-tolerant era, when the number of logical qubits is expected to be limited, this trade-off is crucial. Hence, in this work we focus on the Trotter approximation for Hamiltonian simulation.
Within the Trotter approximation, the target Hamiltonian is decomposed into easy-to-simulate (or fast-forwardable) Hamiltonian fragments:
| | 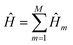 | (1) |
and the exact unitary evolution operator for an arbitrary simulation time
τ is approximated using the time evolution of the fragments
Ĥm. The decomposition in
eqn (1) is non unique and each such decomposition can result in drastically different quantum resources. The goal of the paper is to address the question of how to find the best decomposition scheme among the available options. The second-order Trotter approximation is given by
| | 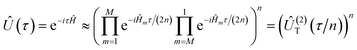 | (2) |
where the approximation is exact up to second order in
τ. This approximate representation of the exact time evolution operator introduces a deviation in the spectrum of the simulated time evolution unitary with respect to the exact one. For estimation of energy eigenvalues through QPE under a fixed target error, it is therefore crucial to rationalize the scaling of this deviation with the time scale used for discretization of the total simulation time as well as its dependence with different Hamiltonian partitioning schemes. The estimation of this deviation is also needed for choosing the evolution time-step and the overall error analysis.
Recently, upper bounds were formulated for the norm of the difference between propagators,
| | 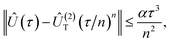 | (3) |
| | 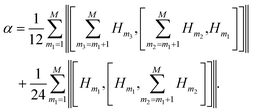 | (4) |
which allowed one to estimate the effect of the Trotter approximation on the accuracy of dynamics.
6 These estimates can be used to derive upper bounds for the energy error in QPE.
7 In what follows, for brevity, we will refer to the time step as
t =
τ/
n. However, it is known in general that the Trotter upper bounds are relatively loose and using them could lead to underestimation of appropriate time-step.
8 Considering that with some simplifications
α values can be evaluated and used to differentiate various Hamiltonian partitionings,
9 it is interesting to examine how accurate
α-based trends are compared to those using the exact Trotter approximation error in eigenvalues.
In ref. 10, it was shown that, unlike the operator norm error α, an alternative error estimator based on time-independent perturbation theory correlates more strongly with the exact error when the Hamiltonian fragments Ĥm are Pauli operators. Here, we investigate whether this estimator can also be used to distinguish and select the most suitable Hamiltonian partitioning scheme for a given molecule. Such an estimator can be built by representing the Trotter propagator as
| | | Û(2)T(t) = e−itĤeff(t) | (5) |
and performing perturbative analysis of the
Ĥeff(
t) spectrum. Even though perturbative estimates are not upper bounds, they can be used for differentiating between various Hamiltonian partitioning schemes. As for predicting the Trotter step, one can use perturbative estimates as a first step in the iterative procedure suggested recently.
11
II. Perturbative error estimates
Time-independent perturbation theory is built by considering Baker–Campbell–Hausdorff expansion of the second order Trotter evolution operator in eqn (5)| | 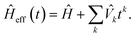 | (6) |
By construction [see eqn (2)], Û(2)T(t)Û(2)T(−t) = 1, implying Ĥeff(t) = Ĥeff(−t). Therefore, only even order ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) k's survive in eqn (6). The leading term is then given by [see Appendix D]
k's survive in eqn (6). The leading term is then given by [see Appendix D]
| | 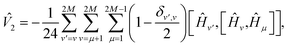 | (7) |
where
HM+i =
HM+1−i for
i = 1 to
M. Note that in spite of
t dependence of
Ĥeff, we do not need time-dependent perturbation theory since we are interested in eigenvalues of
Ĥeff as a function of
t. Eigenvalues of
Ĥeff can be obtained as perturbative series starting from those of
Ĥ. Focusing on the ground state energy
E0, the correction from first-order perturbation theory can be written as
E(1)GS = 〈ϕ0|![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) 2|ϕ0〉t2, 2|ϕ0〉t2, |
where |
ϕ0〉 is the electronic ground state. Note that next correction to energy will be fourth order in time. This implies, the ground state energy of
Heff is
| | 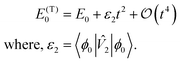 | (8) |
Calculating ε2 requires knowledge of the ground state of Ĥ. Since it is not accessible for a general Hamiltonian, we approximate ε2 using approximate eigenstate |ψ0〉 obtained via cost efficient classical methods, as suggested in ref. 10. We can then define an approximation to ε2 given by
| | εapp = 〈ψ0|![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) 2|ψ0〉. 2|ψ0〉. | (9) |
The difference |ε2 − εapp| is expected to become smaller with larger overlap |〈ϕ0|ψ0〉|.
III. Results
Here we assess correlations of exact Trotter approximation error with estimates based on operator norm error as well as perturbative estimates, for various Hamiltonian partitionings described in Appendix A. We also calculate upper bounds on T-gates for the ground energy estimation problem under QPE using different error estimators. The Trotter approximation errors are obtained for electronic Hamiltonians of small molecules (H2, LiH, BeH2, H2O, and NH3) where we establish the non-reliability of α and merits of perturbative estimates in ranking partitioning schemes. We then consider bond stretching of N2 to study robustness of εapp against the quality of approximate state |ψ0〉 used. |ψ0〉 is obtained as a CISD approximation to the FCI ground state. For H2, LiH, and BeH2, the bond length is chosen to be 1. For H2O and NH3, the bond length is chosen to be 1.9. For N2, we vary the bond length from 1.9 × re to 2.3 × re, where re = 1.098 is the equilibrium bond length. The exact Trotter approximation errors |ΔET| = |E(T)0 − E0| are computed by numerical diagonalization of Ĥ and Ĥeff [eqn (5)] as described in Appendix C.
A. Exact Trotter approximation errors
We define ε = ΔET/t2 to represent the exact Trotter approximation error and examine the correlations between ε and the error estimators in Table 1. Column 2 shows that error estimator α is unreliable in predicting the partitioning scheme with lowest Trotter error. Because of this, we have considered an α-like estimator| | | αe = ‖Û(t) − Û(2)T(t)‖/t3. | (10) |
Table 1 Pearson correlation of different Trotter error estimators with the true Trotter error ε = ΔET/t2. Definitions of α and αe are given in eqn (4) and (10) respectively. For each molecule, the correlation is obtained by evaluating the errors for 9 different Hamiltonian partitionings described in Appendix A. The data used for calculating correlations is provided in Appendix E
| Molecule |
ε vs. α
|
ε vs. α
e
|
| H2 |
0.50 |
0.40 |
| LiH |
0.10 |
−0.61 |
| BeH2 |
0.41 |
−0.45 |
| H2O |
−0.01 |
−0.22 |
| NH3 |
0.30 |
−0.10 |
α
e captures the exact error in the time propagator introduced by the Trotter approximation. However, the correlation between ε and αe is also seen to be low from column 3, and in fact negative in many cases. This discrepancy can be understood as a consequence of α and αe being worst-case scenario metrics for the deviation (with respect to exact unitary propagation) that ensue from the Trotter approximation rather than a measure of deviation with respect to the eigenspectrum of the target simulated Hamiltonian.
On the other hand, since 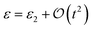 (follows from eqn (8)), for small t, which is mostly the case for ground state energy estimation, ε2 should capture ε almost exactly. A similar correlation calculation as in Table 1 between ε and ε2 leads to a Pearson correlation coefficient of 1.0 for all the molecules considered. Most importantly, correlation between ε vs. εapp also stays close to one with the lowest correlation coefficient being 0.98 for NH3.
(follows from eqn (8)), for small t, which is mostly the case for ground state energy estimation, ε2 should capture ε almost exactly. A similar correlation calculation as in Table 1 between ε and ε2 leads to a Pearson correlation coefficient of 1.0 for all the molecules considered. Most importantly, correlation between ε vs. εapp also stays close to one with the lowest correlation coefficient being 0.98 for NH3.
Having established the unreliability of α, we now investigate the behavior of εapp as a function of quality of |ψ0〉. We consider 10e8o active space of N2 at 5 different bond lengths. Since calculating ε can be expensive, we instead find the correlation between ε2 and εapp. This can be justified from the discussion in the previous paragraph. The results are shown in Table 2. We see that despite the overlaps being as small as 60%, the correlation stays near perfect. This shows the utility of εapp in ranking the partitionings, even at low overlaps.
Table 2 Table to study robustness of εapp against the quality of the approximate state used, with bond stretching of N2 in 10e8o orbital active space as an example. Column one notes the factor by which the equilibrium bond length is stretched. Column two denotes the overlap of CISD approximation to the ground state (|ψ0〉) with FCI solution (|ϕ0〉). The last column notes the correlation between the leading order perturbative correction to Trotter error evaluated using FCI state (ε2), against using CISD state (εapp), across 9 different partitioning of the Hamiltonian. Aggregating the data across all geometries and partitionings leads to a correlation of 0.97. The data to calculate correlations is provided in Appendix E
| Bond stretch factor |
|〈ϕ0|ψ0〉|2 (%) |
ε
2
vs. ε
app correlation |
| 1.9 |
77.12 |
1.00 |
| 2.0 |
71.39 |
0.99 |
| 2.1 |
66.53 |
1.00 |
| 2.2 |
62.63 |
0.99 |
| 2.3 |
59.61 |
1.00 |
B. Resource efficiency
For the set of small molecules we studied, Fig. 1 shows the upper bounds on T-gates required for QPE under a target accuracy based on three different values for Trotter error. The three values come from (1) the exact scaling of Trotter approximation error ε, (2) approximate perturbative estimate εapp, and (3) operator norm error α, all three evaluated for the most efficient Hamiltonian partitioning scheme of each molecule. The actual values are listed in Tables 10 and 11 in Appendix F where we note the T-gate bounds for the best three partitioning schemes. Even though upper bound estimations on T-gate count based on the α mostly predict best performance of qubit decompositions, they tend to consistently overrate the FC SI and QWC SI methods. α based T gate count overestimates T gates by more than an order of magnitude for H2O and NH3. The overestimation is expected to grow as the sizes of molecules or the basis sets increase, since this leads to larger norm of the Hamiltonian and its fragments, and hence the error operators in eqn (4). Thus, using α′s lead to drastic overestimations of resources needed to obtain energies using the Trotter approximation and QPE. On the other hand, we see that εapp-based estimator accurately captures the right order of magnitude of the T-gate numbers as obtained by ε. Also, the εapp-based estimator correctly suggests qubit partition methods as the most accurate compared to their fermionic counterparts. Due to similarity of T-gate numbers for various qubit partitionings (see Table 11), the ranking based on εapp and ε are different, in spite of the high degree of εapp − ε correlation. Since all the best Hamiltonian partitioning methods have very similar resource estimations, and their particular order is of little importance, εapp can be a good substitute for ε. Thus, estimators of Trotter error based on perturbative expression [eqn (8)] and a classically-accessible approximation to the electronic ground state, provide better correlation than commutator-norm-based counterparts, even for the strongly correlated molecular configurations.
 |
| | Fig. 1 Upper bounds on T-gates required for quantum phase estimation of ground-state energy with a target accuracy of 1.6 mHartree for the most efficient Hamiltonian partitioning scheme of each molecule. | |
IV. Discussion
Since estimating εapp requires a good ground-state approximation, what fidelity to expect for industrially relevant systems becomes important. Unlike in the small systems studied here, exact evaluation of the overlap becomes exponentially hard as system size grows. In the broader context of realizing quantum advantage in quantum chemistry through QPE, concerns have been raised about the feasibility of preparing initial states with sufficient overlap for systems that are classically intractable,12 contrary to earlier optimistic predictions.13 Recent works, however, have begun to address these challenges.14,15 Through a bond-dimension extrapolation calculation, the authors of ref. 15 argue that for large molecules such as FeMoco (see Table 1), overlap estimates of classical approximations to low-lying eigenstates can be made as high as 90%. More generally, ref. 16 provides expressions for upper and lower bounds on overlap that require only Hamiltonian moments and approximate eigenvalues. Using this method, one can assess the reliability of εapp even for large systems. These results suggest that obtaining reliable εapp values should not be a bottleneck for ranking partitioning schemes.
While we have primarily focused on estimating Trotter error, there are additional contributors to the final cost of estimating the ground-state energy with QPE (see Appendix F). For example, an initial state with low ground-state fidelity p0 leads to a longer runtime, scaling as 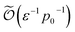 ,17 where ε is the QPE error arising from the finite number of repetitions of the time propagator. It should be noted, however, that ε is introduced in addition to ε2 from the Trotter approximation. Thus, even if QPE error is made small, Trotter error can still prevent achieving chemical accuracy. The Trotter time step can be reduced arbitrarily to overcome this, but doing so only increases the gate depth due to the larger number of repetitions required to reach the same total time. Hence, we believe it is important to specifically analyze Trotter error and how it depends on the choice of Hamiltonian partitioning. In our estimation of the T-gate upper bound, we do not fix the Trotter or QPE error individually; instead, we require that their sum (together with the error from compilation to T-gates) remain below the target accuracy. Under this constraint, we vary these errors to minimize the T-gate upper bound. Since this optimization is nonlinear with many local minima, it is difficult to comment on the exact relationship between Trotter error and QPE error at fixed target accuracy.
,17 where ε is the QPE error arising from the finite number of repetitions of the time propagator. It should be noted, however, that ε is introduced in addition to ε2 from the Trotter approximation. Thus, even if QPE error is made small, Trotter error can still prevent achieving chemical accuracy. The Trotter time step can be reduced arbitrarily to overcome this, but doing so only increases the gate depth due to the larger number of repetitions required to reach the same total time. Hence, we believe it is important to specifically analyze Trotter error and how it depends on the choice of Hamiltonian partitioning. In our estimation of the T-gate upper bound, we do not fix the Trotter or QPE error individually; instead, we require that their sum (together with the error from compilation to T-gates) remain below the target accuracy. Under this constraint, we vary these errors to minimize the T-gate upper bound. Since this optimization is nonlinear with many local minima, it is difficult to comment on the exact relationship between Trotter error and QPE error at fixed target accuracy.
V. Conclusions
We have calculated exact errors associated with the second order Trotter approximation for small molecules and different Hamiltonian partitionings. Previously derived commutator norm based upper bound, α, was shown to have low correlation with the induced exact error in energy due to Trotter approximation. This confirmed the loose character of the α based upper bounds for energies, which makes these upper bounds inadequate in picking the best partitioning scheme and hence determining the true resources needed to achieve target accuracy in energy. The alternative estimate of the Trotter approximation error based on perturbative analysis of the effective Hamiltonian eigen-spectrum performed much better. The T gate upper bound estimates based on α were orders of magnitude higher than those predicted by the exact Trotter error. However, estimates based on εapp produced correct order of T gate estimates.
Substituting the exact ground eigenstate with a classically easy to obtain counterpart in calculating perturbation corrections resulted in strong correlation with exact error, even in the case of strongly correlated molecular configurations. Specifically, the method produced accurate results in the case of multiple stretched geometries of N2, where the CISD ground states have overlaps as low as 60% with respect to the exact ground state. This solidifies the utility of using εapp in ranking Hamiltonian partitioning schemes for the ground state energy estimation problem under QPE. For electronic systems with a higher degree of multiconfigurational character, one can find approximations to the global ground state using more sophisticated polynomial-in-time scaling methods, and hence make use of the tools developed here. These estimations of the Trotter approximation error raise two questions for future research: (1) how to optimize efficiently the Hamiltonian partitioning and ordering of its fragments based on the obtained error estimates; and (2) how to obtain upper bounds instead of approximations for the error estimates based on the eigen-spectrum analysis of Heff. Answering the second question will allow one to set an optimal Trotter time step for resource efficient simulation under a target energy eigenvalue estimation accuracy. An interesting direction to explore would be whether the evaluation of εapp can be performed efficiently on a quantum computer. Since many quantum algorithms exist to generate approximations to the ground state, obtaining a better estimate of ε2 would be particularly useful. However, because the error operator ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) 2 is more complex than the Hamiltonian itself, evaluating its expectation value may be costly. Further research is therefore needed to assess whether a quantum computer can offer a practical benefit in this context.
2 is more complex than the Hamiltonian itself, evaluating its expectation value may be costly. Further research is therefore needed to assess whether a quantum computer can offer a practical benefit in this context.
Conflicts of interest
There are no conflicts to declare.
Data availability
The code to generate the Hamiltonian fragments and calculate the exact and approximate Trotter errors can be found at https://github.com/Shashank-G-M/Perturbative_Trotter_Error. The same has been archived on Zenodo with DOI: https://zenodo.org/records/15327942.
Appendix A: Fermionic and qubit-based Hamiltonian decomposition methods
Here, we discuss the methods we used to decompose electronic Hamiltonians into fast-forwardable fragments using fermionic- and qubit-based methods. The second quantized representation of the molecular electronic Hamiltonian with N single particle spin-orbitals under this representation is| | 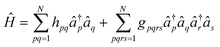 | (A1) |
where a†p (aq) is the creation (annihilation) fermionic operator for the pth spin-orbital, hpq and gpqrs are one- and two-electron integrals.18
(1) Fermionic partitioning methods
These partitioning methods are built upon the solvability of one-electron Hamiltonians using orbital rotations, according to| | 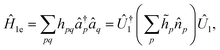 | (A2) |
| | 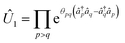 | (A3) |
where ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) p = â†pâq occupation number operators,
p = â†pâq occupation number operators, ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) p are real constants, and Û1 is an orbital rotation parameterized by the amplitudes θpq. Orbital rotations can also be employed to solve two-electron Hamiltonians that are squares of one-electron Hamiltonians as follows:
p are real constants, and Û1 is an orbital rotation parameterized by the amplitudes θpq. Orbital rotations can also be employed to solve two-electron Hamiltonians that are squares of one-electron Hamiltonians as follows:| | 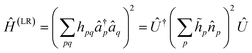 | (A4) |
| | 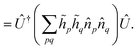 | (A5) |
The matrix with entries λpq = ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) p
p![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) q is a rank-deficient one. The form of two-electron solvable Hamiltonians by means of orbital rotations in (A4) can be straightforwardly generalized by lifting the rank-deficient character of λ matrix and regarding it as a full-rank Hermitian matrix:
q is a rank-deficient one. The form of two-electron solvable Hamiltonians by means of orbital rotations in (A4) can be straightforwardly generalized by lifting the rank-deficient character of λ matrix and regarding it as a full-rank Hermitian matrix:
| | 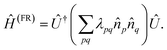 | (A6) |
The fermionic methods that follow are classified according to whether the Hamiltonian decomposition yields fast-forwardable fragments with low- or full-rank character.
Greedy full rank optimization (GFRO).
The approach uses orbital rotations to diagonalize the one-electron part and approximate the two-body interaction terms featured in eqn (A1) as a sum of full-rank Hamiltonian fragments of the form (A6)19| | 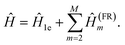 | (A7) |
The decomposition is carried out in a greedy fashion to select an optimal Hamiltonian fragment Ĥ(FR)i+1 [eqn (A6)] that minimizes the L1 norm of the ![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) (i+1) tensor at the ith iteration:
(i+1) tensor at the ith iteration:
| | 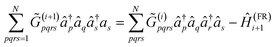 | (A8) |
for
i ≥ 1 and
![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) (1)pqrs
(1)pqrs =
gpqrs, as a function of parameters {
λ(m)pq} and {
θ(m)}.
Low-rank (LR) decomposition.
This partitioning method is based on regarding the two-electron integral tensor gpqrs in eqn (A1) as a square matrix with composite indices along each dimension. It has been shown20 that rank-deficient Hamiltonian fragments can be efficiently found by means of nested factorizations on this matrix, such that| | 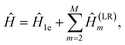 | (A9) |
where| | 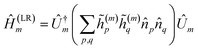 | (A10) |
Pre- and post-processing of Hamiltonian fragments.
So far, the one-body electronic terms of the Hamiltonian in eqn (A1) have been relegated given their straightforward orbital-rotation solvability. However, the one-electron Hamiltonian in (A1) can be partitioned in the same footing as the discussed methods by merging the former in the two-body electronic terms as follows| | 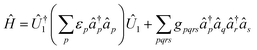 | (A11) |
| | 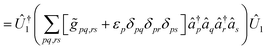 | (A12) |
| | 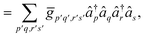 | (A13) |
the decomposition of the ensuing two-electron Hamiltonian can be carried out with the fermionic techniques discussed above. For computational ease, in this work we consider the decomposition of the Hamiltonian (A13) with the GFRO approach, and refer to our combined scheme as SD GFRO, where SD stands for “singles and doubles” in analogy to the terminology used in the electronic structure literature for single and double fermionic excitation operators. In addition to the pre-processing discussed above, we consider a post-processing technique that usually lowers the Trotter approximation error estimator α and relies on the removal of the one-body electron contributions encoded within each of the two-body Hamiltonian fragments and grouping the former in a single one-body electronic sub-Hamiltonian. This is accomplished by employing the approach based in ref. 21, where two-body interaction terms are written as a Linear Combination of Unitaries (LCU), with a concomitant adjustment of the one-body Hamiltonian contributions:9| | 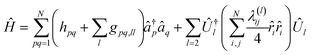 | (A14) |
| |  | (A15) |
(2) Qubit-based partitioning methods
When the Hamiltonian (A1) is mapped to N interacting two-level systems through encodings such as Jordan–Wigner or Bravyi–Kitaev, the Hamiltonian thus obtained is of the form,
where, cn are numerical coefficients and ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) n are tensor products of single-qubit Pauli operators and the identity,
n are tensor products of single-qubit Pauli operators and the identity, ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) (n)k =
(n)k = ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) k,ŷk,ẑk,Îk, acting on the kth qubit. The Fully Commuting (FC) grouping partitions Ĥq into Ĥ(FC)n fragments containing commuting Pauli products:
k,ŷk,ẑk,Îk, acting on the kth qubit. The Fully Commuting (FC) grouping partitions Ĥq into Ĥ(FC)n fragments containing commuting Pauli products:
if ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) i, i,![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) j ∈ Ĥ(FC)n then [ j ∈ Ĥ(FC)n then [![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) i, i,![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) j] = 0. j] = 0. |
This FC condition ensures that Ĥ(FC)n can be transformed, through a series of Clifford group transformations, into sums of only products of Pauli ẑk operators.22,23 We also consider a grouping with a more strict condition known as qubit-wise commutativity (QWC), where each single-qubit Pauli operator in one product commutes with its counterpart in the other product. For example, ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 1ŷ2Î3 and
1ŷ2Î3 and ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 1Î2ẑ3 have QWC as [
1Î2ẑ3 have QWC as [![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 1,
1,![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 1] = 0, [ŷ2,Î2] = 0, [Î3,ẑ3] = 0. Hence, both terms must also fully commute. The converse does not always hold true. For example,
1] = 0, [ŷ2,Î2] = 0, [Î3,ẑ3] = 0. Hence, both terms must also fully commute. The converse does not always hold true. For example, ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 1
1![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 2 and ŷ1ŷ2 are fully commuting but not qubit-wise commuting.24
2 and ŷ1ŷ2 are fully commuting but not qubit-wise commuting.24
For the FC and QWC partitioning techniques, we work with the largest-first (LF) heuristic and the Sorted Insertion (SI) algorithm. The SI algorithm is based on a greedy partitioning of the Hamiltonian, which results in concentrated coefficients cn in the first found Hamiltonian fragments. The LF algorithm, in contrast, yields a homogeneous distribution in the magnitudes of the cn coefficients across Hamiltonian fragments, which usually results in a smaller number of fragments compared to the SI version.24,25
Appendix B: Details of the Hamiltonians and wavefunctions
The Hamiltonians were generated using the STO-3G basis and the Jordan–Wigner transformations for qubit encodings as implemented in the OpenFermion package.26 The nuclear geometries for the molecules are given by R(H–H) = 1 Å (H2), R(Li–H) = 1 Å (LiH) and R(Be–H) = 1 Å with collinear atomic arrangement (BeH2), R(OH) = 1.9 Å and ∠HOH = 104.5° (H2O); and R(N–H) = 1.9 Å with ∠HNH = 107° (NH3). The ground state CISD wavefunction is generated using the OpenFermion package.
Appendix C: Computation of errors for the second order Trotter approximation
From eqn (5) of the main text, Ĥeff is computed through| | Ĥeff = it−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(Û(2)T(t)), ln(Û(2)T(t)), | (C1) |
where 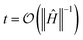 . ε's are obtained according to ε = t−2|E(T)0 − E0|, where E(T)0 (E0) is the ground state energy of Ĥeff (Ĥ). All these calculations were performed using the python Scipy library.27 To reduce computational overhead in our calculations, we take advantage of the fact that the initial state |ψ〉 belongs to a particular irreducible representation of the molecular symmetries: the number of electrons,
. ε's are obtained according to ε = t−2|E(T)0 − E0|, where E(T)0 (E0) is the ground state energy of Ĥeff (Ĥ). All these calculations were performed using the python Scipy library.27 To reduce computational overhead in our calculations, we take advantage of the fact that the initial state |ψ〉 belongs to a particular irreducible representation of the molecular symmetries: the number of electrons, ![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) e, the electron spin, Ŝ2, and its projection, Ŝz. Selecting symmetry adapted states for the neutral singlet molecular forms allowed to reduce the Hamiltonian sub-spaces by almost two orders of magnitude. Similarly, for qubit-based partitioning methods, we use qubit tapering to reduce the system size of NH3 from a 16-qubit system to a 14-qubit system.28 Since the number qubit fragments and their sizes are usually large for BeH2, H2O and NH3, instead of exponentiating each fragment exactly, we approximate the exponential using Taylor series up to 11th order in time. We make use of the Niagara compute cluster hosted by SciNet29 for memory intensive calculations. The Trotter approximation error depends on the order in which individual unitaries e−itĤn are applied.30 The code to generate Hamiltonian fragments and calculate the Trotter error can be accessed at https://doi.org/10.5281/zenodo.15327942.
e, the electron spin, Ŝ2, and its projection, Ŝz. Selecting symmetry adapted states for the neutral singlet molecular forms allowed to reduce the Hamiltonian sub-spaces by almost two orders of magnitude. Similarly, for qubit-based partitioning methods, we use qubit tapering to reduce the system size of NH3 from a 16-qubit system to a 14-qubit system.28 Since the number qubit fragments and their sizes are usually large for BeH2, H2O and NH3, instead of exponentiating each fragment exactly, we approximate the exponential using Taylor series up to 11th order in time. We make use of the Niagara compute cluster hosted by SciNet29 for memory intensive calculations. The Trotter approximation error depends on the order in which individual unitaries e−itĤn are applied.30 The code to generate Hamiltonian fragments and calculate the Trotter error can be accessed at https://doi.org/10.5281/zenodo.15327942.
Appendix D: Effective Hamiltonian derivation based on BCH expansion
In this section we generalize the BCH formula, usually defined for two Hamiltonian fragments, to an arbitrary number of fragments N. We will use mathematical induction with a starting point:| | | e−iH2te−iH1t = exp(−iH(2)efft), | (D1) |
where
To obtain the form of the effective Hamiltonian for N fragments, H(N)eff we extend eqn (D1) to the three-fragment case:
where
 becomes
We note that  can be written in the form
| | 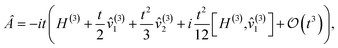 | (D2) |
where
Finally, to show that the form (D2) can be generalized for an arbitrary number of Hamiltonian fragments, we use induction:
where
By using
![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) (n+1)1 = (n+1)1 = ![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) (n)1 − i[Ĥn+1,Ĥ(n)] (n)1 − i[Ĥn+1,Ĥ(n)] |
![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) (n+1)2 = (n+1)2 = ![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) (n)2 − 12[Hn+1,[Hn+1,H(n)]] − i[Hn+1, (n)2 − 12[Hn+1,[Hn+1,H(n)]] − i[Hn+1,![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) (n)1] (n)1] |
[Ĥ(n+1),![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) (n+1)1] = [H(n), (n+1)1] = [H(n),![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) (n)1] − i[H(n),[Hn+1,H(n)]] + [Hn+1, (n)1] − i[H(n),[Hn+1,H(n)]] + [Hn+1,![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) (n)1] − i[Hn+1,[Hn+1,H(n)]] (n)1] − i[Hn+1,[Hn+1,H(n)]] |
we have
Therefore, for Hamiltonian H decomposed into N Hamiltonian fragments, the effective Hamiltonian Heff is
| | 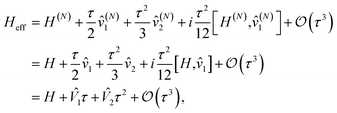 | (D3) |
where
| | 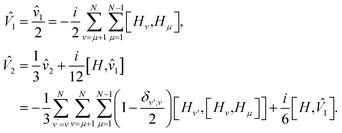 | (D4) |
To get the special case of second order Trotter, use N = 2M, where M is the number of Hamiltonian fragments, and HM+i = HM+1−i for i = 1 to M. Also, each of the fragment will have to be rescaled by a factor of half, as we repeat each fragment twice in the second order Trotter formula [see eqn (2)]. With this constraint, for every commutator [Hμ, Hν] in the expression of ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) 1, there exists a commutator [Hν, Hμ] with the same coefficient. Thus,
1, there exists a commutator [Hν, Hμ] with the same coefficient. Thus, ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) 1 equals zero. Using the same constraint in the expression of
1 equals zero. Using the same constraint in the expression of ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) 2, we recover eqn (7).
2, we recover eqn (7).
Appendix E: Compendium of different Trotter approximation error upper bounds
Tables 3–5 compile Trotter approximation error estimates based on ε, α, and αe quantities. Tables 6 and 7 summarize εapp and ε2 values for H2, LiH, BeH2, and NH3. Tables 8 and 9 summarize the same for N2. These results are obtained by considering the Trotterized unitary:
where the ordering of Hamiltonian fragments was taken as found by the different partition methods with no further post-processing.
Table 3
ε values obtained from true Trotter approximation error scaling for different fermionic and qubit-based partitioning methods and molecules
| Molecule |
QWC LF |
QWC SI |
FC LF |
FC SI |
LR LCU |
GFRO LCU |
LR |
GFRO |
SD GFRO |
| H2 |
3.3 × 10−3 |
3.3 × 10−3 |
3.3 × 10−3 |
3.3 × 10−3 |
3.3 × 10−3 |
3.3 × 10−3 |
2.8 × 10−3 |
2.8 × 10−3 |
3.1 × 10−3 |
| LiH |
3.2 × 10−3 |
2.2 × 10−3 |
3.0 × 10−3 |
2.4 × 10−3 |
3.3 × 10−3 |
3.4 × 10−3 |
4.7 × 10−2 |
5.0 × 10−2 |
1.8 × 10−2 |
| BeH2 |
1.4 × 10−2 |
1.1 × 10−2 |
2.3 × 10−2 |
8.8 × 10−3 |
9.3 × 10−3 |
9.6 × 10−3 |
2.9 × 10−2 |
3.3 × 10−2 |
2.0 × 10−2 |
| H2O |
6.2 × 10−3 |
4.8 × 10−3 |
2.4 × 10−2 |
2.9 × 10−3 |
2.4 × 10−2 |
2.5 × 10−2 |
1.4 × 10−1 |
1.3 × 10−1 |
2.6 × 10−2 |
| NH3 |
1.1 × 10−2 |
1.0 × 10−2 |
9.0 × 10−2 |
1.5 × 10−2 |
2.0 × 10−2 |
2.0 × 10−2 |
1.7 × 10−1 |
1.4 × 10−1 |
2.9 × 10−2 |
Table 4 Values of Trotter approximation error upper bound α as defined in eqn (4)
| Molecule |
QWC LF |
QWC SI |
FC LF |
FC SI |
LCU |
GFRO LCU |
LR |
GFRO |
SD GFRO |
| H2 |
0.02 |
0.02 |
0.02 |
0.02 |
0.02 |
0.02 |
0.02 |
0.02 |
0.02 |
| LiH |
1.07 |
0.26 |
0.63 |
0.26 |
0.13 |
0.12 |
0.52 |
0.46 |
0.23 |
| BeH2 |
4.22 |
1.02 |
4.96 |
0.99 |
0.58 |
0.55 |
2.36 |
2.03 |
1.13 |
| H2O |
79.41 |
28.73 |
181.56 |
27.86 |
15.30 |
15.06 |
52.37 |
48.27 |
27.88 |
| NH3 |
51.66 |
16.36 |
65.99 |
16.02 |
7.81 |
7.64 |
28.43 |
25.79 |
14.51 |
Table 5 Values of αe = ‖ÛT(t) − Û(2)T(t)‖/t3
| Molecule |
QWC LF |
QWC SI |
FC LF |
FC SI |
LR LCU |
GFRO LCU |
LR |
GFRO |
SD GFRO |
| H2 |
0.02 |
0.01 |
0.02 |
0.01 |
0.01 |
0.01 |
0.01 |
0.01 |
0.01 |
| LiH |
0.22 |
0.18 |
0.25 |
0.18 |
0.10 |
0.10 |
0.07 |
0.08 |
0.06 |
| BeH2 |
0.67 |
0.75 |
0.81 |
0.76 |
0.42 |
0.43 |
0.29 |
0.35 |
0.36 |
| H2O |
23.25 |
23.42 |
46.45 |
23.45 |
1.85 |
11.86 |
15.67 |
14.88 |
12.87 |
| NH3 |
11.23 |
11.23 |
15.86 |
11.21 |
6.55 |
6.56 |
7.25 |
7.05 |
6.03 |
Table 6
ε
app = 〈ψ0|![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) 2|ψ0〉 for different Hamiltonian decomposition methods and molecules
2|ψ0〉 for different Hamiltonian decomposition methods and molecules
| Molecule |
QWC-LF |
QWC-SI |
FC-LF |
FC-SI |
LR LCU |
GFRO LCU |
LR |
GFRO |
SD-GFRO |
| H2 |
3.24 × 10−3 |
3.24 × 10−3 |
3.24 × 10−3 |
3.24 × 10−3 |
3.24 × 10−3 |
3.24 × 10−3 |
2.77 × 10−3 |
2.78 × 10−3 |
3.00 × 10−3 |
| LiH |
3.26 × 10−3 |
2.18 × 10−3 |
3.02 × 10−3 |
2.46 × 10−3 |
3.30 × 10−3 |
3.39 × 10−3 |
4.72 × 10−2 |
4.99 × 10−2 |
1.82 × 10−2 |
| BeH2 |
1.38 × 10−2 |
1.12 × 10−2 |
2.25 × 10−2 |
8.93 × 10−3 |
9.49 × 10−3 |
9.83 × 10−3 |
2.89 × 10−2 |
3.36 × 10−2 |
1.98 × 10−2 |
| H2O |
9.78 × 10−3 |
8.04 × 10−3 |
1.99 × 10−2 |
6.03 × 10−3 |
3.22 × 10−2 |
3.52 × 10−2 |
1.78 × 10−1 |
1.67 × 10−1 |
3.48 × 10−2 |
| NH3 |
1.31 × 10−2 |
1.57 × 10−2 |
7.79 × 10−2 |
1.05 × 10−2 |
3.33 × 10−2 |
3.44 × 10−2 |
2.34 × 10−1 |
2.09 × 10−1 |
4.75 × 10−2 |
Table 7
ε
2 = 〈ϕ0|![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) 2|ϕ0〉 for different Hamiltonian decomposition methods and molecules
2|ϕ0〉 for different Hamiltonian decomposition methods and molecules
| Molecule |
QWC-LF |
QWC-SI |
FC-LF |
FC-SI |
LR LCU |
GFRO LCU |
LR |
GFRO |
SD-GFRO |
| H2 |
3.24 × 10−3 |
3.24 × 10−3 |
3.24 × 10−3 |
3.24 × 10−3 |
3.24 × 10−3 |
3.24 × 10−3 |
2.77 × 10−3 |
2.78 × 10−3 |
3.00 × 10−3 |
| LiH |
3.25 × 10−3 |
2.16 × 10−3 |
3.01 × 10−3 |
2.45 × 10−3 |
3.30 × 10−3 |
3.39 × 10−3 |
4.72 × 10−2 |
4.99 × 10−2 |
1.82 × 10−2 |
| BeH2 |
1.37 × 10−2 |
1.10 × 10−2 |
2.27 × 10−2 |
8.76 × 10−3 |
9.30 × 10−3 |
9.63 × 10−3 |
2.87 × 10−2 |
3.34 × 10−2 |
1.96 × 10−2 |
| H2O |
6.22 × 10−3 |
4.76 × 10−3 |
2.36 × 10−2 |
2.85 × 10−3 |
2.37 × 10−2 |
2.51 × 10−2 |
1.42 × 10−1 |
1.28 × 10−1 |
2.58 × 10−2 |
| NH3 |
1.15 × 10−2 |
9.98 × 10−3 |
8.95 × 10−2 |
1.52 × 10−2 |
2.00 × 10−2 |
1.98 × 10−2 |
1.65 × 10−1 |
1.38 × 10−1 |
2.94 × 10−2 |
Table 8
ε
app = 〈ψ0|![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) 2|ψ0〉 for N2 at various bond lengths
2|ψ0〉 for N2 at various bond lengths
| Bond stretch factor |
QWC-LF |
QWC-SI |
FC-LF |
FC-SI |
LR LCU |
GFRO LCU |
LR |
GFRO |
SD-GFRO |
| 1.9 |
1.22 × 10−2 |
1.01 × 10−2 |
6.26 × 10−2 |
1.13 × 10−2 |
7.20 × 10−3 |
7.49 × 10−3 |
1.75 × 10−2 |
2.15 × 10−2 |
9.63 × 10−3 |
| 2.0 |
1.28 × 10−2 |
1.20 × 10−2 |
4.98 × 10−2 |
1.18 × 10−2 |
5.95 × 10−3 |
6.28 × 10−3 |
1.35 × 10−2 |
1.66 × 10−2 |
9.42 × 10−3 |
| 2.1 |
9.23 × 10−3 |
6.81 × 10−3 |
5.55 × 10−2 |
6.66 × 10−3 |
4.99 × 10−3 |
5.39 × 10−3 |
1.05 × 10−2 |
1.32 × 10−2 |
7.76 × 10−3 |
| 2.2 |
8.71 × 10−3 |
6.40 × 10−3 |
5.38 × 10−2 |
6.41 × 10−3 |
4.25 × 10−3 |
4.64 × 10−3 |
8.29 × 10−3 |
1.10 × 10−2 |
5.90 × 10−3 |
| 2.3 |
1.20 × 10−2 |
5.93 × 10−3 |
3.46 × 10−2 |
5.72 × 10−3 |
3.66 × 10−3 |
4.02 × 10−3 |
6.54 × 10−3 |
9.98 × 10−3 |
4.98 × 10−3 |
Table 9
ε
2 = 〈ϕ0|![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) 2|ϕ0〉 for N2 at various bond lengths
2|ϕ0〉 for N2 at various bond lengths
| Bond stretch factor |
QWC-LF |
QWC-SI |
FC-LF |
FC-SI |
LR LCU |
GFRO LCU |
LR |
GFRO |
SD-GFRO |
| 1.9 |
1.01 × 10−2 |
3.72 × 10−3 |
5.55 × 10−2 |
4.64 × 10−3 |
1.72 × 10−3 |
2.29 × 10−3 |
9.65 × 10−3 |
1.50 × 10−2 |
5.25 × 10−3 |
| 2.0 |
1.03 × 10−2 |
4.60 × 10−3 |
4.84 × 10−2 |
4.46 × 10−3 |
9.60 × 10−4 |
1.52 × 10−3 |
6.53 × 10−3 |
1.10 × 10−2 |
5.24 × 10−3 |
| 2.1 |
8.06 × 10−3 |
1.99 × 10−3 |
4.48 × 10−2 |
1.77 × 10−3 |
4.70 × 10−4 |
1.07 × 10−3 |
4.61 × 10−3 |
8.45 × 10−3 |
4.16 × 10−3 |
| 2.2 |
8.09 × 10−3 |
1.63 × 10−3 |
4.30 × 10−2 |
1.65 × 10−3 |
1.56 × 10−4 |
7.06 × 10−4 |
3.41 × 10−3 |
6.86 × 10−3 |
3.07 × 10−3 |
| 2.3 |
1.30 × 10−2 |
1.47 × 10−3 |
4.55 × 10−2 |
1.25 × 10−3 |
−4.50 × 10−5 |
4.93 × 10−4 |
2.65 × 10−3 |
6.26 × 10−3 |
2.71 × 10−3 |
Appendix F: T-gate count upper bound estimations
Upper-bound for T-gate counts for a fixed target error εTot in energy eigenvalue estimation in a Trotterized quantum phase estimation algorithm can be formulated in light of previous works.31,32 The total T-gate count NT7,32 is given bywhere NR is the number of single-qubit rotations needed for the implementation of a single Trotter step in a quantum computer. NHT refers to the number of T gates needed to compile one single qubit rotation (for a fixed target error εHT) and NPE is the number of Trotter steps required to resolve the target energy eigenvalue under a target uncertainty εPE, the latter scaling as t−1, t being the total simulation time. Using our results that describe the energy deviation in the estimated ground-state energy eigenvalue due to the Trotter approximation, according to the relation εΔt2 = ΔET, we find the Trotter step Δt according to a target error εTS, given by 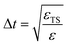 . The number of Trotter steps needed for a target uncertainty in phase estimation under adaptive phase estimation techniques is given by
. The number of Trotter steps needed for a target uncertainty in phase estimation under adaptive phase estimation techniques is given by| |  | (F2) |
Finally, the number of T gates needed to compile one single qubit rotation for a fixed target error εHT is 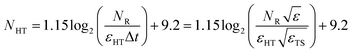 . Putting everything together we arrive at
. Putting everything together we arrive at
| | 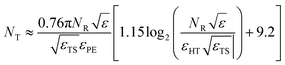 | (F3) |
In the worst case, the errors due to the three sources discussed above, add linearly32 and to guarantee that the total error is at most εTot we assume
| | | εTot = εTS + εPE + εHT. | (F4) |
Thus, we can minimize the number of T-gates NT over the target errors in eqn (F3) subject to the constraint (F4), for an estimation of T-gate under a target error εTot. In this work, we have taken εTot = 1.6 × 10−3 Hartree, the chemical accuracy. The T-gate upper bounds based on ε, α, and εapp are provided in Tables 10 and 11.
Table 10 Best resource-efficient Hamiltonian decomposition methods for eigenvalue estimation within chemical accuracy with a Trotterized QPE algorithm. T-gate count NT is given in parenthesis
| Molecule |
ε-based |
α-based |
| 1st best (NT) |
2nd best (NT) |
3nd best (NT) |
1st best (NT) |
2nd best (NT) |
3nd best (NT) |
| H2 |
QWC LF (6.2 × 106) |
QWC SI (6.2 × 106) |
FC LF (6.2 × 106) |
QWC SI (1.4 × 107) |
FC SI (1.4 × 107) |
QWC LF (1.5 × 107) |
| LiH |
QWC SI (2.5 × 108) |
FC SI (2.7 × 108) |
FC LF (3.0 × 108) |
FC SI (2.9 × 109) |
QWC SI (2.9 × 109) |
FC LF (4.7 × 109) |
| BeH2 |
FC SI (5.5 × 108) |
QWC SI (6.2 × 108) |
QWC LF (7.0 × 108) |
FC SI (6.3 × 109) |
QWC SI (6.4 × 109) |
QWC LF (1.3 × 1010) |
| H2O |
FC SI (5.1 × 108) |
QWC SI (6.7 × 108) |
QWC LF (7.7 × 108) |
FC SI (5.9 × 1010) |
QWC SI (6.0 × 1010) |
QWC LF (1.0 × 1011) |
| NH3 |
QWC SI (9.8 × 108) |
QWC LF (1.0 × 109) |
FC SI (1.2 × 109) |
FC SI (4.4 × 1010) |
QWC SI (4.5 × 1010) |
QWC LF (8.1 × 1010) |
Table 11 Best resource-efficient Hamiltonian decomposition methods for eigenvalue estimation within chemical accuracy with a Trotterized QPE algorithm. T-gate count NT is given in parenthesis
| Molecule |
ε
app-based |
| 1st best (NT) |
2nd best (NT) |
3nd best (NT) |
| H2 |
QWC LF (6.2 × 106) |
QWC SI (6.2 × 106) |
FC LF (6.2 × 106) |
| LiH |
QWC SI (2.5 × 108) |
FC SI (2.7 × 108) |
FC LF (3.0 × 108) |
| BeH2 |
FC SI (5.6 × 108) |
QWC SI (6.2 × 108) |
QWC LF (7.0 × 108) |
| H2O |
FC SI (7.6 × 108) |
QWC SI (8.8 × 108) |
QWC LF (9.7 × 108) |
| NH3 |
FC SI (1.0 × 109) |
QWC LF (1.1 × 109) |
QWC SI (1.2 × 109) |
Acknowledgements
The authors would like to thank Nathan Wiebe for useful discussions. L. A. M. M. is grateful to the Center for Quantum Information and Quantum Control (CQIQC) for a postdoctoral fellowship. P. D. K. is grateful to Mitacs for the Globalink research award. A. F. I. acknowledges financial support from the Natural Sciences and Engineering Council of Canada (NSERC). This research was partly enabled by the support of Compute Ontario (https://www.computeontario.ca) and the Digital Research Alliance of Canada (https://www.alliancecan.ca). Part of the computations were performed on the Niagara supercomputer at the SciNet HPC Consortium. SciNet is funded by Innovation, Science, and Economic Development Canada, the Digital Research Alliance of Canada, the Ontario Research Fund: Research Excellence, and the University of Toronto.
References
-
T. Hoefler, T. Haener and M. Troyer, Disentangling hype from practicality: On realistically achieving quantum advantage, arXiv, 2023, preprint, arXiv:2307.00523, DOI:10.48550/arXiv.2307.00523.
- L. Bassman Oftelie, M. Urbanek, M. Metcalf, J. Carter, A. F. Kemper and W. A. de Jong, Simulating quantum materials with digital quantum computers, Quantum Sci. Technol., 2021, 6, 043002 CrossRef.
- M. Suzuki, Fractal decomposition of exponential operators with applications to many-body theories and monte carlo simulations, Phys. Lett. A, 1990, 146, 319–323 CrossRef.
-
A. M. Childs and N. Wiebe, Hamiltonian simulation using linear combinations of unitary operations, arXiv, 2012, preprint, arXiv:1202.5822, DOI:10.48550/arXiv.1202.5822.
- H. L. Guang and I. L. Chuang, Hamiltonian Simulation by Qubitization, Quantum, 2019, 3, 163 CrossRef.
- A. M. Childs, Y. Su, M. C. Tran, N. Wiebe and S. Zhu, Theory of trotter error with commutator scaling, Phys. Rev. X, 2021, 11, 011020 CAS.
- M. Reiher, N. Wiebe, K. M. Svore, D. Wecker and M. Troyer, Elucidating reaction mechanisms on quantum computers, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 7555–7560 CrossRef CAS PubMed.
-
D. Poulin, M. B. Hastings, D. Wecker, N. Wiebe, A. C. Doherty and T. Matthias, Trotter step size required for accurate quantum simulation of quantum chemistry, arXiv, 2014, preprint, arXiv:1406.4920, DOI:10.48550/arXiv.1406.4920.
- L. A. Martínez-Martínez, T.-C. Yen and A. F. Izmaylov, Assessment of various Hamiltonian partitionings for the electronic structure problem on a quantum computer using the Trotter approximation, Quantum, 2023, 7, 1086 CrossRef.
- R. Babbush, J. McClean, D. Wecker, A. Aspuru-Guzik and N. Wiebe, Chemical basis of trotter-suzuki errors in quantum chemistry simulation, Phys. Rev. A, 2015, 91, 022311 CrossRef.
-
G. Rendon, W. Jacob and N. Wiebe, Improved error scaling for trotter simulations through extrapolation, arXiv, 2022, preprint, arXiv:1406.4920, DOI:10.48550/arXiv.1406.4920.
- S. Lee, J. Lee, H. Zhai, Y. Tong, A. M. Dalzell, A. Kumar, P. Helms, J. Gray, Z.-H. Cui, W. Liu, M. Kastoryano, R. Babbush, J. Preskill, D. R. Reichman, E. T. Campbell, E. F. Valeev, L. Lin and G. K.-L. Chan, Evaluating the evidence for exponential quantum advantage in ground-state quantum chemistry, Nat. Commun., 2023, 14 Search PubMed.
-
N. M. Tubman, C. Mejuto-Zaera, J. M. Epstein, D. Hait, D. S. Levine, W. J. Huggins, Z. Jiang, J. R. McClean, R. Babbush, M. Head-Gordon and K. B. Whaley, Postponing the orthogonality catastrophe: efficient state preparation for electronic structure simulations on quantum devices, arXiv, 2018, preprint, arXiv:1809.05523, DOI:10.48550/arXiv.1809.05523.
- P. J. Ollitrault, C. L. Cortes, J. F. Gonthier, R. M. Parrish, D. Rocca, G.-L. Anselmetti, M. Degroote, N. Moll, R. Santagati and M. Streif, Enhancing initial state overlap through orbital optimization for faster molecular electronic ground-state energy estimation, Phys. Rev. Lett., 2024, 133, 250601 CrossRef CAS PubMed.
- D. W. Berry, Y. Tong, T. Khattar, A. White, T. In Kim, G. H. Low, S. Boixo, Z. Ding, L. Lin, S. Lee, G. K.-L. Chan, R. Babbush and N. C. Rubin, Rapid initial-state preparation for the quantum simulation of strongly correlated molecules, PRX Quantum, 2025, 6, 020327 CrossRef.
-
J. Lin and A. F. Izmaylov, Bounds on a wavefunction overlap with hamiltonian eigen-states: Performance guarantees for the quantum phase estimation algorithm, arXiv, 2025, preprint, arXiv:2503.12224, DOI:10.48550/arXiv.2307.00523.
- L. Lin and Y. Tong, Heisenberg-limited ground-state energy estimation for early fault-tolerant quantum computers, PRX Quantum, 2022, 3, 010318 CrossRef.
-
T. Helgaker, P. Jørgensen and J. Olsen, Molecular Electronic Structure Theory, John Wiley & Sons, Ltd., Chichester, 2000 Search PubMed.
- T.-C. Yen and A. F. Izmaylov, Cartan subalgebra approach to efficient measurements of quantum observables, PRX Quantum, 2021, 2, 040320 CrossRef.
- M. Motta, E. Ye, J. R. McClean, Z. Li, A. J. Minnich, R. Babbush and G. K.-L. Chan, Low rank representations for quantum simulation of electronic structure, npj Quantum Inf., 2021, 7, 83 CrossRef.
- J. Lee, D. W. Berry, G. Craig, W. J. Huggins, J. R. McClean, N. Wiebe and B. Ryan, Even more efficient quantum computations of chemistry through tensor hypercontraction, PRX Quantum, 2021, 2, 030305 CrossRef.
- Z. Pierce Bansingh, T.-C. Yen, P. D. Johnson and A. F. Izmaylov, Fidelity overhead for nonlocal measurements in variational quantum algorithms, J. Phys. Chem. A, 2022, 126, 7007–7012 CrossRef PubMed.
- E. Van Den Berg and K. Temme, Circuit optimization of hamiltonian simulation by simultaneous diagonalization of pauli clusters, Quantum, 2020, 4, 322 CrossRef.
- T.-C. Yen, V. Verteletskyi and A. F. Izmaylov, Measuring all compatible operators in one series of single-qubit measurements using unitary transformations, J. Chem. Theory Comput., 2020, 16, 2400–2409 CrossRef CAS PubMed.
- V. Vladyslav, T.-C. Yen and A. F. Izmaylov, Measurement optimization in the variational quantum eigensolver using a minimum clique cover, J. Chem. Phys., 2020, 152, 124114 CrossRef PubMed.
- J. R. McClean, N. C. Rubin, K. J. Sung, I. D. Kivlichan, X. Bonet-Monroig, Y. Cao, C. Dai, E. S. Fried, G. Craig and B. Gimby,
et al., Openfermion: the electronic structure package for quantum computers, Quantum Sci. Technol., 2020, 5, 034014 CrossRef.
- P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser, J. Bright, S. J. van der Walt, M. Brett, J. Wilson, K. J. Millman, N. Mayorov, A. R. J. Nelson, E. Jones, R. Kern, E. Larson, C. J. Carey, İ. Polat, Yu Feng, E. W. Moore, J. VanderPlas, D. Laxalde, J. Perktold, R. Cimrman, I. Henriksen, E. A. Quintero, C. R. Harris, A. M. Archibald, A. H. Ribeiro, F. Pedregosa, P. van Mulbregt and SciPy 1.0 Contributors, SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python, Nat. Methods, 2020, 17, 261–272 CrossRef CAS PubMed.
-
S. Bravyi, J. M. Gambetta, A. Mezzacapo and K. Temme, Tapering off qubits to simulate fermionic hamiltonians, arXiv, 2017, preprint, arXiv:1701.08213, DOI:10.48550/arXiv.1701.08213.
-
M. Ponce, R. van Zon, S. Northrup, D. Gruner, J. Chen, F. Ertinaz, A. Fedoseev, L. Groer, F. Mao, B. C. Mundim, M. Nolta, J. Pinto, M. Saldarriaga, V. Slavnic, E. Spence, C.-H. Yu and W. R. Peltier, Deploying a top-100 supercomputer
for large parallel workloads: the niagara supercomputer, in Practice and Experience in Advanced Research Computing 2019: Rise of the Machines (Learning). PEARC '19, Association for Computing Machinery, New York, NY, USA, 2019 Search PubMed.
- A. Tranter, P. J. Love, F. Mintert, N. Wiebe and P. V. Coveney, Ordering of trotterization: Impact on errors in quantum simulation of electronic structure, Entropy, 2019, 21, 1218 CrossRef CAS.
- D. W. Berry, D. W. Berry, B. Higgins, S. D. Bartlett, M. W. Mitchell, G. J. Pryde and H. M. Wiseman, How to perform the most accurate possible phase measurements, Phys. Rev. A: At., Mol., Opt. Phys., 2009, 80, 052114 CrossRef.
- I. D. Kivlichan, G. Craig, D. W. Berry, N. Wiebe, J. McClean, W. Sun, Z. Jiang, N. Rubin, A. Fowler, A. Aspuru-Guzik, H. Neven and B. Ryan, Improved Fault-Tolerant Quantum Simulation of Condensed-Phase Correlated Electrons via Trotterization, Quantum, 2020, 4, 296 CrossRef.
Footnote |
| † These authors contributed equally to this work. |
|
| This journal is © The Royal Society of Chemistry 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article ab,
Luis A.
Martínez-Martínez†
ab,
Prathami Divakar
Kamath†
ab,
Luis A.
Martínez-Martínez†
ab,
Prathami Divakar
Kamath†
 c and
Artur F.
Izmaylov
c and
Artur F.
Izmaylov
 *ab
*ab
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos−1(Ĥ/λ)) when given access to an LCU decomposition of a Hamiltonian, where λ is the induced 1-norm of the LCU.5 Unlike the Trotter approximation, Qubitization can encode the Hamiltonian exactly. This allows a straightforward cost analysis with tight bounds on T-gate counts in terms of target accuracy. The downside, however, is the significant number of ancillas required, which are not needed in the Trotter approximation. In the early fault-tolerant era, when the number of logical qubits is expected to be limited, this trade-off is crucial. Hence, in this work we focus on the Trotter approximation for Hamiltonian simulation.
cos−1(Ĥ/λ)) when given access to an LCU decomposition of a Hamiltonian, where λ is the induced 1-norm of the LCU.5 Unlike the Trotter approximation, Qubitization can encode the Hamiltonian exactly. This allows a straightforward cost analysis with tight bounds on T-gate counts in terms of target accuracy. The downside, however, is the significant number of ancillas required, which are not needed in the Trotter approximation. In the early fault-tolerant era, when the number of logical qubits is expected to be limited, this trade-off is crucial. Hence, in this work we focus on the Trotter approximation for Hamiltonian simulation.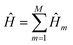
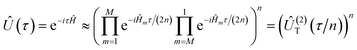
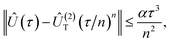
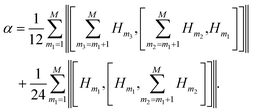
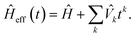
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) k's survive in eqn (6). The leading term is then given by [see Appendix D]
k's survive in eqn (6). The leading term is then given by [see Appendix D]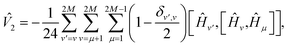
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) 2|ϕ0〉t2,
2|ϕ0〉t2,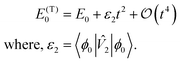
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) 2|ψ0〉.
2|ψ0〉.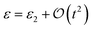 (follows from eqn (8)), for small t, which is mostly the case for ground state energy estimation, ε2 should capture ε almost exactly. A similar correlation calculation as in Table 1 between ε and ε2 leads to a Pearson correlation coefficient of 1.0 for all the molecules considered. Most importantly, correlation between ε vs. εapp also stays close to one with the lowest correlation coefficient being 0.98 for NH3.
(follows from eqn (8)), for small t, which is mostly the case for ground state energy estimation, ε2 should capture ε almost exactly. A similar correlation calculation as in Table 1 between ε and ε2 leads to a Pearson correlation coefficient of 1.0 for all the molecules considered. Most importantly, correlation between ε vs. εapp also stays close to one with the lowest correlation coefficient being 0.98 for NH3.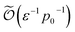 ,17 where ε is the QPE error arising from the finite number of repetitions of the time propagator. It should be noted, however, that ε is introduced in addition to ε2 from the Trotter approximation. Thus, even if QPE error is made small, Trotter error can still prevent achieving chemical accuracy. The Trotter time step can be reduced arbitrarily to overcome this, but doing so only increases the gate depth due to the larger number of repetitions required to reach the same total time. Hence, we believe it is important to specifically analyze Trotter error and how it depends on the choice of Hamiltonian partitioning. In our estimation of the T-gate upper bound, we do not fix the Trotter or QPE error individually; instead, we require that their sum (together with the error from compilation to T-gates) remain below the target accuracy. Under this constraint, we vary these errors to minimize the T-gate upper bound. Since this optimization is nonlinear with many local minima, it is difficult to comment on the exact relationship between Trotter error and QPE error at fixed target accuracy.
,17 where ε is the QPE error arising from the finite number of repetitions of the time propagator. It should be noted, however, that ε is introduced in addition to ε2 from the Trotter approximation. Thus, even if QPE error is made small, Trotter error can still prevent achieving chemical accuracy. The Trotter time step can be reduced arbitrarily to overcome this, but doing so only increases the gate depth due to the larger number of repetitions required to reach the same total time. Hence, we believe it is important to specifically analyze Trotter error and how it depends on the choice of Hamiltonian partitioning. In our estimation of the T-gate upper bound, we do not fix the Trotter or QPE error individually; instead, we require that their sum (together with the error from compilation to T-gates) remain below the target accuracy. Under this constraint, we vary these errors to minimize the T-gate upper bound. Since this optimization is nonlinear with many local minima, it is difficult to comment on the exact relationship between Trotter error and QPE error at fixed target accuracy.![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) 2 is more complex than the Hamiltonian itself, evaluating its expectation value may be costly. Further research is therefore needed to assess whether a quantum computer can offer a practical benefit in this context.
2 is more complex than the Hamiltonian itself, evaluating its expectation value may be costly. Further research is therefore needed to assess whether a quantum computer can offer a practical benefit in this context.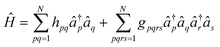
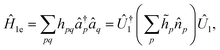
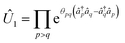
![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) p = â†pâq occupation number operators,
p = â†pâq occupation number operators, ![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) p are real constants, and Û1 is an orbital rotation parameterized by the amplitudes θpq. Orbital rotations can also be employed to solve two-electron Hamiltonians that are squares of one-electron Hamiltonians as follows:
p are real constants, and Û1 is an orbital rotation parameterized by the amplitudes θpq. Orbital rotations can also be employed to solve two-electron Hamiltonians that are squares of one-electron Hamiltonians as follows: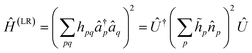
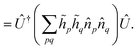
![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) p
p![[h with combining tilde]](https://www.rsc.org/images/entities/i_char_0068_0303.gif) q is a rank-deficient one. The form of two-electron solvable Hamiltonians by means of orbital rotations in (A4) can be straightforwardly generalized by lifting the rank-deficient character of λ matrix and regarding it as a full-rank Hermitian matrix:
q is a rank-deficient one. The form of two-electron solvable Hamiltonians by means of orbital rotations in (A4) can be straightforwardly generalized by lifting the rank-deficient character of λ matrix and regarding it as a full-rank Hermitian matrix: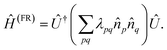
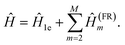
![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) (i+1) tensor at the ith iteration:
(i+1) tensor at the ith iteration: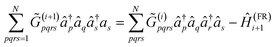
![[G with combining tilde]](https://www.rsc.org/images/entities/i_char_0047_0303.gif) (1)pqrs = gpqrs, as a function of parameters {λ(m)pq} and {θ(m)}.
(1)pqrs = gpqrs, as a function of parameters {λ(m)pq} and {θ(m)}.
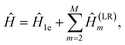
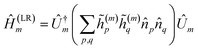
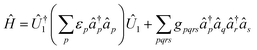
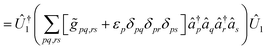
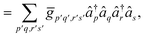
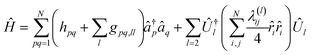

![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) n are tensor products of single-qubit Pauli operators and the identity,
n are tensor products of single-qubit Pauli operators and the identity, ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) (n)k =
(n)k = ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) k,ŷk,ẑk,Îk, acting on the kth qubit. The Fully Commuting (FC) grouping partitions Ĥq into Ĥ(FC)n fragments containing commuting Pauli products:
k,ŷk,ẑk,Îk, acting on the kth qubit. The Fully Commuting (FC) grouping partitions Ĥq into Ĥ(FC)n fragments containing commuting Pauli products:![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) i,
i,![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) j ∈ Ĥ(FC)n then [
j ∈ Ĥ(FC)n then [![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) i,
i,![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) j] = 0.
j] = 0.![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 1ŷ2Î3 and
1ŷ2Î3 and ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 1Î2ẑ3 have QWC as [
1Î2ẑ3 have QWC as [![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 1,
1,![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 1] = 0, [ŷ2,Î2] = 0, [Î3,ẑ3] = 0. Hence, both terms must also fully commute. The converse does not always hold true. For example,
1] = 0, [ŷ2,Î2] = 0, [Î3,ẑ3] = 0. Hence, both terms must also fully commute. The converse does not always hold true. For example, ![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 1
1![[x with combining circumflex]](https://www.rsc.org/images/entities/i_char_0078_0302.gif) 2 and ŷ1ŷ2 are fully commuting but not qubit-wise commuting.24
2 and ŷ1ŷ2 are fully commuting but not qubit-wise commuting.24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(Û(2)T(t)),
ln(Û(2)T(t)),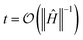 . ε's are obtained according to ε = t−2|E(T)0 − E0|, where E(T)0 (E0) is the ground state energy of Ĥeff (Ĥ). All these calculations were performed using the python Scipy library.27 To reduce computational overhead in our calculations, we take advantage of the fact that the initial state |ψ〉 belongs to a particular irreducible representation of the molecular symmetries: the number of electrons,
. ε's are obtained according to ε = t−2|E(T)0 − E0|, where E(T)0 (E0) is the ground state energy of Ĥeff (Ĥ). All these calculations were performed using the python Scipy library.27 To reduce computational overhead in our calculations, we take advantage of the fact that the initial state |ψ〉 belongs to a particular irreducible representation of the molecular symmetries: the number of electrons, ![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) e, the electron spin, Ŝ2, and its projection, Ŝz. Selecting symmetry adapted states for the neutral singlet molecular forms allowed to reduce the Hamiltonian sub-spaces by almost two orders of magnitude. Similarly, for qubit-based partitioning methods, we use qubit tapering to reduce the system size of NH3 from a 16-qubit system to a 14-qubit system.28 Since the number qubit fragments and their sizes are usually large for BeH2, H2O and NH3, instead of exponentiating each fragment exactly, we approximate the exponential using Taylor series up to 11th order in time. We make use of the Niagara compute cluster hosted by SciNet29 for memory intensive calculations. The Trotter approximation error depends on the order in which individual unitaries e−itĤn are applied.30 The code to generate Hamiltonian fragments and calculate the Trotter error can be accessed at https://doi.org/10.5281/zenodo.15327942.
e, the electron spin, Ŝ2, and its projection, Ŝz. Selecting symmetry adapted states for the neutral singlet molecular forms allowed to reduce the Hamiltonian sub-spaces by almost two orders of magnitude. Similarly, for qubit-based partitioning methods, we use qubit tapering to reduce the system size of NH3 from a 16-qubit system to a 14-qubit system.28 Since the number qubit fragments and their sizes are usually large for BeH2, H2O and NH3, instead of exponentiating each fragment exactly, we approximate the exponential using Taylor series up to 11th order in time. We make use of the Niagara compute cluster hosted by SciNet29 for memory intensive calculations. The Trotter approximation error depends on the order in which individual unitaries e−itĤn are applied.30 The code to generate Hamiltonian fragments and calculate the Trotter error can be accessed at https://doi.org/10.5281/zenodo.15327942.
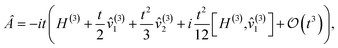
![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) (n+1)1 =
(n+1)1 = ![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) (n)1 − i[Ĥn+1,Ĥ(n)]
(n)1 − i[Ĥn+1,Ĥ(n)]![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) (n+1)2 =
(n+1)2 = ![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) (n)2 − 12[Hn+1,[Hn+1,H(n)]] − i[Hn+1,
(n)2 − 12[Hn+1,[Hn+1,H(n)]] − i[Hn+1,![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) (n)1]
(n)1]![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) (n+1)1] = [H(n),
(n+1)1] = [H(n),![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) (n)1] − i[H(n),[Hn+1,H(n)]] + [Hn+1,
(n)1] − i[H(n),[Hn+1,H(n)]] + [Hn+1,![[v with combining circumflex]](https://www.rsc.org/images/entities/i_char_0076_0302.gif) (n)1] − i[Hn+1,[Hn+1,H(n)]]
(n)1] − i[Hn+1,[Hn+1,H(n)]]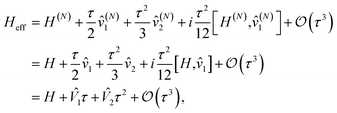
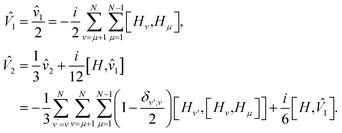
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) 1, there exists a commutator [Hν, Hμ] with the same coefficient. Thus,
1, there exists a commutator [Hν, Hμ] with the same coefficient. Thus, ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) 1 equals zero. Using the same constraint in the expression of
1 equals zero. Using the same constraint in the expression of ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) 2, we recover eqn (7).
2, we recover eqn (7).![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) 2|ψ0〉 for different Hamiltonian decomposition methods and molecules
2|ψ0〉 for different Hamiltonian decomposition methods and molecules
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) 2|ϕ0〉 for different Hamiltonian decomposition methods and molecules
2|ϕ0〉 for different Hamiltonian decomposition methods and molecules
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) 2|ψ0〉 for N2 at various bond lengths
2|ψ0〉 for N2 at various bond lengths
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) 2|ϕ0〉 for N2 at various bond lengths
2|ϕ0〉 for N2 at various bond lengths
 . The number of Trotter steps needed for a target uncertainty in phase estimation under adaptive phase estimation techniques is given by
. The number of Trotter steps needed for a target uncertainty in phase estimation under adaptive phase estimation techniques is given by
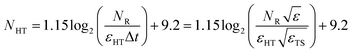 . Putting everything together we arrive at
. Putting everything together we arrive at