Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Physics-informed Gaussian process classification for constraint-aware alloy design†
Christofer
Hardcastle
 a,
Ryan
O'Mullan
a,
Raymundo
Arróyave
abc and
Brent
Vela
a,
Ryan
O'Mullan
a,
Raymundo
Arróyave
abc and
Brent
Vela
 *a
*a
aDepartment of Materials Science and Engineering, Texas A&M University, College Station, TX 77843, USA. E-mail: brentvela@tamu.edu
bJ. Mike Walker '66 Department of Mechanical Engineering, Texas A&M University, College Station, TX 77843, USA
cWm Michael Barnes '64 Department of Industrial and Systems Engineering, Texas A&M University, College Station, TX 77843, USA
First published on 18th June 2025
Abstract
Alloy design can be framed as a constraint-satisfaction problem. Building on previous methodologies, we propose equipping Gaussian Process Classifiers (GPCs) with physics-informed prior mean functions to model the centers of feasible design spaces. Through three case studies, we highlight the utility of informative priors for handling constraints on continuous and categorical properties. (1) Phase stability: by incorporating CALPHAD predictions as priors for solid-solution phase stability, we enhance model validation using a publicly available XRD dataset. (2) Phase stability prediction refinement: we demonstrate an in silico active learning approach to efficiently correct phase diagrams. (3) Continuous property thresholds: by embedding priors into continuous property models, we accelerate the discovery of alloys meeting specific property thresholds via active learning. In each case, integrating physics-based insights into the classification framework substantially improved model performance, demonstrating an efficient strategy for constraint-aware alloy design.
1 Introduction
Due to the multitude of performance requirements in materials development, alloy design is often more accurately framed as a constraint satisfaction problem rather than a pure optimization problem.1–4 In this framework,5 the objective shifts from optimizing a single function to identifying one—or all—solutions that satisfy all imposed constraints. This perspective is particularly relevant to alloy design, where the violation of even a single constraint can render a material unsuitable for a specific application. Consequently, it is imperative to develop methods that efficiently navigate feasible design spaces while reducing the reliance on costly experiments.6,7 For example, phase stability constraints are particularly common in alloy design,8,9 as specific phases are often desired while deleterious phases need to be avoided. X-ray diffraction (XRD) or microscopy at multiple resolutions are typically employed to determine the presence of various phases in bulk alloy samples. Likewise, high-temperature compression/tension measurements are common objectives in alloy design schemes10–12 yet are difficult and expensive to execute.13Due to the combinatorial vastness of alloy design spaces, the time and financial costs of brute-force experimental exploration become prohibitive.7 To alleviate this burden, computational techniques—such as the modified Hume-Rothery rules and CALPHAD-based approaches—have been widely employed as a first approximation for phase stability assessments and predictions.14,15 Although heuristics like the modified Hume-Rothery rules enable rapid screening of potential single-phase solid solutions, their accuracy is limited for complex multi-component systems; moreover, they cannot predict phase stability as a function of temperature or identify specific intermetallic phases.14 In contrast, CALPHAD techniques offer higher accuracy but rely heavily on thermodynamic databases15 that are often labor-intensive to calibrate and less adaptable to the dynamic incorporation of new data in iterative experimental campaigns.16 Similarly, in the context of yield strength, several inexpensive analytical models17–19 predict various strengthening mechanisms; however, these models exhibit limited accuracy when compared to ground-truth experimental measurements.
Recent advances in machine learning have demonstrated significant promise in addressing these challenges. In particular, adaptive models that utilize active learning can dynamically update predictions of material properties as new experimental data become available.20,21 Nonetheless, purely data-driven approaches often overlook valuable physical insights, thereby limiting their reliability when data are sparse or incomplete. When alloy design problems are highly constrained, we believe it is more appropriate to frame the design process as a constraint satisfaction problem rather than a pure optimization problem. In our previous work,11,22 we demonstrated that incorporating physics-informed priors into Gaussian Process Regressors (GPRs) significantly improved both the physical accuracy and predictive performance of the models, leading to more efficient Bayesian optimization strategies.11 In other research,7 we explored how active learning could be used to refine the feasible design space in Bayesian optimization; however, the Gaussian Process Classifiers (GPCs) employed were purely data-driven and lacked informative priors mean functions.
In this study, we address the challenge of dynamically updating predictive models for constrained properties—as new experimental data become available—by proposing a Bayesian classification approach that seamlessly integrates prior knowledge derived from physics-based models. Specifically, we introduce a physics-informed classification method to handle both continuous and categorical constraints in alloy design, targeting properties such as phase stability and yield strength. This approach not only refines predictions with incoming data but also enhances model interpretability and reliability in scenarios where data acquisition is expensive or time-consuming. Moreover, the probabilistic framework enables rigorous quantification of classification uncertainty, which is crucial for informed design and decision-making.
We validate our method through three case studies:
(1) To demonstrate its utility for categorical classification, we benchmark the proposed method using a publicly available dataset on phase stability in high entropy alloys.23
(2) We extend the method to active learning for categorical constraints, demonstrating its ability to construct accurate phase stability predictions with minimal ground-truth data.
(3) Finally, we apply the method to active learning for continuous constraints, specifically yield strength. In this case, equipping Gaussian Process Classifiers (GPCs) with informative priors significantly enhances both classification performance and the active learning of feasible design spaces compared to purely data-driven techniques.
2 Methods
2.1 Gaussian process classification for categorical data
In our previous work,11,22 we demonstrated how any Gaussian Process Regressor (GPR) can be equipped with a non-zero prior mean function. This is achieved by training a GPR on the differences between the training data and the prior predictions for that data. Specifically, the model is trained to predict the error in the prior prediction for each data point in the training set. For new data points, the model's predicted error is added to the prior prediction to obtain a final prediction. Mathematically, this approach is equivalent to using a GPR with a non-zero mean function.24 The expression for a physics-informed posterior mean function and standard deviation is shown in eqn (1). | (1) |
 , and σGP2(x*) represents the corresponding posterior variance, quantifying predictive uncertainty. The prior mean function m(·) may incorporate physics-based insight. The training inputs are XN = {x1, …, xN} with observations yN = [y1, …, yN]T. The covariance vector K(XN, x*) = [k(x1, x*), …, k(xN, x*)]T and the matrix K(XN, XN) has entries k(xi, xj). Here, k(·,·) is the kernel measuring similarity between inputs, σn2 is the Gaussian noise variance, and I is the N × N identity matrix.
, and σGP2(x*) represents the corresponding posterior variance, quantifying predictive uncertainty. The prior mean function m(·) may incorporate physics-based insight. The training inputs are XN = {x1, …, xN} with observations yN = [y1, …, yN]T. The covariance vector K(XN, x*) = [k(x1, x*), …, k(xN, x*)]T and the matrix K(XN, XN) has entries k(xi, xj). Here, k(·,·) is the kernel measuring similarity between inputs, σn2 is the Gaussian noise variance, and I is the N × N identity matrix.
In the case of regression, we found that on average, models utilizing this method converge during Bayesian optimization faster than standard GPRs trained on the same data.11 This method can also be extended to classification by adjusting the prior mean function of the latent Gaussian Process (GP) required during GP classification.
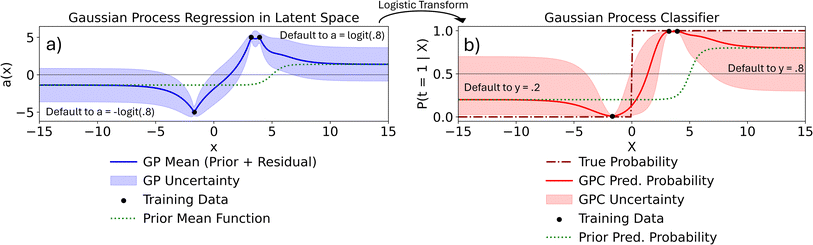
Using notation from ref. 25, the goal of GP classification is to predict the probability that any test point x* belongs to class t = 1 where t = {0, 1}. To do this GPCs rely on an unobserved latent function a(·) to map input features x to real label probabilities y ∈ (0, 1). Example of this latent GP is shown in Fig. 1a. To model this latent function we place a GP prior on it:
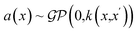 | (2) |
In order to convert output of the latent GP into valid probabilities we pass it through a response function. After passing the latent GP a(x) through a response function we obtain valid probabilities y(x) ∈ (0, 1) that t = 1. An example of this is shown in Fig. 1b. A common choice of response function is the logistic sigmoid:
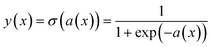 | (3) |
Once ‘squashed’ through the logistic sigmoid, the latent GP a becomes a non-Gaussian stochastic process y. At a test point x* this y(x) defines a Bernoulli distribution for the class label t i.e. if y = 0.7 there is a 70% chance that t = 1. In order to predict the probability that a test point x* belongs to class t = 1 the integral form of Bayesian theorem must be used
| y(x*) = ∫p(t* = 1∣a*)p(a*∣tN)da* | (4) |
In order to equip GP classifiers with informative prior mean functions, in this work, we adopt a less rigourous but practical approximation. Specifically, we create a latent GP, a and this GP regressor is trained with binary class labels y ∈ {−5, 5} using a Gaussian likelihood. Using a Gaussian likelihood, the equations for the posterior mean and standard deviations hold (eqn (1)). This is important as an informative prior mean function m(·) can be defined in this equation. In order to predict the class probability y(x*) at test point x*, the posterior mean μ(x*) of the GP a(x*) is then passed through a logistic sigmoid, transforming it to be a number between 0 and 1. This is shown in eqn (5).
| y(x) = σ(m(x) + K(XN, x)T [K(XN, XN) + σn2I]−1(tN − m(XN))) | (5) |
The use of GP regressors for classification has precedent; for instance, Dai et al.20 constructed a GPC using a similar methodology. However, their work did not modify the prior mean function of the latent GP. In contrast, in this work we modify the prior mean function of the latent GP. Specifically, instead of a uniform prior mean function, we have a user-defined prior mean function. To train the proposed framework ground-truth class observations tN and the prior class prediction m(XN) at points XN. To predict the class probability y(x*) at test point x* only the prior class prediction m(x*) is required as an input.
To handle multi-class classification, we employ an ensemble of one-vs-rest classifiers. In this approach, each class i is associated with its own GPR ai, which is responsible for predicting the error in the prior probability for that specific class. Once we have the individual probabilities for each class, yi, we can apply various normalization techniques to generate a multi-class probabilistic prediction for a particular class, k. The probabilistic prediction that a data point x* belongs to class k, p(k|x*, tN), is the output of an ensemble of one-vs-rest classifiers. This process involves taking the raw output probabilities from each classifier and normalizing them so that they sum to 1, thus transforming the predictions into a valid probability distribution over all classes. This normalization is essential for interpreting the predictions as a set of probabilities. The formula for normalizing the probabilities is shown in eqn (6) where σ(ak(x)) is the raw probability (score) from the binary classifier for the class of interest k and the denominator is the sum of all the raw probabilities for all n classes
 | (6) |
This method ensures that the probabilities are bound between 0 and 1, but it does not always account for the relative confidence of the classifiers. An alternative approach is to use softmax normalization, which normalizes the probabilities and considers each classifier's relative confidence. The softmax function converts the raw class probabilities into a distribution where the sum of all probabilities equals 1. This ensures that the resulting probabilities represent the likelihood of each class, making them directly comparable. Additionally, the softmax function amplifies the differences between class scores, making it particularly useful when there is a large disparity in classifier confidence.
The softmax function in eqn (7), where σ(ak(x)) is the raw probability (logit) from the classifier for class k. The denominator is the sum of the exponentiated probabilities for all n classes, ensuring that the probabilities sum to 1.
 | (7) |
2.2 Gaussian process classification for continuous data
Classification can be extended to continuous properties by assessing whether a property exceeds or falls below a specific threshold, such as meeting or failing to meet a property constraint. This approach is particularly relevant in alloy design, where the objective is often to create an alloy that satisfies multiple constraints rather than optimizing a single property.6 In these scenarios, it is crucial not only to classify whether the constraints are met but also to quantify the confidence in each prediction. This classification task can be achieved using a GPR.Consider the example of the classification of continuous properties in Fig. 2. In this senario we are modeling an unobserved function f. The goal is to predicted the probability that at a particular point x* the function f is greater than a lower threshold c, i.e. p(f(x*) > c). A GPR is trained on a limited number of observations (red dots). Based on these observations, the GPR will interpolate and extrapolate f values across the x domain. Predictions from GPRs are normal distributions. For each value of x in the domain, the GPR returns the mean prediction and standard deviation (each prediction is Gaussian and is determined by the posterior distribution over functions26). Since each prediction is a normal distribution, the probability that a property is above a threshold can be found using the Cumulative Distribution Function (CDF), as shown in as shown in eqn (8). Similarly, the probability that a property falls below threshold can be found by subtracting the CDF from 1.
This is shown graphically in Fig. 2a we take an arbitrary test point (green dot) and calculate the probability that it is above or below a threshold (dashed red line). Once the probability of exceeding or falling below a threshold is determined, the property is classified as meeting the constraint if the probability is greater than 0.5. Otherwise, it is classified as failing to meet the constraint.
 | (8) |
2.3 Classification error metrics
To evaluate model performance, we calculated six classification metrics for predictions on the test subsets: accuracy, precision, recall, F1-score, log-loss, and multi-class Brier loss. Accuracy measures the proportion of correctly classified samples, as defined in eqn (9) where TP, TN, FP, and FN represent the counts of true positives, true negatives, false positives, and false negatives, respectively. Precision quantifies the fraction of predicted positive cases that are true positives, as defined in eqn (10). Recall indicates the proportion of correctly identified positive cases, as defined in eqn (11). The F1-score combines precision and recall into a single harmonic mean to summarize the test's accuracy, providing a balanced measure that accounts for both false positives and false negatives, as defined in eqn (12). Log-loss (eqn (13)) and Brier loss (eqn (14)) evaluate the accuracy of predicted probabilities by penalizing incorrect confidence levels. In these equations N is the total number of data points, R is the number of classes, fti is the predicted probability of class i for data point t, and oti is 1 if t belongs to class i, otherwise 0. | (9) |
 | (10) |
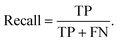 | (11) |
 | (12) |
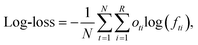 | (13) |
 | (14) |
3 Case study: benchmark against experimental data
First, to demonstrate the benefit of informative priors in static classification examples,23 we benchmark our proposed method against a dataset of experimentally classified phase stability data. Specifically, we utilize a dataset of experimentally labeled phase stability data and their corresponding homogenization temperatures, and employ CALPHAD models to predict the expected equilibrium phases under these conditions. The dataset used in this work is provided in the code repository associated with this work. These CALPHAD predictions are then treated as the prior for probabilistic classification. Next, the database is shuffled and split into training and test sets. Using the training set, the prior probabilities (derived from the CALPHAD phase predictions) for the test set are updated based on the training data (experimental phase labels). The accuracy, precision, recall, F1-score, Brier-loss, and log-loss scores are computed for both the multi-class scenario and several one-vs-rest scenarios. Our method outperforms both the CALPHAD prior model and purely data-driven “vanilla” GPCs.3.1 Experimental dataset
In this experimental case study, we evaluated the predictive performance of GPCs with informative priors by comparing their predictions to experimental phase stability data. The dataset, curated by Machaka et al.,23 provides comprehensive information on the phase stability of various High Entropy Alloys (HEAs), including details on alloy synthesis methods, processing conditions (e.g., cold or hot work), heat treatment temperatures, and the resulting phases. To minimize confounding factors, we filtered the dataset to include only as-cast alloys that underwent homogenization heat treatments, excluding those subjected to further processing such as hot or cold working. This filtering was applied to approximate equilibrium conditions, aligning with the predictive capabilities of CALPHAD-based prior models, which focus on equilibrium phase stability. This approach ensures that the experimental data is consistent with the assumptions of the computational framework. Although this simplification in this case study limits the method's applicability under non-equilibrium processing conditions, it was chosen deliberately to isolate and quantify the benefit of well-matched informative priors. Inclusion of phase stability data dominated by strong non-equilibrium effects would devaluate the informativeness of the prior. For more details on the effect of ‘harmful’ priors, see the Section 6.Although the original dataset categorized alloys into seven phase labels, this study focused on the four most common: single-phase FCC alloys, FCC alloys with secondary phases (FCC + Sec.), single-phase BCC alloys, and BCC alloys with secondary phases (BCC + Sec.). Although this proposed method can accommodate classification problems beyond 4 classes, insufficient data for the remaining three labels, particularly after filtering, required this simplification. For the purposes of this study, a 4-label classification framework provides a robust benchmark to validate the proposed method. After filtering, the dataset contained 86 usable data points: in order to facilitate reproducibility and further research, the cleaned and processed dataset is publicly available in the code repository associated with this work.
3.2 Physics-informed prior for phase stability
The source of prior information for phase stability was the ‘Calculation of Phase Diagrams’ (CALPHAD) predictions generated using Thermo-Calc's Python equilibrium module.27 This module utilizes the TCHEA6 thermodynamic database,28 which was specifically chosen for its suitability in modeling compositionally complex alloys. In our previous work,11 we rigorously evaluated the accuracy of Thermo-Calc's equilibrium module for predicting phase stability and demonstrated its reliability for alloy design applications. Based on these findings, we considered this module a robust and credible source of prior information for this case study.Phase stability predictions were generated using Thermo-Calc for each alloy in the filtered dataset at its respective homogenization/heat treatment temperature, representing the equilibrium phases expected under those conditions. Although cooling rates can affect phase formation in practice, these predictions are used solely as prior information and are refined by experimental data. We acknowledge that factors like cooling rates can introduce confounding effects that sometimes reduce the accuracy of Thermo-Calc predictions; however, equilibrium CALPHAD predictions provide a reasonable initial approximation for phase stability—an approximation that can be updated in light of experimental data. In fact, correcting the prior model with data is the main goal of the proposed framework.
The Thermo-Calc equilibrium module predicts the mole fractions of various microstructures. The prior phase classification from Thermo-Calc was assigned according to the following rules:
• If the FCC mole fraction for a data point is ϕFCC ≥ 0.99, it is classified as single-phase FCC.
• If ϕFCC ≥ 0.5 but less than 0.99, it is classified as FCC with a secondary phase (FCC + Sec.).
• The same thresholds are applied to BCC mole fractions for classification as single-phase BCC or BCC + Sec.
After establishing phase predictions from Thermo-Calc, we quantified our confidence in these prior class predictions using class probabilities. These probabilities reflect the level of certainty associated with a particular classification, whether derived from a vanilla GPC or an informed GPC. In the case of an uninformed GPC, the prior class probability is 50%/50%. For an informed GPC, the prior class probability is assigned according to the designer's judgment. An example of this informed prior class probability is shown in Fig. 1.
The prior probabilities are detailed in Table 1. For instance, if the prior classification for an alloy is single-phase FCC, the confidence is distributed as follows: a 50% probability of being single-phase FCC, a 40% probability of being FCC with secondary phases, and a 5% probability of either being single-phase BCC or BCC with secondary phases. These prior probabilities are intuitive because if Thermo-Calc predicts an alloy to be single-phase FCC, the highest prior probability is assigned to the FCC class. However, because secondary phases may form within the FCC matrix during cooling, the FCC + Sec. class is assigned the second-highest probability. Conversely, if an alloy is predicted to be FCC by Thermo-Calc, it is unlikely to exhibit a BCC matrix experimentally. In other words, while we trust Thermo-Calc's ability to distinguish between FCC and BCC, we are less confident in its ability to differentiate between FCC and FCC + Sec. and to differentiate between BCC and BCC + Sec.
| Prior probability | |||||
|---|---|---|---|---|---|
| FCC | FCC + Sec. | BCC | BCC + Sec. | ||
| Prior pred. | FCC | 50% | 40% | 5% | 5% |
| FCC + Sec. | 40% | 50% | 5% | 5% | |
| BCC | 5% | 5% | 50% | 40% | |
| BCC + Sec. | 5% | 5% | 40% | 50% | |
3.3 Training the Gaussian processes classifiers
To implement the informative GPCs described in the Methods section, we developed a custom class based on Gaussian Process Regressors (GPRs). For each one-vs-rest GPC, a latent GPR is first trained on the class observations, where positive class observations are set to y = 5 and negative ones to y = −5. This latent GPR is then passed through a logistic sigmoid transformation to constrain the outputs between 0 and 1, yielding valid probabilities. The code for this implementation is available in the associated Code Ocean repository.The GPRs used in this active learning scheme employ an additive kernel composed of a Radial Basis Function (RBF) kernel and a White Noise (WN) kernel, as defined in eqn (15). In eqn (15), k(x, x′) represents the covariance function between input points x and x′. The first term corresponds to the RBF kernel, where σf2 is the signal variance, controlling the amplitude of function variations, and  is the characteristic length scale, determining how quickly correlations decay with distance. The second term accounts for white noise, where σn2 is the noise variance, and δ(x, x′) is the Kronecker delta function. Selecting an appropriate kernel is inherently challenging and often depends on expert judgment; this choice implicitly assumes specific correlation patterns and functional shapes. The RBF + WN additive kernel is a standard choice that works well in practice.
is the characteristic length scale, determining how quickly correlations decay with distance. The second term accounts for white noise, where σn2 is the noise variance, and δ(x, x′) is the Kronecker delta function. Selecting an appropriate kernel is inherently challenging and often depends on expert judgment; this choice implicitly assumes specific correlation patterns and functional shapes. The RBF + WN additive kernel is a standard choice that works well in practice.
Kernel hyperparameters were optimized by maximizing the log-marginal likelihood using the L-BFGS-B algorithm as implemented in Scikit-Learn.29 To ensure robust optimization, we performed 10 optimizer restarts for each GPR. For the RBF kernel, the optimization was constrained to search for length scales between 5 atomic percent (at%) and 100 at%. This range was chosen based the observation that barycentric spaces cannot have length scales exceeding 100 at%. These constraints help ensure that the kernel parameters remain physically meaningful and aligned with the characteristics of the sampled data.
 | (15) |
Table 2 summarizes the 10 alloy features used to train the model. For brevity, specific details on these features can be found at ref. 30. All features are functions of an alloy's chemical composition and were calculated using Matminer's  featurizer.31 These were determined to be useful in predicting solid solution phase stability by Wen et al.30 While more sophisticated feature selection could be performed, this work aims to highlight the effect of physics-informed prior mean functions during GP classification and does not necessarily identify the most relevant features for phase classification.
featurizer.31 These were determined to be useful in predicting solid solution phase stability by Wen et al.30 While more sophisticated feature selection could be performed, this work aims to highlight the effect of physics-informed prior mean functions during GP classification and does not necessarily identify the most relevant features for phase classification.
| Yang delta | Yang omega |
|---|---|
| APE mean | Radii local mismatch |
| Radii gamma | Configuration entropy |
| Atomic weight mean | Total weight |
| Lambda entropy | Electronegativity delta |
3.4 Experimental benchmarking results
Three models were benchmarked to illustrate the impact of incorporating a physics-informed prior into GPCs: two control models and the proposed model. The first control model was a GPC with an uninformed prior mean function, which assigned equal probabilities (25%) to all predictions in the four-class case. In the case of four-class classification problems, 25% probability for all 4 classes represents the state of maximum information entropy, reflecting the highest level of uncertainty in predictions. The second control model consisted solely of the CALPHAD phase predictions. The third model was a GPC with a prior mean function defined by CALPHAD phase predictions. The values of these priors are reported in Table 1. As mentioned in Section 3.3 the latent GPs in both GP classifiers were equipped with the same kernel and training settings as the uninformed GPC, specifically the RBF + WN additive kernel, as described in eqn (15).Benchmarking the models on a small dataset necessitated the use of cross-validation. We employed stratified Monte Carlo cross-validation, generating 500 random 20%/80% train/test splits. This approach differs from the more typical 80%/20% splitting and reflects the reality of data-sparse scenarios in alloy design, where experimental data is often prohibitively expensive to collect. Stratification was crucial to maintain the class ratio in both training and testing subsets, ensuring consistency across splits.
Using box-and-whisker plots to display each error metric across the cross-validation splits, Fig. 3 summarizes the overall predictive performance of the three models across all classes. In the context of predicting phase stability as a 4-class classification problem, it is evident that the informed model exhibits, on average, improved accuracy and recall. Although the median precision values of the uninformed and informed classifiers are similar, the interquartile range (IQR) indicates that the CALPHAD-informed model performs more consistently, whereas the uninformed model displays greater variability—an undesirable outcome. We prefer that models perform well and perform well consistently. Furthermore, employing any GPC is preferable to using a model with unquantified uncertainty in its predictions (i.e., a non-probabilistic model).
As clearly demonstrated by the plots, the GPC with the physics-informed prior outperforms both control models on most metrics. The interquartile ranges for accuracy, recall, F1-score, and Brier loss show significant improvements over the control models, with more subtle enhancements in precision and log-loss. To further evaluate each model's ability to correctly identify specific classes, separate analyses of the predictions over the 500 splits were performed and are reported in the ESI.†
4 Case study: active learning of categorical constraints
Phase stability constraints are particularly common in alloy design, where specific phases are desired and deleterious phases need to be avoided.12,32,33 To assess phase stability, X-ray diffraction (XRD) experiments are typically employed to determine the presence of various phases in bulk alloy samples. However, given the large number of candidate alloys, even ternary alloy systems, the time and cost associated with XRD experiments make a brute-force experimental exploration infeasible.7 To mitigate this burden, computational techniques have emerged to complement experimental efforts in alloy design.Simple heuristics, such as modified Hume-Rothery rules, have been extended to screen for alloys, particularly medium and high entropy alloys, that form single-phase solid solutions.14 These methods are computationally inexpensive, allowing for rapid preliminary screening of large compositional spaces.15,34 However, these heuristics for phase stability have shortcomings. Their accuracy is often limited.14 Moreover, these heuristics cannot predict phase stability as a function of temperature. Furthermore, these modified Hume-Rothery rules are only valid in determining if HCP, FCC, BCC or intermetallic phases are likely to form, however these metrics do not provide details about what intermetallic phase is likely to form.
Beyond simple heuristic models, CALculation of PHAse Diagram (CALPHAD) techniques have been employed to predict phase stability in HEA design, particularly in high-throughput computational workflows.15 The accuracy of CALPHAD predictions relies heavily on the quality and relevance of the underlying thermodynamic databases. CALPHAD databases require careful calibration of parameters to match experimental results. This restricts their applicability in closed-loop experimental alloy design campaigns, where data are dynamic and must be quickly incorporated into models to inform subsequent experiments.
Recent advances in machine learning have demonstrated the potential for on-the-fly updating of phase stability models during experimental campaigns. Machine learning models, particularly those used for classification, can be continuously trained as new data become available, allowing for adaptive, data-driven optimization strategies.20,21,35 This is known as active learning (AL) of constraints. However, these approaches often neglect valuable physical insights and can suffer from a dependence on large amounts of training data, limiting their effectiveness when data are sparse or incomplete.
Physics-constrained active learning of phase diagrams have been achived using graph-based techniques such as in the CAMEO framework.36 Of particular interest to this work, Ament et al.37 employed a physics-informed kernel within a GP-based active learning framework to accelerate the construction of phase diagrams by incorporating prior physical knowledge into the model's covariance structure. While this approach has its merits, our work introduces a novel and complementary strategy: incorporating physics through the modification of the GP prior mean function. Since a GP is fully defined by both its mean and covariance functions, embedding domain-specific physical insights directly into the prior mean offers an alternative pathway for guiding predictions—especially beneficial when fast-acting prior models for specific properties are available. In contrast to kernel modification, which is better suited for capturing global trends and symmetries,37 adjusting the prior mean function provides a more targeted method for integrating known local physical behaviors.
In this in silico case study, we address the challenge of dynamically updating phase stability models as new experimental data become available. Here, the valence electron concentration (VEC) serves as the prior belief regarding the stability of FCC and BCC phases in the Fe–Ni–Cr alloy system at 1000 °C. The ground truth for phase stability is provided by Thermo-Calc equilibrium calculations, using the TCHEA6 high entropy alloy database.28 The objective of this case study is to construct the most accurate isopleth phase stability predictions with the fewest possible queries of the ground truth. Our results demonstrate that active learning schemes incorporating simple yet informative priors outperform those relying solely on vanilla GPCs. This approach aligns with recent efforts to develop closed-loop alloy design frameworks, making this a well-motivated case study.
4.1 Models for prior and ground-truth
The Valence Electron Concentration (VEC) of an alloy is defined as the weighted sum of the valence electron concentrations of its constituent elements. Numerous studies38–41 have shown that VEC is an effective descriptor for predicting single-phase stability and for delineating the boundary between FCC and BCC phase stability. In particular, alloys with a VEC above 8 tend to exhibit FCC structures, while those with a VEC below 6.87 are typically BCC.41 This suggests that alloys with VEC values between 6.87 and 8 are likely to display dual-phase (BCC + FCC) behavior. The formula for calculating VEC is given in eqn (16), where ci represents the atomic fraction of element i and vi is the valence electron concentration of element i. | (16) |
We assign prior probabilities based on predictions from the prior model (i.e., the VEC). These probabilities are detailed in Table 3. For example, if an alloy has a VEC greater than 8, our degree of belief that the alloy is FCC is represented by a 54% probability. Conversely, we assign a 23% probability each to the alloy being dual-phase or BCC.
| Prior probability | ||||
|---|---|---|---|---|
| FCC | Dual | BCC | ||
| Prior pred. | FCC | 54% | 23% | 23% |
| Dual | 23% | 54% | 23% | |
| BCC | 23% | 23% | 54% | |
Regarding the ground truth model for this in silico example, we consider Thermo-Calc's equilibrium calculator—equipped with the TCHEA6 database28—as the ground truth. We queried this calculator at 1000 °C for all candidate alloys, which yielded the decision boundaries (i.e., phase boundaries) shown as black dashed lines in Fig. 4. The code for the ground-truth model is available in the repository associated with this work.
4.2 Gaussian processes and active learning parameters
The Gaussian Process Regressors (GPRs) used in this active learning scheme employed an additive kernel that combines a Radial Basis Function (RBF) kernel with a White Noise kernel (WN), as defined in eqn (15). Selecting an appropriate kernel is inherently challenging and often relies on expert judgment, since this choice implicitly assumes specific correlation patterns and functional shapes for the underlying process. The RBF + WN additive kernel is a standard choice in such applications.The kernel hyperparameters were optimized by maximizing the log-marginal likelihood using the L-BFGS-B algorithm, as implemented in scikit-learn. To ensure robust optimization, we performed 50 optimizer restarts for each GPR. The first run used the kernel's initial parameter estimates, while the remaining runs initialized parameters by sampling log-uniformly from the allowed parameter space, ensuring thorough exploration.
For the RBF kernel, the optimization was constrained to search for length scales between 5 atomic percent (at%) and 100 at%. Again this range was chosen based on the fact that barycentric spaces do not have properties that vary at lengthscale greater than 100 at%. These constraints ensured that the kernel parameters remained physically meaningful and aligned with the characteristics of the sampled data. The active learning framework for categorical properties used a GPfor the surrogate model and maximum Shannon entropy for the acquisition function.42
4.3 Categorical active learning case study results
To evaluate the impact of informative priors on Bayesian active learning for phase stability predictions within the Fe–Ni–Co system at 1000 °C, we compared a physics-informed active learning scheme to a physics-uninformed scheme. Each scheme operated under a fixed budget of 25 queries to the ground truth per active learning campaign. Fig. 4 shows an example of a single active learning campaign. Class probabilities in this 3-class scenario are visualized using an RGB color scheme. For instance, if an alloy is predicted to be FCC with 100% confidence (i.e., a probability of 1.0), the corresponding RGB value is [0, 255, 0], resulting in a bright green color in the ternary diagram. Similarly, alloys predicted to be dual-phase with 100% confidence are plotted as blue (RGB = [0, 0, 255]). If the model predicts equal probabilities for all three phases (33%/33%/33%), the RGB value is [85, 85, 85], and the alloy is displayed as gray, indicating the highest Shannon entropy and, consequently, the greatest uncertainty in the prediction.42The top row shows the progression of the vanilla active learning (AL) campaign, while the bottom row displays that of the physics-informed AL campaign. At the 5th iteration, the physics-informed approach already leverages its prior knowledge (e.g., phase predictions from the VEC) to accurately delineate the decision boundary between the FCC and dual-phase regions, though it still struggles to separate the dual-phase from the BCC region. At the 10th iteration, the physics-informed model achieves better recall for the BCC class than the vanilla model; however, predictions in the BCC region are rendered in purple, indicating uncertainty between a pure BCC phase and a mixed FCC + BCC state—while clearly ruling out single-phase FCC (green). By the 15th iteration, the physics-informed scheme further refines its predictions, markedly improving recall for the minority BCC class. Finally, at the 20th iteration, the vanilla AL scheme reveals its limitations in handling class imbalance by heavily biasing predictions toward the dominant FCC + BCC (blue) region, whereas the physics-informed model consistently converges toward the true decision boundaries across all phase regions.
Running a single AL campaign is insufficient for benchmarking because a favorable or unfavorable random initialization could unduly influence the results. To address this, we report the distribution of metrics across multiple AL campaigns as a function of iteration, providing a more robust assessment of each method's average performance and progression. Specifically, we run 200 AL campaigns, each with a budget of 25 queries of the ground truth. For each campaign, the six classification metrics described in Section 2.3 were recorded at each iteration. The average error metrics and their standard deviations, as a function of AL iteration, are plotted in Fig. 5.
The proposed method (blue) shows improved accuracy on average, indicating better overall performance compared to the control model. Furthermore, the standard deviation of accuracy decreases in later iterations, suggesting that the method consistently achieves higher accuracy and is robust to random initializations. In contrast, the control model (red) exhibits a wide accuracy standard deviation that even increases slightly in later iterations, indicating that its performance is less consistent over time and more sensitive to the initial ‘seed query’ of the AL scheme.
5 Case study: informative priors for continuous constraint satisfaction
In alloy design, the goal is often to identify an alloy that meets all specified thresholds with high confidence rather than to find the absolute optimal alloy in terms of individual properties.6 We contend that, in most real-world examples, quantifying the probability of meeting critical constraints43 is more important than maximizing any single property. Using the methods described in Section 2.2, we develop an active learning scheme to identify the set of W–Nb–Ta alloys with a yield strength exceeding 100 MPa at 1300 °C using as few queries as possible. This constraint is adapted from the performance requirements of ARPA-e's ULTIMATE program, which strongly motivates this case study.44 The confidence that an alloy meets this threshold is represented by the probability mass of the predicted normal distribution (from the GPR model) that falls below 100 MPa. Fig. 2 provides a visual demonstration of this classification. Although this is a synthetic problem, it is motivated by previous works.11,12 Our study demonstrates that equipping GPR models with physics-informed prior mean functions accelerates the identification of alloys that satisfy the yield strength threshold.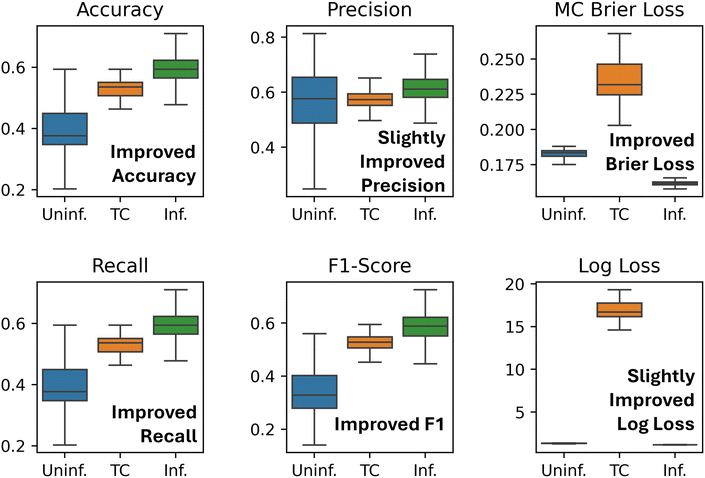 | ||
| Fig. 3 Model errors for the standard GPC (Uninf.), Thermo-Calc (TC), and the GPC with the physics-informed prior (Inf.) when predicting across all phases. | ||
5.1 Ground-truth and prior models for high-temperature yield strength
The Curtin–Maresca model provides a mechanistic framework for predicting the yield strength of BCC high-entropy alloys (HEAs).18 Rooted in dislocation theory, this model accounts for the influence of atomic-scale heterogeneities inherent in multicomponent alloys. Specifically, the yield strength is attributed to the resistance encountered by dislocations as they move through a heterogeneous lattice. Such lattice heterogeneities arise from variations in atomic size, elastic modulus, and other local properties due to the random distribution of constituent elements in the alloy.The critical resolved shear stress is calculated based on the statistical interactions between dislocations and local obstacles, incorporating both temperature and strain rate dependencies. The model employs the following equation to estimate the yield stress:
 | (17) |
![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) is the applied value, typically set to
is the applied value, typically set to ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) = 10−3 s−1, and
= 10−3 s−1, and ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) 0 is the reference strain rate, estimated to be
0 is the reference strain rate, estimated to be ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) 0 = 104 s−1. This equation provides a lower-bound estimate for tensile yield strength, as validated in recent studies.11,45
0 = 104 s−1. This equation provides a lower-bound estimate for tensile yield strength, as validated in recent studies.11,45
In this work, the Maresca–Curtin model queried at 1300 °C was used as the ground truth for high-temperature yield strength. The model queried at 25 °C was considered the prior. While this is only a toy problem, it emulates a scenario where room-temperature yield strength serves as a proxy for high-temperature yield strength. This prior is updated iteratively.
5.2 Gaussian processes and active learning parameters
The active learning framework for continuous properties used a Gaussian Process for the surrogate model and maximum Shannon entropy for the acquisition function.42 The GPRs used in the framework employed the RBF kernel. Since this case involved a straightforward binary classification problem using an analytical model as the ground truth, the White Noise (WN) kernel was omitted. In this study, the RBF kernel models how the 1300 °C yield strength varies with composition in the Nb–Ta–W alloy system. As in previous case studies, the kernel hyperparameters were optimized by maximizing the log-marginal likelihood using the L-BFGS-B algorithm in scikit-learn. To ensure robust optimization, each GPR underwent 50 optimizer restarts.For the RBF kernel, the optimization was restricted to length scales between 5 atomic percent (at%) and 100 at%. This range was chosen based on the Nb–Ta–W alloy space's sampling resolution of 5 at% and the observation that barycentric spaces typically do not exhibit length scales beyond 100 at%. These constraints ensured that the kernel parameters remained physically meaningful and aligned with the characteristics of the sampled data.
5.3 Continous active learning case study results
To demonstrate the effect of a physics-informed prior during active learning (AL) of constraint boundaries for continuous properties, we equipped one AL scheme with a prior mean function and benchmarked it against an AL scheme without a prior mean function. As mentioned in Section 5.1, the ground truth is provided by the Maresca–Curtin model queried at 1300 °C, representing a difficult-to-attain high-temperature tensile measurement. In contrast, the prior in this work is obtained by querying the Maresca–Curtin model at room temperature, representing an easier-to-obtain value.The model with a physics-informed prior outperforms the model without a prior during the initial iterations of the AL campaign. For example, in iteration 1, the yield strength prediction from the vanilla GPR is constant across the design space, meaning that all alloys receive the same prediction. However, the GPR with the informative prior exhibits a more complex prediction even when provided with only a single data point. The initial predicted decision boundary (i.e., the threshold for alloys having high-temperature yield strength greater than the target value) is more accurately defined. An example of this is shown in Fig. 7. Both AL schemes were initialized 200 times and ran for 15 iterations. The average performance metrics for each model were plotted as a function of iteration and are shown in Fig. 6.
For the first seven iterations, the model with prior data exhibits higher average accuracy and recall. In addition, its average Brier loss and average F1 score are higher for the first eight iterations. The average precision is consistently higher, and the average log loss is consistently lower for the model with prior data. Although the confidence intervals for recall overlap between the two models, the model without prior knowledge shows a notably high standard deviation in recall—exceeding its mean recall value in the first iteration. For all other metrics, the confidence intervals of the two models do not overlap during the first two to four iterations, and the standard deviation is initially lower for the model with a prior.
6 Limitations and advantages
In these case studies we demonstrated the benefit of equipping GPs with informative prior mean functions during static and active learning tasks. However, there are some important limitations to consider.The proposed method depends greatly on the quality of the prior mean function used. To demonstrate this, we present a case study that examines the effect of prior model quality on Bayesian active learning outcomes. Specifically, we compare the performance of the framework using the Iris dataset from the  library. The model is equipped with (i) a well-aligned informative prior, (ii) a deliberately misleading or ‘harmful prior, and (iii) no prior. These priors can be seen in Fig. 8, while Fig. 9 shows a single instance of active learning. As in previous benchmarks, we conducted 200 active learning runs for each scheme to obtain statistically robust comparisons of average performance. The resulting error distributions are shown in Fig. 10. The results indicate that while informative priors can substantially accelerate learning, poor priors can significantly degrade performance. This underscores the critical role of prior selection and highlights a well-known limitation of Bayesian approaches: their sensitivity to prior assumptions, especially in data-scarce settings.
library. The model is equipped with (i) a well-aligned informative prior, (ii) a deliberately misleading or ‘harmful prior, and (iii) no prior. These priors can be seen in Fig. 8, while Fig. 9 shows a single instance of active learning. As in previous benchmarks, we conducted 200 active learning runs for each scheme to obtain statistically robust comparisons of average performance. The resulting error distributions are shown in Fig. 10. The results indicate that while informative priors can substantially accelerate learning, poor priors can significantly degrade performance. This underscores the critical role of prior selection and highlights a well-known limitation of Bayesian approaches: their sensitivity to prior assumptions, especially in data-scarce settings.
Beyond sensitivity to priors, the computational cost of the proposed framework warrants consideration. While this work primarily emphasizes reducing experimental costs in alloy discovery, the implementation of the framework also incurs computational overhead. Specifically, the method requires querying an informative prior model and training a GP on the discrepancy between the prior and the observed ground truth. As such, the throughput of class prediction depends both on the computational cost of evaluating the prior model and on the training set size used for the GP.
In this study, the most computationally expensive component is the CALPHAD equilibrium calculation step, which serves as the prior model. For example, performing equilibrium calculations over the Fe–Ni–Cr compositional space used in the study (comprising of 1372 distinct alloys) requires approximately 24 minutes when run sequentially on a single core. For larger alloy systems, querying a CALPHAD prior can be parallelized efficiently across compositions, substantially reducing wall time when distributed across multiple cores. Examples of this are provided in ref. 4, 12 and 44.
Training the GP model itself also incurs computational cost,26 particularly due to its cubic scaling with the number of training points, i.e., 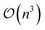 . While this scaling presents challenges for large datasets, it is well-suited to the low-data regime commonly encountered in alloy design. In practice, the training time for the classification problems considered in this work remained well within practical limits, with individual GPC models trained in a matter of minutes on standard desktop hardware.
. While this scaling presents challenges for large datasets, it is well-suited to the low-data regime commonly encountered in alloy design. In practice, the training time for the classification problems considered in this work remained well within practical limits, with individual GPC models trained in a matter of minutes on standard desktop hardware.
Thus, while the proposed framework introduces some computational cost i.e. the cost of quering a prior model across a design space and training a GP, these remain manageable within the scale of current alloy discovery problems, and the benefits of reduced experimental burden and improved sample efficiency outweigh the computational overhead in many practical scenarios.
Despite these limitations, the proposed method offers several advantages.
Other machine learning methods such as deep neural networks or random forests—have been applied to phase stability prediction, Gaussian Process Classifiers (GPCs) offer several key advantages that justify their use here. First, GPCs are natively amenable to Bayesian active learning and active classification, since they intrinsically quantify predictive uncertainty. This uncertainty quantification is what enables Bayesian active learning. Moreover, Gaussian Process–based methods are already the default choice in many materials-informatics studies, especially in data-sparse regimes.46,47 Our approach therefore builds directly upon a well-established framework, augmenting it with physics-informed priors and active learning strategies.
In addition, GPCs provide superior interpretability compared to “black-box” models like neural networks. Using Automatic Relevance Determination (ARD) kernels, GPC hyperparameters such as length scales reveal the relative importance and spatial influence of individual input features. By inspecting these length scales, one can discern which compositional or processing variables exert the strongest effect on the latent classification function, thus gaining direct insight into the underlying physics. In contrast, neural networks often require post-hoc interpretation methods and can obscure the mechanistic relationship between inputs and predictions. Furthermore, the proposed method explicitly models the discrepancy between the physical model and observed data. This discrepancy highlights where and how the prior physical understanding breaks down, providing insights into the underlying alloy behavior.
7 Conclusion
In materials design, objectives and constraints play distinct yet complementary roles. Objectives represent desirable material properties that we seek to optimize, while constraints define non-negotiable requirements that a material must satisfy, typically ensuring that it meets minimum performance standards. In previous work,11,22 we demonstrated that Bayesian optimization for property optimization (i.e., maximizing or minimizing objective properties) can be accelerated by incorporating informative priors. In this study, we extend this concept to classification and the active learning of decision boundaries. Specifically, we enhanced Gaussian Process Classifiers (GPCs) with physics-informed priors to make the exploration of material design spaces both more efficient and cost-effective. Our case studies demonstrate that physics-informed prior mean functions can improve the predictive performance of GPCs in alloy design.The impact of this work lies in its potential contribution to accelerating materials discovery and optimization through physics-informed machine learning. Specifically, we develop a Gaussian Process framework that integrates prior scientific knowledge to improve probabilistic classification and regression in both categorical and continuous design spaces. For categorical variables, we introduce informative prior mean functions into GP classifiers— an approach that, to our knowledge, is unprecedented in materials science. For continuous variables, we combine threshold-based classification and informative priors within a GP regressor to predict the likelihood that a material satisfies critical performance constraints. This enables more targeted exploration of design spaces, making our method particularly powerful for constraint-driven materials optimization.
Given the improvements in active learning-based discovery demonstrated in our case studies, we conclude that incorporating physics-informed priors into the alloy design workflow has the potential to significantly reduce computational and experimental costs while enhancing model accuracy and efficiency. The proposed methodology aligns with recent initiatives focused on Integrated Computational Materials Engineering (ICME)-enabled closed-loop design platforms and autonomous materials discovery. Moreover, the approach is easily implemented using only scikit-learn and open-access code, ensuring broad accessibility.
Data availability
The code used for the case studies presented in this paper is publicly available on Zenodo at https://zenodo.org/records/15683743 and can be accessed via the DOI: https://doi.org/10.5281/zenodo.15683742.Author contributions
Christofer Hardcastle: writing – original draft, writing – review & editing, visualization, software, investigation, formal analysis, data curation. Ryan O'Mullan: writing – original draft, visualization, software, validation, investigation, formal analysis, data curation. Raymundo Arróyave: writing – review & editing, project administration, funding acquisition. Brent Vela: writing – original draft, writing – review & editing, visualization, software, investigation, formal analysis, data curation, conceptualization, methodology, supervision.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
We acknowledge the support from the U.S. Department of Energy (DOE) ARPA-E ULTIMATE Program through Project DE-AR0001427. RA also acknowledges the Army Research Laboratory (ARL) for support through Cooperative Agreement Number W911NF-22-2-0106, as part of the High-throughput Materials Discovery for Extreme Conditions (HTMDEC) program as supported by the BIRDSHOT Center at Texas A&M University. BV acknowledges the support of NSF through Grant No. 1746932 (GRFP) and 1545403 (NRT-D3EM). Computations were conducted at the Texas A&M University High-Performance Research Computing (HPRC) facility. During the preparation of this work the authors used GPT-4-turbo in order to ideate/brainstorm alternative sentence structures and stylistic choices in limited sections of the paper. After using this tool/service, the authors reviewed and edited the content as needed and take full responsibility for the content of the publication.References
- J. Broucek, D. Khatamsaz, C. Cakirhan, S. H. Zadeh, M. Fan, G. Vazquez, K. Atli, X. Qian, R. Arroyave and I. Karaman, Design of high-temperature nicutihf shape memory alloys with minimum thermal hysteresis using bayesian optimization, Acta Mater., 2024, 120651, DOI:10.1016/j.actamat.2024.120651 . https://www.sciencedirect.com/science/article/pii/S1359645424009996.
- W. Yang, S. Lin, Q. Wang, C. Liu, J. Qin and J. Zhang, Accelerated design of l12-strengthened single crystal high entropy alloy based on machine learning and multi-objective optimization, Mater. Adv., 2024, 5, 5772–5780 RSC.
- W. Xu, E. Diesen, T. He, K. Reuter and J. T. Margraf, Discovering high entropy alloy electrocatalysts in vast composition spaces with multiobjective optimization, J. Am. Chem. Soc., 2024, 146(11), 7698–7707 CrossRef CAS PubMed.
- C. Acemi, B. Vela, E. Norris, W. Trehern, K. C. Atli, C. Cleek, R. Arróyave and I. Karaman, Multi-objective, multi-constraint high-throughput design, synthesis, and characterization of tungsten-containing refractory multi-principal element alloys, Acta Mater., 2024, 281, 120379 CrossRef CAS.
- R. Arróyave, S. Gibbons, E. Galvan and R. Malak, The inverse phase stability problem as a constraint satisfaction problem: Application to materials design, JOM, 2016, 68, 1385–1395 CrossRef.
- A. Abu-Odeh, E. Galvan, T. Kirk, H. Mao, Q. Chen, P. Mason, R. Malak and R. Arróyave, Efficient exploration of the high entropy alloy composition-phase space, Acta Mater., 2018, 152, 41–57, DOI:10.1016/j.actamat.2018.04.012 . https://www.sciencedirect.com/science/article/pii/S1359645418302854.
- D. Khatamsaz, B. Vela, P. Singh, D. D. Johnson, D. L. Allaire and R. Arróyave, Bayesian optimization with active learning of design constraints using an entropy-based approach, npj Comput. Mater., 2023, 9, 1–14 CrossRef . https://api.semanticscholar.org/CorpusID:257902688.
- T. M. Pollock and A. Van der Ven, The evolving landscape for alloy design, MRS Bull., 2019, 44(4), 238–246, DOI:10.1557/mrs.2019.69.
- A. B. Peters, D. Zhang, S. Chen, C. Ott, C. Oses, S. Curtarolo, I. McCue, T. M. Pollock and S. Eswarappa Prameela, Materials design for hypersonics, Nat. Commun., 2024, 15(1), 3328 CrossRef CAS PubMed.
- J. Qi, X. Fan, D. I. Hoyos, M. Widom, P. K. Liaw and J. Poon, Integrated design of aluminum-enriched high-entropy refractory b2 alloys with synergy of high strength and ductility, Sci. Adv., 2024, 10(49), eadq0083 CrossRef CAS PubMed.
- B. Vela, D. Khatamsaz, C. Acemi, I. Karaman and R. Arróyave, Data-augmented modeling for yield strength of refractory high entropy alloys: A bayesian approach, Acta Mater., 2023, 261, 119351, DOI:10.1016/j.actamat.2023.119351 . https://www.sciencedirect.com/science/article/pii/S135964542300681X.
- B. Vela, C. Acemi, P. Singh, T. Kirk, W. Trehern, E. Norris, D. D. Johnson, I. Karaman and R. Arróyave, High-throughput exploration of the wmovtanbal refractory multi-principal-element alloys under multiple-property constraints, Acta Mater., 2023, 248, 118784, DOI:10.1016/j.actamat.2023.118784 . https://www.sciencedirect.com/science/article/pii/S1359645423001155.
- B. Skrotzki, J. Olbricht and H.-J. Kühn, High temperature mechanical testing of metals, in Handbook of Mechanics of Materials, Springer Nature Singapore Pte Ltd, 2018, pp. 1–38 Search PubMed.
- M. C. Troparevsky, J. R. Morris, M. Daene, Y. Wang, A. R. Lupini and G. M. Stocks, Beyond atomic sizes and hume-rothery rules: understanding and predicting high-entropy alloys, JOM, 2015, 67, 2350–2363 CrossRef CAS.
- R. Li, L. Xie, W. Y. Wang, P. K. Liaw and Y. Zhang, High-throughput calculations for high-entropy alloys: a brief review, Front. Mater., 2020, 7, 290 CrossRef.
- C. Zhang and Y. Yang, The calphad approach for heas: Challenges and opportunities, MRS Bull., 2022, 47(2), 158–167 CrossRef.
- S. Rao, C. Woodward, B. Akdim, O. N. Senkov and D. Miracle, Theory of solid solution strengthening of bcc chemically complex alloys, Acta Mater., 2021, 209, 116758 CrossRef CAS.
- F. Maresca and W. A. Curtin, Mechanistic origin of high strength in refractory bcc high entropy alloys up to 1900k, Acta Mater., 2020, 182, 235–249 CrossRef CAS.
- S. Rao, E. Antillon, C. Woodward, B. Akdim, T. Parthasarathy and O. Senkov, Solution hardening in body-centered cubic quaternary alloys interpreted using suzuki's kink-solute interaction model, Scr. Mater., 2019, 165, 103–106 CrossRef CAS.
- C. Dai and S. C. Glotzer, Efficient phase diagram sampling by active learning, J. Phys. Chem. B, 2020, 124(7), 1275–1284 CrossRef CAS PubMed.
- A. Koizumi, G. Deffrennes, K. Terayama and R. Tamura, Performance of uncertainty-based active learning for efficient approximation of black-box functions in materials science, Sci. Rep., 2024, 14(1), 27019 CrossRef CAS PubMed.
- P. Morcos, B. Vela, C. Acemi, A. Elwany, I. Karaman and R. Arróyave, Data-augmented modeling in laser powder bed fusion: A bayesian approach, Addit. Manuf., 2024, 96, 104545, DOI:10.1016/j.addma.2024.104545 . https://www.sciencedirect.com/science/article/pii/S2214860424005918.
- R. Machaka, G. T. Motsi, L. M. Raganya, P. M. Radingoana and S. Chikosha, Machine learning-based prediction of phases in high-entropy alloys: A data article, Data Brief, 2021, 38, 107346, DOI:10.1016/j.dib.2021.107346 . https://www.sciencedirect.com/science/article/pii/S2352340921006302.
- D. Bagnell, Statistical techniques in robotics (16-831, f09), lecture #21: Gaussian process – part 2, scribed by Stephane Ross, 2009, https://www.cs.cmu.edu/16831-f09/ Search PubMed.
- C. M. Bishop and N. M. Nasrabadi, Pattern recognition and machine learning, Springer, 2006, vol. 4 Search PubMed.
- C. E. Rasmussen and H. Nickisch, Gaussian processes for machine learning (gpml) toolbox, J. Mach. Learn. Res., 2010, 11, 3011–3015 Search PubMed.
- Tc-python api programmer guide 2021b, accessed: May 2024, https://thermocalc.com/wp-content/uploads/Documentation/Archive/2020-2024/2021b/2021b-tc-python-api-programmer-guide.pdf.
- Thermo-calc software tchea6 database, accessed: May 2024, https://www.engineering-eye.com/THERMOCALC/details/db/pdf/thermo-calc/2022b/TCHEA6_technical_info.pdf.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and E. Duchesnay, Scikit-learn: Machine learning in Python, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- C. Wen, Y. Zhang, C. Wang, D. Xue, Y. Bai, S. Antonov, L. Dai, T. Lookman and Y. Su, Machine learning assisted design of high entropy alloys with desired property, Acta Mater., 2019, 170, 109–117, DOI:10.1016/j.actamat.2019.03.010 . https://www.sciencedirect.com/science/article/pii/S1359645419301430.
- L. Ward, A. Dunn, A. Faghaninia, N. E. R. Zimmermann, S. Bajaj, Q. Wang, J. H. Montoya, J. Chen, K. Bystrom, M. Dylla, K. Chard, M. Asta, K. Persson, G. J. Snyder, I. Foster and A. Jain, Matminer: An open source toolkit for materials data mining, Comput. Mater. Sci., 2018, 152, 60–69 CrossRef.
- B. Vela, S. Mehalic, S. Sheikh, A. Elwany, I. Karaman and R. Arróyave, Evaluating the intrinsic resistance to balling of alloys: A high-throughput physics-informed and data-enabled approach, Addit. Manuf. Lett., 2022, 3, 100085 CrossRef.
- T. M. Pollock and A. Van der Ven, The evolving landscape for alloy design, MRS Bull., 2019, 44(4), 238–246 CrossRef CAS.
- Y. Wu and Y. Zhang, Design and high-throughput screening of high entropy alloys, Advances in High-Entropy Alloys-Materials Research, Exotic Properties and Applications, 2021, pp. 1–16 Search PubMed.
- M. Zhu, J. Yao, M. Mynatt, H. Pugzlys, S. Li, S. Bacallado, Q. Zhao and C. Jia, Active learning for discovering complex phase diagrams with Gaussian processes, arXiv, 2024, preprint, arXiv:2409.07042, DOI:10.48550/arXiv.2409.07042.
- A. G. Kusne, H. Yu, C. Wu, H. Zhang, J. Hattrick-Simpers, B. DeCost, S. Sarker, C. Oses, C. Toher and S. Curtarolo, et al., On-the-fly closed-loop materials discovery via bayesian active learning, Nat. Commun., 2020, 11(1), 5966 CrossRef CAS PubMed.
- S. Ament, M. Amsler, D. R. Sutherland, M.-C. Chang, D. Guevarra, A. B. Connolly, J. M. Gregoire, M. O. Thompson, C. P. Gomes and R. B. Van Dover, Autonomous materials synthesis via hierarchical active learning of nonequilibrium phase diagrams, Sci. Adv., 2021, 7(51), eabg4930 CrossRef CAS PubMed.
- S. S. Basu, P. P. Jana and M. Ghosh, A new insight into the phase stability in high entropy alloys, Mater. Today Commun., 2023, 37, 107394 CrossRef CAS.
- R. Arróyave, Phase stability through machine learning, J. Phase Equilib. Diffus., 2022, 43(6), 606–628 CrossRef.
- I. Alam, M. A. Adaan-Nyiak and A. A. Tiamiyu, Revisiting the phase stability rules in the design of high-entropy alloys: A case study of quaternary alloys produced by mechanical alloying, Intermetallics, 2023, 159, 107919 CrossRef CAS.
- S. Guo, C. Ng, J. Lu and C. Liu, Effect of valence electron concentration on stability of fcc or bcc phase in high entropy alloys, J. Appl. Phys., 2011, 109(10), 103505 CrossRef.
- D. W. Chen and Y. H. Jin, An active learning algorithm based on shannon entropy for constraint-based clustering, IEEE Access, 2020, 8, 171447–171456 Search PubMed.
- S. F. Ghoreishi and D. Allaire, Multi-information source constrained bayesian optimization, Struct. Multidiscip. Optim., 2019, 59, 977–991 CrossRef.
- R. Arroyave, Ultimate: Birdshot. final technical report, Tech. rep., Texas A & M Univ., College Station, TX (United States), 2024 Search PubMed.
- C. Baruffi, F. Maresca and W. Curtin, Screw vs. edge dislocation strengthening in body-centered-cubic high entropy alloys and implications for guided alloy design, MRS Commun., 2022, 12(6), 1111–1118 CrossRef CAS.
- D. Xue, P. V. Balachandran, J. Hogden, J. Theiler, D. Xue and T. Lookman, Accelerated search for materials with targeted properties by adaptive design, Nat. Commun., 2016, 7(1), 11241, DOI:10.1038/ncomms11241.
- S. K. Achar and J. A. Keith, Small data machine learning approaches in molecular and materials science, Chem. Rev., 2024, 124(24), 13571–13573, DOI:10.1021/acs.chemrev.4c00957.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5dd00084j |
| This journal is © The Royal Society of Chemistry 2025 |