BayBE: a Bayesian Back End for experimental planning in the low-to-no-data regime

Abstract

Due to its potential for high-dimensional black-box optimization and automation, Bayesian optimization(BO) is an excellent match for the iterative low-to-no-data regime many experimentalist practice in. It can be cumbersome to make BO work for real-world problems, as the application of code frameworks focusing only on implementing the core loop often requires substantial adaptation. Furthermore, with an extremely active research community, it can be challenging to find, select and learn the right components and code frameworks that best match the specific problem at hand. This is striking, as the BO framework in principle is highly modular, and such fragmentation is a headwind for the adoption of BO in industry. In this work, we present the Bayesian Back End (BayBE), an open-source framework for BO in real-world industrial contexts. Besides core BO, BayBE provides a wide range of additions relevant for practitioners, four of which we highlight in case studies in the domains of chemical reactions and housing prices: The impact of (i) chemical and (ii) custom categorical encodings; (iii) transfer learning BO; and (iv) automatic stopping of unpromising campaigns. These features can reduce the average number of experiments by at least 50%, cost and time requirements being reduced by the same factor compared to default implementations such as one-hot encoding. With this, we engage interested users and researchers from either industrial or academic backgrounds, and actively invite them to evaluate and contribute to the framework.

---

1 Introduction

Chemical, materials, and pharmaceutical industries are facing an ever-growing complexity in the experimental effort to create their products. For instance, the ratio of R&D spending to total sales in the pharmaceutical industry increased from 11.9% to 17.7% from 2008 to 2019.¹ As pointed out by Bannigan et al.,² a 51-fold increase in R&D spending has only led to a two-fold increase in approved FDA drugs between 1980 and 2020.³ Overall, this is not unexpected as any industry will progressively transition from readily achievable objectives to more complex issues to address. This, in turn, creates new challenges for all fields participating in physical product development, from synthesis of compounds and materials to formulation screening and process optimization.

Traditional ways of approaching these growing experimental challenges, including some of their downsides, are typically:

(1) Unsystematic: this often involves human judgment coming from a longstanding expertise. While this is not an issue per se, humans are not good at optimizing many variables and targets simultaneously, often falling back into simplistic one-at-a-time approaches. Beyond that, human bias has also been identified as a potential issue,⁴ increasing the risk of masking important factors or getting trapped with suboptimal settings.

(2) Classical design of experiments (DOE): DOE offers a mathematically sound way to produce a plan to gather results in an information-efficient way.^4,5 However, it comes with limited options to include prior data, often uses too simplistic models, and struggles with high-cardinality categorical parameters.^6,7

(3) Brute-force via high throughput-screening (HTS): HTS is often enabled by technical achievements allowing to screen a large number of samples. Due to the combinatorial explosion of parameter combinations, HTS still remains unfeasible in most cases, while in other cases the design spaces are reduced as a compromise to make it amenable to HTS.^8,9

Bayesian optimization (BO) has emerged as a formidable tool for conquering complex search spaces in both academic and industry settings. Due to its inherent ability to balance exploration and exploitation, it offers the prospect of global optimization.^10,11

Moreover, BO aligns nicely with the data regime in which most experimental campaigns operate: in contrast to many of the impressive achievements that the deep learning field has produced,¹² the vast majority of chemistry and materials science problems in daily industrial context do not have the big data basis required for deep learning. On the other hand, most industrial problems are too complex to be modeled directly by entirely mechanistic (non-data-driven) methods, such as fluid dynamics¹³ or density functional theory.¹⁴

Thus, by far the most common practice to tackle design problems is to work in an iterative manner, performing make-test-learn cycles while generating a small amount of data. We term this regime the low-to-no-data regime. Since this is also the modus operandi of BO, whilst also being flexible to start from any kind of data situation, BO is a natural match for experimental planning. BO has already been applied in various problem domains, e.g. reaction conditions,^15,16 mixtures,^17–19 biological assays,²⁰ or exploring chemical compound space.^21–24

Despite the growing adoption of BO, applying it in realistic scenarios still requires much adaptation because many aspects are not handled well by implementations focusing only on the core optimization loop. As an example, label encoding does not usually take into consideration the chemical nature of the entities (such as solvents, ligands or bases) represented by the labels. Simple one-hot encoding distorts the useful relations between substances in chemical space by imposing a uniform distance between labels. Since BO use cases are extremely frequent and interest from even non-technical experts increases steadily, such important technical details contribute to forming an adoption barrier.

To address this barrier and to assemble all required tools needed to perform industrial BO, we created the open-source Python package BayBE (Bayesian Back End), released under a non-restrictive Apache-2.0 license.²⁵ It provides easy access to the core BO methodology, while also including a range of very useful additions that are at the disposal of the user within a few lines of code: (1) chemical and custom categorical encodings; (2) minimization, maximization, and target matching in discrete, continuous, or hybrid parameter spaces; (3) multi-target optimization via desirability scalarization or Pareto-front search; (4) model insights such as parameter importance; (5) distributed asynchronous workflows between several experimenters and support for partial measurements; (6) active learning; (7) bandit optimization; (8) full serializability of all objects, and (9) transfer learning for unlocking data treasures found in similar experiments. Beyond this, the code undergoes extensive review, integration testing, and hypothesis tests, and we provide comprehensive user guides and templates with educational character.²⁶

The need for bringing BO to real-world labs is also reflected in the many recent frameworks developed around this topic to achieve similar goals, such as ,²⁷ ,²⁸ ,²⁹ ,³⁰ ,³¹ ,^{32 33} or ;³⁴ as well as commercial offerings.^35–39

In this work, following a brief explanation of the BO methodology and our investigation process, we show four case studies utilizing features mentioned beforehand that we found to be most relevant in realistic use cases: (i) the impact of chemical and (ii) custom encodings for categorical variables; (iii) transfer learning between chemical reactions performed under slightly different conditions; and (iv) automatic stopping of unpromising campaigns.

2 Methods

We provide detailed explanations of the methods applied in their respective subsections of Section 3, while this section contains a summary of BO basics, backtesting, and how results and outcomes are evaluated.

BO aims to sequentially optimize an expensive-to-obtain, unknown objective function f, which typically delivers noisy and gradient-free information.¹¹ To this end, two main components are used: first, a probabilistic surrogate model f̂ of the objective function f, and second, an acquisition function α encoding the optimization strategy³⁰ for proposing new measurements. In its most basic variant, optimizing the function f is performed by repeating the following steps:⁴⁰

• Update the probabilistic model f̂ of f using all available data D.

• Maximize the acquisition function α computed from f̂.

• Evaluate the true objective function f at the calculated maximizer of α and update D.

Optimizing the function f is typically referred to as a BO campaign. Critical is the choice of suitable α, as it balances exploration and exploitation by considering both the predicted values and their associated uncertainty. This results in enhanced robustness against becoming trapped in local minima. Most often, the expected improvement (EI) is used, integrating the probability-weighted model prediction that is higher than the currently best observed value.^41,42 Special acquisition functions are available as well, e.g. for active learning⁴³ or custom control of the exploration/exploitation trade-off.⁴⁴ If not mentioned differently, we are using EI and Gaussian Process (GP) models throughout.

A GP defines a probability distribution over functions, offering a non-parametric Bayesian approach. Formally, a GP is a collection of random variables which have a joint Gaussian distribution. It is fully specified by a mean function µ(x) and a covariance function k(x,x̂) commonly referred to as kernel. k(x,x̂) models the covariance between function values at points x and x̂. By carefully choosing k, it is also possible to include prior information, e.g. knowledge about an underlying periodicity. For a finite set of input points {x₁, …, x_n}, the corresponding vector of function values f = {f(x₁), …, f(x_n)} follows a multivariate Gaussian distribution: , where the mean vector µ has elements µ_i = µ(x_i) and the covariance matrix K has elements K_ij = k(x_i, x_j).

In contrast to supervised machine learning, the outcome of BO campaigns is not commonly judged by regression or classification metrics.⁴⁵ Rather, one is primarily interested in the trajectory the optimization takes, considering the specific problem and corresponding setup at hand. The latter includes a translation of the experimental parameters, constraints, and targets into a machine-treatable language. Typically, there are several choices to make, which we refer to as the overall settings. Examples for settings are the parameter types (e.g. discrete or continuous numerical), the encodings for categorical parameters, and the surrogate model.

To judge the BO performance of a given problem and setting, backtesting is frequently the method of choice in the computer science domain. This approach is well known, e.g. also in financial modeling⁴⁶ for evaluation on historical data. It is a Monte Carlo (MC) like procedure, where entire BO campaign trajectories with different initial conditions are repeated. Backtesting with different settings provides insights into their influence on the campaign. For a backtest in the context of BO, we need a lookup mechanism (e.g. on historical data) or oracle corresponding to the black-box function f, which provides the target values for any proposed set of input parameter values. BayBE provides utilities to quickly perform these backtests,⁴⁷ enabling the study of various algorithms and settings without having to worry about things like parallelization. The full recommend-measure loop is repeated several times to account for random effects, e.g. caused by the selection of starting points or stochastic components of the recommendation algorithm. If not mentioned differently, all results in this work are obtained by choosing a different set of initial measurements randomly for each MC run (although this behavior can be configured flexibly in BayBE).

The outcome of the aforementioned process is an average trajectory, in the sense that the measurements of the target are averaged point-wise per iteration. We refer to this as an optimization curve, see e.g. Fig. 1b. Visualizing the optimization curves across several settings for a fixed problem indicates which settings are superior and should be preferred for actual campaigns. We generally judge the resulting plot in two aspects:

Fig. 1 Chemical encodings: (a) Illustration of different encodings applied to molecular substances. The top and bottom solvents are chemically very similar and both are less similar to the central solvent. This is not reflected in the numbers generated by integer (INT) and one-hot (OHE) encodings. By contrast, an encoding with chemically meaningful quantities reveals the similarities. (b) Optimization performance for the direct arylation reaction from Shields et al.,¹⁵ with the task to maximize reaction yield among 1728 possible combinations. Each curve corresponds to different encodings used for the categorical labels belonging to the substance entries of bases, ligands and solvents. The dashed lines mark the number of experiments needed to reach a reasonably high yield of 90% for MORDRED and OHE. This backtest was performed with 100 Monte-Carlo iterations, and shaded areas indicate 95% confidence intervals.

(1) Is the global optimum found? If so, how fast and stable is the convergence?

(2) How steep is the optimization curve at the initial iterations? We judge this by the number of iterations until 90% of the best possible value has been reached.

We note that in the traditional machine learning literature, the first aspect is often emphasized. However, industrial applications can have different goals. It can be more valuable to obtain a sufficiently good result (close but not identical to the global optimum) in a small number of experiments. Take, for instance, reaction condition screening in medicinal chemistry: usually, it is not critical to find a perfect set of conditions with 100% yield. Instead reaching a problem-specific lower limit might already be acceptable to move the project forward. While it is difficult to generalize what qualifies as sufficiently good and how many constitute a small number of experiments, these questions are typically clear for domain experts who understand the objectives, time characteristics and budget limits of their specific problem. Thus, our assessment of BO performance will focus more on the second aspect.

3 Results

To highlight some of the features mentioned in the introduction, we present four case studies. These use-cases highlight the concepts that are impactful additions to the basic BO workflow when used in practice. However, to the best of our knowledge, these are still somewhat underutilized and underappreciated.

3.1 Chemical encodings

One important aspect of real-world campaigns in chemical, pharmaceutical, or materials industries is that they work with substances as parameters. The choice of which substance to choose as solvent, ligand, base, phase agent, buffer, or mixture component appears frequently. This comprises a choice between a set of categories, corresponding to the available substances (e.g. identified by their name). To be treatable by tabular machine learning models, these labels are transformed into a machine-interpretable representation, typically a numerical encoding.

Two often used encodings are integer (INT) and one-hot encoding (OHE).⁴⁸ These approaches have severe downsides, as they can impose spurious orders and distances between the labels. Fig. 1a illustrates this issue. Consider the three depicted solvents, where solvents 1 and 3 are extremely similar, and both are dissimilar to solvent 2. If this situation is encoded with integers 1, 2, 3, the imposed order does not reflect the underlying chemical similarity. Instead, solvents 1 and 3 would always be more similar to solvent 2 than to each other – the exact opposite of the preposition. This can have detrimental effects on the machine learning model, e.g. for a random forest performing binary splits along the ordered histogram of values. Since molecules can generally not be ordered along one dimension, INT encoding is a poor choice for substance representations. A similar argument can be made for OHE encoding, where all labels are represented as orthogonal unit vectors. This imposes a uniform pairwise distance, which also does not capture the similarities in chemical space.

In the case of chemical categorical parameters, a straightforward improvement is to use chemical descriptors⁴⁹ as encoding. Similar to OHE, this leads to a multivariate representation of the labels but with a structure reflecting the actual (dis-)similarities in multiple dimensions of chemical variability (see also Fig. 1a). For small molecules, this can easily be achieved by using common cheminformatics libraries such as 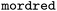^50,51 or .⁵² Alternatives to this descriptor-based approach are latent space representations, which have successfully been applied in chemical BO,⁵³ but will not be investigated further here.

In addition to generating these descriptors, BayBE performs a (user-configurable) feature reduction via sequentially selecting descriptors and including a descriptor only if it has a Pearson correlation below a certain threshold (0.7 being applied in this work). This reduces the dimensionality of the search space while limiting information loss, and results in a different set of descriptors being used for each problem, depending on the substances behind the labels.

Fig. 1b demonstrates the impact of using different encodings for a chemical use case. We utilize the dataset from Shields et al.,¹⁵ where reaction conditions for a direct arylation have been optimized. The temperature and concentration of the substrate are modeled as discrete numerical parameters, and the solvent, base, and ligand substances as discrete categorical parameters. The latter three can be encoded in various ways, as displayed in the legend. Since all possible parameter combinations were tested in the lab, we can perform a backtest on this dataset.

First, we note that there is a tremendous difference between the optimization curves for different encodings in the investigated scenario. The aforementioned encodings from 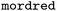(MORDRED) and 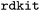(RDKIT2DDESCRIPTORS) perform best, both in the early and late trajectory. In contrast, OHE encoding performs poorly, in parts even worse than random exploration. The encoding with extended connectivity fingerprints (ECFP⁵⁴) performs worse than the other chemical encodings, but still better than OHE.

As practical consideration, we highlight a potential early stop of this campaign at a 90% yield with dashed lines. This identifies after how many experiments the MORDRED and OHE trajectories reach this yield on average. With 16 experiments, MORDRED needs less than half the number of iterations compared to OHE, which requires 37 experiments. Hence, in practice, such a simple switch from categorical encodings to chemical encodings can save as much as 50% of the invested time or budget.

Additionally, we also investigated the performance of ,⁵⁵ a popular BO package in the data science community. With default settings, uses a probabilistic surrogate⁵⁶ that does not employ any numerical representation for labels and instead models their sampling probabilities directly. For the given problem, we find that the performance to be poor, i.e. on par with random exploration. We attribute this in part to the inability to use chemical encodings, causing difficulties for the underlying tree-based model.⁵⁵ Beyond this consideration, the framework is also unable to perform batch optimization – another important feature required for real-world campaigns, which often need to run experiments in parallel. We see the strengths of more in searching highly nested spaces, commonly encountered in hyperparameter optimization, where the underlying search space cannot be easily represented in tabular form.

Finally, we note that the similarity between chemicals can be directly incorporated into the model architecture instead of using a tabular encoding of their labels, by employing an appropriate kernel for the underlying surrogate model. This has been done, for instance, using Tanimoto or SMILES string kernels⁵⁷ in Gaussian processes. As long as the induced similarity measures are reasonable, we can expect comparable performance from both approaches.

3.2 Custom encodings

Using the ideas from Section 3.1, we can enable the use of arbitrary categorical parameters. Although BayBE provides built-in chemical encodings for small molecules, these might not be the best choice for larger substances that are either not correctly identified by a single molecular graph, where the molecular graph is unknown, or where the relevant properties cannot even be gleaned from the molecular graph. Chemical examples for this are polymers, biomolecules, strongly folded molecules or mixtures. This also opens the avenue to think beyond chemicals and substances, as there are quantities that are categorical but have no chemical nature, such as ZIP codes or vendors.

In many cases, we can craft context-specific numeric representations as alternatives to the generic INT and OHE encodings, provided there exists some underlying structure that is relevant to identify similarities between the otherwise randomly ordered labels. For example, it is common to characterize a polymer by its molecular weight and glass transition temperature.⁵⁸ We call these representations custom encodings.

Custom encodings can comprise computational and experimental values, offering users an opportunity to collaborate with subject-matter experts to identify or measure advanced descriptors that they believe are important to the campaign. BayBE supports the use of any custom descriptor set via a dedicated custom parameter type. Thinking beyond pure optimization performance, this can be a great help in lowering the adoption barrier to engage experimentalists and decision makers going beyond pure black-box modeling – an aspect that should not be underestimated.

To illustrate the impact in such a situation, we take the California housing data set⁵⁹ and consider the task of finding the highest house price through BO. Although this is not a common use case in itself, we can imagine it as a proxy for, e.g. political or advertisement campaigns that do not have the budget to perform a large-scale screening to find regions with desired properties.

First, we pre-process the data to add the latitude and longitude of each region in the data set, as well as its ZIP code. We then model the data using a BO campaign with the ZIP code as the only parameter. The spatial distribution of the ZIP code values, as well as the spatial distribution of the median house value (MEDV, maximization target of the campaign) can be seen in Fig. 2a and b. The ordering of ZIP codes taken as numbers increases roughly from south to north. However, a certain arbitrariness can be seen by looking at the highlighted regions with the largest ZIP codes (red stars). Furthermore, the numerical ordering of ZIP codes does not match with the spatial distribution of the MEDV in panel b. Thus, we anticipate that a spatial encoding of ZIP values can boost the optimization performance in this case.

Fig. 2 Custom encodings: (a) spatial distribution of locations in the California housing data set⁵⁹ as identified by their ZIP code. Color coding corresponds to numerical magnitude, and the largest five ZIP codes are highlighted by stars. Each point on the map corresponds to a distinct ZIP code. (b) The same as (a) but color-coded according to the median house value (MEDV) of the region identified by the ZIP code. (c) Optimization performance for different encodings of the ZIP code parameter. The inlay above the legend shows the histogram of MEDV, which is the target property of the maximization task. Dashed lines indicate when a high MEDV value of 4.5 was found, shown for our custom encoding and OHE. This backtest was performed with 200 Monte-Carlo iterations, and shaded areas indicate 95% confidence intervals.

This hypothesis is confirmed in Fig. 2c, where the OHE and INT encodings perform as badly as random search. The latitude–longitude encoding of the ZIP codes causes a much better convergence to the best possible value of 5. When stopping the campaign at a near-optimal value of 4.5 (dashed lines), we find that our simple custom encoding needs 12 iterations on average, while OHE needs 23 – a saving in experimental budget and time of almost 50%.

3.3 Transfer learning

Another downside that standard BO shares with DOE is that campaigns in slightly different environments still need to be run fully independently. This means if one or several campaigns in similar but not quite identical environments were already run (referred to as source campaigns), the next campaign (referred to as target campaign) would still need to start from scratch, even though the results of the source campaigns may contain valuable information for the target campaign. There are plenty of industrially relevant examples for such a situation:

• Reaction conditions: while campaigns optimizing reaction conditions for different substrates are not identical, they can share a large amount of similarity, especially if they optimize the same reaction type (such as industrial workhorses like Suzuki or Buchwald couplings).

• Site transfer: a complex calibrated piece of equipment might need to be moved between two locations. In the new location, it does not work as well as in the original location, requiring renewed calibration. Ideally, the latter should be informed by the calibration that was performed in the first location.

• Cell culture media: finding growth media for cells is often done in identical parameter spaces. However, if a new type of cell is used, the corresponding campaign usually starts from scratch. If there are similar cell types (e.g. liver cells, but from different mammals), information transfer of pre-existing source campaigns should be possible.

• Vendor change: in case a material needs to be obtained from a replacement vendor due to unavailability, there can be severe implications even though the materials are supposedly equivalent. We can still assume some degree of similarity between the campaign associated with material from the old vendor and the campaign using the new material. This situation can be encountered in fields such as the semiconductor industry, where complex materials are utilized and even transportation can have an influence.

The examples above are comparable in that they describe several tasks, i.e. represented by the source and target campaigns and their respective data sets, which are very similar but not exactly identical. Due to their differences, a naive combination of data without any further consideration is clearly suboptimal.

The approach to utilize data from similar but not identical campaigns can be called transfer learning in the BO context (TL-BO), borrowing from the deep learning literature where transfer learning describes the reutilization of models originally trained for other tasks. It is closely related to multi-fidelity BO (MF-BO), where target measurements can be done at different levels of complexity and cost, such as the simulation of a property versus an actual experiment.^60,61 While the underlying surrogate-based treatments in MF-BO and TL-BO are extremely similar, they differ mainly in their usage. In MF-BO, the user is interested in adding results from different fidelities and also being recommended the optimal fidelity to measure in the next iteration. In TL-BO, the fidelities can be seen as different tasks, however, the user in practice will always restrict the recommendation to one (or few) tasks corresponding to the currently active campaign, i.e. not switch between fidelities during a campaign. For further information about the terminology, the interested reader is referred to our user guide.⁶²

In case the differences between campaigns are known and measured (e.g. the temperature used in different labs for exactly the same reaction condition optimization), the data can be mixed by adding explicit parameters accounting for them. The target campaign would then be restricted to run only at the currently relevant temperature, but data from other campaigns (i.e. other temperatures) could still be ingested.

However, in general, the exact parameters that distinguish the tasks are not known. Moreover, even if they were known, they are typically not measured. It might also be the case that there are so many task-specific parameters that explicitly modeling them would render the entire problem infeasible for BO. These situations are, for instance, encountered for the cell culture media example, where the exact differences between cell types are not easy to enumerate.

Consequently, it is attractive to enable the TL-BO approach via implicit modeling of the differences between tasks. For this, we follow the ansatz proposed by Bonilla et al.,⁶³ which allows to abstract differences between any two tasks into a single number – their inter-task covariance. For a GP model, this is achieved by augmenting the kernel used for regular parameters with an explicit index kernel component,

k_TL(x,x̂,t,t̂) = k_GP(x,x̂)·k_index(t,t̂) (1)

where k_TL is the overall pair-wise covariance kernel of the GP in the TL-BO case, k_GP(x,x̂) is the standard kernel used for the non-task parameters (vectors x for the first point and x̂ for the second), and k_index is the kernel for the task parameter (t for the first point and t̂ for the second). Alternatives to this model-based approach to TL-BO exist,⁶⁴ but are not investigated further here.

Note that t is a regular categorical parameter with integer encoding – it just gets special treatment in the model. Within BayBE, users can also provide their own models, but the treatment of task parameters is highly dependent on the architecture and might require a different approach to enable TL-BO. k_index can be represented as a simple covariance matrix capturing the relationships between all possible tasks,

k_index(i,j) = δ_i,jVar(i) + (1 − δ_i,j)Cov(i,j) (2)

where δ is the Kronecker delta, Var(i) is a variance component of data belonging to task i, and Cov(i, j) models the covariance between tasks i and j. Since these matrix elements need to be learned from data, it can be expected that this approach generally performs worse than the explicit modeling mentioned before. However, in practice, it is this implicit ansatz that enables the application of TL-BO in the first place, as explicit modeling is almost always unfeasible for the reasons discussed earlier.

We compare both modeling approaches for TL-BO in Fig. 3. For demonstration, we choose the direct arylation reaction from Section 3.1. Since there were three explicit temperatures, we can act like these are results from three different labs, which performed the otherwise identical experiments. While this is a constructed example, it is not unreasonable that such situations arise in the real world, as mismatches in settings and calibrations are likely one major cause of differences between different campaigns on an otherwise identical task. As a target campaign, we choose the middle temperature and assume that the yield for this setting is to be maximized. The data from lower/higher temperatures have a Pearson correlation of 0.88/0.91 to the middle temperature, respectively. Our setup means that there are twice as many source data points as parameter combinations in the target campaign. This allows us to sub-sample different amounts of the source data (corresponding to different color hues in Fig. 3), which further enables us to assess how many source data points are needed to positively affect the target campaign.

Fig. 3 Assessment of transfer learning: We optimize the reaction data from Shields et al.¹⁵ for high yield, split into three sub-sets based on the temperature (90, 105, and 120 °C). The optimization was done for the middle temperature (referred to as target data or campaign), treating the data from the lower/higher temperature as source data. This mimics a situation where a lab gets auxiliary data on a supposedly identical task with hidden parameters (known to be the temperature for this example) being slightly different. The left panel models this via an explicit numerical parameter for the temperature, while the right panel models this via the transfer learning procedure described in the text. Colors visualize different amounts of source data ingested into the target campaign before starting it. Note that the two models employ different kernels and hence have different performance even when no source data are used (blue curves). This plot was generated from 100 Monte Carlo runs, which also randomized the source data sampling. Shaded areas indicate 95% confidence intervals.

In essence, we find the expected behavior, in that the implicitly modeled transfer learning (right panel) performs slightly worse than the transfer via explicit parameter (left panel). However, the performance improvement over no transfer learning (blue curves corresponding to no ingested source data) is significant in both approaches. The optimization curves are particularly improved in the early phase, which is of immense practical value. It is also remarkable that even for small amount of source data utilized (green and orange curves) there is already a substantial improvement. For the task parameter variant, we can also see that there is a sort of saturation, as curves belonging to larger amounts of source data ingested (red, purple and brown) differ less from each other. Indeed, we have indications that the fit procedure for the surrogate model has a strong influence on the results and seems to be more challenging for the task parameter case. Preliminary results from our ongoing work on more robust settings indicate that an even better TL-BO performance is possible.

This study was repeated for all other combinations of temperatures as well as concentrations (which also had three distinct possible values) and the outcome can be found in the ESI.† The very same model-based approach to TL-BO has also been successfully tested for chemical reactions by Taylor et al.⁶⁵ These results suggest that TL-BO can be a game changer in the industry. There are countless and frequent optimization campaigns for materials or chemistry that have been run in similar but not identical contexts in the past. Therefore, TL-BO can be the key that truly unlocks the data lakes many companies have been building in the last decades.

3.4 Automatic campaign-stopping

Budget and time considerations are important for experimental campaigns and can even mean that suboptimal results are preferred if achieved quickly. The reduction of cost and time is one of the main reasons to use BO in the first place. However, one major downside of the vanilla BO approach is that it requires a fixed search space to be defined before optimization can begin. If no acceptable target value lies within this space, the campaign is effectively futile. One solution to this is to make the search space dynamically self-adjusting, which can be tricky implementation-wise and comes with its own challenges.^66,67 A much simpler remedy for this situation is stopping unpromising campaigns based on a criterion that relates to the probability of improving the best result any further.

We tested this behavior on the same reaction data as in Section 3.1, where we removed candidates with yields above 80% to make the best point of stopping non-obvious. This is not strictly required to demonstrate the effectiveness of the algorithm, but more closely resembles a situation encountered in the lab: since 100% yield is the physical limit, we would trivially know to stop there without any data-driven considerations. By contrast, if an optimization curve seemingly flattens out before the physical limit, knowing when to stop is not trivial but very useful from a budget perspective. To identify the stopping point, we calculate the expected improvement (EI) acquisition values and stop the campaign when fewer than 50% of remaining candidates have an EI of at least 0.5% yield. We anticipate that there are many more viable stopping criteria to achieve something similar and encourage further study.

As demonstrated in Fig. 4, this simple EI criterion already works surprisingly well: all five interrupted campaigns have reached the best accessible target value of 80%, successfully realizing that there is nothing to gain from further experimentation. The plot also shows a trajectory that has a near-optimal yield right from the start – this might also happen in practice and highlights the importance of deciding how long to keep looking for further improvements.

Fig. 4 Automatic campaign stopping: Average trajectory of uninterrupted optimization campaigns (blue) versus five campaigns that were interrupted when the EI-based stopping criterion was hit. This test was performed on the same reaction data as in Fig. 1, but with candidates that achieved a yield above 80% removed from the search space to make the best point of stopping non-obvious. The transparent circles indicate when a campaign was stopped. The shaded areas indicate 95% confidence intervals from 20 MC runs.

4 Conclusions

We introduced the Bayesian Back End as all-in-one-place computational toolbox for real-world BO. Through four case studies on some of its features, we demonstrated how additions to the vanilla BO approach can have a tremendous impact on experimental campaigns. We consider chemical and custom encodings an easy improvement over the prevalent OHE, as well as a binding element allowing collaboration between computational, experimental, and data scientific contributors. We believe it is always worth spending more time on the encoding of categorical variables than is currently appreciated, and encourage readers to utilize custom encodings that offer the prospect of better BO campaigns for any conceivable categorical parameter. Similarly, automatic criteria applied to judge a campaign's current status, including its chance of continued success or underlying model fit qualities, are promising. Further work is currently underway to provide more features in this direction.

Transfer learning in the context of BO was highlighted and studied for a chemical reaction. We reiterate the tremendous impact TL-BO has for large corporations in possession of data for many similar campaigns, or in shared data environments such as collaborative consortia. We found a strong speedup of the optimization campaigns when combining data from similar but not identical campaigns via TL-BO, which allows transfer learning in many situations where explicit modeling of parameters that distinguishes tasks is practically not possible. The benefits beyond cost-savings are reduced go-to-market times, which is critical in today's increasing development pace and fast moving markets.

Looking forward, we anticipate many more developments in the thriving field around real-world BO, in both the technical and adoption aspects. For instance, how to robustly incorporate human knowledge into the BO process is an ongoing field of research^68–70 that we are excited to include in the future, also for reasons of lowering adoption barriers of experimentalists running traditional campaigns.

Data availability

All technical functions discussed in this work are consolidated in the Python package , available open-source under an Apache-2.0 license on GitHub at https://github.com/emdgroup/baybe. A Zenodo snapshot of the baybe repository of the version used for the manuscript (0.12.2) is available at https://doi.org/10.5281/zenodo.15204129. The code and data needed to create the backtests and figures is also available on GitHub https://github.com/emdgroup/baybe-paper and via a Zenodo snapshot https://doi.org/10.5281/zenodo.15204164.

Author contributions

MF, AŠ and AVH are the core developers of the Python package utilized in this work. MF created the code and plots for Fig. 1, 2 and 4. MM created the code and plots for Fig. 3. RR contributed to the code and plots for Fig. 4. AŠ and AVH contributed to ideating all shown examples. KH and FL contributed to the development of the software and methodology. MW, WH and JGB supervised the project. MF wrote the original manuscript draft. All authors contributed to the draft review and editing.

Conflicts of interest

During the creation of the results, all authors were employed by Merck KGaA, Darmstadt, Germany or one of its subsidiaries. Merck KGaA, Darmstadt, Germany is a partner of the Acceleration Consortium. JGB is founder of Quastify GmbH.

Acknowledgements

We thank Alex Lee, Di Jin, Daniel Weber, Alexander Wieczorek, Julie Fang, Julian Streibel, Roya Javadi, Arkadiusz Donajski, Catalin Gheorghe Stetco and Lisa Neuner for contributing to the BayBE ecosystem. We are grateful to Laura Matz, Philipp Harbach and Subbu Iyer for their support and sponsoring of this project. We acknowledge the support of the Acceleration consortium, in particular Sterling G. Baird, Padraic Foley and Alán Aspuru-Guzik. We also thank Hergen Schultze, Behrang Shafei, Dominik Linzner and Jakob Zeitler for fruitful discussions.

Notes and references

1. A. Sertkaya, T. Beleche, A. Jessup and B. D. Sommers, JAMA Netw. Open, 2024, 7, e2415445.
2. P. Bannigan, R. J. Hickman, A. Aspuru-Guzik and C. Allen, Adv. Healthcare Mater., 2024, 13, 2401312.
3. Research and Development in the Pharmaceutical Industry, Congressional Budget Office, https://www.cbo.gov/publication/57025, 2021.
4. J. Antony, Design of experiments for engineers and scientists, Elsevier, 2023.
5. P. F. de Aguiar, B. Bourguignon, M. Khots, D. Massart and R. Phan-Than-Luu, Chemom. Intell. Lab. Syst., 1995, 30, 199–210.
6. N. Costa, Total Qual. Manag., 2019, 31, 772–789.
7. M. Tanco, E. Viles and L. Pozueta, Advances in electrical engineering and computational science, 2009, 611–621.
8. R. Macarron, M. N. Banks, D. Bojanic, D. J. Burns, D. A. Cirovic, T. Garyantes, D. V. Green, R. P. Hertzberg, W. P. Janzen and J. W. Paslay, et al., Nat. Rev. Drug Discov., 2011, 10, 188–195.
9. V. Blay, B. Tolani, S. P. Ho and M. R. Arkin, Drug Discov. Today, 2020, 25, 1807–1821.
10. J. Mockus, Bayesian Approach to Global Optimization: Theory and Applications, Springer Netherlands, Dordrecht, 1989, vol. 37.
11. R. Garnett, Bayesian Optimization, Cambridge University Press, Cambridge, United Kingdom, 2023.
12. S. Dong, P. Wang and K. Abbas, Comput. Sci. Rev., 2021, 40, 100379.
13. R. K. Raman, Y. Dewang and J. Raghuwanshi, International Journal of LNCT, 2018, 2, 137–143.
14. A. M. Teale, T. Helgaker, A. Savin, C. Adamo, B. Aradi, A. V. Arbuznikov, P. W. Ayers, E. J. Baerends, V. Barone, P. Calaminici, E. Cancès, E. A. Carter, P. K. Chattaraj, H. Chermette, I. Ciofini, T. D. Crawford, F. D. Proft, J. F. Dobson, C. Draxl, T. Frauenheim, E. Fromager, P. Fuentealba, L. Gagliardi, G. Galli, J. Gao, P. Geerlings, N. Gidopoulos, P. M. W. Gill, P. Gori-Giorgi, A. Görling, T. Gould, S. Grimme, O. Gritsenko, H. J. A. Jensen, E. R. Johnson, R. O. Jones, M. Kaupp, A. M. Köster, L. Kronik, A. I. Krylov, S. Kvaal, A. Laestadius, M. Levy, M. Lewin, S. Liu, P.-F. Loos, N. T. Maitra, F. Neese, J. P. Perdew, K. Pernal, P. Pernot, P. Piecuch, E. Rebolini, L. Reining, P. Romaniello, A. Ruzsinszky, D. R. Salahub, M. Scheffler, P. Schwerdtfeger, V. N. Staroverov, J. Sun, E. Tellgren, D. J. Tozer, S. B. Trickey, C. A. Ullrich, A. Vela, G. Vignale, T. A. Wesolowski, X. Xu and W. Yang, Phys. Chem. Chem. Phys., 2022, 24, 28700–28781.
15. B. J. Shields, J. Stevens, J. Li, M. Parasram, F. Damani, J. I. M. Alvarado, J. M. Janey, R. P. Adams and A. G. Doyle, Nature, 2021, 590, 89–96.
16. J. Guo, B. Ranković and P. Schwaller, Chimia, 2023, 77, 31–38.
17. H. C. Herbol, W. Hu, P. Frazier, P. Clancy and M. Poloczek, npj Comput. Mater., 2018, 4, 51.
18. E. Saleh, A. Tarawneh, M. Naser, M. Abedi and G. Almasabha, Constr. Build. Mater., 2022, 330, 127270.
19. T. Rosenkranz, M. von der Haar, A. Šošić, J. G. Brandenburg and N. Banik, Digital selection of viscosity reducing excipients for protein formulations, US pat. 18/559906, 2024.
20. R. Sedgwick, J. P. Goertz, M. M. Stevens, R. Misener and M. van der Wilk, Biotechnol. Bioeng., 2025, 122, 189–210.
21. L. Schaufelberger, J. T. Blaskovits, R. Laplaza, K. Jorner and C. Corminboeuf, Angew. Chem., Int. Ed., 2025, 64, e202415056.
22. R.-R. Griffiths and J. M. Hernández-Lobato, Chem. Sci., 2020, 11, 577–586.
23. X. Li, Y. Che, L. Chen, T. Liu, K. Wang, L. Liu, H. Yang, E. O. Pyzer-Knapp and A. I. Cooper, Nat. Chem., 2024, 1–9.
24. F. Strieth-Kalthoff, H. Hao, V. Rathore, J. Derasp, T. Gaudin, N. H. Angello, M. Seifrid, E. Trushina, M. Guy and J. Liu, et al., Science, 2024, 384, eadk9227.
25. BayBE – A Bayesian Back End for Design of Experiments, https://emdgroup.github.io/baybe/stable/.
26. BayBE user guide, https://emdgroup.github.io/baybe/stable/userguide/userguide.html.
27. J. A. G. Torres, S. H. Lau, P. Anchuri, J. M. Stevens, J. E. Tabora, J. Li, A. Borovika, R. P. Adams and A. G. Doyle, J. Am. Chem. Soc., 2022, 144, 19999–20007.
28. R. J. Hickman, M. Sim, S. Pablo-García, G. Tom, I. Woolhouse, H. Hao, Z. Bao, P. Bannigan, C. Allen and M. Aldeghi, et al., Digital Discovery, 2025, 4(4), 1006–1029.
29. J. P. Dürholt, T. S. Asche, J. Kleinekorte, G. Mancino-Ball, B. Schiller, S. Sung, J. Keupp, A. Osburg, T. Boyne, R. Misener, R. Eldred, W. S. Costa, C. Kappatou, R. M. Lee, D. Linzner, D. Walz, N. Wulkow and B. Shafei, BoFire: Bayesian Optimization Framework Intended for Real Experiments, 2024, https://arxiv.org/abs/2408.05040.
30. M. Balandat, B. Karrer, D. Jiang, S. Daulton, B. Letham, A. G. Wilson and E. Bakshy, Adv. Neural Inf. Process Syst., 2020, 21524–21538.
31. K. Kandasamy, K. R. Vysyaraju, W. Neiswanger, B. Paria, C. R. Collins, J. Schneider, B. Poczos and E. P. Xing, J. Mach. Learn. Res., 2020, 21, 1–27.
32. S. G. Baird, A. R. Falkowski and T. D. Sparks, arXiv, 2025, preprint, arXiv:2502.06815,  DOI:10.48550/arXiv.2502.06815.
33. A. M. Mroz, P. N. Toka, E. A. del Río Chanona and K. E. Jelfs, Faraday Discuss., 2025, 256, 221–234.
34. S. Bertelsen, S. Carlsen, S. Furbo, M. B. Nielsen, A. Obdrup and R. Taaning, J. Chem. Inf. Model., 2025, 65(4), 1702–1707.
35. D. P. Gutierrez, L. M. Folkmann, H. Tribukait and L. M. Roch, Chimia, 2023, 77, 7–16.
36. D. Gala, G. Becker, K. Kaul, D. Marcelo, A. Hegde, S. Moisselin, C. Fuda, S. Doraiswamy, V. Verma and X. Wu, SPE Annual Technical Conference and Exhibition?, 2023, p. D032S023R002.
37. G. J. Dovonon and J. Zeitler, arXiv, 2023, preprint, arXiv:2312.12633,  DOI:10.48550/arXiv.2312.12633.
38. M. Eskandari, L. Puiman and J. Zeitler, arXiv, 2023, preprint, arXiv:2311.05776,  DOI:10.48550/arXiv.2311.05776.
39. B. Folie and M. Hutchinson, Mach. Learn.: Sci. Technol., 2023, 4, 015022.
40. P. I. Frazier, A Tutorial on Bayesian Optimization, 2018.
41. D. R. Jones, M. Schonlau and W. J. Welch, J. Global Optim., 1998, 13, 455–492.
42. S. Ament, S. Daulton, D. Eriksson, M. Balandat and E. Bakshy, Adv. Neural Inf. Process Syst., 2023, 36, 20577–20612.
43. S. Seo, M. Wallat, T. Graepel and K. Obermayer, Proceedings of the IEEE-INNS-ENNS International Joint Conference on Neural Networks. IJCNN 2000. Neural Computing: New Challenges and Perspectives for the New Millennium, 2000, vol. 3, pp. 241–246.
44. F. Hase, L. M. Roch, C. Kreisbeck and A. Aspuru-Guzik, ACS Cent. Sci., 2018, 4, 1134–1145.
45. V. Beiranvand, W. Hare and Y. Lucet, Optim. Eng., 2017, 18, 815–848.
46. P. Christoffersen, Encyclopedia of Quantitative Finance, John Wiley & Sons, Ltd, 2010.
47. BayBE user guide on backtest simulations, https://emdgroup.github.io/baybe/paper/simulation.
48. E. C. Garrido-Merchán and D. Hernández-Lobato, Neurocomputing, 2020, 380, 20–35.
49. J. Adamczyk and P. Ludynia, SoftwareX, 2024, 28, 101944.
50. H. Moriwaki, Y.-S. Tian, N. Kawashita and T. Takagi, J. Cheminform., 2018, 10, 4.
51. mordred-community – A community-maintained version of the mordred molecular descriptor calculator, https://github.com/JacksonBurns/mordred-community.
52. RDKit: Open-source Cheminformatics, 2024.
53. N. Aldulaijan, J. A. Marsden, J. A. Manson and A. D. Clayton, React. Chem. Eng., 2024, 9, 308–316.
54. D. Rogers and M. Hahn, J. Chem. Inf. Model., 2010, 50, 742–754.
55. T. Akiba, S. Sano, T. Yanase, T. Ohta and M. Koyama, Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2019.
56. S. Watanabe, arXiv, 2023, preprint, arXiv:2304.11127.
57. R.-R. Griffiths, L. Klarner, H. Moss, A. Ravuri, S. Truong, Y. Du, S. Stanton, G. Tom, B. Rankovic and A. Jamasb, et al., Adv. Neural Inf. Process Syst., 2024, 36, 76923–76946.
58. R. Xie, A. R. Weisen, Y. Lee, M. A. Aplan, A. M. Fenton, A. E. Masucci, F. Kempe, M. Sommer, C. W. Pester and R. H. Colby, et al., Nat. Commun., 2020, 11, 893.
59. R. Kelley Pace and R. Barry, Stat. Probab. Lett., 1997, 33, 291–297.
60. J. Wu, S. Toscano-Palmerin, P. I. Frazier and A. G. Wilson, Uncertainty in Artificial Intelligence, 2020, pp. 788–798.
61. E. Judge, M. Azzouzi, A. M. Mroz, A. del Rio Chanona and K. E. Jelfs, Applying Multi-Fidelity Bayesian Optimization in Chemistry: Open Challenges and Major Considerations, 2024, https://arxiv.org/abs/2409.07190.
62. BayBE user guide on transfer learning, https://emdgroup.github.io/baybe/paper/transfer_learning.
63. E. V. Bonilla, K. Chai and C. Williams, Adv. Neural Inf. Process Syst., 2007 , https://papers.nips.cc/paper_files/paper/2007/hash/66368270ffd51418ec58bd793f2d9b1b-Abstract.html.
64. T. Bai, Y. Li, Y. Shen, X. Zhang, W. Zhang and B. Cui, arXiv, 2023, preprint, arXiv:2302.05927,  DOI:10.48550/arXiv.2302.05927.
65. C. J. Taylor, K. C. Felton, D. Wigh, M. I. Jeraal, R. Grainger, G. Chessari, C. N. Johnson and A. A. Lapkin, ACS Cent. Sci., 2023, 9, 957–968.
66. H. Ha, S. Rana, S. Gupta, T. Nguyen, H. Tran-The and S. Venkatesh, Adv. Neural Inf. Process Syst., 2019 , https://papers.nips.cc/paper_files/paper/2019/hash/ccf0304d099baecfbe7ff6844e1f6d91-Abstract.html.
67. L. Papenmeier, L. Nardi and M. Poloczek, Adv. Neural Inf. Process Syst., 2022, 11586–11601.
68. A. I. Cooper, P. Courtney, K. Darvish, M. Eckhoff, H. Fakhruldeen, A. Gabrielli, A. Garg, S. Haddadin, K. Harada, J. Hein et al., arXiv, 2025, preprint, arXiv:2501.06847,  DOI:10.48550/arXiv.2501.06847.
69. R. Guay-Hottin, L. Kardassevitch, H. Pham, G. Lajoie and M. Bonizzato, Knowledge-Based Systems, 2025, 113039.
70. Q. Feng, Z. J. Lin, Y. Zhang, B. Letham, J. Markovic-Voronov, R.-R. Griffiths, P. I. Frazier and E. Bakshy, NeurIPS 2024 Workshop on Bayesian Decision-making and Uncertainty, 2024.

---

Footnotes

† Electronic supplementary information (ESI) available: Correlation analysis and further results for the transfer learning study. See DOI: https://doi.org/10.1039/d5dd00050e

‡ These authors contributed equally to this work.

---