BoTier: multi-objective Bayesian optimization with tiered objective structures

Abstract

Scientific optimization problems are usually concerned with balancing multiple competing objectives that express preferences over both the outcomes of an experiment (e.g. maximize reaction yield) and the corresponding input parameters (e.g. minimize the use of an expensive reagent). In practice, operational and economic considerations often establish a hierarchy of these objectives, which must be reflected in algorithms for sample-efficient experiment planning. Herein, we introduce BoTier, a software library that can flexibly represent a hierarchy of preferences over experiment outcomes and input parameters. We provide systematic benchmarks on synthetic and real-life surfaces, demonstrating the robust applicability of BoTier across a number of use cases. Importantly, BoTier is implemented in an auto-differentiable fashion, enabling seamless integration with the BoTorch library, thereby facilitating adoption by the scientific community.

---

1 Introduction

Multi-objective optimization (MOO) – the task of finding a global optimum that simultaneously satisifies a set of optimization criteria – is a common problem in many fields of science and engineering.^1–5 As an example, a new drug needs to simultaneously optimize target activity, side effects, bioavailability and metabolic profile; similarly, a new material must meet several demands relating to properties, stability or synthesizability. Usually, such objectives are conflicting, so any optimal solution represents a trade-off between them. In many scenarios, finding these optimal solutions is cumbersome, especially in a setting in which experimental evaluations are expensive – creating a need for efficient experiment planning algorithms. Over the past decade, Bayesian Optimization (BO) has become the de-facto choice for sample-efficient iterative optimization of black-box functions,^6–8 and has found particular popularity in the context of autonomous experimentation with self-driving laboratories (SDLs).^9,10

In scientific optimization problems, the primary objective(s) are generally derived from the outcome of an experiment. In reaction optimization (Fig. 1a), for example, this could be the yield of the desired product, or the quantity of an undesired side product. At the same time, secondary optimization objectives can include preferences over input parameters, such as minimizing the loading of an expensive catalyst, or minimizing the reaction temperature to lower energy consumption.^11–13 It is worth noting that such considerations imply that certain objectives are prioritized over others, establishing a known hierarchy.^14–16

Fig. 1 MOO with preferences over experiment inputs and outputs. (A) Example from chemical reaction optimization. (B) Optimization with two conflicting objectives. (C) In multi-objective BO, objectives are often scalarized into a single score, which is used as the optimization goal. This can be done in under implicit (“score than predict”, left) or explicit (“predict then score”, right) objective modeling.

In MOO, a solution in which further improving one objective is detrimental to at least one other objective is called a Pareto optimum,¹⁷ and the set of all Pareto optima is referred to as the Pareto front (Fig. 1b). In an ideal scenario, knowing the entire Pareto front would enable optimal post-hoc decisions, accounting for all inter-objective trade-offs. Accordingly, the past decades have seen significant advances in hypervolume-based approaches to map the Pareto front.^18,19 However, Pareto-oriented optimization may spend significant experimental resources on mapping regions of the Pareto front that are not of interest to the researcher (Fig. 1b). Therefore, when relative objective importances are known, scalarizing multiple objectives into a single score can help guide the optimization to desired regions of the Pareto front.^1,13,20

In practice, such scalar scores are often used in a manner that can be described as implicit objective modeling (Fig. 1c left). Here, for each observation, the multiple objective values are first combined into a single scalar score, and standard single-objective BO is then employed to optimize this score over the search space.^1,20 While straightforward, this aggregate-then-predict approach has two main drawbacks: (a) when input-based objectives are included, the relationship between score and input parameters is provided only implicitly to the surrogate, and must therefore be “re-learned”. For example, in the reaction optimization scenario shown in Fig. 1a, the surrogate would have to learn how catalyst loading and temperature influence the final score, even though this relation is known a-priori in analytical form. This redundancy is likely to reduce optimization efficiency. (b) The scalar score itself is artificial and may lack physical meaning, which can hinder the design of effective priors.^21,22

Therefore, scalarization would ideally be employed in a predict-then-aggregate manner (Fig. 1c), which, requires manipulating multiple posterior distributions, therefore complicating practical implementation. In this context, Frazier and co-workers introduced the concept of composite objective functions,²³ where a real-valued function is applied only after building surrogate models, and demonstrated that their posteriors can be approximated by Monte-Carlo integration. When applied to scalarization in MOO, we refer to this strategy as explicit objective modeling.

Combining the principle of hierarchical MOO with the idea of explicit objective modeling, we herein introduce BoTier as a flexible framework for MOO which enables tiered preferences over both experiment inputs and outputs. The main contributions of this paper include (1) the formulation of an improved, auto-differentiable hierarchical composite score; (2) its open-source implementation as an extension of the BoTorch library; and (3) systematic benchmarks on analytical surfaces and real-world chemistry examples, showcasing how BoTier can efficiently navigate MOO problems in the context of scientific optimization.

2 Formulation of BoTier

2.1 Multi-objective optimization

In MOO, the goal is to optimize several often conflicting objectives simultaneously. Formally, each set of input parameters x ∈ X is associated with N objective values {ψ_i(x)}_i=1^N. Here, x represents a vector of input parameters, X is the domain from which these parameters are chosen, and each ψ_i(x) denotes the i-th objective evaluated at x – which can come from either an experimental evaluation at x, or from a user-defined preference over x.

2.2 Scalarization functions

Given a set of N objectives {ψ_i}_i=1^N, a scalarization function φ: [Doublestruck R]^N → [Doublestruck R] combines these objective values into a single score that reflects user preferences, and serves as the eventual optimization goal. In the context of hierarchical optimization, this was pioneered by Aspuru-Guzik and co-workers, who introduced Chimera χ as an additive scalarization function.²⁴ In eqn (1), χ is shown for the case where each objective is to be maximized. We assume that the objectives are sorted by their hierarchy, i.e. ψ₁ is the most important, ψ₂ is the second-most important, etc. Each objective has a user-defined “satisfaction threshold” t_i. The component-wise formulation of χ then ensures that the contribution of objective ψ_i to the score is only considered if all superordinate objectives {ψ_j}_j<i meet their respective thresholds. Additionally, the contribution of each objective is shifted by the highest observed values of all superordinate objectives to ensure continuity of χ. If all objectives meet their thresholds, the primary objective is used for optimization (third summand in eqn (1)).Here, H(x) denotes the Heaviside step function.

Although Chimera is widely used for MOO, its current formulation is limited to implicit objective modeling scenarios, where χ is computed for all K observations, {(ψ₁(x_k), ψ₂(x_k),…,ψ_N(x_k))}_k=1^K. Since the value of χ for a single observation depends on all other observations considered at the same time, batch-wise evaluation of χ is not possible in its current form. Moreover, its implementation is not auto-differentiable, limiting its usefulness as a composite score for BO.

2.3 Formulation of BoTier

We address these limitations by proposing an alternative hierarchical scalarization function designed as a composite score for explicit objective modeling. Without loss of generality, we assume a maximization problem for each objective, and define

As in Chimera, the product 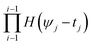ensures that an objective ψ_i contributes to Ξ only after all superordinate objectives {ψ_j}_j<i have met their satisfaction thresholds. When ψ_i is below its threshold t_i, it becomes the limiting objective in that region of parameter space, and min (ψ_i, t_i) returns ψ_i. Otherwise, t_i is added to the score, preserving continuity of Ξ. Empirically, we confirm that this formulation is consistent with the ranking behavior of Chimera (ESI,† section 4). In addition, all ψ_i can be normalized to the range [0, 1] based on expert knowledge. This normalization, albeit optional, places gradients of Ξ on a consistent scale for all x ∈ X.

Our implementation of Ξ employs continuously differentiable approximations for both min (x₁, x₂) and H(x) (see (ESI),† section 1), enabling the automatic propagation of gradients through Ξ(x) using the PyTorch framework. This approach supports gradient-based techniques for optimizing any acquisition function computed on top of Ξ, ensuring robust optimization even in high-dimensional spaces. Therefore, BoTier integrates seamlessly with the widespread BoTorch ecosystem for BO, and can be flexibly combined with different single- or multi-task surrogate models, and acquisition functions. When applied in the context of explicit objective modeling, Ξ can be evaluated over both experiment inputs and model outputs (i.e., posterior distributions) using Monte-Carlo integration (see ESI,† section 1.3 for details).^25,26 We provide BoTier as a lightweight Python library, which can be installed from the Python Package Index (PyPI).

3 Experimental use cases

We evaluated the applicability and limitations of BoTier through benchmark studies on analytical test surfaces and real-life optimization problems from chemistry and materials science. Our investigations focused on two key algorithmic choices and their influence on sample efficiency in multi-objective BO: (a) the use of BoTier compared to other MOO strategies; and (b) the application of explicit compared to implicit objective modeling.

All empirical optimization runs were performed using BO workflows implemented in BoTorch. Unless otherwise noted, we employed a Gaussian Process (GP) surrogate model with the Expected Improvement (EI) acquisition function and a batch size of 1. Each run was repeated 50 times from different random seed points to ensure statistical significance. Sobol sampling was used as a model-free baseline. The complete code for reproducing all experiments is available on our GitHub repository.

First, we evaluated several MOO strategies on four analytical multiobjective surfaces from the BoTorch library. These multidimensional (2—10D) benchmark functions typically exhibit non-linear, non-convex behavior within a bounded search space. To simulate a scenario with both input- and output-dependent objectives, each of these two-objective problems was augmented by a third objective that depends solely on the function inputs (see ESI†). Fig. 2 summarizes the general trends observed across all surfaces; a detailed, problem-specific comparison between the algorithms is provided in the ESI.† Across all tasks, we found that BoTier, when used in an implicit objective modeling scenario, already led to faster convergence toward the optimum value of Ξ compared to Chimera (Fig. 2, top row). Likewise, the number of experiments needed to find conditions that satisfy the first objective, the first two objectives, or all three objectives, was consistently lower (Fig. 2 bottom row). In every case, using BoTier under explicit objective modeling further accelerated optimization. We initially attributed this improvement to the surrogate model no longer needing to “re-discover” known correlations between inputs and objectives. Surprisingly, this finding persisted for the original two-objective problems in which all objectives depend solely on experiment outputs (see ESI,† Section 2.2). Although a systematic analysis is beyond the scope of this study, these findings suggest that learning two independent distributions is seemingly simpler than capturing a more complex joint distribution, as required in the case of implicit objective modeling. In fact, multi-output GP surrogates, that try to capture correlations between objectives, did not improve optimization performance compared to single-task GP models in most cases (Fig. S12 and S17†).

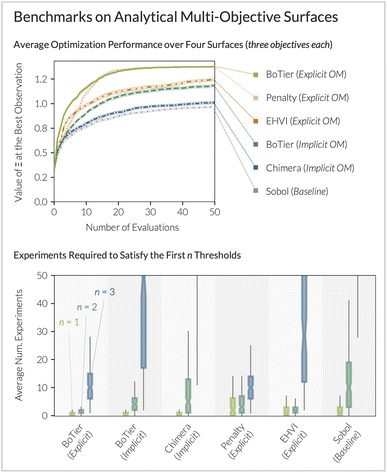Fig. 2 Benchmarks of MOO strategies on four analytical surfaces, each extended by an input-dependent objective (see ESI† for details). Top panel: best observed value of Ξ as a function of the number of experimental evaluations. All statistics were calculated on 50 independent campaigns on each surface. Intervals are plotted as the standard error. Bottom panel: Number of experiments required to satisfy the first objective (n = 1, green); the first two objectives (n = 2, dark green); or all three objectives (n = 3, blue).

Moreover, we evaluated BoTier against a threshold-based, non-hierarchical composite score: a penalty-based scalarization introduced by deMello and co-workers.²⁷ The widespread Pareto-oriented Expected Hypervolume Improvement (EHVI) acquisition function was tested as a reference.²⁸ While optimization behavior varied by problem (see ESI,† Sections 2.2 and 2.3), several trends emerged: Compared to BoTier, the penalty-based scoring often takes more evaluations to satisfy the early objectives in the hierarchy. The identification of points that satisfy all objective criteria is achieved at a comparable experimental budget, highlighting the general efficiency of explicit objective modeling. As expected, EHVI, lacking preferences for any “region” of the Pareto front, required substantially more experiments to identify Pareto-optimal points that satisfy all criteria (see Fig. 2 and ESI†). These benchmarks confirm the feasibility of BoTier's formulation and its effectiveness as a composite score in explicit objective modeling.

Encouraged by these results, we tested BoTier on chemical reaction optimization scenarios which are highly relevant to self-driving laboratories. Following the emulator strategy described by Häse et al.,²⁹ first, a supervised ML model was trained on an external, labeled dataset. The resulting model was then used as an emulator, substituting for actual wet-lab experiments, and could be queried with any set of input parameters proposed during a BO campaign. Specifically, we investigated the following problems: condition optimization in a heterocyclic Suzuki–Miyaura coupling,²⁹ an enzymatic alkoxylation reaction,²⁹ a synthesis of silver nanoparticles monitored via spectrophotometry,³⁰ and an amine monoalkylation.³¹ All optimization runs were performed using a GP surrogate with the EI acquisition function, running 50 iterations from different random seed points, as described above.

Fig. 3b illustrates the Suzuki–Miyaura coupling example, which is optimized over reagent stoichiometry, catalyst loading, base loading and reaction temperature. Process chemistry considerations define a three-tier objective hierarchy, consisting of (1) maximized product yield, (2) minimized cost of all reactants and reagents, and (3) minimized reaction temperature. Benchmarking different MOO algorithms on this problem shows that BoTier is the only strategy capable of identifying reaction conditions that simultaneously meet all thresholds. By contrast, a statistical, model-free Sobol sampling baseline (see ESI† for further details) rapidly found high-yielding conditions, but failed to keep cost and temperature low. Similarly, neither Chimera with implicit objective modeling nor the evaluation of the full Pareto front (EHVI) identified satisfactory conditions in the given budget.

Fig. 3 Evaluation of different MOO strategies for chemical reaction optimization. (A) Optimization performance on different emulated reaction optimization problems. Number of experiments required to satisfy the first n objectives. (B) Case study of a Suzuki–Miyaura coupling. Plots show the median objective values across 50 independent runs, with shaded areas indicating the 20th and 80th percentiles. See ESI† for further details.

Similar trends were observed for the other emulated problems (Fig. 3a). Notably, we observed cases in which BoTier and EHVI satisfy the criteria at similar rates (Fig. 3a, panels 2 and 4); which occurred when the objectives did not strongly compete (see Fig. S21 and S23† for further details). Overall, if a hierarchy between objectives exists, BoTier proved to be a robust scalarization function which, across all cases investigated, never performed worse, but often notably better than existing MOO methods – particularly when used as a composite score in explicit objective modeling.

4 Outlook and perspectives

We have introduced BoTier as a flexible composite score for hierarchical multi-objective BO. Based on our benchmark studies, we formulate the following empirical guidelines for MOO:

(1) Use hierarchical objectives when a hierarchy exists. If the objectives, whether input- and output-dependent, are subject to a well-defined priority structure, BoTier offers a robust objective to encode and optimize these preferences. Our benchmarks show that, in these cases, hierarchical methods can more rapidly identify desirable optima than approaches that seek to map the entire Pareto front.

(2) Favor explicit over implicit objective modeling whenever possible. Across all problems studied, explicit objective modeling consistently outperformed implicit objective modeling approaches, often yielding substantial speedups. In no case did an implicit modeling approach prove superior. We foresee that this effect will be even more pronounced when incorporating priors over physically meaningful quantities.

To encourage broader adoption, BoTier is provided as a lightweight, open-source extension to the BoTorch library. Looking ahead, we are exploring its applications in self-driving laboratories, where hierarchical optimization can be especially valuable for balancing complex objectives including materials properties, synthetic feasibility, cost, and sustainability. We anticipate that BoTier will be a valuable addition to the optimization toolbox for autonomous research systems.

Data availability

The software package is available on Github under https://github.com/fsk-lab/botier, and can be obtained from the Python Package Index (PyPI) at https://pypi.org/project/botier. BoTier 1.0.0 was used for all experiments presented in this study. The release, including all code, scripts and datasets, has been archived on Zenodo at the following DOI: https://doi.org/10.5281/zenodo.15305205.

Author contributions

Conceptualization: F. S.-K.; Data Curation: M. H., L. G., F. S.-K.; formal analysis: M. H., L. G., F. S.-K.; funding acquisition: F. S.-K.; investigation: M. H., L. G., F. S.-K.; methodology: M. H., F. S.-K.; project administration: F. S.-K.; resources: F. S.-K.; software: M. H., F. S.-K.; supervision: F. S.-K.; validation: M. H., L. G., F. S.-K.; visualization: M. H., F. S.-K.; writing – original draft: F. S.-K.; writing – review & editing: M. H., L. G., F.S.-K.

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. J. C. Fromer and C. W. Coley, Patterns, 2023, 4, 100678.
2. A. S. Vel, D. Cortés-Borda and F.-X. Felpin, React. Chem. Eng., 2024, 9, 2882–2891.
3. B. J. Shields, J. Stevens, J. Li, M. Parasram, F. Damani, J. I. Martinez Alvardo, J. M. Janey, R. P. Adams and A. G. Doyle, Nature, 2021, 590, 89–96.
4. N. H. Angello, V. Rathore, W. Beker, A. Wołos, E. R. Jira, R. Roszak, T. C. Wu, C. M. Schroeder, A. Aspuru-Guzik, B. A. Grzybowski and M. D. Burke, Science, 2022, 378, 399–405.
5. B. Shi, T. Lookman and D. Xue, Mater. Genome Eng. Adv., 2023, 1, e14.
6. J. Snoek, H. Larochelle and R. P. Adams, Advances in Neural Information Processing Systems, 2012.
7. P. I. Frazier, A Tutorial on Bayesian Optimization, 2018, https://arxiv.org/abs/1807.02811.
8. R. Garnett, Bayesian Optimization, Cambridge University Press, 2023.
9. G. Tom, S. P. Schmid, S. G. Baird, Y. Cao, K. Darvish, H. Hao, S. Lo, S. Pablo-García, E. M. Rajaonson, M. Skreta, N. Yoshikawa, S. Corapi, G. D. Akkoc, F. Strieth-Kalthoff, M. Seifrid and A. Aspuru-Guzik, Chem. Rev., 2024, 124, 9633–9732.
10. F. Strieth-Kalthoff, H. Hao, V. Rathore, J. Derasp, T. Gaudin, N. H. Angello, M. Seifrid, E. Trushina, M. Guy, J. Liu, X. Tang, M. Mamada, W. Wang, T. Tsagaantsooj, C. Lavigne, R. Pollice, T. C. Wu, K. Hotta, L. Bodo, S. Li, M. Haddadnia, A. Wołos, R. Roszak, C. T. Ser, C. Bozal-Ginesta, R. J. Hickman, J. Vestfrid, A. Aguilar-Granda, E. L. Klimareva, R. C. Sigerson, W. Hou, D. Gahler, S. Lach, A. Warzybok, O. Borodin, S. Rohrbach, B. Sanchez-Lengeling, C. Adachi, B. A. Grzybowski, L. Cronin, J. E. Hein, M. D. Burke and A. Aspuru-Guzik, Science, 2024, 384, eadk9227.
11. A. D. Clayton, J. A. Manson, C. J. Taylor, T. W. Chamberlain, B. A. Taylor, G. Clemens and R. A. Bourne, React. Chem. Eng., 2019, 4, 1545–1554.
12. J. A. G. Torres, S. H. Lau, P. Anchuri, J. M. Stevens, J. E. Tabora, J. Li, A. Borovika, R. P. Adams and A. G. Doyle, J. Am. Chem. Soc., 2022, 144, 19999–20007.
13. C. J. Taylor, A. Pomberger, K. C. Felton, R. Grainger, M. Barecka, T. W. Chamberlain, R. A. Bourne, C. N. Johnson and A. A. Lapkin, Chem. Rev., 2023, 123, 3089–3126.
14. F. Waltz, IEEE Trans. Autom. Control, 1967, 12, 179–180.
15. W. Stadler, Multicriteria Optimization in Engineering and in the Sciences, Springer Nature, 1988.
16. M. Rentmeesters, W. Tsai and K.-J. Lin, Proceedings of the 2nd IEEE International Conference on Engineering of Complex Computer Systems, 1996, pp. 76–79.
17. K. Deb, in Multi-objective Optimisation Using Evolutionary Algorithms: An Introduction, ed. L. Wang, A. H. C. Ng and K. Deb, Springer London, London, 2011, pp. 3–34.
18. M. Emmerich, K. Giannakoglou and B. Naujoks, IEEE Trans. Evol. Comput., 2006, 421–439.
19. S. Daulton, M. Balandat and E. Bakshy, Proceedings of the 34th International Conference on Neural Information Processing Systems, 2020.
20. T. Chugh, IEEE Congress on Evolutionary Computation, IEEE Congress of Evolutionary Computation (CEC) pp. pp. 1–8.
21. L. Klarner, T. G. J. Rudner, G. M. Morris, C. Deane and Y. W. Teh, Proceedings of the 41th International Conference on Machine Learning, 2024.
22. A. Kristiadi, F. Strieth-Kalthoff, M. Skreta, P. Poupart, A. Aspuru-Guzik and G. Pleiss, Proceedings of the 41th International Conference on Machine Learning, 2024.
23. R. Astudillo and P. Frazier, Proceedings of the 36th International Conference on Machine Learning, 2019, pp. 354–363.
24. F. Häse, L. M. Roch and A. Aspuru-Guzik, Chem. Sci., 2018, 9, 7642–7655.
25. M. Balandat, B. Karrer, D. Jiang, S. Daulton, B. Letham, A. G. Wilson and E. Bakshy, Advances in Neural Information Processing Systems, 2020, pp. 21524–21538.
26. S. Daulton, X. Wan, D. Eriksson, M. Balandat, M. A. Osborne and E. Bakshy, Advances in Neural Information Processing Systems, 2022, pp. 12760 – 12774.
27. B. E. Walker, J. H. Bannock, A. M. Nightingale and J. C. deMello, React. Chem. Eng., 2017, 2, 785–798.
28. M. T. M. Emmerich, A. H. Deutz and J. W. Klinkenberg, IEEE Congress of Evolutionary Computation (CEC), 2011, pp. 2147–2154.
29. F. Häse, M. Aldeghi, R. J. Hickman, L. M. Roch, M. Christensen, E. Liles, J. E. Hein and A. Aspuru-Guzik, Mach. Learn. Sci. Technol., 2021, 2, 035021.
30. F. Mekki-Berrada, Z. Ren, T. Huang, W. K. Wong, F. Zheng, J. Xie, I. P. S. Tian, S. Jayavelu, Z. Mahfoud, D. Bash, K. Hippalgaonkar, S. Khan, T. Buonassisi, Q. Li and X. Wang, npj Comput. Mater., 2021, 7, 55.
31. A. M. Schweidtmann, A. D. Clayton, N. Holmes, E. Badford, R. A. Bourne and A. A. Lapkin, Chem. Eng. J., 2018, 352, 277–282.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5dd00039d

---