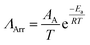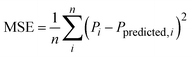Uncovering ion transport mechanisms in ionic liquids using data science

Abstract

Batteries play a key role in the energy transition but suffer from safety concerns arising from the electrochemical instability of organic electrolytes. Ionic liquids are emerging as promising, non-flammable electrolytes for next-generation batteries. Yet, designing ionic liquids to facilitate redox ion transport has proven challenging, because ionic liquids are concentrated electrolytes where ion–ion interactions cause pronounced deviation from classical electrolyte scaling theories which assume viscosity governs mobility. Machine learning studies show that ionic liquid transport properties are challenging to predict from molecular descriptors, preventing rational design. Here, we pursue a broader data-centric approach to provide insight into ionic liquid design by merging databases of experimental properties and computational molecular features for 218 ionic liquids across 127 publications. We find that ionic liquids are well-described by a modified Arrhenius model that captures structure-driven ion transport in correlated electrolytes, yielding energy barriers of around 20–30 kJ mol⁻¹. This exhibits remarkable agreement with the approximately 25 kJ mol⁻¹ screened ion pair interaction energy derived from surface forces measurements, suggesting links between mechanisms of ion transport and interfacial screening. We also use machine learning models to find that molecular features can predict some properties, such as density, while failing to predict properties that rely on long-range correlations, such as viscous dissipation. Our study reveals that data science tools can be leveraged to reveal non-classical transport scaling relationships and alternative materials descriptors that promise to be transformative for designing ionic liquids and other correlated electrolytes for next-generation batteries. All data and models are shared as open-source code.

---

Introduction

Climate change remediation requires the widespread deployment of energy storage devices, raising increasing challenges for battery safety as the scale of battery use increases. For example, the U.S. Product Safety Commission reported over 25 000 battery safety incidents from over 400 types of consumer battery products in 2012–2017.¹ These failure events arise from a dependence on high conductivity liquid electrolytes which is often achieved by using low viscosity, yet flammable and degradable, organic solvents.^2–4 As such, there is a pressing need to develop new classes of safe electrolytes with efficient ion transport to address these challenges.

Ionic liquids are defined as salts with melting points below 100 °C, and many ionic liquids are in fact room temperature liquids. Ionic liquids are composed of bulky, asymmetric cations and anions that maintain strong electrostatic interactions, but charge delocalization and asymmetry hinder formation of crystal structures to lower melting points. Currently, ionic liquids are under extensive investigation as novel electrolytes that promise to improve battery safety and performance as ionic liquids exhibit a variety of desirable electrolyte properties, arising from strong ion–ion interactions, including non-flammability, electrochemical stability, and intrinsic ionic conductivity.^5–10

The strong ion–ion interactions in ionic liquids lead to the formation of nanostructured correlated ion networks, which creates opportunities to modulate ion transport pathways at the molecular level via changes in ion assembly.^5,11–13 For example, recent studies show that replacing an alkyl substituent with an ether substituent on a common imidazolium ionic liquid cation eliminates the formation of nanoscale nonpolar domains often associated with ionic liquids, thereby improving ion transport.^14,15 Similar nanoscale structuring is used to sculpt ion transport pathways in solid and polymeric electrolytes.^11,16,17 The capabilities of selectively tuning electrolyte nanostructure by altering ions and their substituents makes ionic liquids ideal materials for which to develop structure–property relationships and provide new avenues for modulating electrolyte performance under conditions of high ion concentration.^18–21

Currently, many groups in the ionic liquids community are investigating how ion–ion interactions between large numbers of ions exceeding molecular distances impact critical properties, such as viscosity and conductivity. Increasingly, a picture is emerging whereby collective interactions between large numbers of constituent ions play a key role in governing materials properties. Yet, prior literature has often modelled ion transport in ionic liquids using classical dilute electrolyte theories with the goal of simplifying design criteria.^{5,7,8,22–24} For example, classical dilute electrolyte theories clearly predict inverse scaling relationships between viscosity and conductivity. The commonly used Nernst–Einstein model is often a first approach benchmark ionic liquid conductivity according to viscosity and ionic radii.^7,24 Yet, recent studies show ionic liquids often deviate significantly from these hydrodynamic models,^5,8,19,25,26 and that ionic correlations play leading roles in governing ionic liquid conductivity.^13,15,27

Machine learning models (ML) have also been used to predict ionic liquid properties, like conductivity, from computational molecular descriptors.^8,28–31 This enables material property prediction without requiring experimental data beforehand, including properties such as density, gas solubility, conductivity, viscosity, and melting point to screen ionic liquids for various applications.^8,28,30–34 However, developing a ML model with suitable accuracy often requires complex “black-box” ML approaches, offering limited mechanistic insights into origins of materials properties.^8,31 In contrast, simpler interpretable models often fail to accurately capture the diverse range of ionic liquid conductivity.³¹

Many different types of information have been used to develop ML models for ionic liquid properties, including experimental measurements, 2D and 3D molecular structures for individual ions, and electronic properties for individual ions.^{7,8,28,29,31,35,36} Models with the highest reported accuracy often employ complex descriptors such as electronic state and connectivity indices, however it is not simple to translate these descriptors into obvious ion choices for ionic liquids.³¹ Importantly, widely-available modeling descriptors explored to date only consider features of isolated single ions and cannot capture the collective influence of interactions between ion pairs or larger correlated ion networks.^37–39 Notably, features that contain descriptions of microphase structure are often missing in ionic liquid property modeling, likely due to the limited scope of experimental techniques such as X-ray or neutron scattering data.

In this work, we aim to advance towards development of data science and ML frameworks that can be leveraged to advance understanding of how collective ionic interactions impact ion transport mechanisms in ionic liquids. Notably, we show how this approach can enable derivation of non-classical transport scaling relationships to evaluate different plausible models of ion transport in neat ionic liquids.

Our approach reveals a previously unexplored molecular descriptor, the barrier for ion mobility, which highlights links between ionic screening and ion mobility in ionic liquids. Importantly, this molecular descriptor, the screened ion pair interaction energy, promises to be readily accessible computationally. We then explore the extent to which structural similarity can explain ionic liquid conductivity trends by examining the ionic liquid design space. Lastly, we predict ionic liquid conductivity using ML models and our dataset of ionic liquid descriptors to clarify the extent to which molecular information can predict transport properties.

Electrolyte design models

The Nernst–Einstein model is a classical electrolyte design model that is widely used to describe the ion conductivity of electrolytes:
here, Λ [S m² mol⁻¹] is molar conductivity, N_A [mol⁻¹] is Avogadro's number, e [1.602 × 10⁻¹⁹ C] is the electronic charge, k [J K⁻¹] is Boltzmann's constant, T [K] is temperature, v is the stoichiometric coefficient of each ion, z is ion charge, and D [m² s⁻¹] is the ion diffusion coefficient. The Nernst–Einstein model predicts molar conductivities based on the diffusion coefficient of each ion in the electrolyte, which can be further simplified using Stokes–Einstein model for hard sphere diffusion:
here, ions are approximated as spheres subject only to bulk viscous forces. The symbol r [m] denotes the ion hydrodynamic radius and η [Pa s] is the bulk viscosity.

The modified Arrhenius equation

and the Vogel–Tammann–Fulcher equation
have been used to model conductivity as a kinetic step in “hole theory” models and are primarily used in solid and polymeric systems but have also been applied to ionic liquids in limited cases.^16,40 In these models, A_Arr [S m² mol⁻¹] and A_VTF [S m² (mol⁻¹ K⁻¹)] are pre-exponential factors, E_a [kJ mol⁻¹] is the activation energy, R [kJ (mol⁻¹ K⁻¹)] is the gas constant, T [K] is temperature, and T₀ [K] is an empirical temperature offset. These equations model ion transport as moving between adjacent coordination sites within the medium,^14–16,25 a form of structural diffusion that is increasingly thought to decouple ion mobility from viscosity. These models can robustly predict temperature dependence of conductivity in polymeric ionic liquids and room temperature ionic liquids, suggesting the important contribution of structural diffusion to transport processes in these materials, yet analyses of these models in ionic liquids remains limited.^{17,26,35,41,42}

The Vogel–Tammann–Fulcher model applies a temperature offset, T₀, to the modified Arrhenius equation and is often used to describe materials where non-Boltzmann distributed relaxation mechanisms with different time and energy scales exist concurrently, often at temperatures near a phase transition or glass transition point.^40,43 Compared to the modified Arrhenius model, the Vogel–Tammann–Fulcher model was found to better describe the interplay of ion-hopping and bulk material mobility near glass transition temperatures.^16,40 However, the empirical temperature offset often differs from the glassy transition temperature and does not have a conclusive physical meaning in ionic liquids.^16,35 At temperatures ∼50 K above the glass transition temperature, the Vogel–Tammann–Fulcher equation converges to the modified Arrhenius equation, and the temperature offset has negligible effects.⁴⁴ As glass transition temperatures for room temperature ionic liquids are often between 150–250 K,^25,45,46 we assume room temperature to be sufficiently above the glass transition in our study and use the modified Arrhenius model.

Results and discussion

We combined 2D molecular, 3D molecular, and bulk property descriptors to create a database of ionic liquid materials properties to analyze structure–property and property–scaling relationships. This database contains structure, shape, and polarity information to provide molecular insights on ionic liquid bulk properties. Experimentally-reported conductivity, viscosity, density, heat capacity, and melting point data is collected from the NIST ILThermo database of ionic liquid properties shown in Table 1.^47,48

Table 1 Experimental bulk properties

Descriptor name	Range	Units
Temperature^47,48	273–363	K
Molar conductivity^47,48	0.13–9.72	S cm^2 mol^−1
Viscosity^47,48	4.9–11 500	mPa s
Density^47,48	934.7–1625.9	kg m^−3
Heat capacity^47,48	306.5–1409	J mol^−1 K^−1
Melting point^47,48	236.3–317.6	K

---

Computed molecular descriptors from PubChem^37,38 and RDKit³⁹ libraries are shown in Table 2. RDKit and PubChem molecular descriptors are widely available for single ions and are calculated using the MMFF94s forcefield to provide ionic liquid molecular details for analysis. These descriptors were down selected from a broad library of descriptors based on mathematical simplicity and application to experimental design. Descriptions of each descriptor can be found in Tables S1–S4 in the ESI.†

Table 2 Molecular descriptors

Descriptor name	Cation range	Anion range	Units
Atom count^37	13–62	3–36
Bond count^37	12–63	2–35
Rotatable bond count^37	0–15	0 – 9
Rotatable bond fraction^37	0–0.241	0–0.257
Hydrogen bond acceptors^37	0–2	2–15
Hydrogen bond donor^37	0–2	0–2
Molecular weight^37	74.1–364.5	45.02–380.2
Valence electrons^39	30–146	16–128
Volume^38	63.3–304.2	34.2–195.5	Å^3
Ionic radius^38	2.47–4.17	2.01–3.60	Å
Cation/anion volume ratio^38	0.874–1.344	—
Avg. sphericity^39	0.725–0.996	0.296–1.00
Avg. asphericity^39	0.054–0.774	0.000–1.00
Rel. Std. Dev. sphericity^39	0.0–8.5	0.0–4.7	%
Rel. Std. Dev. asphericity^39	0.0–47.5	0.0–33.8	%
Polar area^37	0.0–39.7	13.9–103.0	Å^2
Hydrogen bond donor interactions^37	0–22	0–2
Log P^37	−1 to 7	−4.2 to 3.6
Max. partial charge^39	−0.46 to −0.07	−0.87 to −0.36	e
Min. partial charge^39	0.09–0.35	−0.08 to 0.52	e

---

Nernst–Einstein conductivity scaling analysis

The Nernst–Einstein ion transport model has an extensive history as being a benchmark for evaluating deviations from classical viscosity–conductivity scaling in ionic liquids.^{5,7,8,22–24} Using reported viscosity, density, and ionic radii for each ionic liquid, we obtain hydrodynamic estimates for molar conductivity. While the Nernst–Einstein model assumes independent ion motion, which is necessarily incorrect in ionic liquids, it is often used as a first-pass analysis in concentrated electrolytes to understand how ion transport deviates from ion transport in ideal strong electrolytes. Often, concentrated electrolytes exhibit notable deviations from Nernst–Einstein predictions, and the mechanistic origins of these deviations are subject to ongoing discussion and investigation.^5,7,8

Using simulated ion volumes and spherical ion geometry, which is a Nernst–Einstein model assumption, we calculate an upper-limit prediction for hydrodynamic ion mobility using the Nernst–Einstein equation. This yields what is often assumed to be an upper bound for molar conductivity experiment measurements. Fig. 1 shows a parity plot of the Nernst–Einstein molar conductivity prediction and experimental conductivity measurements for 218 ionic liquids, which is an expanded analysis on a similar approach reported previously by our group.⁸

Fig. 1 Parity plot comparing hydrodynamic predictions of molar conductivity from the Nernst–Einstein model and experimentally reported molar conductivities for 218 ionic liquids at various temperatures. Ionic liquids which exhibit molar conductivities greater than hydrodynamic model predictions are labeled as super-hydrodynamic and demonstrate super-hydrodynamic conductivity–viscosity scaling. Ionic liquids which exhibit 70% to 100% of Nernst–Einstein predictions are labeled strong electrolytes and ionic liquids which exhibit less than 70% of Nernst–Einstein predictions are labeled as weak electrolytes.

We compare Nernst–Einstein predictions and experimental measurements utilizing the ratio of experimental measurements over Nernst–Einstein predictions, which we will call the “Nernst–Einstein Ratio” (sometimes referred to as “ionicity” or “inverse Haven ratio”) in Fig. 1.

here, Λ_EXP [S m² mol⁻¹] is the measured experimental molar conductivity and Λ_NE [S m² mol⁻¹] is the Nernst–Einstein molar conductivity prediction. We find many ionic liquids exhibit measured molar conductivities greater than Nernst–Einstein hydrodynamic model predictions of molar conductivity.⁸ These are labeled as super-hydrodynamic and exhibit ion transport which supersedes viscous transport limitations.

In agreement with several studies on ionic liquid property scaling, we observe a decoupling of viscosity and conductivity in a broad selection of ionic liquids.^8,23,35,49 This decoupling is thought to arise from strong ionic and polar intermolecular interactions^12,26,50 which can drive nanoscale ionic liquid structuring.^{6,13,15,21,27,51,52} However, clarifying how individual ion structures contribute to structure formation and conductivity–viscosity decoupling remains challenging.

Hybrid conductivity modeling

To better understand the origin of this viscosity–conductivity decoupling, we created a ML model to learn deviations from the Nernst–Einstein model using 3D structural and energetic descriptors to correct Nernst–Einstein conductivity predictions. The difference between measured conductivities and Nernst–Einstein predictions, hereon referred to as residual conductivity,

Residual conductivity = Λ_Exp − Λ_NE

can help elucidate which molecular descriptors drive deviations from classical hydrodynamic transport models.

Our hybrid ML model combines Nernst–Einstein and a random forest model to rank RDKit descriptor importance for predicting ionic liquid conductivity. Starting with viscosity and ionic radii, a greedy selection algorithm is used to add the RDKit descriptor which best improves model performance. Results are shown in Table 3.

Table 3 Hybrid ML cumulative performance as additional properties and RDKit descriptors are added to a random forest regression model

Added variables	Cumulative mean squared error (S cm^2 mol^−1)^2	Cumulative model R^2
None (Nernst–Einstein baseline)	0.99	0.72
Viscosity, cation radius, anion radius	0.86	0.75
Cation polar area	0.67	0.81
Anion hydrogen bond donor count	0.62	0.82
Anion valence electrons	0.61	0.83
Anion hydrogen bond acceptor count	0.60	0.83
All	0.80	0.77

---

The hybrid model shows improvements upon the Nernst–Einstein model as we add additional molecular features. The selected descriptors in order of improved model performance are cation polar area, anion hydrogen bond donor count, anion valence electrons, and anion hydrogen bond acceptor count. Additional descriptors did not improve performance and eventually worsened performance due to the model overfitting when all RDKit descriptors are input to the model.

We find that hydrodynamic variables only minimally contribute to residual conductivity predictions, as inputting viscosity and ion radii to our random forest model only slightly improved model performance. This lack of improvement broadly implies that deviations from the Nernst–Einstein model are non-hydrodynamic in nature. Instead, new molecular information, scaling theories, and/or transport mechanisms are needed to describe observed conductivity with increased accuracy.

From RDKit descriptors, we observe that polarity and electronic information best compliment hydrodynamic information for ionic liquid conductivity modeling. These descriptors begin to provide information about ion interactions that are not accounted for in classical hydrodynamic models. For example, polar area provides insight about resonant structures and charge delocalization, and cation polar area can distinguish aromatic cations such as imidazolium and pyridinium which have delocalized electrostatic interactions with anions.6,53,54

Modified Arrhenius model

To further investigate non-hydrodynamic transport mechanisms in ionic liquids, we explore ionic liquid conductivity using a modified Arrhenius model and ion hopping framework.16,40 We use a modified Arrhenius model in combination with the combined database we developed to derive a modified Arrhenius scaling theory to conductivity data. Here, the modified Arrhenius model is fitted to each unique ionic liquid containing more than 5 reported conductivity measurements at different temperatures. Fig. 2 shows a parity plot of these modified Arrhenius model fits and experimental measurements. While the modified Arrhenius model does not provide predictive capabilities for new ionic liquids, we find the derived scaling model collapses conductivity–temperature scaling in ionic liquids, surpassing accuracies achieved by any hydrodynamic models, such as the Nernst–Einstein model in Fig. 1, explored to date.

Fig. 2 Molar conductivity fit using the modified Arrhenius equation vs. experimentally reported molar conductivities. Ionic liquids with at least 5 temperature dependent conductivity measurements were fit. Nearly all ionic liquids seem to be modeled well by the thermally activated diffusion as described by the modified Arrhenius equation's conductivity-temperature scaling relationship.

The modified Arrhenius equation is a model that originates from use of statistical mechanics to describe defect-driven structural ion transport. In this model, transport is governed by adjacency to local defects in a medium structure, which act as ion coordination sites.^16,35 Ions jump between sites with a probability dictated by the relative magnitudes of ion–ion interaction energy barriers and thermal fluctuations in a process described by “hole theory”.^16,40,44 Hence, the universal agreement between this derived theory and ion conductivity in ionic liquids implies that non-hydrodynamic mechanisms play a key role in ion mobility in ionic liquids.

Importantly, using the modified Arrhenius model to make conductivity predictions requires knowledge of activation energies to capture the temperature dependence of conductivity, so we explore how activation energies inferred from this analysis for existing ionic liquids compare to known physical and chemical properties. We compare conductivity activation energies to reported interaction energies measured from surface force measurements and density functional theory (DFT) calculated ion dissociation energies reported in literature in Table 4. Since DFT dissociation energies were calculated for ionic liquid ions in vacuum, the energies reported here are normalized by its respective ionic liquid dielectric permittivity to estimate ion dissociation energies in a dielectric fluid as a simplified approach to estimating how surrounding ions impact pairwise cation–anion interactions via dielectric screening.⁵⁵

Table 4 Fit, measured, and calculated ionic liquid dissociation energies for select ionic liquids. 95% confidence intervals are included from our modified Arrhenius model fit for our fit activation energies

Ionic liquid	Modeled activation energy (kJ mol^−1)	Measured interaction energy (kJ mol^−1)	DFT interaction energy (kJ mol^−1)
1-Ethyl-3-methylimidazolium BF4	26.7 ± 2.9	—	25.4 (ref. 54, 56 and 57)
1-Butyl-3-methylimidazolium BF4	32.4 ± 1.5	—	29.5 (ref. 57 and 58)
			35.6 (ref. 56 and 58)
1-Ethyl-3-methylimidazolium CF3SO3	19.9 ± 1.9	—	18.3 (ref. 54 and 56)
			23.4 (ref. 54 and 57)
1-Ethyl-3-methylimidazolium bis(trifluoromethanesulfonyl)imide	23.3 ± 1.0	23.0 (ref. 55)	26.5 (ref. 54, 55 and 57)
			28.4 (ref. 54 and 56)
1-Propyl-3-methylimidazolium bis(trifluoromethanesulfonyl)imide	29.4 ± 2.7	23.6 (ref. 55)	—
1-Butyl-3-methylimidazolium bis(trifluoromethanesulfonyl)imide	28.9 ± 0.8	25.8 (ref. 55)	27.3 (ref. 55)

---

The inferred activation barriers are in remarkable agreement with interaction energies for ionic liquids measured and calculated in literature. Agreement between the ion–pair interaction energies and modeled activation energies implies that measured or DFT predicted ion interaction energies may be used to predict temperature dependence of ionic liquid conductivity. Yet, we note the existing availability of DFT or measured ion interaction energies is limited primarily to imidazolium-based ionic liquids. This finding supports emerging theories that ion conduction may occur via thermally activated desolvation mechanisms in ionic liquids as we find the energy barrier for ion transport to be equivalent to simulated ion pair interaction energies.^14,35,55 Therefore, we suggest that ion dissociation plays a key role in ionic liquid ion mobility.

As interaction energies are available only for a small subset of ionic liquids, we additionally explore correlations between ion transport and electrostatic screening for 20 ionic liquids using dielectric permittivity data reported by Bennet, et al.⁵⁶ Here, we observe that conductivity activation energies decrease as the reported dielectric permittivity increases as shown in Fig. 3. These 20 ionic liquids have a greater diversity of anions and are reported in Table S8 in the ESI.†

Fig. 3 Activation energies fit using the modified Arrhenius equation vs. reported dielectric permittivities. A negative correlation between conductivity activation energies and permittivity suggests that weak electrostatic screening and long-range ionic interactions increase energy barriers for ion transport in ionic liquids and decreases conductivity.

Examining the negative correlation between reported dielectric permittivity and fit activation energy in Fig. 3, we find that ionic liquids with low permittivities, and thus poor electrostatic screening,⁵⁹ have the highest energy barriers for ion transport. This trend is likely due to ionic correlations induced by long-range electrostatic interactions in these materials. Interestingly, this correlation suggests a unification of ion mobility and ion screening in ionic liquids, and we suggest dielectric permittivity to be a new potential descriptor for evaluating conductivity via experiment, DFT, or GNN.³⁴

Overall, we conclude that ionic liquid electrostatics interactions and ionic correlations must be dominant factors in ionic liquid ion transport. Our observations reinforce the idea that ion transport is dependent on ion desolvation and ion-network reorganization. Ultimately, we find agreement between Arrhenius model activation energies, experimental interaction energies, and DFT as well as correlation with dielectric permittivity which suggests new avenues for evaluating ion transport by predicting ion interaction energies.

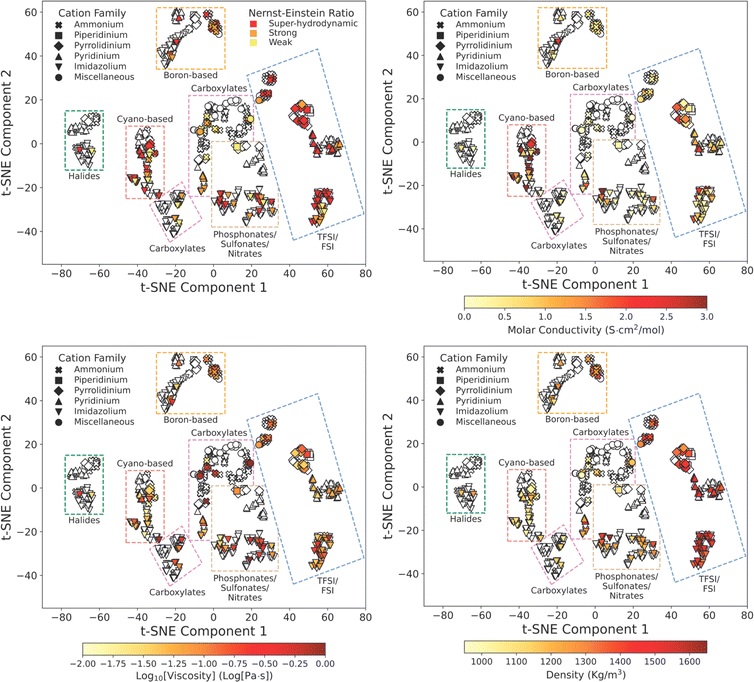
Ionic liquid property mapping

Additionally, given the extremely large number of potential ionic liquids, we explore the extent to which molecular similarity dictates properties across the ionic liquid design space. We visualize the ionic liquid design space by mapping molecular similarity onto a 2D latent space using unsupervised dimensionality reduction. We use t-Distributed Stochastic Neighbor Embedding (t-SNE) to map ionic liquids while retaining local and global similarity distributions. Fig. 4 shows the resulting molecular map overlayed with ionic liquid properties at 298 K to elucidate structure–property correlations. We observe that t-SNE clusters naturally organize according to ionic charge and charge-carrier identity. Anion families appear to globally sort along t-SNE component 1 and cation families locally sort along t-SNE component 2 within each cluster. This clustering is consistent with the common classification of ionic liquids according to their anion and cation charge family.

Fig. 4 Projections of molecular similarity overlayed with Nernst–Einstein ratio (top left), molar conductivity (top right), log10[viscosity] (bottom left), and density (bottom right) all at 298 K. Ionic liquids missing property data are colored white. Ionic liquids are clustered according to their structural similarities using t-stochastic neighbor embedding to preserve local and global ionic liquid distributions then overlayed with physical properties to identify underlying structure–property trends. Strong structure–property trends arise from clustering with ionic liquid density that are not observed for ionic liquid transport properties suggesting a direct correlation between ionic liquid density and structure that does not exist for ionic liquid transport properties.

Our approach to ionic liquid mapping distinctly captures global trends in ionic liquid density as molecules with similar atomistic compositions possess similar densities due to the additive nature of atomic masses and volumes. From this mapping, we observe that ionic liquid density is strongly correlated to anion identity. This is explained by the greater diversity in anion atomic composition. Anions containing sulfur, phosphorous, and fluorine have higher densities than carbon and nitrogen composed anions and are located at larger t-SNE component 2 values. As ionic liquid cations in our database are mostly comprised of carbon, and nitrogen, we correspondingly find little variation in density between cation families along t-SNE component 2.

Ionic liquid conductivity, viscosity, and Nernst–Einstein ratio trends are not clearly described by our t-SNE clustering as many clusters contain a wide range of property values. This indicates that ionic liquids with similar 2D structures can exhibit a wide range of transport behaviors, and that additional information is required to distinguish transport behavior in ionic liquids.

For example, 1-butyl-3-methylimidazolium tetrafluoroborate and 1-butyl-2,3-methylimidazolium tetrafluoroborate are clustered closely together as boron-based imidazolium ionic liquids in Fig. 4 but exhibit a 4-fold difference in viscosity. Here, methylation of the C2 proton on 1-butyl-3-methylimidazolium results in an increase in viscosity due to a reduction in the cation conformational entropy,⁶⁰ highlighting the challenge in predicting transport properties from ion identity alone. Instead, the assembly of ions into heterogeneous nanoscale domains is likely to be key for many ionic liquid transport properties, and it appears challenging to learn this nanostructure information directly from individual ion identity.

Although t-SNE projections do not fully capture transport property trends in ionic liquids, we identify notable characteristics across ionic liquid cation and anion families. For anion families, we find carboxylate, phosphonate, sulfonate, and boron-based anions exhibit the highest viscosities and lowest molar conductivities. Molecular transport in these ionic liquids may be limited by strong ion–ion associations.^11,61

In contrast, dicyanamide and bis(trifluoromethanesulfonyl)imide ionic liquids exhibit a wide range of molar conductivities despite consistently low viscosities. This decoupled transport behavior in dicyanamide and bis(trifluoromethanesulfonyl)imide ionic liquids is evidence for how molecular structure and interactions can drive deviations from classical hydrodynamic transport. The low viscosities in dicyanamide and bis(trifluoromethanesulfonyl)imide ionic liquids are explained by delocalized anion charge centers and asymmetric geometry which reduces charge density and can reduce site-specific electrostatic interactions.⁶² However, ion transport in these ionic liquids may further depend on local ion coordination that is specific to each unique ion pair combination.^27,62–64

Observing cation families, we find ammonium cations tend to exhibit the highest viscosities and lowest molar conductivities. Pyrrolidinium and piperidinium ionic liquids exhibit the lowest viscosities while imidazolium and pyridinium cations exhibit the highest molar conductivities. Interestingly, we find that pyrrolidinium and pyridinium cations paired with bis(trifluoromethanesulfonyl)imide anions often exceed hydrodynamic ion transport predictions yet remain minimally studied in literature.³⁵ The increase in super-hydrodynamic ion transport in pyrrolidinium-based ionic liquids compared to imidazolium-based ionic liquids may arise from greater steric shielding of the cation core which may increase ion mobility by weakening electrostatic counter-ion attraction.^65,66

Overall, we observed a strong decoupling between viscosity and conductivity across ionic liquid cation and anion families. We find that high viscosities limit molar conductivity in ionic liquids, yet low viscosities do not necessitate high molar conductivities. Intriguingly, molar conductivity appears to be more sensitive to ionic liquid structure than viscosity and may be more dependent on ionic correlations. To better understand the differences in underlying mechanisms across ionic liquid properties, we explore the ability to predict these properties using the various types of available chemical information within our dataset.

Machine learning property modeling

A long-standing challenge in modeling ionic liquid properties is understanding what kind of information is required to predict each property.^30,31 To determine if broader ML modeling can be competitive with the modified Arrhenius scaling theory derived above, we create four sets of ionic liquid descriptors from our data set and input them into a fully connected feed-forward neural network to predict various ionic liquid properties. Here, we use molecular connectivity graphs, scalar molecular descriptors, bulk ionic liquid properties, and a combination of molecular descriptors and bulk properties. We note that our graph representations are highly simplified and only capture connectivity. Table 5 shows the test results of each target property and input representation.

Table 5 Neural network test set prediction R², MSE, and RMSE

Predicted property	Connectivity graph	Computational RDKit descriptors	Remaining experimental bulk properties	RDKit descriptors + bulk properties
Molar conductivity (S cm^2 mol^−1)	R^2 = 0.50	R^2 = 0.76	R^2 = 0.73	R^2 = 0.82
	MSE = 1.75	MSE = 0.823	MSE = 0.941	MSE = 0.662
	RMSE = 1.32	RMSE = 0.91	RMSE = 0.97	RMSE = 0.79
Density (kg m^−3)	R^2 = 0.73	R^2 = 0.96	R^2 = 0.02	R^2 = 0.97
	MSE = 7414	MSE = 1190	MSE = 26773	MSE = 838
	RMSE = 86.1	RMSE = 34.5	RMSE = 164	RMSE = 29
Viscosity (Pa s)	R^2 = 0.06	R^2 = 0.08	R^2 = 0.23	R^2 = 0.09
	MSE = 0.122	MSE = 0.12	MSE = 0.100	MSE = 0.118
	RMSE = 0.35	RMSE = 0.35	RMSE = 0.32	RMSE = 0.34
Heat capacity (J mol^−1 K^−1)	R^2 = 0.75	R^2 = 0.84	R^2 = 0.11	R^2 = 0.79
	MSE = 4380	MSE = 2780	MSE = 15356	MSE = 362
	RMSE = 66.2	RMSE = 52.7	RMSE = 124	RMSE = 60.2
Melting point (K)	R^2 = 0.02	R^2 = 0.06	R^2 = 0.11	R^2 = 0.06
	MSE = 317	MSE = 305	MSE = 288	MSE = 306
	RMSE = 17.8	RMSE = 17.5	RMSE = 16.9	RMSE = 17.5
Residual conductivity (S cm^2 mol^−1)	R^2 = 0.02	R^2 = 0.35	R^2 = 0.01	R^2 = 0.11
	MSE = 0.966	MSE = 0.644	MSE = 0.977	MSE = 0.881
	RMSE = 0.98	RMSE = 0.80	RMSE = 0.99	RMSE = 0.94

---

We find that connectivity graphs are suitable for predicting density and heat capacity but insufficient for predicting all other properties. Using RDKit descriptors, we achieve the highest accuracies for all properties except melting point which cannot be predicted with any ionic liquid representation. Similar to our results using a hybrid ML model, we find that a neural network can predict conductivity using viscosity with accuracy comparable to the Nernst–Einstein model. However, we find no additional property-scaling relationships within our dataset.

Finally, combining molecular descriptors with measured properties, we find that our model significantly improves molar conductivity predictions which agrees with hybrid modeling results. For all other properties studied, however, we do not observe any significant improvement from combining RDKit descriptors with bulk properties over RDKit descriptors alone.

2D molecular connectivity graphs

We find that molecular structure information alone is suitable for predicting density and heat capacity, in agreement with previous studies,^32,67 but insufficient for predicting other properties. Density is well modeled by 2D structure likely due to its dependence on atomic composition and size which is easily captured in a 2D representation. Further, heat capacity is governed primarily by rotational and translational degrees of freedom, which is also represented by molecular connectivity.

Our 2D graph does not capture intermolecular interactions, however, and cannot model viscosity or melting temperature. Interestingly, we find 2D structure capable of modeling conductivity with moderate accuracy (R² = 0.50) but incapable of predicting residual conductivity when Nernst–Einstein predictions of conductivity are subtracted out (R² = 0.02). We conclude that the 2D model is modeling is capturing a relationship between size and conductivity but not transport-relevant intermolecular interactions since the 2D graph neural networks cannot model viscosity nor non-hydrodynamic contributions to conductivity. Overall, we find that 2D structure is capable of modeling ionic liquid properties which are independent of intermolecular interactions and collective assembly.

3D RDKit descriptors

RDKit descriptors provide higher resolution information about single-ion molecular structure, conformational flexibility, and polarity compared to 2D graphs which best improve property modeling for our studied properties. We observe that RDKit descriptors improve density and heat capacity predictions, likely because atomistic features are now embedded as molecular descriptors. This additional information also enables suitable predictions for molar conductivity and best predicts residual conductivity of the representations tested. As RDKit cheminformatic descriptors add 3D structural information, the resulting models improve upon all ionic liquid property predictions compared to 2D connectivity.

Density predictions are greatly improved by the inclusion of molecular weight and simulated molecular volume. Similarly, heat capacity predictions improve with the inclusion of 3D features as we include conformational flexibility, which is calculated from the variance in shape from molecular simulations using RDKit. RDKit simulated descriptors provided the highest accuracy for density and heat capacity predictions as 3D molecular information can easily describe these material properties.

Molar conductivity model predictions are improved to accuracies comparable to Nernst–Einstein model predictions using RDKit cheminformatic 3D structural descriptors. However, our model does not require any experimental measurements in contrast to the Nernst–Einstein model. This model thus provides the benefit of predictive capability without prior knowledge of any physical properties. However, the model still suffers from the same limitations as our hybrid model and is only recommended to be used for initial ionic liquid conductivity estimates.

We find that residual conductivity is best modeled using RDKit descriptors and reinforces that polarity and electronic information best describes deviations from hydrodynamic transport. Information regarding ionic liquid conformational distributions and partial charges prove useful for describing ion transport in ionic liquids as they relate to local ion transport phenomena, such as ion hopping. We recommend that polar and electrostatic interactions be further investigated for modeling ion transport in ionic liquids.

Finally, we find that RDKit cheminformatic 3D structural descriptors cannot be used to model ionic liquid viscosity or melting point. Since these ions are simulated individually in vacuum, interactions cannot be calculated to predict the molecular correlations which drive viscous forces. Similarly, conformational geometries without intermolecular force calculations are too inaccurate to predict molecular packing for melting point predictions. These results agree with previous studies modeling viscosity^30–32 and melting point^30,33 using 2D or 3D molecular structure which find that ionic liquid viscosity and melting point are difficult to model without intermolecular force calculations.³¹ We conclude that a scalable approach for modeling or predicting intermolecular interactions in ionic liquids would provide significant advantages in achieving accurate predictions for efficient screening of ionic liquid viscosity and melting temperature.

Bulk property scaling

Experimental bulk property descriptors best represent the net molecular behavior of ionic liquid materials; however, they do not provide molecular details to deconvolute contributing molecular forces. Using bulk properties for property predictions, we analyze an interesting lack of reciprocity between viscosity and conductivity predictions; however, we do not report any other property-scaling relationships within our dataset.

Interestingly, although viscosity is a suitable predictor of conductivity (R² = 0.73), we find that conductivity is a poor predictor of viscosity (R² = 0.23). While viscosity provides information about the average mobility of large ensembles of ions useful for modeling ion motion, the local mobility of individual ions does not appear to provide the same level of information about the mobility of the bulk ionic liquid molecules. Viscosity is especially dependent on many intermolecular forces present in ionic liquid materials and likely requires information on longer–range correlations than conductivity to identify all contributing forces.

Such conductivity–viscosity decoupling matches prior understandings that ion conduction and viscous dissipation can inherently occur on different length and time scales in correlated materials.⁶⁸ For example, Phillipi, et al. reported ionic liquid viscosity to be equally impacted by the molecular compression caused by coulombic attractions and electrostatic restrictions to mobility resulting from a structured charge network.⁶⁹ The interplay of these intermolecular interactions across large length scales would require the development of new computational descriptors to model such behavior for viscosity predictions.

Conclusions

In this work, we demonstrate how the classical Nernst–Einstein model captures the general trend of ionic liquid conductivity–viscosity scaling (R² = 0.72), but that many ionic liquids significantly deviate from this model. We use a hybrid ML to correct the Nernst–Einstein model and find that cation polar area, anion hydrogen bond donor count, anion valence electrons, and anion hydrogen bond acceptor count are the best readily available RDKit descriptors for improving upon classical hydrodynamic model predictions (R² = 0.83). These models fail to predict conductivity with high accuracy, however, and highlight the limitations of the Nernst–Einstein for describing ion transport in ionic liquids.

Critically, we find that a modified Arrhenius model derived using data science approaches, which describes defect-driven transport in structured electrolytes, broadly collapses molar conductivity in ionic liquids to a universal scaling (R² = 0.99). We report activation energy barriers, which are inferred from this model by fitting experimental conductivity–temperature measurements, that match values obtained from experimental surface forces measurements and Density Functional Theory (DFT) calculations, highlighting that ionic correlations are crucial in describing ion transport.

Our findings suggest a general link between electrostatic screening and ion transport in ionic liquids and points to new avenues for predicting ion conductivity in ionic liquids using interaction energies and permittivities. Altogether, our findings suggest that ion transport in ionic liquids occurs via thermally-activated ion desolvation and that ion–ion interaction strengths within coordinated ionic liquid networks are important considerations for rationally modeling ionic liquid conductivity.

Next, we create a map of the ionic liquid molecular design space to identify ion transport property trends across similar ionic liquids using unsupervised dimensionality reduction. We find that ionic liquids cluster by similar charge centers but exhibit strikingly varied transport properties. This clustering visualizes viscosity–conductivity decoupling and depicts the challenges in exploiting ionic liquid motifs for electrolyte design. We observe that the most conductive ionic liquids are composed of cations and anions with delocalized charges and steric shielding which weaken counter-ion coordination. Interestingly, we observe that while high viscosity often limits molar conductivity, low viscosity ionic liquids yield a large range of molar conductivities, suggesting that bulk transport is important, but not solely responsible, for capturing the broad range of conductivity values in ionic liquids.

Finally, we create ML models to predict conductivity, using sets of 2D molecular connectivity graphs, RDKit molecular descriptors, and experimental properties as model inputs. We find that RDKit molecular descriptors generally provided the highest accuracy because of the range of information represented by these descriptors. Using RDKit descriptors, we find that some properties are dictated solely by individual ion properties and do not require information about ion–ion interactions, such as heat capacity (R² = 0.84) and density (R² = 0.96). However, properties that are governed by a collection of ion–ion interactions are more challenging to predict with high accuracy, including residual conductivity (R² = 0.35), viscosity (R² = 0.08), and melting point (R² = 0.06).

By contrasting our ability to predict ionic liquid conductivity across various data-centric methods, we identify a need for ionic liquid representations which can describe ion–ion interactions and higher-order ionic correlations. Our results suggest that electrostatic screening and ionic correlations play significant roles in ionic liquid ion mobility and identify ion dissociation energies as a new descriptor for understanding ion transport in ionic liquid. Most importantly, our results show how data science can be used to suggest new opportunities to identify, predict, and understand non-classical ion transport mechanisms in next-generation electrolytes.

Methods

3D RDKit descriptors

We used reported experimental viscosity, conductivity, density, melting point, and heat capacity data from ILThermo v2.0 shown in Table 1.^47,48 Data was pre-processed to remove values with reported experimental uncertainty greater than 15%. We used computational descriptors from PubChem3D using PubChemPy v1.0.4 (ref. 37 and 38) and RDKit v2024.3.5,³⁹ shown in Table 2, to evaluate structure–property relationships. RDKit properties include individual ion properties from molecular dynamics simulations, which are simulated 50 times using MMFF94 s force fields. Average values and standard deviations were used as molecular descriptors. Ionic radii were computed using the radius of a sphere with equivalent volume as computed ion volumes. Atoms with sp³ d² hybridization, primarily PF₆, and single atom ions could not be modeled using RDKit and were excluded. Ions containing Re or more than 15 rotatable bonds, such as the C₁₆MIm cation, did not contain PubChem3D data and were excluded. The final dataset consisted of 2224 temperature dependent viscosity, density, and conductivity data points for 218 ionic liquids from 127 publications collected from ILThermo. Heat capacity data consisted of 857 temperature dependent heat capacity data points for 70 ionic liquids from 40 publications collected from ILThermo. Melting point data consisted of melting temperatures at atmospheric pressure for 75 ionic liquids from 44 publications collected from ILThermo.

Data test-train split

We used 5-fold cross validation during training, validation, and hyperparameter tuning for all ML models. Model architecture and data splits were kept constant during hyperparameter tuning. Model learning rates and number of epochs were adjusted to minimize MSE. The best performing hyperparameters for each model are reported in the ESI† and associated GitHub. The dataset was split by unique ionic liquid compound names to ensure the same ionic liquid does not appear in both the training and test set for a given split, even when measurements were at different temperatures. This approach ensures that models do not simply learn temperature-dependence of all ionic liquids during training and then interpolate values in the test set. We provide a prediction value for each data point in the presented regression plots.

Ionic liquid mapping

One-hot encoded molecular fingerprints were created for every cation and anion using RDKit's MACCS Keys generation function. These fingerprints encode the presence or absence of each of the 166 molecular fragments in the MACCS Keys library.³⁹ Corresponding cation and anion molecular fingerprints are concatenated to create a 332-key fingerprint for each ionic liquid.

Ionic liquid structural similarity was evaluated using the generated molecular fingerprints and Tanimoto similarity. The Tanimoto similarity of two ions is calculated by dividing the number of shared MACCS Keys fragments by the total number of MACCS Keys fragments present amongst the two ion molecular fingerprints. Pairwise Tanimoto similarity is calculated for each ion and its co-ions to create a cation similarity matrix and anion similarity matrix with diagonals of 0 for self-similarity. The matrices were concatenated to create an N × 2N similarity matrix, where N is the number of unique ionic liquids, containing the similarity of each ionic liquid's ions with the ions of every other ionic liquid. t-Distributed Stochastic Neighbor Embedding was used to project this similarity matrix onto a 2D latent space and visualize the diversity of studied ionic liquids. t-SNE reduces data dimensionality while retaining local and global data structure for high-dimensional datasets.⁶⁸ The similarity matrix was reduced to 2 latent dimensions for further analysis.

Graph neural network

To model bulk ionic liquid properties using 2D molecular structure, we trained a graph neural network using molecular connectivity graph representations of ionic liquids. To create molecular connectivity graphs, atoms were represented as nodes and covalent bonds as edges to create adjacency matrices.^70,71 To produce consistent graphs without additional convolution, we use each molecule's canonical SMILE representation and RDKit's adjacency matrix function, these graphs were depicted in matrix form as square adjacency matrices; row/columns represent graph nodes, and binary matrix elements indicate edges between. To create uniform sized matrices, ion adjacency matrices were padded to size 33 × 33 with additional rows and columns of 0s. Matrices were then flattened into 1089 element vectors and cation–anion pairs were concatenated to create a 2178 element vector for each ionic liquid. These vectors were input into a 5-layer, feed-forward artificial neural network to predict ionic liquid properties. The neural network architecture consisted of a 2178 node input layer; 4 hidden layers of 64, 32, 16, and 8 nodes; and a 1 node linear output layer. ReLU and sigmoid activation functions as shown in Fig. 5, Adam optimization, constant learning rates, and early stopping were used to train the neural network using the PyTorch ML framework.⁷²

Fig. 5 Illustration of graph neural network (GNN) architecture used for making physical property predictions. Molecular connectivity is encoded into an adjacency matrix where rows and columns represent atoms, and entries represent if respective atoms are directly bonded. For GNN predictions, only molecular connectivity and temperature are used to predict physical properties, providing insight into if molecular structure, even lacking atomic identity and molecular forces information, can capture differences in physical properties for ionic liquids.

Artificial neural network

Artificial neural networks were trained to model ionic liquid properties using ionic liquid molecular descriptors and ionic liquid properties. Scalar inputs were derived from RDKit simulations and ILThermo. Input layer sizes varied from 2 to 52 as feature sets were alternated between experimental measurements, computationally derived individual ion features, and a combination of both feature sets. The neural network consisted of 4 hidden layers (2 hidden layers of 64 and 32 nodes with sigmoid activation functions then 2 hidden layers of 16 and 8 ReLU activation functions) and a 1 node linear output layer. Adam optimization and constant learning rates were used to train the neural network using the PyTorch ML framework.⁷²

Hybrid modeling

A hybrid ML model was created to rank descriptor importance for predicting deviations in molar conductivity from the Nernst–Einstein model by combining the Nernst–Einstein molar conductivity predictions with a random forest regression model:

We chose to use a random forest for this modeling as it yielded more consistent results as we updated model inputs. Beginning with viscosity and ion radii, inputs to the random forest model are updated iteratively using a greedy selection algorithm to include an additional input descriptor per iteration. In every model iteration, each RDKit descriptor is individually added to the random forest model then the model is trained and evaluated using 5-fold cross validation. The descriptor which provides the lowest mean squared error (MSE) is added to the model and the iterative steps are repeated until no further improvements in MSE are recorded, providing a ranked list of feature importance in predicting molar conductivity deviations.

Modified arrhenius model fit

To linearly fit conductivity and infer activation energy barriers using the modified Arrhenius model, the model equation is linearized to the following form:

We employ a linear regression to fit the regression coefficient and constant for each ionic liquid with more than 5 reported conductivity measurements at varying temperatures. Here, Λ_i is molar conductivities of ionic liquid i, the regression coefficient is , and the constant is ln(A_A). 95% confidence intervals are reported for the regressed parameters using standard error of regressed coefficients.

Model assessment

Mean squared error

Root Mean Squared Error

and coefficient of determination (R²)
were used to evaluate model performance. P is the modeled property, P_i is the measured value, P_predicted,i is the model prediction, and n is the total number of data points.

Data availability

All data and code needed to reproduce the analysis is available in the GitHub repository https://github.com/zavalab/ML/tree/master/IonicLiquids and is published on Zenodo at https://doi.org/10.5281/zenodo.15047258.

Author contributions

Research was conceptualized by M. A. G., V. M. Z., R. K. C., and J. E. U. Data was curated by R. K. C. and J. E. U. Formal Analysis was performed by J. E. U. Funding was acquired by M. A. G. and V. M. Z. Investigations were performed by J. E. U. Computational studies were performed by J. E. U. Data was analyzed by M. A. G., V. M. Z., R. K. C., and J. E. U. Methodology was developed by R. K. C. and J. E. U. Project Administration by M. A. G. and V. M. Z. Software was developed by R. K. C. and J. E. U. Resources were provided by M. A. G. and V. M. Z. Research was supervised by M. A. G. and V. M. Z. Result validation was performed by J. E. U. Visualizations were created by M. A. G., V. M. Z., R. K. C. and J. E. U. Written by M. A. G., V. M. Z., R. K. C., and J. E. U. Reviewed and Edited by M. A. G., V. M. Z., R. K. C., and J. E. U.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Support for this research was provided by the University of Wisconsin–Madison Office of the Vice Chancellor for Research with funding from the Wisconsin Alumni Research Foundation via the Research Forward project entitled “Accelerating the Discovery of Electrolyte Systems for Safe and Sustainable Energy Storage”. This material is based upon work supported by the National Science Foundation Graduate Research Fellowship Program under Grant No. DGE-2137424. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.

References

1. D. Lee, Consumer Product Safety Commission 2018.
2. M. Kaliaperumal, M. S. Dharanendrakumar, S. Prasanna, K. V. Abhishek, R. K. Chidambaram, S. Adams, K. Zaghib and M. V. Reddy, Materials, 2021, 14, 5676.
3. L. Kong, C. Li, J. Jiang and M. G. Pecht, Energies, 2018, 11, 2191.
4. P. V. Chombo and Y. Laoonual, J. Power Sources, 2020, 478, 228649.
5. P. Nurnberg, J. Atik, O. Borodin, M. Winter, E. Paillard and M. Schonhoff, J. Am. Chem. Soc., 2022, 144, 4657–4666.
6. J. C. Araque, J. J. Hettige and C. J. Margulis, J. Phys. Chem. B, 2015, 119, 12727–12740.
7. O. Nordness and J. F. Brennecke, Chem. Rev., 2020, 120, 12873–12902.
8. R. K. Cashen, M. M. Donoghue, A. J. Schmeiser and M. A. Gebbie, J. Phys. Chem. B, 2022, 126, 6039–6051.
9. M. Watanabe, M. L. Thomas, S. Zhang, K. Ueno, T. Yasuda and K. Dokko, Chem. Rev., 2017, 117, 7190–7239.
10. T. Welton, Biophys. Rev., 2018, 10, 691–706.
11. K. D. Fong, J. Self, B. D. McCloskey and K. A. Persson, Macromolecules, 2021, 54, 2575–2591.
12. D. Rauber, F. Philippi, B. Kuttich, J. Becker, T. Kraus, P. Hunt, T. Welton, R. Hempelmann and C. W. M. Kay, Phys. Chem. Chem. Phys., 2021, 23, 21042–21064.
13. F. Philippi, D. Pugh, D. Rauber, T. Welton and P. A. Hunt, Chem. Sci., 2020, 11, 6405–6422.
14. J. C. Araque, S. K. Yadav, M. Shadeck, M. Maroncelli and C. J. Margulis, J. Phys. Chem. B, 2015, 119, 7015–7029.
15. W. D. Amith, J. C. Araque and C. J. Margulis, J. Ionic Liq., 2022, 2, 100012.
16. L. Caradant, N. Verdier, G. Foran, D. Lepage, A. Prebe, D. Ayme-Perrot and M. Dolle, ACS Appl. Polym. Mater., 2021, 3, 6694–6704.
17. V. Delhorbe, D. Bresser, H. Mendil-Jakani, P. Rannou, L. Bernard, T. Gutel, S. Lyonnard and L. Picard, Macromolecules, 2017, 50, 4309–4321.
18. O. Borodin, J. Self, K. Persson, C. Wang and K. Xu, Joule, 2020, 4, 69–100.
19. C. A. Angell, Y. Ansari and Z. F. Zhao, Faraday Discuss., 2012, 154, 9–27.
20. D. Larcher and J. M. Tarascon, Nat. Chem., 2015, 7, 19–29.
21. M. A. Gebbie, A. M. Smith, H. A. Dobbs, A. A. Lee, G. G. Warr, X. Banquy, M. Valtiner, M. W. Rutland, J. N. Israelachvili, S. Perkin and R. Atkin, Chem. Commun., 2017, 53, 1214–1224.
22. A. Mariani, M. Bonomo, X. P. Gao, B. Centrella, A. Nucara, R. Buscaino, A. Barge, N. Barbero, L. Gontrani and S. Passerini, J. Mol. Liq., 2021, 324, 115069.
23. F. Philippi, D. Rauber, J. Zapp, C. Prasang, D. Scheschkewitz and R. Hempelmann, Chemphyschem, 2019, 20, 443–455.
24. D. R. MacFarlane, M. Forsyth, E. I. Izgorodina, A. P. Abbott, G. Annat and K. Fraser, Phys. Chem. Chem. Phys., 2009, 11, 4962–4967.
25. W. Xu, E. I. Cooper and C. A. Angell, J. Phys. Chem. B, 2003, 107, 6170–6178.
26. M. Videa and C. A. Angell, J. Phys. Chem. B, 1999, 103, 4185–4190.
27. H. K. Kashyap, H. V. R. Annapureddy, F. O. Raineri and C. J. Margulis, J. Phys. Chem. B, 2011, 115, 13212–13221.
28. P. Dhakal and J. K. Shah, Mol. Syst. Des. Eng., 2022, 7, 1344–1353.
29. P. Dhakal and J. K. Shah, Fluid Phase Equilibr., 2021, 549, 113208.
30. I. Baskin, A. Epshtein and Y. Ein-Eli, J. Mol. Liq., 2022, 351, 118616.
31. S. Koutsoukos, F. Philippi, F. Malaret and T. Welton, Chem. Sci., 2021, 12, 6820–6843.
32. J. O. Valderrama, J. M. Muñoz and R. E. Rojas, Korean J. Chem. Eng., 2011, 28, 1451–1457.
33. V. Venkatraman, S. Evjen, H. K. Knuutila, A. Fiksdahl and B. K. Alsberg, J. Mol. Liq., 2018, 264, 318–326.
34. S.-C. Li, H. Wu, A. Menon, K. A. Spiekermann, Y.-P. Li and W. H. Green, J. Am. Chem. Soc., 2024, 146, 23103–23120.
35. P. Nancarrow, A. Al-Othman, D. K. Mital and S. Dopking, Energy, 2021, 220.
36. F. Philippi and T. Welton, Phys. Chem. Chem. Phys., 2021, 23, 6993–7021.
37. S. Kim, J. Chen, T. Cheng, A. Gindulyte, J. He, S. He, Q. Li, B. A. Shoemaker, P. A. Thiessen, B. Yu, L. Zaslavsky, J. Zhang and E. E. Bolton, Nucleic Acids Res., 2021, 49, D1388–d1395.
38. E. E. Bolton, J. Chen, S. Kim, L. Han, S. He, W. Shi, V. Simonyan, Y. Sun, P. A. Thiessen, J. Wang, B. Yu, J. Zhang and S. H. Bryant, J. Cheminform., 2011, 3, 32.
39. RDKit: Open-Source Cheminformatics Software, https://www.rdkit.org/, accessed 8/8/2022, 2022.
40. S. B. Aziz, T. J. Woo, M. F. Z. Kadir and H. M. Ahmed, J. Sci., 2018, 3, 1–17.
41. A. P. Abbott, ChemPhysChem, 2004, 5, 1242–1246.
42. A. P. Abbott, ChemPhysChem, 2005, 6, 2502–2505.
43. J. Vila, P. Ginés, J. M. Pico, C. Franjo, E. Jiménez, L. M. Varela and O. Cabeza, Fluid Phase Equilibr/, 2006, 242, 141–146.
44. P. Bruce, Solid State Electrochemistry, Cambridge University Press, New York, NY, 1995.
45. S. M. Mousavisafavi, S. A. Mirkhani, F. Gharagheizi and J. Akbari, J. Therm. Anal. Calorim., 2013, 111, 235–246.
46. S. A. Mirkhani, F. Gharagheizi, P. Ilani-Kashkouli and N. Farahani, Thermochim. Acta, 2012, 543, 88–95.
47. A. F. Kazakov, J. W. Magee, R. D. Chirico, V. Diky, K. G. Kroenlein, C. D. Muzny and M. D. Frenkel, Ionic Liquids Database - ILThermo (v2.0), 2013.
48. D. Qian, M. Chris, K. Andrei, D. Vladimir, M. Joe, W. Jason, C. Robert, M. Kenneth and F. Michael, J. Chem. Eng. Data, 2007, 1151–1159.
49. K. R. Harris, J. Phys. Chem. B, 2019, 123, 7014–7023.
50. A. Knorr, P. Stange, K. Fumino, F. Weinhold and R. Ludwig, ChemPhysChem, 2016, 17, 458–462.
51. H. V. R. Annapureddy, H. K. Kashyap, P. M. De Biase and C. J. Margulis, J. Phys. Chem. B, 2010, 114, 16838–16846.
52. R. Hayes, G. G. Warr and R. Atkin, Chem. Rev., 2015, 115, 6357–6426.
53. C. Wu, A. De Visscher and I. D. Gates, J. Phys. Chem. B, 2018, 122, 6771–6780.
54. S. Tsuzuki, H. Tokuda, K. Hayamizu and M. Watanabe, J. Phys. Chem. B, 2005, 109, 16474–16481.
55. M. A. Gebbie, H. A. Dobbs, M. Valtiner and J. N. Israelachvili, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 7432–7437.
56. E. L. Bennett, C. Song, Y. Huang and J. Xiao, J. Mol. Liq., 2019, 294, 111571.
57. H. Weingärtner, Z. Phys. Chem., 2006, 220, 1395–1405.
58. P. A. Hunt, I. R. Gould and B. Kirchner, Aust. J. Chem., 2007, 60, 9–14.
59. J. N. Israelachvili, Intermolecular and Surface Forces, Academic Press, 255 Wyman St, Waltham, MA 02451, USA, 3 edn, 2011.
60. P. A. Hunt, J. Phys. Chem. B, 2007, 111, 4844–4853.
61. M. Ue, J. Electrochem. Soc., 1994, 141, 3336.
62. K. B. Dhungana, L. F. O. Faria, B. Wu, M. Liang, M. C. C. Ribeiro, C. J. Margulis and E. W. Castner Jr, J. Chem. Phys., 2016, 145.
63. D. Penley, X. Y. Wang, Y. Y. Lee, M. N. Garaga, R. Ghahremani, S. Greenbaum, E. J. Maginn and B. Gurkan, J. Chem. Eng. Data, 2022, 67, 1810–1823.
64. J. McAlpine, A. Bloemendal, J. E. Dahl, R. M. K. Carlson, I. A. Guzei, C. F. M. Clewett, B. O. Tkachenko, P. R. Schreiner and M. A. Gebbie, Chem. Mater., 2023, 35, 3545–3554.
65. H. Tokuda, K. Ishii, M. A. B. H. Susan, S. Tsuzuki, K. Hayamizu and M. Watanabe, J. Phys. Chem. B, 2006, 110, 2833–2839.
66. T. Vogl, P. Goodrich, J. Jacquemin, S. Passerini and A. Balducci, J. Phys. Chem. C, 2016, 120, 8525–8533.
67. J. O. Valderrama and R. E. Rojas, Fluid Phase Equilibr., 2010, 297, 107–112.
68. M. McLin and C. A. Angell, J. Phys. Chem., 1988, 92, 2083–2086.
69. F. Philippi, D. Rauber, K. L. Eliasen, N. Bouscharain, K. Niss, C. W. M. Kay and T. Welton, Chem. Sci., 2022, 13, 2735–2743.
70. C. M. Bishop and H. Bishop, Deep Learning: Foundations and Concepts, Springer, Cham, Switzerland, 2024.
71. D. Grattarola, D. Zambon, F. M. Bianchi and C. Alippi, IIEEE Trans. Neural Network. Learn. Syst., 2024, 35, 2708–2718.
72. A. Paszke, S. Gross, F. Massa, A. Lerer, J. Bradbury, G. Chanan, T. Killeen, Z. Lin, N. Gimelshein and L. Antiga, Adv. Neural Inf. Process. Syst., 2019, 32, 8024–8035.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dd00378k

---