Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
pyRheo: an open-source Python package for complex rheology†
Isaac Y.
Miranda-Valdez
 *,
Aaro
Niinistö
,
Tero
Mäkinen
*,
Aaro
Niinistö
,
Tero
Mäkinen
 ,
Juha
Lejon
,
Juha
Koivisto
,
Juha
Lejon
,
Juha
Koivisto
 and
Mikko J.
Alava
and
Mikko J.
Alava
Department of Applied Physics, Aalto University, P. O. Box 15600, 00076 Aalto, Espoo, Finland. E-mail: isaac.mirandavaldez@aalto.fi
First published on 20th March 2025
Abstract
Mathematical modeling is a powerful tool in rheology, and we present pyRheo, an open-source package for Python designed to streamline the analysis of creep, stress relaxation, small amplitude oscillatory shear, and steady shear flow tests. pyRheo contains a comprehensive selection of viscoelastic models, including fractional order approaches. It integrates model selection and fitting features and employs machine intelligence to suggest a model to describe a given dataset. The package fits the suggested model or one chosen by the user. An advantage of using pyRheo is that it addresses challenges associated with sensitivity to initial guesses in parameter optimization. It allows the user to iteratively search for the best initial guesses, avoiding convergence to local minima. We discuss the capabilities of pyRheo and compare them to other tools for rheological modeling of soft matter. We demonstrate that pyRheo significantly reduces the computation time required to fit high-performance viscoelastic models.
Introduction
Soft matter, such as cells, tissues, and polymers, displays complexity in its composition, structure, and dynamic properties. As such, soft matter exhibits a time-dependent response in its mechanical properties known as viscoelasticity.1–3 Quantifying the viscoelastic behavior of soft matter is critical for inferring its dynamics and microstructure. Rheology, as the branch of physics concerned with the deformation of matter, uses mathematical modeling to classify the viscoelastic response of soft matter. Furthermore, rheology abstracts parameters that can enable characterizing and predicting the response of soft matter at short and long timescales. The latter is of pivotal importance in the manufacturing and design of many materials and has widespread applications in fields such as tissue engineering, cell growth, and disease screening.4–7Mathematical modeling in rheology is a gateway to understanding the structure–property relationship for soft matter. However, choosing a model, data processing of the experimental measurements, and curve-fitting routines can represent a steep learning curve in conducting and interpreting viscoelastic experiments, due to the highly nonlinear nature of the behavior. For example, rheological models based on fractional order derivatives commonly require a curve-fitting routine that involves computationally expensive operations, such as the Mittag–Leffler function—most commonly represented by an infinite sum of terms containing the gamma function.8–10 Another challenge in the mathematical modeling of viscoelasticity is defining a cost function that allows selecting a model and further finding its parameters.11–13 Therefore, choosing a model and inferring its parameters are two critical decisions that are highly uncertain and have non-unique solutions.13
Currently, there are numerous open-source rheological tools. For example, Boudara et al.14 developed RepTate which offers comprehensive tools for analyzing linear and nonlinear rheological data. In particular, RepTate provides an interface to analyze entangled polymer melts using theoretical frameworks such as the Likhtman–McLeish theory and multi-mode Maxwell analysis. Other remarkable efforts include the work of Luciano et al.,15 who designed oreo to analyze nonlinear rheological data, and the work of Tassieri et al.16 who developed i-Rheo to infer linear viscoelastic properties with Fourier transform analysis. Additionally, Shanbhag17 developed pyReSpect as a tool to extract relaxation spectra from stress relaxation experiments. Nonetheless, despite these great efforts, no open-source tools for Python integrate rheological frameworks based on fractional calculus. Therefore, this work introduces pyRheo, an open-source Python package that assists in model selection and fitting procedures for several types of rheology experiments.
pyRheo focuses on streamlining the mathematical modeling of rheological data obtained in the linear viscoelastic regime using fractional rheology.18–20 First, pyRheo uses machine intelligence to suggest a rheological model likely to describe a provided dataset. Then, it allows users to fit the proposed model or choose a different one. pyRheo enables the user to automatically or manually choose from several fractional rheological models. pyRheo focuses on fractional order viscoelastic models which have proved to be able to provide valuable insights into soft materials, such as food gels, structured fluids, biological tissues, cells, and polymers.21–27 For example, fractional models have allowed linking the microstructure of colloidal gels to their relaxation spectrum and elasticity.19,20
pyRheo is highlighted as a tool for analyzing rheological data readily and as an interface that can be coupled with machine learning algorithms widely available for Python.28 The following sections demonstrate pyRheo's features. We present a set of robust validations against experimental results and other public toolkits to check the accuracy and computational performance of our code package in characterizing soft materials such as biological tissues, polymers, foams, foodstuff, and gels. We note that pyRheo is available via its GitHub repository, where all the Python scripts to compute every single example presented in this paper and its ESI† are available as Jupyter Notebooks. Furthermore, we have created a simple graphical user interface (GUI) for those users whose programming skills may limit their access to pyRheo. The GUI file can be found in the GitHub repository.
Results
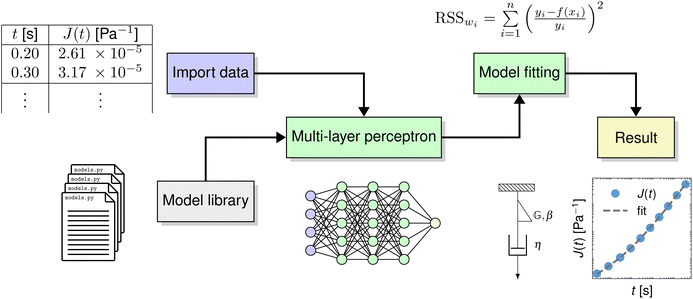
Fig. 1 highlights, in green boxes, the two primary features of pyRheo: (i) it utilizes machine learning to determine which model best fits the user's rheological data, and (ii) it fits a rheological model to that data. The workflow of pyRheo is summarized in four steps: (1) importing data, (2) selecting a model, (3) fitting the model, and (4) analyzing the results. ESI Note 1† details these four steps, while ESI Note 2† describes all the models available in pyRheo, including their constitutive equations and representative plots. In step (2), users have the option to call a pre-trained machine learning model, specifically a Multi-Layer Perceptron (MLP), which can help infer the model that most likely describes the provided dataset. ESI Note 3† explains how the MLP model was trained and assesses its performance using synthetic data.Model prediction and fitting
To demonstrate that pyRheo's capabilities lead to accurate and computationally efficient performance, we evaluate pyRheo using data from existing literature. In this section, we present the results obtained from fitting creep and stress relaxation data of two biological materials. Furthermore, we show how users of pyRheo can take advantage of available Python packages specifically designed for rheology. For instance, Lennon et al.29 have developed a robust algorithm for creating master curves based on Gaussian process regression. Here, as well as in some of the demonstrations provided in ESI Note 4,† we showcase the results of integrating Lennon et al.'s29 package with pyRheo.First, we test the performance of pyRheo using the creep data measured for a perihepatic abscess reported by Shih et al.30 and the stress relaxation data of a fish muscle reported by Song et al.2. The first step in pyRheo's workflow is to import the rheological data of creep compliance J(t) and relaxation modulus G(t) into the MLP model. In the cases shown in Fig. 2a and b, the MLP model classifies the data from creep as FractionalKelvinVoigt and stress relaxation as FractionalMaxwell. FractionalKelvinVoigt consists of two springpots connected in parallel, whereas FractionalMaxwell is built by two springpots connected in series (see insets in Fig. 2).2 The predicted model is automatically fitted to each dataset by pyRheo, and the fitting results are depicted by the dashed lines in Fig. 2a and b.
 | ||
| Fig. 2 Creep and stress relaxation data classified and fitted with pyRheo. (a) Creep compliance J(t) of a perihepatic abscess sample. The curve is fitted using the auto function in pyRheo, which classifies the data as a FractionalKelvinVoigt. (b) Relaxation modulus G(t) of a fish muscle classified and fitted with FractionalMaxwell. The raw data of the perihepatic abscess was reproduced from Shih et al.30 and the data of the fish muscle from Song et al.2 | ||
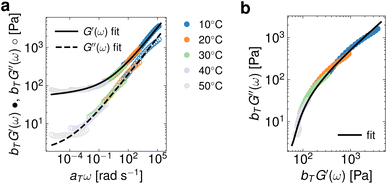
In Fig. 3, we showcase an instance of coupling Lennon et al.'s29 package with pyRheo to analyze the small amplitude oscillatory shear (SAOS) data of an interpenetrating-network hydrogel made of cellulose nanofibers and methylcellulose. We import the master curve data from G′(ω) and G′′(ω) to the MLP classifier of pyRheo. The MLP classifies the G′(ω) and G′′(ω) data as a FractionalKelvinVoigt. The result of fitting this model to the master curve data is depicted by the solid and dashed lines in Fig. 3a. Furthermore, we demonstrate in Fig. 3b how to utilize the model predictions generated with pyRheo to easily construct other visualizations such as Cole–Cole diagrams. This is feasible because pyRheo stores the model results as an object the user can call to, for example, predict the material response according to a specified ω range. Consequently, this flexibility allows for estimating model predictions to higher and lower ω values.
pyRheo's model fitting and prediction tools are specifically designed to address fractional order viscoelastic models, as these models provide a more succinct representation of viscoelastic phenomena compared to traditional multi-mode fitting methodologies, such as generalized Maxwell models. This advantage becomes particularly pronounced when characterizing the linear viscoelastic response of entangled polymer melts.
As illustrated in Fig. 4, we compare the fitting outcomes for a polyisoprene melt using the FractionalZener model (depicted in Fig. 4a) with those obtained from a generalized Maxwell model employing eight modes (shown in Fig. 4b). Both models effectively capture the behavior of the storage modulus G′(ω) and the loss modulus G′′(ω). Notably, the fractional order model necessitates only six parameters, whereas the generalized Maxwell model requires 16 parameters, thereby illustrating the enhanced efficiency of the fractional framework. Schmidt et al.31 have thoroughly discussed the potential of fractional frameworks in comparison to generalized approaches.
 | ||
| Fig. 4 Comparison between pyRheo and RepTate frameworks applied to describe the small amplitude oscillatory shear (SAOS) data of a polyisoprene melt (data from Boudara et al.14). (a) pyRheo fitting using FractionalZener. (b) RepTate fitting using a generalized Maxwell model with eight modes. | ||
This section is complemented by additional results in ESI Note 4,† where we present more fitting routines, which include materials such as mucus, foams, polymer networks, gels, plastics, food colloids, and polysaccharides. The examples included in ESI Note 4† present data analysis from steady shear flow experiments, which are not detailed in the main article due to their lower computational complexity. For transparency, every demonstration with pyRheo is available as a Jupyter Notebook on the pyRheo GitHub page, which users can test and adapt to suit their needs.
Performance of Mittag–Leffler function in pyRheo
When using fractional rheological models, one often encounters the Mittag–Leffler (ML) function in the constitutive equation of the rheological model.10 The ML function is expensive to compute as it is represented by an infinite sum of terms with gamma functions Γ. In its generalized form, the ML function uses the following notation, | (1) |
There are several methods for numerically computing the ML function, either through the numerical inversion of its Laplace transform or by using mixed techniques, including Taylor series, asymptotic series, and integral representations.32 Notable examples of these methods can be found in the algorithms developed by Garrappa33 and Podlubny.34
In fitting routines, the computational demands of the ML function can become increasingly sensitive to the size of the dataset. This often leads to exponential growth in computation time as the dataset expands. The latter is common in master curve fitting and creep and stress relaxation tests, where the sampling rate is higher than in SAOS and steady shear flow tests. Current methods for reducing the computation time of the ML function typically involve downsampling. However, this process introduces uncertainty and can lead to non-unique outcomes in the fitting. The computational demand of the ML function is also evident when the fitting involves iterative optimization of multiple parameters; poor initial parameter guesses can result in slower convergence or even lead to convergence to a local minima. Consequently, finding the best model parameters may require restarting the optimization with a different initial guess for the model parameters.
To the best of our knowledge, using Padé approximations to compute rheological models has not been extensively researched. Thus, pyRheo exploits the Padé approach to reduce the computation time spent in fitting fractional rheological models by implementing the ML function based on the global Padé approximations proposed by Zeng and Chen32 and Sarumi et al.35. In Fig. 5, we compare the performance of pyRheo against popular methodologies for fitting fractional rheological models, which are based on the MATLAB toolkit published by Song et al.2 and the RHEOS package for Julia programming language.36 The MATLAB toolkit uses Garrappa's algorithm33 to compute the ML function, whereas RHEOS uses Gorenflo et al.'s37 approach.
 | ||
| Fig. 5 Performance comparison of fitting routines across pyRheo (Python), MATLAB, and RHEOS (Julia) for the relaxation modulus G(t) of polyethylene (PE) and fish muscle. (a) Fitting results for PE from each implementation using FractionalZenerSolidS. (b) Normalized computation times tn for fitting routines on PE; RHEOS required downsampling to 20% of the dataset, while pyRheo and MATLAB processed the full dataset. (c) Fitting results for fish muscle from each implementation using FractionalMaxwell, based on Song et al.2. (d) Normalized computation times tn for fish muscle fitting; RHEOS required downsampling to 10%, while others used the complete dataset. All computations were on a system with an Intel Core i5-12600K CPU at 3.7 GHz, 31 GB RAM, and 1 TB SSD, running Ubuntu 20.04. | ||
Accordingly, in Fig. 5a, we fitted a FractionalZenerSolidS to the relaxation modulus G(t) of a polyethylene (PE) sample to show the applications of pyRheo in other fields of soft matter. For the examples reported here, we chose Pade32 in pyRheo; in other words, a second-order global Padé approximation. Fig. 5b displays the computation time spent in fitting the stress relaxation data of PE. The fitting requires computing the one-parameter ML function (i.e., b = 1). pyRheo, MATLAB, and RHEOS yield similar parameter values, as seen in Table 1. However, it is essential to note that the computation times tn vary significantly among the three implementations. For the stress relaxation data of PE, pyRheo identifies the optimal parameters one to three orders of magnitude faster than MATLAB and RHEOS, respectively. We normalize the computation times by the size of the dataset to enable a fair performance comparison across the different implementations. In the case of RHEOS, we downsampled the PE dataset to contain 20% (tn is obtained by multiplying the real time by a factor of five) of the original one since the computation time extended beyond the capabilities of a desktop computer.
In Fig. 5c, we show again the stress relaxation data of the fish muscle from Fig. 2b. Fig. 5d shows that the computation of FractionalMaxwell is more time-consuming than that of the FractionalZenerSolidS. The latter is due to the multi-parametric nature of the ML function used in the FractionalMaxwell. Again, in Table 1, we observe that the three implementations find similar parameter values for the fish muscle. Nonetheless, the computation times with pyRheo are shorter than those needed by MATLAB and RHEOS. pyRheo leverages the computational efficiency of the ML function thanks to the global Padé approximation. Again, we normalized the computation times for the fish muscle data to enable a fair performance comparison across the different implementations. In the case of RHEOS, we downsampled the datasets to contain 10% of the original ones (i.e., tn is the real computation time scaled by a factor of ten).
In addition to the global Padé approximation, we also programmed in pyRheo the option to use Garrappa's algorithm33 for the evaluation of the Mittag–Leffler function. The algorithm was adapted from its MATLAB script.38 The inclusion of Garrappa's algorithm allows users to benefit from its robust computation method, especially in cases where the Mittag–Leffler function needs to be evaluated for parameters that pose challenges for the global Padé approximation. This flexibility is crucial as it ensures that accurate and reliable results can be obtained across a broader range of applications and parameter settings, reinforcing pyRheo's position as a trusted tool for researchers and engineers in rheology.
In ESI Notes 5 and 6,† we detail the global Padé approximations and provide examples demonstrating the differences between the global Padé approximation and Garrappa's algorithm when computing the FractionalMaxwellGel, FractionalMaxwellLiquid, and FractionalMaxwell. These examples showcase the accuracy and reliability of each algorithm in various scenarios. Such detailed comparisons help users make informed decisions about which algorithm to employ for their specific needs, thereby enhancing the overall utility and effectiveness of pyRheo in addressing complex rheological analyses.
Discussion
Our Python package, pyRheo, delivers significant computational improvements that enable using fractional order viscoelastic models to describe soft materials effectively. These models have often been overlooked due to their computational complexity, making their implementation non-intuitive and challenging. In recent years, we have seen increasing use of fractional frameworks to describe the linear viscoelastic data of soft matter.1,2,20,24,25,27 This is because the parameters in fractional models can be linked to the material microstructure.19 Furthermore, they offer a more compact description of SAOS, creep, and stress relaxation experiments than traditional multi-mode Maxwell frameworks. For example, in Fig. 4, we compare the fitting for the SAOS data of an entangled polyisoprene melt sample using a pyRheo's fractional model (Fig. 4a) and RepTate's implementation of the generalized Maxwell model with eight modes (Fig. 4b). While pyRheo is not intended to replace other open-access rheological tools like RepTate, it is a complementary resource for the soft matter community. pyRheo finally addresses the need for Python packages that include fractional viscoelastic models and offers effective computation options.Our work demonstrates how to reduce the computational cost of fitting routines involving the ML function, which is part of many models constitutive equations for creep compliance J(t) and relaxation modulus G(t). We decreased the computation times by utilizing Padé approximations to compute the ML function. This advancement allows for exploring a wider range of models and methodologies, requiring fewer resources and less time. Besides faster computation of models with the ML function, the Padé approximation enables pyRheo to offer a solution to a common problem in fitting routines of rheological models, which is sensitivity to the initial guesses. Commonly, a bad choice of initial guess might lead the parameter optimization process to converge to local minima. pyRheo presents two solutions to determine the initial guesses: random search and Bayesian optimization (BO).28
In the data analyzed in Fig. 3 and 5, we have implemented a random search of initial guesses. In all cases, we have fixed a maximum of ten restarts of the optimization algorithm that seeks to minimize the weighted residual sum of squares RSSwi. As shown in Fig. 5, our brute-force approach combined with the global optimization algorithms from SciPy39 yields faster computations than the MATLAB and RHEOS implementations. On the other hand, in ESI Note 7,† our BO approach was also shown to be effective in finding suitable initial guesses for fitting the creep data of a mucus gel. Our work reveals how random search and BO methodologies, techniques that are used in hyperparameter tuning of machine learning, can be adapted to traditional fitting routines.
The fitting tools available in pyRheo, along with its integrated machine intelligence, position it as a valuable resource for developing automated laboratories capable of conducting high-throughput testing and analysis. In the future, the Multi-Layer Perceptron (MLP) classifier could assist high-throughput rheometers in reformulating and optimizing materials. However, it is important to note that the current MLP classifier integrated into pyRheo cannot label rheological data related to Zener models. This limitation arises because the responses of Zener models overlap with those of Maxwell and Kelvin–Voigt models. One potential strategy to address this issue would be to use multi-label classifiers.
We have also integrated in pyRheo an option for the user to simply call a model's function (evaluators class). This option allows the user to compute the fractional models by assigning fixed values to the model parameters, as shown in the plots in ESI Note 2.† As shown by Miranda-Valdez et al.,40 this evaluator class offers the user flexibility to design their own problems.
Methods
pyRheo's methodology has two main features: (i) providing a machine learning decision of what model likely describes the rheological data and (ii) fitting a rheological model to the data. Based on these two features the package can analyze creep, stress relaxation, SAOS, and steady shear flow data.Step 1: importing data
First, the user should import the data pertinent to the type of rheological dataset. Depending on the specific nature of the dataset, users should import the relevant features and their corresponding class (creep, stress relaxation, SAOS, or SteadyShear) following Table 2. pyRheo is designed to work with material functions, so one must provide at least two data vectors. For example, for creep and stress relaxation data, it is expected to import a time t vector together with its corresponding material function J(t) or G(t). Alternatively, for SAOS data, the user must import angular frequency ω and the materials functions storage modulus G′(ω) and loss modulus G′′(ω).Step 2: model selection
After importing the data, the user shall select to analyze their data using the auto method or by manually specifying a model according to Table 2. The auto method uses a pre-trained neural network based on a Multi-Layer Perceptron (MLP). Each class has its own MLP classifier, which has been trained using 1 million computations of the corresponding material function (e.g., J(t)) derived from the constitutive equations of the Maxwell, SpringPot, FractionalMaxwellGel, FractionalMaxwellLiquid, FractionalMaxwell, and FractionalKelvinVoigt.The accuracy (with synthetic data) of the MLP classifiers ranges from 70 to 80%. We suggest using the auto method as a first approximation to identify the type of rheological behavior. More detailed information about the machine learning training process and performance is disclosed in the ESI.†
Step 3: model fitting
Parameter optimization with pyRheo follows the common practice of minimizing the weighted residual sum of squares,2,13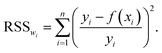 | (2) |
Users may define their own initial guesses and parameter bounds (automatic bounds and random initial guesses by default). Then, to minimize RSSwi, users can choose from several minimization algorithms implemented on SciPy,39 such as Nelder–Mead, Powell, and L-BFGS-B (Powell by default).
As shown in Table 2, an advantage of using pyRheo is that it addresses the challenges associated with sensitivity to initial guesses in parameter optimization. In other words, if an initial guess is close to a local minimum, the minimization algorithm may converge there instead of the global minimum. Therefore, pyRheo allows the user to restart the fitting process multiple times with random initial parameter values and then take as the final result the iteration with the lowest RSSwi. By generating a diverse set of random starting points, this brute-force approach increases the likelihood of exploring different regions of the parameter space, thus avoiding local minima.
Another method that pyRheo offers for defining initial guesses is Bayesian Optimization (BO).41–43 In this approach, pyRheo creates a mapping from the parameter space  to the error space
to the error space  using Gaussian Process Regression (GPR), represented as
using Gaussian Process Regression (GPR), represented as  where g is the Gaussian Process. The surrogate model
where g is the Gaussian Process. The surrogate model  is developed by computing the constitutive equation of the target model with fixed parameter values and then recording the difference (residuals) between this computation and the data being analyzed. The goal of BO is to minimize ε by exploring various combinations of parameter values, guided by an acquisition function known as expected improvement, which balances exploration and exploitation of the parameter space. Afterward, pyRheo uses the BO solution as the initial guess for the minimization algorithm. Miranda-Valdez et al.40 present this methodology in detail and expand it further.
is developed by computing the constitutive equation of the target model with fixed parameter values and then recording the difference (residuals) between this computation and the data being analyzed. The goal of BO is to minimize ε by exploring various combinations of parameter values, guided by an acquisition function known as expected improvement, which balances exploration and exploitation of the parameter space. Afterward, pyRheo uses the BO solution as the initial guess for the minimization algorithm. Miranda-Valdez et al.40 present this methodology in detail and expand it further.
Step 4: analysis of results
After fitting the target model to the rheological data, the results are stored as an object variable that contains all the necessary components for prediction, visualization, and further data analysis. Users can learn more from pyRheo's documentation and the examples available on its GitHub repository.Data availability
The code for pyRheo, data analysis scripts of this article, and the data for this article are available at pyRheo's Github at https://github.com/mirandi1/pyRheo.git with https://doi.org/10.5281/zenodo.15041024. The version of the code employed for this study is version 1.0.1.Author contributions
Isaac Y. Miranda-Valdez: conceptualization, methodology, software, formal analysis, visualization, investigation, data curation, writing – original draft, writing – review & editing, project administration, and funding acquisition. Aaro Niinistö: investigation and software. Tero Mäkinen: validation and writing – review & editing. Juha Lejon: investigation. Juha Koivisto: supervision, validation, writing – review & editing, funding acquisition. Mikko J. Alava: supervision, validation, writing – review & editing, funding acquisition, project administration.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Dr Jesús G. Puente-Córdova for his suggestions and feedback during the conceptualization of pyRheo as well as for sharing experimental data for testing tasks. I. M. V. acknowledges the Vilho, Yrjö, and Kalle Väisälä Foundation of the Finnish Academy of Science and Letters for personal funding. M. J. A. acknowledges funding from the Finnish Cultural Foundation. M. J. A., J. K., T. M. and I. M. V. acknowledge funding from Business Finland (211909, 211989). M. J. A. and J. K. acknowledge funding from FinnCERES flagship (151830423), Business Finland (211835), and Future Makers Programs. Aalto Science-IT project is acknowledged for computational resources.Notes and references
- A. Bonfanti, J. L. Kaplan, G. Charras and A. Kabla, Soft Matter, 2020, 16, 6002–6020 RSC.
- J. Song, N. Holten-Andersen and G. H. McKinley, Soft Matter, 2023, 19, 7885–7906 RSC.
- R. G. Ricarte and S. Shanbhag, Polym. Chem., 2024, 15, 815–846 RSC.
- J. Steinwachs, C. Metzner, K. Skodzek, N. Lang, I. Thievessen, C. Mark, S. Münster, K. E. Aifantis and B. Fabry, Nat. Methods, 2016, 13, 171–176 CrossRef CAS.
- F. Serwane, A. Mongera, P. Rowghanian, D. A. Kealhofer, A. A. Lucio, Z. M. Hockenbery and O. Campàs, Nat. Methods, 2017, 14, 181–186 CrossRef CAS PubMed.
- P.-H. Wu, D. R.-B. Aroush, A. Asnacios, W.-C. Chen, M. E. Dokukin, B. L. Doss, P. Durand-Smet, A. Ekpenyong, J. Guck and N. V. Guz, et al. , Nat. Methods, 2018, 15, 491–498 CrossRef CAS PubMed.
- M. A. Liegeois, M. Braunreuther, A. R. Charbit, W. W. Raymond, M. Tang, P. G. Woodruff, S. A. Christenson, M. Castro, S. C. Erzurum and E. Israel, et al. , JCI Insight, 2024, 9, e181024 CrossRef PubMed.
- H. J. Haubold, A. M. Mathai and R. K. Saxena, J. Appl. Math., 2011, 2011, 1–51 CrossRef.
- A. Jaishankar and G. H. McKinley, J. Rheol., 2014, 58, 1751–1788 CrossRef CAS.
- F. Mainardi, Entropy, 2020, 22, 1359 CrossRef PubMed.
- R. H. Ewoldt, M. T. Johnston and L. M. Caretta, in Experimental Challenges of Shear Rheology: How to Avoid Bad Data, ed. S. E. Spagnolie, Springer New York, New York, NY, 2015, pp. 207–241 Search PubMed.
- J. B. Freund and R. H. Ewoldt, J. Rheol., 2015, 59, 667–701 CrossRef CAS.
- P. K. Singh, J. M. Soulages and R. H. Ewoldt, Rheol. Acta, 2019, 58, 341–359 CrossRef CAS.
- V. A. H. Boudara, D. J. Read and J. Ramírez, J. Rheol., 2020, 64, 709–722 CrossRef CAS.
- G. Luciano, S. Berretta, K. H. Liland, G. J. Donley and S. A. Rogers, SoftwareX, 2021, 15, 100769 CrossRef.
- M. Tassieri, M. Laurati, D. J. Curtis, D. W. Auhl, S. Coppola, A. Scalfati, K. Hawkins, P. R. Williams and J. M. Cooper, J. Rheol., 2016, 60, 649–660 CrossRef CAS.
- S. Shanbhag, Macromol. Theory Simul., 2019, 28, 1900005 Search PubMed.
- A. Jaishankar and G. H. McKinley, Proc. R. Soc. A, 2013, 469, 20120284 Search PubMed.
- M. Bantawa, B. Keshavarz, M. Geri, M. Bouzid, T. Divoux, G. H. McKinley and E. Del Gado, Nat. Phys., 2023, 19, 1178–1184 Search PubMed.
- B. Keshavarz, D. G. Rodrigues, J.-B. Champenois, M. G. Frith, J. Ilavsky, M. Geri, T. Divoux, G. H. McKinley and A. Poulesquen, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2022339118 CAS.
- T. Faber, A. Jaishankar and G. H. McKinley, Food Hydrocolloids, 2017, 62, 325–339 CAS.
- I. Y. Miranda-Valdez, J. G. Puente-Córdova, F. Y. Rentería-Baltiérrez, L. Fliri, M. Hummel, A. Puisto, J. Koivisto and M. J. Alava, Food Hydrocolloids, 2024, 147, 109334 CAS.
- M. Caputo, J. M. Carcione and F. Cavallini, Ultrasound Med. Biol., 2011, 37, 996–1004 Search PubMed.
- J. Bauland, G. Manna, T. Divoux and T. Gibaud, Phys. Rev. Mater., 2024, 8, L072601 CAS.
- G. Legrand, G. P. Baeza, M. Peyla, L. Porcar, C. Fernández-De-Alba, S. Manneville and T. Divoux, ACS Macro Lett., 2024, 234–239 CAS.
- A. Y. Tiong, S. Crawford, N. C. Jones, G. H. McKinley, W. Batchelor and L. van't Hag, Food Struct., 2024, 40, 100374 CAS.
- I. Y. Miranda-Valdez, M. Sourroubille, T. Mäkinen, J. G. Puente-Córdova, A. Puisto, J. Koivisto and M. J. Alava, Cellulose, 2024, 31, 1545–1558 CAS.
- I. Y. Miranda-Valdez, T. Mäkinen, S. Coffeng, A. Päivänsalo, L. Jannuzzi, L. Viitanen, J. Koivisto and M. J. Alava, Mater. Horiz., 2025, 12, 1855–1862 CAS.
- K. R. Lennon, G. H. McKinley and J. W. Swan, Data-Centric Engineering, 2023, 4, e13 Search PubMed.
- A. Shih, S. J. Chung, O. B. Shende, S. E. Herwald, A. M. Vezeridis and G. G. Fuller, Phys. Fluids, 2024, 36, 111919 CAS.
- R. F. Schmidt, H. H. Winter and M. Gradzielski, Soft Matter, 2024, 20, 7914–7925 CAS.
- C. Zeng and Y. Q. Chen, Fract. Calc. Appl. Anal., 2015, 18, 1492–1506 Search PubMed.
- R. Garrappa, SIAM J. Numer. Anal., 2015, 53, 1350–1369 CrossRef.
- D. Sierociuk, I. Podlubny and I. Petras, IEEE Trans. Control Syst. Technol., 2013, 21, 459–466 Search PubMed.
- I. O. Sarumi, K. M. Furati and A. Q. M. Khaliq, J. Sci. Comput., 2020, 82, 1–27 CrossRef.
- J. Kaplan, A. Bonfanti and A. Kabla, RHEOS.jl – A Julia package for rheology data analysis, 2019 Search PubMed.
- R. Gorenflo, J. Loutchko and Y. Loutchko, Fract. Calc. Appl. Anal., 2002, 5, 491–518 Search PubMed.
- R. Garrappa, The Mittag–Leffler Function, 2024, https://www.mathworks.com/matlabcentral/fileexchange/48154-the-mittag-leffler-function, MATLAB Central File Exchange, retrieved November 12, 2024 Search PubMed.
- P. Virtanen, R. Gommers, T. E. Oliphant, M. Haberland, T. Reddy, D. Cournapeau, E. Burovski, P. Peterson, W. Weckesser, J. Bright, S. J. van der Walt, M. Brett, J. Wilson, K. J. Millman, N. Mayorov, A. R. J. Nelson, E. Jones, R. Kern, E. Larson, C. J. Carey, İ. Polat, Y. Feng, E. W. Moore, J. VanderPlas, D. Laxalde, J. Perktold, R. Cimrman, I. Henriksen, E. A. Quintero, C. R. Harris, A. M. Archibald, A. H. Ribeiro, F. Pedregosa, P. van Mulbregt and SciPy 1.0 Contributors, Nat. Methods, 2020, 17, 261–272 CrossRef CAS PubMed.
- I. Y. Miranda-Valdez, T. Mäkinen, J. Koivisto and M. J. Alava, Bayesian optimization to infer parameters in viscoelasticity, 2025, https://arxiv.org/abs/2502.19132 Search PubMed.
- T. Head, MechCoder, G. Louppe, I. Shcherbatyi, fcharras, Z. Vinícius, cmmalone, C. Schröder, nel215, N. Campos, T. Young, S. Cereda, T. Fan, rene rex, K. K. Shi, J. Schwabedal, carlosdanielcsantos, Hvass-Labs, M. Pak and A. Fabisch, scikit-optimize/scikit-optimize: v0.5.2, 2018 Search PubMed.
- I. Y. Miranda-Valdez, L. Viitanen, J. Mac Intyre, A. Puisto, J. Koivisto and M. Alava, Carbohydr. Polym., 2022, 298, 119921 CrossRef CAS PubMed.
- V. Torsti, T. Mäkinen, S. Bonfanti, J. Koivisto and M. J. Alava, APL Mach. Learn., 2024, 2, 016119 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5dd00021a |
| This journal is © The Royal Society of Chemistry 2025 |






![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif)