Open Access Article
Open Access ArticleComprehensive sampling of coverage effects in catalysis by leveraging generalization in neural network models†
Daniel
Schwalbe-Koda
 *abd,
Nitish
Govindarajan
*abd,
Nitish
Govindarajan
 *acd and
Joel B.
Varley
ad
*acd and
Joel B.
Varley
ad
aMaterials Science Division, Lawrence Livermore National Laboratory, Livermore, CA 94550, USA
bDepartment of Materials Science and Engineering, University of California, Los Angeles, Los Angeles, CA 90095, USA. E-mail: dskoda@ucla.edu
cSchool of Chemistry, Chemical Engineering, and Biotechnology, Nanyang Technological University, 21 Nanyang Link, Singapore 637371, Singapore. E-mail: nitish.govindarajan@ntu.edu.sg
dLaboratory for Energy Applications for the Future (LEAF), Lawrence Livermore National Laboratory, Livermore, CA 94550, USA
First published on 9th December 2024
Abstract
Sampling high-coverage configurations and predicting adsorbate–adsorbate interactions on surfaces are highly relevant to understand realistic interfaces in heterogeneous catalysis. However, the combinatorial explosion in the number of adsorbate configurations among diverse site environments presents a considerable challenge in accurately estimating these interactions. Here, we propose a strategy combining high-throughput simulation pipelines and a neural network-based model with the MACE architecture to increase sampling efficiency and speed. By training the models on unrelaxed structures and energies, which can be quickly obtained from single-point DFT calculations, we achieve excellent performance for both in-domain and out-of-domain predictions, including generalization to different facets, coverage regimes and low-energy configurations. From this systematic understanding of model robustness, we exhaustively sample the configuration phase space of catalytic systems without active learning. In particular, by predicting binding energies for over 14 million structures within the neural network model and the simulated annealing method, we predict coverage-dependent adsorption energies for CO adsorption on six Cu facets (111, 100, 211, 331, 410 and 711) and the co-adsorption of CO and CHOH on Rh(111). When validated by targeted post-sampling relaxations, our results for CO on Cu correctly reproduce experimental interaction energies reported in the literature, and provide atomistic insights on the site occupancy of steps and terraces for the six facets at all coverage regimes. Additionally, the arrangement of CO on the Rh(111) surface is demonstrated to substantially impact the activation barriers for the CHOH bond scission, illustrating the importance of comprehensive sampling on reaction kinetics. Our findings demonstrate that simplified data generation routines and evaluating generalization of neural networks can be deployed at scale to understand lateral interactions on surfaces, paving the way towards realistic modeling of heterogeneous catalytic processes.
Introduction
Understanding the interaction between surfaces and adsorbates is crucial for several applications in surface science and heterogeneous catalysis. Advances in density functional theory (DFT) and computational methods enabled accurately estimating adsorption energies of several molecules and reaction intermediates on metal surfaces,1,2 resulting in the rational design and discovery of (electro)catalysts for several technologically relevant applications.3–6 Although atomistic studies often focus on adsorbate–surface interactions, it is well known that lateral interactions between adsorbates, often referred to as adsorbate–adsorbate interactions, can strongly influence catalytic activity, selectivity and surface stability under operating conditions.7–9 For example, changing adsorbate coverages can influence binding site preferences and, in turn, strongly affect the activity and selectivity of important reactions such as the hydrogen evolution reaction (HER)10 and carbon dioxide reduction reaction (CO2RR),11 among many others. Therefore, it is highly desirable to develop a comprehensive understanding of lateral interactions and in turn, coverage effects, to study surface catalyzed processes.Given the multitude of site types and the combinatorial increase in the number of configurations with adsorbate coverage, exhaustive sampling and estimation of coverage-dependent adsorption energies are intractable using DFT simulations. This is especially true when larger supercell sizes are used to quantify coverage effects at longer length scales, and remain challenging even for small adsorbates with few degrees of freedom, such as *H or *CO. As a result, surrogate models bootstrapped from DFT simulations have been used to explore the large configurational space to estimate coverage-dependent adsorption energies.12 Examples of such surrogate models include: (1) analytical relationships based on first or higher order lateral interaction models,13–15 (2) cluster expansion based approaches that include a sum of on-site, two- and higher-body interactions,8,16–19 and (3) machine learning (ML) based approaches, including neural networks (NNs), that predict total adsorption energies from atom-centered descriptors.20–23 Each of these strategies has advantages and limitations. For instance, analytical expressions that are often used to account for lateral interactions in mean-field microkinetic models are computationally efficient, but rely on sampling of limited configurations at discrete coverages and use interpolated functional forms (e.g., piecewise-linear)13 to estimate coverage-dependent adsorption energies. As spatial correlations are not accounted for in such models, they can lead to large errors in the prediction of surface coverages and catalytic activity.24 Cluster expansion approaches explicitly account for spatial correlations between adsorbates and have been extensively used in lattice based kinetic Monte Carlo (kMC) simulations.25 However, cluster expansion requires selecting (small) discrete clusters whose complexity increases exponentially with number of adsorbates and active sites. This also hinders the transferability of these models beyond a single (low symmetry) facet type, particularly to higher index facets that have more complex active site environments. Finally, ML-based approaches are data-intensive and require careful analysis to avoid generalization failures when used beyond their training datasets. As such, these methods rely on active learning to augment training sets whenever novel coverage configurations are found,21 or on incremental model training by stepwise generation of coverage configurations.22 When using relaxed configurations obtained from DFT-based geometry optimizations, ML approaches require larger computational resources to accurately sample the entire configuration space of interest, including high adsorbate coverages, co-adsorption, and low symmetry surfaces with diverse site environments.
In this work, we introduce a fast and scalable data pipeline for quantifying coverage effects on catalyst surfaces using high-throughput workflows and ML, with an emphasis on generalization and transferability. In particular, we use the MACE architecture,26 based on many-body message passing neural networks exhibiting good generalization behavior,26,27 to predict coverage dependent adsorption energies with high accuracy for both in- and out-of-domain tasks. Using binding energies for unrelaxed structures as training data, MACE models exhibit high accuracy across different facets, coverage regimes, and thoroughly sample combinatorial spaces of coverage configurations without retraining the model. By combining the NN model with workflow management implemented in mkite,28 we sampled over 14 million configurations of CO adsorbed on six Cu facets (111, 100, 211, 331, 410 and 711) with varying coordination environments, which are systems of relevance for electrochemical CO2 reduction.29 Binding energies of the most stable structures, as predicted with the NN model, are computed with single-point DFT calculations and demonstrated to agree nearly perfectly with the predictions. Our approach is further validated using over a thousand structural relaxations, from which differential binding curves and trends are obtained for coverage-dependent *CO adsorption on the six Cu facets. Finally, we demonstrate that our pipeline is also applicable to co-adsorption systems using the *CHOH intermediate on CO-covered Rh(111), an active catalyst for thermal CO hydrogenation, as a case study.15 This combination of simpler data generation and understanding of NN generalization demonstrates how new ML pipelines can be developed and employed to model increasingly complex interfaces in heterogeneous catalysis at scale.
Results and discussion
Designing a data-efficient pipeline for coverage-dependent adsorption energies
The accuracy of ML predictions is often intrinsically connected to the training set used to create the models. Especially within NN potentials, predicting coverage effects in surface catalysts often rely on active learning strategies21,22 or expert curation23 when generating training data. This ensures that models continue to perform well as new regions of the configuration space are sampled, thus avoiding the generation of “adversarial examples” in the potential energy landscape30 or failures when generalization to unseen configurations.27,31 Furthermore, because the input data often comes from DFT relaxations, producing enough data points to train the model imposes a large cost on the developer, especially as larger surfaces and adsorbates are investigated. To explore how improving generalization and avoiding relaxations can be beneficial for modeling lateral interactions, we first explore coverage-dependent binding energies of CO adsorbed on six different Cu facets (111, 100, 211, 331, 410, and 711). These facets span a wide range of adsorption site environments and accessible *CO coverages, and correspond to the predominant facets in Cu at zero applied potential according to Wulff constructions.32 Furthermore, surface coverage and adsorbate–adsorbate interactions of *CO, a key intermediate during electrochemical CO2 and CO reduction, have been shown to have a strong influence on kinetics and selectivity towards the different multi-carbon products.33–36 Thus, it is important to obtain realistic models for these lateral interactions and minimize artifacts from periodic boundary conditions observed in small supercell models. To do that, large orthogonal supercells containing at least 16 surface atoms were used as initial slabs where adsorbates where distributed (see Table S1 and Fig. S1†). As these structures contain from 64 to 144 high-symmetric adsorption sites (Fig. S2†), creating unique adsorbate configurations using enumeration-based approaches37,38 is no longer feasible. If brute force enumerations were used to build configurations in mid- to high-coverage regimes, the number of adsorbate configurations could reach the order of hundreds of millions to billions of configurations per facet per coverage (Table S2†), forming complex interaction networks between adsorbates and surface (Fig. 1a) and posing a challenge to data sampling and evaluation.To efficiently generate data for combinatorial adsorption spaces while also avoiding active learning loops, we propose to: (1) train a model on unrelaxed energies (i.e., single-point DFT calculations) from randomly sampled configurations, and (2) extend beyond this limited space by assessing the generalization behavior of the ML models. Because sampling the space of relaxed structures with ML models is much more expensive and less reliable than that of unrelaxed structures, step (1) reduces the computational cost associated with performing structural relaxations when creating training data. As a consequence, more data can be generated to train the ML models at a reduced computational expense. A second benefit of our approach is bypassing the need for active learning approaches, simplifying the simulation workflows. Fig. 1b summarizes the data generation strategy for this work, and the complete relationship between workflow objects implemented in mkite is shown on Fig. S3.† Instead of enumerating configurations, we randomly sampled configurations on a per-facet, per-coverage basis (see the Methods section for details). In particular, we generated up to 100 unique configurations for each facet and coverage where nCO < 10 (low coverage regime) and 50 unique configurations per facet and coverage where 10 ≤ nCO ≤ 18 (high coverage regime). These configurations were generated by randomly sampling adsorption sites that avoid distances smaller than 2.0 Å (1.7 Å) between adsorbates in the low (high) coverage regime, then deduplicating symmetrically equivalent structures (see Methods). This resulted in 6793 configurations for the different CO coverages and Cu facets considered in this work (Table S3†). Then, single-point DFT simulations are used to compute unrelaxed binding energies of *CO adsorbed on the Cu facets of interest. These randomly sampled distributions span a wide range of energies, as exemplified in Fig. 1c for low and high *CO coverages on Cu(111), and detailed in Fig. S4 and S5.† Already from the randomly generated data, known trends from the sampling outcomes can be observed. For example, at higher coverages, average binding energies tend to shift towards higher energies in all facets (Fig. S4†), although with different magnitudes in each facet due to different binding sites.
Because randomly sampled datasets are often not representative of the lowest-energy structures, quantitative analysis of the physical phenomena cannot be performed until the configuration space is thoroughly sampled. To evaluate how models generalize beyond these datasets, we proposed five tests to assess the performance of NN models beyond their training domain (Fig. 1d). In addition to in-domain train-test splits, additional errors metrics can be obtained by: training the model on data from one facet and testing it on data from another facet; training the model on lower coverages of a single facet and testing it on higher coverages of the same facet; or omitting certain coverages from the training set. These tests can provide additional information to assess generalization behavior, thus helping decide if a model can reliably obtain low-energy structures despite being trained on a higher-energy dataset.
In- and out-of-domain performance of binding energy predictions
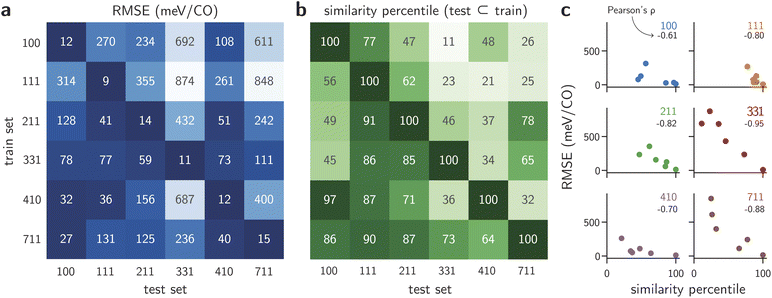
Using the dataset of nearly 7000 unrelaxed *CO binding energies, we trained MACE models on a per-facet basis and evaluated them according to the generalization protocols defined above. The model and training parameters were chosen based on correlations between hyperparameters and generalization performance from previous work.26,27,39 However, because the screening strategy proposed here avoids training a force field and rather focuses only on binding energies, an invariant model (L = 0) was used (see Methods). Fig. 2a shows the performance of the models when trained on one facet (rows) and tested on all other facets (columns). The test root mean square error (RMSE) of the *CO binding energies for in-domain data is shown in the diagonal of the matrix, and corresponds to the lowest error obtained for each training set. As expected, each model exhibits excellent performance when tested against held-out data within the same distribution, with RMSEs lower than 15 meV per CO for all the six Cu facets and averaged across all coverage regimes. When predictions are performed on facets different from the training set, on the other hand, errors are strongly dependent on the facet identity of the training set. Although all training and test sets have similar sizes (Table S3†), models trained on low-symmetry facets such as Cu(331) or Cu(711) exhibit much lower generalization errors, under 111 meV per CO for Cu(331) and 236 meV per CO for Cu(711). Although errors on the order of 100 meV per CO can be large in many cases for catalytic applications, the models retain excellent correlation between predicted and true binding energies (Fig. S6†). In contrast, MACE models trained on the low index facets Cu(100) and Cu(111) fail to predict binding energies of the other facets within reasonable accuracy, with errors larger than 800 meV per CO in some cases. Not only do the models trained on flat surfaces predict CO binding energies on stepped surfaces with smaller accuracy, but they also fail to adequately generalize between Cu(100) and Cu(111). At the same time, models trained on stepped facets often predict unrelaxed binding energies of *CO on Cu(100) and Cu(111) with errors below 131 meV per CO.To explain the facet dependence of the aforementioned errors, we first evaluated whether models are indeed performing in out-of-distribution assumptions. Given that binding sites in higher-index facets can be represented using binding sites from low-index facets,40 it is relevant to quantify the extent of their similarity from an ML standpoint, thus beyond the microfacet notation. To perform this analysis independently of the learned features, we represented the adsorption sites of all facets using a fixed descriptor, namely the Smooth Overlap of Atomic Positions (SOAP)41 (see Methods). Then, by performing all pairwise comparisons between adsorption sites across all facets, we obtained a measure of similarity between the sets of unique adsorption sites. Because the resulting similarity between two facets corresponds to a matrix, we compute the Hausdorff distance between sites, which is a measure of how far is the furthest point of the test set compared to all points in the train set. Finally, the similarities are then compared based on their percentile within the distribution of all similarities. These results are shown in Fig. 2b. Although a qualitative visualization can help visualize the richness of the binding space (Fig. S7†), the quantitative analysis in Fig. 2b further confirms that adsorption sites from low-index facets are indeed contained in all stepped surfaces from an ML perspective, as shown by the higher percentiles in the columns of Cu(100) and Cu(111). Interestingly, however, adsorption sites from Cu(100) are more similar to those in Cu(111) than the other way around, explaining the asymmetry of generalization errors between Cu(100) and Cu(111). Similar patterns can be observed across Cu(211), Cu(331), and Cu(711). In fact, when the RMSE in Fig. 2a is visualized against the similarity in Fig. 2b, reasonable correlations are found between the results, as shown in Fig. 2c. The Pearson correlation coefficient between the two quantities ranges from −0.61 (for Cu(100) as the test set) to −0.95 (for Cu(331) as the test set). Errors scale similarly across facets, with the exception of Cu(410). Its RMSE values remain consistently lower than its counterparts when used as a test set, which could be an artifact of lower coverages when the number of *CO adsorbates is normalized by the number of surface sites. Indeed, the distribution of binding energies for Cu(410) is closer to those from the (100, 111, 211) facets than to those observed in the lower-symmetry counterparts (331, 711) (Fig. S5†). This suggests that, in addition to similarity in binding sites, the performance of the models is also connected to the coverage and density of adsorbates. Importantly, it also emphasizes that, from a machine learning perspective, the results do not correspond plainly to an ill-defined interpolation. Rather, the test data is far away from the entire training set and thus is not guaranteed to be within reasonable ranges of interpolation. While these absolute thresholds are challenging to determine in a universal way, the analysis shows that the model performance is strongly related to the surrogate metric of “extrapolation” shown in Fig. 2.
To test whether generalization across number of adsorbates plays a substantial role in the models, we compared models trained with different coverage regimes (Fig. 1d). The results of the comparison are shown in Fig. 3a. Errors of models trained and tested on all coverages (dark blue in 3a) are equivalent to those in Fig. 2a, and serve as a baseline for this test. First, we trained per-facet models on subsets of the data by adding all even coverages to the training set and all odd coverages in the test set. The results, depicted in Fig. 3a as “different covs.” (cyan), show that slightly worse performances are found despite half of the coverages being discarded. Fig. S8† further shows that, beyond the error values, correlation coefficients also remain nearly perfect for the test set predictions. This observation implies not only that the model can properly interpolate within the space of coverages, but also that future dataset construction can be optimized by removing some intermediate coverages. This approach could drastically reduce the total number of single-point DFT calculations to be performed when generating the initial training set. Secondly, we verified whether models trained on low-coverage structures (nCO < 10) could accurately predict binding energies from high-coverage structures (nCO ≥ 10). In a previous work,22 this approach was performed in a step-wise manner to ensure the reliability of predictions, but coupling step-by-step exploration and model retraining can be time-consuming. Ideally, a model with high generalization capacity could bypass the need for sequential data generation and predict directly the binding energies for higher coverage regimes. Fig. 3a shows that, although the RMSE degrades when models are tested on substantially higher coverages, errors remain small compared to the baseline (red bars). Even in the worst case in Fig. 3a, obtained with models trained on low-coverage structures for Cu(711), correlation coefficients for the predictions remain nearly perfect (Fig. S9†). This remarkable performance suggests that accurate models of lateral interactions are being learned within the MACE models, and offer reliable predictions outside of their training domain. Moreover, the lower error of Cu(410) compared to other stepped facets further confirms the previous hypothesis that lateral interaction models between *CO adsorbates are either easier to fit within Cu(410) compared to Cu(211), Cu(331), and Cu(711), or more limited in scope given the larger lateral sizes of the Cu(410) supercells under study (Table S1†).
Given the success of the MACE models in predicting binding energies beyond their training domain, we evaluated whether a single model could be created for all facets and all coverages at once without loss of accuracy. This would suggest that the MACE models are able to capture all binding energies in a single model, facilitating and increasing the convenience of sampling new structures with a single model. Fig. 3c shows a breakdown of the test RMSE values for the MACE model trained on the entire dataset (all facets and coverages) at once. Errors for individual facets are equivalent to the in-domain RMSE values shown in Fig. 2a, with deviations on the order of 1 meV per CO. Across all facets and coverages, the RMSE is found to be uniform and generally smaller than 20 meV per CO. This further confirms the ability of the models to represent the entire configuration space of *CO adsorbates on Cu within different facets and coverages.
To better understand whether this performance could have been achieved without the MACE models, we systematically decreased the complexity of the architectures and models themselves. Because of the diversity in adsorption sites for Cu(711) (see Fig. 2b), we selected this facet as the training set for this study. First, we reduced the number of body-order correlations (ν) in MACE to understand whether complex many-body interactions can substantially affect the errors. Fig. 3c shows that small test error differences are found for in-domain data when 3-body (ν = 2) and 4-body messages (ν = 3) are used, but the performance degrades more substantially when the model is restricted to use 2-body (ν = 1) messages. These observations are similar to those in ref. 26. The trends in Fig. 3c also remain constant across smaller dataset sizes, and illustrate that the representation capacity of the models are likely limited by the interaction order. To further test this result, we verified whether simpler models can obtain comparable performance to MACE (Fig. 3d). For instance, we trained a NN on the SOAP fingerprint centered on the adsorbates, as well as a plain SchNet model,42 which is similar to the recently proposed ACE-GCN,22 to predict binding energies of all Cu facets after being trained on Cu(711) configurations. Although the in-domain performance of both models were reasonable, with 41 and 29 meV per CO RMSE when the models were tested on held-out Cu(711) data, the average RMSE for out-of-domain test sets in both systems was much higher, at 201 and 174 meV per CO, compared to an average RMSE of 112 meV per CO for the MACE model (see also Fig. S11†). Following the clue from Fig. 3c on the role of many-body interactions, we tested a simple model that explicitly accounts for lateral interactions when computing the binding energy. The simplified model, which decomposes the binding energy into site-centered contributions and lateral interactions (see ESI Text and Fig. S10†), exhibits a substantial improvement over SchNet in terms of generalization behavior (Fig. 3d and S11†) despite using a fixed descriptor. Remarkably, the simplified NN model shows a smaller error when generalizing from Cu(711) to Cu(211) or Cu(331) than MACE (Fig. S11†), but a larger error for the other facets. We hypothesize that this effect reflects the larger similarity between the SOAP vectors of adsorption sites from Cu(711) in the training set and the ones from Cu(211) and Cu(331) in the test set, as shown in Fig. 2b. On the other hand, this observation also indicates that while learnable representations in MACE effectively capture environments beyond those in the Cu(711) training set, it slightly compromises the ability to understand other specific facets despite their similarity (Fig. 2b). Furthermore, this behavior may not be exclusive to the MACE architecture and can be likely achieved by other models demonstrating near state-of-the-art performance in recent benchmarks.43,44 Nevertheless, this example further demonstrates that improved generalization behavior in coverage-dependent interactions can be improved by the priors in the NN architecture, and thus are not entirely explained by correlations in the dataset of *CO on Cu facets.
Sampling low-energy, high-coverage configurations of *CO on Cu
The reliability of the models under out-of-distribution regimes is essential to support their use in the final proposed “extrapolation test” of interest, where low-energy structures are sampled despite being outside of the training distribution (Fig. 1d). When ML models cannot generalize well, sampling low-energy structures often fails because adversarial examples—i.e., points outside of the training set predicted to be much lower in energy because of failures in generalization—are typically sampled along with the true ground states. As previously mentioned, these problems can be mitigated by retraining the model within an active learning loop, at the expense of higher costs and a human-in-the-loop evaluating the model performance. The excellent precision and accuracy of the MACE model in predicting coverage-dependent binding energies across different tests, however, supports their deployment for sampling new configurations of *CO on Cu facets without further retraining. Then, after sampling, the results can be easily validated by comparing targeted single-point DFT calculations and the evaluations from the model.To extensively sample the configuration space of nCO on the six Cu facets, we used a Markov chain Monte Carlo (MCMC) sampling strategy within the Metropolis–Hastings45,46 and simulated annealing47 algorithms (see Methods). An example of the temperature and energy profiles from the MCMC sampling for Cu(410) with nCO = 10 is shown in Fig. 4a. By taking advantage of batched evaluation of the NN model, we sampled 1000 replicas in parallel for each nCO and facet, resulting in over 14.5 million energy evaluations to sample the lowest energy configurations (see Fig. S12 and S13†). The sampling method systematically sampled low energy configurations despite starting from random structures (Fig. S14†), demonstrating the success of the sampling approach. To validate whether the model predictions were accurate and the low energy structures are not generalization failures, we ranked the structures by energy and selected the top-3 unique configurations per facet and per coverage for DFT evaluation. After performing 312 single-point calculations for these systems, we compared their unrelaxed binding energies against the original dataset. Fig. 4b shows that the DFT-calculated binding energies of MCMC-sampled structures (red) are substantially lower in energy than the original dataset (dark blue), as expected. This shift towards lower DFT energies is also visualized on the total, per-facet distributions of energies (Fig. 4c). Therefore, the MACE model trained on all facets was effective in sampling low-energy configurations without active learning loops and despite being trained on a dataset of randomly sampled structures. When the performance of the model is assessed by comparing the predicted binding energies for the top sampled structures and the resulting DFT values, a near-perfect correlation is found (Fig. 4d). Although the RMSE of predictions (91 meV per CO) is higher than the baseline test errors (<15 meV per CO), the Spearman's correlation coefficient is equal to 0.999. This indicates that the model predicts shifted energies with respect to the ground truth due to a skewed training set, but reproduces all correlations in the underlying data. The strategy also enabled sampling higher coverage configurations (nCO > 18) for the Cu(410) case which were initially absent from the training set (see Fig. 4b), further supporting the model's ability to generalize towards higher coverages in a production analysis.
Validating the strategy with structural relaxations and binding energy curves
So far, the results for the different coverages and Cu facets are based on unrelaxed configurations and binding energies. Because the sampling strategy creates unrelaxed structures and the model performs well in predicting their unrelaxed energies, the data is efficiently generated and later validated with single-point DFT calculations. Ultimately, however, we are interested in obtaining the lowest-energy configurations according to relaxed structures from geometry optimizations, as the corresponding *CO adsorbates can move substantially from their initial positions, especially in high coverage regimes. For example, surface reconstructions can further lower the energy of the system, or adsorbate–adsorbate interactions may displace the *CO molecules from their high-symmetry adsorption sites while lowering the overall energy of the system. Previous work has shown that correlations between relaxed energies and model predictions can be less than ideal, especially if systems with significant reconstruction are taken into consideration.22 Therefore, it is important to evaluate whether sampling unrelaxed configurations also reasonably samples the trends in relaxed ones.To evaluate correlations between relaxed and unrelaxed energies, we performed DFT relaxations for 675 configurations from the original (thus randomly sampled) dataset across all facets and coverage regimes. These data points were obtained by attempting to relax a subset of nearly 2000 configurations whose unrelaxed energies were lower than its counterparts on a per-facet, per-coverage basis. However, not all structural relaxations led to systems where all *CO remained adsorbed on the Cu facet. Most of the relaxation calculations for the original dataset had to be stopped due to desorption of *CO from the facet, or large wall times expected for job completion on the high-performance computing cluster. Therefore, the final 675 relaxed structures and energies only represent the subset of successful relaxations. Although this is an inherent bias in the data—e.g., systems for which there is desorption have a single-point energy in the training set, but not relaxed energies—it still represents the subspace of interest, which is that of structures with faster DFT relaxations and closer to the local optima. In this sense, the absence of high-energy structures (including desorbed ones) is exactly the phase space of interest and does not affect the conclusions regarding the predicted desorption energies. Aiming to sample this space allows us to focus on the effect of low-energy configurations of *CO on Cu facets in their bound states.
First, we verified if relaxed binding energies correlate with their unrelaxed counterparts. If the energies are completely uncorrelated, this would suggest that sampling unrelaxed structures is not a good strategy for exploring the space of relaxed configurations. Fig. 5a illustrates this correlation for Cu(410) (see Fig. S15† for all facets). The Spearman's correlation coefficient (ρS) between relaxed and unrelaxed binding energies of *CO on Cu(410) is 0.58, suggesting that lower unrelaxed energies usually lead to systems with lower relaxed energies. Similar trends are found among other facets, with most values of ρS higher than 0.5. The only exception is Cu(711), for which fewer data points are available, with a correlation coefficient of 0.350. On the other hand, the best correlation coefficient found for Cu(211) (ρS = 0.739). To quantify whether relaxing the lowest unrelaxed energies often leads to the lowest relaxed binding energies, we computed the recall of the top-N relaxed energies given the top-N unrelaxed ones. Fig. 5b exemplifies this recall for Cu(410) for three different cases and compares it to the expected recall for a baseline, random sampling method. The recall is always better than the baseline when the top-5, top-10, and top-15 (un)relaxed structures are considered, exhibiting a higher area under the recall curve and quick rise with low percentiles of unrelaxed energies. Similar trends are observed for other facets (Fig. S16†), with particularly successful results for Cu(100), Cu(211), Cu(331), and Cu(711). The case of Cu(111) shows a mismatch between the structures with lowest unrelaxed energies and relaxed ones, as also seen in Fig. S15.† For some coverages, the best configurations of *CO on Cu do not have the top unrelaxed energies, but intermediate values that require further sampling of the unrelaxed configurations to obtain the lowest energy configurations of the original dataset.
Given the reasonable agreement between unrelaxed and relaxed energies from the recall curves, we verified whether relaxed energies could be inferred directly from unrelaxed ones on a per-facet, per-coverage basis. To do so, we analyzed the distribution of relaxed binding energies across all systems under study. Fig. S17 and S18† show that the range of relaxed binding energies is much smaller than the range of unrelaxed binding energies in the original dataset (compare with Fig. S4†). In fact, even when systems with different unrelaxed energies are selected, they often collapse to very similar relaxed energies, as shown by the small standard deviation from Fig. S4.† Because structural relaxations may substantially rearrange the position of the adsorbates on the surface, structures with different unrelaxed energies may relax towards similar structures, with the difference between unrelaxed energies compensated by sufficient structural reconstruction. To verify this hypothesis, we compared the relaxation energy difference (ΔEb = E(relax)b − E(unrelax)b) with the unrelaxed binding energies on a per-facet manner. Fig. S19† shows a nearly-linear relationship between ΔEb and the unrelaxed binding energies, suggesting that even across different coverages and facets, improvements in energy due to relaxation are related to the initial unrelaxed binding affinities. This suggests that systems with higher unrelaxed energies may still undergo relaxation to lower energies given enough reconstruction and provided that structural rearrangement is achieved within DFT relaxation trajectories. To further verify this claim, we quantified the structural reconstruction of each trajectory by comparing the initial and final configuration using the Pointwise Distance Distribution (PDD).48 This structural invariant is continuous, guaranteed to recover identical structures, and has been proven useful to compare a range of materials.48,49 Furthermore, it bypasses the need for root mean square deviations (RMSD) along the relaxation trajectory, which can be deceptive depending on the atom assignment, the periodic boundary conditions, and the number of atoms over which the deviations were averaged against. Fig. 5c and S20† further confirm that these differences in binding energy are due to rearrangement of atom positions on the surface, with strong correlations between ΔEb and the PDD distance. As expected, configurations with higher nCO undergo larger restructuring during geometry relaxations (higher PDD distance). Taken together, these results suggest that sampling configurations with low unrelaxed energies can lead to smaller ΔEb and, consequently, may require fewer relaxation steps to converge. Although recalling the ground state configuration cannot be guaranteed within any method, our approach provides an efficient strategy to minimize the significant computational cost associated with structural relaxations.
The previous results show that relaxing structures with low unrelaxed binding energies on a per-facet, per-coverage basis is an efficient way to estimate low-energy relaxed structures without having to exhaustively sample the space of relaxed structures. To evaluate the properties of interest, we performed geometry optimizations for all 312 low-energy structures obtained from the MCMC sampling using DFT calculations (see Methods). When the resulting energies from the sampled dataset are compared with the energies from the original dataset, we found that the sampled structures relax to lower energies than their counterparts (Fig. S21†), further supporting the previous results. The only exception is Cu(111), as expected from the shifted recall curves in Fig. S16.† Using the final low-energy (relaxed) structures allows us to investigate the coverage of *CO on specific adsorption sites for the different facets. For example, the coverage-dependent occupancy of *CO adsorbates on the sites of Cu(410) is shown in Fig. 5d. To avoid labeling the surface atoms with discrete coordination numbers after reconstruction upon geometry optimization, we computed an average coordination number (aCN) for each copper atom on the surface using a sum over neighbors defined from a smooth cutoff (see Methods). Then, for each carbon atom, we compute the average coordination of the binding site by taking the average of aCN of all the neighboring copper atoms. Fig. 5d shows with a red bar the aCN of each CO for the lowest energy structure associated with each coverage. At low coverage, *CO adsorbs preferentially on undercoordinated sites that have lower aCN values, specifically the on-top sites on steps (see also Fig. 5e and S22† for a visual guide). After step sites are occupied, lateral repulsion between adsorbates forces the occupancy of higher coordination sites, with a larger preference for terrace sites (aCN < 11) for coverages above 0.25 monolayer (nCO = 6 in our slab model). Then, as the coverage continues to increase, the occupancy of terrace and overcoordinated sites increases, with high preference for on-top sites, until all sites are occupied. This behavior agrees very well with *CO desorption experiments on Cu(410). For example, Makino and Okada50 verified with infrared reflection-adsorption spectroscopy (IRAS) and temperature-programmed desorption (TPD) that the preferential adsorption sites for *CO at low coverages is the on-top site of steps, with their saturation point at ≈0.25 monolayer. Similar behavior is found for all stepped facets considered in this work, where *CO preferentially adsorbed on the undercoordinated sites at low coverages, and structural relaxations tilted the *CO adsorbates away from each other due to lateral interactions. On the other hand, for the flat Cu(100) and Cu(111) surfaces, the relaxation led to geometrical deviation of adsorbates from their initial configuration only at higher coverages (Fig. S23–S28†). Our results show that Cu(100) is preferred over Cu(111) at higher CO coverages, as also proposed from other experimental and computational investigations.35 Additionally, we find that the on-top sites are occupied at low coverages, with the occupancy of the multi-coordinated sites (hollow, bridge) increasing at higher coverages (Fig. S23 and S24†).
To further illustrate how the calculated results can predict the experimental behavior of these systems, we computed the differential binding energy curves of *CO on all facets. By considering all relaxations, we computed the Boltzmann average of relaxed binding energies on a per-coverage, per-facet basis. Then, we fitted a piecewise continuous and differentiable linear-cubic polynomial to the integral binding energy (see Methods). The data points and fitted integral binding energy curve are shown in Fig. S29.† Then, by differentiating the integral binding energy curve with respect to the coverage, we obtained the differential binding energy curves in Fig. 6. A qualitative analysis of Fig. 6 highlights the similar behaviors of *CO adsorption on Cu(100) and Cu(111), given the similar adsorption modes on the flat surfaces (also see Fig. S23 and S24†). However, Cu(100) allows up to 0.7 monolayer of *CO coverage, with lateral repulsions starting at 0.66 monolayer, in contrast to lower thresholds for Cu(111). This finding is in excellent agreement with experimental observations,51 where lateral repulsions (i.e., appearance of a shoulder peak in the TPD spectra) is observed to dominate the adsorption at 0.6 monolayer. The behavior of Cu(711) also shows a large saturation point for *CO, with increasing differential binding energies near 0.5 monolayer. However, due to the nature of the stepped surface (Fig. S28†), *CO adsorption energies are more favorable compared to (100) and (111), shifting the differential binding energies down. In the case of the other stepped surfaces, Cu(211) and Cu(331) have similar adsorption energies at the low coverage regime, but their smaller curvature reflects the less favorable energies of terrace sites occupied at higher coverages compared to undercoordinated steps (Fig. S25 and S26†). Indeed, for Cu(211), it was observed that CO prefers to bind upright on the top sites of the step edge based on DFT calculations and scanning tunneling microscopy (STM) imaging experiments.52 At coverages greater than 0.5ML, the authors note that obtaining the most favorable adsorption geometry was non-trivial, with both top–top and top-bridge configurations being reported in experiments. Both these observations are consistent with the lowest energy configurations we obtain for Cu(211) for different coverages as shown in Fig. S25.† Furthermore, when the differential binding energy of these facets are compared against experimental results, good agreement is found despite the limitations of the RPBE functional in predicting the low-coverage binding preferences and *CO adsorption energies on Cu compared to experiments.53 Cu(100) and Cu(111) have experimental desorption energies at low coverages equal to 530 ± 15 and 490 ± 15 meV per CO,50 respectively, while our computed values are 432 and 440 meV per CO. Cu(211) exhibits an experimental *CO desorption energy of 605 ± 15 meV per CO (attributed to the step-edge),50 similar to our calculated desorption energy of 619 meV per CO at low coverage. Finally, Cu(410) exhibits an experimental desorption energy of 725 ± 31 meV per CO (attributed to the step-edge),50 in excellent agreement with the calculated value of 728 meV per CO from the binding energy curve at low coverage where *CO exclusively occupies the step-edges (Fig. S27†). Taken together, these results further validate the combination of fast data pipelines, ML-accelerated sampling, and selective relaxation when predicting coverage-dependent binding energies for *CO on Cu. The overall agreement of our results with experimental observations offer a roadmap on the extension of these methods towards other catalyst systems—for instance, to accelerate the sampling of potential- and coverage-dependent adsorption energies and properties relevant in electrocatalysis.54
Sampling the co-adsorption of *CO and *CHOH on Rh(111)
As a second example, we show that the proposed workflow can also be used to study the co-adsorption of different adsorbate species. In particular, we sampled the adsorption of *CHOH with increasing *CO coverage on Rh(111). This system was motivated by the fact that Rh is an active catalyst for the conversion of syngas to C2+ oxygenates,15 where both species play an important role in the reaction. To explore the space of *CHOH and *CO on Rh(111), we first computed the binding energies of *CHOH on Rh(111) in the absence of CO species using a supercell with 9 surface sites. Then, the geometry of the system was optimized and the four lowest-energy configurations were selected. The most stable configuration was *CHOH on a top site, followed by three different conformations on bridge sites. Afterwards, similarly to the *CO on Cu system, we generated data by randomly sampling configurations of *CO on the four CHOH-adsorbed Rh(111) systems, followed by single-point DFT calculations to obtain unrelaxed binding energies. A MACE model was then trained to predict unrelaxed binding energies of co-adsorbed systems across all CO coverages. The model performance was evaluated on a held-out test set, leading to the parity plot in Fig. 7a. Despite the existence of two co-adsorbates and the range of coverages, the model successfully predicted binding energies of the enumerated systems, with a total RMSE of 8 meV per CO. Although the initial four configurations of *CHOH on Rh(111) are kept constant, the binding energy due to *CO coverage accounted for the presence of the co-adsorbate species. If the coverages of both adsorbates are changed simultaneously, the same approach would be applicable, though at a much higher cost given the increased combinatorial space. Using this model, we then explored the space of *CO configurations using the MCMC and simulated annealing approach (see Fig. S31† for an example profile). Fig. 7b shows that unrelaxed binding energies of original (blue) configurations are higher than the top-3 sampled (red) ones, in line with the results in Fig. 4b for CO on copper. Because the configurations of one and two CO adsorbates had been exhaustively sampled, we only sampled cases with at least three CO adsorbates, obtaining the lowest energy states in all but one coverage (see Fig. S32† for the configurations).To further exemplify the importance of configurational sampling in modeling reactions where co-adsorption plays a role, we computed the activation barriers for *CH–OH bond scission on Rh(111) in the presence of three different CO configurations with the same coverage of 0.55 monolayer. The barriers were calculated using the nudged elastic band (NEB) method and DFT simulations using CO configurations with initial unrelaxed energies of 0, 150, and 250 meV relative to the lowest energy structure. The results of the NEB calculations are summarized in Fig. 7c (see Fig. S33† for detailed NEB trajectories). Because of the structural relaxations prior to NEB calculations, the energy differences between the three initial systems changed slightly to 0, 72, and 286 meV, but still conserved the energy ranking. All systems are observed to undergo not only the *CH–OH bond scission, but also different restructuring of the adsorbate configurations during the reaction pathway. Because sterical hindrance from *CO does not allow the formation of separate *CH and *OH products, the reaction progresses by first reorganizing the CO into a higher energy state. The energy barrier for this restructuring depends on the initial configuration, with configurations 1 and 3 in Fig. 7c showing barriers of 0.46 and 0.38 eV for this restructuring, leading to intermediate structures less stable than the initial ones. Whereas in system 1 the restructuring is due to CO rearrangement on the surface, in system 3 this increase in energy is associated with the inversion the OH configuration instead (Fig. S34†). After this restructuring, both systems proceed with the CH–OH bond scission on the Rh(111) surface with minor rearrangements of CO adsorbates on the surface. However, even though the energy of restructured configuration 1 is similar to the energy of initial configuration 3 (see also Table S4†), configurations 1 and 3 exhibit energy barriers of 0.85 and 1.98 eV with respect to the intermediate state, respectively (Fig. 7d), demonstrating that the initial arrangement of CO strongly influences the reaction kinetics. As another example, configuration 2 does not show a single barrier with the formation of a more stable intermediate, but the pathway only increases in energy relative to the initial state until the CH–OH bond scission. In our simulations, this led to a concerted CH–OH bond breaking and CO rearrangement, with a single barrier of 1.31 eV along the reaction pathway (see also Fig. S32 and S33†). Because these three systems vary only by the initial *CO arrangement, but exhibit substantially different energetics (both kinetic and thermodynamic) and reaction pathways, this example demonstrates the importance of sampling low-energy configurations and how leveraging generalization in ML models can facilitate this sampling method. Importantly, because exploring combinatorial spaces of co-adsorption can be overly expensive, we showed how data-efficient pipelines can enable a more realistic representation of these and other complex interfaces.
Conclusions
In this work, we proposed an efficient data pipeline to sample combinatorial spaces of adsorbate coverage configurations and estimate coverage-dependent adsorption energies. Instead of relying on expensive active learning loops and relaxed energy data to train a ML model, we instead ensured NN models were capable of generalizing under multiple regimes, and then proceeded to sample new structures. By using unrelaxed structures to train ML models, we also avoided expensive data generation and retraining workflows. In combination with targeted structural relaxations, we obtained coverage-dependent binding energies of CO adsorbed on six low- and high-index copper facets. Results from the computed differential binding energy and ground-state structures agree well with experimental observations from the literature, and support the usefulness of the approach. Finally, we show our sampling strategy can also be used to obtain configurations in the cases of co-adsorption, and demonstrate how reaction pathways and the associated kinetics of CHOH bond scission on Rh(111), a crucial step during syngas conversion can change substantially depending on the configuration of adsorbed CO at a given coverage. Overall, our combined approach on data generation pipelines and evaluation of ML generalization demonstrates how scalable workflows can be developed and employed to model increasingly complex interfaces in heterogeneous catalysis. Future work can explore the dependence of increased number of adsorbates, facets, and composition in the generalization of NN models. The combinatorial explosion of parameters may become the limiting factor for energy prediction models, which would then require even better generalization power to be extended towards kinetic models.Methods
Density functional theory calculations
| Eb = EnCO+surf − Esurf − nECO(g), | (1) |
Simulation workflow
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) was initially relaxed using DFT calculations, and a lattice parameter of 2.60 Å was obtained. Then, surfaces for all copper facets (111, 100, 211, 331, 410 and 711) were generated using the Atomic Simulation Environment,64 and constrained to have at least 6 layers and lateral size of 9 Å. The atomic positions of the two topmost layers were then relaxed using DFT, as described above. A similar procedure was adopted for Rh, but only the Rh(111) facet was considered in our study of co-adsorption. A supercell containing 6 layers and 9 surface sites was created for Rh(111).
m) was initially relaxed using DFT calculations, and a lattice parameter of 2.60 Å was obtained. Then, surfaces for all copper facets (111, 100, 211, 331, 410 and 711) were generated using the Atomic Simulation Environment,64 and constrained to have at least 6 layers and lateral size of 9 Å. The atomic positions of the two topmost layers were then relaxed using DFT, as described above. A similar procedure was adopted for Rh, but only the Rh(111) facet was considered in our study of co-adsorption. A supercell containing 6 layers and 9 surface sites was created for Rh(111).
 recipe in the
recipe in the  package (v 0.1.1). The generator takes in a surface and a single adsorbate as inputs. Then, it identifies all distinct high-symmetry adsorption sites on the surface using the AdsorbateSiteFinder class65 implemented in pymatgen.66 Because fully enumerating all combinations of adsorption sites with n adsorbates is intractable (see Table S2† for rough estimates), we instead randomly sampled n different adsorption sites and checked whether the distances between sampled sites is larger than a given threshold, ensuring there is no overlap between adsorbate positions. For lower coverages (n < 10), this threshold was set to 2.0 Å, while for higher coverages (n ≥ 10) this threshold was set to 1.7 Å. The sampling and checking procedure is repeated until a desired number of configurations is achieved or if a maximum number of attempts is reached. In our case, we sampled up to 100 valid configurations for lower coverages (n < 10) and 50 valid configurations for higher coverages (n ≥ 10) for all facets, with a maximum of 106 attempts. For all these systems, adsorbates were placed 2.0 Å away from the surface, including on the step sites. This distance was selected to be close to equilibrium distances between CO and Cu. Whereas this is a hyperparameter, it is not expected to strongly influence the overall workflow if it remained within reasonable ranges (e.g., 1.8 or 2.2 Å), as all energy shifts would likely retain the major trends. For the cases of co-adsorption, this procedure was first performed with *CHOH as the only adsorbate. As discussed in the main text, the four most favorable structures created from *CHOH adsorption were used as initial structures for sampling the CO coverage.
package (v 0.1.1). The generator takes in a surface and a single adsorbate as inputs. Then, it identifies all distinct high-symmetry adsorption sites on the surface using the AdsorbateSiteFinder class65 implemented in pymatgen.66 Because fully enumerating all combinations of adsorption sites with n adsorbates is intractable (see Table S2† for rough estimates), we instead randomly sampled n different adsorption sites and checked whether the distances between sampled sites is larger than a given threshold, ensuring there is no overlap between adsorbate positions. For lower coverages (n < 10), this threshold was set to 2.0 Å, while for higher coverages (n ≥ 10) this threshold was set to 1.7 Å. The sampling and checking procedure is repeated until a desired number of configurations is achieved or if a maximum number of attempts is reached. In our case, we sampled up to 100 valid configurations for lower coverages (n < 10) and 50 valid configurations for higher coverages (n ≥ 10) for all facets, with a maximum of 106 attempts. For all these systems, adsorbates were placed 2.0 Å away from the surface, including on the step sites. This distance was selected to be close to equilibrium distances between CO and Cu. Whereas this is a hyperparameter, it is not expected to strongly influence the overall workflow if it remained within reasonable ranges (e.g., 1.8 or 2.2 Å), as all energy shifts would likely retain the major trends. For the cases of co-adsorption, this procedure was first performed with *CHOH as the only adsorbate. As discussed in the main text, the four most favorable structures created from *CHOH adsorption were used as initial structures for sampling the CO coverage.
Unsupervised learning analysis
 (v. 2.1.0).67 The cosine distance was used to obtain the distance between two environments.
(v. 2.1.0).67 The cosine distance was used to obtain the distance between two environments.
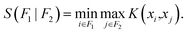 | (2) |
 package in Python (v. 0.5.3). The 2D UMAP plot was produced by using the cosine distance between binding sites, and using 10 neighbors as parameter.
package in Python (v. 0.5.3). The 2D UMAP plot was produced by using the cosine distance between binding sites, and using 10 neighbors as parameter.
 package (https://github.com/dwiddo/average-minimum-distance, v. 1.4.1).48 A total of k = 50 neighbors were used when computing the PDD matrices. The final distance between the two structures is the earth mover's distance between the PDD matrices.
package (https://github.com/dwiddo/average-minimum-distance, v. 1.4.1).48 A total of k = 50 neighbors were used when computing the PDD matrices. The final distance between the two structures is the earth mover's distance between the PDD matrices.
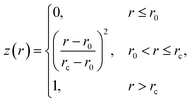 | (3) |
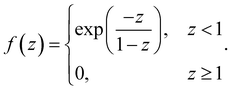 | (4) |
For each CO adsorbed on the copper surfaces, the coordination number reported in Fig. 5d is the coordination number of the closest copper atom. In the case of near-degeneracies of distances, defined when the k-nearest neighbors have distances within 0.05 Å of the smallest distance, the reported aCN is the average of aCNs of all k neighboring atoms.
Deep learning models
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20
20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 for train/validation/test. This ensures that there is no data imbalance between splits, which could bias the results. One exception is the case where only one or two adsorbates are on the surface. Because of their importance for on-site energy predictions and their scarcity, all configurations with nCO ≤ 2 were added to the training set only, and none to validation and tests sets. The dataset splits were then aggregated on a per-facet basis to train individual models per facet, and concatenated together for the all-facet model. As figures of merit such as root mean squared error depend on test splits, all comparisons between models (such as Fig. 3) were performed using the exact same train–validation–test splits.
20 for train/validation/test. This ensures that there is no data imbalance between splits, which could bias the results. One exception is the case where only one or two adsorbates are on the surface. Because of their importance for on-site energy predictions and their scarcity, all configurations with nCO ≤ 2 were added to the training set only, and none to validation and tests sets. The dataset splits were then aggregated on a per-facet basis to train individual models per facet, and concatenated together for the all-facet model. As figures of merit such as root mean squared error depend on test splits, all comparisons between models (such as Fig. 3) were performed using the exact same train–validation–test splits.
 . The number of radial basis functions was set to 8, with a cutoff of 5.0 Å.
. The number of radial basis functions was set to 8, with a cutoff of 5.0 Å.
 (v. 2.1.0).67 A simple feedforward neural network was implemented in PyTorch to predict atom-centered contributions which are later summed to obtain the total binding energy of the system. The NN model had 3 hidden layers with 600 neurons each, mish activation function, and an input size of 539, corresponding to the length of the SOAP vector. A mean squared error loss was used to train the models. NN parameters were updated using the AdamW optimizer71 using a learning rate of 10−3, weight decay of 10−2, default β values of β1 = 0.9, β2 = 0.999, and ε = 10−8. The learning rate was reduced by a factor of 0.5 when the loss plateaus for 20 consecutive epochs, and the model was trained for 900 epochs in four NVIDIA V100 GPUs in the Lassen supercomputer, with a batch size of 50. A stochastic weight averaging (SWA) callback was also used after epoch 700, with a starting learning rate of 3 × 10−4 and cosine annealing function every 10 epochs. Training and evaluation routines were implemented using PyTorch Lightning.
(v. 2.1.0).67 A simple feedforward neural network was implemented in PyTorch to predict atom-centered contributions which are later summed to obtain the total binding energy of the system. The NN model had 3 hidden layers with 600 neurons each, mish activation function, and an input size of 539, corresponding to the length of the SOAP vector. A mean squared error loss was used to train the models. NN parameters were updated using the AdamW optimizer71 using a learning rate of 10−3, weight decay of 10−2, default β values of β1 = 0.9, β2 = 0.999, and ε = 10−8. The learning rate was reduced by a factor of 0.5 when the loss plateaus for 20 consecutive epochs, and the model was trained for 900 epochs in four NVIDIA V100 GPUs in the Lassen supercomputer, with a batch size of 50. A stochastic weight averaging (SWA) callback was also used after epoch 700, with a starting learning rate of 3 × 10−4 and cosine annealing function every 10 epochs. Training and evaluation routines were implemented using PyTorch Lightning.
Monte Carlo sampling
Sampling of new surface configurations is performed in a per-facet, per-coverage basis. Given a facet and a number of adsorbates, initial configurations are generated by randomly sampling valid combinations of adsorption sites and placing the adsorbates at the selected points (as outlined in the “Simulation workflow” subsection above). Then, the energy of the structures is evaluated with the production MACE models trained with the data from all the surface facets and coverages. Because the energies can be evaluated in batches, the evaluation step is performed for all structures at once, with a batch size of 20. This allows for 1000 replicas of the Monte Carlo sampling to be performed in parallel.The sampling procedure follows the Metropolis–Hastings algorithm within the simulated annealing method. The cooling profile is chosen to be a quadratic decay, following the equation
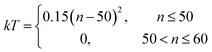 | (5) |
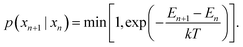 | (6) |
Although more sophisticated sampling strategies have shown to improve the acceptance ratios,21 the simpler, parallelized implementation of the MCMC algorithm demonstrated enough success in sampling the configuration space of the cases studied in this work (see Fig. S12 and S13†).
Differential binding energies
Following the work of Grabow et al.,13 the binding energy of a system was computed using eqn (1) and normalized by the number of adsorbates n of the system, Eb/n. Then, the integral binding energy is computed by multiplying the coverage θ by the average binding energy,| E(int)b = θEb/n, | (7) |
 | (8) |
To avoid computing numerical derivatives of the models, we fitted a piecewise continuous and differentiable polynomial for the integral binding energy curves,
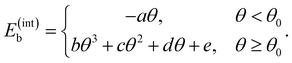 | (9) |
The equation above can be simplified when the function and its first and second derivatives are constrained to be continuous at θ = θ0, leading to
To fit the three parameters (a, b, θ0) to a relevant binding energy curve, relaxed energies were averaged using a Boltzmann average at 298 K of energies on a per-facet, per-coverage basis. Then, the parameters for the integral binding energy (eqn (7)) were obtained using the non-linear least squares method implemented in SciPy.
Data and code availability
All third-party code necessary to reproduce the results in this manuscript are described in the Methods section. The scripts and raw data required to reproduce, analyze, and visualize all results and figures in this manuscript are available on GitHub at https://github.com/dskoda/ML-Coverage. Persistent links for the data are available at Zenodo under the following DOIs: https://dx.doi.org/10.5281/zenodo.13801296 and https://dx.doi.org/10.5281/zenodo.14079367.Author contributions
Daniel Schwalbe-Koda: conceptualization; data curation; formal analysis; investigation; methodology; software; validation; visualization; writing – original draft; writing – review & editing; funding acquisition; supervision. Nitish Govindarajan: conceptualization; data curation; formal analysis; investigation; methodology; validation; visualization; writing – original draft; writing – review & editing; supervision. Joel Varley: conceptualization; formal analysis; writing – original draft; writing – review & editing; funding acquisition; supervision.Conflicts of interest
The authors have no conflicts to disclose.Acknowledgements
This work was performed under the auspices of the U.S. Department of Energy by Lawrence Livermore National Laboratory (LLNL) under Contract DE-AC52-07NA27344. D. S.-K. and N. G. acknowledge funding from the Laboratory Directed Research and Development (LDRD) Program at LLNL under project tracking code 22-ERD-055. N. G. and J. B. V. acknowledge the U.S. Department of Energy's Office of Energy Efficiency and Renewable Energy (EERE) under the Advanced Manufacturing Office (AMO) funding opportunity announcement DE-FOA-0002252. The authors also acknowledge computational support from Livermore Computing under the LLNL Institutional Computing Grand Challenge program and LDRD allocation. The views expressed herein do not necessarily represent the view of the U.S. Department of Energy or the United States Government. Manuscript released as LLNL-JRNL-858286.References
- A. Patra, J. E. Bates, J. Sun and J. P. Perdew, Properties of real metallic surfaces: Effects of density functional semilocality and van der Waals nonlocality, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E9188–E9196 CrossRef CAS.
- S. Mallikarjun Sharada, R. K. B. Karlsson, Y. Maimaiti, J. Voss and T. Bligaard, Adsorption on transition metal surfaces: Transferability and accuracy of DFT using the ADS41 dataset, Phys. Rev. B, 2019, 100, 035439 CrossRef.
- J. K. Nørskov, T. Bligaard, J. Rossmeisl and C. H. Christensen, Towards the computational design of solid catalysts, Nat. Chem., 2009, 1, 37–46 CrossRef PubMed.
- A. J. Medford, A. Vojvodic, J. S. Hummelshøj, J. Voss, F. Abild-Pedersen, F. Studt, T. Bligaard, A. Nilsson and J. K. Nørskov, From the Sabatier principle to a predictive theory of transition-metal heterogeneous catalysis, J. Catal., 2015, 328, 36–42 CrossRef CAS.
- Z. W. Seh, J. Kibsgaard, C. F. Dickens, I. Chorkendorff, J. K. Nørskov and T. F. Jaramillo, Combining theory and experiment in electrocatalysis: Insights into materials design, Science, 2017, 355, eaad4998 CrossRef PubMed.
- J. Peng, D. Schwalbe-Koda, K. Akkiraju, T. Xie, L. Giordano, Y. Yu, C. J. Eom, J. R. Lunger, D. J. Zheng, R. R. Rao, S. Muy, J. C. Grossman, K. Reuter, R. Gómez-Bombarelli and Y. Shao-Horn, Human- and Machine-Centred Designs of Molecules and Materials for Sustainability and Decarbonization, Nat. Rev. Mater., 2022, 7, 991–1009 CrossRef.
- A. Goswami, H. Ma and W. F. Schneider, Consequences of adsorbate-adsorbate interactions for apparent kinetics of surface catalytic reactions, J. Catal., 2022, 405, 410–418 CrossRef CAS.
- M. Deimel, H. Prats, M. Seibt, K. Reuter and M. Andersen, Selectivity Trends and Role of Adsorbate–Adsorbate Interactions in CO Hydrogenation on Rhodium Catalysts, ACS Catal., 2022, 12, 7907–7917 CrossRef CAS.
- M. T. Tang, Z. W. Ulissi and K. Chan, Theoretical Investigations of Transition Metal Surface Energies under Lattice Strain and CO Environment, J. Phys. Chem. C, 2018, 122, 14481–14487 CrossRef CAS.
- P. Lindgren, G. Kastlunger and A. A. Peterson, A Challenge to the G ∼ 0 Interpretation of Hydrogen Evolution, ACS Catal., 2020, 10, 121–128 CrossRef CAS.
- F. Li, et al., Molecular tuning of CO2-to-ethylene conversion, Nature, 2020, 577, 509–513 CrossRef CAS PubMed.
- T. Mou, X. Han, H. Zhu and H. Xin, Machine learning of lateral adsorbate interactions in surface reaction kinetics, Curr. Opin. Chem. Eng., 2022, 36, 100825 CrossRef.
- L. C. Grabow, B. Hvolbæk and J. K. Nørskov, Understanding trends in catalytic activity: the effect of adsorbate–adsorbate interactions for CO oxidation over transition metals, Top. Catal., 2010, 53, 298–310 CrossRef CAS.
- R. B. Getman and W. F. Schneider, DFT-Based Coverage-Dependent Model of Pt-Catalyzed NO Oxidation, ChemCatChem, 2010, 2, 1450–1460 CrossRef CAS.
- N. Yang, A. J. Medford, X. Liu, F. Studt, T. Bligaard, S. F. Bent and J. K. Nørskov, Intrinsic Selectivity and Structure Sensitivity of Rhodium Catalysts for C2+ Oxygenate Production, J. Am. Chem. Soc., 2016, 138, 3705–3714 CrossRef CAS PubMed.
- D. J. Schmidt, W. Chen, C. Wolverton and W. F. Schneider, Performance of Cluster Expansions of Coverage-Dependent Adsorption of Atomic Oxygen on Pt(111), J. Chem. Theory Comput., 2012, 8, 264–273 CrossRef CAS.
- J. Nielsen, M. d'Avezac, J. Hetherington and M. Stamatakis, Parallel Kinetic Monte Carlo Simulation Framework Incorporating Accurate Models of Adsorbate Lateral Interactions, J. Chem. Phys., 2013, 139, 224706 CrossRef PubMed.
- L. M. Herder, J. M. Bray and W. F. Schneider, Comparison of cluster expansion fitting algorithms for interactions at surfaces, Surf. Sci., 2015, 640, 104–111 CrossRef CAS.
- M. Pineda and M. Stamatakis, Beyond mean-field approximations for accurate and computationally efficient models of on-lattice chemical kinetics, J. Chem. Phys., 2017, 147, 024105 CrossRef CAS.
- F. Liu, S. Yang and A. J. Medford, Scalable approach to high coverages on oxides via iterative training of a machine-learning algorithm, ChemCatChem, 2020, 12, 4317–4330 CrossRef CAS.
- V. Sumaria and P. Sautet, CO organization at ambient pressure on stepped Pt surfaces: first principles modeling accelerated by neural networks, Chem. Sci., 2021, 12, 15543–15555 RSC.
- P. G. Ghanekar, S. Deshpande and J. Greeley, Adsorbate chemical environment-based machine learning framework for heterogeneous catalysis, Nat. Commun., 2022, 13, 5788 CrossRef CAS PubMed.
- B. Klumpers, E. J. Hensen and I. A. Filot, Lateral Interactions of Dynamic Adlayer Structures from Artificial Neural Networks, J. Phys. Chem. C, 2022, 126, 5529–5540 CrossRef CAS.
- X. Li and L. C. Grabow, Evaluating the benefits of kinetic Monte Carlo and microkinetic modeling for catalyst design studies in the presence of lateral interactions, Catal. Today, 2022, 387, 150–158 CrossRef CAS.
- F. Hess, Efficient Implementation of Cluster Expansion Models in Surface Kinetic Monte Carlo Simulations with Lateral Interactions: Subtraction Schemes, Supersites, and the Supercluster Contraction, J. Comput. Chem., 2019, 40, 2664–2676 CrossRef CAS.
- I. Batatia, D. P. Kovacs, G. Simm, C. Ortner and G. Csanyi, MACE: Higher Order Equivariant Message Passing Neural Networks for Fast and Accurate Force Fields, Adv. Neural Inf. Process. Syst., 2022, 11423–11436 Search PubMed.
- J. A. Vita and D. Schwalbe-Koda, Data efficiency and extrapolation trends in neural network interatomic potentials, Mach. Learn.: Sci. Technol., 2023, 4, 035031 Search PubMed.
- D. Schwalbe-Koda, mkite: A distributed computing platform for high-throughput materials simulations, Comput. Mater. Sci., 2023, 230, 112439 CrossRef CAS.
- S. Nitopi, E. Bertheussen, S. B. Scott, X. Liu, A. K. Engstfeld, S. Horch, B. Seger, I. E. L. Stephens, K. Chan, C. Hahn, J. K. Nørskov, T. F. Jaramillo and I. Chorkendorff, Progress and Perspectives of Electrochemical CO2 Reduction on Copper in Aqueous Electrolyte, Chem. Rev., 2019, 119, 7610–7672 CrossRef CAS PubMed.
- D. Schwalbe-Koda, A. R. Tan and R. Gómez-Bombarelli, Differentiable sampling of molecular geometries with uncertainty-based adversarial attacks, Nat. Commun., 2021, 12, 5104 CrossRef CAS.
- X. Fu, Z. Wu, W. Wang, T. Xie, S. Keten, R. Gomez-Bombarelli and T. S. Jaakkola, Forces are not Enough: Benchmark and Critical Evaluation for Machine Learning Force Fields with Molecular Simulations, Transactions on Machine Learning Research, 2023 Search PubMed.
- H. Yu, N. Govindarajan, S. E. Weitzner, R. F. Serra-Maia, S. A. Akhade and J. B. Varley, Theoretical Investigation of the Adsorbate and Potential-Induced Stability of Cu Facets During Electrochemical CO2 and CO Reduction, ChemPhysChem, 2024, 25, e202300959 CrossRef CAS.
- R. B. Sandberg, J. H. Montoya, K. Chan and J. K. Nørskov, CO-CO Coupling on Cu Facets: Coverage, Strain and Field Effects, Surf. Sci., 2016, 654, 56–62 CrossRef CAS.
- J. Li, Z. Wang, C. McCallum, Y. Xu, F. Li, Y. Wang, C. M. Gabardo, C.-T. Dinh, T.-T. Zhuang, L. Wang, J. Y. Howe, Y. Ren, E. H. Sargent and D. Sinton, Constraining CO Coverage on Copper Promotes High-Efficiency Ethylene Electroproduction, Nat. Catal., 2019, 2, 1124–1131 CrossRef CAS.
- Y. Wang, et al., Catalyst Synthesis under CO2 Electroreduction Favours Faceting and Promotes Renewable Fuels Electrosynthesis, Nat. Catal., 2020, 3, 98–106 CrossRef CAS.
- X. Kong, J. Zhao, J. Ke, C. Wang, S. Li, R. Si, B. Liu, J. Zeng and Z. Geng, Understanding the Effect of *CO Coverage on C–C Coupling toward CO2 Electroreduction, Nano Lett., 2022, 22, 3801–3808 CrossRef CAS PubMed.
- J. R. Boes, O. Mamun, K. Winther and T. Bligaard, Graph theory approach to high-throughput surface adsorption structure generation, J. Phys. Chem. A, 2019, 123, 2281–2285 CrossRef CAS PubMed.
- S. Deshpande, T. Maxson and J. Greeley, Graph theory approach to determine configurations of multidentate and high coverage adsorbates for heterogeneous catalysis, npj Comput. Mater., 2020, 6, 79 CrossRef CAS.
- D. P. Kovács, I. Batatia, E. S. Arany and G. Csányi, Evaluation of the MACE Force Field Architecture: From Medicinal Chemistry to Materials Science, J. Chem. Phys., 2023, 159, 044118 CrossRef.
- M. Van Hove and G. Somorjai, A new microfacet notation for high-Miller-index surfaces of cubic materials with terrace, step and kink structures, Surf. Sci., 1980, 92, 489–518 CrossRef CAS.
- A. P. Bartók, R. Kondor and G. Csányi, On Representing Chemical Environments, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 184115 CrossRef.
- K. T. Schütt, P.-J. Kindermans, H. E. Sauceda, S. Chmiela, A. Tkatchenko and K.-R. Müller, SchNet: A continuous-filter convolutional neural network for modeling quantum interactions, in Proceedings of the 31st International Conference on Neural Information Processing Systems (NIPS'17), Curran Associates Inc., Red Hook, NY, USA, 2017, pp. 992–1002 Search PubMed.
- Y.-L. Liao, B. Wood, A. Das and T. Smidt, EquiformerV2: Improved Equivariant Transformer for Scaling to Higher-Degree Representations, International Conference on Learning Representations (ICLR), 2024 Search PubMed.
- L. Chanussot, A. Das, S. Goyal, T. Lavril, M. Shuaibi, M. Riviere, K. Tran, J. Heras-Domingo, C. Ho and W. Hu, others Open catalyst 2020 (OC20) dataset and community challenges, ACS Catal., 2021, 11, 6059–6072 CrossRef CAS.
- N. Metropolis, A. W. Rosenbluth, M. N. Rosenbluth, A. H. Teller and E. Teller, Equation of state calculations by fast computing machines, J. Chem. Phys., 1953, 21, 1087–1092 CrossRef CAS.
- W. K. Hastings, Monte Carlo Sampling Methods Using Markov Chains and Their Applications, Biometrika, 1970, 57, 97–109 CrossRef.
- S. Kirkpatrick, C. D. Gelatt Jr and M. P. Vecchi, Optimization by simulated annealing, Science, 1983, 220, 671–680 CrossRef CAS PubMed.
- D. Widdowson and V. Kurlin, Resolving the data ambiguity for periodic crystals, Adv. Neural Inf. Process. Syst., 2022, 35, 24625–24638 Search PubMed.
- D. Schwalbe-Koda, D. E. Widdowson, T. A. Pham and V. A. Kurlin, Inorganic synthesis-structure maps in zeolites with machine learning and crystallographic distances, Digital Discovery, 2023, 2, 1911–1924 RSC.
- T. Makino and M. Okada, CO Adsorption on Regularly Stepped Cu(410) Surface, Surf. Sci., 2014, 628, 36–40 CrossRef CAS.
- A. Kokalj, T. Makino and M. Okada, DFT and TPD study of the role of steps in the adsorption of CO on copper: Cu (4 1 0) versus Cu (1 0 0), J. Phys.: Condens. Matter, 2017, 29, 194001 CrossRef PubMed.
- M. Gajdoš, A. Eichler, J. Hafner, G. Meyer and K.-H. Rieder, CO adsorption on a Cu (211) surface: First-principle calculation and STM study, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035402 CrossRef.
- C. N. Lininger, J. A. Gauthier, W.-L. Li, E. Rossomme, V. V. Welborn, Z. Lin, T. Head-Gordon, M. Head-Gordon and A. T. Bell, Challenges for density functional theory: calculation of CO adsorption on electrocatalytically relevant metals, Phys. Chem. Chem. Phys., 2021, 23, 9394–9406 RSC.
- G. Kastlunger, L. Wang, N. Govindarajan, H. H. Heenen, S. Ringe, T. Jaramillo, C. Hahn and K. Chan, Using pH Dependence to Understand Mechanisms in Electrochemical CO Reduction, ACS Catal., 2022, 12, 4344–4357 CrossRef CAS.
- G. Kresse and J. Furthmüller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- B. Hammer, L. B. Hansen and J. K. Nørskov, Improved adsorption energetics within density-functional theory using revised Perdew-Burke-Ernzerhof functionals, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 7413 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, A climbing image nudged elastic band method for finding saddle points and minimum energy paths, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- G. Henkelman and H. Jónsson, A dimer method for finding saddle points on high dimensional potential surfaces using only first derivatives, J. Chem. Phys., 1999, 111, 7010–7022 CrossRef CAS.
- A. Hjorth Larsen, et al., The atomic simulation environment—a Python library for working with atoms, J. Phys.: Condens. Matter, 2017, 29, 273002 CrossRef PubMed.
- J. H. Montoya and K. A. Persson, A high-throughput framework for determining adsorption energies on solid surfaces, npj Comput. Mater., 2017, 3, 14 CrossRef.
- S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Python Materials Genomics (pymatgen): A robust, open-source python library for materials analysis, Comput. Mater. Sci., 2013, 68, 314–319 CrossRef CAS.
- J. Laakso, L. Himanen, H. Homm, E. V. Morooka, M. O. Jäger, M. Todorović and P. Rinke, Updates to the DScribe library: New descriptors and derivatives, J. Chem. Phys., 2023, 158, 234802 CrossRef CAS.
- L. McInnes, J. Healy and J. MelvilleUMAP: Uniform manifold approximation and projection for dimension reduction, arXiv, 2018, preprint, arXiv:1802.03426, DOI:10.48550/arXiv.1802.03426.
- D. Kingma and J. Ba, Adam: A Method for Stochastic Optimization, International Conference on Learning Representations (ICLR), San Diego, CA, USA, 2015 Search PubMed.
- S. J. Reddi, S. Kale and S. Kumar, On the Convergence of Adam and Beyond, International Conference on Learning Representations, 2018 Search PubMed.
- I. Loshchilov and F. Hutter, Decoupled Weight Decay Regularization, International Conference on Learning Representations, 2019 Search PubMed.
- K. T. Schütt, P. Kessel, M. Gastegger, K. A. Nicoli, A. Tkatchenko and K.-R. Müller, SchNetPack: A Deep Learning Toolbox For Atomistic Systems, J. Chem. Theory Comput., 2019, 15, 448–455 CrossRef.
- K. T. Schütt, S. S. P. Hessmann, N. W. A. Gebauer, J. Lederer and M. Gastegger, SchNetPack 2.0: A neural network toolbox for atomistic machine learning, J. Chem. Phys., 2023, 158, 144801 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dd00328d |
| This journal is © The Royal Society of Chemistry 2025 |