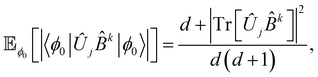Efficient strategies for reducing sampling error in quantum Krylov subspace diagonalization
Received
4th October 2024
, Accepted 17th February 2025
First published on 21st March 2025
Abstract
Within the realm of early fault-tolerant quantum computing (EFTQC), quantum Krylov subspace diagonalization (QKSD) has emerged as a promising quantum algorithm for the approximate Hamiltonian diagonalization via projection onto the quantum Krylov subspace. However, the algorithm often requires solving an ill-conditioned generalized eigenvalue problem (GEVP) involving erroneous matrix pairs, which can significantly distort the solution. Since EFTQC assumes limited-scale error correction, finite sampling error becomes a dominant source of error in these matrices. This work focuses on quantifying sampling errors during the measurement of matrix element in the projected Hamiltonian examining two measurement approaches based on the Hamiltonian decompositions: the linear combination of unitaries and diagonalizable fragments. To reduce sampling error within a fixed budget of quantum circuit repetitions, we propose two measurement strategies: the shifting technique and coefficient splitting. The shifting technique eliminates redundant Hamiltonian components that annihilate either the bra or ket states, while coefficient splitting optimizes the measurement of common terms across different circuits. Numerical experiments with electronic structures of small molecules demonstrate the effectiveness of these strategies, reducing sampling costs by a factor of 20–500.
I. Introduction
Recent advancements in quantum computing devices, particularly in terms of the scale and coherence time,1–7 have significantly heightened expectations for their ability to perform efficient quantum simulations. These advancements promise to deepen our understanding of many-body quantum systems, such as electronic structure in chemical systems.8–10 This anticipation is driven by the expected stability, controllability, and scalability of universal quantum computers being developed across various platforms, including ion traps,2,3 photons,4,5 and superconductors.6,7
Currently, the field is progressing through the era of noisy and intermediate-scale quantum computers (NISQ).11,12 This phase marks a regime of quantum computation which is hard to be simulated using classical computers, while quantum error correction is absent due to the limited scalability, inherent noises, and decoherence of current devices. Within this context, the variational quantum eigensolver (VQE) has been primarily discussed as an algorithm for quantum simulation.13,14 Based on the variational principle, VQE employs quantum-classical hybrid optimization of a parameterized ansatz, implementable within a shallow quantum circuit to approximate specific eigenstates of the target system. However, the expected quantum advantage—based on the classical hardness of simulating the ansatz—is negated by errors in estimating cost function for each optimization step, particularly associated with barren plateau problem.15–19 Furthermore, the absence of the error correction results in the errors accumulating significantly, thus limiting the scalable quantum advantage in VQE.
This naturally shifts our attention towards early fault-tolerant quantum computing (EFTQC) as a viable next step beyond NISQ era. The feasibility of EFTQC is further supported by decreasing hardware error rates that are approaching the threshold for the error correction20–22 and an emergence of a small-scale demonstration of logical qubits.23 EFTQC is introduced within a framework of scale-limited quantum error correction, where the error rate for logical qubits increases with the size of the quantum circuit.24 Consequently, unlike fully fault-tolerant quantum computing, EFTQC cannot arbitrarily scale the number of logical qubits or the use of non-Clifford operations, thereby limiting the practical implementation of quantum phase estimation.25 To address these limitations, EFTQC algorithms typically aim to compromise between the circuit size and the number of repetitions. Quantum phase estimation requires M = O(|γ0|−2) repetitions of a circuit with real-time propagators (e−iĤtk) with the total propagation time,  , where |γ0| and εalg denote the initial overlap and algorithm accuracy, respectively.25 Here, the real-time propagator is usually approximately implemented by Suzuki–Trotterization.26,27 In contrast, EFTQC algorithms use shorter propagators, t < O(εalg−1), but increase the number of repetitions, M > O(|γ0|−2).28–33 An alternative approach within EFTQC utilizes the block encoding scheme,34 which, while exact, demands significantly more resources than Trotterization with a minimal Trotter steps. Although reducing Trotterization errors necessitates more Trotter steps, thus approaching the resource demands of block encoding, the limitations of near-future hardware render small-scale Trotterization a more feasible option.
, where |γ0| and εalg denote the initial overlap and algorithm accuracy, respectively.25 Here, the real-time propagator is usually approximately implemented by Suzuki–Trotterization.26,27 In contrast, EFTQC algorithms use shorter propagators, t < O(εalg−1), but increase the number of repetitions, M > O(|γ0|−2).28–33 An alternative approach within EFTQC utilizes the block encoding scheme,34 which, while exact, demands significantly more resources than Trotterization with a minimal Trotter steps. Although reducing Trotterization errors necessitates more Trotter steps, thus approaching the resource demands of block encoding, the limitations of near-future hardware render small-scale Trotterization a more feasible option.
Within the domain of EFTQC algorithms, quantum Krylov subspace diagonalization (QKSD) is being explored as a promising candidate for quantum simulation algorithm.32,33 QKSD employs quantum circuits to project the Hamiltonian onto the Krylov subspace, a reduced-dimensional space that is classically solvable. This approach is potentially feasible because the extremal eigenvalues of the projected matrix converge exponentially fast to those of the original Hamiltonian, provided the projection remains unperturbed and the overlap between the eigenstate and the initial state is large.35 However, this advantage is counterbalanced by the challenge associated with ill-conditioning of the eigenvalue problem, where perturbations in the projected matrix can significantly distort the accuracy of the approximated eigenvalues.35,36 These perturbations mainly arise from imperfect error correction, Trotterization error, and finite sampling error. As EFTQC stabilizes and expands, the first two factors can be suppressed. However, despite the discussion of the measurement problem in QKSD,36 strategies to tackle this problem have not been suggested.
QKSD involves measuring the matrix elements, Hkl = 〈ϕk|Ĥ|ϕl〉, across a finite basis {|ϕk〉 = e−iĤkΔt|ϕ0〉} that spans the Krylov subspace with a reference state |ϕ0〉. While other bases have been proposed, such as |ϕk〉 = Ĥk|ϕ0〉37 and |ϕk〉 = e−Ĥkβ|ϕ0〉,38 we focus on QKSD with the real-time evolution operator due to its simplicity and practical viability for EFTQC. Consequently, a primary objective in this scenario is to minimize the sampling error when measuring the matrix elements. Although this specific measurement problem has not been tackled, several measurement strategies have been proposed for the standard expectation values.39–46 In general, the direct measurement of 〈ψ|Ĥ|ψ〉 with a single circuit is impractical, as measurement is constrained to the Pauli-Z basis, which requires the implementation of a unitary operator that fully diagonalizes Ĥ. As an alternative, Ĥ is decomposed into a linear combination of fragmented Hamiltonians, which can be efficiently diagonalized with implementable unitaries, and the results for each fragment are aggregated.39,42,46 The goal then becomes to minimize the sampling error by optimally fragmenting Ĥ and allocating the number of circuit repetitions among these fragments. This optimization can be formulated as a combinatorial problem, akin to NP-hard clique covering problems,42,46 for which a heuristic solution has been developed.39 Additionally, this issue has been expanded into a continuous optimization problem that considers approximated covariances between fragments.40,44 On the other hand, randomized measurement strategies, known as classical shadow techniques, have been developed.47–49 While these methods are superior when measuring multiple expectation values simultaneously, deterministic methods generally outperform them when measuring a single expectation value 〈Ĥ〉.40,41,50 Since our case involves measuring 〈ϕk|Ĥ|ϕl〉, we focus on deterministic measurement strategies in this work.
These developments resolve the measurement problems associated with standard expectation values. In this paper, we aim to adapt these methods to the QKSD framework. To accomplish this, we analyze the measurement problem of the matrix elements with two decomposition scenarios for Ĥ: linear combination of unitaries (LCU) and fragmented Hamiltonians (FH). Specifically, we focus on quantifying and mitigating the sampling errors for these scenarios, applying strategies originally designed for standard expectation values to enhance measurement accuracy in QKSD. Notably, the strategies that we propose can be applied to the general measurement of transitional amplitudes, 〈ϕk|Ĥ|ϕl〉, which can be utilized for the design of algorithms beyond QKSD.
The organization of the paper is as follows. First, a brief preliminary of the QKSD is provided in Section II, followed by the analyses of the two measurement methods for the matrix elements and the associated errors in Section III. Section IV demonstrates how conventional methods39,40,51,52 are converted to reduce the sampling errors for QKSD, highlighting that a method initially devised for reducing the simulation cost of LCU51,52 is transferable to the measurement problem. Finally, we numerically validate these reduction methods by solving the electronic structure problems of small molecules as case studies in Section V.
II. QKSD
Before considering the measurement problem in QKSD, this section reviews the QKSD method for estimating the spectrum of a Hamiltonian Ĥ, as originally introduced in ref. 32 and 33.
QKSD estimates approximated eigenstates of a Hamiltonian Ĥ with the following ansatz:
| |  | (1) |
where
is the normalization factor, and

, and
n is the Krylov order. This ansatz fully covers vectors in the Krylov subspace,

, where |
ϕk〉=
![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) k
k|
ϕ0〉 is defined by a reference state |
ϕ0〉 and the base operator,
| | ![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) = e−iΔtĤ. = e−iΔtĤ. | (2) |
This exponential function is approximated by the Trotterization. There are other choices for ![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) , such as Ĥ, which is analogous to the classical Krylov method,37 and imaginary time evolution (e−βĤ).38 Although we only focus on the real-time evolution operator, which is widely discussed, the methods that will be described in the Section IV can be expanded to the other choices of
, such as Ĥ, which is analogous to the classical Krylov method,37 and imaginary time evolution (e−βĤ).38 Although we only focus on the real-time evolution operator, which is widely discussed, the methods that will be described in the Section IV can be expanded to the other choices of ![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) because they are approximated by linear combinations or products of real-time propagators.
because they are approximated by linear combinations or products of real-time propagators.
Using the ansatz (eqn (1)) in the variational principle with w as optimized parameters leads to the following generalized eigenvalue problem (GEVP)
where
E(n) is an approximate eigenvalue, and the
n ×
n Hamiltonian matrix
H and overlap matrix
S are defined as
| | Hkl = 〈ϕk|Ĥ|ϕl〉 = 〈ϕ0|![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) †kĤ †kĤ![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) l|ϕ0〉 = H0,l−k l|ϕ0〉 = H0,l−k | (4) |
| | Skl = 〈ϕk|ϕl〉 = 〈ϕ0|![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) †k †k![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) l|ϕ0〉 = S0,l–k. l|ϕ0〉 = S0,l–k. | (5) |
These matrices are obtained by quantum algorithms using EFTQC circuits and measurements. Note that S has the structure of a Toeplitz matrix, Sk,l = S0,l–k, because ![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) is unitary. Furthermore, since [Ĥ,
is unitary. Furthermore, since [Ĥ,![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) ] = 0, H becomes a Toeplitz matrix as well. Therefore, rather than n2, only n elements are required to construct each matrices.
] = 0, H becomes a Toeplitz matrix as well. Therefore, rather than n2, only n elements are required to construct each matrices.
For systems with large energy gaps, the lowest solution of eqn (3) converges to the ground state energy of Ĥ exponentially fast with n.35 However, the GEVP in eqn (3) can become ill-conditioned for larger n's, which makes QKSD sensitive to noise in matrix elements of H and S.
III. Measurement of QKSD matrix elements
In the quantum subroutine that estimates the elements of H and S, the quantum uncertainty predominantly induces the matrix perturbation. This perturbation, coupled with the ill-conditioned GEVP (eqn (3)), may introduce a significant error in the solution. In this section, we develop methods for estimating Hamiltonian matrix elements,and the analysis of the associated sampling error.
Since, rather than the matrix element, only the measurements of standard expectation values of 〈Φ|Ôj|Φ〉 with easily diagonalizable Ôj's are possible at the circuit level, it is necessary to express eqn (6) in terms of 〈Φ|Ôj|Φ〉 using certain states |Φ〉 and simple operators Ôj. To translate eqn (6) into standard expectations, we consider two approaches: the Hadamard and the extended swap tests. In both approaches, the problem is addressed by partitioning the Hamiltonian into diagonalizable Hermitian or implementable unitary operators. In the Hadamard test, the Hamiltonian is presented as an LCU:  , where each unitary Ûj is implemented to estimate the overlap between |ϕ0〉 and Ûj|ϕk〉 (Fig. 1a). In the extended swap test, Ĥ is decomposed as a sum of fragments:
, where each unitary Ûj is implemented to estimate the overlap between |ϕ0〉 and Ûj|ϕk〉 (Fig. 1a). In the extended swap test, Ĥ is decomposed as a sum of fragments:  , where
, where ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) j is diagonal and the corresponding diagonalizing unitary
j is diagonal and the corresponding diagonalizing unitary ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) j can be implemented efficiently. Then, the extended swap test is conducted with the circuits of Hadamard tests which estimate 〈ϕ0|ϕk〉, while including the measurement of system qubits with the basis represented by
j can be implemented efficiently. Then, the extended swap test is conducted with the circuits of Hadamard tests which estimate 〈ϕ0|ϕk〉, while including the measurement of system qubits with the basis represented by ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) j (Fig. 1b). Note that in the extended swap test, the overlap matrix elements can be measured simultaneously by measuring the ancilla qubit, which corresponds to a Hadamard test circuit that measures S0,k = 〈ϕ0|e−ikΔtĤ|ϕ0〉. This simultaneous measurement capability is not available in the Hadamard test when measuring the Hamiltonian in its LCU form.
j (Fig. 1b). Note that in the extended swap test, the overlap matrix elements can be measured simultaneously by measuring the ancilla qubit, which corresponds to a Hadamard test circuit that measures S0,k = 〈ϕ0|e−ikΔtĤ|ϕ0〉. This simultaneous measurement capability is not available in the Hadamard test when measuring the Hamiltonian in its LCU form.
 |
| | Fig. 1 Circuit diagrams for (a) the Hadamard test and (b) the extended swap test to estimate the j-th fragment of the Hamiltonian matrix element, 〈ϕ0|Ĥ|ϕk〉 (see eqn (11) and (18)); here, ![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) x(y) operator rotates x(y) operator rotates ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) z basis into z basis into ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) x ( x (![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) y) basis and is adopted to estimate the real (imaginary) part of the amplitude for the second operator applied to the ancilla qubit. y) basis and is adopted to estimate the real (imaginary) part of the amplitude for the second operator applied to the ancilla qubit. | |
This work mainly focuses on analyzing and improving the sampling error determined by the decomposition of the observable, which is not required for the case of the overlap matrix element,  . In a previous work,36 it was shown that the sampling variance of S0k are determined identically across the test algorithms as:
. In a previous work,36 it was shown that the sampling variance of S0k are determined identically across the test algorithms as:
| |  | (7) |
where
mR and
mI are the fraction of total shots,
M, allocated to measure real and imaginary parts of
S0k, respectively (
mR +
mI = 1). The ideal allocation that minimizing the variance is
m(opt)R ∝ (1 − Re[
S0k]
2)
1/2 and
m(opt)I ∝ (1 − Im[
S0k]
2)
1/2, which is, however, infeasible to be estimated before measuring
S0k. If we take Haar averaging of the states, |
ϕ0〉 and |
ϕk〉,
mR =
mI = 1/2 is achieved from Lemma 2 in Appendix A. The corresponding variance is related to the amplitude of the matrix element as
| |  | (8) |
In the rest of this section, we quantify the sampling error associated with the Hamiltonian matrix elements and examine how the decomposition of Ĥ affects this error.
A Hadamard test
An LCU decomposition of Ĥ is| |  | (9) |
where Ûj is unitary, and βj is a real and positive coefficient. Such decomposition was originally motivated in the context of Hamiltonian simulation problem53 and then expanded to the measurement problem.54,55 The simulation cost in LCU based approach scales linearly with the L1 norm of the coefficients,  . In the Hadamard test, we are going to show that the sampling cost to estimate eqn (6) within a certain level of accuracy is proportional to ‖β‖12.
. In the Hadamard test, we are going to show that the sampling cost to estimate eqn (6) within a certain level of accuracy is proportional to ‖β‖12.
The matrix element in eqn (6) can be viewed as the weighted sum of overlaps between |ϕ0〉 and Ûj|ϕk〉:
| |  | (10) |
Fig. 1a depicts the circuit that estimates 〈ϕ0|Ûj|ϕk〉. To derive the sampling cost, eqn (6) is translated to standard expectations as
| |  | (11) |
where
| |  | (12) |
is prepared with an additional qubit and the conditional evolution unitary. The additional qubit is measured in
![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) x
x and
![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) y
y bases, corresponding to the real and imaginary parts of 〈
ϕ0|
Ûj|
ϕk〉, respectively. Thus, 2
Nβ independent measurements of

and

with a set of states

complete the total estimation of a matrix element in
eqn (11).
For measuring the expectation value of eqn (11), the variance is:
| |  | (13) |
where
| |  | (14) |
Also, M denotes the total number of shots to measure H0k, and mjX is the fraction of shots for 〈Φ0k;j|ÔX|Φ0k;j〉  .
.
Given LCU decomposition, finding the optimal shot allocation m to minimize eqn (13) is a convex problem, which is analytically solved by
| | | m(opt)jX ∝ βjVar[ÔX]Φ0k;j1/2. | (15) |
However, since Var[ÔX]Φ0k;j are not known in advance, they are estimated by taking Haar-averaging over the states |ϕ0〉 and |ϕk〉. This results in a sub-optimal allocation instead, m(subopt)jX ∝ βj, which is independent of the unknown variances. Furthermore, such allocation leads to the averaged variance as shown below:
| | 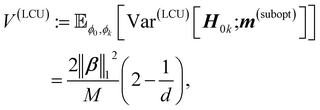 | (16) |
where
d is the dimension of the Hilbert space, which is generally exponentially large. The proof of
eqn (16) is provided in Appendix A. The number of total shots more than
| |  | (17) |
is required to make the total uncertainty less than
ε with a high probability, which shows that the sampling cost is proportional to ‖
β‖
12. This result indicates that an LCU decomposition of
Ĥ with lower ‖
β‖
1 can potentially reduce the number of samplings, while maintaining accuracy.
B Extended swap test
The extended swap test32 estimates the matrix element through the measurement of| | 〈ϕ0|Ĥ|ϕk〉 = 〈Φ0k|(![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) x + i x + i![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) y) ⊗ Ĥ|Φ0k〉, y) ⊗ Ĥ|Φ0k〉, | (18) |
where
However, the direct measurement of eqn (18) is possible only when Ĥ is an Ising form. In general, Ĥ can be expressed as a sum of diagonalizable fragment Hamiltonians:
| |  | (19) |
where
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) j
j can be efficiently implemented to diagonalize
Ĥj onto the computational basis, yielding an Ising Hamiltonian
![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) j
j. Then, the measurement can be performed for each
Ĥj. For example, if
Ĥj is composed of mutually commuting Pauli operators, the unitary
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) j
j can be efficiently determined and implemented as a Clifford circuit with the gate count of
O(
Nq2), where
Nq is the number of qubits.
39,56,57
After substituting Ĥ in eqn (18) by (19), the total variance of the estimator is
| |  | (20) |
where
Ôj,R(I) =
![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) x(y)
x(y) ⊗
Ĥj, and the quantum variance of
Ôj is
| |  | (21) |
with
As in LCU decomposition, the optimal shot allocation, m(opt)jX ∝ Var[ÔjX]Φ0k;j1/2, is hard to estimate in advance. In order to find a sub-optimal allocation, m(subopt), we perform Haar averaging on the variance over the states, |ϕ0〉 and |ϕk〉. According to the result in Appendix A, this averaging produces m(subopt)jR(I) ∝ (Tr[Ĥj2]/d)1/2. Furthermore, for the case of Pauli decomposition, the value of (Tr[Ĥj2]/d)1/2 is efficiently determined as the L2 norm of Pauli coefficients in Ĥj, as elaborated in Appendix B.
The total averaged variance is
| |  | (22) |
where

. The corresponding measurement cost,
| |  | (23) |
scales quadratically with the ‖
γ‖
1, which plays the same role as ‖
β‖
1 in the LCU case.
We can find the similarity between the variances of LCU and FH, (see eqn (16) and (22)). Let us write the decompositions for both cases (eqn (9) and (19)) as
| |  | (24) |
where
![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) j
j ∈ {
βjÛj,
Ĥj}. Then, the partial variances,
eqn (14) (multiplied by
βj) and
(21), are generalized into a single form:
| |  | (25) |
where
X0k;j ∈ {
R0k;j,
I0k;j} is an estimator for the real or imaginary part of 〈
ϕ0|
![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) j
j|
ϕk〉.
Moreover, the decomposition norms, ‖β‖1 and ‖γ‖1 in eqn (16) and (22), are regarded as:
| |  | (26) |
Correspondingly, the sampling cost is given by:
| |  | (27) |
Thus, regardless of the test algorithms, ‖ζ‖1 serves as a metric of decomposition assessing the finite sampling error, akin to the measurements of standard expectation values.39,55
IV. Sampling cost reduction
In this section, we propose techniques to reduce the sampling cost discussed in the previous section. This is done by adapting the cost reduction techniques for the measurement of standard expectation, 〈ϕ|Ĥ|ϕ〉,39,40,44 to the measurement of matrix elements. Such adaptation is simply done by replacing the standard variance, 〈Ôj2〉–〈Ôj〉2, by the variance for the matrix elements represented in eqn (14) and (21). We propose a method to optimize the decomposition, {Ûj} or {Ĥj}, to achieve smaller variance analogous to the approach in previous work.39 Furthermore, the dependence of the sampling cost on ‖ζ‖1, as shown in eqn (27), allows us to use methods that reduce ‖ζ‖1.
A Shifting technique
Here, we introduce a technique to reduce the norm ‖ζ‖1, and consequently, lower expected sampling costs, by shifting the Hamiltonian. Before developing the technique, let's clarify the notation for the norm, ‖ζA(Ĥ)‖1, which indicates the norm of the decomposition achieved on Ĥ using a specific deterministic algorithm, A. This clarification is crucial because the decomposition applied to Ĥ is not unique without specifying the algorithm A. As an example of A, a greedy algorithm-based  heuristically finds a decomposition by Pauli operators that yields a relatively small norm.39
heuristically finds a decomposition by Pauli operators that yields a relatively small norm.39
The shifting technique involves finding an operator ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) that shifts the Hamiltonian and minimizes the norm of the shifted decomposition:
that shifts the Hamiltonian and minimizes the norm of the shifted decomposition:
| |  | (28) |
where
A is a fixed polynomial time algorithm performing a decomposition, and the Hermitian operator
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif)
is parameterized by
τ, enabling the use of classical optimization algorithms. Additionally, we impose a constraint on
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif)
(
τ), that is
| | ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) (τ)|ϕ0〉 = t(τ)|ϕ0〉, (τ)|ϕ0〉 = t(τ)|ϕ0〉, | (29) |
for a known factor
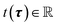
. Note that
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif)
is not required to commute with
Ĥ, unlike symmetry operators. The necessity of this constraint will be presented with the rest of procedure.
After the optimization of eqn (28), we then employ test algorithms explained in Section III to estimate the shifted Hamiltonian matrix H − T, consuming reduced cost (‖ζA(Ĥ − ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) )‖12 ≤ ‖ζA(Ĥ)‖12). Here, H − T is defined as a Toeplitz matrix satisfying
)‖12 ≤ ‖ζA(Ĥ)‖12). Here, H − T is defined as a Toeplitz matrix satisfying
| | [H − T]kl = 〈ϕ0|(Ĥ − ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) )|ϕl−k〉. )|ϕl−k〉. | (30) |
Then, the GEVP with the shifted Hamiltonian matrix is
| | | (H − T)w = Sw(E(n) − t), | (31) |
because the original matrix element is written in terms of the shifted matrix element as shown below:
and
H −
T is Toeplitz as defined in
eqn (30). Thus, the constraints of
eqn (29) and
(30) enables the recovery of the solutions of the original GEVP,
E(n) from that of shifted one by simply adding
t.
Here, we give an example of designing and parameterizing ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) dedicated to the electronic structure problem. In many cases, the reference state, |ϕ0〉 is chosen as a simple state, such as Hartree Fock (HF) ground state or a configuration state function (CSF) which is a symmetry-adapted state composed of a small number of Slater determinants. Some or all orbitals in such reference states are separately occupied or unoccupied, which is represented as:
dedicated to the electronic structure problem. In many cases, the reference state, |ϕ0〉 is chosen as a simple state, such as Hartree Fock (HF) ground state or a configuration state function (CSF) which is a symmetry-adapted state composed of a small number of Slater determinants. Some or all orbitals in such reference states are separately occupied or unoccupied, which is represented as:
| |  | (32) |
where ‘occ’ and ‘virt’ denote the sets of occupied and virtual orbitals, respectively, and |
ϕ0(r)〉 is possibly entangled and in the remainder system, satisfying |
ϕ0(r)〉〈
ϕ0(r)| = Tr
occ,virt[|
ϕ0〉〈
ϕ0|]. In a HF ground state, all orbitals are either occupied or unoccupied while a CSF state may involve some entangled state |
ϕ0(r)〉. Furthermore, an electronic structure Hamiltonian is represented as
| |  | (33) |
where
Norb denotes the number of total orbitals and the notations of the symmetric excitation operators
Êrs =
â†râs +
â†sâr and the number operators
![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) q
q =
â†qâq are employed.
Then, the shift operator can be designed to cover one- and two-body terms in the Hamiltonian and to satisfy eqn (29), which has the following form:
| |  | (34) |
Here, the sets of orbital indices,  and
and 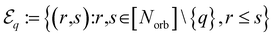 are defined, and δq∈occ is an identity if q ∈ occ, zero otherwise. The indices r and s range over the entire orbital set except q to make
are defined, and δq∈occ is an identity if q ∈ occ, zero otherwise. The indices r and s range over the entire orbital set except q to make ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) Hermitian and to avoid duplication with the one-body number operator, since
Hermitian and to avoid duplication with the one-body number operator, since ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) q2 =
q2 = ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) q. Note that the two-body terms with Êrs
q. Note that the two-body terms with Êrs![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) q for q ∈ virt annihilate |ϕ0〉, as do Êrs(
q for q ∈ virt annihilate |ϕ0〉, as do Êrs(![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) q − 1) for q ∈ occ. Therefore, the corresponding shift factor is determined as
q − 1) for q ∈ occ. Therefore, the corresponding shift factor is determined as
| |  | (35) |
The optimal τ can be found using iterative optimization algorithms like  or
or  with the number of parameters of |τ| = O(Norb3). However, the optimization overhead is reduced if we adopt a decomposition algorithm where each term in eqn (33) is regarded as a fragment, as detailed in Appendix D. By using this reduced optimization, the optimal parameters are found as
with the number of parameters of |τ| = O(Norb3). However, the optimization overhead is reduced if we adopt a decomposition algorithm where each term in eqn (33) is regarded as a fragment, as detailed in Appendix D. By using this reduced optimization, the optimal parameters are found as
| |  | (36) |
After this optimization, the entire number operators, along with a significant portion of one-body Hamiltonian, are discarded. Consequently, only a part of the two-body Hamiltonian needs to be measured.
The shifting technique is also applicable to other algorithms that require the measurement of aÔ(τ) := 〈ϕ0|Ôe−iĤτ|ϕ0〉 for some Hermitian operator Ô. With the extended swap test, one can efficiently estimate aÔ(τ) from the measurement of aÔ−![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) (τ) and
(τ) and  , which are always measurable simultaneously.
, which are always measurable simultaneously.
B Iterative coefficient splitting
In contrast to the shifting technique, which minimizes the state-averaged costs (eqn (16) and (22)), this section focuses on optimizing the state-dependent costs (eqn (13) and (20)). As one approach, we apply iterative coefficient splitting (ICS), initially designed for standard measurements,40 to the problem of measuring the matrix elements.
Given a qubit Hamiltonian,  , where
, where 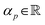 and
and  , ICS seeks a decomposition into measurable operators that minimizes the total variance. Note that measurable operators here involve not only Hermitian operators but also scaled unitaries, which are used for the Hadamard test. As reviewed in Appendix B, such a decomposition in Pauli basis is written as:
, ICS seeks a decomposition into measurable operators that minimizes the total variance. Note that measurable operators here involve not only Hermitian operators but also scaled unitaries, which are used for the Hadamard test. As reviewed in Appendix B, such a decomposition in Pauli basis is written as:
| |  | (37) |
where
![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) j
j are measurable operators and the corresponding sets of Pauli indices,
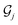
, are predetermined by a decomposition algorithm like

. Importantly, these

sets may not be disjoint, meaning the same operator
![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) p
p can belong to multiple sets. Correspondingly, the coefficient
αp is split across these sets, satisfying the condition:
| |  | (38) |
ICS leverages the flexibility of coefficient splitting to minimize the total variance, which is thus treated as a function of the split coefficients α and the shot allocation m:
| |  | (39) |
where the vectors of split coefficients are defined as

and

. The partial variance for
![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) j
j (
eqn (25)) is expressed as a quadratic form in terms of the split coefficients

:
| |  | (40) |
Here, the Pauli covariance for the real part is determined as:
| | 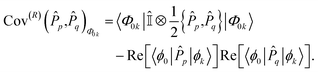 | (41) |
The detailed derivation is provided in Appendix C. The covariance for the imaginary part is obtained by replacing Re with Im in eqn (41).
To proceed with the optimization of eqn (39), the covariances need to be estimated beforehand. A direct and precise calculation of eqn (41) requires a state, |ϕk〉 = e−iĤtk|ϕ0〉, which is classically difficult to obtain. Therefore, the covariance is approximated using configuration interaction single and double (CISD) ground state, |CISD〉, and its energy, ECISD:
| | | |ϕk〉 ≈ e−iECISDtk|CISD〉. | (42) |
Then, the optimization problem is given as:
| |  | (43) |
Here,
α and
m, denote the split coefficients and the shot allocation, respectively. Although optimizing both
α and
m does not have a closed-form solution, the each step of alternating optimization—by fixing one variable (
α or
m) while optimizing the other—is a convex problem. When
m is held constant, constrained quadratic programming can be employed for optimizing
α, because the variance is expressed as a quadratic form of
α as shown in
eqn (40). Conversely, when optimizing
m with a fixed
α, the Lagrangian multiplier method is utilized, which results in
| |  | (44) |
Overall, adapting the ICS method to the measurement problem for the matrix elements involves three additional key features compared to ref. 40: (1) including scaled unitaries as measurable objects, (2) defining covariances between anticommuting Pauli operators, (3) employing the CISD proxy state for the time-evolved state.
V. Numerical results
Here, we present numerical illustrations of our theoretical developments by examining the electronic structures of small molecules: H2, H4, LiH, BeH2 and H2O, using the STO-3G basis set. The fermionic Hamiltonians are transformed to qubit operators by the Bravyi–Kitaev mapping with two-qubit reduction.58,59
For the QKSD setting, we use the Hartree–Fock ground as the reference state |ϕ0〉. The time step for the propagator is chosen as Δt = π/ΔE1, following the choice in ref. 35, Theorem 3.1, where ΔE1 represents the first spectral gap. In practical scenario where the spectral gap is difficult to estimate in advance, a sufficiently large time step is often chosen to mitigate ill-conditioning, although this comes at the cost of increased circuit depth. The dependency of the conditioning on the time step has been numerically studied in ref. 37, Appendix A-2. Also, in order to focus on the finite sampling error, we assume that the exact propagator ![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) = e−iĤΔt is available, which does not involve Trotterization error. The QKSD order is set to n = Nq + 1, where Nq is the number of qubits. In this setting, the overhead for the classical GEVP is exponentially small compare to the direct diagonalization, while the error induced by the projection onto the quantum Krylov space is exponentially small as shown in ref. 35, Theorem 3.1. We observed that the error caused by the Krylov projection is bounded as |E0(n) − E0|<10−4 Ha in the electronic structures of our interest, where E0 is the true ground state energy of Ĥ.
= e−iĤΔt is available, which does not involve Trotterization error. The QKSD order is set to n = Nq + 1, where Nq is the number of qubits. In this setting, the overhead for the classical GEVP is exponentially small compare to the direct diagonalization, while the error induced by the projection onto the quantum Krylov space is exponentially small as shown in ref. 35, Theorem 3.1. We observed that the error caused by the Krylov projection is bounded as |E0(n) − E0|<10−4 Ha in the electronic structures of our interest, where E0 is the true ground state energy of Ĥ.
The reduction in the norm achieved through the shifting operator in eqn (34) is presented in Table 1. Overall, the shifting technique reduced the norm more than 74%. The relative reductions are larger in the LCU case because the shifting removes large Ẑ-type Pauli operators. These operators cannot be grouped together in the LCU decomposition, leading to a larger norm when they were not removed. The details are provided in Appendix B. However, the resulting costs of LCU remain higher than those for FH, which implies that FH allows more efficient measurement.
Table 1 LCU(β) and FH(γ) decomposition norms with and without shifting.  is adopted as decomposition algorithm. Shifting operators
is adopted as decomposition algorithm. Shifting operators ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) are chosen as eqn (34) and optimized by the
are chosen as eqn (34) and optimized by the  algorithm after assigning the parameters shown in eqn (36)
algorithm after assigning the parameters shown in eqn (36)
| Norm (Hartree) |
H2 |
H4 |
LiH |
BeH2 |
H2O |
| ‖βSI(Ĥ)‖1 |
0.8405 |
6.0055 |
9.9902 |
16.4482 |
57.3794 |
‖βSI(Ĥ − ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) )‖1 )‖1 |
0.1812 |
1.1278 |
0.4739 |
1.3582 |
2.0035 |
| Reduction (LCU, %) |
78.4 |
81.2 |
95.3 |
91.7 |
96.5 |
| ‖γSI(Ĥ)‖1 |
0.7397 |
2.0310 |
2.5254 |
4.7003 |
21.9723 |
‖γSI(Ĥ − ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) )‖1 )‖1 |
0.1812 |
0.5288 |
0.3268 |
0.7857 |
1.1727 |
| Reduction (FH, %) |
75.50 |
74.0 |
87.1 |
83.3 |
94.7 |
The exact and empirical measurement costs for each scenario, both with and without the techniques described in Section IV, are tabulated in Table 2. The measurement costs obtained by the experiments approximate the exact costs described in eqn (13) and (20) within the error caused by the finite number of experiments. Generally, the cost reduction tends to increase with the system size. Also, a significant portion of the reduction is attributed to the shifting technique, which correlates closely with the squared reduction ratio in Table 1. This correlation suggests that Mε2 ∝ ‖ζ‖12, aligning with the relationship previously established in eqn (27).
Table 2 The measurement costs Mε2 for the (shifted) matrix elements 〈ϕ0|Ĥ(−![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) )|ϕk〉, averaged over k, are separately displayed for the cases with and without applying ICS and/or shift techniques from the measurement setting obtained from
)|ϕk〉, averaged over k, are separately displayed for the cases with and without applying ICS and/or shift techniques from the measurement setting obtained from  (denoted as ‘SI’). The costs are estimated by directly computing eqn (20) and (13). The values in the parenthesis are averaged empirical variances obtained by 1000 independent runs of QKSD algorithm for each setting. The sub-optimal shot allocations are used if ICS is not employed, while shot allocations of the ICS output are adopted otherwise. The result of ICS based on the true state |ϕk〉 and phased CISD proxy are shown. Note that ICS by true state is not practically achievable
(denoted as ‘SI’). The costs are estimated by directly computing eqn (20) and (13). The values in the parenthesis are averaged empirical variances obtained by 1000 independent runs of QKSD algorithm for each setting. The sub-optimal shot allocations are used if ICS is not employed, while shot allocations of the ICS output are adopted otherwise. The result of ICS based on the true state |ϕk〉 and phased CISD proxy are shown. Note that ICS by true state is not practically achievable
|
Mε
2 (Hartree2) |
H2 |
H4 |
LiH |
BeH2 |
H2O |
| LCU |
SI |
1.51 |
(1.50) |
81.40 |
(82.53) |
213.60 |
(215.62) |
598.29 |
(600.75) |
7265.04 |
(7290.16) |
| ICS (True) |
0.88 |
(0.87) |
69.84 |
(69.77) |
185.04 |
(182.27) |
534.46 |
(534.83) |
6534.53 |
(6508.27) |
| ICS (CISD) |
0.92 |
(0.90) |
70.11 |
(71.19) |
185.34 |
(184.59) |
536.47 |
(529.47) |
6550.79 |
(6561.18) |
| Shift |
0.13 |
(0.13) |
5.08 |
(5.01) |
0.89 |
(0.91) |
7.37 |
(7.38) |
16.04 |
(15.77) |
| Shift, ICS |
0.13 |
(0.13) |
4.82 |
(4.85) |
0.80 |
(0.79) |
6.97 |
(7.03) |
14.53 |
(14.50) |
| FH |
SI |
2.18 |
(2.24) |
34.66 |
(34.27) |
50.19 |
(50.25) |
151.65 |
(149.91) |
2284.67 |
(2287.81) |
| ICS (True) |
1.29 |
(1.29) |
18.32 |
(18.32) |
26.43 |
(26.29) |
88.00 |
(87.51) |
1528.96 |
(1529.87) |
| ICS (CISD) |
1.42 |
(1.44) |
18.74 |
(18.60) |
26.48 |
(26.18) |
89.52 |
(89.90) |
1535.81 |
(1523.23) |
| Shift |
0.13 |
(0.13) |
1.61 |
(1.60) |
0.67 |
(0.67) |
3.01 |
(3.01) |
6.44 |
(6.44) |
| Shift, ICS |
0.13 |
(0.13) |
0.80 |
(0.79) |
0.37 |
(0.36) |
1.46 |
(1.47) |
3.25 |
(3.25) |
Furthermore, we validated the approximation of Pauli covariance (eqn (41)) using the CISD proxy (eqn (42)) by comparing ICS results obtained with both the proxy and the true Krylov basis state, as shown in Table 2.
However, we observed that for the LCU cases, the ICS method performed less effectively than the FH cases. As shown in Appendix B, a scaled unitary fragment, βjÛj, is constructed by grouping mutually anticommuting Pauli operators, while commuting ones form a Hamiltonian fragment, Ĥj. In general, because the anticommutation between Pauli operators occurs less frequently, there are fewer opportunities for the Pauli operators to be grouped to form a unitary. This makes the coefficient splitting with LCU less effective.
As shown in Fig. 2, we compare the perturbed ground state energies of the electronic Hamiltonian of H2O, obtained by the QKSD algorithm, with and without applying the reduction techniques. We observed the unperturbed QKSD energy, E(n), is close to the full configuration interaction (FCI) energy (|E(n) − EFCI| ≈ 0.1 mHa).
 |
| | Fig. 2 Histogram of the error of the estimated ground state energies (Ẽ0(n→n′) − EFCI) of the electronic structure Hamiltonian of H2O with different measurement settings obtained from QKSD algorithm with the thresholding by eqn (45) and the finite number of shots of M = 108. The horizontal axis represents the errors in the atomic unit (mHa), and the vertical one denotes the frequency of the each histogram bin. The histogram is plotted using the perturbed QKSD energies from 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 independent and identical experiments. Here, the optimal thresholding of eqn (45) is applied to mitigate the sampling error, further reducing the Krylov dimension from n = 9 to n′ = 3. In the FH case, two different values of n′ = 2, 3 were observed across the random experiments, resulting in the two peaks in the histogram. Ẽ(n→n′) and E(n→n′) denote the QKSD ground state energies with and without considering the effect of sampling error, respectively. E(n) represents the QKSD ground state energy without error or thresholding. 000 independent and identical experiments. Here, the optimal thresholding of eqn (45) is applied to mitigate the sampling error, further reducing the Krylov dimension from n = 9 to n′ = 3. In the FH case, two different values of n′ = 2, 3 were observed across the random experiments, resulting in the two peaks in the histogram. Ẽ(n→n′) and E(n→n′) denote the QKSD ground state energies with and without considering the effect of sampling error, respectively. E(n) represents the QKSD ground state energy without error or thresholding. | |
We also employed a classical postprocessing called basis thresholding to alleviate the numerical instability of GEVP.35,36 Since small singular values in S significantly amplify the perturbation to the eigenvalue E(n), the thresholding technique further projects the GEVP onto the singular basis of S with corresponding singular values larger than a certain value εth > 0. However, the thresholding also discards the information about the eigenstates, not only the error, which biases thresholded QKSD energy. Thus, by adjusting εth, the thresholding establishes a trade-off, reducing the effect of the statistical error in H and S while introducing additional projection error. Within this trade-off, the optimal εth was heuristically found in ref. 36 to be:
| |  | (45) |
where
MS is the number of shots used to construct
S with the Hadamard or extended swap test. Note that for the case of errors other than the sampling error are present, an automated thresholding
60 can be adopted. We denote
n′ as the dimension of the thresholded problem and
E(n→n′) as corresponding eigenvalue.
Despite the bias caused by the projection error, the effect of the matrix perturbation is minimized. In the FH case, the application of the shifting technique and ICS resulted in the perturbed QKSD solution being concentrated within chemical accuracy (|Ẽ0(n→n′) − EFCI| <1.6 mHa), whereas most results without these techniques deviated beyond chemical accuracy.
VI. Conclusion
In this work, we analyzed the finite sampling errors that arise when projecting the Hamiltonian onto the quantum Krylov subspace with quantum algorithms. The measurement cost analyses of two scenarios, LCU and FH decomposition, converge to a unified perspective, where the decomposition rules and circuit construction are different. We also showed that the expected cost is analogous to the LCU 1-norm, which has the same definition in the context of block encoding.53 Such analogies enable the translation of methods originally motivated to reduce the costs in LCU simulation51,52 and the expectation measurement39,40 to the problem of measuring matrix elements. Especially, adopting the symmetry shift51,52 to the measurement problem eases the constraint on the shift operator, and thus provides larger cost reduction. Although the shifting technique is more effective in the LCU case, the measurement cost is observed to be lower in the FH case.
Despite of the effort to reduce the measurement cost, achieving the chemical accuracy by QKSD in practice remains still challenging, as the corresponding GEVP is often ill-conditioned. Note that in our application of QKSD to the H2O system, the results were fitted within the chemical accuracy by using 108 shots, which can be considered expensive. In classical Krylov subspace diagonalization, the perturbation on the GEVP matrices mainly depends on the round off or floating point error, which decreases exponentially to the number of bits of the data type, although the calculation of the matrix elements takes exponentially long time. On the other hand, governed by the standard quantum limit, the matrix perturbation in QKSD decays with the square root of the number of measurements, which is much slower than the classical KSD, while each measurement takes polynomial time. Therefore, if exponential precision for the matrix element is required because of the ill-conditioning, it is not yet obvious that QKSD is superior to the classical counterpart in terms of running time to achieve a certain precision in the estimated eigenvalues.
As discussed in Section III, we observed that the extended swap test, enabled by FH decomposition, allows for the simultaneous measurement of both the overlap and Hamiltonian matrices:
due to commutativity between

and
Ĥ ⊗
![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) x(y)
x(y). This idea can be extended to the other EFTQC algorithms. Based on our knowledge, recently developed EFTQC algorithms other than QKSD focus on extracting the spectrum only from the autocorrelation function,
a(
t) := 〈
ϕ0|e
−iĤt|
ϕ0〉. However, those algorithms can be more refined by adopting the simultaneous measurement of
aÔ(
t) := 〈
ϕ0|
Ôe
−iĤt|
ϕ0〉 for some observable
Ô. For instance, the first derivative of
a(
t) can be directly calculated from
aĤ(
t). This measurement, which can be done precisely if the techniques introduced in this work are adopted, only requires overheads of
O(
Nq2) Clifford operations. These operations do not need additional logical qubits and present an endurable cost for EFTQCs. Given this rationale, our future research direction involves exploring EFTQC algorithms including
aÔ(
t) in the spectrum extraction.
Code availability
The data and code that support the findings of this study are openly available in https://github.com/snow0369/ofex. The repository contains the full source code to reproduce the results presented in this work. All scripts and related data are licensed under MIT License, allowing for reuse and adaptation with proper attribution.
Data availability
The Python package for the techniques introduced in this work (shifting and iterative coefficient splitting) is available at ref. 61. Furthermore, the raw data for numerical results are available at ref. 62 along with the reproducing scripts.
Author contributions
GL: conceptualization, methodology, software, validation, formal analysis, investigation, data curation, writing – original draft preparation, writing – review & editing, visualization, funding acquisition. SC: methodology, software. JH: conceptualization, investigation, resources, writing – review & editing, supervision, project administration, funding acquisition. AFI: conceptualization, methodology, formal analysis, investigation, resources, writing – review & editing, visualization, supervision, project administration, funding acquisition.
Conflicts of interest
There are no conflicts of interest to declare.
Appendices
Appendix A: averaged variance on H0k
In this section, we derive the state-independent variance, represented by eqn (16) and (22), by averaging the states |ϕ0〉 and |ϕk〉 over the independent uniform Haar distributions  . Before proceeding with the derivation, we introduce three lemmas that will be instrumental in this process. Throughout this section,
. Before proceeding with the derivation, we introduce three lemmas that will be instrumental in this process. Throughout this section,  is abbreviated as
is abbreviated as  unless otherwise mentioned.
unless otherwise mentioned.
Lemma 1: for any normal operator  , the following equality holds:
, the following equality holds:
| |  | (A1) |
Proof: for any operator  , the averaged conjugation is known as
, the averaged conjugation is known as
| |  | (A2) |
as a consequence of Schur's lemma and the left and right invariance of the Haar measure, where

is the uniform Haar distribution over the unitary group of dimension
d. Therefore, we can state
| |  | (A3) |
Finally, by applying eqn (A3) consecutively, we have:
Lemma 2: for any normal operator  , the following equality holds:
, the following equality holds:
| | 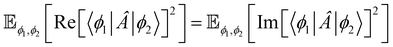 | (A4) |
Proof: because of the unitary-invariant property of Haar measure,  is always identical to
is always identical to  for any function f. Therefore, the following proves eqn (A4):
for any function f. Therefore, the following proves eqn (A4):
| |  | (A5) |
| |  | (A6) |
| | 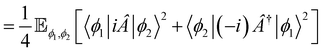 | (A7) |
| | 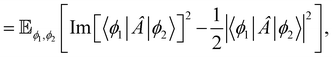 | (A8) |
where
eqn (A6) and
(A8) are obtained using

and

, respectively, for

. Additionally,
eqn (A7) is derived by replacing |
ϕ2〉 with
i|
ϕ2〉.
Lemma 3: for any normal operator  , the following equality holds:
, the following equality holds:
| |  | (A9) |
Proof: because  is normal, we can perform the eigendecomposition to an arbitrary state as  , where Â|ψi〉 = ai|ψi〉 and γi = 〈ψi|ϕ〉. Then the Haar averaging over |ϕ〉 is identical to the averaging {γi}i=1d over d-dimensional complex unit sphere,
, where Â|ψi〉 = ai|ψi〉 and γi = 〈ψi|ϕ〉. Then the Haar averaging over |ϕ〉 is identical to the averaging {γi}i=1d over d-dimensional complex unit sphere,  , where
, where  denotes the complex projective space. Therefore, it can be shown that
denotes the complex projective space. Therefore, it can be shown that
| |  | (A10) |
| |  | (A11) |
| |  | (A12) |
| |  | (A13) |
| |  | (A14) |
| |  | (A15) |
where

denotes
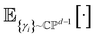
and
eqn (A13) holds because of ref.
63, Theorem 2.6.
For the case of LCU decomposition, the Haar-averaged partial variance in eqn (14) is identically determined over X and j as
| |  | (A16) |
by applying Lemmas 1 and 2 with
 =
Ûj. Therefore, the sub-optimal shot allocation,
| |  | (A17) |
is obtained by replacing Var[
ÔX]
ϕ0k;j in
eqn (15) with the expected variance, where the denominator is set to satisfy the normalization constraint,
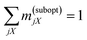
.
The variance with the sub-optimal shot allocation is derived from eqn (13) by assigning eqn (A17), which is
| | 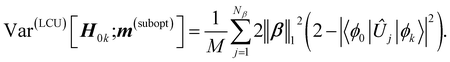 | (A18) |
Finally, by Lemma 1, the Haar averaging of |〈ϕ0|Ûj|ϕk〉|2 both over ϕ0 and ϕk results in eqn (16).
Furthermore, because |ϕk〉 = ![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) k|ϕ0〉 is an evolved state from |ϕ0〉, we can consider averaging the variance over single state |ϕ0〉, fixing the evolution operator,
k|ϕ0〉 is an evolved state from |ϕ0〉, we can consider averaging the variance over single state |ϕ0〉, fixing the evolution operator, ![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) k. Then from eqn (A18), |〈ϕ0|Ûj|ϕk〉|2 = |〈ϕ0|Ûj
k. Then from eqn (A18), |〈ϕ0|Ûj|ϕk〉|2 = |〈ϕ0|Ûj![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) k|ϕ0〉|2 needs to be averaged over |ϕ0〉. Using Lemma 3 with  = Ûj
k|ϕ0〉|2 needs to be averaged over |ϕ0〉. Using Lemma 3 with  = Ûj![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) k, we can show that
k, we can show that
and thus
because 0 ≤ |Tr[
Ûj![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) k
k]|
2 ≤
d2. Finally, the total averaged variance is bounded by
| |  | (A19) |
which is approximately less than the expected variance considering the two states independently (
eqn (16).)
In FH case, the shots for real and imaginary parts are identically allocated (mjR = mjI ≕ mj/2) because of Lemma 2, similar to the LCU case. Therefore, the variances for the real and imaginary parts in eqn (21) can be directly added, yielding
| |  | (A20) |
In eqn (21), the expected second moment is determined as  , while the last term,
, while the last term,  is obtained using Lemma 1. Finally, the expected variance of jth fragment is derived as below:
is obtained using Lemma 1. Finally, the expected variance of jth fragment is derived as below:
| | 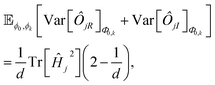 | (A21) |
which results in a total averaged variance of
eqn (22) with the sub-optimal allocation
mj ∝ Tr[
Ĥj2]
1/2.
Similar to the LCU case, if we take the expectation only on |ϕ0〉, we have
| |  | (A22) |
Appendix B: grouping Pauli operators
In this section, we review the partitioning of qubit Hamiltonian in a form of LCU and FH. Also, the expressions of ‖β‖1 and ‖γ‖1 are presented with respect to the Pauli coefficients.
A qubit Hamiltonian Ĥ is expressed as
| | 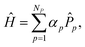 | (B1) |
where
![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) p
p ∈ {
Î,
![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) x
x,
![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) y
y,
![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) z
z}
⊗Nq is an
Nq-qubit Pauli operator and its coefficient is

.
First, we review the derivation of LCU in Pauli basis,54,55 which is described as
| |  | (B2) |
Here, a Pauli term
αp![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) p
p can be separated to the multiple groups

. Thus,
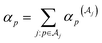
for all 1 ≤
p ≤
Np, should be imposed for the partitioned coefficients. Also, if the anticommutation conditions of different Pauli operators within a group holds:
| |  | (B3) |
each partition,

, becomes a scaled unitary,
βjÛj. Then,

is found consequently, and the norm becomes
| |  | (B4) |
Furthermore, a circuit realization of controlled Ûj is known, which requires  two-qubit gates.55
two-qubit gates.55
Now, for the case of FH, Pauli operators are grouped together if all pairs of the operators in a group commute:
| |  | (B5) |
where
| |  | (B6) |
and

. For each of
Ĥj, one can construct a diagonalizing Clifford circuit,
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) j
j, taking

two-qubit gates. Furthermore, one can find the FH decomposition norm, ‖
γ‖
1 in terms of Pauli coefficients:
| |  | (B7) |
Here, note that we used  because the trace of Pauli operators except the identity is zero.
because the trace of Pauli operators except the identity is zero.
The two norms described in eqn (B4) and (B7) shares a common expression as the sum of the L2 norms of Pauli coefficients. We can consider decomposing eqn (B1) without grouping, Ĥj = βjÛj = αj![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) j, which is also an LCU and an FH simultaneously. However, in such case, the norm ‖β‖1 = ‖γ‖1 = ‖α‖1 becomes larger than that of grouped Pauli case because the sum of L2 norms of grouped Pauli coefficients is smaller than the L1 norm.
j, which is also an LCU and an FH simultaneously. However, in such case, the norm ‖β‖1 = ‖γ‖1 = ‖α‖1 becomes larger than that of grouped Pauli case because the sum of L2 norms of grouped Pauli coefficients is smaller than the L1 norm.
Pauli groupings are not unique and can be translated to a clique covering problem on the (anti-)commutation graph. The commutation graph, denoted as  , encodes the commutativity between Pauli operators. Specifically, the nodes in V correspond to individual Pauli operators: V = {vp : 1 ≤ p ≤ NP} with a node weight function w(vp) = αp. Also, undirected and unweighted edges connect nodes whose corresponding operators commute
, encodes the commutativity between Pauli operators. Specifically, the nodes in V correspond to individual Pauli operators: V = {vp : 1 ≤ p ≤ NP} with a node weight function w(vp) = αp. Also, undirected and unweighted edges connect nodes whose corresponding operators commute  . The anticommutation graph,
. The anticommutation graph,  , shares the same node set with
, shares the same node set with  but connects nodes with anticommuting operators
but connects nodes with anticommuting operators  . Because any two Pauli operators either commute or anticommute, these graphs are complements, meaning that
. Because any two Pauli operators either commute or anticommute, these graphs are complements, meaning that  .
.
In such setting, minimizing eqn (B4) and (B7) translates to finding a clique covering that minimizes the sum of the clique weights. Each weight is defined as a L2 norm of node weights covered by each clique. Like other clique covering problems, this is an NP-hard problem. However, a heuristic and greedy algorithm called  often outperform other heuristic algorithms as demonstrated in ref. 39. The original work on
often outperform other heuristic algorithms as demonstrated in ref. 39. The original work on  aimed to minimize the cost of measuring standard expectation values, so it only considered the commutation graph. However, we extend the algorithm to the anticommutation case to reduce the cost of the LCU measurements by simply modifying its grouping condition.
aimed to minimize the cost of measuring standard expectation values, so it only considered the commutation graph. However, we extend the algorithm to the anticommutation case to reduce the cost of the LCU measurements by simply modifying its grouping condition.
In the numerical results of Section V, the Ẑ-type operators, which dominate the example Hamiltonians, correspond to the number operators in the fermionic representation. In the LCU decomposition, these operators are not grouped due to their mutual commutativity, resulting in a larger LCU norm than FH norm (‖βSI(Ĥ)‖ ≥ ‖γSI(Ĥ)‖) because large coefficients are treated separately. However, the shifting technique effectively eliminates these operators, significantly reducing the norm ‖βSI(Ĥ − ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) )‖. In the FH decomposition, Ẑ-type operators are naturally grouped together, which contribute to the norm less significantly than the LCU case. Consequently, the impact of the shifting technique is less pronounced in the FH case compared to the LCU case. Nevertheless, the shifted FH decomposition still achieves a smaller norm than the shifted LCU decomposition.
)‖. In the FH decomposition, Ẑ-type operators are naturally grouped together, which contribute to the norm less significantly than the LCU case. Consequently, the impact of the shifting technique is less pronounced in the FH case compared to the LCU case. Nevertheless, the shifted FH decomposition still achieves a smaller norm than the shifted LCU decomposition.
Appendix C: Pauli covariance
In this section derives the Pauli covariance for measuring the matrix element (eqn (41)). Starting from the partial variance in eqn (25), and substituting  , which is analogous to eqn (B2) or (B5), we obtain:
, which is analogous to eqn (B2) or (B5), we obtain:| |  | (C1) |
Comparing eqn (40) and (C1) suggests defining the covariance as the expression within the bracket. However, this definition violates the symmetric property of the covariance because ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) p
p![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) q is not necessarily identical to
q is not necessarily identical to ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) q
q![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) p. Therefore, to ensure the symmetry, we superpose the product of operators in both orders, (p, q) and (q, p). This results in the definition of the covariance as eqn (41).
p. Therefore, to ensure the symmetry, we superpose the product of operators in both orders, (p, q) and (q, p). This results in the definition of the covariance as eqn (41).
Appendix D: efficient shifting technique for electronic structure problem
Here, we describe an efficient procedure of optimizing eqn (28) for an electronic structure Hamiltonian. If ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) is given as eqn (34), the number of real parameters determining
is given as eqn (34), the number of real parameters determining ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) is:
is:| |  | (D1) |
where Nocc and Nvirt denote the number of occupied and virtual orbitals, respectively. This number scales as O(Norb3) and makes the optimization computationally expensive. In the rest of the section, we show an alternative and efficient method for the minimization of the norm by the shift technique.
We consider that the Hamiltonian Ĥ is given as an electronic structure Hamiltonian in eqn (33), whose the indices are determined for the unique terms:
| |  | (D2) |
where
The set  with the size of
with the size of  represents the indices of Hermitian two-body operators avoiding the duplication from the following eight-fold symmetries:
represents the indices of Hermitian two-body operators avoiding the duplication from the following eight-fold symmetries:
| gpqrs = gqprs = gpqsr = gqpsr = grspq = gsrpq = grsqp = gsrqp, |
and squared number operators (
p =
q =
r =
s), which are absorbed into one-body number operators due to the idempotent property (
![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) p2
p2 =
![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) p
p).
In order to realize the efficient optimization, we find a part affected by the shift among the terms in eqn (D2). The terms relevant to eqn (34) are selected to construct the partial Hamiltonian, Ĥ(s):
| |  | (D3) |
where the modified coefficients are
Such coefficients are determined by the following transformation to make the form of the Hamiltonian consistent to the shift operator:
| |  | (D4) |
for all
r ≠
q and
s ≠
q. Because the rest of the Hamiltonian (
Ĥ −
Ĥ(s)) is invariant to the shifting with respect to the term-wise grouping algorithm, denoted as
T, we focus on the following norm minimization:
| |  | (D5) |
Here, Ĥ(s) − ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) (τ) is given as
(τ) is given as
| |  | (D6) |
Note that the each operators in eqn (D6) contributes to the norm as shown below:
| |  | (D7) |
for
r ≠
q and
s ≠
q. Therefore, the norm with term-wise grouping is determined as
| |  | (D8) |
The first summation becomes zero by assigning
| |  | (D9) |
Furthermore, because the variables, τ(2)qrs for  such that
such that
| |  | (D10) |
are only included in the third summation, they are also determined as
| |  | (D11) |
However, the rest of the variables, τ(2)qrs for  occur both in the second and the third summations, where
occur both in the second and the third summations, where
| | 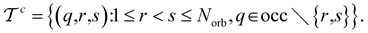 | (D12) |
After the assignment of eqn (D9) and (D11), the minimization problem of eqn (D8) is then reduced to
| |  | (D13) |
where

denotes the shift operator
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif)
with the partial assignment and

denotes the set of variables,
τ(2)qrs with

. Furthermore, minimizing
eqn (D13) is identical to the separated optimizations:
| |  | (D14) |
for each (
r,
s) with respect to the variables,

, where

and
| |  | (D15) |
and

. We provide a pictorial procedure to solve
eqn (D14) in
Fig. 3. Although the solution for 2-dimensional problem is shown, this can be extended to

-dimensional problem by considering hyperplane instead of lines in the figure. Every

satisfying
| |  | (D16) |
for all
r and
s, identically results in the optimal value of
eqn (D14), which is
| |  | (D17) |
 |
| | Fig. 3 A pictorial approach for the optimization of eqn (D14). For the simplicity, the super- and subscripts (rs) are omitted, and it is assumed that μ is two-dimensional and A > 0. In figure (a), for a fixed μ★, the green diamond-shaped plot and the orange parallel lines denote all the points of μ such that ‖μ‖1 = ‖μ★‖1 and P(μ) = P(μ★), respectively. It is shown that P(μ★) + ‖μ★‖1 ≥ A must be satisfied for the intersections between two plots to be established, and thus μ★ exists. In figure (b), for a fixed ‖μ‖1, the optimal points are found, as indicated by the red line, with the corresponding optimal value of P(μ★) + ‖μ★‖1 = A. By varying ‖μ‖1, these points are expanded to the shaded area in figure (c). For the case of A ≤ 0, the plots are symmetrically transposed about the origin, resulting in the optimal points of 0 ≤ ‖μ★‖1 ≤ − A and μ1★,μ2★ ≤ 0. | |
Note that assigning τ(2)★qrs = ![[g with combining tilde]](https://www.rsc.org/images/entities/i_char_0067_0303.gif) rsqq for all
rsqq for all  satisfies eqn (D16), which is analogous to eqn (D11).
satisfies eqn (D16), which is analogous to eqn (D11).
Therefore, we conclude that the parameters
| | | τ(2)qrs = 4grsqq − 2grqsq | (D19) |
lead to the optimal shift with respect to the term-wise grouping algorithm. However, strictly to say, the above simplification only holds for the fragment Hamiltonian, as
![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) r
r and
Êrs![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) q
q are Hermitian, not unitary. Although
![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) q
q can be written as a unitary operator (
![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) q
q = 2
![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) q
q − 1), our current understanding of representing a unitary operator as a linear combination of one-body excitation operators remains insufficient to establish an analogous reduction for the LCU case. Therefore, this work adopts the same shift operator for both LCU decomposition as an interim solution, leaving the parameter reduction for the LCU case as a future work.
Acknowledgements
A. F. I. acknowledges financial support from the Natural Sciences and Engineering Council of Canada (NSERC). G. L. acknowledges the support from the Education and Training Program of the Quantum Information Research Support Center, funded through the National Research Foundation of Korea (NRF) by the Ministry of Science and ICT (MSIT) of Korean government (NRF-2021M3H3A1036573). Additionally, this work was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF), funded by the Ministry of Education, Science and Technology (NRF-2022M3H3A106307411, NRF-2023M3K5A1094813). This work was also partly supported by Institute for Information & communications Technology Promotion (IITP) grant funded by the Korea government(MSIP) (No. 2019-0-00003, Research and Development of Core technologies for Programming, Running, Implementing and Validating of Fault-Tolerant Quantum Computing System). The Ministry of Trade, Industry, and Energy (MOTIE), Korea, also partly supported this research under the Industrial Innovation Infrastructure Development Project (No. RS-2024-00466693).
References
- K. Wintersperger, F. Dommert, T. Ehmer, A. Hoursanov, J. Klepsch and W. Mauerer,
et al., Neutral atom quantum computing hardware: performance and end-user perspective, EPJ Quantum Technol., 2023, 10(1), 32 CrossRef.
- S. Debnath, N. M. Linke, C. Figgatt, K. A. Landsman, K. Wright and C. Monroe, Demonstration of a small programmable quantum computer with atomic qubits, Nature, 2016, 536(7614), 63–66 CrossRef CAS PubMed.
- M. F. Brandl, M. W. van Mourik, L. Postler, A. Nolf, K. Lakhmanskiy and R. R. Paiva,
et al., Cryogenic setup for trapped ion quantum computing, Rev. Sci. Instrum., 2016, 87(11), 113103 CrossRef CAS PubMed.
- X. L. Wang, L. K. Chen, W. Li, H. L. Huang, C. Liu and C. Chen,
et al., Experimental Ten-Photon Entanglement, Phys. Rev. Lett., 2016, 117, 210502 Search PubMed.
- X. Qiang, X. Zhou, J. Wang, C. M. Wilkes, T. Loke and S. O'Gara,
et al., Large-scale silicon quantum photonics implementing arbitrary two-qubit processing, Nat. Photonics, 2018, 12(9), 534–539 CAS.
- J. M. Chow, J. M. Gambetta, A. D. Córcoles, S. T. Merkel, J. A. Smolin and C. Rigetti,
et al., Universal Quantum Gate Set Approaching Fault-Tolerant Thresholds with Superconducting Qubits, Phys. Rev. Lett., 2012, 109, 060501 Search PubMed.
- G. Wendin, Quantum information processing with superconducting circuits: a review, Rep. Prog. Phys., 2017, 80(10), 106001 CAS.
- Y. Cao, J. Romero, J. P. Olson, M. Degroote, P. D. Johnson and M. Kieferová,
et al., Quantum Chemistry in the Age of Quantum Computing, Chem. Rev., 2019, 119(19), 10856–10915 CAS , PMID: 31469277..
- S. McArdle, S. Endo, A. Aspuru-Guzik, S. C. Benjamin and X. Yuan, Quantum computational chemistry, Rev. Mod. Phys., 2020, 92, 015003 CAS.
- B. Bauer, S. Bravyi, M. Motta and G. K. L. Chan, Quantum Algorithms for Quantum Chemistry and Quantum Materials Science, Chem. Rev., 2020, 120(22), 12685–12717 CAS , PMID: 33090772..
- J. Preskill, Quantum Computing in the NISQ era and beyond, Quantum, 2018, 2, 79 Search PubMed.
- K. Bharti, A. Cervera-Lierta, T. H. Kyaw, T. Haug, S. Alperin-Lea and A. Anand,
et al., Noisy intermediate-scale quantum algorithms, Rev. Mod. Phys., 2022, 94, 015004 CAS.
- M. Cerezo, A. Arrasmith, R. Babbush, S. C. Benjamin, S. Endo and K. Fujii,
et al., Variational quantum algorithms, Nat. Rev. Phys., 2021, 3(9), 625–644 Search PubMed.
- J. Tilly, H. Chen, S. Cao, D. Picozzi, K. Setia and Y. Li,
et al., The Variational Quantum Eigensolver: A review of methods and best practices, Phys. Rep., 2022, 986, 1–128 Search PubMed.
- J. R. McClean, S. Boixo, V. N. Smelyanskiy, R. Babbush and H. Neven, Barren plateaus in quantum neural network training landscapes, Nat. Commun., 2018, 9(1), 4812 CrossRef PubMed.
- M. Cerezo, A. Sone, T. Volkoff, L. Cincio and P. J. Coles, Cost function dependent barren plateaus in shallow parametrized quantum circuits, Nat. Commun., 2021, 12(1), 1791 CrossRef CAS PubMed.
- S. Wang, E. Fontana, M. Cerezo, K. Sharma, A. Sone and L. Cincio,
et al., Noise-induced barren plateaus in variational quantum algorithms, Nat. Commun., 2021, 12(1), 6961 CrossRef CAS PubMed.
- M. Cerezo and P. J. Coles, Higher order derivatives of quantum neural networks with barren plateaus, Quantum Sci. Technol., 2021, 6(3), 035006 CrossRef.
- A. Arrasmith, M. Cerezo, P. Czarnik, L. Cincio and P. J. Coles, Effect of barren plateaus on gradient-free optimization, Quantum, 2021, 5, 558 CrossRef.
- X. Xue, M. Russ, N. Samkharadze, B. Undseth, A. Sammak and G. Scappucci,
et al., Quantum logic with spin qubits crossing the surface code threshold, Nature, 2022, 601(7893), 343–347 CrossRef CAS PubMed.
- R. Blume-Kohout, J. K. Gamble, E. Nielsen, K. Rudinger, J. Mizrahi and K. Fortier,
et al., Demonstration of qubit operations below a rigorous fault tolerance threshold with gate set tomography, Nat. Commun., 2017, 8(1), 14485 CrossRef CAS PubMed.
- L. Postler, S. Heuβen, I. Pogorelov, M. Rispler, T. Feldker and M. Meth,
et al., Demonstration of fault-tolerant universal quantum gate operations, Nature, 2022, 605(7911), 675–680 CrossRef CAS PubMed.
- D. Bluvstein, S. J. Evered, A. A. Geim, S. H. Li, H. Zhou and T. Manovitz,
et al., Logical quantum processor based on reconfigurable atom arrays, Nature, 2024, 626(7997), 58–65 CrossRef CAS PubMed.
- A. Katabarwa, K. Gratsea, A. Caesura and P. D. Johnson, Early Fault-Tolerant Quantum Computing, PRX Quantum, 2024, 5(2), 020101 CrossRef.
- D. S. Abrams and S. Lloyd, Quantum Algorithm Providing Exponential Speed Increase for Finding Eigenvalues and Eigenvectors, Phys. Rev. Lett., 1999, 83, 5162–5165 Search PubMed.
- M. Suzuki, Fractal decomposition of exponential operators with applications to many-body theories and Monte Carlo simulations, Phys. Lett. A, 1990, 146(6), 319–323 CrossRef.
-
Finding Exponential Product Formulas of Higher Orders, ed. Hatano N., Suzuki M., Das A. and K Chakrabarti B., Springer Berlin Heidelberg, Berlin, Heidelberg, 2005, pp. 37–68 Search PubMed.
- R. D. Somma, Quantum eigenvalue estimation via time series analysis, New J. Phys., 2019, 21(12), 123025 CrossRef.
- R. Zhang, G. Wang and P. Johnson, Computing Ground State Properties with Early Fault-Tolerant Quantum Computers, Quantum, 2022, 6, 761 CrossRef.
- Z. Ding and L. Lin, Even Shorter Quantum Circuit for Phase Estimation on Early Fault-Tolerant Quantum Computers with Applications to Ground-State Energy Estimation, Phys. Rev. X, 2023, 4, 020331 Search PubMed.
- Z. Ding and L. Lin, Simultaneous estimation of multiple eigenvalues with short-depth quantum circuit on early fault-tolerant quantum computers, Quantum, 2023, 7, 1136 CrossRef.
-
R. M. Parrish and P. L. McMahon, Quantum Filter Diagonalization: Quantum Eigendecomposition without Full Quantum Phase Estimation, arXiv, 2019, arXiv:1909.08925, DOI:10.48550/arXiv.1909.08925.
- N. H. Stair, R. Huang and F. A. Evangelista, A Multireference Quantum Krylov Algorithm for Strongly Correlated Electrons, J. Chem. Theory Comput., 2020, 16(4), 2236–2245 CrossRef CAS PubMed.
- W. Kirby, M. Motta and A. Mezzacapo, Exact and efficient Lanczos method on a quantum computer, Quantum, 2023, 7, 1018 CrossRef.
- E. N. Epperly, L. Lin and Y. Nakatsukasa, A Theory of Quantum Subspace Diagonalization, SIAM J. Matrix Anal. Appl., 2022, 43(3), 1263–1290 CrossRef.
- G. Lee, D. Lee and J. Huh, Sampling Error Analysis in Quantum Krylov Subspace Diagonalization, Quantum, 2024, 8, 1477 CrossRef.
- K. Seki and S. Yunoki, Quantum Power Method by a Superposition of Time-Evolved States, Phys. Rev. X, 2021, 2, 010333 Search PubMed.
- M. Motta, C. Sun, A. T. K. Tan, M. J. O'Rourke, E. Ye and A. J. Minnich,
et al., Determining eigenstates and thermal states on a quantum computer using quantum imaginary time evolution, Nat. Phys., 2020, 16(2), 205–210 Search PubMed.
- O. Crawford, B. Straaten, D. Wang, T. Parks, E. Campbell and S. Brierley, Efficient quantum measurement of Pauli operators in the presence of finite sampling error, Quantum, 2021, 5, 385 Search PubMed.
- T. C. Yen, A. Ganeshram and A. F. Izmaylov, Deterministic improvements of quantum measurements with grouping of compatible operators, non-local transformations, and covariance estimates, NPJ Quantum Inf., 2023, 9(1), 14 Search PubMed.
- S. Choi and A. F. Izmaylov, Measurement Optimization Techniques for Excited Electronic States in Near-Term Quantum Computing Algorithms, J. Chem. Theory Comput., 2023, 19(11), 3184–3193 CrossRef CAS PubMed , PMID: 37224265..
- T. C. Yen, V. Verteletskyi and A. F. Izmaylov, Measuring All Compatible Operators in One Series of Single-Qubit Measurements Using Unitary Transformations, J. Chem. Theory Comput., 2020, 16(4), 2400–2409 CrossRef CAS PubMed , PMID: 32150412..
- S. Choi, T. C. Yen and A. F. Izmaylov, Improving Quantum Measurements by Introducing “Ghost” Pauli Products, J. Chem. Theory Comput., 2022, 18(12), 7394–7402 CrossRef CAS PubMed , PMID: 36332111..
- S. Choi, I. Loaiza and A. F. Izmaylov, Fluid fermionic fragments for optimizing quantum measurements of electronic Hamiltonians in the variational quantum eigensolver, Quantum, 2023, 7, 889 CrossRef.
- T. C. Yen and A. F. Izmaylov, Cartan Subalgebra Approach to Efficient Measurements of Quantum Observables, Phys. Rev. X, 2021, 2, 040320 Search PubMed.
- V. Verteletskyi, T. C. Yen and A. F. Izmaylov, Measurement optimization in the variational quantum eigensolver using a minimum clique cover, J. Chem. Phys., 2020, 152(12), 124114 CrossRef CAS PubMed.
- H. Y. Huang, R. Kueng and J. Preskill, Predicting many properties of a quantum system from very few measurements, Nat. Phys., 2020, 16(10), 1050–1057, DOI:10.1038/s41567-020-0932-7.
-
C. Hadfield, S. Bravyi, R. Raymond and A. Mezzacapo, Measurements of Quantum Hamiltonians with Locally-Biased Classical Shadows, arXiv, 2020, arXiv:2006.15788, DOI:10.48550/arXiv.2006.15788.
- H. Y. Huang, R. Kueng and J. Preskill, Efficient Estimation of Pauli Observables by Derandomization, Phys. Rev. Lett., 2021, 127, 030503, DOI:10.1103/PhysRevLett.127.030503.
- Y. Nakamura, Y. Yano and N. Yoshioka, Adaptive measurement strategy for quantum subspace methods, New J. Phys., 2024, 26(3), 033028, DOI:10.1088/1367-2630/ad2c3b.
- I. Loaiza and A. F. Izmaylov, Block-Invariant Symmetry Shift: Preprocessing Technique for Second-Quantized Hamiltonians to Improve Their Decompositions to Linear Combination of Unitaries, J. Chem. Theory Comput., 2023, 19(22), 8201–8209 CrossRef CAS PubMed , PMID: 37939198..
- I. Loaiza, A. M. Khah, N. Wiebe and A. F. Izmaylov, Reducing molecular electronic Hamiltonian simulation cost for linear combination of unitaries approaches, Quantum Sci. Technol., 2023, 8(3), 035019 CrossRef.
- A. M. Childs and N. Wiebe, Hamiltonian simulation using linear combinations of unitary operations, Quantum Inf. Comput., 2012, 12(11–12), 901–924 Search PubMed.
- A. F. Izmaylov, T. C. Yen, R. A. Lang and V. Verteletskyi, Unitary Partitioning Approach to the Measurement Problem in the Variational Quantum Eigensolver Method, J. Chem. Theory Comput., 2020, 16(1), 190–195 CrossRef PubMed , PMID: 31747266..
- A. Zhao, A. Tranter, W. M. Kirby, S. F. Ung, A. Miyake and P. J. Love, Measurement reduction in variational quantum algorithms, Phys. Rev. A, 2020, 101, 062322 CrossRef CAS.
-
Y.-C. Zheng, C.-Y. Lai, T. A. Brun and L.-C. Kwek, Depth reduction for quantum Clifford circuits through Pauli measurements, arXiv, 2018, arXiv:1805.12082, DOI:10.48550/arXiv.1805.12082.
-
P. Gokhale, O. Angiuli, Y. Ding, K. Gui, T. Tomesh, M. Suchara, M. Martonosi and F. T. Chong, Minimizing State Preparations in Variational Quantum Eigensolver by Partitioning into Commuting Families, arXiv, 2019, arXiv:1907.13623, DOI:10.48550/arXiv.1907.13623.
- J. T. Seeley, M. J. Richard and P. J. Love, The Bravyi-Kitaev transformation for quantum computation of electronic structure, J. Chem. Phys., 2012, 137(22), 224109 CrossRef PubMed.
-
S. Bravyi, J. M. Gambetta, A. Mezzacapo and K. Temme, Tapering off qubits to simulate fermionic Hamiltonians, arXiv, 2017, arXiv:1701.08213, DOI:10.48550/arXiv.1701.08213.
-
N. Yoshioka, M. Amico, W. Kirby, P. Jurcevic, A. Dutt, B. Fuller, S. Garion, H. Haas, I. Hamamura, A. Ivrii, R. Majumdar, Z. Minev, M. Motta, B. Pokharel, P. Rivero, K. Sharma, C. J. Wood, A. Javadi-Abhari and A. Mezzacapo, Diagonalization of large many-body Hamiltonians on a quantum processor, arXiv, 2024, arXiv:2407.14431, DOI:10.48550/arXiv.2407.14431.
-
G. Lee, Openfermion Expansion Toolkit, GitHub, 2024, https://github.com/snow0369/ofex Search PubMed.
-
G. Lee, Measurement Strategies for QKSD, GitHub, 2024, https://github.com/snow0369/eff_qksd_script Search PubMed.
- A. Roy and S. Suda, Complex Spherical Designs and Codes, J. Combin. Designs, 2014, 22(3), 105–148 CrossRef.
|
| This journal is © The Royal Society of Chemistry 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Seonghoon
Choi
a,
Seonghoon
Choi
 bc,
Joonsuk
Huh
bc,
Joonsuk
Huh
 *d and
Artur F.
Izmaylov
*d and
Artur F.
Izmaylov
 *bc
*bc
 , where |γ0| and εalg denote the initial overlap and algorithm accuracy, respectively.25 Here, the real-time propagator is usually approximately implemented by Suzuki–Trotterization.26,27 In contrast, EFTQC algorithms use shorter propagators, t < O(εalg−1), but increase the number of repetitions, M > O(|γ0|−2).28–33 An alternative approach within EFTQC utilizes the block encoding scheme,34 which, while exact, demands significantly more resources than Trotterization with a minimal Trotter steps. Although reducing Trotterization errors necessitates more Trotter steps, thus approaching the resource demands of block encoding, the limitations of near-future hardware render small-scale Trotterization a more feasible option.
, where |γ0| and εalg denote the initial overlap and algorithm accuracy, respectively.25 Here, the real-time propagator is usually approximately implemented by Suzuki–Trotterization.26,27 In contrast, EFTQC algorithms use shorter propagators, t < O(εalg−1), but increase the number of repetitions, M > O(|γ0|−2).28–33 An alternative approach within EFTQC utilizes the block encoding scheme,34 which, while exact, demands significantly more resources than Trotterization with a minimal Trotter steps. Although reducing Trotterization errors necessitates more Trotter steps, thus approaching the resource demands of block encoding, the limitations of near-future hardware render small-scale Trotterization a more feasible option.
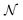 is the normalization factor, and
is the normalization factor, and  , and n is the Krylov order. This ansatz fully covers vectors in the Krylov subspace,
, and n is the Krylov order. This ansatz fully covers vectors in the Krylov subspace,  , where |ϕk〉=
, where |ϕk〉=![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) k|ϕ0〉 is defined by a reference state |ϕ0〉 and the base operator,
k|ϕ0〉 is defined by a reference state |ϕ0〉 and the base operator,![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) = e−iΔtĤ.
= e−iΔtĤ.![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) , such as Ĥ, which is analogous to the classical Krylov method,37 and imaginary time evolution (e−βĤ).38 Although we only focus on the real-time evolution operator, which is widely discussed, the methods that will be described in the Section IV can be expanded to the other choices of
, such as Ĥ, which is analogous to the classical Krylov method,37 and imaginary time evolution (e−βĤ).38 Although we only focus on the real-time evolution operator, which is widely discussed, the methods that will be described in the Section IV can be expanded to the other choices of ![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) because they are approximated by linear combinations or products of real-time propagators.
because they are approximated by linear combinations or products of real-time propagators.![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) †kĤ
†kĤ![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) l|ϕ0〉 = H0,l−k
l|ϕ0〉 = H0,l−k![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) †k
†k![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) l|ϕ0〉 = S0,l–k.
l|ϕ0〉 = S0,l–k.![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) is unitary. Furthermore, since [Ĥ,
is unitary. Furthermore, since [Ĥ,![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) ] = 0, H becomes a Toeplitz matrix as well. Therefore, rather than n2, only n elements are required to construct each matrices.
] = 0, H becomes a Toeplitz matrix as well. Therefore, rather than n2, only n elements are required to construct each matrices. , where each unitary Ûj is implemented to estimate the overlap between |ϕ0〉 and Ûj|ϕk〉 (Fig. 1a). In the extended swap test, Ĥ is decomposed as a sum of fragments:
, where each unitary Ûj is implemented to estimate the overlap between |ϕ0〉 and Ûj|ϕk〉 (Fig. 1a). In the extended swap test, Ĥ is decomposed as a sum of fragments:  , where
, where ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) j is diagonal and the corresponding diagonalizing unitary
j is diagonal and the corresponding diagonalizing unitary ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) j can be implemented efficiently. Then, the extended swap test is conducted with the circuits of Hadamard tests which estimate 〈ϕ0|ϕk〉, while including the measurement of system qubits with the basis represented by
j can be implemented efficiently. Then, the extended swap test is conducted with the circuits of Hadamard tests which estimate 〈ϕ0|ϕk〉, while including the measurement of system qubits with the basis represented by ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) j (Fig. 1b). Note that in the extended swap test, the overlap matrix elements can be measured simultaneously by measuring the ancilla qubit, which corresponds to a Hadamard test circuit that measures S0,k = 〈ϕ0|e−ikΔtĤ|ϕ0〉. This simultaneous measurement capability is not available in the Hadamard test when measuring the Hamiltonian in its LCU form.
j (Fig. 1b). Note that in the extended swap test, the overlap matrix elements can be measured simultaneously by measuring the ancilla qubit, which corresponds to a Hadamard test circuit that measures S0,k = 〈ϕ0|e−ikΔtĤ|ϕ0〉. This simultaneous measurement capability is not available in the Hadamard test when measuring the Hamiltonian in its LCU form.
![[R with combining circumflex]](https://www.rsc.org/images/entities/i_char_0052_0302.gif) x(y) operator rotates
x(y) operator rotates ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) z basis into
z basis into ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) x (
x (![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) y) basis and is adopted to estimate the real (imaginary) part of the amplitude for the second operator applied to the ancilla qubit.
y) basis and is adopted to estimate the real (imaginary) part of the amplitude for the second operator applied to the ancilla qubit. . In a previous work,36 it was shown that the sampling variance of S0k are determined identically across the test algorithms as:
. In a previous work,36 it was shown that the sampling variance of S0k are determined identically across the test algorithms as:


 . In the Hadamard test, we are going to show that the sampling cost to estimate eqn (6) within a certain level of accuracy is proportional to ‖β‖12.
. In the Hadamard test, we are going to show that the sampling cost to estimate eqn (6) within a certain level of accuracy is proportional to ‖β‖12.



![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) x and
x and ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) y bases, corresponding to the real and imaginary parts of 〈ϕ0|Ûj|ϕk〉, respectively. Thus, 2Nβ independent measurements of
y bases, corresponding to the real and imaginary parts of 〈ϕ0|Ûj|ϕk〉, respectively. Thus, 2Nβ independent measurements of  and
and  with a set of states
with a set of states  complete the total estimation of a matrix element in eqn (11).
complete the total estimation of a matrix element in eqn (11).


 .
.

![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) x + i
x + i![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) y) ⊗ Ĥ|Φ0k〉,
y) ⊗ Ĥ|Φ0k〉,
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) j can be efficiently implemented to diagonalize Ĥj onto the computational basis, yielding an Ising Hamiltonian
j can be efficiently implemented to diagonalize Ĥj onto the computational basis, yielding an Ising Hamiltonian ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) j. Then, the measurement can be performed for each Ĥj. For example, if Ĥj is composed of mutually commuting Pauli operators, the unitary
j. Then, the measurement can be performed for each Ĥj. For example, if Ĥj is composed of mutually commuting Pauli operators, the unitary ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) j can be efficiently determined and implemented as a Clifford circuit with the gate count of O(Nq2), where Nq is the number of qubits.39,56,57
j can be efficiently determined and implemented as a Clifford circuit with the gate count of O(Nq2), where Nq is the number of qubits.39,56,57

![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) x(y) ⊗ Ĥj, and the quantum variance of Ôj is
x(y) ⊗ Ĥj, and the quantum variance of Ôj is

 . The corresponding measurement cost,
. The corresponding measurement cost,

![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) j ∈ {βjÛj,Ĥj}. Then, the partial variances, eqn (14) (multiplied by βj) and (21), are generalized into a single form:
j ∈ {βjÛj,Ĥj}. Then, the partial variances, eqn (14) (multiplied by βj) and (21), are generalized into a single form:
![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) j|ϕk〉.
j|ϕk〉.


 heuristically finds a decomposition by Pauli operators that yields a relatively small norm.39
heuristically finds a decomposition by Pauli operators that yields a relatively small norm.39
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) that shifts the Hamiltonian and minimizes the norm of the shifted decomposition:
that shifts the Hamiltonian and minimizes the norm of the shifted decomposition:
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) is parameterized by τ, enabling the use of classical optimization algorithms. Additionally, we impose a constraint on
is parameterized by τ, enabling the use of classical optimization algorithms. Additionally, we impose a constraint on ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) (τ), that is
(τ), that is![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) (τ)|ϕ0〉 = t(τ)|ϕ0〉,
(τ)|ϕ0〉 = t(τ)|ϕ0〉,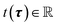 . Note that
. Note that ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) is not required to commute with Ĥ, unlike symmetry operators. The necessity of this constraint will be presented with the rest of procedure.
is not required to commute with Ĥ, unlike symmetry operators. The necessity of this constraint will be presented with the rest of procedure.
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) )‖12 ≤ ‖ζA(Ĥ)‖12). Here, H − T is defined as a Toeplitz matrix satisfying
)‖12 ≤ ‖ζA(Ĥ)‖12). Here, H − T is defined as a Toeplitz matrix satisfying![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) )|ϕl−k〉.
)|ϕl−k〉.![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) dedicated to the electronic structure problem. In many cases, the reference state, |ϕ0〉 is chosen as a simple state, such as Hartree Fock (HF) ground state or a configuration state function (CSF) which is a symmetry-adapted state composed of a small number of Slater determinants. Some or all orbitals in such reference states are separately occupied or unoccupied, which is represented as:
dedicated to the electronic structure problem. In many cases, the reference state, |ϕ0〉 is chosen as a simple state, such as Hartree Fock (HF) ground state or a configuration state function (CSF) which is a symmetry-adapted state composed of a small number of Slater determinants. Some or all orbitals in such reference states are separately occupied or unoccupied, which is represented as:

![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) q = â†qâq are employed.
q = â†qâq are employed.

 and
and 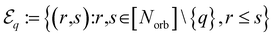 are defined, and δq∈occ is an identity if q ∈ occ, zero otherwise. The indices r and s range over the entire orbital set except q to make
are defined, and δq∈occ is an identity if q ∈ occ, zero otherwise. The indices r and s range over the entire orbital set except q to make ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) Hermitian and to avoid duplication with the one-body number operator, since
Hermitian and to avoid duplication with the one-body number operator, since ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) q2 =
q2 = ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) q. Note that the two-body terms with Êrs
q. Note that the two-body terms with Êrs![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) q for q ∈ virt annihilate |ϕ0〉, as do Êrs(
q for q ∈ virt annihilate |ϕ0〉, as do Êrs(![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) q − 1) for q ∈ occ. Therefore, the corresponding shift factor is determined as
q − 1) for q ∈ occ. Therefore, the corresponding shift factor is determined as
 or
or  with the number of parameters of |τ| = O(Norb3). However, the optimization overhead is reduced if we adopt a decomposition algorithm where each term in eqn (33) is regarded as a fragment, as detailed in Appendix D. By using this reduced optimization, the optimal parameters are found as
with the number of parameters of |τ| = O(Norb3). However, the optimization overhead is reduced if we adopt a decomposition algorithm where each term in eqn (33) is regarded as a fragment, as detailed in Appendix D. By using this reduced optimization, the optimal parameters are found as
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) (τ) and
(τ) and  , which are always measurable simultaneously.
, which are always measurable simultaneously. , where
, where 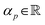 and
and  , ICS seeks a decomposition into measurable operators that minimizes the total variance. Note that measurable operators here involve not only Hermitian operators but also scaled unitaries, which are used for the Hadamard test. As reviewed in Appendix B, such a decomposition in Pauli basis is written as:
, ICS seeks a decomposition into measurable operators that minimizes the total variance. Note that measurable operators here involve not only Hermitian operators but also scaled unitaries, which are used for the Hadamard test. As reviewed in Appendix B, such a decomposition in Pauli basis is written as:
![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) j are measurable operators and the corresponding sets of Pauli indices,
j are measurable operators and the corresponding sets of Pauli indices, 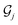 , are predetermined by a decomposition algorithm like
, are predetermined by a decomposition algorithm like  . Importantly, these
. Importantly, these  sets may not be disjoint, meaning the same operator
sets may not be disjoint, meaning the same operator ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) p can belong to multiple sets. Correspondingly, the coefficient αp is split across these sets, satisfying the condition:
p can belong to multiple sets. Correspondingly, the coefficient αp is split across these sets, satisfying the condition:

 and
and  . The partial variance for
. The partial variance for ![[N with combining circumflex]](https://www.rsc.org/images/entities/i_char_004e_0302.gif) j (eqn (25)) is expressed as a quadratic form in terms of the split coefficients
j (eqn (25)) is expressed as a quadratic form in terms of the split coefficients  :
:
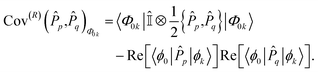


![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) = e−iĤΔt is available, which does not involve Trotterization error. The QKSD order is set to n = Nq + 1, where Nq is the number of qubits. In this setting, the overhead for the classical GEVP is exponentially small compare to the direct diagonalization, while the error induced by the projection onto the quantum Krylov space is exponentially small as shown in ref. 35, Theorem 3.1. We observed that the error caused by the Krylov projection is bounded as |E0(n) − E0|<10−4 Ha in the electronic structures of our interest, where E0 is the true ground state energy of Ĥ.
= e−iĤΔt is available, which does not involve Trotterization error. The QKSD order is set to n = Nq + 1, where Nq is the number of qubits. In this setting, the overhead for the classical GEVP is exponentially small compare to the direct diagonalization, while the error induced by the projection onto the quantum Krylov space is exponentially small as shown in ref. 35, Theorem 3.1. We observed that the error caused by the Krylov projection is bounded as |E0(n) − E0|<10−4 Ha in the electronic structures of our interest, where E0 is the true ground state energy of Ĥ. is adopted as decomposition algorithm. Shifting operators
is adopted as decomposition algorithm. Shifting operators ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) are chosen as eqn (34) and optimized by the
are chosen as eqn (34) and optimized by the  algorithm after assigning the parameters shown in eqn (36)
algorithm after assigning the parameters shown in eqn (36)
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) )‖1
)‖1![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) )‖1
)‖1![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) )|ϕk〉, averaged over k, are separately displayed for the cases with and without applying ICS and/or shift techniques from the measurement setting obtained from
)|ϕk〉, averaged over k, are separately displayed for the cases with and without applying ICS and/or shift techniques from the measurement setting obtained from  (denoted as ‘SI’). The costs are estimated by directly computing eqn (20) and (13). The values in the parenthesis are averaged empirical variances obtained by 1000 independent runs of QKSD algorithm for each setting. The sub-optimal shot allocations are used if ICS is not employed, while shot allocations of the ICS output are adopted otherwise. The result of ICS based on the true state |ϕk〉 and phased CISD proxy are shown. Note that ICS by true state is not practically achievable
(denoted as ‘SI’). The costs are estimated by directly computing eqn (20) and (13). The values in the parenthesis are averaged empirical variances obtained by 1000 independent runs of QKSD algorithm for each setting. The sub-optimal shot allocations are used if ICS is not employed, while shot allocations of the ICS output are adopted otherwise. The result of ICS based on the true state |ϕk〉 and phased CISD proxy are shown. Note that ICS by true state is not practically achievable

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 independent and identical experiments. Here, the optimal thresholding of eqn (45) is applied to mitigate the sampling error, further reducing the Krylov dimension from n = 9 to n′ = 3. In the FH case, two different values of n′ = 2, 3 were observed across the random experiments, resulting in the two peaks in the histogram. Ẽ(n→n′) and E(n→n′) denote the QKSD ground state energies with and without considering the effect of sampling error, respectively. E(n) represents the QKSD ground state energy without error or thresholding.
000 independent and identical experiments. Here, the optimal thresholding of eqn (45) is applied to mitigate the sampling error, further reducing the Krylov dimension from n = 9 to n′ = 3. In the FH case, two different values of n′ = 2, 3 were observed across the random experiments, resulting in the two peaks in the histogram. Ẽ(n→n′) and E(n→n′) denote the QKSD ground state energies with and without considering the effect of sampling error, respectively. E(n) represents the QKSD ground state energy without error or thresholding.
 and Ĥ ⊗
and Ĥ ⊗ ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) x(y). This idea can be extended to the other EFTQC algorithms. Based on our knowledge, recently developed EFTQC algorithms other than QKSD focus on extracting the spectrum only from the autocorrelation function, a(t) := 〈ϕ0|e−iĤt|ϕ0〉. However, those algorithms can be more refined by adopting the simultaneous measurement of aÔ(t) := 〈ϕ0|Ôe−iĤt|ϕ0〉 for some observable Ô. For instance, the first derivative of a(t) can be directly calculated from aĤ(t). This measurement, which can be done precisely if the techniques introduced in this work are adopted, only requires overheads of O(Nq2) Clifford operations. These operations do not need additional logical qubits and present an endurable cost for EFTQCs. Given this rationale, our future research direction involves exploring EFTQC algorithms including aÔ(t) in the spectrum extraction.
x(y). This idea can be extended to the other EFTQC algorithms. Based on our knowledge, recently developed EFTQC algorithms other than QKSD focus on extracting the spectrum only from the autocorrelation function, a(t) := 〈ϕ0|e−iĤt|ϕ0〉. However, those algorithms can be more refined by adopting the simultaneous measurement of aÔ(t) := 〈ϕ0|Ôe−iĤt|ϕ0〉 for some observable Ô. For instance, the first derivative of a(t) can be directly calculated from aĤ(t). This measurement, which can be done precisely if the techniques introduced in this work are adopted, only requires overheads of O(Nq2) Clifford operations. These operations do not need additional logical qubits and present an endurable cost for EFTQCs. Given this rationale, our future research direction involves exploring EFTQC algorithms including aÔ(t) in the spectrum extraction.
 . Before proceeding with the derivation, we introduce three lemmas that will be instrumental in this process. Throughout this section,
. Before proceeding with the derivation, we introduce three lemmas that will be instrumental in this process. Throughout this section,  is abbreviated as
is abbreviated as  unless otherwise mentioned.
unless otherwise mentioned.
 , the following equality holds:
, the following equality holds:
 , the averaged conjugation is known as
, the averaged conjugation is known as
 is the uniform Haar distribution over the unitary group of dimension d. Therefore, we can state
is the uniform Haar distribution over the unitary group of dimension d. Therefore, we can state
 , the following equality holds:
, the following equality holds: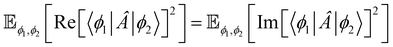
 is always identical to
is always identical to  for any function f. Therefore, the following proves eqn (A4):
for any function f. Therefore, the following proves eqn (A4):

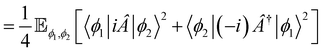
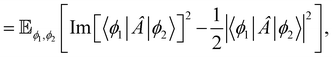
 and
and  , respectively, for
, respectively, for  . Additionally, eqn (A7) is derived by replacing |ϕ2〉 with i|ϕ2〉.
. Additionally, eqn (A7) is derived by replacing |ϕ2〉 with i|ϕ2〉.
 , the following equality holds:
, the following equality holds:
 , where Â|ψi〉 = ai|ψi〉 and γi = 〈ψi|ϕ〉. Then the Haar averaging over |ϕ〉 is identical to the averaging {γi}i=1d over d-dimensional complex unit sphere,
, where Â|ψi〉 = ai|ψi〉 and γi = 〈ψi|ϕ〉. Then the Haar averaging over |ϕ〉 is identical to the averaging {γi}i=1d over d-dimensional complex unit sphere,  , where
, where  denotes the complex projective space. Therefore, it can be shown that
denotes the complex projective space. Therefore, it can be shown that





 denotes
denotes 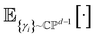 and eqn (A13) holds because of ref. 63, Theorem 2.6.
and eqn (A13) holds because of ref. 63, Theorem 2.6.


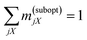 .
.
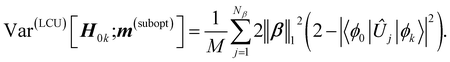
![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) k|ϕ0〉 is an evolved state from |ϕ0〉, we can consider averaging the variance over single state |ϕ0〉, fixing the evolution operator,
k|ϕ0〉 is an evolved state from |ϕ0〉, we can consider averaging the variance over single state |ϕ0〉, fixing the evolution operator, ![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) k. Then from eqn (A18), |〈ϕ0|Ûj|ϕk〉|2 = |〈ϕ0|Ûj
k. Then from eqn (A18), |〈ϕ0|Ûj|ϕk〉|2 = |〈ϕ0|Ûj![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) k|ϕ0〉|2 needs to be averaged over |ϕ0〉. Using Lemma 3 with  = Ûj
k|ϕ0〉|2 needs to be averaged over |ϕ0〉. Using Lemma 3 with  = Ûj![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) k, we can show that
k, we can show that![[B with combining circumflex]](https://www.rsc.org/images/entities/i_char_0042_0302.gif) k]|2 ≤ d2. Finally, the total averaged variance is bounded by
k]|2 ≤ d2. Finally, the total averaged variance is bounded by

 , while the last term,
, while the last term,  is obtained using Lemma 1. Finally, the expected variance of jth fragment is derived as below:
is obtained using Lemma 1. Finally, the expected variance of jth fragment is derived as below: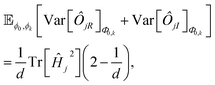

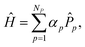
![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) p ∈ {Î,
p ∈ {Î, ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) x,
x, ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) y,
y, ![[small sigma, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e111.gif) z}⊗Nq is an Nq-qubit Pauli operator and its coefficient is
z}⊗Nq is an Nq-qubit Pauli operator and its coefficient is  .
.

![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) p can be separated to the multiple groups
p can be separated to the multiple groups  . Thus,
. Thus, 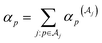 for all 1 ≤ p ≤ Np, should be imposed for the partitioned coefficients. Also, if the anticommutation conditions of different Pauli operators within a group holds:
for all 1 ≤ p ≤ Np, should be imposed for the partitioned coefficients. Also, if the anticommutation conditions of different Pauli operators within a group holds:
 , becomes a scaled unitary, βjÛj. Then,
, becomes a scaled unitary, βjÛj. Then,  is found consequently, and the norm becomes
is found consequently, and the norm becomes
 two-qubit gates.55
two-qubit gates.55

 . For each of Ĥj, one can construct a diagonalizing Clifford circuit,
. For each of Ĥj, one can construct a diagonalizing Clifford circuit, ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) j, taking
j, taking  two-qubit gates. Furthermore, one can find the FH decomposition norm, ‖γ‖1 in terms of Pauli coefficients:
two-qubit gates. Furthermore, one can find the FH decomposition norm, ‖γ‖1 in terms of Pauli coefficients:
 because the trace of Pauli operators except the identity is zero.
because the trace of Pauli operators except the identity is zero.![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) j, which is also an LCU and an FH simultaneously. However, in such case, the norm ‖β‖1 = ‖γ‖1 = ‖α‖1 becomes larger than that of grouped Pauli case because the sum of L2 norms of grouped Pauli coefficients is smaller than the L1 norm.
j, which is also an LCU and an FH simultaneously. However, in such case, the norm ‖β‖1 = ‖γ‖1 = ‖α‖1 becomes larger than that of grouped Pauli case because the sum of L2 norms of grouped Pauli coefficients is smaller than the L1 norm. , encodes the commutativity between Pauli operators. Specifically, the nodes in V correspond to individual Pauli operators: V = {vp : 1 ≤ p ≤ NP} with a node weight function w(vp) = αp. Also, undirected and unweighted edges connect nodes whose corresponding operators commute
, encodes the commutativity between Pauli operators. Specifically, the nodes in V correspond to individual Pauli operators: V = {vp : 1 ≤ p ≤ NP} with a node weight function w(vp) = αp. Also, undirected and unweighted edges connect nodes whose corresponding operators commute  . The anticommutation graph,
. The anticommutation graph,  , shares the same node set with
, shares the same node set with  but connects nodes with anticommuting operators
but connects nodes with anticommuting operators  . Because any two Pauli operators either commute or anticommute, these graphs are complements, meaning that
. Because any two Pauli operators either commute or anticommute, these graphs are complements, meaning that  .
. often outperform other heuristic algorithms as demonstrated in ref. 39. The original work on
often outperform other heuristic algorithms as demonstrated in ref. 39. The original work on  aimed to minimize the cost of measuring standard expectation values, so it only considered the commutation graph. However, we extend the algorithm to the anticommutation case to reduce the cost of the LCU measurements by simply modifying its grouping condition.
aimed to minimize the cost of measuring standard expectation values, so it only considered the commutation graph. However, we extend the algorithm to the anticommutation case to reduce the cost of the LCU measurements by simply modifying its grouping condition.![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) )‖. In the FH decomposition, Ẑ-type operators are naturally grouped together, which contribute to the norm less significantly than the LCU case. Consequently, the impact of the shifting technique is less pronounced in the FH case compared to the LCU case. Nevertheless, the shifted FH decomposition still achieves a smaller norm than the shifted LCU decomposition.
)‖. In the FH decomposition, Ẑ-type operators are naturally grouped together, which contribute to the norm less significantly than the LCU case. Consequently, the impact of the shifting technique is less pronounced in the FH case compared to the LCU case. Nevertheless, the shifted FH decomposition still achieves a smaller norm than the shifted LCU decomposition. , which is analogous to eqn (B2) or (B5), we obtain:
, which is analogous to eqn (B2) or (B5), we obtain:
![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) p
p![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) q is not necessarily identical to
q is not necessarily identical to ![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) q
q![[P with combining circumflex]](https://www.rsc.org/images/entities/i_char_0050_0302.gif) p. Therefore, to ensure the symmetry, we superpose the product of operators in both orders, (p, q) and (q, p). This results in the definition of the covariance as eqn (41).
p. Therefore, to ensure the symmetry, we superpose the product of operators in both orders, (p, q) and (q, p). This results in the definition of the covariance as eqn (41).![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) is given as eqn (34), the number of real parameters determining
is given as eqn (34), the number of real parameters determining ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) is:
is:

 with the size of
with the size of  represents the indices of Hermitian two-body operators avoiding the duplication from the following eight-fold symmetries:
represents the indices of Hermitian two-body operators avoiding the duplication from the following eight-fold symmetries:![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) p2 =
p2 = ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) p).
p).



![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) (τ) is given as
(τ) is given as



 such that
such that

 occur both in the second and the third summations, where
occur both in the second and the third summations, where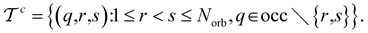

 denotes the shift operator
denotes the shift operator ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) with the partial assignment and
with the partial assignment and  denotes the set of variables, τ(2)qrs with
denotes the set of variables, τ(2)qrs with  . Furthermore, minimizing eqn (D13) is identical to the separated optimizations:
. Furthermore, minimizing eqn (D13) is identical to the separated optimizations:
 , where
, where  and
and
 . We provide a pictorial procedure to solve eqn (D14) in Fig. 3. Although the solution for 2-dimensional problem is shown, this can be extended to
. We provide a pictorial procedure to solve eqn (D14) in Fig. 3. Although the solution for 2-dimensional problem is shown, this can be extended to  -dimensional problem by considering hyperplane instead of lines in the figure. Every
-dimensional problem by considering hyperplane instead of lines in the figure. Every  satisfying
satisfying


![[g with combining tilde]](https://www.rsc.org/images/entities/i_char_0067_0303.gif) rsqq for all
rsqq for all  satisfies eqn (D16), which is analogous to eqn (D11).
satisfies eqn (D16), which is analogous to eqn (D11).![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) r and Êrs
r and Êrs![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) q are Hermitian, not unitary. Although
q are Hermitian, not unitary. Although ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) q can be written as a unitary operator (
q can be written as a unitary operator (![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) q = 2
q = 2![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) q − 1), our current understanding of representing a unitary operator as a linear combination of one-body excitation operators remains insufficient to establish an analogous reduction for the LCU case. Therefore, this work adopts the same shift operator for both LCU decomposition as an interim solution, leaving the parameter reduction for the LCU case as a future work.
q − 1), our current understanding of representing a unitary operator as a linear combination of one-body excitation operators remains insufficient to establish an analogous reduction for the LCU case. Therefore, this work adopts the same shift operator for both LCU decomposition as an interim solution, leaving the parameter reduction for the LCU case as a future work.