Artificial intelligence-assisted electrochemical sensors for qualitative and semi-quantitative multiplexed analyses

Abstract

This research utilises Artificial Intelligence (AI) to enhance electrochemical peak resolution and lower detection limits in voltammetric analysis, focusing on complex, multiplex real matrices analyses. The study investigated the quinone family, hydroquinone, benzoquinone, and catechol analysed individually and in mixtures using cyclic and square wave voltammetry. The ferrocyanide/ferricyanide redox couple was included as a standard redox probe to provide a reference for method validation.

---

Artificial intelligence (AI) has emerged as a paradigm-shifting technology, bringing about significant changes across sectors through its capacity to facilitate sophisticated data processing, identify patterns, and generate predictive analytics.^1,2

Electrochemical sensors (ESs), an industry historically dependent on established analytical methods, are presently undergoing substantial advancements due to AI.^3,4 In general, ESs, which measure electrical signals generated by chemical reactions, have long been utilized in a wide array of applications, including environmental monitoring, clinical diagnostics, food safety, and industrial process control.^5–7 However, they often face limitations in detecting low-abundance analytes and interpreting complex signal patterns, particularly in the case of multiplexed analysis of complex matrices.¹

Integrating AI with ESs represents a transformative advancement in analytical science, significantly enhancing these devices' sensitivity, specificity, and functionality.⁸ AI-assisted ESs offer a promising solution to these challenges by leveraging advanced AI algorithms, such as machine learning (ML) and deep learning (DL), to process and analyze complex datasets with high precision.^9,10 In particular, AI algorithms enable to discern subtle patterns and correlations within data that are typically imperceptible to conventional analytical methods.¹¹ This capability significantly improves the sensors' ability to detect low-concentration analytes in complex samples, enhancing their overall sensitivity and specificity.^6,11–14 Moreover, AI-powered sensors can perform real-time data analysis, providing immediate feedback and enabling swift decision-making, which is crucial in applications requiring rapid responses. Another significant advantage of AI-based ESs is their ability to automate calibration processes and error detection.¹⁵ This automation ensures consistent accuracy and reliability of sensor readings without the need for manual intervention.^16,17 Additionally, AI enables predictive maintenance by analyzing performance trends and identifying signs of sensor degradation before failure occurs, thereby reducing downtime and maintenance costs.¹⁸ Furthermore, it was recently evidenced that AI-assisted ESs also exhibit remarkable adaptability, learning capabilities and data augmentation possibility.^18–20 These sensors can continuously improve their performance by learning from new data inputs, allowing them to handle various analytes and environmental conditions. This adaptability makes AI-enhanced sensors highly versatile and suitable for diverse applications.^21,22

Despite their numerous advantages, deploying AI-assisted sensors involves increasingly complex hardware and software. AI algorithms require large datasets for training and validation, which can be resource-intensive to acquire and process.²³ Moreover, implementing AI techniques necessitates significant computational power, particularly for real-time data processing and deep learning applications, which can be a limiting factor in resource-constrained settings.²⁴ Additionally, AI models, especially deep learning networks, often operate as “black boxes”, providing limited insight into the underlying mechanisms of their decisions, which can be a disadvantage in applications where understanding the rationale behind sensor readings is crucial.²⁵

Herein, AI is proposed as a solution for resolving peak overlap in electrochemical signals when the target analytes show similar discharge potential and electrochemical behaviour. This is a significant challenge, especially in complex samples where multiple electroactive species with similar redox potential may be present simultaneously. There are a few examples of a similar approach in the literature but limited to more simplistic experiments. For example, De Oliveira Filho et al. (2023), developed an AI-integrated method for the selective detection of dopamine (DA) in a complex matrix like cerebrospinal fluid.²⁶ However, the challenge addressed is less complex than ours, since this case only involves two interferents (uric acid and ascorbic acid). In this work, the quinone family were examined as a case study for proof of concept. A mixture including hydroquinone (HQ), benzoquinone (BQ), catechol (CT), adding ferrocyanide (FC) as reference electroactive probes, at various ratios and concentrations was qualitatively and quantitatively analysed using cyclic voltammetry (CV). In addition, to further challenge the system and assess the AI model's potential, the analyte samples were prepared in deionized (dW) and tap water (tW) (Table 1).

Table 1 Analytical parameters obtained by analysing different Fe, HQ, Bz and Ct concentrations in dW and tW samples

	Fe		HQ		Bz		Ct
	dW	tW	dW	tW	dW	tW	dW	tW
Cyclic voltammetry (CV)
LOD (μM)	12.2	13.1	14.4	14.6	9.4	9.8	8.8	10.2
LOQ (μM)	45.4	50.3	39.2	41.2	26.2	32.2	25.1	34.1
RSD%	10	12	10	11	11	11	9	10
Square wave voltammetry (SWV)
LOD (μM)	2.1	2.8	0.8	1.3	1.8	2.7	2.4	4.2
LOQ (μM)	6.9	9.1	2.9	4.3	6.3	8.7	7.3	13.6
RSD%	9	10	8	9	8	10	8	10

---

To perform this investigation, bare screen-printed electrodes (SPEs) were employed for voltammetric analyses of separate solutions of the selected analytes using CV and square wave voltammetry (SWV). SPEs used in this study are custom-made and consist of three components: a working electrode (WE) and counter electrode (CE) made from graphite ink, and a reference electrode (RE) fabricated using silver/silver chloride ink. Each SPE measures 3 × 1 cm, with the WE having an active surface area of 0.07 cm². Measurements were performed at each concentration (0.01 μM to 2 mM) in triplicate. Key analytical parameters, including the limit of detection (LOD), limit of quantification (LOQ), and reproducibility (RSD%), were calculated. As shown in Table 2, the performance of the SPEs in dW was similar to that in tW. However, a slight decrease in reproducibility was noted (RSD% always <12%, calculated on the media of all measurements for each analyte), likely attributable to the increased complexity of the real matrix.

Table 2 Detailed architecture of the Convolutional Neural Network (CNN) model used in this study, including the type of layer, output shape, kernel size, and the number of parameters for each layer. The model consists of convolutional, pooling, flattening, dense, and regularization layers, ending with a softmax activation for classification

Layer (type)	Output shape	Size	Param #
Input	(None, 224, 224, 3)
Conv2D	(None, 222, 222, 48)	3	1.344
MaxPooling2D	(None, 111, 111, 48)	2	0
Conv2D	(None, 109, 109, 48)	3	20.784
MaxPooling2D	(None, 54, 54, 48)	2	0
Conv2D	(None, 52, 52, 32)	3	13.856
MaxPooling2D	(None, 26, 26, 32)	2	0
Conv2D	(None, 24, 24, 32)	3	9.248
MaxPooling2D	(None, 12, 12, 32)	2	0
Conv2D	(None, 10, 10, 16)	3	4.624
MaxPooling2D	(None, 5, 5, 16)	2	0
Conv2D	(None, 3, 3, 8)	3	1.160
MaxPooling2D	(None, 1, 1, 8)	2	0
Flatten	(None, 8)		0
Dense (ReLu)	(None, 64)		576
Dropout (0.5)	(None, 64)		0
Dense (ReLu)	(None, 5)		325
Batch normalization	(None, 5)		30
Activation softmax	(None, 5)		0
	Total param #		51 947

---

After conducting a classical characterization of SPEs to determine the redox potentials of every single probe in tW (Fe: −0.26 V, 0.24 V; Bz: −0.650 V, 0.02 V, 0.610 V; HQ: −0.35 V, 0.35 V; Ct: −0.18 V, 0.25 V) and to evaluate the performance limits of our devices, a more complex analysis was undertaken. Specifically, CV was employed to qualitatively identify each redox probe within a mixed solution containing all probes at a fixed concentration of 2 mM. The results, shown in Fig. 1a, reveal CVs and indicate the difficulty of identifying all species, evidenced by the presence of only two distinct oxidation and reduction peaks. The literature reports various methods involving redox mediators, modified electrodes, and specific nanomaterials. However, these approaches are often time-consuming, costly, and not fully efficient. Additionally, challenges in qualitative analysis encountered in CV persist in SWV of the same mixed samples. As illustrated in Fig. 1b, it is evident that multiple redox probes undergo oxidation within the specified potential window. However, accurately identifying and labelling the peaks presents a significant challenge. Consequently, utilizing an SPE makes it nearly impossible to recognize each electroactive species qualitatively and then quantitatively determine their concentrations.^27–31

Fig. 1 Electrochemical characterization of a mixture of Fe, Bz, HQ and Ct (all 2 mM). In (a) CV and (b) SWV voltammograms recorded in tW. An example of curves of at least 3 analyzed SPEs is presented (RSD% < 13%).

For this reason, a method based on Machine Learning was developed for the qualitative (classification) and quantitative analysis of complex organic samples. The Gramian Angular Field (GAF) transformation was employed to convert CV signals into images, enabling 2D Convolutional Neural Networks (CNNs) to effectively capture both local and global dependencies in the data, which are critical for resolving overlapping electrochemical signals.³² The GAF transformation allows the encoding of time-series data into an image format, preserving both temporal and amplitude relationships in a way that makes these global dependencies more accessible to 2D CNNs. As a result, the proposed approach enhances the model's ability to resolve mixed analyte signals by leveraging the strengths of 2D convolutional layers in capturing spatial dependencies.

The initial phase of the proposed methodology entails converting I–V cycles derived from CV and SWV into an equivalent RGB image format. This conversion utilizes the GAF transformation. Briefly, the process begins with a time series X = {x₁, x₂, …, x_n} of n real-valued observations. Since the vector X is normalized, all its values fall within the interval [−1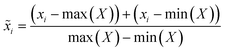,1].

The re-scaled vector X̃ is represented in polar coordinates by associating each value with its angular cosine, Φ_i, and the corresponding time instant with its radius, r. This can be described by the following equations:

Here, t_i represents the time stamp and N is a constant factor used to regularize the span of the polar coordinate system.

This transformation has two key properties: (i) it is bijective since cos(Φ) is monotonic when Φ ∈ [0, π]; (ii) unlike Cartesian coordinates, polar coordinates preserve the absolute temporal relationships.

The Gramian summation angular field (GASF) and Gramian difference angular field (GADF) are defined as follows:

Using these transformations, each I–V cycle is converted into an image. Specifically, the GASF related to the potential is mapped to the red (R) colour plane, and the GADF and GASF related to the current are mapped to the green (G) and blue (B) planes, respectively. Examples of the resulting RGB images, corresponding to the detection of BQ in water solution, are shown in Fig. 2. After converting all 75 cycles into RGB images, we trained a deep neural network (DNN) to classify them. Specifically, we used a convolutional neural network (CNN), which mimics the animal visual cortex by having neurons respond to stimuli in overlapping receptive fields. CNNs require minimal preprocessing, as they automatically optimize filters (or kernels) through machine learning, unlike traditional algorithms where filters are manually designed.

Fig. 2 GBR representation of GAF from (a) hydrochinone, (b) cathecol and (c) hydrochinone–benzoquinone obtained using CV as analytical technique.

Our CNN comprises six blocks with 2D convolution (kernel size 3 × 3), max pooling (stride of 2), and two fully connected layers, including a hidden layer of 64 units, a dropout of 0.5, and an output layer of 3 units. This structure was chosen to minimize complexity and prevent overfitting, as detailed in Table 2.

As described in the following, the dataset generated by CV experiments contains 75 experimental points, each referring to the characterization of HQ, BQ, CT, and FC in tW. Three experiments have been conducted. The first with shuffled data, the second and third with data organized in terms of concentrations. In the shuffled data experiment, the 75 images were divided randomly in training, validation, and testing in a ratio of 70%, 15%, and 15%, respectively. We used the division reported in Table 3 in the other two experiments. Thus, the models have been trained only with specific concentrations in terms of μM.

Table 3 Image distribution for the second (a) and third (b) experiments

Set	Concentrations (mM)		Number of images
Experiment	(a)	(b)
Training	0.5, 0.1, 0.01	2, 0.5, 0.01	45
Validation	2	1	15
Test	1	0.1	15

---

As shown in Table 3, three concentrations were used for training and two others for validation and testing. In the first experiment (a), the highest concentrations were used for testing, while in the second experiment (b), training was performed on concentrations distributed between the minimum and maximum.

Training on a Dell laptop with a Core i9 processor, 64GB RAM, and an NVIDIA 4080 GPU took about ten minutes to converge at epoch 1200. As a deep learning framework, we used Keras version 2.4.0 with TensorFlow version 2.4.0 as the back end. During the network training, the following hyperparameters were used: epochs 400, patience 100, optimizer Stochastic Gradient Descent, learning rate 0.0001, momentum 0.9, loss categorical cross-entropy, metrics accuracy, batch size: 16. At the end of each epoch, the loss was evaluated on the validation set to save the best-performing model and avoid overfitting. An early stopping policy with a patience of 100 epochs was used to halt training if the loss did not improve.

Fig. 3 shows the accuracy and loss curves during training. Notably, the validation set had a lower loss and higher accuracy than the training set, likely due to the dropout layer, which sets 50% of features to zero during training, making the model more robust during validation when all features are used.

Fig. 3 The confusion matrices for the three experiments are in (a–c). As a row, the predicted values, and as a column, the ground truth. In all the experiments, there is only one error (confusion) between the mix of hydroquinone/benzoquinone and ferrocyanide. The (d and e) subfigures describe the trend of the loss and accuracy, respectively, on training (red) and validation (blue).

The training phase reached a plateau at epoch 1100, with no further decrease in validation loss for 100 epochs, prompting the stop of training. The model saved at this point was used for testing. Global performance was assessed using accuracy and a confusion matrix (CM). A CM summarizes the results of the testing phase on different classes. The CM_ij element represented the percentage of elements labelled as class i and predicted as class j. The ideal case is represented by a diagonal matrix, meaning that all class samples were correctly classified. Furthermore, the global accuracy can be evaluated as the ratio between the CM trace (sum of the correctly classified) and the sum of all CM values.

Conclusions

The fusion of AI with electrochemical sensors holds immense potential to revolutionize analytical methodologies across various fields. In this study, we introduce an AI-driven approach for the qualitative and quantitative analysis of complex matrices comprising multiple electroactive species with overlapping electrochemical profiles and achieving a Limit of Detection (LOD) of CV to micromolar levels. By significantly enhancing analytical precision in complex environments, this approach presents a robust and scalable solution for intricate chemical analyses. This convergence promises to open new avenues for research and application, ultimately contributing to advancements in environmental protection, healthcare, food safety, and industrial processes.

Data availability

The data and source code supporting this article are available at: https://github.com/mariomolinara/CHEM_GAF_CNN and can be referenced using the DOI: https://doi.org/10.5281/zenodo.14601909.

Author contributions

Conceptualization, R. C., M. M.; methodology, R. C., M. M., A. M., L. M.; software, R. C., M. M., A. M., L. M.; investigation, R. C., M. M., A. L.; resources, L. M., A. M., and M. M.; data curation R. C., M. M.; writing—original draft preparation R. C., M. M.; writing—review and editing, R. C., M. M., A. M., L. M.; funding acquisition, A. M., L. M. All authors have read and agreed to the published version of the manuscript. All authors participated in reviewing and editing the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The research leading to these results has received funding from the Project “SENS-AI, Environmental Sensing with Artificial Intelligence” CUP H53D23000520006, funded by EU in NextGenerationEU plan through the Italian “Bando Prin 2022 – D.D. 104 del 02-02-2022′′ by MUR (2023–2025).

Notes and references

1. S. Chen, et al. , Fundam. Res., 2023, S2667325823003588.
2. A. Aldoseri, et al. , Sustainability, 2024, 16, 1790.
3. C. Zhu, et al. , Anal. Chem., 2015, 87, 230–249.
4. A. T. Lawal, et al. , Sens. BioSensing Res., 2023, 41, 100571.
5. L. Zhang, et al. , Adv. Sens. Energy Mater., 2023, 2, 100081.
6. M. M. Shanbhag, et al. , Chem. Eng. J. Adv., 2023, 16, 100516.
7. R. Cancelliere, et al. , Trac. Trends Anal. Chem., 2024, 117949.
8. R. Cardoso Rial, et al. , Talanta, 2024, 274, 125949.
9. M. Molinara, et al. , Sensors, 2022, 22, 8032.
10. Y. Zhao, et al. , Biomicrofluidics, 2023, 17, 041301.
11. L. Sangiorgi, et al. , Sensors, 2024, 24, 1396.
12. L. Chen, et al. , Sensors, 2024, 24, 2958.
13. C. Wang, et al. , Bioelectron. Med., 2023, 9, 17.
14. J. Wu, et al. , Nat. Rev. Bioeng., 2023, 1, 346–360.
15. C. D. Flynn, et al. , Diagnostics, 2024, 14, 1100.
16. J. H. Kim, et al. , Biomed. Eng. Lett., 2021, 11, 309–334.
17. I. Rojek, et al. , Appl. Sci., 2023, 13, 4971.
18. T. T. Um, et al., Proceedings 19th ACM, 2017, pp. 216–220.
19. T. Sun, et al. , Nano–Micro Lett., 2024, 16, 14.
20. M. Saeidi, et al. , Biosensors, 2023, 13, 823.
21. H. Adamu, et al. , Energy Adv., 2023, 2, 615–645.
22. Y. Zhang, et al. , Biosens. Bioelectron., 2023, 219, 114825.
23. A. Aldoseri, et al. , Appl. Sci., 2023, 13, 7082.
24. I. H. Sarker, SN Comput. Sci., 2021, 2, 420.
25. V. Hassija, et al. , Cogn. Comput., 2024, 16, 45–74.
26. J. I. De Oliveira Filho, et al. , Adv. Inf. Syst., 2023, 5, 2300227.
27. R. Qureshi, et al., TechRxiv, 2023, preprint,  DOI:10.36227/techrxiv.22293442.
28. E. Bainomugisha, et al. , Soc. Impact, 2024, 3, 100044.
29. Y. Wu, et al. , Food Chem. Toxicol., 2022, 169, 113398.
30. G. F. Giordano, et al. , Anal. Bioanal. Chem., 2023, 415, 3683–3692.
31. Z. Zhou, et al. , Curr. Res. Food Sci., 2024, 8, 100679.
32. S. Shajari, et al. , Sensors, 2023, 23, 9498.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dd00318g

---