Atlas: a brain for self-driving laboratories

Abstract

Self-driving laboratories (SDLs) are next-generation research and development platforms for closed-loop, autonomous experimentation that combine ideas from artificial intelligence, robotics, and high-performance computing. A critical component of SDLs is the decision-making algorithm used to prioritize experiments to be performed. This SDL “brain” often relies on optimization strategies that are guided by machine learning models, such as Bayesian optimization. However, the diversity of hardware constraints and scientific questions being tackled by SDLs require the availability of a set of flexible algorithms that have yet to be implemented in a single software tool. Here, we report Atlas, an application-agnostic Python library for Bayesian optimization that is specifically tailored to the needs of SDLs. Atlas provides facile access to state-of-the-art, model-based optimization algorithms—including mixed-parameter, multi-objective, constrained, robust, multi-fidelity, meta-learning, asynchronous, and molecular optimization—as an all-in-one tool that is expected to suit the majority of specialized SDL needs. After a brief description of its core capabilities, we demonstrate Atlas' utility by optimizing the oxidation potential of metal complexes with an autonomous electrochemical experimentation platform. We expect Atlas to expand the breadth of design and discovery problems in the natural sciences that are immediately addressable with SDLs.

---

1. Introduction

Self-driving laboratories (SDLs) are advanced technological platforms that use artificial intelligence, robotics, and high-performance computing to perform complex research tasks autonomously, that is, without human intervention. Such platforms aim to streamline and enhance the efficiency of scientific experimentation, research, and analytical processes.^1–8 SDLs can accelerate the rate at which advanced materials, functional molecules, and industrial processes are designed by enhancing productivity, throughput, accuracy, and reproducibility. Early-stage SDLs have targeted diverse research and development goals, including chemical reaction and process optimization,^9–19 the design of nanomaterials,^20–23 and light-harvesting materials,^24–27 to name a few.^28–32

The cornerstone of an SDL is its decision-making algorithm (here informally referred to as its “brain”), which is typically implemented as a data-driven experiment planning strategy. Compared to less dynamic strategies such as Design of Experiment,^33–35 data-driven approaches leverage feedback from previously completed experiments to inform subsequent recommendations of experimental parameters, resulting in superior sample efficiency. Although many such strategies have been proposed, including gradient-based optimizers,³⁶ evolutionary strategies,^37–42 and reinforcement learning,^43,44 Bayesian optimization (BO)^45–47 has recently emerged as the most popular choice. BO is a sequential optimization strategy for expensive-to-evaluate black-box functions based on machine-learned approximations of the target objective being optimized.

Python libraries for general-purpose BO are plentiful. Popular examples include scikit-learn,^48,49 GPyOpt,⁵⁰ HyperOpt,^51–54 SMAC3,^55,56 Dragonfly,⁵⁷ HEBO,⁵⁸ BoTorch,⁵⁹ Ax,⁶⁰ and Vizier,^61,62 amongst others. Most of the aforementioned libraries are primarily scoped toward optimization of machine learning (ML) model hyperparameters, and often lack specific functionality requisite for the experimental sciences. For example, the proposed parameters for hyperparameter tuning are generally expected to be executed exactly, while in a SDL it might be impossible to control experimental conditions to high levels of precision.^63,64 Other requirements for broad applicability of BO in experimental sciences include constrained optimization, with a priori known (physical hardware restrictions, safety concerns)^65,66 and unknown (failed/abandoned synthesis, inadequate conditions for property measurement)^67–72 constraint functions, as well as the ability for asynchronous experimental execution (i.e. recommendation of new parameters before a complete batch of corresponding measurements are available).^73,74 Although several such libraries do contain the low-level infrastructure necessary to implement more advanced optimization techniques, it remains an expert-level task to correctly organize the required building blocks to produce a working prototype. Software libraries for data-driven decision-making in SDLs and experimental sciences have also been reported.^20,75–82 While these studies constitute important landmarks in the burgeoning field of SDLs, most target specific experimental frameworks and/or narrow problem types and do not cover the full extent of requirements needed for a truly general-purpose tool.

In this work, we introduce Atlas, an Object-Oriented Python library for BO that was designed with the broadest applicability to SDLs and experimental science in mind. Fig. 1 shows a summary of the main experiment-planning capabilities of Atlas along with its place within the closed-loop experimentation paradigm. Atlas intends to provide practitioners of autonomous science with state-of-the-art BO algorithms while abstracting away all complex implementation details. We strived to provide researchers with the numerous, application-agnostic features often required for the successful deployment of BO in practice. This flexibility is expected to allow researchers to focus on customizing their experimental or computational protocols and expand the set of design and discovery problems that BO and SDLs can tackle. Additionally, Atlas features a modular architecture, is freely available, and is built on top of robust deep learning libraries such as BOTorch, GPyTorch, and PyTorch. This design not only facilitates advanced users in modifying the code, customizing algorithms, and integrating new ones, but also ensures access to the performance and reliability of established Bayesian optimization libraries. This paper is organized as follows: Section 2 provides a brief review of BO and its components. Section 3 lists the notable features of the Atlas library and gives code snippet examples for each feature. Finally, Section 4 describes a real-world demonstration of Atlas used in conjunction with ChemOS 2.0,⁸³ an SDL orchestration software, to optimize the oxidation potential of metal complexes in a cyclic voltammetry experiment.

Fig. 1 Conceptual figure showing the important capabilities of Atlas, as well as its place in a closed-loop experimentation cycle utilized by an SDL.

2. Overview of Bayesian optimization for experiment planning

In this section, we briefly review the basic principles of Bayesian optimization as a primer for discussion of the capabilities of Atlas in Section 3.

2.1. Bayesian optimization

Optimization problems involve identifying parameters, x, that produce the most desirable outcome for an objective function, f(x). For a minimization problem, the solution is the set of parameters that minimizes f(x),where is the parameter space, i.e. a structured input domain that can be explored during optimization. In a BO setting, the objective function is considered to be a black-box function, meaning its structure is a priori unknown, and can only be sequentially resolved by empirical measurement. Black-box functions also do not provide access to gradient information, and measurements are typically expected to be corrupted by noise.

Measurements are collected sequentially, either in batches or one-by-one. After collection of a measurement y corresponding to the parameter x, the surrogate model is trained on the dataset of all available observations, 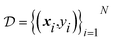. An acquisition function is then computed based on the surrogate model. The maximum of this function defines the set of parameters expected to provide maximal utility, and corresponds to the parameter recommended for subsequent measurement. Typically, this iterative procedure is repeated until a pre-defined stopping criterion, such as the exhaustion of an experimental budget, is met. Algorithm 1 shows pseudocode for a BO loop, and Fig. 2 visualizes the procedure. The first set of parameters is often not recommended by BO, but are rather produced by random sampling, a low-discrepancy sequence, or an experimental design strategy. This is known as the initial design phase.

Fig. 2 Conceptual figure showing Bayesian optimization of a 1d function. In this example, the surrogate model is a GP with a Matérn 5/2 kernel, and the acquisition function is the expected improvement criterion.

2.1.1. Acquisition functions. The surrogate model is constructed to approximate the objective function f(x) and can be queried for mean and uncertainty estimates of the objective across the parameter space. Acquisition functions, α(x), are used to guide the selection of parameter recommendations using the surrogate model's prediction. Specifically, maximization of α(x) reveals the parameters x_next for subsequent measurement.

Several acquisition functions are available for use in Atlas, including the upper and lower confidence bound, expected improvement, probability of improvement, variance-based sampling, and greedy sampling. Our library also features several specialty acquisition functions for more advanced BO concepts, including general parameter optimization (Section 3.5), multi-fidelity optimization (Section 3.6), and meta-learning enhanced optimization (Section 3.7).

2.1.2. Acquisition function optimization. A crucial subroutine in BO is the optimization of the acquisition function. Several factors influence the aptitude of optimization strategies for this task, including the types of parameters making up the parameter space and its volume. Atlas provides 3 distinct acquisition function optimization strategies that are each suited for specific problem types: (i) a constrained gradient optimizer based on SLSQP^59,84 or Adam,⁸⁵ (ii) a constrained genetic algorithm (GA) optimizer based on the PyMOOlibrary,⁸⁶ and (iii) a constrained GA based on the DEAPlibrary.^87,88 Gradient strategies are well-suited for problems with fully-continuous parameter spaces, while GA strategies are well-suited for mixed-parameter problems and fully discrete/categorical problems with large Cartesian product spaces.

2.2. Gaussian processes

A crucial component of the BO framework is the surrogate model, an ML model which produces an estimate of the true objective function given a dataset of observations. Many ML models have been used as BO surrogates, including Bayesian neural networks, tree-based models, and kernel smoothing, but the most prevelant and well-studied choice is the Gaussian process (GP).⁸⁹ GPs are non-parametric probabilistic ML models. They are a collection of random variables such that the joint distribution of each finite set of variables is a multivariate normal. GPs are characterized by a mean, m(x), and covariance function, k(x, x′), and are written as

For experiment planning applications, inputs x are vectors of parameters of the experiment. Conveniently, the mean and variance of a GP can be written in closed form. For query parameters, x̂(i.e. those which do not yet have an associated measurement), the GP returns a predictive mean [small mu, Greek, circumflex] and variance [small sigma, Greek, circumflex]².

2.2.1. Kernel functions. The choice of covariance or kernel function k(x, x′) is an crucial inductive bias for a GP model, and should be selected according to the characteristics of the objective function being modelled. A popular choice for continuous input domains is the Matérn kernel,where d(·,·) is the Euclidian distance, K_ν(·) is a modified Bessel function, and Γ(·) is the Gamma function. The Matérn kernel also has an additional parameter, ν, which controls the smoothness of the resulting function (fixed at 5/2 in Atlas), and is a lengthscale hyperparameter. Atlas uses a Matérn 5/2 kernel for continuous and numerical discrete input domains, but also supports categorical, mixed continuous/discrete-categorical, and molecular input domains. For categorical spaces in which inputs are one-hot-encoded, we use a kernel function based on Hamming distances,where d_Hamming(x,x′) = 0 if x = x′ and = 1 if x ≠ x′. Automatic relevance determination (ARD)⁹⁰ is used for this kernel for all input dimensions. For mixed continuous/discrete-categorical spaces, we use a mixed kernel comprising Matérn 5/2 and Hamming parts,where x_cont and x_cat are the continuous/discrete and categorical portions of the input vector, respectively. The reader is referred to Section 3.8 for discussion of the kernel used for molecular input domains.

2.2.2. Gaussian process training. Fitting a GP to a dataset of observations involes choosing hyperparameters of the kernel function (collectively referred to as θ) and the likelihood noise σ_y². Hyperparameters are chosen by minimizing the negative log marginal likelihood,y ∈ [Doublestruck R]ⁿ is a vector of n objective measurements, X ∈ [Doublestruck R]^n×d is the design matrix of n d-dimensional input vectors. K_θ(X,X) is a kernel matrix such that each entry [K_θ]_i,j = k(x_i,x_j). σ_y²I is the variance of Gaussian noise on the measurements y. Note that the first term encourages the model's fit to the training data, while the second penalizes overly complex models.⁹¹ This inherent regularization is attractive for modelling in a low-data setting, such as the initial stages of a sequential model-based optimization campaign.

2.2.3. Variational Gaussian process classifier. Atlas uses a GP-based binary classifier to learn the feasible-infeasible boundaries in parameter space for optimization problems with unknown constraints. This capability is explained in detail in Section 3.2. Here, we provide details of the GP classifier itself.

For feasibility classification using a GP, exact inference is intractable. Thus, Atlas approximates the classification posterior using variational inference. Assume a dataset of n binary constraint function c(x) measurements, , where ỹ ∈ {0,1} (0 for feasible measurements and 1 for infeasible measurements). For brevity, we denote the n feasibility measurements as ỹ= {ỹ_i}_i=1ⁿ and the design matrix as X = {x_i}_i=1n. GP classification squashes the latent GP output f through a sigmoidal inverse-link function, and a Bernoulli likelihood function conditions the function values. The joint distribution of the feasibility measurements and the latent values is

where is the Bernoulli distribution, and is the usual prior for the values of the GP.

Atlas' classifier adopts an inducing point approach, in which the latent variables are augmented with additional inducing points. Our strategy follows closely to the one detailed in Hensman et al.,⁹² where a bound on the marginal likelihood for classification problems in derived. This bound is optimized by adjusting the hyperparameters of the GP kernel, parameters of the multivariate normal variational distribution, and the inducing inputs/points simultaneously using stochastic gradient descent. The classification approach is implemented using the GpyTorch library,⁹³ and has the added benefit of scaling more favourably with than does exact GP inference.

3. Atlas library overview

Atlas users interact with the package via a high-level “ask-tell” interface, in which a instance is iteratively queried for parameters, some physical or computational measurement is completed, and the parameter-measurement pairs are added to a Olympus instance. Olympus^80,81 is a complementary experiment-planning framework developed by our research group that provides an interface to Atlas. For example, Olympus implements an abstraction for a generic experiment planning strategy, from which all Atlas strategies inherit. Also, the Olympus object is used for storing optimization trajectories and meta-information. Olympus also provides definitions of parameter types and spaces, and achievement scalarizing functions for multi-objective optimization, all of which are used by Atlas.

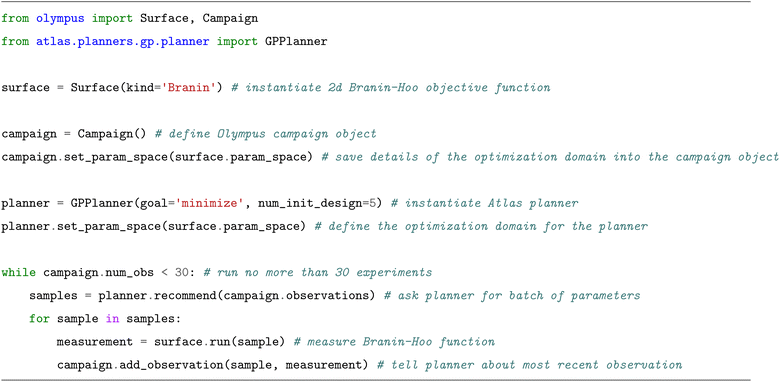
To demonstrate the usage of our software, we present a minimal code example in which the (aussian rocess ) from Atlas is used to minimize the Branin-Hoo surface,⁹⁴. “Ask-tell” experimentation proceeds iteratively by generating parameters to be measured using the planner's method, and informing the Olympus 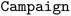instance about the corresponding measurement using its 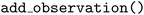method. We opt to use a flexible “ask-tell” interface to remain application-agnostic, as well as allow for analysis and customization of the optimization loops. Measurement steps usually involve calls to specialized robotic laboratory equipment or computational simulation packages, which can be fully customized by the user. Fig. 3 visualizes the results of this simple example. The argument to the constructor defines the number of parameters to recommend in the initial design phase. This value defaults to 5 and will not be listed as an argument in subsequent examples for brevity.

Fig. 3 Visualization of the minimal code optimization of the 2d Branin-Hoo surface using Atlas. The left-most subplot shows a contour plot of the Branin-Hoo surface with its triply-degenerate global minimum highlighted with pink stars. The center subplot shows the location of the parameters recommended by Atlas as gray crosses. The right-most subplot shows the optimization regret trace.

Atlas supports parameter spaces consisting of continuous, discrete, and categorical parameters, and arbitrary combinations thereof, in sequential or batched optimization mode. The definition of vector-valued descriptors for categorical parameter options is also supported.⁷⁹ BO strategies in Atlas primarily use GP surrogate models,⁸⁹ and use the low-level infrastructure of the PyTorch,⁹⁵ GpyTorch⁹³ and BoTorch⁵⁹ libraries. In the following section, the main capabilities of Atlas (Fig. 1) are explained. For more information on each concept, please visit the Atlas GitHub,⁹⁶ documentation, and tutorial notebook. Importantly, Atlas allows users to combine its key capabilities to suit their specialized needs. Barring a few incompatibilities (described in detail in our documentation), capabilities can be combined and interchanged freely. For example, the a priori known and unknown constraints can be used for any parameter space, with any acquisition function, acquisition optimizer, and any planner. Multi-objective optimization via ASFs, robust optimization, and asynchronous optimization can also be used in this way.

3.1. A priori known constraints

Using a simple interface, users can specify arbitrary known constraint functions on the parameter space, which results in portions of the space being omitted from consideration by planners.⁶⁵ This would increase the efficiency of the optimization, as the model would not make any suggestions that are known to be infeasible, avoiding costly experimental evaluations. We also supply convenient ways to specify commonly occurring known constraint types, including compositional (simplex),⁶⁶ permutation (ordering),⁶⁶ pending experiments, or process-constrained batches.⁹⁷

The following code snippet shows the instantiation of the with a user-defined constraint function for the surface, . Constraint functions are Python callables which return a boolean value, 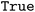for feasible (infeasible) parameters, and are passed to the constructor of as a list using the argument.

Next, we show an example of a special known constraint case built into Atlas: compositional or simplex constraints. This constraint type is useful when parameters (or a subset thereof) must lie on a standard n-simplex, i.e.. Such constraints are commonly encountered in SDL applications.⁶⁶

To demonstrate this constraint type, we use the dataset from Olympus, which reports high-throughput screens for oxygen evolution reaction (OER) activity by systematically exploring high-dimensional chemical spaces.^98,99 The dataset is a discrete library of 2121 catalysts, comprising all unary, binary, ternary and quaternary compositions from unique 6 element sets at 10% intervals. The composition system of the dataset is Mn–Fe–Co–Ni–La–Ce. Olympus emulates the discrete dataset with a Bayesian neural network (BNN) to produce noisy virtual measurements.¹⁰⁰ Fractional compositions must lie on the standard 6-simplex . The following code snippet shows instantiation of the for this problem. The 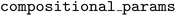argument takes a list of integers representing the parameter space indices to be treated with the compositional constraint. In this case, all 6 parameters are subject to the constraint.

Lastly, we show an example using the pending experiment known constraint type. The interpretation of this constraint is simple: parameters that have been assigned to measurement, but for which the experiments have not been completed yet, must be avoided by the planner to avoid duplicate recommendation. Note that duplicate parameters are still permitted, as long as the other axes of the recommendation parameter space are varied. Atlas provides a simple method for all planners to set pending experiments. The planner's method can be called at any time within an optimization campaign to inform the planner about parameter settings to be avoided. This method takes as an argument , which is a list of Olympus 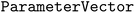objects. Each subsequent call overwrites the pending parameters from the last iteration. To remove all the pending experiments, one can use the planner's method.

3.2. A priori unknown constraints

The inclusion of (not a number) objective values is supported, which could occur due to attempted but failed experimental measurements. Several strategies are provided which learn the unknown constraint function on the fly, using a GP-based binary feasibility classifier (explained in detail in Section 2.2.3). These predictions are used in conjunction with the typical regression surrogate model to parameterize feasibility-aware acquisition functions, α_c(x). All acquisition function types in Atlas have a feasibility-aware analogue.

We provide an example optimization of the Branin-Hoo surface with an a priori unknown constraint function c(x), visualized by the shaded region in Fig. 4. The example uses the feasibility-interpolated acquisition strategy with the UCB acquisition function. Two additional arguments to the constructor are required for optimization with unknown constraints. 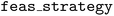indicates the feasibility-aware acquisition type, and the 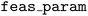argument indicates the associated parameter. The strategies interpolate between the vanilla acquisition function α(x) and the conditional output of the feasibility classifier, P(feasible|x) using the following expression:

α_c(x) = (1 − c^t) × α(x) + c^t × P(feasible|x) (9)

c is the ratio of infeasible measurements to total measurements, and t ∈ [Doublestruck R]₊ is a parameter (specified with the argument) which controls risk when it comes to selecting infeasible parameters. Here, smaller values of t de-emphasize the feasibility classifier's contribution (second term in eqn (9)) and thus indicate more risk, while larger values do the opposite and represent less risk.

Fig. 4 Visualization of an a priori unknown constraint optimization benchmark on the 2d Branin-Hoo surface using Atlas. The left-most subplot shows a contour plot of the Branin-Hoo surface with its triply-degenerate global minimum highlighted with pink stars, and the constrained regions shaded. The plot also shows the locations of the (in)feasible parameters recommended by Atlas as (white)gray crosses (recommended using the strategy). The center subplot shows regret traces for each strategy averaged over 100 independent executions. The right-most subplot shows distributions of percentages of infeasible measurements (i.e. objective values) produced by each strategy during a run.

Fig. 4 shows the results of a larger benchmark of feasibility-aware acquisition strategies in Atlas on the 2d constrained Branin-Hoo surface. The legend of the center subplot lists the unknown constraint strategies and associated parameters available for use in Atlas. We omit a full discussion and benchmark of these strategies, as they will be thoroughly detailed in an upcoming manuscript. Briefly, the strategy is a simple baseline approach which does not use the feasibility classifier. Instead, the objective value of infeasible measurements is replaced by the current worst feasible measurement in .⁷¹ Although this strategy is effective for avoiding infeasible measurements (lowest % infeasible measurements in right-most subplot), optimization performance is sacrificed, especially when the optimum of the problem is located close to an infeasible region. is among the top performers for this example.

3.3. Multi-objective optimization

Atlas supports multi-objective optimization for all planners by using achievement scalarizing functions (ASFs) defined in Olympus. Multi-objective problems feature an objective space corresponding to a set of n > 1 objective functions 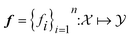to be optimized concurrently. ASF transforms a vector of objective measurements to a scalar merit value, which is processed by the optimizer. Available ASF types are Chimera,¹⁰¹ Hypervolume,^102–105 Chebyshev,^106,107 and Weighted Sum.^108,109

As an illustrative example of multi-objective optimization in Atlas, we use the dataset from Olympus, which reports computed photophysical properties for 3458 organic molecules synthesized from three groups of molecular building blocks – A, B, and C (resulting in A–B–C–B–A pentamers shown in Fig. 5a).¹¹⁰ Each molecule was subjected to a computational protocol consisting of cheminformatic, semi-empirical and ab initio quantum chemical steps to compute absorption and emission spectra, as well as fluorescence rates. The objectives for this dataset are (i) the peak score, a dimensionless quantity given by the fraction of the fluorescence power spectral density that falls within the 400–460 nm region (to be maximized), (ii) the spectral overlap of the absorption and emission spectra (to be minimized), and (iii) the fluorescence rate (to be maximized).

Fig. 5 (a) Reaction scheme of iterative Suzuki–Miyaura cross-coupling reaction proposed to synthesize symmetric A–B–C–B–A pentamers in the dataset. (b) Individual objective traces corresponding to the experiment with the best hypervolume value as a function of the number of transpired experiments. Solid lines represent the mean objective values averaged over 50 independent runs and shaded regions represent the 95% confidence interval.

The Hypervolume ASF is used for this example. One must include additional arguments to the 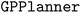constructor, namely, a boolean value for , the name of the ASF for , the objective space as an Olympus object, and a list of representing the individual optimization goals for each objective (either or ). For parameter spaces with categorical parameters, note that we can toggle between using a descriptor representation for the options and one-hot encodings using the argument.

Fig. 5b shows the results of a larger scale benchmark experiment where the performance of the is compared to a random search on the 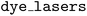dataset. Each subplot shows traces of the objective values associated with the measurement assigned the best hypervolume as a function of the number of evaluations. While the peak score and fluorescence rate traces are comparable between strategies, the is able to identify candidate molecules with lower spectral overlap between absorption and emission spectra (a proxy for reduced losses from self-absorption of emitted light) significantly quicker than random sampling. This indicates better multi-objective optimization performance.

3.4. Robust optimization

For all planners and parameter types, we have integrated the Golem algorithm,⁶³ which allows users to identify optimal solutions that are robust to input parameter uncertainty. This helps ensure reproducible performance of optimized experimental protocols and processes.

In order to demonstrate how Golem is integrated into Atlas, we reproduce the setup of the noisy high-performance liquid chromatography (HPLC) protocol optimization experiment from the original publication.⁶³ In this application, an HPLC protocol is calibrated by adjusting 6 process parameters with the goal of maximizing the amount of drawn sample reaching the detector (referred to as the peak area). It is assumed that input parameters P1 (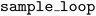) and P3 are subject to significant noise, and that the other four parameters are noiseless. Normally distributed noise truncated at zero is used for both parameters, with standard deviations of 0.008 mL and 0.08 mL for P1 and P3, respectively. The HPLC response is emulated within the Olympus package using BNNs ( dataset).

The problem setup for this example is shown in the following code snippet. For all planners, the constructor argument is available, which expects a dictionary whose keys are parameter names for which the user would like to specify an input uncertainty distribution. The corresponding values are themselves dictionaries, for which the user must specify the distribution type and its associated parameters. Golem ships with a diverse set of distribution types, which are detailed in its documentation. For all parameters not itemized within the argument, Atlas automatically assigns them a distribution, meaning no uncertainty/noiseless.

3.5. Optimization for generalizable parameters

Atlas includes a strategy based on BO and variance-based active learning¹¹¹ to identify sets of parameters from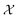 that result in average-best performance over a set of variables S = {s_i}_i=1^N. Instead of optimizing objective function f(x), the objective 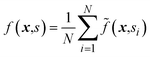is targeted. Our strategy is inspired by the approach reported by Angello et al.,¹¹² which was used to design chemical reaction conditions resulting in high yields across a range of substrates. Importantly, this approach alleviates one from having to measure the full objective function for each recommended set of parameters, which can become costly when the number of general parameter options are large.

As an illustrative example, we consider the - datasets from Olympus, which report the yield and catalyst turnover number for flow-based Suzuki–Miyaura coupling reactions with varying substrates shown in Fig. 6a and b.¹¹³ There are three continuous parameters (temperature, residence time, and catalyst loading) and one categorical parameter (Pd catalyst ligand). The objective is to simultaneously maximize both the yield and catalyst turnover number across all four substrates with the general parameter optimization strategy. Since this is also a multi-objective optimization problem, we use the Hypervolume ASF.

Fig. 6 (a) Scheme for the Suzuki–Miyaura cross-coupling of two heterocycles in the presence of 1,8-diazabicyclo[5.4.0]undec-7-ene (DBU) and THF/water. (b) Structure of the substrates in each of the four Suzuki–Miyaura reaction cases, corresponding to the datasets and general parameter. (c) Results of the comparative optimization experiment. Boxplots show the normalized average hypervolume across the four reactions for solutions from 50 independent runs (larger hypervolume is better). The experimental budget for these runs was 30 measurements.

The following code snippet describes the setup for this example. We add an additional categorical parameter named , which comprises the general parameter options (in our case these are the different possible substrates for the Suzuki–Miyaura reaction encoded as Roman numerals). For general parameter problems, the argument of the planner must be set to . Similar to the known constraints problems outlined in Section 3.1, the constructor takes an argument called , which must be a list of integers representing the parameter space indices of those parameters to be treated as general parameters. In our case, only the first parameter, , is a general parameter.

Fig. 6c shows the results of a larger scale benchmark experiment on this problem. We compare the performance of the general parameter optimization strategy in Atlas to a strategy in which, for each set of recommended parameters, we measure the full objective, i.e.. Effectively, the latter strategy must make 4 objective measurements for each set of recommended parameters, while the general parameter strategy must only make 1. The box plots in Fig. 6c show the hypervolume of solutions identified by each strategy averaged over the 4 reaction types. On average, the general parameter strategy produces larger hypervolumes, indicating superior multi-objective optimization performance.

3.6. Multi-fidelity optimization

Multi-fidelity BO targets problems where two or more “information sources” are available to the researcher. Typically, the information sources generate measurements of the same property at different levels of fidelity, precision, or accuracy, and are available at varying cost. For instance, a chemical property could be estimated using a crude but inexpensive simulation (low-fidelity) as a proxy for an accurate but expensive experimental determination (high-fidelity). Multi-fidelity strategies are quickly becoming a popular approach for resource-intensive problems in chemistry and materials science.^114–120 Atlas provides a based on the trace-aware knowledge gradient^121,122 and augmented-EI (aEI) acquisition functions¹²³ which allows for the inclusion of an arbitrary number of information sources with discrete fidelity levels.

To illustrate multi-fidelity BO with Atlas, we use a dataset of simulated band gaps for 192 hybrid organic–inorganic perovskite (HOIP) materials reported by Kim et al.¹²⁴ HOIP candidates are designed from a set of 4 halide anions, 3 group-IV cations and 16 organic anions. Electronic and geometric descriptors of the HOIP components are available through Olympus. Two density functional theory (DFT) information sources are available for all 192 HOIP candidates.

• Low-fidelity: band gaps computed using the generalized gradient approximation (GGA), E^GGA_g.¹²⁵

• High-fidelity: band gaps computed using the Heyd–Scuseria–Ernzerhof (HSE06) exchange-correlation functional, E^HSE06_g.^126,127

The GGA level of theory is computationally feasible for these systems but is known to underestimate E_g by 30%.¹²⁵ The HSE06 level of theory is expected to be on par with experimentally determined band gaps but is computationally restrictive. We omit a detailed comparison of the computational methods and estimate the HSE06 level of theory to be an order of magnitude more expensive than the GGA level.

The following code snippet sets up this multi-fidelity optimization problem using Atlas' 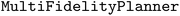. We've defined helper functions to measure the objective at each fidelity level ( table provided on GitHub repo), and a function to compute the cumulative experimental cost. The 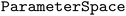is constructed with an additional fidelity parameter, , which is a instance with options corresponding to the expense of low-fidelity information sources relative to the high- or target fidelity source organized in increasing order. By convention, Atlas expects the target fidelity to have a value of 1.0, while the lower fidelity levels have values 0.0 < s < 1.0. Here, the choice of 0.1 for the E^GGA_g determinations reflects our estimate that GGA is an order of magnitude cheaper than HSE06. The constructor of the must receive one additional argument, 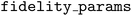, which is the parameter space index of the fidelity parameter .

Note that for this example, we define the BO stopping criterion to be a cumulative experimental cost budget rather than the number of transpired objective evaluations. By default, the automatically determines which fidelity level to measure the objective at each iteration. However, an SDL researcher may want to further customize their multi-fidelity optimization campaign such that, for example, they can alternate between batches of low- and high-fidelity measurements. Atlas enables such customized campaigns by allowing the user to specify the fidelity level they wish for the parameters to be measured for the upcoming batch of recommendations. One may set the 's attribute by calling the method and specifying the desired level. Atlas employs constrained acquisition function optimization to deliver the desired parameter recommendations. The following code snippet revisits the HOIP example and assumes the researcher desires to alternate between low- and high-fidelity measurements.

Fig. 7 shows the results of a larger-scale benchmark comparison between Atlas' and on the perovskites problem. Boxplots show the cumulative simulation cost taken to identify the perovskite with the lowest HSE06 bandgap, E^HSE06_g in the dataset over 100 independently seeded runs for each strategy. The also has access to bandgap measurements at the GGA level (with an E^GGA_g to E^HSE06_g measurement ratio of 8 : 1), while the has access to E^HSE06_g measurements only. The ratio of low-to high-fidelity measurements is set to 8 : 1 for the , i.e., the planner is provided with 8 low-fidelity measurements followed by 1 high-fidelity measurement. We note that this is completely user-controlled, and can be changed per iteration using the 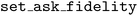method. On average, the achieves the lowest high-fidelity bandgap with a cost of 13.9 ± 0.56 a.u., while the achives this with a cost of only 9.6 ± 0.35 a.u. These results demonstrate the ability of multi-fidelity BO strategies to leverage inexpensive measurements to augment cost-effective optimization of resource-intensive objectives in SDLs.

Fig. 7 Results of multi-fidelity optimization benchmark using the HOIP dataset from Kim et al.¹²⁴ Boxplots show the cumulative simulation cost incurred before identification of the perovskite material with the smallest HSE06 bandgap in the dataset. Each strategy is run 100 independent times. The also has access to bandgap measurements at the GGA level (with an E^GGA_g to E^HSE06_g measurement ratio of 8 : 1), while the has access to E^HSE06_g measurements only.

3.7. Meta-/few-shot learning enhanced optimization

With Atlas, users may easily incorporate data from historical optimization campaigns. These source tasks can be leveraged to accelerate the optimization rate on a novel campaign by using one of two meta-/few-shot learning planners: the Ranking-Weighted Gaussian Process Ensemble planner (ref. 128 and 129) and the Deep Kernel Transfer planner .^130,131 Importantly, these strategies can each transcend the innate design restrictions of typical BO by inferring an inductive bias implicitly from data. In SDLs, this amounts to learning inductive biases that closely resemble particular concepts in chemistry or materials science, and then applying them to related optimization problems. Such approaches have been used to optimize chemical reactions in SDL applications.^132,133

We use the datasets from Olympus to showcase the aptitude of meta-/few-shot learning planners to accelerate optimization given historical optimization campaign data. The datasets comprise 5 datasets which each report the yield of Pd-catalyzed Buchwald–Hartwig amination reactions of aryl halides (3 options) with 4-methylaniline in the presence of varying isoxazole additives (22 options), Pd catalyst ligands (4 options), and bases (3 options).¹³⁴ Each dataset consists of 792 yield measurements. The reaction scheme is shown in Fig. 8a. We compare the ability of the to maximize reaction yield on a particular target dataset after meta-training on yield measurements from the other 4 datasets. 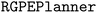For instance, if the target dataset is , the has access to measurements from the 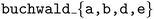datasets. As a baseline, we optimize each target reaction using Atlas' , which has no access to historical reaction data.

Fig. 8 (a) Reaction scheme for the Buchwald–Hartwig datasets. (b) Optimization traces comparing the performance of Atlas' and on 3 target reaction datasets. Solid traces show the mean taken over 50 independently seeded runs. Shaded regions show the 95% confidence interval. Horizontal dotted lines indicate the maximum possible yield reported by Ahneman et al.¹³⁴ for each reaction product.

The following code snippet shows the problem setup. The 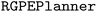or takes an argument called , which must be a list of dictionaries containing the source task data ( are provided for this example in the GitHub repo).

Fig. 8b shows the results of this comparative experiment for 3 target reaction products: 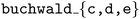. In each case, the is able to identify higher yields with fewer objective evaluations compared to the by using intuition gleaned from meta-training on related reaction data.

3.8. Optimization over molecular domains

For optimization over molecular spaces, we provide a specialized GP kernel function that is compatible with all planners and is based on the Tanimoto distance kernel.^82,93 The Tanimoto kernel is a general similarity metric^135,136 defined for binary vectors x, x′ ∈ {0,1}^d for d ≥ 1 aswhere 〈·,·〉 is the Euclidean inner product, ‖·‖ is the Euclidean norm, and σ_f² is the kernel's signal variance hyperparameter. Several binary vector representations of molecules are available, but perhaps the most well known are extended-connectivity fingerprints (ECFPs).¹³⁷

Atlas allows for use of any molecular representation based on binary vectors. Users must only specify, to the constructor of the planner, the indices that identify molecular parameters with the parameter space using the argument. Molecular parameters must be of type categorical, with options corresponding to unique molecules. Users may then define their descriptors as the corresponding binary vectors. We show a simple example in which we intend to minimize the aqueous solubility of molecules in the ESOL dataset.¹³⁸

While it has been shown that using physicochemical descriptor-based representations of molecules in a BO setting can accelerate optimization rate,^79,139 other studies have found that expert-crafted descriptors did not out-perform simpler representations like fingerprints or even one-hot-encodings.¹⁴⁰ Given the apparent dependence of optimal molecular representation on the characteristics of the optimization problem at hand, Atlas provides users with the flexibility to represent molecular parameters in several ways: either with binary vectors or continuous vectors containing properties extracted from other methods, such as DFT or experimental data.

3.9. Asynchronous experimental execution

In many SDL applications, researchers have access to multiple robotic or computational workers and may parallelize measurements. When performing batched BO in a setting where there is variability in measurement times for each individual experiment, it is important to operate an SDL asynchronously, where a worker starts a new experiment immediately after completion of the previous experiment.¹⁴¹ This approach has been shown to be overall more efficient than waiting for an entire batch of experiments to complete before commencing the next batch.^73,74

We provide template scripts for an asynchronous SDL setup on our GitHub repo. In this example, we optimize a surface from Olympus using 3 workers, each of which can perform a measurement for a single set of parameters. Workers can be assigned parameters to measure in parallel using multiprocessing, and measurement duration is set to be variable. Upon receiving a measurement, Atlas re-trains its surrogate model, but also conditions its recommendations on pending experiments, i.e. those that have been assigned to a worker but whose measurement has not completed (the reader is referred to Section 3.1 for additional information on setting pending parameter constraints in Atlas). This is achieved with a built-in mechanism to generate fictitious measurements, y′ for pending parameters, x′. Specifically, we adopt the hallucination or kriging believer strategy first reported by Ginsbourger et al.,^73,74 which imputes the expected value of each pending parameter,

where is the current dataset of observations. The fictitious measurement y′ is then used to augment the dataset of observations, i.e.. Unlike other strategies that merely block recommendations based on pending experiments, hallucinations incorporate this information by updating the model's variance while keeping the mean constant. Atlas maintains a “priority queue” of recommended parameters that is immediately updated in light of new measurements, such that parameter proposals are always informed by the most recent observations. Proposals in the priority queue are then delegated to measurement workers as they become available.

4. Experimental demonstration

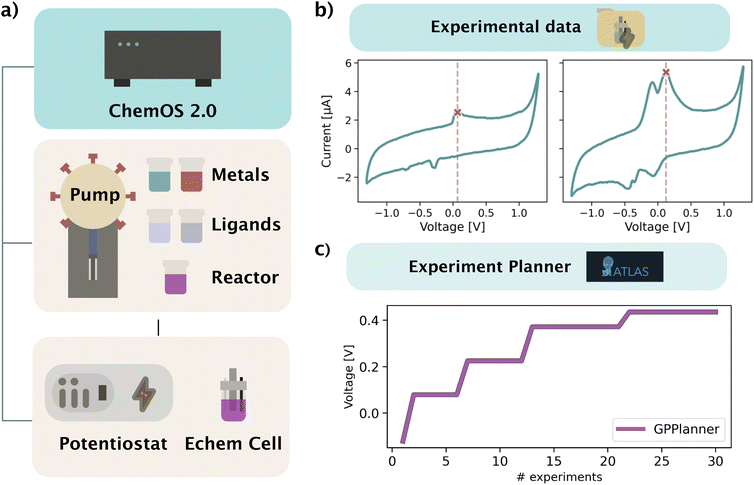
In this section, we outline an experimental demonstration highlighting the use of Atlas in a simple SDL. Specifically, we show how Atlas is combined with ChemOS 2.0,⁸³ an SDL orchestration software, to optimize the oxidation potential of a set of metal complexes in a cyclic voltammetry (CV) experiment. Fig. 9a depicts the experimental setup. The electrochemical SDL consists of two hardware parts: the automatic complexation robot module and the E-chem analyzer module, both of which are controlled remotely from ChemOS 2.0. ChemOS 2.0 hosts Atlas, and iteratively sends jobs to the E-chem setup for each evaluation step of the optimization campaign. In turn, it receives the raw data and the treated oxidation potential from the instrument after execution of the CV experiment. ChemOS 2.0 saves the raw CV data in its internal experimental database and also saves the results of the optimization campaign. Data for the experiment reported in this work has all been stored on ChemOS 2.0.

Fig. 9 (a) Schematic diagram of automated electrochemical SDL setup. (b) Two examples of cyclic voltammograms measured during the campaign. The oxidation peak is identified using in-house software and is marked with a red cross and vertical dotted line. (c) Optimization trace showing the maximum oxidation peak voltage identified by Atlas' as a function of the number of completed experiments.

The automatic complexation robot is a flow-based system based on a syringe pump and selection valves driven by a Python controller developed in-house. Upon receiving instructions, it runs automatic complexation by transferring designated amounts of stock solutions (metal, ligand, electrolyte, buffer and water) to the reactor, conducts a reactor mixing step, transfers the sample to the flow cell of the E-chem module, and invokes the electrochemistry measurements. A standard clean-up step is executed after the electrochemistry is finished. The E-chem analyzer consists of a flow cell equipped with a printed electrode and a low-cost potentiostat controlled by Python software. The electrochemistry measurement is invoked by ChemOS 2.0 to measure the sample in the flow cell. In the context of this demonstration, a fixed parameter CV experiment is conducted for all samples. The raw data collected from the potentiostat is streamed to ChemOS 2.0 for further processing, and cleaning instructions are sent to the complexation robot.

The parameter space for this experiment consists of 4 parameters, which are summarized in Table 1. The ligand options are H₂O, pyridine, and ethylenediamine. The metal options are silver(I) and copper(II). The objective of the optimization is to maximize the voltage of the oxidation peak. The of Atlas is run for 40 iterations, the first 5 of which are randomly selected initial design points. Results of the optimization experiment are shown in Fig. 9b and c. Fig. 9b shows two cyclic voltammograms collected during the optimization. The voltage peak is selected using in-house software and is identified on the figure with a red cross and red vertical dotted line. Fig. 9c shows the maximum voltage peak identified by the as a function of the number of transpired experiments.

Table 1 Parameter space for the electrochemical SDL demonstration with Atlas

Parameter	Type	Range/num options	Description	Descriptors
a Discrete parameter has a stride of 1.
Ligand	Categorical	3	Ligand identity	No
Metal	Categorical	2	Metal identity	No
# Mixings	Discrete	[1–10]^a	Number of pump mixing steps	N/A
Ratio	Continuous	[1.0–9.0]	Ligand/metal ratio	N/A

---

5. Conclusion

In summary, we introduce Atlas, a Bayesian optimization package with a comprehensive set of features designed to suit most experimental settings and enable model-guided optimization in SDLs. Among the capabilities currently available are optimizations over mixed-parameter, constrained, and molecular domains, in addition to supporting multi-objective and multi-fidelity optimizations, as well as robust optimization and the incorporation of past knowledge via meta-learning. Atlas uses Gaussian process surrogate models, and is built upon PyTorch,⁹⁵ GpyTorch,⁹³ and BoTorch.⁵⁹ It exposes its broad set of capabilities via the Olympus⁸⁰ interface, and it integrates with ChemOS 2.0 (ref. 83) for SDL deployment. Atlas is an open-source software, it is distributed under the MIT permissive license, and comes with a documentation that includes examples for all case scenarios discussed in this manuscript. We expect Atlas to be able to cover a much broader set of SDL setups and research challenges than the Bayesian optimization packages developed to date.

Data availability

Atlas is available on GitHub at https://github.com/aspuru-guzik-group/atlas under an MIT license. The measurements generated in the electrochemical SDL demonstration have been added to the Olympus package as an emulated called , on which users may benchmark experiment planning strategies (https://github.com/aspuru-guzik-group/olympus/tree/dev/src/olympus/datasets/dataset_electrochem) ChemOS 2.0 is available on GitHub at https://github.com/malcolmsimgithub/ChemOS2.0 under an MIT license.

Conflicts of interest

A. A.-G. is a founding member of Kebotix, Inc. R. J. H., Z. B., P. B., C. A. and A. A.-G. are founding members of Intrepid Labs, 15073383 Canada Inc.

Acknowledgements

The authors thank Dr Felix Strieth-Kalthoff, Dr Martin Seifrid, Dr Shengyang Sun, Dr Roger Grosse, Dr Robert Black, Guodong Zhang, and Erfan Fathei for contribution to valuable discussion. R. J. H. gratefully acknowledges the Natural Sciences and Engineering Research Council of Canada (NSERC) for provision of the Postgraduate Scholarships-Doctoral Program (PGSD3-534584-2019), as well as support from the Vector Institute. G. T. is supported by NSERC and the Vector Institute. C. A. acknowledges an NSERC Discovery grant (RGPIN-2022-04910). A. A.-G. acknowledges support from the Canada 150 Research Chairs program and CIFAR, as well as the generous support of Dr Anders G. Frøseth. This research was undertaken thanks in part to funding provided to the University of Toronto's Acceleration Consortium from the Canada First Research Excellence Fund (CFREF). Computations reported in this work were performed on the computing clusters of the Vector Institute and on the Niagara supercomputer at the SciNet HPC Consortium.^142,143 Resources used in preparing this research were provided, in part, by the Province of Ontario, the Government of Canada through CIFAR, and companies sponsoring the Vector Institute. SciNet is funded by the Canada Foundation for Innovation, the Government of Ontario, Ontario Research Fund – Research Excellence, and by the University of Toronto.

References

1. F. Häse, L. M. Roch and A. Aspuru-Guzik, Next-Generation Experimentation with Self-Driving Laboratories, Trends Chem., 2019, 1(3), 282–291.
2. E. Stach, B. DeCost, A. G. Kusne, J. Hattrick-Simpers, K. A. Brown and K. G. Reyes, et al., Autonomous experimentation systems for materials development: A community perspective, Matter, 2021, 4(9), 2702–2726 . https://www.sciencedirect.com/science/article/pii/S2590238521003064.
3. C. W. Coley, N. S. Eyke and K. F. Jensen, Autonomous Discovery in the Chemical Sciences Part I: Progress, Angew. Chem., Int. Ed., 2020, 59(51), 22858–22893.
4. C. W. Coley, N. S. Eyke and K. F. Jensen, Autonomous Discovery in the Chemical Sciences Part II: Outlook, Angew. Chem., Int. Ed., 2020, 59(52), 23414–23436.
5. M. M. Flores-Leonar, L. M. Mejía-Mendoza, A. Aguilar-Granda, B. Sanchez-Lengeling, H. Tribukait and C. Amador-Bedolla, et al., Materials Acceleration Platforms: On the way to autonomous experimentation, Curr. Opin. Green Sustainable Chem., 2020, 25, 100370.
6. H. S. Stein and J. M. Gregoire, Progress and prospects for accelerating materials science with automated and autonomous workflows, Chem. Sci., 2019, 10(42), 9640–9649.
7. J. Yano, K. J. Gaffney, J. Gregoire, L. Hung, A. Ourmazd and J. Schrier, et al., The case for data science in experimental chemistry: examples and recommendations, Nat. Rev. Chem., 2022, 6, 357–370 . https://www.nature.com/articles/s41570-022-00382-w.
8. G. Tom, S. P. Schmid, S. G. Baird, Y. Cao, K. Darvish and H. Hao, et al., Self-driving laboratories for chemistry and materials science, Chem. Rev., 2024, 124(16), 9633–9732.
9. J. P. McMullen and K. F. Jensen, An automated microfluidic system for online optimization in chemical synthesis, Org. Process Res. Dev., 2010, 14(5), 1169–1176.
10. D. E. Fitzpatrick, C. Battilocchio and S. V. Ley, A novel internet-based reaction monitoring, control and autonomous self-optimization platform for chemical synthesis, Org. Process Res. Dev., 2016, 20(2), 386–394.
11. D. Cortés-Borda, E. Wimmer, B. Gouilleux, E. Barré, N. Oger and L. Goulamaly, et al., An Autonomous Self-Optimizing Flow Reactor for the Synthesis of Natural Product Carpanone, J. Org. Chem., 2018, 83(23), 14286–14299.
12. B. E. Walker, J. H. Bannock, A. M. Nightingale and J. C. deMello, Tuning reaction products by constrained optimisation, React. Chem. Eng., 2017, 2(5), 785–798.
13. S. Krishnadasan, R. Brown, A. Demello and J. Demello, Intelligent routes to the controlled synthesis of nanoparticles, Lab Chip, 2007, 7(11), 1434–1441.
14. L. M. Baumgartner, C. W. Coley, B. J. Reizman, K. W. Gao and K. F. Jensen, Optimum catalyst selection over continuous and discrete process variables with a single droplet microfluidic reaction platform, React. Chem. Eng., 2018, 3(3), 301–311.
15. A. M. Schweidtmann, A. D. Clayton, N. Holmes, E. Bradford, R. A. Bourne and A. A. Lapkin, Machine learning meets continuous flow chemistry: Automated optimization towards the Pareto front of multiple objectives, Chem. Eng. J., 2018, 177–282.
16. A. C. Bédard, A. Adamo, K. C. Aroh, M. G. Russell, A. A. Bedermann and J. Torosian, et al., Reconfigurable system for automated optimization of diverse chemical reactions, Science, 2018, 361(6408), 1220–1225.
17. M. Christensen, L. P. E. Yunker, F. Adedeji, F. Häse, L. M. Roch and T. Gensch, et al., Data-science driven autonomous process optimization, Commun. Chem., 2021, 4(1), 1–12.
18. A. M. K. Nambiar, C. P. Breen, T. Hart, T. Kulesza, T. F. Jamison and K. F. Jensen, Bayesian Optimization of Computer-Proposed Multistep Synthetic Routes on an Automated Robotic Flow Platform, ACS Cent. Sci., 2022, 8(6), 825–836.
19. J. M. Granda, L. Donina, V. Dragone, D. L. Long and L. Cronin, Controlling an organic synthesis robot with machine learning to search for new reactivity, Nature, 2018, 559(7714), 377–381.
20. P. Nikolaev, D. Hooper, F. Webber, R. Rao, K. Decker and M. Krein, et al., Autonomy in materials research: a case study in carbon nanotube growth, npj Comput. Mater., 2016, 2(1), 1–6.
21. K. Vaddi, H. T. Chiang and L. D. Pozzo, Autonomous retrosynthesis of gold nanoparticles via spectral shape matching, Digit. Discov., 2022, 1(4), 502–510.
22. R. J. Hickman, P. Bannigan, Z. Bao, A. Aspuru-Guzik and C. Allen, Self-driving laboratories: A paradigm shift in nanomedicine development, Matter, 2023, 6(4), 1071–1081.
23. A. Deshwal, C. M Simon and J. Rao Doppa, Bayesian optimization of nanoporous materials, Mol. Syst. Des. Eng., 2021, 6(12), 1066–1086.
24. B. P. MacLeod, F. G. L. Parlane, T. D. Morrissey, F. Häse, L. M. Roch and K. E. Dettelbach, et al., Self-driving laboratory for accelerated discovery of thin-film materials, Sci. Adv., 2020, 6(20), eaaz8867 . https://advances.sciencemag.org/content/6/20/eaaz8867.
25. B. P. MacLeod, F. G. L. Parlane, C. C. Rupnow, K. E. Dettelbach, M. S. Elliott and T. D. Morrissey, et al., A self-driving laboratory advances the Pareto front for material properties, Nat. Commun., 2022, 13(1), 995 . https://www.nature.com/articles/s41467-022-28580-6.
26. N. T. P. Hartono, M. Ani Najeeb, Z. Li, P. W. Nega, C. A. Fleming and X. Sun, et al., Principled Exploration of Bipyridine and Terpyridine Additives to Promote Methylammonium Lead Iodide Perovskite Crystallization, Cryst. Growth Des., 2022, 22(9), 5424–5431.
27. S. Sun, A. Tiihonen, F. Oviedo, Z. Liu, J. Thapa and Y. Zhao, et al., A data fusion approach to optimize compositional stability of halide perovskites, Matter, 2021, 4(4), 1305–1322.
28. B. Burger, P. M. Maffettone, V. V. Gusev, C. M. Aitchison, Y. Bai and X. Wang, et al., A mobile robotic chemist, Nature, 2020, 583(7815), 237–241.
29. M. J. Tamasi, R. A. Patel, C. H. Borca, S. Kosuri, H. Mugnier and R. Upadhya, et al., Machine Learning on a Robotic Platform for the Design of Polymer–Protein Hybrids, Adv. Mater., 2022, 34(30), 2201809.
30. M. J. Tamasi and A. J. Gormley, Biologic formulation in a self-driving biomaterials lab, Cell Rep. Phys. Sci., 2022, 3(9), 101041 . https://www.sciencedirect.com/science/article/pii/S2666386422003356.
31. M. M. Noack, K. G. Yager, M. Fukuto, G. S. Doerk, R. Li and J. A. Sethian, A kriging-based approach to autonomous experimentation with applications to X-ray scattering, Sci. Rep., 2019, 9(1), 1–19.
32. B. Rohr, H. S. Stein, D. Guevarra, Y. Wang, J. A. Haber and M. Aykol, et al., Benchmarking the acceleration of materials discovery by sequential learning, Chem. Sci., 2020, 11(10), 2696–2706.
33. R. A. Fisher, The design of experiments, Oliver and Boyd, Edinburgh; London, 1937.
34. G. E. P. Box, J. S. Hunter and W. G. Hunter, Statistics for experimenters: design, innovation and discovery, 2005, vol. 2.
35. M. J. Anderson and P. J. Whitcomb, DOE simplified: practical tools for effective experimentation, CRC Press, 2016.
36. A. Lucia and J. Xu, Chemical process optimization using Newton-like methods, Comput. Chem. Eng., 1990, 14(2), 119–138.
37. I. Rechenberg, Evolutionsstrategien, in Simulationsmethoden in der Medizin und Biologie, Springer, 1978, pp. 83–114.
38. H. P. Schwefel, Evolutionsstrategien für die numerische optimierung, in Numerische Optimierung von Computer-Modellen mittels der Evolutionsstrategie, Springer, 1977, pp. 123–176.
39. G. Zames, N. Ajlouni, N. Ajlouni, N. Ajlouni, J. Holland and W. Hills, et al., Genetic algorithms in search, optimization and machine learning, Inf. Technol. J., 1981, 3(1), 301–302.
40. J. R. Koza and J. R. Koza, Genetic programming: on the programming of computers by means of natural selection, MIT press, 1992, vol. 1.
41. M. Srinivas and L. M. Patnaik, Genetic algorithms: A survey, Computer, 1994, 27(6), 17–26.
42. D. Wierstra, T. Schaul, T. Glasmachers, Y. Sun, J. Peters and J. Schmidhuber, Natural evolution strategies, J. Mach. Learn. Res., 2014, 15(1), 949–980.
43. Z. Zhou, X. Li and R. N. Zare, Optimizing Chemical Reactions with Deep Reinforcement Learning, ACS Cent. Sci., 2017, 3(12), 1337–1344,  DOI:10.1021/acscentsci.7b00492.
44. C. Beeler, S. G. Subramanian, K. Sprague, N. Chatti, C. Bellinger, M. Shahen, et al., ChemGymRL: An Interactive Framework for Reinforcement Learning for Digital Chemistry, 2023.
45. J. Močkus, On Bayesian methods for seeking the extremum, in Optimization techniques IFIP technical conference, Springer, 1975, pp. 400–404.
46. J. Mockus, V. Tiesis and A. Zilinskas, The application of Bayesian methods for seeking the extremum, J. Glob. Optim., 1978, 2, 117–129.
47. J. Mockus, Bayesian approach to global optimization: theory and applications, Springer Science & Business Media, 2012, vol. 37.
48. F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion and O. Grisel, et al., Scikit-learn: Machine Learning in Python, J. Mach. Learn. Res., 2011, 12, 2825–2830.
49. L. Buitinck, G. Louppe, M. Blondel, F. Pedregosa, A. Mueller, O. Grisel, et al., API design for machine learning software: experiences from the scikit-learn project, in ECML PKDD Workshop: Languages for Data Mining and Machine Learning, 2013, pp. 108–122.
50. The GPyOpt authors, GPyOpt: A Bayesian Optimization framework in python, 2016, http://github.com/SheffieldML/GPyOpt.
51. J. S. Bergstra, R. Bardenet, Y. Bengio and B. Kégl, Algorithms for hyper-parameter optimization, in Advances in neural information processing systems, 2011, pp. 2546–2554.
52. J. S. Bergstra and Y. Bengio, Random search for hyper-parameter optimization, J. Mach. Learn. Res., 2012, 13(Feb), 281–305.
53. J. S. Bergstra, D. Yamins and D. D. Cox, Making a science of model search: Hyperparameter optimization in hundreds of dimensions for vision architectures, JMLR, 2013.
54. J. Bergstra, B. Komer, C. Eliasmith, D. Yamins and D. D. Cox, Hyperopt: a Python library for model selection and hyperparameter optimization, Comput. Sci. Discov., 2015, 8(1), 014008 . http://stacks.iop.org/1749-4699/8/i=1/a=014008.
55. M. Lindauer, K. Eggensperger, M. Feurer, A. Biedenkapp, D. Deng, C. Benjamins, et al., SMAC3: A Versatile Bayesian Optimization Package for Hyperparameter Optimization, 2021.
56. M. Lindauer, K. Eggensperger, M. Feurer, S. Falkner, A. Biedenkapp, F. Hutter, SMAC v3: Algorithm Configuration in Python, GitHub, 2017, https://github.com/automl/SMAC3.
57. K. Kandasamy, K. R. Vysyaraju, W. Neiswanger, B. Paria, C. R. Collins and J. Schneider, et al., Tuning Hyperparameters without Grad Students: Scalable and Robust Bayesian Optimisation with Dragonfly, J. Mach. Learn. Res., 2020, 21(81), 1–27.
58. A. I. Cowen-Rivers, W. Lyu, R. Tutunov, Z. Wang, A. Grosnit, R. R. Griffiths, A. M. Maraval, H. Jianye, J. Wang, J. Peters and H. Bou-Ammar, HEBO: Pushing The Limits of Sample-Efficient Hyper-parameter Optimisation, J. Artif. Int. Res., 2022, 74 DOI:10.1613/jair.1.13643.
59. M. Balandat, B. Karrer, D. R. Jiang, S. Daulton, B. Letham, A. G. Wilson, et al., BoTorch: A Framework for Efficient Monte-Carlo Bayesian Optimization, in Advances in Neural Information Processing Systems, 2020, vol. 33, http://arxiv.org/abs/1910.06403.
60. The Ax authors, Ax: Adaptive Experimentation Platform, GitHub, 2023, https://github.com/facebook/Ax.
61. X. Song, S. Perel, C. Lee, G. Kochanski and D. Golovin, Open Source Vizier: Distributed Infrastructure and API for Reliable and Flexible Black-box Optimization, in Automated Machine Learning Conference, Systems Track (AutoML-Conf Systems), 2022.
62. D. Golovin, B. Solnik, S. Moitra, G. Kochanski, J. Karro and D. Sculley, Google Vizier: A Service for Black-Box Optimization, in Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, ACM, Halifax, NS, Canada, 2017, pp. 1487–1495,  DOI:10.1145/3097983.3098043.
63. M. Aldeghi, F. Häse, R. J. Hickman, I. Tamblyn and A. Aspuru-Guzik, Golem: an algorithm for robust experiment and process optimization, Chem. Sci., 2021, 12, 14792–14807.
64. S. Daulton, S. Cakmak, M. Balandat, M. A. Osborne, E. Zhou and E. Bakshy, Robust Multi-Objective Bayesian Optimization Under Input Noise, in K. Chaudhuri, S. Jegelka, L. Song, C. Szepesvari, G. Niu and S. Sabato, ed. Proceedings of the 39th International Conference on Machine Learning. vol. 162 of Proceedings of Machine Learning Research, PMLR, 2022, pp. 4831–4866.
65. R. J. Hickman, M. Aldeghi, F. Häse and A. Aspuru-Guzik, Bayesian optimization with known experimental and design constraints for chemistry applications, Digit. Discov., 2022, 1, 732–744.
66. S. G. Baird, J. R. Hall and T. D. Sparks, Compactness matters: Improving Bayesian optimization efficiency of materials formulations through invariant search spaces, Comput. Mater. Sci., 2023, 224, 112134.
67. J. Snoek, H. Larochelle and R. P. Adams, Practical Bayesian Optimization of Machine Learning Algorithms, arXiv, 2012, preprint, arXiv:1206.2944,  DOI:10.48550/arXiv.1206.2944, http://arxiv.org/abs/1206.2944.
68. M. A. Gelbart, J. Snoek and R. P. Adams, Bayesian optimization with unknown constraints, in Proceedings of the Thirtieth Conference on Uncertainty in Artificial Intelligence (UAI'14), AUAI Press, Arlington, Virginia, USA, 2014, pp. 250–259,  DOI:10.5555/3020751.3020778.
69. R. B. Gramacy and H. K. H. Lee, Optimization Under Unknown Constraints, arXiv, 2010, preprint, arXiv:1004.4027,  DOI:10.48550/arXiv.1004.4027, http://arxiv.org/abs/1004.4027.
70. C. Antonio, Sequential model based optimization of partially defined functions under unknown constraints, J. Global Optim., 2021, 79(2), 281–303,  DOI:10.1007/s10898-019-00860-4.
71. Y. K. Wakabayashi, T. Otsuka, Y. Krockenberger, H. Sawada, Y. Taniyasu and H. Yamamoto, Bayesian Optimization with Experimental Failure for High-Throughput Materials Growth, npj Comput. Mater., 2022, 8, 180.
72. D. Khatamsaz, B. Vela and P. Singh, et al., Bayesian optimization with active learning of design constraints using an entropy-based approach, npj Comput. Mater., 2023, 9, 49.
73. D. Ginsbourger, J. Janusevskis and R. L. Riche, Dealing with asynchronicity in parallel Gaussian Process based global optimization, 2011.
74. T. Desautels, A. Krause and J. W. Burdick, Parallelizing Exploration-Exploitation Tradeoffs in Gaussian Process Bandit Optimization, J. Mach. Learn. Res., 2014, 15(119), 4053–4103.
75. B. J. Shields, J. Stevens, J. Li, M. Parasram, F. Damani and J. I. M. Alvarado, et al., Bayesian reaction optimization as a tool for chemical synthesis, Nature, 2021, 590(7844), 89–96.
76. J. Torres, S. Lau, P. Anchuri, J. Stevens, J. Tabora, J. Li, A. Borovika, R. Adams and A. Doyle, A Multi-Objective Active Learning Platform and Web App for Reaction Optimization, J. Am. Chem. Soc., 2022, 144(43), 19999–20007.
77. K. C. Felton, J. G. Rittig and A. A. Lapkin, Summit: Benchmarking Machine Learning Methods for Reaction Optimisation, Chem. Methods, 2021, 1(2), 116–122.
78. F. Häse, L. M. Roch, C. Kreisbeck and A. Aspuru-Guzik, Phoenics: A Bayesian Optimizer for Chemistry, ACS Cent. Sci., 2018, 4(9), 1134–1145.
79. F. Häse, M. Aldeghi, R. J. Hickman, L. M. Roch and A. Aspuru-Guzik, Gryffin: An algorithm for Bayesian optimization of categorical variables informed by expert knowledge, Applied Physics Reviews, 2021, 8(3), 031406,  DOI:10.1063/5.0048164.
80. F. Häse, M. Aldeghi, R. J. Hickman, L. M. Roch, M. Christensen and E. Liles, et al., Olympus: a benchmarking framework for noisy optimization and experiment planning, Mach. Learn.: Sci. Technol., 2021, 2(3), 035021,  DOI:10.1088/2632-2153/abedc8.
81. R. Hickman, P. Parakh, A. Cheng, Q. Ai, J. Schrier and M. Aldeghi, et al., Olympus, enhanced: benchmarking mixed-parameter and multi-objective optimization in chemistry and materials science, ChemRxiv, 2023, preprint,  DOI:10.26434/chemrxiv-2023-74w8d.
82. R. R. Griffiths, L. Klarner, H. B. Moss, A. Ravuri, S. Truong, B. Rankovic, et al., GAUCHE: A Library for Gaussian Processes in Chemistry, 2022.
83. M. Sim, M. G. Vakili, F. Strieth-Kalthoff, H. Hao, R. J. Hickman, S. Miret, S. Pablo-García and A. Aspuru-Guzik, ChemOS 2.0: An orchestration architecture for chemical self-driving laboratories, Matter, 2024, 7(9), 2959–2977.
84. D. Kraft, et al., A software package for sequential quadratic programming, 1988.
85. D. P. Kingma and J. Ba, Adam: A Method for Stochastic Optimization, arXiv, 2017, preprint, arXiv:1412.6980,  DOI:10.48550/arXiv.1412.6980, http://arxiv.org/abs/1412.6980.
86. J. Blank and K. Deb, pymoo: Multi-Objective Optimization in Python, IEEE Access, 2020, 8, 89497–89509.
87. F. A. Fortin, F. M. De Rainville, M. A. Gardner, M. Parizeau and C. Gagné, DEAP: Evolutionary Algorithms Made Easy, J. Mach. Learn. Res., 2012, 13, 2171–2175.
88. F. M. De Rainville, F. A. Fortin, M. A. Gardner, M. Parizeau and C. Gagné, Deap: A python framework for evolutionary algorithms, in Proceedings of the 14th annual conference companion on Genetic and evolutionary computation, 2012, pp. 85–92.
89. C. E. Rasmussen and C. K. I. Williams, Gaussian processes for machine learning, Adaptive computation and machine learning, MIT Press, 2006.
90. R. M. Neal, Bayesian Learning for Neural Networks. vol. 118 of Lecture Notes in Statistics, ed. P. Bickel, P. Diggle, S. Fienberg, K. Krickeberg, I. Olkin, N. Wermuth, et al., Springer, New York, NY, 1996,  DOI:10.1007/978-1-4612-0745-0.
91. C. Rasmussen and Z. Ghahramani, Occam’ s Razor, in Advances in Neural Information Processing Systems, vol. 13, MIT Press, 2000.
92. J. Hensman, A. G. de G Matthews and Z. Ghahramani, Scalable Variational Gaussian Process Classification, in International Conference on Artificial Intelligence and Statistics, 2014.
93. J. R. Gardner, G. Pleiss, D. Bindel, K. Q. Weinberger and A. G. Wilson, GPyTorch: Blackbox Matrix-Matrix Gaussian Process Inference with GPU Acceleration, in Advances in Neural Information Processing Systems, 2018.
94. Towards global optimisation 2, ed. G. P. Szego and L. C. W. Dixon, Amsterdam; New York: New York: North-Holland Pub. Co.; sole distributors for the U.S.A. and Canada, Elsevier, North-Holland, 1978.
95. A. Paszke, S. Gross, F. Massa, A. Lerer, J. Bradbury, G. Chanan, et al., PyTorch: An Imperative Style, High-Performance Deep Learning Library, in Advances in Neural Information Processing Systems 32, Curran Associates, Inc., 2019, pp. 8024–8035.
96. The Atlas authors, Atlas: A Brain for Self-driving Laboratories, GitHub, 2023, https://github.com/aspuru-guzik-group/atlas.
97. P. Vellanki, S. Rana, S. Gupta, D. Rubin, A. Sutti, T. Dorin, et al., Process-constrained batch Bayesian optimisation, in Advances in Neural Information Processing Systems, vol. 30, Curran Associates, Inc., 2017.
98. E. Soedarmadji, H. S. Stein, S. K. Suram, D. Guevarra and J. M. Gregoire, Tracking materials science data lineage to manage millions of materials experiments and analyses, npj Comput. Mater., 2019, 5(1), 1–9.
99. H. S. Stein, D. Guevarra, A. Shinde, R. J. R. Jones, J. M. Gregoire and J. A. Haber, Functional mapping reveals mechanistic clusters for OER catalysis across (Cu–Mn–Ta–Co–Sn–Fe)Ox composition and pH space, Mater. Horiz., 2019, 6(6), 1251–1258.
100. C. Blundell, J. Cornebise, K. Kavukcuoglu and D. Wierstra, Weight Uncertainty in Neural Network, Proceedings of the 32nd International Conference on Machine Learning, Proceedings of Machine Learning Research, 2015, vol. 37, pp. 1613–1622, Available from https://proceedings.mlr.press/v37/blundell15.html.
101. F. Häse, L. M. Roch and A. Aspuru-Guzik, Chimera: enabling hierarchy based multi-objective optimization for self-driving laboratories, Chem. Sci., 2018, 9(39), 7642–7655 . http://xlink.rsc.org/?DOI=C8SC02239A.
102. E. Zitzler and L. Thiele, Multiobjective optimization using evolutionary algorithms — A comparative case study, in Parallel Problem Solving from Nature — PPSN V, Lecture Notes in Computer Science, ed. A. E. Eiben, T. Bäck, M. Schoenauer and H. P. Schwefel, Springer, Berlin, Heidelberg, 1998, pp. 292–301.
103. J. D. Knowles, D. W. Corne and M. Fleischer, Bounded archiving using the lebesgue measure, in The 2003 Congress on Evolutionary Computation, 2003, CEC ’03, 2003, vol. 4, pp. 2490–2497.
104. M. Li and X. Yao, Quality Evaluation of Solution Sets in Multiobjective Optimisation: A Survey, ACM Comput. Surv., 2019, 52(2), 1–38.
105. A. P. Guerreiro, C. M. Fonseca and L. Paquete, The Hypervolume Indicator: Problems and Algorithms, ACM Comput. Surv., 2021, 54(6), 1–42 . ArXiv:2005.00515 [cs]. Available from: http://arxiv.org/abs/2005.00515.
106. J. Knowles and E. J. Hughes, Multiobjective optimization on a budget of 250 evaluations, in Evolutionary Multi-Criterion Optimization (EMO-2005), ed. C. Coello, et al, Springer-Verlag, 2005, vol. 3410 of LNCS.
107. J. Knowles, ParEGO: a hybrid algorithm with on-line landscape approximation for expensive multiobjective optimization problems, IEEE Trans. Evol. Comput., 2006, 10(1), 50–66.
108. I. Y. Kim and O. L. de Weck, Adaptive weighted sum method for multiobjective optimization: a new method for Pareto front generation, Struct. Multidiscip. Optim., 2006, 31(2), 105–116.
109. C. A. C. Coello, S. Gonz&aacute, L. Brambila, G. F. Josu&eacute and M. G. C. Tapia, et al., Evolutionary multiobjective optimization: open research areas and some challenges lying ahead, Complex Intell. Syst., 2020, 6(2), 221–237.
110. M. Seifrid, R. J. Hickman, A. Aguilar-Granda, C. Lavigne, J. Vestfrid, T. C. Wu, et al., Routescore: Punching the Ticket to More Efficient Materials Development, 2021, https://chemrxiv.org/engage/chemrxiv/article-details/60f085e88ae3a7499b78400f.
111. B. Settles, Active Learning, Synthesis Lectures on Artificial Intelligence and Machine Learning, Morgan & Claypool Publishers, 2012, vol. 6, 1, pp. 1–114.
112. N. H. Angello, V. Rathore, W. Beker, A. Wołos, E. R. Jira and R. Roszak, et al., Closed-loop optimization of general reaction conditions for heteroaryl Suzuki-Miyaura coupling, Science, 2022, 378(6618), 399–405.
113. B. J. Reizman, Y. M. Wang, S. L. Buchwald and K. F. Jensen, Suzuki–Miyaura cross-coupling optimization enabled by automated feedback, React. Chem. Eng., 2016, 1(6), 658–666.
114. C. Fare, P. Fenner, M. Benatan, A. Varsi and E. O. Pyzer-Knapp, A multi-fidelity machine learning approach to high throughput materials screening, npj Comput. Mater., 2022, 8(1), 1–9 . https://www.nature.com/articles/s41524-022-00947-9.
115. D. Bash, Y. Cai, V. Chellappan, S. L. Wong, X. Yang and P. Kumar, et al., Multi-Fidelity High-Throughput Optimization of Electrical Conductivity in P3HT-CNT Composites, Adv. Funct. Mater., 2021, 2102606.
116. A. Patra, R. Batra, A. Chandrasekaran, C. Kim, T. D. Huan and R. Ramprasad, A multi-fidelity information-fusion approach to machine learn and predict polymer bandgap, Comput. Mater. Sci., 2020, 172, 109286.
117. A. Tran, J. Tranchida, T. Wildey and A. P. Thompson, Multi-fidelity machine-learning with uncertainty quantification and Bayesian optimization for materials design: Application to ternary random alloys, J. Chem. Phys., 2020, 153(7), 074705 . https://aip.scitation.org/doi/10.1063/5.0015672.
118. A. Tran, T. Wildey and S. McCann, sMF-BO-2CoGP: A Sequential Multi-Fidelity Constrained Bayesian Optimization Framework for Design Applications, J. Comput. Inf. Sci. Eng., 2020, 20(3), 031007.
119. N. Gantzler, A. Deshwal, J. R. Doppa and C. Simon, Multi-fidelity Bayesian Optimization of Covalent Organic Frameworks for Xenon/Krypton Separations, ChemRxiv, 2023 DOI:10.26434/chemrxiv-2023-jfzrf-v2 , https://chemrxiv.org/engage/chemrxiv/article-details/64970d6a4821a835f355c8b9.
120. A. E. Gongora, K. L. Snapp, E. Whiting, P. Riley, K. G. Reyes and E. F. Morgan, et al., Using simulation to accelerate autonomous experimentation: A case study using mechanics, iScience, 2021, 24(4), 102262.
121. M. Poloczek, J. Wang and P. Frazier, Multi-Information Source Optimization, in Advances in Neural Information Processing Systems, Curran Associates, Inc., 2017, vol. 30.
122. J. Wu, S. Toscano-Palmerin, P. I. Frazier and A. G. Wilson, Practical Multi-fidelity Bayesian Optimization for Hyperparameter Tuning, arXiv, 2019, preprint, arXiv:1903.04703,  DOI:10.48550/arXiv.1903.04703, http://arxiv.org/abs/1903.04703.
123. D. Huang, T. T. Allen, W. I. Notz and R. A. Miller, Sequential kriging optimization using multiple-fidelity evaluations, Struct. Multidiscip. Optim., 2006, 32(5), 369–382.
124. C. Kim, T. Doan Huan, S. Krishnan and R. Ramprasad, A hybrid organic-inorganic perovskite dataset, Sci. Data, 2017, 4(170057), 1–11.
125. J. P. Perdew, Density functional theory and the band gap problem, Int. J. Quantum Chem., 1985, 28(S19), 497–523.
126. J. Heyd, G. E. Scuseria and M. Ernzerhof, Hybrid functionals based on a screened Coulomb potential, J. Chem. Phys., 2003, 118(18), 8207–8215.
127. A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, Influence of the exchange screening parameter on the performance of screened hybrid functionals, J. Chem. Phys., 2006, 125(22), 224106.
128. M. Feurer, B. Letham and E. Bakshy, Scalable Meta-Learning for Bayesian Optimization using Ranking-Weighted Gaussian Process Ensembles, ICML 2018 AutoML Workshop, 2018.
129. M. Feurer, B. Letham, F. Hutter and E. Bakshy, Practical Transfer Learning for Bayesian Optimization, arXiv, 2021, preprint, arXiv:1802.02219,  DOI:10.48550/arXiv.1802.02219.
130. M. Patacchiola, J. Turner, E. J. Crowley, M. O’ Boyle and A. J. Storkey, Bayesian Meta-Learning for the Few-Shot Setting via Deep Kernels, in Advances in Neural Information Processing Systems, Curran Associates, Inc., 2020, vol. 33, pp. 16108–16118.
131. M. Wistuba, N. Schilling and L. Schmidt-Thieme, Scalable Gaussian process-based transfer surrogates for hyperparameter optimization, Mach. Learn., 2018, 107(1), 43–78,  DOI:10.1007/s10994-017-5684-y.
132. C. J. Taylor, K. C. Felton, D. Wigh, M. I. Jeraal, R. Grainger and G. Chessari, et al., Accelerated Chemical Reaction Optimization Using Multi-Task Learning, ACS Cent. Sci., 2023, 9(5), 957–968.
133. R. J. Hickman, J. Ruža, H. Tribukait, L. M. Roch and A. García-Durán, Equipping data-driven experiment planning for Self-driving Laboratories with semantic memory: case studies of transfer learning in chemical reaction optimization, React. Chem. Eng., 2023, 8, 2284–2296.
134. D. T. Ahneman, J. G. Estrada, S. Lin, S. D. Dreher and A. G. Doyle, Predicting reaction performance in C–N cross-coupling using machine learning, Science, 2018, 360(6385), 186–190,  DOI:10.1126/science.aar5169.
135. J. C. Gower, A General Coefficient of Similarity and Some of Its Properties, Biometrics, 1971, 27(4), 857–871 . https://www.jstor.org/stable/2528823.
136. L. Ralaivola, S. J. Swamidass, H. Saigo and P. Baldi, Graph kernels for chemical informatics, Neural Network., 2005, 18(8), 1093–1110.
137. D. Rogers and M. Hahn, Extended-Connectivity Fingerprints, J. Chem. Inf. Model., 2010, 50(5), 742–754,  DOI:10.1021/ci100050t.
138. J. S. Delaney, ESOL: Estimating Aqueous Solubility Directly from Molecular Structure, J. Chem. Inf. Comput. Sci., 2004, 44(3), 1000–1005,  DOI:10.1021/ci034243x.
139. G. Tom, R. J. Hickman, A. Zinzuwadia, A. Mohajeri, B. Sanchez-Lengeling and A. Aspuru-Guzik, Calibration and generalizability of probabilistic models on low-data chemical datasets with DIONYSUS, Digit. Discov., 2023, 2(3), 759–774.
140. A. Pomberger, A. A. Pedrina McCarthy, A. Khan, S. Sung, C. J. Taylor and M. J. Gaunt, et al., The effect of chemical representation on active machine learning towards closed-loop optimization, React. Chem. Eng., 2022, 7, 1368–1379.
141. K. Kandasamy, A. Krishnamurthy, J. Schneider and B. Poczos, Parallelised Bayesian Optimisation via Thompson Sampling, in Proceedings of the Twenty-First International Conference on Artificial Intelligence and Statistics, PMLR, 2018, pp. 133–142, ISSN: 2640-3498.
142. M. Ponce, R. van Zon, S. Northrup, D. Gruner, J. Chen, F. Ertinaz, et al., Deploying a top-100 supercomputer for large parallel workloads: The niagara supercomputer, in Proceedings of the Practice and Experience in Advanced Research Computing on Rise of the Machines (learning), 2019, pp. 1–8.
143. C. Loken, D. Gruner, L. Groer, R. Peltier, N. Bunn and M. Craig, et al., SciNet: lessons learned from building a power-efficient top-20 system and data centre, J. Phys. Conf., 2010, 256, 012026.

---

Footnote

† Current address: Bayer Research and Innovation Center, 238 Main St, Cambridge, MA 02142, USA.

---