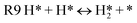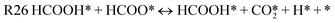Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Elucidating the essential role of hydrogen bonding and direct H-transfer in transfer hydrogenation on transition metal catalysts†
Aojie
Li
and
Srinivas
Rangarajan
 *
*
Department of Chemical and Biomolecular Engineering, Lehigh University, Bethlehem, PA 18015, USA. E-mail: srr516@lehigh.edu
First published on 19th May 2025
Abstract
Catalytic transfer hydrogenation (CTH) employs molecular hydrogen donors such as isopropanol and formic acid as H source. Using periodic density functional theory (DFT) and microkinetic modeling, here we show that direct hydrogen atom transfer between a donor and acceptor is kinetically feasible on transition metal catalysts especially if the donor and the acceptor (or intermediates derived from them) can interact via hydrogen bonding. This direct hydrogen transfer opens up new hydrogenation pathways not available in conventional hydrogenation with H2. The mechanism of catalytic hydrogen transfer between formic acid, and a model acceptor, viz. formaldehyde (HCHO, the smallest carbonyl compound), on Cu(111) is first studied to conceptually explain the role of indirect and direct hydrogenation routes and the effect of surface coverages and concomitant destabilization. Our results show that (1), when HCOOH and HCHO are both present, hydrogen bonded complexes may form that enable direct hydrogen transfer which can then be kinetically relevant; (2), the direct hydrogen transfer with formic acid results in three times higher reaction rate (compared to using molecular H2 under the same conditions). We finally show that hydrogen bonded complexes arise in a number of other CTH reactions on transition metal catalysts (furfural and lignin hydrogenolysis, reduction of nitrates, nitriles, etc.), potentially indicating the generality of our results to more practical chemistries.
1. Introduction
Catalytic hydrogenation and hydrogenolysis are typically carried out using gaseous molecular hydrogen (H2) as the hydrogen source (also known as “direct hydrogenation”). Alternatively, these chemistries can be carried out by using organic hydrogen donors such as alcohols and formic acid (HCOOH) as the reductant, instead of H2; these reactions are termed catalytic transfer hydrogenation or hydrogenolysis (CTH, see Fig. 1). The organic hydrogen donors employed in CTH are soluble in the liquid phase and can be activated at low temperatures, enabling reduction at milder conditions; the donors themselves can be produced via electrocatalytic routes, thereby permitting sustainable alternatives to using methane-derived hydrogen. CTH has been widely studied to reduce a variety of molecules such as ketones,1 aldehydes,2 styrene oxide,3 furfural,4 phenol,5 cyclohexanone,6 nitroarenes,7 nitrile,8 nitrate,9 olefins,10 lignin11etc. on homogeneous and heterogeneous catalysts; the spectrum of donors include formic acid,12 2-propanol,13 methanol,14 and cyclohexanol.15 More recently, CTH has seen wide application in biomass conversion,16 especially using molecules such as formic acid (that can also be produced as a byproduct of biomass upgrading); transfer hydrogenation has also been suggested as a milder option to hydrogenate hydrogen-lean unsaturated molecules (e.g. dibenzyltoluene) to liquid organic hydrogen carriers (LOHCs).17 | ||
| Fig. 1 A schematic comparison between catalytic transfer hydrogenation/hydrogenolysis (CTH) using an organic hydrogen donor and conventional hydrogenation using H2. | ||
Transition metal catalysts such as Pd,18 Cu,19 and Ru (ref. 20) are an important class of materials used in CTH for both hydrogenation21 and hydrogenolysis,22 particularly in biomass conversion. However, the mechanism of CTH is not completely well-understood. On metals, CTH is often postulated to occur through “indirect metal hydride mechanism” wherein the donor first dehydrogenates to produce surface hydrogen atoms (H*) which then is consumed by the acceptor (Fig. 2). Such a mechanism would essentially be identical to that of conventional hydrogenation, once H* is formed on the surface. Alternatively, hydrogen transfer (H-transfer) between the donor and the acceptor, similar to Meerwein–Ponndorf–Verley (MPV) reductions on Lewis acid catalyst, could lead to “direct” hydrogenation. Yu and Spencer showed experimental evidence for direct hydrogen transfer from HCOOH in a model study involving cis-trans isomerization of a functionalized alkene on Pd/C catalyst; in particular, using DCOOH directly led to deuterium incorporation in the trans product while HCOOD resulted in no D in the product at all suggesting that the formyl hydrogen was exclusively involved in this chemistry.23 DFT-derived microkinetic models for HCOOH decomposition on Pt and Pd have also shown that H-transfer between the reactant and abundant surface intermediates such as CO* are kinetically relevant.24,25 Furthermore, multiple studies have demonstrated the relative efficacy of CTH compared to direct hydrogenation using H2 on transition metal catalysts. Li et al., for instance, found that under the same reaction conditions (and concentration of H source, H2 or formic acid), quinoline hydrogenation was three times higher on Co@OMNC catalyst.26 Xu et al. showed that the conversion of furfural during hydrogenation with formic acid on mesoporous N-doped carbon encapsulated Co catalysts (Co–N–C) was higher than with H2 for a given reaction time.27 In the absence of transport limitations, the mechanistic origin of such higher activities is not clear. The indirect mechanism can explain this observation if (1) the formation of H* from dissociation of H2 is rate controlling on these catalysts while the dehydrogenation of formic acid is more facile leading to a higher concentration of H* on the surface for consumption by the acceptor, or (2) the formation of H* is quasi-equilibrated but is greater in the presence of the donor than with H2 due to more favorable thermochemistry. The direct route can also explain this observation if indirect hydrogenation steps with H* (or dissociation of H2) are rate-controlling in the case of H2 while using a molecular donor enables faster hydrogen transfer. Finally, donors such as formic acid can also generate abundant surface intermediates such as CO* and HCOO* (depending on the catalyst and its binding to C or O atoms); these intermediates can destabilize all other intermediates and transition states and participate in reactions through mediating H-transfer, thereby influencing the overall rates. The exact role of each of these possibilities still remain unclear and will, expectedly, change from system to system.
In this work, we use a combination of density functional theory (DFT) and coverage-cognizant microkinetic modeling to conceptually explain the mechanism of catalytic hydrogen transfer between a common donor, viz. HCOOH, and a model acceptor, viz. formaldehyde (HCHO, the smallest carbonyl compound), on Cu(111). While hydrogenation of formaldehyde to methanol is not industrially significant, this chemistry is an excellent model system as it allows us to rigorously explicate the role of indirect and direct hydrogenation routes and the effect of surface coverages and concomitant destabilization. We select Cu(111) as the reference surface for simplicity and because of its activity for formic acid dehydrogenation.28,29 We show that when HCOOH and HCHO are both present, hydrogen bonded complexes may form between them or intermediates derived from them; such complexes enable direct hydrogen transfer which can then be kinetically relevant. The direct hydrogen transfer, indeed, results in a significantly higher reaction rate (compared to using molecular H2 under same conditions), we discuss the origin of this higher activity with regard to new pathways, and differences in surface intermediates and rate determining steps. We show that hydrogen bonded complexes arise in a number of other CTH systems, potentially indicating the generality of our results to more practical chemistries.
2. Method
2.1 Density functional theory calculations
Periodic plane wave DFT calculations in this study were performed using the Vienna ab initio simulation package (VASP30–32). The exchange–correlation functionals were described by the Perdew–Burke–Ernzerhof (PBE) exchange correlation functional33 with the DFT-D3 dispersion correction method of Grimme.34 Projector-augmented wave (PAW) pseudopotentials35,36 were used with an energy cut off of 500 eV.Cu(111) surface was modeled using a 3 × 3 periodic slab with four layers, containing 36 Cu atoms in each supercell. Each supercell has lattice parameters a = 7.57 Å, b = 7.57 Å, c = 20.18 Å. The 3 × 3 × 4 Cu(111) slab was selected as the representative model for subsequent calculations after careful consideration, as it offers a good balance between accuracy and computational efficiency. We benchmarked the binding energies and relative energies of several key intermediates (e.g., CH3O*, CH3OH*, H*, HCOOH*, HCOO*, HCHO*) on both 3 × 3 × 4 and 4 × 4 × 4 Cu(111) slab models, the max difference between the two models is 0.04 eV, indicating that the smaller 3 × 3 × 4 Cu(111) surface does not exhibit noticeable dispersion effects that would compromise the accuracy of the energy calculations. The bulk lattice constant of copper was computed to be 3.57 Å, which is consistent with the experimental value 3.62 Å.37 The bottom two layers of the slab were fixed to simulate the bulk and a 15 Å vacuum perpendicular to the surface (z-direction) was employed to avoid interactions with the neighboring slab. The Brillouin zone was sampled with a gamma centered 6 × 6 × 1 k-point mesh. Self-consistent field (SCF) calculations had an electronic convergence criterion of 10−4 eV; additionally, the geometric convergence criterion was set so that the norm of forces on all atoms were smaller than 0.05 eV Å−1. Further, a first order Methfessel–Paxton smearing38 was utilized with a width of 0.1 eV. All gas phase calculations (of isolated molecules) were computed using the same settings (except with a Gaussian smearing with a width of 0.05 eV) in a large cell so that there was at least 10 Å of vacuum in all directions.
Activation barriers and minimum energy paths for each elementary step were carried out using climbing image nudged elastic band (CI-NEB) method,39 which was discretized by seven images between the initial and final states; the force convergence for these calculations were set at of 0.1 eV/A.
Several structures were carefully identified and relaxed for each adsorbate (and pairs of co-adsorbates to probe initial states of reactions); care was taken to consider plausible intermolecular hydrogen bonding when co-adsorbates had hydroxy group (–OH) and carbonyl groups. Similarly, several candidate pathways were evaluated to identify the lowest energy transition state structures (and corresponding activation barriers of the elementary steps).
For gas phase species, their binding energies (BE) onto the surface are calculated as:
| BE = Emolecule+slab − Eslab − Egaseous molecule | (1) |
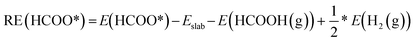 | (2) |
To compute kinetic and thermodynamic quantities at non-zero temperatures for microkinetic modeling, temperature corrections were applied as described by Grabow and Mavrikakis40 to obtain Shomate parameters. DFT-derived thermochemical quantities of gas phase molecules are often incorrect for species containing C–O unsaturation; to this end, we corrected the enthalpies of CO, HCOOH, and HCHO to match NIST-derived values for heats of reference reactions. See ESI† S1 for more details.
The complexation energy (CE) of hydrogen-bonded intermediates with formic acid (“molecule-HCOOH”) is used to determine the stability of hydrogen bonding and is calculated as:
| CEmolecule-HCOOH* = Emolecule-HCOOH* − E(molecule*) − E(HCOOH*) + Eslab | (3) |
Simulated IR intensities of each vibrational mode are calculated based on atomic displacements and Born effective charges, based on Karhánek et al.41 More specifically, the dipole moment change is derived in the direction perpendicular to the slab (which means the Born effective charge matrix and eigenvector are both only kept in z direction) and was then squared to give the IR intensity of the vibrational mode.
2.2 Microkinetic models
Mean-field microkinetic models (MKMs) were built as a continuous stirred tank reactor (CSTR) to mimic low conversion. The surface species were assumed to be uniformly distributed and characterized by a “mean” coverage although accounting for denticity (bidentate vs. monodentate species). All simulations were carried out at a total fixed pressure of 1 atm and temperatures within 353–393 K (based on HCOOH decomposition conditions). The partial pressures of the reactants were kept low (0.062–0.092 atm for HCOOH and 0.014–0.017 atm for hydrogen, with the rest being inert) and flow rates were set to a high enough value to ensure the conversion was low (<0.1%) to maintain differential conditions. The model was formulated as a time-varying CSTR and was simulated until steady state. The base condition is 1 atm and 373 K with partial pressure of PHCOOH = 0.077 atm, PH2 = 0.154 atm.All reactions in the network were elementary steps and were considered to be reversible. The model ensured thermodynamic consistency; specifically (1) all activation barriers are ensured to be positive and greater than the corresponding reaction enthalpy, and (2) the ratio of the forward and reverse rate constants is the equilibrium constant of the step. The specific steps included in the model evolved as the model complexity changed and are discussed in detail in section 3. Since multiple NEB calculations were carried out and several transition state energies were obtained for each elementary step, the activation enthalpies for each elementary step were determined based on the lowest transition state energy and the infinitely separated initial states. The kinetic rate constant for each elementary step was calculated using transition state theory, except for adsorption steps where the collision theory (as discussed in Motagamwala and Dumesic42) was used. In the process of evaluating elementary steps in the direct hydrogen transfer mechanism, if the donor and acceptor could form stable hydrogen-bonded complexes, we introduced new intermediates to represent these hydrogen-bonded complexes (for example, “CH3OHHCOO*” as the hydrogen-bonded complex for CH3O* and HCOOH*) and included additional reactions to illustrate the formation of hydrogen bonding and the transfer of the hydrogen atom. Those additional reactions designed for direct hydrogen transfer mechanism can be found in ESI† S2.
Incorporating coverage effect is crucial to ensure that model predictions align with the quantities measured in reaction kinetics experiments,25,43–45 and it is important to maintain consistency between the surface coverages predicted by microkinetic modeling (MKM) and those assumed in DFT calculations. Various methods for including coverage effects have been discussed by Nolen et al.46 When needed, we incorporate coverage effects as polynomial terms, similar to Bhandari et al.,24 enabling the calculation of destabilization/stabilization of the states with respect to energies at a reference coverage.
3. Results
To rigorously contrast H2 and HCOOH as the hydrogen source, we need to account for a comprehensive reaction network in either case and be cognizant of relevant abundant surface intermediates and their effect on thermokinetic parameters. We begin by discussing the results of DFT calculations and microkinetic modeling on Cu(111). The model results showed a substantial coverage of intermediates on the surface, therefore, we then re-computed DFT energies with appropriate coverages of intermediates and re-solved the microkinetic model to account for the corrections to the energies as a function of intermediate coverages. The final coverage-cognizant model is used to elucidate the reaction mechanism. Achieving coverage cognizance is critical as abundant surface intermediates and their influence on the chemistry and kinetics can vary between conventional and transfer hydrogenation systems.3.1 Microkinetic modeling of HCHO hydrogenation on Cu(111)
Periodic DFT calculations were carried out for all relevant surface intermediates on the Cu(111) surface (detailed structure could be found in ESI† S3). The adsorption modes are chemisorptive for open shell species; for some closed shell species such as hydrogen and CO2, the adsorption is physisorptive (binding energy of −0.11 eV and −0.24 eV), while formic acid, formaldehyde, and CO are relatively strongly chemisorbed (binding energy of −1.11 eV to −0.43 eV). These results are consistent with Grabow and Mavrikakis,40 albeit that our binding energies are larger in magnitude due to dispersive interactions that are taken into account here.
Upon computing co-adsorbed states (as a starting point for direct hydrogen transfer steps), our DFT results showed that hydrogen-bonded complexes form between OH (hydroxyl) groups of donor and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O (carbonyl) or OH (hydroxyl) groups of the acceptor. In particular, as shown in Fig. 4, hydrogen-bonded pairs were seen for HCOOH–HCHO*, HCOOH–CH3O*, HCOO–HCOOH*, COOH–HCHO*, and COOH–CH3OH*.
O (carbonyl) or OH (hydroxyl) groups of the acceptor. In particular, as shown in Fig. 4, hydrogen-bonded pairs were seen for HCOOH–HCHO*, HCOOH–CH3O*, HCOO–HCOOH*, COOH–HCHO*, and COOH–CH3OH*.
To ensure that these structures are not an artifact of the chosen functional, we computed single-point energies (using structures derived from the reference PBE-D3 functional) with seven alternative functionals: PBE-D2,50 PBE-dDsC,51,52 PBE-D3-with Becke–Johnson damping function,53 SCAN-rVV10,54 optPBE,55 SCAN,56 and r2SCAN-rVV10.57 Specifically, using each of these functionals, we re-computed the (1) complexation energy of the hydrogen-bonded structure CH3OHHCOO* (viz., CH3O* + HCOOH* ↔ CH3OHHCOO*) and (2) activation energy of the transfer hydrogenation step CH3O* + HCOOH* ↔ CH3OH* + HCOO* involving the hydrogen-bonded complex; both energies are computed based on infinitely separated initial states, as shown in Table 1. The complexation energy of CH3OHHCOO* was found to be −0.54 eV and activation energy for the corresponding elementary step is 0.13 eV with the PBE-D3 functional. Subsequent application of seven different functionals yielded a range of complexation energies from −0.63 eV to −0.55 eV (one exception of −0.80 eV by optPBE), and activation energies within the range of 0.08 eV to 0.14 eV (with the exception of 0 eV by PBE-D2 and PBE-dDsC). Notably, all of these functionals are qualitatively consistent in that they show that the hydrogen-bonded complex is stable and facilitates direct hydrogen transfer.
| Name of the functional | E(complexation of CH3OHHCOO*)/eV | E(activation)/eV |
|---|---|---|
| PBE-D3 | −0.55 | 0.13 |
| PBE-D2 | −0.59 | 0.00 |
| PBE-dDsC | −0.59 | 0.00 |
| PBE-D3-with Becke–Johnson damping function | −0.55 | 0.15 |
| SCAN-rVV10 | −0.55 | 0.19 |
| optPBE | −0.80 | 0.15 |
| SCAN | −0.61 | 0.14 |
| r2SCAN-rVV10 | −0.63 | 0.08 |
Not all co-adsorbates led to hydrogen bond formation, therefore, while Fig. 3 lists all possible direct hydrogen transfer steps, only those were considered for full transition state search where the initial state co-adsorbates have a hydrogen bonding between the donor and the acceptor via the hydrogen that needs to be transferred. For instance, hydrogen transfer from the OH group of formic acid to the carbonyl oxygen of HCHO* was considered as there is a hydrogen bond between the donor and the acceptor via this specific H atom. On the other hand, the transfer of the hydrogen from the carbon atom of formic acid to either the oxygen or the carbon of HCHO* (to form CH2OH* or CH3O*) were both ruled out because no viable hydrogen bond existed between the donor and acceptor via this hydrogen. This process of elimination resulted in six direct hydrogen transfer steps 22–26 as shown in Fig. 3.
Temperature-corrected enthalpies and entropies, computed from DFT-derived Shomate parameters (see section 2 and Grabow and Mavrikakis40) were used to develop microkinetic models (MKMs) for clean Cu(111), details could be found in ESI† S4, and NEB calculations that are used to find the transition state of each elementary steps on clean Cu(111) surface could be found in ESI† S5. To explore the effect of direct hydrogen transfer in enhancing reaction kinetics, we simultaneously built two versions of the model, each with a slightly different reaction network; the first considers only HCOOH as the hydrogen source (referred to as the “HCOOH-cofeed” model) and comprises steps 1–26; the second considers molecular hydrogen (H2) as the source (“H2-cofeed” model) and comprises only steps 5–21 (i.e. not involving formic acid reactions or the direct hydrogen transfer steps).
In the absence of any energy corrections due to lateral interactions with spectators, our models showed high coverages of HCOO*, H*, or CH3O*. Approximate corrections to species and transition state energies were, therefore, included based on DFT-derived differential binding energies of these intermediates. These corrections allowed, as a first step, to compare the two model versions under similar conditions of gas phase H concentration and temperature. The details of the first (no corrections) and second (approximate corrections) iterations and model predictions are in S6 of the ESI.† The “HCOOH-cofeed” model predicted orders of magnitude higher rates than the “H2-cofeed” model, due to a direct hydrogen transfer mediated by the H-bonded complexation. In particular, direct hydrogen transfer from HCOOH* to CH3O*, via the formation of the H-bonded CH3OHHCOO*, to finally form CH3OH* was a kinetically relevant step. The models predicted high surface coverages of intermediates; in particular, the “HCOOH-cofeed” model had a HCOO* coverage of 0.2 monolayer (ML) while the CH3O* coverage of “H2-cofeed” model was ∼0.3 ML indicating that the surface environment can be different in CTH, thereby also resulting in different reaction kinetics.
The transition states and species of the “HCOOH-cofeed” model were recomputed with respect to 2/9th ML HCOO* coverage on the surface and the “H2-cofeed” model based on 3/9th ML CH3O* surface coverage (based on model results). The adsorption structures of the relevant surface intermediates for “HCOOH-cofeed” model are shown in Fig. 5, while those for the “H2-cofeed” model can be found in ESI† S7. Details of NEB calculations that are used to find the transition state of selected elementary steps on 2/9th HCOO*-covered and 3/9th CH3O*-covered Cu(111) surface are in ESI† S8 and S9 respectively.
HCOO* coverages and CH3O* coverages can, in general, stabilize or destabilize intermediates, as shown in Fig. 6. Our DFT results highlight the potential formation of hydrogen-bonded complexes between HCOO* and certain surface intermediates such as HCOOH*, CH2OH*, and CH3OH*, and they exhibit binding energy stabilization ranging from 0.26 to 0.4 eV.  does not exhibit hydrogen bonding with HCOO*, however, its binding energy is more negative likely due to the additional dispersion stabilization with HCOO*.
does not exhibit hydrogen bonding with HCOO*, however, its binding energy is more negative likely due to the additional dispersion stabilization with HCOO*.  also experiences stabilization of approximately 0.16 eV; HCHO* and CH3O* exhibit negligible changes in binding (relative) energy in the presence of HCOO*, because they do not form any hydrogen binding with formate; H* and HCOO* experience destabilization respectively by 0.12 eV and 0.3 eV. On the 3/9th ML CH3O*-covered surface, HCHO*, CH3OH* and
also experiences stabilization of approximately 0.16 eV; HCHO* and CH3O* exhibit negligible changes in binding (relative) energy in the presence of HCOO*, because they do not form any hydrogen binding with formate; H* and HCOO* experience destabilization respectively by 0.12 eV and 0.3 eV. On the 3/9th ML CH3O*-covered surface, HCHO*, CH3OH* and  are stabilized by 0.24 eV, 0.23 eV and 0.12 eV respectively;
are stabilized by 0.24 eV, 0.23 eV and 0.12 eV respectively;  and CH2OH* exhibit negligible changes in binding energy; H* and CH3O* are destabilized respectively by 0.13 eV and 0.36 eV. The detailed data for binding energy comparison are in S10 of ESI.†
and CH2OH* exhibit negligible changes in binding energy; H* and CH3O* are destabilized respectively by 0.13 eV and 0.36 eV. The detailed data for binding energy comparison are in S10 of ESI.†
 | ||
| Fig. 6 Comparison of binding (relative) energies of different intermediates on clean Cu(111) surface, 2/9th ML HCOO*-covered Cu(111) surface and 3/9th ML CH3O*-covered Cu(111) surface. By comparing the binding energies on two covered surfaces to clean surface, intermediates are ordered from both stabilized (far left) to both destabilized (far right). The binding (relative) energy for open-shell species COOH*, CH2OH*, OH*, CH3O*, CHO*, HCOO*, H* are calculated based on the relative energy as defined in eqn (2). Since the 3/9th ML CH3O*-covered Cu(111) surface only appears in “H2-cofeed” case, the binding (relative) energy of HCOOH*, HCOO* and COOH* in the presence of 3/9th ML CH3O* are not calculated. | ||
Activation barriers for elementary steps are also affected differently in the presence of HCOO* and CH3O*, as shown in Table 2. Interestingly, the presence of 2/9th ML HCOO* coverage leads to a reduction in the activation barriers of most indirect hydrogen transfer elementary steps, but increases the activation energy for the direct hydrogen transfer steps with HCOOH*. The 3/9th ML CH3O* coverage leads to an increase in the activation barrier for the first hydrogenation step of HCHO* to CH3O*, but leads to a decrease in the activation energy of the second hydrogenation step from CH3O* to CH3OH*.
The presence of 2/9th ML HCOO* introduces a new elementary step for facilitating the direct hydrogen transfer. In particular, the CH3OHHCOO* complex can, in addition to dissociating into physiosorbed CH3OH(g) and surface HCOO* as described in R25(b) in ESI† Table S2, undergo C–H dissociation of the “HCOO” portion to CO2(g) and H*. We term this new elementary step as R27: CH3OHHCOO* ↔ CH3OH* + CO2(g) + H* (as shown in R27 of Fig. S6 in ESI†). This step has a higher barrier (Table 2) in the presence of 2/9th ML of HCOO* compared to the clean surface.
The complicated effect of HCOO* necessitates correctly accounting for the destabilization due to lateral repulsive interactions of some adsorbates and stabilization due to hydrogen bonding for others. For “HCOOH-cofeed” model, therefore, we calculated Shomate parameters for all intermediates and transition states with 2/9th ML HCOO* on the surface and input them to the microkinetic model as the reference energetics i.e. we implicitly set 2/9th ML HCOO* surface as the “reference” surface. This allows the MKM to account for the stabilization due to hydrogen bonding at the higher coverage of HCOO*. Further, polynomial-based stabilization/destabilization terms were also included and calculated based on 2/9th ML HCOO* surface as the “reference” surface for the “HCOOH-cofeed” model. These complications, however, do not arise for “H2-cofeed” case, therefore, we keep the clean surface as reference and include coverage-dependent stabilization/destabilization terms based on this state.
The “HCOOH-cofeed” model additionally required a few iterative refinement steps where we systematically added new destabilization terms if the coverage of certain intermediates was calculated to be higher than 1/9th ML. This ultimately resulted in adding cross- and self-destabilization terms with respect to HCOO* and CH3O*, and self-destabilization terms for HCOOH* and CH3OH*. The detailed information of the Shomate parameters at the reference coverage for “HCOOH-cofeed” model and the destabilization terms used for both models are all given and explained in S11–S13 of the ESI.†
The coverages of relevant intermediates under different reaction conditions are shown in Fig. 7. Our new “HCOOH-cofeed” model predicted a coverage of 2/9th ML HCOOx* (HCOOx* here comprises of HCOO* and the methanol-formate hydrogen-bonded complex CH3OHHCOO*), 6/9th ML vacant sites. Our new “H2-cofeed” model predicted a 3/9th ML CH3O* coverage, 1/9th ML H*, and 5/9th ML vacant sites. Therefore, we have fully coverage-cognizant microkinetic models for both cases whereby the predicted coverages fall within the range of DFT coverages considered.
Fig. 8 compares the hydrogenation rate for two models, with HCOOH and H2 cofeed, at various temperatures. With the explicit coverage effect, we note that, (1) the hydrogenation rates in both cases are significantly higher than those for clean surface models (see Fig. S3(a) in the ESI† for model results using the clean surface energetics and approximate corrections) thereby indicating the importance of explicitly including coverage effects, and (2) the hydrogenation rate while cofeeding HCOOH is three (3) times higher than with using molecular H2, thus indicating the efficacy of CTH.
Fig. 9 below shows the reaction fluxes in the network for the final “HCOOH-cofeed” model at 373 K, 1 atm, with partial pressure of HCHO and HCOOH being 0.15 and 0.08 respectively (and rest inert). The most dominant pathway to form methanol involves hydrogenation of HCHO* by a surface H* (indirect step) to form a methoxy, following which an HCOOH* can directly transfer hydrogen to CH3O*, thereby forming the hydrogen-bonded intermediate CH3OHHCOO*; CH3OH portion of this complex stabilizes the transition state of the C–H dissociation of formate (HCOO*) part of the complex and ultimately forms CH3OH* and an H* (and releasing a molecule of CO2). This hydrogenation pathway is at least 8 orders of magnitude larger (in rate) than a purely indirect pathway (i.e. successive hydrogenation by surface H* to form methanol); the results are consistent with the degrees of rate control (as shown in Table 3), which indicates that the hydrogenation of HCHO* by surface H* and direct hydrogen transfer from HCOOH* to CH3O* are rate-controlling. This pathway accounts for 96% of the flux to consume (CH3OHHCOO*) and thereby HCOO* dissociation; the remaining 4% of the flux involves desorption of methanol to form HCOO* which can then decompose via the HCOOH co-catalysis route (as proposed by Chen and Mavrikakis47,48 and Lin et al.49). At the reference condition shown in Fig. 9, the most abundant surface intermediate is HCOOx* (∼0.2 ML); all the other intermediates have low coverage, and the surface is mostly vacant (∼0.6 ML). Clearly, the model results indicate that both direct and indirect steps are likely to play a role in CTH; the direct step, once again, is aided by the formation of H-bonded complexes.
Table 3 shows that CH3O* hydrogenation and H2 dissociation are rate-controlling in the “H2-cofeed” model. Both steps are avoided in “HCOOH-cofeed” case, because CH3O* hydrogenation is preferred to occur via direct H-transfer and H2 dissociation is not kinetically relevant. Intermediates of HCOOH decomposition, viz. HCOO* and even COOH*, form H-bonded complexes with HCHO*, its hydrogenated intermediates (CH3O*, CH2OH*), and CH3OH*. These complexes not only facilitate H-transfer, but they also facilitate dehydrogenation steps (e.g. CH3OHHCOO* dissociation to CH3OH(g), H*, and CO2(g) as shown in Fig. 12). The results also point to the effect of surface coverages during H2 and HCOOH cofeeds. Clearly, the abundant surface intermediates are different in the two cases (CH3O* for the “H2-cofeed” case and HCOO* for the “HCOOH-cofeed” case), resulting in a substantially different surface environment and, consequently, reaction energetics (and rate/equilibrium constants). Such changes can influence the availability of H* even if direct routes are not available for a hydrogen donor (e.g. using cyclohexane as an H-donor). Therefore, all three factors, viz., facile reactions of formic acid relative to H2 dissociation, the feasibility of alternate pathways (direct H-transfer) and new species aided by hydrogen-bonding, and relative differences in surface environment (and ensuing destabilization/stabilization of key intermediates and transition states), contribute to the higher CTH rate relative to the “H2-cofeed” case in this reaction system.
3.2 Computed infrared spectra of H-bonded complex
To evaluate if hydrogen-bonded species were likely to have distinct vibrational signatures, we calculated the IR spectra for the most stable configurations of HCOO*, CH3OH*, and their hydrogen-bonded complex, CH3OHHCOO* (Fig. 10). For HCOO* in its most stable bidentate form, we observed a peak at 1312 cm−1, corresponding to the symmetric O–C–O stretching mode. Additionally, within the 1200–1400 cm−1 range, we identified an IR-inactive vibrational mode at 1287 cm−1, attributed to in-plane C–H stretching (as described by Chutia et al.58) or O–C–H scissoring (as described by Xu et al.59). For CH3OH*, we detected a weak peak at 1299 cm−1, associated with O–H scissoring. In the hydrogen-bonded CH3OHHCOO* complex, three IR-active peaks appeared at 1301 cm−1, 1315 cm−1, and 1382 cm−1, corresponding to O–C–H scissoring on the HCOO portion of the complex, O–C–O stretching on HCOO influenced by its interaction with CH3OH, and O–H scissoring on the CH3OH portion, respectively.We observed that hydrogen bonding not only shifts existing IR-active vibrational modes but also generates new IR-active modes. While the symmetric O–C–O stretching mode shifted by just 3 cm−1, the O–H scissoring on the CH3OH* part shifted significantly by 83 cm−1, indicating that hydrogen bonding has a greater impact on CH3OH* than on HCOO*. Furthermore, the O–C–H scissoring mode, which is IR-inactive in isolated HCOO*, becomes active in the H-bonded complex, likely due to the breaking of the symmetry in the HCOO* portion.
3.3 Nature of transferred hydrogen
Bader charge analysis60 and DDEC6 atomic population analysis61,62 were used to investigate the nature of the transferred H atom. As shown in Table 4, the transferring H atom at the transition state is protic (charge on H is +0.65 using the Bader approach and +0.35 using DDEC6). Therefore, protic solvents such as water could modulate the activity of these H-transfer steps further and increase CTH rates.3.4 Universality of direct H-transfer
That the formation of hydrogen bonding opens up new routes for hydrogenation of HCHO indicates that other CTH systems may also exhibit such interactions (and reaction pathways). Since CTH has been shown to occur in hydrogenation of furfural,4 nitrate reduction,9 hydrogenation of nitriles,8,63 and hydrogenolysis of nitroarenes,7 we explored the interaction of various oxygen- and nitrogen-containing molecules with formic acid on three representative metal surfaces. In particular, we considered the interaction of furfural, acetonitrile, NO3, and nitromethane with HCOOH on Cu(111), Pd(111), and Pt(111).In our DFT calculations, we use a 3 × 3 × 4 surface supercell (36 metal atoms in each supercell) for H-bonded complex of HCOOH with acetonitrile, nitromethane, and nitrate, while a 4 × 4 × 4 surface supercell (64 metal atoms in each supercell) is used for furfural considering the molecule size. All hydrogen-bonded structures are stable as shown in Fig. 10. Indeed, the complexation energy, which determines the strength of H-bonded complex, varies from being thermoneutral to ∼−0.7 eV across all molecules and surfaces (Fig. 11). Therefore, direct H-transfer is likely in all these cases. Notably, the higher stability of these complexes on Cu indicates that direct H-transfer is particularly likely on this catalyst than on Pt and Pd. The strength of a complex depends upon the stability of the individual surface adsorbates (i.e., the binding energy of the four molecules and formic acid). The origin of the relative stability of hydrogen bonded complexes on Cu can be explained for furfural and acetonitrile based on the relatively lower binding energy of these adsorbates on Cu compared to Pd and Pt; for NO3 and CH3NO2, the complexation energy inversely tracks the binding energy of formic acid. While detailed kinetic models are necessary for confirmation, our results indicate that direct hydrogen transfer on transition metal catalysts is more general, especially when the donor and acceptors (or intermediates derived from them) can form hydrogen bonded complexes.
4. Conclusions
By integrating density functional theory (DFT) with coverage-cognizant microkinetic modeling, we elucidate the mechanism of catalytic hydrogen transfer between a common donor, HCOOH, and a model acceptor, formaldehyde, on Cu(111). Our findings reveal that when both HCOOH and HCHO are present, hydrogen-bonded complexes can form between them or their intermediates. These complexes not only facilitate an alternative direct hydrogen transfer between the donor and acceptor but also make the decomposition of HCOOH more favorable compared to the dissociation of H2. Specifically, flux analysis and the degrees of rate control indicate that the primary pathway for methanol formation from HCHO involves the initial hydrogenation of HCHO* by a surface H* (an indirect step) to produce methoxy (HCHO* + H* ↔ CH3O*). The methoxy then forms a hydrogen-bonded complex with HCOOH (CH3OHHCOO*), which enables direct hydrogen transfer from HCOOH to CH3O*. The CH3OH fragment of this resulting complex stabilizes the transition state of C–H dissociation in formate (HCOO*), resulting in CH3OH* and H*, and the release of a CO2 molecule (CH3O* + HCOOH* ↔ CH3OHHCOO* ↔ CH3OH(g) + H* + CO2(g)).Furthermore, we observed that surface coverages of HCOO* and CH3O* can stabilize or destabilize intermediates, thereby kinetically affecting the hydrogenation rate. Together, these factors indicate that the interplay of facile decomposition of the hydrogen donor, new reaction pathways enabling direct hydrogen transfer, and different abundant surface intermediates (and associated impact on energetics) can all contribute to higher CTH rates. In addition, we find that the transferring hydrogen atom is positively charged and can plausibly be further stabilized in protic solvents. While results on another catalyst (or catalytic site) may be different, and intrinsic errors in the chosen level of theory can lead to overall errors in predicted rates, we hold that our principal result, viz., the formation of hydrogen-bonded complexes and ensuing direct hydrogen transfer, are key to this class of reactions on metal catalysts. Indeed, our exploratory results indicate that hydrogen bonded complexes are present between HCOOH and several acceptors on different metals, suggesting that our findings have broader applicability to practical systems.
Data availability
All DFT calculations were carried out using VASP (https://www.vasp.at/). This software requires a user license purchasable from the developers. The version used is 5.4.4. Detailed energies and associated kinetics of all elementary steps (in the form of Shomate parameters) are given in the supporting information. Microkinetic modeling was carried out using an in-house software described in https://pubs.acs.org/doi/full/10.1021/acs.jpcc.7b08089.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was financially supported by the NSF CAREER grant (#2045550). Portions of this research were conducted on Lehigh University's Research Computing infrastructure partially supported by NSF Award #2019035. This work also used Stampede2 at TACC, and Expanse at SDSC through allocation CTS170035 from the Advanced Cyberinfrastructure Coordination Ecosystem: Services & Support (ACCESS) program, which is supported by National Science Foundation grants (#2138259, #2138286, #2138307, #2137603, and #2138296). The authors thank Adhika Setiawan from Lehigh University for adapting open source IR scripts for surface adsorbate calculations.References
- S. Dayan, F. Arslan and N. Kalaycioglu Ozpozan, Ru(II) Impregnated Al2O3, Fe3O4, SiO2 and N-Coordinate Ruthenium(II) Arene Complexes: Multifunctional Catalysts in the Hydrogenation of Nitroarenes and the Transfer Hydrogenation of Aryl Ketones, Appl. Catal., B, 2015, 164, 305–315, DOI:10.1016/j.apcatb.2014.09.025.
- Y. Gao, S. Jaenicke and G. K. Chuah, Highly Efficient Transfer Hydrogenation of Aldehydes and Ketones Using Potassium Formate over AlO(OH)-Entrapped Ruthenium Catalysts, Appl. Catal., A, 2014, 484, 51–58, DOI:10.1016/j.apcata.2014.07.010.
- E. A. Baghdady, D. K. Schwartz and J. Will Medlin, Effects of Surface Hydrophobicity on Catalytic Transfer Hydrogenation of Styrene with Formic Acid in a Biphasic Mixture, ACS Appl. Mater. Interfaces, 2022, 14(29), 33457–33462, DOI:10.1021/acsami.2c11732.
- Z. An and J. Li, Recent Advances in the Catalytic Transfer Hydrogenation of Furfural to Furfuryl Alcohol over Heterogeneous Catalysts, Green Chem., 2022, 24(5), 1780–1808, 10.1039/d1gc04440k.
- D. Zhang, F. Ye, T. Xue, Y. Guan and Y. M. Wang, Transfer Hydrogenation of Phenol on Supported Pd Catalysts Using Formic Acid as an Alternative Hydrogen Source, Catal. Today, 2014, 234, 133–138, DOI:10.1016/j.cattod.2014.02.039.
- M. Blanco, P. Álvarez, C. Blanco, M. V. Jiménez, J. Fernández-Tornos, J. J. Pérez-Torrente, L. A. Oro and R. Menéndez, Enhanced Hydrogen-Transfer Catalytic Activity of Iridium N-Heterocyclic Carbenes by Covalent Attachment on Carbon Nanotubes, ACS Catal., 2013, 3(6), 1307–1317, DOI:10.1021/cs4000798.
- A. H. Romero, Reduction of Nitroarenes via Catalytic Transfer Hydrogenation Using Formic Acid as Hydrogen Source: A Comprehensive Review, ChemistrySelect, 2020, 5(42), 13054–13075, DOI:10.1002/slct.202002838.
- L. Liu, J. Li, Y. Ai, Y. Liu, J. Xiong, H. Wang, Y. Qiao, W. Liu, S. Tan, S. Feng, K. Wang, H. Sun and Q. Liang, A Ppm Level Rh-Based Composite as an Ecofriendly Catalyst for Transfer Hydrogenation of Nitriles: Triple Guarantee of Selectivity for Primary Amines, Green Chem., 2019, 21(6), 1390–1395, 10.1039/c8gc03595d.
- Y. Ding, W. Sun, W. Yang and Q. Li, Formic Acid as the In-Situ Hydrogen Source for Catalytic Reduction of Nitrate in Water by PdAg Alloy Nanoparticles Supported on Amine-Functionalized SiO2, Appl. Catal., B, 2017, 203, 372–380, DOI:10.1016/j.apcatb.2016.10.048.
- D. A. Bulushev and J. R. H. Ross, Vapour Phase Hydrogenation of Olefins by Formic Acid over a Pd/C Catalyst, Catal. Today, 2011, 163(1), 42–46, DOI:10.1016/j.cattod.2010.01.055.
- J. Zhang, Catalytic Transfer Hydrogenolysis as an Efficient Route in Cleavage of Lignin and Model Compounds, Green Energy Environ., 2018, 3(4), 328–334, DOI:10.1016/j.gee.2018.08.001.
- R. Nie, Y. Tao, Y. Nie, T. Lu, J. Wang, Y. Zhang, X. Lu and C. C. Xu, Recent Advances in Catalytic Transfer Hydrogenation with Formic Acid over Heterogeneous Transition Metal Catalysts, ACS Catal., 2021, 11(3), 1071–1095, DOI:10.1021/acscatal.0c04939.
- M. Gopiraman, S. Ganesh Babu, Z. Khatri, W. Kai, Y. A. Kim, M. Endo, R. Karvembu and I. S. Kim, Dry Synthesis of Easily Tunable Nano Ruthenium Supported on Graphene: Novel Nanocatalysts for Aerial Oxidation of Alcohols and Transfer Hydrogenation of Ketones, J. Phys. Chem. C, 2013, 117(45), 23582–23596, DOI:10.1021/jp402978q.
- Y. Zhao, F. Pan, H. Li, G. Q. Xu and W. Chen, Titania-Photocatalyzed Transfer Hydrogenation Reactions with Methanol as a Hydrogen Source: Enhanced Catalytic Performance by Pd-Pt Alloy at Ambient Temperature, ChemCatChem, 2014, 6(2), 454–458, DOI:10.1002/cctc.201300905.
- N. Siddiqui, R. Khatun, V. K. Mishra, T. S. Khan, C. Samanta and R. Bal, Selective Transfer Hydrogenation of Biomass Derived Furanic Molecules Using Cyclohexanol as a Hydrogen Donor over Nanostructured Cu/MgO Catalyst, Mol. Catal., 2021, 513, 111812, DOI:10.1016/j.mcat.2021.111812.
- M. J. Gilkey and B. Xu, Heterogeneous Catalytic Transfer Hydrogenation as an Effective Pathway in Biomass Upgrading, ACS Catal., 2016, 6(3), 1420–1436, DOI:10.1021/acscatal.5b02171.
- D. Zakgeym, T. Engl, Y. Mahayni, K. Müller, M. Wolf and P. Wasserscheid, Development of an Efficient Pt/SiO2 Catalyst for the Transfer Hydrogenation from Perhydro-Dibenzyltoluene to Acetone, Appl. Catal., A, 2022, 639, 118644, DOI:10.1016/j.apcata.2022.118644.
- Y. M. Lu, H. Z. Zhu, W. G. Li, B. Hu and S. H. Yu, Size-Controllable Palladium Nanoparticles Immobilized on Carbon Nanospheres for Nitroaromatic Hydrogenation, J. Mater. Chem. A, 2013, 1(11), 3783–3788, 10.1039/c3ta00159h.
- W. Gong, C. Chen, R. Fan, H. Zhang, G. Wang and H. Zhao, Transfer-Hydrogenation of Furfural and Levulinic Acid over Supported Copper Catalyst, Fuel, 2018, 231, 165–171, DOI:10.1016/j.fuel.2018.05.075.
- P. Panagiotopoulou and D. G. Vlachos, Liquid Phase Catalytic Transfer Hydrogenation of Furfural over a Ru/C Catalyst, Appl. Catal., A, 2014, 480, 17–24, DOI:10.1016/j.apcata.2014.04.018.
- X. Chang, A. F. Liu, B. Cai, J. Y. Luo, H. Pan and Y. B. Huang, Catalytic Transfer Hydrogenation of Furfural to 2-Methylfuran and 2-Methyltetrahydrofuran over Bimetallic Copper–Palladium Catalysts, ChemSusChem, 2016, 9(23), 3330–3337, DOI:10.1002/cssc.201601122.
- X. Liu, B. Yin, W. Zhang, X. Yu, Y. Du, S. Zhao, G. Zhang, M. Liu, H. Yan, M. Abbotsi-Dogbey, S. T. Al-Absi, S. Yeredil, C. Yang, J. Shen, W. Yan and X. Jin, Catalytic Transfer Hydrogenolysis of Glycerol over Heterogeneous Catalysts: A Short Review on Mechanistic Studies, Chem. Rec., 2021, 21(7), 1792–1810, DOI:10.1002/tcr.202100037.
- J. Yu and J. B. Spencer, Evidence for Direct Hydride Delivery from Formic Acid in Transfer Hydrogenation, Chem. – Eur. J., 1999, 5(8), 2237–2240, DOI:10.1002/(SICI)1521-3765(19990802)5:8<2237::AID-CHEM2237>3.0.CO;2-O.
- S. Bhandari, S. Rangarajan, S. Li, J. Scaranto, S. Singh, C. T. Maravelias, J. A. Dumesic and M. Mavrikakis, A Coverage Self-Consistent Microkinetic Model for Vapor-Phase Formic Acid Decomposition over Pd/C Catalysts, ACS Catal., 2023, 13(6), 3655–3667, DOI:10.1021/acscatal.2c06078.
- S. Bhandari, S. Rangarajan, C. T. Maravelias, J. A. Dumesic and M. Mavrikakis, Reaction Mechanism of Vapor-Phase Formic Acid Decomposition over Platinum Catalysts: DFT, Reaction Kinetics Experiments, and Microkinetic Modeling, ACS Catal., 2020, 10(7), 4112–4126, DOI:10.1021/acscatal.9b05424.
- G. Li, H. Yang, H. Zhang, Z. Qi, M. Chen, W. Hu, L. Tian, R. Nie and W. Huang, Encapsulation of Nonprecious Metal into Ordered Mesoporous N-Doped Carbon for Efficient Quinoline Transfer Hydrogenation with Formic Acid, ACS Catal., 2018, 8(9), 8396–8405, DOI:10.1021/acscatal.8b01404.
- L. Xu, R. Nie, X. Lyu, J. Wang and X. Lu, Selective Hydrogenation of Furfural to Furfuryl Alcohol without External Hydrogen over N-Doped Carbon Confined Co Catalysts, Fuel Process. Technol., 2020, 197, 106205, DOI:10.1016/j.fuproc.2019.106205.
- J. A. Herron, J. Scaranto, P. Ferrin, S. Li and M. Mavrikakis, Trends in Formic Acid Decomposition on Model Transition Metal Surfaces: A Density Functional Theory Study, ACS Catal., 2014, 4(12), 4434–4445, DOI:10.1021/cs500737p.
- G. Ruehl, S. E. Harman, O. M. Gluth, D. H. Lavoy and C. T. Campbell, Energetics of Adsorbed Formate and Formic Acid on Cu(111) by Calorimetry, ACS Catal., 2022, 12(17), 10950–10960, DOI:10.1021/acscatal.2c02608.
- G. Kresse and J. Hafner, Ab Initio Molecular Dynamics for Liquid Metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47(1), 558–561, DOI:10.1103/PhysRevB.47.558.
- G. Kresse and J. Furthmüller, Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set, Comput. Mater. Sci., 1996, 6(1), 15–50, DOI:10.1016/0927-0256(96)00008-0.
- G. Kresse and J. Furthmüller, Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(16), 11169–11186, DOI:10.1103/PhysRevB.54.11169.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868, DOI:10.1103/PhysRevLett.77.3865.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu, J. Chem. Phys., 2010, 132(15), 154104, DOI:10.1063/1.3382344.
- D. Joubert, From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59(3), 1758–1775, DOI:10.1103/PhysRevB.59.1758.
- P. E. Blöchl, Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50(24), 17953–17979, DOI:10.1103/PhysRevB.50.17953.
- D. R. Lide, Handbook of Chemistry and Physics, 76th edn, 1996 Search PubMed.
- M. Methfessel and A. T. Paxton, High-Precision Sampling for Brillouin-Zone Integration in Metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40(6), 3616–3621, DOI:10.1103/PhysRevB.40.3616.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, Climbing Image Nudged Elastic Band Method for Finding Saddle Points and Minimum Energy Paths, J. Chem. Phys., 2000, 113(22), 9901–9904, DOI:10.1063/1.1329672.
- L. C. Grabow and M. Mavrikakis, Mechanism of Methanol Synthesis on Cu through CO2 and CO Hydrogenation, ACS Catal., 2011, 1(4), 365–384, DOI:10.1021/cs200055d.
- D. Karhánek, T. Bučko and J. Hafner, A Density-Functional Study of the Adsorption of Methane-Thiol on the (111) Surfaces of the Ni-Group Metals: II. Vibrational Spectroscopy, J. Phys.: Condens. Matter, 2010, 22(26), 265006, DOI:10.1088/0953-8984/22/26/265006.
- A. H. Motagamwala and J. A. Dumesic, Microkinetic Modeling: A Tool for Rational Catalyst Design, Chem. Rev., 2021, 121(2), 1049–1076, DOI:10.1021/acs.chemrev.0c00394.
- S. Bhandari, S. Rangarajan and M. Mavrikakis, Combining Computational Modeling with Reaction Kinetics Experiments for Elucidating the in Situ Nature of the Active Site in Catalysis, Acc. Chem. Res., 2020, 53(9), 1893–1904, DOI:10.1021/acs.accounts.0c00340.
- Z. Wang, W. Xie, Y. Xu, Y. Han, J. Xu and P. Hu, Comprehensive Understanding of Ethylene Epoxidation on Copper Catalysts: A Microkinetic Study with Coverage Effects, Catal. Sci. Technol., 2024, 14(18), 5291–5303, 10.1039/d4cy00617h.
- L. C. Grabow, A. A. Gokhale, S. T. Evans, J. A. Dumesic and M. Mavrikakis, Mechanism of the Water Gas Shift Reaction on Pt: First Principles, Experiments, and Microkinetic Modeling, J. Phys. Chem. C, 2008, 112(12), 4608–4617, DOI:10.1021/jp7099702.
- M. A. Nolen, C. A. Farberow and S. Kwon, Incorporating Coverage-Dependent Reaction Barriers into First-Principles-Based Microkinetic Models: Approaches and Challenges, ACS Catal., 2024, 14206–14218, DOI:10.1021/acscatal.4c03358.
- B. W. J. Chen and M. Mavrikakis, Formic Acid: A Hydrogen-Bonding Cocatalyst for Formate Decomposition, ACS Catal., 2020, 10(19), 10812–10825, DOI:10.1021/acscatal.0c02902.
- B. W. J. Chen, S. Bhandari and M. Mavrikakis, Role of Hydrogen-Bonded Bimolecular Formic Acid-Formate Complexes for Formic Acid Decomposition on Copper: A Combined First-Principles and Microkinetic Modeling Study, ACS Catal., 2021, 11(7), 4349–4361, DOI:10.1021/acscatal.0c05695.
- T. C. Lin, U. De La Torre, A. Hejazi, S. Kwon and E. Iglesia, Unimolecular and Bimolecular Formic Acid Decomposition Routes on Dispersed Cu Nanoparticles, J. Catal., 2021, 404, 814–831, DOI:10.1016/j.jcat.2021.08.049.
- S. Grimme, Semiempirical GGA-Type Density Functional Constructed with a Long-Range Dispersion Correction, J. Comput. Chem., 2006, 27(15), 1787–1799, DOI:10.1002/jcc.20495.
- S. N. Steinmann and C. Corminboeuf, A Generalized-Gradient Approximation Exchange Hole Model for Dispersion Coefficients, J. Chem. Phys., 2011, 134(4), 044117, DOI:10.1063/1.3545985.
- S. N. Steinmann and C. Corminboeuf, Comprehensive Benchmarking of a Density-Dependent Dispersion Correction, J. Chem. Theory Comput., 2011, 7(11), 3567–3577, DOI:10.1021/ct200602x.
- S. Grimme, S. Ehrlich and L. Goerigk, Effect of the Damping Function in Dispersion Corrected Density Functional Theory, J. Comput. Chem., 2011, 32(7), 1456–1465, DOI:10.1002/jcc.21759.
- H. Peng, Z. H. Yang, J. P. Perdew and J. Sun, Versatile van Der Waals Density Functional Based on a Meta-Generalized Gradient Approximation, Phys. Rev. X, 2016, 6(4), 041005, DOI:10.1103/PhysRevX.6.041005.
- J. Klimeš, D. R. Bowler and A. Michaelides, Chemical Accuracy for the van Der Waals Density Functional, J. Phys.: Condens. Matter, 2010, 22(2), 022201, DOI:10.1088/0953-8984/22/2/022201.
- J. Sun, A. Ruzsinszky and J. Perdew, Strongly Constrained and Appropriately Normed Semilocal Density Functional, Phys. Rev. Lett., 2015, 115(3), 036402, DOI:10.1103/PhysRevLett.115.036402.
- J. Ning, M. Kothakonda, J. W. Furness, A. D. Kaplan, S. Ehlert, J. G. Brandenburg, J. P. Perdew and J. Sun, Workhorse Minimally Empirical Dispersion-Corrected Density Functional with Tests for Weakly Bound Systems: R2SCAN+rVV10, Phys. Rev. B, 2022, 106(7), 075422, DOI:10.1103/PhysRevB.106.075422.
- A. Chutia, I. P. Silverwood, M. R. Farrow, D. O. Scanlon, P. P. Wells, M. Bowker, S. F. Parker and C. R. A. Catlow, Adsorption of Formate Species on Cu(h,k,l) Low Index Surfaces, Surf. Sci., 2016, 653, 45–54, DOI:10.1016/j.susc.2016.05.002.
- L. Xu, J. Lin, Y. Bai and M. Mavrikakis, Atomic and Molecular Adsorption on Cu(111), Top. Catal., 2018, 61(9), 736–750, DOI:10.1007/s11244-018-0943-0.
- G. Henkelman, A. Arnaldsson and H. Jónsson, A Fast and Robust Algorithm for Bader Decomposition of Charge Density, Comput. Mater. Sci., 2006, 36(3), 354–360, DOI:10.1016/j.commatsci.2005.04.010.
- T. A. Manz and N. G. Limas, Introducing DDEC6 Atomic Population Analysis: Part 1. Charge Partitioning Theory and Methodology, RSC Adv., 2016, 6(53), 47771–47801, 10.1039/c6ra04656h.
- N. G. Limas and T. A. Manz, Introducing DDEC6 Atomic Population Analysis: Part 2. Computed Results for a Wide Range of Periodic and Nonperiodic Materials, RSC Adv., 2016, 6(51), 45727–45747, 10.1039/c6ra05507a.
- M. Vilches-Herrera, S. Werkmeister, K. Junge, A. Börner and M. Beller, Selective Catalytic Transfer Hydrogenation of Nitriles to Primary Amines Using Pd/C, Catal. Sci. Technol., 2014, 4(3), 629–632, 10.1039/c3cy00854a.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cy00238a |
| This journal is © The Royal Society of Chemistry 2025 |