Rapid and selective formic acid dehydrogenation catalysis by molecular ruthenium hydrides supported by rigid PCcarbeneP pincer ligands†
Laurie J.
Donnelly
 ,
Benjamin S.
Gelfand
,
Benjamin S.
Gelfand
 and
Warren E.
Piers
and
Warren E.
Piers
 *
*
Department of Chemistry, University of Calgary, 2500 University Drive NW, Calgary, Alberta T2N 1N4, Canada. E-mail: wpiers@ucalgary.ca
First published on 27th November 2024
Abstract
A series of four molecular ruthenium hydrido complexes supported by previously reported rigid PCcarbeneP pincer ligand frameworks were evaluated as formic acid dehydrogenation (FAD) catalysts. The ligands in the complexes LRRu(H)X (R = H, NMe2; X = Cl, κ2-O2CH) differ in the electron richness by substitution on the aryl groups linking the di-iso-propylphosphine arms to the central carbene donor. We find that only the unsubstituted (R = H) chloro and formato complexes are effective catalyst precursors; the NMe2 substituted derivatives decompose under catalytic conditions. However, the two compounds LHRu(H)X are highly active (TOF = 1300–4200 h−1), long lived (TON up to 122![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) and selective (dihydrogen and carbon dioxide are the sole products) at 21 °C with no base additives necessary in 13 M formic acid in water/dioxane. These performance metrics compare well with state of the art catalysts operating under ambient conditions. Mechanistic experiments support a simple two-step mechanism involving rate limiting protonolysis of the Ru–H by formic acid to release H2 and rapid loss of CO2via β-elimination from the resulting formato complex.
000) and selective (dihydrogen and carbon dioxide are the sole products) at 21 °C with no base additives necessary in 13 M formic acid in water/dioxane. These performance metrics compare well with state of the art catalysts operating under ambient conditions. Mechanistic experiments support a simple two-step mechanism involving rate limiting protonolysis of the Ru–H by formic acid to release H2 and rapid loss of CO2via β-elimination from the resulting formato complex.
Introduction
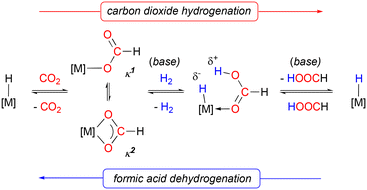
In discussions regarding societal transitioning from fossil fuels to less polluting, sustainable fuels, dihydrogen is often presented as an attractive alternative,1 provided its production can be driven by renewable energy sources and its storage and transport can be done safely and economically. With regard to the latter concern, a major practical limitation in using hydrogen as a fuel is the low volumetric energy of H2 gas (1.4 kW h L−1 at 70 MPa),2 and the attendant difficulties in its widespread distribution. Potential solutions to this issue include H2 adsorption into porous heterogeneous materials like metal–organic frameworks or storage in the form of metal hydrides, which suffer from low volumetric capacities and poor reversibility, respectively.3An alternative means of H2 storage and transport uses reversible hydrogenation reactions and one of the most promising chemical storage systems is formic acid, since it is a relatively non-toxic liquid with low volativity under ambient conditions with a high gravimetric H2 capacity (4.4 wt% resulting in energy density of 1.77 kW h L−1) and low flammability.2 Formic acid is available through biomass degradation or CO2 hydrogenation.4 If formic acid dehydrogenation (FAD) can be made efficient,5 this in theory implements a carbon-neutral cycle for storing and releasing H2 (Fig. 1). However, the high kinetic barrier to dehydrogenation for liberation of H2 (ref. 6 and 7) from formic acid means that effective catalysts for “hydrogen on demand” from this carrier are needed.
Although FAD is a thermodynamically favoured reaction, selectivity is also an issue. Thermal decomposition can follow two pathways: the dehydrogenation pathway, giving CO2 and H2, and the dehydration pathway giving CO and H2O.8 Therefore, a catalyst is also beneficial in directing the selectivity of the process for production of clean H2. Accordingly, there has been intense interest in catalysts that can dehydrogenate formic acid with high activity, longevity and selectivity.5 These can take the form of heterogeneous systems9 or, more germane to the work reported here, homogeneous molecular catalysts.10,11
While there have been some notable recent advances in the use of molecular catalysts based on earth abundant metals such as manganese12,13 or iron,14,15 with few exceptions these catalysts are unable to rival the TON or TOF performance of precious metal-based systems that use ruthenium or iridium.10 Focusing on the former metal, several ruthenium hydride catalyst precursors exhibit exceptionally high turnover numbers (TONs) and reasonable turnover frequencies (TOFs), Chart 1. Beller et al. reported a ruthenium hydride catalyst formed in situ from [RuCl2(benzene)]2 and 1,2-bisdiphenylphosphinoethane16 that eventually demonstrated a TON over one million with a modest TOF of 1000 h−1 at 25 °C.17
Several molecular catalysts with PNP pincer ligands capable of ligand cooperativity18 have also proven highly effective. Pidko et al. reported a PNP ruthenium hydride that showed high activities towards FAD (257![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 h−1 at 90 °C).19,20 Huang et al. reported a related PNP ruthenium hydride that achieved a TON of over one million with a TOF of 7333 h−1 at 90 °C.21 While these systems were highly active, they required basic additives to avoid decomposition under acidic conditions. Acid sensitivity is a common limitation of FAD catalysts and only a handful of base-free FAD catalysts have been reported.22,23 Within the context of (PNP)Ru catalyst precursors, a noteworthy base-free catalyst was reported by Milstein et al. using a PNP-supported ruthenium hydride that could dehydrogenate neat formic acid, producing over one million turnovers with a rate of 3067 h−1.24 In order to achieve these performance metrics, most of these and other catalysts require elevated temperature (60–95 °C) and at room temperature, while TONs are maintained or improved, TOFs are significantly dampened. In general, for these systems, the TOF is governed mechanistically by rate limiting elimination of CO2 from higher energy κ1 metal formate intermediates.25
000 h−1 at 90 °C).19,20 Huang et al. reported a related PNP ruthenium hydride that achieved a TON of over one million with a TOF of 7333 h−1 at 90 °C.21 While these systems were highly active, they required basic additives to avoid decomposition under acidic conditions. Acid sensitivity is a common limitation of FAD catalysts and only a handful of base-free FAD catalysts have been reported.22,23 Within the context of (PNP)Ru catalyst precursors, a noteworthy base-free catalyst was reported by Milstein et al. using a PNP-supported ruthenium hydride that could dehydrogenate neat formic acid, producing over one million turnovers with a rate of 3067 h−1.24 In order to achieve these performance metrics, most of these and other catalysts require elevated temperature (60–95 °C) and at room temperature, while TONs are maintained or improved, TOFs are significantly dampened. In general, for these systems, the TOF is governed mechanistically by rate limiting elimination of CO2 from higher energy κ1 metal formate intermediates.25
Recently we reported ruthenium hydrides supported by an advanced generation of our rigid PCcarbeneP family of pincer ligands26LRRu(H)X (R = H, NMe2; X = Cl, κ2-O2CH, Chart 1).27 These complexes were initially studied in the context of CO2 hydrogenation and (somewhat to our surprise) we found them to be almost completely inactive for this process. Mechanistic and chemical studies showed this to be related to the extremely facile deinsertion of CO2 from the formato intermediates presumably formed upon insertion of CO2 into the Ru–H bond of these complexes, i.e., LRRu(κn-O2CH)X (n = 1, X = Cl; n = 2, x = κ2-O2CH). As we concluded in the previous contribution,27 this suggests that these compounds should facilitate FAD catalysis as opposed to the reverse reaction. Here we show this to be the case, demonstrating that the complex where R = H is an extremely active, stable platform for highly selective, base additive free formic acid dehydrogenation catalysis at room temperature.
Results and discussion
A. FAD catalysis
Formic acid typically contains up to 15 mole% H2O, therefore it is necessary that the precatalysts are water stable to engage in FAD catalysis. Although quite oxygen sensitive,‡ all four derivatives LRRu(H)X (R = H, NMe2; X = Cl, κ2-OOCH) proved completely stable when treated with degassed H2O. None of the complexes were soluble in aqueous formic acid solutions, even at milligram per 100 mL concentrations, so an organic solvent additive was necessary to solubilize the catalyst precursors in the catalytic medium. Commonly, water-miscible solvents like DMF, DMSO, and 1,4-dioxane are used in FAD catalysis,21,25,28 although liquid amines can also serve the dual purpose of catalyst solubilizer and Lewis basic additive to drive catalysis.17,28 For precatalysts LRRu(H)X (particularly the R = H derivatives), we have found that strongly donating solvents (specifically acetonitrile in this case) can induce a 1,2-hydride to carbene-carbon shift to form a PCalkylP complex;27 this is a primary mode by which these ligands engage in cooperativity for stoichiometric29–33 and catalytic34–38 transformations. In this context, transfer of the Ru–H to the ligand carbene carbon shuts down FAD catalysis (see mechanistic discussion below), so we used minimal amounts of the weakly-coordinating solvent 1,4-dioxane to solubilize the precatalysts in aqueous formic acid.Initial small-scale experiments were conducted by dissolving the four ruthenium hydride precursors in ≈0.1 mL of dioxane in vial sealed with a septum under argon and adding ≈0.6 mL of 1.15 M aqueous, argon sparged formic acid solutions. For the R = H complexes LHRu(H)X, immediate, visible evolution of gas was observed. Through analysis of the headspace by gas chromatography (GC), the gases evolved were determined to be H2 and CO2; no detectable amounts of CO were observed (detection limit ≈50 ppb). For the two LNMe2Ru(H)X catalyst precursors, gas evolution was significantly less vigorous, and solutions underwent a rapid orange to purple color change upon which catalysis halted, leaving most of the formic acid substrate intact. Subsequent experiments therefore focussed exclusively on the LHRu(H)X catalyst precursors.
Larger scale catalytic reactions were performed using a simple system that captures the evolved gas in an inverted graduate cylinder; the set-up is similar to what other researchers have employed for evaluation of molecular FAD catalysts15,21,24 and is depicted schematically in Fig. S1.† Results of various experiments are summarized in Table 1. Catalyst precursors were dissolved in 1,4-dioxane in the reaction flask and the process initiated by injection of an amount of degassed, commercial grade (88%) formic acid through the flask septum at room temperature (21 °C). Under optimized conditions, both LHRu(H)Cl and LHRu(H)-κ2-O2CH mediate complete, selective conversion (TON = 6900) of formic acid to H2 and CO2 (Table 1, entries 1 and 2). The reaction selectivity was confirmed by GC analysis and to confirm the complete conversion of formic acid, the reaction solution was assayed using 1H NMR spectroscopy, using sodium benzoate as an internal standard. The κ2 formato catalyst precursor is ≈4× more active that the chlorido derivative. When determining the minimum amount of dioxane solubilizer required, it was found that formic acid concentrations above the 13 M used for the optimized runs leads to a halting of catalysis. For LHRu(H)-κ2-O2CH, gas evolution ceases completely at 15 M formic acid, while LHRu(H)Cl remained highly active for a few minutes before the rate began to decline (Table 1, entry 3), with gas production stopping completely after 27 minutes. Experiments analogous to that in entry 3 which included basic additives like triethylamine or sodium formate19,21,28,39,40 gave the same results. Furthermore, these additives did not enhance the activity of the catalysts as found in entries 1 and 2, indicating that FAD catalysis using LHRu(H)X do not require basic additives to be effective. The decline or lack of activity observed at [HCOOH] > 13 M appears to be a solubility issue, where catalyst precipitation in more concentrated formic acid stops the catalytic reaction. Consistent with this hypothesis, injection of more 1,4-dioxane to entry 3 solutions leads to a resumption of gas evolution at comparable activities to those observed for entries 1 and 2. As expected, activity can be increased by raising the temperature to 40 °C (entries 4 and 5); we did not explore higher temperature regimes. It should also be noted that no reaction occurred in the absence of catalyst. Furthermore, as shown in entry 8, the complex [Ru(p-cymene)Cl2]2 (which is the starting material used to prepare complexes LHRu(H)X27), is completely inactive under these conditions. This simple precursor has been shown mediate FAD catalysis, albeit under much different conditions and rather poorly.28
| Entry | Catalyst | T (°C) | TON | TOF (h−1) |
|---|---|---|---|---|
| a Optimized conditions, performed in triplicate, room temperature: 0.0015 mmol of catalyst dissolved in 2.0 mL 1,4-dioxane, 4.5 mL of 88% formic acid added (13 M). Deviations in calculated TOFs were no greater than ±5% based on the difference of the slopes in plots of gas volume vs. time. b 0.0015 mmol of catalyst dissolved in 2.0 mL 1,4-dioxane, 5.0 mL 88% formic acid added (15 M). c 0.004 mmol of catalyst in 2.5 mL 1,4-dioxane, 23 mL of 88% formic acid added at a rate of 0.86 mL per hour. d 0.003 mmol catalyst dissolved in 2.0 mL dioxane, 5 sequential additions of 0.45 mL 88% formic acid, TOF reported for first addition. | ||||
| 1a | L R Ru(H)Cl | 21 | 6900 | 1300(65) |
| 2a | L H Ru(H)-κ 2 -O 2 CH | 21 | 6900 | 4170(200) |
| 3b | L R Ru(H)Cl | 21 | 1926 | — |
| 4a | L R Ru(H)Cl | 40 | 6900 | 1850(90) |
| 5a | L H Ru(H)-κ 2 -O 2 CH | 40 | 6900 | 8000(400) |
| 6c | L H Ru(H)-κ 2 -O 2 CH | 21 | 122![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 735 735 |
— |
| 7d | L H Ru(H)-κ 2 -O 2 CH | 21 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
3850 |
| 8a | [Ru(p-cymene)Cl2]2 | 21 | 0 | 0 |
To obtain a better indication as to the longevity of catalyst precursors LHRu(H)X in comparison to related systems with high TONs (Chart 1), we conducted catalytic runs with substantially lower catalyst loadings (Table 1, entry 6). Being limited by the formic acid concentration as described above, we used a syringe pump to add 23.00 mL of 88% formic acid at a rate of 0.86 mL per hour to 0.004 mmol of the more active catalyst, LHRu(H)-κ2-O2CH, in 2.5 mL of 1,4-dioxane. The reaction was stopped once the addition was complete (∼27 hours), at which point no further gas evolution was observed. Based on integration of the 1H NMR spectrum, ∼93% conversion was reached with a total of ≈120![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 turnovers. The rate of gas production could not be measured with this high volume of gas, although the gas evolution did appear to slow after several hours before stopping after 24 hours. Given the oxygen sensitivity of the catalyst precursor, we attribute the halting of catalysis to eventual degradation of the catalyst due to the seepage of trace oxygen into the system and view these turnover numbers as representing a minimum value under the conditions employed.
000 turnovers. The rate of gas production could not be measured with this high volume of gas, although the gas evolution did appear to slow after several hours before stopping after 24 hours. Given the oxygen sensitivity of the catalyst precursor, we attribute the halting of catalysis to eventual degradation of the catalyst due to the seepage of trace oxygen into the system and view these turnover numbers as representing a minimum value under the conditions employed.
Finally, we also probed the question of catalyst longevity by conducting five successive single injection cycles (Table 1, entry 7; Fig. 2) of substrate, using LHRu(H)-κ2-O2CH as the catalyst precursor. In this experiment, after each injection of formic acid substrate charge, the evolved gases in the inverted graduated cylinder were removed in vacuo and the reaction vessel recharged with formic acid. As shown in Fig. 2, resumption of gas evolution was instantaneous upon reintroduction of substrate. However, while the first two cycles showed the same rate within error (∼2%) the rate during the third cycle dropped by ≈25%. The 4th cycle showed a further drop in the rate of gas evolution to ≈58% slower than that of the first cycle (note, this 4th charge occurred several hours after the 3rd charge had been fully converted). By the 5th cycle the rate was slowing during the reaction, even as formic acid was present in large excess. These experiments demonstrate that LHRu(H)-κ2-O2CH exhibits remarkable stability over long periods of time, likely limited primarily by its oxygen sensitivity.
 | ||
| Fig. 2 Graph of the volume of gas formed over time in 5 cycles of formic acid dehydrogenation catalyzed by LHRu(H)-κ2-O2CH. | ||
B. Mechanism
When FAD reactions mediated by LHRu(H)X are monitored by 31P{1H} NMR spectroscopy, the catalyst precursors are the only species observable during catalysis (Fig. S2†). Stoichiometric reactions of LHRu(H)X and one equivalent of H13CO2H, when monitored by 13C{1H} NMR spectroscopy (Fig. S3,† X = Cl; S4, X = κ2-O2CH) show signals only for 13CO2 product, with no intermediates observed in either case; for LHRu(H)-κ2-O2CH, small amounts of label are incorporated into the formato ligand of the precatalyst, consistent with previous observations.27Together, these observations point to a rate limiting protonolysis of the hydride ligands in LHRu(H)X by HCOOH (pKa = 3.75 (ref. 41)), to release H2 and form the unobserved intermediates I (X = Cl) and II (X = κ2-O2CH) depicted in Scheme 1. In our previous contribution, we attempted to prepare these compounds but found them to be prone to rapid loss of CO2, producing LHRu(H)X cleanly and quantitatively. These two steps constitute a simple mechanism for formic acid dehydrogenation. We note here that when more strongly donating solvents like acetonitrile are used to solubilize the catalyst, catalysis is shut down because of the 1,2-hydride transfer to the carbene carbon induced by such solvents.27 Thus, maintaining the Ru–H moiety is essential for catalysis. The enhanced activity observed for the formato precatalyst LHRu(H)-κ2-O2CH likely stems from its more rapid reaction with formic acid in the first rate determining protonolysis step in comparison to the chlorido version LHRu(H)Cl. In the stoichiometric reactions with H13CO2H mentioned above (Fig. S3 and S4†), the degradation of formic acid is essentially instantaneous for the former while for the latter it takes 15–20 minutes to fully convert.
The products of rate determining protonolysis, intermediates I and II, Scheme 1, rapidly release CO2 to complete the cycle. Noting that the hydrido formates previously reported undergo loss of CO2 at a much slower rate, the question arises as to why elimination of CO2 from I and II are so facile in comparison. We propose that the disparity is related to differing trans influence for a hydrido ligand vs. the chlorido and κ1-formato ligands in I and II. Presumably, in order to undergo β-elimination to release carbon dioxide, slippage of the κ2-formato ligands in I and II to a κ1 structure must occur in order to access the proposed β-elimination type transition states TS-Cl and TS-O2CH shown in Scheme 1. (Although II already has one κ1-formato ligand, it is not able to β-eliminate due to coordinative saturation). Indeed, both structural and computation evidence suggests that the Otrans bonds (highlighted in pink in Scheme 1) are shortened significantly in in silico or chemical model structures of I and II in comparison with the formato hydride LRRu(H)-κ2-O2CH structures.
For example, the β-elimination immune benzoate complex LNMe2Ru(Cl)-κ2-O2CPh was prepared and structurally characterized for comparison to the published structure of LNMe2Ru(H)-κ2-O2CH.27 The benzoate was readily prepared via reaction of LNMe2RuCl2 and NaO2CPh; further details can be found in the ESI.† Interestingly, this compound can also be cleanly prepared by treatment of LNMe2Ru(H)Cl with benzoic acid (pKa = 4.20 (ref. 42)), a weaker acid than formic acid. This observation supports the initial protonolysis step proposed in Scheme 1. In any case, crystals of model complex LNMe2Ru(Cl)-κ2-O2CPh were obtained from benzene solutions layered with pentane, and the molecular structure of this compound is shown in Fig. 3. In comparison to the reported structure of LNMe2Ru(H)-κ2-O2CH,27 where the difference between the Ru–O(1) and Ru–O(2) is only 0.081 Å, this disparity in LNMe2Ru(Cl)-κ2-O2CPh is substantially larger at 0.222 Å. This is mainly due to an elongation of Ru–O(2)trans bond in the hydrido formate in comparison to the same bond in the chloro benzoate, consistent with the greater trans influence expected for the hydrido ligand in the former complex. With a larger disparity between the Ru–O(1)/Ru–O(2) distance, the benzoate ligand in LNMe2Ru(Cl)-κ2-O2CPh is more energetically inclined to access the κ1 mode than the formato ligand in LNMe2Ru(H)-κ2-O2CH and provides some circumstantial support for the notion that weaker trans influence ligands favor κ1-formato structures and more facile CO2 loss from intermediates like I and II.
A more direct comparison between LRRu(X)-κ2-O2CH (here, X is H vs. Cl) was obtained computationally using DFT methodology (bp3w91-SDD for Ru; def2TZVP for Cl, P, O, Ccarbene; def2SVP for the remaining atoms) to compute the ground state structures of the four complexes. Full computational details and coordinates can be found in the ESI.† The calculated structures of LRRu(H)-κ2-O2CH once again showed differences in Ru–Ocis and Ru–Otrans bond lengths of less than 0.1 Å and a more stabilized κ2 structure; the metrical parameters obtained for the R = NMe2 complex are in good agreement with the experimentally determined structure.27 As found for the model benzoate structure discussed above, the calculated structures of the chlorido derivatives LRRu(Cl)-κ2-O2CH had a much greater difference between these two bond lengths: Δ (Ru–Ocis/Ru–Otrans) = 0.282 Å for R = H and 0.272 Å for R = NMe2 (Fig. S5†). This further substantiates the notion that the replacement of the hydride with a chloride pushes the formate closer to a κ1 coordination mode, which would be expected to lower the barrier for β-H elimination assuming this requires slippage to a κ1 formate to allow access to the TS-Cl or TS-O2CH transition structures. It should also be noted that since the X ligand in II is a second formato ligand, CO2 elimination from this species is statistically favored in comparison to I and may also contribute to the overall higher activity observed for this catalyst relative to the chlorido derivative.
Conclusions
In this study, we evaluated four PCcarbeneP pincer complexes LRRu(H)X as formic acid dehydrogenation catalysts. While the R = NMe2 derivatives undergo rapid stoichiometric reactivity with HCOOH, they are not stable under typical catalytic conditions. However, the unsubstituted derivatives (R = H) are highly effective catalysts for the selective conversion of formic acid to dihydrogen and carbon dioxide at room temperature, without the need for Lewis base additives. Both for X = Cl and κ2-O2CH, the catalysts exhibit high turnover numbers and reasonable turnover frequencies, with the latter being about 3–4 times as active. Mechanistic studies support a two-step mechanism where the resting state of the catalysts are the hydrido precursors. Rate limiting protonolysis followed by rapid CO2 elimination completes the simple catalytic cycle.In comparison to the state-of-the-art molecular catalysts based on ruthenium depicted in Chart 1, compounds LHRu(H)X perform very well. In most instances, the TOF values observed here at 21 °C are comparable to those observed for other systems at >90 °C, the exception being the system reported by Pidko et al.19,20 While we report somewhat lower TON values than the systems listed in Chart 1, the value of ≈122![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 we obtain is a lower limit; the somewhat rudimentary nature of our experimental set up, coupled with the oxygen sensitivity of our catalyst systems limits our ability to more accurately evaluate the true longevity of these catalysts. The system most comparable to the catalysts LHRu(H)X reported here is the chemically more simple catalyst of Beller et al.16 While it has demonstrated high turnover numbers, this was evaluated in a more sophisticated apparatus than ours;17 in terms of TOF under similar conditions, the performance of LHRu(H)-κ2-O2CH is about 4× faster than the Beller system, and without the need for amine base additives.
000 we obtain is a lower limit; the somewhat rudimentary nature of our experimental set up, coupled with the oxygen sensitivity of our catalyst systems limits our ability to more accurately evaluate the true longevity of these catalysts. The system most comparable to the catalysts LHRu(H)X reported here is the chemically more simple catalyst of Beller et al.16 While it has demonstrated high turnover numbers, this was evaluated in a more sophisticated apparatus than ours;17 in terms of TOF under similar conditions, the performance of LHRu(H)-κ2-O2CH is about 4× faster than the Beller system, and without the need for amine base additives.
Data availability
The data supporting this article have been included as part of the ESI.†Author contributions
Experiments, computations and data analysis were carried out by LJD. The manuscript was prepared with contributions from LJD and WEP. BSG performed X-Ray crystallographic analysis on LNMe2Ru(Cl)-κ2-O2CPh.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was funded by the Natural Sciences and Engineering Research Council of Canada through a Discovery Grant to WEP. WEP also acknowledges and thanks the Canada Research Chairs program for a Tier I CRC (2020-2027). LJD thanks NSERD for a PGS-D award and the Province of Alberta for and Alberta Graduate Excellence Scholarship (AGES).Notes and references
- I. P. Jain, Int. J. Hydrogen Energy, 2009, 34, 7368–7378 CrossRef CAS.
- J. Eppinger and K.-W. Huang, ACS Energy Lett., 2017, 2, 188–195 CrossRef CAS.
- M. Yadav and Q. Xu, Energy Environ. Sci., 2012, 5, 9698–9725 RSC.
- M. Tawalbeh, R. M. N. Javed, A. Al-Othman, F. Almomani and S. Ajith, Environ. Technol. Innovation, 2023, 31, 103217 CrossRef CAS.
- A. Wang, P. He, J. Wu, N. Chen, C. Pan, E. Shi, H. Jia, T. Hu, K. He, Q. Cai and R. Shen, Energy Fuels, 2023, 37, 17075–17093 CrossRef CAS.
- S. Satyapal, J. Petrovic, C. Read, G. Thomas and G. Ordaz, Catal. Today, 2007, 120, 246–256 CrossRef CAS.
- G. Sievi, D. Geburtig, T. Skeledzic, A. Bösmann, P. Preuster, O. Brummel, F. Waidhas, M. A. Montero, P. Khanipour, I. Katsounaros, J. Libuda, K. J. J. Mayrhofer and P. Wasserscheid, Energy Environ. Sci., 2019, 12, 2305–2314 RSC.
- W. L. Nelson and C. J. Engelder, J. Phys. Chem., 1926, 30, 470–475 CrossRef CAS.
- R. Xu, W. Lu, S. Toan, Z. Zhou, C. K. Russell, Z. Sun and Z. Sun, J. Mater. Chem. A, 2021, 9, 24241–24260 RSC.
- N. Onishi, R. Kanega, H. Kawanami and Y. Himeda, Molecules, 2022, 27, 455 CrossRef CAS.
- C. Guan, Y. Pan, T. Zhang, M. J. Ajitha and K.-W. Huang, Chem. – Asian J., 2020, 15, 937–946 CrossRef CAS PubMed.
- N. H. Anderson, J. Boncella and A. M. Tondreau, Chem. – Eur. J., 2019, 25, 10557–10560 CrossRef CAS.
- A. Léval, H. Junge and M. Beller, Catal. Sci. Technol., 2020, 10, 3931–3937 RSC.
- A. Boddien, D. Mellmann, F. Gärtner, R. Jackstell, H. Junge, P. J. Dyson, G. Laurenczy, R. Ludwig and M. Beller, Science, 2011, 333, 1733–1736 CrossRef CAS PubMed.
- E. A. Bielinski, P. O. Lagaditis, Y. Zhang, B. Q. Mercado, C. Würtele, W. H. Bernskoetter, N. Hazari and S. Schneider, J. Am. Chem. Soc., 2014, 136, 10234–10237 CrossRef CAS.
- A. Boddien, B. Loges, H. Junge, F. Gärtner, J. R. Noyes and M. Beller, Adv. Synth. Catal., 2009, 351, 2517–2520 CrossRef CAS.
- P. Sponholz, D. Mellmann, H. Junge and M. Beller, ChemSusChem, 2013, 6, 1172–1176 CrossRef CAS.
- J. R. Khusnutdinova and D. Milstein, Angew. Chem., Int. Ed., 2015, 54, 12236–12273 CrossRef CAS PubMed.
- G. A. Filonenko, R. van Putten, E. N. Schulpen, E. J. M. Hensen and E. A. Pidko, ChemCatChem, 2014, 6, 1526–1530 CrossRef CAS.
- G. A. Filonenko, E. J. M. Hensen and E. A. Pidko, Catal. Sci. Technol., 2014, 4, 3474–3485 RSC.
- Y. Pan, C.-L. Pan, Y. Zhang, H. Li, S. Min, X. Guo, B. Zheng, H. Chen, A. Anders, Z. Lai, J. Zheng and K.-W. Huang, Chem. – Asian J., 2016, 11, 1357–1360 CrossRef CAS PubMed.
- Y. Himeda, Green Chem., 2009, 11, 2018–2022 RSC.
- Z. Wang, S.-M. Lu, J. Li, J. Wang and C. Li, Chem. – Eur. J., 2015, 21, 12592–12595 CrossRef CAS.
- S. Kar, M. Rauch, G. Leitus, Y. Ben-David and D. Milstein, Nat. Catal., 2021, 4, 193–201 CrossRef CAS PubMed.
- D. P. Estes, M. Leutzsch, L. Schubert, A. Bordet and W. Leitner, ACS Catal., 2020, 10, 2990–2998 CrossRef CAS.
- R. A. Manzano and R. D. Young, Coord. Chem. Rev., 2021, 449, 214215 CrossRef CAS.
- L. J. Donnelly, J.-B. Lin, B. S. Gelfand, C. Y. Chang and W. E. Piers, Dalton Trans., 2024, 53, 1862–1869 RSC.
- B. Loges, A. Boddien, H. Junge and M. Beller, Angew. Chem., Int. Ed., 2008, 47, 3962–3965 CrossRef CAS.
- R. J. Burford, W. E. Piers and M. Parvez, Organometallics, 2012, 31, 2949–2952 CrossRef CAS.
- L. E. Doyle, W. E. Piers and J. Borau-Garcia, J. Am. Chem. Soc., 2015, 137, 2187–2190 CrossRef CAS PubMed.
- L. E. Doyle, W. E. Piers, J. Borau-Garcia, M. J. Sgro and D. M. Spasyuk, Chem. Sci., 2016, 7, 921–931 RSC.
- D. V. Gutsulyak, W. E. Piers, J. Borau-Garcia and M. Parvez, J. Am. Chem. Soc., 2013, 135, 11776–11779 CrossRef CAS PubMed.
- E. A. LaPierre, W. E. Piers, D. M. Spasyuk and D. W. Bi, Chem. Commun., 2016, 52, 1361–1364 RSC.
- J. Borau-Garcia, D. V. Gutsulyak, R. J. Burford and W. E. Piers, Dalton Trans., 2015, 44, 12082–12085 RSC.
- J. D. Smith, G. Durrant, D. H. Ess, B. S. Gelfand and W. E. Piers, Chem. Sci., 2020, 11, 10705–10717 RSC.
- W. Weng, S. Parkin and O. V. Ozerov, Organometallics, 2006, 25, 5345–5354 CrossRef CAS.
- A. V. Polukeev and O. F. Wendt, Organometallics, 2017, 36, 639–649 CrossRef CAS.
- H. Tinnermann, S. Sung, B. A. Cala, H. J. Gill and R. D. Young, Organometallics, 2020, 39, 797–803 CrossRef CAS.
- J. F. Hull, Y. Himeda, W.-H. Wang, B. Hashiguchi, R. Periana, D. J. Szalda, J. T. Muckerman and E. Fujita, Nat. Chem., 2012, 4, 383–388 CrossRef CAS PubMed.
- A. Vatsa and S. K. Padhi, New J. Chem., 2022, 46, 15723–15731 RSC.
- J. A. Riddick and W. B. Bunger, Techniques of Chemistry: Organic Solvents, John Wiley and Sons Ltd., New York, 4th edn, 1985 Search PubMed.
- W. M. Haynes, CRC Handbook of Chemistry and Physics, CRC Press Inc., Boca Raton, 91st edn, 2010 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: General Experimental details, synthesis and characterization of all new compounds, catalytic procedures, computational details and crystallographic parameters for CCDC 2400771. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4cy01346h |
| ‡ Unpublished results in the form of a crystal structure and 31P NMR data suggest that phosphine oxidation is the primary avenue of decomposition for these compounds in the presence of O2 and other O atom transfer agents. Further elucidation of these products is beyond the scope of this article, but we note that oxygen poisoning of catalysis is rapid and irreversible in the context of the FAD process reported here. |
| This journal is © The Royal Society of Chemistry 2025 |