Chemical kinetic mechanism for selective catalytic reduction of nitrogen oxides†
Received
9th October 2024
, Accepted 5th December 2024
First published on 5th December 2024
Abstract
A generic chemical kinetic mechanism for nitric oxide reduction by ammonia is developed exploiting similarities in redox cycles exhibited by different catalysts. The mechanism comprises 28 reactions, the rate constants of which were estimated through analysis of the individual sub-processes and identifying the overall rate with the rate of the limiting step. The chemical kinetics so developed was used to simulate operation of several catalysts in a plug flow reactor. These simulations show that, after taking into account differences in feed gas composition, active site concentration and residence time, varying only one kinetic parameter, namely activation energy for the low-temperature catalytic site oxidation allows one to reconcile the observed differences between copper and iron exchanged zeolites and cerium dioxide with tungsta on titania. Prediction of the NO conversion by vanadia at high temperatures required changes of two kinetic parameters.
1 Introduction
Removal of nitric oxide from exhaust or flue gas is required for a great variety of applications ranging from a passenger car engine to a large power plant, and selective catalytic reduction (SCR) of NO by ammonia is often the only practical means of achieving this. It is therefore not surprising that there is a wealth of literature, see e.g. review of Han et al.1 or Fig. 1 in Lian et al.2 illustrating the exponential growth of the number of publications in recent years, devoted to investigation of SCR surface reactions and their pathways, undertaken through experiments and/or numerical modelling. However, perhaps owing to the complexity and large number of possible transition states, the rate analysis is largely limited to some individual possible reactions with few notable exceptions, e.g. Janssens et al.3 Regardless of the exact composition of the catalyst, the SCR proceeds as a cyclic process with two or more interlinked pathways. One of these chemical pathways results in a reduction, during which the catalyst metal lowers the number of its valent bonds and another pathway involves oxidation where the number of valent bonds is restored by reaction with the free oxygen typically present in exhaust or flue gas, e.g. Topsøe et al.4 and Han et al.1 The operating temperature of an SCR may also vary from less than 450 K at the cold start to more than 900 K at full load, thus complicating the direct translation of laboratory catalyst kinetic studies, usually performed in a much smaller temperature range, into an applied numerical model.
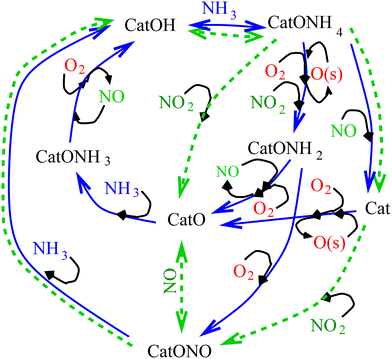 |
| | Fig. 1 Graphical representation of the proposed kinetic scheme of selective catalytic reduction of nitric oxide by ammonia. | |
A number of SCR models represent the processes in terms of net reactions compounding together physisorption, chemical adsorption, surface diffusion and chemical transformations, e.g. Olsson et al.5 or De-La-Torre et al.6 In such approaches, the rate expressions are found by fitting the rate coefficients to match simulation results to one or several experiments and it is difficult to estimate the generality of the obtained expressions, the range of operating conditions and the types of catalysts to which they are applicable. The kinetic experiments are usually conducted in micro-reactors with characteristic dimensions of a few millimetres filled with powder catalysts, e.g. Chatterjee et al.7 Arguably, the use of micro-reactors eliminates the influence of mass transfer from the gas phase to the catalyst surface. The temperature of the micro-reactor is homogeneous and tightly controlled, and flow rates through it are so small as to eliminate any spatial variation in gas and surface species concentrations. On the other hand, quantum chemistry simulations using either analytical forms of molecular orbitals, e.g. German and Sheintuch,8 or density functional theory, e.g. Arnarson et al.,9 are very useful in establishing the structure of possible transition states and the rate of associated reactions but owing to their heavy computational requirements, they are necessarily restricted to a limited number of configurations. Yet, together with available measurements, these methods allow one to clarify the mechanisms of the rate-limiting processes, that is conditions under which the overall rate of NO conversion is constrained by an elementary step of the chemical kinetics or physical kinetics, e.g. physisorption at or diffusion to the catalyst surface from the bulk of gas. Nonetheless, despite the progress achieved in studies of different factors in the selective catalytic reduction of nitric oxide by ammonia NH3, see e.g. Kim et al.,10 there does not seem to exist a comprehensive mathematical description of the latter including both physical and chemical rates of individual processes. Development of such a model is attempted here based on the generalised kinetics whereby the formulated kinetic pathways exploit the similarity of the redox cycles for the different types of catalysts and the rate constants for individual chemical reactions are estimated as average values across the range of catalysts. While this generalisation necessarily entails lower accuracy than the one attainable with fine tuning of the rates for a specific type of catalyst or SCR system design, it is worth emphasising that, owing to the complexity of the numerical modelling of flow and reactions in the SCR, a number of other assumptions are inevitable and the loss of accuracy caused by the use of generalised kinetics in simulations of a complete SCR system may well be smaller than that caused by other simplifications, e.g. the pattern of reducing agent spray entering the catalyst, e.g. if ammonia comes from decomposition of urea water solution as is commonly done in automotive applications.
The purpose of this work is thus to consider the generic elementary steps involved in NO reduction and estimate their rates from well-established dependencies. This is done with the hope that the resulting model, while perhaps not tuned to any particular type of catalyst, would nonetheless be capable of yielding an accuracy sufficient for an a priori analysis of a wide range of SCR exhaust aftertreatment systems through numerical simulations resolving simultaneously the gas flow and SCR chemistry. As shown by Jin et al.11 a number of SCR catalysts have similar properties in terms of porosity, in the range 0.3…0.4, characteristic pore dimension, circa 10 nm, overall concentration of active sites, 0.5…1.5 × 10−3 mole cm−3, and an attempt to utilise these similarities is made here through formulation of a generalised chemical kinetic mechanism and consideration of both physical and chemical steps in SCR processes.
2 Physical and chemical kinetics in SCR catalysts
The starting point in the development of this kinetic mechanism was the assumption that any catalytic site irrespective of its nature and composition may be attributed the same reaction rate constants. Though this assumption is obviously wrong as, e.g. it is well known that iron catalysts have much lower catalytic activity at lower temperatures compared to copper-exchanged zeolites or vanadia–tungsta catalysts, it proved nonetheless very useful in establishing the baseline kinetic mechanism, and estimating its rate constants. Departing from there, the difference in performance of different types of catalysts could then be reflected in changes of only a few rate constants while most of the scheme remains the same reflecting the generic features of SCR chemistry.
In what follows, Cat denotes the catalytic complex, e.g. Cu2+ in Cu – exchanged zeolites, or V5+ for vanadia catalysts, and Z denotes a substrate surface site capable of physisorption, e.g. SiOAl site for a zeolite or TiO2 for a vanadia/tungsta catalyst. Charge changes are disregarded, that is Cat− and Cat species are lumped together. Both surface and gaseous species are described in terms of their molar concentrations: this allows for a straightforward account of the surface coverage factor but makes it difficult to describe the neighbouring effects and the latter are neglected here. The differences between the activity of oligomeric, dimeric and polymeric active centres are reflected through introduction of several competing paths, the relative importance of which changes with temperature, catalyst loading and composition of the feed gas. Essentially, a given catalyst surface is imagined as a uniform substrate with a fixed molar surface density ns of sites with a uniform fraction of oligomeric active sites.
This surface has a specific volumetric surface area identified here with the BET area; hence it is assumed that all reactions proceed either by the Eley–Rideal mechanism or in an adsorbed monolayer. It is assumed that, other than the catalytic sites, there are only 3 surface species: NH3(s), NO2(s) and O(s); the study of the role of the physiosorbed water and formation and reactions of surface hydroxyl are left for the subsequent work.
Two key catalytically active species in this mechanism are CatOH, designating the sites with Brønsted acidity, and CatO, a combination species with Lewis acidity. Together with the sites in an intermediate state they participate in a catalytic cycle shown in Fig. 1. The relative proportion of the CatOH and CatO sites existing in a degassed catalyst is an important characteristic of the latter: for vanadia-based catalysts with virtually no Lewis acidity all active sites are taken as CatOH, while for metal-replaced zeolites the active sites are assumed to be mostly CatO. In order to make the model under development generic, i.e. applicable to variety of catalysts, it is proposed to combine mechanistically the pre-existing Lewis sites together with derivative CatO, e.g. produced by the sequence of reactions R1, R7 and R11 even though the valency of the catalyst metal would not be the same. This ansatz of lumping together catalyst sites with unequal valencies, hence possibly reactivity, is made solely to keep the model as simple as possible. It should be emphasised that both types of acidity refer to the catalyst sites and the effects of acidities on the substrate, see e.g. Ravi et al.,12 are not considered: in this model the substrate itself is chemically passive but the three surface species adsorbed on it are reactive.
Fig. 1 depicts the summary of the proposed mechanism; in it, the main SCR loops are shown in blue solid lines, while the reactions pertinent to the so-called fast SCR loop involving NO2 are shown as green dashed lines. Evacuation of the main reaction products, water vapour and nitrogen is not shown in order to simplify the diagram. It should be noticed that the reaction pathway involving the formation of nitrates at the catalytic site is represented here by reactions involving the CatONO complex; this aspect is further discussed below. As may be seen from Fig. 1, the proposed mechanism includes also the pathways for ammonia and NO oxidation at elevated temperatures, thus enabling simulations of effects of catalyst overheating. However, nitrous oxide N2O and its reactions are excluded from the mechanism: it should be noticed that under most conditions, the yield of N2O is very small at least in automotive applications. Competition between reactions involving NO and O2 determines a progressive shift between different pathways of the redox cycle to ammonia oxidation at temperatures above 400 °C leading to worsening of NO conversion at more or less constant consumption of ammonia. The individual steps of the mechanism are considered in the subsequent sections.
In order to facilitate the inclusion of the proposed mechanism into the flow simulations, the rates of reactions and concentrations of both surface and gaseous species are expressed in this work as volumetric molar concentrations, following common convention for description of homogeneous reacting media. For a surface species Y, the volumetric concentration [Y] is related to the coverage fraction ΘY and the surface concentration 〈Y〉 as:
where
ns is the total molar surface concentration and
![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif)
is the BET surface area of the catalyst per unit volume. Here and in what follows the square and angle brackets denote specific quantities per unit volume and surface, respectively. In the estimations of the rate constants below, the value of
ns = 1.5 × 10
−1 mole per cm
2 is taken as constant for all types of catalysts; this value corresponds to approximately 3 Å spacing between the molecules at the surface: for most SCR catalysts, the typical inter-site distance on the surface is
rs ≈ 2–3 Å. The BET area,
i.e. catalyst specific surface area
![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif)
, an input parameter to this model, lies in the range of several tens to several hundred m
2 cm
−3.
2.1 Adsorption of ammonia
There is ample experimental evidence that sorption of NH3 may produce both strongly chemisorbed and weakly physiosorbed ammonia (Topsøe et al.,4 Ma et al.,13 and Hahn et al.)14 The strong chemisorption of ammonia on a catalyst Brønsted acid site leads to the formation of bound ammonium, Han et al.:1| |  | (R1) |
with a reverse process of desorption of NH3 from the active site. This step is common for any catalyst site with Brønsted acidity, e.g. vanadia (Topsøe et al.,4 Inomata et al.),15 Nb–Cs (Ma et al.),13 or Cu-exchanged zeolite (Janssens et al.)3 Reaction of the Brønsted site with NO is ruled out owing to the evidence from experiments of Inomata et al.15 and DFT simulations of Arnarson et al.16 for vanadia catalysts with various dopants.
The rate W1f of formation of ammonium bound on the catalytically active site, reaction R1, is determined by the ammonia diffusion from the gas phase proceeding with zero activation energy (Busca et al.),17 with an accommodation steric factor ψ (sometimes also referred to as the “sticking coefficient”) within the possible range of values 102–1 with the larger values for molecular adsorption:
where
FNH3 is the molar flux of NH
3 from the bulk of the gas phase to the unit surface of the catalyst. The above expression incorporates the temperature
T and pressure
p dependency through the average thermal velocity
vNH3 and the molar density NH
3:
| |  | (2) |
Here
Rg is the universal gas constant, and
MNH3 is the molecular weight of ammonia.
Eqn (2) assumes the equipartition of translational degrees of freedom. The specific surface area of the CatOH species 〈
SCatOH〉 in
eqn (1) is simply related to the CatOH concentration as:
| |  | (3) |
and, using the above expressions, the rate
W1f becomes:
| |  | (4) |
where the “pseudo-pre-exponential factor”,
k1f, may be estimated as
k1f ≈ 4 × 10
11T0.5 (
k1f ≈ 10
13 cm
3 per mole s at
T = 600 K); the accommodation steric factor, or “sticking probability”,
ψ1f is taken here as one, a common value for molecular adsorption (Zhdanov).
18
Because k1f is effectively the rate of collisions of gas molecules with a unit surface, in what follows its value will be used as the upper limit for the pre-exponential factor of other reactions involving gaseous species. Zero activation energy and ψ in the range 0.1–1 are common for molecular adsorption on active catalyst sites, Zhdanov.18
For a typical SCR catalyst, ΘCatOH, the surface fraction of the Brønsted acid sites, lies in the range from 0.01, (or, obviously, even 0 for catalysts which do not exhibit protonation, e.g. Lietti et al.19) to a rather extreme value of ΘCatOH = 0.6, Alemany et al.,20 with typical values for most industrial catalysts of 0.02–0.04; thus [CatOH] ranges from 10−4 to 10−3 mole per cm3. With the values in the middle of this range, eqn (4) yields the inverse characteristic time of NH3 adsorption k1f[CatOH] ≈ 3 × 109 s−1. It is worth noticing that, though eqn (2) and (4) use expressions for thermal velocity in the bulk gas phase, the characteristic time of adsorption so obtained is very close to that of gaseous diffusion over a distance, e.g. pore diameter, of rp = 2 × 10−6 cm:
| |  | (5) |
It should also be mentioned that the above estimation of the inverse characteristic time is well within the range recommended by Zhdanov
18 but much larger than the values in the range of 10
3–10
4 s
−1 used previously in some applied simulations,
e.g. Chatterjee
et al.,
7,21 Schmeisser
et al.22
Reverse reaction to (R1) is the desorption of strongly bound NH3 from the active site, the characteristic time of which is
| |  | (6) |
where the pre-exponential factor for desorption
kdes may be estimated using analysis of Campbell
et al.23 involving the difference of entropies
S of the adsorbed NH
3(s) and gaseous NH
3 species:
| |  | (7) |
where
kB and
h are Boltzmann and Planck constants, respectively,

. The entropy
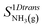
of gaseous ammonia with one translational degree of freedom removed may be estimated Campbell
et al.23 at
T0 = 298 K using the standard entropy of formation of argon
S0AR as:
| | 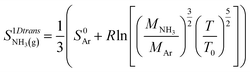 | (8) |
where the
MNH3 and
MAr are the molecular weights of ammonia and argon, respectively. Using the tabulated values Vargaftik
24 of
S0AR = 18.6R
g,
SNH3(400 K) = 205 J mole
−1 K
−1, one may obtain that the pre-factor in
eqn (7) at
T = 400 K,
k1b ≈ 8.4 × 10
14 s
−1 increasing to
k1b ≈ 1.6 × 10
15 s
−1 at 600 K. This estimation does not depend on the nature of the sorbent.
The activation energy for desorption of NH3 strongly adsorbed on the Brønsted sites was derived from temperature-programmed desorption experiments in Colombo et al.25 as E1b ≈ 106–116 kJ per mole. Using these values in eqn (6), one obtains at 400 K the characteristic time for desorption τdes ≈ 0.28 s, i.e. about eight orders of magnitude larger than the characteristic time for adsorption owing to the large activation energy of desorption. For different types of zeolites and silica–alumina catalysts with significant concentration of the acid cites, fairly wide distributions of the desorption activation energy were measured in Masuda et al.26 with maximum probabilities in the range of 70–110 kJ per mole. Thus, in the lower range of temperatures typical for SCR operation, the equilibrium of reaction R1 is strongly shifted to absorption on active sites.
An alternative path of CatONH4 formation is through the Langmuir–Hinshelwood mechanism, i.e. weak physisorption of NH3 on the metal oxide sites of the substrate Z with subsequent surface diffusion to and chemisorption at an active site:
| |  | (R2) |
| |  | (R3) |
Strictly speaking, the rates of these processes depend on the nature of the substrate and the structure of the surface. Even though it has been shown that for some catalysts,
e.g. V/W/TiO
2, NH
3 sorption on TiO
2 is molecular with the accommodation factor
ψ2 in the range 0.2–0.4, Diebold and Madey,
27 in the presence of oxygen or surface hydroxyl radicals from dissociatively adsorbed water vapour, chemisorption may not be excluded, see
e.g. Dastoor
et al.28 Following the arguments for the rate of adsorption on the active sites, the rate of physisorption on the substrate per unit catalyst volume may be estimated as
proceeding with zero activation energy and
ψ2 ≈ 0.25. The concentration of
Z is [
Z] =
ΘZns![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif)
where
ΘZ is the ratio of surface sites capable of physisorption to the total surface molecular concentration,
e.g. ΘZ = 1 for the tungsta substrate and for SSZ zeolites
ΘZ may be taken as equal to the Al/Si molar ratio.
The rate of desorption of weakly sorbed NH3(s) is
| | 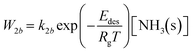 | (10) |
The pre-exponential factor in the above equation may be estimated using the same procedure involving the difference in entropies:
k2b ≈ 2.6 × 10
12 T [s
−1] in the temperature range relevant for SCR operation. Modelling of Colombo
et al.25 used the activation energy
Edes = 46.5 kJ per mole for the desorption of weakly adsorbed NH
3 for Fe-activated zeolite. However, using synchrotron PXRD experiments Ye
et al.29 showed for H-ZSM-5 zeolite a distribution of the desorption energies with peaks at 7, 21 and 113 kJ per mole corresponding to activation barriers for very weak interactions, N–H⋯O, hydrogen bonding N–H⋯N, and strong Brønsted acid–base adduct formation O⋯+HN, respectively. Here it is assumed that the adsorption on the substrate is through the formation of hydrogen bonds only, thus the desorption activation energy is taken as
E2b = 42 kJ per mole: the chemisorption is considered only on the catalytically active sites but not on the substrate. The reason for this is that, while adsorption of water always present in the exhaust is likely to increase the prominence of NH
3 sorption through hydrogen bonding, co-adsorption of water and ammonia on passive surfaces is beyond the scope of the present work.
Taking into account that the amount of the available sorption sites [Z] remains approximately constant, as it is verified below, the ratio of concentrations of physiosorbed and gaseous ammonia may be found if reaction R2 is in partial equilibrium:
| |  | (11) |
This ratio may be estimated at 400 K at 6 × 10
−4 with temperature rise decreasing this ratio further still. Work of Campbell
et al.23 showed that the pre-exponential
k1b has only a weak, within one order of magnitude, dependency on the adsorbate structure or composition, however, the issue of chemisorption of NH
3 on hydroxyl layers in the presence of water vapour in the gas,
e.g. forming the O*HNH
3 complex in the substrate, would deserve a further study.
Formation of CatONH4 from the weakly adsorbed ammonia proceeds through surface diffusion of the ammonia to a much heavier, hence less mobile, catalytic site, followed by reaction R3. The characteristic time for the surface diffusion is 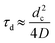 where dc is an average distance between two catalyst sites, dc ∼ (ΘCatOHnsNA)−1/2 and D is the surface diffusivity. The activation energy for surface diffusion is low, Zhdanov,18 and, assuming a typical value of D ≈ 10−3 cm2 s−1,30 one may estimate τd ≈ 1.4 × 10−12 s−1. Therefore, the rate of reaction R3 between two surface species:
where dc is an average distance between two catalyst sites, dc ∼ (ΘCatOHnsNA)−1/2 and D is the surface diffusivity. The activation energy for surface diffusion is low, Zhdanov,18 and, assuming a typical value of D ≈ 10−3 cm2 s−1,30 one may estimate τd ≈ 1.4 × 10−12 s−1. Therefore, the rate of reaction R3 between two surface species:
| |  | (12) |
may be assumed to proceed with very low activation energy
E3 ≈ 0, Chorkendorff and Niemanrsverdriet,
30 and its pre-exponential factor
k3 may be estimated as follows.
As reaction R3 is an addition, its activated complex is the same as the final product, and its formation comes with loss of two translational and one rotational degree of freedom (DOF) of NH3(s). For one translational DOF of a physiosorbed molecule, the partition function  where the cell size d is essentially the distance between two sorption sites, d ≈ rs:
where the cell size d is essentially the distance between two sorption sites, d ≈ rs:
and the thermal wavelength at 400 K
Thus, one translational DOF partition function
qT = 15. For one rotational DOF the partition function
qR may be estimated as
with the rotational temperatures Π
1,2,3 = 13.6, 13.6, and 8.9 K for ammonia. Thus at 400 K
qR ≈ 7. Then the characteristic reaction time
τ3 for
reaction R3 may be found as
| | 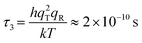 | (13) |
This time is much, by about two orders of magnitude, larger than the surface diffusion time
τd found above, therefore the chemical transformation is the limiting stage defining the pre-exponential factor
k3. When the rate of a bimolecular reaction is written for the molar concentrations of surface species its pre-exponential factor becomes:
| | 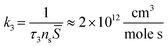 | (14) |
It is worth mentioning that the above value is about one order of magnitude larger that the values that may be derived from the recommendations of Zhdanov
18 for the frequency
ν of the bimolecular reaction between the adsorbed species,
ν = 10
13–10
14 s
−1. One may also see that the
reaction R3 is much faster than ammonia desorption, especially for a lower range of SCR operation temperatures. Taking into account fast surface diffusion and relatively fast reaction time, as well as the low equilibrium ratio of physiosorbed ammonia concentration to that of gaseous NH
3, one may see why the weakly adsorbed ammonia is commonly not detected in experiments, see
e.g. Inomata
et al.:
15 effectively,
reaction R3 acts as a fast sink for relatively small amounts of physiosorbed NH
3(s).
In formulation of the proposed mechanism it is assumed that both gaseous and physiosorbed ammonia adducts molecularly on Lewis acid cites: this assumption is supported by the spectroscopic observations of Suárez et al.31 This assumption leads to the following reactions:
| |  | (R4) |
| |  | (R5) |
As a matter of fact, chemisorption of NH
3 on CatO and formation of CatONH
3 through a valent bond involves electron transfer from NH
3 and is therefore equivalent to an action of a Lewis acid cite, except that in this case CatO may also be a derivative site formed as a part of the catalytic cycle. A number of novel catalysts, however, do not exhibit Brønsted acidity at all, Jin
et al.,
11 Han
et al.,
1 and for those
reaction R4 should be taken as the departure point for description of the SCR redox cycles.
As shown in Arnarson et al.,9reaction R4 has a relatively low activation energy of E3 = 7.4 kcal per mole for reduced CatO while pre-existing, i.e. non-reduced Lewis sites should chemisorb NH3(g) with an activation barrier greater than or at least equal to E3 and a much smaller accommodation factor, Yin et al.32 However, doping catalysts, e.g. vanadia with CeO2, accelerates chemisorption, Han et al.,1 thus increasing the accommodation factor and lowering the activation energy. Hence, the rate constants for reaction R4 may be estimated as ψ4k1f with lowered ψ4 = 0.3 to account for asymmetry of NO and E3 = 30 kJ per mole. The low value of the activation energy for the adsorption at the Lewis site is also in agreement with Marberger et al.,33 see also ref. 6 therein.
Reaction R5 is a bimolecular association of two surface species, thus for it one may safely assume zero activation energy and the characteristic frequency factor of 1014 s−1, Zhdanov,18 corresponding to the pre-exponential factor of  . On the other hand, the pre-exponential factor for the surface diffusion kd ≈ (τdns
. On the other hand, the pre-exponential factor for the surface diffusion kd ≈ (τdns![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) )−1 may be estimated as
)−1 may be estimated as  , thus this reaction is diffusion-controlled, non-activated and k5 = kd.
, thus this reaction is diffusion-controlled, non-activated and k5 = kd.
2.1.1 Redox cycles.
The envisaged normal SCR cycle comprises two steps of NO reduction and one step of oxidation with O2 in order to satisfy the overall stoichiometry. Reactions with NO or oxygen proceed in parallel for most states of the catalytic site, starting with the complex CatONH4 formed in reactions R1 and R3, see Fig. 1. The reaction of the complex CatONH4 with gaseous NO forms gaseous water, nitrogen, and a reduced active catalyst site:| |  | (R6) |
This reaction has been very extensively studied, see e.g. Arnarson et al.9 It may be thought as a succession of several steps: diffusion of NO with formation of an activated complex and consequent split of the latter, and evacuation, either by the surface diffusion or desorption of H2O, N2, and H2O again: a priori any of these steps may be rate limiting under a particular set of conditions.
The overall rate of reaction R6 may therefore be represented as:
| |  | (15) |
where
WNO is the rate of formation of the transition state CatONH
4NO,
WsH2O and
WeH2O are the rates of water scission and removal from the site,
i.e. desorption and surface diffusion,
WsN2 and
WeN2 are the rate of molecular nitrogen scission and removal, respectively. The rates of these individual steps may be estimated as follows.
Results of DFT simulations by Arnarson et al.9 show that formation of the transition state proceeds with activation energy ENO of 13.6 kcal per mole. Invoking a usual Arrhenius expression for its rate:
| |  | (16) |
the pre-exponential factor
kNO should be determined by the rate of flow of NO from the gas phase. Similar to the previous derivation for NH
3,
kNO may be written as
While data on the accommodation factor
ψNO are not available and its precise value depends on the nature of the catalyst, it may be tentatively estimated as
ψNO ≈ 005, the value in the range between the ranges for molecular and associative adsorption. Thus

yielding the characteristic time of this reaction of order of 0.2 s for typical NO molar densities in an exhaust gas at 600 K.
Scission of both water and nitrogen occurs with zero activation energy, and does not activate any additional degrees of freedom in the transition state, hence their pre-exponent factors are those of the monomolecular reaction of an adsorbed species, for which a typical value (Zhdanov)18 is  , e.g. at T = 500 K ksH2O = ksN2 = 1013 s−1, hence
, e.g. at T = 500 K ksH2O = ksN2 = 1013 s−1, hence
| | | WsH2O = WsN2 = ks[CatONH4NO] | (17) |
It is obvious that the scission step is much faster than the formation of the activated complex CatONH
4NO at any temperature, hence it cannot be rate limiting.
The rate of removal of products, e.g. water, away from the active site, is the sum of the rates of desorption WdesH2O from the active site and the surface diffusion, WdiffH2O away from the site:
| | | WeH2O = WdiffH2O + WdesH2O | (18) |
The pre-exponential factors for the desorption are determined following the same procedure of Campbell
et al.23 invoking entropy differences at 400 K and 600 K as:
| kdesH2O(400K) = 7.0 × 1014 s−1 kdesH2O(600K) = 1.3 × 1015 s−1 |
| kdesN2(400K) = 5.9 × 1014 s−1 kdesN2(600K) = 9.7 × 1014 s−1 |
The activation energy for the desorption from the active site is estimated here from the measurements of the rate of desorption extrapolated to unity coverage,
Θ = 1. For N
2 the experiments of Scholten
et al.34 on desorption from iron films yield
EdesN2(
Θ) = 55.0 − 29.2
Θ[kcal
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
per
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
mole] with the value extrapolated to full coverage
EdesN2 = 25.8 kcal per mole; this value is adopted here as an average for different substrates owing to the lack of data for other types of catalyst substrates. For the desorption of water, the activation energy reported for zeolites in Fan
et al.35 changed from approximately 20 kcal per mole at lower temperatures, 300–450 K, to just above 70 kcal per mole at 600–700 K; the reported value also depended, albeit with a smaller variation, upon the zeolite structure and what alkali metal, Li or Na, cations were used for charge compensation. The average value, measured in Fan
et al.35 at temperatures of 500–600 K, of
EdesH2O ≈ 40 kcal per mole, was about twice larger than the value of 18 kcal per mole reported for different TiO
2 crystals in Henderson.
36 Close to the latter, values of approximately 15 kcal per mole were reported for different types of zeolites in Prokof'ev
et al.37 and similar figures of 16.6 kcal per mole for silica in Feng
et al.38 For the overall rate estimations, the value of
EdesH2O = 20 kcal per mole is retained here.
Compared to desorption, the surface diffusion has very low activation energy which may safely be assumed as zero, and its rate constants may be estimated as, Campbell et al.:23
| |  | (19) |
leading to:
| kdiffH2O(400K) = 2.0 × 1010 s−1 kdesH2O(600K) = 1.4 × 1010 s−1 |
| kdesN2(400K) = 1.6 × 1010 s−1 kdesN2(600K) = 1.1 × 1010 s−1 |
Comparing these values with the rates of desorption, one may see that for nitrogen the surface diffusion is faster than the desorption over the entire range of temperatures relevant to SCR operation (300–1000 K) and in the range of 300–900 K for water. Moreover, one may also see that the product removal is many orders of magnitude faster than the chemisorption
reaction R6, hence, to a very good approximation the overall rate is given by the limiting step
eqn (16).
Reaction R6 or one of its variations features in every kinetic scheme of SCR operation, meanwhile reactions of ammonium bound on a catalytic site with molecular gaseous oxygen are, with notable exceptions of Arnarson et al.9 and Cheng et al.,39 invariably absent from consideration. This is rather surprising as a typical exhaust gas contains at least ten times more O2 than NO. In order to clarify the pathways of reactions involving oxygen, consider the following reaction, a partial oxidation of bound ammonium:
| |  | (R7) |
producing physiosorbed atomic oxygen O(s). The above reaction is a very much simplified but stoichiometrically correct representation of several elementary steps analysed in Arnarson
et al.,
9 it may be inferred from their analysis that this
reaction R7 proceeds with the overall activation energy of
E7 = 215 kcal per mole. Its pre-exponential factor, determined by the flux of gaseous O
2, may be estimated in the same manner as it was done for
reactions R2 and
R6:

with the accommodation factor
ψ7 ≈ 1. Owing to its larger activation energy, this reaction is about four orders of magnitude slower than
reaction R6 at low temperatures, but with the rise of temperature the difference progressively decreases so that at approximately 950 K both reactions proceed at the same rate. Following the same method as for
reaction R6, it may be shown that neither scission nor evacuation of the products is the rate-limiting step.
In principle, the same rate constants as for reaction R7 may also be ascribed to other reactions consuming gaseous oxygen, e.g. oxidation of the reduced active site Cat formed in reaction R6:
| |  | (R8) |
or further steps in oxidation of bound ammonium following
reaction R7:
| |  | (R9) |
| | 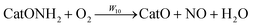 | (R10) |
with the sum of the accommodation factors for the latter two reactions equal to or less than one so that their summary pre-exponential does not exceed the gaseous oxygen diffusive flux, hence values
ψ9 =
ψ10 = 0.5 are taken here. The above three reactions describe two alternative oxidation pathways and, in order to distinguish low-temperature and high-temperature branches,
reaction R8 is ascribed the activation energy of
E8 of 80 kJ per mole, a value lower than
E7 while the activation energies for
reactions R9 and
R10 are taken larger than
E7, at
E9 =
E10 = 125 kJ per mole.
In parallel with the above oxidation reactions, CatONH2 also reduces NO as:
| |  | (R11) |
with the activation energy equal or somewhat smaller than that of
reaction R6; owing to the lack of other data, the same rate constants are taken for this reaction as for
reaction R6.
The cycle of active site transformations envisaged so far to represent the so-called normal SCR operation may now be closed with the following two reactions returning the active site its Brønsted acidity:
| |  | (R12) |
| |  | (R13) |
It has been noticed that, compared with Brønsted sites, the Lewis sites have higher reactivity. As the pre-exponential factors for the two above reactions are determined by the rate of diffusion of NO and O
2 from the gas phase, both proportional to
k1f, and they are likely to have only a small difference in the accommodation factors, the latter may be taken essentially equal to those for
reactions R6 and
R7. The higher reactivity of the CatONH
3 state may thus only be reflected through the activation energies for the above two reactions being lower than those of the counterpart reactions with CatONH
4. As a first approximation, the activation energy for reaction of CatONH
3 with oxygen is taken the same as for CatONH
4 as
E13 = 21.4 kcal per mole but reduced by 20% for reaction with NO,
E12 ≈ 11 kcal per mole.
While reactions R12 and R13 complete the normal SCR cycle ensuring correct stoichiometry, there is a significant body of evidence, e.g. Nova et al.,40 Ma et al.41 that oxidation of active sites proceeds through formation of nitrates, e.g. CatONH4NO3 and a set of reactions with overall stoichiometry of CatNO3 + NH4 → CatO + 2H2O + N2. Furthermore, the presence of NO2 in exhaust gas, as e.g. may be formed in diesel engines at the cold start and at low loads, may lead to the SCR cycle proceeding in the so-called “fast SCR” mode with different stoichiometry, Koebel et al.,42 Leistner et al.43 It should be noticed that taking into account the surface atomic oxygen species O(s) means that, even if there is no nitrogen dioxide in the exhaust, it could be produced through direct reaction NO(g) + O(s) → NO2 introduced later as reaction R16, hence, NO2 kinetic pathways should be taken into account too. Increased SCR activity at low temperatures favouring adsorption over desorption suggests that sorbed NO2(s) species should be considered alongside gaseous NO2(g), and this is considered in the next section.
The rates of reactions of oxidation by physiosorbed atomic oxygen and another surface species, e.g.:
| |  | (R14) |
| |  | (R15) |
are determined by the surface diffusion of O(s) as the active catalytic species are much less mobile owing to their larger molecular mass. The pre-exponential factor for the above reactions is of the order
k11 =
k12 ≈ 5 × 10
12 cm
3 per mole per s, and these reactions proceed with zero activation energy owing to the high reactivity of the atomic oxygen. It is interesting to notice that, at least in principle, a switch of the reduction cycle to the so-called fast SCR loop involving NO
2 may be initiated by the following surface reaction proceeding on a substrate, even if there is no nitrogen dioxide originally in the exhaust:
| |  | (R16) |
The rate of
reaction R16 is determined by the NO diffusion from the gas phase, thus

with unity accommodation factor and zero activation energy.
2.2 NO2 pathway and fast SCR
The usual interpretation of the so-called “fast SCR” cycle is that it involves gaseous nitrogen dioxide NO2 in concentration comparable to that of NO.42,43 While combustion in modern either spark or compression ignition engines does not commonly produce NO2 in any significant amounts, it may be expected that for certain operating conditions it could be formed in the exhaust circuit from NO through gas phase reactions with oxygen or water vapour. The mechanism of NO2 formation in the gas phase is beyond the scope of this work, nonetheless, assuming that NO2 is present in the exhaust, the previous investigations of the fast SCR mechanism, see e.g. Arnarson et al.,9 highlight the CatONO complex as the principal surface intermediate. Consideration of this complex and its pathways in this model also represents reactions involving well-documented nitrate species, e.g. Ma et al.,41 involved as intermediates in the SCR cycle.
Other than reaction R9, CatONO may be formed in reactions involving both gaseous and surface species:
| |  | (R17) |
| |  | (R18) |
| |  | (R19) |
According to the meaning of CatO as Lewis acid sites adopted in this model,
reaction R17 means chemisorption of NO on an active site, hence, the desorption should also be considered for consistency with analysis of
reaction R1. Weak NO adsorption on the substrate is not considered following the findings of Lietti
et al.19 and Sivachandiran
et al.44
The desorption activation energies E17b and E18b depend on the type of catalyst and, arguably, the substrate and composition of the exhaust gas; using a single value for either in this model is, by necessity, a compromise aiming at applicability to several catalyst types. Adsorption and desorption of NO were studied quite extensively, in particular in relation to the oxidation on platinum catalysts, e.g. Ghosh et al.,45 Crocoll et al.,46 and storage in absorbers, e.g. Villamaina et al.,47 Ambast et al.48 It was found that increase of water vapour or carbon monoxide coverage fraction of the catalyst inhibits the desorption while oxygen promotes it. For example, for dry and oxygen saturated Pt catalysts, desorption activation energies of 114 and 104 kJ per mole, respectively, were reported by Crocoll et al.46 At the same time, experiments of Lietti et al.19 reported virtually no adsorption of NO in vanadia catalysts thus indicating a very small desorption activation energy and a strong shift of equilibrium in reaction R17 to the left. Work of Wentworth et al.49 quoted the range of 90–140 kJ per mole and, accepting temperature as a proxy for the coverage fraction, proposed an expression for desorption activation energy decreasing from 105 to approximately 75 kJ per mole over the range of temperatures encountered in an automotive SCR. Very strong suppression of NO adsorption by water vapour was noticed by Despres et al.50 Adsorption of NO in Cu-exchanged zeolites proceeds through formation of copper mono- or dinitrosyls with the bond energies dependent on the zeolite structure and coordination of the N–O bonds: clearly, no single value may be attributed to the diverse cases. A binding energy of 22 kcal per mole average over different configurations is reported by Treesukol et al.51 for Cu-exchanged ZSM5 zeolite. Therefore, a compromise value of E17b of 78 kJ per mole is adopted here from pragmatic considerations that this value should describe the equilibrium shift in reaction R17 from strong absorption at low temperatures to nearly complete desorption at higher temperatures of typical automotive SCR conditions.
If one defines the equilibrium constant for reaction R17 as
| |  | (20) |
and takes into account that fugacity coefficients for the surface species are very close to one, one may see that a nearly complete desorption means
Kdes ≈ [NO]
10 where the typical NO concentration in the exhaust gas is [NO]
0 ∼ 10
−8 mole per cm
3. Estimating the pre-exponential factors as
ψ17fk17f = 3 × 10
11T1/2 cm
3 per mole per s and
k17b = 2 × 10
13 1 s
−1 (Baetzold and Somorjai),
52 and assuming that at 500 K there is no appreciable adsorption, one may obtain
E17b = 78 kJ per mole. This value is about 20% less than the 105 kJ per mole calculated with
ab initio methods in Zhanpeisov
et al.53 for Cu+ model zeolites, but very close to the values obtained in Treesukol
et al.51 and experiments discussed therein.
Strong chemisorption of NO2 on Cu–β zeolite was noticed in Wilken et al.54 The reversible reaction R18 describes chemisorption and desorption of gaseous NO2 on a modified active site; thus, its forward step is non-activated and the activation energy for the reverse step is the same as the heat of NO2 adsorption, reported as 65 kJ per mole for Cu–β zeolite in Wilken et al.54 The pre-exponential factors may be estimated as ψ18fk18f = 1.5 × 1010T1/2 cm3 per mole per s and k18b = 2 × 1013 1 s−1. Accepting these values and the results of experiments of Sivachandiran et al.44 showing that most (97%) NO2 is strongly absorbed on tungsta with a desorption temperature of about 580 K leads to the value of E18b = 120 kJ per mole and this value is adopted here. The rate of bimolecular association, reaction R19, is determined by the non-activated surface diffusion of NO2(s), k19 ≈ 3 × 1012 cm3 per mole per s, E19 = 0.
Reactions with either gaseous or physiosorbed ammonia transform the complex CatONO representing nitrates back to the Brønsted acid site CatOH, the departure point for the redox cycles envisaged here:
| |  | (R20) |
| |  | (R21) |
As follows from the DFT simulations of Arnarson
et al.,
9reaction R20 should have an activation barrier,
EF20 = 7.9 kcal per mole and its pre-exponential factor is the same as of
reaction R1. The pre-exponential factor of the non-activated
reaction R21 is determined by the surface diffusion of NH
3(s),
k21 ≈ 4 × 10
12 cm
3 per mole per s.
Nitrogen dioxide is involved in the fast SCR cycle and reactions of oxidation of nitric oxide and ammonia. Within the postulated set of species, the following reactions may be envisaged for the fast SCR cycle, see the green lines in Fig. 1:
| |  | (R22) |
| |  | (R23) |
together with their counterparts involving physiosorbed NO
2(s). To reflect the greater reactivity of NO
2 compared to NO in the lower temperature range, the activation energy for each of the two above reactions is taken as
E22 =
E23 =

. The pre-exponential factors for these reactions are taken equal to those of
reaction R18. The reactions involving physiosorbed NO
2(s) will have zero activation energy and their pre-exponential factors equal one for
reaction R19.
Finally, development of this kinetic mechanism is completed with inclusion of further three reactions, the first two for oxidation of the CatONO site with oxygen and the last one for adsorption of NO2 on the substrate:
| |  | (R24) |
| |  | (R25) |
| |  | (R26) |
the rate constants of which are estimated in the same manner as for similar reactions considered above, with the only exception of a lower accommodation factor taken as 0.05 for
reaction R26.
The values of the rate constants given in this section were taken as the base line common for all types of catalysts but some adjustments proved necessary in order to achieve quantitative agreement with the measurements used for the assessment of the scheme: this procedure is described below. The complete mechanism with the recommended values of the catalyst-dependent rate constants may be found in the ESI.†
3 Model assessment: numerical implementation
The developed kinetic model is assessed using simulations of a one-dimensional adiabatic plug reactor representing very common micro-reactor experimental setups. The simulated plug flow reactor has a volume of 1 cm3 and length of 1 cm with its inlet taken as the origin x = 0 cm and outlet situated at x = 1 cm where x is the direction of the flow. The total amount of catalyst placed in this reactor was taken as 1 g. The temperature and pressure were constant and for each species an unsteady transport equation was solved for its molar concentration Y neglecting the changes in the density ρ of the gas flow caused by variations of the molecular weight caused by chemical reactions:| | 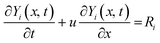 | (21) |
where i is the species number, u is the gas flow velocity for the species in the gas phase and u = 0 for the surface species and Ri is the total rate of change of the i-th species molar concentration. As the amount of catalyst in the simulations is assumed constant, in order to match conditions of different experiments, u in eqn (21) is taken as the inverse specific residence time, i.e. space velocity per unit mass of catalyst. The initial conditions for the surface species were calculated assuming constant total molar surface concentration ns = 1.5 × 109 mole per cm2 and values of either CatOH or CatO proportional to the molar fraction of catalyst sites. Thus, a catalyst is characterised in this formulation with its specific surface area and catalyst loading only, hence, in order to match the experimental conditions the specific area of this 1 g of catalyst was taken as the total area of catalyst used in the experiments. This procedure ensured that the simulations use exact total molar amounts of active catalytic sites and residence times as used in the experiments chosen for the model assessment.
Eqn (21) was discretised over a grid of N nodes in the x direction using a simple finite volume method with a first-order upwind difference (Patankar);55 most simulations shown below were conducted with either 100 or 200 nodes; 100 nodes were sufficient to achieve grid independence. Time integration of eqn (21) was performed using SEULEX software implementing an extrapolation algorithm with variable step size based on a linearly implicit Euler method, Hairer and Wanner.56 The final simulation time was set so as to ensure achievement of stationary outlet gas composition and it was typically of the order of a few thousand seconds. The time step δt for the simulations was set to satisfy the Courant–Friedrichs–Lewy (CFL) condition, uδt < δx = 1/(N − 1), that is the gas flow advanced less than one grid node during one time step.
4 Model assessment: results and discussion
The proposed generic kinetic mechanism was assessed by simulating several experimental studies of SCR operation performed with different catalysts with varying catalyst loading, surface area, feed gas composition, temperatures and GSHV, i.e. residence time. The first application has been done for copper-exchanged zeolites, SSZ-13 and SAPO-34 studied by Leistner et al.,43 see Fig. 2–4. These experiments used 30 mg of SSZ with a BET area of 4.39 × 106 cm2 g−1 and 60 mg of SAPO-34 with a BET area of 5.44 × 106 cm2 g−1, hence, the surface area of the simulated 1 g catalyst, and ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) was set equal to 1.32 × 105 cm2 for SSZ-13 and 3.26 × 105 cm2 for SAPO-34. Catalyst loading was determined from the molar ratios of copper to other elements and the initial surface molar fraction of CatO was set to xCatO = 0.045 and xCatO = 0.012 for SSZ-13 and SAPO-34, respectively. The initial molar fraction of other species was set to zero. The GSHV for both zeolites was given as 30
was set equal to 1.32 × 105 cm2 for SSZ-13 and 3.26 × 105 cm2 for SAPO-34. Catalyst loading was determined from the molar ratios of copper to other elements and the initial surface molar fraction of CatO was set to xCatO = 0.045 and xCatO = 0.012 for SSZ-13 and SAPO-34, respectively. The initial molar fraction of other species was set to zero. The GSHV for both zeolites was given as 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 h−1 corresponding to the residence time of 0.12 s and the linear gas velocity of u = 84 cm s−1 for the simulated 1 cm-long catalyst.
300 h−1 corresponding to the residence time of 0.12 s and the linear gas velocity of u = 84 cm s−1 for the simulated 1 cm-long catalyst.
 |
| | Fig. 2 Transient composition of the gas and concentration of the surface species at the outlet of the Cu/SAPO-34 catalyst in SCR operation at 150 °C (top), 350 °C (middle), 550 °C (bottom). The inserts on the right show the magnified period around achieving the steady-state operation. The notation is the same as on the main figure on the left. The inlet gas composition is: xNO = xNH3 = 400 ppm, xO2 = 8%, xH2O = 5% with the rest being N2. The inlet gas velocity is 8.4 cm s−1. | |
 |
| | Fig. 3 Reaction rates in established steady-state SCR operation along the length of the Cu/SAPO-34 catalyst at 150 °C (top), 350 °C (middle), 550 °C (bottom). The inserts on the right discern the main redox cycle reaction rates with exception of reaction R1: the notation is the same as on the main figure on the left. The inlet gas composition is: xNO = xNH3 = 400 ppm, xO2 = 8%, xH2O = 5% with the rest being N2. The inlet gas velocity is 8.4 cm s−1. | |
 |
| | Fig. 4 NO conversion vs. temperature for two copper-exchanged zeolites for SCR operation. The inlet gas composition is: xNO = xNH3 = 400 ppm, xO2 = 8%, xH2O = 5% with the rest being N2. The inlet gas velocity is 8.4 cm s−1. Symbols are measurements of Leistner et al.43 | |
Fig. 2 shows the temporal variation of the composition of the gas and concentration of the surface species at the outlet of the Cu/SAPO-34 catalyst at low, medium and high temperature in the range typical of the SCR operation. Clearly, the substrate surface sites have the highest molar concentration, followed by nitrogen. At the initial period, all ammonia but very little NO are adsorbed, and the duration of this transient period depends on the temperature: the longest duration is at medium temperatures corresponding to the optimum SCR conversions. At low temperature, after approximately 500 s, [NH3] and [NO] at the outlet stabilise at the same value: this demonstrates that the proposed scheme does respect the stoichiometry of the normal SCR conversion. The catalyst sites, initially all in the CatO state, shown as diamonds in Fig. 2, transition to, in order of decreasing concentrations, CatONH4 (shown there as triangles pointing left), Cat (triangles up), CatONH2 (triangles right), and CatONH3 (stars), while the concentrations of CatOH and NH3(s) are at least two orders of magnitude smaller than the latter and the concentrations of other surface species are negligible. This distribution of the catalytic sites strongly suggests that the redox cycle proceeds through the sequence of reactions R4, R12, R1 and R6, with the oxidation step concluding the cycle in reactions R8 and R15. Large amounts of CatONH4 and Cat indicate that either reaction R8 or reaction R6 is a limiting step for the entire cycle; the combination of NO conversion well below 100% and abundance of molecular oxygen suggests that the rate limitation is caused by the slowness of the chemical reaction rather than mass transfer. Hence, under these conditions the rate of conversion will scale linearly with the catalyst loading or total amount and inversely with the residence time.
The reaction sequence suggested above for the low temperature is corroborated with the calculation of the reaction rates shown in Fig. 3. It is seen that the rates of formation of ammonium and physisorption of ammonia are much larger than the rates of the reactions in the redox cycle and they therefore are equilibrated with their reverse reactions of desorption. The reactions of the main redox cycle, see the figure in the top right of Fig. 3, have progressively diminishing, but approximately the same, rates: reaction R12 (triangles right), reaction R4 (bold dotted line), reaction R6 (large circles), but the oxidation reaction R8 producing surface atomic oxygen is much slower; reaction R15 consuming O(s) is slower still. Thus, for this low temperature the catalyst re-oxidation is the limiting step.
Returning to the concentration of species shown in Fig. 2, one may see that the temperature increase to 350 °C resulted in a very large increase of CatOH (squares) and a very strong decrease in concentration of Cat (triangles up) thus indicating that now the active site reduction reaction R6 is gradually replacing oxidation as the redox cycle limiting step. Indeed, this is confirmed by direct comparison of the rates: reaction R6 (large circles) and reaction R8 (straight crosses) now proceed at the same rate, noticeably slower than other parts of the redox pathway operational at low temperatures. As may be expected, the rate of every individual step is very much increased with the temperature rise, however, it is noticeable that the reaction rates in a steady-state operation decrease significantly, by nearly three orders of magnitude towards the catalyst exit; a simple explanation to this fact is that the overall amount and increased reactivity of the active sites at this temperature consume most of the ammonia closer to the inlet, thus one may safely assume that under these conditions the conversion rate close to 100% may be maintained even for considerably larger gas debits, i.e. much smaller residence times. Finally, it should be noticed that now much faster oxidation step reaction R8 produces amounts of O(s) sufficient to trigger a second alternative redox pathway proceeding with oxidation of CatONH4viareaction R14 (dash-dot-dot line) and resulting in the rate of reduction viareaction R11 comparable with the total conversion rate of the low temperature cycle.
Further temperature increase to 550 °C, see the bottom row of Fig. 2 and 3, leads to sub-optimal SCR operation with the NO conversion rate decreasing by more than 20%, see Fig. 4. The concentration of the active states in the intermediate states CatONH4, CatONH3 and CatONH2 drops by two orders of magnitude compared with the case of 350 °C: this indicates that the redox cycle rate is now limited by the ammonia desorption and ammonium dissociation with the equilibrium of both reactions R1 and R2 shifted to the left. In principle, temperature increase may slow down the low-temperature redox cycle, owing to the equilibrium of reaction R17 and R18 shifted to the left, but this factor is not important under the investigated conditions. Thus, the overall efficiency of SCR conversion does not seem to have a single limiting factor, and the changing competition between the different pathways may, at least qualitatively, explain the “sea-gull shape” of the efficiency dependency upon temperature for a given catalyst, Gao et al.57
Comparing predictions of this mechanism with the measurements of Leistner et al.,43 see Fig. 4, one may see that SSZ-13 exhibits a drop of SCR efficiency at high temperatures smaller than SAPO-34 does; while differences in catalyst loading and the surface explain a part of this difference, cf. solid and dashed lines in Fig. 4, a noticeable difference remains. Both zeolites are copper-exchanged, thus the reason is unlikely to be related to the reactivity of the active sites. Based on predictions of the present model, one may suggest that the very likely reason for this difference is that SSZ-13 has a slightly larger activation barrier to weakly bound ammonia desorption: a modest increase of activation energy of reverse reaction R2 allows a very good match of the SCR efficiency (not shown) observed with this zeolite.
One of the base assumptions in the development of this mechanism was that different active catalytic sites may be characterised with the same rate constants; while this assumption is very convenient for estimation of rate constants, it is clearly inaccurate: as may be seen from Fig. 5, the SCR conversion observed for Fe-exchanged zeolite is much worse at low temperatures than that for Cu-exchanged ones considered previously and simulations with the rate constants of the base model (not shown) overpredict the performance for the temperatures below 300 °C in comparison with measurements of Hahn et al.14 These measurements employed a reactor with a much larger total catalyst amount, and hence, a total area of 2.46 × 106 cm2, catalyst loading xCatO = 0.008 and twice larger GSHV, yielding a linear feed velocity of u = 15.3 cm s−1, the value matching their residence time. The higher amount of catalyst sites may explain the superior performance at temperatures of 450 °C and above, but it cannot account for poor low-temperature conversion; thus, the question arises of how many alterations are required for the base mechanism to represent this type of catalyst. According to the above rate analysis, the conversion rate at low temperatures is limited by reaction R8, therefore, the rate of the latter is the defining factor for the degree of conversion. It proved that the increase of the activation energy of this reaction from 80 to 95 kJ per mole brings the low-temperature conversion for Fe-exchanged zeolite into the correct range, see Fig. 5. While the agreement is not ideal, it is remarkable that a change of a single kinetic parameter allows one within the present kinetic mechanism to reconcile iron and copper zeolite-based catalysts.
 |
| | Fig. 5 NH3 and NO conversion vs. temperature for SCR operation with Fe-exchanged HBEA zeolite, Hahn et al.14 The inlet gas composition is: xNO = xNH3 = 500 ppm, xO2 = 5%, with the rest being N2. The inlet gas velocity is 15.3 cm s−1, ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) = 2.46 × 106 cm2, the initial catalyst loading is xCatO = 0.008. Symbols are measurements of Hahn et al.14 = 2.46 × 106 cm2, the initial catalyst loading is xCatO = 0.008. Symbols are measurements of Hahn et al.14 | |
Compared to zeolites, catalysts on the TiO2 substrate, such as vanadia–tungsta ones, have much smaller specific surface areas, hence, for comparable catalyst loading, they have smaller concentration of active sites, yet they are widely used when the size of the SCR converter is not very important, e.g. in marine and power generation applications. Two such catalysts, CeO2 and V2O5 on the TiO2 substrate, were simulated here for conditions of experiments of Huang et al.58 and the outcomes are shown in Fig. 6. For V2O5 the experimental conditions were matched with the simulated catalyst area of ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) = 5.89 × 104 cm2, catalyst loading of xCatOH = 0.03 and for CeO2:
= 5.89 × 104 cm2, catalyst loading of xCatOH = 0.03 and for CeO2: ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) = 1.26 × 105 cm2 with xCatOH = 0.1, i.e. the latter had approximately 6 times more active sites. Similar to Fe-exchanged zeolite, and despite the relatively high active site concentration, the cerium dioxide catalyst exhibits poor low-temperature conversion for both SCR operation and NH3 oxidation not captured with the baseline set of rate constants. However, as it was the case with the Fe-exchanged zeolite, the increase of the activation energy for reaction R8 to 90 kJ per mole has allowed a reasonably good agreement to be achieved with the measurements of Huang et al.58 with the exception of ammonia oxidation at 450 K underpredicted by approximately 10%.
= 1.26 × 105 cm2 with xCatOH = 0.1, i.e. the latter had approximately 6 times more active sites. Similar to Fe-exchanged zeolite, and despite the relatively high active site concentration, the cerium dioxide catalyst exhibits poor low-temperature conversion for both SCR operation and NH3 oxidation not captured with the baseline set of rate constants. However, as it was the case with the Fe-exchanged zeolite, the increase of the activation energy for reaction R8 to 90 kJ per mole has allowed a reasonably good agreement to be achieved with the measurements of Huang et al.58 with the exception of ammonia oxidation at 450 K underpredicted by approximately 10%.
 |
| | Fig. 6 Left: NH3 and NO conversion vs. temperature for SCR operation of two catalysts, CeO2 and V2O5, on a tungsta substrate. Right: NH3 conversion vs. temperature for the same catalysts for ammonia oxidation. The inlet gas composition is for SCR: xNO = xNH3 = 500 ppm, for ammonia oxidation xNH3 = 500 ppm, with xO2 = 2% with the rest being N2 for both cases. The inlet gas velocity is 3.3 cm s−1. Symbols are measurements of Huang et al.58 | |
Of all the catalysts simulated so far, the vanadia–tungsta on titania one of Huang et al.58 has the lowest surface and active site concentration and the highest residence time; at higher temperatures the measurements showed a significant decrease of NO conversion, while the NH3 consumption remained nearly complete. The baseline set of the rate constants showed in this case a good agreement at lower temperatures, but at high temperatures the predicted conversion of both NO and NH3 was smaller than those measured for both SCR and NH3 oxidation. The reaction rate analysis showed that in this case the high temperature redox pathway proceeding through oxidation of CatONH2, rather than the Cat intermediate see Fig. 1, was very slow. Therefore, activation energies for reactions R7 and R9 were decreased to 85 and 95 kJ per mole, respectively; the results are shown in Fig. 6. While this change allowed one to obtain a fairly good agreement for NH3 conversion under all conditions, the present kinetics still overpredicted NO conversion at temperatures above 400 °C. The diverging degrees of ammonia and nitric oxide conversion were, however, shown in Huang et al.58 to be caused by the formation of nitrous oxide N2O, the detailed mechanism of which has so far not been considered in SCR chemical kinetic mechanisms. Clearly, inclusion of the chemical pathways for nitrous oxide formation would be a desirable next step in the development of SCR kinetic schemes. Another aspect well worthy of comment and a further investigation is representation of the role of water in the exhaust gas.
The current formulation assumes that the water in the exhaust or flue gas is chemically inert; it is formed as a product in the redox cycles but its concentration does not affect the reaction rates. At the same time, there does exist experimental evidence that water concentration in the gas phase affects the SCR reaction rates. Work of Nova et al.59 demonstrated that addition of up to 5% vol. of H2O decreases SCR conversion efficiency in a vanadia–tungsta catalyst but it does not affect the rates of NH3 adsorption or desorption. Because of this it was argued that its role cannot be reduced to surface coverage competition. DFT simulations of Broclawik et al.60 of the same type of catalyst demonstrated the possibility of low temperature water dissociation leading to the formation of active hydroxyls bound to tungsten ions; however, this process creates stronger Brønsted sites and thus it should promote rather than inhibit SCR conversion. This finding explains that addition of tungsta to vanadia catalysts significantly improves low-temperature SCR performance but it does not explain the inhibiting effect of increasing water concentration in the flue gas to be scrubbed. At the same time, addition of a fixed amount of water markedly increased NO conversion in several Cu-exchanged zeolites at higher, above 400 °C, temperatures, Fedyna et al.,61 while at lower, between 100 and 200 °C, temperatures water could inhibit, promote or leave the conversion unchanged. The promotion of catalytic activity was attributed to transition of isolated copper ions and their dimers to Cu2+–OH− centres, Fedyna et al.,61 as confirmed spectroscopically. The proposed mechanism does have distinct low and high-temperature pathways but the question to which extent reactions on the different structures with copper cations may be lumped together in the adopted generalised kinetics scheme should at present be considered open. It is worth mentioning that formation of metal-hydroxyl groups was associated with the N2O reactions in DFT simulations of Song et al.62 performed for a Mn-doped ceria catalyst thus indicating that the N2O and H2O pathways should be considered together in the subsequent developments of this, or indeed, any other kinetic scheme for SCR catalysts.
5 Conclusions
It is remarkable that a patently wrong departure point, namely assuming the same reactivity for different SCR catalytic sites, has proved rather fruitful in allowing to develop a new generic chemical kinetic scheme aimed at exploiting similarities in reduction–oxidation catalytic cycles for nitric oxide reduction to nitrogen by ammonia. This generic scheme comprises 28 reactions involving 16 species where a catalytically active site may be in 7 states. The rate constants for these reactions were estimated through analysis of the individual sub-processes and identifying the overall rate with the rate of the limiting sub-process. The chemical kinetics so developed was used to simulate operation of several catalysts through matching catalyst concentration and residence times. These simulations show that, after taking into account differences in feed gas composition, active site concentration and residence time, varying only one kinetic parameter, namely activation energy for the low-temperature pathway allows one to reconcile the observed differences between copper and iron exchanged zeolites and cerium dioxide on tungsta. These simulations show that it is plausible that differences in the operating regime of a catalytic converter matter at least as much as the nature of the catalyst sites.
In what concerns the development of this chemical kinetics, vanadia on TiO2 appears different from other catalysts as achieving a similar agreement of its simulations with the observed rates of SCR conversion required changes of activation energy of two high-temperature active site oxidation reactions. Its simulations have also identified pathway(s) of nitrous oxide formation as essential for description of its high-temperature behaviour and consideration of effects of addition of water to the gas to be scrubbed indicates that this pathway should be considered alongside water adsorption and dissociation on the catalyst surface.
Data availability
The developed chemical kinetic mechanism and its rate constants are supplied in CHEMKIN format as the ESI.† The simulation data and the code are available upon request.
Author contributions
AAB: kinetic mechanism formulation, simulations and manuscript, APM: simulations and manuscript.
Conflicts of interest
There are no conflicts of interest to declare.
Acknowledgements
APM acknowledges the financial support through RDF studentship from Northumbria University.
References
- L. Han, S. Cai, M. Gao, J. Y. Hasegawa, P. Wang, J. Zhang, L. Shi and D. Zhang, Chem. Rev., 2019, 119, 10916–10976 CrossRef CAS PubMed.
- Z. Lian, Y. Li, W. Shan and H. He, Catalysts, 2020, 10, 1421 CrossRef CAS.
- T. V. W. Janssens, H. Falsig, L. F. Lundegaard, P. N. R. Vennestrøm, S. B. Rasmussen, P. G. Moses, F. Giordanino, E. Borfecchia, K. A. Lomachenko, C. Lamberti, S. Bordiga, A. Godiksen, S. Mossin and P. Beato, ACS Catal., 2015, 5, 2832–2845 CrossRef CAS.
- N. Y. Topsøe, J. A. Dumesic and H. Topsøe, J. Catal., 1995, 151, 241–252 CrossRef.
- L. Olsson, K. Wijayanti, K. Leistner, A. Kumar, S. Y. Joshi, K. Kamasamudram, N. W. Currier and A. Yezerets, Appl. Catal., B, 2016, 183, 394–406 CrossRef CAS.
- U. De-La-Torre, B. Pereda-Ayo, M. Gutiérrez-Ortiz, J. González-Marcos and J. González-Velasco, Catal. Today, 2017, 296, 95–104 CrossRef CAS.
-
D. Chatterjee, T. Burkhardt, B. Bandl-Konrad, T. Braun, E. Tronconi, I. Nova and C. Ciardelli, SAE Technical Papers 2005-01-0965, 2005 Search PubMed.
- E. D. German and M. Sheintuch, Russ. J. Phys. Chem. B, 2007, 1, 357–376 CrossRef.
- L. Arnarson, H. Falsig, S. B. Rasmussen, J. V. Lauritsen and P. G. Moses, J. Catal., 2017, 346, 188–197 CrossRef CAS.
- M.-J. Kim, J.-R. Youn, S.-J. Lee, I.-S. Ryu, S. Chan Nam, S. Kwan Jeong and S. Goo Jeon, J. Ind. Eng. Chem., 2022, 108, 438–448 CrossRef CAS.
- Q. Jin, M. Chen, X. Tao, B. Lu, J. Shen, Y. Shen and Y. Zeng, Appl. Surf. Sci., 2020, 512, 145757 CrossRef CAS.
- M. Ravi, V. L. Sushkevich and J. A. van Bokhoven, Chem. Sci., 2021, 12, 4094–4103 RSC.
- Z. Ma, X. Wu, H. Härelind, D. Weng, B. Wang and Z. Si, J. Mol. Catal. A: Chem., 2016, 423, 172–180 CrossRef CAS.
- C. Hahn, J. Seidel, F. Mertens and S. Kureti, Phys. Chem. Chem. Phys., 2022, 24, 7493–7504 RSC.
- M. Inomata, A. Miyaoto and M. Yuichi, J. Catal., 1980, 62, 140–148 CrossRef CAS.
- L. Arnarson, H. Falsig, S. B. Rasmussen, J. V. Lauritsen and P. G. Moses, Phys. Chem. Chem. Phys., 2016, 18, 17071 RSC.
- G. Busca, L. Lietti, G. Ramis and F. Berti, Appl. Catal., B, 1998, 18, 1–36 CrossRef CAS.
-
V. Zhdanov, Elementary physico-chemical processes on a surface, “Nauka”, Siberian Section, Novosibirsk, 1988 Search PubMed.
- L. Lietti, G. Ramis, F. Berti, G. Toledo, D. Robba, G. Busca and P. Forzatti, Catal. Today, 1998, 42, 101–116 CrossRef CAS.
- L. J. Alemany, L. Lietti, N. Ferlazzo, P. Forzatti, G. Busca, E. Giamello and F. Bregani, J. Catal., 1995, 155, 117–130 CrossRef CAS.
-
D. Chatterjee, T. Burkhardt, M. Weibel, I. Nova, A. Grossale and E. Tronconi, SAE Technical Papers 2007-01-1136, 2007, vol. 2007 Search PubMed.
- V. Schmeisser, M. Weibel, L. Sebastian Hernando, I. Nova, E. Tronconi and M. P. Ruggeri, SAE Int. J. Commer. Veh., 2013, 6, 190–199 CrossRef.
- C. T. Campbell, L. Árnadóttir and J. R. Sellers, Z. Phys. Chem., 2013, 227, 1435–1454 CAS.
-
N. B. Vargaftik, Handbook of Physical Properties of Liquids and Gases, Pure Substances and Mixtures, Springer-Verlag Berlin Heidelberg, 2nd edn, 1975 Search PubMed.
- M. Colombo, I. Nova, E. Tronconi, V. Schmeißer, B. Bandl-Konrad and L. Zimmermann, Appl. Catal., B, 2012, 111–112, 106–118 CrossRef CAS.
- T. Masuda, Y. Fujikata, H. Ikeda, S. Matsushita and K. Hashimoto, Appl. Catal., A, 1997, 162, 29–40 CrossRef CAS.
- U. Diebold and T. E. Madey, J. Vac. Sci. Technol., A, 1992, 10, 2327–2335 CrossRef CAS.
- H. E. Dastoor, P. Gardner and D. A. King, Surf. Sci., 1993, 289, 279–289 CrossRef CAS.
- L. Ye, B. T. Lo, J. Qu, I. Wilkinson, T. Hughes, C. A. Murray, C. C. Tang and S. C. E. Tsang, Chem. Commun., 2016, 52, 3422–3425 RSC.
-
I. Chorkendorff and J. Niemanrsverdriet, Concepts of modern catalysis and kinetics, Wiley-VCH Verlag, Weinheim, 2nd edn, 2007 Search PubMed.
- S. Suárez, S. Jung, P. Avila, P. Grange and J. Blanco, Catal. Today, 2022, 75, 331–338 CrossRef.
- X. Yin, H. Han, I. Gunji, A. Endou, S. S. Cheettu Ammal, M. Kubo and A. Miyamoto, J. Phys. Chem. B, 1999, 103, 4701–4706 CrossRef CAS.
- A. Marberger, D. Ferri, M. Elsener and O. Kröcher, Angew. Chem., Int. Ed., 2016, 55, 11989–11994 CrossRef CAS PubMed.
- J. J. Scholten, P. Zwietering, J. A. Konvalinka and J. H. De Boer, Trans. Faraday Soc., 1959, 55, 2166–2179 RSC.
- M. Fan, H. Panezai, J. Sun, S. Bai and X. Wu, J. Phys. Chem. C, 2014, 118, 23761–23767 CrossRef CAS.
- M. A. Henderson, Surf. Sci., 1994, 319, 315–328 CrossRef CAS.
- V. Y. Prokof'ev, N. E. Gordina, T. N. Borisova and N. V. Shamanaeva, Microporous Mesoporous Mater., 2019, 280, 116–123 CrossRef.
- A. Feng, B. J. McCoy, Z. A. Munir and D. E. Cagliostro, J. Colloid Interface Sci., 1996, 180, 276–284 CrossRef CAS.
- Y. Cheng, W. Song, J. Liu, H. Zheng, Z. Zhao, C. Xu, Y. Wei and E. J. M. Hensen, ACS Catal., 2017, 7, 3883–3892 CrossRef CAS PubMed.
- I. Nova, C. Ciardelli, E. Tronconi, D. Chatterjee and M. Weibel, AIChE J., 2009, 55, 1514–1529 CrossRef CAS.
- Z. Ma, X. Wu, H. Härelind, D. Weng, B. Wang and Z. Si, J. Mol. Catal. A: Chem., 2016, 423, 172–180 CrossRef CAS.
- M. Koebel, G. Madia and M. Elsener, Catal. Today, 2002, 73, 239–247 CrossRef CAS.
- K. Leistner, O. Mihai, K. Wijayanti, A. Kumar, K. Kamasamudram, N. Currier, A. Yezerets and L. Olsson, Catal. Today, 2015, 258, 49–55 CrossRef CAS.
- L. Sivachandiran, F. Thevenet, P. Gravejat and A. Rousseau, Appl. Catal., B, 2013, 142–143, 196–204 CrossRef CAS.
- R. S. Ghosh, M. P. Harold and D. Wang, Chem. Eng. J., 2021, 418, 129065 CrossRef CAS.
- M. Crocoll, S. Kureti and W. Weisweiler, J. Catal., 2005, 229, 480–489 CrossRef CAS.
- R. Villamaina, U. Iacobone, I. Nova, E. Tronconi, M. P. Ruggeri, L. Mantarosie, J. Collier and D. Thompsett, Appl. Catal., B, 2021, 284, 119724 CrossRef CAS.
- M. Ambast, A. Gupta, B. M. M. Rahman, L. C. Grabow and M. P. Harold, Appl. Catal., B, 2021, 286, 119871 CrossRef CAS.
- T. Wentworth, S. Loya, C. Depcik and S. Susan Stagg-Williams, React. Kinet., Mech. Catal., 2016, 117, 15–34 CrossRef CAS.
- J. Despres, M. Koebel, O. Kröcher, M. Elsener and A. Wokaun, Microporous Mesoporous Mater., 2003, 58, 175–183 CrossRef CAS.
- P. Treesukol, J. Limtrakul and T. N. Truong, J. Phys. Chem. B, 2001, 105, 2421–2428 CrossRef CAS.
- R. Baetzold and G. Somorjai, J. Catal., 1976, 45, 94–105 CrossRef CAS.
- N. Zhanpeisov, H. Nakatsuji, M. Hada, H. Nakai and M. Anpo, Catal. Lett., 1996, 42, 173–176 CrossRef CAS.
- N. Wilken, K. Kamasamudram, N. Currier, J. Li, A. Yezerets and L. Olsson, Catal. Today, 2010, 151, 237–243 CrossRef CAS.
-
S. Patankar, Numerical Heat Transfer and Fluid Flow, Hemisphere Publ, Washington D.C., 1980 Search PubMed.
-
E. Hairer and G. Wanner, Solving ordinary differential equations II. Stiff and differential-algebraic problems. Springer series in computational mathematics 14, Springer-Verlag, Berlin, 2nd edn, 1996 Search PubMed.
- F. Gao, E. D. Walter, M. Kollar, Y. Wang, J. Szanyi and C. H. Peden, J. Catal., 2014, 319, 1–14 CrossRef CAS.
- N. Huang, Y. Geng, S. Xiong, X. Huang, L. Kong, S. Yang, Y. Peng, J. Chen and J. Lia, Catal. Commun., 2019, 121, 84–88 CrossRef CAS.
- I. Nova, L. Lietti, E. Tronconi and P. Forzatti, Catal. Today, 2000, 60, 73–82 CrossRef CAS.
- E. Broclawik, A. Góra and M. Najbar, J. Mol. Catal. A: Chem., 2001, 166, 31–38 CrossRef CAS.
- M. Fedyna, P. Legutko, M. Marzec and Z. Sojka, Appl. Catal., B, 2025, 361, 124632 CrossRef CAS.
- W. Song, J. Liu, H. Zheng, S. Ma, Y. Wei, A. Duan, G. Jiang, Z. Zhao and E. J. M. Hensen, Catal. Sci. Technol., 2016, 6, 2120–2128 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available: The kinetic scheme and thermochemical data. See DOI: https://doi.org/10.1039/d4cy01205d |
| ‡ Current address: Clean Air Ltd, Mill Street, Farnworth, Bolton, BL4 7BH, UK. |
|
| This journal is © The Royal Society of Chemistry 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article * and
Andrew P.
Manning‡
* and
Andrew P.
Manning‡


![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) is the BET surface area of the catalyst per unit volume. Here and in what follows the square and angle brackets denote specific quantities per unit volume and surface, respectively. In the estimations of the rate constants below, the value of ns = 1.5 × 10−1 mole per cm2 is taken as constant for all types of catalysts; this value corresponds to approximately 3 Å spacing between the molecules at the surface: for most SCR catalysts, the typical inter-site distance on the surface is rs ≈ 2–3 Å. The BET area, i.e. catalyst specific surface area
is the BET surface area of the catalyst per unit volume. Here and in what follows the square and angle brackets denote specific quantities per unit volume and surface, respectively. In the estimations of the rate constants below, the value of ns = 1.5 × 10−1 mole per cm2 is taken as constant for all types of catalysts; this value corresponds to approximately 3 Å spacing between the molecules at the surface: for most SCR catalysts, the typical inter-site distance on the surface is rs ≈ 2–3 Å. The BET area, i.e. catalyst specific surface area ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) , an input parameter to this model, lies in the range of several tens to several hundred m2 cm−3.
, an input parameter to this model, lies in the range of several tens to several hundred m2 cm−3.







 . The entropy
. The entropy  of gaseous ammonia with one translational degree of freedom removed may be estimated Campbell et al.23 at T0 = 298 K using the standard entropy of formation of argon S0AR as:
of gaseous ammonia with one translational degree of freedom removed may be estimated Campbell et al.23 at T0 = 298 K using the standard entropy of formation of argon S0AR as: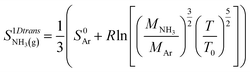


![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) where ΘZ is the ratio of surface sites capable of physisorption to the total surface molecular concentration, e.g. ΘZ = 1 for the tungsta substrate and for SSZ zeolites ΘZ may be taken as equal to the Al/Si molar ratio.
where ΘZ is the ratio of surface sites capable of physisorption to the total surface molecular concentration, e.g. ΘZ = 1 for the tungsta substrate and for SSZ zeolites ΘZ may be taken as equal to the Al/Si molar ratio.
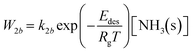

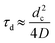 where dc is an average distance between two catalyst sites, dc ∼ (ΘCatOHnsNA)−1/2 and D is the surface diffusivity. The activation energy for surface diffusion is low, Zhdanov,18 and, assuming a typical value of D ≈ 10−3 cm2 s−1,30 one may estimate τd ≈ 1.4 × 10−12 s−1. Therefore, the rate of reaction R3 between two surface species:
where dc is an average distance between two catalyst sites, dc ∼ (ΘCatOHnsNA)−1/2 and D is the surface diffusivity. The activation energy for surface diffusion is low, Zhdanov,18 and, assuming a typical value of D ≈ 10−3 cm2 s−1,30 one may estimate τd ≈ 1.4 × 10−12 s−1. Therefore, the rate of reaction R3 between two surface species:
 where the cell size d is essentially the distance between two sorption sites, d ≈ rs:
where the cell size d is essentially the distance between two sorption sites, d ≈ rs: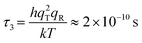
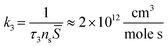


 . On the other hand, the pre-exponential factor for the surface diffusion kd ≈ (τdns
. On the other hand, the pre-exponential factor for the surface diffusion kd ≈ (τdns![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) )−1 may be estimated as
)−1 may be estimated as  , thus this reaction is diffusion-controlled, non-activated and k5 = kd.
, thus this reaction is diffusion-controlled, non-activated and k5 = kd.


 yielding the characteristic time of this reaction of order of 0.2 s for typical NO molar densities in an exhaust gas at 600 K.
yielding the characteristic time of this reaction of order of 0.2 s for typical NO molar densities in an exhaust gas at 600 K.
 , e.g. at T = 500 K ksH2O = ksN2 = 1013 s−1, hence
, e.g. at T = 500 K ksH2O = ksN2 = 1013 s−1, hence![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) per
per![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) mole] with the value extrapolated to full coverage EdesN2 = 25.8 kcal per mole; this value is adopted here as an average for different substrates owing to the lack of data for other types of catalyst substrates. For the desorption of water, the activation energy reported for zeolites in Fan et al.35 changed from approximately 20 kcal per mole at lower temperatures, 300–450 K, to just above 70 kcal per mole at 600–700 K; the reported value also depended, albeit with a smaller variation, upon the zeolite structure and what alkali metal, Li or Na, cations were used for charge compensation. The average value, measured in Fan et al.35 at temperatures of 500–600 K, of EdesH2O ≈ 40 kcal per mole, was about twice larger than the value of 18 kcal per mole reported for different TiO2 crystals in Henderson.36 Close to the latter, values of approximately 15 kcal per mole were reported for different types of zeolites in Prokof'ev et al.37 and similar figures of 16.6 kcal per mole for silica in Feng et al.38 For the overall rate estimations, the value of EdesH2O = 20 kcal per mole is retained here.
mole] with the value extrapolated to full coverage EdesN2 = 25.8 kcal per mole; this value is adopted here as an average for different substrates owing to the lack of data for other types of catalyst substrates. For the desorption of water, the activation energy reported for zeolites in Fan et al.35 changed from approximately 20 kcal per mole at lower temperatures, 300–450 K, to just above 70 kcal per mole at 600–700 K; the reported value also depended, albeit with a smaller variation, upon the zeolite structure and what alkali metal, Li or Na, cations were used for charge compensation. The average value, measured in Fan et al.35 at temperatures of 500–600 K, of EdesH2O ≈ 40 kcal per mole, was about twice larger than the value of 18 kcal per mole reported for different TiO2 crystals in Henderson.36 Close to the latter, values of approximately 15 kcal per mole were reported for different types of zeolites in Prokof'ev et al.37 and similar figures of 16.6 kcal per mole for silica in Feng et al.38 For the overall rate estimations, the value of EdesH2O = 20 kcal per mole is retained here.


 with the accommodation factor ψ7 ≈ 1. Owing to its larger activation energy, this reaction is about four orders of magnitude slower than reaction R6 at low temperatures, but with the rise of temperature the difference progressively decreases so that at approximately 950 K both reactions proceed at the same rate. Following the same method as for reaction R6, it may be shown that neither scission nor evacuation of the products is the rate-limiting step.
with the accommodation factor ψ7 ≈ 1. Owing to its larger activation energy, this reaction is about four orders of magnitude slower than reaction R6 at low temperatures, but with the rise of temperature the difference progressively decreases so that at approximately 950 K both reactions proceed at the same rate. Following the same method as for reaction R6, it may be shown that neither scission nor evacuation of the products is the rate-limiting step.








 with unity accommodation factor and zero activation energy.
with unity accommodation factor and zero activation energy.








 . The pre-exponential factors for these reactions are taken equal to those of reaction R18. The reactions involving physiosorbed NO2(s) will have zero activation energy and their pre-exponential factors equal one for reaction R19.
. The pre-exponential factors for these reactions are taken equal to those of reaction R18. The reactions involving physiosorbed NO2(s) will have zero activation energy and their pre-exponential factors equal one for reaction R19.



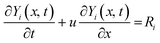
![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) was set equal to 1.32 × 105 cm2 for SSZ-13 and 3.26 × 105 cm2 for SAPO-34. Catalyst loading was determined from the molar ratios of copper to other elements and the initial surface molar fraction of CatO was set to xCatO = 0.045 and xCatO = 0.012 for SSZ-13 and SAPO-34, respectively. The initial molar fraction of other species was set to zero. The GSHV for both zeolites was given as 30
was set equal to 1.32 × 105 cm2 for SSZ-13 and 3.26 × 105 cm2 for SAPO-34. Catalyst loading was determined from the molar ratios of copper to other elements and the initial surface molar fraction of CatO was set to xCatO = 0.045 and xCatO = 0.012 for SSZ-13 and SAPO-34, respectively. The initial molar fraction of other species was set to zero. The GSHV for both zeolites was given as 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 h−1 corresponding to the residence time of 0.12 s and the linear gas velocity of u = 84 cm s−1 for the simulated 1 cm-long catalyst.
300 h−1 corresponding to the residence time of 0.12 s and the linear gas velocity of u = 84 cm s−1 for the simulated 1 cm-long catalyst.



![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) = 2.46 × 106 cm2, the initial catalyst loading is xCatO = 0.008. Symbols are measurements of Hahn et al.14
= 2.46 × 106 cm2, the initial catalyst loading is xCatO = 0.008. Symbols are measurements of Hahn et al.14![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) = 5.89 × 104 cm2, catalyst loading of xCatOH = 0.03 and for CeO2:
= 5.89 × 104 cm2, catalyst loading of xCatOH = 0.03 and for CeO2: ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) = 1.26 × 105 cm2 with xCatOH = 0.1, i.e. the latter had approximately 6 times more active sites. Similar to Fe-exchanged zeolite, and despite the relatively high active site concentration, the cerium dioxide catalyst exhibits poor low-temperature conversion for both SCR operation and NH3 oxidation not captured with the baseline set of rate constants. However, as it was the case with the Fe-exchanged zeolite, the increase of the activation energy for reaction R8 to 90 kJ per mole has allowed a reasonably good agreement to be achieved with the measurements of Huang et al.58 with the exception of ammonia oxidation at 450 K underpredicted by approximately 10%.
= 1.26 × 105 cm2 with xCatOH = 0.1, i.e. the latter had approximately 6 times more active sites. Similar to Fe-exchanged zeolite, and despite the relatively high active site concentration, the cerium dioxide catalyst exhibits poor low-temperature conversion for both SCR operation and NH3 oxidation not captured with the baseline set of rate constants. However, as it was the case with the Fe-exchanged zeolite, the increase of the activation energy for reaction R8 to 90 kJ per mole has allowed a reasonably good agreement to be achieved with the measurements of Huang et al.58 with the exception of ammonia oxidation at 450 K underpredicted by approximately 10%.






