Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Twenty years after: scaling relations in oxygen electrocatalysis and beyond
Vladislav
Ivanistsev
 a,
Ritums
Cepitis
a,
Ritums
Cepitis
 b,
Jan
Rossmeisl
b,
Jan
Rossmeisl
 c and
Nadezda
Kongi
c and
Nadezda
Kongi
 *d
*d
aDepartment of Chemistry, University of Latvia, Jelgavas iela 1, LV-1004 Riga, Latvia
bInstitute of Electrochemistry, University of Alicante, E-03080 Alicante, Spain
cDepartment of Chemistry, Center for High Entropy Alloy Catalysis, University of Copenhagen, Universitetsparken 5, 2100 Copenhagen, Denmark
dInstitute of Chemistry, University of Tartu, Ravila 14a, 50411 Tartu, Estonia. E-mail: nadezda.kongi@ut.ee
First published on 3rd November 2025
Abstract
Since the 2000s, so-called scaling relations have been recognised as a limiting factor in electrocatalysis. Overcoming these constraints is essential to advance energy conversion technologies such as electrolysers, fuel cells, and metal–air batteries. This review presents key concepts, tools, and manipulation strategies required to deal with the scaling relations in oxygen electrocatalysis, chosen as a representative case. Special attention is given to the catalyst's geometry as an emerging central variable in electrocatalysis – one whose influence is only beginning to be systematically understood. Building on geometric and chemical grounds, this review offers a structured tutorial for the theory-driven design of electrocatalysts the deliberate manipulation of scaling relations.
Key learning points1. Definition of scaling relations. The review explains scaling relations in three complementary ways: (1) by expressing them through adsorption energies; (2) by formulating them as chemical and physical equations; and (3) by illustrating them as straight path lines on the theoretical volcano plot, which connects adsorption energy with catalytic activity. 2. Origin of scaling relations. The commonly accepted thermodynamic explanation of scaling relations is presented, together with additional geometrical and chemical perspectives that give the reader a broader understanding of how these relations arise. 3. Classification of strategies to manipulate scaling relations. The review identifies five general strategies for manipulating scaling relations. Each strategy is: (1) explained using examples from the literature; (2) supported by original numerical estimates; (3) ordered chronologically to reflect how the field has developed; and (4) discussed in the context of future directions. 4. Two governing principles in electrocatalysis. Two main principles are discussed: the well-established Sabatier principle, which states that optimal activity is achieved when binding is “neither too strong nor too weak”, and the emerging principle that both activity and selectivity depend on two adsorption sites being neither “too far nor too close”. 5. Verification of the principles and strategies. The review explains why it is important, and also feasible, to use these principles and strategies in both experiments and simulations. |
1 Introduction
This review focuses on the scaling relations – correlations between adsorption energies of reaction intermediates.1–4 This concept emerged twenty years ago, in 2005, when Rossmeisl et al. discovered linear relations between the adsorption energies for OH and OOH vs. O on a set of metal surfaces.5 The term “scaling relations” was first introduced in 2007 by Abild-Pedersen et al., who reported that the adsorption energy of OH, CHx, and NHx is proportional to the adsorption energy of corresponding atoms: O, C, and N.1,2 Thus, scaling relations proved essential in mainstream multi-step electrocatalytic reactions, such as O2, CO2, and N2 reduction.6–9 Further research on the scaling relations provided an understanding of the chemical limitations in electrocatalytic reactions.10–14 Furthermore, it laid the foundation for more efficient catalyst design.15,16In 2024, Calle-Vallejo concluded that scaling relations are regarded by many as a top priority in electrocatalysis and raised questions: “whether we know of any materials that unmistakably break scaling relations and, more importantly, if the breaking of a problematic scaling relation is the end of all troubles in electrocatalysis.”17 Calle-Vallejo has expressed his views on the scaling relations in electrocatalysis of CO2 reduction reaction and showed a concrete example of Cu(100) breaking the scaling relation in CO reduction to ethylene. Most interestingly, the title of the article “What we talk about when we talk about breaking scaling relations” highlights the ambiguity existing in the field where experimentalists and theoreticians refer to breaking the scaling relations with a variety of meaning. Even the use of the term “breaking” is slightly different in Calle-Vallejo's and our review. To resolve such ambiguity, this review addresses the same, above stated, questions by focusing on examples from oxygen electrocatalysis: starting with definitions, providing classification, and then generalising the conclusions to other multi-step reactions.
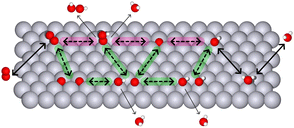
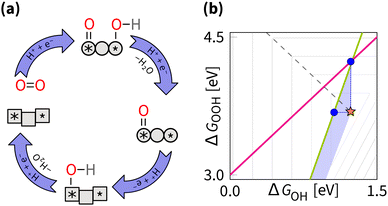
Oxygen electrocatalysis involves O2, H2O2, and H2O molecules (Fig. 1). In particular, the four-electron transformations from oxygen to water and vice versa are known as the oxygen reduction reaction (ORR) and oxygen evolution reaction (OER). For these reactions, the overpotential – the additional potential (beyond the thermodynamic requirement) needed to drive a reaction at a certain rate – can be expressed in terms of adsorption energies that are determined by a specific scaling relation (Section 3). For clarity, we focus on the ORR, which plays a key role in electrochemical energy conversion and is especially significant in applications like fuel cells and metal–air batteries. In these devices, catalysts enhance the ORR by adsorbing intermediates, such as OH, OOH, and O, and facilitating their transformation through various ORR mechanisms, summarised in Fig. 1.
In the 2000s, it became clear that adsorption energies of OH, OOH, and O intermediates are correlated by the scaling relations, which can be used to predict trends in the catalytic activity.2 Further research on the scaling relations caused a paradigm shift in ORR catalysis.18 In particular, in 2011, Stephens et al. introduced the concept of tuning.19 They experimentally varied catalytic activity within the theoretical limits of the OOH–OH scaling relation: by adjusting the OH adsorption energy, they predictably increased the catalytic activity of Pt-based catalysts. They also showed that tuning leads to the “volcano top” – the point of optimal catalytic activity for ORR – thus revealing a strategy for the theory-driven design of ORR catalysts. Shortly after, Koper suggested that the OOH–OH scaling relation is the most problematic step, and, therefore, the experimental challenge for oxygen electrocatalysis is to avoid or minimise the difference in intermediate energies.20
With the identification of the problematic scaling relation in oxygen electrocatalysis, came suggestions for a new strategy alternative to tuning – breaking the OOH–OH scaling relation.21,22 Montemore and Medlin noted that although “the OH vs. OOH scaling relation appears to be particularly hard to break,” it could be altered by stabilising interactions.3 For example, provided by spectator groups that form a hydrogen bond with the OOH intermediate.23 Interestingly, earlier experiments attempting to verify breaking strategy found no significant improvement in electrocatalytic ORR and OER performance, at the same time observing, that in principle it is possible to decrease the problematic intermediate adsorption energy differences.24
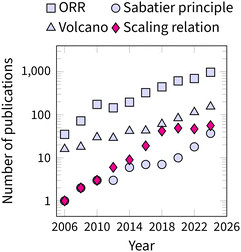
The recognition of scaling relations as the fundamental limitation in ORR catalysis is evident from the growing number of articles on ORR research in Fig. 2. In 2015, Vojvodic and Nørskov even suggested a special term, “circumventing” for any strategy that moves beyond the OOH–OH scaling relation.25 Consequently, the challenge of “circumventing the scaling relations” has become central to the advancement of ORR catalysis.9,26–28
In 2016, Busch et al. posed an important question: “How is it possible to go beyond the top of the volcano?” – which refers to the limit established by the OOH–OH scaling relation.29 They suggested overcoming this limit by avoiding the problematic OOH intermediate. This simple idea of “switching” to an alternative mechanism is referred as the switching strategy in recent literature.30,31
In this review, we define the fourth strategy – pushing, which is simultaneously switching to an alternative mechanism and using stabilising interactions, similar to the breaking strategy. In 2024, we introduced the term “bypassing” for the fifth strategy, which employs two states to decouple the adsorption energies and thus completely eliminate all scaling relations.32 Here, we also suggest “manipulating” as the most general term for overcoming as well as working within the limits set by all of scaling relations. This additional term means controlling any form of scaling relations to your advantage, thus, it should be better suited when discussing scaling relations than the commonly used circumventing.
Altogether, this review provides a set of terms and definitions for five general strategies for manipulating scaling relations in electrocatalysis. These strategies are: tuning, breaking, switching, pushing, and bypassing. They are defined with the thermodynamic approximation, i.e., simplifying the full complexity of the processes happening at interfaces to an assumption that there is one rate limiting step described by its free-energy “height”. More realistic approaches are reviewed in ref. 20, 33 and 34. Still, below, we show how the experimental, computational, and theoretical insights fit into the proposed classification, without the need to overcomplicate things. Thus, we suggest to use that knowledge to direct future research.
2 Mechanisms
To begin discussing strategies, we first remind what happens during oxygen electrocatalysis. Let us assume that the four-electron ORR in an acidic aqueous electrolyte proceeds via one of the two mechanisms with OH, OOH, and O intermediates on an adsorption site (*):Associative mechanism:
| * + O2 + (H+ + e−) ⇌ *OOH |
| *OOH + (H+ + e−) ⇌ *O + H2O |
| or *H2O + *OOH + (H+ + e−) ⇌ *OH + *OH + H2O |
| *O + (H+ + e−) ⇌ *OH + * |
| *OH + (H+ + e−) ⇌ * + H2O |
| 2* + O2 + (H+ + e−) ⇌ *O + *OH |
| *O + *OH + (H+ + e−) ⇌ *O + * + H2O |
| or *O + *OH + (H+ + e−) ⇌ *OH + *OH |
| *O + * + (H+ + e−) ⇌ *OH + * |
| *OH + * + (H+ + e−) ⇌ 2* + H2O |
The form and coordination of the intermediates depend on many factors, such as pH, coverage, and catalyst geometry. For example, in alkaline media, the OOH intermediate can be present as O2−.35 Without going deeper into such peculiarities, we focus on the simplified mechanisms as presented above, from two perspectives: geometrical and chemical.
2.1 Geometrical perspective
Experimental evidence shows that the associative mechanism dominates most known catalysts.36,37 The reason is geometric: the associative mechanism requires only a single atom in the active site, while the dissociative mechanism needs at least two neighbouring atoms to accommodate both dissociation products. Even if all surface atoms are nearby and active, as on metal surfaces, the mechanism does not switch from associative to dissociative. Nørskov et al., in their classic 2004 paper “On the origin of the overpotential for oxygen reduction in fuel cells,” rationalized the dominance of the associative mechanism specifically on the Pt(111) surface.38 Twenty years later, their explanation was generalized as follows: metal surfaces preferentially adsorb O on hollow sites and OH on top sites, which introduces a spatial mismatch that prevents the dissociative mechanism on pure metals.39Unlike metal surfaces, single-atom site catalysts (SACs) allow for on-top adsorption only. Furthermore, dual-atom site catalysts (DACs) allow for the adsorption of dissociation products on two neighbouring atoms as illustrated in Fig. 3.
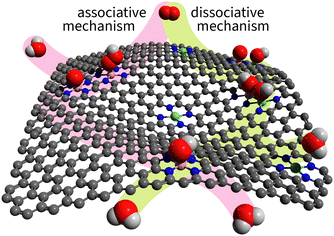 | ||
| Fig. 3 Illustration of associative and dissociative mechanisms on SACs and DACs. The associative path is highlighted in light magenta; the dissociative path – light green. | ||
In addition, according to the Brønsted–Evans–Polanyi principle, the dissociation barrier scales linearly with the adsorption energy.39,40 That can be perceived as “kinetic” scaling relations.10 One of the key parameters controlling the barrier is the inter-atomic distance.31 To balance thermodynamics with kinetics, the two acting atoms must be positioned at an optimal distance – neither too close (to avoid the repulsion effect on the adsorption energy) nor too far (to avoid the range effect on the dissociation energy barrier). For details, see Section 5.3.
At this point, let us briefly discuss the distinction between electronic and geometric effects in electrocatalysis. The number of atoms within the same active site constitutes the material's composition, which is directly related to its electronic structure. Herewith, two catalysts of the same composition can differ in geometry, like in the case of curved DACs.31 The distance between atoms within an active site has a geometric meaning; however, it is still directly related to the electronic structure, like in the case of strained Pt-skin.41,42 In these cases, the electronic structure of the active site dominates the catalysis. Thus, we suggest classifying the causing curvature and strain effects as electronic (or mixed). On transition metals, generalised coordination number has been suggested as an interesting descriptor, incorporating aspects of both composition by considering first and second nearest neighbouring atoms and geometry by including parameter for strain to account for ref. 43.
While both compositional and geometric effects often interplay in the catalysis and can affect the scaling relations,44 only when the geometry variation affects the mechanism and intermediates, such as switching between mechanisms (from associative to dissociative),12,35 and promoting additional interaction (like H-bonding),45,46 we suggest classifying underlying effects as geometric.
2.2 Chemical perspective
In chemistry, the mechanism defines how the bonds are transformed. Chemistry laws set limitations on bonds and their strengths, which in turn determine the adsorption energies and the scaling relations. The adsorption energy is used as the key descriptor in ORR catalysis, and its values are routinely predicted with density functional theory (DFT) calculations.16,47,48 The challenge is to relate this microscopic descriptor to macroscopic activity. For that, the adsorption energy (E) is turned into free energy (G) by adding the relevant thermodynamic terms: zero point energy (ZPE), enthalpy entropy TS, and various corrections:
entropy TS, and various corrections: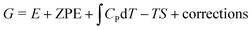 | (1) |
In practice, free energy values for only three intermediates – OOH, OH, O – are relevant for ORR. The common framework for relating these values to electrode potential is by utilising the computational hydrogen electrode (CHE).38 In brief, the electrochemical energy of proton–electron transfer steps at potential U (vs. reversible hydrogen electrode, RHE) is referenced as:
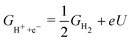 | (2) |
The free energies of the relevant adsorption intermediates are then calculated as:
 | (3) |
| ΔGO = GO − G* − GH2O + GH2 + 2eU | (4) |
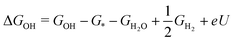 | (5) |
Note that all quantities (besides eU) can be calculated using theoretical formulas, quantum chemical approaches like DFT, as well as machine learning (ML).52,53 Regardless of the method used – with DFT or ML and using CHE or some superior framework54–56 – the scaling relations remain an empirical observation consistently emerging in ORR catalysis.57,58
3 Scaling relations
3.1 General form
Advancement of ORR catalysis is deeply rooted in understanding and manipulating the scaling relations. These relations can be generalized for any two intermediates on the same catalyst:| ΔGA = αA,BΔGB + βA,B. | (6) |
| βA,B = αA,Bβ1 + β2 | (7) |
Two characteristic correlations between ΔGOOH, ΔGOH, and ΔGO are shown in Fig. 4. These scaling relations constrain oxygen electrocatalysis across different classes of catalysts.39,61 Below, we examine the parameters of these correlations, offering an original perspective alongside the consensus view.
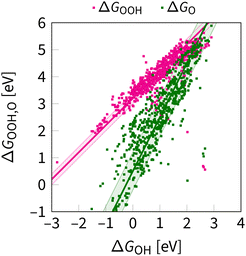 | ||
| Fig. 4 OOH–OH and O–OH scaling relations as obtained at the DFT level in ref. 62 and 63. The shaded region indicates the uncertainty in the scaling relations, as evaluated for the first time in this review. The lines are given by eqn (8) and (10). | ||
3.2 Case of ΔGOOHvs. ΔGOH
| ΔGOOH = ΔGOH + 3.2 ± 0.2 eV. | (8) |
 .68
.68
An alternative explanation is that the value of 3.2 eV in eqn (8) is a consequence of the destabilization of the oxygen–oxygen bond, transitioning from a double bond in O2 to a single bond in OOH. Specifically, from eqn (7), it follows that β = β1 + β2 if α = 1, where β2 represent the difference between the the formation free energy values for H2 and H2O (2.46 eV), and β1 is derived from the difference in the dissociation energy values of the bonds between half a double and a single oxygen–oxygen bond. The estimated range for β1 is from 0.40 to 0.84 eV, based on the bond dissociation energies of O2 and peroxides, such as H2O2, and CH3CO3H.69,70 Consequently, when considering these factors, β is approximately 3.1 ± 0.2 eV. Although indicative of the general trend, this value is subject to variations because of factors contributing to the adsorption energy, such as solvation and on-surface-mediated interactions.71–73
3.3 Case of ΔGOvs. ΔGOH
| ΔGO = 2ΔGOH + (GO + GH2O + G*− 2GOH) | (9) |
| ΔGO = 2ΔGOH + 0.5 ± 0.7 eV | (10) |
It agrees with the reported OH–O scaling with intercepts from −0.2 to 1.3 eV for distinct families of catalysts.58,76,79
3.4 Case of ΔGO/OHvs. ΔGOH
| ΔGO/OH = ΔGO + ΔGOH = 3ΔGOH + 0.5 ± 0.7 eV | (11) |
4 Volcano
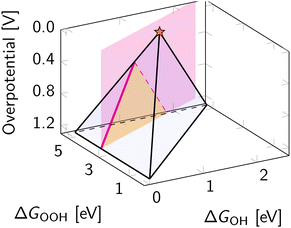
Eqn (8), (10) and (11) form a theoretical framework, known as volcano. The volcano is a central tool for understanding electrocatalysis. It can be constructed to represent overpotential or activity as “altitude” based on thermodynamics and kinetics, respectively.29,81 In this review, we focus on the ORR volcano that correlates adsorption energies with the deviation from the ORR thermodynamic equilibrium potential of 1.23 V. Fig. 5 presents a 3D view of this overpotential volcano, as first reported in 2016.29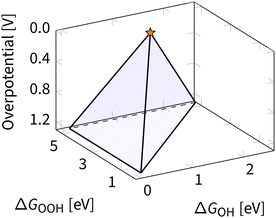 | ||
| Fig. 5 Three-dimensional overpotential volcano for ORR. The star indicates the apex of the volcano – an ideal catalyst with zero overpotential. | ||
4.1 Constructing the volcano
The ORR overpotential (ηORR) is expressed in terms of the adsorption energies as | (12) |
 | (13) |
In Fig. 5, each of the planes in the resulting volcano corresponds to the overpotential arising due to a different limiting step in eqn (13). Accounting for other limiting steps and intermediates introduces kinks to these planes.82–86 Accounting for the ORR kinetics smooths and shifts the volcano apex.87 These details are omitted below to narrow the focus to the apex of the volcano, representing the ideal ORR catalyst. In ORR research, discovering the ideal catalyst is the ultimate target, which remains elusive because of the scaling relations – fixed climbing routes on the volcano plot.
4.2 Climbing the volcano
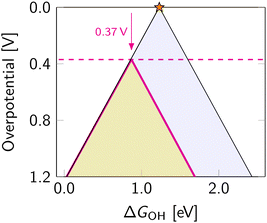
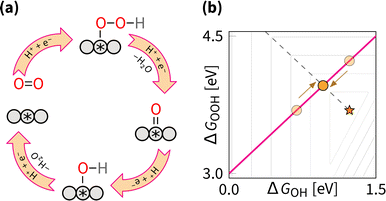
The scaling relations define the paths on the volcano planes that are accessible for climbing to the apex. In the graphical representation of the overpotential volcano, the OOH–OH scaling relation appears as a plane (Fig. 6). The intersection of the overpotential volcano surface and that plane determines the theoretically achievable overpotential values. All catalysts following the OOH–OH scaling relation appear on that line, forming the theoretically accessible path on the volcano's surface. Thus, while the volcano is three-dimensional, in practice, the search for optimal catalysts occurs in two dimensions. Therefore, it is common to reduce the problem's dimensionality by considering the volcano's projections.The most commonly used projection is ηORRvs. ΔGOH (Fig. 7). This side view adheres to the Sabatier principle,88 suggesting that optimal catalyst activity is achieved when the adsorbate binds neither too strongly nor too weakly. However, due to scaling constraints, the optimal adsorption energy of OH is not at the ideal 1.23 eV but rather lower (Fig. 7). That is, the best-predicted overpotential is around  for eqn (12) and (8). Notably, the experimental results in Fig. 8 converge to that limiting overpotential. As can be seen, scaling relations have been limiting progress in ORR catalysis for over twenty years. Consequently, improving oxygen electrocatalysis falls behind the growing demand for sustainable energetics.47,89 That sets the circumventing scaling relations as the central challenge in the current research on ORR catalysis.
for eqn (12) and (8). Notably, the experimental results in Fig. 8 converge to that limiting overpotential. As can be seen, scaling relations have been limiting progress in ORR catalysis for over twenty years. Consequently, improving oxygen electrocatalysis falls behind the growing demand for sustainable energetics.47,89 That sets the circumventing scaling relations as the central challenge in the current research on ORR catalysis.
 | ||
| Fig. 8 Timeline of experimentally observed overpotentials (half-wave potential, E1/2) for ORR. Data obtained from ref. 35 and 90–117. The magenta line indicates the limit set by the OOH–OH scaling relation with an intercept of 3.0 eV. The four values above the magenta line are achieved by circumventing the OOH–OH scaling relation through two strategies: breaking (cyan) and switching (green).35,92–94 Catalysts with platinum group metals (PGM) are marked with a five-pointed star; metal–nitrogen–carbon (M–N–C) catalysts are marked with a three-pointed star. | ||
While the side view of the volcano offers valuable insights into the Sabatier principle, it obscures opportunities for climbing higher. In subsequent discussions, the top view of ΔGOOHvs. ΔGOH is used, as shown in Fig. 9. This bird's eye view simplifies the scaling relation to a single line traversing the volcano. Notably, this line does not intersect with the ideal catalyst position, marked by a star. The goal of any strategy is to set a path as close to that star as possible.
| Surface | OOH–OH scaling relation/eV | Ref. |
|---|---|---|
| M(100) | ΔGOOH = 0.96 × ΔGOH + 3.32 | 5, 61 and 119–121 |
| M(111) | ΔGOOH = 0.96 × ΔGOH + 3.23 | 5, 61 and 119–121 |
| M-HEA | ΔGOOH = 0.76 × ΔGOH + 3.22 | 122 |
| MxOy | ΔGOOH = 0.77 × ΔGOH + 3.28 | 58, 62 and 123 |
| MN4 | ΔGOOH = 0.77 × ΔGOH + 3.25 | 21 |
| M2N6 | ΔGOOH = 0.87 × ΔGOH + 3.34 | 80 and 124–126 |
| MOF | ΔGOOH = 0.85 × ΔGOH + 3.06 | 77 and 86 |
| MPF | ΔGOOH = 0.78 × ΔGOH + 3.17 | 127 |
5 Manipulating the scaling relations
Advancing ORR catalysis involves developing strategies to manipulate the scaling relations, each targeting specific terms in eqn (6):1. Tuning: adjusting ΔGOH to about 0.86–0.96 eV to optimize the catalyst performance within the constraints of the OOH–OH scaling relation. This strategy involves fine-tuning the adsorption energies to achieve a balance that adheres to the Sabatier principle.
2. Breaking: decreasing βOOH/OH from 3.2 eV to the ideal value of 2.46 eV by stabilising OOH relative to OH. This strategy focuses on introducing spectators around active sites to induce stabilising interaction and thus shift the β value.
3. Switching: increasing α from 1 to 2.5–3 by switching from an associative to a dissociative mechanism. This strategy enables reaction pathways that avoid the OOH intermediate and requires two atoms, which are neither too far nor too close.
4. Pushing: changing α from 1 to 2.5–3 and adjusting βO/OH to O by stabilising O/OH relative to OH. This strategy requires controlling the interaction between intermediates, active sites, and spectators.
5. Bypassing: switching between two states with optimal adsorption energies for O/OH (3.69 eV) and OH (1.23 eV). For example, by introducing a dynamic surface that can reversibly change geometry at high turnover frequencies. This strategy aims to optimize the adsorption values for specific intermediates during the reaction cycle.
Each strategy offers a unique approach to enhancing ORR catalysis, with its efficiency depending on the specific catalyst's features and operational conditions. By exploring these general strategies, researchers can push the boundaries of what is currently achievable. We illustrate how the development of more active, stable, and sustainable catalysts for ORR has evolved through the prism of the suggested classification of the scaling relations.
5.1 Tuning the OOH–OH scaling relation
The OOH–OH scaling relation implies the ORR associative mechanism. Adjusting ΔGOH moves the catalyst along the scaling relation, as shown in the schematic representation in Fig. 10. This strategy is the most thoroughly studied. Although it does not allow circumventing the scaling relations, it enables catalysts to be optimized toward the peak of the Sabatier volcano in Fig. 7. The optimal tuning corresponds to the intercept of the scaling plane with the volcano edge (ΔGOOH + ΔGOH = 4.92 eV), giving an optimal range of ΔGOH from 0.86 eV to 0.96 eV. That gives the minimum predicted overpotential of 0.27–0.37 V.The effect of the tuning strategy can be mathematically explored with the δ optimization (where δ is the optimisable adjustment in ΔGOH value), for the full description of the strategy we refer readers to the ref. 128, where the optimisation has been applied to OER for five classes of materials. Notably, the generalisable findings of the optimisation procedure were that the tuning is more effective for catalysts with high overpotentials, and becomes less effective for catalysts at low overpotentials.
Adjusting ΔGOH for Pt-based catalysts was thoroughly studied using combined experimental and computational approaches. The main direction of adjustment is weakening the adsorption of OH on a given surface relative to the well-defined Pt(111) surface. Table 2 summarizes the combined computational and experimental studies linking the measured and predicted activities to the electronic and geometric structures of the catalysts. These studies revealed several specific effects for tuning the OOH–OH scaling relation in the ORR catalysis, including modification of surface electronic structure (strain effect129–132), and introduction of alloying elements (alloy effect133,134). Both are based on the Sabatier principle and empirical evidence that Pt(111) overbinds OH by 0.1 eV.61 The latter assumption was experimentally verified by plotting the potential corresponding to the OH half-coverage versus the ratio of two current density values at 0.9 V vs. RHE: jk/jk,Pt(111)).135 On that basis, it is possible to plot the relative experimental activities against the relative calculated OH adsorption energy, as shown in Fig. 11.
| Example catalyst | Type of tuning the OH–OOH scaling relation | Relative activity | Ref. |
|---|---|---|---|
| Co/Pt(111) | Straining Pt(111) overlayer with Co layers | 13 | 152 |
| Ni/Pt(111) | Straining Pt(111) overlayer with Pt3Ni | >10 | 141 and 143 |
| Y/Pt(111) | Straining Pt(111) overlayer with Pt3Y | 6–10 | 144, 153 and 154 |
| Cu/Pt(111) | Liganding Pt(111) 2nd layer with Cu | 2–10 | 19 and 155 |
| Gd/Pt(111) | Straining Pt(111) overlayer with Pt5Ln | 3–6 | 142, 156 and 157 |
| Pt45Pd45Co10 | Optimizing distribution of ads. energies | 13 | 158 |
| Pd–Ru HEAs | Optimizing distribution of ads. energies | 2 | 159–161 |
 | ||
| Fig. 11 Relative activity vs. relative adsorption energy of OH on metals and alloys. Relative activity is the ratio of two current density values at 0.9 V vs. RHE: jk/jk,Pt(111). Energy difference values were calculated at the DFT level. All data points are taken from ref. 19, 130, 135 and 140–151. The dashed magenta line indicates a limitation beyond the OOH–OH scaling relation. The black lines are defined by equation jk/jk,Pt(111) = exp(ΔΔGOHF/RT), where ΔΔGOH = ΔGOH,apex − |ΔGOH − ΔGOH,apex| The limiting magenta line, corresponding to a scaling given by jk/jk,Pt(111) = exp(0.5 × ΔΔGOHF/RT). | ||
In Fig. 11, a sharp Frontier in activities immediately catches the eye. It signifies a fundamental limitation that currently lacks a consistent explanation. One can apply incrementalism thinking to use the scaling relation as a foundation to consider microkinetic modelling and coverage calculation.40 However, this approach results in a frontline with a slope of 0,136 whether the observed slope is 0.5 (Fig. 11). Such value could correspond to the O–OH scaling relation with α = 1.5. Thus, the scaling relations could be more than meets the eye, because for some families of catalysts, such scaling is indeed predicted.58,118,137,138 A more plausible alternative is that two OH groups form instead of a single O intermediate being formed at the Pt-based catalysts, as predicted by Tripković et al.139 Both scenarios require detailed analysis of the research gap, illustrated in Fig. 11. Within the incremental approach, one should apply step by step thermodynamic CHE-based calculations, then apply microkinetic modelling and also account for coverage as well as other interfacial effects. Alternatively, within an essentialism thinking, one can simply extend the definition of scaling relations as correlation between reaction-step free energies that already include kinetic barriers and coverage-dependent free energies. In that case, Fig. 11 might present the reality without any need for incremental adjustment because the calculated adsorption free-energies are proportional to the reaction-step free energies. For instance, through the Brønsted–Evans–Polanyi principle.
For the scope of this review, we focus below on the standard correlation between adsorption energies while assuming that kinetics, coverage, solvation, and other essential terms remain negligible or counterbalance each other. Besides, we avoid in-depth discussion of specific effects, such as the above-mentioned strain and alloy effect, to avoid misinterpretations and focus on the five general strategies. As follows from the list given in Section 5.2, there are over a dozen of specific effects that allow tuning the OOH–OH scaling relation. As these effects have been repeatedly and thoroughly reviewed in the literature, we simply highlight that their essence can either be electronic or geometric, as suggested in ref. 10 and 25 and revised in Section 2.1.
5.2 Breaking the OOH–OH scaling relation
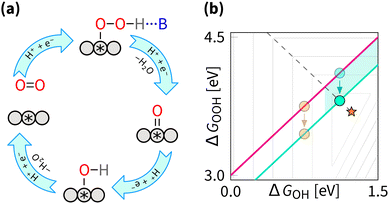
Breaking the OOH–OH scaling relation is a challenging and active area of ORR research. The key to breaking is in stabilising OOH intermediate relative to OH, i.e., decreasing the intercept β to 2.46 eV. Similarly to the tuning strategy, the breaking strategy can be mathematically be explored by the δ–ε optimisation (where the ε describes the stabilisation of ΔGOOH).162 Interestingly, the results from the δ–ε optimisation observe that while tuning improves majority of catalysts, breaking provides further improvements only for a small subset of catalysts.128 From the volcano perspective, this is illustrated by the shaded blue region in Fig. 12(b), where only the catalysts that are moved closer to the apex are expected to show improvement from breaking. Exner provides a more comprehensive perspective on breaking the OOH and OH scaling relation and its effect on electrocatalytic activity in OER,163 and statistical analysis,164 suggesting that decreasing the intercept β to 2.76 eV provides statistically more significant improvement in catalytic activity.From experimental perspective, the breaking has been fulfilled for the reaction opposite to the ORR – oxygen evolution reaction (OER). For OER, breaking was enabled by the cationic vacancies and adjacent active sites, enabling tunable hydrogen bonding.165,166 Notably, the breaking does not have to affect the OOH intermediate directly – in OER, DACs can enable intramolecular hydrogen transfer, leading to effective stabilisation of the OOH intermediate.167 For OER, it is also possible to switch the mechanism from the adsorbate evolving mechanism to the lattice oxygen-mediated mechanism, where the lattice oxygen in the catalyst directly participates in the reaction and provides the required selective stabilization of intermediates.11,57,168–172 Effects similar to those described above for OER were predicted to enhance the ORR by (1) introducing p states, (2) introducing a proton acceptor group (spectator), (3) introducing a second adsorption site, (4) introducing a nanoconfinement, (5) introducing a defect, (6) adjusting coordination environment, (7) adjusting pH, adjusting field, (8) adjusting solvation, (9) applying the strain effect, (10) applying the ligand effect, (11) applying curvature effect, (12) applying cocktail effect, to name just a dozen out of many.16,26,47,173–176 Regardless of terminology, the listed effects fall under either the tuning or the breaking strategy.
While for the ORR the tuning strategy has been verified experimentally numerous times since 2011 (Section 5.1), there was no experimental evidence for breaking until 2023, when Zong et al. synthesized a DAC with Fe and P active sites (PN3FeN3). The phosphorus site turns into P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O which acts as a spectator that selectively stabilises OOH through hydrogen bond.177 More recently, OOH hydrogen bonding with spectator from microporous environment has been observed.178 In essence, breaking is selective OOH stabilization relative to OH as sketched in Fig. 12. In principle, the effect of such stabilization should be comparable to the H2O2·H2O bond strength of 0.3 eV.179,180 A similar stabilization of 0.3 eV was predicted by Sours et al. and Yang et al. for models with OH spectator accepting a hydrogen bond from the OOH intermediate.45,46 With this value, the minimum ORR overpotential for the breaking strategy can be estimated as
O which acts as a spectator that selectively stabilises OOH through hydrogen bond.177 More recently, OOH hydrogen bonding with spectator from microporous environment has been observed.178 In essence, breaking is selective OOH stabilization relative to OH as sketched in Fig. 12. In principle, the effect of such stabilization should be comparable to the H2O2·H2O bond strength of 0.3 eV.179,180 A similar stabilization of 0.3 eV was predicted by Sours et al. and Yang et al. for models with OH spectator accepting a hydrogen bond from the OOH intermediate.45,46 With this value, the minimum ORR overpotential for the breaking strategy can be estimated as 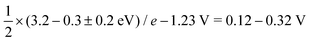 using eqn (8) and (12).
using eqn (8) and (12).
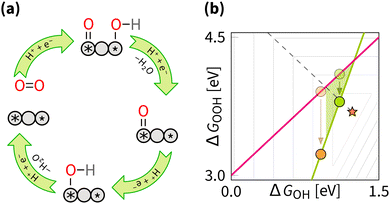
5.3 Switching between two scaling relations
To overcome the scaling relation between the adsorption energy of OH and OOH, a promising strategy is to avoid the OOH intermediate by directing the ORR through the dissociative mechanism. As illustrated in Fig. 13, this approach replaces OOH with two intermediates, O and OH, adsorbed at distinct sites. These two sites can act together in the mechanism when they are neither too far nor too close. Herewith, two sites can be situated in different geometries: within the same plane, facing each other, or taking in-between orientation. Let us examine the concept of switching using examples of coplanar and cofacial DACs.![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond during protonation, and desorbs OH from the platinum site at half-wave potential (E1/2) of 1.05 V.92 Similarly, at Pt/MnO2, a Pt–Mn DAC adsorbs O2, dissociates the O
O bond during protonation, and desorbs OH from the platinum site at half-wave potential (E1/2) of 1.05 V.92 Similarly, at Pt/MnO2, a Pt–Mn DAC adsorbs O2, dissociates the O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond during protonation, and desorbs OH from the manganese site with E1/2 of 0.93 V.93 These studies provide in situ spectroscopic evidence for the dissociative mechanism of these materials, proving that the switching strategy is feasible.
O bond during protonation, and desorbs OH from the manganese site with E1/2 of 0.93 V.93 These studies provide in situ spectroscopic evidence for the dissociative mechanism of these materials, proving that the switching strategy is feasible.
Due to challenges in identifying the active sites and intermediates, there was no strong evidence that switching occurs on metal–nitrogen–carbon (M–N–C) based DACs until the works of Zhou et al.12 and Huang et al.35 presenting FePtN6 and Fe2N6 DACs along with proving the mechanism switching with infrared spectroscopy. Several experimental studies of M2N6 and defective carbon DACs suspected switching to be responsible for the enhanced activity, but lacked structural characterization to confirm the dissociative mechanism.181–187 Herewith, computations predict that only certain DACs (Fe2N6, FeCoN6, Co2N6) favor the dissociative mechanism over the associative one.80,188 These DACs show higher activity in experiments than corresponding SACs,182,189 and indeed can be attributed to switching due to spectroscopic evidence provided for Fe2N6 active site.35 Recently, the FeCoN6–OH active site has been experimentally shown to switch to the dissociative mechanism.190
A viable alternative to Fe2N6 is BFeN4. It is predicted to enable the dissociative mechanism by adsorbing oxygen intermediates at the boron site.191 BFeN4 DACs were synthesized and showed higher activity than FeN4 SACs.192,193 In the absence of spectroscopic evidence for switching, these results might instead reflect tuning or breaking (like with PN3FeN3 in Section 5.2). Still, these examples demonstrate opportunities in composing planar DACs with non-metal active sites, potentially capable of switching between the scaling relations.
In addition to the compositional expansion, another direction is exploring the geometrical features of DACs, such as inter-atomic distance and curvature. The role of inter-atomic distance was revealed in experimental studies of coplanar DACs,184,194 where the inter-atomic distance was continuously varied, and a clear trend in catalytic activity was observed. The supporting DFT calculations showed a non-linear effect of the distance on the electronic structure (e.g., spin-density), resembling the well-known strain modulation.18,42 Similarly, the curvature alternation also affects the electronic structure and consequently alters the catalytic activity.131,195–201 Most importantly, changes in geometry through inter-atomic distance and curvature variation can switch between the associative and dissociative mechanisms. In the latter case, the geometric effect can be described by analogy to the Sabatier principle: optimal catalysis occurs when the inter-atomic distance within an active site is neither too far nor too close.
However, for coplanar DACs, the optimal distances for switching and breaking are almost the same – 2.5 Å (Fig. 14). That makes spectroscopic confirmation essential for identifying the mechanism and the manipulation strategy. Herewith, if the catalyst situated on the right leg of volcano (Fig. 7 and 11), signals of OOH in the spectra together with enhanced activity does not necessarily imply breaking,94,202 as OOH could be part of competing process of H2O2 formation. On the contrary, For cofacial DACs, the intersite distance is clearly different: 7.2 Å for breaking and 4.5 Å for switching (Fig. 14). We suggest using these numbers when designing catalysts for switching.
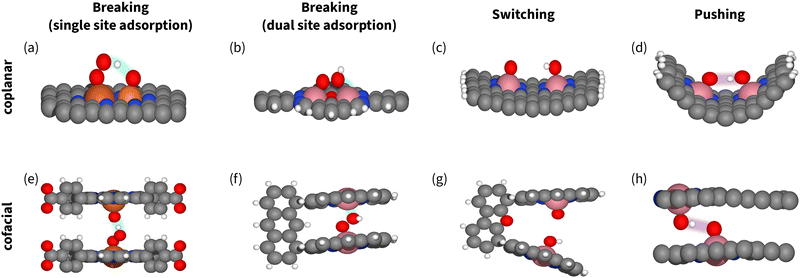 | ||
| Fig. 14 Models of catalysts enabling breaking (a), (b), (e) and (f), switching (c) and (g), and pushing (d) and (h), showing the neither too far nor too close principle. Carbon atoms are gray, oxygen atoms are red, hydrogen atoms are white, iron atoms are dark orange, phosphorous atoms are light orange, and cobalt atoms are pink. The stabilization interactions with spectators or secondary adsorption sites are highlighted. (a) Coplanar P–Fe sites,177 (b) coplanar Robson-type macrocycle with Co2N4O2 active site94,202 (c) coplanar DAC with Fe2N6 active site,35 (d) coplanar curved catalyst with two CoN4 active sites,32 (e) cofacial slit-pore with Fe–N4 active sites,45 (f) and (g) cofacial packman catalyst,81 (h) cofacial slit-pore with shifted Fe–N4 active sites enabling hydrogen bonding.203 | ||
In terms of numbers, the optimum of switching corresponds to the intercept of the scaling plane with the volcano edge (ΔGOOH + ΔGOH = 4.92 eV). In principle, assuming α = 3 and β = 0.5, the optimal ΔGOH = 1.10 eV yielding a predicted overpotential of 1.23 − (3 × 1.10 − 1.10)/2 = 0.13 V.
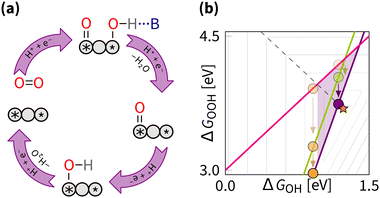
5.4 Pushing the O/OH–OH scaling relation
The DFT predictions for the dissociative mechanism show that the O/OH–OH scaling can be pushed closer to the ideal catalysts (Fig. 15). The pushing strategy involves stabilising O/OH relative to OH, similar to stabilising OOH relative to OH in the breaking strategy. That is achieved by varying the value of β in the scaling equation. The ideal catalyst can be achieved by approaching α = 3 and β = 0 eV or α = 2.5 and β = 0.6 eV in eqn (11).DFT calculations predict overpotentials as low as 0.15 V for Pacman Co–Co diporphyrin anthracene and curved coplanar 2CoN4 models that realize the pushing strategy through liganding and curving.31,81 It is interesting to note that the first model is clearly inspired by nature, namely enzymes, while the second model refers to artificial M–N–C catalysts. Both studies illustrate the vital role of simulations in the discovery, synthesis, and verification of superior catalysts. In particular, let us stress that without computer simulations, the design of dipophyrin complexes (mimicking enzymatic biocatalysis) stagnated at a modest catalytic activity for decades, after being introduced in the 1960s.213 The introduction of computational models allowed for more deliberate design, including the predictions of improved ORR activity via the pushing strategy.39 Based on these theoretical insights, the synthesis of layered Fe–N–C nanotubes with Fe–Fe active sites led to the development of DACs with significantly reduced overpotential.90 With this example, we illustrate that it is better to light the way forward with purpose than to stumble in the dark, hoping for chance discovery. Thus, whether inspired by nature or driven by theory and data, one benefits from deliberately choosing a specific effect (Section 5.2 within one of the general strategies for manipulating the scaling relation rather than relying on serendipity. In principle, assuming α = 3 and β = 0.20, the optimum ΔGOH = 1.18 eV, which results in the minimum predicted overpotential of 1.23 − (3 × 1.18 − 1.18)/2 = 0.05 V.
5.5 Bypassing the scaling relations
The possibility of completely decoupling adsorption energies to design better ORR catalysts is a fascinating idea worth considering. This idea implies switching between two catalyst states during the reaction cycle, each having an optimal adsorption energy value for O/OH and OH (Fig. 16). Computer modelling is well-suited to test any opportunity to advance closer to the ideal ORR catalyst. The recently simulated 2CoN4 DAC model illustrates two geometric states – one with ideal adsorption of O/OH and another with ideal adsorption of OH.32 That model shows that achieving the ideal values of ΔG on the same catalyst is possible via the curvature effect with a predicted overpotential is nearly 0 V. Transitioning between states is expected to occur via the geometric adaptation of the catalysts during the reaction cycle. Similarly, for a 2ZnN4 DAC model, geometry adaptation also gives in simulations a 0 V overpotential.207Here let us recall the dynamic geometry adaption of subnanometer Pt clusters that show bypassing of all scaling relations.215 However, interesting question is whether experimentally possible or such particles would turn into less reactive, yet more stable species. At first sight, geometry adaptation for stable materials at the turnover frequency of the ORR seems hardly imaginable in practice. Looking closer, it becomes clear that the essence of achieving the ideal catalyst lies in transitions between states, which need not be geometric. In particular, this means a single electronic or geometric state for one intermediate, and another electronic or geometric state for the other intermediate. One DFT study demonstrates an inspiring concept of high-frequency switching between electronic states by the electric field.13 For ORR, a more recent combined experimental and DFT study, has shown that the structure of the active site can dynamically change due to quasi-covalent Fe–F bond.216 Overall, considering more than one state of an active site is a powerful idea to bypass the scaling relations and design better ORR catalysts, which could overcome the stagnating state-of-the-art frontier (Fig. 8).
6 Summary and outlook
6.1 Scaling relations' classification in brief
This review refines existing and proposes new definitions for general strategies of manipulating scaling relations: tuning, breaking, switching, pushing, and bypassing. This classification provides a foundation for addressing challenges posed by the scaling relations. In brief, in any multi-step reaction, there is a predominant reaction mechanism limited by the main scaling relation that can be tuned or broken. For such reactions, it is possible to switch to an alternative mechanism and push it towards the limits imposed by the alternative scaling relations. In principle, it is possible to bypass all scaling relations by involving at least two states. This review focused on the oxygen reduction reaction (ORR) as an example and revealed the following.The tuning strategy focuses on the OOH–OH scaling as the limiting factor in the predominant mechanism of oxygen electrocatalytic reduction to water. However, in Section 5.1, we speculated that the O–OH or 2OH–OH scalings could also be a significant constraint. Herewith, we derive both OOH–OH and O–OH scaling relations based on bond strengths. In this way, we offer a chemically intuitive perspective, where altering the electronic structure of a catalyst tunes its activity within the limit set by the OOH–OH scaling relation.
The breaking strategy, in theory, exceeds the limit of the OOH–OH scaling by stabilising the OOH intermediate. Selective stabilization of OOH requires precise structural control, which can be achieved using metal–organic frameworks (MOFs) and metal–nitrogen–carbons (M–N–C).
The switching strategy relies on the presence of two active sites to favour the dissociative ORR mechanism. DACs are, therefore, a promising discovery platform for implementing this strategy.35,183,191 Herewith, it is essential to experimentally confirm the switching mechanism with in situ spectroscopy.
The pushing strategy combines the stabilization effect with mechanism switching, and DACs incorporated into organic frameworks with spectators could offer a solution. As for 2025, the pushing strategy has not yet been verified experimentally.
The bypassing strategy promises to completely eliminate the constraints of the scaling relations by using two distinct states (electronic, geometric, photonic, or similar) to decouple the adsorption energies of intermediates.
Fig. 17 summarizes five strategies in the form of volcanoes with minimal overpotentials and examples of computational predictions and experimental verifications for ORR. For the bypassing strategy, we refer to cytochrome c oxidase as an example of how enzymes in nature adapt during the ORR reaction to bypass the scaling relations.217
 | ||
| Fig. 17 Classification of strategies for manipulating the scaling relations in ORR. Circles indicate chosen experimental results and squares – theoretical predictions. Tuning: varying of OH adsorption energy; theoretical prediction for Pt(111); experimental result for FePc/CoPc@CNT catalyst.218 Breaking: stabilising OOH relative to OH; theoretical prediction for slit-pore system;45 experimental result from Fe,P-DAS@MPC catalyst;177 switching: by enabling the dissociative mechanism; theoretical prediction for dual-catalysts;138 experimental data point for DAC with Pt–Fe active site.92 Pushing: combining stabilization effect with mechanism switching; no theoretical or experimental data points so far. Bypassing: transitioning between states during the reaction cycle; theoretical prediction for geometry-adaptive M–N–C catalyst;32 experimental data point for cytochrome c oxidase.217 | ||
6.2 Scaling relations' classification in numbers
Scaling relations help to quantify the correlations between adsorption energies, catalytic structures, and overpotential (or activity). Each of the five strategies in Table 3 is characterized by distinct numerical parameters that determine the minimal overpotential.| Strategy | α | β | Scaling | ΔGOH/eV | d O–O/Å | d M–M/Å | η/V | Ref. |
|---|---|---|---|---|---|---|---|---|
| a The distance in pushing should be greater than in the switching case to enable a hydrogen bond between O and OH, while in bypassing the geometry is adaptive and should be similar to the switching case. | ||||||||
| Tuning | 1 | 3.20 | OOH–OH | 0.86 | — | — | 0.37 | |
| Tuning | 1 | 3.00 | OOH–OH | 0.96 | — | — | 0.27 | |
| Breaking | 1 | 2.70 | OOH–OH | 1.11 | 2.8 (3.4) | 2.7 (7.2) | 0.12 | 45, 94, 177 and 214 |
| Switching | 3 | 0.50 | O/OH–OH | 1.10 | 2.5 (2.8) | 2.5 (4.5) | 0.13 | 12, 31, 35 and 184 |
| Pushing | 3 | 0.20 | O/OH–OH | 1.18 | 0.05 | |||
| Bypassing | — | — | — | 1.23 | 0 | 32 | ||
The tuning strategy focuses on optimising the OOH–OH scaling relation. For this approach, the optimal OH adsorption energy of 0.86–0.96 eV corresponds to an overpotential of 0.37–0.27 V.
The breaking strategy aims to stabilise the OOH intermediate relative to OH, reducing the OOH–OH scaling limit. The optimal OH adsorption energy after stabilization is approximately 1.11 eV, which corresponds to an overpotential of 0.12 V. This strategy requires a spectator that can stabilise OOH. The characteristic bond lengths between the most distant oxygen atoms (O–O) ∼ 3.4 Å (in cofacial DACs) or ∼2.8 Å (in coplanar DACs) and two active sites are ∼7.2 Å (in cofacial DACs) or ∼2.7 Å (in coplanar DACs).45,94,177,214
The switching strategy relies on dual active sites to enable dissociative mechanisms. In switching, the repulsion between the O/OH and OH intermediates is typically around 0.5 eV, resulting in optimal overpotential of 0.13 eV. The optimal bond lengths for this strategy are ∼2.5 Å for both the O–O and M–M distances in the coplanar case, or ∼2.8 Å for O–O distance and ∼4.5 Å for M–M distance in the cofacial case.12,31,35,184
The pushing strategy combines the effects of stabilization and switching, maintaining a balance between stabilising intermediates and facilitating reactions. The stabilization may reduce the repulsion between the O/OH and OH intermediates to 0.3 eV, reducing the overpotential to 0.05 V. For this strategy, bond lengths should be slightly larger than in the switching case.
The bypassing strategy completely decouples adsorption energies and thus eliminates scaling constraints. This strategy achieves a theoretical zero overpotential (η = 0), with characteristic bond lengths similar to the switching case. Natural systems, such as cytochrome c oxidase, inspire this approach through their ability to spatially and electronically separate catalytic states.219
These numerical estimates serve as a foundation for catalyst development. For example, tuning strategies have been successfully applied to Pt-based alloys, where straining and liganding optimize the OOH–OH scaling relation.130,134 Similarly, breaking, switching, and pushing strategies offer pathways for designing catalysts with high-entropy alloys (HEAs), metal–nitrogen–carbons (M–N–C), metal–organic frameworks (MOFs), and molecular complexes.28,45,175,220,221 By integrating these principles with theoretical and experimental data, researchers can systematically explore various chemical spaces to develop highly efficient catalysts.
6.3 Scaling relations' classification on a timeline
Progress in scaling relations research highlights the effectiveness of integrating theory, experiments, and computational simulations. Collaboration across these disciplines has consistently advanced the understanding and application of scaling relations in electrocatalysis, particularly in the oxygen reduction reaction (ORR). As noted by Seh et al., a systematic combination of these approaches has revealed broader principles that guide the rational design of catalysts.222Fig. 18 highlights milestones in the exploration of scaling relations. The timelines emphasize the iterative nature of progress in this field, where theoretical predictions guide experimental efforts, and experimental results refine theoretical predictions. For example, tuning strategies for Pt-based catalysts were first proposed through computational models and later confirmed by experimental studies that focused on strain and ligand effects. Breaking strategies have evolved similarly, with experimental stabilization of OOH intermediates validating earlier theoretical predictions of minimum overpotentials. Switching strategies, implemented in DACs, required in situ spectroscopic evidence to confirm the mechanism changes predicted by theory.224
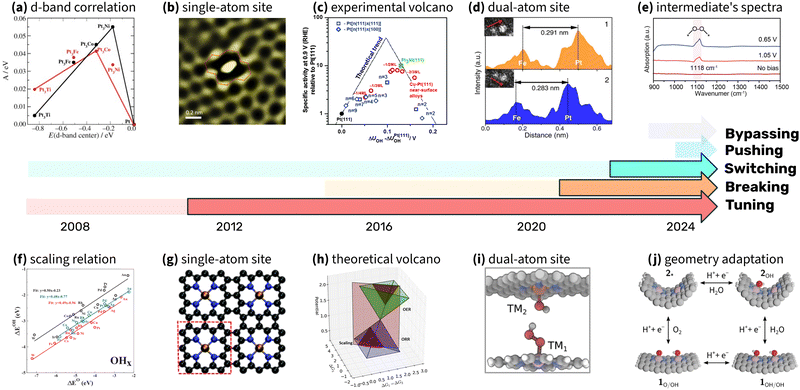 | ||
| Fig. 18 Timeline of milestones in ORR research, highlighting the interplay between theory, experiments, and simulations. Five distinct strategies – tuning, breaking, switching, pushing, and bypassing – are represented with five timelines. Each timeline begins with theoretical predictions (pale colors) and transitions to experimental validation (vivid colors). Insets above the timelines illustrate key experimental breakthroughs, while insets below highlight critical theoretical and computational advancements that shaped the field. (a) Activity correlation with experimentally measured d-band center (reproduced with permission from ref. 140, copyright 2006, John Wiley and Sons), (b) image of single-atom site (reproduced with permission from ref. 223, copyright 2018, Elsevier), (c) experimental volcano plot (reproduced with permission from ref. 135, copyright 2014, Royal Society of Chemistry), (d) dual atome site characterisation (reproduced with permission from ref. 12, copyright 2022, Springer Nature), (e) SR-FTIR spectra of oxygen reduction intermediate (reproduced with permission from ref. 93, copyright 2023, American Chemical Society), (f) scaling relations (reproduced with permission from ref. 1, copyright 2007, American Physical Society), (g) example of single atom site (reproduced with permission from ref. 21, copyright 2011, Royal Society of Chemistry), (h) theoretical volcano (reproduced with permission from ref. 29, copyright 2016, Elsevier), (i) dual atom site example (reproduced with permission from ref. 45, copyright 2020, American Chemical Society), (j) geometry adaptive catalysis (reproduced with permission from ref. 32, copyright 2024, Royal Society of Chemistry). | ||
6.4 Scaling relations' classification and material classes
The overviewed literature shows the general consensus that the scaling relations are universal for all catalysts. First, most of the catalysts prefer the associative mechanism. Thus, most of them allow for the tuning strategy although with slightly different intercept and slope for different material classes. Second, if the deviation is large enough to be considered as the breaking of the OOH–OH scaling relation that is through a stabilisation of OOH relative to OH Nevertheless, let us note several important points regarding different material classes.Electrocatalysts can be grouped by their structural character. Bulk materials with extended surfaces include metals, alloys, HEAs, oxides, mixed oxides, HEOs, MXenes, and carbon materials, while catalysts with atomistic sites include M–N–C, MOFs, COFs, and molecular complexes. These materials can also be distinguished by their degree of structural order. M–N–C, HEAs, and HEOs are stochastic, while surfaces like Pt(hkl) or molecular FePc are well-defined.
Examples from these material classes are discussed in the sections above in regard to their activity, which is governed by scaling relations. The activity exhibits systematic deviations as shown in Table 1. Even larger differences are seen in stability, which varies more widely across these material classes than their activity or selectivity. For instance, Pt-based catalysts such as Pt-alloy nanopolyhedra and nanowires often degrade through dissolution of less noble metals, migration and coalescence of Pt atoms, and gradual loss of their shape and dispersion under potential cycling, all of which are further accelerated by carbon support corrosion.225 In contrast, M–N–C catalysts suffer from demetallation, carbon matrix corrosion induced by reactive oxygen species, protonation of N-groups that deactivates sites, and micropore flooding that limits oxygen transport.226 These degradation mechanisms illustrate how stability differs fundamentally between these material classes, beyond the effects of scaling relations on activity and selectivity. Another relevant aspect is the ratio of catalytically active atoms to all other atoms, whether exposed on the surface or buried in the bulk. In this regard, HEAs and M–N–C catalysts are similar, as the activity of their central atoms is determined by their neighbouring atoms. This raises the open question of whether HEA and M–N–C catalysts can ever achieve the activity of strained Pt-skin, even if their central atoms possessed ΔG value optimal for tuning the OOH–OH scaling relation in Fig. 11.227,228
6.5 Scaling relations' classification in future vision
While single-step electrocatalysis (like hydrogen evolution) can be described using a 2D volcano with a 0 V overpotential apex, multi-step electrocatalysis (like oxygen reduction) exhibits a more complex nature, approximated by a 3D volcano with several hardly reachable apexes. This complexity can, to some extent, be rationalized through scaling relations.229,230 These scaling relations adhere to fundamental chemical laws, defining paths on the 3D volcano that can be traversed by modifying the electronic and geometric structures of catalysts. Optimising the electronic structure aligns with the Sabatier principle, while for geometric structure, a new principle emerges: neither too far nor too close. All of these concepts integrate seamlessly into the proposed classification, making it broadly applicable to any multi-step electrocatalytic reaction.At this point, it is worth recalling that electrocatalysis involves three key properties: activity, selectivity, and stability. Scaling relations within the CHE framework map the landscape of activity and selectivity, yet stability follows a different logic, set by reaction conditions and catalyst properties. Catalysts are often described as “any substance that increases the rate of a reaction without itself being consumed”, yet in reality they degrade. Many of the catalysts that excel at manipulating the scaling relations are inherently unstable. This controversy resembles the CAP theorem in computer science231 – just as no system can deliver consistency, availability, and partition tolerance at once, electrocatalysis may face a similar trilemma between activity, selectivity, and stability. Especially in oxygen electrocatalysis, where oxygen molecules and protons facilitate corrosion of catalysts and their support.
Refocussing back on the scaling relations, let us summarise that the presented classification is applicable to the oxygen evolution reaction (OER) – a slightly more complex reverse of the ORR. Furthermore, the analysis extends naturally to multifunctional catalysis, such as bifunctional OER and ORR catalysts for air-batteries.232–234 When applied to bifunctional oxygen electrocatalysis (on the same catalyst), as the volcano plot for bifunctional catalysis has plateau,235 the advantages of the switching strategy become evident. For example, this strategy achieves an optimal overpotential of 0.45 V, compared to the tuning strategy, which even for the best catalysts imposes a fixed overpotential of 0.74 V, derived as β − 2.46.236
The classification extends beyond electrocatalysis of oxygen to nitrogen, carbon and other elements, as well as the combinations, such as urea electrosynthesis. The general message is that in multi-step reactions, there is one predominant mechanism that can be tuned or even broken. By switching to an alternative mechanism, catalysis can be further pushed towards the limit, potentially bypassing all scaling relations to achieve ideal performance.
Author contributions
Vladislav Ivanistsev and Ritums Cepitis: conceptualization, methodology, validation, formal analysis, writing – original draft, writing – review & editing, visualization. Nadezda Kongi and Jan Rossmeisl: conceptualization, validation, writing – review & editing, project administration, funding acquisition.Conflicts of interest
There are no conflicts to declare.Data availability
All data and scripts required to reproduce the figures presented in this article are openly available at https://gitlab.com/doublelayer/chemsocrev_2025_scaling-relations.Acknowledgements
V. I. and J. R. acknowledge the Danish National Research Foundation Centers of Excellence, the Center for High Entropy Alloys Catalysis (DNRF149), and the Independent Research Fund Denmark (0217-00014B). V. I. receives funding from the European Union's Horizon 2020 research and innovation program under the Marie Skłodowska-Curie (101031656). This research was also supported by the Estonian Ministry of Education and Research (TK210) and the Estonian Research Council (grant STP52 and PUTJD1244).References
- F. Abild-Pedersen, J. Greeley, F. Studt, J. Rossmeisl, T. R. Munter, P. G. Moses, E. Skúlason, T. Bligaard and J. K. Nørskov, Phys. Rev. Lett., 2007, 99, 016105 CrossRef CAS PubMed.
- G. Jones, T. Bligaard, F. Abild-Pedersen and J. K. Nørskov, J. Phys.: Condens. Matter, 2008, 20, 064239 CrossRef CAS PubMed.
- M. M. Montemore and J. W. Medlin, Catal. Sci. Technol., 2014, 4, 3748–3761 RSC.
- S. Vijay, G. Kastlunger, K. Chan and J. K. Nørskov, J. Chem. Phys., 2022, 156, 231102 CrossRef CAS PubMed.
- J. Rossmeisl, A. Logadottir and J. K. Nørskov, Chem. Phys., 2005, 319, 178–184 CrossRef CAS.
- J. H. Montoya, C. Tsai, A. Vojvodic and J. K. Nørskov, ChemSusChem, 2015, 8, 2180–2186 CrossRef CAS PubMed.
- M. J. Kolb, D. Loffreda, P. Sautet and F. Calle-Vallejo, J. Catal., 2021, 395, 136–142 CrossRef CAS.
- W. Nie and C. C. L. McCrory, Dalton Trans., 2022, 51, 6993–7010 RSC.
- S. M. Stratton, S. Zhang and M. M. Montemore, Surf. Sci. Rep., 2023, 78, 100597 CrossRef CAS.
- J. Pérez-Ramírez and N. López, Nat. Catal., 2019, 2, 971–976 CrossRef.
- Z.-F. Huang, S. Xi, J. Song, S. Dou, X. Li, Y. Du, C. Diao, Z. J. Xu and X. Wang, Nat. Commun., 2021, 12, 3992 CrossRef CAS PubMed.
- W. Zhou, H. Su, W. Cheng, Y. Li, J. Jiang, M. Liu, F. Yu, W. Wang, S. Wei and Q. Liu, Nat. Commun., 2022, 13, 6414 CrossRef CAS PubMed.
- S. Jung, C. Pizzolitto, P. Biasi, P. J. Dauenhauer and T. Birol, Nat. Commun., 2023, 14, 7795 CrossRef CAS PubMed.
- G. Yasin, A. Kumar, S. Ajmal, M. Asim Mushtaq, M. Tabish, A. Saad, M. A. Assiri, M. Tariq Nazir and Q. Zhuo, Coord. Chem. Rev., 2024, 501, 215589 CrossRef CAS.
- J. Greeley, Annu. Rev. Chem. Biomol. Eng., 2016, 7, 605–635 CrossRef PubMed.
- Z.-J. Zhao, S. Liu, S. Zha, D. Cheng, F. Studt, G. Henkelman and J. Gong, Nat. Rev. Mater., 2019, 4, 792–804 CrossRef.
- F. Calle-Vallejo, Appl. Phys. Rev., 2024, 11, 021305 CAS.
- A. Kulkarni, S. Siahrostami, A. Patel and J. K. Nørskov, Chem. Rev., 2018, 118, 2302–2312 CrossRef CAS PubMed.
- I. E. L. Stephens, A. S. Bondarenko, F. J. Perez-Alonso, F. Calle-Vallejo, L. Bech, T. P. Johansson, A. K. Jepsen, R. Frydendal, B. P. Knudsen, J. Rossmeisl and I. Chorkendorff, J. Am. Chem. Soc., 2011, 133, 5485–5491 CrossRef CAS PubMed.
- M. T. M. Koper, Chem. Sci., 2013, 4, 2710–2723 RSC.
- F. Calle-Vallejo, J. I. Martínez and J. Rossmeisl, Phys. Chem. Chem. Phys., 2011, 13, 15639 RSC.
- F. Calle-Vallejo, J. I. Martínez, J. M. García-Lastra, E. Abad and M. T. M. Koper, Surf. Sci., 2013, 607, 47–53 CrossRef CAS.
- E. G. Ciapina, P. P. Lopes, R. Subbaraman, E. A. Ticianelli, V. Stamenkovic, D. Strmcnik and N. M. Markovic, Electrochem. Commun., 2015, 60, 30–33 CrossRef CAS.
- J. D. Baran, H. Grönbeck and A. Hellman, J. Am. Chem. Soc., 2014, 136, 1320–1326 CrossRef CAS PubMed.
- A. Vojvodic and J. K. Nørskov, Nat. Sci. Rev., 2015, 2, 140–143 CrossRef CAS.
- Z.-F. Huang, J. Song, S. Dou, X. Li, J. Wang and X. Wang, Matter, 2019, 1, 1494–1518 CrossRef.
- L. E. B. Lucchetti, J. M. de Almeida and S. Siahrostami, EES Catal., 2024, 2, 1037–1058 RSC.
- A.-I. Hutu, E. Pervolarakis, I. N. Remediakis, H. H. Kristoffersen and J. Rossmeisl, J. Phys. Chem. C, 2024, 128, 10251–10258 CrossRef CAS.
- M. Busch, N. B. Halck, U. I. Kramm, S. Siahrostami, P. Krtil and J. Rossmeisl, Nano Energy, 2016, 29, 126–135 CrossRef CAS.
- J. Liu, H. Xu, J. Zhu and D. Cheng, JACS Au, 2023, 3, 3031–3044 CrossRef CAS PubMed.
- R. Cepitis, N. Kongi, J. Rossmeisl and V. Ivaništšev, ACS Energy Lett., 2023, 8, 1330–1335 CrossRef CAS PubMed.
- R. Cepitis, V. Ivaništšev, J. Rossmeisl and N. Kongi, Catal. Sci. Technol., 2024, 14, 2105–2113 RSC.
- K. S. Exner, Chin. J. Catal., 2022, 43, 2871–2880 CrossRef CAS.
- L. Miao, W. Jia, X. Cao and L. Jiao, Chem. Soc. Rev., 2024, 53, 2771–2807 RSC.
- Z. Huang, M. Li, X. Yang, T. Zhang, X. Wang, W. Song, J. Zhang, H. Wang, Y. Chen, J. Ding and W. Hu, J. Am. Chem. Soc., 2024, 146, 24842–24854 CrossRef CAS PubMed.
- C. F. Dickens, J. H. Montoya, A. R. Kulkarni, M. Bajdich and J. K. Nørskov, Surf. Sci., 2019, 681, 122–129 CrossRef CAS.
- Y. Lian, J. Xu, W. Zhou, Y. Lin and J. Bai, Molecules, 2024, 29, 771 CrossRef CAS PubMed.
- J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, J. Phys. Chem. B, 2004, 108, 17886–17892 CrossRef PubMed.
- H. Wan, A. W. Jensen, M. Escudero-Escribano and J. Rossmeisl, ACS Catal., 2020, 10, 5979–5989 CrossRef CAS.
- H. A. Hansen, V. Viswanathan and J. K. Nørskov, J. Phys. Chem. C, 2014, 118, 6706–6718 CrossRef CAS.
- S. Kattel and G. Wang, J. Chem. Phys., 2014, 141, 124713 CrossRef PubMed.
- Z. Hou, C. Cui, Y. Li, Y. Gao, D. Zhu, Y. Gu, G. Pan, Y. Zhu and T. Zhang, Adv. Mater., 2023, 35, 2209876 CrossRef CAS PubMed.
- F. Calle-Vallejo, Adv. Sci., 2023, 10, 2207644 CrossRef CAS PubMed.
- A. Brito-Ravicini and F. Calle-Vallejo, Exploration, 2022, 2, 20210062 CrossRef CAS PubMed.
- T. Sours, A. Patel, J. Nørskov, S. Siahrostami and A. Kulkarni, J. Phys. Chem. Lett., 2020, 11, 10029–10036 CrossRef CAS PubMed.
- L. Yang, Y. Zhang, Y. Huang, L. Deng, Q. Luo, X. Li and J. Jiang, ChemSusChem, 2023, 16, e202300082 CrossRef CAS PubMed.
- J. Zhang, H. B. Yang, D. Zhou and B. Liu, Chem. Rev., 2022, 122, 17028–17072 CrossRef CAS PubMed.
- H. Liu, J. Li, J. Arbiol, B. Yang and P. Tang, EcoEnergy, 2023, 1, 154–185 CrossRef.
- B. Kirchhoff, A. Ivanov, E. Skúlason, T. Jacob, D. Fantauzzi and H. Jónsson, J. Chem. Theory Comput., 2021, 17, 6405–6415 CrossRef CAS PubMed.
- A. Bagger, I. E. Castelli, M. H. Hansen and J. Rossmeisl, in Handbook of Materials Modeling, ed. W. Andreoni and S. Yip, Springer International Publishing, Cham, 2020, pp. 1473–1503 Search PubMed.
- F. Calle-Vallejo, A. Krabbe and J. M. García-Lastra, Chem. Sci., 2017, 8, 124–130 RSC.
- N. Ma, Y. Zhang, Y. Wang, C. Huang, J. Zhao, B. Liang and J. Fan, Appl. Surf. Sci., 2023, 628, 157225 CrossRef CAS.
- J. R. Lunger, J. Karaguesian, H. Chun, J. Peng, Y. Tseo, C. H. Shan, B. Han, Y. Shao-Horn and R. Gomez-Bombarelli, Atom-by-Atom Design of Metal Oxide Catalysts for the Oxygen Evolution Reaction with Machine Learning, 2023 Search PubMed.
- M. H. Hansen and J. Rossmeisl, J. Phys. Chem. C, 2016, 120, 29135–29143 CrossRef CAS.
- M. Busch, E. Ahlberg and K. Laasonen, Phys. Chem. Chem. Phys., 2021, 23, 11727–11737 RSC.
- M. M. Melander, T. Wu, T. Weckman and K. Honkala, npj Comput. Mater., 2024, 10, 1–11 CrossRef.
- M. J. Craig, G. Coulter, E. Dolan, J. Soriano-López, E. Mates-Torres, W. Schmitt and M. García-Melchor, Nat. Commun., 2019, 10, 4993 CrossRef PubMed.
- H. Li, S. Kelly, D. Guevarra, Z. Wang, Y. Wang, J. A. Haber, M. Anand, G. T. K. K. Gunasooriya, C. S. Abraham, S. Vijay, J. M. Gregoire and J. K. Nørskov, Nat. Catal., 2021, 4, 463–468 CrossRef CAS.
- F. Calle-Vallejo, D. Loffreda, M. T. M. Koper and P. Sautet, Nat. Chem., 2015, 7, 403–410 CrossRef CAS PubMed.
- F. Calle-Vallejo, J. I. Martínez, J. M. García-Lastra, J. Rossmeisl and M. T. M. Koper, Phys. Rev. Lett., 2012, 108, 116103 CrossRef CAS PubMed.
- V. Viswanathan, H. A. Hansen, J. Rossmeisl and J. K. Nørskov, ACS Catal., 2012, 2, 1654–1660 CrossRef CAS.
- S. Divanis, T. Kutlusoy, I. M. Ingmer Boye, I. C. Man and J. Rossmeisl, Chem. Sci., 2020, 11, 2943–2950 RSC.
- E. Romeo, F. Illas and F. Calle-Vallejo, Chem. Sci., 2023, 14, 3622–3629 RSC.
- M. T. Koper, J. Electroanal. Chem., 2011, 660, 254–260 CrossRef CAS.
- E. Sargeant, F. Illas, P. Rodríguez and F. Calle-Vallejo, Electrochim. Acta, 2022, 426, 140799 CrossRef CAS.
- R. Christensen, H. A. Hansen, C. F. Dickens, J. K. Nørskov and T. Vegge, J. Phys. Chem. C, 2016, 120, 24910–24916 CrossRef CAS.
- V. Viswanathan and H. A. Hansen, Top. Catal., 2014, 57, 215–221 CrossRef CAS.
- in CRC Handbook of Chemistry and Physics, ed. D. R. Lide, W. M. Haynes and T. J. Bruno, CRC Press, 97th edn, 2017 Search PubMed.
- R. D. Bach and H. B. Schlegel, J. Phys. Chem. A, 2020, 124, 4742–4751 CrossRef CAS PubMed.
- D. J. Carmona, P. Jaque and E. Vöhringer-Martinez, Theor. Chem. Acc., 2020, 139, 102 Search PubMed.
- S.-J. Shin, D. H. Kim, G. Bae, S. Ringe, H. Choi, H.-K. Lim, C. H. Choi and H. Kim, Nat. Commun., 2022, 13, 174 Search PubMed.
- S. Ringe, N. G. Hörmann, H. Oberhofer and K. Reuter, Chem. Rev., 2022, 122, 10777–10820 CrossRef CAS PubMed.
- Y. Qin, P. Li, Z. Li, T. Wu and Y. Su, J. Phys. Chem. C, 2023, 127, 4934–4941 CrossRef CAS.
- S. Back and Y. Jung, ChemCatChem, 2017, 9, 3173–3179 CrossRef CAS.
- Y. Singh, S. Back and Y. Jung, Phys. Chem. Chem. Phys., 2018, 20, 21095–21104 RSC.
- C. F. Dickens, C. Kirk and J. K. Nørskov, J. Phys. Chem. C, 2019, 123, 18960–18977 CrossRef CAS.
- X. Chen, Y. Li and X. Zhao, Surf. Interfaces, 2023, 38, 102821 CrossRef CAS.
- K. A. Moltved and K. P. Kepp, ChemPhysChem, 2020, 21, 2173–2186 CrossRef CAS PubMed.
- M. Busch, A. Fabrizio, S. Luber, J. Hutter and C. Corminboeuf, J. Phys. Chem. C, 2018, 122, 12404–12412 CrossRef CAS.
- P. Lv, W. Lv, D. Wu, G. Tang, X. Yan, Z. Lu and D. Ma, Phys. Rev. Appl., 2023, 19, 054094 CrossRef CAS.
- H. Wan, T. M. Østergaard, L. Arnarson and J. Rossmeisl, ACS Sustainable Chem. Eng., 2019, 7, 611–617 CrossRef CAS.
- M. Busch, Curr. Opin. Electrochem., 2018, 9, 278–284 CrossRef CAS.
- K. S. Exner, Adv. Sci., 2023, 10, 2305505 CrossRef CAS PubMed.
- K. S. Exner, JPhys Energy, 2023, 5, 014008 CrossRef CAS.
- K. S. Exner, Curr. Opin. Electrochem., 2023, 39, 101284 CrossRef.
- I. Barlocco, G. Di Liberto and G. Pacchioni, Catal. Today, 2024, 427, 114409 CrossRef CAS.
- K. S. Exner, Int. J. Hydrogen Energy, 2020, 45, 27221–27229 CrossRef CAS.
- P. Sabatier, Ber. Dtsch. Chem. Ges., 1911, 44, 1984–2001 CrossRef CAS.
- T. J. Shaldehi and S. Rowshanzamir, Sci. Rep., 2024, 14, 14201 CrossRef CAS PubMed.
- J. Woo, J. S. Lim, T. Lim, D. S. Baek, J. H. Kim, J. H. Lee, H. Y. Jeong, C. H. Choi and S. H. Joo, EES Catal., 2023, 1, 62–73 RSC.
- H. Tian, A. Song, P. Zhang, K. Sun, J. Wang, B. Sun, Q. Fan, G. Shao, C. Chen, H. Liu, Y. Li and G. Wang, Adv. Mater., 2023, 35, 2210714 CrossRef CAS PubMed.
- R. Gao, J. Wang, Z.-F. Huang, R. Zhang, W. Wang, L. Pan, J. Zhang, W. Zhu, X. Zhang, C. Shi, J. Lim and J.-J. Zou, Nat Energy, 2021, 6, 614–623 CrossRef CAS.
- F. Liu, R. Gao, C. Shi, L. Pan, Z.-F. Huang, X. Zhang and J.-J. Zou, J. Am. Chem. Soc., 2023, 145, 25252–25263 CrossRef CAS PubMed.
- Z. Zhang, Z. Xing, X. Luo, C. Cheng and X. Liu, Nat. Commun., 2025, 16, 921 CrossRef CAS PubMed.
- W. Yang, X. Liu, X. Yue, J. Jia and S. Guo, J. Am. Chem. Soc., 2015, 137, 1436–1439 CrossRef CAS PubMed.
- P. Yin, T. Yao, Y. Wu, L. Zheng, Y. Lin, W. Liu, H. Ju, J. Zhu, X. Hong, Z. Deng, G. Zhou, S. Wei and Y. Li, Angew. Chem., Int. Ed., 2016, 55, 10800–10805 CrossRef CAS PubMed.
- Y. Chen, S. Ji, Y. Wang, J. Dong, W. Chen, Z. Li, R. Shen, L. Zheng, Z. Zhuang, D. Wang and Y. Li, Angew. Chem., Int. Ed., 2017, 56, 6937–6941 CrossRef CAS PubMed.
- R. Jiang, L. Li, T. Sheng, G. Hu, Y. Chen and L. Wang, J. Am. Chem. Soc., 2018, 140, 11594–11598 CrossRef CAS PubMed.
- C. Zhu, Q. Shi, B. Z. Xu, S. Fu, G. Wan, C. Yang, S. Yao, J. Song, H. Zhou, D. Du, S. P. Beckman, D. Su and Y. Lin, Adv. Energy Mater., 2018, 8, 1801956 CrossRef.
- J. Han, X. Meng, L. Lu, J. Bian, Z. Li and C. Sun, Adv. Funct. Mater., 2019, 29, 1808872 CrossRef CAS.
- Z. Yang, Y. Wang, M. Zhu, Z. Li, W. Chen, W. Wei, T. Yuan, Y. Qu, Q. Xu, C. Zhao, X. Wang, P. Li, Y. Li, Y. Wu and Y. Li, ACS Catal., 2019, 9, 2158–2163 CrossRef CAS.
- K. Chen, K. Liu, P. An, H. Li, Y. Lin, J. Hu, C. Jia, J. Fu, H. Li, H. Liu, Z. Lin, W. Li, J. Li, Y.-R. Lu, T.-S. Chan, N. Zhang and M. Liu, Nat. Commun., 2020, 11, 4173 CrossRef CAS PubMed.
- H. Shang, X. Zhou, J. Dong, A. Li, X. Zhao, Q. Liu, Y. Lin, J. Pei, Z. Li, Z. Jiang, D. Zhou, L. Zheng, Y. Wang, J. Zhou, Z. Yang, R. Cao, R. Sarangi, T. Sun, X. Yang, X. Zheng, W. Yan, Z. Zhuang, J. Li, W. Chen, D. Wang, J. Zhang and Y. Li, Nat. Commun., 2020, 11, 3049 CrossRef CAS PubMed.
- Y. Chen, R. Gao, S. Ji, H. Li, K. Tang, P. Jiang, H. Hu, Z. Zhang, H. Hao, Q. Qu, X. Liang, W. Chen, J. Dong, D. Wang and Y. Li, Angew. Chem., Int. Ed., 2021, 60, 3212–3221 CrossRef CAS PubMed.
- X. Xie, L. Peng, H. Yang, G. I. N. Waterhouse, L. Shang and T. Zhang, Adv. Mater., 2021, 33, 2101038 CrossRef CAS PubMed.
- J. Han, H. Bao, J.-Q. Wang, L. Zheng, S. Sun, Z. L. Wang and C. Sun, Appl. Catal., B, 2021, 280, 119411 CrossRef CAS.
- A. Han, X. Wang, K. Tang, Z. Zhang, C. Ye, K. Kong, H. Hu, L. Zheng, P. Jiang, C. Zhao, Q. Zhang, D. Wang and Y. Li, Angew. Chem., Int. Ed., 2021, 60, 19262–19271 CrossRef CAS PubMed.
- H. Karimi-Maleh, C. Karaman, O. Karaman, F. Karimi, Y. Vasseghian, L. Fu, M. Baghayeri, J. Rouhi, P. Senthil Kumar, P.-L. Show, S. Rajendran, A. L. Sanati and A. Mirabi, J. Nanostruct. Chem., 2022, 12, 429–439 CrossRef CAS.
- T. Cui, Y.-P. Wang, T. Ye, J. Wu, Z. Chen, J. Li, Y. Lei, D. Wang and Y. Li, Angew. Chem., Int. Ed., 2022, 61, e202115219 CrossRef CAS PubMed.
- R. Li and D. Wang, Nano Res., 2022, 15, 6888–6923 CrossRef CAS.
- M.-T. Chen, Z.-X. Huang, X. Ye, L. Zhang, J.-J. Feng and A.-J. Wang, J. Colloid Interface Sci., 2023, 637, 216–224 CrossRef CAS PubMed.
- A. Bala Musa, M. Tabish, A. Kumar, M. Selvaraj, M. Abubaker Khan, B. M. Al-Shehri, M. Arif, M. Asim Mushtaq, S. Ibraheem, Y. Slimani, S. Ajmal, T. Anh Nguyen and G. Yasin, Chem. Eng. J., 2023, 451, 138684 CrossRef CAS.
- H. Chang, Y.-F. Guo, X. Liu, P.-F. Wang, Y. Xie and T.-F. Yi, Appl. Catal., B, 2023, 327, 122469 CrossRef CAS.
- J. Huo, X. Cao, Y. Tian, L. Li, J. Qu, Y. Xie, X. Nie, Y. Zhao, J. Zhang and H. Liu, Nanoscale, 2023, 15, 5448–5457 RSC.
- T. Tang, Y. Wang, J. Han, Q. Zhang, X. Bai, X. Niu, Z. Wang and J. Guan, Chin. J. Catal., 2023, 46, 48–55 CrossRef CAS.
- K. Tiido, N. Alexeyeva, M. Couillard, C. Bock, B. R. MacDougall and K. Tammeveski, Electrochim. Acta, 2013, 107, 509–517 CrossRef CAS.
- N. Alexeyeva, A. Sarapuu, K. Tammeveski, F. J. Vidal-Iglesias, J. Solla-Gullón and J. M. Feliu, Electrochim. Acta, 2011, 56, 6702–6708 CrossRef CAS.
- N. Karmodak and Jens K. Nørskov, Angewandte Chemie, 2023, 135, e202311113 CrossRef.
- J. Greeley, J. Rossmeisl, A. Hellmann and J. K. Norskov, Z. Phys. Chem., 2007, 221, 1209–1220 CrossRef CAS.
- H. A. Hansen, J. Rossmeisl and J. K. Nørskov, Phys. Chem. Chem. Phys., 2008, 10, 3722 RSC.
- J. Rossmeisl, J. K. Nørskov, C. D. Taylor, M. J. Janik and M. Neurock, J. Phys. Chem. B, 2006, 110, 21833–21839 CrossRef CAS PubMed.
- J. K. Pedersen, T. A. A. Batchelor, D. Yan, L. E. J. Skjegstad and J. Rossmeisl, Curr. Opin. Electrochem., 2021, 26, 100651 CrossRef CAS.
- O. Piqué, F. Illas and F. Calle-Vallejo, Phys. Chem. Chem. Phys., 2020, 22, 6797–6803 RSC.
- Y. Meng, C. Yin, K. Li, H. Tang, Y. Wang and Z. Wu, ACS Sustainable Chem. Eng., 2019, 7, 17273–17281 CrossRef CAS.
- J. Xu, A. Elangovan, J. Li and B. Liu, J. Phys. Chem. C, 2021, 125, 2334–2344 CrossRef CAS.
- J. Tang, Z. Zeng, H. Liang, Z. Wang, W. Nong, Z. Yang, C. Qi, Z. Qiao, Y. Li and C. Wang, ACS Omega, 2022, 7, 19794–19803 CrossRef CAS PubMed.
- S. Wannakao, T. Maihom, K. Kongpatpanich, J. Limtrakul and V. Promarak, Phys. Chem. Chem. Phys., 2017, 19, 29540–29548 RSC.
- N. Govindarajan, M. T. M. Koper, E. J. Meijer and F. Calle-Vallejo, ACS Catal., 2019, 9, 4218–4225 CrossRef CAS.
- X. Zhang, Z. Xia, H. Li, S. Yu, S. Wang and G. Sun, New J. Chem., 2020, 44, 6818–6824 RSC.
- R. M. Kluge, R. W. Haid, A. Riss, Y. Bao, K. Seufert, T. O. Schmidt, S. A. Watzele, J. V. Barth, F. Allegretti, W. Auwärter, F. Calle-Vallejo and A. S. Bandarenka, Energy Environ. Sci., 2022, 15, 5181–5191 RSC.
- J. Su, C. B. Musgrave, Y. Song, L. Huang, Y. Liu, G. Li, Y. Xin, P. Xiong, M. M.-J. Li, H. Wu, M. Zhu, H. M. Chen, J. Zhang, H. Shen, B. Z. Tang, M. Robert, W. A. Goddard and R. Ye, Nat. Catal., 2023, 6, 818–828 CrossRef CAS.
- Y. Yuan, Q. Zhang, L. Yang, L. Wang, W. Shi, P. Liu, R. Gao, L. Zheng, Z. Chen and Z. Bai, Adv. Funct. Mater., 2022, 32, 2206081 CrossRef CAS.
- A. Fortunelli, W. A. G. Iii, L. Sementa, G. Barcaro, F. R. Negreiros and A. Jaramillo-Botero, Chem. Sci., 2015, 6, 3915–3925 RSC.
- Z.-P. Wu, D. T. Caracciolo, Y. Maswadeh, J. Wen, Z. Kong, S. Shan, J. A. Vargas, S. Yan, E. Hopkins, K. Park, A. Sharma, Y. Ren, V. Petkov, L. Wang and C.-J. Zhong, Nat. Commun., 2021, 12, 859 CrossRef CAS PubMed.
- A. S. Bandarenka, H. A. Hansen, J. Rossmeisl and I. E. L. Stephens, Phys. Chem. Chem. Phys., 2014, 16, 13625 RSC.
- S. R. Kelly, C. Kirk, K. Chan and J. K. Nørskov, J. Phys. Chem. C, 2020, 124, 14581–14591 CrossRef CAS.
- D. Zhou, J. Wei, Z.-D. He, M.-L. Xu, Y.-X. Chen and J. Huang, J. Phys. Chem. C, 2020, 124, 13672–13678 CrossRef CAS.
- M. Li, R. Lu, Y. Mao, Z. Hu and Z. Wang, J. Phys. Chem. C, 2024, 128, 1964–1970 CrossRef CAS.
- V. Tripković, E. Skúlason, S. Siahrostami, J. K. Nørskov and J. Rossmeisl, Electrochim. Acta, 2010, 55, 7975–7981 CrossRef.
- V. Stamenkovic, B. S. Mun, K. J. J. Mayrhofer, P. N. Ross, N. M. Markovic, J. Rossmeisl, J. Greeley and J. K. Nørskov, Angew. Chem., Int. Ed., 2006, 45, 2897–2901 CrossRef CAS PubMed.
- V. R. Stamenkovic, B. Fowler, B. S. Mun, G. Wang, P. N. Ross, C. A. Lucas and N. M. Marković, Science, 2007, 315, 493–497 CrossRef CAS PubMed.
- M. Escudero-Escribano, P. Malacrida, M. H. Hansen, U. G. Vej-Hansen, A. Velázquez-Palenzuela, V. Tripkovic, J. Schiøtz, J. Rossmeisl, I. E. L. Stephens and I. Chorkendorff, Science, 2016, 352, 73–76 CrossRef CAS PubMed.
- V. R. Stamenkovic, B. S. Mun, M. Arenz, K. J. J. Mayrhofer, C. A. Lucas, G. Wang, P. N. Ross and N. M. Markovic, Nat. Mater., 2007, 6, 241–247 CrossRef CAS PubMed.
- J. Greeley, I. E. L. Stephens, A. S. Bondarenko, T. P. Johansson, H. A. Hansen, T. F. Jaramillo, J. Rossmeisl, I. Chorkendorff and J. K. Nørskov, Nat. Chem., 2009, 1, 552–556 CrossRef CAS PubMed.
- S.-h Kim, Y. Kang and H. C. Ham, Energies, 2021, 14, 7814 CrossRef CAS.
- J. Zhang, M. B. Vukmirovic, Y. Xu, M. Mavrikakis and R. R. Adzic, Angewandte Chemie, 2005, 117, 2170–2173 CrossRef.
- A. U. Nilekar and M. Mavrikakis, Surf. Sci., 2008, 602, L89–L94 CrossRef CAS.
- W.-P. Zhou, X. Yang, M. B. Vukmirovic, B. E. Koel, J. Jiao, G. Peng, M. Mavrikakis and R. R. Adzic, J. Am. Chem. Soc., 2009, 131, 12755–12762 CrossRef CAS PubMed.
- A. Hitotsuyanagi, M. Nakamura and N. Hoshi, Electrochim. Acta, 2012, 82, 512–516 CrossRef CAS.
- A. Kuzume, E. Herrero and J. M. Feliu, J. Electroanal. Chem., 2007, 599, 333–343 CrossRef CAS.
- J. Huang, L. Sementa, Z. Liu, G. Barcaro, M. Feng, E. Liu, L. Jiao, M. Xu, D. Leshchev, S.-J. Lee, M. Li, C. Wan, E. Zhu, Y. Liu, B. Peng, X. Duan, W. A. Goddard, A. Fortunelli, Q. Jia and Y. Huang, Nat. Catal., 2022, 5, 513–523 CrossRef CAS.
- S. Kaneko, R. Myochi, S. Takahashi, N. Todoroki, T. Wadayama and T. Tanabe, J. Phys. Chem. Lett., 2017, 8, 5360–5365 CrossRef CAS PubMed.
- S. J. Yoo, K.-S. Lee, S. J. Hwang, Y.-H. Cho, S.-K. Kim, J. W. Yun, Y.-E. Sung and T.-H. Lim, Int. J. Hydrogen Energy, 2012, 37, 9758–9765 CrossRef CAS.
- R. Brown, M. Vorokhta, I. Khalakhan, M. Dopita, T. Vonderach, T. Skála, N. Lindahl, I. Matolínová, H. Grönbeck, K. M. Neyman, V. Matolín and B. Wickman, ACS Appl. Mater. Interfaces, 2020, 12, 4454–4462 CrossRef CAS PubMed.
- K. D. Jensen, J. Tymoczko, J. Rossmeisl, A. S. Bandarenka, I. Chorkendorff, M. Escudero-Escribano and I. E. L. Stephens, Angew. Chem., Int. Ed., 2018, 57, 2800–2805 CrossRef CAS PubMed.
- R. M. Kluge, E. Psaltis, R. W. Haid, S. Hou, T. O. Schmidt, O. Schneider, B. Garlyyev, F. Calle-Vallejo and A. S. Bandarenka, ACS Appl. Mater. Interfaces, 2022, 14, 19604–19613 CrossRef CAS PubMed.
- M. Escudero-Escribano, A. Verdaguer-Casadevall, P. Malacrida, U. Grønbjerg, B. P. Knudsen, A. K. Jepsen, J. Rossmeisl, I. E. L. Stephens and I. Chorkendorff, J. Am. Chem. Soc., 2012, 134, 16476–16479 CrossRef CAS PubMed.
- M. Torihata, M. Nakamura, N. Todoroki, T. Wadayama and N. Hoshi, Electrochem. Commun., 2021, 125, 107007 CrossRef CAS.
- L. Banko, O. A. Krysiak, J. K. Pedersen, B. Xiao, A. Savan, T. Löffler, S. Baha, J. Rossmeisl, W. Schuhmann and A. Ludwig, Adv. Energy Mater., 2022, 12, 2103312 CrossRef CAS.
- C. M. Clausen, O. A. Krysiak, L. Banko, J. K. Pedersen, W. Schuhmann, A. Ludwig and J. Rossmeisl, Angew. Chem., Int. Ed., 2023, 62, e202307187 CrossRef CAS PubMed.
- J. K. Pedersen, C. M. Clausen, O. A. Krysiak, B. Xiao, T. A. A. Batchelor, T. Löffler, V. A. Mints, L. Banko, M. Arenz, A. Savan, W. Schuhmann, A. Ludwig and J. Rossmeisl, Angew. Chem., Int. Ed., 2021, 60, 24144–24152 CrossRef CAS PubMed.
- N. Azcona-Aliende, P. Rodriguez and F. Calle-Vallejo, ChemSusChem, 2025, n/a, 2501198 Search PubMed.
- K. S. Exner, Chem. Catal., 2021, 1, 258–271 CAS.
- S. Razzaq and K. S. Exner, Electrochim. Acta, 2022, 412, 140125 CrossRef CAS.
- P. Ma, C. Feng, Y. Kong, D. Wang, M. Zuo, S. Wang, R. Wang, L. Kuang, X. Ding, S. Zhou, Z. Zhang, J. Zeng and J. Bao, Chem. Catal., 2022, 2, 2764–2777 CAS.
- P. Ma, H. Cao, Q. Hao, R. Wang, W. Liu, M. Zuo, C. Jia, Z. Zhang and J. Bao, Angew. Chem., Int. Ed., 2024, 63, e202404418 CrossRef CAS PubMed.
- Z. Zhang, H. Zhao, S. Xi, X. Zhao, X. Chi, H. Bin Yang, Z. Chen, X. Yu, Y.-G. Wang, B. Liu and P. Chen, Nat. Commun., 2025, 16, 1301 CrossRef CAS PubMed.
- N. Bendtsen Halck, V. Petrykin, P. Krtil and J. Rossmeisl, Phys. Chem. Chem. Phys., 2014, 16, 13682–13688 RSC.
- H. Hajiyani and R. Pentcheva, ACS Catal., 2018, 8, 11773–11782 CrossRef CAS.
- J. Zhang, J. Liu, L. Xi, Y. Yu, N. Chen, S. Sun, W. Wang, K. M. Lange and B. Zhang, J. Am. Chem. Soc., 2018, 140, 3876–3879 CrossRef CAS PubMed.
- Z.-W. Gao, J.-Y. Liu, X.-M. Chen, X.-L. Zheng, J. Mao, H. Liu, T. Ma, L. Li, W.-C. Wang and X.-W. Du, Adv. Mater., 2019, 31, 1804769 CrossRef PubMed.
- K. L. Svane, Curr. Opin. Electrochem., 2025, 51, 101670 CrossRef CAS.
- L. Li, K. Yuan and Y. Chen, Acc. Mater. Res., 2022, 3, 584–596 CrossRef CAS.
- G. Yasin, S. Ibrahim, S. Ajmal, S. Ibraheem, S. Ali, A. K. Nadda, G. Zhang, J. Kaur, T. Maiyalagan, R. K. Gupta and A. Kumar, Coord. Chem. Rev., 2022, 469, 214669 CrossRef CAS.
- J. Chen and Y. Ji, Chin. J. Catal., 2022, 43, 2889–2897 CrossRef CAS.
- J. Zhang, Z. Liang, Z. Li, S. Qu, Y. Cao, H. Zheng and R. Cao, Sustainable Energy Fuels, 2025, 9, 3152–3181 RSC.
- L. Zong, K. Fan, P. Li, F. Lu, B. Li and L. Wang, Adv. Energy Mater., 2023, 13, 2203611 CrossRef CAS.
- H. Liu, P. Li, K. Fan, F. Lu, Q. Sun, Q. Zhang, B. Li, Y. Shu, L. Zong and L. Wang, Angewandte Chemie, 2025, 137, e202501307 CrossRef.
- D.-M. Du, A.-P. Fu and Z.-Y. Zhou, J. Mol. Struct.: THEOCHEM, 2005, 717, 127–132 CrossRef CAS.
- D. J. Arismendi-Arrieta, A. Sen, A. Eriksson, P. Broqvist, J. Kullgren and K. Hermansson, J. Chem. Phys., 2023, 159, 194701 CrossRef CAS PubMed.
- J. Wang, Z. Huang, W. Liu, C. Chang, H. Tang, Z. Li, W. Chen, C. Jia, T. Yao, S. Wei, Y. Wu and Y. Li, J. Am. Chem. Soc., 2017, 139, 17281–17284 CrossRef CAS PubMed.
- G. Yang, J. Zhu, P. Yuan, Y. Hu, G. Qu, B.-A. Lu, X. Xue, H. Yin, W. Cheng, J. Cheng, W. Xu, J. Li, J. Hu, S. Mu and J.-N. Zhang, Nat. Commun., 2021, 12, 1734 CrossRef CAS PubMed.
- G. Dey, R. Jana, S. Saifi, R. Kumar, D. Bhattacharyya, A. Datta, A. S. K. Sinha and A. Aijaz, ACS Nano, 2023, 17, 19155–19167 CrossRef CAS PubMed.
- Y. Xie, X. Chen, K. Sun, J. Zhang, W.-H. Lai, H. Liu and G. Wang, Angew. Chem., Int. Ed., 2023, 62, e202301833 CrossRef CAS PubMed.
- H. Xia, R. Pang, X. Dong, Q. Liu, J. Chen, E. Wang and J. Li, J. Am. Chem. Soc., 2023, 145, 25695–25704 CrossRef CAS PubMed.
- A. Kumar, K. Sun, X. Duan, S. Tian and X. Sun, Chem. Mater., 2022, 34, 5598–5606 CrossRef CAS.
- L. Li, X. Tang, S. Huang, C. Lu, D. Lützenkirchen-Hecht, K. Yuan, X. Zhuang and Y. Chen, Angew. Chem., Int. Ed., 2023, 62, e202301642 CrossRef CAS PubMed.
- F. Wang, W. Xie, L. Yang, D. Xie and S. Lin, J. Catal., 2021, 396, 215–223 CrossRef CAS.
- J. Wang, W. Liu, G. Luo, Z. Li, C. Zhao, H. Zhang, M. Zhu, Q. Xu, X. Wang, C. Zhao, Y. Qu, Z. Yang, T. Yao, Y. Li, Y. Lin, Y. Wu and Y. Li, Energy Environ. Sci., 2018, 11, 3375–3379 RSC.
- X. Wang, Y. Zeng, P. Wang, X. Wang, K. Li, L. Lu, J. Zhu, C. Liu, M. Xiao and W. Xing, Angew. Chem., Int. Ed., 2025, n/a, e202509360 Search PubMed.
- A. G. Saputro, A. K. Fajrial, A. L. Maulana, F. Fathurrahman, M. K. Agusta, F. T. Akbar and H. K. Dipojono, J. Phys. Chem. C, 2020, 124, 11383–11391 CrossRef CAS.
- K. Yuan, S. Sfaelou, M. Qiu, D. Lützenkirchen-Hecht, X. Zhuang, Y. Chen, C. Yuan, X. Feng and U. Scherf, ACS Energy Lett., 2018, 3, 252–260 CrossRef CAS.
- Y.-M. Zhao, L.-M. Liao, G.-Q. Yu, P.-J. Wei and J.-G. Liu, ChemElectroChem, 2019, 6, 1754–1760 CrossRef CAS.
- Z. Jin, P. Li, Y. Meng, Z. Fang, D. Xiao and G. Yu, Nat. Catal., 2021, 4, 615–622 CrossRef CAS.
- X. Li, X. Wu, Y. Zhao, Y. Lin, J. Zhao, C. Wu, H. Liu, L. Shan, L. Yang, L. Song and J. Jiang, Adv. Mater., 2023, 35, 2302467 CrossRef CAS PubMed.
- T. Kropp and M. Mavrikakis, J. Catal., 2020, 390, 67–71 CrossRef CAS.
- J. Yang, Z. Wang, C.-X. Huang, Y. Zhang, Q. Zhang, C. Chen, J. Du, X. Zhou, Y. Zhang, H. Zhou, L. Wang, X. Zheng, L. Gu, L.-M. Yang and Y. Wu, Angew. Chem., Int. Ed., 2021, 60, 22722–22728 CrossRef CAS PubMed.
- G. Han, X. Zhang, W. Liu, Q. Zhang, Z. Wang, J. Cheng, T. Yao, L. Gu, C. Du, Y. Gao and G. Yin, Nat. Commun., 2021, 12, 6335 CrossRef CAS PubMed.
- Y. Wang, Z. Bao, M. Shi, Z. Liang, R. Cao and H. Zheng, Chem. – Eur. J., 2021, 28, e202102915 CrossRef PubMed.
- J. Li, W. Xia, Y. Guo, R. Qi, X. Xu, D. Jiang, T. Wang, Y. Sugahara, J. He and Y. Yamauchi, Chem. Eng. J., 2023, 477, 146841 CrossRef CAS.
- H. Hu, P. Zhang, B.-B. Xiao and J.-L. Mi, ACS Appl. Mater. Interfaces, 2023, 15, 23170–23184 CrossRef CAS PubMed.
- Z. Zhang, C. Chen, R. Xu, X.-B. Chen, H. Lu, Z. Shi, Y. Han and S. Feng, Adv. Mater., 2024, 36, 2403549 CrossRef CAS PubMed.
- K. L. Svane, H. A. Hansen and T. Vegge, J. Catal., 2021, 393, 230–237 CrossRef CAS.
- A. Pedersen, J. Barrio, A. Li, R. Jervis, D. J. L. Brett, M. M. Titirici and I. E. L. Stephens, Adv. Energy Mater., 2022, 12, 2102715 CrossRef CAS.
- K. Mittra, S. Samanta, A. Singha, K. Sengupta and S. Chatterjee, in Oxygen Reduction Reaction, ed. K. Sengupta, S. Chatterjee and K. Dutta, Elsevier, 2022, pp. 45–77 Search PubMed.
- M. R. Crawley, D. Zhang, A. N. Oldacre, C. M. Beavers, A. E. Friedman and T. R. Cook, J. Am. Chem. Soc., 2021, 143, 1098–1106 CrossRef CAS PubMed.
- X. Li, S. Duan, E. Sharman, Y. Zhao, L. Yang, Z. Zhuo, P. Cui, J. Jiang and Y. Luo, J. Mater. Chem. A, 2020, 8, 10193–10198 RSC.
- H. Arima, M. Wada, T. Nakazono and T. Wada, Inorg. Chem., 2021, 60, 9402–9415 CrossRef CAS PubMed.
- Q. Cai, L. K. Tran, T. Qiu, J. W. Eddy, T.-N. Pham, G. P. A. Yap and J. Rosenthal, Inorg. Chem., 2022, 61, 5442–5451 CrossRef CAS PubMed.
- Y.-H. Wang, P. E. Schneider, Z. K. Goldsmith, B. Mondal, S. Hammes-Schiffer and S. S. Stahl, ACS Cent. Sci., 2019, 5, 1024–1034 CrossRef CAS PubMed.
- Y.-H. Wang, B. Mondal and S. S. Stahl, ACS Catal., 2020, 10, 12031–12039 CrossRef CAS.
- D. Zhang, M. R. Crawley, A. N. Oldacre, L. J. Kyle, S. N. MacMillan and T. R. Cook, Inorg. Chem., 2023, 62, 1766–1775 CrossRef CAS PubMed.
- J. P. Collman, R. Boulatov, C. J. Sunderland and L. Fu, Chem. Rev., 2004, 104, 561–588 CrossRef CAS PubMed.
- Y. Hao, S.-F. Hung, W.-J. Zeng, Y. Wang, C. Zhang, C.-H. Kuo, L. Wang, S. Zhao, Y. Zhang, H.-Y. Chen and S. Peng, J. Am. Chem. Soc., 2023, 145, 23659–23669 CrossRef CAS PubMed.
- B. Zandkarimi and A. N. Alexandrova, J. Phys. Chem. Lett., 2019, 10, 460–467 CrossRef PubMed.
- X. Wang, K. Li, Y. Zeng, W. Liu, L. Lu, M. Shao, M. Xiao, C. Liu, J. Zhu and W. Xing, Angewandte Chemie, 2025, n/a, e202513102 Search PubMed.
- C. H. Kjaergaard, J. Rossmeisl and J. K. Nørskov, Inorg. Chem., 2010, 49, 3567–3572 CrossRef CAS PubMed.
- C. Chen, Y. Li, A. Huang, X. Liu, J. Li, Y. Zhang, Z. Chen, Z. Zhuang, Y. Wu, W.-C. Cheong, X. Tan, K. Sun, Z. Xu, D. Liu, Z. Wang, K. Zhou and C. Chen, J. Am. Chem. Soc., 2023, 145, 21273–21283 CrossRef CAS PubMed.
- A. Shimada, F. Hara, K. Shinzawa-Itoh, N. Kanehisa, E. Yamashita, K. Muramoto, T. Tsukihara and S. Yoshikawa, J. Biol. Chem., 2021, 297, 100967 CrossRef CAS PubMed.
- L. Feng, K.-Y. Wang, E. Joseph and H.-C. Zhou, Trends Chem., 2020, 2, 555–568 CrossRef CAS.
- Y. Zhou, R. Lu, X. Tao, Z. Qiu, G. Chen, J. Yang, Y. Zhao, X. Feng and K. Müllen, J. Am. Chem. Soc., 2023, 145, 3647–3655 CrossRef CAS PubMed.
- Z. W. Seh, J. Kibsgaard, C. F. Dickens, I. Chorkendorff, J. K. Nørskov and T. F. Jaramillo, Science, 2017, 355, eaad4998 CrossRef PubMed.
- L. Zhang, Y. Jia, G. Gao, X. Yan, N. Chen, J. Chen, M. T. Soo, B. Wood, D. Yang, A. Du and X. Yao, Chem, 2018, 4, 285–297 CAS.
- M. T. Darby, M. Stamatakis, A. Michaelides, E. Charles. and H. Sykes, J. Phys. Chem. Lett., 2018, 9, 5636–5646 CrossRef CAS PubMed.
- R. Lin, X. Cai, H. Zeng and Z. Yu, Adv. Mater., 2018, 30, 1705332 CrossRef PubMed.
- Q. Ma, H. Jin, J. Zhu, Z. Li, H. Xu, B. Liu, Z. Zhang, J. Ma and S. Mu, Adv. Sci., 2021, 8, 2102209 CrossRef CAS PubMed.
- F.-Y. Chen, Z.-Y. Wu, Z. Adler and H. Wang, Joule, 2021, 5, 1704–1731 CrossRef CAS.
- H. Li, Y. Lin, J. Duan, Q. Wen, Y. Liu and T. Zhai, Chem. Soc. Rev., 2024, 53, 10709–10740 RSC.
- K. S. Exner, Acc. Chem. Res., 2024, 57, 1336–1345 CrossRef CAS PubMed.
- M. Sokolov and K. S. Exner, Chem. Catal., 2024, 4, 101039 CAS.
- D. E. A. Brewer and D. E. A. Brewer, PODC, 2000, pp. 343–477 Search PubMed.
- S. Chandrasekaran, R. Hu, L. Yao, L. Sui, Y. Liu, A. Abdelkader, Y. Li, X. Ren and L. Deng, Nano-Micro Lett., 2023, 15, 48 CrossRef CAS PubMed.
- J. Sheng, S. Zhu, G. Jia, X. Liu and Y. Li, Nano Res., 2021, 14, 4541–4547 CrossRef CAS.
- S. Hosseini, S. Masoudi Soltani and Y.-Y. Li, Chem. Eng. J., 2021, 408, 127241 CrossRef CAS.
- M. J. Kolb and F. Calle-Vallejo, J. Mater. Chem. A, 2022, 10, 5937–5941 RSC.
- R. Cepitis, A. Kosimov, V. Ivaništšev and N. Kongi, Multi-Functional Electrocatalysts: Fundamentals and Applications, Royal Society of Chemistry, 2024, vol. 46, pp. 357–354 Search PubMed.
| This journal is © The Royal Society of Chemistry 2025 |