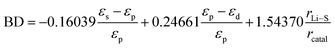Reactivity descriptors for sulfur redox kinetics in lithium–sulfur batteries: from mechanistic insights to machine learning driven catalyst design

Abstract

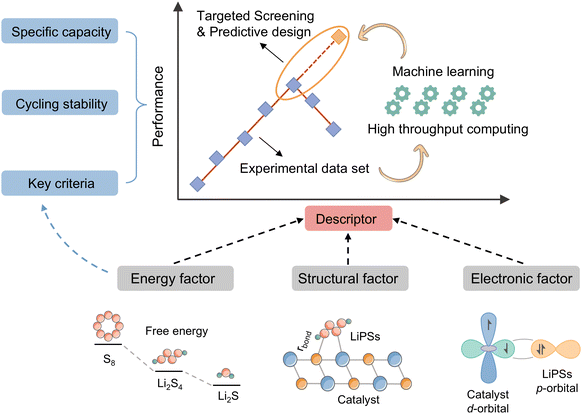
The judicious selection of catalytic materials has emerged as a critical strategy for addressing the notorious lithium polysulfide (LiPS) shuttle effect and sluggish sulfur reduction reaction (SRR) kinetics in lithium sulfur batteries (LSBs). While traditional catalyst development has relied heavily on empirical trial-and-error approaches, recent advances in reactivity descriptor theory offer the potential to understand the mechanisms inherent in the SRR and to revolutionize the catalyst development paradigm, but a comprehensive understanding of the role and origins of descriptors in the SRR remains lacking. This review systematically examines validated descriptor-based research paradigms and their significant advances in LSBs. Firstly, we elucidate critical LiPS intermediates and rate-limiting steps in the SRR process, and present a summary of the role played by descriptors, establishing fundamental connections to descriptor functionality. Subsequently, we delineate the operational principles of three primary descriptor categories (electronic, structural, and energy descriptors) and the establishment of scaling relationships based on them. Moreover, advanced descriptor constructs are also explored, including comprehensive descriptors with multi-factor integration and other types of descriptors. In particular, we summarize how emerging artificial intelligence (AI) methodologies can facilitate the further development and application of descriptors. Ultimately, we envision great potential for clarifying the scope of applicability, developing universal descriptors, integrating with AI, and breaking the scaling relationships to accurately identify and design highly active catalysts.

---

Ziqing Yao

Ziqing Yao obtained his BS degree from the College of Science, National University of Defense Technology in 2023. Currently, he is studying as a PhD student in Prof. Chunman Zheng's group at the College of Aerospace Science and Engineering, National University of Defense Technology. His current research focuses on high specific energy lithium-ion batteries and artificial intelligence-assisted battery material design.

Chunman Zheng

Prof. Chunman Zheng obtained his PhD from the National University of Defense Technology in 2006 and joined the faculty in 2007. He was a visiting scholar at the University of St Andrews in 2012 and is currently a Professor in the College of Aerospace Science and Engineering. His research interests include novel electrode materials, high-performance energy storage devices, and power systems in extreme environments.

Weiwei Sun

Weiwei Sun is an associate researcher at the College of Aerospace Science and Engineering, National University of Defense Technology. He received his BS and PhD degrees from Wuhan University in 2008 and 2015, respectively. He studied as a visiting PhD student at the Hong Kong Polytechnic University from 2011 to 2012. After that, he worked as a postdoctoral researcher at the National University of Defense Technology from 2017 to 2021. His research mainly focuses on high-voltage cathode materials, catalysts for lithium–sulfur batteries, and applications of artificial intelligence in materials development.

---

1 Introduction

In pursuit of developing power batteries for electric vehicles and energy storage systems integral to large-scale power grids, humanity is striving to innovate battery systems. As one of the most promising candidates, lithium–sulfur (Li–S) batteries (LSBs) have attracted considerable attention due to their ultra-high theoretical energy densities of 2600 Wh kg⁻¹ and 2800 Wh L⁻¹.^1–4 Furthermore, sulfur is a naturally abundant, low-cost, and environmentally friendly by-product of petroleum, which contributes to the goal of carbon neutrality for humanity.^5–7 In contrast to conventional lithium-ion batteries with inserted metal oxide cathodes (e.g. LiCoO₂, LiFePO₄, LiNi_xCo_yMn_zO₂, etc.), Li–S batteries represent a transition from conventional insertion electrochemistry to innovative conversion electrochemistry, enabling a substantial storage capacity through a reversible two electron per sulfur atom redox reaction.^8,9 Reversible redox reactions on the cathode side in Li–S batteries occur between sulfur (S₈), lithium polysulfides (LiPSs) (Li₂S_x, 4 ≤ x ≤ 8) and lithium sulfide (Li₂S₂/Li₂S), as illustrated in Fig. 1a. The conversion process follows the sequence: S₈ ⇋ Li₂S₈ ⇋ Li₂S₆ ⇋ Li₂S₄ (⇋Li₂S₂) ⇋ Li₂S (Fig. 1b). Despite the promising future of LSBs, the challenges of practical application are also formidable, including slow reaction kinetics and detrimental shuttling effects of LiPSs.^10–14 The incorporation of appropriate catalysts into LSBs has been demonstrated to facilitate the adsorption of LiPS molecules, while reducing the activation energy associated with the rate-determining step without influencing the redox pathway.^15–19 The LSB charge/discharge curves illustrated in Fig. 1c illustrate that the catalyst reduces the Li₂S nucleation/disintegration energy barrier and lowers the polarization voltage, thereby substantially improving the performance of LSBs.^20,21

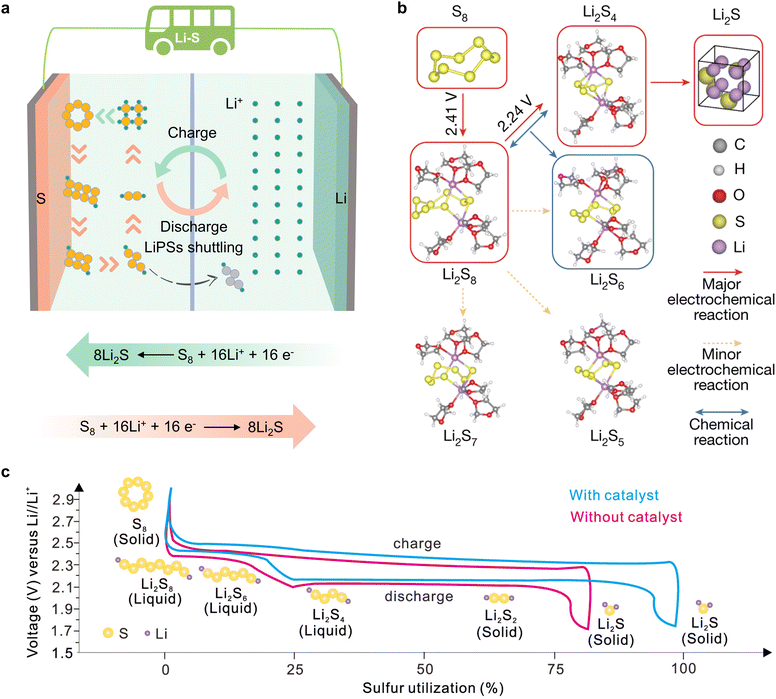Fig. 1 (a) Schematic diagram of orbital interactions between polysulfides and various catalysts. (b) The dominant reaction mechanism suggested by DFT energetics: S₈ → Li₂S₈ → 2Li₂S₄ → 8Li₂S (Li₂S₈ + Li₂S₄ ⇌ 2Li₂S₆), in which the chemical disproportionation part is shown in parentheses. Solid red and dotted yellow lines indicate major and minor electrochemical reactions, respectively, and blue lines indicate chemical reactions. Major products are indicated by red and blue boxes, corresponding to electrochemical and chemical origin, respectively. Reproduced with permission. Copyright 2024, Springer Nature.⁹ (c) Schematic of the charge–discharge process of the sulfur cathode. Reproduced with permission. Copyright 2024, American Chemical Society.²⁰

Following a period of research and development, there has been a notable increase in the variety of catalyst materials that can be applied in Li–S batteries, including mono-metals,²² (high-entropy) alloys,^23–28 metal sulfides,^29–32 metal oxides,^33–35 metal nitrides,^36–39 metal phosphides,^40–42 metal borides,⁴³ non-metals,^44–46 heterojunctions,^47–50 MXenes,^51,52 and perovskites⁵³ as well as single-atom^54–56 and dual-atom catalysts.^20,57–59 Most of these catalytic materials are heterogeneous catalysts, implying that the active sites are difficult to identify and understand, and, hence, it is challenging to develop and tailor catalyst functionality for Li–S batteries with a certain purpose. The intricate structure of catalysts for Li–S batteries and the paucity of in situ characterization techniques render traditional catalyst design methods reliant on trial-and-error experimentation. Fortunately, in the current era of artificial intelligence (AI), computer technology offers a powerful and direct approach to catalyst design, utilizing technologies such as high-throughput computing (HTC) and machine learning (ML).^60–66 Nevertheless, the deployment of these sophisticated algorithms for the identification and prediction of catalysts for LSBs necessitates the establishment of suitable quantifiable criteria, termed descriptors, derived from the physical or chemical properties of the reaction system, also known as reactivity descriptors. Accurate descriptors can describe the energy conditions involved in the reaction network through the electronic and structural properties of the catalyst, thus describing the kinetics of the overall reaction. By mapping the high-dimensional parameter space of chemical reactions to a low-dimensional description space, it is feasible to reduce the computational resources consumed in the screening and prediction of ideal catalysts.

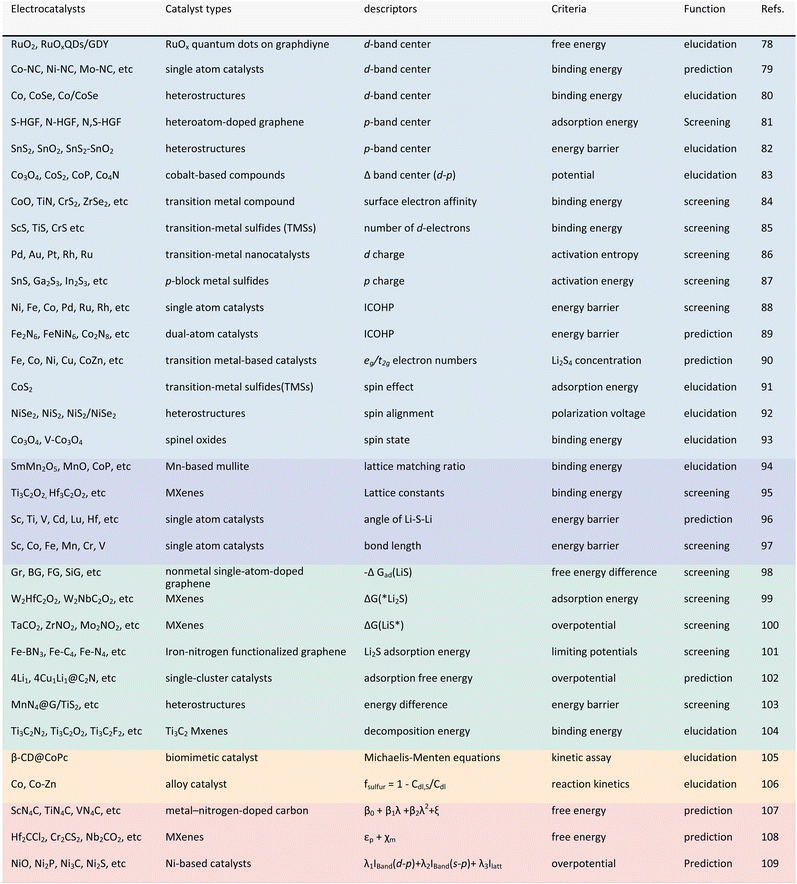
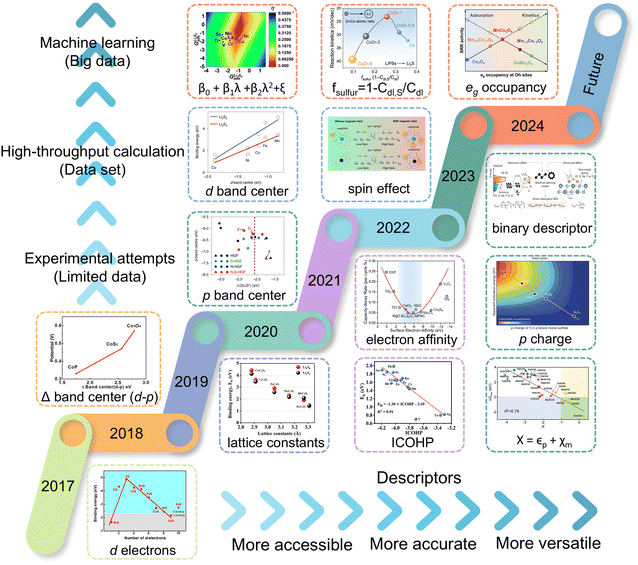
In other catalytic reactions, such as the oxygen evolution reaction (OER), hydrogen evolution reaction (HER), oxygen reduction reaction (ORR), nitrogen reduction reaction (NRR), etc., relatively mature scaling relationships have been established for heterogeneous catalytic reactions, that is, the mathematical relationship between the descriptor and the catalytic performance criterion, is usually linear or volcanic.^67–77 However, the development of descriptors for the sulfur reduction reaction (SRR) in Li–S batteries remains in the nascent stage, and the establishment of scaling relationships is not yet systematic. As illustrated in Fig. 2, the quantity of pertinent literature has increased since this issue was initially identified in 2017, particularly over the past three years. Despite the explosive growth in research on SRR descriptors in recent years, a lack of summarization of existing results and scientific guidance has led to confusion regarding the range of catalysts to which descriptors are applicable, their functions, and the construction and subsequent development of new descriptors. It is thus evident that a systematic review of reactivity descriptors for Li–S battery catalysts is imperative for the advancement of efficient catalysts. Table 1 provides an overview of the types of catalysts studied in a portion of the research papers, accompanied by the corresponding descriptors, key criteria, etc. The various descriptors can be classified into three main categories according to differences in emphasis: electronic descriptors, structural descriptors and energetic descriptors, in addition to the reconciling binary descriptors (which incorporate two of the electronic, structural, or other properties). When examining the role of different descriptors in designing novel catalysts and understanding the origins of catalytic activity, we have summarized their functions into three categories: screening, prediction, and elucidation, as shown in the “Function” column of Table 1. “Screening” refers to selecting the most active catalysts from a limited set of candidates using descriptors; “prediction” involves designing ideal catalysts rationally; and “elucidation” means explaining the origin of catalyst activity through reactive descriptors.

Fig. 2 Schematic representation of the number of publications in the field of descriptors for Li–S batteries.

Table 1 Descriptors that have been studied in LSBs and the corresponding catalyst species.^78–109 Different background colors represent different kinds of reactivity descriptors: electronic descriptors (blue), structural descriptors (purple), energetic descriptors (green), electrochemical descriptors (yellow) and multivariate descriptors (red)

---

The choice of descriptors is contingent on the type of catalyst in question. For instance, the renowned d-band center can be effectively applied to metal compounds, but its use is not recommended for non-metal catalysts. Similarly, while adsorption energy (E_ad) can directly describe the catalytic activity of a catalyst, its acquisition is not straightforward. Furthermore, the intricate catalytic process of a Li–S battery, which involves 16 electrons, presents a significant challenge in accurately assessing the catalytic activity using a single descriptor based on a specific intermediate. In light of the preceding discourse, the reactivity descriptor efficacy of Li–S batteries is hereby summarized and demonstrated in Fig. 3.

Fig. 3 Schematic of the combined efficacy of reactive descriptors.

In this review, we comb through the reactivity descriptors and scaling relationships for sulfur-catalyzed conversion that have been studied in recent years (Fig. 4), aiming to provide the following insights: firstly, we comprehensively summarize the reactivity descriptors mapped in the high-dimensional feature space of the SRR reaction and form reasonable categories, systematically elucidate the origin of the catalytic activity in the adsorption and conversion process of LiPSs from the descriptor viewpoint, and meanwhile, study the proportionality between different reactivity descriptors and catalytic activity on this basis. Next, advanced generic descriptor development paradigms such as binary descriptors are then explored, and we also emphasize the importance of generic descriptors for establishing a unified activity standard for Li–S chemical catalysts. In addition, we summarize in detail the great advantages of the win–win fusion of descriptor engineering and machine learning, and propose a new research paradigm guide for the development of efficient lithium–sulfur catalysts in the age of artificial intelligence. Finally, we look at potential future directions for LSB descriptor research, emphasizing the attractive prospects of combining reactivity descriptors with artificial intelligence techniques for catalyst activity prediction and efficient development. Notably, this review will provide a guide for researchers involved in a wide range of metal–sulfur battery research, novel catalyst development, and machine learning applications in materials, as well as provide tremendous opportunities for disciplinary crossover and the establishment of new research paradigms for catalyst development.

Fig. 4 Schematic diagram of orbital interactions between polysulfides and various catalysts.

2 Electronic descriptors

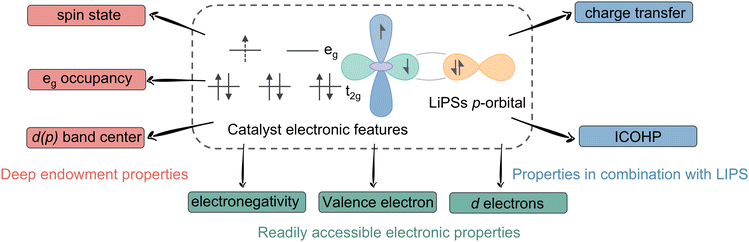
Electronic descriptors are reactivity descriptors based on the catalyst's own electronic configuration, which encompasses the arrangement of electrons in the s, p, d and other orbitals. This includes direct properties such as electronegativity and the number of electrons, as well as secondary properties represented by the d-band center, which must be obtained indirectly through mathematical or other means. Given that the catalytic conversion of lithium polysulfide hinges on the transfer of electrons at the active site, electronic descriptors occupy a pivotal role and are pertinent to the majority of metal-based catalysts. The electronic descriptors that have been proven to be reliable thus far are d-band center, d-electron derived properties and fresh spin configuration descriptors.

2.1 d-Band center

The d-band center is defined as the average energy of electrons projected into the d-orbital, which can be mathematically expressed as follows: . Combining density functional theory (DFT) and mathematical expressions, the d-band center of a certain substance is then identified. The d-band theory has been extensively employed since its initial proposal by Hammer and Nørskov in the 1990s,¹¹⁰ and has progressively emerged as a pivotal nexus between the electronic properties of metals and their chemical reactivity, which in turn has facilitated a deeper comprehension of bond formation and reactivity in catalysis. As illustrated in Fig. 5, the adsorption of simple atoms or molecules on a metal surface gives rise to interactions between the s/p-state electrons of the adsorbate and the d-band of the metal atom, resulting in splitting of the energy levels and the formation of opposite bonding and antibonding states. If the energy of the surface energy levels of the adsorbate and catalyst is higher than the bonding state but lower than the antibonding state, it can be inferred that the antibonding state is occupied. In this case, the system energy is unfavorable, which leads to weak adsorption or even desorption, and vice versa.

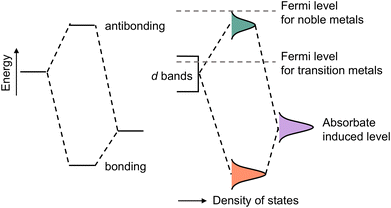Fig. 5 Schematic illustration of the interaction between two electronic states. Adapted with permission. Copyright 1995, Springer Nature.¹¹⁰

In the case of transition metal (TM) catalysts, the d-band center is an ideal descriptor, but the intrinsic relationship between “d-band center – adsorption strength – catalytic activity” is not straightforward. Liu et al. elucidated the bonding mechanism between metal atoms in different d states and polysulfides using porous carbon nanofiber catalysts embedded with different transition metals (M-PCNF-3, M = Fe, Co, Ni, Cu) in Fig. 6a.¹¹¹ The higher the energy of the d-band center with respect to the lower Fermi energy level (E_f), the less populated the antibonding orbitals formed by the 3d orbitals with the lowest unoccupied orbitals of the polysulfides, and the greater the metal active center adsorption of the polysulfides. The adsorption energies of Li₂S₂, Li₂S₄ and Li₂S₆, as obtained from DFT calculations, demonstrate a strictly proportional scaling relationship between the adsorption strength and the energy of the d-band center (Fig. 6b). Therefore, the d-band center provides an accurate description of the strength of adsorption.

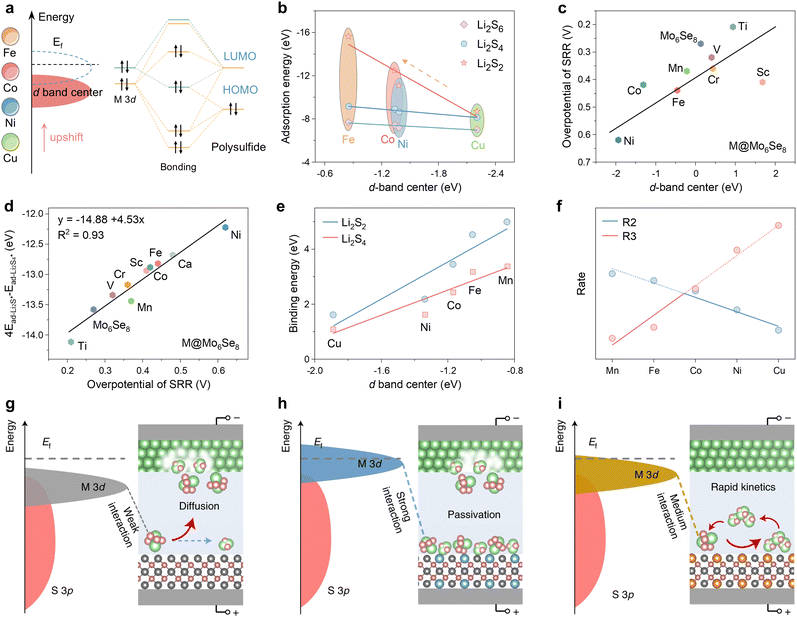Fig. 6 (a) Schematic diagram of orbital interactions between polysulfides and various catalysts. (b) The correlation analysis between the d-band center and adsorption energy. Adapted with permission. Copyright 2024, Wiley-VCH.¹¹¹ (c) Linear relationship between the overpotential of the SRR and 4E_ad-Li2S*–E_ad-Li2S4*. (d) Relationship between the overpotential of SRR and the d-band center of M@Mo₆Se₈ and Mo₆Se₈ systems. Adapted with permission. Copyright 2024, The Royal Society of Chemistry.¹¹² (e) Relationship of binding energy to d-band center. (f) Volcano plots of rates with respect to different dopants (the blue and red lines represent reactions (2) or (3) as the rate-determining steps, respectively). (g)–(i) Schematic illustration of weak (g), strong (h) and medium (i) interactions of polysulfides with catalysts. Reproduced (adapted) with permission. Copyright 2022, Springer Nature.¹¹³

The Chevrel phase Mo₆Se₈ doped with different TM atoms can also employ the d-band center descriptor, a strategy that was identified as an effective means of reducing the overpotential of the sulfur reduction reaction by Duan et al.¹¹² In this study, a linear scaling relationship was identified between the overpotential and the d-band center energy (Fig. 6c). Consequently, a linear relationship exists between the overpotential and 4E_ad-Li2S*–E_ad-Li2S4* with an R² value of 0.93 (Fig. 6d). This energy can be employed as a criterion for catalytic activity, demonstrating that the d-band center can effectively describe complex reactions in catalysts doped with TM elements. The binding energies of polysulfide intermediates in different TM-doped zinc sulfide (M_0.125Zn_0.875S) catalysts, illustrated in Fig. 6e, depend proportionally on the d-band center of the active site as shown in Fig. 6b.¹¹³ The linear scaling observed for intermediate states typically gives rise to the Brønsted–Evans–Polanyi (BEP) relationship (E_a = αΔE + β), which allows for the correlation of activation energy (E_a) with reaction enthalpy (ΔE) with two scaling factors (α, β).^114–116 The authors have devised an ingenious method for streamlining the pivotal liquid–solid conversion phase of Li₂S₄ to Li₂S₂:

Li₂S₄ + * → Li₂S₄*

Li₂S₄* + 2Li⁺ + 2e⁻ + * → 2Li₂S₂*

2Li₂S₂* → 2Li₂S₂ + 2*

This approach entails integrating the BEP relationship to establish a correlation between the rate constants R2 and R3 of the (2), (3) reaction and the reaction enthalpy and obtain a volcano plot of the reaction rate, as illustrated in Fig. 6f, which reveals that the reaction rate exhibits an initial increase before declining as the d-band center upshift from Cu to Mn. Yet the reaction rate attains its maximum reactivity at Co_0.125Z_0.875S. This phenomenon indicates that the d-band centers result in elevated transition state adsorption energies; however, the enhanced adsorption energies do not necessarily correlate with increased catalytic activity. The Sabatier principle, as it pertains to multiphase catalysis, posits that the interactions between the intermediate and the catalyst should be balanced, eschewing either overly strong or overly weak interactions.^117,118 Furthermore, it asserts that only moderate adsorption is necessary to achieve maximum catalytic activity. Similarly, Shen et al. reached the conclusion that strong adsorption of Li₂S₂ reduces the exposure rate of the catalyst's free active sites, thereby causing the catalyst to become passivated (Fig. 6g–i).¹¹³ As a result, a volcano curve is formed.

The d-band center descriptor has been a highly successful model in the context of metal-based catalysts. Nevertheless, in the case of metal compounds, the overall electronic structure is not only shaped by the metal d-orbitals; the non-metal p-orbitals also exert a significant influence. Given this, p-charge related properties such as the p-band center theory and the d–p energy level difference (ΔE_d–p) have been put forth as supplementary descriptors.

The p-band center is comparable to the d-band center in terms of both definition and expression, but the p-band has been considerably less investigated. While it is widely acknowledged that d-orbital partially filled metal centers are active sites for charge transfer and non-homogeneous catalysis, the considerable disparity in the activity of transition metal-based catalysts with different anions also necessitates theoretical elucidation. In light of the success of the d-band model and chemical bonding theory as a descriptor of transition metal surface activity, Hua et al. put forth the proposition that the p-charge of S in p-block metal sulfides (p-MSs) could serve as a reactivity descriptor for the catalytic conversion of LPSs.⁸⁷ They proceeded to establish a linear scaling relationship between the p-electron gain and the activation entropy of adsorption (ΔS⁰*) and the apparent activation energy (E_a).¹¹⁹ It is demonstrated that Bi₂S₃ attains the greatest p-charge gain, which consequently results in the formation of the greatest number of thiosulfate intermediates, ultimately leading to a reduction in E_a and an enhancement in electrocatalytic activity for the SRR (Fig. 7a and b). Peng et al. investigated the optimal adsorption strength and catalytic activity of intermediates in heteroatom-doped holey graphene framework (HGF) systems, employing the p-band center as a descriptor (Fig. 7c and d).⁸¹ As illustrated in Fig. 7c, there is a definitive correlation between the overpotential and the adsorption energy (ΔG(LiS*)) of the critical precursor LiS* under the catalysis of various heteroatom-doped holey graphene framework (HGF), including N-HGF, S-HGF, and N, S-HGF. Furthermore, in Fig. 7d, the p-band centers of different HGF catalysts were used as electronic descriptors to investigate the relationship with ΔG(LiS*). It was found that N and S element doping can regulate the position of carbon atoms' p orbitals to an intermediate energy level, thereby manipulating the adsorption strength to a moderate level and enhancing catalytic activity. DFT calculations have demonstrated that a non-metallic catalyst plays a pivotal role in the process, with the key function being the bonding between the p orbitals of catalytic center and polysulfides.

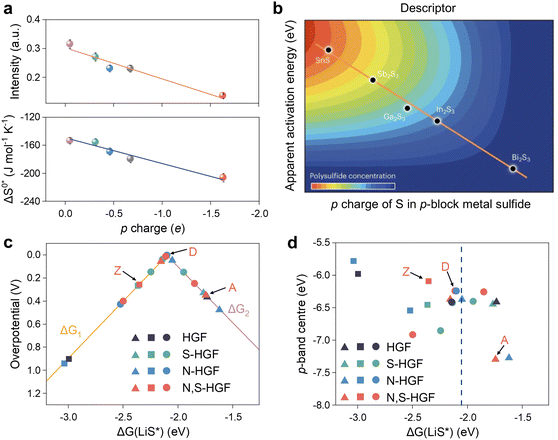Fig. 7 (a) Relationship between the p charge of S in p-MS and ΔS⁰* and E_a for Li₂S_n to Li₂S conversion in the SRR. Error bars indicate the standard deviation of measurements from three independent coin cells. (b) The correlation analysis between the d-band center and adsorption energy. Reproduced (adapted) with permission. Copyright 2023, Springer Nature.⁸⁷ (c) A volcano plot linking the overpotential for the final step to the adsorption energies of the LiS radical intermediate on different active sites. (d) The relationship between the p-band center and LiS* adsorption energy at different active carbons. The blue dashed line represents the adsorption energy associated with the top of the volcano in (c). Adapted with permission. Copyright 2020, Springer Nature.⁸¹

In addition to considering the p- and d-band properties as discrete entities, the energy difference between the two has also been investigated as a potential descriptor. Zhou et al. were the first to elucidate the nature of the modulation of the p-band contributions of different non-metallic elements in the study of the catalytic conversion of LiPSs by cobalt-based compounds, i.e., the higher the p-band center is with respect to the Fermi energy level, the smaller the energy gap between Co-3d and the anion-2p, which implies greater orbital hybridization and valence-band electronic contributions, thus driving the exchange of electrons for the liquid–solid conversion of LiPSs.⁸³ Therefore, the scaling relationship in Fig. 8a depicts that the CoP with the lowest ΔE_d–p has the lowest sulfur reduction potential. In a recent study, Dong et al. developed a concept of periodic expansion catalysis based on the analysis of a range of molecular catalysts with RuP₂ configurations (RuP₂, RuN₂, FeP₂, FeP₂).¹²⁰ Their findings ascertained the crucial role of ΔE_d–p in this concept. In contrast, the smallest ΔE_d–p (3.21 eV) of RuP₂ suggests that the d-electrons of Ru are more likely to be delocalized and diffuse outward from a single Ru atom into a P–Ru–P polyatomic system as illustrated in Fig. 8b. Typically, the delocalized electrons are more reactive and more readily transferred to LiPSs, which ultimately improves the kinetics of the SRR process.¹²¹ In order to investigate 2D MXene materials with complex structures and compositions, Fang et al. employed an HTC method to screen extensive MXene databases.¹⁰⁸ They then attempted to utilize the p-band center (Fig. 8c) and d–p energy band difference (Fig. 8d) descriptors in the exploration process. The linear fitting results demonstrate that the Gibbs free energy change (ΔG) between the initial and final states of the SRR process is proportional to the p-band center and inversely proportional to ΔE_d–p, for the same reason previously described. Notably, the scaling relationship with ΔE_d–p as the descriptor exhibits an R² value of 0.66, which is higher than that of 0.59 for the p-band center, thereby rendering ΔE_d–p a more reliable descriptor.

Fig. 8 (a) Schematic diagram of the effect of the p–d band gap (ΔE_d–p) on the adsorption strength of lithium polysulfide. Reproduced with permission. Copyright 2022, American Chemical Society.¹²⁰ (b) Scaling relationship between the the d band (d–p) center and Li–S redox potentials for CoP, CoS₂, and Co₃O₄, respectively. Adapted with permission. Copyright 2018, Elseiver.⁸³ (c) and (d) Relationships between ΔG and (c) the p-band center and (d) Δ(p–d) of different MXenes. Adapted with permission. Copyright 2023, American Chemical Society.¹⁰⁸

It is regrettable that, despite the efficacy of these two single descriptors in studies with a limited number of samples, they fail to establish a satisfactory scaling relationship for the effective screening and prediction of MXene catalysts in a comprehensive library. Overall, the d-band center theory has been widely employed to elucidate the interactions between active sites and adsorbates in electrocatalysis, with considerable success in metal-based catalysts, including metal monomers and alloys, metal compounds, MXenes, and so forth. Moreover, p-band center and d–p energy level differences have been employed to elucidate the impact of non-metallic elements on the valence band electrons of the active center. Nevertheless, the prevailing approach in SRR currently entails the exclusive consideration of the position of the d-band center, with a paucity of investigation into the width and shape of the d-band, as well as the prospective applications of the position of the highest Hilbert peak, which indicates the potential for further development of the d-band center descriptor.^122,123

2.2 d Electron derived properties

Excluding the successful d-band model, the electronic structure properties of the catalyst have a multitude of d electron derived properties that serve as valid reactivity descriptors for the sulfur cathode. Cui et al. employed an intrinsic property of the cathode material, the ability of surface electron acceptance, designated as surface electron affinity (ΔV_SEA), as a quantitative screening principle for catalysts (Fig. 9a).⁸⁴ This descriptor was determined using the following equation:
ΔV_SEA was calculated by numerical discretization, where S_a is the calculated catalyst surface area, S₀ is the normalized standard specific surface area, and q_max is the maximum electron acceptance accommodated on the neutral surface, as determined by the energy inflection induced by successive electron additions.

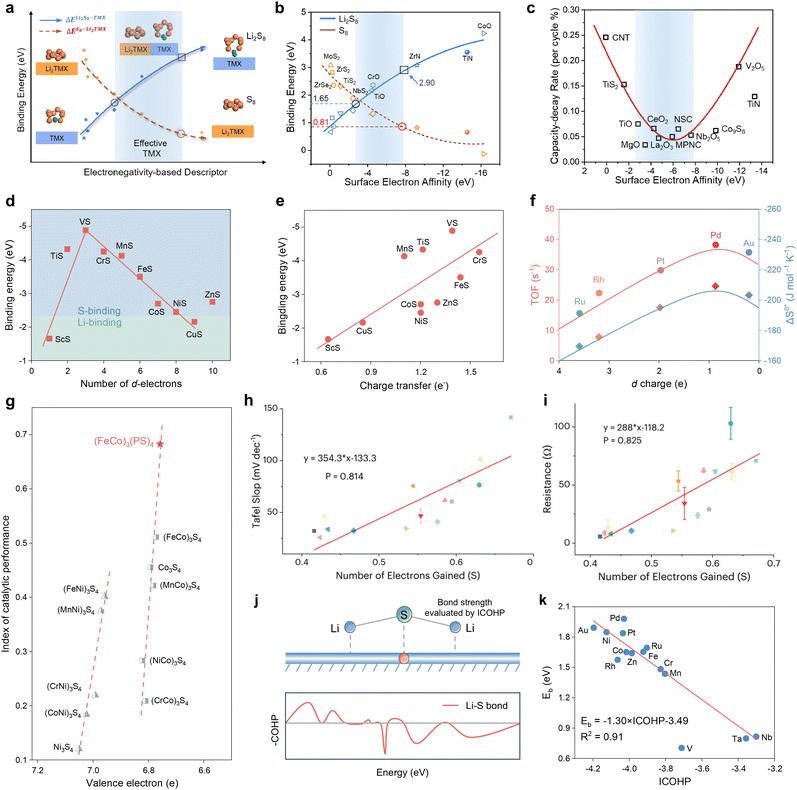Fig. 9 (a) A schematic illustration of the correlation between adsorption strength with electronegativity descriptor between S₈ (Li₂S₈) and the anchoring material TMX. (b) Correlation curve of the binding energy of Li₂S₈ and S₈ on different anchoring materials with surface electron affinity, fitted by the polynomial method. (c) The relationship between capacity-decay rate (per cycle) and surface electron affinity obtained from previous reports and this work. Reproduced with permission. Copyright 2021, Elsevier.⁸⁴ (d) Periodic law of binding energy. (e) Linear relationship of binding energy vs. charge transfer. Adapted with permission. Copyright 2017, American Chemical Society.⁸⁵ (f) The relationship between the value of the d orbital vacancy and the turn-over frequency and the entropy of activation for the reduction of polysulfides to insoluble lithium sulfide.⁸⁶ (g) Catalytic performance index plotted against the valence electron descriptor. Adapted with permission. Copyright 2025, Wiley-VCH.¹²⁴ (h) Experimental relationship between the Tafel slopes determined from symmetric cells with M-MoS₂ electrodes and the number of electrons gained by lattice sulfur. (i) Experimental relationship between the charge transfer resistance determined from symmetric cells with M-MoS₂ electrodes and the number of electrons gained by lattice sulfur. Adapted with permission. Copyright 2025, American Chemical Society.¹²⁵ (j) Schematic diagram for the mechanism of Li₂S decomposition and COHP for VN₄@G. (k) Scatter plots of E_b versus ICOHP of the Li–S interaction. The red line represents the corresponding linear relationships. Adapted with permission. Copyright 2021, Wiley-VCH.⁸⁸

Surface electron affinity is an electronegativity-based descriptor, which is essentially an extension of the concept of atomic electronegativity and characterizes the electron attraction tendency of a specific atom.¹²⁶ As illustrated in Fig. 9b, DFT calculations and experimental tests confirm that for transition metal compounds (TMX) with surface electron affinity potentials between −2.66 and −7.96 eV, there is an optimal binding energy between the catalyst and adsorbate. This not only prevents the dissolution of LiPSs, but also exhibits good electronic conductivity, a phenomenon that can be attributed to Sabatier theorem. The above prediction is corroborated by the volcano relationship between cycling performance and ΔV_SEA for a series of TMXs in Fig. 9c, which demonstrates that surface electron affinity is a reliable descriptor that can be applied to establish quantitative criteria for the screening of catalysts and the optimization of performance.

The current studies posit that the anchoring of adsorbates on the catalyst surface is contingent upon the formation of chemical bonds, specifically in LSBs, the formation of chemical bonds between the catalyst and Li or S of LiPSs. In the case of TMXs, the number of d-electrons which exhibit high activity, affects the formation of bonds and determines the bonding object. In contrast to the Li bonding induced by dipole–dipole interactions, the transition metal bonding with S is of greater strength, due to the fact that it is the charge transfer that induces the formation of the bond.^127,128 The determinants of the two anchoring effects were initially identified as being somewhat ambiguous by Chen et al. and subsequently subjected to a comprehensive investigation within the transition metal sulfide population.⁸⁵ The Mulliken charge analysis results indicate that ScS and CuS exhibit Li-binding-dominated anchoring effects, whereas the remaining objects are in S-binding configurations. This is evidenced by a clear volcano shape of the binding energies versus the number of d electrons of the respective transition metal sulfides, as illustrated in Fig. 9d. The transitions occurring at VS are attributed to the equilibrium between the number of valence electrons and the number of d orbitals in the unoccupied orbitals. Moreover, the linear proportionality between the number of electrons transferred to the d orbitals of the catalytic material by lithium polysulfide and the binding energy presented in Fig. 9e, offers a potential means of predicting the adsorption energy by charge transfer, which in combination with the Sabatier principle then describes catalytic activity. Interestingly, Sun et al. subsequently proposed the use of vacancies in the TM d-orbital electrons, termed d-charges, to describe both the activation entropy (S) of LiPS adsorption and the inversion frequency (TOF) of Li₂S₂/Li₂S precipitation as a reflection of the kinetic parameter of the SRR in their study of TM nano-catalysts loaded on ordered mesoporous carbon.⁸⁶ The results illustrated in Fig. 9f show that the d-orbital vacancies are volcanic for both discriminants in the studied local space, where Pd exhibits the highest S and TOF, implying the success of the d-orbital electron vacancy descriptor.

In the third period of transition metals, the d-orbital electrons are known to be highly correlated with valence electrons, thereby influencing bonding activity with other atoms. Accordingly, Shen et al. attempted to use the electronic model as a reactivity descriptor to guide the design of cationic and anionic co-doped spinel sulfide catalysts, and established an accurate scaling relationship between the number of valence electrons and catalytic activity, which successfully predicted the design of (FeCo)₃(PS)₄ catalysts with the highest number of valence electrons (Fig. 9g).¹²⁴

Moreover, this study demonstrates the unique role of the lattice sulfur sites in the catalyst in promoting the conversion process of lithium polysulfide. Zhang et al. investigated the interactions between metal sites and adjacent lattice sulfur atoms in a metal–MoS₂ (M–MoS₂) catalyst system and analyzed the scaling relationship between lattice sulfur electron density and sulfur species reduction activity using the number of electrons gained by lattice S as descriptors.¹²⁵ As demonstrated in Fig. 9h and i, the quantity of lattice sulfur-acquired electrons exhibits a direct linear correlation with the Tafel slope of the symmetric cell CV curve, as well as the charge-transfer impedance. This provides a theoretical framework for the design and development of heteroatom-doped MoS₂ catalysts.

In addition to the readily accessible properties associated with the number of electrons, there is a crystal orbital Hamiltonian layout based on the electronic density of states and a corresponding energy integral value, which quantifies the strength of the catalyst's bonding to lithium polysulfide and thus shows potential as a reactivity descriptor. Specifically, Zeng et al. screened single metal atom catalysts embedded in graphene coordinated by four nitrogen atoms (MN₄@G) for evaluation by quantifying the strength of Li–S binding bonds using ICOHP values. As illustrated in Fig. 9j and k, a strong linear correlation is evident between ICOHP and the Li₂S decomposition energy barrier (E_b). A decrease in ICOHP value is indicative of an increase in the strength of the Li–S interaction, and vice versa. The robust scaling relationship provides a robust foundation for the prediction and screening of reaction descriptors.

In crystal field theory, the five orbitals of 3d typically split into t_2g (d_xy, d_yz, d_xz) and e_g (d_xy, d_xy), which possess disparate energy levels in the octahedral field. Both are intimately associated with the formation of bonding and antibonding orbitals in the catalytic process. The concept of e_g occupancy descriptors was initially proposed in 2011 by Suntivich et al. in the context of OER catalysis of perovskite oxides.¹³¹ Similarly, Bai et al. applied perovskite oxides to the catalytic conversion of LiPSs, demonstrating that the e_g occupancy approach remained effective, as illustrated in Fig. 10a and b.¹²⁹ In the case of Li₂S, for example, during its adsorption on the surface of the perovskite oxide, the p orbitals of S and the d orbitals of the central metal atoms form σ and π hybridization orbitals, depending on whether or not the orientations are matched. Once the p–d hybridization is complete, the bonding orbitals σ and π, as well as the antibonding orbitals σ* and π*, are formed. According to the Hund's rule and the energy minimization principle, the electrons in the Li₂S adsorption configuration initially occupy the bonding orbitals to reduce the energy of the system, then the non-bonding orbitals and finally the antibonding orbitals. Consequently, the occupancy of the σ* antibonding orbitals (e_g) plays a pivotal role in determining the adsorption strength of polysulfide intermediates. Magnetic measurements indicate that the d-electron configurations of LaCrO₃, LaFeO₃, and LaCoO₃ are t³_2ge⁰_g, t³_2ge²_g, and t³_2ge^1.08_g, respectively. Furthermore, distinct e_g fillings result in disparate d-band center and d–p band gap. Notably, LaCoO₃ demonstrates optimal adsorption strength and the most rapid lithium polysulfide conversion due to its moderate e_g occupancy. Similarly, the intrinsic SRR activity exhibits a volcano-shaped distribution relative to the average e_g occupancy of the octahedral (Oh) site in the different spinel-phase oxides shown in Fig. 10c.¹³⁰ As with the perovskite oxides, this can be also attributed to the antibonding orbital occupancy. Specifically, low e_g occupancy provides undue intermediate adsorption strength and induces active site passivation, which in turn leads to catalyst poisoning. Increasing the e_g occupancy is beneficial in mitigating the poisoning effect, but an excessively high e_g occupancy will result in the LiPSs drifting away, consequently triggering severe shuttle effects. Therefore, the apex of the volcano trend between SRR kinetics and e_g occupancy of transition metals at the Oh site in Li–S batteries is situated at the midpoint of the range of 0.45, which is the consequence of a compromise between the adsorption and conversion of LiPSs. Due to the accurate description of the catalytic conversion of LiPSs by e_g occupancy, it can also be further used to predict new catalyst types. In a recent study, Li et al. investigated the kinetic trends of Li–S batteries in conjunction with Le Chatelier's principle, established a proportionality between polysulfide concentration and antibonding orbital occupancy and identified the crucial role of e_g in transition metal-based catalysts in determining polysulfide concentration as well as in the prediction of SRR kinetics.⁹⁰ The researchers determined the e_g/t_2g ratios of the different metal monomers by DFT calculations and synchrotron-based near-edge X-ray adsorption fine structure (NEXAFS) of the metal L-edge, subsequently obtaining a correlation with the experimental Li₂S₄ concentration, as illustrated in Fig. 10d. Surprisingly, both curves exhibit a linear trend, which suggests that regulating the e_g/t_2g ratio may potentially regulate the concentration of LiPSs and the kinetics of SRR. Considering the balance of the Sabatier principle, the researchers devised CoZn binary clusters with an intermediate e_g occupancy, with the e_g/t_2g ratio of Cu > Zn > Ni > Co > Fe as a guiding parameter (Fig. 10e). At last, the distinctive superiority of CoZn alloys was effectively validated. In general, the s-state of a metal is typically delocalized and exhibits consistency across different metals, whereas the d-state is localized and exhibits notable variations, which is why the d-electron correlation properties are effective descriptors for catalytic reactivity in the SRR.

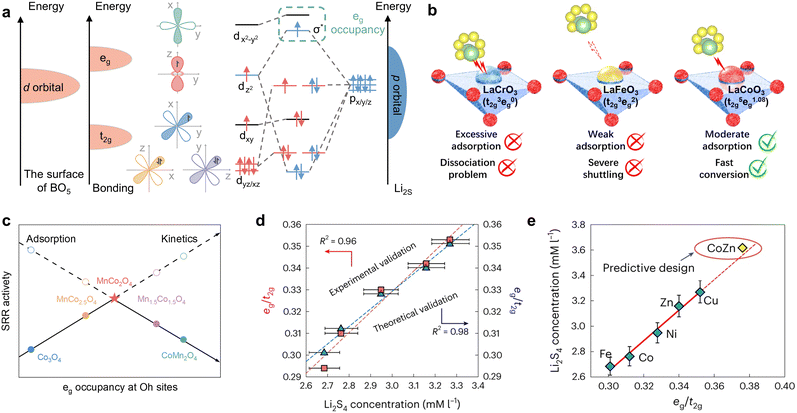Fig. 10 (a) and (b) Schematic illustration of (a) d–p orbital hybridization of transition metal (d_xy/xz/yz, d_x²−y², and d_z²) and Li₂S (p_x/y/z) during the adsorption process between perovskite oxide and polysulfides, and (b) polysulfide regulation with different e_g occupation on the surface of perovskite oxides (LaCrO₃, LaFeO₃, and LaCoO₃). Reproduced (adapted) with permission. Copyright 2024, Elsevier.¹²⁹ (c) Correlation of SRR activity and average e_g occupancy at Oh sites for Mn_xCo_3−xO₄. Adapted with permission. Copyright 2024, Wiley-VCH.¹³⁰ (d) Theoretical and experimental confirmation of the SRR kinetic trend with DOS-based and NEXAFS-based e_g/t_2g ratios for the different catalysts. (e) Design for a CoZn binary cluster catalyst with a good balance of e_g/t_2g electron numbers. The solid red line is the linear fitting for Fe, Co, Ni, Cu and Zn catalysts, and CoZn catalyst can be predictably designed by extrapolating the solid line to obtain a higher e_g/t_2g number with higher polysulfide concentrations (as indicated by the dotted line). Reproduced with permission. Copyright 2024, Springer Nature.⁹⁰

2.3 Spin configuration

The aforementioned e_g occupancy descriptor is applied to catalysts with different metal centers. However, for a given metal center, different e_g orbital occupations correspond to different spin configurations, which are also referred to as spin states. In the field of quantum physics, spin is defined as the angular momentum carried by elementary particles. Spin states, meanwhile, refer to the configuration of electrons in TMs.

The theoretical basis for the use of spin states as SRR reactivity descriptors can be elucidated through an in-depth investigation of several key models. These include the MOT,¹³⁵ a model underpinning chemical bonding theory, the LFT,¹³⁶ an applied theoretical framework for transition metal compounds and complexes, and the CFT, an energy model for the spin states of transition metal elements. The spin pairing energy and the crystal field splitting energy, in conjunction, determine the spin state of the electron, which can be classified as low spin (LS), intermediate spin (IS) and high spin (HS). Given that systems typically exhibit low total energy, those with high crystal field splitting energy will predominantly tend to be LS characteristics, whereas systems with low crystal field splitting energy will predominantly manifest HS. Moreover, a larger magnetic moment is typically observed in HS metal atoms, while a smaller moment is characteristic of LS metal atoms.^137–139 Although metal-based catalysts have intrinsic spin states, the application of external magnetic fields, crystal field, ligand field, stress field, and other stimuli can alter spin states through the spin injection effect and spin polarization.

The field of electrocatalysis has historically concentrated its research efforts on the aforementioned readily accessible characteristics, such as electronegativity, electron count, and energy band structure. However, there has been a paucity of attention directed towards spin-related properties. A number of recent studies have demonstrated that the presence of different spin states gives rise to alterations in the adsorption behavior and reaction rate between the catalyst and key intermediates, which in turn affects the catalytic activity, specifically the bonding and conversion rate of LiPSs in Li–S batteries. The underlying reason is that spin polarization has a significant impact on the bonding, hybridization ability and charge transport properties of catalytic materials. Optimizing the quantum spin exchange interactions of the catalytic system has the potential to increase the spin selection of the activation barriers, the spin correlation electron mobility and the spin potentials. This may result in a reduction of the electron repulsion in the catalyst orbitals and an improvement in the adsorption strength and kinetics of the conversion.

Zhang et al. significantly enhanced the adsorption capacity and SRR reaction kinetics of LiPSs in the presence of CoS_x, a classical catalyst, by employing an external magnetic field generated by a permanent magnet.⁹¹ The calculations of spin density and density of states demonstrate that the augmentation of the magnetic moment of the ligand hole under the influence of an external magnetic field propels the Co electrons to leapfrog from LS to HS, consequently generating additional unpaired electrons in the Co 3d orbitals, as illustrated in Fig. 11a. The consequences of spin polarization are illustrated in Fig. 11a and b, which depicts the high-spin electronic sheet array, resulting in increased overlap between the Co 3d and S 2p orbitals and stronger ligand hole-associated d–p hybridization. This promotes charge transfer to the active site. Additionally, according to the principle of angular momentum conservation, the interaction between the catalyst and the adsorbate induces a slight electron repulsion effect, which enhances the conductivity and mitigates the reduction energy barrier of sulfur. It is not only the external magnetic field that has the capacity to alter the spin configuration of the metal center, the ligand field strategy is also capable of this effect. Du et al. implemented an F-ligand strategy to regulate the electron distribution and energy level arrangement of the Mg center by anchoring Mg phthalocyanine (MgPc) to a fluorinated carbon nanotube substrate (denoted as MgPc@FCNT), which significantly accelerated the conversion kinetics of LiPSs through manipulation of spin polarized electrons of MgPc (Fig. 11c).¹³² The researchers reported that MgPc@FCNT exhibits axially displaced single active Mg sites and optimized quantum spin-exchange interactions. Moreover, DFT theoretical calculations demonstrated that the spin polarization of the catalyst not only increases the adsorption energy of LiPS intermediates but also facilitates the electron tunneling process in LSBs. In a recent study, Li et al. used a combination of experimental and theoretical analyses to investigate the modulation of LiPS co-catalysis in spinel oxides.¹³³ The findings suggest that the nature of this modulation is determined by the competition between the adsorption of intermediates at Co³⁺ tetrahedral (Td) and Mn³⁺ octahedral (Oh) sites on the Mn_Oh³⁺–O–Co_Td³⁺ backbone. As illustrated in Fig. 11d, the high spin active site Co_Td³⁺ (t³_2ge³_g) with stronger Co–S covalency, which is subject to super-exchange interactions of Mn_Oh³⁺–O–Co_Td³⁺, continuously immobilizes LiPSs. Meanwhile, spin-polarized electrons with spin upwards are observed near the Fermi energy level in Fig. 11e, which suggests that Mn Oh sites with Jahn–Teller activity can make 3d orbitals off-domain and exhibit semi-metallic properties. For Mn Oh and Co Td two-site catalysis of LiPSs, this acts as a polarization channel, facilitating electron transfer and elongating the d_z² orbitals, allowing for the emergence of suitable specific orbital catalytic activity. This work differs from previous studies on the intrinsic spin configuration that regulates the metal center of catalysis, as it investigates the structure–efficacy relationship between electronic structure changes triggered by different metal coordination structures and SRR kinetics and deciphers the spin code in the synergistic and efficient catalysis of high spin Mn_Oh³⁺–O–Co_Td³⁺ bimetallics, i.e., Mn facilitates the adsorption of LiPSs by Co through the bridging of O 2p electrons, thereby enhancing the adsorption of LiPSs by Co_Td and promoting the conversion of LiPSs at the Mn_Oh site (Fig. 11f).

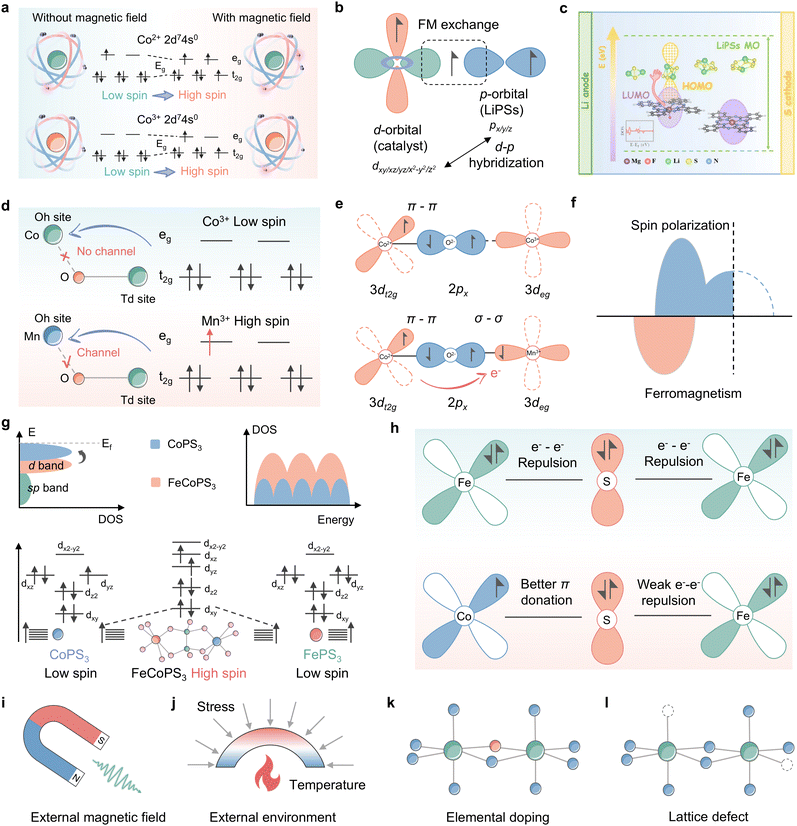Fig. 11 (a) CNF/CoS_x electrode under a magnetic field and no magnetic field for LiPS conversion: a scheme of the electron transition of Co from a low to a high spin state. (b) Schematic of spin-exchange mechanisms in LiPS conversion. Adapted with permission. Copyright 2022, Wiley-VCH.⁹¹ (c) Schematic illustration of the redox kinetics of lithium–sulfur batteries accelerated by quantum spin-exchange interactions. Reproduced with permission. Copyright 2024, Springer.¹³² (d) Illustration of the orbital splitting of Co_Oh³⁺, the corresponding Co_Oh–O–Co_Td spin channel (top) and Mn_Oh³⁺, corresponding Mn_Oh–O–Co_Td spin channel (bottom). (e) Schematic illustration of the spin polarization for Mn_Oh-doped Co₃O₄. (f) Co_Oh³⁺–O–Co_Td²⁺ (localized electronic structure) and Mn_Oh³⁺–O–Co_Td³⁺ (delocalized electronic structure). Adapted with permission. Copyright 2022, Wiley-VCH.¹³³ (g) Electronic configurations of the 3d orbital for CoPS₃, FePS₃, and FeCoPS₃. (h) Schematic representation of the electronic coupling between Fe and Co in FeCoPS₃. Adapted with permission. Copyright 2023, American Chemical Society.¹³⁴ (i)–(l) Schematic illustration of the spin state modulation mode: (i) external magnetic field; (j) external environment including stress, temperature and so on; (k) elemental doping and (l) lattice defect.

Not coincidentally, bimetallic phosphorus trisulfide embedded in nitrogen-doped hollow carbon nanocubes derived from Prussian blue analogues (FeCoPS₃/NCs) has been employed as a research object to elucidate the relationship between the catalytic activity and spin-state configuration of Li–S batteries.¹³⁴ Fig. 11g illustrates how the orbital spin splitting in FeCoPS₃ triggers a shift in the electronic structure from a low spin state to a high spin state, resulting in a greater number of unpaired electrons in the 3d orbitals compared to CoPS₃ and FePS₃. The presence of non-simplex orbitals elevates the d-band center and enhances the number of active electronic states. As with CoMn spinel oxide, the electron transfer process of FeCoPS₃ is shown in Fig. 11h, where the enhancement of the π-donation effect between Co–S, resulting from the coupling of Fe²⁺ to Co²⁺, gives rise to a transfer of electrons from Fe to Co. The accelerated electron transport facilitated by the enhanced spin structure of FeCoPS₃ is beneficial for SRR dynamics in comparison to the electron–electron repulsion with bridging S²⁻, which is induced by the fully occupied t_2g orbitals in FePS₃. A further consideration of the effect of spin configuration reveals that d_xy and d_yz become non-simplex energy levels in FeCoPS₃ due to the presence of heterometallics. Moreover, the fillable energy levels near the Fermi energy level increase and the energy level spacing decreases, thereby creating a tendency for electrons to be filled with single electrons. This results in a shift from low spin to high spin. In the high-spin state, the number of free electrons increases, thereby facilitating interaction with LiPSs via orbital hybridization. This enhances the probability of orbital hybridization, improves the adsorption strength of LiPSs and provides potential reaction pathways. These studies provide insights into the scaling relationship between spin states and the adsorption and conversion of LiPSs in the active site, allowing spin states to be employed as reactivity descriptors to guide the design of ideal catalysts.

In conclusion, it can be stated that the spin state is an inherent property of the material system that determines electron transport capacity, significantly impacts the catalytic conversion process of LiPSs by the catalyst, and has the potential to be a leading candidate for the subsequent generation of accurate electronic descriptors. As illustrated in Fig. 11i–l, several well-established schemes for spin state modulation are provided, including external magnetic field, external environment for synthesis, elemental doping, and lattice defects.^140–142 The selection of appropriate spin regulations for different systems, followed by the elucidation of the relationship between spin state and catalytic activity and the construction of a catalytic model will promote the development of spin descriptors for lithium–sulfur batteries.

2.4 How the electronic descriptors guide the experiments

Electronic descriptors are the most effective tools for describing the intermediate transformations and adsorption of LiPSs, which are summarized in Fig. 12. As previously discussed, electronic descriptors, including d-band centers, d–p energy differences, spin states, and so forth, can modulate the adsorption strength of LiPSs through charge effects. For instance, increasing the d-band center of active sites typically enhances the adsorption capacity of intermediates and mitigates the shuttle effect. In accordance with the guidance of physicochemical theories, linear or volcano-like scalar relationships can typically be obtained by combining the Sabatier principle and the BEP relationship. In conclusion, the following steps may be employed in the practical application of electronic descriptors for the guidance of experiments: (i) obtain the target electronic features of active sites using experimental measurements, theoretical calculations or existing databases; (ii) theoretical explanation of the source of SRR catalytic activity and determination of the adsorption intensity interval for high activity; and (iii) selection of target catalysts within an appropriate range based on the scalar relationship, or alternatively, disrupting the existing scaling relationship to obtain better catalysts through elemental doping, modulation of the coordination environment, external force fields, and so forth.

Fig. 12 Summary of electronic descriptors.

3 Structural descriptors

As a variety of electronic descriptors have yielded insights into the mechanism of electronic interactions between catalyst active sites and polysulfides and have been useful in predicting catalyst activity, structural characterization remains an indispensable perspective for understanding the kinetic processes of LiPS adsorption and conversion. The advent of structural descriptors, initially inspired by the structural sensitivity of certain catalytic systems, has led to the establishment of a scaling relationship between active site geometry and catalytic performance. In recent years, these descriptors have also been applied to SRR processes.^143–145 Notably, structural descriptors are typically more accessible and cost-effective to utilize in comparison to electronic descriptors. The structural descriptors that have been shown to be valid so far are mainly the lattice parameter dependent properties as well as factors such as bond lengths and bond angles of the catalysts and LiPSs combined.

3.1 Lattice parameters and nature of bonding with LiPSs

Wang et al. employed geometrical structure analysis to determine that the distance between two active sites on the lattice-exposed (001) surface is comparable to the distances observed between S and Li atoms in polysulfides in the study of Mn-based mullite SmMn₂O₅.⁹⁴ This finding suggests that SmMn₂O₅ may possess a structural basis for high catalytic activity, particularly in terms of LiPS adsorption. Furthermore, synthesis of the preceding research on catalytic materials, including h-BAs, MnO, CoP, etc., reveals a positive and proportional linear relationship between the lattice match ratio and the Li₂S₆ adsorption energy (Fig. 13a). In light of this, the authors also postulated the ultra-high binding energy of the vanadium nitride (VN) system with a lattice matching percentage of 98.1% for LiPSs from the database, a hypothesis that was subsequently validated through experimentation. More directly, Li et al. employed the lattice constant as a reactivity descriptor for Ti₂CO₂ and six additional M₃C₂O₂ (M = Cr, V, Ti, Nb, Hf, and Zr) MXenes in SRR, yielding noteworthy outcomes.⁹⁵ As illustrated in Fig. 13b, the binding energy of soluble Li₈S₈ to Li₂S₆ increases with decreasing MXene lattice constants, suggesting that a smaller catalyst size may enhance the anchoring effect on LiPSs. Nevertheless, it is likely that this phenomenon is exclusive to MXene-based catalysts.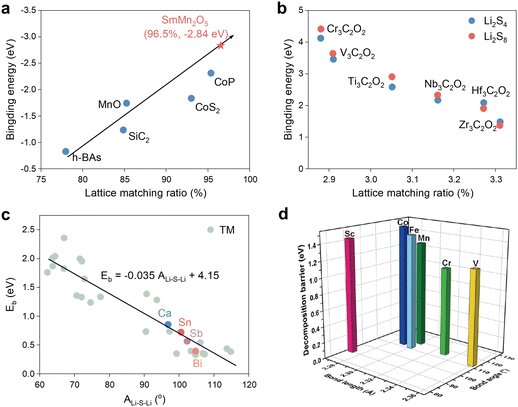

Fig. 13 (a) Relationship between the binding energies of Li₂S₆ on different SRR electrocatalysts and the corresponding lattice match percentage. Adapted with permission. Copyright 2022, Wiley-VCH.⁹⁴ (b) The binding energies for Li₂S₈ and Li₂S₄ as a function of the lattice constants of M₃C₂O₂ (M = Cr, V, Ti, Nb, Hf and Zr) MXenes. Adapted with permission. Copyright 2019, The Royal Society of Chemistry.⁹⁵ (c) Comparison of E_b predicted by the E_b–A_Li–S–Li linear relationship and calculated by the CI-NEB method (colored circles) for Ca@g-C₃N₄, Sn@g-C₃N₄, Sb@g-C₃N₄, and Bi@g-C₃N₄. Adapted with permission. Copyright 2024, Wiley-VCH.⁹⁶ (d) Li–S bond lengths and Li–S-Li bond angles of the adsorbed Li₂S and Li₂S decomposition energy barriers on M–N₃ (M = Sc, V, Cr, Mn, Fe, Co) centers. Reproduced with permission. Copyright 2023, Springer.⁹⁷

Furthermore, following an investigation into a range of descriptors, including Bader charge transfer (ΔQ_M), ICOHP_Li–N and distance between TM atoms above the substrate plane (d_{M_out}), Wu et al. identified the Li–S–Li angle after Li₂S adsorption (A_Li–S–Li), as shown in Fig. 13c, as the most effective descriptor. Subsequently, A_Li–S–Li was subsequently used to screen g-C₃N₄-loaded d- and p-block metal-center single atom catalysts with success. The specificity of A_Li–S–Li was also acknowledged by Song et al., and the impact of Li–S bond length on the Li₂S decomposition energy barrier was also examined in Fig. 13d.⁹⁷ It is evident that longer Li–S and larger angles demonstrate, as in the preceding study, lower decomposition energy barriers and thus higher catalytic activity.

In regard to the aforementioned validated structure descriptors, it can be observed that they predominantly encompass the structural characteristics of the catalyst itself, in addition to those pertaining to the adsorption structure of LiPSs. Obviously, the former is more readily obtainable but has a more limited scope of applicability. In contrast, the latter is not directly accessible but provides a more precise characterization of the energy barriers governing the decomposition of Li₂S. This is due to the fact that the core of SRR catalytic process is electron transfer within the active site, which poses a significant challenge to the comprehension of the reaction mechanism from a structural perspective. Hence, structural descriptors are rarely employed as reactivity descriptors in practical applications. Instead, they are usually integrated with electronic and energy descriptors to generate binary universal descriptors, which will be elaborated upon in the subsequent sections.

3.2 How the structural descriptors guide the experiments

In the extant literature, the structural descriptors predominantly consider the structural properties of the catalyst itself and the structural characteristics of the active sites subsequent to adsorption with LiPSs. Generally, the intrinsic structure of catalytic material is defined by readily accessible properties that can influence the adsorption of polysulfide intermediates through mechanisms such as spatial site resistance. However, the applicability and accuracy of these effects are limited. In practical projects, the impact of the structural characteristics of potential catalytic materials on the reaction activity can be evaluated on a case-by-case basis. This allows for the potential establishment of unique scalar relationships and the development of catalysts with the desired activity through lattice engineering. Incidentally, structural properties typically exhibit enhanced performance when integrated with other factors as multivariate descriptors.

4 Energy descriptors

The 16e⁻ SRR process in LSBs is characterized by the involvement of multiple steps and intermediates, which give rise to highly complex energy changes. Although the recognized rate-limiting step is the conversion between Li₂S₂ and Li₂S, the kinetic reaction paths for the conversion between the two are not deterministic for catalysts with different effects. Accordingly, it is usually necessary to construct multiple reaction paths in order to discriminate based on the energy differences. Therefore, the optimization of the energy during the catalytic conversion of LiPSs by catalysts represents an important basis for judging the catalytic activity. Nevertheless, it is evident that the conventional methodologies for energy determination are inadequate for the large-scale development of catalysts. Fortunately, with the advancement of computer simulation technology and the enhancement of computational capabilities, the energy changes during the SRR were investigated using HTC with ML and employed as a reactivity descriptor for the catalytic process, defined as the energy descriptor.

4.1 Key energies in the SRR

The energy descriptors that have been the subject of investigation are primarily Gibbs free energy changes occurring before and after the reactions of a range of pivotal intermediates. Wu et al. carried out a comprehensive thermodynamic analysis of the catalytic SRR process in non-metallic graphene-based nitrogen atom doped materials, introducing −ΔG_ad(LiS) as an effective catalyst, which represents the Gibbs free energy change before and after the adsorption transformation of LiS intermediates.⁹⁸ Fig. 14a illustrates a comprehensive volcano plot between the descriptor ΔG_ad(LiS) and the total Gibbs free energy (ΔG) of the SRR. This plot allows for the straightforward determination of a ΔG_ad(LiS) value of approximately −1.72 eV, which serves as an indicator of a high-quality catalyst for the purpose of screening and prediction of non-metallic single atom catalysts. With regard to transition metal single atom catalysts, Zhang et al. devised the adsorption energies of the intermediates *LiS and *LiS₂ as descriptors for the purpose of predicting the reaction pathways, reaction steps and overpotentials.¹⁴⁶ Fig. 14b and c illustrate the BEP relational volcano plots constructed for *LiS₂ and *LiS, which demonstrate the equilibrium potential E⁰ = 1.66 V for the conversion of Li₂S₃ to Li₂S/Li₂S₂ at this potential. This potential exhibits an optimal adsorption energy for the reaction and a higher catalyst activity. In accordance with the aforementioned guideline, Ti single-atom catalysts exhibiting optimal performance and a coordination environment of P₁N₃ was identified and validated. Subsequently, Shou et al. constructed a two-dimensional activity volcano plot for the MXene-catalyzed SRR process using ΔG(*Li₂S) and ΔG(*LiS) as illustrated in Fig. 14d and employed HTC to screen and identify potential catalysts from 420 types of MXenes.⁹⁹ It was found that ΔG(*Li₂S) in area 1 and area 2 are similar, however, there was a rapid increase in catalytic activity with a decrease in ΔG(*LiS), indicating that the limiting factor in activity is ΔG(*LiS). Furthermore, the authors extended a new one-dimensional density of states electronic fingerprint similarity as a reactivity descriptor for the catalytic conversion of LiPSs, based on the energy descriptor, which achieved a screening accuracy of 93%. Boteju et al. also employed the Gibbs free energy change of the intermediate state *LiS as a pivotal descriptor, devising a volcano scaling relationship with the thermodynamic overpotential (Fig. 14e), which aided the systematic screening and assessment of the catalytic activity of diverse MXene structures.¹⁰⁰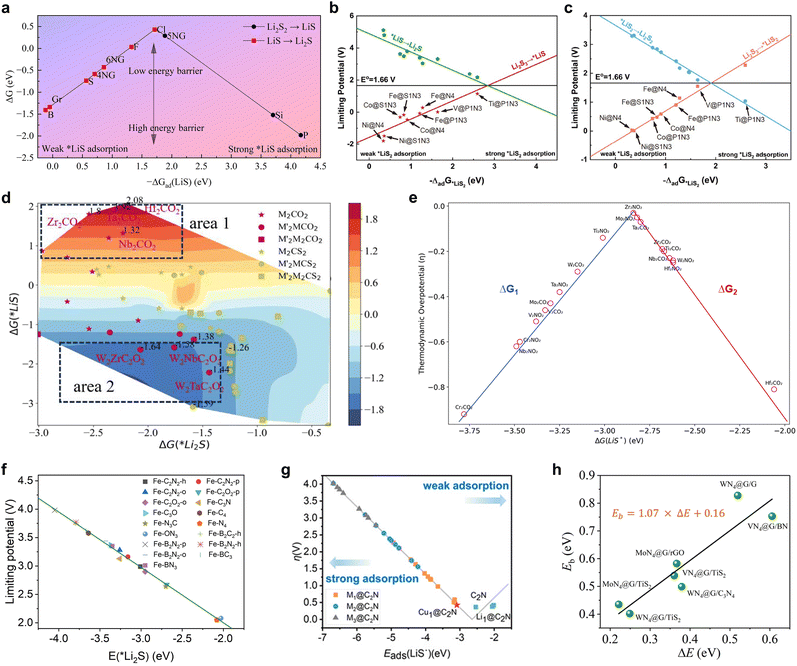

Fig. 14 (a) Catalytic performance volcano plot with respect to ΔG_ad(LiS). Reproduced with permission. Copyright 2024, American Chemical Society.⁹⁸ (b) Limiting potentials for the *LiS associated reaction pathways in the Li₂S₃RR. (c) Limiting potentials for the *LiS₂ associated reaction pathways in the Li₂S₃RR. Reproduced with permission. Copyright 2024, Springer.¹⁴⁶ (d) Two-dimensional (quasi) activity volcano plot for the SRR process, shown with two independent descriptors: ΔG(*Li₂S)and ΔG(*LiS). Reproduced with permission. Copyright 2024, American Chemical Society.⁹⁹ (e) Volcano plot between the thermodynamic overpotential and the reaction Gibbs free energy. Reproduced with permission. Copyright 2024, American Chemical Society.¹⁰⁰ (f) Linear relationship between Li₂S adsorption energies and limiting potentials. Reproduced with permission. Copyright 2024, Wiley-VCH.¹⁰¹ (g) Volcano relationship between the overpotential in the SRR process and the adsorption energy of LiS˙ on various substrates (including C₂N, Li₁@C₂N, Cu₁@C₂N, etc.). Reproduced with permission. Copyright 2024, American Chemical Society.¹⁰² (h) Calculated values of E_b using the CI-NEB method (green balls) for representative heterostructures as a function of ΔE. Reproduced with permission. Copyright 2024, The Royal Society of Chemistry.¹⁰³

In addition to the Gibbs free energy, which is closely related to the reaction thermodynamics, the energy descriptors involved in the LiPS reduction process are the adsorption energies of the key intermediates. While the adsorption energy of LiPSs is typically combined with the BEP relationship as a key indicator of catalytic activity when using electronic descriptors, structural descriptors, and so forth, the adsorption energy itself is also a highly accurate descriptor of reactivity. For instance, Yuan et al. employed the adsorption energy of Li₂S as a reactivity descriptor in their study of iron–nitrogen functional graphene catalysts with different coordination environments, which demonstrated a high correlation with the confinement potential in the SRR (Fig. 14f).¹⁰¹ Not only modifying the coordination environment, but altering the metal center represents an effective strategy for modulating catalytic activity. Chen et al. conducted a comprehensive investigation into the chemical mechanisms and catalytic dependence of single-, double- and even triple-atom catalysts loaded on C₂N (M_n@C₂N, where M is a transition metal atom and n = 1–3) as a model to investigate the pivotal stages of the SRR process.¹⁰² Fig. 14g illustrates the inverted volcano relationship between the adsorption energy of the intermediate LiS and the overpotential of the process, which unmistakably demonstrates the superiority of monoatomic catalysts. As a result, Cu₁@C₂N was selected due to the lowest overpotential of 0.426 V compared to other catalysts and this criterion provided guidance for the screening of SRR catalysts. Furthermore, Liang et al. defined the locally applicable energy descriptor ΔE = E(*Li + *LiS) − E(*Li₂S), which was applied to several N₄-coordinated monatomic catalysts.¹⁰³ As shown in Fig. 14h, ΔE demonstrates a favorable linear scaling relationship with the Li₂S decomposition energy barrier (E_b), thus offering a novel perspective on the emergence of new energy descriptors. Indeed, the activity of catalysts in multiphase catalysis is synergistically governed by a variety of electronic and structural factors, which are ultimately mapped onto the energy change of the process.

4.2 How the energy descriptors guide the experiments

Energy descriptors are distinct from electronic and structural descriptors in that they are intrinsic properties of chemical reactions, consequently ensuring a high degree of accuracy. As previously stated, the LiS intermediate adsorption energy, the Gibbs free energy change, and the Li₂S decomposition energy are crucial parameters for evaluating the adsorption and catalytic conversion activity of LiPSs. In the study of energy descriptors, strict linear or volcano-like scalar relationships are typically obtained, which is crucial for the screening and prediction of highly active catalysts. Nevertheless, the acquisition of energy data for the SRR, catalyzed by a multitude of diverse catalysts, is a more arduous and resource-intensive process than the other two descriptors. Due to their excellent accuracy and high inaccessibility, energy properties are frequently employed as activity criteria in descriptor studies, making significant contributions to the field.

5 Binary descriptors and others

Despite the encouraging outcomes observed in SRR catalysis studies using the aforementioned electronic, structural and energy descriptors, they have not yet surpassed the constraints of single-property descriptors and the inaccuracy that persists in certain instances. This is precisely due to the fact that catalytic activity is influenced by a multitude of factors, making it a formidable challenge to accurately describe or predict activity based on a single feature. Fortunately, the advancement of computer technology has prompted some studies to point out that the application of HTC and ML techniques can effectively identify the constitutive relationships of catalyst ensembles and ascertain the various features influencing the catalytic performance. This, in turn, enables the construction of a multi-feature descriptor, also known as a binary descriptor, following comprehensive analysis.^147–149

5.1 Highly integrated binary descriptor

To date, binary descriptors have either been composed of different electronic properties or a combination of electronic properties and structural features. As illustrated in Fig. 15a, Fang et al. established a correlation between the local chemical reactivity of MXene materials and the p-band centers (ε_p) of the terminals, as well as the Pauli electronegativity¹⁵⁰ (χ_m) of the subsurface transition metals.¹⁰⁸ They proceeded to construct a binary descriptor, X = ε_p + χ_m, and successfully obtained thousands of MXene data points by utilizing the HTC technique, thereby fitted the scaling relationship between X and the energy criterion. It is clear that an elevated X value is indicative of a greater reaction driving force (ΔG), which can be employed to identify high-activity catalysts (green area), such as Sc₂CS₂, Ti₂CS₂, and so forth. Impressively, the R² value of 0.78 for the scalar relationship fit with X as the reactivity descriptor is considerably higher than the R² values for the p-band center and p–d band center fits, which are 0.59 and 0.66, respectively. In contrast to the construction of binary descriptors through the straightforward summation of ε_p and χ_m, Shen et al. leverage machine learning algorithms to develop innovative composite electronic feature quadratic function descriptors, thereby offering fresh insights into the formulation of binary universal descriptors.¹⁰⁷ The researchers investigated the intrinsic d–p coupling at the center of the metal by means of a Hamiltonian model constructed with a single-atom catalyst, and found that the d–p coupling strength λ (λ = ε_p/ε_d) describes the wavefunction overlap and that the larger λ is, the larger the wavefunction overlap is in the vicinity of the Fermi energy level. Therefore, λ is more representative as a descriptor than ε_p and ε_d (Fig. 15c). Subsequently, utilizing λ as a physical parameter and integrating it with the ML algorithm, a distinctive descriptor in the format of β₀ + β₁λ + β₂λ₂ + ε is devised, which demonstrates a definitive scalar correlation with the Gibbs free energy of LiPSs transformed into a decisive velocity step. The establishment of this descriptor not only provides a novel method for the screening of Li–S battery catalysts, but also elucidates the physical nature of the SRR kinetics by effectively providing a generic description of the LiPS conversion during the construction process.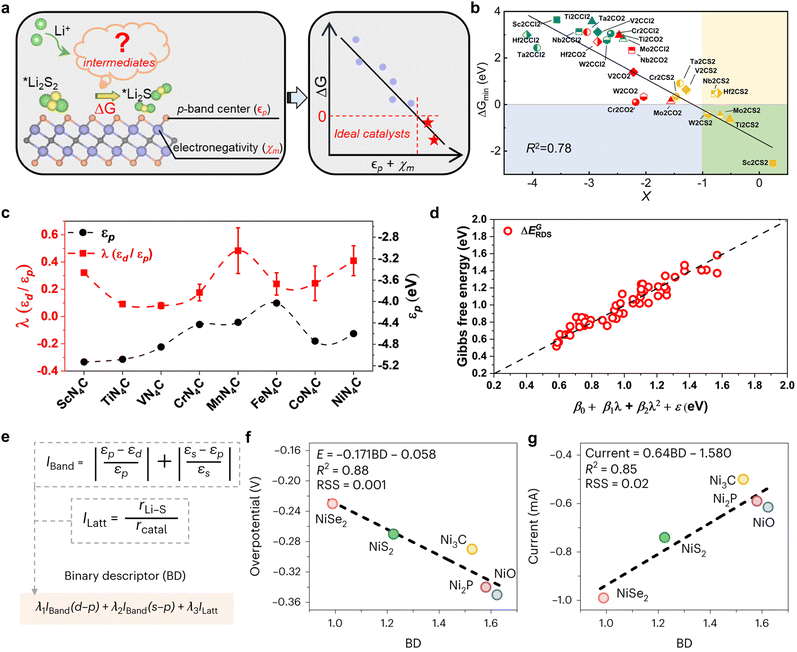

Fig. 15 (a) Relationship between descriptors based on p-band centers and electronegativity construction and the energy criteria for LiPS conversion. (b) Scaling relationship between ΔG_min and descriptor X. The MXenes in the green area are ideal electrocatalysts in the model. Reproduced with permission. Copyright 2023, American Chemical Society.¹⁰⁸ (c) The calculated ε_p and the corresponding λ of the TMNCs system, which are approximately obtained from the DOS calculation. (d) The relationship curve fitting between descriptors obtained from the quadratic polynomial algorithm and Gibbs energy barriers l is a physical quantity associated with ε_d/ε_p, Δd, ΔE_ion, M_ratio, and R_ratio; β₀, β₁, β₂ and ε are the coefficients corresponding to the quadratic polynomial fitting. Δd denotes the vertical nearest distance between metal and non-metal atoms; the electronic structural information of the metal is characterized by the metal's first ionization energy ΔE_ion; the mole mass ratio and atomic radius ratio between metal and non-metal atoms are represented by M_ratio and R_ratio, respectively. Reproduced with permission. Copyright 2024, The Royal Society of Chemistry.¹⁰⁷ (e) Development of the BD simultaneously considering electronic and structural effects. I_band and I_latt are dimensionless, and hence BD is also dimensionless. (f) and (g) Linear regression fitting between the overpotential (f) and peak current (g) and the BD. Reproduced with permission. Copyright 2023, Springer Nature.¹⁰⁹

While the above binary descriptors based on electronic properties have demonstrated a high degree of accuracy in the study of MXene or single-atom catalyst materials, the incorporation of binary descriptors for structural properties is expected for catalyst species that are more structure-dependent, such as transition metal compounds. As illustrated in Fig. 15e, Han et al. captured the electronic and structural contributions of the Ni-based catalytic system and designed a binary descriptor for the catalytic transformation of polysulfides, comprising energy band matching (I_band) and lattice mismatch (I_latt) indices, through the use of ML for the purpose of design assistance. The coefficients λ₁, λ₂ and λ₃ of the linear combination in the binary descriptor expression indicate the relative weights of the electronic and structural effects, while the presence of the parameters ensures the accuracy and generality of the model. Following machine learning to solve the deterministic coefficients using genetic algorithms and Monte Carlo simulations on small samples of experimental values of overpotential iteratively, a potential solution is obtained as follows:

The optimal solution, as determined by the binary descriptor, yields R values of 0.88 and 0.85 in the linear scaling relationship with the overpotential and peak current, respectively. These values are significantly higher than the fitting accuracy of the electronic or structural parameters alone. Furthermore, the elevated coefficient of the structural feature identified by I_latt underscores its significance for catalytic activity, as it correlates with the reaction energy barrier and diffusion resistance. Ultimately, an array of applicability tests on non-nickel-based catalysts substantiated the superior performance of binary descriptors in reorienting the design of catalysts for Li–S batteries.

In conclusion, the thoughtful consideration of factors affecting catalytic activity and the rigorous construction of binary descriptors render them more applicable than single-property descriptors. They are therefore competitive candidates for the design of universal descriptors for catalytic materials. In particular, binary descriptors are well suited to computer technology, and the two complement each other, thus accelerating the design of universal reactivity descriptors.

5.2 Descriptors based on electrochemical principles

In Li–S batteries, the catalytic process of sulfur reduction is not the sole mechanism at play; electrochemical reactions also play a role. Therefore, it is prudent to consider the design of reactivity descriptors from an electrochemical perspective. In the case of biomass catalysts comprising intricate functional groups, it is challenging to ascertain the electronic and structural characteristics. Consequently, the elucidation of catalytic descriptors from electrochemical reaction processes is of paramount importance. Dong et al. synthesized β-CD@CoPC mimetic catalysts for LSBs by injecting cobalt-sulfonated phthalocyamine (CoPC) into β-cyclodextrin (β-CD) cavities, and employed one of the most prevalent models of enzyme kinetics in biochemistry, the Michaelis–Menten equation, which is typically represented as V = V_max × [S]/(K_m + [S]).¹⁰⁵ The equation is derived from standard UV-vis spectra, wherein the Michaelis constant K_m, a pivotal parameter, corresponds to the substrate concentration at half-saturation and serves as a measure of the binding affinity of the substrate for the enzyme (Fig. 16a). A lower K_m value indicates tighter binding between the substrate and the enzyme, whereas a higher K_m value suggests looser binding.^151–153 In accordance with the Lambert–Beer law, the equations and the value of the equilibrium constant (K_m) can be refined following the acquisition of the instantaneous concentration of polysulfides and the reaction rate at each potential. The fitting results demonstrate a perfect fit, indicating that the dynamic structural evolution of the β-CD@CoPC catalyst facilitates the transfer and conversion of LiPSs. This further identifies the Michaelis constant K_m as a key descriptor of the enzyme activity of the mimetic catalyst in LSBs. It is noteworthy that Geng et al. highlighted the pivotal function of the electric double layer (EDL) region in the SRR process.¹⁰⁶ Specifically, the robust binding of polysulfides to the catalyst surface results in the disruption of EDL, which in turn causes a rapid decline in catalyst efficiency. In order to quantify the competitive adsorption of sulfur species in EDLs, the study proposes the introduction of an experimentally measurable competitive adsorption factor (f_sulfur, which can be obtained by ) and suggests an alloying method to modulate f_sulfur by enhancing the p–d hybridization of the alloying metal with the electrolyte solvent. As illustrated in Fig. 16b, the SRR kinetics were enhanced for Co–Zn alloy catalysts with a reduction in Zn content. This was due to an increase in adsorption strength and an improvement in electron transfer efficiency for LiPSs. Nevertheless, when a specific f_sulfur threshold was surpassed, the rise in f signified an excess of sulfur adsorption, which resulted in the disruption of the electric double layer (EDL) and impeded the mass transfer and desorption of polysulfides. This type of volcano-like scaling relationship demonstrates the potential of the competing adsorption factor f_sulfur as a reactivity descriptor. Furthermore, as can be derived from the electrochemical mechanism, it exhibits excellent theoretical universality.

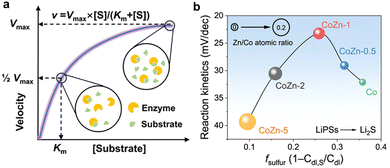Fig. 16 (a) The rectangular hyperbola exemplified by the Michaelis–Menten equation. K_m as the substrate concentration at which the curve attains half of the maximum rate. Reproduced with permission. Copyright 2024, Wiley-VCH.¹⁰⁵ (b) The volcano-type relationship between sulfur and the kinetics of the LiPSs-to-Li₂S reaction. Reproduced with permission. Copyright 2024, Wiley-VCH.¹⁰⁶

6 AI for reactivity descriptors

The 2024 Nobel Prize, a global phenomenon, was bestowed upon Geoffrey E. Hinton, the pioneering figure in the field of artificial intelligence, further substantiating the assertion that AI has catalyzed a significant transformation in the scientific investigation of humanity. From the perspective of the materials research paradigm in Fig. 17, the field has undergone three distinct phases: experimental science, theoretical science, and computational science. With the advent of the artificial intelligence era, the integration of big data of materials information with AI is emerging as the fourth paradigm, i.e. the research hotspot of AI for Materials Science.^154–156 In the field of SRR electrocatalysis in LSB, machine learning algorithms can efficiently identify proportional relationships between catalytic performance and key reactivity descriptors by utilizing experimental data from high-throughput experiments and computational data from simulations (e.g., DFT).^157,158 Furthermore, the machine learning research model is capable of identifying the most accurate descriptors from a vast array of potential descriptors, thereby enabling the development of automated catalyst screening workflows and significantly reducing the financial and temporal costs associated with research. In addition, the rapid advancement of large language models will lead to an enhancement in the pattern recognition abilities of AI, thus accelerating the development process of catalytic materials.^159,160

Fig. 17 The evolution of the materials research paradigm.

6.1 AI-assisted screening and prediction of catalysts

Fig. 18a presents the four-step workflow for machine learning-assisted catalyst development proposed by Han et al.,¹⁰⁹ which mirrors the general steps of the research model: (i) feature extraction, which involves obtaining basic multidimensional features from a database, including electronic features, structural features, and other relevant factors of the catalyst. (ii) Training data: the requisite database for training is obtained through experimental and theoretical calculations. (iii) Determination of descriptors: the effects of various input parameters on catalytic activity are evaluated by well-established machine learning algorithms, such as genetic algorithms and Monte Carlo simulations, in order to identify the most important descriptors or to determine the coefficients of the predefined descriptors. (iv) Validation: predict high-performance catalysts using the scalar relationships obtained by ML and validate them in experiments.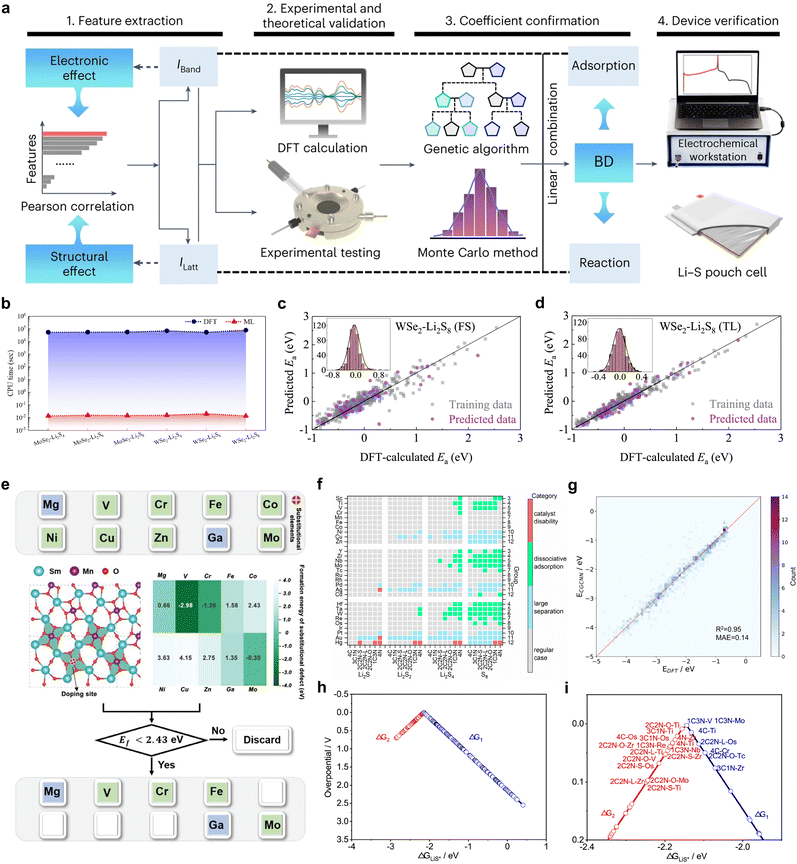

Fig. 18 (a) The overall workflow diagram, showing the steps of feature extraction, experimental and DFT analysis, coefficient confirmation and device verification. Reproduced with permission. Copyright 2023, Springer Nature.¹⁰⁹ (b) Comparison of CPU computational time for MoSe₂/WSe₂ towards three lithium polysulfides. (c) and (d) Correlation plots of binding energy against DFT and ML, along with histograms of error distributions between DFT and ML. (c) was obtained by FS training, while (d) was obtained by TL training. Reproduced with permission. Copyright 2021, Elseiver.¹⁶¹ (e) The flowchart of screening the substitutional elements. Reproduced with permission. Copyright 2022, Wiley-VCH.¹⁶² (f) Categories of adsorption configurations based on 812 data points. The gray block represents the regular case (C1); the blue, the large separation (C2); the green, the dissociative adsorption (C3); and the red, catalyst disability (C4). (g) Two dimensional histograms of DFT calculated and ML predicted adsorption energy of LiPSs. The color scale is used to illustrate the magnitude of number in samples. (h) Volcano plots for all catalysts. (i) Volcano plots for catalysts with an overpotential lower than 0.1 V. Reproduced with permission. Copyright 2021, American Chemical Society.¹⁶³

The efficiency of machine learning has been markedly enhanced in comparison to the third paradigm's direct utilization of computer simulation techniques. In a study conducted by Zhang et al., the use of machine learning to predict the binding energy upon uptake of LiPSs in MoSe₂ as a sulfur host yielded results six orders of magnitude faster than those obtained through DFT (Fig. 18b).¹⁶¹ In detail, the from scratch (FS) training utilizing DFT to predict Li₂S₈ binding energy outcomes are contrasted with the results of the migration learning approach in conjunction with machine learning, as illustrated in Fig. 18c and d. In this AI-assisted binding energy prediction model, the researchers employ the local environment matrix from the DeePMD-kit program as a descriptor. This descriptor is then used as an input vector for the artificial neural network, which is operated to output the predicted value of the adsorption energy of LiPSs. The histograms of Gaussian distributions with a non-zero median in the inset demonstrate that the average absolute errors of the latter training and prediction data are merely 0.07 eV and 0.1 eV, which is only half of the error of the results of the FS approach. This serves to exemplify the unrivalled competitiveness of machine learning in the prediction and screening of Li–S battery catalysts.

Nevertheless, in the context of limited sample sizes, computational simulation techniques such as DFT continue to represent a valuable supplementary approach to ML, facilitating the generation of the datasets necessary for algorithmic operations. In the study of SmMn₂O₅-catalyzed SRR, Wang et al. employed DFT calculations in conjunction with interpretable machine learning to analyze descriptors related to electronic features and polysulfide binding energies with a view to identifying suitable doping elements in a process illustrated in Fig. 18e.¹⁶² Specifically, the non-linear operator applied in supervised learning algorithm sure independent screening and sparse Operator (SISSO) operates on a combination of multiple feature parameters to construct a doping element screening framework and predict the catalytic activity after doping. By establishing a defect formation energy threshold of no greater than 2.43 eV and utilizing an algorithm to evaluate the defect energies of disparate dopant elements calculated by DFT, six optimal metal elements, such as Mg and Ga, etc. were preliminary identified to substitute the Mn atoms within the octahedral ligand unit. Further SISSO studies show that charge transfer, electronegativity differences and the figure of merit jointly determine the binding strength of Li₂S₄, with Mg elemental doping exhibiting the optimal predicted value. The processing of limited data, such as that pertaining to defective mullite, can be efficiently conducted directly using DFT-assisted ML. In contrast, high-throughput-assisted machine learning is a necessary approach for the processing of candidate catalysts with a large space of structural variations. In the case of combinations of single-atom catalysts and elementally doped carbon materials, the conventional trial-and-error methods and conventional DFT calculations are no longer sufficient. Therefore, Lian et al. proposed a ML model based on high-throughput computing to screen loaded SACs on nitrogen-doped carbon.¹⁶³ As demonstrated in Fig. 18f, the researchers categorized the adsorption configurations of the four polysulfide molecules (Li₂S, Li₂S₂, Li₂S₄ and S₈) on the 203 SAC catalysts into four distinct categories, comprising the conventional case (C1, 607), the large separation (C2, 100), the dissociative adsorption (C3, 94), and catalyst failure (C4, 11). These categories exhibited notable differences in terms of their bonding sites, bond lengths of the binding site, and other characteristics. Subsequently, the 812 data points from high throughput DFT calculations were employed as the training, validation, and test set for the machine learning algorithm, operating within the framework of the crystal graph convolutional neural networks (CGCNNs), for the purposes of classification and regression. The regression results presented in Fig. 18g demonstrate a mean absolute error (MAE) of 0.14 for the entire dataset, which evinces a high degree of robustness. The regression model generated through ML was employed to predict the adsorption energies of several LiPSs (e.g., LiS, Li₂S₃, Li₂S₅, Li₂S₇, etc.) that were initially excluded from the training set. The MAE of the model also remained consistent with the scaling relationship of the regression model, indicating reliable predictive ability. Ultimately, the potential-limiting step was identified as either G1 or G2, based on the substantial data predicted by the regression model and the adsorption energy of the pivotal intermediate LiS. This conclusion is supported by the volcano diagram, as illustrated in Fig. 18h. Furthermore, a scaling relationship between specific SAC and overpotential was prepared (Fig. 18i), which also exhibited a strictly volcanic character. Based on the Fig. 18i screening, V, Mo, Ti, Zr, and Os were identified as the most promising SACs, as they are located at the top of the volcano curve and produce very small overpotentials.

In recent years, there has been considerable success achieved with AI-assisted catalyst design models relying on reactive descriptors. However, it should be noted that descriptors are not the sole link between artificial intelligence and catalyst research. The efficacy of graph neural network (GNNs) algorithms for the analysis of generalized graph data, including recurrent graph neural networks (RecGNNs), convolutional graph neural networks (ConvGNNs), and graph autoencoders (GAEs), has been demonstrated in the context of accurately identifying active sites of catalysts and determining activity differences without reliance on descriptors.^164–166 Consequently, the integration of diverse algorithms for processing graph data and descriptor-activity matrix data is anticipated to further propel the advancement of artificial intelligence-assisted catalyst design research paradigms, to promote SRR catalytic mechanism studies, and to drive the development of high-activity catalysts.

6.2 AI-assisted quantitative determination of precise descriptors

In light of the above, machine learning offers a promising solution for the processing and modelling of large amounts of data obtained through experiments and simulations. With the assistance of suitable descriptors, it enables the efficient prediction and design of novel catalysts, thereby rendering fully automated catalyst design a realistic prospect in the near future. Furthermore, in the context of the growing volume of data, the selection of appropriate descriptors can be facilitated through the automated extraction of relevant features, such as Pearson correlation coefficient (PCC), from extensive data sets. The application of statistical tools, such as correlation heat maps, to evaluate the precision of diverse potential descriptors has the potential to yield more robust descriptors of reactivity when sufficient data is available.

In a comprehensive investigation of 3d transition metal-embedded nitrogen-doped defective black scale carbide (TM@N₄-CP) single-atom catalysts, Xia et al. proposed a virtual four-step screening strategy to evaluate the potential influence of finite candidate structures on SRR kinetics (Fig. 19a).¹⁶⁷ Following the acquisition of the properties of E_a(LiPSs), ICOHP, and so forth, for a series of TM@N₄-CP through DFT calculations, PCC was employed to analyze the correlation between the two features, and the PCC of the two variables (X, Y) is defined as , where cov denotes the covariance and σ represents the standard deviation. A P-value of 1 or −1 corresponds to a strong positive or negative correlation, respectively. As illustrated in Fig. 19b and c, the adsorption energies of the majority of intermediates at the catalytic site exhibited a robust linear correlation, with a particularly strong correlation between φ and E_a(*S) (P = 0.85). In addition, both rate-determining step (RDS) and E_barrier demonstrated a positive correlation with ICOHP_TM–S and E_a(*Li₂S), with P-values of 0.86, 0.95, 0.94 and 0.86, respectively. Conversely, B(Li₁–S) exhibited a negative correlation with RDS and E_barrier, with P-values of −0.90 and −0.95, respectively. Ultimately, the ICOHP value of the TM–S bond and the adsorption energy of the intermediate *Li₂S were established as descriptors of the SRR reaction kinetics through the heat map analysis of numerous key parameters, which provided a feasible strategy for the rational retrieval of the defining characteristics of the LSB active catalysts. More generally, Wu et al. also conducted a comprehensive examination of the capacity of the 16 potential descriptors to predict the Li₂S decomposition energy E_b through the utilization of the PPC matrix heatmap illustrated in Fig. 19d within the SACs study.⁹⁶ Their findings demonstrated that A_Li–S–Li and ΔQ_TM exhibited the most pronounced negative and positive correlations, respectively, with E_b. In light of the pivotal role played by the adsorption energy of lithium polysulfide, Wang et al. posited Li₂S₄ as a benchmark and delved into the interrelationship between individual properties and the adsorption energy of Li₂S₄, calculating the PCCs of the eight features illustrated in Fig. 19e.¹⁶² Among the aforementioned properties, the d-band center (ε_d) and Bader charge (Q_M) of the elementally doped defective SmMn₂O₅ active metal site exhibited the lowest positive correlation coefficient (PCC) and the weakest correlation with the binding energy. Furthermore, radargram analysis (Fig. 19f) revealed a strong positive correlation between the Bader charges of Li atoms (Q_Li) and a strong negative correlation between the Bader charges of O atoms (Q_O) and the binding energy. The corresponding P-values were 0.77 and −0.77, respectively. The authors then employ a compressed stem-knowledge interpretable ML algorithm that identifies the sure independence screening and sparsifying operator, combines these strongly correlated parameters, and proposes novel physically meaningful mathematical models as descriptors:

E_b = k₁ × (Q_Li + Q_O) + k₂ × [(Q_s + Δ_x) − WF] + k₃

where k₁, k₂, and k₃ are 56.304, −0.943, and −397.02, respectively. Moreover, Qi et al. employed graphene/electrode heterostructure loaded single atoms as SRR catalytic materials and discovered that the van der Waals (vdW) interactions of the LiPS intermediates also determine the strength of their binding to the active site.¹⁶⁸ In evaluating this correlation using PCC, the researchers found that vdW is a more compelling descriptor than ICOHP_TM–S, a traditional measure, as evidenced by the higher PCC values and R² of the linear regression shown in Fig. 19g.

Fig. 19 (a) Schematic diagram of the virtual four-step strategy for SAC screening in LiSBs. (b) and (c) Heatmaps of the Pearson correlation coefficient matrix of the related descriptors with (b) the adsorption energy of S₈/LiPSs, and (c) RDS and E_barrier. Reproduced with permission. Copyright 2023, Elseiver.¹⁶⁷ (d) Heatmaps of the Pearson correlation coefficient matrix. The values on the heatmap are the PCCs between the corresponding two parameters. Reproduced with permission. Copyright 2024, Wiley-VCH.⁹⁶ (e) and (f) The correlation (Pearson correlation coefficient) between a single parameter and the binding energy of Li₂S₄. Reproduced with permission. Copyright 2022, Wiley-VCH.¹⁶² (g) Linear correlations of the RDS and E_barrier with the ICOHP and the vdW ratio of S₈. Reproduced with permission. Copyright 2023, Elseiver.¹⁶⁸

In brief, the substantial quantity of data yielded by machine learning or high-throughput data, when integrated with statistical tools, enables the quantitative assessment of the precision of candidate descriptors, thereby accelerating the development of accurate and comprehensive generic SRR descriptors.

7 Summary and outlook

The sluggish solid-state redox kinetics and the catastrophic lithium polysulfide shuttle effect remain the main bottlenecks that impede the practical implementation of lithium–sulfur batteries. Consequently, the rational design and development of catalytic materials with optimal electrocatalytic activity, moderate adsorption strength, environmentally benign characteristics, and long-term stability have emerged as pivotal objectives in the scientific community's pursuit of high-energy-density and durable lithium–sulfur batteries. Recent advances in reactivity descriptor theory have emerged as a transformative paradigm, enabling mechanistic elucidation of LiPS conversion pathways and accelerating ab initio catalyst development. This review systematically examines multiphase catalytic mechanisms in sulfur reduction reaction, with particular emphasis on established catalyst archetypes. We additionally discuss the correlations between different descriptor categories (electronic, structural, energetic, and binary descriptors) and critical polysulfide intermediates, while mapping their applicability boundaries between catalyst species and multiple descriptors to guide future research trajectories. Furthermore, we explore the integration of descriptor theory with artificial intelligence frameworks for next-generation catalyst discovery.

Despite the cross-disciplinary synergies between the SRR and related electrocatalytic processes (OER, ORR, NRR, and beyond), the identification of precise and comprehensive descriptors to elucidate the distinctions in catalytic properties and to inform the design of catalysts remains an open scientific challenge. On the one hand, reactive descriptors exhibit limited transferability due to their dependence on the specific atomic composition and spatial structure of the catalyst. Generating universal fusion descriptors iteratively using a single property requires advanced technologies such as reliable databases and machine learning. On the other hand, after establishing a linear or volcano-shaped scaling relationship between precise descriptors and catalytic activity, the challenge lies in experimentally realizing the prediction of highly active catalysts based on scaling relationships, even surpassing activity thresholds, to expand a more comprehensive catalytic perspective. Achieving these objectives necessitates a considerable investment of effort, with a particular focus on the following areas.

7.1 Establishing catalyst-descriptor correspondence frameworks

Current LSB studies have proposed a number of valuable descriptors, including the d-band center theory, e_g-orbital occupancy, spin-state configurations, and so forth. However, for a wide variety of catalysts, they are typically applicable to only one or some descriptors. Hence, elucidating the correlation between catalyst types and descriptors can offer intuitive guidance for subsequent studies. To this end, we further classified the descriptors and corresponding catalyst types that have been validated in Li–S batteries in recent years, as illustrated in Fig. 20. Our analysis reveals that most descriptors demonstrate non-exclusive relationships with catalyst classes, necessitating appropriate corrections or pairing with other catalyst features in practice. For instance, in the utilization of the d-band center descriptor, it is occasionally essential to consider the energy polarity discrepancy with the p-band, or to integrate it with additional structural characteristics such as bond lengths, with the objective of achieving more precise screening and prediction of the target catalysts. While the Sankey diagram in Fig. 20 provides a preliminary catalyst-descriptor correspondence framework, its practical implementation demands rigorous validation through combinatorial experimental-computational approaches. Notably, descriptor development must address the inherent trade-off between universality and specificity across heterogeneous catalytic systems.

Fig. 20 Sankey diagram of correspondence between catalyst types and descriptors based on literatures.

7.2 Multidimensional descriptor engineering

In order to seek out universal SRR reactivity descriptors, it is essential to undertake a comprehensive examination of the electronic, structural, and energetic characteristics of catalytic reactions. Electronic features, such as d-band centers and electronegativity, play an important role in the mechanism of adsorption-conversion dynamics of LiPSs at a deeper level. In addition, structural features, such as bond lengths and bond angles, impact the LiPSs binding through the effect of spatial site resistance. Moreover, energetic features, such as Gibbs free energy and adsorption energy, serve as direct criteria for reactivity. These features act in concert to determine the activity of a catalyst. Therefore, to accurately characterize the catalytic activity, it is advisable to consider them collectively in order to construct a universal descriptor. Of course, there have also been attempts to provide a novel perspective on the electrochemical processes of Li–S batteries, which has involved the design of universal descriptors based on the Michaelis constant and the double electric layer, etc. In general, despite considerable efforts by researchers to develop universal multivariate descriptors and to identify scalar relationships with catalytic activity, most multivariate descriptors remain constrained by oversimplified linear scaling relationships. Accordingly, there is still considerable work to be done before a comprehensive and integrated universal descriptor can be developed to fully characterize catalytic activity in the SRR.

7.3 AI-driven descriptors discovery

The current rapid development of artificial intelligence technology has brought about a transformative research paradigm in materials research, in which machine learning, represented by active learning algorithms using big data, such as genetic algorithms, Monte Carlo simulation, support vector regression, and neural networks, has already made a significant impact in the field of computational catalysis. In particular, datasets generated by ML or HTC in conjunction with statistical methods, such as Pearson heat map analysis and regression model predictions, facilitate the quantitative identification of key descriptors that influence catalytic performance. Specifically, on the one hand when seeking a descriptor applicable to a specific catalytic system, ML can be integrated with statistical tools, such as Pearson's heat map, regression model, and others, to examine the influence of certain factors derived from databases, allowing for the identification of the optimal descriptor in a quantitative manner, which is of particular importance in the context of the SRR process, where a number of factors, including lattice parameter, electronegativity, number of electrons in the d-orbitals, and ionization energy, have the potential to impact catalytic activity. On the other hand, the validated reactivity descriptors are employed as algorithmic parameters to screen and predict novel potential catalytic materials for LSBs, e.g., through the utilization of DFT-trained ML models to predict the adsorption energies of LiPSs on emerging catalysts, ICOHP, and so forth, in order to evaluate the binding strengths and predict the catalytic performance. Notwithstanding the considerable advances made by ML algorithms in the field of catalytic descriptor research, the acquisition of extensive, high-quality databases is still a prerequisite for the training of reliable ML models. At the present time, the most viable methods for obtaining target datasets principally comprise small samples based on experimental values, datasets generated using high-throughput DFT computing, third-party datasets from extant literatures, and open-source data platforms such as open catalyst project (OCP),¹⁶⁹ catalysis-hub (CatHub),¹⁷⁰ and AlphaMat.^171,172 This necessitates substantial computational simulation or experimental work, which can be financially burdensome. Consequently, the comprehensive deployment of ML methodologies in catalysis necessitates the development of cost-effective algorithms, such as those based on multimodal few-shot learning models,¹⁷³ Monte Carlo tree search algorithms with policy gradients,¹⁷⁴ and multi-view machine-learned frameworks.¹⁷⁵

7.4 Breaking the scaling relationship of existing descriptors

As the saying goes, “Out with the old, in with the new.” The same is true for the scaling relationships established in existing SRR descriptor studies. In the event of a disruption to a scaling relationship, efforts are made to establish new scalar relationships, which can facilitate the comprehension of intricate catalytic mechanisms and the development of innovative catalysts. For instance, in linear or volcano-like scalar relationships obtained with a d-band center descriptor in transition metal oxides, the activity of the catalyst can be modified by heterogeneous elemental doping to generate points or regions of enhanced activity compared to those observed in the previous scalar relationship. Similarly, valuable means of overcoming the limitations of the scalar relationship include the use of surface strains, changing ligands, and external force fields. When attempting to establish new scaling relationships, it is important to take into consideration statistical reliability indicators such as the coefficient of determination, error bars and confidence intervals. Many current studies overlook this aspect, yet it is beneficial for quantitatively assessing the accuracy and applicability of scaling relationships. An accurate scaling relationship facilitates the screening and prediction of potential catalysts based on descriptors, while breaking this scaling relationship allows for the search for unknown temptations outside of the law, which seems to be more important in scientific exploration.

Author contributions

W. S. and Z. Y. conceived and designed the project. Z. Y. and Y. Z. carried out the literature research. Q. G. and Y. L. participated in useful discussions. W. S. and C. Z. directed the project. S. L. helped to polish the article. Z. Y. and W. S. co-wrote the manuscript with contributions from all authors.

Conflicts of interest

The authors declare no conflicts of interest.

Data availability

No primary research results, software or code have been included and no new data were generated or analyzed as part of this review.

Acknowledgements

The authors acknowledge the financial support from the high-level innovation talent training plan of the National University of Defense Technology.

Notes and references

1. A. Manthiram, Y. Fu, S.-H. Chung, C. Zu and Y.-S. Su, Chem. Rev., 2014, 114, 11751–11787.
2. Z. W. Seh, Y. Sun, Q. Zhang and Y. Cui, Chem. Soc. Rev., 2016, 45, 5605–5634.
3. G. Zhou, H. Chen and Y. Cui, Nat. Energy, 2022, 7, 312–319.
4. S. Zhou, J. Shi, S. Liu, G. Li, F. Pei, Y. Chen, J. Deng, Q. Zheng, J. Li, C. Zhao, I. Hwang, C.-J. Sun, Y. Liu, Y. Deng, L. Huang, Y. Qiao, G.-L. Xu, J.-F. Chen, K. Amine, S.-G. Sun and H.-G. Liao, Nature, 2023, 621, 75–81.
5. X. Hong, J. Mei, L. Wen, Y. Tong, A. J. Vasileff, L. Wang, J. Liang, Z. Sun and S. X. Dou, Adv. Mater., 2019, 31, 1802822.
6. P. G. Bruce, S. A. Freunberger, L. J. Hardwick and J.-M. Tarascon, Nat. Mater., 2012, 11, 19–29.
7. W. J. Chung, J. J. Griebel, E. T. Kim, H. Yoon, A. G. Simmonds, H. J. Ji, P. T. Dirlam, R. S. Glass, J. J. Wie, N. A. Nguyen, B. W. Guralnick, J. Park, Á. Somogyi, P. Theato, M. E. Mackay, Y.-E. Sung, K. Char and J. Pyun, Nat. Chem., 2013, 5, 518–524.
8. X. Ji, K. T. Lee and L. F. Nazar, Nat. Mater., 2009, 8, 500–506.
9. R. Liu, Z. Wei, L. Peng, L. Zhang, A. Zohar, R. Schoeppner, P. Wang, C. Wan, D. Zhu, H. Liu, Z. Wang, S. H. Tolbert, B. Dunn, Y. Huang, P. Sautet and X. Duan, Nature, 2024, 626, 98–104.
10. A. Bhargav and A. Manthiram, Energy, 2023, 1, 100012.
11. A. Bhargav, J. He, A. Gupta and A. Manthiram, Joule, 2020, 4, 285–291.
12. Y. V. Mikhaylik and J. R. Akridge, J. Electrochem. Soc., 2004, 151, A1969.
13. T. Zhang, M. Marinescu, S. Walus and G. J. Offer, Electrochim. Acta, 2016, 219, 502–508.
14. H. Pan, Z. Cheng, Z. Zhou, S. Xie, W. Zhang, N. Han, W. Guo, J. Fransaer, J. Luo, A. Cabot and M. Wübbenhorst, Nano-Micro Lett., 2023, 15, 165.
15. M. Wild, L. O’Neill, T. Zhang, R. Purkayastha, G. Minton, M. Marinescu and G. J. Offer, Energy Environ. Sci., 2015, 8, 3477–3494.
16. H. Ye, M. Li, T. Liu, Y. Li and J. Lu, ACS Energy Lett., 2020, 5, 2234–2245.
17. Y. Fu, Z. Wu, Y. Yuan, P. Chen, L. Yu, L. Yuan, Q. Han, Y. Lan, W. Bai, E. Kan, C. Huang, X. Ouyang, X. Wang, J. Zhu and J. Lu, Nat. Commun., 2020, 11, 845.
18. M. Zhao, B.-Q. Li, X. Chen, J. Xie, H. Yuan and J.-Q. Huang, Chem, 2020, 6, 3297–3311.
19. P. Wang, B. Xi, M. Huang, W. Chen, J. Feng and S. Xiong, Adv. Energy Mater., 2021, 11, 2002893.
20. G. Cai, H. Lv, G. Zhang, D. Liu, J. Zhang, J. Zhu, J. Xu, X. Kong, S. Jin, X. Wu and H. Ji, J. Am. Chem. Soc., 2024, 146, 13055–13065.
21. B. Song, L. Su, X. Liu, W. Gao, T. Wang, Y. Ma, Y. Zhong, X. Cheng, Z. Zhu, J. He and Y. Wu, Electron, 2023, 1, e13.
22. Q. Gu, Y. Qi, W. Hua, T. Shang, J. Chen, L. Jiang, L. Li, M. Lu, Y. Zhang, X. Liu, Y. Wan and B. Zhang, J. Energy Chem., 2022, 69, 490–496.
23. F. Han, Z. Wang, Q. Jin, L. Fan, K. Tao, L. Li, L. Shi, H.-Q. Lu, Z. Zhang, J. Li, X. Zhang and L. Wu, ACS Nano, 2024, 18, 15167–15176.
24. P. Zeng, C. Liu, X. Zhao, C. Yuan, Y. Chen, H. Lin and L. Zhang, ACS Nano, 2020, 14, 11558–11569.
25. X. Ren, Q. Wang, Y. Pu, Q. Sun, W. Sun and L. Lu, Adv. Mater., 2023, 35, 2304120.
26. N. Gao, Y. Zhang, C. Chen, B. Li, W. Li, H. Lu, L. Yu, S. Zheng and B. Wang, J. Mater. Chem. A, 2022, 10, 8378–8389.
27. M. Li, H. Wang, X. Wang, J. Ren and R. Wang, J. Mater. Chem. A, 2022, 10, 21327–21335.
28. Z. Qiao, F. Zhou, Q. Zhang, F. Pei, H. Zheng, W. Xu, P. Liu, Y. Ma, Q. Xie, L. Wang, X. Fang and D.-L. Peng, Energy Storage Mater., 2019, 23, 62–71.
29. Z. Li, I. Sami, J. Yang, J. Li, R. V. Kumar and M. Chhowalla, Nat. Energy, 2023, 8, 84–93.
30. C. Zhao, G.-L. Xu, Z. Yu, L. Zhang, I. Hwang, Y.-X. Mo, Y. Ren, L. Cheng, C.-J. Sun, Y. Ren, X. Zuo, J.-T. Li, S.-G. Sun, K. Amine and T. Zhao, Nat. Nanotechnol., 2021, 16, 166–173.
31. G. Zhou, H. Tian, Y. Jin, X. Tao, B. Liu, R. Zhang, Z. W. Seh, D. Zhuo, Y. Liu, J. Sun, J. Zhao, C. Zu, D. S. Wu, Q. Zhang and Y. Cui, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 840–845.
32. W. Sun, S. Liu, Y. Li, D. Wang, Q. Guo, X. Hong, K. Xie, Z. Ma, C. Zheng and S. Xiong, Adv. Funct. Mater., 2022, 32, 2205471.
33. S. Wang, R. Hu, D. Yuan, L. Zhang, C. Wu, T. Ma, W. Yan, R. Wang, L. Liu, X. Jiang, H. Liu, S. Dou, Y. Dou and J. Xu, Carbon Energy, 2023, 5, e329.
34. H. Zhang, M. Zhang, R. Liu, T. He, L. Xiang, X. Wu, Z. Piao, Y. Jia, C. Zhang, H. Li, F. Xu, G. Zhou and Y. Mai, Nat. Commun., 2024, 15, 5451.
35. H. Raza, J. Cheng, J. Wang, S. Kandasamy, G. Zheng and G. Chen, Nano Res. Energy, 2024, 3, e9120116.
36. X. Zhang, T. Yang, Y. Zhang, X. Wang, J. Wang, Y. Li, A. Yu, X. Wang and Z. Chen, Adv. Mater., 2023, 35, 2208470.
37. T. Wang, Q. Dong, F. Wang, R. Xu, C. Tong, D. Su, M. Shao, C. Li and Z. Wei, Matter, 2024, 7, 1035–1053.
38. L. Zhang, P. Liang, H. B. Shu, X. L. Man, X. Q. Du, D. L. Chao, Z. G. Liu, Y. P. Sun, H. Z. Wan and H. Wang, J. Colloid Interface Sci., 2018, 529, 426–431.
39. W. Sun, C. Liu, Y. Li, S. Luo, S. Liu, X. Hong, K. Xie, Y. Liu, X. Tan and C. Zheng, ACS Nano, 2019, 13, 12137–12147.
40. B. Zhang, L. Wang, B. Wang, Y. Zhai, S. Zeng, M. Zhang, Y. Qian and L. Xu, Nano Res., 2022, 15, 4058–4067.
41. K. Liao, A. Bhargav and A. Manthiram, ACS Appl. Energy Mater., 2023, 6, 9585–9593.
42. Q. Yang, X. Wei, X. Cao, L. Chen, L. Song, L. Kong, W. Sun, K. Xie and Y. Song, Chem. Eng. J., 2023, 452, 139638.
43. G. Chen, H. Li, Y. Wang, Y. Ding, P. Qian, K. Zhang, H. Zeng and G. Li, Batteries Supercaps, 2024, 7, e202400128.
44. J. Zhou, C. Shu, J. Cui, C. Peng, Y. Liu, W. Hua, L. Simonelli, Y. Wu, S. X. Dou and W. Tang, Carbon Energy, 2024, 6, e460.
45. Z. Wang, M. Feng, H. Sun, G. Li, Q. Fu, H. Li, J. Liu, L. Sun, A. Mauger, C. M. Julien, H. Xie and Z. Chen, Nano Energy, 2019, 59, 390–398.
46. Q. Zheng, Q. Hou, Z. Shu, G. Liu, X. Fan, K. Wang, J. Fan, R. Yuan, M. Zheng and Q. Dong, Angew. Chem., Int. Ed., 2023, 62, e202308726.
47. J. Li, Z. Wang, K. Shi, Y. Wu, W. Huang, Y. Min, Q. Liu and Z. Liang, Adv. Energy Mater., 2023, 14, 2303546.
48. W. Xia, Y. Chen, W. Wang, Y. Lu, Y. Chen, M. Chen and X. Yang, Chem. Eng. J., 2023, 458, 141477.
49. R. Xu, H. Tang, Y. Zhou, F. Wang, H. Wang, M. Shao, C. Li and Z. Wei, Chem. Sci., 2022, 13, 6224–6232.
50. W. Xia, Y. Chen, M. Han, X. Wu, H. Yang, K. Fu, M. Chen, X. Wang and H. Shu, Adv. Funct. Mater., 2024, 34, 2400262.
51. L. Chen, Y. Sun, X. Wei, L. Song, G. Tao, X. Cao, D. Wang, G. Zhou and Y. Song, Adv. Mater., 2023, 35, 2300771.
52. T. Zhang, L. Zhang and Y. Hou, eScience, 2022, 2, 164–182.
53. Y. Xiong, L. Jin, Q. Li, S. Hong, L. Liu, J. Li, J. Cai, Z. Yang, Z. Zhang and J. Yu, ACS Appl. Energy Mater., 2024, 7, 3718–3728.
54. J. Wang, W. Qiu, G. Li, J. Liu, D. Luo, Y. Zhang, Y. Zhao, G. Zhou, L. Shui, X. Wang and Z. Chen, Energy Storage Mater., 2022, 46, 269–277.
55. S. Jia, S. Zhao, Z. Xu, C. Ma, T. Yang, L. Pan, J. Liu, Y. Wang, T. Zhang, X. Sun, N. Liu, Y. Zhang and Z. Chen, Appl. Catal., B, 2024, 351, 124012.
56. W. Xu, S. Lang, K. Wang, R. Zeng, H. Li, X. Feng, M. R. Krumov, S.-M. Bak, C. J. Pollock, J. Yeo, Y. Du and H. D. Abruña, Sci. Adv., 2023, 9, eadi5108.
57. Q. Wu, K. Chen, Z. Shadike and C. Li, ACS Nano, 2024, 18, 13468–13483.
58. X. Sun, Y. Qiu, B. Jiang, Z. Chen, C. Zhao, H. Zhou, L. Yang, L. Fan, Y. Zhang and N. Zhang, Nat. Commun., 2023, 14, 291.
59. Y. Zhang, Energy Storage Mater., 2023, 63, 103026.
60. P. M. Attia, A. Grover, N. Jin, K. A. Severson, T. M. Markov, Y.-H. Liao, M. H. Chen, B. Cheong, N. Perkins, Z. Yang, P. K. Herring, M. Aykol, S. J. Harris, R. D. Braatz, S. Ermon and W. C. Chueh, Nature, 2020, 578, 397–402.
61. M. Meuwly, Chem. Rev., 2021, 121, 10218–10239.
62. Y. Zuo, M. Qin, C. Chen, W. Ye, X. Li, J. Luo and S. P. Ong, Mater. Today, 2021, 51, 126–135.
63. P. Friederich, F. Häse, J. Proppe and A. Aspuru-Guzik, Nat. Mater., 2021, 20, 750–761.
64. J. Fang, M. Xie, X. He, J. Zhang, J. Hu, Y. Chen, Y. Yang and Q. Jin, Mater. Today Commun., 2022, 33, 104900.
65. V. L. Deringer, M. A. Caro and G. Csányi, Adv. Mater., 2019, 31, 1902765.
66. J. Greeley, T. F. Jaramillo, J. Bonde, I. Chorkendorff and J. K. Nørskov, Nat. Mater., 2006, 5, 909–913.
67. Z. Zhang, P. Ma, L. Luo, X. Ding, S. Zhou and J. Zeng, Angew. Chem., Int. Ed., 2023, 62, e202216837.
68. X. Sun, R. B. Araujo, E. C. Dos Santos, Y. Sang, H. Liu and X. Yu, Chem. Soc. Rev., 2024, 53, 7392–7425.
69. Y.-A. Zhu, W.-Q. Yan, X.-G. Zhou and W.-K. Yuan, Chin. J. Chem. Eng., 2022, 41, 22–28.
70. K. Wang and L. Dou, Nat. Nanotechnol., 2022, 17, 562–563.
71. Z.-J. Zhao, S. Liu, S. Zha, D. Cheng, F. Studt, G. Henkelman and J. Gong, Nat. Rev. Mater., 2019, 4, 792–804.
72. F. Abild-Pedersen, J. Greeley, F. Studt, J. Rossmeisl, T. R. Munter, P. G. Moses, E. Skúlason, T. Bligaard and J. K. Nørskov, Phys. Rev. Lett., 2007, 99, 016105.
73. Z. Fang, W. Zhao, T. Shen, D. Qiu, Y. Lv, X. Hou and Y. Hou, Precis. Chem., 2023, 1, 395–417.
74. W. H. Lee, M. H. Han, Y.-J. Ko, B. K. Min, K. H. Chae and H.-S. Oh, Nat. Commun., 2022, 13, 605.
75. T. Sun, Z. Tang, W. Zang, Z. Li, J. Li, Z. Li, L. Cao, J. S. Dominic Rodriguez, C. O. M. Mariano, H. Xu, P. Lyu, X. Hai, H. Lin, X. Sheng, J. Shi, Y. Zheng, Y.-R. Lu, Q. He, J. Chen, K. S. Novoselov, C.-H. Chuang, S. Xi, X. Luo and J. Lu, Nat. Nanotechnol., 2023, 18, 763–771.
76. C.-X. Zhao, X. Liu, J.-N. Liu, J. Wang, X. Wan, X.-Y. Li, C. Tang, C. Wang, L. Song, J. Shui, H.-J. Peng, B.-Q. Li and Q. Zhang, J. Am. Chem. Soc., 2023, 145, 27531–27538.
77. Y. Li, Y. Ji, Y. Zhao, J. Chen, S. Zheng, X. Sang, B. Yang, Z. Li, L. Lei, Z. Wen, X. Feng and Y. Hou, Adv. Mater., 2022, 34, 2202240.
78. Z. Wang, C. Song, H. Shen, S. Ma, G. Li and Y. Li, Adv. Mater., 2024, 36, 2307786.
79. Z. Lian, H. Wu, W. Yang, H. Xiao, L. Ma, J. Zhang, J. Zi, X. Chen and H. Li, Chem. Catal., 2023, 3, 100824.
80. Y. Wen, Z. Shen, J. Hui, H. Zhang and Q. Zhu, Adv. Energy Mater., 2023, 13, 2204345.
81. L. Peng, Z. Wei, C. Wan, J. Li, Z. Chen, D. Zhu, D. Baumann, H. Liu, C. S. Allen, X. Xu, A. I. Kirkland, I. Shakir, Z. Almutairi, S. Tolbert, B. Dunn, Y. Huang, P. Sautet and X. Duan, Nat. Catal., 2020, 3, 762–770.
82. W. Liu, J. Feng, C. Zhang, C. Shi, S. Chen, T. Wang, X. Zhao, L. Zhang and J. Song, Chem. Eng. J., 2024, 490, 151526.
83. J. Zhou, X. Liu, L. Zhu, J. Zhou, Y. Guan, L. Chen, S. Niu, J. Cai, D. Sun, Y. Zhu, J. Du, G. Wang and Y. Qian, Joule, 2018, 2, 2681–2693.
84. M. Cui, Z. Zheng, J. Wang, Y. Wang, X. Zhao, R. Ma and J. Liu, Energy Storage Mater., 2021, 35, 577–585.
85. X. Chen, H.-J. Peng, R. Zhang, T.-Z. Hou, J.-Q. Huang, B. Li and Q. Zhang, ACS Energy Lett., 2017, 2, 795–801.
86. Y. Sun, J. Wang, T. Shang, Z. Li, K. Li, X. Wang, H. Luo, W. Lv, L. Jiang and Y. Wan, Angew. Chem., Int. Ed., 2023, 62, e202306791.
87. W. Hua, T. Shang, H. Li, Y. Sun, Y. Guo, J. Xia, C. Geng, Z. Hu, L. Peng, Z. Han, C. Zhang, W. Lv and Y. Wan, Nat. Catal., 2023, 6, 174–184.
88. Z. Zeng, W. Nong, Y. Li and C. Wang, Adv. Sci., 2021, 8, 2102809.
89. X. Chen, H. Lv and X. Wu, Energy Storage Mater., 2024, 65, 103187.
90. H. Li, R. Meng, C. Ye, A. Tadich, W. Hua, Q. Gu, B. Johannessen, X. Chen, K. Davey and S.-Z. Qiao, Nat. Nanotechnol., 2024, 19, 792–799.
91. C. Y. Zhang, C. Zhang, G. W. Sun, J. L. Pan, L. Gong, G. Z. Sun, J. J. Biendicho, L. Balcells, X. L. Fan, J. R. Morante, J. Y. Zhou and A. Cabot, Angew. Chem., Int. Ed., 2022, 61, e202211570.
92. C. Huang, J. Yu, C. Y. Zhang, Z. Cui, J. Chen, W. Lai, Y. Lei, B. Nan, X. Lu, R. He, L. Gong, J. Li, C. Li, X. Qi, Q. Xue, J. Y. Zhou, X. Qi, L. Balcells, J. Arbiol and A. Cabot, Adv. Mater., 2024, 36, 2400810.
93. W. Zhou, M. Chen, D. Zhao, C. Zhu, N. Wang, W. Lei, Y. Guo and L. Li, Adv. Funct. Mater., 2024, 34, 2402114.
94. L. Wang, W. Hua, X. Wan, Z. Feng, Z. Hu, H. Li, J. Niu, L. Wang, A. Wang, J. Liu, X. Lang, G. Wang, W. Li, Q. Yang and W. Wang, Adv. Mater., 2022, 34, 2110279.
95. N. Li, Q. Meng, X. Zhu, Z. Li, J. Ma, C. Huang, J. Song and J. Fan, Nanoscale, 2019, 11, 8485–8493.
96. S. Wu, C. Wang, H. Liang, W. Nong, Z. Zeng, Y. Li and C. Wang, Small, 2024, 20, 2305161.
97. C. Song, F. Hu, T. Zhang, S. Liu, W. Jiang, Z. Song, Z. Wang, M. Yao and X. Jian, Sci. China Mater., 2023, 66, 4411–4418.
98. M. Wu, Z. Wei, K. Fei, W. Xiao, J. Wu, X. Xu, Y. Zhao and Q. He, J. Phys. Chem. C, 2024, 128, 6551–6561.
99. H. Shou, Q. Zhou, S. Wei, H. Liu, H. Lv, X. Wu and L. Song, JACS Au, 2024, 3, 930–939.
100. T. Boteju, S. Ponnurangam and V. Thangadurai, J. Phys. Chem. C, 2024, 128, 3652–3661.
101. H. Yuan, J. Yang and Y.-W. Zhang, Chemistry, 2024, 19, e202400199.
102. X. Chen, H. Lv and X. Wu, J. Phys. Chem. Lett., 2024, 15, 3425–3433.
103. H. Liang, Z. Zeng, Z. Qiao, Y. Li and C. Wang, Phys. Chem. Chem. Phys., 2024, 26, 5858–5867.
104. D. Wang, F. Li, R. Lian, J. Xu, D. Kan, Y. Liu, G. Chen, Y. Gogotsi and Y. Wei, ACS Nano, 2019, 13, 11078–11086.
105. Y. Dong, H. Zhang, D. Cai, S. Yang, P. Ying, T. Li, J. Zou, M. Shu, R. Li, J. Wang, K. Xiao, X. Zhou, H. Nie, X. Fan and Z. Yang, Adv. Funct. Mater., 2024, 34, 2406455.
106. C. Geng, X. Jiang, S. Hong, L. Wang, Y. Zhao, J. Qi, J. Shi, J. Wang, L. Peng, Z. Hu, Y. Guo, F. Jin, Q. Yang and W. Lv, Adv. Mater., 2024, 36, 2407741.
107. J. Shen, Z. Liang, T. Gu, Z. Sun, Y. Wu, X. Liu, J. Liu, X. Zhang, J. Liu, L. Shen, M. Zhu and J. Liu, Energy Environ. Sci., 2024, 17, 6034.
108. M. Fang, J. Han, S. He, J.-C. Ren, S. Li and W. Liu, J. Am. Chem. Soc., 2023, 145, 12601–12608.
109. Z. Han, R. Gao, T. Wang, S. Tao, Y. Jia, Z. Lao, M. Zhang, J. Zhou, C. Li, Z. Piao, X. Zhang and G. Zhou, Nat. Catal., 2023, 6, 1073–1086.
110. B. Hammer and J. K. Nørskov, Nature, 1995, 376, 238–240.
111. M. Liu, R. Hou, P. Zhang, Y. Li, G. Shao and P. Zhang, Small, 2024, 20, 2402725.
112. T. Duan, D. Fan, Z. Ma and Y. Pei, Nanoscale, 2024, 16, 5352–5361.
113. Z. Shen, X. Jin, J. Tian, M. Li, Y. Yuan, S. Zhang, S. Fang, X. Fan, W. Xu, H. Lu, J. Lu and H. Zhang, Nat. Catal., 2022, 5, 555–563.
114. T. Bligaard, J. K. Nørskov, S. Dahl, J. Matthiesen, C. H. Christensen and J. Sehested, J. Catal., 2004, 224, 206–217.
115. J. Cheng, P. Hu, P. Ellis, S. French, G. Kelly and C. M. Lok, J. Phys. Chem. C, 2008, 112, 1308–1311.
116. R. A. Van Santen, M. Neurock and S. G. Shetty, Chem. Rev., 2010, 110, 2005–2048.
117. S. Hu and W.-X. Li, Science, 2021, 374, 1360–1365.
118. A. J. Medford, A. Vojvodic, J. S. Hummelshøj, J. Voss, F. Abild-Pedersen, F. Studt, T. Bligaard, A. Nilsson and J. K. Nørskov, J. Catal., 2015, 328, 36–42.
119. A. Pan, T. Biswas, A. K. Rakshit and S. P. Moulik, J. Phys. Chem. B, 2015, 119, 15876–15884.
120. Y. Dong, D. Cai, T. Li, S. Yang, X. Zhou, Y. Ge, H. Tang, H. Nie and Z. Yang, ACS Nano, 2022, 16, 6414–6425.
121. S. Kong, X. Lv, X. Wang, Z. Liu, Z. Li, B. Jia, D. Sun, C. Yang, L. Liu, A. Guan, J. Wang, G. Zheng and F. Huang, Nat. Catal., 2023, 6, 6–15.
122. A. Vojvodic, J. K. Nørskov and F. Abild-Pedersen, Top. Catal., 2014, 57, 25–32.
123. H. Xin, A. Vojvodic, J. Voss, J. K. Nørskov and F. Abild-Pedersen, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 115114.
124. Z. Shen, P. Song, W. Xie, L. Tannesia, K. Tang, Y. Sun, S. Xi and Z. J. Xu, Adv. Mater., 2025, 37, 2418090.
125. C. Y. Zhang, J. Yu, C. Huang, G. Sun, L. Balcells, J. Li, X. Qi, C. Z. Yi, J. Herrero-Martín, L. Simonelli, F. Fauth, R. He, X. Pan, J. Li, J. Arbiol, J. Y. Zhou and A. Cabot, J. Am. Chem. Soc., 2025, 147, 7070–7082.
126. K. Ruthenberg and J. C. Martínez González, Found. Chem., 2017, 19, 61–75.
127. T. Hou, W. Xu, X. Chen, H. Peng, J. Huang and Q. Zhang, Angew. Chem., Int. Ed., 2017, 56, 8178–8182.
128. J. K. Nørskov, F. Abild-Pedersen, F. Studt and T. Bligaard, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 937–943.
129. Z. Bai, Z. Wang, T. Wang, Z. Wu, R. Li, X. Gao, Y. Bai and K. Sun, Energy Storage Mater., 2024, 71, 103657.
130. L. Wang, H. Li, T. Yan, C. Yuan, G. Liu, G. Zhao, P. Zeng and L. Zhang, Adv. Funct. Mater., 2024, 34, 2404184.
131. J. Suntivich, K. J. May, H. A. Gasteiger, J. B. Goodenough and Y. Shao-Horn, Science, 2011, 334, 1383–1385.
132. Y. Du, W. Chen, Y. Wang, Y. Yu, K. Guo, G. Qu and J. Zhang, Nano-Micro Lett., 2024, 16, 100.
133. H. Li, P. Shi, L. Wang, T. Yan, T. Guo, X. Xia, C. Chen, J. Mao, D. Sun and L. Zhang, Angew. Chem., Int. Ed., 2023, 62, e202216286.
134. H. Li, M. Chuai, X. Xiao, Y. Jia, B. Chen, C. Li, Z. Piao, Z. Lao, M. Zhang, R. Gao, B. Zhang, Z. Han, J. Yang and G. Zhou, J. Am. Chem. Soc., 2023, 145, 22516–22526.
135. A. Streitwieser and H. W. Salzberg, J. Electrochem. Soc., 1962, 109, 116C.
136. J. S. Griffith and L. E. Orgel, Q. Rev., Chem. Soc., 1957, 11, 381.
137. I. Abdelwahab, D. Kumar, T. Bian, H. Zheng, H. Gao, F. Hu, A. McClelland, K. Leng, W. L. Wilson, J. Yin, H. Yang and K. P. Loh, Science, 2024, 385, 311–317.
138. J. Zhou, X. Liu, L. Zhu, S. Niu, J. Cai, X. Zheng, J. Ye, Y. Lin, Z. Zhu, D. Sun, Z. Li, Y. Zang, Y. Wu, J. Xiao, Q. Liu, Y. Zhu, G. Wang and Y. Qian, Chem, 2020, 6, 221–233.
139. Y. Zhang, Q. Wu, J. Z. Y. Seow, Y. Jia, X. Ren and Z. J. Xu, Chem. Soc. Rev., 2024, 53, 8123–8136.
140. L. Lin, Y. Ni, L. Shang, L. Wang, Z. Yan, Q. Zhao and J. Chen, Angew. Chem., Int. Ed., 2024, 63, e202319518.
141. A. Yu, Y. Zhang, S. Zhu, T. Wu and Z. J. Xu, Nat. Energy, 2025, 10, 435–447.
142. X. Zhang, X. Zhang, X. Wang, G. Cui, H. Pan and W. Sun, Energy Environ. Sci., 2025, 18, 3553–3567.
143. Z.-J. Zhao, R. Mu, X. Wang and J. Gong, Langmuir, 2017, 33, 8700–8706.
144. W. Zhu, L. Zhang, P. Yang, C. Hu, Z. Luo, X. Chang, Z. Zhao and J. Gong, Angew. Chem., Int. Ed., 2018, 57, 11544–11548.
145. V. Fung, F. F. Tao and D. Jiang, J. Phys. Chem. Lett., 2017, 8, 2206–2211.
146. H. Zhang, H. Xue, C. Wei, J. Sun, J. Xu and F. Tang, Sci. China Mater., 2024, 67, 2683–2693.
147. S. Curtarolo, G. L. W. Hart, M. B. Nardelli, N. Mingo, S. Sanvito and O. Levy, Nat. Mater., 2013, 12, 191–201.
148. J. Greeley, Annu. Rev. Chem. Biomol. Eng., 2016, 7, 605–635.
149. M. M. Montemore and J. W. Medlin, Catal. Sci. Technol., 2014, 4, 3748–3761.
150. L. Pauling, The nature of the chemical bond, Cornell University Press, 1960, vol. 350.
151. S. Cestellos-Blanco, H. Zhang, J. M. Kim, Y. Shen and P. Yang, Nat. Catal., 2020, 3, 245–255.
152. T. Li, D. Cai, S. Yang, Y. Dong, S. Yu, C. Liang, X. Zhou, Y. Ge, K. Xiao, H. Nie and Z. Yang, Adv. Mater., 2022, 34, 2207074.
153. L. L. K. Taylor, I. A. Riddell and M. M. J. Smulders, Angew. Chem., Int. Ed., 2019, 58, 1280–1307.
154. X. Lin, X. Du, S. Wu, S. Zhen, W. Liu, C. Pei, P. Zhang, Z.-J. Zhao and J. Gong, Nat. Commun., 2024, 15, 8169.
155. Y. Wang, X. Feng, D. Guo, H. Hsu, J. Hou, F. Zhang, C. Xu, X. Chen, L. Wang, Q. Zhang and M. Ouyang, Joule, 2024, 8, 2639–2651.
156. R. Ding, J. Chen, Y. Chen, J. Liu, Y. Bando and X. Wang, Chem. Soc. Rev., 2024, 53, 11390–11461.
157. Y. Chang, I. Benlolo, Y. Bai, C. Reimer, D. Zhou, H. Zhang, H. Matsumura, H. Choubisa, X.-Y. Li, W. Chen, P. Ou, I. Tamblyn and E. H. Sargent, Matter, 2024, 7, 4099–4113.
158. X. Duan, Y. Li, J. Zhao, M. Zhang, X. Wang, L. Zhang, X. Ma, Y. Qu and P. Zhang, J. Am. Chem. Soc., 2024, 147, 651–661.
159. Y. Yuan, Y. Gao, J. Zhang, Y. Gao, C. Wang, X. Chen and Q. Zhang, Energy Storage Sci. Technol., 2024, 13, 2907–2919.
160. Y. Jia, Z. Wang, Z. Han, J. Li, M. Zhang, Z. Lao, Y. Han, R. Gao, J. Gao, Z. Zheng, A. Chen, H. Li, R. Mao, K. Tao, J. Li and G. Zhou, Joule, 2025, 101878.
161. H. Zhang, Z. Wang, J. Ren, J. Liu and J. Li, Energy Storage Mater., 2021, 35, 88–98.
162. L. Wang, Z. Hu, X. Wan, W. Hua, H. Li, Q. Yang and W. Wang, Adv. Energy Mater., 2022, 12, 2200340.
163. Z. Lian, M. Yang, F. Jan and B. Li, J. Phys. Chem. Lett., 2021, 12, 7053–7059.
164. D. Chen, L. Chen, Q.-C. Zhao, Z.-X. Yang, C. Shang and Z.-P. Liu, Nat. Catal., 2024, 7, 536–545.
165. Q.-C. Zhao, L. Chen, S. Ma and Z.-P. Liu, Nat. Commun., 2025, 16, 3720.
166. P. Zhang, C. Shang, Z. Liu, J.-H. Yang and X.-G. Gong, J. Mater. Chem. A, 2023, 11, 5370–5379.
167. J. Xia, R. Cao, L. Zhao and Q. Wu, J. Colloid Interface Sci., 2023, 630, 317–327.
168. S. Qi, C. Li, G. Chen and M. Zhao, J. Energy Chem., 2024, 97, 738–746.
169. L. Chanussot, A. Das, S. Goyal, T. Lavril, M. Shuaibi, M. Riviere, K. Tran, J. Heras-Domingo, C. Ho, W. Hu, A. Palizhati, A. Sriram, B. Wood, J. Yoon, D. Parikh, C. L. Zitnick and Z. Ulissi, ACS Catal., 2021, 11, 6059–6072.
170. X. Zhang, Y. Tian, L. Chen, X. Hu and Z. Zhou, J. Phys. Chem. Lett., 2022, 13, 7920–7930.
171. Z. Wang, A. Chen, K. Tao, J. Cai, Y. Han, J. Gao, S. Ye, S. Wang, I. Ali and J. Li, npj Comput. Mater., 2023, 9, 130.
172. M. Suvarna and J. Pérez-Ramírez, Nat. Catal., 2024, 7, 624–635.
173. Y. Wanyan, X. Yang, C. Chen and C. Xu, 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), IEEE, Vancouver, BC, Canada, 2023, pp. 6492–6502.
174. Z. Song, Q. Zhou, S. Lu, S. Dieb, C. Ling and J. Wang, J. Phys. Chem. Lett., 2023, 14, 3594–3601.
175. Z. Han, A. Chen, Z. Li, M. Zhang, Z. Wang, L. Yang, R. Gao, Y. Jia, G. Ji, Z. Lao, X. Xiao, K. Tao, J. Gao, W. Lv, T. Wang, J. Li and G. Zhou, Nat. Commun., 2024, 15, 8433.

---