Models and simulations of structural DNA nanotechnology reveal fundamental principles of self-assembly

Abstract

DNA is not only a centrally important molecule in biology: the specificity of bonding that allows it to be the primary information storage medium for life has also allowed it to become one of the most promising materials for designing intricate, self-assembling structures at the nanoscale. While the applications of these structures are both broad and highly promising, the self-assembly process itself has attracted interest not only for the practical applications of designing structures with more efficient assembly pathways, but also due to a desire to understand the principles underlying self-assembling systems more generally, of which DNA-based systems provide intriguing and unique examples. Here, we review the fundamental physical principles that underpin the self-assembly process in the field of DNA nanotechnology, with a specific focus on simulation and modelling and what we can learn from them. In particular, we compare and contrast DNA origami and bricks and briefly outline other approaches, with an overview of concepts such as cooperativity, nucleation and hysteresis; we also explain how nucleation barriers can be controlled and why they can be helpful in ensuring error-free assembly. While high-resolution models may be needed to obtain accurate system-specific properties, often very simple coarse-grained models are sufficient to extract the fundamentals of the underlying physics and can enable us to gain deep insight. By combining experimental and simulation approaches to understand the details of the self-assembly process, we can optimise its yields and fidelity, which may in turn facilitate its use in practical applications.

---

1 Introduction

The need for precise control in the manufacturing and assembly of structures at small length scales has led to some of the most important technological advances of the last century. This control usually comes from assembly methods that are ‘top-down’: an assembling machine contains the information necessary for the final structure, and adds or subtracts components or material to reach it. By contrast, in ‘bottom-up’ assembly, the components themselves contain the information of the final structure, and will self-assemble given sufficient time and appropriate conditions. Both approaches are commonly seen in biological contexts:¹ for example, ribosomal polypeptide synthesis is an example of top-down assembly, while the folding of a polypeptide chain is an example of bottom-up assembly. Hijacking and mimicking these biological systems provides a route to assembling designed structures at small scales.

In contrast to proteins, nucleic acids have highly specific interactions between a small number of monomer types, which makes them particularly amenable for repurposing as a self-assembling material. Structural DNA nanotechnology entails the creation and use of materials made of or with DNA, which contrasts with technologies relating to DNA's information-storage capabilities. Because these systems are based on biological molecules, they have the advantage of being naturally compatible with biological systems, although their applications extend far beyond. Moreover, in many DNA-based systems, each molecule in the target structure is distinct: we know precisely where each molecule is in a correctly assembled structure. Such structures are sometimes described as ‘addressable’,² and this property can enable such structures to be functionalised readily in precisely determined locations, which has significant implications for their utility in applications.³

The idea of using DNA to construct functional structures was initially conceived by Seeman in the early 1980s,^4–6 when he began to explore the use of branched helices and so-called sticky ends (i.e. unpaired overhangs of single-stranded DNA (ssDNA) at the ends of helices) to go beyond the linear helical structures typically found in cells. Such synthetic building blocks with complementary dangling ends can form periodic structures,⁶ and were in a sense the beginning of DNA nanotechnology; they have therefore been investigated in some depth.^7,8 Since then, there has been great interest in pushing the limits of the size and intricacy of the structures that can be designed and assembled with DNA. However, for the following two decades, studies mostly focused on individual structural motifs or periodic 2D or 3D arrays comprising one or several of these motifs.⁹ These methods are limited in the scope of structures that can be made and, in the case of periodic designs, the necessity of extensive purification and precise stoichiometry to achieve appreciable size and yield. In the last two decades, two approaches have emerged that circumvent these issues: DNA origami and DNA bricks.

1.1 DNA nanotechnology is dominated by three methods: origami, bricks and coated colloids

The potential for creating intricate, designable nanostructures with DNA building blocks, and their possible applications, began to be fully appreciated only when the DNA origami method was first introduced.¹⁰ In this method, a long ssDNA ‘scaffold’ strand is folded into its target structure by hybridising with a much larger number of short, carefully designed ‘staple’ strands that bond with multiple domains of the scaffold strand and thus serve to fold it in a designed way [Fig. 1(a)]. As the staples and scaffold bond with one another, double helices are formed; the rigidity of the double-helical structure provides the final structure with considerable mechanical stability. The helices are connected to each other by crossovers between individual strands on adjacent helices, typically forming four-way ‘Holliday’¹¹ junctions.⁴ Because a DNA double helix has a natural twist, a suitable choice of domain lengths can thus result in complex curvature.¹² Junctions between helices must occur at carefully selected intervals to ensure that the dihedral angle is consistent with the target structure arising from the approximate 10.5 base pairs needed per helical turn of B-form DNA [Fig. 2].

Fig. 1 Schematic illustrations of (a) DNA-origami and (b) DNA-brick systems. In (a), a long scaffold is folded into the target structure by staple strands, which are of different lengths and can link parts of the scaffold that are topologically distant, which enables complex structures to be designed. In (b), all DNA molecules are relatively short, have the same number of neighbours except at the edges and faces, and come together in a simple, predictable pattern. The complexity of the target structure arises not from changing the bonding pattern, but from removing some bricks from the structure with the maximum possible connectivity. In both (a) and (b), the parts of the sequence that bond in the target structure are shown in the same base colour, with the long scaffold strand in (a) shown in a darker hue. The target structure is planar for clarity, but its 3D shape depends on the lengths of the domains, which affects dihedral angles [see Fig. 2].

Fig. 2 Crossover dihedral angles in B-DNA. We show pictorial representations of double-stranded B-DNA as a function of the number of base pairs in two orientations. The bottom row shows an orthogonal Newman-like projection of the pink helical strand only onto the helical plane. The position of the pink helical strand from the centre of the double helix (black line) is shown by a blue and red arrow at the start and end of the sequence. These arrows give an indication of the current phase of the helical twist. The position of the paired helix is at the negative of this vector. When another DNA molecule forms a crossover after 8 base pairs, it thus forms an angle of approximately 90° with the start of the pink helical strand. If crossovers occur at 8-base intervals, the resulting structure is therefore approximately cubic.

Over the last two decades, it has been shown that by carefully designing the connectivity, both simple and complex connected shapes can be constructed, including dynamic, stimuli-responsive structures with flexible joints.^13–19 DNA-origami structures can even act as building blocks themselves and assemble into still higher-order structures.^20–22 It is now also possible to produce ssDNA origami, in which the scaffold folds without the aid of staples.²³ The advantages provided by DNA origami have stimulated numerous investigations exploring design and assembly methods, structural and functional classes, and applications in both medical and non-medical fields. The addressability of the target structure offers precise control over their functionalisation,^3,24 which, for example, allows such structures to serve as carriers of antibodies used to target cancer cells²⁵ and helps in the design of artificial photosynthetic pathways.²⁶ There have been many reviews of DNA origami and its possible applications.^{3,9,17,19,27–60} Tentative steps have even been made towards the commercialisation of the technology.⁶¹

In contrast to DNA origami, the self-assembly of DNA tiles⁶² and bricks^63,64 to give two- and three-dimensional target structures, respectively, forgoes the long ssDNA scaffold strand [Fig. 1(b)], and has thus sometimes been referred to as ‘staple-only DNA origami’.⁶⁵ As with origami, DNA tiles and bricks can be designed to assemble in particular ways by relying on Watson–Crick complementarity. The idea behind Seeman's periodic crystals⁶ made with DNA was extended in the early 2010s to create finite target structures; in this context, all building blocks are relatively short DNA molecules, with the sequence of each molecule split into several domains in such a way that each domain is bonded with different ‘neighbouring’ molecules in the target structure. Such neighbouring domains are chosen to have unique complementary sequences, meaning that the correct pairing has a considerably more favourable enthalpy of hybridisation than incorrect pairings, and the target structure is therefore energetically favoured at low enough temperatures. As with DNA origami, the length of each domain is carefully chosen to give the correct target geometry. For example, a three-dimensional cubic assembly of helical strands in the target structure is achieved with 8 base pairs per domain,⁶³ which correspond to approximately three quarters of a helical turn [Fig. 2]. Many target structures have been shown to be possible to form in a modular way, simply by leaving out some components,^{51,62–64,66} but the method has also been extended to allow for multiple possible bonding partners when encoding for multiple target structures simultaneously.⁶⁷ Unlike with DNA origami, where the staple strands largely have to be redesigned for every possible target structure, in DNA-brick systems, considerable complexity of the target structure can thus be designed in a simple way; however, the fact that there is no central molecule with many connections to the staple strands means that the final target structure can be less compact than for analogous DNA-origami designs.⁶⁸

Finally, we can make use of building blocks larger than individual DNA molecules in the self-assembly process. By coating colloidal particles with DNA molecules, the hybridisation properties of DNA can be used to enable designed, complex structures to be formed in colloidal systems.^69–75 The self-assembly of such building blocks has been studied in depth using both computer simulations and theoretical models.^76–81 While the fundamental design principles are similar for all DNA-based building blocks, ultimately relying on the specificity of Watson–Crick pairings to enable designed interactions with complementary sequences to be preferred over any incidental interactions, there are further subtleties involved in the self-assembly of DNA-coated colloids, depending on the placement and length of the DNA strands in question and the manner in which they are tethered to the underlying colloidal particles; these are discussed in a review by Angioletti-Uberti.⁸² Furthermore, in a very recent review, Jacobs and Rogers discuss the physics of DNA-coated colloid self-assembly in detail, as well as the current open questions of designing dynamical self-assembly pathways and assembling multiple target structures from the same building blocks.⁸³ We do not therefore focus on DNA-coated colloids any further in this review.

The rules for designing DNA systems with a particular final structure are well understood and there are a number of tools to assist the design of such structures.^68,84–87 Although such tools enable us to design the final structure of choice, the underlying assembly thermodynamics and kinetics (e.g. the order and cooperativity of staple bonding in the case of DNA origami) of such systems are rather less well understood, and well-designed final structures may simply not assemble in appreciable yields. A fuller understanding of the underlying physics – and the possible bottlenecks and reasons the self-assembly can go awry – is therefore crucial in the design both of structures that assemble most efficiently into their target structure and their associated assembly protocols.

While there has been appreciable progress in understanding fundamental aspects of DNA self-assembly from experiment, there are sometimes certain contradictions in the findings and limitations in the approaches taken. For example, studies using spectroscopic measurements to track the progress of DNA-origami self-assembly have found hysteresis,^66,88–92 with annealing occurring at a lower temperature than melting, which implies the presence of significant free-energy barriers to assembly. By contrast, using atomic-force microscopy, another study found that the melting and annealing pathways are largely the reverse of one another, with the associated temperatures being approximately the same.⁹³ It can be difficult to pin down experimentally the specific reason for such differences; however, models and simulations of DNA self-assembly, and specifically of DNA-origami and DNA-brick systems, have managed to fill in many of the gaps left by experimental approaches. Moreover, simulations can help inform the choice of experimental designs, as was shown in the context of the self-assembly of dodecagonal quasicrystals,^94,95 and are therefore an excellent tool both for exploring design space more cheaply than in experiment and for developing and testing hypotheses that allow us to gain insight into the fundamentals of the process.

In this review, we focus on how we can understand the self-assembly of DNA-based nanoscale structures using computer simulations, and specifically on the fundamental physics governing the self-assembly process (Section 2). We discuss in Section 2.1 how cooperativity arises in DNA-based architectures and what its implications are for the self-assembly process. We explain how self-assembly can be treated in a way analogous to a phase transition and how we can study the corresponding nucleation step. Although the presence of a nucleation barrier slows down the self-assembly process, it can make it more robust to misassembly [Section 2.2]. We show that in some circumstances, it is even possible to design nucleation barriers [Section 2.3]. Although much of the underlying physics can ultimately be understood qualitatively with simple pictorial models, in order to build up enough data that we can subsequently interpret to create such models, we have to be able to study the relevant self-assembly processes numerically; in order to do this, we use detailed simulation methods, as we outline in Section 2.4. The kind of model that we choose to simulate depends on the kind of questions we would like to address, and we explore models at different levels of resolution in Section 3. Finally, in Section 4, we offer a summary of the main lessons to be learnt from computer simulations of DNA self-assembly and outline some questions that remain open.

2 DNA-based self-assembly is governed by the underlying physics

Self-assembly is by definition a non-equilibrium process: in the broadest terms, the system begins in some starting configuration and either relaxes or is driven from this configuration to a more ordered one.⁹⁶ The final assembled state may be a dynamic or dissipative one,^97–99 in that it is a steady state in a system that requires continuous energy input, although such a process may also be referred to as ‘self-organisation’.⁹⁶ For example, under application of a shear flow, specific distributions of DNA colloid structures can be designed to self-assemble,¹⁰⁰ while DNA origami can be fibrillised by a light source with the help of a small-molecule pH regulator.¹⁰¹ However, most literature has focused on the case in which the final assembled state is either the equilibrium one or a metastable one that can be assumed to be at local equilibrium, and we will also do so here.

In such cases, the nature of the assembly process often looks similar to that of a liquid–solid transition, although of course it does not strictly speaking entail a phase transition in the sense that the target structure is of a finite size and not a bulk phase. In a first-order phase transition such as freezing, there is usually a degree of hysteresis: a liquid can often be supercooled considerably before it spontaneously freezes in the absence of an external nucleation seed, and this means that the transition between the two phases occurs at different temperatures when the system is cooled (freezing) and when it is subsequently heated (melting) [Fig. 3(a)]. This occurs through the process of nucleation and growth, and often the reason hysteresis occurs in self-assembly can be traced to the presence of a free-energy barrier to nucleation [Fig. 3(b) and (c)]. The free energy in this context is usually thought of as a projection of the potential-energy surface onto a suitable ‘order parameter’, a metric quantifying the degree of ordering in the system. Sometimes, free energies expressed as a function of an order parameter are known as ‘Landau’ free energies¹⁰² or potentials of mean force.¹⁰³ Generally, suitable order parameters are physically intuitive quantities, such as the size of the largest cluster in the system in the context of nucleation,¹⁰⁴ and should correspond to some component of the reaction co-ordinate; if they do not, interpreting their meaning rapidly becomes opaque.¹⁰⁵

Fig. 3 Illustrations of the meanings of some common terms in self-assembly. In (a)(i), we show a schematic plot of the degree of assembly as a function of temperature. At low temperatures, the assembled structure is thermodynamically stable, and at high temperatures, the disassembled structure in solution is favourable. However, because of a kinetic barrier (see panel (b)), if we cool the disassembled system from a high temperature, assembly begins at a lower temperature than if we heat up an assembled structure. The difference between the temperatures that the transition occurs at in opposite directions is known as hysteresis. However, the temperatures involved are not uniquely defined, both because the nucleation process is stochastic and because it depends on the protocol itself. The faster we cool the system, the more we can overshoot the equilibrium changeover temperature. Disassembly is often less affected by the rate of heating because the barrier is often lower than for assembly, or even essentially non-existent. In (a)(ii), we show one of the hallmarks of cooperativity: if bonding becomes more favourable once the first bond is formed, for example because of a lower entropic cost to bonding the second bonded pair, the equilibrium degree of assembly will increase much more sharply than if every pair were independent. In (b), to illustrate the origins of hysteresis, we show an example Landau free energy as a function of a reaction co-ordinate at different temperatures. If a system is in a metastable state and the free-energy barrier is large, the rate of the phase transition is negligible and a metastable phase can become very long-lived: the system exhibits hysteresis. In (c), we show examples of nucleation free-energy barriers. In (i), we illustrate the classical nucleation theory result for a phase transition. Initially, formation of a new phase entails the creation of an interface, where particles on the surface have fewer bonding interactions than in the bulk condensed phase, but also less entropy than in the dilute phase, and such cluster formation is therefore free-energetically disfavourable. Only once a critical nucleus size is reached does the phase transition become favourable. The interfacial term scales with the surface of the cluster (∼R² for a spherical cluster of radius R), while the bulk term scales with its volume (∼R³). In (ii), we show a schematic illustration of what often happens with highly directional bonding: the critical nucleus often corresponds to an incomplete ’cycle’, and adding an additional molecule allows the system to form two bonds to close it, making it energetically much more favourable for a similar loss of entropy. For sufficiently small critical cluster sizes in highly cooperative transitions, this can result in noticeable jaggedness of the free-energy profile.

As an illustration of how hysteresis can come about, we illustrate in Fig. 3(b) the Landau free energy as a function of the reaction co-ordinate at different temperatures. In this example, phase α is stable at high temperatures and phase β is stable at low temperatures. However, if the system is initially in phase α and is then cooled rapidly, although the thermodynamically stable phase β has a lower free energy overall at this temperature (i.e. ΔG < 0), in order to reach it, the system must overcome a free-energy barrier Δ^‡G > 0. The probability of reaching the top of the barrier is proportional to the Boltzmann factor exp(−Δ^‡G/k_BT), and so if Δ^‡G ≫ k_BT, then the rate is negligible and the metastable phase is very long-lived; in other words, the phase transition does not occur at accessible timescales and hysteresis ensues.

In DNA self-assembly, typically, in the initial unassembled state at room temperature, the DNA molecules present are partially hybridised and kinetically trapped in locally stable states, where any further assembly is kinetically arrested. The first step of the self-assembly process thus generally begins with an initial melting step, in which the temperature is increased sufficiently so that all DNA molecules become unhybridised and the system contains a solution of ssDNA. Then, most commonly, the temperature is slowly lowered at a controlled and empirically optimised rate, in order to ensure that nucleation governs the assembly process: this allows correct assembly to occur in a predictable and controlled manner, as we discuss in Section 2.2. However, in some cases, it is also possible to start from a high-temperature disassembled state and cool it to a fixed temperature, eschewing that part of the cooling process where not much happens; such ‘isothermal’ assembly is possible if the nucleation temperature is at least approximately known,^64,106,107 and in such cases assembly can be achieved particularly quickly and efficiently. Control parameters other than temperature are possible, such as chemical denaturants^108,109 or mechanical pulling;¹¹⁰ however, here, we focus on temperature, as this is the most common control parameter for driving assembly.

In order to understand the physics behind these assembly protocols, in the following we outline the major driving forces involved. Specifically, we argue that one crucial aspect in driving the successful self-assembly of compact structures that can robustly be self-assembled is cooperativity [Section 2.1], which ensures that once assembly begins, there is a collective drive towards increasing the size of the growing target structure. We also explore how we can probe the nucleation barrier that gives rise to hysteresis [Section 2.2], and how nucleation barriers can be fine-tuned to ensure that the system assembles the way we design it to, and how they can be removed altogether if our target application calls for nucleation-free assembly [Section 2.3]. We illustrate all these points by lessons learnt from computer simulations. Finally, we summarise the fundamental ideas behind the computer simulation methods that we can use to obtain these kinds of insights [Section 2.4].

2.1 Cooperativity is a fundamental aspect of self-assembly

Non-covalent chemical cooperativity is the phenomenon wherein the free energy of formation of a molecular complex or assembly is not equal to the free energy of a reference state where the individual non-covalent bonds occur in isolation from each other.^111–113 This cooperativity can be either positive or negative, depending on whether the free energy of forming the assembly is more or less favourable than the reference state, respectively. The details of cooperativity between various pairs of non-covalent bonds, such as how nearby cation–π bonds and hydrogen bonds interact, have been extensively studied.^112,113

In self-assembling DNA systems, we often take a coarser view of cooperativity by focusing on the steepness of the melting/annealing curve [Fig. 3(a)(ii)], which may be quantified via the Hill coefficient.¹¹¹ When considering the cooperativity of two DNA strands hybridising, one choice of reference state might be the isolated bonding of the individual nucleotides [Fig. 4(a)(i)] that make up the two strands [Fig. 4(a)(ii)]. One could then consider the detailed interactions between the base pair and its neighbours, in particular the way the hydrogen bonds and π–π interactions between the nitrogenous bases of the nucleotides are affected by the fact that multiple base pairs occur in sequence along the backbone in the system of interest. For studying cooperativity in DNA bricks, DNA origami or DNA-coated colloidal systems, such a detailed reference state may not be ideal: the effects of cooperativity on the assembly of these systems on this scale are roughly the same when considering base pairs and their nearest neighbours, and such a choice of reference state would obscure the differentiating effects that occur on longer length and time scales. We discuss the trade-offs inherent in selecting a model resolution below in Section 3.

Fig. 4 Cooperativity in DNA self-assembly. In (a)(i) and (b)(i), we show two possible reference states for studying cooperativity in DNA self-assembly. The reference state in (a)(i) is the bonding of individual nucleotides in isolation, which could act as a reference for studying the cooperativity involved in the bonding of two strands of DNA composed of the same nucleotides, as shown in (a)(ii). For studying cooperativity on larger scales, such as in (b)(ii), a more convenient reference state is the bonding of whole strands corresponding to independent domains, as shown in (b)(i). In (c), we show a series of domain bonding events for the assembly of the same toy DNA origami as shown in (b)(ii) in order to demonstrate the different possibilities for loop formation, as discussed in the main text. The two staples are labelled A and B, as shown. The bonded domain pairs in each state are indicated by ringed labels, indicating the staple strand (A or B) and the domain on the strand (1 or 2).

In all forms of DNA-based self-assembly, cooperativity beyond that involved in simple strand hybridisation plays a key role. Perhaps some of the most complex examples of cooperativity in the assembly of DNA-based structures are those found in DNA-origami self-assembly. In order to understand the main drivers of cooperativity in such systems, it is usually more convenient to choose a different reference state instead of the fully independent nucleotides considered in Fig. 4(a)(i). An attractive alternative is to consider whole domains as defined in the design of the system being studied instead. For example, in a DNA-origami system with two staples, each comprising two (say) 16-nucleotide domains [Fig. 4(b)(ii)], a helpful reference system might be one that comprises four 16-nucleotide domains from the staples and four 16-nucleotide domains from the scaffold strand, with both the scaffold and the staples cut up into their individual domains [Fig. 4(b)(i)]. Further, the bonding of each pair of complementary domains in the reference state occurs in isolation as an independent system. With such a short scaffold strand, there is no fundamental distinction between DNA origami and DNA bricks, and so this particular example could equally be considered to be an example of DNA-brick self-assembly. The effects of cooperativity on the finer scale of the hybridisation of individual nucleotides can be captured in a model such as the SantaLucia nearest-neighbour (NN) model, which gives the free energy of hybridisation of any two strands of DNA by considering the local cooperativity of a given base pair with its nearest neighbours. We describe this model further in Section 3.1. Because this NN model has been so well experimentally verified for strand hybridisation free energies and melting temperatures, it is often used to calculate the reference melting curve directly, avoiding the need to synthesise and assemble the reference system experimentally. In the following discussion of domain-level cooperativity, we refer to free-energy gains and costs relative to a reference system with no domain-level cooperativity in which the domains bond to their complementary pairs independently [Fig. 4(b)(i)].

The closure of loops in DNA origami provides ample opportunities for cooperativity. In this context, loop closure refers to the bonding of one domain of DNA to another such that when tracing the backbone of single- or double-stranded regions, a closed topological loop is formed; we show examples of two possible pathways with loop-closure events in Fig. 4(c). In DNA origami, loop formation occurs when staples bond fully to the scaffold. As the first domain of a staple bonds to the scaffold strand, there is a favourable enthalpy change as the two strands hybridise; however, since the two molecules are now bonded, they have to move in concert with one another. The reduction in both the translational and conformational states available to the system means that such bonding entails an entropic penalty. These gains and costs of bonding the first domain of a staple are unaffected by the presence or absence of existing loops in the configuration of the system. However, the bonding of subsequent domains of the same staple depend significantly on what kinds of loops form, since such bonding events occur within the same overall structure, and there is no analogous loss of translational degrees of freedom upon bonding. In contrast to the reference system, the entropic cost of such additional bonding has thus been reduced. Although strictly speaking, the fact that the scaffold and staple strand are bonded through at least one domain does not mean they are one molecule, any subsequent bonding beyond the first is often referred to as being ‘intramolecular’.

On the other hand, an additional cost is introduced relative to the reference system by the formation of loops with the scaffold. When a loop is formed, the scaffold becomes more constrained, which results in an entropic penalty that does not occur in the reference system. The size of the entropic cost of this loop formation depends on the order in which the staple domains bond to the scaffold, and in sufficiently small toy systems, the different possible loops that can form along the assembly pathway can be explicitly enumerated. As an example, let us consider the formation of the same target structure we have already been considering in Fig. 4(b)(ii). Starting from the state shown at the centre of Fig. 4(c), when both staples A and B have one domain bonded to the scaffold, if domain A2 of staple A bonds first (the lower pathway in the figure), it must close a loop of two domains on the scaffold, whereas if domain B2 of staple B bonds first (the upper pathway in the figure), the loop formed comprises four domains on the scaffold, which entails a larger entropic penalty. Conversely, if staple B does bond fully first, the final bonding of domain 2 of staple A will itself have a reduced entropic cost as it forms the final remaining loop with the scaffold strand. The two effects thus act in different directions and which pathway dominates depends on the relative rates of the steps. Empirically, we know that the pathway is likely to be dominated by the initial closure of smaller loops¹¹⁴ (i.e. the lower pathway in the figure), but even with such a simple set-up, it is not completely trivial to justify ‘by eye’ which pathway is faster and thus more likely to dominate. With such a small system, it is of course possible to calculate the full partition function by enumeration, allowing for a detailed understanding of the assembly process; however, in larger origami designs, and in fact even in only slightly larger toy systems, such a combinatorial problem in the analytical calculations of free energies quickly becomes intractable, as the number of different pathways to assembly explodes with the number of staples and domains in a design.

Simulations run with DNA origami-specific models have demonstrated that loop penalties do not outweigh the gains of intramolecular bonding, but do have a significant impact on the overall degree of cooperativity. For example, we have calculated free energies of assembly along different order parameters and were able to show that once a staple bonds with its first domain, it will typically bond fully before additional staples bond.¹¹⁵ In other words, the entropy loss on intramolecular staple bonding is considerably lower than the penalty paid for loop formation. This result was subsequently confirmed by Najafi,¹¹⁴ who calculated similar free-energy profiles for a broader range of designs using an extended version of a model⁸⁹ that was itself specifically designed to handle the calculation of loop-closure penalties for the assembly of DNA origami (see Section 3.3 for details). In these models, varying the strength of the parameter that controls the cost of forming loops significantly changes the degree of cooperativity in the system's melting and annealing curves.^89,114 The presence of double crossover motifs has a particularly strong effect on cooperativity, as the bonding of the first staple in the motif creates the shortest possible loop for the bonding of the second staple.¹¹⁴ However, these simulation studies have focused on relatively simple designs; more complex origami designs may result in a different balance of such driving forces.¹¹⁶

Not all cooperative effects in DNA-origami self-assembly are intramolecular; intermolecular effects also play an important role, primarily in the form of coaxial stacking interactions between helices formed by different staples. These are the same interactions that occur between each adjacent base pair in two contiguous strands of hybridised DNA (e.g. the π–π interactions between the nitrogenous bases, which contribute roughly half of the stability of the helix¹¹⁷), but now occurring between three strands (i.e. the scaffold and two distinct staple strands). In the final structures of DNA-origami designs, such stacking interactions are commonly found at crossovers between nearby helices. In the simulation studies already mentioned, stacking was generally found to be important for cooperativity, in particular nucleation barriers, which we will return to in Section 2.3, and for selectivity. In simulations with our model,¹¹⁸ a high degree of stacking, which could be achieved by increasing the number of domains per staple (i.e. increasing their valency), led to a particularly sharp transition with respect to the system temperature between fully unassembled and fully assembled states. Such a sharp transition can be used as a form of selectivity: the system is highly sensitive to an environmental change, translating it into a nearly binary switch. Selectivity has been studied more extensively in the context of DNA colloids,¹¹⁹ DNA stars¹²⁰ and more broadly in multivalent systems,¹²¹ where ‘superselectivity’ can be used to discriminate strongly between binding to different receptors or surfaces.¹²² Generally, superselectivity is a manifestation of cooperativity.

Although there is a complex interplay between competing enthalpic and entropic effects with many possible self-assembly pathways, having an understanding, even at a qualitative level, of how cooperativity can enhance some pathways at the expense of others, can help us to design target structures that assemble in a more robust way. We explain in the next section how we can use the same ideas of cooperativity to understand the nature of critical nucleation clusters in the self-assembly process.

2.2 Nucleation barriers allow for error-free assembly

As outlined above, one characteristic feature of self-assembly is hysteresis [Fig. 3(a)], which is clearly observed in the self-assembly of DNA tiles and bricks.^107,123 Computer simulations can help us to gain a molecular-level insight into the nature of this nucleation-like process. In particular, a simple patchy-particle-like model of DNA bricks on a lattice, whose design principles we describe more fully in Section 3.2, qualitatively reproduces many experimental observations,¹²⁴ and it can thus allow us to learn about the fundamental physics of the self-assembly process.

As the temperature of the solution of DNA building-block molecules is reduced, the target structure becomes progressively enthalpically favoured. However, when the system is in a metastable melt, before self-assembly has begun, the first stage of the self-assembly process is disfavoured. When the first two DNA molecules come together and hybridise, they can by construction only do so with a small part of their overall sequence, since each molecule has several neighbours in the target structure. As with the initial bonding of staples to a DNA-origami scaffold discussed above, this initial bonding results in the loss of a considerable amount of translational entropy.¹²⁴

The competition between the favourable enthalpic and the disfavourable entropic contributions results in a free-energy barrier to nucleation [Fig. 3(c)]: it is initially unfavourable for molecules to come together until a critical cluster size is reached. The height of the barrier depends on temperature since the higher the temperature, the more entropic considerations – which favour the solution phase – outweigh enthalpic ones that may favour assembly. Indeed, in the context of DNA self-assembly, the strength of the hydrogen bonding between base pairs itself depends on temperature, as hybridisation too has an entropic component; the temperature dependence of the nucleation free-energy barrier is thus even more pronounced. A statistical-mechanical treatment shows that the critical size is associated with the formation of a closed loop of mutually connected molecules; when a molecule completes a loop, two bonds are formed, resulting in a considerable enthalpic stabilisation for a similar overall loss of entropy, and this results in a decrease in the free energy.^123,125,126 The resulting free-energy profile as a function of the structure size is rather jagged¹²⁴ [Fig. 3(c)(ii)], although, as expected, this jaggedness is less pronounced as the number of nearest neighbours increases¹²⁷ and when the model is allowed to go off-lattice.¹²⁸ There is similar evidence of a nucleation barrier with more detailed models of DNA.¹²⁹

Although it may seem at first glance that a nucleation barrier is an undesirable feature of the self-assembly process, since it effectively slows down the assembly kinetics, it is in fact quite the opposite. A nucleation barrier is essential for the target structure to form in high yields.¹²⁴ At temperatures at which the fully assembled target structure is stable, there is a considerable enthalpic gain in forming clusters. As a result, if no nucleation barrier existed, clusters of partially assembled structures would form everywhere in the reaction mixture [Fig. 5(b)]. This would deplete the monomers required to build each target structure individually, while the partially assembled fragments would not be able to combine in an error-free manner, since the structures are addressable and would need to fit each other perfectly. Having a nucleation barrier ensures that the target structures form relatively rarely, and so when a post-critical cluster occurs, it is likely to be far from all others; this means that growth is more likely to be gradual, indeed almost reversible,^8,126via monomer addition, rather than by several partially formed clusters coming together and aggregating [Fig. 5(a)]. As such clusters grow, their hydrodynamic radius increases and they become progressively slower, meaning partially formed clusters are less likely to encounter one another.¹²³ If the temperature at which assembly is attempted is low enough for the nucleation barrier to disappear, the non-designed interactions are so strong that partially assembled structures readily aggregate, resulting in poor yields of the target structure^{123,124,126,130} [Fig. 5(c)].

Fig. 5 Schematic illustrations of correct and incorrect assembly. Building blocks are illustrated in red when they are in a disordered state (either in solution or as part of an aggregate) and in blue when forming part of the ordered target structure. In (a), we illustrate the nucleation-and-growth picture of addressable self-assembly. If there is a nucleation barrier of a suitable magnitude, nucleation is a rare event and any critical clusters that form will be far away from one another. As a result, they can each recruit monomers into the target structure. In addressable self-assembly, generally there needs to be a final cooling step for the target structure to form to completion, including those building blocks on faces and edges that have fewer connections than at the centre, and are thus less enthalpically favourable. In (b), we assume the system is cooled to a temperature so low that the nucleation barrier is too small for the desired assembly outcome; in this case, post-critical clusters can form in numerous locations, and the resulting clusters deplete the local monomer concentration. Since clusters are hydrodynamically larger than monomers, it becomes progressively more difficult to bring clusters into the correct location, and cluster growth can become arrested and must rely on (generally locally disfavourable) Ostwald ripening. In (c), we show a case where the system has been cooled even further, where the contribution of the entropy loss to the free energy is less significant and any interactions between building blocks, even if they are not the designed interactions, are favourable, and a kinetic aggregate forms instead of the target structure. Finally, in (d), we illustrate seeded nucleation: if a pre-formed boundary brick is present, illustrated by a cyan chain, it can reduce the nucleation barrier as other molecules attach to the boundary brick. A post-critical cluster can thus form at relatively high temperatures, where system dynamics are faster, and the target structure can thus grow rapidly.

The fact that DNA-brick structures are finite means that any molecules near the corners and faces of the structure will have fewer neighbouring molecules with which to hybridise; however, attaching such molecules to the target structure still entails a significant loss of entropy and at temperatures at which there is a nucleation barrier, only partial assembly is possible.¹²⁵ In principle, gradually cooling the system can allow for a nucleation event to occur at a relatively high temperature where a significant nucleation barrier ensures error-free growth, and subsequently for full assembly to be possible as the temperature is decreased. An alternative approach in which the self-assembly can be made more robust is to include ‘boundary bricks’, i.e. longer molecules with more neighbours at the faces and edges of the target structure.⁶³ Such molecules can form longer, more enthalpically favoured connections to the rest of the structure, outweighing the disfavourable entropic cost of full assembly at higher temperatures, and enabling the target structure to assemble successfully without the final gradual cooling otherwise required. Moreover, with such an approach, the nucleation barrier itself can readily be tuned,^123,130,131 as the strongly bonded corner and face fragments can provide a nucleation seed, and can facilitate isothermal assembly as long as the optimal temperature range is already known.¹³⁰ If nucleation occurs at specific longer boundary bricks because the free-energy barrier to nucleation is reduced specifically for these parts of the structure, this can enable the controlled crossing of the nucleation barrier at relatively high temperatures [Fig. 5(d)]; moreover, the system can avoid monomer depletion issues illustrated in Fig. 5(b) because nucleation is not favoured everywhere, but only at the relatively few boundary bricks present in solution. Self-assembly yields can thus be dramatically improved by optimising only a small part of the target structure.^123,130

2.3 Nucleation barriers can be designed in DNA-origami systems

In contrast to DNA bricks, equivalent nucleation barriers are not required for error-free assembly of DNA-origami structures. To show this, we previously simulated the assembly of several small origami designs with a coarse-grained model¹¹⁸ (see Section 3.3 for details of the model). From the simulations, we calculated free energies as a function of two order parameters for assembly: the number of bonded staples, and the number of fully bonded staples. These projections of the free energy revealed the assembly was mostly downhill to the favoured state, with the favoured state shifting towards the assembled state as the temperature is lowered, unless certain design conditions have been met, which we discuss below.

Simulations with a different model provide further evidence that nucleation barriers are not necessary for successful assembly of origami structures. DeLuca et al.¹³² studied a helical bundle design with three domains per staple and found that the assembly process was characterised by two stages. In the first stage, the staples bond to their first and second domains, but not their third. After a sufficient number of staples are bonded, the system undergoes a global collapse involving a zipping mechanism in which the third domains of the bonded staples bond. In the second stage, the remaining staples slowly bond until full assembly is achieved. While free energies were not calculated, the consistency of the global collapse after a specific duration of simulation time implies that the collapse is not a rare event, but part of pathway that is downhill in free energy along the reaction co-ordinate. Some care should be taken in interpreting the results of these simulations, however, as they were carried out at room temperature with a high staple concentration, which are not conditions representative of what is typically used experimentally for assembly. While it is possible to carry out assembly at room temperature, this typically requires the use of specific buffers¹⁰⁶ or chemical denaturants.^108,109 Here, assembly is made favourable by not including misbonding (i.e. domains bonding to other domains with which they are not fully complementary) and by including only a single copy of each staple in the simulation box, which prevents blocked states (i.e. those where two or more copies of a staple bond to its complementary domains, blocking a single staple from bonding fully).

That most DNA-origami structures do not have nucleation barriers and yet still are able to assemble with acceptable yield may seem surprising given the discussion in the previous section about the importance of these barriers in the self-assembly of DNA bricks. The question then becomes how the partly assembled structures do not start to aggregate by staples bonding their complementary domains on multiple scaffolds, how misbonding of staples to off-target domains does not make the assembly time scale infeasible, or how the scaffold domains do not become ‘blocked’ by the bonding of multiple staple strands of the same type to domains on the same scaffold that a single staple should connect in the target structure.

In fact, in the highest-resolution simulations of DNA self-assembly, Snodin et al.¹³³ found one of the greatest kinetic hindrances to full assembly was precisely such blocking, although misbonding, especially of a bonded domain to adjacent domains, also had a substantial effect. However, the results of these high-resolution simulations are not straightforward to interpret, as full assembly was simulated only a single time, using a model with base-pair averaged bonding energies, employing much higher staple strand concentrations than is typical in experiments, and employing a design that lacks long-ranged staple crossovers. It may well be that the timescale of blocking resolution is fast enough not to be a limiting factor in realistic experimental assembly conditions. In contrast to these simulations, coarse-grained simulations of small DNA origamis in which assembly occurs without nucleation barriers¹¹⁸ also revealed that staples tend to bond fully once they find their first domain to the scaffold. When this is the case, since the staple is fully bonded, partially assembled structures are less prone to aggregation than DNA bricks; we discuss larger systems when this is not the case below. Moreover, the complete bonding of a staple may explain why blocking at typical staple concentrations does not occur frequently and is therefore not a major hindrance to correct assembly. Finally, although the coarse-grained model also included misbonding, simulations showed that under typical assembly conditions, staples spend little time in misbonded states.

While apparently not necessary to ensure successful self-assembly in DNA-origami systems, nucleation barriers could still be introduced to increase both the speed and yield of assembly in isothermal conditions. Three methods of introducing nucleation barriers into origami designs have been demonstrated. The first involves exploiting the intermolecular cooperativity that results from coaxial base stacking between the helices formed by different staples. By increasing the valency of a staple, namely by increasing the number of its domains, the number of crossovers that the staple is involved in increases, which increases the number of stacking interactions (see Section 2.1) and, in turn, the degree of cooperativity in its bonding.

Simulations with coarse-grained models^114,118 indicate that stacking interactions can lead to nucleation barriers. In our simulations,¹¹⁸ we showed this by increasing the number of domains per staple in a system with a high density of crossovers between staples, and thus a high number of stacking interactions; this led to the presence of a nucleation barrier. Alternatively, rather than increasing the number of stacking interactions per staple, one could increase the strength of stacking by modifying the design such that the strongest stacking pairs occur in these stacking positions at crossovers, or by using alternative nucleobases. By designing a subset of staples that interact via coaxial stacking to be the most stable staples in the system, a nucleation barrier could be introduced such that assembly can begin in a specific region of the target structure and preferentially grow from there as the temperature is lowered further; that initial bonding of staples can be controlled by their thermal stability is something that has been demonstrated experimentally.¹³⁴

However, simply having many or strong stacking interactions is an insufficient condition on its own for a barrier to exist. Additionally, and critically, the staples, or some subset of the staples, must be monodisperse in their individual melting temperatures (i.e. their melting temperatures assuming no cooperativity). Otherwise, if staple–scaffold interactions are sufficiently nonuniform, a more enthalpically favourable cluster can form at higher temperatures where those interactions happen to be stronger than elsewhere. A stacking interaction, which is a comparatively weak enthalpic factor, may then not be sufficient at such a high temperature to counteract the entropic loss of recruiting a further staple and lower the nucleation barrier enough to enable the system to cross it, and so no assembly occurs. By contrast, as the temperature is lowered, the remaining hybridisation interactions rapidly become more enthalpically favourable and so no nucleation barrier needs to be overcome.

The second and third method for designing nucleation barriers (as well confirmation of the first) were demonstrated in a set of simulations run by Najafi¹¹⁴ with an extended version of a model developed to account explicitly for loop entropy costs,⁸⁹ which we mentioned in Section 2.1 and detail in Section 3.3. The second method involves the formation of loops, or in other words, a barrier due to intramolecular rather than intermolecular factors, as was the case with stacking. Free-energy projections similar to those studied in ref. 118 were also considered by Najafi,¹¹⁴ who found a barrier consistent with the bonding of the staple that spanned the longest segment of the scaffold, a span much longer than any considered in ref. 118. Such a barrier occurs only after many previous staples have already bonded to the scaffold, with the order in which they bond largely determined by the length of the loop that the staples close. However, this barrier, like those that occur with sufficient stacking interactions, also depends on the staples being sufficiently monodisperse.

Finally, in the third method, the idea is that two competing staple sets are used,¹¹⁴ with the staples in one set coating the scaffold and thereby preventing misbonding and aggregation while the temperature is lowered well below the temperature that would otherwise be required for assembly of the given design. When bonded, staples in this first set result in the system forming a simple large double-helical ring. The second set of staples, namely those intended to be incorporated in the final structure, are then introduced. This staple set is designed to have stronger bonding than the first, and in particular, each staple in the second set is designed to be able to replace staples in the first set via toe-hold mediated exchange. Although this method was only demonstrated with homogeneous staple bonding enthalpies, which tends to result in the location of the nucleation seed to be random, it was shown that assembly pathways are those spread from that initial rare staple exchange.¹¹⁴ With such an approach, nucleation once again becomes the rate-controlling step and enables efficient, error-free assembly to occur at much lower temperatures¹¹⁴ than might otherwise be feasible; moreover, controlling nucleation in this manner promises to be much more easily achievable in practical applications.

2.4 Simulations can be used to learn about thermodynamics and kinetics

Understanding how systems self-assemble is not a straightforward endeavour. As we discussed above, self-assembly is a non-equilibrium process. This is true even in the simplest case, where the system starts in a metastable state and relaxes towards the assembled state with no active driving forces. So how then, for example, can we know how to quantify a suitable free-energy barrier?

We will discuss the choice of model resolution below [Section 3], but it is clear that the large numbers of distinct components and the fact that DNA molecules are themselves made up of many atoms will mean that most systems will not be possible to simulate using highly detailed models. The kinds of simple models that are commonly used to gain fundamental physical insight often contain piecewise-continuous potentials that make implementations in molecular dynamics codes more challenging, and many coarse-grained simulations have thus used the Monte-Carlo (MC) algorithm¹³⁵ with a periodic simulation box. In such simulations, the system is evolved in configuration space using stochastic moves with the underlying distribution defined by the acceptance criterion. The commonly used Metropolis algorithm specifically samples from the Boltzmann distribution. Stochastic moves can be physical (e.g. rotations or translations), but one important advantage of MC methods when equilibrating a system is that non-physical moves, such as particles moving through each other, are just as valid as physical ones. However, to obtain dynamic information or approximate trajectories, usually moves must be sufficiently local for MC trajectories to approximate molecular-dynamics simulations.¹³⁶

When clusters form in a system, using single-particle moves is usually doomed to fail at accessible time scales, since to move a cluster one particle at a time would necessitate its break-up in the process. To approximate the underlying dynamics, one can use the virtual-move MC algorithm^137,138 or a simpler hybrid scheme accounting separately for cluster diffusion and cluster growth and shrinkage¹³⁹ to improve sampling efficiency. By using such algorithms, simulations of the system remain as realistic as possible given the model resolution. Indeed, by comparing ratios of properties such as diffusivities determined in simulations to those known from experiment, and repeating the procedure for a range of different systems of interest, we can help ascertain how reasonable a description of each such property the model is likely to provide, and so in turn how much faith we can have in its results and predictions.

Such coarse-grained simulations are often sufficient even to describe the nucleation process itself. For example, brute-force trajectories can be analysed in order to determine whether the process is governed by a stochastic rare-event nucleation step by checking if the lag times are Poisson-distributed.¹⁴⁰ However, in order to understand the underlying physics, we often like to think about the energetic and entropic factors that may give rise to a free-energy barrier to nucleation. Although the true reaction co-ordinate may be a very complicated collective variable of the system, in order to make qualitative progress, it is convenient to determine the free energy as a function of a suitable low-dimensional order parameter that can quantify the progress of the self-assembly process. If such an order parameter is identified, we can use brute-force simulations to find the mean first-passage time,¹⁴¹i.e. the mean time necessary for the system to first reach a certain value of the order parameter. The mean first-passage time could be used to find an approximate measure of the rate of nucleation, the critical cluster size and the Zeldovich factor¹⁴² for nucleation.¹⁴³ For MC simulations with coarse-grained potentials, the rate itself is not likely to be a realistic quantity compared to experiment; nevertheless, coupled with classical nucleation theory, the approach can help us to determine crudely whether the free-energy barrier increases or decreases as some parameter of the system is varied with a minimum of effort, provided the nucleation event is sufficiently frequent to capture in brute-force simulations.¹³¹

Both the thermodynamics and the kinetics of a system are ultimately controlled by the underlying potential-energy landscape. For sufficiently small systems, it may be possible to investigate the full potential-energy landscape¹⁴⁴ of addressable systems; however, this is generally infeasible for large target structures. Instead, we usually investigate the free energy as a projection of the potential-energy landscape onto a suitable order parameter, which is feasible to explore even for larger systems.^145,146 To determine an approximate free-energy profile as a function of some order parameter for such systems, there are several possible approaches. Conceptually the simplest may be umbrella sampling,^147,148 where in the Metropolis acceptance criterion we use a biased Boltzmann distribution to force the sampling of previously unsampled regions, even if they are free-energetically disfavourable. A similar method to adaptive umbrella sampling in molecular-dynamics simulations is metadynamics.¹⁴⁹

A powerful alternative method to enhance sampling is replica-exchange Monte Carlo (REMC),^150–153 where several replicas of the system are simulated in parallel, with different replicas using perturbed hamiltonians that can in some way depend on the order parameter. By allowing these replicas to be exchanged with one another with a suitable probability, if the exchange variables provide a good proxy for sampling across the relevant range of the order parameters of interest, less well sampled regions for the unperturbed hamiltonian can be explored. Data from simulations of multiple states can then be reweighted to the state of interest;¹⁵⁴ often, this is achieved with the weighted histogram analysis method (WHAM)¹⁵⁵ by binning the data into histograms, or with the multi-Bennett acceptance ratio (MBAR) method,^156,157 which does not require binning. Both methods can be used to combine and reweight the results of multi-window umbrella-sampling simulations or REMC simulations to take advantage of data at states other than those of interest.

With these methods, a free-energy profile similar to Fig. 3(c) can be constructed, which, as discussed above, can offer us significant insight into what governs the self-assembly process. However, it is worth emphasising again that the free energy is a projection of the potential-energy landscape onto a particular order parameter. The quality of the free-energy profile depends on how sensible the order parameter is and how relevant it is to the true reaction co-ordinate.^105,140 The free energy as a function of a well-chosen order parameter can give us a great deal of insight, but a poorly chosen one is at best misleading.

3 Challenges in selecting model resolution

In general, when modelling any system, the choice of model resolution is a compromise between accuracy (higher resolution) and tractability (lower resolution), with the latter typically referring to the computational resources required to run simulations with the model. To deal with this issue, the first step is to identify the elements of the system expected to be relevant to the problem at hand, and consider the relative magnitude of their impacts. These elements can often be organised hierarchically, with those at the bottom involving smaller length- and time-scales. Investigating their relevance can inform the level of detail required in a model so that it can be used to answer the questions of interest.

As with self-assembly designs themselves, there are various approaches to coarse-graining,¹⁵⁸ including ‘bottom-up’ approaches, where higher-resolution models are used to parameterise a coarse-grained potential, for example with iterative Boltzmann inversion¹⁵⁹ or force matching,¹⁶⁰ and ‘top-down’ approaches, where approximations of the fundamental physical driving forces are made, typically to match known experimental data, allowing for complex features and behaviour to emerge.

There is generally no unique solution when coarse-graining high-resolution models in a bottom-up approach,^161,162 whilst for the top-down approach, the risk may be that we need to understand the underlying system sufficiently well to know what kinds of physical interactions are important, and the predictions resulting from such top-down approaches crucially depend on what a model was designed to account for.¹⁶³ Although coarse-grained models are sometimes placed low on the accuracy scale compared to high-resolution models, this is not always a fair assessment of their performance; ‘accuracy’ is this context is dependent on the property that is being studied. Such models can be very accurate at modelling the phenomenon they were designed to model, but it can be dangerous to apply a coarse-grained model parameterised for studying one property to a different class of problem without understanding what the consequences of doing this are.

In the context of DNA specifically, a great variety of models have been developed.^164–169 These span the gamut of particle resolution, ranging from atomistic,¹⁶⁸ sub-nucleotide coarse-grained models,^{168,170–195} single and multiple nucleotide coarse-grained models,^196–204 single and multiple base-pair coarse-grained models,^205–208 to continuum models.²⁰⁹ Some are intended as general DNA models, while others are designed with specific applications in mind. For example, models of DNA that are more statistical in nature have been designed to gain a better understanding of the fundamentals of hybridisation and denaturation of strands.^210–217 A thorough review of the state of the art in the choice of model resolution in computer simulations of DNA self-assembly was recently written by DeLuca and co-workers;¹⁶⁴ in particular, they provide a careful exposition of the comparison between simulations and experimental data, as well as on the study of material properties of already assembled structures. Here, we therefore offer only a brief overview of the relevant material with a focus on the models that we have already discussed in previous sections.

3.1 DNA hybridisation is well-described with a nearest-neighbour model

For questions regarding DNA self-assembly, there must always be some underlying description of the hybridisation free energy of contiguous strands of DNA. DNA hybridisation is actually itself a rather complex process, involving multiple specific hydrogen-bond and base-stacking interactions, interactions with cations in solution, and the stretching and twisting of internal bonds as a balance is achieved between the new non-covalent bonds with the configuration of the existing internal covalent bonds. To account for such interactions precisely would require a very detailed model. However, the fine details of hybridisation are likely not too important in understanding the broad strokes, and perhaps even the finer nuances, of the details of the pathways involved in self-assembly, as evidenced by the success of a plethora of coarse-grained potentials in describing the process.

For most models of DNA self-assembly, an empirically parameterised model is used to describe the free energies of hybridisation of two strands of DNA.²¹² A naïve approach to calculating the free-energy change upon hybridisation of two strands would be to sum the free-energy contribution of each base pair, with different contributions from A/T base pairs and C/G base pairs, plus some additional free-energy cost of bringing the two strands together. However, in addition to the difference in hydrogen bonding between base pairs, there are differences in the interactions (e.g. the base stacking) between different combinations of base pairs. In what is commonly referred to as the nearest-neighbour (NN) approach,²¹² the two directly adjacent nucleotides are considered to provide sufficient context for calculating an accurate contribution to the free energy of hybridisation, such that

where is the standard state NN Gibbs energy of hybridisation, n is the number of base pairs, and is the contribution of the pair of base pairs at positions i and i + 1 to the standard-state NN Gibbs energy. This results in ten parameters instead of only two, corresponding to ten distinct combinations of base pairs. 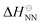The number of parameters doubles if a temperature dependence of the free energy is desired, as now the enthalpy and entropy are required separately, with where is the standard state NN enthalpy and is the standard state NN entropy. One could consider going even further and including the next-nearest neighbours, but this was found to lead to little increase in accuracy.²¹²

To determine the parameters for a NN model, one can measure the melting temperatures for a set of sequences across a range of concentrations, providing the enthalpies and entropies for each sequence, which can then be used in a linear regression. The enthalpies and entropies are usually assumed to be independent of temperature, so the validity of the parameters decreases when the temperature deviates too far from the melting temperatures of the sequences used in the parameterisation, although this dependence can be accounted for.^218–220 These models have also been modified to account for varying salt concentrations.^212,220,221 Besides fully hybridised states, NN models can also account for single internal and terminal mismatches,^222–226 dangling ends,²²⁷ various loops and bulges, and coaxial stacking between separate strands.²¹² A number of groups have derived NN parameter sets, but the most successful of them was derived by the SantaLucia group.^212,222,228

3.2 A minimal model gives significant insight into DNA-brick self-assembly

In the original formulation of DNA-brick systems, Ke and co-workers used 32-nucleotide ssDNA molecules made up of four domains.⁶³ In the target structure, each of these domains hybridised with other distinct DNA-brick molecules. As shown in Fig. 2, the dihedral angle between strands at a crossover, when the domain length is 8 base pairs, is approximately 90°, resulting in an approximately cubic lattice. In order to model such systems, we wanted to design a coarse-grained potential that was simple enough to be computationally tractable while capturing the fundamental physics. Ke and co-workers noticed that the centres of mass of each DNA-brick molecule in the fully assembled target structure form a distorted diamond lattice,⁶³ and to a first level of approximation, we therefore modelled each DNA-brick molecule as a patchy particle with tetrahedrally arranged patches [Fig. 6(a)].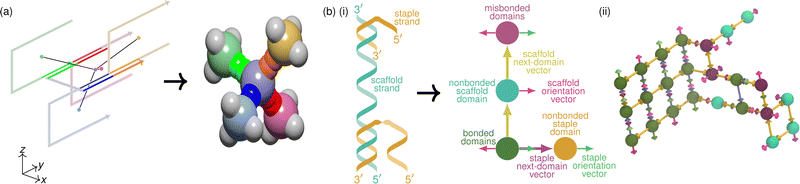

Fig. 6 Coarse-graining DNA bricks and DNA origami. In (a), we show a pictorial representation of DNA bricks in a fragment of the target structure similar to Fig. 1. A DNA molecule in the xy plane is shown with its four neighbours, each in the yz plane, assuming a 90° dihedral angle. Arrows indicate the helical direction of each molecule, and complementary strands are shown in red, green, blue and orange. The centre of each molecule is highlighted with a coloured circle, and these centres are connected with lines to show the roughly tetrahedral connectivity⁶³ in space of the central molecule. We also show the corresponding patchy-particle representation:¹²⁴ each particle corresponds to one of the coloured centres in the left-hand schematic, with pairs of patches of the same colour corresponding to complementary sequences. In (b)(i), we show an example of a mapping from a strand representation of a DNA-origami system to the lattice model of ref. 115 and 118. Each domain on the scaffold and staple strands is represented as an occupied lattice site, but a lattice site can also be occupied doubly to represent either correctly or incorrectly bonded domains, as illustrated. The vectors indicated in the diagram are used to implement the model's state space and energy potential for describing allowed configurations and their energies. In (ii), we show an illustration of a simulation snapshot of a partially assembled DNA origami with this model.

The fundamentals of DNA hybridisation are captured in the model by assigning a unique sequence to each patch, such that sequences of patches that point at each other in the target structure are complementary. The effective interaction energies between the two nearest patches on different particles are then computed by finding the longest complementary sequence match and using the NN model (Section 3.1) to compute the free energy of hybridisation,²¹² assuming that the patches are suitably close to interact.

We then used both lattice¹²⁴ and off-lattice¹²⁸ Monte-Carlo simulations to investigate the self-assembly process. For the off-lattice potential, we used the Kern–Frenkel potential.²²⁹ This potential is effectively a square well with an additional angular dependence that ensures that only patches pointing at each other within a certain width can interact favourably. The appropriate interaction energy also has to be modulated by taking into account this width; we compute it by determining the equilibrium constant for dimerisation from statistical mechanics and imposing agreement with the NN model for the same pair of molecules.¹²⁸

Even though such a model of DNA bricks is very minimal, it nevertheless captures most of the interesting self-assembly behaviour observed in experiment,^{123–128,130,131} such as how nucleation barriers prevent large-scale misassembly or how boundary bricks can enable a self-assembly pathway to be designed, as discussed in Section 2.2. This good qualitative agreement suggests that it is not principally the details of the structure of the building blocks that matter, but that the self-assembly process is fundamentally governed by their connectivity, addressability and specificity.¹²⁴ Indeed in principle the building blocks do not need to be DNA-based at all. It is worth bearing in mind, however, that it is not a priori obvious that a model as simple as this would have led to the conclusions we have outlined above; specifically, in native-contact-based Gō models, denatured proteins do not readily fold back to the native assembled form.²³⁰ The good agreement with experiment in this case is itself a useful observation, as it suggests both that the model is capturing the fundamentals of DNA interactions well enough and that the fine details of the interactions and geometry are apparently not driving the self-assembly process.

3.3 Multiple models of DNA origami complement each other in describing self-assembly and assembled states

Some approaches to modelling DNA origami are intended or only feasible for studying the assembled state. Because most experimental characterisation of folded states is in the form of atomic-force microscopy, which requires the origami structure to be adsorbed on a surface, these studies of assembled states provide a much needed glimpse at the structure when free in solution, as well as a way to study their mechanical properties. The brute-force approach is to use fully atomistic simulations, which in addition to mechanical properties can also be used to study the dynamics of the assembled structures.^231,232 Unfortunately, such simulations are time consuming and include much more detail than is necessary if one is interested only in the mechanical properties of assembled states. A more popular and successful approach with such a focus has been developed,^14,233,234 in which DNA double helices are modelled as finite-element elastic rods rigidly connected to other double helices, whilst single-stranded DNA is modelled as a finite-element approximation of a freely jointed chain; the system is relaxed from a given initial state to find a force-balanced equilibrium state. A later model that takes a more discrete approach to studying mechanical properties has also been developed.²³⁵ Alternatively, rather than choosing a single resolution, multi-scale approaches have been developed for studying the assembled state.^236–240

To answer questions regarding assembly pathways for DNA origami, the level of detail must be sufficient to allow for the inclusion of both the intermolecular and intramolecular forms of cooperativity, which in this case is primarily the reduction in translational entropy costs of having multiple domains per staple, the loop-closure costs of linking the scaffold with the staples and the coaxial stacking between helices formed by different staples (see Section 2.1 for further discussion). On the other hand, the level of detail must not be too high so that it does not become infeasible to run simulations that are sufficiently long to capture the entire assembly process, and, further, to gather sufficient statistics to be able to compute quantities such as free energies accurately. Attempts at modelling this process have included both top-down and bottom-up approaches, and different choices have been made about the features of the systems that should be accounted for. These include models that extend the NN model of DNA hybridisation described above, lattice and off-lattice models that coarse-grain to the level of domains, and more general and detailed coarse-grained DNA models applied to this particular problem.

With the NN approach as a foundation, Arbona, Aimé and Elezgaray^90–92 modelled the assembly process as a series of equilibrium reactions to calculate the likelihood that a particular staple or individual staple domain is bonded to its complementary domain(s) on the scaffold at a given temperature. To calculate the equilibrium constants of each reaction, they introduced a model for the free-energy change upon bonding of each staple, ΔG = ΔG_NN + ΔG_top, where ΔG_NN is from the NN model and ΔG_top is the contribution from the topology of the system in its current bonded state. To solve their equations, they made a number of assumptions. The first was to assume that staples bond fully and only to the correct domains. The second was to assume that if the probability of one staple bonding to the scaffold is greater than another, then that staple will always bond first. Perhaps most fundamental, however, are the assumptions involved in calculating ΔG_top, which involves considering the free-energy cost of forming loops when new staples form. They calculated the loop contribution by empirically modulating another term from the NN model that gives the free-energy cost of hybridising two strands when a segment of one of the strands has extra, non-complementary bases that stick out and form a bulge. These extensions to the NN model represent a starting point for modelling DNA-origami self-assembly. However, the strong assumptions made resulted in a thermodynamically inconsistent model,⁸⁹ and this provided an impetus for further model development.

In particular, the lack of a timescale in statistical approaches led Dannenberg et al.⁸⁹ and Dunn et al.⁸⁸ to formulate their model as a continuous-time Markov chain (CTMC), where the state space is described by the bonding states of each staple type in the system, which allows a clearer link to the kinetics of the assembly process. The state space is described by the states of each staple type in the system, where a two-domain staple can either be non-bonded, bonded to one, the other, or both scaffold domains, or have two copies, one at each domain. In a later extension of the model,¹¹⁴ state spaces with up to three domains per staple, as well as toehold-mediated exchange between two different staple types bonding a shared segment of the scaffold were made possible to simulate. The absolute values of the rate constants are estimated by assuming the reverse rate to be the unbonding rate of an isolated duplex. The CTMC is simulated by selecting a timestep interval and a temperature change rate, and cycling between an initial and final temperature. As before, the NN model is used for the basic hybridisation free energy, supplemented with a term to include the effects of topology, but here an additional term is added to describe stacking interactions between staple domains on separate staples bonded to contiguous segments of the scaffold, ΔG_stack. The stacking term is also based on the NN model; the sequence-averaged value is multiplied by a parameter tuned during the parameterisation of the model. The topology term is taken to be the free-energy change upon breaking and forming loops in the system, and the total contribution relative to the fully non-bonded state is

where G^top_s is the absolute free energy in state s, G^top_null is the absolute free energy in the non-bonded state, L(s) is the set of loops in state s and ΔG^loop_j is the free energy of forming loop j. For 2D origami designs, the loops can be unambiguously identified, whilst more complex designs require a simplified approach, where only free-energy changes resulting from the formation or dissolution of the smallest loop are assumed to be relevant.⁸⁹ The loop free energies are calculated from the probability that the ends of the loop come together within an arbitrarily small distance when not constrained, assuming the probability distribution can be described by that of a freely jointed chain, resulting inwhere γ and C are parameterised constants, and E[r²]_loop is the mean squared distance between the two ends.

These approaches directly extend the NN approach and allow the assembly process for reasonably sized target structures to be simulated in under an hour on current computers, and have led to some important insights into the self-assembly process (see Section 2). Nevertheless, the efficiency advantage that such statistical models provide comes at the price of having no explicit geometric representation of the system and making fairly strong assumptions about the entropic changes that occur during assembly. Furthermore, in ref. 88, an ad hoc exclusion algorithm is used to reject configurations that are not on a pre-defined folding path as a proxy for steric constraints. Finally, these models ignore the possibility that staples may bond, albeit less strongly, to incorrect domains.

In contrast to these top down approaches based on the NN model, Snodin et al.¹³³ used a more popular higher resolution model known as oxDNA^241–246 that was developed to simulate DNA self-assembly. This model is coarse-grained to the level of nucleotides, which are rigid and resolve the backbone from the base in the potential. The potential includes a spring potential for the backbone, excluded-volume interactions for the backbone and base, as well as hydrogen bonding base-stacking interactions that have an angular component. It was parameterised by matching to structural, thermodynamic and mechanical properties with a trial-and-error approach. The model has been successfully used to study mechanical properties of DNA-origami structures,^242,247 as well as their stability upon force-induced unravelling.²⁴⁸ In the application of this model to DNA-origami self-assembly, a full assembly event was captured in unbiased simulations of the system, which allowed the process to be studied in unprecedented detail.¹³³ However, because of the level of detail that oxDNA provides, simulations of a small origami design with only short loops present in the final structure took several months on a cluster with GPU acceleration. Moreover, it was found to be necessary to use staple concentrations in excess of those typically used in experimental assembly conditions. This is not just a matter of speeding up the kinetics: such high concentrations shift the equilibrium between free and bonded staple strands towards the bonded states.

In order to fill the gap between the more detailed models of DNA such as oxDNA and the less detailed models described above, we developed a model of DNA origami that does include an explicit model of the geometry of the system but is still sufficiently coarse-grained to allow for the simulation of the assembly process.^115,118 The model, inspired by the lattice model of DNA bricks described in Section 3.2, is lattice-based and at the level of resolution of domains. Each domain is represented as an occupancy on the lattice, and has both a next-domain vector and an orientation vector associated with it [Fig. 6(b)]. A given lattice site can have an occupancy of up to two domains, in which case they are considered to be hybridised, with the hybridisation occurring between the longest contiguous section of complementary nucleotides between the domains. In other words, any two domains are able to hybridise, meaning that misbonding is taken into account. The next-domain vector points to the neighbouring lattice site that the next domain along the same chain occupies, if it exists, while the orientation vector, very roughly, points from the helical axis to the location of the strand at the end of the domain. The orientation vector is included to retain information on the current phase of a double helix, which puts a constraint on where strand crossovers can occur between two different helices.

The energy potential for our model comprises a bonding term, a stacking term and a steric term, and is in general a function of the lattice occupancies, the next-domain vectors and the orientation vectors in the system. The bonding term is based on the free energy of hybridisation from the NN model of ref. 212, using the longest contiguous complementary sequence between two hybridised domains (i.e. domains occupying the same lattice site). The NN free energies are modified in a similar way to the DNA-brick model discussed in Section 3.2, such that the equilibrium constants are consistent with the degrees of freedom that are accounted for explicitly in this model.^118,249 The stacking term accounts for the free energy associated with the coaxial stacking between two helices formed by separate pairs of domains, which may share one or both strands. Finally, the steric term accounts for the excluded-volume interactions that are implied by the lattice occupancies, the next-domain vectors and the orientation vectors of the system, and essentially prevents model states that do not correspond to realistic underlying configurations of the system.

With this model, we can directly simulate the assembly process of some small origami designs and even calculate free energies projected on some relevant order parameters; however, the model still requires custom simulation methods and significant computational resources to compute thermodynamic properties. In particular, to achieve sufficient statistics for free-energy calculations, the umbrella sampling, REMC and MBAR methods discussed in Section 2.4 were combined with custom MC move types, and required several days of simulation across multiple CPU threads for each design studied. Moreover, some of the assumptions made in the model's design do limit the scope of its applicability. For example, the staple concentrations are assumed to be constant over the course of assembly, which assumes a significant reservoir of building blocks exists. More fundamentally, the designs able to be modelled are limited to those that can be represented on a cubic lattice, and the lattice nature means that dynamical quantities can only be estimated indirectly through MC simulations. Finally, although the geometry of the system is modelled explicitly, the entropy costs of loop formation can only be correct up to some constant,^118,249 and are unlikely to be very precise given that they were not explicitly parameterised in this relatively coarse model. Despite these caveats, the model is sufficiently powerful to allow us to gain significant insights into the self-assembly process, as detailed in Section 2.

Finally, another model at a similar level of resolution as that of ref. 115, but that is off-lattice, has very recently been proposed.¹³² Since it can be used in molecular-dynamics (MD) simulations, it could be used to study kinetics. The model explicitly accounts for mechanical properties of double-stranded (ds) DNA.¹³² It resolves 8-nucleotide domains as beads and the potential is parameterised with a bottom-up approach, with the oxDNA model as the higher-resolution model. In particular, the hybridisation energy in the energy potential contains a term that is smoothly switched on as a function of the distance between two domains. This dependence is determined by calculating free energies from simulations performed with oxDNA as a function of the distance between the two domains in question. In addition, the harmonic potentials used to describe the stretching and bending terms are switchable in order to capture the different mechanical properties between ssDNA and dsDNA. However, some potentially important interactions are not included in the model in its current form: the complementary pairings are programmed in such that no misbonding is included and there is no term for coaxial stacking between domains. Nevertheless, the model holds significant potential to provide insight into the assembly process and promises to be particularly useful in understanding the unique aspects involved the assembly of 3D designs or designs with intrinsic mechanical strain.

Because of the inherent challenges in studying the self-assembly of DNA origami, where we must account for the folding of a long scaffold strand alongside the strong, specific bonding of a potentially large number of unique staple strands,²⁵⁰ there is no single best model that could answer all pertinent questions about the process. Each of the models we have discussed here entails different trade-offs between resolution and computational tractability, and makes different choices regarding the most relevant features to include and the assumptions and approximations that are deemed acceptable. Although each model has its own strengths and weaknesses, they complement each other, and by combining a range of models with different simulation techniques and piecing together the insights each offers, we can begin to understand the self-assembly process at an intuitive level.

4 Conclusions

In this review, we have shown that DNA nanotechnology provides a rich set of behaviours that we can use to understand fundamental thermodynamics and kinetics, from designing assembly pathways to probing phenomena such as nucleation and growth. On the other hand, we discussed how a full understanding of the underlying physics is important from an applications perspective, as it furthers our ability to design target structures that assemble correctly, rapidly and cheaply, and are as stable (or unstable) as a given application calls for. We have argued that, even if large systems cannot usually be simulated at a very fine all-atom resolution, considerable insight can be gained by coarse-graining and using models that are best suited for the level of understanding we are trying to achieve. While ultimately, it is of course experimental observations that give us the ground truth and inform us of what is and what is not important, we have outlined some of the successes of the use of computer simulations and how they tie in with experimental observations.

We hope that by doing so, we have shown how useful simulations can be in interpreting and framing experimental observations, understanding possible self-assembly pathways at the molecular level, and helping to design pathways to optimise assembly yields. Using simulations alongside experiments has proved especially productive. In recent years, encouragingly, most simulation codes have been made available alongside the papers in which they were introduced, which can democratise access to them and enable everyone to play with and test various models. One must bear in mind, however, that simulations ought not to be used as a ‘black box’ without a clear understanding of how they work and what their limitations are likely to be: it is very easy to be misled by a simulation that may look persuasive at first glance but that may not be modelling the right physics for the problem at hand.

Furthermore, although toy systems can often give us a great amount of insight, there are important caveats when generalising any broad principles that simulations using them appear to reveal. For example, although simulations on small two-dimensional DNA-origami systems indicate that staple strands bond fully once the first domain bonds with the scaffold,^114,115 in an experimental study of a larger 3D-lattice-based system with more domains per staple than those considered in the simulation studies, there is evidence that this observation does not hold in such systems.¹¹⁶ This is not an indictment of simulations: it is after all obvious that the conclusion must depend on the design of the system, since in the limit of a staple with many domains, there is a considerably larger entropic cost to bonding the entire staple strand than in their smaller analogues. Instead, the result underlines on the one hand the need for further simulation studies to gain a deeper understanding of ever more complex experimental results, and, on the other, the need to exercise caution when generalising results from simpler systems to larger designs.

Here, we have focused entirely on DNA-based self-assembly, but we have not considered the material properties of the target structures in any great detail. It is worth bearing in mind again that coarse-grained models cannot be used to study problems they were not designed for, and it is important to be aware of the limits of applicability of any model we may wish to use for a given application. Specifically, while we can use very simple models to investigate the beginnings of a nucleation process, the same kinds of model are unlikely to be able to estimate, for example, how flexible a particular section of an assembled structure is going to be. Whilst we have not discussed this here, considerable work has been done to understand the material properties of assembled structures using computer simulations, and much of it has been reviewed in the recent work of DeLuca and co-workers.¹³²

Finally, we expect that the use of machine learning may soon play a greater role in predicting the material properties of DNA nanostructures and aid in their design. Already, DNA-origami shape prediction,²⁵¹ detection^252,253 and optimisation,²⁵⁴ and the characterisation of their fluctuations²⁵⁵ have been probed with machine-learning approaches, and one can envisage the development of machine-learned potentials that can bridge the gap between different coarse-grained potentials. However, although training machine-learning models on simulation data may on the one hand help us to come up with sequence designs with desired assembly pathways, characterising the self-assembly process itself will be a rather more challenging endeavour without recourse to computer simulation. In particular, as discussed above, self-assembly is a non-equilibrium process: while machine learning is excellent at providing interpolations in well-sampled space, learning from a smaller set of examples is not its strength. We believe that physics-based modelling will continue to be crucial in gaining an intuitive understanding of self-assembly.

Data availability

No primary research results, software or code have been included and no new data were generated or analysed as part of this review.

Conflicts of interest

There are no conflicts to declare.

References

1. S. Hirschi, T. R. Ward, W. P. Meier, D. J. Müller and D. Fotiadis, Synthetic biology: bottom-up assembly of molecular systems, Chem. Rev., 2022, 122, 16294–16328,  DOI:10.1021/acs.chemrev.2c00339.
2. D. Frenkel, Order through entropy, Nat. Mater., 2015, 14, 9–12,  DOI:10.1038/nmat4178.
3. G. A. Knappe, E.-C. Wamhoff and M. Bathe, Functionalizing DNA origami to investigate and interact with biological systems, Nat. Rev. Mater., 2022, 8, 123–138,  DOI:10.1038/s41578-022-00517-x.
4. N. C. Seeman, Structural DNA Nanotechnology, Cambridge University Press, 2015.
5. N. C. Seeman, Nanomaterials based on DNA, Annu. Rev. Biochem., 2010, 79, 65–87,  DOI:10.1146/annurev-biochem-060308-102244.
6. N. C. Seeman, Nucleic acid junctions and lattices, J. Theor. Biol., 1982, 99, 237–247,  DOI:10.1016/0022-5193(82)90002-9.
7. E. Winfree, F. Liu, L. A. Wenzler and N. C. Seeman, Design and self-assembly of two-dimensional DNA crystals, Nature, 1998, 394, 539–544,  DOI:10.1038/28998.
8. C. G. Evans and E. Winfree, Physical principles for DNA tile self-assembly, Chem. Soc. Rev., 2017, 46, 3808–3829,  10.1039/c6cs00745g.
9. M. Tintoré, R. Eritja and C. Fábrega, DNA nanoarchitectures: steps towards biological applications, ChemBioChem, 2014, 15, 1374–1390,  DOI:10.1002/cbic.201402014.
10. P. W. K. Rothemund, Folding DNA to create nanoscale shapes and patterns, Nature, 2006, 440, 297–302,  DOI:10.1038/nature04586.
11. R. Holliday, A mechanism for gene conversion in fungi, Genet. Res., 1964, 5, 282–304,  DOI:10.1017/S0016672300001233.
12. D. Han, S. Pal, J. Nangreave, Z. Deng, Y. Liu and H. Yan, DNA origami with complex curvatures in three-dimensional space, Science, 2011, 332, 342–346,  DOI:10.1126/science.1202998.
13. S. M. Douglas, H. Dietz, T. Liedl, B. Hoegberg, F. Graf and W. M. Shih, Self-assembly of DNA into nanoscale three-dimensional shapes, Nature, 2009, 459, 414–418,  DOI:10.1038/nature08016.
14. C. E. Castro, F. Kilchherr, D.-N. Kim, E. L. Shiao, T. Wauer, P. Wortmann, M. Bathe and H. Dietz, A primer to scaffolded DNA origami, Nat. Methods, 2011, 8, 221–229,  DOI:10.1038/nmeth.1570.
15. D. Han, S. Pal, Y. Yang, S. Jiang, J. Nangreave, Y. Liu and H. Yan, DNA gridiron nanostructures based on four-arm junctions, Science, 2013, 339, 1412–1415,  DOI:10.1126/science.1232252.
16. E. Benson, A. Mohammed, J. Gardell, S. Masich, E. Czeizler, P. Orponen and B. Hogberg, DNA rendering of polyhedral meshes at the nanoscale, Nature, 2015, 523, 441–444,  DOI:10.1038/nature14586.
17. C. E. Castro, H.-J. Su, A. E. Marras, L. Zhou and J. Johnson, Mechanical design of DNA nanostructures, Nanoscale, 2015, 7, 5913–5921,  10.1039/c4nr07153k.
18. F. Zhang, S. Jiang, S. Wu, Y. Li, C. Mao, Y. Liu and H. Yan, Complex wireframe DNA origami nanostructures with multi-arm junction vertices, Nat. Nanotechnol., 2015, 10, 779–784,  DOI:10.1038/nnano.2015.162.
19. H. Ijäs, S. Nummelin, B. Shen, M. Kostiainen and V. Linko, Dynamic DNA origami devices: from strand-displacement reactions to external-stimuli responsive systems, Int. J. Mol. Sci., 2018, 19, 2114,  DOI:10.3390/ijms19072114.
20. G. Tikhomirov, P. Petersen and L. Qian, Fractal assembly of micrometre-scale DNA origami arrays with arbitrary patterns, Nature, 2017, 552, 67–71,  DOI:10.1038/nature24655.
21. K. F. Wagenbauer, C. Sigl and H. Dietz, Gigadalton-scale shape-programmable DNA assemblies, Nature, 2017, 552, 78–83,  DOI:10.1038/nature24651.
22. M. T. Luu, J. F. Berengut, J. Li, J.-B. Chen, J. K. Daljit Singh, K. Coffi Dit Glieze, M. Turner, K. Skipper, S. Meppat, H. Fowler, W. Close, J. P. K. Doye, A. Abbas and S. F. J. Wickham, Reconfigurable nanomaterials folded from multicomponent chains of DNA origami voxels, Sci. Rob., 2024, 9, eadp2309,  DOI:10.1126/scirobotics.adp2309.
23. D. Han, X. Qi, C. Myhrvold, B. Wang, M. Dai, S. Jiang, M. Bates, Y. Liu, B. An, F. Zhang, H. Yan and P. Yin, Single-stranded DNA and RNA origami, Science, 2017, 358, eaao2648,  DOI:10.1126/science.aao2648.
24. L. Piantanida, J. A. Liddle, W. L. Hughes and J. Majikes, DNA nanostructure decoration: a how-to tutorial, Nanotechnology, 2024, 35, 273001,  DOI:10.1088/1361-6528/ad2ac5.
25. K. F. Wagenbauer, N. Pham, A. Gottschlich, B. Kick, V. Kozina, C. Frank, D. Trninic, P. Stömmer, R. Grünmeier, E. Carlini, C. A. Tsiverioti, S. Kobold, J. J. Funke and H. Dietz, Programmable multispecific DNA-origami-based T-cell engagers, Nat. Nanotechnol., 2023, 18, 1319–1326,  DOI:10.1038/s41565-023-01471-7.
26. J. Gorman, S. M. Hart, T. John, M. A. Castellanos, D. Harris, M. F. Parsons, J. L. Banal, A. P. Willard, G. S. Schlau-Cohen and M. Bathe, Sculpting photoproducts with DNA origami, Chem, 2024, 10, 1553–1575,  DOI:10.1016/j.chempr.2024.03.007.
27. S. Dey, C. Fan, K. V. Gothelf, J. Li, C. Lin, L. Liu, N. Liu, M. A. D. Nijenhuis, B. Saccà, F. C. Simmel, H. Yan and P. Zhan, DNA origami, Nat. Rev. Methods Primers, 2021, 1, 13,  DOI:10.1038/s43586-020-00009-8.
28. D. Balakrishnan, G. D. Wilkens and J. G. Heddle, Delivering DNA origami to cells, Nanomedicine, 2019, 14, 911–925,  DOI:10.2217/nnm-2018-0440.
29. H. Bila, E. E. Kurisinkal and M. M. C. Bastings, Engineering a stable future for DNA-origami as a biomaterial, Biomater. Sci., 2019, 7, 532–541,  10.1039/c8bm01249k.
30. Y. Dong and Y. Mao, DNA origami as scaffolds for self-assembly of lipids and proteins, ChemBioChem, 2019, 20, 2422–2431,  DOI:10.1002/cbic.201900073.
31. S. Fan, D. Wang, A. Kenaan, J. Cheng, D. Cui and J. Song, Create nanoscale patterns with DNA origami, Small, 2019, 15, 1805554,  DOI:10.1002/smll.201805554.
32. S. Ramakrishnan, H. Ijäs, V. Linko and A. Keller, Structural stability of DNA origami nanostructures under application-specific conditions, Comput. Struct. Biotechnol. J., 2018, 16, 342–349,  DOI:10.1016/j.csbj.2018.09.002.
33. Y. Sakai, M. S. Islam, M. Adamiak, S. C.-C. Shiu, J. A. Tanner and J. G. Heddle, DNA aptamers for the functionalisation of DNA origami nanostructures, Genes, 2018, 9, 571,  DOI:10.3390/genes9120571.
34. S. Kogikoski, W. J. Paschoalino and L. T. Kubota, Supramolecular DNA origami nanostructures for use in bioanalytical applications, TrAC, Trends Anal. Chem., 2018, 108, 88–97,  DOI:10.1016/j.trac.2018.08.019.
35. M. Endo and H. Sugiyama, DNA origami nanomachines, Molecules, 2018, 23, 1766,  DOI:10.3390/molecules23071766.
36. S. Loescher, S. Groeer and A. Walther, 3D DNA origami nanoparticles: from basic design principles to emerging applications in soft matter and (bio-)nanosciences, Angew. Chem., Int. Ed., 2018, 57, 10436–10448,  DOI:10.1002/anie.201801700.
37. P. Wang, T. A. Meyer, V. Pan, P. K. Dutta and Y. Ke, The beauty and utility of DNA origami, Chem, 2017, 2, 359–382,  DOI:10.1016/j.chempr.2017.02.009.
38. A. Udomprasert and T. Kangsamaksin, DNA origami applications in cancer therapy, Cancer Sci., 2017, 108, 1535–1543,  DOI:10.1111/cas.13290.
39. F. Hong, F. Zhang, Y. Liu and H. Yan, DNA origami: Scaffolds for creating higher order structures, Chem. Rev., 2017, 117, 12584–12640,  DOI:10.1021/acs.chemrev.6b00825.
40. A. R. Chandrasekaran, N. Anderson, M. Kizer, K. Halvorsen and X. Wang, Beyond the fold: emerging biological applications of DNA origami, ChemBioChem, 2016, 17, 1081–1089,  DOI:10.1002/cbic.201600038.
41. V. Linko, A. Ora and M. A. Kostiainen, DNA nanostructures as smart drug-delivery vehicles and molecular devices, Trends Biotechnol., 2015, 33, 586–594,  DOI:10.1016/j.tibtech.2015.08.001.
42. H. Jabbari, M. Aminpour and C. Montemagno, Computational approaches to nucleic acid origami, ACS Comb. Sci., 2015, 17, 535–547,  DOI:10.1021/acscombsci.5b00079.
43. L. A. Lanier and H. Bermudez, DNA nanostructures: a shift from assembly to applications, Curr. Opin. Chem. Eng., 2015, 7, 93–100,  DOI:10.1016/j.coche.2015.01.001.
44. A. Kuzuya and Y. Ohya, Nanomechanical molecular devices made of DNA origami, Acc. Chem. Res., 2014, 47, 1742–1749,  DOI:10.1021/ar400328v.
45. N. A. W. Bell and U. F. Keyser, Nanopores formed by DNA origami: a review, FEBS Lett., 2014, 588, 3564–3570,  DOI:10.1016/j.febslet.2014.06.013.
46. S. Hernández-Ainsa and U. F. Keyser, DNA origami nanopores: developments, challenges and perspectives, Nanoscale, 2014, 6, 14121–14132,  10.1039/c4nr04094e.
47. I. Bald and A. Keller, Molecular processes studied at a single-molecule level using DNA origami nanostructures and atomic force microscopy, Molecules, 2014, 19, 13803–13823,  DOI:10.3390/molecules190913803.
48. M. Endo and H. Sugiyama, Single-molecule imaging of dynamic motions of biomolecules in DNA origami nanostructures using high-speed atomic force microscopy, Acc. Chem. Res., 2014, 47, 1645–1653,  DOI:10.1021/ar400299m.
49. F. Zhang, J. Nangreave, Y. Liu and H. Yan, Structural DNA nanotechnology: state of the art and future perspective, J. Am. Chem. Soc., 2014, 136, 11198–11211,  DOI:10.1021/ja505101a.
50. V. Linko and H. Dietz, The enabled state of DNA nanotechnology, Curr. Opin. Biotechnol, 2013, 24, 555–561,  DOI:10.1016/j.copbio.2013.02.001.
51. G. Zhang, S. P. Surwade, F. Zhou and H. Liu, DNA nanostructure meets nanofabrication, Chem. Soc. Rev., 2013, 42, 2488–2496,  10.1039/c2cs35302d.
52. I. Saaem and T. H. LaBean, Overview of DNA origami for molecular self-assembly, Wiley Interdiscip. Rev.: Nanomed. Nanobiotechnol., 2013, 5, 150–162,  DOI:10.1002/wnan.1204.
53. B. Saccà and C. M. Niemeyer, DNA origami: the art of folding DNA, Angew. Chem., Int. Ed., 2012, 51, 58–66,  DOI:10.1002/anie.201105846.
54. N. Michelotti, A. Johnson-Buck, A. J. Manzo and N. G. Walter, Beyond DNA origami: the unfolding prospects of nucleic acid nanotechnology, Wiley Interdiscip. Rev.: Nanomed. Nanobiotechnol., 2012, 4, 139–152,  DOI:10.1002/wnan.170.
55. A. Rajendran, M. Endo and H. Sugiyama, Single-molecule analysis using DNA origami, Angew. Chem., Int. Ed., 2012, 51, 874–890,  DOI:10.1002/anie.201102113.
56. O. I. Wilner and I. Willner, Functionalized DNA nanostructures, Chem. Rev., 2012, 112, 2528–2556,  DOI:10.1021/cr200104q.
57. J. Fu, M. Liu, Y. Liu and H. Yan, Spatially-interactive biomolecular networks organized by nucleic acid nanostructures, Acc. Chem. Res., 2012, 45, 1215–1226,  DOI:10.1021/ar200295q.
58. T. Tørring, N. V. Voigt, J. Nangreave, H. Yan and K. V. Gothelf, DNA origami: a quantum leap for self-assembly of complex structures, Chem. Soc. Rev., 2011, 40, 5636–5646,  10.1039/c1cs15057j.
59. W. M. Shih and C. Lin, Knitting complex weaves with DNA origami, Curr. Opin. Struct. Biol., 2010, 20, 276–282,  DOI:10.1016/j.sbi.2010.03.009.
60. J. Nangreave, D. Han, Y. Liu and H. Yan, DNA origami: a history and current perspective, Curr. Opin. Chem. Biol., 2010, 14, 608–615,  DOI:10.1016/j.cbpa.2010.06.182.
61. K. E. Dunn, The business of DNA nanotechnology: commercialization of origami and other technologies, Molecules, 2020, 25, 377,  DOI:10.3390/molecules25020377.
62. B. Wei, M. Dai and P. Yin, Complex shapes self-assembled from single-stranded DNA tiles, Nature, 2012, 485, 623–626,  DOI:10.1038/nature11075.
63. Y. Ke, L. L. Ong, W. M. Shih and P. Yin, Three-dimensional structures self-assembled from DNA bricks, Science, 2012, 338, 1177–1183,  DOI:10.1126/science.1227268.
64. L. L. Ong, N. Hanikel, O. K. Yaghi, C. Grun, M. T. Strauss, P. Bron, J. Lai-Kee-Him, F. Schueder, B. Wang, P. Wang, J. Y. Kishi, C. Myhrvold, A. Zhu, R. Jungmann, G. Bellot, Y. Ke and P. Yin, Programmable self-assembly of three-dimensional nanostructures from, Nature, 2017, 552, 72–77,  DOI:10.1038/nature24648.
65. M. Yang, D. Bakker, D. Raghu and I. T. S. Li, A single strand: a simplified approach to DNA origami, Front. Chem., 2023, 11, 1126177,  DOI:10.3389/fchem.2023.1126177.
66. X. Wei, J. Nangreave, S. Jiang, H. Yan and Y. Liu, Mapping the thermal behavior of DNA origami nanostructures, J. Am. Chem. Soc., 2013, 135, 6165–6176,  DOI:10.1021/ja4000728.
67. C. G. Evans, J. O'Brien, E. Winfree and A. Murugan, Pattern recognition in the nucleation kinetics of non-equilibrium self-assembly, Nature, 2024, 625, 500–507,  DOI:10.1038/s41586-023-06890-z.
68. S. M. Slone, C.-Y. Li, J. Yoo and A. Aksimentiev, Molecular mechanics of DNA bricks: in situ structure, mechanical properties and ionic conductivity, New J. Phys., 2016, 18, 055012,  DOI:10.1088/1367-2630/18/5/055012.
69. C. A. Mirkin, R. L. Letsinger, R. C. Mucic and J. J. Storhoff, A DNA-based method for rationally assembling nanoparticles into macroscopic materials, Nature, 1996, 382, 607–609,  DOI:10.1038/382607a0.
70. A. P. Alivisatos, K. P. Johnsson, X. Peng, T. E. Wilson, C. J. Loweth, M. P. Bruchez and P. G. Schultz, Organization of “nanocrystal molecules” using DNA, Nature, 1996, 382, 609–611,  DOI:10.1038/382609a0.
71. A. V. Tkachenko, Morphological diversity of DNA-colloidal self-assembly, Phys. Rev. Lett., 2002, 89, 148303,  DOI:10.1103/PhysRevLett.89.148303.
72. L. Di Michele and E. Eiser, Developments in understanding and controlling self assembly of DNA-functionalized colloids, Phys. Chem. Chem. Phys., 2013, 15, 3115–3129,  10.1039/c3cp43841d.
73. W. B. Rogers, W. M. Shih and V. N. Manoharan, Using DNA to program the self-assembly of colloidal nanoparticles and microparticles, Nat. Rev. Mater., 2016, 1, 16008,  DOI:10.1038/natrevmats.2016.8.
74. T. Zhang, D. Lyu, W. Xu, Y. Mu and Y. Wang, Programming self-assembled materials With DNA-coated colloids, Front. Phys., 2021, 9, 672375,  DOI:10.3389/fphy.2021.672375.
75. D. Samanta, W. Zhou, S. B. Ebrahimi, S. H. Petrosko and C. A. Mirkin, Programmable matter: the nanoparticle atom and DNA bond, Adv. Mater., 2022, 34, 2107875,  DOI:10.1002/adma.202107875.
76. M. E. Leunissen, R. Dreyfus, R. Sha, T. Wang, N. C. Seeman, D. J. Pine and P. M. Chaikin, Towards self-replicating materials of DNA-functionalized colloids, Soft Matter, 2009, 5, 2422–2430,  10.1039/b817679e.
77. M. E. Leunissen and D. Frenkel, Numerical study of DNA-functionalized microparticles and nanoparticles: explicit pair potentials and their implications for phase behavior, J. Chem. Phys., 2011, 134, 084702,  DOI:10.1063/1.3557794.
78. J. D. Halverson and A. V. Tkachenko, DNA-programmed mesoscopic architecture, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 062310,  DOI:10.1103/PhysRevE.87.062310.
79. P. Varilly, S. Angioletti-Uberti, B. M. Mognetti and D. Frenkel, A general theory of DNA-mediated and other valence-limited colloidal interactions, J. Chem. Phys., 2012, 137, 094108,  DOI:10.1063/1.4748100.
80. S. Angioletti-Uberti, B. M. Mognetti and D. Frenkel, Re-entrant melting as a design principle for DNA-coated colloids, Nat. Mater., 2012, 11, 518–522,  DOI:10.1038/nmat3314.
81. S. Angioletti-Uberti, B. M. Mognetti and D. Frenkel, Theory and simulation of DNA-coated colloids: a guide for rational design, Phys. Chem. Chem. Phys., 2016, 18, 6373–6393,  10.1039/c5cp06981e.
82. S. Angioletti-Uberti, in Self-Assembly of Nano- and Micro-structured Materials using Colloidal Engineering, ed. D. Chakrabarti and S. Sacanna, Elsevier, 2019, vol. 13, pp. 87–123 DOI:10.1016/b978-0-08-102302-0.00005-5.
83. W. M. Jacobs and W. B. Rogers, Assembly of complex colloidal systems using DNA, arXiv, 2024, preprint, arXiv:2409.08988 DOI:10.48550/arXiv.2409.08988.
84. S. M. Douglas, A. H. Marblestone, S. Teerapittayanon, A. Vazquez, G. M. Church and W. M. Shih, Rapid prototyping of 3D DNA-origami shapes with caDNAno, Nucleic Acids Res., 2009, 37, 5001–5006,  DOI:10.1093/nar/gkp436.
85. D. Doty, B. L. Lee and T. Stérin, DNA 2020, Dagstuhl, Germany, 2020, pp. 9:1–17 DOI:10.4230/lipics.dna.2020.9.
86. S. K. Gupta, F. Joshi, A. Agrawal, S. Deb, M. Sajfutdinow, D. Limbachiya, D. M. Smith and M. K. Gupta, 3DNA: a tool for sculpting brick-based DNA nanostructures, SynBio, 2023, 1, 226–238,  DOI:10.3390/synbio1030016.
87. W. G. Pfeifer, C.-M. Huang, M. G. Poirier, G. Arya and C. E. Castro, Versatile computer-aided design of free-form DNA nanostructures and assemblies, Sci. Adv., 2023, 9, eadi0697,  DOI:10.1126/sciadv.adi0697.
88. K. E. Dunn, F. Dannenberg, T. E. Ouldridge, M. Kwiatkowska, A. J. Turberfield and J. Bath, Guiding the folding pathway of DNA origami, Nature, 2015, 525, 82,  DOI:10.1038/nature14860.
89. F. Dannenberg, K. E. Dunn, J. Bath, M. Kwiatkowska, A. J. Turberfield and T. E. Ouldridge, Modelling DNA origami self-assembly at the domain level, J. Chem. Phys., 2015, 143, 165102,  DOI:10.1063/1.4933426.
90. J.-M. Arbona, J.-P. Aimé and J. Elezgaray, Cooperativity in the annealing of DNA origamis, J. Chem. Phys., 2013, 138, 015105,  DOI:10.1063/1.4773405.
91. J.-M. Arbona, J. Elezgaray and J.-P. Aimé, Modelling the folding of DNA origami, Europhys. Lett., 2012, 100, 28006,  DOI:10.1209/0295-5075/100/28006.
92. J.-M. Arbona, J.-P. Aimé and J. Elezgaray, Folding of DNA origamis, Front. Life Sci., 2012, 6, 11–18,  DOI:10.1080/21553769.2013.768556.
93. J. L. T. Wah, C. David, S. Rudiuk, D. Baigl and A. Estevez-Torres, Observing and controlling the folding pathway of DNA origami at the nanoscale, ACS Nano, 2016, 10, 1978–1987,  DOI:10.1021/acsnano.5b05972.
94. A. Reinhardt, J. S. Schreck, F. Romano and J. P. K. Doye, Self-assembly of two-dimensional binary quasicrystals: a possible route to a DNA quasicrystal, J. Phys.: Condens. Matter, 2017, 29, 014006,  DOI:10.1088/0953-8984/29/1/014006.
95. L. Liu, Z. Li, Y. Li and C. Mao, Rational design and self-assembly of two-dimensional, dodecagonal DNA quasicrystals, J. Am. Chem. Soc., 2019, 141, 4248–4251,  DOI:10.1021/jacs.9b00843.
96. S. Whitelam and R. L. Jack, The statistical mechanics of dynamic pathways to self-assembly, Annu. Rev. Phys. Chem., 2015, 66, 143–163,  DOI:10.1146/annurev-physchem-040214-121215.
97. G. M. Whitesides and B. Grzybowski, Self-assembly at all scales, Science, 2002, 295, 2418–2421,  DOI:10.1126/science.1070821.
98. S. Nag and G. Bisker, Driven self-assembly of patchy particles overcoming equilibrium limitations, J. Chem. Theory Comput., 2024, 20, 7700–7707,  DOI:10.1021/acs.jctc.4c01118.
99. S. Nag and G. Bisker, Dissipative self-assembly of patchy particles under nonequilibrium drive: a computational study, J. Chem. Theory Comput., 2024, 20, 8844–8861,  DOI:10.1021/acs.jctc.4c00856.
100. A. Das and D. T. Limmer, Nonequilibrium design strategies for functional colloidal assemblies, Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2217242120,  DOI:10.1073/pnas.2217242120.
101. W. R. Berg, J. F. Berengut, C. Bai, L. Wimberger, L. K. Lee and F. J. Rizzuto, Light-activated assembly of DNA origami into dissipative fibrils, Angew. Chem., Int. Ed., 2023, 62, e202314458,  DOI:10.1002/anie.202314458.
102. L. D. Landau, K teorii fazovykh perekhodov I, Zh. Eksp. Teor. Fiz., 1937, 7, 19.
103. M. E. Tuckerman, Statistical mechanics: Theory and molecular simulation, Oxford University Press, 2023.
104. P.-R. ten Wolde, M. J. Ruiz-Montero and D. Frenkel, Simulation of homogeneous crystal nucleation close to coexistence, Faraday Discuss., 1996, 104, 93–110,  10.1039/fd9960400093.
105. D. Frenkel, Simulations: the dark side, Eur. Phys. J. Plus, 2013, 128, 10,  DOI:10.1140/epjp/i2013-13010-8.
106. C. Rossi-Gendron, F. El Fakih, L. Bourdon, K. Nakazawa, J. Finkel, N. Triomphe, L. Chocron, M. Endo, H. Sugiyama, G. Bellot, M. Morel, S. Rudiuk and D. Baigl, Isothermal self-assembly of multicomponent and evolutive DNA nanostructures, Nat. Nanotechnol., 2023, 18, 1311–1318,  DOI:10.1038/s41565-023-01468-2.
107. J.-P. J. Sobczak, T. G. Martin, T. Gerling and H. Dietz, Rapid folding of DNA into nanoscale shapes at constant temperature, Science, 2012, 338, 1458–1461,  DOI:10.1126/science.1229919.
108. A. Kopielski, A. Schneider, A. Csaki and W. Fritzsche, Isothermal DNA origami folding: avoiding denaturing conditions for one-pot, hybrid-component annealing, Nanoscale, 2015, 7, 2102–2106,  10.1039/c4nr04176c.
109. Z. Zhang, J. Song, F. Besenbacher, M. Dong and K. V. Gothelf, Self-assembly of DNA origami and single-stranded tile structures at room temperature, Angew. Chem., Int. Ed., 2013, 52, 9219–9223,  DOI:10.1002/anie.201303611.
110. W. Bae, K. Kim, D. Min, J.-K. Ryu, C. Hyeon and T.-Y. Yoon, Programmed folding of DNA origami structures through single-molecule force control, Nat. Commun., 2014, 5, 5654,  DOI:10.1038/ncomms6654.
111. C. A. Hunter and H. L. Anderson, What is cooperativity?, Angew. Chem., Int. Ed., 2009, 48, 7488–7499,  DOI:10.1002/anie.200902490.
112. A. S. Mahadevi and G. N. Sastry, Cooperativity in noncovalent interactions, Chem. Rev., 2016, 116, 2775–2825,  DOI:10.1021/cr500344e.
113. L. K. S. von Krbek, C. A. Schalley and P. Thordarson, Assessing cooperativity in supramolecular systems, Chem. Soc. Rev., 2017, 46, 2622–2637,  10.1039/c7cs00063d.
114. B. Najafi, PhD thesis, University of Oxford, 2022 DOI:10.5287/ora-n6jdo9qaw.
115. A. Cumberworth, A. Reinhardt and D. Frenkel, Lattice models and Monte Carlo methods for simulating DNA origami self-assembly, J. Chem. Phys., 2018, 149, 234905,  DOI:10.1063/1.5051835.
116. F. Schneider, N. Möritz and H. Dietz, The sequence of events during folding of a DNA origami, Sci. Adv., 2019, 5, eaaw1412,  DOI:10.1126/sciadv.aaw1412.
117. E. T. Kool, Hydrogen bonding, base stacking, and steric effects in DNA replication, Annu. Rev. Biophys. Biomol. Struct., 2001, 30, 1–22,  DOI:10.1146/annurev.biophys.30.1.1.
118. A. Cumberworth, D. Frenkel and A. Reinhardt, Simulations of DNA-origami self-assembly reveal design-dependent nucleation barriers, Nano Lett., 2022, 22, 6916–6922,  DOI:10.1021/acs.nanolett.2c01372.
119. C. Linne, D. Visco, S. Angioletti-Uberti, L. Laan and D. J. Kraft, Direct visualization of superselective colloid-surface binding mediated by multivalent interactions, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2106036118,  DOI:10.1073/pnas.2106036118.
120. C. Linne, E. Heemskerk, J. W. Zwanikken, D. J. Kraft and L. Laan, Optimality and cooperativity in superselective surface binding by multivalent DNA nanostars, Soft Matter, 2024, 20, 8515–8523,  10.1039/d4sm00704b.
121. G. V. Dubacheva, T. Curk and R. P. Richter, Determinants of superselectivity–Practical concepts for application in biology and medicine, Acc. Chem. Res., 2023, 56, 729–739,  DOI:10.1021/acs.accounts.2c00672.
122. A. T. R. Christy, H. Kusumaatmaja and M. A. Miller, Control of superselectivity by crowding in three-dimensional hosts, Phys. Rev. Lett., 2021, 126, 028002,  DOI:10.1103/PhysRevLett.126.028002.
123. M. Sajfutdinow, W. M. Jacobs, A. Reinhardt, C. Schneider and D. M. Smith, Direct observation and rational design of nucleation behavior in addressable self-assembly, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E5877–E5886,  DOI:10.1073/pnas.1806010115.
124. A. Reinhardt and D. Frenkel, Numerical evidence for nucleated self-assembly of DNA brick structures, Phys. Rev. Lett., 2014, 112, 238103,  DOI:10.1103/PhysRevLett.112.238103.
125. W. M. Jacobs, A. Reinhardt and D. Frenkel, Communication: theoretical prediction of free-energy landscapes for complex self-assembly, J. Chem. Phys., 2015, 142, 021101,  DOI:10.1063/1.4905670.
126. W. M. Jacobs, A. Reinhardt and D. Frenkel, Rational design of self-assembly pathways for complex multicomponent structures, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 6313–6318,  DOI:10.1073/pnas.1502210112.
127. A. Reinhardt, C. P. Ho and D. Frenkel, Effects of co-ordination number on the nucleation behaviour in many-component self-assembly, Faraday Discuss., 2016, 186, 215–228,  10.1039/c5fd00135h.
128. A. Reinhardt and D. Frenkel, DNA brick self-assembly with an off-lattice potential, Soft Matter, 2016, 12, 6253–6260,  10.1039/c6sm01031h.
129. P. Fonseca, F. Romano, J. S. Schreck, T. E. Ouldridge, J. P. K. Doye and A. A. Louis, Multi-scale coarse-graining for the study of assembly pathways in DNA-brick self-assembly, J. Chem. Phys., 2018, 148, 134910,  DOI:10.1063/1.5019344.
130. Y. Zhang, A. Reinhardt, P. Wang, J. Song and Y. Ke, Programming the nucleation of DNA brick self-assembly with a seeding strand, Angew. Chem., Int. Ed., 2020, 59, 8594–8600,  DOI:10.1002/anie.201915063.
131. H. K. Wayment-Steele, D. Frenkel and A. Reinhardt, Investigating the role of boundary bricks in DNA brick self-assembly, Soft Matter, 2017, 13, 1670–1680,  10.1039/c6sm02719a.
132. M. DeLuca, D. Duke, T. Ye, M. Poirier, Y. Ke, C. Castro and G. Arya, Mechanism of DNA origami folding elucidated by mesoscopic simulations, Nat. Commun., 2024, 15, 3015,  DOI:10.1038/s41467-024-46998-y.
133. B. E. K. Snodin, F. Romano, L. Rovigatti, T. E. Ouldridge, A. A. Louis and J. P. K. Doye, Direct simulation of the self-assembly of a small DNA origami, ACS Nano, 2016, 10, 1724–1737,  DOI:10.1021/acsnano.5b05865.
134. S. Gambietz, L. J. Stenke and B. Saccà, Sequence-dependent folding of monolayered DNA origami domains, Nanoscale, 2023, 15, 13120–13132,  10.1039/d3nr02537c.
135. N. Metropolis, A. W. Rosenbluth, M. N. Rosenbluth, A. H. Teller and E. Teller, Equation of state calculations by fast computing machines, J. Chem. Phys., 1953, 21, 1087–1092,  DOI:10.1063/1.1699114.
136. H. E. A. Huitema and J. P. van der Eerden, Can Monte Carlo simulation describe dynamics? A test on Lennard-Jones systems, J. Chem. Phys., 1999, 110, 3267–3274,  DOI:10.1063/1.478192.
137. S. Whitelam and P. L. Geissler, Avoiding unphysical kinetic traps in Monte Carlo simulations of strongly attractive particles, J. Chem. Phys., 2007, 127, 154101,  DOI:10.1063/1.2790421.
138. Š. Růžička and M. P. Allen, Collective translational and rotational Monte Carlo moves for attractive particles, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 033307,  DOI:10.1103/PhysRevE.89.033307.
139. J. Madge and M. A. Miller, Design strategies for self-assembly of discrete targets, J. Chem. Phys., 2015, 143, 044905,  DOI:10.1063/1.4927671.
140. K. E. Blow, D. Quigley and G. C. Sosso, The seven deadly sins: when computing crystal nucleation rates, the devil is in the details, J. Chem. Phys., 2021, 155, 040901,  DOI:10.1063/5.0055248.
141. J. Wedekind, R. Strey and D. Reguera, New method to analyze simulations of activated processes, J. Chem. Phys., 2007, 126, 134103,  DOI:10.1063/1.2713401.
142. J. B. Zeldovich, On the theory of new phase formation; cavitation, Acta Physicochim. URSS, 1943, 18, 1–22.
143. X. Tang, F. Tian, T. Xu, L. Li and A. Reinhardt, Numerical calculation of free-energy barriers for entangled polymer nucleation, J. Chem. Phys., 2020, 152, 224904,  DOI:10.1063/5.0009716.
144. D. J. Wales, Atomic clusters with addressable complexity, J. Chem. Phys., 2017, 146, 054306,  DOI:10.1063/1.4974838.
145. A. E. Marras, Z. Shi, M. G. Lindell, R. A. Patton, C.-M. Huang, L. Zhou, H.-J. Su, G. Arya and C. E. Castro, Cation-activated avidity for rapid reconfiguration of DNA nanodevices, ACS Nano, 2018, 12, 9484–9494,  DOI:10.1021/acsnano.8b04817.
146. Z. Shi and G. Arya, Free energy landscape of salt-actuated reconfigurable DNA nanodevices, Nucleic Acids Res., 2019, 48, 548–560,  DOI:10.1093/nar/gkz1137.
147. G. M. Torrie and J. P. Valleau, Nonphysical sampling distributions in Monte Carlo free-energy estimation: umbrella sampling, J. Comput. Phys., 1977, 23, 187–199,  DOI:10.1016/0021-9991(77)90121-8.
148. M. Mezei, Adaptive umbrella sampling: self-consistent determination of the non-Boltzmann bias, J. Comput. Phys., 1987, 68, 237–248,  DOI:10.1016/0021-9991(87)90054-4.
149. A. Laio and F. L. Gervasio, Metadynamics: a method to simulate rare events and reconstruct the free energy in biophysics, chemistry and material science, Rep. Prog. Phys., 2008, 71, 126601,  DOI:10.1088/0034-4885/71/12/126601.
150. Q. Yan and J. J. de Pablo, Hyper-parallel tempering Monte Carlo: application to the Lennard-Jones fluid and the restricted primitive model, J. Chem. Phys., 1999, 111, 9509–9516,  DOI:10.1063/1.480282.
151. Y. Sugita, A. Kitao and Y. Okamoto, Multidimensional replica-exchange method for free-energy calculations, J. Chem. Phys., 2000, 113, 6042–6051,  DOI:10.1063/1.1308516.
152. H. Fukunishi, O. Watanabe and S. Takada, On the Hamiltonian replica exchange method for efficient sampling of biomolecular systems: application to protein structure prediction, J. Chem. Phys., 2002, 116, 9058–9067,  DOI:10.1063/1.1472510.
153. M. Lingenheil, R. Denschlag, G. Mathias and P. Tavan, Efficiency of exchange schemes in replica exchange, Chem. Phys. Lett., 2009, 478, 80–84,  DOI:10.1016/j.cplett.2009.07.039.
154. A. M. Ferrenberg and R. H. Swendsen, Optimized Monte Carlo data analysis, Phys. Rev. Lett., 1989, 63, 1195–1198,  DOI:10.1103/PhysRevLett.63.1195.
155. S. Kumar, J. M. Rosenberg, D. Bouzida, R. H. Swendsen and P. A. Kollman, The weighted histogram analysis method for free-energy calculations on biomolecules. I. The method, J. Comput. Chem., 1992, 13, 1011–1021,  DOI:10.1002/jcc.540130812.
156. M. R. Shirts and J. D. Chodera, Statistically optimal analysis of samples from multiple equilibrium states, J. Chem. Phys., 2008, 129, 124105,  DOI:10.1063/1.2978177.
157. J. D. Chodera, A simple method for automated equilibration detection in molecular simulations, J. Chem. Theory Comput., 2016, 12, 1799–1805,  DOI:10.1021/acs.jctc.5b00784.
158. W. G. Noid, Perspective: coarse-grained models for biomolecular systems, J. Chem. Phys., 2013, 139, 090901,  DOI:10.1063/1.4818908.
159. D. Reith, M. Pütz and F. Müller-Plathe, Deriving effective mesoscale potentials from atomistic simulations, J. Comput. Chem., 2003, 24, 1624–1636,  DOI:10.1002/jcc.10307.
160. F. Ercolessi and J. B. Adams, Interatomic potentials from first-principles calculations: the force-matching method, Europhys. Lett., 1994, 26, 583–588,  DOI:10.1209/0295-5075/26/8/005.
161. M. E. Johnson, T. Head-Gordon and A. A. Louis, Representability problems for coarse-grained water potentials, J. Chem. Phys., 2007, 126, 144509,  DOI:10.1063/1.2715953.
162. A. Reinhardt and B. Cheng, Quantum-mechanical exploration of the phase diagram of water, Nat. Commun., 2021, 12, 588,  DOI:10.1038/s41467-020-20821-w.
163. J. A. Joseph, A. Reinhardt, A. Aguirre, P. Y. Chew, K. O. Russell, J. R. Espinosa, A. Garaizar and R. Collepardo-Guevara, Physics-driven coarse-grained model for biomolecular phase separation with near-quantitative accuracy, Nat. Comput. Sci., 2021, 1, 732–743,  DOI:10.1038/s43588-021-00155-3.
164. M. DeLuca, S. Sensale, P.-A. Lin and G. Arya, Prediction and control in DNA nanotechnology, ACS Appl. Bio Mater., 2024, 7, 626–645,  DOI:10.1021/acsabm.2c01045.
165. P. D. Dans, J. Walther, H. Gómez and M. Orozco, Multiscale simulation of DNA, Curr. Opin. Struct. Biol., 2016, 37, 29–45,  DOI:10.1016/j.sbi.2015.11.011.
166. T. Dršata and F. Lankaš, Multiscale modelling of DNA mechanics, J. Phys.: Condens. Matter, 2015, 27, 323102,  DOI:10.1088/0953-8984/27/32/323102.
167. T. E. Ouldridge, DNA nanotechnology: understanding and optimisation through simulation, Mol. Phys., 2015, 113, 1–15,  DOI:10.1080/00268976.2014.975293.
168. C. Maffeo, J. Yoo, J. Comer, D. B. Wells, B. Luan and A. Aksimentiev, Close encounters with DNA, J. Phys.: Condens. Matter, 2014, 26, 413101,  DOI:10.1088/0953-8984/26/41/413101.
169. J. P. K. Doye, T. E. Ouldridge, A. A. Louis, F. Romano, P. Sulc, C. Matek, B. E. K. Snodin, L. Rovigatti, J. S. Schreck, R. M. Harrison and W. P. J. Smith, Coarse-graining DNA for simulations of DNA nanotechnology, Phys. Chem. Chem. Phys., 2013, 15, 20395–20414,  10.1039/c3cp53545b.
170. G. S. Freeman, D. M. Hinckley, J. P. Lequieu, J. K. Whitmer and J. J. de Pablo, Coarse-grained modeling of DNA curvature, J. Chem. Phys., 2014, 141, 165103,  DOI:10.1063/1.4897649.
171. N. Korolev, D. Luo, A. P. Lyubartsev and L. Nordenskiöld, A coarse-grained DNA model parameterized from atomistic simulations by inverse Monte Carlo, Polymers, 2014, 6, 1655,  DOI:10.3390/polym6061655.
172. T. Cragnolini, P. Derreumaux and S. Pasquali, Coarse-grained simulations of RNA and DNA duplexes, J. Phys. Chem. B, 2013, 117, 8047–8060,  DOI:10.1021/jp400786b.
173. O. Gonzalez, D. Petkevičiūtė and J. H. Maddocks, A sequence-dependent rigid-base model of DNA, J. Chem. Phys., 2013, 138, 055102,  DOI:10.1063/1.4789411.
174. Y. He, M. Maciejczyk, S. Ołdziej, H. A. Scheraga and A. Liwo, Mean-field interactions between nucleic-acid-base dipoles can drive the formation of a double helix, Phys. Rev. Lett., 2013, 110, 098101,  DOI:10.1103/PhysRevLett.110.098101.
175. D. M. Hinckley, G. S. Freeman, J. K. Whitmer and J. J. de Pablo, An experimentally-informed coarse-grained 3-site-per-nucleotide model of DNA: structure, thermodynamics, and dynamics of hybridization, J. Chem. Phys., 2013, 139, 144903,  DOI:10.1063/1.4822042.
176. L. E. Edens, J. A. Brozik and D. J. Keller, Coarse-grained model DNA: structure, sequences, stems, circles, hairpins, J. Phys. Chem. B, 2012, 116, 14735–14743,  DOI:10.1021/jp3009095.
177. C. W. Hsu, M. Fyta, G. Lakatos, S. Melchionna and E. Kaxiras, Ab initio determination of coarse-grained interactions in double-stranded DNA, J. Chem. Phys., 2012, 137, 105102,  DOI:10.1063/1.4748105.
178. I. Kikot, A. Savin, E. Zubova, M. Mazo, E. Gusarova, L. Manevitch and A. Onufriev, New coarse-grained DNA model, Biophysics, 2011, 56, 387–392,  DOI:10.1134/S0006350911030109.
179. C. Knorowski, S. Burleigh and A. Travesset, Dynamics and statics of DNA-programmable nanoparticle self-assembly and crystallization, Phys. Rev. Lett., 2011, 106, 215501,  DOI:10.1103/PhysRevLett.106.215501.
180. M. C. Linak, R. Tourdot and K. D. Dorfman, Moving beyond Watson–Crick models of coarse grained DNA dynamics, J. Chem. Phys., 2011, 135, 205102,  DOI:10.1063/1.3662137.
181. P. D. Dans, A. Zeida, M. R. Machado and S. Pantano, A coarse grained model for atomic-detailed DNA simulations with explicit electrostatics, J. Chem. Theory Comput., 2010, 6, 1711–1725,  DOI:10.1021/ct900653p.
182. A. Morriss-Andrews, J. Rottler and S. S. Plotkin, A systematically coarse-grained model for DNA and its predictions for persistence length, stacking, twist, and chirality, J. Chem. Phys., 2010, 132, 035105,  DOI:10.1063/1.3269994.
183. A. Savelyev and G. A. Papoian, Chemically accurate coarse graining of double-stranded DNA, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 20340–20345,  DOI:10.1073/pnas.1001163107.
184. M. Sayar, B. Avşaroğlu and K. Alkan, Twist-writhe partitioning in a coarse-grained DNA minicircle model, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 041916,  DOI:10.1103/PhysRevE.81.041916.
185. N. B. Tito and J. M. Stubbs, Application of a coarse-grained model for DNA to homo- and heterogeneous melting equilibria, Chem. Phys. Lett., 2010, 485, 354–359,  DOI:10.1016/j.cplett.2009.12.079.
186. M. Kenward and K. D. Dorfman, Brownian dynamics simulations of single-stranded DNA hairpins, J. Chem. Phys., 2009, 130, 095101,  DOI:10.1063/1.3078795.
187. F. Lankas, O. Gonzalez, L. M. Heffler, G. Stoll, M. Moakher and J. H. Maddocks, On the parameterization of rigid base and basepair models of DNA from molecular dynamics simulations, Phys. Chem. Chem. Phys., 2009, 11, 10565–10588,  10.1039/b919565n.
188. S. Niewieczerzał and M. Cieplak, Stretching and twisting of the DNA duplexes in coarse-grained dynamical models, J. Phys.: Condens. Matter, 2009, 21, 474221,  DOI:10.1088/0953-8984/21/47/474221.
189. E. Sambriski, D. Schwartz and J. de Pablo, A mesoscale model of DNA and its renaturation, Biophys. J., 2009, 96, 1675–1690,  DOI:10.1016/j.bpj.2008.09.061.
190. N. B. Becker and R. Everaers, From rigid base pairs to semiflexible polymers: coarse-graining DNA, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 021923,  DOI:10.1103/PhysRevE.76.021923.
191. T. A. Knotts, N. Rathore, D. C. Schwartz and J. J. de Pablo, A coarse grain model for DNA, J. Chem. Phys., 2007, 126, 084901,  DOI:10.1063/1.2431804.
192. F. W. Starr and F. Sciortino, Model for assembly and gelation of four-armed DNA dendrimers, J. Phys.: Condens. Matter, 2006, 18, L347,  DOI:10.1088/0953-8984/18/26/L02.
193. H. L. Tepper and G. A. Voth, A coarse-grained model for double-helix molecules in solution: spontaneous helix formation and equilibrium properties, J. Chem. Phys., 2005, 122, 124906,  DOI:10.1063/1.1869417.
194. K. Drukker, G. Wu and G. C. Schatz, Model simulations of DNA denaturation dynamics, J. Chem. Phys., 2001, 114, 579–590,  DOI:10.1063/1.1329137.
195. W. K. Olson, A. A. Gorin, X.-J. Lu, L. M. Hock and V. B. Zhurkin, DNA sequence-dependent deformability deduced from protein–DNA crystal complexes, Proc. Natl. Acad. Sci. U. S. A., 1998, 95, 11163–11168,  DOI:10.1073/pnas.95.19.11163.
196. F. Tosti Guerra, E. Poppleton, P. Šulc and L. Rovigatti, ANNaMo: coarse-grained modelling for folding and assembly of RNA and DNA systems, J. Chem. Phys., 2024, 160, 205102,  DOI:10.1063/5.0202829.
197. A. Naômé, A. Laaksonen and D. P. Vercauteren, A solvent-mediated coarse-grained model of DNA derived with the systematic Newton inversion method, J. Chem. Theory Comput., 2014, 10, 3541–3549,  DOI:10.1021/ct500222s.
198. A. K. Dasanna, N. Destainville, J. Palmeri and M. Manghi, Slow closure of denaturation bubbles in DNA: twist matters, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 052703,  DOI:10.1103/PhysRevE.87.052703.
199. C. Svaneborg, LAMMPS framework for dynamic bonding and an application modeling DNA, Comput. Phys. Commun., 2012, 183, 1793–1802,  DOI:10.1016/j.cpc.2012.03.005.
200. J. C. Araque, A. Z. Panagiotopoulos and M. A. Robert, Lattice model of oligonucleotide hybridization in solution. I. Model and thermodynamics, J. Chem. Phys., 2011, 134, 165103,  DOI:10.1063/1.3568145.
201. K. Doi, T. Haga, H. Shintaku and S. Kawano, Development of coarse-graining DNA models for single-nucleotide resolution analysis, Philos. Trans. R. Soc., A, 2010, 368, 2615–2628,  DOI:10.1098/rsta.2010.0068.
202. F. Trovato and V. Tozzini, Supercoiling and local denaturation of plasmids with a minimalist DNA model, J. Phys. Chem. B, 2008, 112, 13197–13200,  DOI:10.1021/jp807085d.
203. S. P. Mielke, N. Grønbech-Jensen, V. V. Krishnan, W. H. Fink and C. J. Benham, Brownian dynamics simulations of sequence-dependent duplex denaturation in dynamically superhelical DNA, J. Chem. Phys., 2005, 123, 124911,  DOI:10.1063/1.2038767.
204. M. Sales-Pardo, R. Guimerà, A. A. Moreira, J. Widom and L. A. N. Amaral, Mesoscopic modeling for nucleic acid chain dynamics, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 051902,  DOI:10.1103/PhysRevE.71.051902.
205. X. Li, C. M. Schroeder and K. D. Dorfman, Modeling the stretching of wormlike chains in the presence of excluded volume, Soft Matter, 2015, 11, 5947–5954,  10.1039/c5sm01333j.
206. G. T. Barkema, D. Panja and J. M. J. van Leeuwen, Semiflexible polymer dynamics with a bead-spring model, J. Stat. Mech.: Theory Exp., 2014, 2014, P11008,  DOI:10.1088/1742-5468/2014/11/P11008.
207. J. G. de la Torre, J. G. H. Cifre, Á. Ortega, R. R. Schmidt, M. X. Fernandes, H. E. P. Sánchez and R. Pamies, SIMUFLEX: algorithms and tools for simulation of the conformation and dynamics of flexible molecules and nanoparticles in dilute solution, J. Chem. Theory Comput., 2009, 5, 2606–2618,  DOI:10.1021/ct900269n.
208. A. K. Mazur, Kinetic and thermodynamic DNA elasticity at micro- and mesoscopic scales, J. Phys. Chem. B, 2009, 113, 2077–2089,  DOI:10.1021/jp8098945.
209. C. Bustamante, J. Marko, E. Siggia and S. Smith, Entropic elasticity of λ-phage DNA, Science, 1994, 265, 1599–1600,  DOI:10.1126/science.8079175.
210. D. Jost and R. Everaers, A unified Poland-Scheraga model of oligo- and polynucleotide DNA melting: salt effects and predictive power, Biophys. J., 2009, 96, 1056–1067,  DOI:10.1529/biophysj.108.134031.
211. R. Everaers, S. Kumar and C. Simm, Unified description of poly- and oligonucleotide DNA melting: nearest-neighbor, Poland-Sheraga, and lattice models, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 041918,  DOI:10.1103/PhysRevE.75.041918.
212. J. SantaLucia Jr and D. Hicks, The thermodynamics of DNA structural motifs, Annu. Rev. Biophys. Biomol. Struct., 2004, 33, 415–440,  DOI:10.1146/annurev.biophys.32.110601.141800.
213. T. Garel and H. Orland, Generalized Poland-Scheraga model for DNA hybridization, Biopolymers, 2004, 75, 453–467,  DOI:10.1002/bip.20140.
214. C. Richard and A. Guttmann, Poland-Scheraga models and the DNA denaturation transition, J. Stat. Phys., 2004, 115, 925–947,  DOI:10.1023/B:JOSS.0000022370.48118.8b.
215. T. Dauxois, M. Peyrard and A. R. Bishop, Entropy-driven DNA denaturation, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1993, 47, R44–47,  DOI:10.1103/PhysRevE.47.R44.
216. M. Peyrard and A. R. Bishop, Statistical mechanics of a nonlinear model for DNA denaturation, Phys. Rev. Lett., 1989, 62, 2755–2758,  DOI:10.1103/PhysRevLett.62.2755.
217. D. Poland and H. A. Scheraga, Occurrence of a phase transition in nucleic acid models, J. Chem. Phys., 1966, 45, 1464–1469,  DOI:10.1063/1.1727786.
218. I. Rouzina and V. A. Bloomfield, Heat capacity effects on the melting of DNA. 1. General aspects, Biophys. J., 1999, 77, 3242–3251,  DOI:10.1016/S0006-3495(99)77155-9.
219. I. Rouzina and V. A. Bloomfield, Heat capacity effects on the melting of DNA. 2. Analysis of nearest-neighbor base pair effects, Biophys. J., 1999, 77, 3252–3255,  DOI:10.1016/S0006-3495(99)77156-0.
220. R. T. Koehler and N. Peyret, Thermodynamic properties of DNA sequences: characteristic values for the human genome, Bioinformatics, 2005, 21, 3333–3339,  DOI:10.1093/bioinformatics/bti530.
221. R. Owczarzy, B. G. Moreira, Y. You, M. A. Behlke and J. A. Walder, Predicting stability of DNA duplexes in solutions containing magnesium and monovalent cations, Biochemistry, 2008, 47, 5336–5353,  DOI:10.1021/bi702363u.
222. H. T. Allawi and J. SantaLucia Jr, Thermodynamics and NMR of internal G·T mismatches in DNA, Biochemistry, 1997, 36, 10581–10594,  DOI:10.1021/bi962590c.
223. H. T. Allawi and J. SantaLucia Jr, Thermodynamics of internal C·T mismatches in DNA, Nucleic Acids Res., 1998, 26, 2694–2701,  DOI:10.1093/nar/26.11.2694.
224. H. T. Allawi and J. SantaLucia Jr, Nearest-neighbor thermodynamics of internal A·C mismatches in DNA: sequence dependence and pH effects, Biochemistry, 1998, 37, 9435–9444,  DOI:10.1021/bi9803729.
225. H. T. Allawi and J. SantaLucia Jr, Nearest neighbor thermodynamic parameters for internal G·A mismatches in DNA, Biochemistry, 1998, 37, 2170–2179,  DOI:10.1021/bi9724873.
226. N. Peyret, P. A. Seneviratne, H. T. Allawi and J. SantaLucia Jr, Nearest-neighbor thermodynamics and NMR of DNA sequences with internal A·A, C·C, G·G, and T·T mismatches, Biochemistry, 1999, 38, 3468–3477,  DOI:10.1021/bi9825091.
227. S. Bommarito, N. Peyret and J. SantaLucia Jr, Thermodynamic parameters for DNA sequences with dangling ends, Nucleic Acids Res., 2000, 28, 1929–1934,  DOI:10.1093/nar/28.9.1929.
228. J. SantaLucia Jr, A unified view of polymer, dumbbell, and oligonucleotide DNA nearest-neighbor thermodynamics, Proc. Natl. Acad. Sci. U. S. A., 1998, 95, 1460–1465,  DOI:10.1073/pnas.95.4.1460.
229. N. Kern and D. Frenkel, Fluid-fluid coexistence in colloidal systems with short-ranged strongly directional attraction, J. Chem. Phys., 2003, 118, 9882–9889,  DOI:10.1063/1.1569473.
230. Y. Ueda, H. Taketomi and N. Gō, Studies on protein folding, unfolding, and fluctuations by computer simulation. II. A. Three-dimensional lattice model of lysozyme, Biopolymers, 1978, 17, 1531–1548,  DOI:10.1002/bip.1978.360170612.
231. C. Maffeo, J. Yoo and A. Aksimentiev, De novo reconstruction of DNA origami structures through atomistic molecular dynamics simulation, Nucleic Acids Res., 2016, 44, 3013–3019,  DOI:10.1093/nar/gkw155.
232. J. Yoo and A. Aksimentiev, In situ structure and dynamics of DNA origami determined through molecular dynamics simulations, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 20099–20104,  DOI:10.1073/pnas.1316521110.
233. K. Pan, D.-N. Kim, F. Zhang, M. R. Adendorff, H. Yan and M. Bathe, Lattice-free prediction of three-dimensional structure of programmed DNA assemblies, Nat. Commun., 2014, 5, 5578,  DOI:10.1038/ncomms6578.
234. D.-N. Kim, F. Kilchherr, H. Dietz and M. Bathe, Quantitative prediction of 3D solution shape and flexibility of nucleic acid nanostructures, Nucleic Acids Res., 2012, 40, 2862–2868,  DOI:10.1093/nar/gkr1173.
235. R. V. Reshetnikov, A. V. Stolyarova, A. O. Zalevsky, D. Y. Panteleev, G. V. Pavlova, D. V. Klinov, A. V. Golovin and A. D. Protopopova, A coarse-grained model for DNA origami, Nucleic Acids Res., 2018, 46, 1102–1112,  DOI:10.1093/nar/gkx1262.
236. C. Maffeo and A. Aksimentiev, MrDNA: a multi-resolution model for predicting the structure and dynamics of DNA systems, Nucleic Acids Res., 2020, 48, 5135–5146,  DOI:10.1093/nar/gkaa200.
237. J. Y. Lee, J. G. Lee, G. Yun, C. Lee, Y.-J. Kim, K. S. Kim, T. H. Kim and D.-N. Kim, Rapid computational analysis of DNA origami assemblies at near-atomic resolution, ACS Nano, 2021, 15, 1002–1015,  DOI:10.1021/acsnano.0c07717.
238. J. G. Lee, K. S. Kim, J. Y. Lee and D.-N. Kim, Predicting the free-form shape of structured DNA assemblies from their lattice-based design blueprint, ACS Nano, 2022, 16, 4289–4297,  DOI:10.1021/acsnano.1c10347.
239. J. Y. Lee, H. Koh and D.-N. Kim, A computational model for structural dynamics and reconfiguration of DNA assemblies, Nat. Commun., 2023, 14, 7079,  DOI:10.1038/s41467-023-42873-4.
240. J. Y. Lee, Y. Kim and D.-N. Kim, Predicting the effect of binding molecules on the shape and mechanical properties of structured DNA assemblies, Nat. Commun., 2024, 15, 6446,  DOI:10.1038/s41467-024-50871-3.
241. E. J. Ratajczyk, P. Šulc, A. J. Turberfield, J. P. K. Doye and A. A. Louis, Coarse-grained modeling of DNA–RNA hybrids, J. Chem. Phys., 2024, 160, 115101,  DOI:10.1063/5.0199558.
242. J. P. K. Doye, H. Fowler, D. Prešern, J. Bohlin, L. Rovigatti, F. Romano, P. Šulc, C. K. Wong, A. A. Louis, J. S. Schreck, M. C. Engel, M. Matthies, E. Benson, E. Poppleton and B. E. K. Snodin, in DNA and RNA Origami: Methods and Protocols, ed. J. Valero, Humana, New York, NY, 2023, pp. 93–112 DOI:10.1007/978-1-0716-3028-0_6.
243. B. E. K. Snodin, F. Randisi, M. Mosayebi, P. Šulc, J. S. Schreck, F. Romano, T. E. Ouldridge, R. Tsukanov, E. Nir, A. A. Louis and J. P. K. Doye, Introducing improved structural properties and salt dependence into a coarse-grained model of DNA, J. Chem. Phys., 2015, 142, 234901,  DOI:10.1063/1.4921957.
244. P. Šulc, F. Romano, T. E. Ouldridge, L. Rovigatti, J. P. K. Doye and A. A. Louis, Sequence-dependent thermodynamics of a coarse-grained DNA model, J. Chem. Phys., 2012, 137, 135101,  DOI:10.1063/1.4754132.
245. T. E. Ouldridge, A. A. Louis and J. P. K. Doye, Structural, mechanical, and thermodynamic properties of a coarse-grained DNA model, J. Chem. Phys., 2011, 134, 085101,  DOI:10.1063/1.3552946.
246. T. E. Ouldridge, A. A. Louis and J. P. K. Doye, DNA nanotweezers studied with a coarse-grained model of DNA, Phys. Rev. Lett., 2010, 104, 178101,  DOI:10.1103/PhysRevLett.104.178101.
247. B. E. K. Snodin, J. S. Schreck, F. Romano, A. A. Louis and J. P. K. Doye, Coarse-grained modelling of the structural properties of DNA origami, Nucleic Acids Res., 2019, 47, 1585–1597,  DOI:10.1093/nar/gky1304.
248. M. C. Engel, D. M. Smith, M. A. Jobst, M. Sajfutdinow, T. Liedl, F. Romano, L. Rovigatti, A. A. Louis and J. P. K. Doye, Force-induced unravelling of DNA origami, ACS Nano, 2018, 12, 6734–6747,  DOI:10.1021/acsnano.8b01844.
249. A. Cumberworth, PhD thesis, University of Cambridge, 2021 DOI:10.17863/cam.64168.
250. L. Cademartiri and K. J. M. Bishop, Programmable self-assembly, Nat. Mater., 2015, 14, 2–9,  DOI:10.1038/nmat4184.
251. C. Truong-Quoc, J. Y. Lee, K. S. Kim and D.-N. Kim, Prediction of DNA origami shape using graph neural network, Nat. Mater., 2024, 23, 984–992,  DOI:10.1038/s41563-024-01846-8.
252. C. Chen, J. Nie, M. Ma and X. Shi, DNA origami nanostructure detection and yield estimation using deep learning, ACS Synth. Biol., 2023, 12, 524–532,  DOI:10.1021/acssynbio.2c00533.
253. M. Chiriboga, C. M. Green, D. A. Hastman, D. Mathur, Q. Wei, S. A. Díaz, I. L. Medintz and R. Veneziano, Rapid DNA origami nanostructure detection and classification using the YOLOv5 deep convolutional neural network, Sci. Rep., 2022, 12, 3871,  DOI:10.1038/s41598-022-07759-3.
254. E. Benson, M. Lolaico, Y. Tarasov, A. Gådin and B. Högberg, Evolutionary refinement of DNA nanostructures using coarse-grained molecular dynamics simulations, ACS Nano, 2019, 13, 12591–12598,  DOI:10.1021/acsnano.9b03473.
255. Y. Wang, X. Jin and C. Castro, Accelerating the characterization of dynamic DNA origami devices with deep neural networks, Sci. Rep., 2023, 13, 15196,  DOI:10.1038/s41598-023-41459-w.

---