DOI:
10.1039/D5CP03472H
(Review Article)
Phys. Chem. Chem. Phys., 2025,
27, 25232-25253
Review of the tight-binding method applicable to the properties of moiré superlattices
Received
8th September 2025
, Accepted 10th November 2025
First published on 12th November 2025
Abstract
Moiré superlattices have emerged as a versatile platform for exploring a wide range of exotic quantum phenomena. Unlike angstrom-scale materials, the moiré length-scale system contains a large number of atoms, and its electronic structure is significantly modulated by the lattice relaxation. These features pose a huge theoretical challenge. Among the available theoretical approaches, tight-binding (TB) methods are widely employed to predict the electronic, transport, and optical properties of systems such as twisted graphene, twisted transition-metal dichalcogenides (TMDs), and related moiré materials. In this review, we provide a comprehensive overview of atomistic TB Hamiltonians and the numerical techniques commonly used to model graphene-based, TMD-based and hBN-based moiré superlattices. We also discuss the connection between atomistic TB descriptions and effective low-energy continuum models. Two examples of different moiré materials and geometries are provided to emphasize the advantages of the TB methods. This review is intended to serve as a theoretical and practical guide for those seeking to apply TB methods to the study of various properties of moiré superlattices.
1 Introduction
Moiré superlattices can be constructed by stacking two-dimensional materials with relative rotation or slight lattice mismatch, giving rise to long-wavelength interference patterns in their atomic structures.1,2 A famous example is twisted bilayer graphene (TBG), where a small-angle rotation between the graphene layers generates a moiré superlattice with emergent electronic properties, for example, moiré flat band structure.3–5 Such moiré materials have rapidly become a versatile platform for exploring exotic physics,1,6 as well as new opportunities in materials science and chemistry.7–10 Remarkably, experiments have revealed a variety of strongly correlated phenomena and topology in these systems. Unconventional superconductivity and correlated insulating states have been observed in twisted bilayer graphene layers,11–17 multilayer graphene/hexagonal boron nitride (hBN) heterostructures,18–20 as well as in moiré transition-metal dichalcogenides (TMDs).21–24 Beyond superconductivity, moiré systems exhibit tunable ferromagnetism,25–29 ferroelectricity,30–32 and integer and fractional quantum anomalous Hall effects.33–40 These experimental breakthroughs highlight the potential of moiré materials for applications in quantum technologies and optoelectronics,41,42 including quantum computing,43–47 lasing and cavity engineering,41,48–51 and chemical property tuning via twist-angle control.7,8,52–54
Experimental observations on moiré materials also motivate extensive theoretical and numerical efforts to understand these phenomena and provide accurate and robust predictions of the moiré systems. However, theoretical modeling remains challenging because realistic moiré superlattices often contain thousands of atoms.5 In addition, lattice reconstruction and atomic relaxation play critical roles in determining electronic, transport and optical properties of moiré materials.55–62 Several atomistic approaches have been employed to study the electronic structure of moiré superlattices. Density functional theory (DFT) not only supports phenomenological descriptions and synthesis control across diverse two-dimensional (2D) materials,63–65 but also provides accurate descriptions of their electronic structures,66 and has been applied to relatively small and large-angle twised graphene layers, twisted bilayer TMDs and twisted bilayer hBN.67–75 However, its computational cost makes the direct simulation of large-scale moiré superlattices inefficient. At the opposite limit, continuum models offer effective low-energy descriptions that capture essential band features and have been widely used to provide insights into some experimental observations.76–80
Bridging these two methods, the tight-binding (TB) model offers an atomistic yet computationally efficient framework for modeling moiré materials.81–84 Crucially, atomic TB Hamiltonians have been built to simulate a broad variety of 2D materials such as graphene,85,86, TMDs,87,88 black phosphorus,89 and group-IV/V “enes” (silicene/germanene/stanene).90–92 Unlike continuum models, TB retains lattice-level resolution, making it possible to capture the effects of atomic relaxation,93,94 local disorder,95,96 strain,97 and chemical specificity.98–100 Furthermore, the method can be systematically extended to include many-body interactions,101–103 external fields,104 and coupling to lattice or optical degrees of freedom.105 Moreover, TB model is orders of magnitude more efficient than DFT method, enabling conventional numerical simulations of realistic moiré supercells with thousands of atoms. The TB model can be further integrated with advanced real-space linear scaling numerical techniques to simulate up to millions of atoms.82,106–108 Because of this unique balance between accuracy and efficiency, TB method has become a central tool for studying electronic, transport, and optical properties of moiré superlattices across material platforms, from twisted bilayer graphene to hBN- and TMDs-based heterostructures.
In this Review, we focus on TB methods that have been applied to study broad properties of moiré materials such as electronic, transport, and dynamical properties. In Section 2, we introduce widely used TB Hamiltonians in moiré materials including graphene-based, TMDs-based and hBN-based moiré superlattices. In Section 3, we also review the numerical methods in dealing with the large scale TB Hamiltonian matrices and introduce some practical software packages used to study the properties of moiré materials. In Section 4 we then analyze the relation of TB methods to DFT and continuum models used in moiré materials. We also display two typical examples of implementing TB methods to study properties of moiré materials in Section 5.
2 Tight-binding Hamiltonian of moiré materials
In the study of two-dimensional (2D) superlattices, the most commonly investigated materials are graphene, hBN, and transition metal dichalcogenides (TMDs). In homobilayer systems, such as TBG, the superlattice structure is characterized by a single twist angle θ. For certain special twist angles, the superlattice preserves translational symmetry and forms a well-defined commensurate supercell. At these special angles, the two graphene lattices beat in space, giving rise to a moiré period defined by integer numbers of graphene lattice vectors. We refer to these angles as commensurate angles. Another structure of interest is an incommensurate structure, the dodecagonal quasicrystal with θ = 30°.109–111 The atomistic TB model is widely used to study the electronic structures of these superlattices. The starting point for the TB model is the construction of the superlattice. Therefore, in this section, we will first give a brief description of the geometry and then explicitly discuss the TB Hamiltonians of these systems. For simplicity, we limit our attention to moiré systems. The TB Hamiltonian for the incommensurate case is straightforward.
2.1 Moiré geometry
A moiré pattern can be generated in several ways. For example, when two single layers of 2D materials are stacked on top of each other with a relative commensurate angle, a moiré pattern is formed.112 Moiré patterns can also be created solely by applying strain.113 The period of the moiré pattern is determined by the twist angle or lattice mismatch. In this section, we briefly introduce the geometry of the moiré pattern defined by rotation. The general and universal formulas for generating moiré systems are given in ref. 95 and 113.
For the TBG case, the period of the moiré pattern is ref. 114:
| | 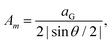 | (1) |
where
aG is the graphene lattice constant. The TBG could be constructed by identifying a common periodicity in the two graphene monolayers. For one layer, we define a supercell with a lattice vector
A1 =
na1 +
ma2, where
a1,2 are the lattice vectors of monolayer graphene, and
m,
n are integers with
n >
m ≥ 1. For the second layer, a supercell with the same size and rotated by an angle
θ can be obtained by taking a lattice vector
A2 = −
ma1 + (
n +
m)
a2. The moiré superlattice is then constructed by rotating the cell with
A1 by
θ/2 and the cell with
A2 by −
θ/2. Each pair of (
n,
m) identifies a commensurate supercell with twist angle
θ as:
| | 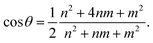 | (2) |
Fig. 1(a) shows a moiré pattern of TBG with
θ = 3.15°, which consists of AA, AB and DW stackings. These stacking configurations have distinct stacking energies, resulting in a strong lattice reconstruction of the system to achieve an equilibrium condition. The moiré pattern can be visualized by means of transmission electron microscopy and scanning tunneling microscopy.
95,115
 |
| | Fig. 1 (a) The atomic structure of TBG with θ = 3.15°. The moiré unit cell is illustrated with a black parallelogram. (b) Band structure of TBG with θ = 5.08° obtained by performing TB (solid line) and ab initio (dot) calculations. In the TB calculation, the hopping parameters are t0 = 2.7 eV and t1 = 0.48 eV. (c) Fermi velocity ratio Vbi/Vmono of TBG versus angle θ. Red dot for the ab initio calculations and black cross for the TB calculations. The velocity close to 0 at angle θ = 1.08° with integer pair (30,31). (d) Distribution of one eigenstate at K point with energy E = 0, in the unit cell of TBG with θ = 1.08°. Black small dots are the positions of all atoms, red dots are atoms where 80% of the states are localized. Inset shows the local density of states (DOS) of the AA stacking (solid red line) and the total DOS (dashed black line). Adapted with permission from ref. 116. Copyright (2010) American Chemical Society. | |
2.2 Graphene-based moiré materials
2.2.1 Single-particle TB method.
The most widely studied moiré materials are graphene-based heterostructures, such as twisted bilayer graphene, twisted trilayer graphene, and twisted multilayer graphene. To describe their electronic structure, single-particle tight-binding models are commonly employed. A typical example is the TB model restricted to the pz orbital, which captures the essential low-energy physics of graphene. The Hamiltonian is written as| |  | (3) |
where 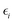 is the onsite energy of the pz orbital at site i, and tij denotes the hopping between pz orbitals at sites i and j. The hopping amplitudes follow the Slater–Koster (SK) relation
is the onsite energy of the pz orbital at site i, and tij denotes the hopping between pz orbitals at sites i and j. The hopping amplitudes follow the Slater–Koster (SK) relation| | | tij = n2Vppσ(rij) + (1 − n2)Vppπ(rij), | (4) |
where rij = |rj − ri| is the distance between sites i and j, and n is the direction cosine along the ez axis perpendicular to the graphene plane. The SK parameters Vppπ and Vppσ are given by ref. 116 and 117| | | Vppπ(rij) = −t0eqπ(1−rij/d)Fc(rij), | (5) |
| | | Vppσ(rij) = t1eqσ(1−rij/h)Fc(rij), | (6) |
where d and h are the nearest in-plane and out-of-plane carbon–carbon distances, respectively. The parameters t0 and t1 set the in-plane and out-of-plane hopping strengths, while qπ and qσ are decay factors satisfying 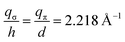 . A smooth cutoff function
. A smooth cutoff function| | 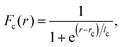 | (7) |
with lc = 0.265 Å and cutoff distance rc = 5.0 Å, is used to suppress long-range hopping terms. According to eqn (5) and (6), the electronic structure varies with SK hopping parameters (t0 and t1) and bond lengths (d and h). For example, by modulating slightly the SK parameters, the first magic angle can be shifted between 1.05° and 1.2°.94 For bilayer graphene case, the equilibrium bond length are d = 1.419 Å and hAA = 3.599 Å, which are reproduced by a DFT + vdW calculation.118 More information on the bound length refers to ref. 93, 114 and 118–120. This minimal pz-orbital model provides a reliable starting point for describing the electronic structure of graphene-based moiré systems. In practice, more refined models are often required to include lattice relaxation, correlation effects, or substrate-induced modifications.
In 2010, Guy Trambly de Laissardière and co-workers derived the above TB model and predicted the electronic structure of TBG at different twist angles.116 The agreement between the ab initio and TB results was excellent (see the red dot and red line in Fig. 1(b)). From the calculated band dispersions along Γ–K, they extracted the velocity of the Dirac states near the K point using 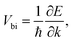 and compared it with the corresponding value in monolayer graphene, Vmono. As shown in Fig. 1(c), the velocity renormalization varies symmetrically around θ = 30°.
and compared it with the corresponding value in monolayer graphene, Vmono. As shown in Fig. 1(c), the velocity renormalization varies symmetrically around θ = 30°.
Within the small-angle regime (θ < 3°), the low-energy bands become flat. At the particular twist angle θ = 1.08°, referred to as the first magic angle, the velocity tends to zero. This value is very close to θ = 1.05°, obtained from the continuum model by Bistritzer and MacDonald,76 and consistent with the experimentally observed magic angle near θ = 1.1°.11 In the flat-band regime, the moiré potential induces a strong peak near the charge neutrality point in the local density of states (DOS) of the AA stacking region, where the states are mainly localized (Fig. 1(d)). This behavior was unexpected at the time, since Dirac electrons in graphene obey the so-called Klein paradox, which makes them difficult to localize with an electrostatic potential.121
A similar TB model was proposed by E. Suárez Morell et al. in 2010, who predicted the magic angle at 1.5°.122 Their model included up to third-nearest-neighbor interlayer hoppings. The precise value of the magic angle depends strongly on the hopping parameters t0 and t1,94 which can be tuned in realistic models to better fit DFT results67,104 or experimental data.94 Moreover, based on the above TB framework, the existence of flat bands has also been demonstrated in twisted trilayer graphene,104,123–126 twisted double bilayer graphene,67,127,128 and twisted multilayer graphene.129–131
The atomistic TB model offers several advantages for studying moiré systems. First, lattice relaxation effects can be incorporated by modifying the distance-dependent hoppings tij in eqn (4) according to the relaxed atomic positions,93,94,119,132 which allows the model to reproduce the observed band gaps between flat and remote bands.12,133 One option to obtain relaxed structures is through the classical simulation package LAMMPS.134 For reference, libraries of lattice relaxation are available for graphene,119 TMDs,135 and hBN136 (LAMMPS potentials are presented in Table 1).
Table 1 Summary of tight-binding (TB) models that have been used for moiré superlattices of three representative material families: (i) twisted bilayer and multilayer graphene, (ii) twisted bilayer hexagonal boron nitride (hBN), and (iii) twisted homobilayer and heterobilayer transition–metal dichalcogenides (TMDs). The second column lists the orbital basis actually used in the TB Hamiltonians (from the simplest pz model for graphene to the 11-orbital Wannier model for TMDs). The third column specifies the intralayer and interlayer hopping functions, including SK parametrizations, range cutoffs, and angle dependences reported in the cited works. The fourth column collects SK-related numerical parameters (lattice constants, onsite energies, hopping amplitudes and decay lengths). The last column summarizes how the atomic structures were relaxed via LAMMPS with corresponding intra- and inter-layer potetials before evaluating SK matrix elements
| Material family |
Orbitals (basis) |
Hopping used (intralayer/interlayer) |
Parameters (SK-related numerics) |
Relaxation (LAMMPS potentials) |
| Moiré graphene (TBG & stacks) |
pz per C |
Intra/inter:116,117tij = n2Vppσ(r) + (1 −n2)Vppπ(r); Vppπ(r) = −t0eqπ(1−r/d)Fc(r); Vppσ(r) = t1eqσ(1−r/h)Fc(r); Fc(r) = (1 + e(r−rc)/lc)−1 |
t
0 = 2.7 eV; t1 = 0.48 eV; qσ/h = qπ/d = 2.218 Å−1; rc = 5.0 Å; lc = 0.265 Å |
Intra:94,119 AIREBO137 LCBOP;138 inter:93,119 |
|
|
|
|
|
Kolmogorov–Crespi (KC)139 |
| Moiré hBN (twisted bilayer) |
pz on B/N |
Intra: (A)140 and (B)141 nearest neighbor (NN) hopping. (c) 6 neighbor hoppings.136 Inter: (A)140tXY⊥(r) = tXYe−α(r−h); (B)141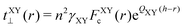 ; (C)136 full SK: Vppπ(r) = −γ0eqπ(1−r/dBN), Vppσ(r) = γ1eqσ(1−r/h) ; (C)136 full SK: Vppπ(r) = −γ0eqπ(1−r/dBN), Vppσ(r) = γ1eqσ(1−r/h) |
(A)140h = 3.33 Å, α = 4.4 Å−1; tNN = 0.15, tBB = 0.7, tNB = 0.3 eV. (B)141h = 3.22 Å, lc = 0.265 Å, rXYc = h + ln(103)/QXY. (C)136dBN = 1.43 Å, h = 3.261 Å; γ0 = 2.7 eV; γ1 ∈ {0.831, 0.6602, 0.3989} eV |
Intra:136 extended Tersoff;142 inter:136 DRIP143,144 |
| Moiré TMDs (twisted homo/hetero) |
11-orbital: 5d (M) + px,y,z on two X; SOC on-site |
Intra: Wannier 11-orbital TB.145 Inter (homobilayer p–p):145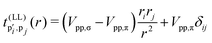 with Vpp,b(r) = νbe−(r/Rb)ηb. Inter (heterobilayer pz–dz2):146 with Vpp,b(r) = νbe−(r/Rb)ηb. Inter (heterobilayer pz–dz2):146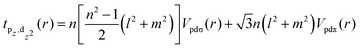 ; Vpd,b(r) = Vb(r/h)αb ; Vpd,b(r) = Vb(r/h)αb![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(βbr/h + γb) cos(βbr/h + γb) |
Homobilayer:147 interlayer cutoff rcut ≈ 5 Å; νb, Rb, ηb from Table V in ref. 145. |
Intra:146,148 Stillinger–Weber (SW);149 inter:146,148 Lennard-Jones (LJ)150/KC135 |
|
|
|
|
Heterobilayer:146 mean interlayer distance h ≈ 3.5 Å; (Vb, αb, βb, γb) from ref. 146 |
|
Second, substrate effects, strain, impurities, and external electric or magnetic fields can be readily implemented within the TB framework. For example, a perpendicular electric field can be introduced by adding an onsite potential term to each site, while a perpendicular magnetic field can be included through the Peierls substitution151
| | 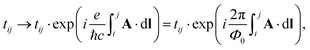 | (8) |
where
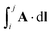
is the line integral of the vector potential from orbital
i to orbital
j, and
Φ0 = 2π
cħ/
e is the flux quantum. For a perpendicular magnetic field along −
z, the Landau gauge
A = (
By,0,0) can be used. This framework enables the study of large-scale properties such as the moiré Hofstadter butterfly in TBG
152 and quantum Hall effect in twisted graphene using linear-scaling methods and linear-response theory.
107,108
2.2.2 TB with electronic interactions.
The localization of electrons in flat bands near the Fermi energy results in strong electronic interactions that cannot be ignored in graphene based moiré materials. For the long range electron-electron interactions, the simplest model is the Hartree approximation, which accounts for a mean field direct interaction between an electron and the surrounding charge density. In TBG, this interaction has been found to be strongest near the magic angle and can be incorporated into the single particle TB model as153–156where| | 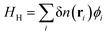 | (10) |
is a self consistent Hartree potential. The electron interaction is replaced by a site-dependent electric potential ϕi, which is determined self consistently through the equation| | 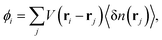 | (11) |
where δn(r) ≡ n(r) − ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) is the deviation of the electron density n(r) from the average density
is the deviation of the electron density n(r) from the average density ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) , and V(ri − rj) is the screened Coulomb interaction. The simplest form of this interaction can be written as153
, and V(ri − rj) is the screened Coulomb interaction. The simplest form of this interaction can be written as153| | 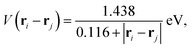 | (12) |
but this potential can take different forms depending on the surrounding environment,154 which has important effects when calculating the electronic interactions. Eqn (9)–(12) define a self consistent iterative scheme to obtain the band structure and eigenstates of the system. From these equations we can deduce the electronic density and then compute the electric potentials ϕi. The electronic density can be expressed in terms of the Bloch eigenstates ψnk(r) (with n the band index and k the crystal momentum) of the Hamiltonian in eqn (9) as| | 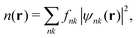 | (13) |
where fnk = 2Θ(εF − εnk) is the occupancy at zero temperature of the state ψnk with eigenvalue εnk, εF is the Fermi energy, and Θ(ε) is the Heaviside step function. In Fig. 2 we show the results of ref. 102, where a TB model with a Hartree potential gives filling dependent renormalized flat bands near the Fermi energy. Similar results are obtained in ref. 153. The TB results are also consistent with those from continuum models including the Hartree potential.157–159
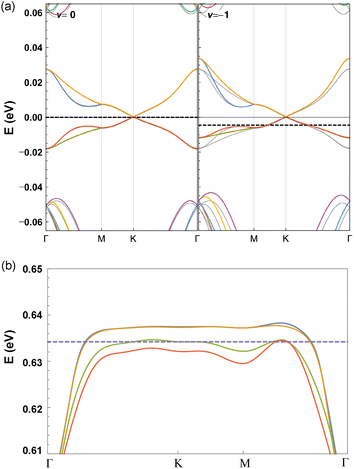 |
| | Fig. 2 (a) The band structure of TBG with θ = 1.08° by taking long-range Hartree corrections into account at electron filling number ν = 0 (left side) and ν = −1 (right side). The gray lines are the band structure without Hartree corrections. The dashed line is the Fermi level at each filling. Adapted with permission from ref. 153. Copyright (2019) by the American Physical Society. (b) The first valence (upper) and conduction (lower) flat bands obtained by including the Hartree-Fock interaction at filling number ν = 0 for TBG with θ = 1.16°. The dashed line is the Fermi level. Adapted with permission from ref. 102. Copyright (2020) by the American Physical Society. | |
To go beyond the Hartree approximation one can consider the Fock contribution, which accounts for the non local electronic interaction. The Fock approximation can be seen as the simplest effective description of the exchange interaction of electrons. Together with the Hartree interaction, this gives the mean field Hartree–Fock approximation. An example of a Hamiltonian with electron–electron interactions in twisted bilayer and trilayer graphene is a mean field Hartree-Fock Hamiltonian of the form102,160–164
| | 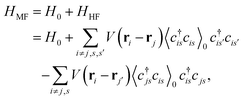 | (14) |
where
H0 is the spin independent non interacting Hamiltonian of
eqn (3),
s(
s′) is the spin quantum number, which can be ignored when considering spin symmetric solutions,
161 and 〈⋯〉
0 denotes the expectation value in a reference state. This HF equation
HMF can be solved self consistently.
102,160–164 We note that the Hartree-Fock solution predicts a gap opening at the Dirac points, as shown in
Fig. 2(b), a result that is also captured by low energy continuum models.
159
2.2.3 TB model with Hubbard-U interaction.
In moiré superlattices, the localized states of flat bands imply strong local electron–electron interaction that could lead to Mott insulating states, ferromagnetism12,25,165,166 and other correlated phases.167 This short range interaction can be described in a minimal way using a local Hubbard term| | 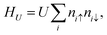 | (15) |
where ni↑ (ni↓) is the electron density operator c†i↑ci↓ (c†i↓ci↑) at each site for pz orbital and U is the interaction strength. In a mean-field approximation, the TB Hamiltonian with the Hubbard-U term can be expressed as168,169| | 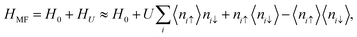 | (16) |
where H0 is a single-particle TB Hamiltonian. The mean-field values 〈ni↑,↓〉 are obtained by iteration until convergence. For TBG around the magic angle, the self-consistent process is typically time-consuming due to the large number of atoms in each moiré unit cell. Therefore, a rescaled non-interacting TB Hamiltonian is proposed to reach an affordable numerical self-consistent calculation. Specially, the low-energy electronic structure of TBG with a small angle θ can be reproduced at a larger angle θ′ that contains a smaller number of atoms.168,169 The rescaled Hamiltonian can be obtained by tuning the parameters in eqn (5) and (6) by the following scaling transformations168| | 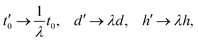 | (17) |
where the dimensionless re-scaling parameter λ is given by| | 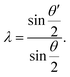 | (18) |
Fig. 3(a) shows the band structure of TBG with θ = 1.5° obtained from a scaled (solid lines) and an unscaled (dashed lines) TB Hamiltonian. The two methods give bands that agree well in the low energy region. The rescaled TB model with a mean field Hubbard U Hamiltonian at the atomic level provides insight into ferromagnetism and Mott insulating states in TBG and other moiré superlattices.168–170 As shown in Fig. 3(b), at half filling of the second band, interactions induce a Stoner instability that splits the flat bands.169
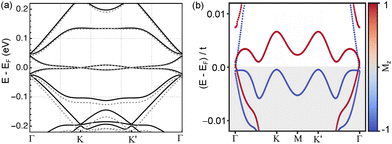 |
| | Fig. 3 (a) Band structure of TBG with θ = 1.5° obtained from a scaled (solid lines) and unscaled (dashed lines) TB models. Adapted with permission from ref. 168. Copyright (2017) by the American Physical Society. (b) The calculated flat bands and spin z magnetization of TBG with angle θ = 0.8° by considering the effect of local mean-field interactions. At angle θ = 0.8°, the second bands from both conduction and valence bands became flat. The interaction strength is U = 2t, where t the nearest-neighbor hopping within one layer, and the electron filling number is ν = −6, corresponding to half-filling of the second band. The red (blue) color indicates a positive (negative) expectation value 〈Sz〉 = Mz of the spin operator. The calculation was performed by using a rescaling method. Adapted with permission from ref. 169. Copyright (2019) by the American Physical Society. | |
2.3 TMDs-based moiré materials
Another family of materials for moiré physics is TMDs, which have attracted growing interest in condensed matter physics. Recently, exciting experimental phenomena, like moiré flat bands, correlated insulating states, interfacial ferroelectricity, Wigner crystals, superconductivity, have been observed in twisted TMDs.21,23,24,147,171,172 TMDs have a triangular geometry that can host both hexagonal (2H) and tetragonal (1T) stackings. In monolayer TMDs, each cell contains one metal and two chalcogenide elements with chemical formula MX2. The geometry and electronic properties vary with different elements. Interestingly, the bilayer moiré pattern can be generated by both identical monolayers (homobilayer) and different monolayers (heterobilayer). In the following, we will describe the TB model for the TMDs homobilayer and heterobilayer.
2.3.1 TB for twisted homobilayer TMDs.
In general there are three TB models for the homobilayer TMDs moiré systems. These three TB models propose very different parameters (onsite energies and SK parameters), but provide electronic structures that are highly consistent. All models adapt an 11-orbital in the monolayer, but consider different interlayer interactions. One of the TB models, discussed by Zhan and coworkers,173,174 considers only the interlayer interactions between the p orbitals of the X atoms at the interface between the two layers. The corresponding TB parameters were developed by Fang and coworkers.145 In the following we describe the theory of this TB model.
The geometry of the TMDs moiré patterns can be defined in the same manner of the graphene moiré systems. The bilayer TB Hamiltonian can be derived by adding an interlayer hopping term to two monolayer Hamiltonians as
| | | Ĥ = Ĥ(1L)1 + Ĥ(1L)2 + Ĥ(2L)int, | (19) |
where the first two terms are the monolayer Hamiltonians and the third term is the interlayer hopping term. The monolayer TB model is constructed from an 11 basis set (five d orbitals from M and three p orbitals from X) as
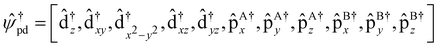
, which contains the on-site energy, the hopping terms between orbitals of the same type at first-neighbor positions, and the hopping terms between orbitals of different type at first- and second-neighbor positions.
145 TB parameters in the single-layer Hamiltonian for MoS
2, MoSe
2, WS
2 and WSe
2 can be obtained from Table 7 of ref.
145. The term
Ĥ(2L)int is the interlayer interaction expressed as
| | 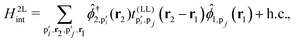 | (20) |
where
![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b5.gif) i,pj
i,pj is the p
j orbital basis of
i-th monolayer. Within the SK parametrization, the interlayer hoppings are expressed as
175| | 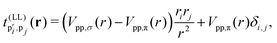 | (21) |
where
r = |
r| and the distance-dependent SK parameter is
| | | Vpp,b = νbe[−(r/Rb)ηb], | (22) |
where
b = σ, π,
νb,
Rb and
ηb are constant values that can be obtained from the ref.
145. The interlayer interactions in twisted homobilayer TMDs are included in the TB Hamiltonian by adding hoppings between p orbitals of chalcogen atoms in top and bottom layers. The cuttoff distance of interlayer hopping can be taken as 5 Å.
148,173,174 The TMDs have two set of bond length values (theoretical and experimental bulk values). For MoS
2, the bond lengths are the in-plane lattice constant
a = 3.18[3.16] Å, unit cell size along the
z direction
h = [12.29] Å, distance alone
z direction between chalcogen layers
dX–X = 3.13[3.17] Å, nearest-neighbor bond betwwen metal and chalgogen atoms
dX–M = 2.41[2.42] Å.
145 Values in brackets are experimental bulk values. More details on the bond length of other TMDs refer to ref.
87 and
145.
Strong spin-orbital coupling (SOC) is a main characteristic in TMDs. By expanding the 11 orbitals to 22, SOC can be incorporated into the TB model. The intralayer Hamiltonian of eqn (19) with SOC is given by145
| | 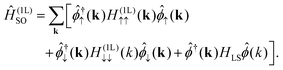 | (23) |
The diagonal blocks in the first term
H(1L)↑↑ =
H(1L)↓↓ =
H(1L) are the intralayer Hamiltonian. These are the spin-independent hopping processes. The effect of spin-orbit coupling,
HLS, is incorporated by the on-site
λSOL·
S term for each atom. Because it is an on-site term, it does not carry momentum dependence and is a constant matrix with elements
| | 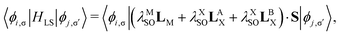 | (24) |
where
λMSO and
λXSO are the SOC strength of the M and X atoms, respectively.
145 Within SOC, the interlayer Hamiltonian will only consider the interaction of electrons with the same spin direction. In this way, the tunable SOC in twisted homobilayer and homotrilayer TMDs were carefully studied.
111,173
Lattice relaxation is also an important effect in TMDs moiré systems that needs to be taken into account in the TB model. When relaxing the system, atoms moves away from its equilibrium position, both in-plane and out-of-plane. Upon relaxation, the intralayer hoppings can be modified through the form176
| | 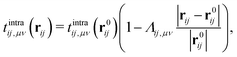 | (25) |
where
tintraij,μν is the intralayer hopping between the
μ orbital of the
i atom and
ν orbital of the
j atom,
r0ij and
rij are the distance between the
i and
j atoms in the equilibrium and relaxed cases, and
Λij,μν is the dimensionless bond-resolved local electron-phonon coupling. It is assumed that
Λij,μν = 3, 4, 5 for the chalcogen–chalcogen pp, chalcogen–metal pd and metal–metal dd hybridizations, respectively.
176 By using the TB model, ultraflat bands were found to exist in TMDs for almost any small twist angles.
173
The second TB model was presented by Venkateswarlu and coworkers.70 In this TB model, the interlayer interaction included p S–p S, d Mo–p S and d Mo–d Mo terms. The TB parameters were set up to correctly match the DFT band structures.
In the third TB model, formulated by Vitale and coworkers,146 the interlayer interactions p;S–p;S and pz;S–dz2;Mo were included. Moreover, they described the interlayer hoppings (p–p and pz–dz2) using different sets of SK parameters for varying interlayer separations. The TB parameters were obtained from a Wannier transformation of the DFT Hamiltonian. Fig. 4 shows the band structures of twisted MoS2 with the same twist angle but derived from different TB models. The results are highly consistent with one another.
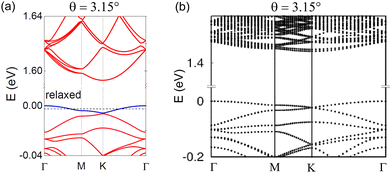 |
| | Fig. 4 Tight-binding band structure of twisted homobilayer MoS2 at θ = 3.15°. (a) Bands obtained from a TB model from ref. 173 and 148. Adapted with permission from ref. 148. Copyright (2022) by the American Physical Society. (b) Bands calculated from the TB model from ref. 146. Adapted under the terms of the CC BY license from ref. 146. Copyright (2021) IOP Publishing. | |
2.3.2 TB for twisted heterobilayer TMDs.
In 2021, by fitting DFT band strutures, Vitale and coworkers extended the work of Fang et al., to construct the TB Hamiltonian for both twisted heterobilayer and homobilayer TMDs. In this TB model, they also consider the interlayer hoppings between chalcogen p and metal dz2 orbitals with a SK expression146| | 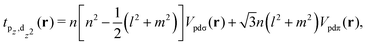 | (26) |
where the directional cosines are defined as l = rx/r, m = ry/r and n = rz/r. To determine the functions Vpdσ(r) and Vpdπ(r), Vitale and coworkers calculated tpz, dz2, tpz,dxz and tpz,dyz for a set of untwisted bilayers with different stacking configurations and different interlayer separations, using a Wannier transformation of the DFT Hamiltonian. Then, a least square fitting process was used to extract Vpdσ and Vpdπ at different interatomic distances. The results were fitted to functions of the type| |  | (27) |
where b = σ, π Vb, αb, βb and γb denote interlayer hopping parameters fitted from DFT calculations, which are dependent on the types of heterostructures of bilayer TMDs.146h = 3.5 Å is an average interlayer distance. All the TB parameters are in ref. 146. Fig. 5 shows the band structures of the TMDs heterostructures containing different species of chalcogens. Similar to the homobilayer case, the highest valence bands are derived from monolayer K/K′ states (Fig. 5(a)) or Γ states (Fig. 5(b)).
 |
| | Fig. 5 Tight-binding band structure of twisted heterobilayer TMDs for (a) twisted bilayer WSe2 /MoS2 and (b) MoSe2 /WS2 heterostructure at twist angle θ = 4.5°.146 Adapted under the terms of the CC BY license from ref. 146 Copyright (2021) IOP Publishing. | |
2.4 hBN-based moiré materials
2.4.1 TB for twisted bilayer hBN.
Similar to TMDs, the bilayer hBN has two possible distinct stacking configurations, the parallel BN/BN and antiparallel alignment BN/NB. In the beginning, the twisted bilayer hBN was studied by DFT calculations, unveiling multi-flat bands at the edges of the bands at an angle θ = 2.64°, and no constraint of magic angles that was similar to the TMDs case.177 Therefore, twisted bilayer hBN could provide an ideal platform to study correlations effects. However, the DFT calculations could only tackle large angle systems. Thus, an atomic TB model was proposed by Walet and Guinea, which could further facilitate finer studies of electronic properties for small angle twisted bilayer hBN.140 In this TB model, the twisted bilayer hBN Hamiltonian is composed of intralayer H1(2) and interlayer H12 partsH1(2) is similar to the single-layer Hamiltonian of graphene and has the form:| | 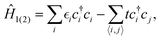 | (29) |
in which i denotes the pz orbital site of B or N atom. 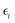 is the onsite energy that has a difference
is the onsite energy that has a difference 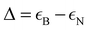 for B and N atoms.178t is the intralayer nearest hopping between B and N. Δ and t are set as 8 eV and 2.33 eV, respectively.140H12 is the interlayer Hamiltonian with the form140
for B and N atoms.178t is the intralayer nearest hopping between B and N. Δ and t are set as 8 eV and 2.33 eV, respectively.140H12 is the interlayer Hamiltonian with the form140| | tXY⊥(r) = tXY![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−α(r − h)), exp(−α(r − h)), | (30) |
where r is the distance between X and Y atoms (X(Y) is B or N) and the empirical parameters are set as h = 3.33 Å, α = 4.4 Å−1, tNN = 0.15 eV, tBB = 0.7 eV and tNB = 0.3 eV in ref. 140. In the above TB model, the hopping term in eqn (30) does not distinguish the atomic species, and assumes one distance-dependent relation for all atoms. However, this model could capture the flat band features and give an explanation of charge polarization in twisted bilayer hBN.140,179
Two additional TB models, fitted from DFT results for twisted bilayer hBN, have been proposed.136,141 One of them, developed by Sponza and coworkers, employs the first nearest-neighbor in-plane Hamiltonian [eqn (29)] with 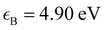 ,
, 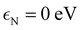 , and t = 2.65 eV, and uses a TBG-like relation that includes only Vppσ for the interlayer hopping.141
, and t = 2.65 eV, and uses a TBG-like relation that includes only Vppσ for the interlayer hopping.141
| | tXY⊥(r)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = = ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n2γXYFXYc(r)exp[QXY(h − r)], n2γXYFXYc(r)exp[QXY(h − r)], | (31) |
where
h = 3.22 Å is the interlayer distance, XY labels the pairings BN, BB, or NN, and
| |  | (32) |
is a smooth function with
lc = 0.265 Å and cutoff distance
rXYc. The values of
γXY and
QXY in
eqn (31) can be found in ref.
141. The cutoff distance
rXYc depends on the value of
QXY according to the relation
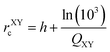
.
Another TB model, developed by Li and coworkers, considered intralayer hoppings up to six neighbors and used onsite energies of 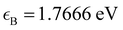 and
and 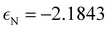 for the first term in eqn (29).136 In addition, the lattice relaxation effect could be incorporated into the intralayer interaction as
for the first term in eqn (29).136 In addition, the lattice relaxation effect could be incorporated into the intralayer interaction as
| |  | (33) |
where
tαβ(
r0,ij) is the intralayer hopping terms of the rigid lattice with distance
r0,ij between atoms
i and
j, and
rij is the relaxed distance.
r0,BB,
r0,BN and
r0,NN can be obtained by using the lattice constant
a = 2.4795 Å of the rigid case. The interlayer hopping terms are determined by the SK relation in
eqn (4) with
| | 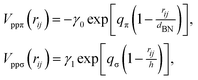 | (34) |
where the intralayer distance is
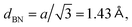
the vertical interlayer distance is
h = 3.261 Å,
γ0 = 2.7 eV, while
γ1 has
γ1 =
tBB′ = 0.831 eV,
γ1 =
tNN′ = 0.6602 eV, or
γ1 =
tBN′ =
tNB′ = 0.3989 eV. The parameters
qπ and
qσ have the relation
| | 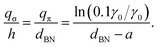 | (35) |
Fig. 6 shows the band structure of twisted bilayer hBN obtained from Li's TB Hamiltonian.
136 The band gap increased significantly after lattice relaxation. The bands from the edges became extremely flat in the small-angle region.
 |
| | Fig. 6 (a) Low-energy valence band and (b) conduction band for the BN/BN stacking with various twist angles, for rigid and relaxed configurations. (c) and (d) are the same plot but for BN/NB. Adapted with permission from ref. 136. Copyright (2024) by the American Physical Society. | |
2.4.2 TB model for graphene/hBN moiré superlattice.
In experiments, hBN is widely used as a substrate to support or encapsulate graphene and twisted graphene layers. Its atomically flat surface and lack of dangling bonds improve the device quality by reducing disorder and enhancing carrier mobility. Because of the lattice mismatch between graphene and hBN, a graphene/hBN superlattice forms even when the lattices are crystallographically aligned. The presence of hBN modifies the electronic properties of graphene, multilayer graphene, and twisted graphene through interlayer interactions between carbon and B or N atoms. The total TB Hamiltonian can be written aswhere Hg and HhBN denote the TB Hamiltonians of graphene and monolayer hBN, respectively. The single layer Hamiltonians Hg and HhBN are as introduced in the previous sections. The key ingredient is the interlayer interaction H⊥, which can be expressed using the Slater–Koster relation in eqn (4), with the same Vppπ and Vppσ as in eqn (5) and (6). In most calculations, the hopping parameters t0 and t1 between a carbon atom and a B or N atom are set to t0 = 2.7 eV and t1 = 0.48 eV. A complementary route is to construct effective hBN potentials within TB models.180 When lattice relaxation is important, combining atomistic TB with classical molecular dynamics provides a practical way to include structural relaxation in TBG on hBN and to quantify its impact on the electronic spectrum.181 The developed theoretical approaches establish the central role of hBN in reshaping the electronic structure of graphene180 and twisted bilayer graphene,181,182 including gap openings at the Dirac point and the appearance of secondary Dirac cones.183–192
3 Computational methods with TB for moiré superlattices
The TB model is a powerful tool for analyzing the physics arising from the moiré systems. In particular, the single-particle band structure of the TB Hamiltonian is a good and accurate starting point to describe the moiré structure and explain the experimental results. However, in these large-scale and complex systems, the loss of angstrom-scale periodicity and possession of moiré-scale period imply that the moiré unit cell contains a large number of atoms. Such large-scale TB Hamiltonian matrix poses a significant theoretical challenge. In the following, we review several methods for dealing with these large-size Hamiltonian matrices.
3.1 Diagonalization method
To analyze electronic properties such as the band structures in Fig. 1, a typical computational method is directly diagonalizing the full TB Hamiltonian Htb to obtain its eigenvalues E and eigenstates ψ satisfyingFor the orthogonal basis, this is a dense Hermitian eigen-problem, with the cost of time and memory scaling as ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (N3) and
(N3) and ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (N2), respectively. The non-orthogonal TB Hamiltonian leads to a generalized form Hψ = ESψ with an overlap matrix S.193 When only a small number of eigenpairs near the Fermi level are required, e.g., bands in a narrow energy window or low-frequency transport/optics, partial-spectrum solvers are markedly efficient tools for sparse TB Hamiltonian matrices. The Krylov method can target extremal or interior eigenvalues. With a shift–invert one iterates on the operatorso that eigenvalues closest to the shift σ ≈ EF converge first.194–199 In practice, full diagonalization remains simple and robust for moderate N, while partial-spectrum solvers become attractive for very large supercells or dense k-meshes focused on a small energy window around EF.
(N2), respectively. The non-orthogonal TB Hamiltonian leads to a generalized form Hψ = ESψ with an overlap matrix S.193 When only a small number of eigenpairs near the Fermi level are required, e.g., bands in a narrow energy window or low-frequency transport/optics, partial-spectrum solvers are markedly efficient tools for sparse TB Hamiltonian matrices. The Krylov method can target extremal or interior eigenvalues. With a shift–invert one iterates on the operatorso that eigenvalues closest to the shift σ ≈ EF converge first.194–199 In practice, full diagonalization remains simple and robust for moderate N, while partial-spectrum solvers become attractive for very large supercells or dense k-meshes focused on a small energy window around EF.
Once {E, ψ} are available, numerous static and dynamical observables can be evaluated via Kubo formulas in the eigenstate basis.200 For example, the optical conductivity can be formulated as201,202
| |  | (39) |
where
gs is the spin degeneracy and D is the dimension of structure, typically set to 2 for 2D materials.
Jα1 and
Jα2 are current operators along the
α1 and
α2 directions, respectively.
nF is the Fermi-Dirac distribution. Eigenvalues
Ekl and eigenstates |
kl〉, with band index
l and momentum
k, are needed to describe optical band transitions between
l and
l′ bands. The integration runs over the whole Brillouin zone (BZ).
3.2 Linear-scaling random state methods
A full diagonalization method will not be very efficient when a moiré supercell contains more than thousands of atoms. For example, the number of atoms in TBG increases rapidly when reducing the angle θ. For instance, the angle θ ≈ 0.22° contains more than 260![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms. The calculation of electronic structures of TBG with tiny angles is numerically challenging. In this case, a linear-scaling method with scale of O(N) has the advantage of tackling the large-scale TB Hamiltonian.106,107,203
000 atoms. The calculation of electronic structures of TBG with tiny angles is numerically challenging. In this case, a linear-scaling method with scale of O(N) has the advantage of tackling the large-scale TB Hamiltonian.106,107,203
One of the linear-scaling methods is the random state kernel polynomial method (KPM).203 For example, the DOS can be expressed as
| | 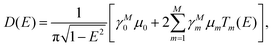 | (40) |
where
E is rescaled to [−1,1] and
γMm is a kernel coefficient; a Jackson kernel, widely used, has the form
| | 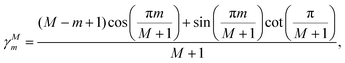 | (41) |
where
Tm(
E) is the Chebyshev polynomial with the recursive relation
| | Tm(x)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = = ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2xTm−1(x) − Tm−2(x). 2xTm−1(x) − Tm−2(x). | (42) |
Here
Tm(
x) = cos[
m![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
arccos(
x)], resulting in
T0(
x) = 1 and
T1(
x) =
x. The parameter
μm is the Chebyshev moment computed through
| | 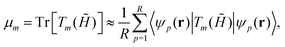 | (43) |
where
ψp(
r) is the random (stochastic) state of the expanded moiré superlattice, and
![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif)
is a rescaled Hamiltonian with eigenvalues ranging for −1 to 1. The error of this approximation is
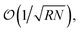
with
R the number of random states and
N the size of the Hamiltonian. The large-scale moiré superlattices naturally give a large
N Hamiltonian that benefits the trace of
eqn (43) convergence, but is hard to be diagonalized. A Kubo-Bastin DC conductivity of large-scale moiré can be computed with
204–206| | 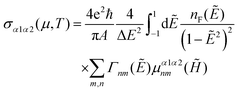 | (44) |
where Δ
E =
E+max −
E−min is the energy range of the spectrum and
Ẽ is the rescaled energy within [−1, 1].
Γnm(
Ẽ) and
μα1α2nm(
![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif)
) are functions of the energy and the Hamiltonian, respectively
| | 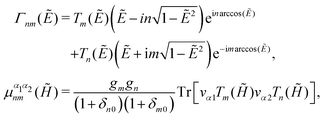 | (45) |
where
gm can be represented as a Lanczos kernel with
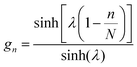
and
λ = 4.
vα1 is the
α1 component of velocity operator

where
l is the distance vector, and the trace can be calculated in a random state basis through
eqn (43).
204 As shown in
Fig. 7, the KPM is a powerful method for modeling the DOS, Direct current (DC) conductivity and conductance in graphene-based moiré systems with tiny angles
207–211 and could facilitate the computation of properties of more complex morié superlattices in the future.
212,213
 |
| | Fig. 7 DC conductivity and DOS calculated from KPM based on the TB model introduced in Section 2.2.1 for TBG over a wide range of angles. Left and right insets display the DC and DOS for small and large angles, respectively. Adapted with permission from ref. 204. Copyright (2018) by the American Physical Society. | |
The tight-binding propagation method (TBPM) is another powerful approach to simulate the broad properties of large-scale moiré materials.107 Compared to KPM, a time-evolution is applied to extract the information of a simulated system.106 For example, the DOS can be calculated as106,107
| | 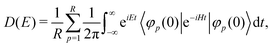 | (46) |
where
φp(0) is the
pth initial random state at
t = 0. The calculation converges with an increasing number of random samples
R and the size of the Hamiltonian
N. Based on TBPM, the optical conductivity can be calculated
106,107| | 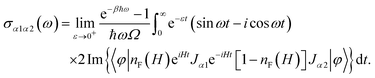 | (47) |
Here,
Ω is the area or volume of the model,
β = 1/
kBT with
kB the Boltzmann constant and
T the temperature. Compared to the
O(
N3) time scaling of
eqn (39), the random-state method scales linearly
O(
N) with the dimension of Hamiltonian in real space. Besides, TBPM can be applied to calculate dynamical properties in both commensurate and incommensurate moiré supperlatice (see
Fig. 8(b)), while the diagonalization method in reciprocal space can only work for commensurate ones (see
Fig. 8(a)). The merits and flexibility of TBPM also make it validly explain experimental phenomena and simulate broad electronic and dynamical properties in various moiré materials (see Section 5).
95,214–217
 |
| | Fig. 8 (a) Evolution of the optical conductivity (solid black lines) of TBG with commensurate angles, calculated by using eqn (39) with exact diagonalization of the TB Hamiltonian. The dashed red circles are the continuum results. Adapted with permission from ref. 218. Copyright (2013) by the American Physical Society. (b) Evolution of the optical conductivity of TBG with varied angles, calculated by using eqn (47) with a combination of TBPM and TB model. Conductivity peaks corresponding optical transitions between VHS of DOS are indicated by arrows in the inset. Adapted with permission from ref. 219. Copyright (2018) by the American Physical Society. | |
3.3 Tight-binding methods with machine learning
A convincing atomic TB model is relevant for exploring properties of morié supperlatices. Recently, machine learning methods have emerged to favor the construction of TB Hamiltonian and investigate the electronic properties of moiré superlattices.220–226 For example, by training various small bilayer stackings of graphene, deep learning-based methods such as DeepH can reproduce electronic structures of a large-scale TBG moiré up to DFT accuracy (see Fig. 9(b)).223,224,227 By similarly preparing the train dataset from real-space DFT calculation as DeepH, HamGNN method can also train and infer the ab initio accuracy TB Hamiltonian of large-scale moiré materials such as twisted bilayer MoS2 as displayed in Fig. 9(a).228,229 While the so-called ab-initial TB Hamiltonian from DeepH and HamGNN is actually a numerical TB Hamiltonian expanded in a group of non-orthogonal and overlapped localized basis, a DeepTB method can generate a semi-empirical SK TB Hamlitonian with ab initio accuracy over a wide range of elements, which could open new possibility to provide accurate SK parameters for generating Hamiltonian for unknown moiré materials.230
 |
| | Fig. 9 (a) Comparison of band structures of twised bilayer MoS2 at θ = 3.5° obtained from machine-learning HamGNN method (lines) and DFT calculation (dots). A band zoom near zero is shown in the inset. Adapted under the terms of the CC BY license from ref. 228. Copyright (2023) the authors. (b) Bands of TBG at θ = 1.08° predicted by DeepH method, compared to those obtained from DFT calculation (red dots) and continuum model (red lines) (Details of continumm model in next section). Adapted under the terms of the CC BY license from ref. 227. Copyright (2023) the authors. | |
3.4 Software packages within TB for modeling moire superlattices
Atomically modeling a moiré material based on TB Hamiltonian contains some typical tasks including the construction of the superlattice, relaxation, building a TB Hamiltonian, employing numerical methods to study properties and postprocessing. There are some useful and versatile software packages facilitating these modeling tasks. Twister is specialized to construct and relax a moiré superlattice.231 Recently, DPmoire provides a means to generate ab-initial accuracy machine-learning force fields specifically tailored for moiré structures,232 which interfaces with molecular dynamics software such as Lammps233 and ASE234 for atomic relaxation. The versatile package KITE incorporates the atomic construction of a moiré superlattice, KPM for calculating transport and optical properties and visualization.108 It also provides the interface with other packages such as Pybinding, which is also based on TB methods with both the exact diagonalization and the KPM.235 TBPLaS is a functional package covering all the procedures required to simulate a moiré superlattice.107 It features with exact diagonalization, TBPM, and KPM to calculate various properties of moiré superlattice. It also has interface with Wannier90,236 Lammps,233 DeepH223 and DeepTB230 to keep its flexibility in considering relaxation and constructing a new Hamiltonian for a moiré superlattice.
4 Fitting TB to low-energy continuum models
The interesting regime of low twist angles in moiré superlattices leads to very large moiré lengths, with up to thousands of atoms per supercell. This naturally imposes a heavy computational cost on atomistic TB simulations. Besides time-consuming limitations, dealing with huge supercells can hinder an intuitive understanding on how the system behavior changes as the twist angle decreases. In addition, going beyond the TB single-particle picture becomes exponentially more difficult as the number of atoms increase. Yet, it is at these large moiré superlattices where the electronic correlations become crucial.
These considerations have motivated the need of having effective continuum descriptions of the electronic properties in moiré systems, which can capture the TB results, but yet are simpler enough to allow efficient extensions of it by including, for instance, correlations effects. Having simpler continuum models can also provide valuable insights on the nature and origin of flat bands in moiré systems.237–242 Furthermore, a continuum model can be constructed even if the systems is incommensurate.76,243 A simple schematic hierarchy of the fitting of TB models to low-energy continuum models is shown in Fig. 10.
 |
| | Fig. 10 Schematic representation of the path from TB models to effective continuum models in TBG. Different approximations are gauged by the properties of the band structure around the magic angle: the emergence of flat bands, their gap with the remote bands, and the particle-hole asymmetry. The later two properties only emerge in the TB model when the system is allowed to relax. The continuum model provides a low-energy description in which the two layers, with Dirac Hamiltonians H1 and H2, are coupled by a moiré potential U with effective hoppings uAA and uAB at the AA and AB/BA stacking regimes. Capturing the three main properties of the flat bands depends, primarily, on the ratio between the hopping energies and the locality of the moiré potential.244–246 From the simple continuum model one can then more easily go beyond the single-particle picture by taking into account many-body interactions. | |
The continuum description rest upon the fact at low twist angles the moiré scale becomes much larger than the atomic length, so the interlayer interaction is dominated by its long wavelength components.76,243 This means that the electronic behavior can be well described by the continuum approximation. The continuum description was originally introduced for TBG in 2007 by Lopes dos Santos et al.,112 for commensurate structures, and later extended to account for incommensurate structures by Bistritzer and MacDonald in 2011.76 The later model allows one to define a moiré Brillouin zone and obtain the band structure of TBG for any low twist angle. These pioneering formulations not only captured the low energy spectra obtained by the TB model, but also allowed one to obtain further simpler models of the flat bands as linear dispersions with a renormalized velocity that vanishes at the magic angle θ ∼ 1.05°.76,112 Since then, many other works have reformulated,77,218,245–251 and extended these continuum models to account for large twist angles,243 lattice relaxation,119,244,252–254 and strain effects.97,113,255–260 The original continuum model of TBG has been further extended to other moiré structures, such as twisted TMDs,71,261,262 twisted hBN,140 twisted graphene/hBN,181,182,263,264 and twisted multilayer graphene.265,266 In what follows we focus on TBG and mostly follow the continuum formulation of Koshino et al.247
The starting point is to define the Bloch wave states in each layer as
| | 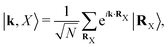 | (48) |
where X = {A
1, B
1, A
2, B
2} is the layer-sublattice index,
N is the number of graphene monolayer cells in each layer, and
Rl are the atomic positions
| | 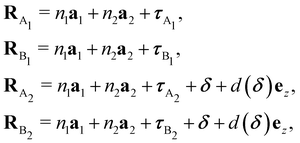 | (49) |
where
a1 =
a(1, 0) and
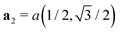
are the monolayer's lattice vectors, while
τX are the sublattice displacements (
τA1 =
τA2 = 0,
τB1 =
τB2 = −
τ1 with
τ1 = (2
a2 −
a1)/3). The displacement vector
δ accounts for the variation in the atomic positions of layer 2 due to its relative rotation with layer 1, while
d(
δ) accounts for the interlayer distance at
δ. When the layers are relatively rotated by a small twist angle
θ, the displacement vector
δ is taken to vary with the real space position
r as
247| | | δ(r) = [R(θ/2) − R(−θ/2)]r. | (50) |
Due to relaxation effects, the corresponding interlayer distance
d(
δ) is not uniform throughout the supercell: it is maximum around the AA stacking with
dAA = 0.36 nm, and minimum around the AB stacking
dAB = 0.335 nm. Koshino
et al.247 interpolated
d as
| | 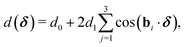 | (51) |
where
b3 = −
b1 −
b2,
d0 = (
dAA + 2
dAB)/3 and
d1 = (
dAA −
dAB)/9.
Assuming that the transfer integral between sites RX and RX′ depends only on their relative distance, the interlayer matrix elements that couple the two layers takes the form ref. 218 and 243
| | 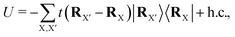 | (52) |
where the transfer integral
t(
R) is given by the SK parametrization in the TB model. Replacing the plane-wave expansion of the Bloch states |
RX〉, and using the continuum description of the displacement vector
δ(
r), leads to the interlayer interaction
| | 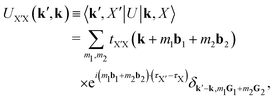 | (53) |
where
Gi = [
R(
θ/2) −
R(−
θ/2)]
bi are the moiré vectors and
tX′X(
q) is the in-plane Fourier transform of the transfer integral
| | 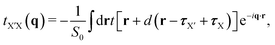 | (54) |
where
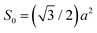
in the unit cell of monolayer graphene.
Fig. 11 shows the variation of the hopping amplitude
t(
q) as a function of momentum
q = |
q|, for different models. The key observation is that
t(
q) decays very rapidly with
q because the interlayer separation exceeds the intralayer carbon–carbon distance by more than a factor of 2.
76
 |
| | Fig. 11 Dependence of the moiré-induced interlayer tunneling on the momentum qa = |q|a, where a ≃ 0.142 nm is the carbon–carbon distance in graphene. The solid, dashed and dot lines correspond to the models described in ref. 267, 268 and 269, respectively. The vertical lines indicates the point kDa, where kD = |K| is the distance of the monlayer's Dirac point. Inset shows the renormalized Fermi velocity v obtained by the Bistritzer–MacDonald continuum model, predicting a series of magic angles where v* vanishes. Adapted under the terms of the CC BY license from ref. 76. Copyright (2011) National Academy of Sciences. | |
Following the Dirac approximation, the momenta in both layers is measured with respect to their Dirac points Kξ (where ξ is the valley index), and the transfer integral in eqn (53) is approximated as 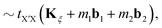 leading to a local moiré potential
leading to a local moiré potential
| | 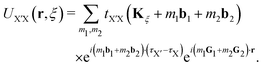 | (55) |
The coupling amplitude
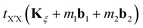
only depends on the distance of the Dirac points to the origin. As
tX′X(
q) decay rapidly with
q, one can take only the first three leading terms (
m1,
m2) = {(0, 0),
ξ(1, 0),
ξ(1, 1)} in the summation over
m1 and
m2. The moiré potential, in matrix form, then takes the well-known form ref.
243 and
247| | | U(r, ξ) = U0 + U1eiξG1·r + U2eiξ(G1+G2)·r, | (56) |
where
76,112| | 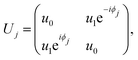 | (57) |
with
ϕj = (
j − 1)2π/3, and
u0 and
u1 are the AA and AB/BA stacking amplitudes given by
247| | 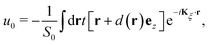 | (58) |
| | 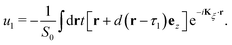 | (59) |
Koshino
et al.247 obtained
u0 = 0.0797 eV and
u1 = 0.0975 eV. Note that for flat TBG, as considered initially in the Bistritzer-MacDonald model,
76 the interlayer distance
d(
r) is constant and thus
u0 =
u1.
Finally, the effective continuum model Hamiltonian for the ξ valley takes the form ref. 247
| | 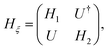 | (60) |
where
Hl is the intralayer Dirac Hamiltonian in layer
l = 1, 2, given by the two-dimensional Weyl equation centered at the
Kl,ξ point
| | | Hl = −ħv[R(lθ/2)(k − Kl,ξ)]·(ξσx, σy). | (61) |
Here
σx and
σy are the Dirac matrices acting on the sublattice space, and ref.
218| | 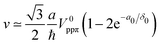 | (62) |
is the Fermi velocity, where
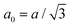
is the carbon–carbon distance and
δ0 = 0.184
a is the decay length,
218 so that the nearest intralayer coupling is 0.1
V0ppπ. With
V0ppπ ∼ −2.7 eV, Koshino
et al. obtained
ħv/
a = 2.1354 eV.
247
To compute the energy bands in the continuum model one expands the Bloch states in plane-waves as
| | 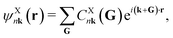 | (63) |
where
n is the moiré band index and
k is a momentum vector in the moiré Brillouin zone. Since each state with momentum
k in one layer is coupled, through the moiré potential, to another state with momentum
k +
G in the other layer, the continuum model Hamiltonian in reciprocal space has no inherent cutoff (any state can be always coupled to another through umklapp processes). However, the relevant low-energy spectra is dominated by the coupling of the states closest to the Dirac points, so in practice it is sufficient to consider a large enough momentum cutoff (
e.g., |
k| < 4|
G1|), up to which the low-energy spectra converges. The caveat is that the lower the twist angle, the stronger the moiré coupling becomes, and thus the more reciprocal vectors one needs to consider for convergence. This again leads to a high-dimension continuum model Hamiltonian (albeit still much smaller than those in the TB models), further motivating yet simpler effective models for the flat bands.
242,250,270–277
The moiré potential given by eqn (55) corresponds to the zeroth order approximation in momenta, i.e., taking k ∼ K in the general expression given by eqn (53). As noted, this results in a local, momentum-independent interlayer tunneling. Although this approximation already captures very well the TB spectra (specially the emergence of flat bands around the magic angle; see Fig. 12), it still cannot capture other important features of the band structure, such as the particle–hole asymmetry of the flat bands due to relaxation effects. To capture such behavior one needs to take into account the contribution of the non-local interlayer tunnelings.
 |
| | Fig. 12 (a) Band structures of rigid twisted bilayer graphene for different commensurate angles θ. The black solid line correspond to the tight-binding results, while the red dotted-line corresponds to the continuum model results with a local moiré potential. Adapted from ref. 218. (b) Comparison between the band structures of rigid and relaxed twisted bilayer graphene at the magic angle θ = 1.05°, obtained by the tight-binding model, and the continuum model with local and non-local (k-dependent) moiré potential. Only the later captures the relaxed particle-hole asymmetry of the tight-binding flat bands. Adapted from ref. 244. | |
The leading order, non-local term follows by expanding the interlayer tunneling tX′X(k) around the Dirac point k = K up to first order in momenta244–246,252
| | 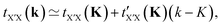 | (64) |
where
| | 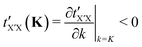 | (65) |
is the non-local tunneling parameter and
K = |
K|. Keeping still the three leading-order Fourier components, the momentum-space matrix elements of the moiré potential then become
| | 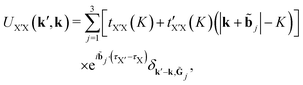 | (66) |
where
![[G with combining tilde]](https://www.rsc.org/images/entities/b_char_0047_0303.gif) 1
1 = 0,
![[G with combining tilde]](https://www.rsc.org/images/entities/b_char_0047_0303.gif) 2
2 =
ξG1,
![[G with combining tilde]](https://www.rsc.org/images/entities/b_char_0047_0303.gif) 3
3 =
ξ(
G1 +
G2) and
![[b with combining tilde]](https://www.rsc.org/images/entities/b_char_0062_0303.gif) 1
1 = 0,
![[b with combining tilde]](https://www.rsc.org/images/entities/b_char_0062_0303.gif) 2
2 =
ξb1,
![[b with combining tilde]](https://www.rsc.org/images/entities/b_char_0062_0303.gif) 3
3 =
ξ(
b1 +
b2). Jihang Zhu
et al.246 estimated the non-local tunneling energies as
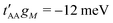
and
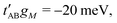
where
gM = |
G1|.
Fig. 12(b) show the continuum band structure, at the magic angle
θ = 1.05°, with and without the non-local moiré potential; only the non-local potential effectively captures the particle-hole asymmetry obtained in the relaxed TB models.
5 Examples of using TB model in moiré systems
In this section, we provide two examples of using the TB model to study the moiré systems. The first example is the theoretical investigation of the electronic properties of graphene quasicrystal,278 and the second example is the theoretical explanation of the Rydberg moiré excitons in WSe2 /TBG heterostructure.215
5.1 Dedocagonal bilayer graphene quasicrystal
When the AA stacking bilayer graphene rotates with an angle of θ = 30°, a dodecagonal bilayer graphene quasicrystal is formed (see Fig. 13(a)). Interestingly, the dodecagonal graphene quasicrystal has a 12-fold rotational symmetry but lacks translational symmetry. The dodecagonal graphene quasicrystal has been investigated by experiments, showing distinct properties from graphene.109,110 The lack of translational symmetry prevents the application of band theory and requires a new method in this system. In 2019, Yu and coworkers explicitly studied the electronic properties of the dedocagonal graphene quasicrystal.278 First, by combining the TBPM and TB methods, they studied the electronic and optical properties (Fig. 13(b) and (c)). In particular, to accurately calculate the characteristics, we adopted a large round disk of graphene quasicrystal with ten million atoms described by the TB Hamiltonian. Such large dimension of TB Hamiltonian was solved by the TBPM method. As shown in Fig. 13(b), compared to the graphene case, the graphene quasicrystal possessed distinct peaks in the DOS spectrum around ±2 eV, which were attributed to the interlayer interaction. In the vicinity of the Fermi level, the DOS was almost the same as the pristine graphene, which indicated that the optical conductivity at low energies was also the same (see Fig. 13(c)). Importantly, peaks emerged around 4.0 ≈ 4.6 eV in the optical spectrum, which were attributed to the VHS of quasicrystal states.
 |
| | Fig. 13 (a) Graphene quasicrystal. (b) DOS obtained from graphene quasicrystal and its approximants. The number of atoms in each unit cell of approximants are in brackets. The DOS of pristine graphene is also plotted. (c) The optical conductivities of graphene quasicrystal, its approximants and graphene. (d) Atomic structure of 4/7 approximant with four unit cells. (e) The eigenstates of 41/71 approximant at −4.2 and −2.76 eV. Red and blue circles represent the states from the top and bottom layers, respectively. (f) Hofstadter's butterflies of 41/71 approximant with magnetic field less than 50 T. Colorbar represents the value of DOS. The blue numbers indicate the indexes of the corresponding Landau levels. Adapted under the terms of the CC BY license from ref. 278. Copyright (2019) the authors. | |
Second, commensurate configurations of TBG with twist angle close to 30° were used as the approximant. In these approximants, the top graphene layer was compressed or stretched to satisfy the condition M × 3d = N × at, with at being the lattice constant of the top graphene with strain. The approximant was named as M/N. The structure of 4/7 approximant is shown in Fig. 13(d). The accuracy of these approximants were varified by comparing the DOS and optical conductivity with those calculated directly from the quasicrystal. Moreover, the quasi-periodicity still remained in the periodic approximants. The eigenstates obtained from the approximant perserved the 12-fold rotational symmetry (Fig. 13(e)). The approximant was used to study the magnetic field effect. Some new Landau levels (LLs) appeared below Fermi level by 1.6 eV when the magnetic field exceeded 10 T. These new LLs followed a two-dimensional Dirac fermion with reduced Fermi velocity of 5.21 × 105 m s−1. Moreover, the LL of n = 0 was missing, but its position was predicted to be around −1.49 eV by interpolation. At this energy, there was a band gap at M point, and the valleys hybridized strongest.
5.2 Rydberg moiré excitons in WSe2/TBG heterostructures
Another example is the observation of the Rydberg moiré excitons in WSe2/TBG heterostructure.215,279 In this system, the induced moiré potential in TBG provided a possible pathway to spatially confine and manipulate the Rydberg excitons in the monolayer WSe2. We named the moiré-trapped Rydberg excitons as Rydberg moiré excitons. For TBG with angle below a crossover angle θ = 1.2°, the lattice relaxation played a significant role in both structural and electronic properties.118,280 In the geometry, the lattice relaxation shrunk the AA region and expanded the AB region to a triangular domain (see the inset of Fig. 14(e)). The states from lowest energy narrow bands were mainly localized in the AA region and states from the remote bands were mainly in the AB region.280 Such lattice reconstruction was relevant in the generation of the Rydberg moiré excitons in WSe2/TBG heterostructures. The lattice relaxation effect could be well captured by a combination of molecular dynamics, TB Hamiltonian and the TBPM methods.
 |
| | Fig. 14 (a) Reflectance contrast spectrum of WSe2/TBG heterostructure with the angle θ = 0.6° in TBG. XRM is the spatial confinement of Rydberg moiré excitons. (b) Photoluminescence spectrum of the same sample measured at the same location. (c) Energy shift of the lowest-energy branch extracted from (a) as a function of n/ns. n is the carrier density and ns is the full filling density of the first narrow band. (d) The TB calculation of local carrier density difference between the states in the AA and AB/BA regions as a function of n/ns. Inset was a schematic exemplification of the XRM with the lowest energy confinement on the electron-doped side. (e) TB calculation of the spatial charge distribution of TBG with θ = 0.6° at different doping densities. The lowest map was a schematic of relaxed TBG with AA, AB and BA stackings. From ref. 215. Reprinted with permission from AAAS. | |
In the WSe2/TBG heterostructure, when the angle in TBG was relatively low, for instance θ = 0.6°, the period λ of the moiré pattern was larger than the exciton size rB (≈7 nm for the 2 s states in monolayer WSe2281). Due to the lattice relaxation, the AA region had a radius of ≈2.6 nm (estimated from the half maximum of the spatially accumulated charge peak), much smaller than rB. Moreover, the accumulated charges in the AA region of the TBG were strong enough to trap the opposite charge of the 2 s exciton. Then, the system was in a strong coupling regime with λ/rB > ≈2.4. In this regime, the Rydberg moiré excitons XRM showed some significant features in the reflectance spectra (see Fig. 14(a)): (1) multiple energy splittings near 1.783 eV, (2) pronounced red shift, (3) narrowed linewidth, indicating a significant enhancement of the interlayer Rydberg exciton-accumulated charge interactions. Such features were confirmed by photoluminescence measurements in Fig. 14(b). The energy shift magnitude |Eshift| from the charge neutrality point (CNP) was extracted, which showed a nonmonotonic dependence on the density. Then, the real-space charge distrubution in TBG was calculated by a combination of the TB Hamiltonian in eqn (3) with TBPM methods, and molecular dynamics for lattice relaxation.215 As shown in Fig. 14(e), in the CNP, the local charge density located mainly in the AA region, which created deep and narrow potential wells for trapping charges of the exciton. The |Eshift| ≈ (eUAA − eUAB/BA) ∝ (nAA − nAB/BA) estimated from the difference in attraction in the AA region and repulsion in the AB/BA region, is plotted in Fig. 14(d). The nonmonotonic trend was similar to the observed result.
6 Summary and perspectives
We have carefully reviewed the single-particle, atomistic TB Hamiltonian for twisted graphene layers. Intralayer and interlayer hoppings in graphene-based moiré materials can be described by the Slater–Koster relation. The single-particle TB Hamiltonian can be combined with Hartree–Fock interactions and a Hubbard-U term within a mean-field approximation. A rescaling strategy can reduce the computational cost of self-consistent mean-field calculations. The SK relation including the pz orbital remains valid when constructing TB Hamiltonians for hBN-based moiré materials, though the hopping parameters fitted from DFT differ from those of graphene-based systems. For TMD-based moiré materials, an ab initial intralayer TB Hamiltonian is needed, while SK relations can be employed to generate an interlayer Hamiltonian. Beyond traditional diagonalization methods, robust linear-scaling approaches can be combined with real-space atomistic TB Hamiltonians to compute diverse properties of moiré materials. Machine-learning methods are accelerating the construction of ab initial-quality TB Hamiltonians for moiré systems. We also summarized how low-energy continuum models can be derived from atomistic TB models. Other low-energy effective lattice models are crucial for understanding electron–electron interaction phenomena in moiré superlattices, but lie beyond the scope of this work.247,248,282–285
As for future prospects of atomistic TB methods for simulating moiré materials, an essential direction is the accurate parameterization of TB Hamiltonians for systems not only with hexagonal lattices (the main focus here) but also with rectangular, kagome, and more general lattices,286 and searching for moiré flat bands in other 2D superlattices. As more experimental results of correlated phases and topology are reported, the TB method is still an accurate enough and powerful tool to understand the origin of the flat band-related correlated phenomena, and needs to be further explored. Building open databases for training deep-learning Hamiltonian models287 will further facilitate data-driven construction and discovery of new interesting moiré superlattices. From the perspective of practice, for simulations of large-scale moiré systems, linear-scaling random-state methods require additional development to ensure compatibility with TB Hamiltonians in non-orthogonal basis.
Conflicts of interest
There are no conflicts to declare.
Data availability
No primary research results, software or code have been included and no new data were generated or analysed as part of this review.
Acknowledgements
IMDEA Nanociencia acknowledges support from the “Severo Ochoa” Programme for Centres of Excellence in R&D (CEX2020-001039-S/AEI/10.13039/501100011033). PAP, FG and ZZ acknowledge support from NOVMOMAT, project PID2022-142162NB-I00 funded by MICIU/AEI/10.13039/501100011033 and by FEDER, UE as well as financial support through the (MAD2D-CM)-MRR MATERIALES AVANZADOS-IMDEA-NC. ZZ acknowledges support from the European Union's Horizon 2020 research and innovation programme under the Marie-Sklodowska Curie grant agreement no. 101034431. FE acknowledges support funding from the European Union's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No 101210351. PAP acknowledges funding by Grant No. JSF-24-05-0002 of the Julian Schwinger Foundation for Physics Research.
References
- E. Y. Andrei, D. K. Efetov, P. Jarillo-Herrero, A. H. MacDonald, K. F. Mak, T. Senthil, E. Tutuc, A. Yazdani and A. F. Young, Nat. Rev. Mater., 2021, 6, 201–206 CrossRef CAS.
- F. He, Y. Zhou, Z. Ye, S.-H. Cho, J. Jeong, X. Meng and Y. Wang, ACS Nano, 2021, 15, 5944–5958 CrossRef CAS PubMed.
- E. Y. Andrei and A. H. MacDonald, Nat. Mater., 2020, 19, 1265–1275 CrossRef CAS PubMed.
- L. Cai and G. Yu, Adv. Mater., 2021, 33, 2004974 CrossRef CAS PubMed.
- S. Carr, S. Fang and E. Kaxiras, Nat. Rev. Mater., 2020, 5, 748–763 CrossRef CAS.
- S. K. Behura, A. Miranda, S. Nayak, K. Johnson, P. Das and N. R. Pradhan, Emergent Mater., 2021, 4, 813–826 CrossRef CAS.
- L. Wang, S. Yin, J. Yang and S. X. Dou, Small, 2023, 19, 2300165 CrossRef CAS PubMed.
- Y. Yu, K. Zhang, H. Parks, M. Babar, S. Carr, I. M. Craig, M. Van Winkle, A. Lyssenko, T. Taniguchi and K. Watanabe,
et al.
, Nat. Chem., 2022, 14, 267–273 CrossRef CAS PubMed.
- V. Hsieh, D. Halbertal, N. R. Finney, Z. Zhu, E. Gerber, M. Pizzochero, E. Kucukbenli, G. R. Schleder, M. Angeli and K. Watanabe,
et al.
, Nano Lett., 2023, 23, 3137–3143 CrossRef CAS PubMed.
- L. Yu, X. Liu, H. Zhang, B. Zhou, Z. Chen, H. Li and L. Zhang, J. Am. Chem. Soc., 2024, 146, 32816–32825 CrossRef CAS PubMed.
- Y. Cao, V. Fatemi, S. Fang, K. Watanabe, T. Taniguchi, E. Kaxiras and P. Jarillo-Herrero, Nature, 2018, 556, 43–50 CrossRef CAS PubMed.
- Y. Cao, V. Fatemi, A. Demir, S. Fang, S. L. Tomarken, J. Y. Luo, J. D. Sanchez-Yamagishi, K. Watanabe, T. Taniguchi and E. Kaxiras,
et al.
, Nature, 2018, 556, 80–84 CrossRef CAS PubMed.
- M. Yankowitz, S. Chen, H. Polshyn, Y. Zhang, K. Watanabe, T. Taniguchi, D. Graf, A. F. Young and C. R. Dean, Science, 2019, 363, 1059–1064 CrossRef CAS PubMed.
- G. W. Burg, J. Zhu, T. Taniguchi, K. Watanabe, A. H. MacDonald and E. Tutuc, Phys. Rev. Lett., 2019, 123, 197702 CrossRef CAS PubMed.
- Y. Saito, J. Ge, K. Watanabe, T. Taniguchi and A. F. Young, Nat. Phys., 2020, 16, 926–930 Search PubMed.
- H. S. Arora, R. Polski, Y. Zhang, A. Thomson, Y. Choi, H. Kim, Z. Lin, I. Z. Wilson, X. Xu and J.-H. Chu,
et al.
, Nature, 2020, 583, 379–384 CrossRef CAS PubMed.
- K. P. Nuckolls, M. Oh, D. Wong, B. Lian, K. Watanabe, T. Taniguchi, B. A. Bernevig and A. Yazdani, Nature, 2020, 588, 610–615 CrossRef CAS PubMed.
- G. Chen, L. Jiang, S. Wu, B. Lyu, H. Li, B. L. Chittari, K. Watanabe, T. Taniguchi, Z. Shi and J. Jung,
et al.
, Nat. Phys., 2019, 15, 237–241 Search PubMed.
- X. Sun, S. Zhang, Z. Liu, H. Zhu, J. Huang, K. Yuan, Z. Wang, K. Watanabe, T. Taniguchi and X. Li,
et al.
, Nat. Commun., 2021, 12, 7196 Search PubMed.
- J. Yang, G. Chen, T. Han, Q. Zhang, Y.-H. Zhang, L. Jiang, B. Lyu, H. Li, K. Watanabe and T. Taniguchi,
et al.
, Science, 2022, 375, 1295–1299 CrossRef CAS PubMed.
- Y. Xu, S. Liu, D. A. Rhodes, K. Watanabe, T. Taniguchi, J. Hone, V. Elser, K. F. Mak and J. Shan, Nature, 2020, 587, 214–218 CrossRef CAS PubMed.
- L. Wang, E.-M. Shih, A. Ghiotto, L. Xian, D. A. Rhodes, C. Tan, M. Claassen, D. M. Kennes, Y. Bai and B. Kim,
et al.
, Nat. Mater., 2020, 19, 861–866 CrossRef CAS PubMed.
- Y. Guo, J. Pack, J. Swann, L. Holtzman, M. Cothrine, K. Watanabe, T. Taniguchi, D. G. Mandrus, K. Barmak and J. Hone,
et al.
, Nature, 2025, 637, 839–845 CrossRef CAS PubMed.
- Y. Xia, Z. Han, K. Watanabe, T. Taniguchi, J. Shan and K. F. Mak, Nature, 2025, 637, 833–838 CrossRef CAS PubMed.
- G. Chen, A. L. Sharpe, E. J. Fox, Y.-H. Zhang, S. Wang, L. Jiang, B. Lyu, H. Li, K. Watanabe and T. Taniguchi,
et al.
, Nature, 2020, 579, 56–61 CrossRef CAS PubMed.
- C. Tschirhart, M. Serlin, H. Polshyn, A. Shragai, Z. Xia, J. Zhu, Y. Zhang, K. Watanabe, T. Taniguchi and M. Huber,
et al.
, Science, 2021, 372, 1323–1327 CrossRef CAS PubMed.
- T. Song, Q.-C. Sun, E. Anderson, C. Wang, J. Qian, T. Taniguchi, K. Watanabe, M. A. McGuire, R. Stöhr and D. Xiao,
et al.
, Science, 2021, 374, 1140–1144 CrossRef CAS PubMed.
- J.-X. Lin, Y.-H. Zhang, E. Morissette, Z. Wang, S. Liu, D. Rhodes, K. Watanabe, T. Taniguchi, J. Hone and J. Li, Science, 2022, 375, 437–441 CrossRef CAS PubMed.
- X. Wang, C. Xiao, H. Park, J. Zhu, C. Wang, T. Taniguchi, K. Watanabe, J. Yan, D. Xiao and D. R. Gamelin,
et al.
, Nature, 2022, 604, 468–473 CrossRef CAS PubMed.
- Z. Zheng, Q. Ma, Z. Bi, S. de La Barrera, M.-H. Liu, N. Mao, Y. Zhang, N. Kiper, K. Watanabe and T. Taniguchi,
et al.
, Nature, 2020, 588, 71–76 CrossRef CAS PubMed.
- S. Zhang, Y. Liu, Z. Sun, X. Chen, B. Li, S. Moore, S. Liu, Z. Wang, S. Rossi and R. Jing,
et al.
, Nat. Commun., 2023, 14, 6200 CrossRef CAS PubMed.
- J. Ding, H. Xiang, W. Zhou, N. Liu, Q. Chen, X. Fang, K. Wang, L. Wu, K. Watanabe and T. Taniguchi,
et al.
, Nat. Commun., 2024, 15, 9087 CrossRef CAS PubMed.
- M. Serlin, C. Tschirhart, H. Polshyn, Y. Zhang, J. Zhu, K. Watanabe, T. Taniguchi, L. Balents and A. Young, Science, 2020, 367, 900–903 CrossRef CAS PubMed.
- T. Li, S. Jiang, B. Shen, Y. Zhang, L. Li, Z. Tao, T. Devakul, K. Watanabe, T. Taniguchi and L. Fu,
et al.
, Nature, 2021, 600, 641–646 CrossRef CAS PubMed.
- H. Park, J. Cai, E. Anderson, Y. Zhang, J. Zhu, X. Liu, C. Wang, W. Holtzmann, C. Hu and Z. Liu,
et al.
, Nature, 2023, 622, 74–79 CrossRef CAS PubMed.
- J. Cai, E. Anderson, C. Wang, X. Zhang, X. Liu, W. Holtzmann, Y. Zhang, F. Fan, T. Taniguchi and K. Watanabe,
et al.
, Nature, 2023, 622, 63–68 CrossRef CAS PubMed.
- F. Xu, Z. Sun, T. Jia, C. Liu, C. Xu, C. Li, Y. Gu, K. Watanabe, T. Taniguchi and B. Tong,
et al.
, Phys. Rev. X, 2023, 13, 031037 CAS.
- Z. Lu, T. Han, Y. Yao, A. P. Reddy, J. Yang, J. Seo, K. Watanabe, T. Taniguchi, L. Fu and L. Ju, Nature, 2024, 626, 759–764 CrossRef CAS PubMed.
- L. Ju, A. H. MacDonald, K. F. Mak, J. Shan and X. Xu, Nat. Rev. Mater., 2024, 9, 455–459 CrossRef.
- Z. Lu, T. Han, Y. Yao, Z. Hadjri, J. Yang, J. Seo, L. Shi, S. Ye, K. Watanabe and T. Taniguchi,
et al.
, Nature, 2025, 1–6 Search PubMed.
- K. Nowakowski, H. Agarwal, S. Slizovskiy, R. Smeyers, X. Wang, Z. Zheng, J. Barrier, D. Barcons Ruiz, G. Li and R. Bertini,
et al.
, Science, 2025, 389, 644–649 CrossRef CAS PubMed.
- B. Du, X. Tian, Z. Chen, Y. Ge, C. Chen, H. Gao, Z. Liu, J. Tung, D. Fixler and S. Wei,
et al.
, Nat. Sci. Rev., 2025, nwaf357 CrossRef PubMed.
- R. Jha, M. Endres, K. Watanabe, T. Taniguchi, M. Banerjee, C. Schönenberger and P. Karnatak, Phys. Rev. Lett., 2025, 134, 216001 CrossRef CAS PubMed.
- Z. Song, Y. Wang, P. Udvarhelyi and P. Narang, Phys. Rev. Lett., 2025, 135, 036201 CrossRef CAS PubMed.
- G. Zheng, S. Iwakiri, E. Portolés, P. Rickhaus, T. Taniguchi, K. Watanabe, T. Ihn, K. Ensslin and F. K. de Vries, Phys. Rev. Res., 2024, 6, L012051 CrossRef CAS.
- S. Kezilebieke, M. N. Huda, V. Vaño, M. Aapro, K. Berke, C. Wang, S. C. Ganguli, S. Głodzik, B. Rzeszotarski and M. Dvorak,
et al.
, Nano Lett., 2022, 22, 4799–4806 CrossRef PubMed.
- F. K. de Vries, E. Portolés, G. Zheng, T. Taniguchi, K. Watanabe, T. Ihn, K. Ensslin and P. Rickhaus, Nat. Nanotechnol., 2021, 16, 760–763 CrossRef CAS PubMed.
- C. Qian,
et al.
, Sci. Adv., 2024, 10, eadk6359 CrossRef CAS PubMed.
- X. Zhang, Y. Long, N. Lu, F. Jian, X. Zhang, Z. Liang, L. He and H. Tang, ACS Appl. Mater. Interfaces, 2024, 16, 68724–68748 CrossRef CAS PubMed.
- X. Yang,
et al.
, Nanoscale, 2024, 16, 2913–2922 RSC.
- Y.-T. Wang,
et al.
, Sci. Adv., 2025, 11, eadv8115 CrossRef CAS PubMed.
- Y. Yu, M. Van Winkle and D. K. Bediako, Trends Chem., 2022, 4, 857–859 CrossRef CAS.
- G. R. Schleder, M. Pizzochero and E. Kaxiras, J. Phys. Chem. Lett., 2023, 14, 8853–8858 CrossRef CAS PubMed.
- G. Zhan, B. Koek, Y. Yuan, Y. Liu, V. Mishra, V. Lenzi, K. Strutyński, C. Li, R. Zhang and X. Zhou,
et al.
, Nat. Chem., 2025, 1–7 Search PubMed.
- M. R. Rosenberger, H.-J. Chuang, M. Phillips, V. P. Oleshko, K. M. McCreary, S. V. Sivaram, C. S. Hellberg and B. T. Jonker, ACS Nano, 2020, 14, 4550–4558 CrossRef CAS PubMed.
- E. Li, J.-X. Hu, X. Feng, Z. Zhou, L. An, K. T. Law, N. Wang and N. Lin, Nat. Commun., 2021, 12, 5601 CrossRef CAS PubMed.
- H. Li, S. Li, M. H. Naik, J. Xie, X. Li, J. Wang, E. Regan, D. Wang, W. Zhao and S. Zhao,
et al.
, Nat. Mater., 2021, 20, 945–950 CrossRef CAS PubMed.
- N. Tilak, G. Li, T. Taniguchi, K. Watanabe and E. Y. Andrei, Nano Lett., 2022, 23, 73–81 CrossRef PubMed.
- D. Halbertal, S. Turkel, C. J. Ciccarino, J. B. Profe, N. Finney, V. Hsieh, K. Watanabe, T. Taniguchi, J. Hone and C. Dean,
et al.
, Nat. Commun., 2022, 13, 7587 CrossRef CAS PubMed.
- S. Zhao, Z. Li, X. Huang, A. Rupp, J. Göser, I. A. Vovk, S. Y. Kruchinin, K. Watanabe, T. Taniguchi and I. Bilgin,
et al.
, Nat. Nanotechnol., 2023, 18, 572–579 CrossRef CAS PubMed.
- M. Van Winkle, I. M. Craig, S. Carr, M. Dandu, K. C. Bustillo, J. Ciston, C. Ophus, T. Taniguchi, K. Watanabe and A. Raja,
et al.
, Nat. Commun., 2023, 14, 2989 CrossRef CAS PubMed.
- Z. Fu, X. Zhou and L. He, J. Phys.: Condens. Matter, 2024, 37, 073001 CrossRef PubMed.
- G. Sfuncia, G. Nicotra, F. Giannazzo, B. Pécz, G. K. Gueorguiev and A. Kakanakova-Georgieva, CrystEngComm, 2023, 25, 5810–5817 RSC.
- M. A. Machado Filho, W. Farmer, C.-L. Hsiao, R. B. dos Santos, L. Hultman, J. Birch, K. Ankit and G. K. Gueorguiev, Cryst. Growth Des., 2024, 24, 4717–4727 CrossRef PubMed.
- N. Mounet, M. Gibertini and P. Schwaller,
et al.
, Nat. Nanotechnol., 2018, 13, 246–252 CrossRef CAS PubMed.
- S. Haastrup, M. Strange and M. Pandey,
et al.
, 2D Mater., 2018, 5, 042002 CrossRef CAS.
- F. Haddadi, Q. Wu, A. J. Kruchkov and O. V. Yazyev, Nano Lett., 2020, 20, 2410–2415 CrossRef CAS PubMed.
- X.-J. Zhao, Y. Yang, D.-B. Zhang and S.-H. Wei, Phys. Rev. Lett., 2020, 124, 086401 Search PubMed.
- M. H. Naik and M. Jain, Phys. Rev. Lett., 2018, 121, 266401 Search PubMed.
- S. Venkateswarlu, A. Honecker and G. Trambly de Laissardière, Phys. Rev. B, 2020, 102, 081103 CrossRef CAS.
- T. Devakul, V. Crépel, Y. Zhang and L. Fu, Nat. Commun., 2021, 12, 6730 CrossRef CAS PubMed.
- Y. Zhang, T. Liu and L. Fu, Phys. Rev. B, 2021, 103, 155142 CrossRef CAS.
- S. Kundu, M. H. Naik, H. Krishnamurthy and M. Jain, Phys. Rev. B, 2022, 105, L081108 CrossRef CAS.
- Y. Jia, J. Yu, J. Liu, J. Herzog-Arbeitman, Z. Qi, H. Pi, N. Regnault, H. Weng, B. A. Bernevig and Q. Wu, Phys. Rev. B, 2024, 109, 205121 CrossRef CAS.
- C. Xu, N. Mao, T. Zeng and Y. Zhang, Phys. Rev. Lett., 2025, 134, 066601 CrossRef CAS PubMed.
- R. Bistritzer and A. H. MacDonald, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 12233–12237 CrossRef CAS PubMed.
- J. Lopes dos Santos, N. Peres and A. Castro Neto, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 155449 CrossRef.
- Y.-W. Chang, Phys. Rev. B, 2023, 108, 155424 CrossRef CAS.
- N. Mao, C. Xu, J. Li, T. Bao, P. Liu, Y. Xu, C. Felser, L. Fu and Y. Zhang, Commun. Phys., 2024, 7, 262 CrossRef CAS.
- N. Morales-Durán, N. Wei, J. Shi and A. H. MacDonald, Phys. Rev. Lett., 2024, 132, 096602 CrossRef PubMed.
- W. M. C. Foulkes and R. Haydock, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 39, 12520 CrossRef PubMed.
- D. Bowler, M. Aoki, C. Goringe, A. Horsfield and D. Pettifor, Modell. Simul. Mater. Sci. Eng., 1997, 5, 199 CrossRef CAS.
- D. Papaconstantopoulos and M. Mehl, J. Phys.: Condens. Matter, 2003, 15, R413 CrossRef CAS.
- Q. Cui and M. Elstner, Phys. Chem. Chem. Phys., 2014, 16, 14368–14377 RSC.
- E. McCann and M. Koshino, Rep. Prog. Phys., 2013, 76, 056503 CrossRef PubMed.
- E. Kogan, V. U. Nazarov, V. M. Silkin and M. Kaveh, Phys. Rev. B, 2014, 89, 165430 CrossRef.
- E. Cappelluti, R. Roldán, J. A. Silva-Guillén, P. Ordejón and F. Guinea, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 075409 CrossRef.
- G.-B. Liu, W.-Y. Shan, Y. Yao, W. Yao and D. Xiao, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 085433 CrossRef.
- A. N. Rudenko and M. I. Katsnelson, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 201408(R) CrossRef.
- M. Nakhaee, M. Yagmurcukardes, S. Ketabi and F. Peeters, Phys. Chem. Chem. Phys., 2019, 21, 15798–15804 RSC.
- R. Chegel and S. Behzad, Sci. Rep., 2020, 10, 704 CrossRef CAS PubMed.
-
M. H. Rahman, S. Mitra and D. A. Redwan, 2020 2nd International Conference on Advanced Information and Communication Technology (ICAICT), 2020, pp. 207–212.
- N. Leconte, S. Javvaji, J. An, A. Samudrala and J. Jung, Phys. Rev. B, 2022, 106, 115410 CrossRef CAS.
- X. Kuang, Z. Zhan and S. Yuan, Phys. Rev. B, 2021, 103, 115431 CrossRef CAS.
- H. Shi, Z. Zhan, Z. Qi, K. Huang, E. V. Veen, J. Á. Silva-Guillén, R. Zhang, P. Li, K. Xie and H. Ji,
et al.
, Nat. Commun., 2020, 11, 371 CrossRef CAS PubMed.
- Y.-N. Ren, Z. Zhan, Y.-W. Liu, C. Yan, S. Yuan and L. He, Nano Lett., 2023, 23, 1836–1842 CrossRef CAS PubMed.
- M. Manna and S. Haddad, Phys. Rev. B, 2021, 103, L201112 CrossRef.
- J. C. Slater and G. F. Koster, Phys. Rev., 1954, 94, 1498 CrossRef CAS.
- M. J. Mehl and D. A. Papaconstantopoulos, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 4519–4530 CrossRef CAS PubMed.
- J.-M. Jancu, R. Scholz, F. Beltram and F. Bassani, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 6493–6507 CrossRef CAS.
- R. Pons, A. Mielke and T. Stauber, Phys. Rev. B, 2020, 102, 235101 CrossRef CAS.
- J. González and T. Stauber, Phys. Rev. B, 2020, 102, 081118 CrossRef.
- S. Bhowmik, B. Ghawri, Y. Park, D. Lee, S. Datta, R. Soni, K. Watanabe, T. Taniguchi, A. Ghosh and J. Jung,
et al.
, Nat. Commun., 2023, 14, 4055 CrossRef CAS PubMed.
- Z. Wu, Z. Zhan and S. Yuan, Sci. China Phys., Mech. Astronomy, 2021, 64, 267811 CrossRef CAS.
- Y. Wang, G. Yu, M. Rösner, M. I. Katsnelson, H.-Q. Lin and S. Yuan, Phys. Rev. X, 2022, 12, 021055 CAS.
- S. Yuan, H. De Raedt and M. I. Katsnelson, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 115448 CrossRef.
- Y. Li, Z. Zhan, X. Kuang, Y. Li and S. Yuan, Comput. Phys. Commun., 2023, 285, 108632 CrossRef CAS.
- S. M. João, M. Anelković, L. Covaci, T. G. Rappoport, J. M. Lopes and A. Ferreira, R. Soc. Open Sci., 2020, 7, 191809 CrossRef PubMed.
- W. Yao, E. Wang, C. Bao, Y. Zhang, K. Zhang, K. Bao, C. K. Chan, C. Chen, J. Avila and M. C. Asensio,
et al.
, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 6928–6933 CrossRef CAS PubMed.
- S. J. Ahn, P. Moon, T.-H. Kim, H.-W. Kim, H.-C. Shin, E. H. Kim, H. W. Cha, S.-J. Kahng, P. Kim, M. Koshino, Y.-W. Son, C.-W. Yang and J. R. Ahn, Science, 2018, 361, 782–786 CrossRef CAS PubMed.
- Y. Li, Z. Zhan and S. Yuan, Phys. Rev. B, 2024, 109, 085118 CrossRef CAS.
- J. Lopes dos Santos, N. Peres and A. Castro Neto, Phys. Rev. Lett., 2007, 99, 256802 CrossRef CAS PubMed.
- F. Escudero, A. Sinner, Z. Zhan, P. A. Pantaleón and F. Guinea, Phys. Rev. Res., 2024, 6, 023203 CrossRef CAS.
- M. Van Wijk, A. Schuring, M. Katsnelson and A. Fasolino, 2D Mater., 2015, 2, 034010 CrossRef.
- H. Yoo, R. Engelke, S. Carr, S. Fang, K. Zhang, P. Cazeaux, S. H. Sung, R. Hovden, A. W. Tsen and T. Taniguchi,
et al.
, Nat. Mater., 2019, 18, 448–453 CrossRef CAS PubMed.
- G. Trambly de Laissardière, D. Mayou and L. Magaud, Nano Lett., 2010, 10, 804–808 CrossRef PubMed.
- G. Trambly de Laissardière, D. Mayou and L. Magaud, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 125413 CrossRef.
- F. Gargiulo and O. V. Yazyev, 2D Mater., 2017, 5, 015019 CrossRef.
- F. Guinea and N. R. Walet, Phys. Rev. B, 2019, 99, 205134 CrossRef CAS.
- K. Zakharchenko, M. Katsnelson and A. Fasolino, Phys. Rev. Lett., 2009, 102, 046808 CrossRef CAS PubMed.
- M. I. Katsnelson, K. S. Novoselov and A. K. Geim, Nat. Phys., 2006, 2, 620–625 Search PubMed.
- E. Suárez Morell, J. Correa, P. Vargas, M. Pacheco and Z. Barticevic, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 121407 CrossRef.
- A. Lopez-Bezanilla and J. Lado, Phys. Rev. Res., 2020, 2, 033357 CrossRef CAS.
- A. Ramires and J. L. Lado, Phys. Rev. Lett., 2021, 127, 026401 CrossRef CAS PubMed.
- Z. Wu, X. Kuang, Z. Zhan and S. Yuan, Phys. Rev. B, 2021, 104, 205104 CrossRef CAS.
- Z. A. Goodwin, L. Klebl, V. Vitale, X. Liang, V. Gogtay, X. van Gorp, D. M. Kennes, A. A. Mostofi and J. Lischner, Phys. Rev. Mater., 2021, 5, 084008 CrossRef CAS.
- F. J. Culchac, R. Del Grande, R. B. Capaz, L. Chico and E. S. Morell, Nanoscale, 2020, 12, 5014–5020 RSC.
- X. Liang, Z. A. Goodwin, V. Vitale, F. Corsetti, A. A. Mostofi and J. Lischner, Phys. Rev. B, 2020, 102, 155146 CrossRef CAS.
- M. L. Perrin, A. Jayaraj, B. Ghawri, K. Watanabe, T. Taniguchi, D. Passerone, M. Calame and J. Zhang, npj 2D Mater. Appl., 2024, 8, 14 CrossRef CAS.
- D. Foo, Z. Zhan, M. M. Al Ezzi, L. Peng, S. Adam and F. Guinea, Phys. Rev. Res., 2024, 6, 013165 CrossRef CAS.
- F. J. Culchac, R. Del Grande, M. G. Menezes and R. B. Capaz, Phys. Rev. B, 2025, 111, 075111 CrossRef CAS.
- N. N. Nam and M. Koshino, Phys. Rev. B, 2017, 96, 075311 CrossRef.
- Y. Cao, J. Luo, V. Fatemi, S. Fang, J. Sanchez-Yamagishi, K. Watanabe, T. Taniguchi, E. Kaxiras and P. Jarillo-Herrero, Phys. Rev. Lett., 2016, 117, 116804 CrossRef CAS PubMed.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- M. H. Naik, I. Maity, P. K. Maiti and M. Jain, J. Phys. Chem. C, 2019, 123, 9770–9778 CrossRef CAS.
- F. Li, D. Lee, N. Leconte, S. Javvaji, Y. D. Kim and J. Jung, Phys. Rev. B, 2024, 110, 155419 CrossRef CAS.
- S. J. Stuart, A. B. Tutein and J. A. Harrison, J. Chem. Phys., 2000, 112, 6472–6486 CrossRef CAS.
- J. H. Los and A. Fasolino, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 024107 CrossRef.
- A. N. Kolmogorov and V. H. Crespi, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 235415 CrossRef.
- N. R. Walet and F. Guinea, Phys. Rev. B, 2021, 103, 125427 CrossRef CAS.
- L. Sponza, V. B. Vu, E. Serrano Richaud, H. Amara and S. Latil, Phys. Rev. B, 2024, 109, L161403 CrossRef CAS.
- J. H. Los, J. M. H. Kroes, K. Albe, R. M. Gordillo, M. I. Katsnelson and A. Fasolino, Phys. Rev. B, 2017, 96, 184108 CrossRef.
- M. Wen, S. Carr, S. Fang, E. Kaxiras and E. B. Tadmor, Phys. Rev. B, 2018, 98, 235404 CrossRef CAS.
- J. Jung, N. Leconte, J. An and Y. Park, Phys. Rev. B, 2024, 110, 024109 CrossRef.
- S. Fang, R. Kuate Defo, S. N. Shirodkar, S. Lieu, G. A. Tritsaris and E. Kaxiras, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 205108 CrossRef.
- V. Vitale, K. Atalar, A. A. Mostofi and J. Lischner, 2D Mater., 2021, 8, 045010 CrossRef CAS.
- Z. Zhang, Y. Wang, K. Watanabe, T. Taniguchi, K. Ueno, E. Tutuc and B. J. LeRoy, Nat. Phys., 2020, 16, 1093–1096 Search PubMed.
- X. Kuang, Z. Zhan and S. Yuan, Phys. Rev. B, 2022, 105, 245415 CrossRef CAS.
- J.-W. Jiang and H. Zhou, Nanotechnology, 2017, 28, 305706 Search PubMed.
- A. K. Rappe, C. J. Casewit, K. S. Colwell, W. A. Goddard and W. M. Skiff, J. Am. Chem. Soc., 1992, 114, 10024–10035 CrossRef CAS.
-
S. V. Vonsovsky and M. I. Katsnelson, Quantum solid-state physics, Springer-Verlag Berlin, Heidelberg, New York, 1989 Search PubMed.
- A. Wania Rodrigues, M. Bieniek, P. Potasz, D. Miravet, R. Thomale, M. Korkusinski and P. Hawrylak, Phys. Rev. B, 2024, 109 DOI:10.1103/PhysRevB.109.075166.
- L. Rademaker, D. A. Abanin and P. Mellado, Phys. Rev. B, 2019, 100, 205114 CrossRef CAS.
- Z. A. Goodwin, V. Vitale, X. Liang, A. A. Mostofi and J. Lischner, Electron. Struct., 2020, 2, 034001 CrossRef CAS.
- A. Fischer, Z. A. Goodwin, A. A. Mostofi, J. Lischner, D. M. Kennes and L. Klebl, npj Quantum Mater., 2022, 7, 5 CrossRef CAS.
- C. T. Cheung, Z. A. Goodwin, V. Vitale, J. Lischner and A. A. Mostofi, Electron. Struct., 2022, 4, 025001 CrossRef CAS.
- F. Guinea and N. R. Walet, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 13174–13179 CrossRef CAS PubMed.
- T. Cea, N. R. Walet and F. Guinea, Phys. Rev. B, 2019, 100, 205113 CrossRef CAS.
- T. Cea and F. Guinea, Phys. Rev. B, 2020, 102, 045107 CrossRef CAS.
- M. Sánchez Sánchez, I. Daz, J. González and T. Stauber, Phys. Rev. Lett., 2024, 133, 266603 CrossRef PubMed.
- M. Sánchez Sánchez and T. Stauber, Phys. Rev. B, 2024, 109, 195167 CrossRef.
- J. González and T. Stauber, Phys. Rev. B, 2021, 104, 115110 CrossRef.
- J. González and T. Stauber, Nat. Commun., 2023, 14, 2746 CrossRef PubMed.
-
M. S. Sánchez, J. González and T. Stauber, arXiv, 2025, preprint, arXiv:2501.09197, DOI: 10.48550/arXiv.2501.09197.
- Y. Tang, L. Li, T. Li, Y. Xu, S. Liu, K. Barmak, K. Watanabe, T. Taniguchi, A. H. MacDonald and J. Shan,
et al.
, Nature, 2020, 579, 353–358 CrossRef CAS PubMed.
- A. Wania Rodrigues, M. Bieniek, D. Miravet and P. Hawrylak, Magnetism and hidden quantum geometry in charge neutral twisted trilayer graphene, arXiv, 2025 Search PubMed , preprint, arXiv:2501.18491.
- A. Jimeno-Pozo, Z. A. H. Goodwin, P. A. Pantaleón, V. Vitale, L. Klebl, D. M. Kennes, A. A. Mostofi, J. Lischner and F. Guinea, Adv. Phys. Res., 2023, 2, 202300048 Search PubMed.
- L. A. Gonzalez-Arraga, J. Lado, F. Guinea and P. San-Jose, Phys. Rev. Lett., 2017, 119, 107201 CrossRef PubMed.
- T. M. Wolf, J. L. Lado, G. Blatter and O. Zilberberg, Phys. Rev. Lett., 2019, 123, 096802 CrossRef CAS PubMed.
- J. Vahedi, R. Peters, A. Missaoui, A. Honecker and G. Trambly de Laissardière, SciPost Phys., 2021, 11, 083 CrossRef CAS.
- A. Weston, E. G. Castanon, V. Enaldiev, F. Ferreira, S. Bhattacharjee, S. Xu, H. Corte-León, Z. Wu, N. Clark and A. Summerfield,
et al.
, Nat. Nanotechnol., 2022, 17, 390–395 CrossRef CAS PubMed.
- E. C. Regan, D. Wang, C. Jin, M. I. Bakti Utama, B. Gao, X. Wei, S. Zhao, W. Zhao, Z. Zhang and K. Yumigeta,
et al.
, Nature, 2020, 579, 359–363 CrossRef CAS PubMed.
- Z. Zhan, Y. Zhang, P. Lv, H. Zhong, G. Yu, F. Guinea, J. Á. Silva-Guillén and S. Yuan, Phys. Rev. B, 2020, 102, 241106 CrossRef CAS.
- Y. Zhang, Z. Zhan, F. Guinea, J. Á. Silva-Guillén and S. Yuan, Phys. Rev. B, 2020, 102, 235418 CrossRef CAS.
- J. C. Slater and G. F. Koster, Phys. Rev., 1954, 94, 1498 CrossRef CAS.
- H. Rostami, R. Roldán, E. Cappelluti, R. Asgari and F. Guinea, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 195402 CrossRef.
- L. Xian, D. M. Kennes, N. Tancogne-Dejean, M. Altarelli and A. Rubio, Nano Lett., 2019, 19, 4934–4940 CrossRef CAS PubMed.
- R. M. Ribeiro and N. M. Peres, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 235312 CrossRef.
- C. Woods, P. Ares, H. Nevison-Andrews, M. Holwill, R. Fabregas, F. Guinea, A. Geim, K. Novoselov, N. Walet and L. Fumagalli, Nat. Commun., 2021, 12, 347 CrossRef CAS PubMed.
- P. Moon and M. Koshino, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 155406 CrossRef.
- M. Long, P. A. Pantaleón, Z. Zhan, F. Guinea, J. Á. Silva-Guillén and S. Yuan, npj Comput. Mater., 2022, 8, 73 CrossRef CAS.
- M. Long, Z. Zhan, P. A. Pantaleón, J. Á. Silva-Guillén, F. Guinea and S. Yuan, Phys. Rev. B, 2023, 107, 115140 CrossRef CAS.
- J. C. W. Song, A. V. Shytov and L. S. Levitov, Phys. Rev. Lett., 2013, 111, 266801 CrossRef PubMed.
- F. Amet, J. R. Williams, K. Watanabe, T. Taniguchi and D. Goldhaber-Gordon, Phys. Rev. Lett., 2013, 110, 216601 CrossRef CAS PubMed.
- B. Hunt, J. D. Sanchez-Yamagishi, A. F. Young, M. Yankowitz, B. J. LeRoy, K. Watanabe, T. Taniguchi, P. Moon, M. Koshino, P. Jarillo-Herrero and R. C. Ashoori, Science, 2013, 340, 1427–1430 CrossRef CAS PubMed.
- R. V. Gorbachev, J. Song, G. L. Yu, F. Kretinin, A. V. Withers, Y. Cao, A. Mishchenko, I. V. Grigorieva, K. S. Novoselov, L. S. Levitov and A. K. Geim, Science, 2014, 346, 448 CrossRef CAS PubMed.
- Z.-G. Chen, Z. Shi, W. Yang, X. Lu, Y. Lai, H. Yan, F. Wang, G. Zhang and Z. Li, Nat. Commun., 2014, 5, 4461 CrossRef CAS PubMed.
- M. Yankowitz, J. Xue and B. J. LeRoy, J. Phys.: Condens. Matter, 2014, 26, 303201 CrossRef PubMed.
- E. Wang, X. Lu, S. Ding, W. Yao, M. Yan, G. Wan, K. Deng, S. Wang, G. Chen, L. Ma, J. Jung, A. V. Fedorov, Y. Zhang, G. Zhang and S. Zhou, Nat. Phys., 2016, 12, 1111–1115 Search PubMed.
- J. Jung, A. M. DaSilva, A. H. MacDonald and S. Adam, Nat. Commun., 2015, 6, 6308 Search PubMed.
- M. Lee, J. R. Wallbank, P. Gallagher, K. Watanabe, T. Taniguchi, V. I. Fal'ko and D. Goldhaber-Gordon, Science, 2016, 353, 1526–1529 CrossRef CAS PubMed.
- H. Kim, N. Leconte, B. L. Chittari, K. Watanabe, T. Taniguchi, A. H. Macdonald, J. Jung and S. Jung, Nano Lett., 2018, 18, 7732–7741 CrossRef CAS PubMed.
-
G. H. Golub and C. F. Van Loan, Matrix Computations, Johns Hopkins University Press, 4th edn, 2013 Search PubMed.
- C. Lanczos, J. Res. Natl. Bur. Stand., 1950, 45, 255–282 CrossRef.
- E. R. Davidson, J. Comput. Phys., 1975, 17, 87–94 CrossRef.
- G. L. G. Sleijpen and H. A. van der Vorst, SIAM Rev., 2000, 42, 267–293 CrossRef.
-
R. B. Lehoucq, D. C. Sorensen and C. Yang, ARPACK Users' Guide: Solution of Large-Scale Eigenvalue Problems with Implicitly Restarted Arnoldi Methods, SIAM, 1998 Search PubMed.
- A. Stathopoulos and J. R. McCombs, ACM Trans. Math. Software, 2010, 37, 21:1–21:30 CrossRef.
- V. Hernández, J. E. Román and V. Vidal, ACM Trans. Math. Software, 2005, 31, 351–362 CrossRef.
- R. Kubo, J. Phys. Soc. Jpn., 1957, 12, 570–586 CrossRef.
- D. Greenwood, Proc. Phys. Soc., 1958, 71, 585–596 CrossRef CAS.
- X. Kuang, P. A. P. Peralta, J. A. Silva-Guillén, S. Yuan, F. Guinea and Z. Zhan, J. Phys.: Condens. Matter, 2024, 36, 173001 CrossRef CAS PubMed.
- A. Weiße, G. Wellein, A. Alvermann and H. Fehske, Rev. Mod. Phys., 2006, 78, 275–306 CrossRef.
- M. Anelković, L. Covaci and F. Peeters, Phys. Rev. Mater., 2018, 2, 034004 CrossRef.
- A. Bastin, C. Lewiner, O. Betbeder-Matibet and P. Nozières, J. Phys. Chem. Solids, 1971, 32, 1811–1824 CrossRef CAS.
- J. H. Garca, L. Covaci and T. G. Rappoport, Phys. Rev. Lett., 2015, 114, 116602 CrossRef PubMed.
- S. G. de Castro, J. M. V. P. Lopes, A. Ferreira and D. Bahamon, Phys. Rev. Lett., 2024, 132, 076302 CrossRef CAS PubMed.
- S. T. Ho and V. N. Do, Phys. Rev. B, 2023, 107, 195141 CrossRef CAS.
- H. A. Le, V.-N. Do and S. T. Ho,
et al.
, Commun. Phys., 2019, 29, 455 CrossRef.
- M. Anelković, S. P. Milovanović, L. Covaci and F. M. Peeters, Nano Lett., 2020, 20, 979–988 CrossRef PubMed.
- S. G. De Castro, A. Ferreira and D. Bahamon, Phys. Rev. B, 2023, 107, 045418 CrossRef CAS.
- Y. Sun, M. Niedermeier, T. V. C. Antao, A. O. Fumega and J. L. Lado, Self-consistent tensor network method for correlated super-moiré matter beyond one billion sites, arXiv, 2025 Search PubMed , preprint, arXiv:2503.04373.
- T. V. C. Antao, Y. Sun, A. O. Fumega and J. L. Lado, Tensor network method for real-space topology in quasicrystal Chern mosaics, arXiv, 2025 Search PubMed , preprint, arXiv:2506.05230.
- G. Yu, Z. Wu, Z. Zhan, M. I. Katsnelson and S. Yuan, Phys. Rev. B, 2020, 102, 115123 CrossRef CAS.
- Q. Hu, Z. Zhan, H. Cui, Y. Zhang, F. Jin, X. Zhao, M. Zhang, Z. Wang, Q. Zhang and K. Watanabe,
et al.
, Science, 2023, 380, 1367–1372 CrossRef CAS PubMed.
- S. Cui, C. Jiang, Z. Zhan, T. Wilson, N. Zhang, X. Xie, S. Yuan, H. Wang, C. Lewandowski and G. Ni, Nano Lett., 2024, 24, 11490–11496 CrossRef CAS PubMed.
- C.-Y. Hao, Z. Zhan, P. A. Pantaleón, J.-Q. He, Y.-X. Zhao, K. Watanabe, T. Taniguchi, F. Guinea and L. He, Nat. Commun., 2024, 15, 8437 CrossRef CAS PubMed.
- P. Moon and M. Koshino, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 205404 CrossRef.
- H. A. Le and V. N. Do, Phys. Rev. B, 2018, 97, 125136 CrossRef CAS.
- S. Yang, J. Chen, C.-F. Liu and M. Chen, Phys. Rev. B, 2024, 110, 235410 CrossRef CAS.
- D. Liu, M. Luskin and S. Carr, Phys. Rev. Res., 2022, 4, 043224 CrossRef CAS.
- G. A. Tritsaris, S. Carr, Z. Zhu, Y. Xie, S. B. Torrisi, J. Tang, M. Mattheakis, D. T. Larson and E. Kaxiras, 2D Mater., 2020, 7, 035028 CrossRef.
- H. Li, Z. Wang, N. Zou, M. Ye, R. Xu, X. Gong, W. Duan and Y. Xu, Nat. Comput. Sci., 2022, 2, 367–377 CrossRef PubMed.
- H. Li, Z. Tang, X. Gong, N. Zou, W. Duan and Y. Xu, Nat. Comput. Sci., 2023, 3, 321–327 CrossRef PubMed.
- Z. Tang, H. Li, P. Lin, X. Gong, G. Jin, L. He, H. Jiang, X. Ren, W. Duan and Y. Xu, Nat. Commun., 2024, 15, 8815 CrossRef CAS PubMed.
-
M. H. Gobbo Khun, L. Silva and D. Bahamon, arXiv, 2025, preprint, arXiv:2502, DOI: 10.48550/arXiv.2502.
- X. Gong, H. Li, N. Zou, R. Xu, W. Duan and Y. Xu, Nat. Commun., 2023, 14, 2848 CrossRef CAS PubMed.
- Y. Zhong, H. Yu, M. Su, X. Gong and H. Xiang, npj Comput. Mater., 2023, 9, 182 CrossRef.
- Y. Zhong, H. Yu, J. Yang, X. Guo, H. Xiang and X. Gong, Chin. Phys. Lett., 2024, 41, 077103 CrossRef.
- Q. Gu, Z. Zhouyin, S. K. Pandey, P. Zhang, L. Zhang and W. E, Nat. Commun., 2024, 15, 6772 CrossRef CAS PubMed.
- S. Naik, M. H. Naik, I. Maity and M. Jain, Comput. Phys. Commun., 2022, 271, 108184 CrossRef CAS.
- J. Liu, Z. Fang, H. Weng and Q. Wu, npj Comput. Mater., 2025, 11, 248 CrossRef.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in 't Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
- A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli and R. Christensen,
et al.
, J. Phys.: Condens. Matter, 2017, 29, 273002 CrossRef PubMed.
-
W. Jakob, pybind11 Documentation, 2024 DOI:10.5281/zenodo.15857181.
- G. Pizzi, V. Vitale, R. Arita, S. Blügel, F. Freimuth, G. Géranton, M. Gibertini, D. Gresch, C. Johnson and T. Koretsune,
et al.
, J. Phys.: Condens. Matter, 2020, 32, 165902 CrossRef CAS PubMed.
- G. Tarnopolsky, A. J. Kruchkov and A. Vishwanath, Phys. Rev. Lett., 2019, 122, 106405 CrossRef CAS PubMed.
- J. Wang, Y. Zheng, A. J. Millis and J. Cano, Phys. Rev. Res., 2021, 3, 023155 CrossRef CAS.
- S. Becker, M. Embree, J. Wittsten and M. Zworski, Phys. Rev. B, 2021, 103, 165113 CrossRef CAS.
- A. B. Watson and M. Luskin, J. Math. Phys., 2021, 62, 091502 CrossRef CAS.
- W.-C. Wang, F.-W. Chen, K.-S. Lin, J. T. Hou, H.-C. Lin and M.-Y. Chou, Phys. Rev. B, 2024, 110, 115154 CrossRef CAS.
- F. Escudero, Phys. Rev. B, 2024, 110, 045442 CrossRef CAS.
- M. Koshino, New J. Phys., 2015, 17, 015014 CrossRef CAS.
- M. Koshino and N. N. Nam, Phys. Rev. B, 2020, 101, 195425 CrossRef CAS.
- A. Garcia-Ruiz, H.-Y. Deng, V. V. Enaldiev and V. I. Fal'ko, Phys. Rev. B, 2021, 104, 085402 CrossRef CAS.
- J. Zhu, I. Torre, M. Polini and A. H. MacDonald, Phys. Rev. B, 2024, 110, L121117 CrossRef CAS.
- M. Koshino, N. F. Yuan, T. Koretsune, M. Ochi, K. Kuroki and L. Fu, Phys. Rev. X, 2018, 8, 031087 CAS.
- J. Kang and O. Vafek, Phys. Rev. X, 2018, 8, 031088 CAS.
- S. Carr, S. Fang, Z. Zhu and E. Kaxiras, Phys. Rev. Res., 2019, 1, 013001 CrossRef CAS.
- B. A. Bernevig, Z.-D. Song, N. Regnault and B. Lian, Phys. Rev. B, 2021, 103, 205411 CrossRef CAS.
- W. Miao, C. Li, X. Han, D. Pan and X. Dai, Phys. Rev. B, 2023, 107, 125112 CrossRef CAS.
-
S. Fang, S. Carr, Z. Zhu, D. Massatt and E. Kaxiras, arXiv, 2019, preprint, arXiv:1908.00058, DOI: 10.48550/arXiv.1908.00058.
- J. Kang and O. Vafek, Phys. Rev. B, 2023, 107, 075408 CrossRef CAS.
- A. Ceferino and F. Guinea, 2D Mater., 2024, 11, 035015 CrossRef CAS.
- Z. Bi, N. F. Yuan and L. Fu, Phys. Rev. B, 2019, 100, 035448 CrossRef CAS.
- L. Balents, SciPost Phys., 2019, 7, 048 CrossRef CAS.
- P. A. Pantaleón, T. Low and F. Guinea, Phys. Rev. B, 2021, 103, 205403 CrossRef.
- F. Mesple, A. Missaoui, T. Cea, L. Huder, F. Guinea, G. Trambly de Laissardière, C. Chapelier and V. T. Renard, Phys. Rev. Lett., 2021, 127, 126405 CrossRef CAS PubMed.
- A. Sinner, P. A. Pantaleón and F. Guinea, Phys. Rev. Lett., 2023, 131, 166402 CrossRef CAS PubMed.
- O. Vafek and J. Kang, Phys. Rev. B, 2023, 107, 075123 CrossRef CAS.
- F. Wu, T. Lovorn, E. Tutuc, I. Martin and A. MacDonald, Phys. Rev. Lett., 2019, 122, 086402 CrossRef CAS PubMed.
- M. Angeli and A. H. MacDonald, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2021826118 CrossRef CAS PubMed.
- J. Jung, E. Laksono, A. M. DaSilva, A. H. MacDonald, M. Mucha-Kruczyński and S. Adam, Phys. Rev. B, 2017, 96, 085442 CrossRef.
- T. Cea, P. A. Pantaleón and F. Guinea, Phys. Rev. B, 2020, 102, 155136 CrossRef CAS.
- D. Waters, R. Su, E. Thompson, A. Okounkova, E. Arreguin-Martinez, M. He, K. Hinds, K. Watanabe, T. Taniguchi and X. Xu,
et al.
, Nat. Commun., 2024, 15, 10552 CrossRef CAS PubMed.
- R. Su, D. Waters, B. Zhou, K. Watanabe, T. Taniguchi, Y.-H. Zhang, M. Yankowitz and J. Folk, Nature, 2025, 637, 1084–1089 CrossRef CAS PubMed.
- V. M. Pereira, A. Castro Neto and N. Peres, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 045401 CrossRef.
- M. Tang, C. Wang, C. Chan and K. Ho, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 979 CrossRef CAS PubMed.
- R. Bistritzer and A. H. MacDonald, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 245412 CrossRef.
- P. San-Jose and E. Prada, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 121408 CrossRef.
- D. K. Efimkin and A. H. MacDonald, Phys. Rev. B, 2018, 98, 035404 CrossRef CAS.
- C. De Beule, F. Dominguez and P. Recher, Phys. Rev. B, 2021, 104, 195410 CrossRef CAS.
- Z.-D. Song and B. A. Bernevig, Phys. Rev. Lett., 2022, 129, 047601 CrossRef CAS PubMed.
- Y.-Z. Chou and S. Das Sarma, Phys. Rev. Lett., 2023, 131, 026501 CrossRef CAS PubMed.
- H. Hu, B. A. Bernevig and A. M. Tsvelik, Phys. Rev. Lett., 2023, 131, 026502 CrossRef CAS PubMed.
- D. Bennett, D. T. Larson, L. Sharma, S. Carr and E. Kaxiras, Phys. Rev. B, 2024, 109, 155422 CrossRef CAS.
- L. L. Lau and P. Coleman, Phys. Rev. X, 2025, 15, 021028 CAS.
- G. Yu, Z. Wu, Z. Zhan, M. I. Katsnelson and S. Yuan, npj Comput. Mater., 2019, 5, 122 CrossRef CAS.
- M. He, J. Cai, H. Zheng, E. Seewald, T. Taniguchi, K. Watanabe, J. Yan, M. Yankowitz, A. Pasupathy and W. Yao,
et al.
, Nat. Mater., 2024, 23, 224–229 CrossRef CAS PubMed.
- V. H. Nguyen, D. Paszko, M. Lamparski, B. Van Troeye, V. Meunier and J.-C. Charlier, 2D Mater., 2021, 8, 035046 CrossRef CAS.
- A. V. Stier, N. P. Wilson, K. A. Velizhanin, J. Kono, X. Xu and S. A. Crooker, Phys. Rev. Lett., 2018, 120, 057405 CrossRef CAS PubMed.
- H. C. Po, L. Zou, A. Vishwanath and T. Senthil, Phys. Rev. X, 2018, 8, 031089 CAS.
- N. F. Q. Yuan and L. Fu, Phys. Rev. B, 2018, 98, 045103 CrossRef CAS.
- J. F. Dodaro, S. A. Kivelson, Y. Schattner, X.-Q. Sun and C. Wang, Phys. Rev. B, 2018, 98, 075154 CrossRef CAS.
- F. Wu, T. Lovorn, E. Tutuc and A. H. MacDonald, Phys. Rev. Lett., 2018, 121, 026402 CrossRef CAS PubMed.
- J. Yu, S. Qian and C.-C. Liu, Phys. Rev. B, 2025, 111, 075434 CrossRef CAS.
-
T. Bao, R. Xu, H. Li, X. Gong, Z. Tang, J. Fu, W. Duan and Y. Xu, arXiv, 2024, preprint, arXiv:2404.06449, DOI: 10.48550/arXiv.2404.06449.
|
| This journal is © the Owner Societies 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  b,
Pierre A.
Pantaleón
b,
Francisco
Guinea
b,
Pierre A.
Pantaleón
b,
Francisco
Guinea
 bc and
Zhen
Zhan
bc and
Zhen
Zhan
 *b
*b
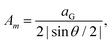
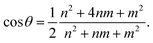


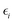 is the onsite energy of the pz orbital at site i, and tij denotes the hopping between pz orbitals at sites i and j. The hopping amplitudes follow the Slater–Koster (SK) relation
is the onsite energy of the pz orbital at site i, and tij denotes the hopping between pz orbitals at sites i and j. The hopping amplitudes follow the Slater–Koster (SK) relation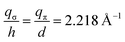 . A smooth cutoff function
. A smooth cutoff function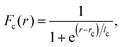
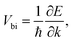 and compared it with the corresponding value in monolayer graphene, Vmono. As shown in Fig. 1(c), the velocity renormalization varies symmetrically around θ = 30°.
and compared it with the corresponding value in monolayer graphene, Vmono. As shown in Fig. 1(c), the velocity renormalization varies symmetrically around θ = 30°.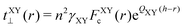 ; (C)136 full SK: Vppπ(r) = −γ0eqπ(1−r/dBN), Vppσ(r) = γ1eqσ(1−r/h)
; (C)136 full SK: Vppπ(r) = −γ0eqπ(1−r/dBN), Vppσ(r) = γ1eqσ(1−r/h)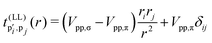 with Vpp,b(r) = νbe−(r/Rb)ηb. Inter (heterobilayer pz–dz2):146
with Vpp,b(r) = νbe−(r/Rb)ηb. Inter (heterobilayer pz–dz2):146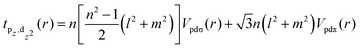 ; Vpd,b(r) = Vb(r/h)αb
; Vpd,b(r) = Vb(r/h)αb![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(βbr/h + γb)
cos(βbr/h + γb)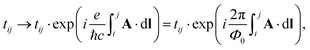
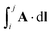 is the line integral of the vector potential from orbital i to orbital j, and Φ0 = 2πcħ/e is the flux quantum. For a perpendicular magnetic field along −z, the Landau gauge A = (By,0,0) can be used. This framework enables the study of large-scale properties such as the moiré Hofstadter butterfly in TBG152 and quantum Hall effect in twisted graphene using linear-scaling methods and linear-response theory.107,108
is the line integral of the vector potential from orbital i to orbital j, and Φ0 = 2πcħ/e is the flux quantum. For a perpendicular magnetic field along −z, the Landau gauge A = (By,0,0) can be used. This framework enables the study of large-scale properties such as the moiré Hofstadter butterfly in TBG152 and quantum Hall effect in twisted graphene using linear-scaling methods and linear-response theory.107,108
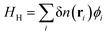
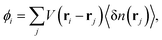
![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) is the deviation of the electron density n(r) from the average density
is the deviation of the electron density n(r) from the average density ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) , and V(ri − rj) is the screened Coulomb interaction. The simplest form of this interaction can be written as153
, and V(ri − rj) is the screened Coulomb interaction. The simplest form of this interaction can be written as153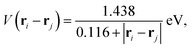
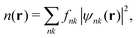

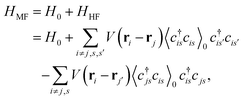
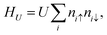
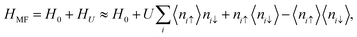
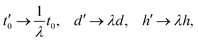
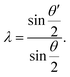

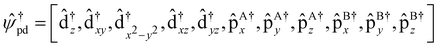 , which contains the on-site energy, the hopping terms between orbitals of the same type at first-neighbor positions, and the hopping terms between orbitals of different type at first- and second-neighbor positions.145 TB parameters in the single-layer Hamiltonian for MoS2, MoSe2, WS2 and WSe2 can be obtained from Table 7 of ref. 145. The term Ĥ(2L)int is the interlayer interaction expressed as
, which contains the on-site energy, the hopping terms between orbitals of the same type at first-neighbor positions, and the hopping terms between orbitals of different type at first- and second-neighbor positions.145 TB parameters in the single-layer Hamiltonian for MoS2, MoSe2, WS2 and WSe2 can be obtained from Table 7 of ref. 145. The term Ĥ(2L)int is the interlayer interaction expressed as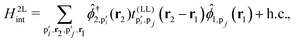
![[small phi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b5.gif) i,pj is the pj orbital basis of i-th monolayer. Within the SK parametrization, the interlayer hoppings are expressed as175
i,pj is the pj orbital basis of i-th monolayer. Within the SK parametrization, the interlayer hoppings are expressed as175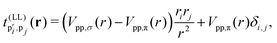
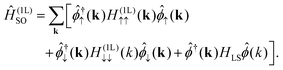
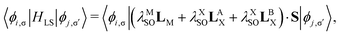
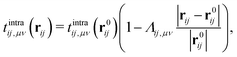

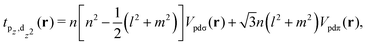

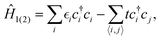
 is the onsite energy that has a difference
is the onsite energy that has a difference  for B and N atoms.178t is the intralayer nearest hopping between B and N. Δ and t are set as 8 eV and 2.33 eV, respectively.140H12 is the interlayer Hamiltonian with the form140
for B and N atoms.178t is the intralayer nearest hopping between B and N. Δ and t are set as 8 eV and 2.33 eV, respectively.140H12 is the interlayer Hamiltonian with the form140![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−α(r − h)),
exp(−α(r − h)),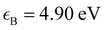 ,
, 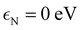 , and t = 2.65 eV, and uses a TBG-like relation that includes only Vppσ for the interlayer hopping.141
, and t = 2.65 eV, and uses a TBG-like relation that includes only Vppσ for the interlayer hopping.141![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
= ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n2γXYFXYc(r)exp[QXY(h − r)],
n2γXYFXYc(r)exp[QXY(h − r)],
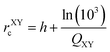 .
.
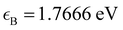 and
and 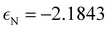 for the first term in eqn (29).136 In addition, the lattice relaxation effect could be incorporated into the intralayer interaction as
for the first term in eqn (29).136 In addition, the lattice relaxation effect could be incorporated into the intralayer interaction as
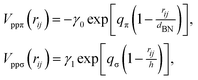
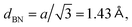 the vertical interlayer distance is h = 3.261 Å, γ0 = 2.7 eV, while γ1 has γ1 = tBB′ = 0.831 eV, γ1 = tNN′ = 0.6602 eV, or γ1 = tBN′ = tNB′ = 0.3989 eV. The parameters qπ and qσ have the relation
the vertical interlayer distance is h = 3.261 Å, γ0 = 2.7 eV, while γ1 has γ1 = tBB′ = 0.831 eV, γ1 = tNN′ = 0.6602 eV, or γ1 = tBN′ = tNB′ = 0.3989 eV. The parameters qπ and qσ have the relation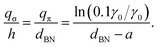

![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (N3) and
(N3) and ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (N2), respectively. The non-orthogonal TB Hamiltonian leads to a generalized form Hψ = ESψ with an overlap matrix S.193 When only a small number of eigenpairs near the Fermi level are required, e.g., bands in a narrow energy window or low-frequency transport/optics, partial-spectrum solvers are markedly efficient tools for sparse TB Hamiltonian matrices. The Krylov method can target extremal or interior eigenvalues. With a shift–invert one iterates on the operator
(N2), respectively. The non-orthogonal TB Hamiltonian leads to a generalized form Hψ = ESψ with an overlap matrix S.193 When only a small number of eigenpairs near the Fermi level are required, e.g., bands in a narrow energy window or low-frequency transport/optics, partial-spectrum solvers are markedly efficient tools for sparse TB Hamiltonian matrices. The Krylov method can target extremal or interior eigenvalues. With a shift–invert one iterates on the operator
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms. The calculation of electronic structures of TBG with tiny angles is numerically challenging. In this case, a linear-scaling method with scale of O(N) has the advantage of tackling the large-scale TB Hamiltonian.106,107,203
000 atoms. The calculation of electronic structures of TBG with tiny angles is numerically challenging. In this case, a linear-scaling method with scale of O(N) has the advantage of tackling the large-scale TB Hamiltonian.106,107,203
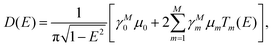
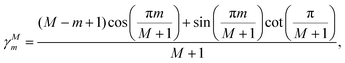
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
= ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2xTm−1(x) − Tm−2(x).
2xTm−1(x) − Tm−2(x).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) arccos(x)], resulting in T0(x) = 1 and T1(x) = x. The parameter μm is the Chebyshev moment computed through
arccos(x)], resulting in T0(x) = 1 and T1(x) = x. The parameter μm is the Chebyshev moment computed through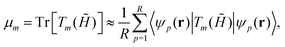
![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) is a rescaled Hamiltonian with eigenvalues ranging for −1 to 1. The error of this approximation is
is a rescaled Hamiltonian with eigenvalues ranging for −1 to 1. The error of this approximation is 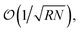 with R the number of random states and N the size of the Hamiltonian. The large-scale moiré superlattices naturally give a large N Hamiltonian that benefits the trace of eqn (43) convergence, but is hard to be diagonalized. A Kubo-Bastin DC conductivity of large-scale moiré can be computed with204–206
with R the number of random states and N the size of the Hamiltonian. The large-scale moiré superlattices naturally give a large N Hamiltonian that benefits the trace of eqn (43) convergence, but is hard to be diagonalized. A Kubo-Bastin DC conductivity of large-scale moiré can be computed with204–206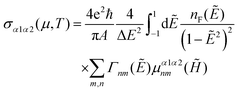
![[H with combining tilde]](https://www.rsc.org/images/entities/i_char_0048_0303.gif) ) are functions of the energy and the Hamiltonian, respectively
) are functions of the energy and the Hamiltonian, respectively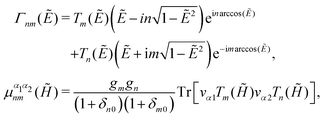
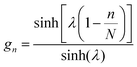 and λ = 4. vα1 is the α1 component of velocity operator
and λ = 4. vα1 is the α1 component of velocity operator  where l is the distance vector, and the trace can be calculated in a random state basis through eqn (43).204 As shown in Fig. 7, the KPM is a powerful method for modeling the DOS, Direct current (DC) conductivity and conductance in graphene-based moiré systems with tiny angles207–211 and could facilitate the computation of properties of more complex morié superlattices in the future.212,213
where l is the distance vector, and the trace can be calculated in a random state basis through eqn (43).204 As shown in Fig. 7, the KPM is a powerful method for modeling the DOS, Direct current (DC) conductivity and conductance in graphene-based moiré systems with tiny angles207–211 and could facilitate the computation of properties of more complex morié superlattices in the future.212,213

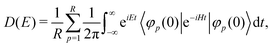
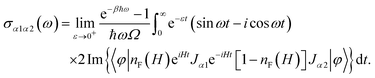



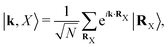
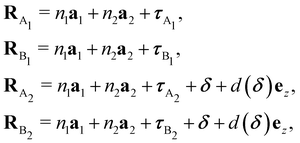
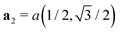 are the monolayer's lattice vectors, while τX are the sublattice displacements (τA1 = τA2 = 0, τB1 = τB2 = −τ1 with τ1 = (2a2 − a1)/3). The displacement vector δ accounts for the variation in the atomic positions of layer 2 due to its relative rotation with layer 1, while d(δ) accounts for the interlayer distance at δ. When the layers are relatively rotated by a small twist angle θ, the displacement vector δ is taken to vary with the real space position r as247
are the monolayer's lattice vectors, while τX are the sublattice displacements (τA1 = τA2 = 0, τB1 = τB2 = −τ1 with τ1 = (2a2 − a1)/3). The displacement vector δ accounts for the variation in the atomic positions of layer 2 due to its relative rotation with layer 1, while d(δ) accounts for the interlayer distance at δ. When the layers are relatively rotated by a small twist angle θ, the displacement vector δ is taken to vary with the real space position r as247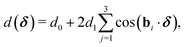
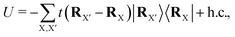
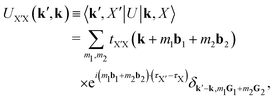
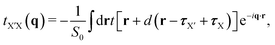
 in the unit cell of monolayer graphene. Fig. 11 shows the variation of the hopping amplitude t(q) as a function of momentum q = |q|, for different models. The key observation is that t(q) decays very rapidly with q because the interlayer separation exceeds the intralayer carbon–carbon distance by more than a factor of 2.76
in the unit cell of monolayer graphene. Fig. 11 shows the variation of the hopping amplitude t(q) as a function of momentum q = |q|, for different models. The key observation is that t(q) decays very rapidly with q because the interlayer separation exceeds the intralayer carbon–carbon distance by more than a factor of 2.76

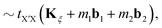 leading to a local moiré potential
leading to a local moiré potential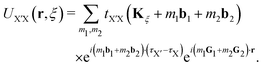
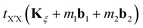 only depends on the distance of the Dirac points to the origin. As tX′X(q) decay rapidly with q, one can take only the first three leading terms (m1, m2) = {(0, 0), ξ(1, 0), ξ(1, 1)} in the summation over m1 and m2. The moiré potential, in matrix form, then takes the well-known form ref. 243 and 247
only depends on the distance of the Dirac points to the origin. As tX′X(q) decay rapidly with q, one can take only the first three leading terms (m1, m2) = {(0, 0), ξ(1, 0), ξ(1, 1)} in the summation over m1 and m2. The moiré potential, in matrix form, then takes the well-known form ref. 243 and 247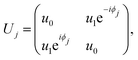
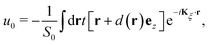
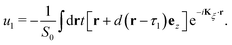
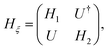
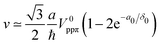
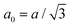 is the carbon–carbon distance and δ0 = 0.184a is the decay length,218 so that the nearest intralayer coupling is 0.1V0ppπ. With V0ppπ ∼ −2.7 eV, Koshino et al. obtained ħv/a = 2.1354 eV.247
is the carbon–carbon distance and δ0 = 0.184a is the decay length,218 so that the nearest intralayer coupling is 0.1V0ppπ. With V0ppπ ∼ −2.7 eV, Koshino et al. obtained ħv/a = 2.1354 eV.247
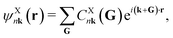

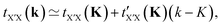
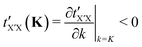
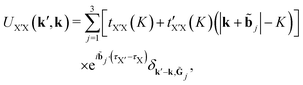
![[G with combining tilde]](https://www.rsc.org/images/entities/b_char_0047_0303.gif) 1 = 0,
1 = 0, ![[G with combining tilde]](https://www.rsc.org/images/entities/b_char_0047_0303.gif) 2 = ξG1,
2 = ξG1, ![[G with combining tilde]](https://www.rsc.org/images/entities/b_char_0047_0303.gif) 3 = ξ(G1 + G2) and
3 = ξ(G1 + G2) and ![[b with combining tilde]](https://www.rsc.org/images/entities/b_char_0062_0303.gif) 1 = 0,
1 = 0, ![[b with combining tilde]](https://www.rsc.org/images/entities/b_char_0062_0303.gif) 2 = ξb1,
2 = ξb1, ![[b with combining tilde]](https://www.rsc.org/images/entities/b_char_0062_0303.gif) 3 = ξ(b1 + b2). Jihang Zhu et al.246 estimated the non-local tunneling energies as
3 = ξ(b1 + b2). Jihang Zhu et al.246 estimated the non-local tunneling energies as 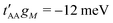 and
and 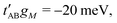 where gM = |G1|. Fig. 12(b) show the continuum band structure, at the magic angle θ = 1.05°, with and without the non-local moiré potential; only the non-local potential effectively captures the particle-hole asymmetry obtained in the relaxed TB models.
where gM = |G1|. Fig. 12(b) show the continuum band structure, at the magic angle θ = 1.05°, with and without the non-local moiré potential; only the non-local potential effectively captures the particle-hole asymmetry obtained in the relaxed TB models.



