SD aromaticity index: a new assessment of aromaticity based on Ramsey spin dipolar contribution to NMR spin–spin coupling constants
M. Natalia C.
Zarycz
 *a,
M. Ayelén
Schiel
*a,
M. Ayelén
Schiel
 a,
Héctor A.
Baldoni
a,
Héctor A.
Baldoni
 b and
Ricardo D.
Enriz
b and
Ricardo D.
Enriz
 a
a
aFacultad de Química, Bioquímica y Farmacia, Instituto Multidisciplinario de Investigaciones Biológicas de San Luis (IMIBIO-SL), CONICET, Universidad Nacional de San Luis, 5700 San Luis, Argentina. E-mail: mnzarycz@gmail.com
bFacultad de Química, Bioquímica y Farmacia, Instituto de Matemáticas Aplicadas (IMASL), CONICET, Universidad Nacional de San Luis, Italia 1556, San Luis, 5700, Argentina
First published on 16th October 2025
Abstract
Aromaticity remains one of the most fundamental yet elusive concepts in chemistry, as no single observable can directly quantify it. In this work, we introduce the spin–dipolar aromaticity index (SDAI), a new descriptor based on the spin–dipolar (SD) contribution to one-bond NMR spin–spin coupling constants. Beyond providing an additional numerical index, SDAI unveils a direct physical manifestation of aromaticity through the magnetic interaction between nuclear spins mediated by delocalized π-electrons. Within the framework of density functional theory (DFT), we analyzed the behavior of the SD term across a representative series of aromatic, nonaromatic, and antiaromatic molecules, including heterocycles, substituted benzenes, fulvenes, and polycyclic hydrocarbons. The calculations show that in aromatic systems, the SD contribution to one bond coupling (1JSD) exhibits nearly uniform values—close to those of benzene—reflecting a collective and homogeneous spin-polarization response of the π-system. In contrast, nonaromatic and antiaromatic compounds display irregular 1JSD patterns, with large bond-to-bond variations that reflect localized π-electron distributions. This magnetic uniformity is therefore a necessary but not sufficient condition for aromaticity: only when the resulting 1JSD values remain comparable to benzene's does genuine aromatic character arise. The aromaticity trends obtained from SDAI closely reproduce those given by electronic and energetic descriptors such as HOMA, PDI, and FLU. Moreover, in molecules where magnetic and electronic criteria diverge, SDAI follows the latter, confirming its consistency with descriptors governed by π-electron delocalization. SDAI thus provides a physically grounded and computationally accessible approach to quantify aromaticity.
1. Introduction
Aromatic compounds, including cyclic hydrocarbons and their heterocyclic analogs, are essential in chemical research and applications, from drug design and polymer synthesis to materials for organic electronics, as well as in biological systems such as DNA and coenzymes.1–10 This importance has driven over a century of studies aimed at understanding the factors governing their chemical and physical properties.5,11–20Despite extensive research, the definition and quantification of aromaticity remain contentious.16,21–23 Aromaticity cannot be defined unequivocally, as there is no physical observable that allows its direct measurement. This chemical unicorn24 is inferred from properties that characterize aromatic systems.5,14,15,17,18,25 A molecule is generally considered aromatic when it exhibits delocalized π-electrons, enhanced energetic stability relative to acyclic analogs, bond-length equalization, diamagnetic ring currents under an external magnetic field, and a tendency toward substitution rather than addition reactions. Although these criteria form a useful framework, they cannot always be consistently applied, and no single property can universally define aromaticity.5,26 Indeed, different indices based on these properties can yield contradictory results.15 This is often attributed to the multidimensional nature of aromaticity, which implies that not all related properties are equally affected.27 While this explanation may be reasonable in some instances, invoking multidimensionality cannot justify cases where certain aromaticity criteria fail or the indices are applied beyond their range of validity.28,29
Since typical aromatic and antiaromatic compounds exhibit diatropic and paratropic ring currents, respectively, under an external magnetic field, magnetic properties are widely used to characterize aromaticity. Methods based on this criterion include magnetic susceptibility anisotropy,30–32 magnetic susceptibility exaltation,33–35 proton NMR chemical shifts,36,37 interatomic magnetizabilities,38 nucleus-independent chemical shifts (NICS),13 and magnetically induced current density (MICD) plots.39–49 Despite its limitations, NICS remains the most widely used approach. Its main drawback is that it measures shielding/deshielding at a single point without revealing the current sources.14,28 Consequently, a NICS value may arise from local atomic currents, adjacent rings, or the ring of interest, leading to misinterpretations as reported for polycyclic hydrocarbons,28,50,51 hydrogen-bonded clusters,52 and all-metal aromatics.53,54 The isotropic NICS(0) and NICS(1) indices give misleading results.14 For monocyclic systems, the most reliable NICS variants are NICS(1)zz and NICS(1)πzz, though they are unsuitable for polycyclic systems. Although these indices better characterize π-electron currents, they should be combined with MICD plots to confirm that the NICS values originate from the ring current rather than from other current–density features14,28 The magnetic criterion faces limitations beyond the ill-defined nature of some derived indices. For example, there are reports of systems with diatropic currents that are not aromatic by energetic or electronic criteria,29,55 and cases of radical ions of benzene and heterocycles exhibiting paratropic currents despite cyclic conjugation.56 These observations have led some authors to question its reliability,29 while others propose distinguishing magnetic aromaticity (based on currents) from intrinsic aromaticity (defined by energetic, electronic, and geometric criteria).55,57 Turning to the geometric criterion, Hiberty, Shaik, and co-workers58 attributed bond equalization in benzene to an anti-distortive σ-electron effect, although later studies revealed an additional contribution from anti-distortive cyclic delocalization energy of the π system.59,60 The energetic criterion is fundamental for characterizing aromaticity, but its use is hindered by the need for an appropriate reference system to isolate stabilization from other energy effects.18 The criterion of cyclic π-electron delocalization is also intrinsic; indeed, several studies have established a direct relationship between the energetic and electronic criteria.12,29,55,61 Nevertheless, as emphasized previously,28 all aromaticity indices have inherent limitations, and overlooking them can lead to misapplication and erroneous conclusions. Therefore, a multifaceted approach using indices based on different physical properties is essential for reliably evaluating the aromatic character of a system.16
Besides magnetic-based indices, the most commonly used aromaticity measures include the aromatic stabilization energy (ASE),18 an energy-based measure; the harmonic oscillator model of aromaticity (HOMA),25 a geometry-based indicator; and electron density-based indices such as the para-delocalization index (PDI),62 the aromatic fluctuation index (FLU)63 and the electron density of delocalized bonds (EDDB).64 A recent and promising contribution to this last category is the set of six new descriptors introduced by Borges Jr. and co-workers, derived from the analysis of delocalized electron density using Stone's distributed multipole analysis (DMA).65
NMR indirect spin–spin coupling constants (J-couplings) are highly sensitive probes of electronic structure, and their accurate prediction is now feasible with modern quantum-chemical methods.66–70J-Coupling depends on σ or π chemical bond character between the coupled nuclei. Such dependency can be analyzed by using the classic Ramsey theory.71 Thus, the Fermi contact (FC) mechanism dominates in σ frameworks; whereas spin–dipolar (SD) and paramagnetic spin–orbital (PSO) terms reflect the presence of π electrons.72–76 Although the role of these non-contact terms in conjugated C–C bonds remains partially unresolved, long-range couplings are known to require π-conjugation, where SD and PSO can outweigh FC.75–77 Our recent study on o-hydroxyaryl Schiff bases77 showed that π-delocalization in the chelate ring produces significant SD and PSO contributions to 2hJ(O–N), affecting the tautomeric equilibrium and corroborating resonance-assisted hydrogen bonding. Moreover, the variation of the SD term with d(NH) closely follows the changes in the PDI, providing novel evidence for a direct relationship between the SD mechanism and π-electron delocalization in cyclic systems.
Since π-electron delocalization in cyclic systems is generally considered the main cause of their aromatic character and considering that the spin–dipolar contribution to J-coupling (JSD) is a highly sensitive probe of the π-electron distribution, analyzing how aromaticity affects this term provides a valuable means to gain physical insight into this elusive property. In fact, we found that the SD contribution to the one-bond J-coupling between nuclei M and N, 1JSD(M,N), exhibits distinctive behavior in aromatic systems: all bonds show nearly identical values, reflecting a homogeneous delocalization of the π-electrons. For instance, at the B3LYP/cc-pVTZ level, in benzene every 1JSD(C,C) coupling is 1.27 Hz, while in other 6π-electron aromatic systems such as C7H7+ and C8H82+ the values decrease slightly to 1.13 and 1.08 Hz, respectively, indicating a reduction of aromatic character with increasing ring size. By contrast, in non-aromatic and antiaromatic systems the 1JSD(C,C) values are not uniform, often around 4 Hz or higher for localized double bonds, directly revealing the lack of π-electron delocalization. Thus, just as bond-length alternation evidences electronic localization, the dispersion of 1JSD(M,N) values constitutes a direct physical manifestation of how the degree of aromaticity modulates the underlying spin interactions responsible for the SD mechanism.
Given that the definition and physical origin of aromaticity remain debated and not fully established, requiring a multifaceted description, several authors have emphasized the need for new descriptors from complementary perspectives.16,21,22,78 Within this context, 1JSD(M,N) emerges as a genuine quantum-physical property that provides new insight into aromaticity by directly probing the π-electron distribution along bonds. The main goal of this study is therefore not merely to propose another index, but to establish a physically grounded descriptor—here termed the spin–dipolar aromaticity index (SDAI)—which formalizes the distinctive behavior of 1JSD(M,N) values: uniform and close to 1.2 Hz in aromatic compounds, and heterogeneous and larger for localized double bonds in non-aromatic or antiaromatic ones. By doing so, this index provides a direct and measurable connection between π-electron delocalization in aromatic/antiaromatic systems and the underlying spin interactions responsible for the spin–dipolar mechanism. Furthermore, we aim to clarify whether SDAI follows more closely the predictions of magnetic or electronic descriptors in molecules where these criteria diverge.29,55 To validate this approach, we applied SDAI to a representative set of cyclic and polycyclic hydrocarbons and their heteroatomic analogues with well-established aromaticity trends, and we compared the results with those from established indices such as HOMA, PDI, FLU, and NICS.
2. Theoretical models
2.1 Origin of NMR J-couplings
This section briefly outlines the physical mechanisms responsible for J-couplings observed in NMR spectra of solutions or gases. While all electronic mechanisms are mentioned, particular focus is placed on those dependent on electron spin. Detailed descriptions of the underlying theory and its quantum-chemical determination are available in textbooks and reviews.66–69Within a non-relativistic framework, Ramsey developed the theory of J-couplings, proposing that nuclear spins interact via electrons located along the coupling pathway.71 The isotropic J-coupling between nuclei K and L is given by the sum of four contributions:
| JKL = JDSOKL + JPSOKL + JFCKL + JSDKL | (1) |
The JDSOKL term is an expectation value of the ground-state wave function and is straightforward to calculate. The PSO, FC, and SD terms were originally formulated as a sum-over-states, requiring knowledge of all singlet (PSO) or triplet (FC, SD) excited states. Although this formulation describes the underlying physics, it is not suitable for computation. In practice, J-couplings are typically evaluated using linear response methods.79,80
Ramsey's formulation distinguishes two types of transmission mechanisms. The first, independent of electron spin, involves interactions between nuclear magnetic fields and electron orbital motion (DSO and PSO). The second, dependent on electron spin, arises from interactions between nuclear magnetic moments and electron spins (FC and SD). In essence, J-coupling occurs when the magnetic field of one nucleus perturbs the surrounding electron cloud, transmitting this disturbance through the electronic system and inducing a secondary magnetic field at the position of the other nucleus. The latter nucleus then interacts with this induced field.
For spin-dependent interactions, one nucleus induces a local polarization of electron spins, leading to a relative excess or deficit of α electrons compared to β electrons. When this polarization occurs at the nuclear positions, the interaction is governed by the FC mechanism. Polarization in the extended dipolar field outside the nuclei is described by the SD term. Although this work is restricted to closed-shell systems, local regions of non-zero spin density (the difference between α- and β-electron densities) may arise. Positive and negative contributions, however, compensate globally so that the total number of α and β electrons remains equal.
The FC contribution arises from nucleus–electron interactions at the nuclear contact surface, involving s-orbitals. It is therefore mainly transmitted through the σ-bond framework and dominates J-couplings in saturated molecules. The SD term originates from interactions away from nuclei and is primarily transmitted through π-systems, becoming significant in unsaturated molecules. Among the spin-independent terms, the DSO contribution is often negligible, though exceptions exist.81 In contrast, the PSO term is typically significant when coupled atoms are linked through π-systems or possess lone pairs.
3. Computational details
All calculations of NMR spectroscopic parameters and geometry optimizations were performed using DFT82 methodology with the Gaussian 16 program package.83 The geometries were optimized using the B3LYP-D3(BJ)84–86 functional with the 6-311++G(d,p) basis set.87J-Couplings were calculated using the B3LYP,84,88 PBE,89 and B3P8688,90 functionals combined with the aug-cc-pVTZ-J,91 ccJ-pVTZ,92 and cc-pVTZ93 basis sets.
Nuclear magnetic shielding constants for the NICS indices were obtained at the B3LYP/aug-cc-pVTZ level using the gauge-independent atomic orbital (GIAO) method.94,95
The optimized geometries were used to compute wavefunctions at the Hartree Fock (HF) level with the cc-pVTZ basis set using Gaussian 16, and the resulting data were employed to calculate delocalization indices (DIs)62 within the quantum theory of atoms in molecules (QTAIM)96 with the Multiwfn software.97
Previous studies have62 shown that DI values for closed-shell systems calculated at the HF level are accurate compared with those from configuration interaction with singles and doubles excitations (CISD), despite a moderate overestimation. Since the qualitative trends are preserved and CISD calculations are computationally prohibitive for the systems studied here, the HF level represents a suitable choice for obtaining reliable DI values.
The geometries of compounds A17–A21 were taken from previous works.29,55 For compounds A19–A21, which are in their lowest triplet state, J-coupling calculations were performed at the UB3LYP/cc-pVTZ level.
4. Results and discussion
4.1 Assessment of Ramsey's terms of carbon–carbon coupling constants as probes of conjugation and aromaticity
If a molecular property is to function as the basis for an aromaticity index, it must distinguish between saturated and unsaturated compounds. Among the latter, its value should vary between systems with conjugated and non-conjugated double bonds, as well as between aromatic, non-aromatic, and antiaromatic frameworks.In this section, we evaluate the behavior of the SD (JSD), PSO (JPSO) and FC (JFC) contributions to J-coupling with the aim of verifying whether any of them meets the requirements to define an aromaticity index.
To properly describe the SD and PSO terms, however, additional tight d- and p-functions are required. The ccJ-pVTZ basis set, optimized by Jensen and co-workers for J-coupling calculations, fulfills this requirement.92 While it has shown excellent performance with coupled-cluster and SOPPA-family methods,100 it had not been tested with the B3LYP, B3P86, and PBE functionals for molecules encompassing diverse carbon hybridizations, such as those in Fig. 1.
 | ||
| Fig. 1 Schematic structures of saturated and unsaturated compounds used to assess the behavior of the J-coupling Ramsey terms. | ||
To evaluate the quality of the chosen functionals and basis sets, we selected 21 molecules (63 J(C,C) values) covering sp3–sp3, sp3–sp2, and sp2–sp2 bond types (see Fig. S1, SI), with experimental values ranging from −2 to 75 Hz (Table S1, SI). Linear regression analyses between calculated and experimental data show excellent agreement (Fig. 2), yielding coefficients R2 > 0.99 for all functional/basis-set combinations. The mean absolute errors (MAEs) were similarly low, ranging from 1.80 to 2.50 Hz (Table S2, SI). The B3P86/aug-cc-pVTZ-J combination provided the lowest MAE (1.80 Hz), but the differences among methods were minor. For instance, switching to the ccJ-pVTZ basis set altered the MAEs by less than 0.23 Hz. These results confirm that both ccJ-pVTZ and aug-cc-pVTZ-J reproduce experimental J-couplings with comparable and reliable accuracy.
A direct comparison of the two basis sets across all three functionals (Fig. S2, SI) further supports their equivalence. The linear correlations for all functionals show slopes close to unity, intercepts near zero, and R2 values of 1.000 for B3LYP and B3P86 and 0.999 for PBE. Given this comparable accuracy, and since ccJ-pVTZ is smaller and computationally more efficient, we selected the B3LYP/ccJ-pVTZ level of theory for the subsequent calculations of Ramsey terms in the molecular systems of Fig. 1.
| Comp. | FC | SD | PSO | Tot | Comp. | FC | SD | PSO | Tot | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 J(C1,C2) | 32.91 | 1.16 | 0.00 | 34.19 | 12 | 1 J(C1,C2) | 81.83 | 3.88 | −10.14 | 75.76 |
| 2 | 1 J(C1,C2) | 33.09 | 1.16 | −0.26 | 34.15 | 1 J(C2,C3) | 40.71 | 0.87 | −1.27 | 40.53 | |
| 2 J(C1,C3) | −0.11 | −0.05 | −0.22 | −0.40 | 1 J(C3,C4) | 32.38 | 1.25 | −0.27 | 33.58 | ||
| 3 | 1 J(C1,C2) | 33.32 | 1.17 | −0.27 | 34.38 | 1 J(C4,C5) | 31.40 | 1.20 | −0.43 | 32.39 | |
| 1 J(C2,C3) | 33.22 | 1.16 | −0.57 | 34.01 | 2 J(C1,C3) | −0.29 | 0.01 | −0.37 | −0.67 | ||
| 2 J(C1,C3) | 0.27 | −0.05 | −0.24 | −0.03 | 2 J(C2,C4) | −1.53 | −0.03 | −0.12 | −1.66 | ||
| 3 J(C1,C4) | 6.42 | 0.03 | 0.01 | 6.40 | 2 J(C3,C5) | −1.30 | −0.05 | −0.12 | −1.44 | ||
| 4 | 1 J(C1,C2) | 33.36 | 1.17 | −0.26 | 34.43 | 3 J(C1,C4) | 6.20 | −0.02 | −0.14 | 6.06 | |
| 1 J(C2,C3) | 33.47 | 1.16 | −0.57 | 34.26 | 3 J(C3,C6) | 3.89 | −0.01 | −0.09 | 3.79 | ||
| 1 J(C3,C4) | 33.50 | 1.16 | −0.57 | 34.29 | 13 | 1 J(C1,C2) | 82.85 | 3.96 | −10.16 | 76.84 | |
| 2 J(C1,C3) | 0.15 | −0.05 | −0.24 | −0.15 | 1 J(C2,C3) | 41.79 | 0.87 | −1.28 | 41.61 | ||
| 2 J(C2,C4) | 0.61 | −0.05 | −0.25 | 0.32 | 2 J(C1,C3) | −0.49 | 0.00 | −0.33 | −0.84 | ||
| 3 J(C1,C4) | 6.16 | 0.04 | 0.00 | 6.14 | 2 J(C2,C4) | −1.89 | −0.02 | 0.05 | −1.83 | ||
| 4 J(C1,C5) | 0.34 | −0.01 | 0.04 | 0.33 | 3 J(C1,C4) | 8.04 | 0.05 | −0.06 | 8.04 | ||
| 5 | 1 J(C1,C2) | 33.35 | 1.17 | −0.26 | 34.42 | 3 J(C3,C6) | 7.46 | 0.00 | −0.16 | 7.28 | |
| 1 J(C2,C3) | 33.52 | 1.16 | −0.57 | 34.32 | 14 | 1 J(C1,C2) | 81.53 | 4.07 | −9.77 | 75.96 | |
| 1 J(C3,C4) | 33.74 | 1.16 | −0.58 | 34.53 | 1 J(C2,C3) | 57.80 | 1.38 | −3.01 | 56.36 | ||
| 1 J(C4,C5) | 33.54 | 1.16 | −0.57 | 34.34 | 2 J(C1,C3) | 1.00 | −1.57 | 0.10 | −0.53 | ||
| 2 J(C1,C3) | 0.17 | −0.05 | −0.24 | −0.13 | 3 J(C1,C4) | 7.89 | 3.50 | 0.69 | 11.98 | ||
| 2 J(C2,C4) | 0.48 | −0.05 | −0.25 | 0.20 | 15 | 1 J(C1,C2) | 81.51 | 4.18 | −9.62 | 76.20 | |
| 3 J(C1,C4) | 5.96 | 0.04 | 0.00 | 5.94 | 1 J(C2,C3) | 61.01 | 1.61 | −3.38 | 59.45 | ||
| 3 J(C2,C5) | 5.92 | 0.04 | −0.01 | 5.90 | 2 J(C1,C3) | 0.71 | −2.28 | 0.14 | −1.47 | ||
| 4 J(C1,C5) | 0.35 | −0.01 | 0.04 | 0.34 | 2 J(C2,C4) | 1.62 | −1.56 | −0.01 | 0.02 | ||
| 5 J(C1,C6) | 0.17 | 0.00 | 0.04 | 0.18 | 3 J(C1,C4) | 8.13 | 3.66 | 0.68 | 12.40 | ||
| 6 | 1 J(C1,C2) | 31.82 | 1.21 | −0.40 | 32.85 | 3 J(C2,C5) | 8.42 | 0.60 | 0.15 | 9.12 | |
| 2 J(C1,C3) | −1.23 | −0.05 | −0.17 | −1.42 | 4 J(C1,C5) | −1.23 | −1.12 | 0.03 | −2.37 | ||
| 3 J(C1,C4) | 2.26 | −0.01 | −0.08 | 2.19 | 5 J(C1,C6) | 1.42 | 2.39 | −0.09 | 3.68 | ||
| 7 | 1 J(C1,C2) | 80.53 | 4.03 | −10.21 | 74.42 | 16 | 1 J(C1,C2) | 81.55 | 4.27 | −9.56 | 76.39 |
| 8 | 1 J(C1,C2) | 82.20 | 4.21 | −10.17 | 76.35 | 1 J(C2,C3) | 61.80 | 1.78 | −3.52 | 60.27 | |
| 1 J(C2,C3) | 42.61 | 0.93 | −0.82 | 42.87 | 2 J(C1,C3) | 0.47 | −2.74 | 0.16 | −2.15 | ||
| 2 J(C1,C3) | 1.16 | 0.03 | −0.33 | 0.79 | 2 J(C2,C4) | 1.43 | −1.59 | −0.03 | −0.22 | ||
| 9 | 1 J(C1,C2) | 81.97 | 4.18 | −10.18 | 76.09 | 2 J(C3,C5) | 1.29 | −2.28 | 0.02 | −0.98 | |
| 1 J(C2,C3) | 42.40 | 0.94 | −1.04 | 42.49 | 3 J(C1,C4) | 8.42 | 3.80 | 0.67 | 12.80 | ||
| 1 J(C3,C4) | 33.81 | 1.20 | −0.15 | 35.02 | 3 J(C2,C5) | 8.74 | 0.84 | 0.18 | 9.71 | ||
| 2 J(C1,C3) | 1.55 | 0.03 | −0.31 | 1.22 | 4 J(C1,C5) | −1.55 | −1.65 | 0.03 | −3.22 | ||
| 2 J(C2,C4) | 0.06 | 0.00 | −0.13 | −0.06 | 4 J(C2,C6) | −1.57 | −1.19 | 0.03 | −2.77 | ||
| 3 J(C1,C4) | 5.53 | 0.02 | 0.14 | 5.61 | 5 J(C1,C6) | 1.76 | 2.61 | −0.10 | 4.22 | ||
| 10 | 1 J(C1,C2) | 82.12 | 4.18 | −10.19 | 76.24 | 5 J(C2,C7) | 1.51 | 0.38 | 0.01 | 1.87 | |
| 1 J(C2,C3) | 42.79 | 0.93 | −1.07 | 42.86 | 6 J(C1,C7) | −1.17 | −0.84 | 0.03 | −2.01 | ||
| 1 J(C3,C4) | 33.90 | 1.19 | −0.45 | 34.84 | 7 J(C1,C8) | 1.08 | 1.92 | 0.05 | 3.03 | ||
| 1 J(C4,C5) | 33.57 | 1.16 | −0.29 | 34.84 | 17 | 1 J(C1,C2) | 84.97 | 4.12 | −9.90 | 79.39 | |
| 2 J(C1,C3) | 1.42 | 0.03 | −0.32 | 1.08 | 1 J(C2,C3) | 59.56 | 0.86 | −2.19 | 58.45 | ||
| 2 J(C2,C4) | 0.58 | 0.00 | −0.14 | 0.46 | 2 J(C1,C3) | −1.28 | 0.01 | −0.11 | −1.39 | ||
| 2 J(C3,C5) | 0.63 | −0.05 | −0.23 | 0.35 | 3 J(C1,C4) | 4.07 | −0.49 | 0.02 | 3.59 | ||
| 3 J(C1,C4) | 5.37 | 0.03 | 0.14 | 5.47 | 3 J(C2,C5) | 4.03 | −0.12 | −0.07 | 3.86 | ||
| 3 J(C2,C5) | 7.15 | 0.04 | 0.02 | 7.16 | 4 J(C1,C5) | −2.38 | 0.10 | 0.01 | −2.26 | ||
| 4 J(C1,C5) | 0.57 | 0.01 | 0.08 | 0.61 | 18 | 1 J(C1,C2) | 65.05 | 1.38 | −7.23 | 59.41 | |
| 11 | 1 J(C1,C2) | 82.75 | 4.23 | −10.18 | 76.92 | 2 J(C1,C3) | −0.99 | −0.90 | 0.06 | −1.84 | |
| 1 J(C2,C3) | 43.94 | 0.92 | −1.06 | 44.01 | 3 J(C1,C4) | 8.65 | 2.00 | 0.54 | 11.19 | ||
| 2 J(C1,C3) | 2.04 | 0.04 | −0.33 | 1.71 | 19 | 1 J(C1,C2) | 58.88 | 1.17 | −7.03 | 53.21 | |
| 2 J(C2,C4) | 0.60 | −0.01 | −0.23 | 0.38 | 2 J(C1,C3) | −1.35 | 1.39 | 2.52 | 2.52 | ||
| 3 J(C1,C4) | 6.39 | 0.05 | 0.06 | 6.42 | 3 J(C1,C4) | 1.03 | −0.63 | 0.11 | 0.49 | ||
| 4 J(C1,C5) | 0.78 | −0.04 | 0.09 | 0.76 | 4 J(C1,C5) | 1.75 | 1.75 | −0.55 | 2.95 |
Across all compounds, the one-bond coupling, 1J(C,C), is the largest. The 1J(C,C) magnitude is primarily determined by the FC contribution, which depends on the hybridization of the coupled atoms and on the presence of a π bond; JSD(C,C) and JPSO(C,C) often provide important corrections depending on the bonding environment. This trend is in line with previous works.70,74,98
4.1.2.1 Saturated compounds. For saturated compounds (1–6), 1J(C,C) values lie around 33 Hz (see Table 1). Two-bond couplings are nearly zero in linear systems but reach ≈−1.4 Hz in cyclohexane; couplings beyond three bonds are negligible. For couplings beyond one bond, the SD and PSO contributions are practically zero. Thus, the through-space mechanism observed for 3J(C,C) in these saturated systems is attributable exclusively to the FC contribution.
4.1.2.2 Compounds with isolated double bonds. For compounds 7–13, 1J(C,C) across a double bond is ≈74–77 Hz, whereas for σ sp3–sp2 1J(C,C) values are ≈40–44 Hz and for σ sp3–sp3 ≈32–35 Hz. Two-bond couplings are small (≈–1.8 to 1.7 Hz) and couplings over more than three bonds vanish; 3J(C,C) remains non-zero because of a through-space mechanism transmitted by JFC.
When a double bond is present between the coupled carbons, the SD and PSO contributions to 1J(C,C) are non-negligible (JSD ≈ 3.9–4.2 Hz; JPSO ≈ −10.2 Hz), although JFC remains dominant; thus reproducing experiment requires inclusion of non-contact terms. For σ sp3–sp2 1J(C,C), the SD and PSO contributions are small (≈0.9 and ≈−1 Hz, respectively) and largely cancel. For couplings beyond one bond in this group, JSD and JPSO are negligible and observable values arise primarily from JFC.
4.1.2.3 Compounds with conjugated double bonds. For compounds 14–19, 1J(C,C) remains the largest coupling and 3J(C,C) is often the next largest. Unlike the previous two groups, couplings over more than three bonds can be detectable (≈−3.2 to 4.2 Hz in the set studied).
4.1.2.4 Acyclic compounds with conjugated double bonds. In linear polyenes (14–16), 1J(C,C) depends strongly on whether the bond is double (≈76 Hz) or σ sp2–sp2 (≈56–60 Hz) and remains nearly constant along a given conjugated chain. The Ramsey contributions to 1J(C,C) in the presence of a double bond are numerically close to those found in compounds with isolated double bonds. For σ sp2–sp2 1J(C,C) in these polyenes, the JSD and JPSO contributions are ≈1.4–1.8 Hz and ≈−3.5 to −3.0 Hz, respectively, while JFC ≈57.8–61.8 Hz. These values differ from σ sp2–sp3 cases, confirming that both JFC and the non-contact terms depend on hybridization and on involvement in a conjugated π system.
In these acyclic conjugated systems, the PSO contribution to couplings beyond one bond is negligible or vanishes, whereas the SD contribution shows characteristic behavior. For 2J(C,C), JSD values (≈−2.7 to −1.6 Hz) are often larger in absolute value than JFC (≈0.5–1.6 Hz), so the total 2J(C,C) is controlled by JSD when the two terms do not cancel. For 3J(C,C), JFC increases (≈7.9–8.7 Hz) relative to saturated systems (≈5.9–6.4 Hz); JSD for 3J(C,C) depends on the number of conjugated bonds in the pathway (≈3.5–3.8 Hz when two conjugated bonds lie in the path, ≈0.6–0.8 Hz when only one does).
For longer-range couplings, JSD values tend to be larger when the coupling pathway is fully conjugated, e.g., 5J(C1,C6) > 4J(C1,C5). At the same time, JFC generally decreases with distance (approaching ≈1 Hz for very long pathways), indicating that JFC is relatively insensitive to extended conjugation while JSD clearly reflects it. Our results show that for some long-range couplings with fully conjugated pathways, such as 5J(C1,C6) and 7J(C1,C8), the JSD contribution exceeds JFC. This finding contrasts with earlier work that considered only JFC.101
4.1.2.5 Cyclic compounds with conjugated/alternated double bonds. Cyclooctatetraene (17) is non-planar and lacks extended π conjugation. Its 1J(C,C) values are similar to those of linear analogues. For double bonds, the Ramsey terms are comparable to those in linear compounds, and for σ sp2–sp2 bonds, JFC is also similar. In contrast, JSD and JPSO decrease substantially for these bonds (by ≈50% and ≈30%, respectively) and nearly vanish for couplings over more than two bonds. This drastic reduction in JSD, compared to linear conjugated systems, identifies it as a sensitive probe for the absence of extended conjugation in cyclic systems.
By contrast, compounds 18 and 19 are aromatic, planar, and possess fully delocalized π systems. Their high structural symmetry makes all bonds equivalent, which results in identical numerical values for all nJ(C,C) couplings of the same range n, as well as for their respective Ramsey terms (nJFC(C,C), nJSD(C,C), and nJPSO(C,C)). However, these equal values arise from different physical origins: nJFC(C,C) is governed by the σ skeleton, whereas nJSD(C,C) and nJPSO(C,C) depend primarily on the π-electron distribution.
In benzene, the FC contributions to 1J(C,C), 2J(C,C), and 3J(C,C) are 65, −1, and 8.6 Hz, respectively, while the PSO contributions are −7.23, 0, and 0.5 Hz. Although both JFC and JPSO reflect the variation in π character of the C–C bond relative to a localized double bond, their overall trends across these couplings resemble those of their linear analogues. In contrast, the SD contributions to 1J(C,C), 2J(C,C), and 3J(C,C) are 1.4, −0.9, and 2.0 Hz, respectively. Remarkably, the SD contribution to 3J(C,C) exceeds that to 1J(C,C), a trend opposite to that observed in conjugated linear compounds for a 1J(C,C) coupling across a double bond.
For compound 19, the FC contribution to 1J(C,C) is 58.9 Hz, while for longer-range couplings, JFC values range between −1.3 and 1.7 Hz. The PSO contributions to 1J(C,C) and 2J(C,C) are −7.0 and 2.5 Hz, respectively, becoming negligible beyond two bonds. Thus, as in benzene, the PSO term does not reveal extended conjugation. Conversely, the SD contributions to 1J(C,C), 2J(C,C), 3J(C,C), and 4J(C,C) are 1.2, 1.4, −0.6, and 1.7 Hz, respectively. These results confirm the sensitivity of the SD term to extended conjugation and, moreover, suggest a π-electron delocalization that differs from that in benzene. In particular, the 1JSD(C,C) value is sensitive to the varying degrees of aromaticity in these systems.
Our results demonstrate that the JSD term can detect cyclic delocalization and exhibits a characteristic pattern distinct from that in acyclic analogues. The SD term of J-couplings reliably reflects the presence and degree of extended π-delocalization, establishing it as the foundation for a new aromaticity index.
4.2 Definition of a novel aromaticity index
To optimize computational efficiency, we evaluated the performance of the cc-pVTZ basis set against ccJ-pVTZ for calculating the SD term of carbon–carbon J-couplings in the compounds shown in Fig. S1 (SI). As detailed in Table S3 (SI), the differences between the basis sets originate primarily from the FC term, as cc-pVTZ lacks the diffuse functions needed to accurately describe the wavefunction at the nucleus. In contrast, the SD and PSO terms show negligible variation.A linear regression of nJSD(C,C) values obtained with cc-pVTZ and ccJ-pVTZ yields an R2 = 0.9998, a slope of 0.904, and an intercept of 0.014 (Fig. S3, SI). This confirms that the cc-pVTZ basis set reliably reproduces the trends in SD term values obtained with ccJ-pVTZ. Therefore, in the remainder of this work, SD terms are calculated at the B3LYP/cc-pVTZ level, unless otherwise stated.
Regarding aromatic systems, two notable features of the SD term are the uniformity and magnitude of its values. For instance, the 1JSD(C,C) value in benzene is 1.27 Hz, compared to 1.08 Hz in the larger, less aromatic cyclooctatetraenyl dication.16
For couplings across more than one bond, however, orbital interactions within the π-system become more complex, making direct comparisons between systems of different ring sizes less straightforward. In contrast, for one-bond couplings, the SD contribution primarily reflects the π-system localized to the bond itself, a direct manifestation of the ring's overall delocalization. Since a key objective is to define an index applicable to both six-membered and other ring sizes, we base our new index on the SD term of the one-bond coupling constant. We define the spin-dipolar aromaticity index (SDAI) as follows:
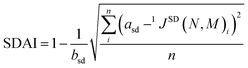 | (2) |
4.3 Performance of SDAI as a new aromaticity index
In this section, we assess the reliability of the SDAI index for evaluating aromaticity in cyclic hydrocarbon and heterocyclic rings belonging to compounds previously classified as aromatic, nonaromatic, or antiaromatic. Our study includes five-membered heterocycles, mono-substituted benzene derivatives, substituted fulvenes and heptafulvenes, three 6π-electron hydrocarbon rings (to test ring-size dependence), and various polycyclic aromatic hydrocarbons comprising both benzenoid and non-benzenoid systems. We also analyze SDAI performance in compounds for which previous studies reported discrepancies between magnetic and electronic descriptors of aromaticity.29,55 These compounds are shown in Fig. 3. | ||
| Fig. 3 Schematic structures of selected compounds used to evaluate the performance of SDAI as a new aromaticity index. | ||
As noted earlier, SDAI takes benzene as the reference aromatic system, with a maximum value of 1. For less aromatic compounds, the SDAI value decreases. According to our results, systems with SDAI > 0.3 are classified as aromatic, while those with values <0.3 are considered nonaromatic or antiaromatic. Within the aromatic group, compounds can be further distinguished as highly aromatic (0.75–1), moderately aromatic (0.45–0.75), or weakly aromatic (0.3–0.45).
We compared SDAI with other indices, including ASE, PDI, FLU, the Shannon Aromaticity (SA),102 the multicenter index (MCI),103 the normalized multicenter index (INB),104 the normalized Giambiagi index (ING),104 NICS(1)zz, and HOMA. The more aromatic a system, the higher the ASE, PDI, MCI, INB, ING, and HOMA values, whereas the FLU and SA indices decrease. For NICS, more negative values correspond to stronger aromaticity. In cases where additional indices are used, we provide the relevant references for their interpretation.
| X | ASEa | NICS(1)zzb | SA × 102![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c |
SDAId |
|---|---|---|---|---|
| a From ref. 26. b Calculated at B3LYP/aug-cc-pVTZ. c From ref. 102. d Calculated at B3LYP/cc-pVTZ. | ||||
| CH− | 22.05 | −34.32 | 2 × 10−7 | 0.727 |
| NH | 20.57 | −31.83 | 0.0958 | 0.438 |
| O | 14.77 | −27.97 | 0.2543 | 0.330 |
| PH | 3.20 | −14.04 | 0.3192 | 0.162 |
| CH2 | 0.00 | −13.12 | 0.4919 | 0.120 |
| AlH | −9.98 | 13.85 | 0.6785 | −0.060 |
| BH | −22.49 | 37.80 | 0.9053 | −1.558 |
Rings with X = CH−, NH, or O are aromatic with six π-electrons, though their aromaticity depends on the heteroatom. In the cyclopentadienyl anion (X = CH−), the negative charge is symmetrically delocalized, giving five equivalent bonds and making it the most aromatic species in the series. In pyrrole (X = NH) and furan (X = O), the heteroatom contributes a lone pair from a p-orbital to the π-system. Both overlap effectively with the carbon 2p-orbitals, but nitrogen donates more efficiently due to its lower electronegativity, so pyrrole is more aromatic than furan. Thus, the aromaticity order is CH− > NH > O.
Systems with X = CH2 or PH are considered non-aromatic, while X = AlH or BH yield antiaromatic species. SDAI reproduces the expected order:
| CH− > NH > O > PH > CH2 > AlH > BH |
| X | FLU1/2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
PDIb | HOMAa | NICS(1)zzc | SDAId |
|---|---|---|---|---|---|
| a From ref. 16. b Calculated at HF/cc-pVTZ. c Calculated at B3LYP/aug-cc-pVTZ. d Calculated at B3LYP/cc-pVTZ. | |||||
| H | 0.000 | 0.100 | 0.989 | −29.80 | 1.000 |
| CH3 | 0.015 | 0.097 | 0.984 | −28.29 | 0.985 |
| CONH2 | 0.021 | 0.096 | 0.984 | −27.82 | 0.984 |
| COOCH3 | 0.023 | 0.095 | 0.983 | −27.83 | 0.980 |
| OH | 0.039 | 0.093 | 0.989 | −27.05 | 0.981 |
| NO2 | 0.029 | 0.093 | 0.994 | −27.87 | 0.975 |
| NH2 | 0.040 | 0.091 | 0.976 | −25.35 | 0.973 |
| CN | 0.031 | 0.094 | 0.977 | −28.14 | 0.970 |
| COCH3 | 0.029 | 0.095 | 0.973 | −27.66 | 0.967 |
| COCl | 0.030 | 0.093 | 0.978 | −27.40 | 0.963 |
| OCH3 | 0.044 | 0.092 | 0.981 | −27.53 | 0.957 |
| CHO | 0.028 | 0.094 | 0.980 | −27.75 | 0.951 |
| NO | 0.043 | 0.091 | 0.981 | −26.27 | 0.922 |
| NN+ | 0.078 | 0.079 | 0.955 | −25.29 | 0.861 |
As expected, SDAI assigns the maximum value (1.0) to unsubstituted benzene. Substituents reduce aromaticity to varying degrees. The NN+ group has the strongest effect (SDAI = 0.861), consistent with other indices, as its electron-withdrawing and negative inductive effects synergistically reduce delocalization. Other strong electron-withdrawing groups, like NO, generally also induce large decreases. In contrast, substituents such as NH2, which possess a strong electron-donating resonance effect that partially compensates for its inductive effect, cause a smaller reduction in aromaticity (SDAI = 0.973). Other groups with weaker electronic effects, like CH3 and OH, yield SDAI values close to 1.0 (0.985 and 0.981, respectively), reflecting their minimal impact on π-electron delocalization.
The trends obtained with SDAI are in line with those from the other indices listed in Table 3, fulfilling the reliability criterion mentioned above. HOMA follows these trends as well, except for NO2, which shows a slightly higher value than benzene, although the difference is minimal (0.005).
These findings support SDAI as a reliable tool for assessing aromaticity in substituted benzenes and detecting subtle changes in electron delocalization. They also underscore the benzene π-system's resistance to substituent-induced perturbations, explaining its remarkable stability and central role in organic chemistry.
| X | HOMAa | MCIa | I NB | NICS(1)zzb | SDAIc |
|---|---|---|---|---|---|
| a From ref. 16. b Calculated at B3LYP/aug-cc-pVTZ. c Calculated at B3LYP/cc-pVTZ. | |||||
| Pentafulvenes | |||||
| NH2+ | −0.83 | −0.008 | −0.0304 | 32.34 | −1.531 |
| O | −1.50 | −0.002 | −0.0231 | 13.45 | −0.516 |
| NH | −0.81 | 0.003 | 0.0258 | 4.67 | −0.254 |
| CH2 | −0.28 | 0.012 | 0.0330 | −4.55 | −0.014 |
| BH2− | 0.48 | 0.051 | 0.0441 | −26.04 | 0.584 |
| Heptafulvenes | |||||
| NH2+ | 0.80 | 0.036 | 0.0327 | −15.04 | 0.643 |
| O | 0.27 | 0.018 | 0.0297 | −6.25 | 0.379 |
| NH | 0.21 | 0.014 | 0.0286 | 4.77 | 0.192 |
| CH2 | 0.16 | 0.011 | 0.0275 | 19.29 | −0.038 |
| BH2− | 0.02 | 0.003 | 0.0224 | 102.20 | −1.339 |
For pentafulvenes, electron-donating substituents enhance aromaticity by stabilizing the 6-π electron form, while electron-withdrawing substituents reduce it by favoring the 4-π electron form. In contrast, in heptafulvenes electron-donating substituents reduce aromaticity by stabilizing the 8π form, whereas electron-withdrawing ones increase it by promoting the 6-π structure.
The SDAI values for the pentafulvenes indicate increasing aromaticity in the order: NH2+ < O < NH < CH2 < BH2−. These results agree with the substituents' electronic properties: X = BH2− leads to aromatic character, X = CH2 and NH to non-aromaticity, and X = O and NH2+ to antiaromaticity. The same order is obtained from the NICS(1)zz, MCI, and INB indices. The HOMA index yields a nearly identical trend but swaps the order for X = NH2+ and X = O. Nonetheless, all indices agree in classifying these two compounds as antiaromatic. Thus, the proposed SDAI index successfully quantifies the aromaticity of both penta- and heptafulvenes.
| Compounds | Ring | HOMAa | PDIb | FLUc | SDAId |
|---|---|---|---|---|---|
| a Calculated at B3LYP/6-311++g(d,p) as implemented in the Multiwfn program. b Calculated at HF/cc-pVTZ. c From ref. 106, except A.10 for ref. 63 and A.16 for ref. 107. d Calculated at B3LYP/cc-pVTZ. | |||||
| A.5 | I | 0.981 | 0.100 | 0.000 | 1.000 |
| A.8 | I | 0.769 | 0.073 | 0.009 | 0.741 |
| A.9 | I/III | 0.854 | 0.081 | 0.005 | 0.837 |
| II | 0.433 | 0.044 | 0.019 | 0.667 | |
| A.10 | I/IV | 0.804 | 0.078 | 0.008 | 0.806 |
| II/III | 0.541 | 0.052 | 0.019 | 0.711 | |
| A.11 | I/III/IV | 0.889 | 0.085 | 0.003 | 0.886 |
| II | 0.047 | 0.026 | 0.023 | 0.773 | |
| A.12 | I/III | 0.854 | 0.072 | 0.006 | 0.859 |
| II/IV | 0.579 | 0.039 | 0.018 | 0.640 | |
| A.13 | I | 0.664 | 0.083 | 0.013 | 0.421 |
| II | −1.570 | 0.063 | −0.833 | ||
| A.14 | I/III | 0.755 | 0.067 | 0.010 | 0.589 |
| II/IV | −0.164 | 0.040 | −0.037 | ||
| A.15 | I | 0.515 | 0.010 | 0.705 | |
| II | 0.278 | 0.015 | 0.662 | ||
| A.16 | I | −0.381 | 0.046 | −2.439 | |
In most cases, the SDAI agrees with the other indices in identifying the most aromatic ring within each system. As expected, SDAI indicates that naphthalene rings (A.8) are less aromatic than benzene. For PAHs with a single Clar structure (A.9, A.11, A.12), SDAI assigns higher aromaticity to rings with π-sextets, in accordance with Clar's rule. Thus, SDAI correctly shows that in phenanthrene (A.9), the outer rings are more aromatic than the inner one, while in pyrene (A.12) rings I and III are more aromatic than II and IV, a finding consistent with the other indices.
For triphenylene (A.11), SDAI yields values of 0.886 and 0.773 for the outer and inner rings, respectively, both within the aromatic range but showing the expected higher aromaticity of the outer rings. The deviations from benzene's aromaticity (0.114 and 0.228) indicate that the inner ring deviates twice as much as the outer ones, though both remain relatively small. SDAI also identifies the lateral rings (I, IV) of chrysene (A.10) as more aromatic than the inner ones (II, III), a finding consistent with the other indices.
In benzocyclobutadiene (A.13), SDAI and HOMA indicate moderate aromaticity for the six-membered ring, whereas PDI and FLU assign higher aromaticity. Additionally, the SDAI value of the four-membered ring (−0.833) indicates antiaromaticity, in line with the other indices.
For compound A.14, SDAI suggests moderate aromaticity for the six-membered rings, while HOMA, PDI, and FLU indicate stronger aromatic character. All indices agree on the non-antiaromatic nature of its five-membered rings.
Regarding azulene (compound A.15), the SDAI and FLU values indicate that the seven-membered ring is more aromatic than the five-membered one, both exhibiting significant aromatic character. In contrast, the HOMA index also identifies the seven-membered ring as the more aromatic ring but assigns it only a moderate aromatic character and an even smaller one to the five-membered ring.
Furthermore, the SDAI value calculated for the 10 π-electron perimeter of azulene (0.820) reveals that the external circuit is more aromatic than the individual five- and seven-membered rings, confirming the predominance of the 10 π-electron perimeter aromaticity recently reported by Dunlop et al.108 For naphthalene, the SDAI value obtained for its 10 π-electron perimeter (0.737) is comparable to those of the individual six-membered rings, in good agreement with the findings of Bakouri et al.,109 where EDDB analysis showed delocalization percentages of 46.8% for the perimeter and 41.3% for each ring.
Finally, the SDAI value for the five-membered rings of pentalene (A.16) indicates that it is a markedly antiaromatic compound, as expected. This result is also supported by the other aromaticity indices analyzed in this study.
| Compounds | NICS(1)zzab | J(r)a |
I
NG × 103![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) f f |
FLUbc | MCIbd | SDAIe |
|---|---|---|---|---|---|---|
| a From ref. 29. b From ref. 55. c From ref. 63. d From ref. 16. e Calculated at UB3LYP/cc-pVTZ. f I NG values are reported multiplied by 103, following the convention of Zhao et al.29 | ||||||
| A.5 | −28.7 | 11.7 | 41.3 | 0.000 | 0.072 | 1.000 |
| A.17 | −25.7 | 10.1 | 11.9 | −0.181 | ||
| A.18 | −25.5 | 10.3 | 11.4 | 0.058 | ||
| A.19 | −32.4 | 0.001 | 0.0275 | 0.671 | ||
| A.20 | −19.3 | 0.237 | 0.0016 | 0.272 | ||
| A.21 | −16.6 | — | 0.053 | 0.0013 | −0.173 | |
Frenking and co-workers29 showed that the 10 π-electron planar systems (N6H6)2+ (A.17) and C4N2H6 (A.18) are not minima on their respective potential energy surfaces (PES), lying 82.0 and 115.5 kcal mol−1 above their most stable acyclic isomers. Nevertheless, magnetic descriptors—NICS(1)zz and current intensity J(r), along with induced current density maps29—indicate that these species sustain a strong diamagnetic ring current comparable to that of benzene, suggesting a high degree of aromaticity. By contrast, the electron delocalization index ING values for A.5, A.17, and A.18 (41.3, 11.9, and 11.4, respectively) show that π-delocalization in (N6H6)2+ and C4N2H6 is much weaker than in benzene. The SDAI values of −0.181 and 0.058, respectively, further suggest that these systems are not aromatic, in agreement with the energetic and electronic criteria reported in ref. 29.
In a recent study, Ottosson and co-workers55 compared the Baird aromaticity110–113 of cyclooctatetraene (A.19) and its BN/CC isosteres B4N4COT-A (A.20) and B4N4COT-B (A.21) in their lowest triplet states (T1). They found that in A.20 and A.21 the magnetic descriptors diverge from the electronic and energetic ones. At T1, both isomers adopt highly symmetric and planar structures similar to A.19; however, 3B4N4COT-A is 128.7 kcal mol−1 lower in energy than 3B4N4COT-B.55 The energetic aspects have been thoroughly discussed in ref. 55; here we simply note that they indicate 3COT is clearly aromatic, whereas 3B4N4COT-A and 3B4N4COT-B are non-aromatic. Regarding the electronic aspect, Ottosson et al. employed the FLU and MCI indices, whose values are listed in Table 7. Both indices classify 3COT as aromatic and the two isomers as non-aromatic. The SDAI values for 3COT, 3B4N4COT-A, and 3B4N4COT-B are 0.671, 0.272, and −0.173, respectively, confirming that 3COT is aromatic, while the two isosteres are non-aromatic. In agreement with energetic data and the MCI index, the SDAI values also reflect the lower stability of 3B4N4COT-B relative to 3B4N4COT-A.
This analysis shows that for molecules where traditional magnetic descriptors diverge from electronic and energetic ones, SDAI reproduces the trends predicted by the latter criteria.
5. Conclusions
In this work, we introduce a new aromaticity index based on the SD contribution to one-bond spin–spin coupling constants, designed to quantify local aromaticity in cyclic and polycyclic systems—the SDAI index. Beyond proposing an additional numerical descriptor, our goal was to reveal a physical manifestation of aromaticity by linking it to an objective NMR parameter—the JSD term. This index demonstrates, for the first time, that aromaticity can be interpreted through a specific magnetic interaction: the coupling between nuclear magnetic moments mediated by delocalized π-electrons.The SD term is computationally straightforward to evaluate. Using the B3LYP, B3P86, and PBE functionals in conjunction with the ccJ-pVTZ basis set, we achieved excellent agreement with experimental J-coupling values for C–C bonds of different hybridizations (sp3–sp3, sp3–sp2, and sp2–sp2). Moreover, calculations with the standard cc-pVTZ basis set reproduced the JSD results obtained with the specialized ccJ-pVTZ and aug-cc-pVTZ sets, showing that SDAI can be efficiently computed with widely available quantum-chemical tools.
We examined the SD, PSO, and FC contributions to nJ(C,C), with n ranging from one to seven bonds, in both linear and cyclic compounds comprising saturated and unsaturated systems. We found that only the SD term reflects extended conjugation, showing distinctive value patterns that allow the detection of aromaticity. Our results show that in polyenes, long-range couplings such as 5J(C1,C6) and 7J(C1,C8) are dominated by the SD term, contrary to earlier studies that neglected this contribution.
We found that the SD contribution to 1J(M,N) acts as a sensitive probe of the magnetic uniformity of the π-system, revealing how electrons transmit spin polarization between adjacent nuclei. In aromatic rings, this response is collective and uniform, yielding 1JSD(M,N) values close to those of benzene. In contrast, nonaromatic and antiaromatic systems display irregular spin polarization, producing large bond-to-bond variations in 1JSD(M,N), which may become negative, vanish, or exceed 4 Hz. A uniform spin-polarization pattern is therefore a necessary but not sufficient condition for aromaticity: when the resulting 1JSD(M,N) values differ significantly from those of benzene—as in the dication [N6H6]2+—the system remains nonaromatic, even though it sustains diatropic ring currents. The SDAI index correctly classifies such systems as nonaromatic.
For a representative series of compounds—including five-membered heterocycles, mono-substituted benzenes, substituted fulvenes and heptafulvenes, and polycyclic hydrocarbons containing both benzenoid and non-benzenoid rings—we show that SDAI reproduces the aromaticity order obtained from established indices such as HOMA, NICS(1)zz, PDI, and FLU. More importantly, in molecules where magnetic descriptors diverge from electronic and energetic ones, SDAI follows the trends of the latter, confirming its reliability as a physically grounded measure of aromaticity.
Unlike most traditional indices based on geometry, energy, or magnetic shielding, SDAI is founded on a physical basis that enables it to detect subtle variations in aromatic character, particularly in ambiguous systems where conventional descriptors may fail. Consequently, SDAI offers a new and complementary perspective that integrates the magnetic and electronic aspects of aromaticity into a single, accessible property.
Our findings demonstrate that the proposed index not only provides additional quantitative information but also deepens our understanding of aromaticity by unveiling a direct quantum-physical manifestation of this phenomenon—one that bridges nuclear magnetic interactions with the delocalized π-electron framework of aromatic systems.
Conflicts of interest
There are no conflicts of interest to declare.Data availability
The data that supports the findings of this study are available within the article and its supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5cp02867a.Acknowledgements
Grants from Universidad Nacional de San Luis (UNSL-Argentina) (PROICO: 02-1418) partially supported this work. Ayelen Schiel acknowledges a post-doctoral fellowship of the CONICET-Argentina. M. N. C. Z.; H. A. B and R. D. E. are members of CIC-CONICET (Consejo Nacional de Investigaciones Científicas y Técnicas).References
- Arene Chemistry: Reaction Mechanisms and Methods for Aromatic Compounds, ed. J. Mortier, John Wiley & Sons, Hoboken, 2016 Search PubMed.
- A. F. Pozharskii, A. T. Soldatenkov and A. R. Katritzky, Heterocycles in Life and Society: An Introduction to Heterocyclic Chemistry, Biochemistry and Applications, John Wiley & Sons, Chichester, 2nd edn, 2011 Search PubMed.
- Structure, Bonding and Reactivity of Heterocyclic Compounds, ed. F. De Proft and P. Geerlings, Springer, Verlag Berlin Heidelberg, Heidelberg, 2014 Search PubMed.
- T. J. Ritchie and S. J. F. MacDonald, Physicochemical descriptors of aromatic character and their use in drug discovery, J. Med. Chem., 2014, 57, 7206–7215 CrossRef CAS PubMed.
- T. M. Krygowski, H. Szatylowicz, O. A. Stasyuk, J. Dominikowska and M. Palusiak, Aromaticity from the viewpoint of molecular geometry: Application to planar systems, Chem. Rev., 2014, 114, 6383–6422 CrossRef CAS PubMed.
- K. P. Vuayalakshmi and C. H. Suresh, Theoretical studies on the carcinogenicity of polycyclic aromatic hydrocarbons, J. Comput. Chem., 2008, 29, 1808–1817 CrossRef PubMed.
- J. D. Hepworth, D. R. Waring and M. J. Waring, Aromatic Chemistry, The Royal Society of Chemistry, Cambridge, 2002 Search PubMed.
- Q. Li, Y. Zhang, Z. Xie, Y. Zhen, W. Hu and H. Dong, Polycyclic aromatic hydrocarbon-based organic semiconductors: ring-closing synthesis and optoelectronic properties, J. Mater. Chem. C, 2022, 10, 2411–2430 RSC.
- J. E. Anthony, Functionalized acenes and heteroacenes for organic electronics, Chem. Rev., 2006, 106, 5028–5048 CrossRef CAS PubMed.
- S. Kilaru, R. Gade, Y. Bhongiri, A. Tripathi, P. Chetti and S. Pola, Organic materials based on hetero polycyclic aromatic hydrocarbons for organic thin-film transistor applications, Mater. Sci. Semicond. Process., 2022, 147, 106730 CrossRef CAS.
- H. Szatylowicz, O. A. Stasyuk, M. Solà and T. M. Krygowski, Aromaticity of nucleic acid bases, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2021, 11, e1509 CAS.
- Z. Badri and C. Foroutan-Nejad, Unification of ground-state aromaticity criteria – structure, electron delocalization, and energy – in light of the quantum chemical topology, Phys. Chem. Chem. Phys., 2016, 18, 11693–11699 RSC.
- A. Stanger, NICS – Past and Present, Eur. J. Org. Chem., 2020, 3120–3127 CrossRef CAS.
- R. Gershoni-Poranne and A. Stanger, Magnetic criteria of aromaticity, Chem. Soc. Rev., 2015, 44, 6597–6615 RSC.
- F. Feixas, E. Matito, J. Poater and M. Solà, Quantifying aromaticity with electron delocalisation measures, Chem. Soc. Rev., 2015, 44, 6434–6451 RSC.
- F. Feixas, E. Matito, J. Poater and M. Solà, On the performance of some aromaticity indices: a critical assessment using a test set, J. Comput. Chem., 2008, 29, 1543–1554 CrossRef CAS PubMed.
- Z. Chen, C. S. Wannere, C. Corminboeuf, R. Puchta and P. von R. Schleyer, Nucleus-Independent Chemical Shifts (NICS) as an Aromaticity Criterion, Chem. Rev., 2005, 105, 3842–3888 CrossRef CAS PubMed.
- M. K. Cyrański, Energetic aspects of cyclic pi-electron delocalization: Evaluation of the methods of estimating aromatic stabilization energies, Chem. Rev., 2005, 105, 3773–3811 CrossRef PubMed.
- A. T. Balaban, D. C. Oniciu and A. R. Katritzky, Aromaticity as a cornerstone of heterocyclic chemistry, Chem. Rev., 2004, 104, 2777–2812 CrossRef CAS PubMed.
- M. Randić, Aromaticity of Polycyclic Conjugated Hydrocarbons, Chem. Rev., 2003, 103, 3449–3605 CrossRef PubMed.
- P. Von Ragué Schleyer, Introduction: Aromaticity, Chem. Rev., 2001, 101, 1115–1117 CrossRef PubMed.
- G. Merino, M. Solà, I. Fernández, C. Foroutan-Nejad, P. Lazzeretti, G. Frenking, H. L. Anderson, D. Sundholm, F. P. Cossío, M. A. Petrukhina, J. Wu, J. I. Wu and A. Restrepo, Aromaticity: Quo Vadis, Chem. Sci., 2023, 14, 5569–5576 RSC.
- H. Ottosson, A focus on aromaticity: fuzzier than ever before?, Chem. Sci., 2023, 14, 5542–5544 RSC.
- G. Frenking and A. Krapp, Unicorns in the world of chemical bonding models, J. Comput. Chem., 2007, 28, 15–24 CrossRef CAS PubMed.
- T. M. Krygowski and M. K. Cyrański, Structural Aspects of Aromaticity, Chem. Rev., 2001, 101, 1385–1419 CrossRef CAS PubMed.
- M. K. Cyrañski, T. M. Krygowski, A. R. Katritzky and P. V. R. Schleyer, To what extent can aromaticity be defined uniquely?, J. Org. Chem., 2002, 67, 1333–1338 CrossRef PubMed.
- A. R. Katritzky, M. Karelson, S. Sild, T. M. Krygowski and K. Jug, Aromaticity as a Quantitative Concept. 7. Aromaticity Reaffirmed as a Multidimensional Characteristic, J. Org. Chem., 1998, 63, 5228–5231 CrossRef CAS.
- P. J. Mayer and H. Ottosson, False Identification of (Anti)aromaticity in Polycyclic Molecules in Ground and Excited States Through Incorrect Use of NICS, J. Phys. Org. Chem., 2025, 38, e70000 CrossRef CAS.
- L. Zhao, R. Grande-Aztatzi, C. Foroutan-Nejad, J. M. Ugalde and G. Frenking, Aromaticity, the Hückel 4n + 2 Rule and Magnetic Current, ChemistrySelect, 2017, 2, 863–870 CrossRef CAS.
- R. C. Benson, C. L. Norris, W. H. Flygare and P. Beak, A Classification of 2- and 4-Pyrone as Nonaromatic on the Basis of Molecular Magnetic Suscepttbility Anisotropies, J. Am. Chem. Soc., 1971, 93, 5591–5593 CrossRef CAS.
- W. H. Flygare, Magnetic interactions in molecules and an analysis of molecular electronic charge distribution from magnetic parameters, Chem. Rev., 1974, 74, 653–687 CrossRef CAS.
- D. H. Sutter and W. H. Flygare, Molecular g Values, Magnetic Suscepttbility Anisotropies, Second Moment of the Charge Distribution, and Molecular Quadrupole Moments in Ethylenimine and Pyrrole, J. Am. Chem. Soc., 1969, 91, 6895–6902 CrossRef CAS.
- H. J. Dauben, J. D. Wilson and J. L. Laity, Diamagnetic Susceptibility Exaltation as a Criterion of Aromaticity, J. Am. Chem. Soc., 1968, 90, 811–813 CrossRef CAS.
- H. J. Dauben, J. D. Wilson and J. L. Laity, Diamagnetic Susceptibility Exaltation in Hydrocarbons, J. Am. Chem. Soc., 1969, 91, 1991–1998 CrossRef CAS.
- F. De Proft and P. Geerlings, Conceptual and computational DFT in the study of aromaticity, Chem. Rev., 2001, 101, 1451–1464 CrossRef CAS PubMed.
- R. H. Mitchell, Measuring Aromaticity by NMR, Chem. Rev., 2001, 101, 1301–1316 CrossRef CAS PubMed.
- R. V. Williams, W. D. Edwards, P. Zhang, D. J. Berg and R. H. Mitchell, Experimental verification of the homoaromaticity of 1,3,5-cycloheptatriene and evaluation of the aromaticity of tropone and the tropylium cation by use of the dimethyldihydropyrene probe, J. Am. Chem. Soc., 2012, 134, 16742–16752 CrossRef CAS PubMed.
- C. Foroutan-Nejad, Interatomic Magnetizability: A QTAIM-Based Approach toward Deciphering Magnetic Aromaticity, J. Phys. Chem. A, 2011, 115, 12555–12560 CrossRef CAS PubMed.
- S. Coriani, P. Lazzeretti, M. Malagoli and R. Zanasi, On CHF calculations of second-order magnetic properties using the method of continuous transformation of origin of the current density, Theor. Chim. Acta, 1994, 89, 181–192 CrossRef CAS.
- P. Lazzeretti, M. Malagoli and R. Zanasi, Computational approach to molecular magnetic properties by continuous transformation of the origin of the current density, Chem. Phys. Lett., 1994, 220, 299–304 CrossRef CAS.
- A. Ghosh, S. Larsen, J. Conradie and C. Foroutan-Nejad, Local versus global aromaticity in azuliporphyrin and benziporphyrin derivatives, Org. Biomol. Chem., 2018, 16, 7964–7970 RSC.
- R. Zanasi, Coupled Hartree–Fock calculations of molecular magnetic properties annihilating the transverse paramagnetic current density, J. Chem. Phys., 1996, 105, 1460–1469 CrossRef CAS.
- E. Steiner and P. W. Fowler, Patterns of ring currents in conjugated molecules: a few-electron model based on orbital contributions, J. Phys. Chem. A, 2001, 105, 9553–9562 CrossRef CAS.
- P. Lazzeretti, Assessment of aromaticity via molecular response properties, Phys. Chem. Chem. Phys., 2004, 6, 217–223 RSC.
- D. Geuenich, K. Hess, F. Köhler and R. Herges, Anisotropy of the induced current density (ACID), a general method to quantify and visualize electronic delocalization, Chem. Rev., 2005, 105, 3758–3772 CrossRef CAS PubMed.
- J. Jusélius, D. Sundholm and J. Gauss, Calculation of current densities using gauge-including atomic orbitals, J. Chem. Phys., 2004, 121, 3952–3963 CrossRef PubMed.
- H. Fliegl, S. Taubert, O. Lehtonen and D. Sundholm, The gauge including magnetically induced current method, Phys. Chem. Chem. Phys., 2011, 13, 20500–20518 RSC.
- D. Sundholm, H. Fliegl and R. J. F. Berger, Calculations of magnetically induced current densities: theory and applications, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2016, 6, 639–678 CAS.
- S. Pathak, R. Bast and K. Ruud, Multiconfigurational Self-Consistent Field Calculations of the Magnetically Induced Current Density Using Gauge-Including Atomic Orbitals, J. Chem. Theory Comput., 2013, 9, 2189–2198 CrossRef CAS PubMed.
- E. Paenurk and R. Gershoni-Poranne, Simple and efficient visualization of aromaticity: bond currents calculated from NICS values, Phys. Chem. Chem. Phys., 2022, 24, 8631–8644 RSC.
- P. Bultinck, S. Fias and R. Ponec, Local Aromaticity in Polycyclic Aromatic Hydrocarbons: Electron Delocalization versus Magnetic Indices, Chem. – Eur. J., 2006, 8813–8818 CrossRef CAS PubMed.
- Y. C. Lin, D. Sundholm and J. Jusélius, On the Aromaticity of the Planar Hydrogen-Bonded (HF)3 Trimer, J. Chem. Theory Comput., 2006, 2, 761–764 CrossRef CAS PubMed.
- Z. Badri, S. Pathak, H. Fliegl, P. Rashidi-Ranjbar, R. Bast, R. Marek, C. Foroutan-Nejad and K. Ruud, All-Metal Aromaticity: Revisiting the Ring Current Model among Transition Metal Clusters, J. Chem. Theory Comput., 2013, 9, 4789–4796 CrossRef CAS PubMed.
- C. Foroutan-Nejad, Is NICS a reliable aromaticity index for transition metal clusters?, Theor. Chem. Acc., 2015, 134, 1–9 Search PubMed.
- P. Preethalayam, N. Proos Vedin, S. Radenković and H. Ottosson, Azaboracyclooctatetraenes reveal that the different aspects of triplet state Baird-aromaticity are nothing but different, J. Phys. Org. Chem., 2023, 36, e4455 CrossRef CAS.
- C. Foroutan-Nejad, Magnetic Antiaromaticity—Paratropicity—Does Not Necessarily Imply Instability, J. Org. Chem., 2023, 88, 14831–14835 CrossRef CAS PubMed.
- T. Janda and C. Foroutan-Nejad, Why is Benzene Unique? Screening Magnetic Properties of C6H6 Isomers, ChemPhysChem, 2018, 19, 2357–2363 CrossRef CAS PubMed.
- S. Shaik, A. Shurki, D. Danovich and P. C. Hiberty, A Different Story of π-DelocalizationThe Distortivity of π-Electrons and Its Chemical Manifestations, Chem. Rev., 2001, 101, 1501–1539 CrossRef CAS PubMed.
- J. P. Malrieu, M. Giequel, P. W. Fowler, C. Lepetit, J. L. Heully and R. Chauvin, Direct Evaluation of Cyclic Contributions to the π Energy of Conjugated Hydrocarbons from Strongly Localized Zero-Order Pictures†, J. Phys. Chem. A, 2008, 112, 13203–13214 CrossRef CAS PubMed.
- C. Angeli and J. P. Malrieu, Aromaticity: an ab Initio Evaluation of the Properly Cyclic Delocalization Energy and the π-Delocalization Energy Distortivity of Benzene, J. Phys. Chem. A, 2008, 112, 11481–11486 CrossRef CAS PubMed.
- J. Jara-Cortés and J. Hernández-Trujillo, Energetic Analysis of Conjugated Hydrocarbons Using the Interacting Quantum Atoms Method, J. Comput. Chem., 2018, 39, 1103–1111 CrossRef PubMed.
- J. Poater, X. Fradera, M. Duran and M. Solà, The delocalization index as an electronic aromaticity criterion: Application to a series of planar polycyclic aromatic hydrocarbons, Chem. – Eur. J., 2003, 9, 400–406 CrossRef CAS PubMed.
- E. Matito, M. Duran and M. Solà, The aromatic fluctuation index (FLU): a new aromaticity index based on electron delocalization, J. Chem. Phys., 2005, 122, 014109 CrossRef PubMed.
- D. W. Szczepanik, M. Andrzejak, J. Dominikowska, B. Pawełek, T. M. Krygowski, H. Szatylowicz and M. Solà, The electron density of delocalized bonds (EDDB) applied for quantifying aromaticity, Phys. Chem. Chem. Phys., 2017, 19, 28970–28981 RSC.
- M. Máximo-Canadas, R. S. S. Oliveira, M. A. S. Oliveira and I. Borges, A New Set of Aromaticity Descriptors Based on the Electron Density Employing the Distributed Multipole Analysis (DMA), ACS Omega, 2025, 10, 14157–14175 CrossRef PubMed.
- H. Günther, NMR Spectroscopy. Basic Principles, Concepts, and Applications in Chemistry, Wiley-VCH, Weinheim, Germany, 3rd edn, 2013 Search PubMed.
- T. Helgaker, M. Jaszunski and K. Ruud, Ab Initio Methods for the Calculation of NMR Shielding and Indirect Spin − Spin Coupling Constants, Chem. Rev., 1999, 99, 293–352 CrossRef CAS PubMed.
- Calculation of NMR and EPR Parameters. Theory and Applications, ed. M. Kaupp, M. Bühl and G. Malkin Vladimir, Wiley-VCH, Weinheim, 2004 Search PubMed.
- T. Helgaker, M. Jaszuński and M. Pecul, The quantum-chemical calculation of NMR indirect spin–spin coupling constants, 2008 Search PubMed.
- L. B. Krivdin, Carbon–carbon spin–spin coupling constants: practical applications of theoretical calculations, Prog. Nucl. Magn. Reson. Spectrosc., 2018, 105, 54–99 CrossRef CAS PubMed.
- N. F. Ramsey, Electron coupled interactions between nuclear spins in molecules, Phys. Rev., 1953, 91, 303–307 CrossRef CAS.
- J. Gräfenstein and D. Cremer, Analysis of the paramagnetic spin–orbit transmission mechanism for NMR spin–spin coupling constants using the paramagnetic spin–orbit density distribution, Chem. Phys. Lett., 2004, 383, 332–342 CrossRef.
- J. Gräfenstein and D. Cremer, Analysis of the spin–dipole transmission mechanism for NMR spin–spin coupling constants using orbital contributions, spin polarization, and spin–dipole energy density distribution, Chem. Phys. Lett., 2004, 387, 415–427 CrossRef.
- D. Cremer, E. Kraka, A. Wu and W. Lüttke, Can One Assess theπ Character of a C–C Bond with the Help of the NMR Spin–Spin Coupling Constants?, ChemPhysChem, 2004, 5, 349–366 CrossRef CAS PubMed.
- P. F. Provasi, G. A. Aucar and S. P. A. Sauer, Large long-range F–F indirect spin-spin coupling constants. Prediction of measurable F–F couplings over a few nanometers, J. Phys. Chem. A, 2004, 108, 5393–5398 CrossRef CAS.
- J. Gräfenstein and D. Cremer, Unusual long-range spin–spin coupling in fluorinated polyenes: a mechanistic analysis, J. Chem. Phys., 2007, 127, 174704 CrossRef PubMed.
- M. N. C. Zarycz, M. A. Schiel, E. Angelina and R. D. Enriz, Covalence and π-electron delocalization influence on hydrogen bonds in proton transfer process of o-hydroxy aryl Schiff bases: a combined NMR and QTAIM analysis, J. Chem. Phys., 2021, 155, 054307 CrossRef CAS PubMed.
- M. Randić, Aromaticity Revisited, Adv. Quantum Chem., 2018, 77, 167–199 CrossRef.
- J. Olsen and P. Jørgensen, Linear and nonlinear response functions for an exact state and for an MCSCF state, J. Chem. Phys., 1985, 82, 3235–3264 CrossRef CAS.
- O. Vahtras, H. Ågren, P. Jørgensen, H. J. A. Jensen, S. B. Padkjær and T. Helgaker, Indirect nuclear spin–spin coupling constants from multiconfiguration linear response theory, J. Chem. Phys., 1992, 96, 6120–6125 CrossRef CAS.
- M. A. Watson, P. Sałek, P. Macak, M. Jaszuński and T. Helgaker, The calculation of indirect nuclear spin–spin coupling constants in large molecules, Chem. – Eur. J., 2004, 10, 4627–4639 CrossRef CAS PubMed.
- W. Kohn and L. J. Sham, Self-consistent equations including exchange and correlation effects, Phys. Rev., 1965, 140, 1133–1138 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, N. J. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 16 Revision C.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, Effect of the Damping Function in Dispersion Corrected Density Functional Theory, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, Self-consistent molecular orbital methods. XX. A basis set for correlated wave functions, J. Chem. Phys., 1980, 72, 650–654 CrossRef CAS.
- A. D. Becke, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. P. Perdew, Density-functional approximation for the correlation energy of the inhomogeneous electron gas, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 CrossRef PubMed.
- P. F. Provasi, G. A. Aucar and S. P. A. Sauer, The effect of lone pairs and electronegativity on the indirect nuclear spin–spin coupling constants in CH2X (X = CH2, NH, O, S): Ab initio calculations using optimized contracted basis sets, J. Chem. Phys., 2001, 115, 1324–1334 CrossRef CAS.
- U. Benedikt, A. A. Auer and F. Jensen, Optimization of augmentation functions for correlated calculations of spin-spin coupling constants and related properties, J. Chem. Phys., 2008, 129, 064111 CrossRef PubMed.
- T. H. Dunning Jr, Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
- K. Wolinski, J. F. Hinton and P. Pulay, Efficient Implementation of the Gauge-Independent Atomic Orbital Method for NMR Chemical Shift Calculations, J. Am. Chem. Soc., 1990, 112, 8251–8260 CrossRef CAS.
- J. R. Cheeseman, G. W. Trucks, T. A. Keith and M. J. Frisch, A comparison of models for calculating nuclear magnetic resonance shielding tensors, J. Chem. Phys., 1996, 104, 5497–5509 CrossRef CAS.
- R. F. W. Bader, Atoms in Molecules A Quantum Theory, Oxford University Press, Oxford, 1994 Search PubMed.
- T. Lu and F. Chen, Multiwfn: a multifunctional wavefunction analyzer, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- K. Kamieńska-Trela and J. Wójcik, High Resolution NMR Spectroscopy: Understanding Molecules and their Electronic Structures, Elsevier, Oxford, 2013, pp. 347–424 Search PubMed.
- R. Suardíaz, C. Pérez, R. Crespo-Otero, J. M. G. De La Vega and J. S. Fabián, Influence of density functionals and basis sets on one-bond carbon-carbon NMR spin-spin coupling constants, J. Chem. Theory Comput., 2008, 4, 448–456 CrossRef PubMed.
- H. Kjr, S. P. A. Sauer and J. Kongsted, Benchmarking NMR indirect nuclear spin-spin coupling constants: SOPPA, SOPPA(CC2), and SOPPA(CCSD) versus CCSD, J. Chem. Phys., 2010, 133, 144106 CrossRef PubMed.
- J. Gräfenstein, T. Tuttle and D. Cremer, Analysis of long-range NMR spin–spin coupling in polyenes and the π-mechanism, Phys. Chem. Chem. Phys., 2005, 7, 452–462 RSC.
- S. Noorizadeh and E. Shakerzadeh, Shannon entropy as a new measure of aromaticity, Shannon aromaticity, Phys. Chem. Chem. Phys., 2010, 12, 4742–4749 RSC.
- P. Bultinck, R. Ponec and S. Van Damme, Multicenter bond indices as a new measure of aromaticity in polycyclic aromatic hydrocarbons, J. Phys. Org. Chem., 2005, 18, 706–718 CrossRef CAS.
- J. Cioslowski, E. Matito and M. Solà, Properties of Aromaticity Indices Based on the One-Electron Density Matrix, J. Phys. Chem. A, 2007, 111, 6521–6525 CrossRef CAS PubMed.
- M. Giambiagi, M. Segre De Giambiagi, C. D. Dos Santos Silva and A. Paiva De Figueiredo, Multicenter bond indices as a measure of aromaticity, Phys. Chem. Chem. Phys., 2000, 2, 3381–3392 RSC.
- J. Dominikowska and M. Palusiak, EL: the new aromaticity measure based on one-electron density function, Struct. Chem., 2012, 23, 1173–1183 CrossRef CAS.
- K. P. Sudhakaran, A. Benny, A. T. John and M. Hariharan, Exploring the influence of graphene on antiaromaticity of pentalene, Phys. Chem. Chem. Phys., 2023, 25, 26986–26990 RSC.
- D. Dunlop, L. Ludvíková, A. Banerjee, H. Ottosson and T. Slanina, Excited-state (anti) aromaticity explains why azulene disobeys Kasha's rule, J. Am. Chem. Soc., 2023, 145, 21569–21575 CrossRef CAS PubMed.
- O. El Bakouri, D. W. Szczepanik, K. Jorner, R. Ayub, P. Bultinck, M. Solà and H. Ottosson, Three-Dimensional Fully π-Conjugated Macrocycles: When 3D-Aromatic and When 2D-Aromatic-in-3D?, J. Am. Chem. Soc., 2022, 144, 8560–8575 CrossRef CAS PubMed.
- N. C. Baird, Quantum organic photochemistry. II. Resonance and aromaticity in the lowest 3.pi⋯pi.* state of cyclic hydrocarbons, J. Am. Chem. Soc., 1972, 94, 4941–4948 CrossRef CAS.
- H. Ottosson, Exciting excited-state aromaticity, Nat. Chem., 2012, 4, 969–971 CrossRef CAS PubMed.
- M. Rosenberg, C. Dahlstrand, K. Kilså and H. Ottosson, Excited State Aromaticity and Antiaromaticity: Opportunities for Photophysical and Photochemical Rationalizations, Chem. Rev., 2014, 114, 5379–5425 CrossRef CAS PubMed.
- J. Yan, T. Slanina, J. Bergman and H. Ottosson, Photochemistry Driven by Excited-State Aromaticity Gain or Antiaromaticity Relief, Chem. – Eur. J., 2023, 29, e202203748 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2025 |

