Open Access Article
Open Access ArticleThird-order nonlinear optical properties of a series of pyrroles and dipyrroles featuring π-conjugated substituents and linkers
Elisha
Bennett
a,
Adil
Alkaş
 b,
Roberto M.
Diaz-Rodriguez
b,
Roberto M.
Diaz-Rodriguez
 b,
Jacob W.
Campbell
b,
Luke A.
Ferguson
b,
Jacob W.
Campbell
b,
Luke A.
Ferguson
 b,
Michael J.
Cotnam
b,
Richard
Cisek
b,
Michael J.
Cotnam
b,
Richard
Cisek
 a,
Alison
Thompson
a,
Alison
Thompson
 *b and
Danielle
Tokarz
*b and
Danielle
Tokarz
 *a
*a
aDepartment of Chemistry, Saint Mary's University, 923 Robie Street, Halifax, Nova Scotia B3H 3C3, Canada. E-mail: Danielle.Tokarz@smu.ca
bDepartment of Chemistry, Dalhousie University, P.O. Box 15000, Halifax, Nova Scotia B3H 4J3, Canada. E-mail: Alison.Thompson@dal.ca
First published on 3rd October 2025
Abstract
The third-order nonlinear optical properties of a series of novel pyrrole-containing compounds were explored. A custom nonlinear optical microscope was used to measure the third harmonic generation (THG) intensity ratio from two interfaces of an ultrasmall cuvette: a glass–solution interface incorporating the pyrrole-containing compound, and an air–glass interface. The THG intensity ratio, along with refractive index measurements of the solution at the laser wavelength (1030 nm) and the third harmonic wavelength (343 nm), were used to calculate χ(3) values of each pyrrole-containing solution. The second hyperpolarisability γ was then extracted from concentration-dependent measurements of χ(3). Trends in the magnitude of γ for the studied pyrrole-containing compounds became apparent, including that several formyl-substituted dipyrrole derivatives exhibited elevated γ values. Further, an enhancement in γ was observed with increasing conjugation length when formyl-substituted dipyrroles with differing internal linkers were studied. Lastly, the complexation of ruthenium by a formyl-substituted dipyrrole enhanced the magnitude of the γ value by ∼3 to ∼300 times, depending on the dipyrrole derivative. These trends can be used to understand the chemical features needed for the emergent development of dyes for THG microscopy.
Introduction
Although principles for designing chemical frameworks exhibiting enhanced second-order nonlinear optical properties are well established, strategies for designing systems with enhanced third-order nonlinear optical properties are less evident.1 It has been observed that systems with extended π conjugation exhibit enhanced third-order nonlinear optical properties.2–4 However, systematic experimental studies investigating related systems for enhancing third-order nonlinear optical properties are scant in comparison to reports discussing second-order nonlinear optical properties.Recently, polyenes and porphyrins, including naturally-occurring carotenoids and chlorophylls, have been reported to have large third-order nonlinear optical properties, a property known as the second hyperpolarisability or γ. The second hyperpolarisability has been shown to be exponentially related to the conjugation length of the molecule, as well as the nature of substituents.5 The second hyperpolarisability has also been shown to be enhanced by charge transfer interactions between electron acceptor and electron donor groups.5
The second hyperpolarisability has been measured using several techniques, including the third harmonic generation (THG) ratio technique, z-scan, Maker fringe, degenerate four wave mixing (DFWM) and the optical Kerr effect. For the work presented herein, the THG ratio technique was chosen for its sensitivity and its utility with small sample volumes of solutions with absorption characteristics.
Carotenoids and chlorophylls were initially proposed as harmonophores, i.e., dyes for THG microscopy,6–8 due to their high THG emission and biocompatibility. β-Carotene has been used as a standard for γ measurements, exhibiting a |γ| value of 7.1 ± 0.4 × 10−41 m2 V−2 at 773 nm, 7 ± 1 × 10−41 m2 V−2 at 830 nm and 4.9 ± 0.8 × 10−41 m2 V−2 at 1028 nm.7 To develop new harmonophores capable of intense THG, systematic investigations of γ values across a range of similar organic frameworks are needed. Determination of the sign of γ is also important, given the cancellation effect on THG.8 With a more thorough fundamental understanding, the effect of conjugation length/type and electron-withdrawing/donating ability will be useful for the design of THG dyes with desired optical properties. Such insight will further enable optimisation of substituents for targeting, desired solubility, etc.
Pyrrole-containing molecules have been extensively explored for their second-order nonlinear optical properties.9–32 When used as an electron donor in a donor–acceptor system, the pyrrole unit can provide a high first hyperpolarisability (β) value while also offering thermal stability.28 However, reports focused on the third-order nonlinear optical properties of simple pyrrole-containing frameworks are limited. To the best of our knowledge, only theoretical studies of the third-order nonlinear optical properties of simple pyrrole-containing frameworks have been reported,33–43 with some focusing on complex pyrrole-containing systems such as BODIPY dyes, porphyrins and phthalocyanines. Toward the goal of better understanding third-order nonlinear optical properties for the development of THG dyes, herein we report use of the THG ratio technique to determine γ values of a series of pyrrole-containing frameworks with varying conjugated linking units.
Materials and methods
Synthesis
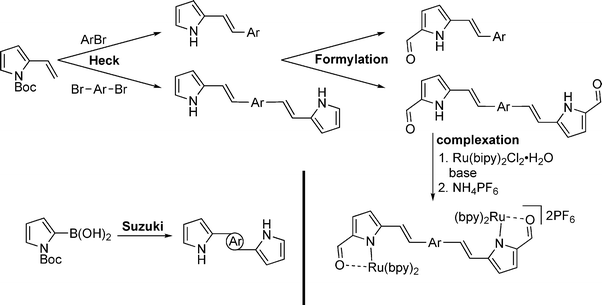
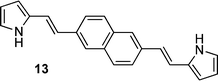
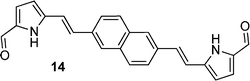
With a focus on materials suited to the incremental incorporation of conjugating moieties, the synthesis of a series of pyrrole-containing materials was targeted as shown in Fig. 1. 2-Vinyl pyrrole served as a convenient building block to which aryl groups were appended via Heck coupling. Complementing the incorporation of vinyl-aryl substituents and linkers, Suzuki coupling using 1-Boc-pyrrole-2-boronic acid enabled preparation of (di)pyrroles directly linked via aryl moieties. A series of monopyrrolic and dipyrrolic frameworks was thus generated. Formylation and subsequent complexation to Ru(II) provided a series of compounds with the incremental incorporation of conjugating moieties to enable a systematic investigation of γ values.THG ratio technique and measurements
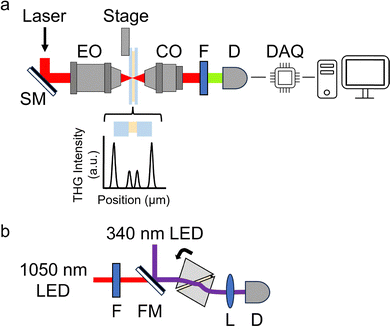
The third-order nonlinear optical properties of each of the 26 conjugated pyrroles, dissolved in THF, were measured. At least four dilutions were assessed for each pyrrole. In each case, two measurements were made: THG intensity ratio, which denotes THG emitted by each system cf. a standard (borosilicate glass); and refractive indexes, at 1030 nm and 343 nm. The spectroscopic setup enabling the THG intensity ratio measurement is unique. A focused laser spot does not generate THG from a homogenous solution, due to the Gouy phase shift. In this case, a relative π phase shift on half of the laser focal volume occurs, rendering full THG cancellation. As a result, THG is not emitted when focused in any homogenous material. However, homogenous solutions containing a harmonophore can be analysed by focusing the laser at the interface between the glass cuvette and the liquid, where the Gouy symmetry is broken. Indeed, THG is emitted when the focal spot is applied to at least two different materials with different refractive index or third-order nonlinear optical susceptibility values. In practice, the laser spot is focused at least 15 μm away from an interface, and the sample is moved in steps of 1 μm across two interfaces, i.e. an air–glass interface and the glass–solution interface, with 100 ms integration time. In this way, two THG intensity profiles are created (four are shown in the graph of Fig. 2a), and then a Gaussian fit is performed to obtain the THG intensity maxima (I in eqn (1)) and widths (b in eqn (2)).For the THG intensity ratio measurement, a nonlinear optical microscope44 was modified (Fig. 2a). A commercial femtosecond pulsed laser (FemtoLux 3, EKSPLA) provided 290 fs pulses at a wavelength of 1030 nm with a pulse repetition rate of 5 MHz. The laser was focused using a 0.25 numerical aperture (NA) air immersion microscope objective (Carl Zeiss Canada Ltd) to minimise optical aberrations from higher NA objectives.45 The THG intensity profiles of the air–glass and glass–solution interfaces were collected in transmission geometry in 1 μm steps using 100 ms integration time, and a custom 0.85 NA collection objective (Omex Technologies, Inc.). Measurements were made using a photomultiplier tube in photon counting mode (H10682-210, Hamamatsu Photonics K. K.), with a data acquisition card (PCIe-6363, NI) and custom software (LabVIEW, NI). The THG signal was filtered with a 10 nm bandwidth filter (65-129, Edmund Optics Inc.) to ensure removal of the laser light and to ensure that only THG signal was collected. However, some conjugated pyrroles are known to fluoresce. Unlike two photon absorption fluorescence at ∼515 nm or higher, which would be easily filtered, any three photon absorption fluorescence, at ∼343 nm, may pass through the 338–348 nm filter window if the Stokes shift for the solution is small. However, in this experiment the THG intensity profiles of the glass–solution interface are measured typically >20 μm past the second interface into the solution, while the THG intensity from a glass–solution interface is diminished after ∼15 μm. Therefore, signal collected when the laser focus is >15 μm inside the contents of the cuvette would indicate that three photon fluorescence is being transmitted through the filter. As such, the presence of any fluorescence is easily confirmed.
For THG intensity ratio measurements, a new capillary tube (5012, VitroCom) was used for each dilution. To minimise evaporation, individual capillary tubes, with 100 μm path lengths and 100 μm thick walls, were sealed with nail polish after introduction of the dilute sample. The capillary tubes were oriented orthogonal to the direction of laser propagation (Fig. 2a), and were translated axially along the laser focal spot using an automated translation stage (ASI) and a LabVIEW microscope control interface programmed in-house. The THG signals generated from the air–glass and glass–solution interfaces of the capillary tube closest to the collection objective were recorded at least ten times per dilution, with the air–glass interface acting as a standard. Any possibility of molecular photodegradation was avoided by ensuring that the THG intensity ratio of the air–glass and glass–solution interfaces remained constant throughout. As noted above, the THG intensities of capillary scans at least 20 μm into each dilution were verified to ensure that no fluorescence was contaminating the THG signal.
In addition to recording the THG intensity from the air–glass and glass–solution interface for each dilution, additional measurements were made using a capillary tube containing neat THF. THG intensity measurements of the air–glass and glass–solvent interfaces were obtained before the solutions of each compound of interest was studied. Measurements were also made after the analysis of the final dilution for each compound. Additionally, THG intensity measurements of the air–glass and glass–solvent interfaces were sparingly made between dilutions.
A refractometer built in-house, based on a previous model,46 was used for measuring the refractive indices of the dilutions (Fig. 2b). The refractometer contained two LED light sources (M340L4 and M1050L2, Thorlabs Inc.) centered at 340 nm and 1050 nm, respectively. The 1050 nm LED had a bandwidth of 60 nm, and therefore light at 1030 nm was obtained using a 10 nm bandwidth optical filter centred at 1030 nm (FLH1030-10, Thorlabs Inc.). The LED light was directed through each dilution of the sample of interest, which was held within a spacer and squeezed between two yttrium aluminum garnet (YAG) prisms (Red Optronics). A custom holder on a motorised rotation stage (CR1-Z7, Thorlabs Inc.) held the prisms and each sample. The light transmitted through the prisms and the sample was focused by a lens and detected by a standard CMOS camera (HD Webcam C270, Logitech). Meanwhile the custom holder was rotated, by the motorised rotation stage, until the intensity of the transmitted light diminished to half – due to total internal reflection at the prism-dilution interface.
Before each measurement, the refractive index of neat THF was determined in order to ensure reliability of the technique. This involved measuring the critical angle for THF, as well as the critical angle of a standard (distilled water). Then, the critical angle of each diluted sample, along with the critical angle of THF, was measured (at least three replicates). The refractive indices were subsequently calculated using the critical angles measured for THF and each diluted sample, and averaged across the replicates. The concentration used to determine the THG intensity ratio, for each sample, was also used for refractive index measurements.
An equation expressing the THG intensity ratio of the glass–solution and air–glass interfaces was then applied to determine the χ(3) of each dilution:47
 | (1) |
 | (2) |
 where: bTHG is the measured full-width half-maximum of the THG intensity peak generated from a glass–solution or air–glass interface. The Δk value is calculated using the expression
where: bTHG is the measured full-width half-maximum of the THG intensity peak generated from a glass–solution or air–glass interface. The Δk value is calculated using the expression  where Δn = nTHG − nlaser and λ is 1030 nm.
where Δn = nTHG − nlaser and λ is 1030 nm.
Previously published values for the χ(3) and refractive indices of Duran borosilicate glass were used where indicated.6,7 The γ value for each compound was subsequently extracted from a plot of χ(3)versus concentration using the following equation:5,48
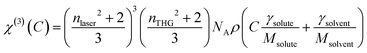 | (3) |
Results and discussion
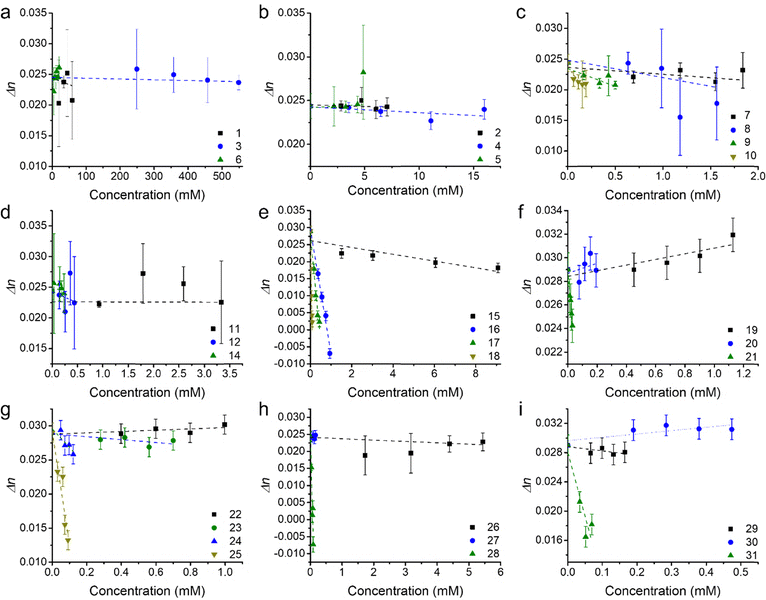
The refractive indices of the diluted samples at the THG (343 nm) and laser (1030 nm) wavelengths (nTHG and nlaser) were measured to obtain dispersion values (Δn = nTHG − nlaser) for each of the core linking units and for the monopyrrolic frameworks. Dispersion values for bromobenzene (1), 2-bromonaphthalene (3) and pyrrole-2-carboxaldehyde (6) are shown in Fig. 3a while the dispersion values for 1,4-dibromobenzene (2), naphthalene (4), and 2,6-dibromonaphthalene (5) are shown in Fig. 3b. The dispersion values for phenyl-appended pyrroles (7–8) and 1,4-phenyl-linked pyrroles (9–10) are shown in Fig. 3c, and those for the naphthyl-appended (11–12) and 2,6-naphthyl-linked pyrroles (13–14) are shown in Fig. 3d. Dispersion values for analogues of 2,1,3-benzothiadiazole (15–18), pyrene (19–21), diphenyl-2,1,3-benzothiadiazole (22–25), biphenyl (26–28) and fluorene (29–31) were similarly evaluated (Fig. 3e–i). Changes in dispersion with increased concentration are due to absorbance at the THG or laser wavelength. In general, the dispersion of the compounds decreased with increasing concentration, except for 5, 6, 19, 20, 22 and 30.The THG intensity ratio for these solutions were measured at the same concentrations as Δn (Fig. 4). Interestingly, the THG intensity ratios of the compounds decreased with increasing concentration, except for 1,4-dibromobenzene (2), 2,6-dibromonaphthalene (5) and the 2-vinyl pyrrole (7).
The refractive index and the THG intensity ratio play a role in determining the value of χ(3). Previous studies have shown that the relationship between χ(3) and increasing concentration mimics the trend in Δn with increasing concentration, when Δn changes drastically with concentration.6,8 The χ(3) values for the compounds in this study decreased with increasing concentration (Fig. 5), except for 5, 6, 19 and 30, where an increase in Δn with increasing concentration was observed. An increase in Δn with increasing concentration was also observed for 20 and 22, which were determined to have χ(3) values that decreased with increasing concentration, following the relationship between their THG intensity ratios and increasing concentration. This may be because the slope of their plots of THG intensity ratios versus concentration (Fig. 4f and g) are much larger (∼22 times larger for 20, and ∼17 times larger for 22) than the slope of their plots of Δn versus concentration (Fig. 3f and g).
The trend in χ(3) values with increasing concentration determines the sign of the extracted γ value. An increase in the value of χ(3) with increasing concentration indicates that the THG emitted by the solution has the same phase with respect to the THG emitted by the solvent, THF: this results in a positive γ value. Consequently, a decrease in the value of χ(3) with increasing concentration indicates that the THG emitted by the solution has the opposite phase with respect to the THG emitted from the solvent, THF: this results in negative γ values.
The choice of solvent is very important for these measurements, and can influence both the sign and magnitude of γ. For instance, the experimental γ values of porphyrins change depending on the solvent used. An increase in the γ value of 3–5 times was observed when porphyrins were dissolved in an acidic medium rather than a neutral medium.49 Furthermore, some porphyrins may form oligomers in nonpolar solvents, and thus electronic coupling effects between pyrrole rings may lead to increased γ values.50
The choice of solvent used herein was THF. This solvent was chosen for a number of reasons including its ability to dissolve the conjugated pyrroles. Furthermore, since THF is a moderately polar aprotic inert solvent, it is not expected that the conjugated pyrroles will oligomerise in this solvent. Cognisant of the need to reduce aggregation, dilutions were chosen such that the ratio of the THG intensity generated at the air–glass and solution–glass interfaces of the capillary tube containing the lowest dilution was aligned with the ratio of the THG intensity generated at the air–glass and solution–glass interfaces of a capillary tube with only neat THF. Since THG is sensitive to changes in refractive index, it is also sensitive to the presence of aggregates greater than ∼20 nm. Therefore, any aggregates larger than ∼20 nm that float through a focal volume during the measurement would alter the THG intensity profile, although these are easily identified and discarded. Since the THG intensity ratio measurement consisted of ten uniform profiles per dilution (i.e. for each diluted sample), any non-uniform profiles were discarded, and extra profiles were run to satisfy the total. It is noted that reduction in concentration due to the presence of the aggregates was unaccounted for. Furthermore, although the refractive index measurement is sensitive to aggregates, these effects were not removed given that the spot size in such experiments is several mm in size. The naphthyl derivative 13 was not fully soluble in THF, and measurements corresponding to this derivative may have benefitted from the use of a different solvent, or by developing a film. However, the use of films with this technique would require superb control over the uniformity of the molecular distribution within the film or a priori knowledge of this distribution.
The magnitude of the γ values of the benzene and naphthalene derivatives (1–6) are generally much smaller than those of the phenyl, naphthyl, 2,1,3-benzothiadiazole, pyrene, diphenyl-benzothiadiazole, biphenyl and fluorene derivatives with exception of 7, 11, 22 and 26. It was observed that much higher concentrations of the benzene and naphthalene derivatives were needed in order to induce an adequate THG intensity ratio difference from measurements of neat solvent (THF). In Fig. 3, the error bars of the Δn values are propagated error values from standard deviations of multiple refractive index measurements. It was observed that the errors for compounds 1–6 (Fig. 3a and b) are higher than those for the Δn values of other compounds (Fig. 4b–i). However, it is noted that the solutions of 1–6 in THF were much more concentrated than were the solutions of other compounds. Therefore, the higher error Δn values associated with these compounds may be due to the presence of small aggregates (<20 nm), or the presence of an ordered structure in solution due to π–π stacking.
Effect of bromination
The magnitude of γ for compounds 1–31 is listed in Table 1. The effect of bromo substitution on the third-order nonlinear optical properties of benzene and naphthalene were explored. A 6-fold increase in the γ value was observed when comparing naphthalene (3) and 2-bromonaphthalene (4). This observation aligns with previous findings that the addition of electron-withdrawing groups results in an increase in the value of γ.7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 8
1, 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 and 8
2 and 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, respectively, mixtures of THF
2, respectively, mixtures of THF![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMSO)
DMSO)
Stark differences are observed between the properties of bromo-substituted benzenes and bromo-substituted naphthalenes. In particular, the γ value of 1,4-dibromobenzene (2) is 50 times smaller than the γ value of bromobenzene (1), while the γ value of 2,6-dibromonaphthalene (5) is ∼8 times greater in magnitude than the γ value of 2-bromonaphthalene (4). This is likely because any enhancement in γ obtained from the addition of electron-withdrawing substituents is cancelled by their symmetrical opposition, whereas the lack of such symmetry in 2,6-dibromonaphthalene instead causes an enhancement: indeed, a higher dipole moment appears to lead to an improved THG.
Phenyl and naphthyl derivatives
The 1,4-phenyl-linked and 2,6-naphthyl-linked pyrroles and dipyrroles were next evaluated. Comparing monopyrroles 7 and 11 with their 2-formyl derivatives 8 and 12, respectively, revealed that the magnitude of γ for the formyl-substituted pyrroles is higher (Table 1), presumably as a consequence of the electron-withdrawing effect of the carbonyl. This difference is much more drastic for 12 than for 8, i.e. an increase in γ of ∼63 times rather than ∼12 times.The dipyrrole 9 features a 1,4-disubstituted phenyl linker flanked by two vinylpyrrole units. This extension in the chain length of the conjugated linker results in an 11-fold increase in γ cf. the monopyrrole 8. Previous DFWM investigations51 at 532 nm involving a disubstituted phenyl linking unit flanked by two vinylpyrrole units appended at ortho and meta positions via imino functionality revealed similar χ(3) values. However, it is unclear how the γ value for the para-substituted phenyl linker (9) compares to that for the ortho- and meta-analogues. Future investigations are needed to explore the influence of 2-, 3-, 4-substitution at the linking phenyl unit upon THG response, and the effect of imino versus alkenyl linking functionality. Certainly 9 and its ortho- and meta-analogues are anticipated to have differing charge transfer donor–acceptor effects.
The effect of formylation upon γ is again seen when comparing the α-free (H atom in the α-position, i.e. 2-position) dipyrrole 9versus its 2-formylated derivative 10 (3-fold increase cf.9) which again may be due to the more electron-withdrawing effect of the carbonyl group. However, the increase in γ is more significant (14-fold) for the 2,6-naphthyl-linked dipyrrole 14cf. the corresponding monopyrrole 12. These trends between the 1,4-phenyl- and 2,6-dinaphthyl-linked systems can be rationalised as for the bromo-substituted benzenes and naphthalenes discussed above, where lack of symmetry in the 1,4-diphenyl- and 2,6-dinaphthyl-linked systems seemingly results in an enhancement in γ.
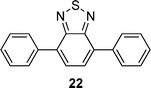
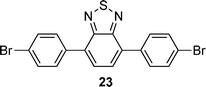
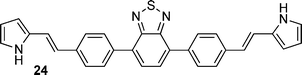
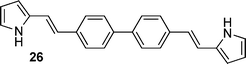
2,1,3-Benzothiadiazole, pyrene, diphenyl-2,1,3-benzothiadiazole, biphenyl and fluorene derivatives
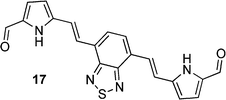
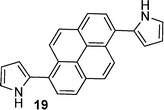
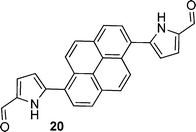
After observing an increase in γ value for dipyrroles linked via 1,4-phenyl and 2,6-dinaphthyl units, presumably as a consequence of increased conjugation across the framework, analogues featuring 2,1,3-benzothiadiazole, pyrene, diphenyl-2,1,3-benzothiadiazole, biphenyl and fluorene units were evaluated (16, 19, 24, 26, 29), as were their diformylated derivatives (17, 20, 25, 27, 20). The effects of these linking units on γ values are previously unreported. However, DFWM studies at 602 nm are reported for benzothiazole, benzimidazole and benzoxazole units. The γ value of benzothiazole was found to be higher than that for benzimidazole and benzoxazole.52 Therefore, it is anticipated that the 2,1,3-benzothiadiazole may exhibit an enhanced γ value due to its enhanced electronic effects cf. the parent compounds. Furthermore, previous studies of biphenyl include its incorporation into tetrabiphenyl ethylene systems featuring four biphenyl groups. Z-Scan studies of these systems at 532 nm have revealed increased third-order nonlinear optical properties due to enhanced π-conjugation.53 Lastly, fluorene-based polymers were determined to exhibit large γ values, as measured using the optical Kerr effect at 830 nm54 and the Maker-Fringe technique at 1200 nm.55As seen for the 1,4-phenyl and 2,6-naphthyl linked analogues studied herein, the formylated dipyrroles exhibited enhanced γ cf. the corresponding α-free species: ∼2.3 times higher for the formylated 4,7-disubstituted-2,1,3-benzothiadiazole-linked dipyrrole 17cf. the α-free analogue 16; ∼1.9 times higher for the formylated 1,6-disubstituted-pyrene-linked dipyrrole 20cf. the α-free analogue 19; ∼6.9 times higher for the formylated 4,7-diphenyl-2,1,3-benzothiadiazole-linked dipyrrole 25cf. the α-free analogue 24; and ∼227 times higher for the formylated 4,4′-biphenyl-linked dipyrrole 27cf. the α-free analogue 26. This enhancement in γ may be due to the lack of symmetry in many of these systems, whereas greater enhancement is observed with derivatives that contain a more flexible core (e.g.27versus20). Dipyrroles linked via a 2,7-fluorenyl unit (29–31) are an exception to this trend, with formylation engendering an 11-fold decrease in γ. The slope of Δn versus concentration is larger for all the formylated analogues except 30, where the slope of the α-free 29 is slightly higher and thus results in a higher value of γ. Interestingly, the absorption maximum of 29 is closer to the third harmonic wavelength (343 nm) than the absorption maximum of 30 (Table 1). As a result, the molar extinction coefficient of 29 is slightly higher at the third harmonic wavelength than for the formylated analogue 30,56 providing a tentative rationale for the decrease in Δn. However, the absorption maxima of compounds 9, 16, 24 and 26 are closer to the third harmonic wavelength than their formylated analogues (10, 17, 25 and 27): the γ values of the formylated analogues are higher, suggesting that, in these compounds, formylation enhances the γ values. A higher molar extinction coefficient at the third harmonic wavelength was also observed for the formylated pyrene-linked system 20, compared to the corresponding α-free dipyrrole 19. Additionally, 20 has a slightly higher molar extinction coefficient than 19 at the second harmonic wavelength, which may contribute to resonance enhancement. The 2,1,3-benzothiadiazole-linked dipyrrole 16 exhibited a similar molar extinction coefficient at the third harmonic wavelength to its formylated analogue 17, and a higher molar extinction coefficient at the second harmonic wavelength.56 In contrast, the related diphenyl-2,1,3-benzothiadiazole-linked dipyrrole 24 exhibits a higher molar extinction coefficient than the corresponding formylated dipyrrole 25 at the third harmonic wavelength, and a slightly higher molar extinction coefficient than 25 at the second harmonic wavelength.56 It should be noted that, due to anomalous dispersion, the refractive index difference may increase or decrease at absorption peaks.
Most formylated analogues (10, 14, 17, 25, 27) were determined to exhibit γ values of magnitudes that were higher than the benchmark standard β-carotene, with exception of the formylated pyrenes (20) and fluorenes (30). Comparing pairs of formylated dipyrroles with differing conjugation lengths, the magnitude of γ evidently increases with an increased extent of conjugation: compare the 1,4-phenyl-linked dipyrrole 10 with the 1,4-biphenyl-linked dipyrrole (27), or the 2,1,3-benzothiadiazole-linked 17 with 25, which bears two additional phenyl groups within the linker unit. Similar observations have been reported for related systems. For example, γ at a wavelength of 1.91 μm was found to increase with increasing bridge length (i.e. the number of double bonds) in donor-bridge-acceptor and acceptor-bridge-acceptor molecular systems consisting of dimethylaniline as the donor, with a variation of double bonds as the bridge, and formyl as the acceptor.57,58
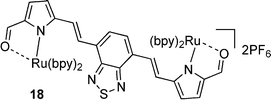
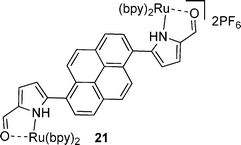
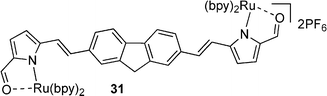
The ruthenium complexes of 17, 20, 27 and 30 exhibited higher γ values compared to the corresponding free ligands, with specific enhancements of: ∼2.9 times higher for 18cf.17; ∼47 times higher for 21cf.20; ∼6.8 times higher for 28cf.27; and ∼308 times higher for 31cf.30. Impressively, these compounds displayed γ values of magnitudes that were higher than the benchmark standard β-carotene.
Given that some conjugated materials fluoresce, the methodology used to measure THG, as described in the THG ratio technique and measurements section above, ensures that only THG signal is collected. Furthermore, as THG and fluorescence are not competing processes it is not expected that fluorescence will reduce THG signal. Interestingly, many of the characteristics of an efficient fluorophore may also be relevant to requirements for a useful harmonophore for THG. For instance, many of the conjugated pyrroles have γ values with magnitudes that are larger than the benchmark standard β-carotene. Furthermore, the ruthenium complexes 18, 21, 28 and 31, as well as 25, have γ values on par with chlorophyll a8 (|γ| = 100 ± 20 × 10−41 m2 V−2 at 1028 nm), which is a well-known highly conjugated chemical framework that produces a γ value that is ∼20× greater than β-carotene; and it is also fluorescent. Many fluorescent frameworks, such as chlorophyll a, have absorption bands in the UV and visible regions. This is advantageous for harmonophores for THG: indeed, electronic or vibrational energy levels at the second harmonic wavelength (515 nm for a 1030 nm laser) and the third harmonic wavelength (343 nm for a 1030 nm laser) can significantly increase THG signal through resonance enhancement.
The use of polymeric materials with extended π-conjugated systems has been demonstrated as an efficient strategy towards achieving larger third-order nonlinearities. Similarly, organometallic compounds with extended π-conjugated systems are also promising as third-order nonlinear optical materials.1 It has been speculated that the interaction of the transition metal d orbitals with conjugated π-orbitals may enhance γ, and that THG may be directly influenced by the types of ligands attached to the metal centre. Recently, ruthenium(II) polypyridyl complexes have been demonstrated to exhibit enhanced third-order nonlinear optical responses, which was proposed to be a consequence of the strong σ-donating ability of the ligands constituting a push–pull system with the ruthenium(II) ion.59 Further, metal-to-ligand charge transfer (MLCT) could play a role in enhancing γ values of ruthenium complexes. In this case, MLCT involves the transfer of electron density from the ruthenium d orbital to a vacant, ligand-localised π* antibonding orbital. This electron transfer increases electron delocalisation over the system, which enhances the third-order nonlinear optical response of the molecule. The charge transfer characteristics of a molecule might therefore be manipulated towards desirable third-order nonlinear optical properties, by tuning metal and ligand combinations.
Table 2 lists the γ enhancement factors, deduced via this study, that amplify the γ values of pyrroles and dipyrroles. These factors include complexation with ruthenium(II), increased conjugation length, formylation and desymmetrisation. These deductions fuel future work to solidify the relevance and generality of these enhancement factors. Future work should further involve performing quantum mechanical calculations regarding the relationship between dipoles and γ values, to support insights by which to design molecular frameworks with enhanced THG signal.
| Specific enhancement | Example compounds |
|---|---|
| Lack of symmetry enhances γ | 5 vs. 4, 10 vs. 9 |
| Increased conjugation length enhances γ | 9 vs. 7, 16 vs. 15, 24 vs. 23 |
| Formylation enhances γ | 7 vs. 8, 9 vs. 10, 11 vs. 12, 16 vs. 17, 19 vs. 20, 24 vs. 25, 26 vs. 27 |
| Complexation with Ru enhances γ | 17 vs. 18, 20 vs. 21, 27 vs. 28, 30 vs. 31 |
Conclusions
The THG intensity ratio technique was used to measure the second hyperpolarisability γ of a series of pyrrole-containing frameworks, to experimentally determine the molecular third-order nonlinear optical properties of this fundamental chemical building block. The THG intensity ratios from (1) a glass–solution interface incorporating the pyrrole-containing molecule and (2) an air–glass interface were measured, along with the refractive index of each pyrrole-containing solution at the laser (1030 nm) and third harmonic (343 nm) wavelengths. These values were used to calculate the χ(3) values of pyrrole-containing solutions. The γ value of each pyrrole-containing framework was then extracted from concentration-dependent χ(3) values. Trends in the magnitude of γ were noted, including that several formyl-substituted dipyrroles showed increased γ compared to the corresponding α-free dipyrroles. The formyl-substituted dipyrroles also exhibited enhancements in the magnitude of γ with increasing conjugation length. Finally, the complexation of ruthenium(II) by formyl-substituted dipyrroles enhanced the corresponding γ values ∼3 to ∼300-fold. The trends emergent from this systematic study bolster knowledge of the electronic and structural features necessary for enhancement of third-order nonlinear optical properties. Correspondingly, these data offer significant insight as regards to key molecular features required for the strategic design of novel dyes for THG microscopy.Author contributions
Conceptualisation: AT and DT. Investigation: EB, AA, RMD-R, JWC, LAF, MJC, RC and DT. Funding acquisition administration and supervision: AT and DT. Writing and editing: RC, DT, AB, AA, RMD-R, JWC and AT.Conflicts of interest
There are no conflicts to declare.Data availability
The data supporting this article have been included as part of the supplementary information (SI). Supplementary information: synthesis of novel compounds, NMR spectra and UV-visible absorption spectral data. See DOI: https://doi.org/10.1039/d5cp02783g.Acknowledgements
We thank Dr M. Lumsden and Mr X. Feng (Dalhousie University) for sharing expertise in NMR spectroscopy and mass spectrometry, respectively, and Dr Deborah A. Smithen for contributions to synthesis. This research was supported in part by: the Canada Research Chairs Program (950-232829), Canada Foundation for Innovation (JELF 39824 for A. T., and JELF 37749 for D. T.), Research Nova Scotia (Research Opportunities Fund 2020-1208 for A. T. and 1868 for D. T.), NSERC of Canada via Discovery Grants, Undergraduate Student Research Awards and the CREATE Training Program in BioActives (510963), Canada's Research Support Fund, and Saint Mary's University.References
- N. J. Long, Organometallic Compounds for Nonlinear Optics-The Search for En-light-enment!, Angew. Chem., Int. Ed. Engl., 1995, 34, 21–38 CrossRef CAS.
- J. P. Hermann, D. Ricard and J. Ducuing, Optical Nonlinearities in Conjugated Systems – Beta-Carotene, Appl. Phys. Lett., 1973, 23, 178–180 CrossRef CAS.
- J. P. Hermann and J. Ducuing, Third-order polarizabilities of long-chain molecules, J. Appl. Phys., 1974, 45, 5100–5102 CrossRef CAS.
- K. C. Rustagi and J. Ducuing, Third-order optical polarizability of conjugated organic molecules, Opt. Commun., 1974, 10, 258–261 CrossRef CAS.
- R. R. Tykwinski, U. Gubler, R. E. Martin, F. Diederich, C. Bosshard and P. Gunter, Structure-property relationships in third order nonlinear optical chromophores, J. Phys. Chem. B, 1998, 102, 4451–4465 CrossRef CAS.
- D. Tokarz, R. Cisek, N. Prent, U. Fekl and V. Barzda, Measuring the molecular second hyperpolarizability in absorptive solutions by the third harmonic generation ratio technique, Anal. Chim. Acta, 2012, 755, 86–92 CrossRef CAS PubMed.
- D. Tokarz, R. Cisek, M. Garbaczewska, D. Sandkuijl, X. Qiu, B. Stewart, J. D. Levine, U. Fekl and V. Barzda, Carotenoid based bio-compatible labels for third harmonic generation microscopy, Phys. Chem. Chem. Phys., 2012, 14, 10653 RSC.
- D. Tokarz, R. Cisek, U. Fekl and V. Barzda, The molecular second hyperpolarizability of the light-harvesting chlorophyll a/b pigment-protein complex of photosystem II, J. Phys. Chem. B, 2013, 117, 11069–11075 CrossRef CAS PubMed.
- R. Bano, K. Ayub, T. Mahmood, M. Arshad, A. Sharif, A. L. Khan, H. AlMohamadi, M. Yasin and M. A. Gilani, Rational design of superalkali-based novel calix[4]pyridine alkalides as high performance nonlinear optical materials, RSC Adv., 2025, 15, 6147–6161 RSC.
- H. Zhang, Y. Yang, H. Xiao, F. Liu, F. Huo, L. Chen, Z. Chen, S. Bo, L. Qiu and Z. Zhen, Enhancement of electro-optic properties of bis(N,N-diethyl)aniline based second order nonlinear chromophores by introducing a stronger electron acceptor and modifying the π-bridge, J. Mater. Chem. C, 2017, 5, 6704–6712 RSC.
- M. Khalid, M. U. Khan, I. Shafiq, R. Hussain, A. Ali, M. Imran, A. A. C. Braga, M. Fayyaz Ur Rehman and M. S. Akram, Structural modulation of π-conjugated linkers in D–π–A dyes based on triphenylamine dicyanovinylene framework to explore the NLO properties, R. Soc. Open Sci., 2021, 8, 210570 CrossRef CAS PubMed.
- X. L. Zheng, C. C. Yang, W. Q. Tian, L. Yang and W. Q. Li, Tuning azulene defects and doping of N atoms in graphene nanosheets: improving nonlinear optical properties of carbon-based nano materials, Phys. E, 2022, 136, 115040 CrossRef CAS.
- M. M. M. Raposo, M. C. R. Castro, A. M. C. Fonseca, P. Schellenberg and M. Belsley, Design, synthesis, and characterization of the electrochemical, nonlinear optical properties, and theoretical studies of novel thienylpyrrole azo dyes bearing benzothiazole acceptor groups, Tetrahedron, 2011, 67, 5189–5198 CrossRef CAS.
- S. S. M. Fernandes, J. Aires-de-Sousa, M. Belsley and M. M. M. Raposo, Synthesis of pyridazine derivatives by Suzuki–Miyaura cross-coupling reaction and evaluation of their optical and electronic properties through experimental and theoretical studies, Molecules, 2018, 23, 3014 CrossRef PubMed.
- F. Liu, H. Xiao, H. Xu, S. Bo, C. Hu, Y. He, J. Liu, Z. Zhen, X. Liu and L. Qiu, Synthesis of chromophores with ultrahigh electro-optic activity: rational combination of the bridge, donor and acceptor groups, Dyes Pigm., 2017, 136, 182–190 CrossRef CAS.
- S. A. Mitchell, Indole adsorption to a lipid monolayer studied by optical second harmonic generation, J. Phys. Chem. B, 2009, 113, 10693–10707 CrossRef CAS PubMed.
- M. A. M. El-Mansy, W. Osman and H. Abdelsalam, The electronic and optical absorption properties of pristine, homo and hetero Bi-nanoclusters, Chem. Phys., 2021, 544, 111113 CrossRef CAS.
- Z. Benková, I. Černušák and P. Zahradník, Theoretical study of static electric properties of benzothiazole containing push–pull systems as potential candidates for NLO materials, Struct. Chem., 2006, 17, 287–300 CrossRef.
- R. N. Singh, A. Kumar, R. K. Tiwari and P. Rawat, Study of spectroscopic, reactivity and NLO properties of synthesized dipyrromethane containing cyanovinylhydrazide using experimental and theoretical approaches, J. Mol. Struct., 2013, 1048, 448–459 CrossRef CAS.
- F. T. Khan, M. Ibrahim, A. Yousuf and M. A. Ali, Extrusion of carbon with SON in heterocycles for enhanced static and dynamic hyperpolarizabilities and light harvesting efficiencies, Chem. Phys., 2025, 596, 112761 CrossRef CAS.
- R. N. Singh, A. Kumar, P. Rawat and A. Srivastsva, Synthesis, spectroscopic and structural evaluation of ethyl 2-cyano-3-{5-[(4-nitro-benzoyl)-hydrazonomethyl]-1H-pyrrol-2-yl}-acrylate using experimental and theoretical approaches, J. Mol. Struct., 2013, 1049, 419–428 CrossRef CAS.
- J. J. Wang, Z. J. Zhou, H. M. He, D. Wu, Y. Li, Z. R. Li and H. X. Zhang, An External Electric Field Manipulated Second-Order Nonlinear Optical Switch of an Electride Molecule: A Long-Range Electron Transfer Forms a Lone Excess Electron Pair and Quenches Singlet Diradical, J. Phys. Chem. C, 2016, 120, 13656–13666 CrossRef CAS.
- Y. Yang, Y. Yan and N. Hou, Evaluation of the second-order nonlinear optical properties of oxasmaragdyrin-BODIPY derivatives, Comput. Theor. Chem., 2025, 1244, 115067 CrossRef CAS.
- P. Rawat and R. N. Singh, Experimental and theoretical study of 4-formyl pyrrole derived aroylhydrazones, J. Mol. Struct., 2015, 1084, 326–339 CrossRef CAS.
- H. Weng, Y. Teng, Q. Sheng, Z. Zhou, X. Huang, Z. Li and T. Zhang, Theoretical study of substituent effects on electride characteristics and the nonlinear optical properties of Li@calix[4]pyrrole, RSC Adv., 2019, 9, 37919–37925 RSC.
- O. P. Kwon, M. Jazbinsek, H. Yun, J. I. Seo, E. M. Kim, Y. S. Lee and P. Günter, Pyrrole-based hydrazone organic nonlinear optical crystals and their polymorphs, Cryst. Growth Des., 2008, 8, 4021–4025 CrossRef CAS.
- F. Liu, H. Wang, Y. Yang, H. Xu, M. Zhang, A. Zhang, S. Bo, Z. Zhen, X. Liu and L. Qiu, Nonlinear optical chromophores containing a novel pyrrole-based bridge: optimization of electro-optic activity and thermal stability by modifying the bridge, J. Mater. Chem. C, 2014, 2, 7785–7795 RSC.
- R. M. F. Batista, S. P. G. Costa, M. Belsley and M. M. M. Raposo, Synthesis and second-order nonlinear optical properties of new chromophores containing benzimidazole, thiophene, and pyrrole heterocycles, Tetrahedron, 2007, 63, 9842–9849 CrossRef CAS.
- M. C. R. Castro, M. Belsley and M. M. M. Raposo, Synthesis and characterization of push-pull bithienylpyrrole NLOphores with enhanced hyperpolarizabilities, Dyes Pigm., 2016, 131, 333–339 CrossRef CAS.
- M. C. R. Castro, M. Belsley and M. M. M. Raposo, Push–pull second harmonic generation chromophores bearing pyrrole and thiazole heterocycles functionalized with several acceptor moieties: syntheses and characterization, Dyes Pigm., 2016, 128, 89–95 CrossRef CAS.
- B. Li, P. Sathishkumar and F. L. Gu, Tuning the first hyperpolarizability of hexaphyrins with different connections of mislinked pyrrole units: a theoretical study, Phys. Chem. Chem. Phys., 2021, 23, 8489–8499 RSC.
- M. C. R. Castro, M. Belsley, A. M. C. Fonseca and M. M. M. Raposo, Synthesis and characterization of novel second-order NLO-chromophores bearing pyrrole as an electron donor group, Tetrahedron, 2012, 68, 8147–8155 CrossRef CAS.
- A. Alparone, H. Reis and M. G. Papadopoulos, Theoretical investigation of the (hyper)polarizabilities of pyrrole Homologues C4H4XH (X = N, P, As, Sb, Bi). A coupled-cluster and density functional theory study, J. Phys. Chem. A, 2006, 110, 5909–5918 CrossRef CAS PubMed.
- N. Islam and S. S. Chimni, Geometrical structure and nonlinear response variations of metal (M = Ni2+, Pd2+, Pt2+) octaphyrin complex derivatives: a DFT study, J. Coord. Chem., 2017, 70, 1221–1236 CrossRef CAS.
- R. Saha, B. B. Skjelstad and S. Pan, In Silico Design and Characterization of a New Molecular Electride: Li@Calix[3]Pyrrole, Chem. – Eur. J., 2024, 38, e202400448 CrossRef PubMed.
- G. T. Yu, W. Chen, F. L. Gu and Y. Aoki, Theoretical study on nonlinear optical properties of the Li+ [calix[4]pyrrole]Li− dimer, trimer and its polymer with diffuse excess electrons, J. Comput. Chem., 2009, 4, 863–870 Search PubMed.
- D. Avci, Ö. Tamer and Y. Atalay, Solvatochromic effect on UV-vis absorption and fluorescence emission spectra, second- and third-order nonlinear optical properties of dicyanovinyl-substituted thienylpyrroles: DFT and TDDFT study, J. Mol. Liq., 2016, 220, 495–503 CrossRef CAS.
- J. Wei, J. Yang, L. Yang, Y. Li and Y. Song, Tunable third-order NLO properties of acene derivatives with molecular structural modification, Int. J. Quantum Chem., 2024, 124, e27354 CrossRef CAS.
- W. Zhu and Y. Jiang, An investigation of the relationships between the bridge atomic charge sum and the molecular polarizabilities of push-pull polyenes, THEOCHEM, 2000, 496, 67–72 CrossRef CAS.
- V. Keshari, W. K. P. Wyekoon, P. N. Prasad, S. P. Kama and F. J. Seiler, Hyperpolarizabilities of Organic Molecules: Ab Initio Time-Dependent Coupled Perturbed Hartree-Fock-Roothaan Studies of Basic Heterocyclic Structures, J. Phys. Chem., 1995, 99, 9045–9050 CrossRef CAS.
- Y. Q. Qiu, H. L. Fan, S. L. Sun, C. G. Liu and Z. M. Su, Theoretical study on the relationship between spin multiplicity effects and nonlinear optical properties of the pyrrole radical (C4H4N), J. Phys. Chem. A, 2008, 112, 83–88 CrossRef CAS PubMed.
- M. Zouaoui-Rabah, L. Bekri, M. Hedidi, A. M. Elhorri and Y. Madaoui, Characteristics of new pyrrolic derivatives and their oligomers using DFT and TD–DFT calculations, J. Mol. Model., 2023, 29, 364 CrossRef CAS PubMed.
- W. Zhu and G. S. Wu, An ab initio study on the first- and third-order polarizabilities of the octupolar heteroaromatic-substituted triazines, J. Phys. Chem. A, 2002, 106, 7216–7221 CrossRef CAS.
- K. Brittain, M. Harvey, R. Cisek, S. Pillai, S. D. Christie and D. Tokarz, Second harmonic generation microscopy of otoconia, Biomed. Opt. Express, 2022, 13, 3593–3600 CrossRef CAS PubMed.
- R. S. Pillai, G. J. Brakenhoff and M. Muller, Analysis of the influence of spherical aberration from focusing through a dielectric slab in quantitative nonlinear optical susceptibility measurements using third-harmonic generation, Opt. Express, 2006, 14, 260–269 CrossRef PubMed.
- K. Purvis, K. Brittain, A. Joseph, R. Cisek and D. Tokarz, Third-order nonlinear optical properties of phycobiliproteins from cyanobacteria and red algae, Chem. Phys. Lett., 2019, 731, 136599 CrossRef CAS.
- V. Shcheslavskiy, G. Petrov and V. V. Yakovlev, Nonlinear optical susceptibility measurements of solutions using third-harmonic generation on the interface, Appl. Phys. Lett., 2003, 82, 3982–3984 CrossRef CAS.
- F. Kajzar, I. Ledoux and J. Zyss, Electric-field-induced optical second-harmonic generation in polydiacetylene solutions, Phys. Rev. A: At., Mol., Opt. Phys., 1987, 36, 2210–2219 CrossRef CAS PubMed.
- K. Kandasamy, S. J. Shetty, P. N. Puntambekar, T. S. Srivastava, T. Kundu and B. P. Singh, Effects of metal substitution on third-order optical non-linearity of porphyrin macrocycle, J. Porphyrins Phthalocyanines, 1999, 3, 81–86 CrossRef CAS.
- L. X. Q. Chen, Nonlinear-optical properties of porphyrin and chlorophyll dimers studied by degenerated four-wave mixing, Proc. SPIE, 1993, 1852, 162–166 CrossRef CAS.
- S. Velmathi and V. Reena, Synthesis, characterization and investigation of the third order NLO properties of pyrrole Schiff bases, Adv. Mater. Res., 2012, 488–489, 377–382 CAS.
- M. Zhao, M. Samoc, P. N. Prasad, B. A. Reinhardt, M. R. Unroe, M. Prazak, R. C. Evers, J. J. Kane, C. Jariwala and M. Sinsky, Studies of the third-order optical nonlinearities of model compounds containing benzothiazole, benzimidazole, and benzoxazole units, Chem. Mater., 1990, 2, 670–678 CrossRef CAS.
- L. Gao, H. Yi, Y. Li, B. Li, J. Cui, H.-R. Yang, L. Zhou and S. Fang, Synthesis and investigation of nonlinear optical properties of biphenyl ethylene derivatives with different substituents, Mater. Lett., 2023, 346, 134433 CrossRef CAS.
- X. Zhan, Y. Liu, D. Zhu, W. Huang and Q. Gong, Large femtosecond third-order nonlinear optical response in a novel donor-acceptor copolymer consisting of ethynylfluorene and tetraphenyldiaminobiphenyl units, Chem. Mater., 2001, 13, 1540–1544 CrossRef CAS.
- G. Ramos-Ortíz, J. L. Maldonado, M. C. G. Hernández, M. G. Zolotukhin, S. Fomine, N. Fröhlich, U. Scherf, F. Galbrecht, E. Preis, M. Salmon, J. Cárdenas and M. I. Chávez, Polymer, 2010, 51, 2351–2359 CrossRef.
- D. A. Smithen, S. Monro, M. Pinto, J. Roque, R. M. Diaz-Rodriguez, H. Yin, C. G. Cameron, A. Thompson and S. A. Mcfarland, Bis[pyrrolyl Ru(II)] triads: a new class of photosensitizers for metal–organic photodynamic therapy, Chem. Sci., 2020, 11, 12047–12069 RSC.
- G. Puccetti, M. Blancharddesce, I. Ledoux, J. M. Lehn and J. Zyss, Chain-Length Dependence of the 3rd-Order Polarizability of Disubstituted Polyenes – Effects of End-Groups and Conjugation Length, J. Phys. Chem., 1993, 97, 9385–9391 CrossRef CAS.
- A. Elizabete, A. Machado, A. Arnóbio and S. Da Gama, Calculations of second hyperpolarizabilities of some polyenic derivatives, J. Mol. Struct.:THEOCHEM, 2003, 1, 21–29 Search PubMed.
- L. Xiao, H. Wang, Q. Zhang, Y. Zhu, J. Luo, Y. Liang, S. Zhang, H. Zhou, Y. Tian and J. Wu, Novel ruthenium(II) polypyridyl complexes containing carbazole with flexible substituents: crystal structure, nonlinear optical properties and DNA-binding interaction, Dyes Pigm., 2015, 113, 165–173 CrossRef CAS.
| This journal is © the Owner Societies 2025 |