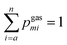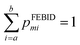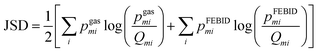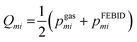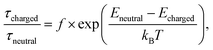Desorption of fragments upon electron impact on adsorbates: implications for electron beam induced deposition

Abstract

A molecular level understanding of surface chemistry involved in the focused electron beam induced deposition (FEBID) with metalorganic molecules is crucial for enhancing the metal content in the fabricated nanostructures. Here, we investigate the FEBID process of trimethyl(methylcyclopentadienyl)platinum(IV) [MeCpPtMe₃] using focused electron beam induced mass spectrometry (FEBiMS), a recently developed in situ analytical technique. A comparison with experimental gas-phase electron impact fragmentation spectra, alongside density–functional theory calculations and molecular dynamics simulations is presented. The results indicate that charged fragments generated via dissociative ionization exhibit strong adsorption to the substrate and lack sufficient kinetic energy to desorb. This suggests that the most observed charged species during FEBID originate from gas-phase fragmentation above the surface. Furthermore, this study proposes processes like charge neutralization and dissociative recombination, not previously considered in FEBID, could be significant contributors to increasing the metal content in the resulting nanostructures.

---

1. Introduction

Techniques for probing a surface through mass analysis of particles ejected by an external trigger, such as secondary ion mass spectrometry (SIMS), are valuable for gaining insights into the chemical composition of a sample. Using a focused particle beam as the trigger, as in scanning electron microscopes (SEMs) or focused ion beam (FIB) systems, allows for detailed imaging of the chemical composition with excellent lateral resolution.¹ In FIB, the ion beam generally induces sputtering, facilitating SIMS depth profiling. FIB-SIMS can be applied to analyse interfaces between different materials or dopant profiles in electronic devices.^1–4

Focused electron beam induced mass spectrometry (FEBiMS) is an analogous technique employing a focused electron beam (FEB) as an external trigger.⁵ FEBiMS monitors electron-induced damage by in situ mass detection of charged fragments generated during irradiation of a material and can be used for in situ monitoring of gas-assisted focused electron beam induced deposition (FEBID).

FEBID is a direct-write nanofabrication technique in which precursor molecules are continuously delivered onto a substrate, where they physisorb and are locally decomposed by a focused electron beam, creating a deposit in the irradiated area. The process also involves the interactions of secondary electrons (SEs, with energy <50 eV) and backscattered electrons (BSEs) interacting with the adsorbates. By controlling the scanning of the electron beam, various patterned 2D and 3D deposits can be fabricated. The technique thus serves as a 3D-nanoprinting tool for several nanotechnological applications.^6–9 For metallic nanostructures, organometallic or inorganic complexes are used as precursors.^10,11 A significant challenge with this approach is obtaining high purity, carbon-free metal nanostructures. Incomplete separation of ligands from metal atoms and co-deposition of already cleaved ligands often result in low metal content in the created nanostructures. Consequently, much attention has been paid in recent years to understanding the electron-induced fragmentation of FEBID precursors. The primary question in these efforts is how many (and which) ligands the precursors lose in collisions with electrons. Common approaches to tackle this question include experiments with precursors in the gas phase,^12–14 their layers condensed on various low-temperature substrates,^15–17 or in the form of clusters.^18,19 These approaches provide useful insight into the radiation-induced chemistry during FEBID. However, the molecular environments used in such experiments are different from the FEBID process environment. In this respect, the FEBiMS method used for in situ monitoring of FEBID can provide insights into mechanisms that are directly responsible for the deposition process.

FEBiMS was successfully applied for in situ monitoring of FEBID using W(CO)₆ as a precursor.⁵ It was also used for monitoring irradiation of grains of non-volatile precursors such as silver and copper carboxylates and ruthenium carbonyls.⁵ Both approaches provided first insights into electron induced decomposition processes under conditions similar to those of a standard FEBID process.

A key unresolved issue in in situ monitoring of FEBID through FEBiMS is the contribution of the electron-induced fragmentation of either adsorbed or gas-phase molecules to the detected signal. An estimate, based on precursor concentrations and electron mean free paths in both the gas and adsorbed phases, suggests that the signal from the condensed phase could be up to 500 times more intense than that from the gas phase, assuming equal fragmentation cross-sections in both phases.⁵ However, the mass spectra recorded during the FEBID process with W(CO)₆ were qualitatively, and surprisingly, similar to the gas-phase spectra available in the literature.

This paper aims to investigate the origin of metal-containing fragments in the FEBiMS signal during FEBID. We have selected the precursor trimethyl(methylcyclopentadienyl)platinum(IV), (CH₃)₃Pt(C₅H₄(CH₃)) or [MeCpPtMe₃], which is widely used for creating local platinum–carbon surface protection deposits for subsequent FIB milling. FEBID structures nanoprinted using MeCpPtMe₃ are employed in gas, temperature, and strain sensors.^20–23 We present the mass spectra obtained during the [MeCpPtMe₃]-assisted FEBID and compare them with the gas-phase mass spectra of MeCpPtMe₃ across an electron-energy range of 10 eV to 30 keV, reflecting the broad energy spectrum of electrons involved in the FEBID process. The aim of this analysis is to investigate the origin of fragments in the FEBID process. Quantum chemical calculations were performed to understand the molecule–substrate interactions for the neutral and charged precursor molecule and its fragments. A possibility of ion desorption through kinetic energy release was also explored using classical reactive molecular dynamics simulations. This study provides valuable insights into the electron-induced deposition process.

2. Experimental methods

2.1 SEM based FEB induced mass spectrometry

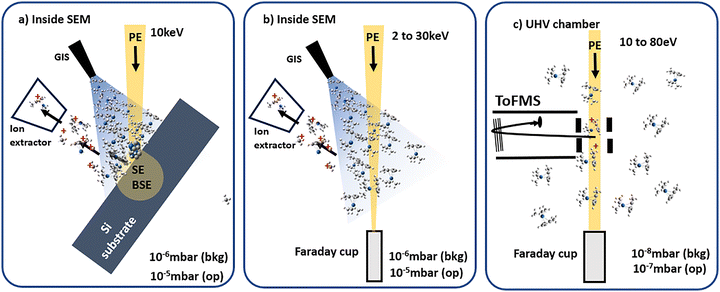
The experimental setup used in this study is described in detail by Jurczyk et al.,⁵ and is shown schematically in Fig. 1a and b. The experiments were conducted in a TESCAN Lyra3 dual-beam system (Brno, Czech Republic), consisting of an SEM, a gallium FIB, and a 5-line gas injection system (GIS) from Orsay Physics (Fuveau, France). It is equipped with a synchronized high-resolution time-of-flight mass spectrometer (ToFMS) from TOFWERK (Thun, Switzerland). The resolution M/ΔM is 2096 at a mass of 320 amu and is 2087 at a mass of 50 amu. The ToF mass spectrometer has an ion extractor at an angle of 55° to the electron beam. Ionic fragments generated inside the chamber are extracted and collected by electrostatic potentials of around 100 V. Every 40 μs, the fragments are released into the ToFMS for mass analysis by an orthogonal voltage pulse. The ToF instrument was originally designed for time-of-flight secondary ion mass spectrometry (ToF-SIMS) and synchronized with a FIB.^4,24 The mass spectrum is collected pixel by pixel as the ion beam scans the surface, with pixels being binned according to the user's preference, resulting in a spatial map for each complete scan. No post-ionization of neutral fragments is involved in the measurement.

Fig. 1 (a) FEBiMS method for in situ monitoring of FEBID inside the SEM. (b) High-energy (1–30 keV) gas-phase experiments inside the SEM. (c) Low-energy (10–80 eV) gas-phase experiments. Abbreviations “bkg” and “op” stand for background and during operation. PE stands for the primary electron beam.

2.1.1 FEBiMS experiments for in situ monitoring the FEBID process. For our purposes, the mass spectra were binned across all scanned pixels to enhance the signal-to-noise ratio, as no spatial map was needed. FEBID was performed on a native oxide Si(100) substrate using a focused electron beam with an energy of 10 keV and a beam current of 8.9 nA. Square deposits were created by scanning an area of 20 × 20 μm² using a serpentine scanning strategy. The MeCpPtMe₃ GIS was maintained at 77 °C, while the substrate was kept at room temperature. The mass spectrum was collected during FEBID with a pixel dwell time of 40 μs enabling coverage of the mass range up to 450 m/q (mass over charge ratio) and a frame size of 256 × 256 pixels.

2.1.2 High energy electron gas phase experiments (1–30 keV) inside the SEM. The same experimental setup was used to investigate the gas-phase electron-induced fragmentation at high electron energies (>1 keV). For this experiment, the substrate was removed from the setup, as shown in Fig. 1b, and a Faraday cup was introduced. These modifications enabled us to study the electron impact dissociation of the gas-phase precursors in the SEM. The base pressure of the chamber was 6.9 × 10⁻⁶ mbar. The chamber pressure rose to approximately 8.2 × 10⁻⁶ mbar when introducing the MeCpPtMe₃ precursor at 60 °C. The GIS was in a standby position to prevent higher molecular flux locally. We collected the mass spectrum at different electron currents at 2 keV electron impact energy and selected the current range of 100–900 pA that satisfies the single collision condition. Since the cross-section for fragmentation decreases with increasing electron energy, this condition holds for higher electron energies. The SEM-based gas-phase electron impact mass spectra were recorded at 2, 5, 10, 20, and 30 keV electron energies.

2.2 Gas phase experiments (10–80 eV)

The low-energy gas-phase mass spectra were measured using a dedicated experimental setup equipped with a tunable monochromatic electron gun and a reflectron time-of-flight (RToF) mass spectrometer (Stefan Kaesdorf, Germany),²⁵ as shown schematically in Fig. 1c. The base pressure in the interaction vacuum chamber was 1 × 10⁻⁸ mbar. The MeCpPtMe₃ sample was introduced into the chamber via a background gas inlet at room temperature, and the whole chamber was thus filled with its vapor to the background pressure of 4.0 × 10⁻⁷ mbar. The electron beam was generated by a magnetically collimated electron gun using a heated tungsten filament as an electron source. The electron beam was pulsed at a frequency of 10 kHz, and the electrons were passed through the interaction region in a field-free environment. After the electrons exited the interaction region, an extraction pulse was applied to extract the ions to the RToF mass spectrometer. The mass resolution of the spectrometer during the present experiments was M/ΔM = 2627 at 320 amu and 691 at 50 amu. Mass spectra were recorded for electron impact energies from 10 to 80 eV in steps of 0.5 eV.

2.3 Experimental data analysis

Mass spectra obtained were discretized by binning ion signals into integer mass units. This was achieved by integrating ion counts within a ±0.4 amu window centred at each integer mass. The chosen bin width exceeds the instrumental mass resolution, thereby ensuring complete capture of each mass peak. Individual mass channels are denoted by mi with corresponding intensities designated as I^gas_mi for gas phase data and I^FEBID_mi for the mass spectra obtained during FEBID.

Quantitative comparison among the three different experimental methodologies was conducted over two distinct mass intervals: 180–340 amu, encompassing Pt-containing fragments, and a broader 0–340 amu range. Empirical intensity values were normalized to construct discrete probability distributions. Specifically, the normalized intensities from gas-phase spectra yield the distribution p^gas_mi while those from FEBID spectra yield p^FEBID_misuch that

and
where the summation bounds (a, b) correspond to either the 180–340 or 0–340 amu range, depending on the analysis.

To quantify spectral similarity, the Jensen–Shannon divergence (JSD) was computed. This symmetric divergence metric, measures the dissimilarity between two probability distributions and is bounded between 0 (identical distributions) and 1 when the logarithm of base 2 is considered. At a given gas phase electron impact energy, E, the JSD between the FEBID mass spectrum and the gas phase spectrum is defined as:

with the intermediate distribution (Q_mi) defined as:
JSD values computed for the 180–340 amu and 0–340 amu mass ranges at a given gas phase electron energy, E, are denoted as h(E) and g(E), respectively.

3. Theoretical methods

3.1 DFT interaction energy calculations

To calculate the interaction between MeCpPtMe₃ and its charged and neutral fragments and the substrate, a quartz (001) surface was modelled as a slab consisting of seven SiO layers. To avoid spurious interactions between the layers, a vacuum space of 30 Å was included in the simulation cell. The lateral dimensions of the simulation cell are 21.38 × 21.38 Ų and the cell was periodically repeated. Where needed, dangling bonds were saturated with hydrogen atoms to ensure a chemically reasonable hydroxyl-terminated surface and a charge-balanced model.

All periodic calculations were performed using the Quickstep module of CP2K (version 2022.1).²⁶ Kohn–Sham density functional theory (DFT) with the Gaussian and plane wave (GPW) method was employed. The Perdew–Burke–Ernzerhof (PBE) functional with D3(BJ) dispersion corrections, paired with the DZVP-MOLOPT-SR-GTH basis set, was used for all structure optimization and interaction energy calculations. For all calculations, a grid cutoff/relative grid cutoff of 400 Ry/50 Ry was used.

The geometry of MeCpPtMe₃ was optimized at the B3LYP/LANL2DZ level using Gaussian16.²⁷ This optimized molecule was subsequently adsorbed in different orientations onto the quartz slab, creating eight different adsorption geometries. Each adsorption configuration, including the adsorbed molecule and the uppermost layer of the slab, was optimized. For MeCpPtMe₃, MeCpPtMe₂, MeCpPtMe, PtMe₃, and Pt, four adsorption geometries were created for each singly charged and neutral fragment and optimized in the same way. In all cases, the basis set superposition error (BSSE)-corrected interaction energy of the most stable adsorption configuration is reported.

3.2 Kinetic energy release calculations

We have analysed the kinetic energy release of the fragments (ions and neutral co-fragments) following the gas-phase ionization of MeCpPtMe₃. This analysis is based on the results of irradiation-driven molecular dynamics (IDMD) simulations presented in Lyshchuk et al.²⁸ The IDMD method,²⁹ implemented in the MBN Explorer software package,³⁰ allows atomistic simulations of irradiation-driven transformations in various molecular and condensed matter systems exposed to radiation. This method was introduced in Sushko et al.,²⁹ and described in detail in several recent reviews and books.^31–33 Briefly, the IDMD-based molecular fragmentation model assumes that, upon ionization, excess energy is transferred from the electronic degrees of freedom of the target molecular system to the motion of nuclei on an ultrafast timescale.^18,28,29,34 At simulation time zero, the excess energy is distributed statistically among the vibrational degrees of freedom of the parent cation MeCpPtMe₃⁺. A classical reactive MD simulation of the nuclear motion was then performed using the reactive rCHARMM force field.³⁵ The parameters of the force field describing the covalent bonded and angular interactions (which change dynamically upon the breakage or formation of covalent bonds) are described in detail in Lyshchuk et al.²⁸ The simulations were conducted with the MBN Explorer software package.³⁰ The IDMD simulations of MeCpPtMe₃ fragmentation recently showed a very good agreement with the experimental data on electron-induced dissociative ionization of gas-phase MeCpPtMe₃ in terms of fragmentation patterns and appearance energies of different fragments.²⁸ In this study, we have analysed the trajectories from these simulations to evaluate the kinetic energy imparted into the fragments during the dissociative ionization.

4. Results and discussion

4.1 Mass spectra of in situ FEBID and gas phase electron impact ionization

Fig. 2 shows the FEBiMS spectrum obtained during FEBID of MeCpPtMe₃ which we refer to as the FEBID spectrum. The mass spectrum shows a series of peaks that are grouped due to the presence of various isotopic forms of Pt, with the following abundances: ¹⁹⁰Pt = 0.01289%, ¹⁹²Pt = 0.7938%, ¹⁹⁴Pt = 32.81%, ¹⁹⁵Pt = 33.79%, ¹⁹⁶Pt =25.29% and ¹⁹⁸Pt = 7.308%.³⁶ In addition, the observed fragments contain varying numbers of hydrogen atoms, with the removal of hydrogen indicated as –nH in Fig. 2. The most intense group of ions corresponds to [MeCpPtMe-nH]⁺, representing the loss of 2 methyl ligands, followed by a second group, [MeCpPt-nH]⁺, corresponding to the loss of three methyl ligands. Ligand stripping down to the bare platinum ion was also observed. Interestingly, the signal at m/q = 197 clearly indicates the presence of a PtH⁺ ion (see Fig. S1 in the SI). A second strong intensity group of ions appears at low masses and corresponds to the ligands (CpMe⁺, Me⁺) and their fragments (MeCp-nH)⁺, (Cp-nH)⁺, CxHn⁺). The intact ligand signals have higher intensities than their respective fragments. Additionally, background gas peaks were observed, including H₂O⁺ from background water vapor and Ga⁺ (m/q = 69) from the liquid ion source of FIB, even though the gallium ion beam was not used in this study. Fig. 3 presents the integer gas-phase mass spectra taken at 2 keV and 80 eV electron energy. These electron energies correspond to the lowest and highest energies used in the experiments described in Sections 2.1 and 2.2, respectively. The raw mass spectra are shown in Fig. S2 of the SI. To facilitate comparison, the mass spectra were normalized by dividing each spectrum by the corresponding sum of all Pt-containing peaks, so that the total intensity of these peaks is equal to 1. It is evident that the degree of fragmentation is greater at 80 eV than at 2 keV. This is well rationalized by the short interaction time and the resulting lower amount of deposited energy for the higher-energy spectrum. The 2 keV mass spectrum measured in the SEM has significant contribution from the residual gases N₂ (venting gas, m/q = 28) and O₂ (m/q = 32). Our 80 eV spectrum is in a very good qualitative agreement with the one measured by Engmann et al.,¹⁴ using a quadrupole mass analyzer in an orthogonal beam setup.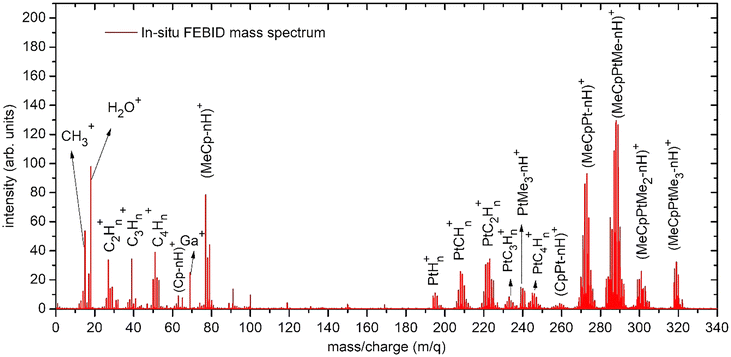

Fig. 2 The mass spectrum collected during the FEBID process with the FEBiMS experimental setup shown in Fig. 1a using the MeCpPtMe₃ precursor with an electron energy of 10 keV with n = 0, 1, 2,… The parent ion with most abundant Pt and C isotopes has m/q = 319. The value for n in (Cp-nH)⁺ can take negative integers.

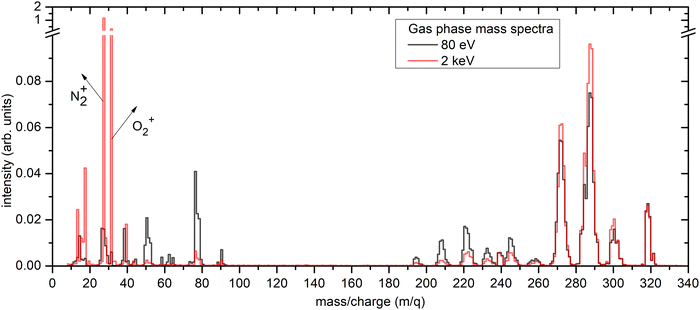Fig. 3 Integer electron impact ionization mass spectra of gas-phase MeCpPtMe₃. Fig. 1b and c show the related experimental setups for the 2 keV and 80 eV measurement, respectively.

4.2 Comparison of in situ FEBID and gas-phase electron impact mass spectra

In gas-assisted FEBID, precursor molecules are delivered to the substrate surface and irradiated with an electron beam, initiating a complex deposition process involving not only primary electrons but also SEs and BSEs. To elucidate the contribution of gas-phase fragmentation in the FEBID mass spectrum, we therefore need to consider a broad electron energy range. We systematically compared gas-phase mass spectra recorded at electron energies ranging from 10 to 80 eV in 0.5 eV increments, alongside spectra acquired at 2, 5, 10, 20, and 30 keV using a SEM, against the in situ FEBID spectrum.

Fig. 4 presents a qualitative comparison of the FEBID spectrum with three gas-phase spectra at energies of 10 eV, 70 eV and 10 keV (the complete mass spectrum can be found in SI, Section S2). We confine the spectra to a mass range of 180–340 amu and normalize such that the sum of the intensities in the mass range 180–340 amu equals one. We can observe that the FEBID spectrum closely matches the 10 keV spectrum above m/q = 241 and the 70 eV spectrum below m/q =230, the difference is clearly visible from the region around m/q = 290. At 10 eV, the mass spectrum is dominated by the parent ion with significant contribution coming from the MeCpPt-nH fragment.

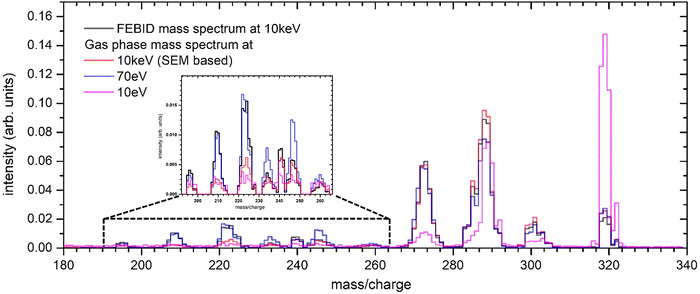Fig. 4 Comparison of normalized integer mass spectra. All spectra are normalized to the sum of all Pt containing mass peaks, i.e. the area below each curve is one.

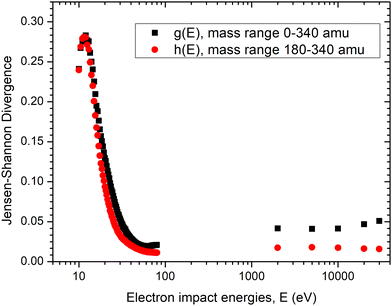
For quantitative comparison, we used the JSD measure and first focused on the mass range of 180–340 amu. We set the values of I^FEBID_mi and I^gas_mi to zero for all ion masses where no signal from MePtCpMe₃ is expected, in order to eliminate the noise contribution to the divergence. Normalization of each spectrum within the 180–340 amu range yielded discrete probability distributions p^gas_mi and p^FEBID_mi enabling the calculation of JSD, denoted as h(E). The resulting values, plotted in Fig. 5 in red, indicate a high degree of spectral similarity between FEBID and gas-phase measurements over the energy range 60 eV to 30 keV, which can be considered constant (the range between 80 eV and 2 keV is unfortunately not covered in the present experiments).

Fig. 5 The value of the Jensen–Shannon divergence used for evaluating the similarity of the 10 keV FEBID mass spectrum with the gas phase spectrum at all gas-phase electron energies. The h(E) and g(E) denote the JSD values at a given electron impact energy, E, for the two mass ranges 180–340 amu and 0–340 amu, respectively. The smaller the JSD the more similar is the gas-phase spectrum to the FEBiMS spectrum.

We further extended the analysis to the full 0–340 amu range (the normalized mass spectra can be found in SI, Section S3) by computing an additional JSD quantity, g(E). A minimum in g(E) occurs near 50 eV, followed by an increase at higher energies.

In both cases, we have observed a high degree of similarity for electron energies greater than 30 eV. This suggests that the dominant fraction of the in situ FEBID signal comes indeed from the gas-phase precursor molecules fragmented above the substrate and the growing deposit. This also shows that the role of SEs around 50 eV in causing the dissociation is important in FEBID. This was already suggested by the observation of negatively charged fragments in the FEBID using W(CO)₆.⁵ Of note is that we have removed the background masses, 18, 28, 32, 69 amu in the analysis. The difference between g(E) and h(E) at higher energies could also imply that the difference in 10 keV FEBID and 10 keV gas-phase mass spectra could be due to the observation of desorbed fragments coming from dissociation of physisorbed molecular fragments. This is particularly notable for the MeCp⁺ fragment, which is prominent in the FEBiMS and 80 eV gas-phase spectrum but almost absent in the 2 keV gas-phase spectrum. This suggests that this fragment was produced by SEs or low energy BSEs dissociating the adsorbates or gas phase molecules above the surface.

4.3 Adsorption energies of fragments to the substrate

The intensity of the charged particle signal, I, is proportional to the number density of precursor molecules, n, the ionization cross section, σ, and the length of the path travelled by the electron beam through the volume filled with molecules, I ∼ nσl. In our experiment, the adsorbed versus gas-phase ratio of ionization events is related as I_FEBID/I_gas ≈ 5 × 10² × σ_FEBID/σ_gas (see the SI of Jurczyk et al.⁵). This relationship suggests that ionization events in the adsorbed phase are dominant when assuming roughly equal cross-sections for both phases. This contradicts the above observations. Moreover, this expression does not account for how many ions from each phase reach the ion extractor and, subsequently, contribute to the ToFMS signal.

To address this, we explored the desorption behavior of charged and neutral fragments via DFT calculations as exemplified in Fig. 6, which shows a MeCpPtMe₃ molecule physisorbed on a hydroxylated quartz slab. Interestingly, the lowest energy configuration is neither with the cyclopentadienyl ring, nor with the three methyl ligands facing the substrate as is often schematically represented.³⁷ This was also observed in previous theoretical studies.^38,39Table 1 compares the calculated adsorption energies of several neutral and singly charged cation fragments observed. Evidently, the charged state increases the adsorption energy drastically: while the adsorption energy of neutral MeCpPtMe₃ to the substrate is 0.62 eV, comparable to the literature values,^38,39 the adsorption energy of the parent cation is 4.4 eV. For the bare platinum atom, the binding energy is 2.06 eV and for Pt⁺ it is 10.05 eV. The higher adsorption energies of cations can be attributed to the stronger electrostatic interactions than the weaker van der Waals interaction of neutral species.

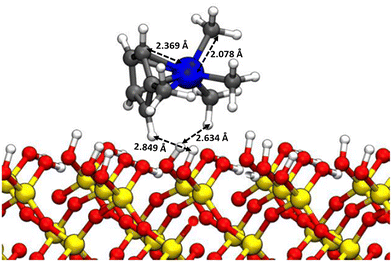Fig. 6 Optimized adsorption geometry of the neutral MeCpPtMe₃ on the hydroxylated SiO₂ slab. Color code: white – H, black – C, blue – Pt, red – O, and yellow – Si.

Table 1 The adsorption energies of the neutral and singly charged positive molecular species on the hydroxylated SiO₂ surface. Me stands for the methyl group (CH₃)

Fragment	Adsorption energy (in eV)
	Singly charged cation	Neutral
MeCpPtMe3	−4.41	−0.62
MeCpPtMe2	−5.91	−0.69
MeCpPtMe	−6.51	−1.63
PtMe3	−7.11	−1.11
Pt	−10.05	−2.06
Me	−5.87	−0.27

---

Hence, ion species created on the substrate surface have to overcome a much larger barrier than the neutrals to desorb. Following an Arrhenius-type dependence, the average thermal desorption time τ ∼ τ₀ exp(−E_ads/k_BT) depends exponentially on the adsorption energy E_ads with T being the temperature, k_B the Boltzmann constant and τ₀ being an inverse of the attempt frequency/escape frequency. The ratio of desorption times for different adsorption energies is given by

f = τ_0charged/τ_0neutral and yields τ_charged/τ_neutral ≈ f × 10⁶⁵ for MeCpPtMe₃⁺versus MeCpPtMe₃ at room temperature (20 °C) when entering the adsorption energies from Table 1. To have comparable desorption rates of ionic vs neutral ligand fragments the pre-exponential factor should be at least 10⁻⁶⁰ which is far beyond the typical vibrational frequencies (10¹³–10¹⁴ s⁻¹). This exemplifies that at room temperature the thermal desorption of cationic species with binding energies in units of eV never happens unless there are other mechanisms taking place. Considering the values for τ₀ = 10⁻¹³ s from Cullen et al.,⁴⁰ time scales of desorption of neutrals are around τ_neutral ≈ 5 ms for the parent molecule. It should be noted that the desorption behavior is more generally expressed using Polanyi–Wigner equation which has a dependence on surface coverage. It was shown theoretically that the Polanyi–Wigner frequency prefactor (can be considered as the Arrhenius pre-factor, attempt frequency) is more than two orders of magnitude greater than the value of 10¹³ s⁻¹ for a specific case.⁴¹ When we apply this correction, we obtain the characteristic desorption time τ_neutral ≈ 50 μs, which is within the order of magnitude of the experimentally determined desorption time of MeCpPtMe₃ on the silicon cantilever.⁴² This would then result in τ_charged ≈ 10⁶¹ s for charged parent ions, implying that they cannot desorb to be detected by ToFMS during FEBID. This applies further to other charged fragments in Table 1 as they have higher binding energy than the parent ion. The charge transfer could take place in the presence of the conductive substrate. This process would lead to the neutralization of fragments which would then enable desorption. However, it should be noted that neutralization of metal-containing fragments would not result in such an effect, as the adsorption energies of these fragments are still high. Consider for example, for Pt containing fragments, such as MeCpPtMe or PtMe₃, the desorption times can reach 10¹⁵ or 10⁶ s, respectively, suggesting that these fragments also do not thermally desorb during the FEBID process.

The adsorption energies reported in Table 1 correspond to the configurations with the highest interaction energy of the molecule with the surface. The existence of some configurations in which charged species have less interaction energy than the neutral is possible. In the SI, Section S4, we show that the adsorption energies for different configurations of MeCpPtMe₃ are smaller than those for the related MeCpPtMe₃⁺ configurations and hence we consider that in general the charged species have higher interaction energy than their corresponding neutrals for the substrate and molecules used in this study. Moreover, it was proven theoretically that equilibration timescales are in the order of picoseconds, much faster than the desorption time.⁴¹ This would support the consideration of the most stable configuration. As the deposit grows, the surface changes from quartz to the deposited material itself. Although values in Table 1 refer to the quartz surface, we think that the considerable difference between interaction energies of neutral and charged species will still be present.

The above considerations on desorption times assumed that the molecules are at room temperature in equilibrium with the substrate after electron impact (k_BT ≈ 25 meV). However, the energy deposited by electrons in the molecules (k_BT ≈ eV range) lead to “hot” molecules where the internal energy distribution of molecules no longer follows a room temperature Boltzmann distribution. The temperature in the Arrhenius expression can be several thousands of kelvins (1 eV corresponds to 11 604.5 K). This eventually can reduce the desorption times by several orders of magnitude. Here, the transfer of deposited energy into the substrate needs to be considered and this aspect is out of the scope of the present work.

4.4 Kinetic energy release of the fragments

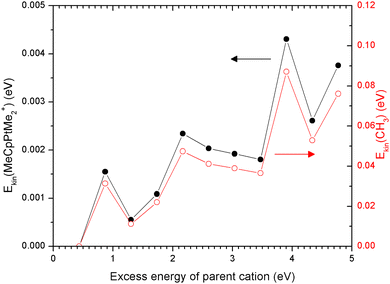
Another factor that could contribute to ion desorption from the substrate is the kinetic energy imparted into the fragment ion in the process of dissociative ionization. Such a desorption process was studied experimentally by Sanche et al.^43,44Fig. 7 shows the results of IDMD simulations²⁸ of electron-induced MeCpPtMe₃ fragmentation in the gas phase, resulting in the formation of a singly-charged MeCpPtMe₂⁺ fragment and a neutral methyl radical as a co-fragment. The horizontal axis shows the excess energy which was put into the parent MeCpPtMe₃⁺ ion at the beginning of the simulation. The vertical axis shows the average kinetic energy of the cationic (left) and neutral methyl (right) fragments at the end of the 500 ps long simulations. These are obtained as kinetic energies of the centers of mass of the two fragments. As expected purely from momentum conservation, the kinetic energies of MeCpPtMe₂⁺ are lower by approximately a factor of 20 (ratio of masses of the two fragments). The sum of the kinetic energies of the products does not equal the input excess energy as the energy is also distributed among the vibrational and rotational degrees of freedom. For the charged fragment, the maximum value of kinetic energy is around 4.5 meV, which is much lower than the eV-range adsorption energy to the substrate (5.9 eV, see Table 1). We thus conclude that for Pt-containing cations, the kinetic energy released in dissociative ionization will not increase their desorption probability. The situation may significantly change upon multiple ionization when multiply charged fragments can decay via Coulomb explosion and cascade processes.⁴⁵ Surprisingly, despite high enough electron energies of impinging electrons to doubly ionize the precursors,^46,47 the mass spectra are dominated by single ionization products as discussed above. For neutral methyl fragments, however, the kinetic energy of up to 0.1 eV is comparable with the binding energy of the methyl radical to the substrate (0.27 eV, see Table 1).

Fig. 7 Calculated average kinetic energy of the MeCpPtMe₂⁺ fragment (left axis) and the neutral methyl fragment (right axis) upon dissociative ionization in the gas phase. The horizontal axis shows the internal energy of the parent cation at the start of the IDMD simulations.

Two aspects concerning these simulations should be discussed. The first is the amount of excess energy. In the electron-impact ionization, the incident collision energy (which goes up to 30 keV in the present experiments) is divided between the two outgoing electrons and the internal energy of the cation (= excess energy). In principle, the excess energy can be much higher than the values considered here. However, it has been shown by Lyshchuk et al.²⁸ that for excess energies higher than 7 eV, the process is more fragmentative, and more than one methyl group is separated. In other words, any detected MeCpPtMe₂⁺ has to originate from a parent cation with less than this amount of excess energy. The second aspect is that the IDMD simulations have been performed for the fragmentation in the gas phase. If the precursors are adsorbed on a substrate, the excess energy can be quenched by the presence of the environment prior to the dissociation.¹⁸ This would probably lead to even lower fragment kinetic energies.

The fact that the neutral methyl fragment has a low adsorption energy and (relatively) high kinetic energy upon its release could indicate the possible explanation of the results of Jurczyk et al.⁵ Upon the irradiation of non-volatile precursor grains of silver and copper carboxylates and ruthenium carbonyls, only the ligands and their fragments were observed in the FEBiMS spectra. It is reasonable to assume that similar effects are operative in these precursor grain irradiation experiments, as presented in our current work. First, only a small part of kinetic energy is imparted into the metal atoms which is insufficient to cause the desorption of metal-containing fragments. Second, the cleaved neutral ligands interact weakly with the substrate, and are much more likely to desorb. They can be further ionized by a second electron collision in the gas phase above the substrate to be collected by the ion extractor in the ToFMS.

Our proposed mechanisms and observations are in line with the experiments of Massey et al.⁴⁸ who irradiated Fe(CO)₅ molecules condensed onto a Pt substrate at 40 K. They collected desorbed ionic fragments either by the ion collector close to the substrate (as in our setup) or by applying a keV-potential pulse on the substrate to be analyzed using a mass spectrometer. They observed ionized ligands (CO)⁺ with a significant signal and no metal containing ions. However, when adding condensed inert xenon monolayers between the Pt and the Fe(CO)₅ film, the signal of the metal containing ions increased with the number of inert Xe monolayers. This was explained through the quenching of image dipole interaction due to the Xe layer⁴⁸ which enabled the desorption of metal-containing ionic fragments. It is worth observing that they applied a voltage of 2.4 kV to the substrate after the electron pulse to collect ions. This voltage should not influence the desorption of ions: let us assume an ion with a binding energy of 1 eV to a substrate which is at a distance of 0.1 nm (typical bond length). A field strength of 1 × 10¹⁰ V m⁻¹ is required to remove it. With 2.4 kV and 10 mm distance between the electrodes as reported in the experiments of Massey et al.,⁴⁸ the field strength amounts to 2.4 × 10⁵ V m⁻¹, which is being orders of magnitude smaller.

4.5 The CH₄⁺ signal

Our results shed some light on a long-standing puzzle in the electron-induced chemistry of MeCpPtMe₃ concerning the non-Pt-containing peak, namely CH₄⁺. Surface-science experiments with electron irradiation of cryogenically condensed thin films of MeCpPtMe₃ showed that the dominant neutral volatile product is methane, CH₄, and no methyl radicals are released.¹⁷ This is very surprising in the view of the MeCpPtMe₃ structure. In contrast, the gas-phase dissociative ionization study of Engmann et al.¹⁴ reported no CH₄⁺ signal.

Detection of this ion by mass spectrometric means is difficult since m/q = 16 coincides with O⁺ ions originating from the residual oxygen and water in high and ultrahigh vacuum systems. However, our TOF spectrometer in the FEBiMS experiment has a mass resolution that can separate masses 15.999 amu (O₂²⁺ and O⁺) and 16.04 amu (CH₄⁺) as shown in Fig. 8. A plausible explanation is that CH₄⁺ observed in the FEBID mass spectrum originates from a CH₄ molecule formed in the adsorbed phase which then desorbs and is ionized by another electron in the gas phase above the substrate.

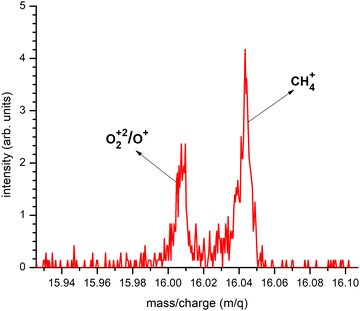Fig. 8 The O₂²⁺/O⁺ and CH₄⁺ fragments in the FEBID mass spectrum at 10 keV electron beam. A similar graph is shown for the SEM based high energy electron impact mass spectrum in the SI (see Fig. S5).

Careful examination of the CH₄⁺ peak in the SEM based high-energy gas phase experiments shows its presence, see Fig. S4 in the SI. We verified the formation of CH₄⁺ in the low-energy gas phase experiments. As the mass analyzer does not have the necessary mass resolution to separate the O₂²⁺/O⁺ and CH₄⁺, we used the ratio of peak intensities at m/q = 16 and m/q =32 and compared it to what is expected from the ionization of pure molecular oxygen. This ratio (shown in SI in Fig. S6) suggests that CH₄⁺ is present also in the low-energy gas-phase mass spectra. Our results suggest that the rearrangement reactions before the dissociation occur in the gas phase under single electron–molecule collision conditions and that the CH₃⁺ fragment efficiently abstracts a hydrogen atom upon leaving the parent molecule. This rearrangement mechanism also justifies the statistical nature of the fragmentation process considered in the IDMD simulations.²⁸

4.6 Implications for FEBID

Our above experimental and theoretical findings show that the majority of the peaks in the spectra obtained during FEBID are coming from the gas phase ionization and fragmentation. However, pairing the experimental results with calculations allows us to draw a conclusion for the FEBID process, which happens on the surface of the sample. For the cases when the charged fragments are produced by the electron beam irradiation, it is possible that significantly fast neutralization processes can lead to desorption of the produced fragments. This includes the potential SE-induced neutralization. To our knowledge, the possible role of SEs in neutralizing the charged fragments has not yet been considered.^49,50 We would like to highlight two facts. The slow SEs will be more efficient in the charge neutralization than the fast primary electrons. The more efficient neutralization will lead to a higher desorption probability of ligands and thus to a higher metal content in the nanoprinted material. The dissociative recombination⁵¹ which involves dissociation after neutralization could also play a role in FEBID. These processes are represented as:

AB⁺ + e⁻ → AB (charge neutralization)

AB⁺ + e⁻ → A + B (dissociative recombination).

Further investigation for understanding the role of these processes could provide insights for FEBID.

5. Conclusions

In this study, we conducted a detailed analysis of the performance of the FEBiMS analytical technique for in situ monitoring of FEBID using the MeCpPtMe₃ precursor. For this purpose, we recorded the surface-based FEBID process mass spectrum at 10 keV and gas phase mass spectra of this precursor at a broad range of electron energies. Their qualitative and quantitative comparison showed that most of the mass spectrometric signals, in particular, of the metal-containing ions during the MeCpPtMe₃ FEBID process originated from the dissociation and ionization of the gas-phase molecules present above the surface and not from the physisorbed molecules. This observation was rationalized by the low probability of the desorption of ions created on the surface. DFT calculations showed that they have considerably higher binding energies and their thermal desorption is not possible. The kinetic energy released in the dissociative ionization process calculated by MD was insufficient to cause their direct desorption. However, the low mass, carbon-containing fragments observed in the FEBiMS spectrum can originate from the dissociation of the molecules on the surface. Further research should be considered to properly differentiate the origin of the low-mass signals, and to properly understand the FEBiMS spectra in their full range. Additionally, from the obtained results, we propose that processes such as charge neutralization and dissociative recombination by SEs and low-energy BSEs may contribute to the low carbon content deposits, which have not been considered for the FEBID in the past, and could be of interest to investigate their cross-sections in comparison to other FEBID processes.

Conflicts of interest

There are no conflicts to declare.

Data availability

The theoretical DFT calculations and experimental data used in this study is available on https://zenodo.org/records/15043934. Molecular dynamics simulations data can be found on https://zenodo.org/records/15043934.

Supplementary information is available. DOI: https://doi.org/10.1039/d5cp02552d.

Acknowledgements

This work was funded by the Swiss National Fund by the COST-SNF project IZCOZ0_205450. C. S. J. and I. U. would like to acknowledge the support by the EU COST Action CA 19140 ‘FIT4NANO’. This work has also been supported by the H2020-MSCA-RISE-2019 project RADON (GA 872494) and by the COST Action CA20129 MultIChem. The work of J. J. was supported by the European Community under the Horizon 2020 Program, Contract No. 101001290 (3DNANOMAG). J. F. and J. K. acknowledge support from the Czech Science Foundation project 21-26601X. H. L. and J. K. acknowledge support from the MEYS Project No. CZ.02.01.01/00/22_008/0004558 (AMULET), Co-funded by the European Union. P. W. gratefully acknowledges the financial support of these studies from Gdańsk University of Technology by the DEC-22/2023/IDUB/IV.2/EUROPIUM grant under the EUROPIUM SHORT-TERM OUTGOING VISITS – ‘Excellence Initiative – Research University’ program.

Notes and references

1. L. Pillatsch, F. Östlund and J. Michler, FIBSIMS: A Review of Secondary Ion Mass Spectrometry for Analytical Dual Beam Focussed Ion Beam Instruments, Prog. Cryst. Growth Charact. Mater., 2019, 65(1), 1–19,  DOI:10.1016/j.pcrysgrow.2018.10.001.
2. J. A. Whitby, F. Östlund, P. Horvath, M. Gabureac, J. L. Riesterer, I. Utke, M. Hohl, L. Sedláček, J. Jiruše, V. Friedli, M. Bechelany and J. Michler, High Spatial Resolution Time-of-Flight Secondary Ion Mass Spectrometry for the Masses: A Novel Orthogonal ToF FIB-SIMS Instrument with In Situ AFM, Adv. Mater. Sci. Eng., 2012, 2012, 1–13,  DOI:10.1155/2012/180437.
3. A. Priebe, I. Utke, L. Pethö and J. Michler, Application of a Gas-Injection System during the FIB-TOF-SIMS Analysis—Influence of Water Vapor and Fluorine Gas on Secondary Ion Signals and Sputtering Rates, Anal. Chem., 2019, 91(18), 11712–11722,  DOI:10.1021/acs.analchem.9b02287.
4. K. Wieczerzak, A. Priebe, I. Utke and J. Michler, Practical Aspects of Focused Ion Beam Time-of-Flight Secondary Ion Mass Spectrometry Analysis Enhanced by Fluorine Gas Coinjection, Chem. Mater., 2021, 33(5), 1581–1593,  DOI:10.1021/acs.chemmater.1c00052.
5. J. Jurczyk, L. Pillatsch, L. Berger, A. Priebe, K. Madajska, C. Kapusta, I. B. Szymańska, J. Michler and I. Utke, In Situ Time-of-Flight Mass Spectrometry of Ionic Fragments Induced by Focused Electron Beam Irradiation: Investigation of Electron Driven Surface Chemistry inside an SEM under High Vacuum, Nanomaterials, 2022, 12(15), 2710,  DOI:10.3390/nano12152710.
6. V. Reisecker, R. Winkler and H. Plank, A Review on Direct-Write Nanoprinting of Functional 3D Structures with Focused Electron Beams, Adv. Funct. Mater., 2024, 34(46), 2407567,  DOI:10.1002/adfm.202407567.
7. J. M. De Teresa, A. Fernández-Pacheco, R. Córdoba, L. Serrano-Ramón, S. Sangiao and M. R. Ibarra, Review of Magnetic Nanostructures Grown by Focused Electron Beam Induced Deposition (FEBID), J. Phys. Appl. Phys., 2016, 49(24), 243003,  DOI:10.1088/0022-3727/49/24/243003.
8. J. M. De Teresa, Nanoscale Direct-Write Fabrication of Superconducting Devices for Application in Quantum Technologies, Mater. Quantum Technol., 2023, 3(1), 013001,  DOI:10.1088/2633-4356/acbefb.
9. M. Huth, F. Porrati and O. V. Dobrovolskiy, Focused Electron Beam Induced Deposition Meets Materials Science, Microelectron. Eng., 2018, 185–186, 9–28,  DOI:10.1016/j.mee.2017.10.012.
10. I. Utke, P. Swiderek, K. Höflich, K. Madajska, J. Jurczyk, P. Martinović and I. B. Szymańska, Coordination and Organometallic Precursors of Group 10 and 11: Focused Electron Beam Induced Deposition of Metals and Insight Gained from Chemical Vapour Deposition, Atomic Layer Deposition, and Fundamental Surface and Gas Phase Studies, Coord. Chem. Rev., 2022, 458, 213851,  DOI:10.1016/j.ccr.2021.213851.
11. S. Barth, M. Huth and F. Jungwirth, Precursors for Direct-Write Nanofabrication with Electrons, J. Mater. Chem. C, 2020, 8(45), 15884–15919,  10.1039/D0TC03689G.
12. R. M. Thorman, P. A. Jensen, J.-C. Yu, S. J. Matsuda, L. McElwee-White, O. Ingólfsson and D. H. Fairbrother, Electron-Induced Reactions of Ru(CO)₄I₂: Gas Phase, Surface, and Electron Beam-Induced Deposition, J. Phys. Chem. C, 2020, 124(19), 10593–10604,  DOI:10.1021/acs.jpcc.0c01801.
13. E. Bilgilisoy, A. Kamali, T. X. Gentner, G. Ballmann, S. Harder, H.-P. Steinrück, H. Marbach and O. Ingólfsson, A Combined Gas-Phase Dissociative Ionization, Dissociative Electron Attachment and Deposition Study on the Potential FEBID Precursor [Au(CH₃)₂Cl]₂, Beilstein J. Nanotechnol., 2023, 14, 1178–1199,  DOI:10.3762/bjnano.14.98.
14. S. Engmann, M. Stano, Š. Matejčík and O. Ingólfsson, Gas Phase Low Energy Electron Induced Decomposition of the Focused Electron Beam Induced Deposition (FEBID) Precursor Trimethyl (Methylcyclopentadienyl) Platinum(IV) (MeCpPtMe₃), Phys. Chem. Chem. Phys., 2012, 14(42), 14611,  10.1039/c2cp42637d.
15. P. Martinović, M. Rohdenburg, A. Butrymowicz, S. Sarigül, P. Huth, R. Denecke, I. B. Szymańska and P. Swiderek, Electron-Induced Decomposition of Different Silver(I) Complexes: Implications for the Design of Precursors for Focused Electron Beam Induced Deposition, Nanomaterials, 2022, 12(10), 1687,  DOI:10.3390/nano12101687.
16. T. P. Ragesh Kumar, I. Unlu, S. Barth, O. Ingólfsson and D. H. Fairbrother, Electron Induced Surface Reactions of HFeCo₃ (CO)₁₂, a Bimetallic Precursor for Focused Electron Beam Induced Deposition (FEBID), J. Phys. Chem. C, 2018, 122(5), 2648–2660,  DOI:10.1021/acs.jpcc.7b08611.
17. J. D. Wnuk, J. M. Gorham, S. G. Rosenberg, W. F. Van Dorp, T. E. Madey, C. W. Hagen and D. H. Fairbrother, Electron Induced Surface Reactions of the Organometallic Precursor Trimethyl(Methylcyclopentadienyl)Platinum(IV), J. Phys. Chem. C, 2009, 113(6), 2487–2496,  DOI:10.1021/jp807824c.
18. B. Andreides, A. V. Verkhovtsev, J. Fedor and A. V. Solov’yov, Role of the Molecular Environment in Quenching the Irradiation-Driven Fragmentation of Fe(CO)₅: A Reactive Molecular Dynamics Study, J. Phys. Chem. A, 2023, 127(17), 3757–3767,  DOI:10.1021/acs.jpca.2c08756.
19. J. Lengyel, J. Fedor and M. Fárník, Ligand Stabilization and Charge Transfer in Dissociative Ionization of Fe(CO)₅ Aggregates, J. Phys. Chem. C, 2016, 120(31), 17810–17816,  DOI:10.1021/acs.jpcc.6b05852.
20. F. Kolb, K. Schmoltner, M. Huth, A. Hohenau, J. Krenn, A. Klug, E. J. W. List and H. Plank, Variable Tunneling Barriers in FEBID Based PtC Metal-Matrix Nanocomposites as a Transducing Element for Humidity Sensing, Nanotechnology, 2013, 24(30), 305501,  DOI:10.1088/0957-4484/24/30/305501.
21. G. Arnold, R. Winkler, M. Stermitz, A. Orthacker, J. Noh, J. D. Fowlkes, G. Kothleitner, M. Huth, P. D. Rack and H. Plank, Tunable 3D Nanoresonators for Gas-Sensing Applications, Adv. Funct. Mater., 2018, 28(19), 1707387,  DOI:10.1002/adfm.201707387.
22. J. Sattelkow, J. E. Fröch, R. Winkler, S. Hummel, C. Schwalb and H. Plank, Three-Dimensional Nanothermistors for Thermal Probing, ACS Appl. Mater. Interfaces, 2019, 11(25), 22655–22667,  DOI:10.1021/acsami.9b04497.
23. M. Dukic, M. Winhold, C. H. Schwalb, J. D. Adams, V. Stavrov, M. Huth and G. E. Fantner, Direct-Write Nanoscale Printing of Nanogranular Tunnelling Strain Sensors for Sub-Micrometre Cantilevers, Nat. Commun., 2016, 7(1), 12487,  DOI:10.1038/ncomms12487.
24. A. Priebe, J.-P. Barnes, T. E. J. Edwards, E. Huszár, L. Pethö and J. Michler, Elemental Characterization of Al Nanoparticles Buried under a Cu Thin Film: TOF-SIMS vs STEM/EDX, Anal. Chem., 2020, 92(18), 12518–12527,  DOI:10.1021/acs.analchem.0c02361.
25. M. Fárník, J. Fedor, J. Kočišek, J. Lengyel, E. Pluhařová, V. Poterya and A. Pysanenko, Pickup and Reactions of Molecules on Clusters Relevant for Atmospheric and Interstellar Processes, Phys. Chem. Chem. Phys., 2021, 23(5), 3195–3213,  10.1039/D0CP06127A.
26. T. D. Kühne, M. Iannuzzi, M. Del Ben, V. V. Rybkin, P. Seewald, F. Stein, T. Laino, R. Z. Khaliullin, O. Schütt, F. Schiffmann, D. Golze, J. Wilhelm, S. Chulkov, M. H. Bani-Hashemian, V. Weber, U. Borštnik, M. Taillefumier, A. S. Jakobovits, A. Lazzaro, H. Pabst, T. Müller, R. Schade, M. Guidon, S. Andermatt, N. Holmberg, G. K. Schenter, A. Hehn, A. Bussy, F. Belleflamme, G. Tabacchi, A. Glöβ, M. Lass, I. Bethune, C. J. Mundy, C. Plessl, M. Watkins, J. VandeVondele, M. Krack and J. Hutter, CP2K: An Electronic Structure and Molecular Dynamics Software Package – Quickstep: Efficient and Accurate Electronic Structure Calculations, J. Chem. Phys., 2020, 152(19), 194103,  DOI:10.1063/5.0007045.
27. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, Williams, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. C.01, 2016.
28. H. Lyshchuk, A. V. Verkhovtsev, J. Kočišek, J. Fedor and A. V. Solov’yov, Release of Neutrals in Electron-Induced Ligand Separation from MeCpPtMe₃: Theory Meets Experiment, J. Phys. Chem. A, 2025, 129(8), 2016–2023,  DOI:10.1021/acs.jpca.4c08259.
29. G. B. Sushko, I. A. Solov’yov and A. V. Solov’yov, Molecular Dynamics for Irradiation Driven Chemistry: Application to the FEBID Process, Eur. Phys. J. D, 2016, 70(10), 217,  DOI:10.1140/epjd/e2016-70283-5.
30. I. A. Solov’yov, A. V. Yakubovich, P. V. Nikolaev, I. Volkovets and A. V. Solov’yov, MesoBioNano Explorer—A Universal Program for Multiscale Computer Simulations of Complex Molecular Structure and Dynamics, J. Comput. Chem., 2012, 33(30), 2412–2439,  DOI:10.1002/jcc.23086.
31. Dynamics of Systems on the Nanoscale, ed. I. A. Solov’yovA. V. Verkhovtsev, A. V. Korol and A. V. Solov’yov, Lecture Notes in Nanoscale Science and Technology, Springer International Publishing, Cham, 2022, vol. 3410 DOI:10.1007/978-3-030-99291-0.
32. A. V. Solov’yov, A. V. Verkhovtsev, N. J. Mason, R. A. Amos, I. Bald, G. Baldacchino, B. Dromey, M. Falk, J. Fedor, L. Gerhards, M. Hausmann, G. Hildenbrand, M. Hrabovský, S. Kadlec, J. Kočišek, F. Lépine, S. Ming, A. Nisbet, K. Ricketts, L. Sala, T. Schlathölter, A. E. H. Wheatley and I. A. Solov’yov, Condensed Matter Systems Exposed to Radiation: Multiscale Theory, Simulations, and Experiment, Chem. Rev., 2024, 124(13), 8014–8129,  DOI:10.1021/acs.chemrev.3c00902.
33. A. V. Verkhovtsev, I. A. Solov’yov and A. V. Solov’yov, Irradiation-Driven Molecular Dynamics: A Review, Eur. Phys. J. D, 2021, 75(7), 213,  DOI:10.1140/epjd/s10053-021-00223-3.
34. P. De Vera, A. Verkhovtsev, G. Sushko and A. V. Solov’yov, Reactive Molecular Dynamics Simulations of Organometallic Compound W(CO)₆ Fragmentation, Eur. Phys. J. D, 2019, 73(10), 215,  DOI:10.1140/epjd/e2019-100232-9.
35. G. B. Sushko, I. A. Solov’yov, A. V. Verkhovtsev, S. N. Volkov and A. V. Solov’yov, Studying Chemical Reactions in Biological Systems with MBN Explorer: Implementation of Molecular Mechanics with Dynamical Topology, Eur. Phys. J. D, 2016, 70(1), 12,  DOI:10.1140/epjd/e2015-60424-9.
36. J. Creech, J. Baker, M. Handler, M. Schiller and M. Bizzarro, Platinum Stable Isotope Ratio Measurements by Double-Spike Multiple Collector ICPMS, J. Anal. At. Spectrom., 2013, 28(6), 853,  10.1039/c3ja50022e.
37. J. A. Spencer, S. G. Rosenberg, M. Barclay, Y.-C. Wu, L. McElwee-White and D. Howard Fairbrother, Understanding the Electron-Stimulated Surface Reactions of Organometallic Complexes to Enable Design of Precursors for Electron Beam-Induced Deposition, Appl. Phys. A: Mater. Sci. Process., 2014, 117(4), 1631–1644,  DOI:10.1007/s00339-014-8570-5.
38. J. Shen, K. Muthukumar, H. O. Jeschke and R. Valentí, Physisorption of an Organometallic Platinum Complex on Silica: An Ab Initio Study, New J. Phys., 2012, 14(7), 073040,  DOI:10.1088/1367-2630/14/7/073040.
39. K. Muthukumar, H. O. Jeschke and R. Valentí, Dynamics and Fragmentation Mechanism of (C₅H₄CH₃)Pt(CH₃)₃ on SiO₂ Surfaces, Beilstein J. Nanotechnol., 2018, 9, 711–720,  DOI:10.3762/bjnano.9.66.
40. J. Cullen, A. Bahm, C. J. Lobo, M. J. Ford and M. Toth, Localized Probing of Gas Molecule Adsorption Energies and Desorption Attempt Frequencies, J. Phys. Chem. C, 2015, 119(28), 15948–15953,  DOI:10.1021/acs.jpcc.5b00918.
41. D. Alfè and M. J. Gillan, Ab Initio Statistical Mechanics of Surface Adsorption and Desorption. I. H₂O on MgO(001) at Low Coverage, J. Chem. Phys., 2007, 127(11), 114709,  DOI:10.1063/1.2772258.
42. V. Friedli, C. Santschi, J. Michler, P. Hoffmann and I. Utke, Mass Sensor for in Situ Monitoring of Focused Ion and Electron Beam Induced Processes, Appl. Phys. Lett., 2007, 90(5), 053106,  DOI:10.1063/1.2435611.
43. Y. Yildirim, M. Balcan, A. D. Bass, P. Cloutier and L. Sanche, Electron Stimulated Desorption of Anions and Cations from Condensed Allyl Glycidyl Ether, Phys. Chem. Chem. Phys., 2010, 12(28), 7950,  10.1039/b925347e.
44. P. Rowntree, H. Sambe, L. Parenteau and L. Sanche, Formation of Anionic Excitations in the Rare-Gas Solids and Their Coupling to Dissociative States of Adsorbed Molecules, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47(8), 4537–4554,  DOI:10.1103/PhysRevB.47.4537.
45. S. Indrajith, P. Rousseau, B. A. Huber, C. Nicolafrancesco, A. Domaracka, K. Grygoryeva, P. Nag, B. Sedmidubská, J. Fedor and J. Kočišek, Decomposition of Iron Pentacarbonyl Induced by Singly and Multiply Charged Ions and Implications for Focused Ion Beam-Induced Deposition, J. Phys. Chem. C, 2019, 123(16), 10639–10645,  DOI:10.1021/acs.jpcc.9b00289.
46. K. Głuch, J. Cytawa and L. Michalak, Electron Impact Ionization of Acrylonitrile, Int. J. Mass Spectrom., 2008, 278(1), 10–14,  DOI:10.1016/j.ijms.2008.07.001.
47. K. Głuch, S. Feil, V. G. Hasan, S. Matt-Leubner, T. Tepnual, O. Echt, V. Grill, P. Scheier and T. D. Märk, Coulomb Explosion of Ions Produced by Electron Impact Ionization of Toluene, Vacuum, 2005, 78(2–4), 187–191,  DOI:10.1016/j.vacuum.2005.01.024.
48. S. Massey, A. D. Bass and L. Sanche, Role of Low-Energy Electrons (<35 eV) in the Degradation of Fe(CO)5 for Focused Electron Beam Induced Deposition Applications: Study by Electron Stimulated Desorption of Negative and Positive Ions, J. Phys. Chem. C, 2015, 119(22), 12708–12719,  DOI:10.1021/acs.jpcc.5b02684.
49. N. G. Adams and D. Smith, Laboratory Studies of Dissociative Recombination and Mutual Neutralization and Their Relevance to Interstellar Chemistry, in Rate Coefficients in Astrochemistry, ed. T. J. Millar and D. A. Williams, Astrophysics and Space Science Library, Springer Netherlands, Dordrecht, 1988, vol. 146, pp. 173–192 DOI:10.1007/978-94-009-3007-0_11.
50. W. D. Geppert and M. Larsson, Experimental Investigations into Astrophysically Relevant Ionic Reactions, Chem. Rev., 2013, 113(12), 8872–8905,  DOI:10.1021/cr400258m.
51. J. Brian, The Dissociative Recombination of Molecular Ions, Phys. Rep., 1990, 186(5), 215–248,  DOI:10.1016/0370-1573(90)90159-Y.

---