Open Access Article
Open Access ArticleThermodynamic properties of lower critical solution temperature (LCST) mixtures for application in energy–water systems†
Jordan D.
Kocher
 a,
Ahmed
Mahfouz
a,
Jesse G.
McDaniel
b and
Akanksha K.
Menon
a,
Ahmed
Mahfouz
a,
Jesse G.
McDaniel
b and
Akanksha K.
Menon
 *a
*a
aGeorge W. Woodruff School of Mechanical Engineering, Georgia Institute of Technology, Atlanta, GA 30332, USA. E-mail: akanksha.menon@me.gatech.edu
bSchool of Chemistry and Biochemistry, Georgia Institute of Technology, Atlanta, GA 30332, USA
First published on 25th June 2025
Abstract
Mixtures that possess a lower critical solution temperature (LCST) phase behavior are homogeneous at temperatures below the LCST and separate into two phases above the LCST. These materials have recently received interest for use in various applications, including refrigeration, dehumidification, desalination, and atmospheric water harvesting. However, proof-of-concept demonstrations of cycles employing these materials have shown poor performance, due to the thermodynamic properties of existing LCST mixtures. This work develops a theoretical framework to evaluate the thermodynamic properties (chemical potential, partial molar enthalpy, and partial molar entropy) required for a mixture to exhibit LCST behavior and meet the application-specific property targets. Our analysis reveals that a hypothetical LCST mixture that would outperform existing ones would need a more negative partial molar enthalpy (to achieve lower chemical potentials), but it would also need a more negative partial molar entropy (to preserve LCST behavior). Specifically, LCST refrigeration and dehumidification would require a partial molar enthalpy and entropy of water that are an order of magnitude greater than existing LCST mixtures, while LCST-based desalination requires properties 2.5× greater than existing mixtures. We show that improved LCST mixtures with lower chemical potentials would necessarily need more heat to induce phase separation, and we derive an expression to predict the enthalpy of separation using water activity data. Finally, we demonstrate that the addition of a hygroscopic additive (e.g., LiCl) to an LCST mixture does not increase the chemical potential difference between the two phases. Overall, this work lays out the thermodynamic framework and target properties that new LCST mixtures must possess and discusses implications for system performance.
Introduction
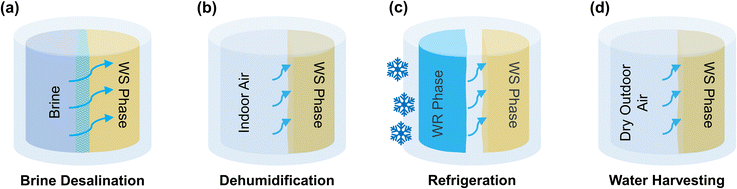
Mixture separation is ubiquitous in the modern world for various energy and water end-uses, such as desalination1–3 and absorption refrigeration.4,5 Some separations are driven by work, such as reverse osmosis for desalination, while others are driven by heat, such as the desorption process used for sorbent regeneration in dehumidifiers6 and sorption refrigerators.5 Distillation is a common method of thermal separation for aqueous solutions, where water is evaporated from the mixture (e.g., seawater) and then condensed to produce fresh water.7–10 However, the latent heat of vaporization of water is orders of magnitude larger than the thermodynamic minimum heat of separation. For example, the minimum heat of separation of water from a solution with a water activity of 0.98 (i.e., seawater) is 14 kJ kg−1 when the ambient temperature is 25 °C and the heat source is at 100 °C, whereas the latent heat of vaporization of water is 2256 kJ kg−1 at 100 °C – this is 161× higher than the theoretical minimum (i.e., thermodynamically reversible case). Distillation systems reduce their heat input to ∼13× the theoretical minimum11 by recycling the latent heat across multiple stages with recuperative heat exchangers, but this improvement in efficiency comes with increased capital costs.Liquid mixtures that possess a lower critical solution temperature (LCST) separate into two immiscible phases when heated above the LCST.12–26 This liquid–liquid thermal separation can be more efficient than vaporization-based distillation methods – for example, an LCST mixture is heated to induce separation, the two immiscible phases (water-rich and water-scarce) are then separated, after which they can be sent through a recuperator to preheat the original mixture. In this manner, the reversible limit of separation heat is approached using a single recuperator, instead of the many stages used in distillation. This in turn could enable highly efficient dehumidification,16–18,27 refrigeration,18 desalination,14,28,29 or atmospheric water harvesting systems.17,30
In aqueous LCST mixtures, the chemical potentials of the two phases after separation determine the performance of the cycle in which the LCST mixture is being used. For example, if the chemical potential of water in the water-scarce phase is not low enough, an LCST dehumidifier would not be able to lower the indoor humidity to sufficiently low levels, an LCST refrigerator would not reach sufficiently low temperatures, and an LCST desalination system would not be able to treat hypersaline brines. Performance will also suffer if the chemical potential of water in the water-rich phase is not high enough – the LCST dehumidifier would not be able to operate when the outdoor humidity is high, and an LCST desalination system would produce very impure permeate, requiring post-treatment to yield fresh water. Thus, it is important to pinpoint the underlying thermophysical properties that LCST mixtures must possess for the aforementioned applications.
However, literature on LCST mixtures leaves a lot to be desired – most prior reports focused on the discovery and/or characterization of new LCST mixtures12,21–24,31 and hydrogels,32–36 while other works discussed new thermodynamic cycles that utilize LCST materials.14,16–19,28,37–40 There are only a couple of studies on the properties that produce LCST behavior in a mixture, but these tend to focus on specific chemistries – for example, the tradeoff between hydrophobicity and hydrophilicity has been identified as a cause of LCST behavior in ionic liquids,12,13 with the hydration state of functional groups in the solute (e.g., carboxylic group in P4444Tf-Leu12) being a key factor. In this work, we address these gaps by taking a more general thermodynamic approach that complements prior materials-focused analyses. This theoretical framework (guided by experimental insights from existing LCST materials) is then applied to establish targets for the thermophysical properties that improved LCST mixtures must possess and discusses its implications for system performance, thus serving as a guide for designing new materials.
For a mixture that exhibits LCST behavior to outperform existing LCST mixtures, we show that the chemical potential, partial molar enthalpy, and partial molar entropy of water must all be more negative. A negative entropy is necessary for the solvent chemical potential to increase with temperature at higher solute concentrations, leading to LCST behavior. Since the entropy is negative, the enthalpy must also be negative for mixing to occur spontaneously at temperatures below the LCST. Using this framework, we provide estimates for the partial molar enthalpy and entropy of water values that ideal LCST mixtures must possess for their application in dehumidification, refrigeration, desalination, and atmospheric water harvesting. We then show that these improved LCST mixtures with lower chemical potentials of water in the water-scarce phase would necessarily require more energy (heat) for phase separation than existing LCST mixtures. Finally, we provide experimental results for the addition of a hygroscopic additive (LiCl) to an LCST mixture, which indicates that this approach will not yield the target properties necessary for the aforementioned applications.
Theory
Thermodynamics of mixtures
For a binary mixture consisting of a solvent (subscript w) and solute (subscript u), eqn (1) is the expression for the Gibbs free energy of the mixture, where μ is the partial molar Gibbs free energy, also known as chemical potential, and ni is the number of moles of species i.41| G = nwμw + nuμu | (1) |
If μ* is the chemical potential of a pure (i.e., unmixed) substance, the Gibbs free energy of the mixture can be expressed as eqn (2), where gmix is the molar free energy of mixing.
 | (2) |
Taking the partial derivative of eqn (2) with respect to nw gives eqn (3), the expression for the chemical potential of the solvent species w within the mixture, μmw.
 | (3) |
The difference between the chemical potential of the mixed and pure substance is defined in eqn (4), where aw is the activity of the solvent species w.
 | (4) |
The partial derivative  can be rewritten as
can be rewritten as  , where x is the solute concentration (mole fraction). The solvent and solute chemical potentials relative to chemical potentials of pure species can then be expressed as eqn (5) and (6), respectively.
, where x is the solute concentration (mole fraction). The solvent and solute chemical potentials relative to chemical potentials of pure species can then be expressed as eqn (5) and (6), respectively.
 | (5) |
 | (6) |
Combining eqn (5) and (6) yields eqn (7) as the relationship between solute and solvent chemical potential.
 | (7) |
Additionally, the Gibbs–Duhem relation yields eqn (8) for the chemical potential of all species in a mixture when temperature and pressure are held constant. For a binary mixture, eqn (8) can be rewritten as eqn (9).
 | (8) |
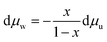 | (9) |
Thus, if the chemical potential of one species (solvent or solute) is known at a particular temperature and pressure, the chemical potential of the other species can be found by integrating the expression in eqn (9).
LCST thermodynamics
In a binary LCST mixture, the two species are miscible at all concentrations when the temperature is below the LCST. Above the LCST, the mixture will separate into two phases when its concentration lies within a certain range (the miscibility gap). This results in a phase diagram shown in Fig. 1a, where the single- and two-phase regions are separated by the binodal (or coexistence) curve.At temperature T2, which is above the LCST, the two concentrations that lie on the binodal curve are xp and xq. These two phases emerge because the sum of the free energies of the two phases is less than that of the corresponding single phase. This is shown in Fig. 1b – the tangent (dashed line) between xp and xq represents the free energy of two coexisting, immiscible phases at those concentrations, and it lies below gmix for any concentration that is greater than xp and less than xq. Therefore, the free energy of the two immiscible phases is lower than the free energy of a single phase at T2, making it thermodynamically favorable. Thus, xp and xq are the two points on the binodal curve at T2, and this method of constructing the phase diagram is known as the “common tangent method”.42 Additional details on the common tangent method are provided in Note S3 (ESI†).
Because the mixture is miscible in all proportions at temperatures below the LCST, no two points on gmix can have a common tangent at T1, which is below the LCST (Fig. 1b). In other words,  must monotonically increase as a function of concentration at temperatures below the LCST
must monotonically increase as a function of concentration at temperatures below the LCST  . By differentiating eqn (5) and (6), it can be seen that μw must monotonically decrease with solute concentration, while μu monotonically increases at temperatures below the LCST (Fig. 1c and d).
. By differentiating eqn (5) and (6), it can be seen that μw must monotonically decrease with solute concentration, while μu monotonically increases at temperatures below the LCST (Fig. 1c and d).
Above the LCST, the two phases with different concentrations are in equilibrium. For this to be the case, the chemical potential of the solvent must be equal at both of these concentrations (eqn (10) and Fig. 1c), as must the chemical potential of the solute (eqn (11) and Fig. 1d).
| μw(xp,T2) = μw(xq,T2) | (10) |
| μu(xp,T2) = μu(xq,T2) | (11) |
This equality of chemical potentials at xp and xq at T2 is already satisfied with the common tangent condition. From eqn (5),  is equal to
is equal to  , which is the left vertical-axis intercept of the tangent in Fig. 1b, while eqn (6) reveals that
, which is the left vertical-axis intercept of the tangent in Fig. 1b, while eqn (6) reveals that  is the right vertical axis intercept. If the two points share a tangent at T2, then they have the same intercepts, and therefore those concentrations have the same chemical potentials at that temperature.
is the right vertical axis intercept. If the two points share a tangent at T2, then they have the same intercepts, and therefore those concentrations have the same chemical potentials at that temperature.
Once the two phases are physically separated and cooled to T1, they would re-mix to form a single phase at this lower temperature. Because of this, the chemical potentials at xp and xq are different at T1. As such, the chemical potential of water at xp must be a stronger or weaker function of temperature than it is at xq. This is depicted in Fig. 1c and d, where the chemical potentials at xp and xq are not equal at T1, but they change by different amounts to become equal when the temperature is increased to T2.
This example illustrates that both solvent and solute chemical potentials must change as a function of temperature for mixtures that possess an LCST, but the magnitude of these changes could be vastly different. The remainder of this work focuses on the chemical potential of the solvent (water), since this is a relevant parameter that determines the performance of many energy and water systems (e.g., refrigeration, dehumidification, and desalination) that utilize LCST mixtures.
Enthalpy, entropy, and chemical potential of water in LCST mixtures
As discussed, the chemical potential of water monotonically decreases with increasing solute concentration at temperatures below the LCST. Then, above the LCST, the chemical potential of water is no longer monotonic, and there exist multiple concentrations at which the chemical potential is equal. This is depicted in Fig. 2, with two scenarios in Fig. 2a that give rise to the equality of chemical potential necessary for LCST behavior to emerge. | ||
Fig. 2 Change in chemical potential of water required to induce phase separation in LCST mixtures. (a) Chemical potential at ambient temperature (T1) and two possible scenarios that would give rise to phase separation at a temperature above the LCST (T2). (b) The chemical potential of water in the “base” mixture at T1 (μw(T1), solid blue curve) and T2 (μw(T2), dashed light blue curve), as well as an “improved” mixture, which has a lower chemical potential than the base mixture at T1 ( , solid orange curve) but the same chemical potential at T2. Eqn (5) is used to obtain the water chemical potential trends of Fig. 2 based on the gmix trends at T1 and T2 shown in Fig. 1b. , solid orange curve) but the same chemical potential at T2. Eqn (5) is used to obtain the water chemical potential trends of Fig. 2 based on the gmix trends at T1 and T2 shown in Fig. 1b. | ||
In the first scenario, the chemical potential of water at xq (higher concentration) increases with temperature to match that at xp, which remains relatively unchanged with temperature. In the second scenario, the chemical potential of water at xp decreases to match that at xq. For the applications discussed in this work, the ideal aqueous LCST mixture would be very close to pure water at xp. In this case, the water activity at xp would be a weak function of temperature. This resembles Scenario 1 in Fig. 2a and is consistent with our experimental data from real LCST mixtures – at xp, the chemical potential of water is relatively unchanged with increasing temperature (shown in Note S1, ESI†). For this reason, we focus on LCST mixtures with properties that correspond to the first scenario for the remainder of this work.
The change in chemical potential of water with an incremental change in temperature (at constant pressure and concentration) is equal to the partial molar entropy of water, ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) w, as described by eqn (12) (derived in Note S2, ESI†).
w, as described by eqn (12) (derived in Note S2, ESI†).
 | (12) |
Because Δμq (change in chemical potential of water at concentration xq upon heating from T1 to T2) is positive for Scenario 1 in Fig. 2a, the inequality in eqn (13) must hold.
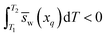 | (13) |
If the partial molar entropy of water at xq, ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) w(xq), is constant with temperature, then the only way for the integral in eqn (13) to be negative is if
w(xq), is constant with temperature, then the only way for the integral in eqn (13) to be negative is if ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) w(xq) is negative. This can arise from a negative entropy of mixing (i.e., a material that becomes more ordered in the presence of water) at a concentration xq; however, in certain cases, a negative value of
w(xq) is negative. This can arise from a negative entropy of mixing (i.e., a material that becomes more ordered in the presence of water) at a concentration xq; however, in certain cases, a negative value of ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) w(xq) can arise from an exclusively positive entropy of mixing (see Note S5, ESI†). If
w(xq) can arise from an exclusively positive entropy of mixing (see Note S5, ESI†). If ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) w(xq) is not constant with temperature, it must be negative within at least some portion of the temperature range T1 to T2, such that the integral in eqn (13) is net negative, for Scenario 1 in Fig. 2a to emerge. This non-linear trend is evident in the chemical potential of water for an LCST ionic liquid shown in Fig. S2a (ESI†). Meanwhile,
w(xq) is not constant with temperature, it must be negative within at least some portion of the temperature range T1 to T2, such that the integral in eqn (13) is net negative, for Scenario 1 in Fig. 2a to emerge. This non-linear trend is evident in the chemical potential of water for an LCST ionic liquid shown in Fig. S2a (ESI†). Meanwhile, ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) w(xp) is small in magnitude given that Δμp (change in chemical potential of water at concentration xp upon heating from T1 to T2) is nearly zero for Scenario 1 in Fig. 2a.
w(xp) is small in magnitude given that Δμp (change in chemical potential of water at concentration xp upon heating from T1 to T2) is nearly zero for Scenario 1 in Fig. 2a.
Eqn (13) would appear to suggest that the partial molar entropy of water is the only parameter necessary to give rise to LCST behavior. But the behavior of LCST mixtures at temperatures below the LCST reveals that the enthalpy is also important. Specifically, the chemical potential of water at concentration xq and temperature T1, μw(xq,T1), must be negative for the two species to be miscible. From eqn (14), this means that the partial molar enthalpy, ![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) w(xq,T1), must also be negative for this to occur.
w(xq,T1), must also be negative for this to occur.
μw(xq,T1) = ![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) w(xq,T1) − T1 w(xq,T1) − T1![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) w(xq,T1) < 0 w(xq,T1) < 0 | (14) |
If the partial molar entropy varies as a function of temperature, so too will the partial molar enthalpy of water, ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) w(xq,T1), according to eqn (15) (derived in Note S2, ESI†). Notably, eqn (15) is true for any substance held at constant pressure and concentration, not just for LCST mixtures.
w(xq,T1), according to eqn (15) (derived in Note S2, ESI†). Notably, eqn (15) is true for any substance held at constant pressure and concentration, not just for LCST mixtures.
 | (15) |
Accordingly, a binary mixture with a partial molar entropy of water that varies with temperature must also have a partial molar enthalpy of water that varies with temperature, and vice versa. At a given concentration (e.g., xq), the enthalpy and entropy of water are inextricably linked viaeqn (15).
Thus, eqn (13) and (14) reveal the necessary properties of LCST mixtures that follow Scenario 1 in Fig. 2a: (i) the partial molar entropy must be negative for the chemical potential of water to increase with temperature, which is the case for existing LCST mixtures (experimental data is shown in Note S1, ESI†), and (ii) the partial molar enthalpy of water must also be negative. A more negative enthalpy than what has been observed in existing LCST mixtures would result in a lower chemical potential at ambient temperature (therefore improving performance as we discuss in the next section). However, since the chemical potential of water at ambient temperature,  , would then be more negative, the new change in chemical potential upon heating,
, would then be more negative, the new change in chemical potential upon heating,  , must be greater (than Δμq) for the mixture to still phase separate at the same temperature T2. Thus, the partial molar entropy in this new and improved LCST mixture must also be more negative. These changes are illustrated in Fig. 2b.
, must be greater (than Δμq) for the mixture to still phase separate at the same temperature T2. Thus, the partial molar entropy in this new and improved LCST mixture must also be more negative. These changes are illustrated in Fig. 2b.
While LCST separation could theoretically arise from Scenario 2, this behavior has not been observed in the aqueous LCST mixtures reported in literature. It is worth noting that both Scenario 1 and Scenario 2 require endothermic separation; that is, heat is absorbed by the mixture as it phase separates at temperatures above the LCST. In Note S6 (ESI†), we show that this behavior applies to all LCST mixtures.
Given the intricate nature of these mixtures, some simplifications must be made to obtain analytical expressions for approximating target properties of LCST mixtures for different energy and water applications properties. First, we assume that the chemical potential of water in the mixture at the water-rich concentration, μw(xp), does not vary strongly with temperature (Scenario 1 in Fig. 2a). Then, because μw(xp,T2) = μw(xq,T2) as shown in Fig. 2a, it holds that μw(xq,T2) ≈ μw(xp,T1). In this case, Δμq, which is the change in chemical potential of water at xq from T1 to T2, is equal to the water chemical potential difference between xp and xq at T1, which we refer to as Δμw – this is illustrated in Fig. 2b. Next, we assume that the partial molar entropy of water at any concentration is constant with temperature, in which case the integration of eqn (12) yields eqn (16). The validity of this assumption is supported by experimental data for the chemical potential of water in both phases, which is approximately linear with temperature for an LCST deep eutectic solvent as shown in Fig. S2b and c (ESI†). Since the chemical potential and partial molar entropy of water are related by eqn (12), if μw varies approximately linearly with temperature, it follows that ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) w is nearly constant or invariant with temperature. When the partial molar entropy of water changes as a function of temperature, eqn (16) represents the average value from T1 to T2.
w is nearly constant or invariant with temperature. When the partial molar entropy of water changes as a function of temperature, eqn (16) represents the average value from T1 to T2.
 | (16) |
In some cases, the chemical potential of water exhibits a non-linear trend with temperature as shown in Fig. S2a (ESI†) for an LCST ionic liquid. To calculate the exact partial molar entropy of water, numerical differentiation of eqn (12) must be performed at either xp or xq depending on which of the two scenarios illustrated in Fig. 2 holds true for that particular LCST mixture. Our final assumption is that the mixture at the water-rich concentration, xp, has properties approximate to those of pure water. This has been observed for many existing LCST mixtures,13,18 and it is a desired trait of an ideal LCST mixture for the applications described in this work. As such, we treat the chemical potential, partial molar enthalpy, and partial molar entropy of water at xp as being negligible based on eqn (4), i.e., μw(xp) ≈ 0, ![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) w(xp) ≈ 0, and
w(xp) ≈ 0, and ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) w(xp) ≈ 0. From this approximation, eqn (17) results for the partial molar entropy of water in the water-scarce phase of an LCST mixture. Meanwhile, combining eqn (14) and (17) yields eqn (18), which provides an approximation for the partial molar enthalpy of water in the water-scarce phase of the LCST mixture.
w(xp) ≈ 0. From this approximation, eqn (17) results for the partial molar entropy of water in the water-scarce phase of an LCST mixture. Meanwhile, combining eqn (14) and (17) yields eqn (18), which provides an approximation for the partial molar enthalpy of water in the water-scarce phase of the LCST mixture.
 | (17) |
 | (18) |
In summary, the partial molar properties at xp are approximated as zero, while the partial molar enthalpy and entropy of water at xq can be expressed entirely in terms T1, T2, and μw(xq,T1).
Application-specific property targets for LCST materials
The thermodynamic framework established thus far can be used to estimate the properties that an ideal LCST mixture must possess for the four applications depicted in Fig. 3. By defining the necessary water activity of the water-scarce phase, we can calculate the corresponding chemical potential, μw(xq,T1), using eqn (4). Desalination1–3,14,28,43,44 requires a water activity as low as 0.75 in the water-scarce phase, as this value corresponds to the activity of saturated brine (26 wt% NaCl). On the other hand, atmospheric water harvesting30,43,45,46 in arid regions requires an activity as low as 0.10, as this corresponds to the relative humidity of ambient air. Air conditioning6,16,17,38,47,48 requires a water activity around 0.40,17 which corresponds to a comfortable indoor relative humidity of 40%,49 and it is also the value needed to produce a temperature drop of ∼10 °C via evaporative cooling (determined from a psychrometric chart).An example calculation of the chemical potential of water in the water-scarce phase for the refrigeration application is as follows: if the ambient temperature is T1 = 300 K, a water activity of 0.40 equates to a chemical potential of μw(xq,T1) = −2285.5 J mol−1 (from eqn (4)). If T2 = 343 K, then ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) w(xq) ≈ −53.2 J mol−1 K−1 (from eqn (17)) and hw(xq) ≈ −18
w(xq) ≈ −53.2 J mol−1 K−1 (from eqn (17)) and hw(xq) ≈ −18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 231 J mol−1 (from eqn (18)). Table 1 summarizes these values (water activity, chemical potential, and partial molar properties) required for LCST refrigeration, along with the values needed for the desalination and atmospheric water harvesting applications.
231 J mol−1 (from eqn (18)). Table 1 summarizes these values (water activity, chemical potential, and partial molar properties) required for LCST refrigeration, along with the values needed for the desalination and atmospheric water harvesting applications.
| Application | Water activity | Chemical potential of water at 300 K (J mol−1) | Partial molar enthalpy of water (J mol−1) | Partial molar entropy of water (J mol−1 K−1) |
|---|---|---|---|---|
| Brine desalination | 0.750 | −717.58 | −5724 | −16.7 |
| Refrigeration or dehumidification | 0.400 | −2285.5 | −18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 231 231 |
−53.2 |
| Atmospheric water harvesting | 0.100 | −5743.5 | −45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 814 814 |
−133.6 |
| OA/LD | 0.890 | −288.1 | — | — |
| PTFA | 0.976 | −60.6 | — | — |
Performance of existing LCST mixtures
Having established these targets for “ideal” mixtures, we can now compare them to existing LCST mixtures. For this, we performed activity measurements on two LCST mixtures based on a deep eutectic solvent and ionic liquid mixed with water (Note S1, ESI†). Oleic acid/lidocaine (OA/LD), a deep eutectic solvent with LCST phase behavior,15 after separation at T2 = 343 K, has a water-scarce phase with a chemical potential of μw(xq,T1) ≈ −290.7 J mol−1 at an ambient temperature of T1 = 300 K. Meanwhile, tetrabutylphosphonium trifluoroacetate (PTFA),13,14 an ionic liquid with LCST phase behavior, has chemical potential of μw(xq,T1) ≈ −60.6 J mol−1 after being separated at 343 K. Comparing the chemical potentials of these existing LCST mixtures with the application-specific targets in Table 1 reveals that the chemical potential of an ideal aqueous LCST mixture is approximately 8× that of OA/LD and 38× that of PTFA at the water-scarce concentration xq. We note that some assumptions were made to obtain these values as previously discussed, and this is valid for an LCST mixture that separates into a water-rich phase that is nearly pure water, as is the case with OA/LD (based on experimental measurements shown in Note S1, ESI†).Notably, Table 1 reveals that it is more realistic for an LCST mixture to possess the properties required for desalination compared to atmospheric water harvesting or refrigeration and dehumidification. The water harvesting case would require a particularly hygroscopic material (water activity ∼0.10; e.g., LiCl) at ambient temperature, which then becomes very hydrophobic (water activity ∼1) when the temperature is raised by tens of degrees – it is unrealistic for a single material to possess these properties. Even for desalination application, the values in Table 1 indicate that the properties of current LCST mixtures based on ionic liquids are much smaller than the target properties. This motivates the need to explore different chemistries and design new materials to achieve the target behavior – OA/LD shows promise, but desalination based on this mixture is yet to be demonstrated.
Heat of separation
Another critical parameter for LCST mixtures is the heat required for phase separation. Some studies in the literature have proposed using LCST hydrogels for dehumidification and atmospheric water harvesting with little energy input.27,30,37,50,51 Some of these works have erroneously neglected the heat of separation/demixing and only considered sensible heating in their energy analyses.37,51 This is because existing LCST hydrogels and liquid mixtures require a small amount of heat (10–40 J g−1 for LCST liquids14 and hydrogels35) to induce phase separation. However, as we showed in the previous section, an LCST mixture with a more negative water-scarce chemical potential (lower water activity) is necessary for applications, but this will be accompanied by a more negative water partial molar enthalpy and entropy (eqn (13) and (14)). An improved LCST mixture would thus require more heat for separation.To evaluate whether the “improved” mixture requires more heat to separate than the “base” mixture in Fig. 2b, we consider the cycle in Fig. 4, in which an LCST mixture, initially at ambient temperature (T1), is heated to T3 (above the LCST) to induce phase separation. Q1 is the heat required to raise the initial mixture temperature, T1, to the LCST, which is an entirely sensible heat (i.e., no heat of separation). Meanwhile, Q2 is the combination of the heat required to induce phase separation (Qsep) and the sensible heat required to raise the temperature of the mixture from the LCST to T3.
In Fig. 4, the two phases have the same chemical potential of water at T3, but when they are physically separated and cooled to ambient temperature, they have different chemical potentials. Because they have different chemical potentials, they can produce work in the process of returning to equilibrium. If a membrane permeable only to water were used to produce this work, then the maximum (i.e., reversible) increment of work that could be produced for a differential amount of water transferred between the two phases, dnw, is given in eqn (19). xWR is the concentration of the water-rich phase (initially at xp), and xWS is the concentration of the water-scarce phase (initially at xq); integrating eqn (19) from state 4 to 1 would yield the total amount of work produced.
| δW = [μw(xWR,T1) − μw(xWS,T1)]dnw | (19) |
Assuming that the specific heat is constant across the separation process, a second law analysis of the entire cycle reveals that both ΔSsep = Q4/T1 and 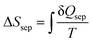 . If we define an effective temperature of separation
. If we define an effective temperature of separation  , then we can write ΔSsep = Qsep/Tsep where Tsep is essentially the thermodynamic average temperature of separation that will always be between the LCST and T3. Meanwhile, a first law analysis of the cycle reveals that W = Qsep − Q4, which can be rewritten in the form expressed in eqn (20).
, then we can write ΔSsep = Qsep/Tsep where Tsep is essentially the thermodynamic average temperature of separation that will always be between the LCST and T3. Meanwhile, a first law analysis of the cycle reveals that W = Qsep − Q4, which can be rewritten in the form expressed in eqn (20).
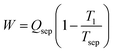 | (20) |
Combining eqn (19) and (20) yields eqn (21) for the enthalpy of separation, where  is the average chemical potential of water difference between the two phases from state 4 to 1 in Fig. 4b, and xi is the initial mixture concentration before separation.
is the average chemical potential of water difference between the two phases from state 4 to 1 in Fig. 4b, and xi is the initial mixture concentration before separation.  is a material property that can be evaluated using eqn (22), which only requires that the chemical potential of water be known for the mixture between the concentrations xWR and xWS at ambient temperature. In eqn (22), w is a dimensionless quantity that represents the transfer of water from the WR phase to the WS phase during process 4 to 1 in Fig. 4b. The units of separation enthalpy in eqn (21) are energy per mol of total mixture before separation. Notably, even though the expression in eqn (21) was derived from the hypothetical cycle in Fig. 4, the enthalpy of separation is a state function, so the expression in eqn (21) is process independent and can be used to calculate the heat of separation for any LCST mixture. The detailed derivations of eqn (21) and (22) are provided in Note S7 (ESI†).
is a material property that can be evaluated using eqn (22), which only requires that the chemical potential of water be known for the mixture between the concentrations xWR and xWS at ambient temperature. In eqn (22), w is a dimensionless quantity that represents the transfer of water from the WR phase to the WS phase during process 4 to 1 in Fig. 4b. The units of separation enthalpy in eqn (21) are energy per mol of total mixture before separation. Notably, even though the expression in eqn (21) was derived from the hypothetical cycle in Fig. 4, the enthalpy of separation is a state function, so the expression in eqn (21) is process independent and can be used to calculate the heat of separation for any LCST mixture. The detailed derivations of eqn (21) and (22) are provided in Note S7 (ESI†).
 | (21) |
 | (22) |
In eqn (21), Tsep is the effective separation temperature and must take a value between T2 and T3 in Fig. 4b. Thus, for regeneration at a given T3, and with knowledge of the binodal curve temperature at the initial mixture concentration (T2), a reasonable estimate can be obtained for the effective separation temperature. Alternatively, Δhsep can be evaluated for the entire possible range of Tsep, which spans [T2,T3].
Using experimental data of the chemical potential of water reported in the literature, the average chemical potential  is tabulated for various LCST mixtures in Table 2. For each mixture, the initial mixture concentration (state 1, before phase separation) is 50 wt% water and 50 wt% ionic liquid or deep eutectic solvent (OA/LD). From this, the enthalpy of separation is estimated, using an approximation for the effective separation temperature:
is tabulated for various LCST mixtures in Table 2. For each mixture, the initial mixture concentration (state 1, before phase separation) is 50 wt% water and 50 wt% ionic liquid or deep eutectic solvent (OA/LD). From this, the enthalpy of separation is estimated, using an approximation for the effective separation temperature:  , where T2 is the binodal curve temperature at 50 wt% (determined from literature data) and T3 is the regeneration temperature, which was taken to be the highest temperature at which the binodal curve data was reported for each mixture (since minimal further phase separation occurs beyond this temperature). The quantity Δw is the number of moles of water transported (per mole of initial mixture) between the WR and WS phase in the hypothetical process 4 to 1 from Fig. 4b. Notably, the calculated values for P4444TFA and P4444DMBS are in excellent agreement with the range of values measured by Haddad et al.10 ∼5 J g−1 using differential scanning calorimetry (DSC). This approach of determining the enthalpy of separation is preferable to a DSC measurement, since the enthalpy of separation of existing LCST mixtures is much smaller than the typical latent heat values used to calibrate the instrument (∼5 J g−1 for LCST mixtures compared to the latent heat of melting ice of 334 J g−1), which could lead to inaccurate measurements.
, where T2 is the binodal curve temperature at 50 wt% (determined from literature data) and T3 is the regeneration temperature, which was taken to be the highest temperature at which the binodal curve data was reported for each mixture (since minimal further phase separation occurs beyond this temperature). The quantity Δw is the number of moles of water transported (per mole of initial mixture) between the WR and WS phase in the hypothetical process 4 to 1 from Fig. 4b. Notably, the calculated values for P4444TFA and P4444DMBS are in excellent agreement with the range of values measured by Haddad et al.10 ∼5 J g−1 using differential scanning calorimetry (DSC). This approach of determining the enthalpy of separation is preferable to a DSC measurement, since the enthalpy of separation of existing LCST mixtures is much smaller than the typical latent heat values used to calibrate the instrument (∼5 J g−1 for LCST mixtures compared to the latent heat of melting ice of 334 J g−1), which could lead to inaccurate measurements.
We can now answer our original question regarding whether an LCST mixture with a greater chemical potential difference  will require more heat input to separate than one with a smaller chemical potential difference (Δμq). Clearly, a more negative value of μw(xWS,T1) would result in greater work output (per eqn (19)). But, as is the case in any reversible heat engine operating between thermal reservoirs at fixed temperatures, more work output requires more heat input to separate (per eqn (20)) – there is “no free lunch”. This increase in separation heat that accompanies greater chemical potential differences can be circumvented to some extent by finding an LCST mixture that phase separates at higher temperatures. Most aqueous LCST mixtures that have been reported in literature separate at temperatures ∼ 10 °C higher than ambient, with a few exceptions that have LCST values around 60 °C (N4444CF3COO and P4444ToS13). Mixtures that separate in the range of 70–90 °C would avoid boiling while still taking advantage of lower heats of separation, making these suitable from an application standpoint.
will require more heat input to separate than one with a smaller chemical potential difference (Δμq). Clearly, a more negative value of μw(xWS,T1) would result in greater work output (per eqn (19)). But, as is the case in any reversible heat engine operating between thermal reservoirs at fixed temperatures, more work output requires more heat input to separate (per eqn (20)) – there is “no free lunch”. This increase in separation heat that accompanies greater chemical potential differences can be circumvented to some extent by finding an LCST mixture that phase separates at higher temperatures. Most aqueous LCST mixtures that have been reported in literature separate at temperatures ∼ 10 °C higher than ambient, with a few exceptions that have LCST values around 60 °C (N4444CF3COO and P4444ToS13). Mixtures that separate in the range of 70–90 °C would avoid boiling while still taking advantage of lower heats of separation, making these suitable from an application standpoint.
LCST behavior with a positive entropy of mixing
In the literature, a negative enthalpy and entropy of mixing are listed as prerequisites for LCST phase behavior (conversely, a positive enthalpy and entropy of mixing are stated as prerequisites for UCST behavior).14,22,52,53 Our finding that LCST phase separation is necessarily endothermic supports these statements. However, we now demonstrate that a negative entropy of mixing is not a strict requirement and that LCST phase behavior can indeed emerge in a mixture that possesses an entropy of mixing that is positive at all concentrations.In Fig. 5, we plot two different hypothetical entropies of mixing (one exclusively negative, one exclusively positive), while also plotting the Gibbs free energy (using the enthalpy of mixing curve provided in Note S5) to reveal that both would possess LCST phase behavior. From Fig. 5b, there is no common tangent at the lower temperature of 300 K (indicating that the mixture is miscible in all proportions), but at 350 K, there is a common tangent (indicating the presence of a miscibility gap). Thus, this mixture possesses LCST phase behavior (phase separation upon heating). Meanwhile, in Fig. 5c, the entropy of mixing is positive at all concentrations. Importantly, the entropy of mixing is lower at the intermediate concentrations. From this entropy of mixing, along with the enthalpy of mixing in Fig. S5b (ESI†), the Gibbs free energy in Fig. 5d is obtained, which again shows no common tangent (i.e., miscibility in all proportions) at 300 K and the presence of a common tangent (i.e., a miscibility gap) at 350 K. Thus, a positive entropy of mixing can indeed lead to LCST phase behavior, provided that the entropy of mixing is lower in the region of the miscibility gap. Furthermore, even though the entropy of mixing is exclusively positive, the partial molar entropies are still negative at certain points (see Note S5, ESI†), because it is dependent not only on the magnitude of the entropy of mixing at a certain point, but also the slope at that point. Thus, the conclusions drawn earlier in this work regarding the partial molar entropy of water being negative at the WS concentration of an LCST mixture are still valid to this hypothetical mixture with a positive entropy of mixing.
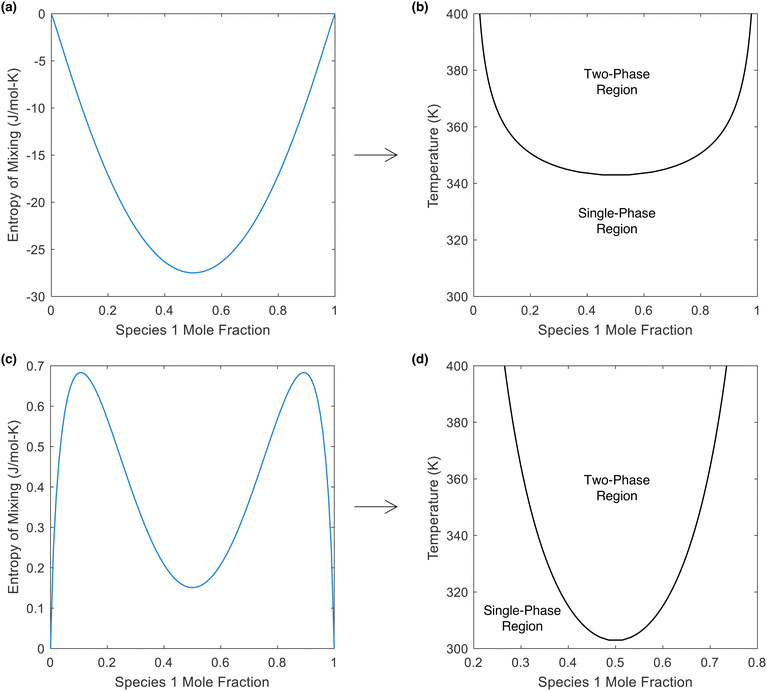 | ||
| Fig. 5 Entropy and phase diagram for two different hypothetical mixtures. (a) Entropy of mixing that is exclusively negative. (b) The LCST phase diagram that results from the entropy of mixing in (a), along with the enthalpy of mixing in Fig. S4b (ESI†). (c) Entropy of mixing that is exclusively positive. (d) The LCST phase diagram that results from the entropy of mixing in (c), along with the enthalpy of mixing in Fig. S5b (ESI†). The phase diagrams in (b) and (d) were obtained using the common tangent method, which was applied to the Gibbs free energy at temperatures between 300 and 400 K. The Gibbs free energy is plotted for each of these hypothetical mixtures in Note S5 (ESI†); the presence of a miscibility gap at higher temperatures is evident for both mixtures, proving that LCST phase behavior can occur with an exclusively positive entropy of mixing. | ||
Given that literature has tied LCST phase behavior to the requirement that the entropy of mixing must be negative, the findings herein could lead to the discovery of new LCST mixtures. This in turn could yield new LCST mixtures that meet the target properties outlined in this work, since the discovery of mixtures with highly negative entropies of mixing is difficult (because the “ideal” contribution to the entropy of mixing is always positive). Furthermore, the insight that LCST phase behavior can emerge in systems with exclusively positive entropies of mixing could also explain the presence of LCST behavior ionic liquid/acetone mixtures54 and ionic liquid mixtures with small perhalogenated hydrocarbons.55 Although the entropy of mixing was not quantified for these mixtures, it is possible that they have a positive entropy of mixing due to the lack of structured/directional hydrogen bonding interactions that contribute to the negative entropy of mixing in aqueous LCST mixtures.
Furthermore, it is important to note that even though the sign of the entropy of mixing is different for the two mixtures explored in Fig. 5, both mixtures would have endothermic phase separation (i.e., they would both absorb heat upon separating). In Note S6 (ESI†), we show that exothermic phase separation is non-physical for an LCST mixture, and any LCST mixture (whether the entropy of mixing is positive or negative) would possess both a positive enthalpy and entropy of separation. This is because the enthalpy and entropy of separation are not simply the inverse of the enthalpy and entropy of mixing; rather, they are determined by the change in enthalpy and entropy of mixing when going from a single-phase state to a biphasic state.
Effect of salt additives on LCST mixtures
Finally, we discuss the effect of adding a hygroscopic salt to an existing LCST mixture as a means to increase Δμq. Previous work has shown that hygroscopic additives impact the sorption behavior of LCST hydrogels in atmospheric water harvesting and dehumidification applications27,30,38 by allowing them to absorb moisture from lower humidities than the pure LCST hydrogel. However, the water chemical potential difference between the dry hydrogel and expelled liquid water after heating was not quantified. In this section, we experimentally measure the chemical potential of water in oleic acid/lidocaine with and without a hygroscopic salt to observe if this improves Δμq.Certain salts, such as LiCl, are very hygroscopic and are often used as desiccants.56,57 As such, we investigated the addition of LiCl to an aqueous mixture of OA/LD, finding that the addition of LiCl does not increase the water chemical potential difference between the two phases as shown in Fig. 6a. Instead, the entire chemical potential curve is shifted down, as depicted in Fig. 6b, such that Δμw is about the same with or without salt. Therefore, while these results warrant further investigation, they indicate that the water chemical potential difference between the two phases is determined by the LCST species within the mixture and adding hygroscopic salts is not a viable method to increase this. Hygroscopic additives will thus not improve existing LCST mixtures to achieve the targets necessary for the applications shown in Table 1. However, adding chloride salts to an LCST mixture can be used to tune the chemical potentials of the two phases at a fixed difference (Δμw). This in turn could be leveraged to shift the chemical potentials of a given LCST mixture around the water activities needed for a particular operation. It could also be used in a multi-stage or cascade configuration to obtain an overall Δμq that is greater than that of a single stage.
We also note that while the focus of this thermodynamic analysis was on aqueous LCST mixtures, the findings can be extended to LCST mixtures with other solvents. In particular, the finding that negative entropy of mixing is not a strict requirement for LCST behavior (as illustrated in Note S5, ESI†) may help rationalize empirical observations of LCST behavior among more general classes of ionic liquid mixtures that do not exhibit structured/directional hydrogen bonding interactions, such as ionic liquid/acetone mixtures54 or ionic liquid mixtures with small perhalogenated hydrocarbons.55
Looking ahead, modern computational methods such as molecular dynamics (MD) simulations and machine learning techniques may substantially aid the design and utilization of novel LCST mixtures for target applications. In this regard, MD simulations provide an atomistic description of the intermolecular interactions and microscopic liquid structure that dictate the molecular thermodynamic properties (e.g., μw(xWS,T1))controlling the phase behavior and application performance (Table 1). From simulations, structure–property relationships can be developed to provide insight into and to predict the complex dependence of thermodynamic parameters on molecular structure, properties, and interactions of the constituent species (e.g., ionic liquids, deep eutectic solvents) in LCST mixtures. Furthermore, MD simulations can be used to develop “bottom-up” molecular thermodynamics models of LCST phase behavior in which the requisite parameters such as molar entropy and enthalpy are computed in a “first-principles” manner directly from the simulations, rather than being empirically parameterized. Because the simulations are “information-rich”, a powerful approach is to take advantage of modern machine learning tools to synthesize the high dimensional, atomistic data into meaningful collective variables or fingerprints that encode quantitative structure–property relationships;58 an approach that has shown promise in predicting LCST phase behavior of complex systems.59 The stringent property requirements for various applications (Table 1) will necessitate a close collaboration of experimental and computational approaches to discover and design new LCST mixtures that meet the outlined criteria.
Conclusion
In this work, we derive the thermodynamic relations relevant to mixtures that possess LCST behavior, which are useful both for designing new materials and for analyzing thermodynamic cycles that utilize these materials. We then use this framework to demonstrate (i) the need for more negative partial molar enthalpies and entropies, (ii) the challenge with utilizing LCST mixtures for applications such as atmospheric water harvesting, (iii) the importance of including the heat of separation in analyses of thermodynamic cycles that utilize LCST mixtures, (iv) that LCST phase behavior can emerge even when the entropy of mixing is positive at all concentrations, and (v) that phase separation of LCST mixtures is always endothermic.For emerging applications of LCST mixtures (air conditioning, desalination, and atmospheric water harvesting), the necessary thermophysical properties are summarized as follows:
• Improved aqueous LCST mixtures must have a lower chemical potential of water at ambient temperature and concentration xq (concentration of the water-scarce phase).
• This lower chemical potential will be caused by a more negative partial molar enthalpy of water. However, to preserve LCST behavior, the partial molar entropy of water must also become more negative.
The chemical potential changes required for LCST mixtures to perform in certain applications (e.g., atmospheric water harvesting) will be harder to achieve than other applications (e.g., desalination). To design materials that achieve the target properties for these applications, it will be important to identify the chemistries that yield more negative partial molar enthalpies of water (i.e., stronger bonding upon the addition of water) and more negative partial molar entropies of water (i.e., more ordering upon the addition of water).
However, there is no “free lunch”; while these ideal LCST mixtures – with lower chemical potentials in the water-scarce phase – would perform better than existing ones (e.g., achieve lower temperatures when used in a refrigeration cycle, absorb moisture from lower humidities, etc.), they would necessarily require more heat for regeneration. This is true not only for liquid LCST mixtures based on ionic liquids and deep eutectic solvents, but also for LCST hydrogels.
Furthermore, adding a salt (LiCl) to existing LCST mixtures lowers the water chemical potential of both the water-rich and water-scarce phases, such that the chemical potential difference between the phases is unchanged. While this behavior can be exploited in certain ways (i.e., multi-stage or cascaded operation), it indicates that hygroscopic additives will not improve the performance of existing LCST materials and new mixtures must be discovered.
Author contributions
Conceptualization: JDK. Methodology: JDK. Investigation: JDK and AM. Visualization: JDK. Resources: JDK and AKM. Writing – original draft: JDK. writing – review & editing: JDK, AM, JGM, and AKM.Conflicts of interest
J. D. K. is the inventor on an international patent (application number PCT/US2023/065629, patent pending), a U. S. patent (application number 18/298796, patent pending), and a provisional patent, which describe various uses of LCST materials in air conditioning cycles. A. K. M. is a co-inventor on US patent number 11845682 that describes the use of LCST materials for desalination. The authors declare that they have no other competing interests.Data availability
The data supporting this article have been included as part of the ESI.†Acknowledgements
J. D. K. acknowledges financial support from the IBUILD Fellowship. This research was performed under an appointment to the Building Technologies Office (BTO) IBUILD-Graduate Research Fellowship administered by the Oak Ridge Institute for Science and Education (ORISE) and managed by Oak Ridge National Laboratory (ORNL) for the U. S. Department of Energy (DOE). ORISE is managed by Oak Ridge Associated Universities (ORAU). All opinions expressed in this paper are the author's and do not necessarily reflect the policies and views of DOE, EERE, BTO, ORISE, ORAU or ORNL. A. K. M acknowledges the Woodruff School of Mechanical Engineering at Georgia Tech for startup funds used to perform this work. The authors would like to thank Dr Andrew Z. Haddad for synthesizing P4444TFA, which was used to provide water activity data of real LCST mixtures in the ESI.†References
- J. Eke, A. Yusuf, A. Giwa and A. Sodiq, Desalination, 2020, 495, 114633 CrossRef CAS.
- M. Elimelech and W. A. Phillip, Science, 2011, 333, 712–717 CrossRef CAS PubMed.
- M. S. Mauter and P. S. Fiske, Energy Environ. Sci., 2020, 13, 3180–3184 RSC.
- T. Berlitz, H. Plank, F. Ziegler and R. Kahn, Int. J. Refrig., 1998, 21, 219–229 CrossRef CAS.
- P. Srikhirin, S. Aphornratana and S. Chungpaibulpatana, Renewable Sustainable Energy Rev., 2001, 5, 343–372 CrossRef CAS.
- K. S. Rambhad, P. V. Walke and D. J. Tidke, Renewable Sustainable Energy Rev., 2016, 59, 73–83 CrossRef CAS.
- A. M. Alklaibi and N. Lior, J. Membr. Sci., 2006, 282, 362–369 CrossRef CAS.
- W. P. Parker, J. D. Kocher and A. K. Menon, Desalination, 2024, 580, 117560 CrossRef CAS.
- J. Swaminathan, H. W. Chung, D. M. Warsinger and J. H. Lienhard, Appl. Energy, 2018, 211, 715–734 CrossRef CAS.
- S. Xu, L. Xu, X. Wu, P. Wang, D. Jin, J. Hu, S. Zhang, Q. Leng and D. Wu, Desalination, 2019, 467, 64–78 CrossRef CAS.
- H. Nassrullah, S. F. Anis, R. Hashaikeh and N. Hilal, Desalination, 2020, 491, 114569 CrossRef CAS.
- Y. Kohno and H. Ohno, Phys. Chem. Chem. Phys., 2012, 14, 5063–5070 RSC.
- E. Kamio, A. Takenaka, T. Takahashi and H. Matsuyama, J. Membr. Sci., 2019, 570–571, 93–102 CrossRef CAS.
- A. Z. Haddad, A. K. Menon, H. Kang, J. J. Urban, R. S. Prasher and R. Kostecki, Environ. Sci. Technol., 2021, 55, 3260–3269 CrossRef CAS PubMed.
- O. Longeras, A. Gautier, K. Ballerat-Busserolles and J.-M. Andanson, ACS Sustainable Chem. Eng., 2020, 8, 12516–12520 CrossRef CAS.
- A. Rana and R. Y. Wang, Energy Convers. Manage., 2024, 301, 118029 CrossRef.
- J. D. Kocher, S. K. Yee and R. Y. Wang, Energy Convers. Manage., 2022, 253, 115158 CrossRef CAS.
- J. D. Kocher, A. K. Menon and S. K. Yee, American Society of Mechanical Engineers Digital Collection, 2023 Search PubMed.
- C.-H. Hsu, C. Ma, N. Bui, Z. Song, A. D. Wilson, R. Kostecki, K. M. Diederichsen, B. D. McCloskey and J. J. Urban, ACS Omega, 2019, 4, 4296–4303 CrossRef CAS PubMed.
- S. Darvishmanesh, B. A. Pethica and S. Sundaresan, Desalination, 2017, 421, 23–31 CrossRef CAS.
- H. Iwasawa, D. Uchida, Y. Hara, M. Tanaka, N. Nakamura, H. Ohno and T. Ichikawa, Adv. Opt. Mater., 2023, 11, 2370081 CrossRef.
- Y. Kohno and H. Ohno, Chem. Commun., 2012, 48, 7119–7130 RSC.
- Y. Kohno, Y. Deguchi and H. Ohno, Chem. Commun., 2012, 48, 11883–11885 RSC.
- S. Saita, Y. Mieno, Y. Kohno and H. Ohno, Chem. Commun., 2014, 50, 15450–15452 RSC.
- S. Saita, Y. Kohno and H. Ohno, Chem. Commun., 2012, 49, 93–95 RSC.
- A. Mahfouz, A. Z. Haddad, J. D. Kocher and A. K. Menon, J. Mater. Chem. A, 2025, 13, 275–288 RSC.
- K. Matsumoto, N. Sakikawa and T. Miyata, Nat. Commun., 2018, 9, 2315 CrossRef PubMed.
- Y. Cai, W. Shen, J. Wei, T. H. Chong, R. Wang, W. B. Krantz, A. G. Fane and X. Hu, Environ. Sci.: Water Res. Technol., 2015, 1, 341–347 RSC.
- A. Z. Haddad, A. K. Menon, R. Revanur, J. Klare, J. J. Urban and R. Kostecki, Ind. Eng. Chem. Res., 2025, 64(15), 7810–7817 CrossRef CAS PubMed.
- F. Zhao, X. Zhou, Y. Liu, Y. Shi, Y. Dai and G. Yu, Adv. Mater., 2019, 31, 1806446 CrossRef PubMed.
- T. Ando, Y. Kohno, N. Nakamura and H. Ohno, Chem. Commun., 2013, 49, 10248–10250 RSC.
- Y. Deguchi, Y. Kohno and H. Ohno, Chem. Commun., 2015, 51, 9287–9290 RSC.
- Y.-H. Chu and C.-Y. Chen, Mater. Chem. Front., 2021, 5, 7286–7290 RSC.
- C. Pelosi, E. Guazzelli, M. Calosi, L. Bernazzani, M. R. Tiné, C. Duce and E. Martinelli, Appl. Sci., 2021, 11, 2711 CrossRef CAS.
- V. Y. Grinberg, A. S. Dubovik, D. V. Kuznetsov, N. V. Grinberg, A. Y. Grosberg and T. Tanaka, Macromolecules, 2000, 33, 8685–8692 CrossRef CAS.
- S. M. Tehrani, Y. Lu and M. A. Winnik, Macromolecules, 2016, 49, 8711–8721 CrossRef CAS.
- J. D. Kocher, MS thesis, Arizona State University, 2019.
- Y. Zeng, J. Woods and S. Cui, Energy Convers. Manage., 2021, 244, 114520 CrossRef CAS.
- J. D. Kocher, WO/2023/201227, 2023.
- J. D. Kocher and R. Wang, US20240117977A1, 2024.
- ed. M. J. Moran, Fundamentals of Engineering Thermodynamics, Wiley, Hoboken, NJ, 8th edn, 2014 Search PubMed.
- D. V. Schroeder, An Introduction to Thermal Physics, Addison Wesley Longman, 2000, pp. 186–200 Search PubMed.
- J. D. Kocher and A. K. Menon, Energy Environ. Sci., 2023, 16, 4983–4993 RSC.
- A. K. Menon, M. Jia, S. Kaur, C. Dames and R. S. Prasher, iScience, 2023, 26, 105966 CrossRef CAS PubMed.
- J. D. Kocher and A. K. Menon, American Society of Mechanical Engineers Digital Collection, 2023 Search PubMed.
- J. Lord, A. Thomas, N. Treat, M. Forkin, R. Bain, P. Dulac, C. H. Behroozi, T. Mamutov, J. Fongheiser, N. Kobilansky, S. Washburn, C. Truesdell, C. Lee and P. H. Schmaelzle, Nature, 2021, 598, 611–617 CrossRef PubMed.
- J. Woods, N. James, E. Kozubal, E. Bonnema, K. Brief, L. Voeller and J. Rivest, Joule, 2022, 6, 726–741 CrossRef CAS.
- E. Kozubal, J. Woods, J. Burch, A. Boranian and T. Merrigan, Desiccant Enhanced Evaporative Air-Conditioning (DEVap): Evaluation of a New Concept in Ultra Efficient Air Conditioning, National Renewable Energy Laboratory, Technical Report, NREL/TP-5500-49722, 2011, DOI:10.2172/1004010.
- Moisture Control, Part of Indoor Air Quality Design Tools for Schools, https://www.epa.gov/iaq-schools/moisture-control-part-indoor-air-quality-design-tools-schools, (accessed January 10, 2023) Search PubMed.
- G. Chen, Phys. Chem. Chem. Phys., 2022, 24, 12329–12345 RSC.
- X. Zhang, Z. Guo, W. Li and D.-J. Lee, Appl. Therm. Eng., 2024, 247, 123095 CrossRef CAS.
- H.-N. Lee and T. P. Lodge, J. Phys. Chem. Lett., 2010, 1, 1962–1966 CrossRef CAS.
- H. Yamauchi and Y. Maeda, J. Phys. Chem. B, 2007, 111, 12964–12968 CrossRef CAS PubMed.
- S. Dong, J. Heyda, J. Yuan and C. A. Schalley, Chem. Commun., 2016, 52, 7970–7973 RSC.
- M. B. Shiflett and A. Yokozeki, Fluid Phase Equilib., 2007, 259, 210–217 CrossRef CAS.
- N. Fumo and D. Y. Goswami, Sol. Energy, 2002, 72, 351–361 CrossRef CAS.
- H. F. Gibbard and G. Scatchard, J. Chem. Eng. Data, 1973, 18, 293–298 CrossRef CAS.
- S. Koutsoukos, F. Philippi, F. Malaret and T. Welton, Chem. Sci., 2021, 12, 6820–6843 RSC.
- H. Jung and A. Yethiraj, J. Phys. Chem. B, 2020, 124, 9230–9238 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp02285a |
| This journal is © the Owner Societies 2025 |