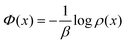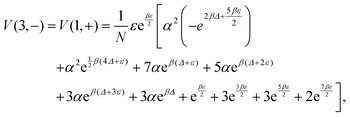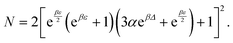Open Access Article
Open Access ArticleNegative specific heats: where Clausius and Boltzmann entropies separate
Lander
Bogers
 ,
Faezeh
Khodabandehlou
and
Christian
Maes
,
Faezeh
Khodabandehlou
and
Christian
Maes

Department of Physics and Astronomy, KU Leuven, Belgium. E-mail: christian.maes@kuleuven.be
First published on 23rd June 2025
Abstract
Steady nonequilibria dissipate energy and, when changing external parameters, an extra or excess heat accompanies the relaxation to the new nonequilibrium condition. For nonequilibrium systems in contact with a thermal bath, the heat capacity is defined as that excess heat per degree temperature for a quasistatic change of the bath temperature. It is fairly common to find negative heat capacities for steady nonequilibrium systems, in contrast with the situation for systems in thermal equilibrium. We discuss and illustrate the origin of that negative thermal response using Markov models. We find that the negativity results from an anticorrelation between quasipotential and (a change in) pseudopotential, the first measuring (excess) heat (and Clausius entropy), and the latter being related to the Boltzmann entropy. It can be quantified via an appropriate choice of effective temperatures.
I. Introduction
There is only one entropy for macroscopic equilibrium systems. The original understanding of the Clausius or thermodynamic entropy S derives from the well-known formula δQrev/T = dS, part of the famous heat theorem from which reversible heat over temperature is an exact differential. While the kinetic interpretation of temperature marked the beginning of statistical mechanics, the notion of heat got its role and place in bookkeeping changes in energy (first law of thermodynamics). So many years later, the work of Boltzmann, Planck and Einstein gave a totally new and statistical meaning to entropy, where we now write S = kB![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) W for the Boltzmann entropy counting the microscopic degeneracy W of a macroscopic condition (at some fixed energy etc.). Miraculously, Boltzmann and Clausius entropies (and others like the Gibbs ensemble entropy) agree under thermodynamic equilibrium, at least for quasilocal interactions. It implies that fluctuations, governed by the Boltzmann entropy, and dissipation, represented by the Clausius entropy, are closely linked as also made explicit in response relations following from the fluctuation–dissipation theorem. Yet, we cannot expect that to remain true and unchanged when we move far away from equilibrium.1–3 For steady nonequilibrium conditions, it is, first of all, unclear how to define the analogues of temperature or entropy, and, more generally, the standard fluctuation–dissipation relations are simply violated when well away from equilibrium.4,5 In other words, Boltzmann and Clausius entropies are bound to separate. The main point of the present paper is to make that statement operational via the study of nonequilibrium heat capacities. Their negativity is the sign of separation, as we will see that the negativity of the heat capacity indicates an anticorrelation between the excess heat and the change in population degeneracy.
W for the Boltzmann entropy counting the microscopic degeneracy W of a macroscopic condition (at some fixed energy etc.). Miraculously, Boltzmann and Clausius entropies (and others like the Gibbs ensemble entropy) agree under thermodynamic equilibrium, at least for quasilocal interactions. It implies that fluctuations, governed by the Boltzmann entropy, and dissipation, represented by the Clausius entropy, are closely linked as also made explicit in response relations following from the fluctuation–dissipation theorem. Yet, we cannot expect that to remain true and unchanged when we move far away from equilibrium.1–3 For steady nonequilibrium conditions, it is, first of all, unclear how to define the analogues of temperature or entropy, and, more generally, the standard fluctuation–dissipation relations are simply violated when well away from equilibrium.4,5 In other words, Boltzmann and Clausius entropies are bound to separate. The main point of the present paper is to make that statement operational via the study of nonequilibrium heat capacities. Their negativity is the sign of separation, as we will see that the negativity of the heat capacity indicates an anticorrelation between the excess heat and the change in population degeneracy.
The thermal response refers to the behavior of a physical system under changes in temperature or when subjected to heat pulses. For a macroscopic system in equilibrium, one can measure the change in its temperature by heating it. That can be done under various constraints Z such as, e.g. for a gas keeping its volume or pressure constant, and gives rise to the standard definitions of (equilibrium) heat capacities CZ(T). In short, δQrevZ = CZ(T)dT where QrevZ is the reversible heat given to the system to increase its temperature by T → T + dT while keeping the constraint Z. Interestingly, heat capacity may on the one hand be used to measure energy, entropy, or enthalpy, and on the other hand inform about the variance (fluctuations) of those potentials in the corresponding equilibrium ensemble. However, those relations are not given when the interaction becomes long-ranged such as for Newtonian gravity or when the system is nonthermodynamic such as in finite-size clusters,6–8 where the equivalence of ensembles is violated; negative heats become possible there.
The situation for nonequilibrium heat capacities is conceptually similar but results in other expressions. We refer to9–16 for introductions and examples.
The interest in the notion of nonequilibrium heat capacity derives from the wish to quantify thermal response, and to understand what information is encoded in it concerning the nonequilibrium condition and its dynamics. A variety of toy-examples have been studied so far,9,10,14,16–18 and sufficient conditions have been formulated for a nonequilibrium extension of the third law of thermodynamics.11,13 It has also been observed that this nonequilibrium heat capacity can become negative, which makes the question of the present paper: to understand the meaning and the origin of that negativity. We focus on models with a discrete state space, that show a typical Schottky anomaly already for zero driving.19,20 Some driven examples of Section VI show an inverted Schottky anomaly, visible already in the right plot of Fig. 3 for the next example. For examples of Markov diffusions with negative specific heats, we refer to;14,17,18,21 the understanding of negativity there is the same as for the jump processes that we consider below.
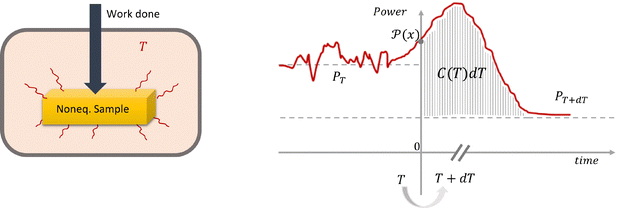
After the Glossary (which is next), Section III reminds the reader of the relevant setup. For nonequilibrium steady conditions, we need an open system, and we identify a thermal bath in its environment where the system dissipates heat. Upon small and slow changes dT in the bath, an excess of heat δQexc = C(T)dT is absorbed by the system that defines the heat capacity C(T) at temperature T of the thermal bath. We ignore from now on in the notation the possibility of different constraints Z, which can act on the system itself and on the bath. It is no longer true that C(T) needs to be positive and indeed we know plenty of examples where C(T) < 0. It is an interesting feature which goes hand in hand with the typical extra we get from nonequilibrium heat capacities: C(T) is able to pick up dynamical or kinetic information about the system which is not available when scanning it in equilibrium.
Section IV gives the theoretical framework for understanding the occurrence and the implication of negative specific heats for nonequilibrium systems. The heat capacity gets written as a covariance in the stationary distribution. The two involved random variables are anticorrelated when the heat capacity is negative. They are related on the one hand to the quasipotential, which gives the expected excess heat,11 and to the pseudopotential, which governs the population statistics in the form −1/β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ρ(x).22 It is there that we see how Clausius and Boltzmann entropies separate.
ρ(x).22 It is there that we see how Clausius and Boltzmann entropies separate.
Section V defines the relevant effective temperatures and we use it to quantify the negativity of the heat capacity. In particular, a sufficient relation follows for that negativity.
Finally, in Section VI we present a number of discrete models with agitated and double-channel transitions to illustrate the theory and the specific origin of negativity at very low and at intermediate temperatures. Each time, we see that the probability of the quasi-ground state (minimizing the quasipotential or expected excess heat) is increasing with temperature (quite unlike the situation for systems in thermal equilibrium) and the effective temperatures (defined with respect to that quasi-ground state) are decreasing with temperature. It indicates a population anomaly (even leading to an inversion): as the temperature of the bath increases, low-lying quasi-energies get more populated. It can also happen without population anomaly when the effective temperatures become almost constant as function of the bath temperature (again, unlike in equilibrium).
II. Glossary
For reference, we start with a short list of words related to nonequilibrium statistical mechanics, introducing concepts that play a role in what follows. Of course, explanations and references do continue, as the various notions appear in their specific roles for the main messages of the paper. This section can be skipped at first reading, to take back when needed.(1) Steady nonequilibrium condition: if we consider an open system, it matters a great deal what boundary conditions and what external forces are applied. A standard setup is that of the so-called canonical ensemble where the system is in weak contact with a thermal bath, and thermal equilibrium is obtained for the system. However, if additionally, rotational forces act on the system, or time-dependent fields, or gradients in chemical potential or pressure are maintained etc. the system may be kept in a steady nonequilibrium condition. An example would be a chemical reactor with sources and sinks, in which the concentrations of the various species are kept stationary while chemical currents are maintained.
(2) Stationary density at temperature T: the open system (as above) is subject to a dynamics, here modeled as a Markov process. It makes sense to define a Master equation giving the updating of probabilities ρ(x,t) of a state x at time t. We can think of ρ(x,t) as the occupation fraction of the state x for many independent identical copies of the system. The Master equation depends on transition rates k(x,y) which indicate the probability per unit time for having a transition x → y when the system is in state x. We assume that k(x,y) is nonzero if and only if k(y,x) is nonzero. The (time-dependent) Master equation for the (time-dependent) probabilities is
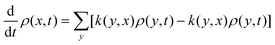 | (II.1) |
The eqn (II.1) gives the time-dependent probability, analogous to the time-dependent solution of Fokker–Planck or Smoluchowski equations. The stationary Master equation puts the left-hand in (II.1) equal to zero. For a finite number of states, all of which can be reached starting from an arbitrary state, it can be shown (Perron–Frobenius theorem) that there is a unique stationary (time-independent) probability ρ:
 | (II.2) |
We call the stationary process an equilibrium process when there is detailed balance: there exists an energy function E(x) so that for all pairs of states x, y,
| k(x,y)e−βE(x) = k(y,x)e−βE(y) | (II.3) |
We are mostly interested in nonequilibrium processes where (II.3) is violated for some pair x, y of system states. On the other hand, we do attach a physical meaning to the ratio
 | (II.4) |
(3) Generators: the backward generator L for a Markov process with transition rate k(x,y) is defined as
is the forward generator, and it appears in the Master eqn (II.1), since
for a probability ν.
(4) Excess heat: the notion of excess heat is explained in Section III and in Fig. 1 in particular. One basically considers the Joule heat flux which is constantly dissipated in a thermal bath for a steady nonequilibrium systems. That heat flux (dissipated power) depends on the temperature of the thermal bath. By changing that temperature, an extra heat flux appears, called excess heat.
(5) Thermal response: for a system that can exchange energy with a (thermal) heat bath at temperature T, we speak about the thermal response when probing system properties as T is varied.
Quasistatic response corresponds to very slow changes in that temperature, with respect to system relaxation times.
Heat capacity measures a thermal response in terms of the excess heat (see above) absorbed by the system.
(6) Quasipotential: the quasipotential V is a certain function of the system state x, taking real values V(x). Sometimes we add a subscript of temperature T, making VT(x), to emphasize its temperature-dependence. In the present paper, the quasipotential is a measure of expected excess heat, when the system is in state x. It is mathematically defined in (III.3).
We take the quasipotential always to be centered, meaning that the expected average 〈V〉 = 0 vanishes for the corresponding stationary probability.
For an equilibrium process, with (II.3), the quasipotential V(x) = E(x) − 〈E〉, reduces to the (centred) energy function.
(7) Pseudopotential: in the case of nonequilibrium processes, we most of the time have no idea or explicit construction of the stationary probability ρ. We call pseudopotential Φ its logarithm
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Z, and its equilibrium expectation 〈Φ〉eq would be a measure of heat. Hence, under detailed balance (equilibrium), the quasipotential and the pseudopotential become directly connected. That is a reflection of the identity under equilibrium between Clausius entropy and Boltzmann entropy.
Z, and its equilibrium expectation 〈Φ〉eq would be a measure of heat. Hence, under detailed balance (equilibrium), the quasipotential and the pseudopotential become directly connected. That is a reflection of the identity under equilibrium between Clausius entropy and Boltzmann entropy.
(8) Expected power versus stationary power: given the heat q(x,y) in the transition x → y we define the expected power (heat flux)
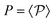 . We can prove that P ≥ 0 with equality if and only if there is detailed balance; see e.g. ref. 25.
. We can prove that P ≥ 0 with equality if and only if there is detailed balance; see e.g. ref. 25.
(9) Covariance: given a probability ρ on the system states, we define the covariance 〈f;g〉 = 〈fg〉 − 〈f〉 〈g〉 (connected two-point function) between any two functions f and g. It measures the correlation, positive or negative, as is important for the understanding of negative specific heat in (IV.3).
(10) Kinetic aspects: to study nonequilibrium regimes, either transient (toward relaxation to equilibrium) or steady (as in the present paper), we need more than the usual thermodynamic functions and principles. Kinetics matters, which is not so surprising from the dynamical perspective. One of the interesting aspects of nonequilibrium calorimetry, is that it can detect some of those kinetic aspects. More specifically, dynamical activities (like in switches and their switching rate) and energy barriers (in transition rates) will be detected and characterized via heat capacities for the nonequilibrium system.
(11) Effective temperature there have appeared various effective temperatures in transient and steady nonequilibrium processes, for example, to restore the (equilibrium) fluctuation–dissipation relation. In the present paper, in (V.2), we use a state-dependent effective temperature T(x). It depends on the state x and also on some reference state x* (not indicated). We will take x* to be a state with minimal quasipotential, and define T(x) starting from the pseudopotential as defined above (and in (V.2)). It gives a measure of population-change or population inversion. Under detailed balance (in equilibrium), T(x) = T is the temperature of the heat bath.
III. Nonequilibrium heat capacity
Consider a stationary nonequilibrium system exchanging energy with a heat bath at temperature T; see Fig. 1. The nonequilibrium is maintained via nonconservative forces, via boundary driving, or via internal fueling as in living matter. Whatever the case, there will be a steady dissipated power of (Joule) heat flowing into the bath, as suggested in the left cartoon of Fig. 1. That heat flow may fluctuate in time, while, on average, it is positive. In general, it depends on various parameters such as the (fixed) temperature T of the bath. For defining the (nonequilibrium) heat capacity, we need the excess heat in a quasistatic temperature variation.26 The shaded area in the right of Fig. 1 is a measure of that heat capacity.For more precision and mathematical details, we refer to the original papers14,17 and to more recent publications.10–12,15,16 Experiments are in progress, with27,28 as early measurements.
The theoretical modeling so far is restricted to Markov processes. We have here time-homogeneous processes Xt that converge exponentially fast to a unique stationary distribution ρ(x), x ∈ K over state space K, satisfying the stationary Master equation of the form L†ρ = 0, where L† is the forward generator. More specifically, let k(x,y) be the transition rate to jump from state x to state y, then the stationary Master equation is
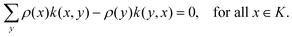 | (III.1) |
The solution ρ is the stationary distribution. To emphasize its temperature dependence, we sometimes denote it by ρT. The subscript T is also used for other quantities.
The backward generator L generates the time evolution in the sense that
| etLg(x) = 〈g(Xt)|X0 = x〉 | (III.2) |
 for state x, and write
for state x, and write  for its stationary value (with stationary distribution ρT and stationary expectations denoted by 〈·〉T). The calculation of that expected heat essentially requires a careful understanding of the first law, but can often be shortened by assuming local detailed as will be made explicit in Example III.1 below.
for its stationary value (with stationary distribution ρT and stationary expectations denoted by 〈·〉T). The calculation of that expected heat essentially requires a careful understanding of the first law, but can often be shortened by assuming local detailed as will be made explicit in Example III.1 below.
After identifying the heat flux  , we define the quasipotential VT = V as the centered function, 〈VT〉T = 0, that solves the Poisson equation,30
, we define the quasipotential VT = V as the centered function, 〈VT〉T = 0, that solves the Poisson equation,30
 | (III.3) |
 is indeed centred. The heat capacity C(T) is then obtained as
is indeed centred. The heat capacity C(T) is then obtained as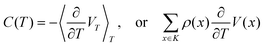 | (III.4) |
 , and thence, V(x) = E(x) − 〈E〉T, which reduces (III.4) to the well-known equilibrium formula for the heat capacity at fixed volume.
, and thence, V(x) = E(x) − 〈E〉T, which reduces (III.4) to the well-known equilibrium formula for the heat capacity at fixed volume.
Example III.1 (agitated three-level system) consider an agitated molecular system, where the hierarchy of energy levels randomly switches. Such a molecular switch can be modelled as a Markov jump process on a ladder with (to be specific) three levels; see Fig. 2. Each leg σ = ± has three states η = 1, 2, 3, so that the states are of the form x = (η,σ). Each state located in σ = − has an energy E(η, −) = (η − 1)ε and the states on σ = + has an energy E(η, +) = (3 − η)ε, and the process is switching legs at rate α. The transition rates are chosen as
 | (III.5) |
The heat flowing to the bath at inverse temperature β equals ε at each transition η → η′ where the level is changing. The changing of legs is work done by external sources.
For completeness, the stationary distribution, the quasipotential and the heat capacity of this three-ladder are calculated in Appendix A. Stationary distributions are obtained by solving the steady master equations. By solving the Poisson equation in (III.3), the quasipotentials of each state are determined, where 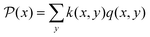 and
and  flowing local detailed balanced condition.23
flowing local detailed balanced condition.23
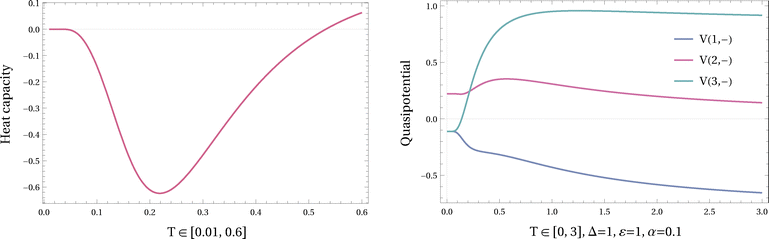
The plots of the heat capacity for varying α, Δ and temperature T are shown in the Fig. 3. Taking α = 0 corresponds to the equilibrium case. For α > 0, the nonequilibrium heat capacity depends kinetically on the barrier Δ and may become negative (here, at low temperatures for large enough Δ).
 | ||
| Fig. 3 Heat capacity of a 3-level ladder as a function of temperature T for different values of α, Δ and ε as defined in the transition rates (III.5). We observe an inverted Schottky anomaly for large enough Δ when ε = 1. | ||
For some regimes of the values, the heat capacity becomes negative and the inverted Schottky anomaly is observed. The dependence of heat capacity on α and Δ is summarized in Fig. 4, where the colors shows different values of the heat capacity.
 | ||
| Fig. 4 The heat capacity of a 3-level ladder as a function of Δ, α and T for fixed ε = 1, the transition rates are given in (III.5). The color bar represents the values of the heat capacity. | ||
This example is continued in Section VI.1.
Example III.2 (heat conducting system, ref. 33). A pleasant and interesting discussion of negative response is contained in the paper by Zia et al.33 We disagree with their identification of the specific heat with the temperature-derivative of the expected energy – that is a procedure that works in equilibrium at constant volume, but is not correct for steady nonequilibria. Yet, their example is very instructive. We repeat it here in the corrected version, using the quasipotential (III.3).
Consider a three-level system (states are a, b, c) in contact with two baths. See Fig. 5, where the two thermal baths are suggested at inverse temperatures β1, β2 and the two energy gaps ε, δ > 0 are shown.
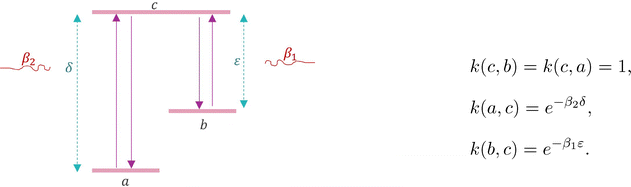 | ||
| Fig. 5 Heat conducting three-level system of Example III.2, after.33 | ||
The stationary distribution is given by  and
and  , where
, where 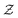 is the normalization. In equilibrium, where β1 = β2 = β, the heat capacity is
is the normalization. In equilibrium, where β1 = β2 = β, the heat capacity is
We look at the nonequilibrium situation where β2 ≠ β1. The system plays the role of a (molecular) conductor between two thermal baths. The heat capacity is now a matrix Cij, i, j = 1, 2 for quantifying the excess heat absorbed by the system from the i-th bath when changing the temperature in bath j. The sum C2,2 + C2,1 + C1,1 + C1,2 = Ceq when β1 = β2.
The expected heat fluxes to bath 2 are:  and
and  and to bath 1 are:
and to bath 1 are:  and
and  . Therefore, solving the Poisson eqn (III.3) gives the quasipotential for bath 1,
. Therefore, solving the Poisson eqn (III.3) gives the quasipotential for bath 1,
and the heat capacity for changing the first temperature is
which is always positive. However, if we look at the heat capacity with respect to the second bath but for changing the temperature of the first bath, we get
which is always negative and means that increasing the first temperature causes extra heat to flow from the system to the second bath; see Fig. 6.
 | ||
| Fig. 6 Heat capacities for Example III.2 quantifying the excess heat absorbed by the system. Parameter values are δ = 3, ε = 1, β2 = 1 in the left plot and β1 = 1 in the right plot. | ||
More relevant is the sum C1,1 + C2,1, which is the total extra heat absorbed by the system when slightly increasing the temperature of the first thermal bath. We have
is positive.
IV. Heat capacity as covariance
For Markov jump processes with a finite state space K, we can rewrite the heat capacity (III.4) as | (IV.1) |
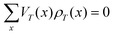 , and where the last expectation 〈·〉T+dT is for the dynamics at temperature T + dT. Under detailed balance, the Kubo formula leads from (IV.1) to the variance of the energy since then and there, VT = E − 〈E〉T. Nonequilibrium response theory is more complicated as it does not only involve a correlation with the heat but also with the frenesy. The resulting expression is formally complicated and does not reveal much specific detail about the negativity of the heat capacity, except that it is clearly the frenetic contribution in general that must be responsible for the negativity; see also ref. 34.
, and where the last expectation 〈·〉T+dT is for the dynamics at temperature T + dT. Under detailed balance, the Kubo formula leads from (IV.1) to the variance of the energy since then and there, VT = E − 〈E〉T. Nonequilibrium response theory is more complicated as it does not only involve a correlation with the heat but also with the frenesy. The resulting expression is formally complicated and does not reveal much specific detail about the negativity of the heat capacity, except that it is clearly the frenetic contribution in general that must be responsible for the negativity; see also ref. 34.
Another way to express heat capacity as a correlation function is less explicit but conceptually more attractive. In fact, the heat capacity (III.4) or (IV.1) can be written as
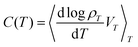 | (IV.2) |
 which is the change in state probability with temperature. We can even make it a covariance between a heat capacity CB(x) derived from the Boltzmann entropy, and a Clausius entropy SC(x) = δQexc(x)/T,
which is the change in state probability with temperature. We can even make it a covariance between a heat capacity CB(x) derived from the Boltzmann entropy, and a Clausius entropy SC(x) = δQexc(x)/T,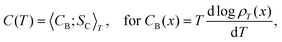 | (IV.3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ρ(x), mimicking the Boltzmann entropy, and the heat capacity (IV.2) gets rewritten as
ρ(x), mimicking the Boltzmann entropy, and the heat capacity (IV.2) gets rewritten as | (IV.4) |
Inspecting (IV.4), the negativity of the nonequilibrium heat capacity signifies at least an anticorrelation between the heat absorbed and the change in occupation with increasing bath temperature. One possibility is that increasing the temperature may, at least in certain regimes, lead to higher occupation of low-energy states. That is not unrelated to the idea of negative temperatures for gravitating or for very inhomogeneous and smaller systems for which the potential energy is anticorrelated with the kinetic energy and/or that fail to satisfy equivalence of ensembles.6–8 What happens is that increasing the temperature may, at least in certain regimes, lead to higher occupation of low-energy states.
V. Negative heat capacity via effective temperatures
Although the covariance identity (IV.2) (or (IV.4)) helps to conceptualize the negativity of the heat capacity, here we look for a sufficient and quantitative condition in terms of effective temperatures. We consider the case where there is a well-defined energy E(x) associated to each state, so that in equilibrium the occupation| ρeq(x) ∼ e−βE(x) | (V.1) |
Fixing the bath temperature T, we denote by x* any specific state that has the smallest quasipotential: for all x,
| ΔV(x) = V(x) − V(x*) ≥ 0 |
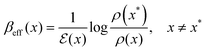 | (V.2) |
 . It may be that there are multiple minima of V and they may give rise to different effective temperatures; we just fix one choice. In equilibrium, with (V.1), βeff(x) = β.
. It may be that there are multiple minima of V and they may give rise to different effective temperatures; we just fix one choice. In equilibrium, with (V.1), βeff(x) = β.
Writing in terms of the inverse bath temperature β, we have
 | (V.3) |
 | (V.4) |
 | (V.5) |
 | (V.6) |
The situation is then as follows:
When there exists a temperature range where 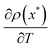 is positive (unlike equilibrium), then a negative heat capacity will arise (and can only arise) from a sufficiently decreasing effective temperature Teff(x) in temperature T (for some state x). We illustrate that in the next section. Indeed, in nonequilibrium, due to the driving, population inversion can occur, and
is positive (unlike equilibrium), then a negative heat capacity will arise (and can only arise) from a sufficiently decreasing effective temperature Teff(x) in temperature T (for some state x). We illustrate that in the next section. Indeed, in nonequilibrium, due to the driving, population inversion can occur, and  is easily made positive for some temperature range.
is easily made positive for some temperature range.
We can also get a negative heat capacity when 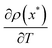 is negative (like in equilibrium), as long as the slope of Teff against T is sufficiently small: we need that
is negative (like in equilibrium), as long as the slope of Teff against T is sufficiently small: we need that  (for some state x). We will encounter that for instance in Fig. 7 and 8 around T = 0.5. It is the situation when the effective temperature (almost) stops to depend on the environment temperature.
(for some state x). We will encounter that for instance in Fig. 7 and 8 around T = 0.5. It is the situation when the effective temperature (almost) stops to depend on the environment temperature.
 | ||
Fig. 8 Left: Stationary occupation of (1, −) in Example III.1, for varying temperatures. The top curve shows the equilibrium case (α = 0), and the lower curve is for α = 0.1. In nonequilibrium there exists a range of temperatures where for Δ = 1, α = 0.1 and ε = 1 in Example III.1,  . Right: Effective temperatures Teff(2, −) and Teff(3, −) (defined from (V.2)) are decreasing in the temperature range where the heat capacity is negative. . Right: Effective temperatures Teff(2, −) and Teff(3, −) (defined from (V.2)) are decreasing in the temperature range where the heat capacity is negative. | ||
As a sufficient condition for negative heat capacity, we then have
 | (V.7) |
We can rewrite (V.7) using the heat bath temperature directly, for easier intuition,
 | (V.8) |
We repeat that the effective temperature (V.2) is defined with respect to some minimizer x* of the quasipotential, and we note that  can also change with temperature T. In many cases at low temperatures x* = g where g denotes the state that maximizes the pseudopotential Φ of (IV.4) and hence the stationary probability, ρT(g) ≥ ρT(x): the dominant state g can then be identified with the state x*, that minimizes the quasipotential. That is certainly the case close-to-equilibrium,12,35 but is not always true in nonequilibrium.
can also change with temperature T. In many cases at low temperatures x* = g where g denotes the state that maximizes the pseudopotential Φ of (IV.4) and hence the stationary probability, ρT(g) ≥ ρT(x): the dominant state g can then be identified with the state x*, that minimizes the quasipotential. That is certainly the case close-to-equilibrium,12,35 but is not always true in nonequilibrium.
VI. Illustrations
We collect a number of discrete examples to clearly illustrate the origin of negative heat capacity as discussed above. We consider basically two regimes for the negativity, at very low, and at intermediate temperatures. The models are not suitable to study high-temperature physics, where we would need to turn to underdamped Langevin processes, possibly for an ideal gas with driven internal degrees of freedom.Example VI.1 (Example III.1 continued: negative heat capacity around zero temperature). The low-temperature behavior of the heat capacity is
Observe that the quasipotential VT((1, −) = x*) is minimal at all temperatures T; see Fig. 7. That minimizer for the quasipotential maximizes the pseudopotential, in the sense that ρ(1, −) = ρ(3, +) ≥ ρ(2, −) = ρ(2, +) ≥ ρ(3, −) = ρ(1, +) for all temperatures as well.
Next, we see from Fig. 8, that the stationary occupation of x* = (1, −) is increasing with temperature over T < 0.5,  , which is different from the equilibrium situation where the ‘ground state’ loses occupation at higher temperature. At the same time, as shown in the right figure, for the same temperature range,
, which is different from the equilibrium situation where the ‘ground state’ loses occupation at higher temperature. At the same time, as shown in the right figure, for the same temperature range,  and
and 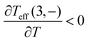 . That produces the negative heat capacity according to (V.8).
. That produces the negative heat capacity according to (V.8).
Example VI.2 (uneven ladder: negative heat capacity at intermediate temperatures). Consider the uneven 3-level ladder, with an unbalanced energy gap, in Fig. 9. The energies E(η,σ) are
| E(1, −) = 0, E(2, −) = 2ε, E(3, −) = 3ε. | (VI.1) |
| k−(1,2) = k+(3,2) = e−β(Δ+ε), k−(2,3) = k+(2,1) = e−β(Δ+ε/2) |
| k+(1,2) = k−(3,2) = e−β(Δ+ε), k+(2,3) = k−(2,1) = e−β(Δ+ε/2) |
| kη(−, +) = kη(+, −) = α > 0, ∀η = 1, 2, 3. |
 | ||
| Fig. 9 Uneven 3-level ladder of Example VI.2. To be compared to the 3-level ladder in Fig. 2; now the energy gaps are unbalanced. | ||
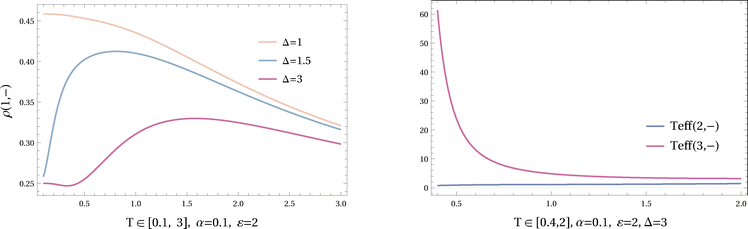
The heat capacity of this system can become negative over intermediate values of temperature for certain values of α, ε and Δ; see Fig. 10, where the heat capacity is plotted for fixed α = 0.1, ε = 2 and different Δ.
 | ||
| Fig. 10 Left: Heat capacity of Example VI.3 for varying temperature, different values of Δ and fixed values of α = 0.1, ε = 2. Right: Quasipotentials at Δ = 3, α = 0.1 and ε = 2, where x* = (1, −). | ||
In Fig. 10, the heat capacity remains positive for Δ = 1. For higher values of Δ, it becomes negative at low temperatures and for even higher values of Δ, it becomes negative at higher (intermediate) temperatures.
For an understanding in terms of (V.8), we observe from Fig. 11 that the stationary occupation of (1, −) can be increasing with temperature for high enough Δ. On the other hand, the effective temperature of the other states located on the leg – are seen for Δ = 3 in the right plot. For the intermediate range of temperatures where the heat capacity is negative, Teff(3, −) is strongly decreasing in temperature.
Example VI.3 (double-channel two-level model with negative heat capacity at intermediate temperatures). Consider the two-level system with states 1 and 2, with possible transitions over two channels, + and −. See Fig. 12, and ref. 17.
 | ||
| Fig. 12 Double-channel 2level-model of Example VI.3. The plus-channel is more reactive than the minus-channel for ϕ > 0 in (VI.2). | ||
The transition rates are
 | (VI.2) |
 . In equilibrium (w = 0),
. In equilibrium (w = 0),  and
and 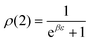 . The analytic expressions for the nonequilibrium stationary distribution, quasipotential and dissipated heat are provided in Appendix B.
. The analytic expressions for the nonequilibrium stationary distribution, quasipotential and dissipated heat are provided in Appendix B.
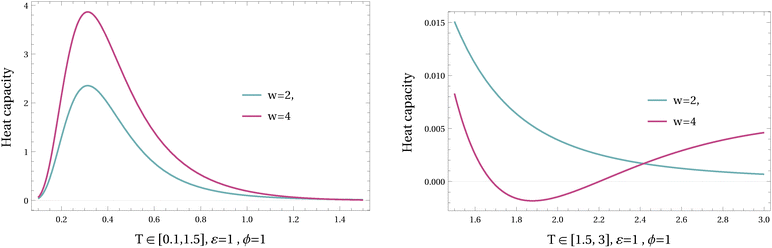
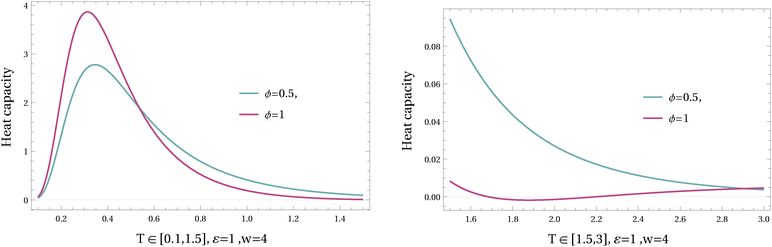
In Fig. 13 and 14, the heat capacity is plotted for different values of ϕ and w in varying temperatures. As it is shown in higher values of driving w the heat capacity can be negative at intermediate temperatures; see Fig. 13. The mechanism is different from the previous example (where the barrier was the relevant variable for the nonequilibrium regime); here it is the asymmetry between the two channels that does the job (of negative heat capacity).
The analytical expression of the heat capacity is given in Appendix B, and there is a transition in ϕ, depending on the driving W, between completely positive and partially negative temperature-regimes of the heat capacity.
The quasipotential is plotted in Fig. 15 as a function of temperature.
V(2) < V(1) for w = 4, ϕ = ε = 1 and T ∈ [1.7,2.2], and x* = 2. For the negativity of the heat capacity we see from Fig. 17 that  is positive for T ∈ [1.7,2.2]. We have plotted the effective temperature of state 2 in Fig. 16.
is positive for T ∈ [1.7,2.2]. We have plotted the effective temperature of state 2 in Fig. 16.
 | ||
| Fig. 16 The effective temperature of state 1 with respect to temperature for Example VI.3. The right plot is the zoom in the range of temperatures where the heat capacity is negative. | ||
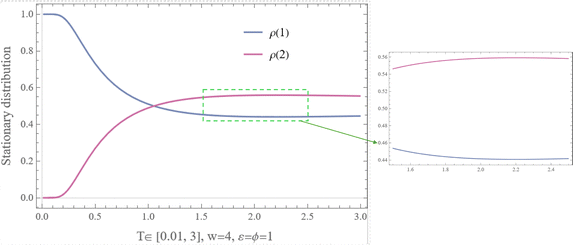 | ||
Fig. 17 Stationary distribution for Example VI.3, with T ∈ [2,10] at w = 4 and ϕ = ε = 1. It is important that  . . | ||
Again, where the effective temperature is decreasing with temperature we get a negative heat capacity; see Fig. 13.
Observe from Fig. 15 that although x* = 1, the stationary probability ρ(1) is not the highest at all temperatures.
VII. Conclusion
For steady nonequilibrium systems, the specific heat at fixed volume is not immediately related to the change of the total average energy with respect to changes in kinetic energy. The latter can be negative for certain equilibrium systems. Instead, the negativity of the specific heat for driven or active systems arises from an anticorrelation between the expected absorbed heat for a given system condition and the change in its population level for increased bath temperature. The former relates to the Clausius entropy, and the latter connects to the Boltzmann entropy. Those entropies do not march together when out of equilibrium, and that is the ultimate reason for the negativity of nonequilibrium heat capacities. The present paper substantiates that claim in quantitative ways and various examples have been used to illustrate the possible scenarios.Conflicts of interest
The authors declare no conflicts of interest.Data availability
The figures represent the result of computer-assisted calculations for the theoretical models, and using publicly available methods described in detail in the main text. No other data nor primary software or code have been used.Appendices
A: Three-level ladder
We include the explicit formulae for Example III.1.Solving the stationary Master equation for the rates given in (III.5), the stationary distribution is
We plot the stationary distribution of the states on the leg σ = − for different values of α, Δ and temperature; see Fig. 18. The ground states (1, −) and (3, +) are the most dominant states. Toward zero temperature for values of Δ > ε/2 all the transition rates become equal (approaching zero); consequently, all states become equivalent.
 | ||
| Fig. 18 Stationary distributions of the three-level ladder given in Example III.1 for different values of α, Δ and temperature T. | ||
The quasipotential equals
where
Since the steady average of the quasipotentials is zero, there must be at least one state with a negative quasipotential. In this example, the states with the highest stationary occupation correspond to those negative quasipotentials.
The heat capacity is computed from (III.4) to be
At very low temperatures with Δ > 0,
With αε > 0, at low temperatures, the heat capacity is negative for Δ > ε/2.
B: Two-channel model
We collect the formulae for Example VI.3; see also ref. 17.The stationary distribution is
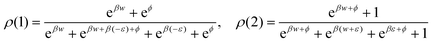 | (B.1) |
The quasipotential is obtained from solving the Poisson eqn (III.3),
where the expected dissipated heat fluxes equal
Hence, the heat capacity is
| a = (eβw+ϕ + eβ(w+ε) + eβε+ϕ + 1)3 |
For w > ε ≥ 0 and all values of ϕ and β, if eϕ(w − ε)(eβw + eβε) > (w + ε)(eβ(w+ε) + 1) and ε(cosh(βw) + cosh(ϕ)) > w![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sinh(ϕ), then the heat capacity is negative. Another condition that leads to negative heat capacity is eϕ(w − ε)(eβw + eβε) < (w + ε)(eβ(w+ε) + 1) and ε(cosh(βw) + cosh(ϕ)) < w
sinh(ϕ), then the heat capacity is negative. Another condition that leads to negative heat capacity is eϕ(w − ε)(eβw + eβε) < (w + ε)(eβ(w+ε) + 1) and ε(cosh(βw) + cosh(ϕ)) < w![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sinh(ϕ). For ϕ = 0; the heat capacity is always positive for w > ε ≥ 0.
sinh(ϕ). For ϕ = 0; the heat capacity is always positive for w > ε ≥ 0.
At very low temperatures,
Acknowledgements
We are grateful to Karel Netočný for many discussions that made this work possible.References
- J. L. Lebowitz, Boltzmann's entropy and time's arrow, Phys. Today, 1993, 46(9), 32–38, DOI:10.1063/1.881363.
- D. Ruelle, Extending the definition of entropy to nonequilibrium steady states, Proc. Natl. Acad. Sci. U. S. A., 2003, 100(6), 3054–3058, DOI:10.1073/pnas.0630567100.
- G. Jona-Lasinio. On Clausius’ approach to entropy and analogies in non-equilibrium, 2023. Available from: https://arxiv.org/abs/2306.04395 Search PubMed.
- C. Maes, Nonequilibrium entropies, Phys. Scr., 2012, 86(5), 058509, DOI:10.1088/0031-8949/86/05/058509.
- M. Baiesi, C. Maes and B. Wynants, The modified Sutherland–Einstein relation for diffusive non-equilibria, Proc. R. Soc. A, 2011, 467, 2792–2809, DOI:10.1098/rspa.2011.0046.
- D. Lynden-Bell, Negative specific heat in astronomy, physics and chemistry, Phys. A, 1999, 263(1), 293–304 CrossRef . Proceedings of the 20th IUPAP International Conference on Statistical Physics. Available from: https://www.sciencedirect.com/science/article/pii/S0378437198005184.
- M. Schmidt, R. Kusche, T. Hippler, J. Donges, W. Kronmüller and B. von Issendorff, et al., Negative heat capacity for a cluster of 147 sodium atoms, Phys. Rev. Lett., 2001, 86, 1191–1194 CrossRef CAS PubMed . Available from: https://link.aps.org/doi/10.1103/PhysRevLett.86.1191.
- W. Thirring, H. Narnhofer and H. A. Posch, Negative specific heat, the thermodynamic limit, and ergodicity, Phys. Rev. Lett., 2003, 91, 130601 CrossRef CAS PubMed . Available from: https://link.aps.org/doi/10.1103/PhysRevLett.91.130601.
- F. Khodabandehlou and I. Maes, Drazin-inverse and heat capacity for driven random walks on the ring, Stochastic Processes Appl., 2023, 164, 337–356, DOI:10.1016/j.spa.2023.07.011.
- F. Khodabandehlou, S. Krekels and I. Maes, Exact computation of heat capacities for active particles on a graph, J. Stat. Mech.:Theory Exp., 2022, 12, 123208, DOI:10.1088/1742-5468/aca4c5.
- F. Khodabandehlou, C. Maes and K. Netočný, A Nernst heat theorem for nonequilibrium jump processes, J. Chem. Phys., 2023, 158(20) DOI:10.1063/5.0142694.
- F. Khodabandehlou and C. Maes, Close-to-equilibrium heat capacity, J. Phys. A:Math. Theor., 2024, 57(20), 205001–205017, DOI:10.1088/1751-8121/ad3ef2.
- F. Khodabandehlou, C. Maes, I. Maes and K. Netočný, The vanishing of excess heat for nonequilibrium processes reaching zero ambient temperature, Ann. Henri Poincare, 2023 DOI:10.1007/s00023-023-01367-1.
- E. Boksenbojm, C. Maes, K. Netočný and J. Pešek, Heat capacity in nonequilibrium steady states, Europhys. Lett., 2011, 96(4), 40001, DOI:10.1209/0295-5075/96/40001.
- C. Maes and K. Netočný, Nonequilibrium calorimetry, J. Stat. Mech.:Theory Exp., 2019, 2019(11), 114004, DOI:10.1088/1742-5468/ab4589.
- E. Rufeil Fiori and C. Maes, Heat capacity of periodically driven two-level systems, Phys. Rev. E, 2024, 110, 024121, DOI:10.1103/PhysRevE.110.024121.
- J. Pešek, E. Boksenbojm and K. Netočný, Model study on steady heat capacity in driven stochastic systems, Cent. Eur. J. Phys., 2012, 10(3), 692–701, DOI:10.2478/s11534-012-0053-8.
- P. Dolai, C. Maes and K. Netočný, Calorimetry for active systems, SciPost Phys., 2023, 14, 126 CrossRef Available from: https://scipost.org/10.21468/SciPostPhys.14.5.126.
- M. d Souza, R. Paupitz and A. Seridonio, et al., Specific heat anomalies in solids described by a multilevel model, Braz. J. Phys., 2016, 46, 206–212, DOI:10.1007/s13538-016-0404-9.
- A. F. Tar. The specific heat of matter at low temperatures. 2003. Available from: https://api.semanticscholar.org/CorpusID:92908264 Search PubMed.
- P. Dolai and C. Maes, Specific heat of a driven lattice gas, Ann. Phys., 2024, 460, 169546, DOI:10.1016/j.aop.2023.169546.
- C. Maes, K. Netočný and W. O’Kelly, Low temperature behavior of nonequilibrium multilevel systems, J. Phys. A:Math. Theor., 2014, 47, 035002, DOI:10.1088/1751-8113/47/3/035002.
- C. Maes, Local detailed balance, SciPost Phys. Lect. Notes, 2021, 32 CrossRef . Available from: https://scipost.org/10.21468/SciPostPhysLectNotes.32.
- C. Maes and K. Netočný, Time-reversal and entropy, J. Stat. Phys., 2003, 110, 269–310, DOI:10.1023/A:1021026930129.
- C. Maes, F. Redig and M. Verschuere, No current without heat, J. Stat. Phys., 2002, 106, 569–587, DOI:10.48550/arXiv.cond-mat/0111281.
- Y. Oono and M. Paniconi, Steady State Thermodynamics, Progr. Theor. Phys. Suppl., 1998, 130, 29–44, DOI:10.1143/PTPS.130.29.
- J. del Cerro and S. Ramos, Specific heat of latgs ferroelectric crystal under dissipative conditions, Ferroelectr. Lett., 1993, 16 DOI:10.1080/07315179308204268.
- F. Jiménez, S. Ramos and J. del Cerro, Influence of a d.c. electric field on the thermal hysteresis behavior of specific heat and dielectric susceptibility of latgs crystals, Ferroelectrics, 1989, 92, 369–373, DOI:10.1080/00150198908211361.
- C. Maes and K. Netočný, Time-reversal and entropy, J. Stat. Phys., 2003, 110, 269, DOI:10.1023/A:1021026930129.
- F. Khodabandehlou, C. Maes and K. Netočný, On the Poisson equation for nonreversible Markov jump processes, J. Math. Phys., 2024, 65(4) DOI:10.1063/5.0184909.
- F. Khodabandehlou and C. Maes, Local detailed balance for active particle models, J. Stat. Mech.:Theory Exp., 2024, 2024(6), 063205, DOI:10.1088/1742-5468/ad5435.
- Y. Tu and Y. Cao, Design principles and optimal performance for molecular motors under realistic constraints, Phys. Rev. E, 2018, 97, 022403 CrossRef CAS PubMed . Available from: https://link.aps.org/doi/10.1103/PhysRevE.97.022403.
- R. K. P. Zia, E. L. Praestgaard and O. G. Mouritsen, Getting more from pushing less: Negative specific heat and conductivity in nonequilibrium steady states, Am. J. Phys., 2002, 70(4), 384–392, DOI:10.1119/1.1427088.
- P. Baerts, U. Basu, C. Maes and S. Safaverdi, The frenetic origin of negative differential response, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2013, 88, 052109, DOI:10.1103/PhysRevE.88.052109.
- C. Maes and K. Netčný, Rigorous meaning of McLennan ensembles, J. Math. Phys., 2010, 51(1) DOI:10.1063/1.3274819.
| This journal is © the Owner Societies 2025 |