Accurate prediction of the energies of the lowest excited states, S₁, T₁, and T₂, of chromophores for improving solar cell applications

Abstract

The lowest singlet excited state and triplet states of acene and polyaromatic hydrocarbon derivatives are calculated using a screened range separated hybrid functional within a polarizable continuum model (SRSH-PCM). Excited state energies are obtained at the time-dependent density functional theory (TDDFT) and the Tamm–Dancoff approximation (TDA) levels. The SRSH-PCM electronic structure protocol successfully incorporates the effect of the electrostatic environment of an active molecule. SRSH-PCM TDDFT excitation energies present a significantly decreased averaged deviation from relevant experimental benchmark energies in comparison to TDA energies. In particular, the energies of the two lowest lying excited triplet states, T₁ and T₂, are predicted with an average error of 0.06 eV and that of the lowest singlet state, S₁, with an average error of 0.11 eV for a molecular test set following a linear fit correction based on a benchmark set. The predictive description of the excited states can be achieved only by properly incorporating effects of the dielectric medium as accomplished by the SRSH-PCM approach. The results highlight the prospect of using SRSH-PCM to uncover molecules bearing optimal properties for singlet fission or triplet–triplet annihilation upconversion applications, where the conditions addressing the energies of these states must be satisfied.

---

1 Introduction

Photovoltaic cells based on organic semiconducting materials continue to draw research activity to materialize the promise of achieving economical and efficient energy production.¹ The technology, however, is fundamentally limited by the Shockley–Queisser relationship,² with functionality capped by energy loss through competing relaxation processes and material absorption cross-section. To overcome these limiting relationships large scale research efforts pursue the design of materials that invoke complementary photophysical processes such as triplet–triplet annihilation upconversion (TTA-UC)³ and singlet fission (SF).^4,5 Furthermore, the design of materials to control and tune triplet excitations can impact such energy generation applications. Light generation applications can also be improved through involving low lying triplet excitations in optoelectronic processes such as thermally activated delayed fluorescence.^6–9

Through such mechanisms of TTA-UC and SF the material absorption spectral range can be extended.¹⁰ Specifically, efficient TTA-UC requires that an intermediate triplet excitation state, T₁, energy is higher than or equal to the energy of the absorbing lowest singlet states, S₁, where 2 × T₁ ≥ S₁. Efficient SF, on the other hand, requires that the energy of the S₁ state is higher than or equal to the formed triplets, where S₁ ≥ 2 × T₁.¹¹ Both processes can be limited by triplet–triplet combination to a higher triplet state, T₂, and therefore require that their energies satisfy T₁ ≤ T₂ × 0.5.¹² Computational studies can play a decisive role in research efforts to uncover materials that bear excited states that meet these requirements for the excited state energies.

A computational approach of predictive quality is required to impact molecular design efforts.¹³ For achieving the predictive quality the approach must tackle well challenges in resolving structure–function relationships affecting relevant energy criteria.¹⁴ Toward this goal, excited state calculations must go beyond gas phase descriptions, reliably addressing the dielectric environment and molecular packing interactions.^12,15,16 In recent years, a DFT framework that addresses the dielectric environment has been developed and benchmarked. In particular, a screened range separated hybrid (SRSH) functional within the polarizable continuum model (PCM), denoted as SRSH-PCM, has been shown to predict energies of frontier orbitals,¹⁷ excited states,^18–20 and charge transfer (CT) states²¹ in a condensed phase remarkably well. The SRSH-PCM approach accounts for the effects of the dielectric environment of organic materials in crystal and solution phases, establishing a high quality and efficient approach to predict excited state energies of organic semiconductors in single molecule calculations.^8,17,19,22

We point out that the noted energetic relationships determining the SF and TTA-UC efficiencies relate to low lying excited states of molecular dimers. Nevertheless, to demonstrate the potential impact on the design of materials this work focuses on calculating low lying excited states of single molecules using SRSH-PCM. Indeed, only such a framework that addresses excited state energies of molecular systems within a condensed phase at a predictive quality can be used to contribute to molecular design research. Future design efforts will use SRSH-PCM to investigate relevant molecular dimer systems,²³ where intermolecular orientation effects are resolved.

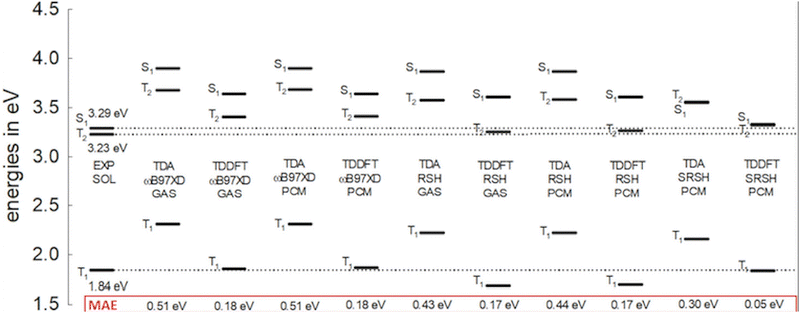
In this study, SRSH-PCM is employed to calculate the lowest excited singlet state, S1 and the two lowest triplet states, T1 and T2, in organic semiconducting materials that are involved in SF and TTA processes. Fig. 1 presents a benchmark set of acene derivatives, including tetracene,²⁴ pentacene,²⁵ PDI,²⁶ and DPH,²⁷ that are widely studied in the context of SF activity. These acenes are complemented by several related molecules with reported measured excited state energies. (Molecule acronyms are introduced in the figure.) We address this set of molecules to establish the success of the calculated values to reproduce the experimental benchmark energies through a linear fit with experimental values. We then proceed and use the linear fit to further improve the agreement of calculated S₁, T₁, and T₂ energies with experimental values of molecules outside the benchmark set. We emphasize that the linear fit parameters provide for a correction measure to improve the agreement of calculated energies with experimental values. The correction is solely based on line parameters obtained by correlating calculated values to experimental values of the benchmark set (see ESI,† Table S1 for the listed experimental excitation energies of both sets^28–38).

Fig. 1 The training set of molecules.

As shown below, SRSH-PCM calculated excitation energies are found to reproduce well the measured values, which are significantly affected by the polarizable environment. The framework's success stands on imposing meaningful dielectric screening of the electronic interactions at the long range. In particular the approach is found to predict exceptionally well energies of the two low lying triplet states,¹⁹ and especially well the important T₁–T₂ energy gap and the triplet states alignment relative to the lowest singlet excitation, S₁. The SRSH-PCM energies are within chemical accuracy of experimental energies without any empirical fitting. The excellent linear fit between the calculated and experimental energies establishes the predictive quality of the approach and at the same time offers a means to further improve the quality of the calculated energies.

2 Computational details

In range-separated hybrid (RSH) functionals and the SRSH framework the electronic Coulomb interactions are range-partitioned using an error function in the following form:^22,39Here, r is the interaction distance, and ω is a tunable range switching parameter. Considering the right-hand side of eqn (1), the first term is used for treating the exact exchange and the second term is used for the semilocal exchange functional. Consequently, the α and β parameters determine the exact and semilocal exchange contributions in the long and the short ranges. Specifically, the exchange–correlation functional takes the following form:where SR and LR stand for the short-range and long-range, respectively, F_x represents the exact exchange, DF_x denotes the semilocal density functional exchange, and DF_c stands for the correlation part of the functional. In this work α is set to 0.2 as widely used in earlier studies.^40–42 (The RSH functional follows α + β = 1, reflecting the LR limit in the gas phase.)

We then invoke the PCM and establish the SRSH-PCM level, where β is reset according to the preset α and the scalar dielectric constant associated with the environment (ε),^17,22 by following the expression

α + β = 1/ε. (3)

We address for completeness the RSH-PCM level, where the PCM is invoked with β at the same value as used in the gas phase tuning (and without changing the range separation parameter).

Using the range separation expression opens the opportunity to align the frontier molecular orbital (MO) energies, the highest occupied MO (HOMO) and the lowest unoccupied MO (LUMO), and match them to the ionization potential (IP) and the electron affinity (EA), respectively. In particular, the range separation parameter, ω, is chosen to minimize the error measure, J(ω),

J(ω) = [ε_HOMO(ω) + E_IP(ω)]² + [ε_LUMO(ω) + E_EA(ω)]². (4)

In the above equation, ε_HOMO and ε_LUMO are the frontier MO energies that are tuned to optimally match the IP and EA, respectively. We point out that in this work SRSH-PCM is based only on gas phase tuning established by the RSH level, and, therefore, can potentially be improved by PCM-based tuning.

Excited-state energies are calculated at the Tamm–Dancoff approximation (TDA) and full time-dependent density functional theory (TDDFT) levels. The effect of the dielectric environment on excited state densities is evaluated at the perturbative state-specific (ptSS) level⁴³ for TDA states, where the electronic response is parameterized by the optical dielectric constant. The ptSS corrections are expected to increase (in absolute value) with the optical dielectric constant and with the CT character of the excited state. In this work, the corrections are found to be minor at about −0.002 eV, reflecting the relatively weak response of the solute excited electron density to the electrostatic environment. A single exception is found for the S₁ state of 1-cyano naphthalene bearing significant CT character leading to a −0.07 eV ptSS correction.

In this study we employ the PBEh as the semilocal functional, therefore addressing the tuned LR-corrected (LRC) hybrid functional (ωPBEh)⁴⁴ as the RSH level. All geometry optimizations of the molecules used in this study are carried out with the ωB97X-D functional⁴⁵ and the cc-pVTZ basis set. The calculated excited states are obtained using the cc-pVTZ basis set. The geometry optimizations and the excited state calculations are performed using the software package Q-Chem version 6.0.2.⁴⁶

The scalar dielectric constant representing the environment is set to 3.5 and the optical dielectric constant parameterizing the ptSS correction is set to 1.4. These values reflect reasonably well the non-polar solvents affecting the considered experimental benchmark data and essentially follow the frameworks affected in related benchmark studies.^9,47,48 Scalar dielectric constants of organic crystals are typically in the range of 3–4.^49–54 See examples of dielectric constants associated with organic materials in a molecular crystal phase listed in the ESI,† Table S2. We also address the sensitivity of the calculated excited state energies to the employed dielectric constant especially in cases of smaller molecules by resolving the excited state energy and dielectric constant relationship, demonstrating the larger dependence of the singlet state over that of triplet states.

3 Results and discussion

3.1 Representative molecule – anthracene

Trends related to the condensed phase effects parameterized by the dielectric constant in the PCM calculations are presented using anthracene as a representative system. Both ωB97X-D and the RSH predict at the gas phase IP/EA values of anthracene quite satisfactorily with matching frontier orbital energies. The RSH functional is associated with a smaller mean absolute error (MAE) between the IP/EA and frontier orbital energies, reflecting the gas phase optimally tuned ω. See the orbital energy gaps presented in the ESI,† Fig. S1. We also point out that the RSH orbital energies align well with the corresponding experimental gas phase IP⁵⁵/EA⁵⁶ energies.

We now consider the condensed phase effects by using PCM-based energies. To highlight the effect of invoking dielectric screening we compare SRSH-PCM energies to those obtained using the corresponding unscreened RSH-PCM energies. We also consider energies based on the ωB97X-D functional used in the geometry optimizations which includes an elaborate fitting process to establish the RS parameter.⁵⁷

Calculated anthracene HOMO/LUMO energies and the corresponding oxidation potentials (OPs) and reduction potentials (RPs) obtained using DFT-PCM are presented in Fig. 2 and compared to the experimentally measured values in the solid state.⁵⁸ As expected, the frontier orbital energies do not match the –OP/–RP energies obtained using the unscreened functionals, ωB97X-D-PCM and RSH-PCM. Also as expected,¹⁷ by introducing screening effects in SRSH-PCM and even without affecting any further tuning the HOMO/LUMO energies nicely match the OP/RP values and appear to also match well the experimental data. Such excellent alignment of the frontier orbital energies with the OP/RP also leads to an improved match of TDDFT calculated excited state energies with measured spectral trends as demonstrated for similar systems.^18,19,21

Fig. 2 Anthracene PCM-calculated HOMO, LUMO (H,L) energies, and –OP,–RP energies, compared to experimental solid-state data.⁵⁸ Only the SRSH-PCM calculated gaps match and reproduce well the experimental solid-state data.

The calculated S₁, T₁, and T₂ energies of anthracene within the PCM and in the gas phase are presented in Fig. 3. (Excited state properties are listed in the ESI,† Table S3.) The lowest excited states in anthracene are predominantly due to HOMO → LUMO transitions (it is important to note that all lowest excitations involve HOMO–LUMO orbital replacements in this study). Consequently, the incorrectly overestimated HOMO–LUMO gaps shown in Fig. 2 using ωB97X-D and RSH in the PCM, where the gaps remain similar to the gas phase values, foreshadow the overestimated excited state energies at these levels, especially for the S₁ state. Indeed, these PCM energies, without the dielectric screening in the functional, are quite similar to the gas phase energies. On the other hand, we also point out that TDA excitation energies based on such traditional functionals are known to compare better with experimental energies than those based on full TDDFT.^59–62 However, this TDA trend in conventional functionals appears to benefit from fortuitous cancellation of errors associated with gas-phase underestimated orbital gaps and therefore negates the goal of predictive calculations.⁶³ On the other hand, TDDFT in the PCM based on SRSH-PCM reproduces well measured excitation state energies, offering a predictive level of calculations. Here we find a MAE of only 0.05 eV for anthracene S₁, T₁, and T₂ state energies, whereas all other levels are associated with larger than 0.15 eV MAEs.

Fig. 3 Anthracene calculated low lying excited state energies, comparing TDA and TDDFT energies to the solid-state measured energies. Lower panel: MAEs from the experimental value. The SRSH-PCM calculated excited state energies are of the smallest MAE of 0.05 eV.

Before we proceed to consider the set of molecules for comprehensive benchmarking, we present the relationship of the excited state energies to the dielectric constant. The dielectric constant represents the molecular environment affecting the excited state energies. To demonstrate these trends, we list the calculated SRSH-PCM excited states within a range of dielectric constants in Table 1. The S₁ energies are found to vary significantly within the range of ε by 0.2 eV, whereas the T₁ and T₂ energies change by less than 0.1 eV within the same range. Notably RSH-PCM energies without the dielectric screening show essentially the same energies across the considered range of dielectric constants. Such vanishing dielectric constant dependence of the RSH-PCM energies is erroneously established, especially, for the S₁ state. See the RSH-PCM calculated energies across the same range of dielectric constants listed in the ESI,† Table S4.

Table 1 Anthracene SRSH-PCM excited state energies (eV) in various solvents parameterized by the scalar dielectric constant (ε). The corresponding RSH-PCM energies are listed in the ESI,¹ Table S4. Also listed is the solvent refractive index (n_D)

Solvent			S1		T1		T2
Name	ε	nD	TDA	TDDFT	TDA	TDDFT	TDA	TDDFT
Cyclohexane	2.02	1.426	3.650	3.419	2.176	1.801	3.565	3.306
Benzene	2.27	1.501	3.624	3.396	2.171	1.813	3.565	3.313
Solid state	3.50	1.400	3.549	3.330	2.155	1.836	3.559	3.323
Anisole	4.33	1.517	3.521	3.305	2.149	1.843	3.557	3.327
Chloroform	4.81	1.446	3.509	3.295	2.148	1.850	3.558	3.332
Chlorobenzene	5.62	1.525	3.494	3.281	2.143	1.850	3.554	3.330
THF	7.58	1.407	3.470	3.260	2.138	1.855	3.553	3.333
DCM	8.93	1.424	3.459	3.250	2.136	1.858	3.552	3.335

---

3.2 Benchmark training set

Ground state energy gaps due to frontier orbital energies and the IP and EA are listed in Table 2 for the benchmark set of molecules shown in Fig. 1. We consider first the energy gap trends, where optimal tuning of ω leads to excellent (within 0.02 eV) correspondence of HOMO and LUMO energies to IP and EA, respectively, for all molecules, with, however, a single exception. The quinoxaline molecule presents a weaker match, presumably due to the delocalized nature of the frontier orbitals. We are pursuing means to improve RSH functional performance also for such challenging cases and plan to report such progress in future publications.

Table 2 Calculated frontier orbitals and –OP/–RP energies (eV) based on RSH, RSH-PCM, and SRSH-PCM levels. The listed RS parameter is obtained by gas phase optimal tuning

Molecule	ω	RSH				RSH-PCM				SRSH-PCM
		HOMO	–OP	LUMO	–EA	HOMO	–OP	LUMO	–RP	HOMO	–OP	LUMO	–RP
Naphthalene	0.216	−8.10	−8.11	0.53	0.51	−8.15	−6.71	0.49	−0.94	−6.39	−6.58	−1.11	−0.96
Anthracene	0.189	−7.28	−7.29	−0.33	−0.33	−7.33	−6.04	−0.36	−1.64	−5.79	−5.93	−1.79	−1.67
Tetracene	0.170	−6.74	−6.75	−0.91	−0.90	−6.78	−5.61	−0.94	−2.11	−5.24	−5.35	−2.37	−2.27
Pentacene	0.156	−6.35	−6.36	−1.33	−1.32	−6.39	−5.31	−1.36	−2.43	−5.12	−5.20	−2.56	−2.48
Perylene	0.177	−6.87	−6.86	−0.70	−0.72	−6.92	−5.75	−0.74	−1.93	−5.51	−5.62	−2.06	−1.97
PDI	0.156	−7.82	−7.81	−2.46	−2.45	−7.62	−6.54	−2.27	−3.29	−6.35	−6.44	−3.43	−3.33
Quinoxaline	0.242	−9.17	−9.36	−0.26	−0.35	−9.19	−7.94	−0.29	−1.87	−7.25	−7.57	−2.01	−1.83
DPB	0.164	−7.21	−7.23	−0.38	−0.37	−7.24	−6.08	−0.40	−1.56	−5.83	−5.95	−1.72	−1.63
DPH	0.156	−6.93	−6.94	−0.65	−0.65	−6.95	−5.85	−0.66	−1.76	−5.62	−5.72	−1.91	−1.83
(E)-Stilbene	0.178	−7.57	−7.58	−0.07	−0.08	−7.61	−6.36	−0.10	−1.35	−6.08	−6.22	−1.52	−1.41
Chrysene	0.176	−7.52	−7.52	0.01	−0.01	−7.57	−6.37	−0.03	−1.24	−6.09	−6.21	−1.41	−1.31
1-Cyano naphthalene	0.206	−8.57	−8.59	−0.42	−0.43	−8.49	−7.11	−0.35	−1.74	−6.80	−6.98	−1.90	−1.75
Triphenylene	0.176	−7.89	−7.88	0.33	0.31	−7.94	−6.73	0.28	−0.94	−6.44	−6.56	−1.11	−1.01
1-Methoxy naphthalene	0.202	−7.58	−7.58	0.71	0.70	−7.67	−6.28	0.61	−0.77	−5.98	−6.16	−0.94	−0.80

---

We address next energies associated with environment effects using PCM calculations. Table 2 lists the calculated energies at the RSH-PCM and SRSH-PCM levels. At the RSH-PCM level the HOMO/LUMO energies remain similar to the gas-phase values.¹⁷ The calculated OP and RP, on the other hand, are strongly affected, again as expected, by the polarizable embedding of the solute. Consequently, the energy differences between the HOMO and –OP and between the LUMO and –RP are significant.

At the SRSH-PCM level, on the other hand, the frontier orbital energies realign within 0.15 eV of the –OP/–RP values and notably even without retuning in the PCM. Quinoxaline presents again an exception reflecting the weaker mismatch at the gas phase, where the SRSH-PCM HOMO energy deviates by 0.3 eV from the –OP. Here, we note that retuning ω in the PCM does not improve error measure for orbital energy matching to IP/EA for quinoxaline. Indeed, this trend of the electronic density response to the environment depends and may vary with the size of the molecule and the degree of delocalization of the frontier orbitals.

The SRSH-PCM calculated excited state energies are presented in Fig. 4 in the form of correlation plots to the experimental energies at both the TDDFT and TDA levels. The energies are listed in the ESI,† Table S5. (For completeness, RSH-PCM excitation energies and their correlation plots are provided in the ESI,† Table S6 and Fig. S2, respectively.) More specifically, the calculated energies of each state are fitted to the experimental values, establishing a linear relationship, E_exp = mE_calc + n. The line equations for S₁, T₁, and T₂ states at the TDDFT-SRSH-PCM level are as follows:

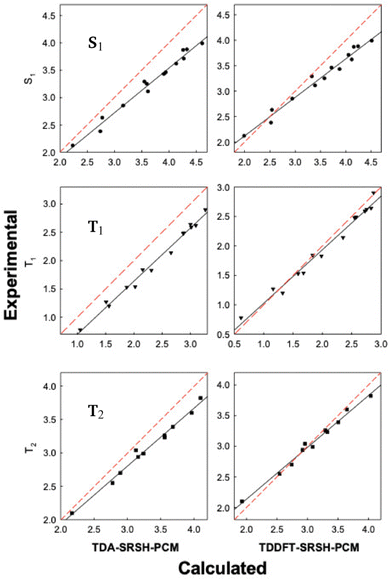Fig. 4 Correlation plots of the calculated excitation energies (eV) vs. the experimental data for the training set molecules (Fig. 1). Red dashed lines of y = x lines represent the perfect fit for comparison.

The linear fit parameters of TDA and TDDFT excited state energies along with the MAEs are listed in Table 3, where we include those based on the RSH-PCM energies as well. Overall, the TDDFT energies present a closer match with experimental values than the TDA energies with significantly smaller MAEs. TDA energies present correlation plots with larger slopes and smaller intercept values than TDDFT. Namely, the TDA tendency to overpredict the excitation energy increases with the energy. TDDFT is found to underpredict the experimental values only at sufficiently low excitation energies. To better gauge the quality of the linear fit we also list the coefficient of determination, R², which is 1.0 in the case of a perfect fit. Notably, all plots are associated with good fits finding R² values larger than 0.96. Regardless of whether TDA or TDDFT is used, the SRSH-PCM approach performs much better than RSH-PCM, reflecting the excellent match of frontier orbital energy levels with the corresponding –OP and –RP values.

Table 3 Linear fit parameters of the correlation plots shown in Fig. 4. Also listed are the calculated vertical excitation energies MAEs (eV) from the experimental training set values

Method	S1				T1				T2
	m	n	R^2	MAE	m	n	R^2	MAE	m	n	R^2	MAE
TDA-RSH-PCM	0.832	0.001	0.996	0.66	0.935	−0.308	0.987	0.47	0.853	0.193	0.994	0.30
TDA-SRSH-PCM	0.819	0.266	0.981	0.40	0.937	−0.236	0.989	0.39	0.867	0.200	0.987	0.24
TDDFT-RSH-PCM	0.760	0.405	0.982	0.50	0.864	0.331	0.961	0.11	0.804	0.579	0.974	0.10
TDDFT-SRSH-PCM	0.758	0.604	0.975	0.29	0.908	0.118	0.981	0.11	0.845	0.448	0.988	0.08

---

More specifically, the TDDFT-SRSH-PCM MAEs for the experimental energies for T₁ and T₂ energies are 0.11 and 0.08 eV, respectively, smaller than that of 0.29 eV for S₁. The relative, while systematic, larger deviation found for the S₁ energies reflects the tendency to further overestimate with the increase of the excitation energy. We emphasize first that the S₁ energies with the linear fit correction are also within chemical accuracy of 0.1 eV deviation. We relate the overestimated S₁ energies to the imposed fixed dielectric constant, where the S₁ states present stronger dependence on the dielectric constant than the triplet excitations as demonstrated above in Table 1. The S₁ energies are found to vary significantly within the range of ε, for example by 0.2 eV for anthracene, whereas the T₁ and T₂ energies change by less than 0.1 eV within the same range. In addition, we emphasize that significantly overestimated S₁ is indicated only for the smaller molecules with the larger excitation energies. Indeed, the smaller molecules typically require tuning within the PCM or even present a challenge for optimal tuning as noted above for quinoxaline. Indeed, as shown in Table 2, the naphthalene case presents a HOMO energy that indicates a 0.2 eV overestimated IP and one of the more overestimated S₁ energies, whereas the larger acenes (anthracene through pentacene) are associated with smaller deviations in both the HOMO from IP and in the calculated S₁ energy from the experimental value. Investigating more precisely the smaller molecules establishes a refinement or a challenge that can be addressed in future studies.

For the triplet states, we found a different trend than for the singlet energies. Here the calculated energies show a similar deviation across the considered set of molecules. This reflects success in addressing the challenge of triplet states in the condensed phase and where the triplet states bear a weaker dependence on the polarizing environment than indicated for the singlet states.^9,19,64,65

The absence of a transition dipole moment in spin-forbidden vertical transitions for triplet states leads to weak interaction with the polarized solute environment and therefore weaker solvent dependence.

3.3 Molecular test set

We next test the applicability of the TDDFT-SRSH-PCM method, where we also validate the linear fits using the set of molecules shown in Fig. 5. The calculated excited state energies are compared to the experimental data,^28–37 presenting a MAE of 0.28 eV for S₁, 0.09 eV for T₁, and 0.12 eV for T₂ states; see the energies listed in Table 4. Such MAEs are quite similar to the values found for the training set listed above in Table 3, confirming a statistically meaningful data set. As established above, improvement of the calculated energies, E_calc, in reproducing the experimental energies within 0.1 eV accuracy is achieved using the linear fit parameters provided above in eqn (5)–(7). The linear-fit corrected SRSH-PCM excited state S₁, T₁, and T₂ energies present significantly smaller MAEs of 0.06 eV for T₁ and T₂ and 0.11 eV for S₁. The SRSH-PCM energies and linear fit corrected energies for the test set molecules are presented in the form of correlation plots in the ESI,† Fig. S3.

Fig. 5 The test set of molecules, where we refer to MCT as 5-chlorotetracene, DCT as 5,11-dichlorotetracene, and TCT as 5,6,11,12-tetrachlorotetracene.

Table 4 SRSH-PCM TDDFT calculated and linear-fit corrected vertical excitation energies (eV) of the test set of molecules (Fig. 5). The experimental excitation energies are provided in the ESI, Table S1

Molecule	RS	SRSH-PCM			Corrected
	(ω)	S1	T1	T2	S1	T1	T2
Pyrene	0.190	3.81	2.18	3.51	3.49	2.10	3.41
Phenanthrene	0.189	4.10	2.77	3.53	3.71	2.63	3.43
Porphyrin	0.164	2.34	1.48	1.82	2.38	1.46	1.99
Dibenzofuran	0.198	4.58	3.21	3.71	4.08	3.03	3.58
Phenazine	0.198	3.12	1.93	2.62	2.97	1.87	2.66
TCT	0.154	2.21	0.87	2.35	2.28	0.91	2.43
DCT	0.160	2.41	1.07	2.45	2.43	1.09	2.52
MCT	0.164	2.48	1.12	2.50	2.48	1.14	2.56
MAE	—	0.28	0.09	0.12	0.11	0.06	0.06

---

The energies listed in Table 4 indicate that TCT, DCT, and MCT molecules have excited states energy alignment that satisfies the requirement for effective SF. In particular, TCT with the lowest band gap among the considered chlorinated tetracene derivatives stands out as a promising candidate for the SF application and therefore for potentially enhancing device efficiencies in photovoltaics.

3.4 Discussion

Design and synthesis of novel molecules, characterization, and the subsequent testing in applications such as SF or TTA-UC tend to be quite expensive and labor-intensive.^10,11,66 Uncovering optimal molecules for these applications is hindered by the difficulty in resolving the T₂ states. There are only a few molecules for which T₂ state energies are reported. To address these challenges, computational studies of the excitation energies can significantly impact molecular design efforts. Such studies, however, to be truly predictive and impactful must account for the condensed phase environment even in cases of non-polar molecules and environments.

In this regard, SRSH-PCM has evolved as a powerful approach achieving accurate condensed phase-affected excited state energies in single molecule calculations.^{17,19,20,67,68} In this study we use this polarization consistent framework to demonstrate the predictive quality of the SRSH-PCM framework. Such predictive quality is necessary for reliably highlighting molecules that satisfy either SF or TTA-UC requirements affecting the excited state energies.

This work shows that SRSH-PCM can be used to predict the energies of T₁ and T₂ states reliably with MAE < 0.1 eV and S₁ with MAE < 0.3 eV, noting the larger deviations found for the relatively smaller molecules. Importantly, the calculated SRSH-PCM TDDFT energies can be improved to offer chemical accuracy of less than 0.1 eV deviation also for S₁ energies by using linear fit correction (the line fit parameters obtained using the benchamrk set are provided for general utility). This trend is especially impressive, given the moderate cost of SRSH-PCM bearing single molecule calculations and corrections based on a simple linear fit. As noted, the S₁ energies present a significant overestimated energy only for the higher energies associated with the smaller molecules. These molecules, while tending to be less relevant as potential candidates for optoelectronic applications, may benefit from pursuing optimal tuning in the PCM.

We also point out that intermolecular interactions in a crystalline environment can affect excited state energies while neglected in a scheme that represents the environment as a dielectric continuum. To fully address such molecular-specific environment effects requires sophisticated embedding protocols as recently reported for the SRSH framework.⁶⁷ Nevertheless, SRSH-PCM has emerged as a highly effective framework to achieve predictive calculations. SRSH-PCM, therefore, bears potential to impact experimental efforts to design molecules with optimal properties for SF and TTA-UC applications. Future studies can readily explore dimers made of candidate molecules as highlighted in this study (TCT, DCT, and MCT) at varied orientations to consider their applicability through the highly efficient SRSH-PCM calculations. We point out that we do not expect that calculated excitation energies based on a single molecule will significantly be affected by the required ω retuning. Indeed in foreseeing calculation of these excited states in dimer systems, a decrease in the dimer tuned ω is projected. We confirm that recalculating the excited states using such a smaller ω parameter by an assumed 10% decrease results in only a negligible change in the excitation energies; see examples in the ESI,† Table S7.

4 Conclusion

In summary, S₁, T₁, and T₂ state energies of polyaromatic hydrocarbon derivatives are successfully predicted using TDDFT with a SRSH functional within the PCM. The SRSH-PCM framework accounts exceptionally well for effects of the polarizable environment on the electronic density of the embedded molecule. The excited state energies calculated using TDA yield a slightly better correlation against the experiment than TDDFT. Nonetheless, comparison of calculated excited state energies with experiment reveals that TDDFT-SRSH-PCM stands out by accurately predicting S₁, T₁, and T₂ energies with MAEs smaller than 0.1 eV. The linear fitting formulas obtained at the TDDFT-SRSH-PCM level in this work can be applied to polyaromatic hydrocarbon derivatives to further improve calculated predictions of excited state energies. Therefore, SRSH-PCM has emerged as an effective framework with potential to impact efforts to design materials suitable for SF or TTA-UC applications, and therefore promise to reduce the time, cost, and efforts in related experimental studies. We, in particular, highlight TCT as a potential candidate for efficient SF applications.

Conflicts of interest

The authors declare no conflict of interest.

Data availability

The data supporting this article have been included as part of the ESI† that provides the following: experimental S₁, T₁, and T₂ energies for molecules shown in Scheme S1 (ESI†); excited state energies, orbital transitions, and oscillator strengths of the transitions with various methods for anthracene; calculated RSH-PCM excited state energies within different solvents for tetracene; excited state energies obtained using RSH-PCM and SRSH-PCM for S₁, T₁, and T₂ at TDA and full TDDFT levels; and comparison of calculated frontier orbital energies with IP/EA energies for ωB97X-D and RSH-GAS methods.

Acknowledgements

This work was supported by the Basic Energy Sciences, Office of Science, U.S. Department of Energy, award DE-SC0025404 and Kent State University.

Notes and references

1. C. Battaglia, A. Cuevas and S. De Wolf, Energy Environ. Sci., 2016, 9, 1552–1576.
2. W. Shockley and H. J. Queisser, J. Appl. Phys., 1961, 32, 510–519.
3. L. Naimovicius, P. Bharmoria and K. Moth-Poulsen, Mater. Chem. Front., 2023, 7, 2297–2315.
4. M. B. Smith and J. Michl, Chem. Rev., 2010, 110, 6891–6936.
5. A. Rao and R. H. Friend, Nat. Rev. Mater., 2017, 2, 17063.
6. D. Barman, K. Narang, R. Gogoi, D. Barman and P. K. Iyer, J. Mater. Chem. C, 2022, 10, 8536–8583.
7. S. E. Seo, H.-S. Choe, H. Cho, H.-I. Kim, J.-H. Kim and O. S. Kwon, J. Mater. Chem. C, 2022, 10, 4483–4496.
8. B. Mandal and B. D. Dunietz, J. Phys. Chem. A, 2023, 127, 216–223.
9. R. Khatri and B. D. Dunietz, J. Phys. Chem. C, 2025, 129, 436–446.
10. S. Ito, T. Nagami and M. Nakano, Phys. Rep., 2018, 34, 85–120.
11. A. J. Carrod, V. Gray and K. Boerjesson, Energy Environ. Sci., 2022, 15, 4982–5016.
12. D. Padula, O. Omar, T. Nematiaram and A. Troisi, Energy Environ. Sci., 2019, 12, 2412–2416.
13. X. P. Wang, S. Y. Gao, Y. Q. Luo, X. Y. Liu, R. Tom, K. J. Zhao, V. Chang and N. Marom, J. Chem. Phys., 2024, 128, 7841–7864.
14. R. Grotjahn, T. M. Maier, J. Michl and M. Kaupp, J. Chem. Theory Comput., 2017, 13, 4984–4996.
15. C. F. Perkinson, D. P. Tabor, M. Einzinger, D. Sheberla, H. Utzat, T. A. Lin, D. N. Congreve, M. G. Bawendi, A. Aspuru-Guzik and M. A. Baldo, J. Chem. Phys., 2019, 151, 121102.
16. D. López-Carballeira and T. Polcar, J. Comput. Chem., 2021, 42, 2241–2249.
17. S. Bhandari, M. Cheung, E. Geva, L. Kronik and B. D. Dunietz, J. Chem. Theory Comput., 2018, 14, 6287–6294.
18. H. Aksu, A. Schubert, E. Geva and B. D. Dunietz, J. Phys. Chem. B, 2019, 123, 8970–8975.
19. K. Begam, S. Bhandari, B. Maiti and B. D. Dunietz, J. Chem. Theory Comput., 2020, 16, 3287.
20. C. Chakravarty, H. Aksu, J. A. Martinez, P. Ramos, M. Pavanello and B. D. Dunietz, J. Phys. Chem. Lett., 2022, 13, 4849.
21. S. Bhandari and B. D. Dunietz, J. Chem. Theory Comput., 2019, 15, 4305.
22. R. Khatri and B. D. Dunietz, J. Chem. Phys., 2023, 159, 071103.
23. J. Zirzlmeier, D. Lehnherr, P. B. Coto, E. T. Chernick, R. Casillas, B. S. Basel, M. Thoss, R. R. Tykwinski and D. M. Guldi, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 5325–5330.
24. M. W. B. Wilson, A. Rao, K. Johnson, S. Gélinas, R. di Pietro, J. Clark and R. H. Friend, J. Am. Chem. Soc., 2013, 135, 16680–16688.
25. M. W. B. Wilson, A. Rao, B. Ehrler and R. H. Friend, Acc. Chem. Res., 2013, 46, 1330–1338.
26. C. Schierl, A. Niazov-Elkan, L. J. W. Shimon, Y. Feldman, B. Rybtchinski and D. M. Guldi, Nanoscale, 2018, 10, 20147–20154.
27. O. Millington, S. Montanaro, A. Leventis, A. Sharma, S. A. Dowland, N. Sawhney, K. J. Fallon, W. X. Zeng, D. G. Congrave, A. J. Musser, A. K. Rao and H. Bronstein, J. Am. Chem. Soc., 2023, 125, 2499–2510.
28. M. Montalti, A. Credi, L. Prodi and M. T. Gandolfi, Handb. Photochem., Taylor & Francis Group, LLC, Boca Raton, 3rd edn, 2006.
29. C. C. Ladwig and R. S. H. Liu, Chem. Phys. Lett., 1975, 35, 563–565.
30. R. E. Kellogg, J. Chem. Phys., 1966, 44, 411–412.
31. C. Burgdorff, T. Kircher and H. G. Lohmannsroben, Spectrochim. Acta, Part A, 1988, 44, 1137–1141.
32. B. J. Baer and E. L. Chronister, J. Chem. Phys., 1994, 100, 23–27.
33. F. Lewitzka, H. G. Lohmannsroben, M. Strauch and W. Luttke, J. Photochem. Photobiol., A, 1991, 61, 191–200.
34. R. Ahmed and A. K. Manna, J. Phys. Chem., 2022, 126, 6594–6603.
35. H. Agren, B. F. Minaev and S. Knuts, J. Phys. Chem., 1994, 98, 3943–3949.
36. F. Vogeler, S. Siegert, C. M. Marian and R. Weinkauf, ChemPhysChem, 2011, 12, 1948–1956.
37. N. Nishi, K. Matsui, M. Kinoshita and J. Higuchi, Mol. Phys., 1979, 38, 1–24.
38. C. Burgdorff, S. Ehrhardt and H. G. Lohmannsroben, J. Phys. Chem., 1991, 95, 4246–4249.
39. T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
40. H. T. Sun, S. Ryno, C. Zhong, M. K. Ravva, Z. R. Sun, T. Körzdörfer and J. L. Brédas, J. Chem. Theory Comput., 2016, 12, 2906–2916.
41. S. Refaely-Abramson, S. Sharifzadeh, N. Govind, J. Autschbach, J. B. Neaton, R. Baer and L. Kronik, Phys. Rev. Lett., 2012, 109, 226405.
42. D. A. Egger, S. Weissman, S. Refaely-Abramson, S. Sharifzadeh, M. Dauth, R. Baer, S. Kümmel, J. B. Neaton, E. Zojer and L. Kronik, J. Chem. Theory Comput., 2014, 10, 1934–1952.
43. Z. Q. You, J. M. Mewes, A. Dreuw and J. M. Herbert, J. Chem. Phys., 2015, 143, 204104.
44. M. A. Rohrdanz, K. M. Martins and J. M. Herbert, J. Chem. Phys., 2009, 130, 054112.
45. T. Körzdörfer and J. L. Brédas, Acc. Chem. Res., 2014, 47, 3284–3291.
46. E. Epifanovsky, A. T. B. Gilbert, X. Feng, J. Lee, Y. Mao, N. Mardirossian, P. Pokhilko, A. F. White, M. P. Coons, A. L. Dempwolff, Z. Gan, D. Hait, P. R. Horn, L. D. Jacobson, I. Kaliman, J. Kussmann, A. W. Lange, K. U. Lao, D. S. Levine, J. Liu, S. C. McKenzie, A. F. Morrison, K. D. Nanda, F. Plasser, D. R. Rehn, M. L. Vidal, Z.-Q. You, Y. Zhu, B. Alam, B. J. Albrecht, A. Aldossary, E. Alguire, J. H. Andersen, V. Athavale, D. Barton, K. Begam, A. Behn, N. Bellonzi, Y. A. Bernard, E. J. Berquist, H. G. A. Burton, A. Carreras, K. Carter-Fenk, R. Chakraborty, A. D. Chien, K. D. Closser, V. Cofer-Shabica, S. Dasgupta, M. de Wergifosse, J. Deng, M. Diedenhofen, H. Do, S. Ehlert, P.-T. Fang, S. Fatehi, Q. Feng, T. Friedhoff, J. Gayvert, Q. Ge, G. Gidofalvi, M. Goldey, J. Gomes, C. E. Gonzalez-Espinoza, S. Gulania, A. O. Gunina, M. W. D. Hanson-Heine, P. H. P. Harbach, A. Hauser, M. F. Herbst, M. Hernandez Vera, M. Hodecker, Z. C. Holden, S. Houck, X. Huang, K. Hui, B. C. Huynh, M. Ivanov, A. Jasz, H. Ji, H. Jiang, B. Kaduk, S. Kähler, K. Khistyaev, J. Kim, G. Kis, P. Klunzinger, Z. Koczor-Benda, J. H. Koh, D. Kosenkov, L. Koulias, T. Kowalczyk, C. M. Krauter, K. Kue, A. Kunitsa, T. Kus, I. Ladjanszki, A. Landau, K. V. Lawler, D. Lefrancois, S. Lehtola, R. R. Li, Y.-P. Li, J. Liang, M. Liebenthal, H.-H. Lin, Y.-S. Lin, F. Liu, K.-Y. Liu, M. Loipersberger, A. Luenser, A. Manjanath, P. Manohar, E. Mansoor, S. F. Manzer, S.-P. Mao, A. V. Marenich, T. Markovich, S. Mason, S. A. Maurer, P. F. McLaughlin, M. F. S. J. Menger, J.-M. Mewes, S. A. Mewes, P. Morgante, J. W. Mullinax, K. J. Oosterbaan, G. Paran, A. C. Paul, S. K. Paul, F. Pavosevic, Z. Pei, S. Prager, E. I. Proynov, A. Rak, E. Ramos-Cordoba, B. Rana, A. E. Rask, A. Rettig, R. M. Richard, F. Rob, E. Rossomme, T. Scheele, M. Scheurer, M. Schneider, N. Sergueev, S. M. Sharada, W. Skomorowski, D. W. Small, C. J. Stein, Y.-C. Su, E. J. Sundstrom, Z. Tao, J. Thirman, G. J. Tornai, T. Tsuchimochi, N. M. Tubman, S. P. Veccham, O. Vydrov, J. Wenzel, J. Witte, A. Yamada, K. Yao, S. Yeganeh, S. R. Yost, A. Zech, I. Y. Zhang, X. Zhang, Y. Zhang, D. Zuev, A. Aspuru-Guzik, A. T. Bell, N. A. Besley, K. B. Bravaya, B. R. Brooks, D. Casanova, J.-D. Chai, S. Coriani, C. J. Cramer, G. Cserey, A. E. DePrince, R. A. DiStasio, A. Dreuw, B. D. Dunietz, T. R. Furlani, W. A. Goddard, S. Hammes-Schiffer, T. Head-Gordon, W. J. Hehre, C.-P. Hsu, T.-C. Jagau, Y. Jung, A. Klamt, J. Kong, D. S. Lambrecht, W. Liang, N. J. Mayhall, C. W. McCurdy, J. B. Neaton, C. Ochsenfeld, J. A. Parkhill, R. Peverati, V. A. Rassolov, Y. Shao, L. V. Slipchenko, T. Stauch, R. P. Steele, J. E. Subotnik, A. J. W. Thom, A. Tkatchenko, D. G. Truhlar, T. Van Voorhis, T. A. Wesolowski, K. B. Whaley, H. L. Woodcock, P. M. Zimmerman, S. Faraji, P. M. W. Gill, M. Head-Gordon, J. M. Herbert and A. I. Krylov, J. Chem. Phys., 2021, 155, 084801.
47. L. Kunze, A. Hansen, S. Grimme and J. Mewes, J. Phys. Chem. Lett., 2021, 12, 8470–8480.
48. T. Froitzheim, S. Grimme and J. Mewes, J. Chem. Theory Comput., 2022, 18, 7702–7713.
49. L. Packman, N. Mallo, A. Raynor, M. L. Gao, M. Babazadeh, H. Jin, D. M. Huang, P. L. Burn, I. R. Gentle and P. E. Shaw, Phys. Chem. Chem. Phys., 2023, 25, 23867–23878.
50. D. Datta and S. Kumar, Sol. Energy Mater. Sol. Cells, 2010, 94, 420–424.
51. J. Brebels, J. V. Manca, L. Lutsen, D. Vanderzande and W. Maes, J. Mater. Chem., 2017, 5, 24037–24050.
52. K. Ishii, M. Kinoshita and H. Kuroda, Bull. Chem. Soc. Jpn., 2006, 46, 3385–3391.
53. C. H. Kim, O. Yaghmazadeh, D. Tondelier, Y. B. Jeong, Y. Bonnassieux and G. Horowitz, J. Appl. Phys., 2011, 109, 083710.
54. U. Kaatze, R. Pottel and P. Schmidt, J. Phys. Chem., 1988, 92, 3669–3674.
55. J. W. Hager and S. C. Wallace, Anal. Chem., 1988, 60, 5–10.
56. N. Ando, M. Mitsui and A. Nakajima, J. Chem. Phys., 2007, 127, 234305.
57. J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620.
58. P. I. Djurovich, E. I. Mayo, S. R. Forrest and M. E. Thompson, Org. Electron., 2009, 10, 515–520.
59. S. Hirata and M. Head-Gordon, Chem. Phys. Lett., 1999, 302, 375–382.
60. M. J. Peach, M. J. Williamson and D. J. Tozer, J. Chem. Theory Comput., 2011, 7, 3578–3585.
61. M. J. Peach and D. J. Tozer, J. Phys. Chem. A, 2012, 116, 9783–9789.
62. Y. Shao, Y. Mei, D. Sundholm and V. R. I. Kaila, J. Chem. Theory Comput., 2020, 16, 587–600.
63. M. Zheng, Y. Li, Y. Wei, L. Chen, X. Zhou and S. Liu, J. Phys. Chem. Lett., 2022, 13, 2507–2515.
64. S. Sarkar, H. P. Hendrickson, D. Lee, F. Devine, J. Jung, E. Geva, J. Kim and B. D. Dunietz, J. Phys. Chem. C, 2017, 121, 3771–3777.
65. K. Begam, H. Aksu and B. D. Dunietz, J. Phys. Chem. B, 2024, 128, 4315–4324.
66. T. Ullrich, P. Pinter, J. Messelberger, P. Haines, R. Kaur, M. M. Hansmann, D. Munz and D. M. Guldi, Angew. Chem., Int. Ed., 2020, 59, 7906–7914.
67. C. Chakravarty, H. Aksu, B. Maiti and B. D. Dunietz, J. Phys. Chem. A, 2021, 125, 7625–7632.
68. H. Aksu, A. Schubert, S. Bhandari, A. Yamada, E. Geva and B. D. Dunietz, J. Phys. Chem. B, 2020, 124, 1987–1994.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp02127h

---