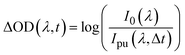Excited state deactivation in phytochemical flavonoids: astragalin and kaempferol

Abstract

Femtosecond transient absorption experiments and ab initio and nonadiabatic dynamics (NAD) simulations have helped to explicate the photophysical dynamics of two ubiquitous members of the flavonoid family, astragalin and kaempferol. Differences between their excited state deactivation mechanisms have been observed and explained. Astragalin exhibits an ultrashort (∼10 ps) S₁ lifetime, whereas that of kaempferol extends approximately twice as long (∼20 ps), explained by the systems’ relative access to a S₁/S₀ conical intersection following excited state intramolecular proton transfer. These findings expound the unexpected role played by sugar substituents in photoprotective flavonoids and justify the use of similar natural derivatives for UV photothermal materials.

---

Introduction

Nature continues to inspire many of humanity's technological advancements.¹ Deference to billions of years of evolutionary development may provide the solution to the last century's global issues.^2–4 Active compounds in plants – phytochemicals – have seen use as preventative medicines and nutraceuticals,^5,6 whilst flora has informed the design of biobased materials.⁷ Phytochemical photo-protectant molecules are of particular interest for biomimetic applications. Due to their dependence on photosynthesis, plants are especially sensitive to the effects of solar radiation and have therefore developed effective and sensitive defensive mechanisms.⁸

Amongst the multitude of natural products which have found use as pharmaceuticals is a group of phenolic species known as flavonoids.⁹ Flavonoids are ubiquitous in fruits, vegetables, stems, flowers, and grains.⁹ Kaempferol is a natural flavonol, the most abundant subgroup of flavonoids,⁹ and has been identified as having antioxidant, antimicrobial, anticancer and neuroprotective properties.¹⁰ The structural features of flavonols, including a C₂=C₃ double bond conjugated with a 4-oxo group and 3-hydroxyl group on the C ring, and 5,7-dihydroxylation on the A ring (see Fig. 1 for atom and ring labelling), are critical to their biological and antioxidant activities.^11–13

Fig. 1 Structures and atom numbering schema (top) and optimized geometries (bottom) of kaempferol (left) and astragalin (right).

In this study, we investigate the photochemistry of kaempferol and its phytochemical 3-O-glucoside, astragalin,¹⁴ both experimentally and theoretically. Astragalin, found in a plethora of plant families,¹⁵ retains many structural characteristics commonplace in bioactive flavonoids, and it was therefore judged as a suitable model for other plant-derived systems capable of antioxidative support against UV damage.¹⁶ Astragalin's glycosyl substitution aids its aqueous solubility and may influence its biochemical properties but would not be expected to significantly influence its photochemistry. As pharmaceutical compounds already in use,^14,15,17,18 astragalin and kaempferol uniquely present themselves as models for dual-purpose natural products, whose applications might bridge the divide between purely cosmeceutical (e.g., antioxidant, anti-aging, cell protection) and specialised medical markets.¹⁹

This study evaluated whether the photochemistry of astragalin was distinct from kaempferol itself, or even from other flavonoids more generally.²⁰ By investigating both the photochemistry of astragalin and kaempferol in a polar (ethanol, dielectric constant ε_r = 25.3²¹) and nonpolar (1,4-dioxane, ε_r = 2.22²¹) solution, and rationalising our findings using computational chemistry, including exploration of ground and excited state geometries, electronic structure and nonadiabatic dynamics (NAD), we have also assessed their ability to act as photothermal materials.²²

Materials and methods

UV-Visible absorption spectroscopy

UV-Visible absorption spectra of both solution samples were recorded using a Cary 60 UV/Vis spectrophotometer before and after irradiation with a simulated solar spectrum (LCS-100, Spectra-Physics, see Fig. S3, ESI†). Solutions of each molecule were made up to ∼0.5 absorbance at their UV-visible origin maximum (λ_max) in a 1 mm path length quartz cuvette for ultrafast experiments.

Femtosecond transient electronic absorption spectroscopy

A detailed description of the femtosecond transient electronic absorption spectroscopy (fs-TEAS) setup has been described previously; a brief overview of the method used is therefore provided below.

Solutions, as described supra, were used as prepared. The ‘pump’ (photoexcitation) wavelength was set to λ_max for each analyte solution, as extracted from UV-visible absorption spectra (see Fig. 2); the pump power was set to ∼500 μW. Our ‘probe’ pulse, a white light supercontinuum (WLS) which ranged from ∼320–720 nm, was generated by focusing ∼0.05 W of a fundamental 800 nm beam into a translating CaF₂ window. The WLS probe was focused and overlapped with the pump beam inside the 1 mm sample cuvette to maximise observed signal. Pump–probe time delay (Δt) was controlled by changing the pathlength of the probe pulse using a gold retroreflector mounted onto a motorised delay stage. Every other pump pulse was blocked by a chopper spinning at 0.5 kHz to directly observe the ‘pump-off’ (I₀) and ‘pump-on’ (I_pu) probe absorbance. The resulting change in optical density (ΔOD) was recorded by focusing the probe beam into a fibre-coupled spectrometer (AvaSpec-ULS1650F, Avantes, Apeldoorn, The Netherlands), and calculated as:

Fig. 2 UV-Visible absorption spectra of kaempferol (red) and astragalin (blue) in ethanol before and after 2 hours’ ‘solar’ irradiation. Shaded plots are approximate profiles of the ‘pump’ pulses used in fs-TEAS for each solution.

Computational details

Stable geometries of astragalin and kaempferol were identified using the conformer-rotamer ensemble sampling tool/version6.4.0 (CREST).^23,24 CREST adopts a meta-dynamic (MTD) scheme for generating conformational ensembles, directly sampling at a semiempirical quantum mechanical (SQM) level. An energy window of 8.0 kcal mol⁻¹ was applied to screen conformational energies at the semiempirical level. This technique utilised the GFN2-xTB method.²⁵ A total of 649 conformers were identified for astragalin, while five were found for kaempferol: kaempferol lacks a glycoside moiety, resulting in fewer conformational degrees of freedom and thereby affording a more straightforward structural analysis. The 100 most stable conformers of astragalin and all conformers of kaempferol were subjected to geometry optimization using density functional theory (DFT) with the B3LYP functional, cc-pVDZ basis set, and D3 dispersion correction.^26,27 Subsequently, the 20 most stable DFT-optimized conformers of astragalin and all DFT-optimized conformers of kaempferol underwent a final optimization using the RI-MP2 theoretical model and cc-pVDZ basis set. The RI-ADC(2) and time dependent density functional theory (TD-DFT) methodologies (using ωB97XD functional²⁸) were used to predict the excitation energies and oscillator strengths associated with the four lowest energy singlet–singlet excitations, for the most stable identified ground state conformers of astragalin and kaempferol in both the gas and implicit solution phases. All calculations used the cc-pVDZ basis set. The polarizable continuum model (PCM)²⁹ and COSMO models were employed to incorporate implicit solvation effects when required.

The MP2/ADC(2)^30–32 calculations were done using the Turbomole suite (version 6.3 and 6.6) and DFT/TD-DFT calculations were performed using Gaussian 16.³³ We investigated nonradiative relaxation mechanisms and PESs by mapping reaction paths with relaxed scan and LIIC and deriving potential energy curves at the cost-effective ADC(2) theoretical level.^23–25 In the relaxed scan, the O₅–H bond length was selected as the reaction coordinate, whose value varies, in 0.06 Å intervals, from 0.99–1.72 Å and 0.99–1.78 Å for astragalin and kaempferol, respectively. The O₅–H bond length was frozen while allowing the remaining degrees of freedom to be optimized. For both systems, the minimum energy S₁/S₀ CI was optimized based on CASSCF(6,6)/6-31G* method, implemented in the Gaussian 16 program.³³ The active space for these calculations comprised six electrons distributed across six molecular orbitals, including three occupied and three virtual orbitals (Fig. S14, ESI†); this active space was selected due to its reported accuracy and feasible computational cost.^34–38 To explore the implicit solvent effects (i.e., of ethanol), the polarizable continuum model (PCM), implemented in Gaussian 16, and the COSMO model in Turbomole (version 6.6) were employed. To connect the S₁ optimized geometry to the CI structure, we used a Python script to generate 16 intervals to determine points on the LIIC potential energy surfaces.

UV-Visible absorption spectra and nonadiabatic dynamics simulations were performed using a mixed quantum-classical trajectory method incorporating decoherence correction (α = 0.1 Hartree), based on TD-ωB97XD/cc-pVDZ theory and implemented via Newton-X (v2.4)^39,40 interfaced with Gaussian 16.³³ The suitability of this computational framework for exploring excited-state deactivation processes has been validated in several prior studies.^34,41–43 To initiate the simulations, 500 initial conditions were sampled from a Wigner distribution (0 K) of normal modes from a harmonic oscillator around the ground-state minimum. The resulting nuclear ensemble was then employed to compute excitation energies and transition dipole moments, enabling simulation of the UV absorption spectrum for the bright S₁ (¹ππ*) state.

Nonadiabatic dynamics simulations were conducted for the ground state (S₀) and the two lowest excited singlet states (S₁ and S₂), initiating the trajectories from S₁ due to its dominant role in UV absorption for both molecular systems. An additional set of 500 initial conditions was generated for S₁ using a Lorentzian line broadening with δ = 0.05 eV. Electronic propagation was carried out using the local diabatization method.^44,45 When state hopping occurred, typically across a finite energy gap, total energy conservation was ensured by rescaling momenta along the direction of the nonadiabatic coupling vector.^46,47 In addition, a bond length criterion of O₄–H₁₂ ≤ 1.0 Å, implemented via a custom Python script, was used to define proton transfer (PT) (see Fig. S10, ESI†).

Initial conditions for the nuclear ensemble method⁴⁸ were sampled within the spectral windows of 3.5 ± 0.1 eV and 3.7 ± 0.1 eV respectively for astragalin and kaempferol, as illustrated in Fig. S9 (ESI†). A total of 103 trajectories for astragalin and 92 trajectories for kaempferol were simulated. Each trajectory was propagated for a maximum of 1500 fs with a nuclear time step of 0.5 fs. Due to limitations inherent to TD-DFT, trajectories were terminated either when the energy gap between S₁ and S₀ dropped below 0.15 eV, or when the maximum simulation time was reached. Energy conservation was satisfactorily maintained throughout the simulations.

Solvent effects on the absorption spectra were investigated using the polarizable continuum model (PCM, water) as implemented in Gaussian 16. To characterize out-of-plane ring distortions during dynamics, Cremer–Pople puckering parameters⁴⁹ were calculated using the PLATON program.⁵⁰

Results

UV-Visible absorption spectroscopy

As is characteristic of other flavonoid systems,⁵¹ two distinct absorption bands (at ∼250 and ∼350 nm) are present in the UV region for kaempferol and astragalin, both in polar (ethanol, see Fig. 2) and nonpolar (1,4-dioxane, see Fig. S1, ESI†) solutions. Extinction coefficients ε for kaempferol in ethanol at 366 nm and astragalin in ethanol at 351 nm were determined as 22 100 ± 170 and 17 320 ± 30 mol⁻¹ dm³ cm⁻¹, respectively (see Fig. S2, ESI†).

Photostability under a simulated solar spectrum was measured by recording UV-visible absorption spectra after 2 hours’ exposure under the equivalent of ‘one Sun’ (shown in ethanol in Fig. 2; the simulated solar spectrum used is shown in Fig. S3, ESI†). Extremely high photostability is observed for astragalin, which is somewhat reduced for kaempferol; as is commonly reported in literature for UV filters, an area under curve index (AUCI) between 280 and 400 nm of 94% was calculated for astragalin and of 87% for kaempferol (see ESI,† Section S1.1), classifying each as photostable.⁵²

Ground state geometry determination

The most stable identified structures of ethanolic kaempferol and astragalin are shown in Fig. 1. As shown, the optimized ground state structures include the O₅H₁₂⋯O₄ hydrogen bond in both systems. Rotation of the C₅ hydroxyl group (O₅H₁₂) to face away from the C₄ carbonyl, removing the hydrogen bonding interactions between these moieties, destabilises kaempferol and astragalin by ∼0.36 and ∼0.32 eV, respectively (see ESI,† Sections S1.2 and S2.3 for further details). Similarly, in kaempferol, a geometry with both C₃ and C₅ hydroxyl groups facing the carbonyl oxygen is stabilized by ∼0.18 eV relative to a conformer with the C₃ hydroxyl oriented away. This appears to result from the loss of the hydrogen bonding interaction between the O₃H₁₁ hydroxyl group and the C₄ carbonyl, and the diminished overlap of p orbitals associated with rings B and C: the steric hindrance between O₃H₁₁ and the proton at C_6′/C_2′ causes a dihedral rotation of ring B ∼40.2° out of the plane of ring C.

Vertical transition energies

Vertical transition energies and oscillator strengths at the ADC(2) level for the optimized structures of astragalin and kaempferol in vacuo, between the ground and four lowest-lying singlet excited states (S₁–S₄), are presented in Table 1. Selected valence molecular orbitals (MOs) of these two molecules are also presented in Fig. 3. For astragalin, the S₁ ← S₀ electronic transition is assigned as ¹ππ*, originating from the highest occupied molecular orbital to the lowest unoccupied molecular orbital (LUMO ← HOMO) (64%) and LUMO ← HOMO−1 (30%) single electron transition. The S₂ ← S₀ transition corresponds to an optically dark ¹nπ* state, dominated by a LUMO ← HOMO−7 transition. The third and fourth singlet electronic transitions are also assigned as optically bright ¹ππ* states, arising from LUMO ← HOMO−1 (51%) and LUMO ← HOMO−2 (65%) for the S₃ ← S₀ and S₄ ← S₀ transitions respectively. Similar electronic transition assignments hold for kaempferol, except for the character of S₂ and S₃ swapping, and we therefore neglect further discussion on this system (see ESI,† Section S1.3 for more information).

Table 1 Vertical transition energies and oscillator strengths for lowest lying electronic transitions in astragalin and kaempferol in vacuo and in implicit ethanol. ADC(2) results were determined based on the MP2 optimized ground state geometries, and TD-DFT results were determined based on the ωB97XD optimized ground state geometries for each system

Transition energy/eV
Molecule	Excited state	ADC (2)/cc-pVDZ		TD-ωB97XD/cc-pVDZ
		Gas phase	COSMO/ethanol	PCM/ethanol
Astragalin (experimental λmax: 351 nm (3.53 eV))	S1 (ππ*)	3.84 (0.3450)	3.76 (0.4482)	3.98 (0.5444)
	S2 (nπ*)	4.12 (0.0038)	4.14 (0.1468)	4.52 (0.0955)
	S3 (ππ*)	4.21 (0.1774)	4.16 (0.0003)	4.75 (0.0049)
	S4 (ππ*)	4.58 (0.0956)	4.49 (0.1413)	4.94 (0.1109)
Kaempferol (experimental λmax: 366 nm (3.39 eV))	S1 (ππ*)	3.61 (0.5306)	3.56 (0.5417)	3.66 (0.6726)
	S2 (ππ*)	4.29 (0.1166)	4.26 (0.1133)	4.45 (0.0708)
	S3 (nπ*)	4.36 (0.0000)	4.31 (0.0034)	4.83 (0.0072)
	S4 (ππ*)	4.62 (0.0447)	4.58 (0.1109)	4.86 (0.0000)

---

Fig. 3 Selected valence MOs which play a prominent role in the lowest lying electronic transitions of astragalin and kaempferol.

We also determined the four lowest lying electronic transitions of the two molecules at ADC(2) level, considering the effect of an implicit solvent based on the COSMO model,⁵³ the results of which are present in Table 1. The S₁ (¹ππ*) ← S₀ electronic transition of both molecules exhibits a slight shift in this implicit model versus in vacuo, and the oscillator strength of subsequent excited states changes. Finally, time-dependent density functional theory (TD-DFT) calculations were performed with ethanol as an implicit solvent. Overall, TD-DFT results are consistent with ADC(2) (see Table 1), demonstrating reliability in describing the electronic structures and photophysics of the systems. Our transition assignments using TD-DFT confirm that the S₁ (¹ππ*) state is responsible for UV absorption in both flavonoids. These results also suggest that solvent interactions play only a minor role in modulating the electronic properties of the systems. Optimized geometries of both systems in the ground (at MP2/cc-pVDZ) and S₁ (at ADC(2)/cc-pVDZ) states are presented in Fig. S4 (ESI†). Both astragalin and kaempferol exhibit a local S₁ minimum, the properties of which may govern their respective photophysics.

Femtosecond transient electronic absorption spectroscopy

Following measurements in the steady-state regime, spectroscopy was done on the ultrafast (femtosecond) timescale. Solutions of both astragalin and kaempferol in ethanol and 1,4-dioxane were analysed using fs-TEAS,⁵⁴ a method long implemented for studying the time-resolved photochemistry of biological chromophores. Each solution was photo-excited at its respective origin band maximum (λ_max, see Fig. 2). Spectral dynamics following photoexcitation were similar in each system, as were kinetics between solvents. Collected transient absorption (TA) spectra, as shown in Fig. 4 for astragalin and kaempferol in ethanol (and in Fig. S5 in 1,4-dioxane, ESI†), were fitted using a global fitting procedure (see ESI,† Section S1.4 for instrument response function (IRF), decay associated spectra (DAS), and residuals from fitting);⁵⁵ lifetimes extracted from this fitting are shown in Table 2.

Fig. 4 Collected TA heatmaps (left) and kinetic traces at excited state absorption maximum (right) of astragalin (blue) and kaempferol (red) in ethanol after photoexcitation with 351 nm and 366 nm light, respectively.

Table 2 Lifetimes extracted from global fitting of TA spectra collected following photoexcitation at λ_pump

Lifetime	Astragalin		Kaempferol
Solvent	Ethanol	1,4-Dioxane	Ethanol	1,4-Dioxane
λpump (nm)	351	347	366	364
τ1 (ps)	8.44 ± 0.07	11.05 ± 0.05	18.40 ± 0.24	16.84 ± 0.09
τ2 (ps)	>2500	>2500	>2500	>2500
IRF (FWHM) (fs)	136 ± 6	106 ± 12	160 ± 18	109 ± 8

---

Photophysics: nonadiabatic dynamics (NAD) simulations and conical intersections

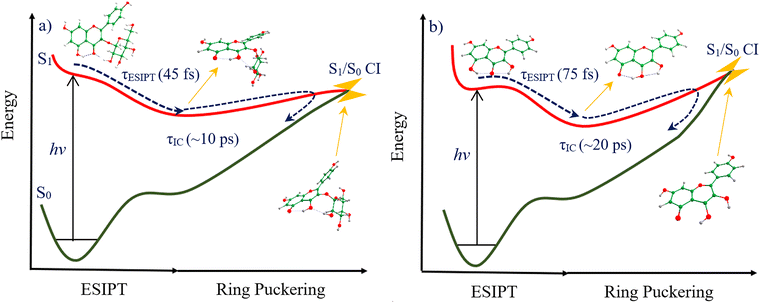
To explore the dynamical behaviour of astragalin and kaempferol following photoexcitation, we undertook NAD simulations based on the TD-ωb97XD/cc-pVDZ theoretical model,^30,56 initialized from the most stable conformer of each molecule. Simulated UV-visible absorption spectra of these two systems (see Fig. S9, ESI†), were generated using the nuclear ensemble approach.⁴⁸ To add from the outset, preliminary TD-DFT calculations (see ESI,† Section S2.5) showed that intersystem crossing (ISC) was unlikely to contribute significantly to the relaxation mechanisms of either system; the energies of triplet states (T₁–T₃) corresponding to configurations generated by relaxing the Franck–Condon (FC) geometry into an energetically accessible local S₁ minimum (where ISC would be most feasible) were further than 0.26 eV away from the vertical S₁ energy. NAD simulations were initialized from the S₁ (¹ππ*) excited state, using the decoherence-corrected fewest switches surface-hopping (DC-FSSH) approach.^57,58 Starting in the optically bright S₁ state, 103 trajectories were generated for astragalin, and 92 for kaempferol; selected trajectories are shown in Fig. 5. Trajectories were run up to 1500 fs for astragalin and 2000 fs for kaempferol. For astragalin, 80% of trajectories accessed a S₁/S₀ CI within 1500 fs; however, for kaempferol, only 10% of the trajectories reached a CI before 2000 fs simulation, indicating the excited state lifetime is substantially longer than this. This difference agrees with what is observed experimentally.

Fig. 5 Energy profiles from selected NAD trajectories of astragalin (a) and kaempferol (b). The black, red and blue curves respectively indicate the ground (S₀), S₁ and S₂ state energies.

In our simulations of astragalin, excited state intramolecular proton transfer (ESIPT) from O₅ to O₄ was observed in 97% of trajectories; the remaining 3% showed ESIPT from the sugar's O_2′′H to O₄. In kaempferol, ESIPT occurred from O₅H₁₂ in 86% of trajectories, and from O₃H₁₁ in the remaining 14%. To evaluate the ESIPT timescale from NAD simulations in both systems (i.e., the time taken for PT to occur from O₅H₁₂), an exponential decay was fitted to O₅H₁₂ proton occupation (see Fig. S10, ESI†).⁵⁹ From this, ESIPT lifetimes of 45 ± 5 fs for astragalin and 75 ± 2 fs for kaempferol were extracted, the latter agreeing with the results of Ji et al.⁶⁰ Both lifetimes are within the IRF for our fs-TEAS experiments (see Table 2) and therefore cannot be observed.

The S₁ lifetime was evaluated from NAD trajectories in a similar way to ESIPT (see Fig. S11, ESI†),⁶⁰ yielding 984 ± 67 fs for astragalin. Conversely, as shown in Fig. 5(b), it is predicted that most of kaempferol's excited population remains trapped in the S₁ excited state; state crossings between S₁ and S₀ were infrequent within 2000 fs. Monitoring astragalin's structure (in trajectories that culminate in S₁/S₀ crossing before 2000 fs) identified key molecular motions that facilitate nonadiabatic coupling. An out-of-plane C₂ distortion, continuing to the end of dynamics, puckers the benzopyran moiety. This ring deformation coordinate steadily increases the ground state energy, until S₁/S₀ state degeneracy is reached, and thus embodies the primary deactivation pathway in astragalin. The distribution of trajectories in the space of Cremer–Pople parameters (θ, Φ) at S₁/S₀ crossings in astragalin, defined by out-of-plane deformation of atoms in the C ring, is shown in Fig. S12 (ESI†).⁴⁹ The C₂ puckering deformation experienced by astragalin's benzopyran moiety is defined by the parameters θ and Φ;^61–63 most S₁/S₀ crossings appear within the range 270° > Φ > 180°, yielding an envelope conformation for the ring structure.

To investigate the excited state deactivation of astragalin and kaempferol further, we have resolved the potential energy surfaces (PESs) and located possible CIs in both systems, using the complete active space self-consistent field (CASSCF) theoretical method (Fig. S4, ESI†). As shown in Table 1, S₁ (¹ππ*) has significant oscillator strength; it is therefore responsible for both astragalin and kaempferol's absorption in the UV region. Consequently, it is anticipated to play a governing role in their photophysics. Relaxing each molecule in S₁ from its FC geometry is accompanied by ESIPT from O₅H₁₂ to O₄. To further explore this, we generated approximate 1D minimum energy paths (MEPs) for S₀ and S₁ through relaxed scans along the proton transfer (PT) coordinate in each system (see Fig. S13, ESI†). As shown, in both systems ESIPT follows a decreasing, and barrierless, S₁ PES. ESIPT should therefore be exothermic, justifying its rapidity.

Taking the final geometries resulting from PT, the minimum S₁/S₀ CIs were determined at the CASSCF (6,6)/6-31G* theoretical level for astragalin and kaempferol (see Fig. S4, ESI†). The active space for CASSCF level consists of three occupied and three virtual orbitals (see Fig. S14, ESI†). As locating CIs does not guarantee a physically related nonradiative deactivation mechanism for the systems, we have determined S₀ and S₁ PESs of both systems along a linear interpolation of internal coordinates (LIIC), connecting the S₁ minimum of each system to the located minimum energy CI (see Fig. S15, ESI†). For both systems the S₁/S₀ CI is accessible, albeit following dissimilar S₁ PES topographies. Thus, following photoexcitation, each molecule can undergo PT on an ultrashort timescale and, following this, approach a S₁/S₀ CI by slight out-of-plane deformation in the benzopyran ring (at C₂). This provides a significant route for internal conversion (IC) by returning the ring to planarity and finally by back-PT to recover the ground state minimum energy structure.

Discussion

Firstly, a brief treatise on properties of the UV-visible absorption spectrum of each system is necessary. From the apparent lack of substantial solvatochromism for astragalin's absorption maximum at ∼350 nm (between in ethanol and in 1,4-dioxane, see Fig. 2 and Fig. S1 respectively, ESI†), we may conclude that the transition corresponding to this band does not generate a dipole-dependent charge transfer (CT) state,⁶⁴ but is instead consistent with local excitation (LE), most likely arising around the central conjugated flavonoid moiety. This is supported by transition densities generated for the S₁ ← S₀ excitation (see ESI,† Section S2.1). Kaempferol's electronic origin band (at ∼365 nm) is similarly insensitive to solvent polarity (see Fig. 2 and Fig. S1, ESI†). The sugar side chain would normally be expected to act as a spectator, but the significant blue shift of astragalin's absorption maximum with respect to kaempferol refutes this.

As mentioned supra, the two absorption bands seen in the UV-visible spectra are ubiquitous in flavonoid systems.⁶⁵ From consideration of the above, it is prudent to assume that photodynamics following excitation to similar respective bands in astragalin and kaempferol would be alike. Vertical excitation energies and oscillator strengths predicted by TD-DFT (Table 1) also explain the origin of experimentally observed absorption between the two most significant absorption bands. Rather than being purely vibronic in origin, nonzero absorption within this region can be attributed to S_2–4 ← S₀ transitions, which are (variably) predicted to be moderately bright for ethanolic astragalin and kaempferol. The oscillator strengths associated with these transitions, however, are far lower than those predicted for the corresponding system's S₁ ← S₀ transition. Exclusively elucidating those relaxation pathways that are followed upon population of S₁ can still therefore offer insight into the overall systems’ photophysics.

Under a simulated solar spectrum, astragalin preserves good stability, with little reduction in observed absorption (Fig. 2). This photostability indicates a predominant relaxation pathway which does not lead to permanent chemical change. Kaempferol's reduced photostability may be explained by an alternative dissociative pathway in the excited state (not explicitly identified), which can be accessed while population resides in S₁.

At first glance, results from ultrafast measurements indicate similar spectral dynamics between flavonoids and solvents. Global fitting of TA data for each system yields two lifetimes, both of which are similar between solvents (Table 2). A broad excited state absorption (ESA) feature, centred at ∼400 nm, is seen in each solvent, for both molecules. The excited state dynamics of both are kinetically uncomplicated. τ₁ is assigned to a convolution of fast ESIPT (potentially within our experimental IRF) and continuous geometry relaxation towards and through the S₁/S₀ CI into the ground state, incorporating back-PT to reform the starting material. Astragalin's faster relaxation in ethanol versus 1,4-dioxane may be explained by enhanced coupling between its glucoside and the surrounding polar environment effecting more efficient vibrational energy dissipation; this would not be seen in the non-glycosylated kaempferol. τ₂ captures unrecovered excited state population. The relaxation pathway identified in NAD simulations of astragalin indicates a strong propensity for efficient regeneration. The identified CI, which 80% of trajectories encountered within the simulation time of 1500 fs, afforded passage to a barrierless path along the ground state PES, featuring steep gradient(s) and 3.48 eV stabilization, back to the FC geometry (see Fig. 6(a)).

Fig. 6 Summary of the nonradiative decay pathway of astragalin (a) and kaempferol (b) photoexcited to S₁. Geometries of relevant optimized structures are inset. Time scales corresponding to excited state intramolecular proton transfer (ESIPT) and internal conversion (IC) are also shown.

From both experimental and theoretical results (i.e., from ab initio PESs and NAD simulations), we summarise the photo-dynamics of astragalin and kaempferol in Fig. 6. Both systems, when initialized at the FC geometry, undergo ultrafast ESIPT (within 45 and 75 fs for astragalin and kaempferol, respectively). Subsequently, both systems experience further conformational change, involving the displacement of C₂, which leads to a puckered benzopyran moiety. This motion drives the system toward an energetically accessible S₁/S₀ CI, where a nonadiabatic transition to the ground state occurs, followed by back-PT in S₀. The net effect of this process is conversion of deleterious UV light to heat, a key criterion for UV filters.

A difference in experimental excited state lifetimes was measured for these two systems (∼10 ps and ∼20 ps for astragalin and kaempferol respectively). Guided by our ab initio calculations’ predictions for S₁/S₀ CIs in both compounds, we seek to explain this. In astragalin, the identified S₁/S₀ CI was predicted to locate lower in energy (0.48 eV) than the vertical S₁ ← S₀ electronic transition energy, meaning there is no barrier on the S₁ PES between the FC geometry and S₁/S₀ CI (see Fig. 6(a)). In kaempferol, we predict that the S₁/S₀ CI locates slightly higher in energy (0.45 eV) than the vertical S₁ ← S₀ transition energy (see Fig. 6(b)); the S₁/S₀ CI cannot be accessed in kaempferol without surmounting this barrier. Expectedly, kaempferol's excited state deactivation, although still facile, is significantly slower than in astragalin. Excited population can experience trapping in the S₁ minimum, from which it could conceivably decay to the ground state (although an emission quantum yield of only ∼1% was observed) or undergo excited state photochemistry, accounting for its degradation.

The shorter excited state lifetime of astragalin, seen both experimentally and computationally, is effected by additional structural complexity conferred by the sugar moiety. The out-of-plane deformation at C₂ is aided, albeit marginally, by the steric interaction of the glucosyl with the B ring. Judicial substitution of saccharides to flavonoids, or selection of appropriately glycosylated natural derivatives, could therefore enhance the efficiency of nonradiative relaxation in these systems.

Conclusion

In this study, we have comprehensively investigated the intrinsic photostability and dynamics of astragalin and kaempferol using a combined experimental and theoretical approach. While both compounds have appreciable UV absorption and undergo excited state intramolecular proton transfer, their ultrafast dynamics differ. Specifically, kaempferol's excited state lifetime is approximately twice that of astragalin, evidenced by prolonged excited state absorption. In astragalin, no potential energy barrier has been predicted before a S₁/S₀ CI, enabling more efficient nonradiative relaxation. In contrast, for kaempferol, a small barrier hinders excited population approaching the S₁/S₀ CI, explaining slower deactivation. These results are qualitatively reflected in nonadiabatic surface hopping dynamics simulations. The shorter excited state lifetime of astragalin compared to kaempferol arises from additional structural complexity introduced by the sugar moiety, aiding the out-of-plane motion of C₂ (benzopyran).

Our results demonstrate the significant role of sugar in enhancing excited state deactivation of flavonoids, comparable to the effect of sugars on the photophysical behaviour of nucleobases.^36,66–69 These findings enhance our understanding of nonradiative pathways in flavonoids and the role of substitution, offering biomimetic insight into designing more photostable materials. Moreover, as two members of the flavonoid family, our results confirm that these systems fulfil the conditions for model nature-inspired UV filters, due both to their strong UV absorption and ultrafast ground state recovery.

Author contributions

S. P. and V. G. S. conceived the presented idea. M. H. carried out the fs-TEAS and steady-state experiments. J. E., M. S. and R. O. performed the computational calculations. J. E. undertook the preliminary computational study. M. H., J. E., M. S., R. O. and V. G. S. analysed the results. M. H., J. E., M. S. and R. O. designed the figures. M. H. wrote the manuscript with input from all authors. R. O., S. P. and V. G. S. supervised the project.

Conflicts of interest

There are no conflicts to declare.

Data availability

The data that support the findings of this study are available upon request.

Acknowledgements

The authors would like to acknowledge the Warwick Centre for Ultrafast Spectroscopy (https://warwick.ac.uk/fac/sci/wcus) for use of the Cary 60 UV/Vis Spectrometer and the fs-TEAS set-up. M. H. was supported by NERC CENTA2 (Grant No. NE/S007350/1). The University of Birmingham's BlueBEAR High Performance Computing (HPC) services are acknowledged. J. E. acknowledges funding from the EPSRC CDT in Modelling of Heterogeneous Systems funded by EP/S022848/1. Computing facilities were provided by the Scientific Computing Research Technology Platform of the University of Warwick through the use of the HPC cluster Avon, and the Sulis Tier 2 platforms at HPC Midlands+ funded by the Engineering and Physical Sciences Research Council (EPSRC), grant number EP/T022108/1. R. O. thanks the support of Royal Society International Exchange (No. IES\R2\232279). The Research Council of the University of Isfahan is kindly appreciated for financial support. The support of the Iran National Science Foundation (insf.org) is also acknowledged (Grant: 4041840). V. G. S. thanks the Royal Society for a Royal Society Industry Fellowship. The authors would like to thank Mibelle Group Biochemistry for supplying the astragalin and kaempferol samples.

Notes and references

1. N. K. Katiyar, G. Goel, S. Hawi and S. Goel, Nature-Inspired Materials: Emerging Trends and Prospects, NPG Asia Mater., 2021, 13(1), 1–16,  DOI:10.1038/s41427-021-00322-y.
2. W. R. Turner, Looking to Nature for Solutions, Nat. Clim. Change, 2018, 8(1), 18–19,  DOI:10.1038/s41558-017-0048-y.
3. Y. H. Cohen and Y. Reich, The Biomimicry Discipline: Boundaries, Definitions, Drivers, Promises and Limits, in Biomimetic Design Method for Innovation and Sustainability, ed. Y. Helfman Cohen and Y. Reich, Springer International Publishing, Cham, 2016, pp. 3–17 DOI:10.1007/978-3-319-33997-9_1.
4. H. Dicks, The Biomimicry Revolution: Learning from Nature How to Inhabit the Earth, Columbia University Press, 2023, p. 320.
5. D. Mihaylova and A. Popova, Phytochemicals of Natural Products: Analysis and Biological Activities, Horticulturae, 2023, 9(2), 167,  DOI:10.3390/horticulturae9020167.
6. A. Kumar, N. P, M. Kumar, A. Jose, V. Tomer, E. Oz, C. Proestos, M. Zeng, T. Elobeid, S. K and F. Oz, Major Phytochemicals: Recent Advances in Health Benefits and Extraction Method, Molecules, 2023, 28(2), 887,  DOI:10.3390/molecules28020887.
7. M. S. Ganewatta, Z. Wang and C. Tang, Chemical Syntheses of Bioinspired and Biomimetic Polymers toward Biobased Materials, Nat. Rev. Chem., 2021, 5(11), 753–772,  DOI:10.1038/s41570-021-00325-x.
8. N. Shubayr, Phytochemicals Properties of Herbal Extracts for Ultraviolet Protection and Skin Health: A Narrative Review, J. Radiat. Res. Appl. Sci., 2023, 16(4), 100729,  DOI:10.1016/j.jrras.2023.100729.
9. A. N. Panche, A. D. Diwan and S. R. Chandra, Flavonoids: An Overview, J. Nutr. Sci., 2016, 5, e47,  DOI:10.1017/jns.2016.41.
10. S. P. Bangar, V. Chaudhary, N. Sharma, V. Bansal, F. Ozogul and J. M. Lorenzo, Kaempferol: A Flavonoid with Wider Biological Activities and Its Applications, Crit. Rev. Food Sci. Nutr., 2023, 63(28), 9580–9604,  DOI:10.1080/10408398.2022.2067121.
11. S. Burda and W. Oleszek, Antioxidant and Antiradical Activities of Flavonoids, J. Agric. Food Chem., 2001, 49(6), 2774–2779,  DOI:10.1021/jf001413m.
12. C. G. Heijnen, G. R. Haenen, F. A. van Acker, W. J. van der Vijgh and A. Bast, Flavonoids as Peroxynitrite Scavengers: The Role of the Hydroxyl Groups, Toxicol. In Vitro, 2001, 15(1), 3–6,  DOI:10.1016/s0887-2333(00)00053-9.
13. F. Perez-Vizcaino and J. Duarte, Flavonols and Cardiovascular Disease, Mol. Aspects Med., 2010, 31(6), 478–494,  DOI:10.1016/j.mam.2010.09.002.
14. J. Chen, K. Zhong, S. Qin, Y. Jing, S. Liu, D. Li and C. Peng, Astragalin: A Food-Origin Flavonoid with Therapeutic Effect for Multiple Diseases, Front. Pharmacol., 2023, 14, 1–18,  DOI:10.3389/fphar.2023.1265960.
15. A. Riaz, A. Rasul, G. Hussain, M. K. Zahoor, F. Jabeen, Z. Subhani, T. Younis, M. Ali, I. Sarfraz and Z. Selamoglu, Astragalin: A Bioactive Phytochemical with Potential Therapeutic Activities, Adv. Pharmacol. Pharm. Sci., 2018, 2018(1), 9794625,  DOI:10.1155/2018/9794625.
16. S. Vazifeh, P. Kananpour, M. Khalilpour, S. V. Eisalou and M. R. Hamblin, Anti-Inflammatory and Immunomodulatory Properties of Lepidium Sativum, BioMed Res. Int., 2022, 2022(1), 3645038,  DOI:10.1155/2022/3645038.
17. J. Ren, Y. Lu, Y. Qian, B. Chen, T. Wu and G. Ji, Recent Progress Regarding Kaempferol for the Treatment of Various Diseases (Review), Exp. Ther. Med., 2019, 18(4), 2759–2776,  DOI:10.3892/etm.2019.7886.
18. A. Y. Chen and Y. C. Chen, A Review of the Dietary Flavonoid, Kaempferol on Human Health and Cancer Chemoprevention, Food Chem., 2013, 138(4), 2099–2107,  DOI:10.1016/j.foodchem.2012.11.139.
19. L. Li, L. Chong, T. Huang, Y. Ma, Y. Li and H. Ding, Natural Products and Extracts from Plants as Natural UV Filters for Sunscreens: A Review, Anim. Models Exp. Med., 2023, 6(3), 183–195,  DOI:10.1002/ame2.12295.
20. M. Sisa, S. L. Bonnet, D. Ferreira and J. H. Van der Westhuizen, Photochemistry of Flavonoids, Molecules, 2010, 15(8), 5196–5245,  DOI:10.3390/molecules15085196.
21. CRC Handbook of Chemistry and Physics, ed. W. M. Haynes, CRC Press, Boca Raton, 95th edn, 2014 DOI:10.1201/b17118.
22. J. Dalton, J. M. Toldo, F. Allais, M. Barbatti and V. G. Stavros, Understanding the Impact of Symmetrical Substitution on the Photodynamics of Sinapate Esters Using Gas-Phase Ultrafast Spectroscopy, J. Phys. Chem. Lett., 2023, 14(39), 8771–8779,  DOI:10.1021/acs.jpclett.3c02134.
23. S. Grimme, Exploration of Chemical Compound, Conformer, and Reaction Space with Meta-Dynamics Simulations Based on Tight-Binding Quantum Chemical Calculations, J. Chem. Theory Comput., 2019, 15(5), 2847–2862,  DOI:10.1021/acs.jctc.9b00143.
24. P. Pracht, F. Bohle and S. Grimme, Automated Exploration of the Low-Energy Chemical Space with Fast Quantum Chemical Methods, Phys. Chem. Chem. Phys., 2020, 22(14), 7169–7192,  10.1039/C9CP06869D.
25. C. Bannwarth, S. Ehlert and S. Grimme, GFN2-xTB—An Accurate and Broadly Parametrized Self-Consistent Tight-Binding Quantum Chemical Method with Multipole Electrostatics and Density-Dependent Dispersion Contributions, J. Chem. Theory Comput., 2019, 15(3), 1652–1671,  DOI:10.1021/acs.jctc.8b01176.
26. A. D. Becke, A New Mixing of Hartree–Fock and Local Density-functional Theories, J. Chem. Phys., 1993, 98(2), 1372–1377,  DOI:10.1063/1.464304.
27. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu, J. Chem. Phys., 2010, 132(15), 154104,  DOI:10.1063/1.3382344.
28. S. Miertuš, E. Scrocco and J. Tomasi, Electrostatic Interaction of a Solute with a Continuum. A Direct Utilizaion of AB Initio Molecular Potentials for the Prevision of Solvent Effects, Chem. Phys., 1981, 55(1), 117–129,  DOI:10.1016/0301-0104(81)85090-2.
29. M. Cossi, N. Rega, G. Scalmani and V. Barone, Energies, Structures, and Electronic Properties of Molecules in Solution with the C-PCM Solvation Model, J. Comput. Chem., 2003, 24(6), 669–681,  DOI:10.1002/jcc.10189.
30. J.-D. Chai and M. Head-Gordon, Long-Range Corrected Hybrid Density Functionals with Damped Atom–Atom Dispersion Corrections, Phys. Chem. Chem. Phys., 2008, 10(44), 6615–6620,  10.1039/B810189B.
31. C. Hättig, Geometry Optimizations with the Coupled-Cluster Model CC2 Using the Resolution-of-the-Identity Approximation, J. Chem. Phys., 2003, 118(17), 7751–7761,  DOI:10.1063/1.1564061.
32. C. Hättig, Structure Optimizations for Excited States with Correlated Second-Order Methods: CC2 and ADC(2), in Advances in Quantum Chemistry, ed. H. J. Å. Jensen, Response Theory and Molecular Properties (A Tribute to Jan Linderberg and Poul Jørgensen), Academic Press, 2005, vol. 50, pp. 37–60 DOI:10.1016/S0065-3276(05)50003-0.
33. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision A3, 2016.
34. R. Omidyan, L. Shahrokh, A. L. Whittock and V. G. Stavros, Theoretical Insights into the Ultrafast Deactivation Mechanism and Photostability of a Natural Sunscreen System: Mycosporine Glycine, J. Phys. Chem. A, 2023, 127(22), 4880–4887,  DOI:10.1021/acs.jpca.3c02360.
35. S. Roshan, M. Hymas, V. G. Stavros and R. Omidyan, New Theoretical Insights on the Nonradiative Relaxation Mechanism of the Core Structure of Mycosporines: The Amino-Cyclohexenone Central Template, J. Chem. Phys., 2024, 161(9), 094301,  DOI:10.1063/5.0222147.
36. M. Salehi, P. Çarçabal and R. Omidyan, Theoretical Insights on the Excited State Deactivation Mechanism in Protonated Adenosine, J. Phys. Chem. A, 2024, 128(50), 10851–10860,  DOI:10.1021/acs.jpca.4c06496.
37. J. M. Woolley, M. Staniforth, M. D. Horbury, G. W. Richings, M. Wills and V. G. Stavros, Unravelling the Photoprotection Properties of Mycosporine Amino Acid Motifs, J. Phys. Chem. Lett., 2018, 9(11), 3043–3048,  DOI:10.1021/acs.jpclett.8b00921.
38. J. M. Toldo, M. T. do Casal and M. Barbatti, Mechanistic Aspects of the Photophysics of UVA Filters Based on Meldrum Derivatives, J. Phys. Chem. A, 2021, 125(25), 5499–5508,  DOI:10.1021/acs.jpca.1c03315.
39. M. Barbatti, G. Granucci, M. Persico, M. Ruckenbauer, M. Vazdar, M. Eckert-Maksić and H. Lischka, The On-the-Fly Surface-Hopping Program System Newton-X: Application to Ab Initio Simulation of the Nonadiabatic Photodynamics of Benchmark Systems, J. Photochem. Photobiol., A, 2007, 190(2), 228–240,  DOI:10.1016/j.jphotochem.2006.12.008.
40. M. Barbatti, M. Ruckenbauer, F. Plasser, J. Pittner, G. Granucci, M. Persico and H. Lischka, Newton-X: A Surface-Hopping Program for Nonadiabatic Molecular Dynamics, Wiley Interdiscip. Rev.:Comput. Mol. Sci., 2014, 4(1), 26–33,  DOI:10.1002/wcms.1158.
41. T. T. Abiola, B. Rioux, J. M. Toldo, J. Alarcan, J. M. Woolley, M. A. P. Turner, D. J. L. Coxon, M. T. Casal, C. do; Peyrot, M. M. Mention, W. J. Buma, M. N. R. Ashfold, A. Braeuning, M. Barbatti, V. G. Stavros and F. Allais, Towards Developing Novel and Sustainable Molecular Light-to-Heat Converters, Chem. Sci., 2021, 12(46), 15239–15252,  10.1039/D1SC05077J.
42. D. Fazzi, M. Barbatti and W. Thiel, Unveiling the Role of Hot Charge-Transfer States in Molecular Aggregates via Nonadiabatic Dynamics, J. Am. Chem. Soc., 2016, 138(13), 4502–4511,  DOI:10.1021/jacs.5b13210.
43. M. Hymas, S. Wongwas, S. Roshan, A. L. Whittock, C. Corre, R. Omidyan and V. G. Stavros, A Multipronged Bioengineering, Spectroscopic and Theoretical Approach in Unravelling the Excited-State Dynamics of the Archetype Mycosporine Amino Acid, J. Phys. Chem. Lett., 2024, 15(29), 7424–7429,  DOI:10.1021/acs.jpclett.4c01254.
44. F. Plasser, G. Granucci, J. Pittner, M. Barbatti, M. Persico and H. Lischka, Surface Hopping Dynamics Using a Locally Diabatic Formalism: Charge Transfer in the Ethylene Dimer Cation and Excited State Dynamics in the 2-Pyridone Dimer, J. Chem. Phys., 2012, 137(22), 22A514,  DOI:10.1063/1.4738960.
45. G. Granucci, M. Persico and A. Toniolo, Direct Semiclassical Simulation of Photochemical Processes with Semiempirical Wave Functions, J. Chem. Phys., 2001, 114(24), 10608–10615,  DOI:10.1063/1.1376633.
46. A. Ferretti, G. Granucci, A. Lami, M. Persico and G. Villani, Quantum Mechanical and Semiclassical Dynamics at a Conical Intersection, J. Chem. Phys., 1996, 104(14), 5517–5527,  DOI:10.1063/1.471791.
47. U. Müller and G. Stock, Surface-Hopping Modeling of Photoinduced Relaxation Dynamics on Coupled Potential-Energy Surfaces, J. Chem. Phys., 1997, 107(16), 6230–6245,  DOI:10.1063/1.474288.
48. R. Crespo-Otero and M. Barbatti, Spectrum Simulation and Decomposition with Nuclear Ensemble: Formal Derivation and Application to Benzene, Furan and 2-Phenylfuran, in Marco Antonio Chaer Nascimento: A Festschrift from Theoretical Chemistry Accounts, ed. F. R. Ornellas and M. João Ramos, Springer, Berlin, Heidelberg, 2014, pp. 89–102 DOI:10.1007/978-3-642-41163-2_9.
49. D. Cremer and J. A. Pople, General definition of ring puckering coordinates, J. Am. Chem. Soc., 1975, 97, 1354–1358,  DOI:10.1021/ja00839a011.
50. A. L. Spek, Single-Crystal Structure Validation with the Program PLATON, J. Appl. Crystallogr., 2003, 36(1), 7–13,  DOI:10.1107/S0021889802022112.
51. D. R. Telange, A. T. Patil, A. Tatode and B. Bhoyar, Development and Validation of UV Spectrophotometric Method for the Estimation of Kaempferol in Kaempferol: Hydrogenated Soy PhosphatidylCholine (HSPC) Complex, Pharm. Methods, 2014, 5(1), 34–38,  DOI:10.5530/phm.2014.1.6.
52. H. Gonzalez, N. Tarras-Wahlberg, B. Strömdahl, A. Juzeniene, J. Moan, O. Larkö, A. Rosén and A.-M. Wennberg, Photostability of Commercial Sunscreens upon Sun Exposure and Irradiation by Ultraviolet Lamps, BMC Dermatol., 2007, 7(1), 1,  DOI:10.1186/1471-5945-7-1.
53. A. Klamt and G. Schüürmann, COSMO: A New Approach to Dielectric Screening in Solvents with Explicit Expressions for the Screening Energy and Its Gradient, J. Chem. Soc., Perkin Trans. 2, 1993,(5), 799–805,  10.1039/P29930000799.
54. R. Berera, R. van Grondelle and J. T. M. Kennis, Ultrafast Transient Absorption Spectroscopy: Principles and Application to Photosynthetic Systems, Photosynth. Res., 2009, 101(2), 105–118,  DOI:10.1007/s11120-009-9454-y.
55. J. J. Snellenburg, S. Laptenok, R. Seger, K. M. Mullen and I. H. M. van Stokkum, Glotaran: A Java-Based Graphical User Interface for the R Package TIMP, J. Stat. Software, 2012, 49, 1–22,  DOI:10.18637/jss.v049.i03.
56. T. H. Dunning, Gaussian Basis Sets for Use in Correlated Molecular Calculations. I. The Atoms Boron through Neon and Hydrogen, J. Chem. Phys., 1989, 90(2), 1007–1023,  DOI:10.1063/1.456153.
57. J. C. Tully, Molecular Dynamics with Electronic Transitions, J. Chem. Phys., 1990, 93(2), 1061–1071,  DOI:10.1063/1.459170.
58. G. Granucci and M. Persico, Critical Appraisal of the Fewest Switches Algorithm for Surface Hopping, J. Chem. Phys., 2007, 126(13), 134114,  DOI:10.1063/1.2715585.
59. R. Mansour, J. M. Toldo, S. Mukherjee, M. Pinheiro and M. Barbatti, Temperature Effects on the Internal Conversion of Excited Adenine and Adenosine, Phys. Chem. Chem. Phys., 2023, 25(40), 27083–27093,  10.1039/D3CP03234E.
60. F. Ji, Z. Wu, M. Wang, Y. Guo, C. Wang, S. Wang and G. Zhao, New Insights into the Excited State Intramolecular Proton Transfer (ESIPT) Competition Mechanism for Different Intramolecular Hydrogen Bonds of Kaempferol and Quercetin in Solution, J. Lumin., 2022, 248, 118914,  DOI:10.1016/j.jlumin.2022.118914.
61. E. Charvati and H. Sun, Potential Energy Surfaces Sampled in Cremer–Pople Coordinates and Represented by Common Force Field Functionals for Small Cyclic Molecules, J. Phys. Chem. A, 2023, 127(11), 2646–2663,  DOI:10.1021/acs.jpca.3c00095.
62. L. Chan, G. R. Hutchison and G. M. Morris, Understanding Ring Puckering in Small Molecules and Cyclic Peptides, J. Chem. Inf. Model., 2021, 61(2), 743–755,  DOI:10.1021/acs.jcim.0c01144.
63. J. Iglesias-Fernández, L. Raich, A. Ardèvol and C. Rovira, The Complete Conformational Free Energy Landscape of β-Xylose Reveals a Two-Fold Catalytic Itinerary for β-Xylanases, Chem. Sci., 2015, 6(2), 1167–1177,  10.1039/C4SC02240H.
64. K. M. C. Davis, Solvent Effects on Charge-Transfer Fluorescence Bands, Nature, 1969, 223(5207), 728,  DOI:10.1038/223728a0.
65. M. Taniguchi, C. A. LaRocca, J. D. Bernat and J. S. Lindsey, Digital Database of Absorption Spectra of Diverse Flavonoids Enables Structural Comparisons and Quantitative Evaluations, J. Nat. Prod., 2023, 86(4), 1087–1119,  DOI:10.1021/acs.jnatprod.2c00720.
66. R. Mansour, J. M. Toldo and M. Barbatti, Role of the Hydrogen Bond on the Internal Conversion of Photoexcited Adenosine, J. Phys. Chem. Lett., 2022, 13(26), 6194–6199,  DOI:10.1021/acs.jpclett.2c01554.
67. R. Szabla, J. Campos, J. E. Šponer, J. Šponer, R. W. Góra and J. D. Sutherland, Excited-State Hydrogen Atom Abstraction Initiates the Photochemistry of β-2′-Deoxycytidine, Chem. Sci., 2015, 6(3), 2035–2043,  10.1039/C4SC03761H.
68. M. J. Janicki, C. L. Kufner, Z. R. Todd, S. C. Kim, D. K. O’Flaherty, J. W. Szostak, J. Šponer, R. W. Góra, D. D. Sasselov and R. Szabla, Ribose Alters the Photochemical Properties of the Nucleobase in Thionated Nucleosides, J. Phys. Chem. Lett., 2021, 12(28), 6707–6713,  DOI:10.1021/acs.jpclett.1c01384.
69. L. Shahrokh, R. Omidyan and G. Azimi, Excited State Deactivation Mechanisms of Protonated Adenine: A Theoretical Study, Phys. Chem. Chem. Phys., 2022, 24(24), 14898–14908,  10.1039/D2CP00106C.

---

Footnotes

† Electronic supplementary information (ESI) available: (1) Experimental and computational details and (2) preliminary computational study. See DOI: https://doi.org/10.1039/d5cp01895a

‡ These authors have contributed equally.

---