Low-energy pathways lead to self-healing defects in CsPbBr₃

Abstract

Self-regulation of free charge carriers in perovskites via Schottky defect formation has been posited as the origin of the well-known defect-tolerance of metal halide perovskite materials. Understanding the mechanisms of self-regulation promises to lead to the fabrication of better performing solar cell materials with higher efficiencies. We investigate many such mechanisms here for CsPbBr₃, a popular representative of a more commercially viable all-inorganic metal halide perovskite. We investigate different atomic-level mechanisms and pathways of the diffusion and recombination of neutral and charged interstitials and vacancies (Schottky pairs) in CsPbBr₃. We use nudged elastic band calculations and ab initio-derived pseudopotentials within quantum ESPRESSO to determine energies of formation and migration and hence the activation energies for these defects. While halide vacancies are known to exhibit low formation energies, the migration of interstitials is less studied. Our calculations uncover interstitial defect pathways capable of producing an activation energy at, or below, the single experimental value of 0.53 eV observed for the slow, temperature-dependent recovery of light-induced conductivity in bulk CsPbBr₃. Our work reveals the existence of a low-energy diffusion pathway involving a concerted “domino effect” of interstitials, with the net result that interstitials can diffuse more readily over longer distances than expected. This observation suggests that defect self-healing can be promoted if the “domino effect” strategy can be engaged.

---

1 Introduction

Metal halide perovskites (MHPs) are one of the most exciting materials classes at the forefront of photovoltaic materials development. They have demonstrated performance comparable to market-leading solar cell materials, as evidenced by the dramatic rise in their power conversion efficiency (PCE) since emerging around 2009.¹ Defect migration and recombination strongly affect device performance and long-term durability and are generally unwanted in photovoltaic devices.² In terms of defect tolerance, metal halide perovskites (MHPs) are known to be more “forgiving” than their silicon solar cell counterparts.^3–5 MHPs, like the entire class of perovskites, adopt the general formula ABX₃, where A is a monovalent cation (MA⁺, FA⁺, Cs⁺), B is a divalent metal cation (Sn²⁺, Pb²⁺), and X is a halide (Br⁻, I⁻, Cl⁻). Early work on MHPs centered on methylammonium (MA) lead iodide (or MAPbI₃). More recently, MHP studies have been migrating towards a focus on all-inorganic perovskites, like CsPbX₃, with band gaps in the range 1.7 to 2.3 eV, depending on the halide. These perovskites have proven to be somewhat more stable in conditions (UV, heat, and humidity) that can degrade MAPbI₃, and other hybrid organic–inorganic perovskites, over time. Due to its importance, we focus our defect studies on CsPbBr₃ alone.

MHPs have unusually low charge carrier recombination rates despite intrinsic defects created during solution processing, and show apparent defect remediation under external stimulus (dark-resting recovery⁶ and proton irradiation⁷). The underlying atomic-level mechanisms and prevalent pathways surrounding MHP defect remediation remain hotly debated.⁸ Cahen et al.'s⁹ review entitled, “Are defects in lead–halide perovskites healed, tolerated, or both?” aptly summarizes this unresolved debate: do defects have an inconsequential effect on MHP material properties, i.e., are the materials defect-tolerant, or are the effects of defects reversible, or at least mitigated, through some self-regulatory processes, i.e., are MHPs able to self-heal? The authors of that review concluded that defect-tolerance need not be viewed as mutually exclusive to self-healing. Rather, defect-tolerance may be a bridging mechanism to longer time-scale self-healing phenomena.

It is important to distinguish between defects that are intrinsic versus extrinsic, surface versus bulk, and charged versus uncharged defects. Here, we define intrinsic defects as atomic substitutions, vacancies, anti-sites, or interstitials. Extrinsic impurities include doping and alloying effects on defect migration.¹⁰ We limit our scope to intrinsic bulk defect migration; work outside our purview considers the importance of surface-assisted defect remediation.^11,12 In particular, Ten Brinck et al. calculated defect formation energy values for interstitial, vacancy, and anti-site defects in non-periodic 3 nm CsPbBr₃ nanoparticles and concluded that the most stable defect position occurs on the surface of the nanoparticle.¹³

Several classes of primary mechanisms have been investigated for intrinsic bulk defect remediation, including trap states,¹⁴ polarons,¹⁵ the Rashba band-splitting mechanism,¹⁶ photon recycling,^17,18 as well as ion or defect migration,¹⁹ or some combination of these. Within the MHP class, there are likely to be mechanistic differences between hybrid organic–inorganic perovskites and entirely inorganic ones. For instance, while evidence suggests polaronic effects mitigate recombination for MAPbI₃,^20,21 CsPbBr₃ has dispersive band-edges (VBM and CBM) that do not support charge carrier localization, i.e., self-trapped charge carriers.²² Österbacka et al. show favorable CsPbBr₃ polaron formation relative to the delocalized electron by only 0.1 eV, notably, within the margin of error for DFT results like the ones considered in this paper.²³ Recent angle-resolved photoelectron emission data interpretations are contradictory as to a polaron signature.^24,25 Finally, it is possible for mechanistic differences to exist even within MHP sub-classes: bulk MAPbBr₃, FAPbBr₃, and CsPbBr₃ demonstrate unique photo-bleaching damage and recovery dynamics exhibiting up to an order of magnitude difference in value.²⁶

While the Rashba band effect explanation initially gained traction, this possibility was definitively ruled out for both MAPbBr₃ or CsPbBr₃; it was later asserted that incorrect structural relaxations were responsible for the previously predicted large Rashba effect.^27,28 The contributions of photon recycling in conjunction with defect migration should be further investigated for both surface and bulk systems.

Experimental measurements and computational estimates of defect activation energies are rare, especially for the all-inorganic perovskite studied in this paper. In this study, we determine activation energies, E_a, computationally: the activation energy can be determined from the sum of the energy to form the defect, E_f, plus the energy to move the defect in the lattice, E_m. Both E_f and E_m can be determined computationally, performed here using density functional theory (DFT) calculations, thus allowing activation energies to be estimated.

In terms of extant defect studies, especially computational studies, a larger volume of prior work exists for hybrid organic–inorganic systems, with methylammonium (MA⁺) and formamidinium (FA⁺) A-site cations in the lattice,^29–31 compared to fewer studies for inorganic MHP systems. Meggiolaro and De Angelis provided a fairly comprehensive review of ab initio-generated formation energies only for MAPbI₃ and offered “best practices” for such calculations.³² Oranskaia et al. found lower hydrogen-bonding strength in MAPbBr₃ than FAPbBr₃ and, consequentially, lower halide migration and defect formation energies (DFE).³³ This finding suggests that careful A-site cation selection may reduce perovskite ion migration.

Turning to the all-inorganic MHPs studied in this paper, Evarestov et al. found that perfect CsPbX₃ structures follow the stability trend, CsPbBr₃ > CsPbI₃ > CsPbCl₃, corroborating neutral defect formation energies for CsPbBr₃ provided by Kang and Wang.^5,34 Xue et al. use an accurate SCAN+rVV103 functional within the VASP DFT codebase to study charged defect formation energies as a function of Fermi level for various anti-site and compound vacancies (PbI₂ or CsPbI₃) within CsPbI₃ systems.³⁵ Balestra et al. conducted a classical molecular dynamics simulation of CsPbBr₃ and mixed halide CsPb(Br_xI_1−x)₃ (x = 1/3, 2/3) systems with a genetically optimized force field across a range of temperatures. The authors determined an Arrhenius-fit ionic diffusion coefficient in CsPbBr₃ and CsPbI₃ systems from which they report an “activation enthalpy” to halide ion diffusion. Since their derivation does not include the formation energy of the defect, this should be considered to be a migration enthalpy.³⁶

Pazoki et al. conducted quantum espresso nudged elastic band (NEB) calculations employing the PBE exchange–correlation functional for MAPbI₃, FAPbI₃, and CsPbI₃. They determined halide vacancy formation energies and corresponding migration energies for the same vacancies to exchange positions with neighboring lattice atoms.³⁷ The authors defined the positional exchange of a vacancy with its lattice neighbor as an ion migration energy rather than a vacancy migration energy as we define it. Neither interstitial studies nor those for anti-sites were considered in Pazoki's study.

Relevant to our methodology presented below, the concept of assigning localized charge does not exist formally within the quantum espresso NEB method. Applied charges, such as a positive vacancy or negative interstitial defect, are applied over the entire simulation area. This charge delocalization is also the case in other common ab initio codes, such as VASP.³⁸

Our calculations were motivated by Tirmzi et al.'s measurements of the slow recovery of light-induced conductivity in CsPbBr₃.³⁹ In these measurements, a charged atomic-force microscope cantilever was brought near the surface of a CsPbBr₃ film and experienced a non-contact friction depending on the sample's total conductivity, electronic plus ionic.⁴⁰ After irradiating the sample with above-bandgap light, Tirmzi et al. observed a prompt increase in friction, as expected from the presence of photo-generated electrons and holes. Electrons and holes recombine on the microsecond timescale in perovskites. After the light was turned off, however, sample friction took 10 s to recover at room temperature. Tirmzi et al. concluded that light-induced mobile ionic defects dominated the sample's conductivity, following:

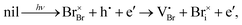in Kröger–Vink notation. The friction recovery time in the dark was temperature-dependent, with an activation energy of E_a = 0.53 ± 0.03 eV (95% confidence interval). A similar conductivity-recovery E_a = 0.58 ± 0.07 eV was measured in (FA_0.79MA_0.16Cs_0.05)_0.97Pb(I_0.84Br_0.16)_2.97.⁴⁰ The associated defect-recovery reaction in the dark is

For this reaction, we would expect the measured E_a to be dominated by the migration energy governing the diffusion of the neutral interstitial 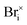. This mechanism is similar to others considered by Poli et al.,⁴¹ and Mosconi et al.,⁴² which suggest light irradiation promotes the annihilation of Frenkel defect pairs. Relevant to our work, Lv et al. observed a reduction in the creation of an energy barrier related to anti-Frenkel disorder due to the presence of vacancies and interstitials in CsPbI₃.⁴³

Given the far fewer studies of migration energies for MHPs, this paper models a number of potential recombination pathways for interstitial, vacancy, and anti-site defects using quantum espresso for density functional calculations in conjunction with nudged elastic band determinations of the energy barriers. Given that the ionic radius for neutral bromine is 1.12 Å, compared to that of the negatively charged bromine anion, 1.95 Å, it could be argued that the anion is too large to squeeze into the interstitial site. Iodine shows a similar trend. As a result, halide interstitials might be expected to have zero charge. But a case can also be made for a negatively charged halide interstitial. This has guided our consideration of both neutral and charged interstitial defects.⁴⁴ In a similar vein, the charge on the vacancies may be either 0 or +1. Pazoki et al. reported an E_m value of 0.21 eV for a halide vacancy in CsPbI₃;³⁷ they do not explicitly state whether the vacancies they modeled were charged or neutral. We will show below that their E_m values fall within a similar range of 0.22 and 0.27 E_m as do our charged and neutral CsPbBr₃ (V_Br) migration energies, respectively; see Table 1.

Table 1 Defect formation, migration and activation energies in CsPbBr₃ from this work and comparison to prior results, where possible

Defect^a	E f (eV)		E m (eV)		E a (eV)
	Formation energy (this work)	Other Ef results	Migration energy	Other Em results
a Br-rich environment.
VBr	2.57	2.67^5	0.27	0.29;^55 0.43^56	2.83
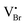
	2.71	2.6^51	0.22	0.27^57	2.93
Bri	0.59–0.63		0.20–0.54	0.21;^55 0.53^39	0.79–1.17
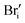
	0.66–0.88	0.70^5	0.19–0.41	—	0.85–1.29
BrPb	1.30	1.40^5	—	—	—
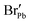
	1.27	1.58^51	—	—	—
PbBr	6.18	6.28^5	—	—	—
	6.31	—	—	—	—
	7.46	—	—	—	—
Bri−Bri split	0.74	—	0.37	—	1.11
(Bri–Bri)′ split	0.81	—	0.33	—	1.14
(Bri−Pbi) split	1.16	—	0.02	—	0.54
(Bri–Pbi)′ split	1.78	—	0.16	0.21^55	1.30

---

Unlike previous studies in the literature, we have calculated both formation and migration energies for a range of defect pathways. This provides us with the ability to calculate activation energies, which is an experimentally accessible property. But it is a property that is in short supply from experimental sources. Coupling nudged elastic band calculations with ab initio pseudopotentials provides accurate estimates for the migration energies. The recovery rate of the conductivity observed by Tirmzi and co-workers³⁹ was not noticeably different near grain boundaries, suggesting they were observing a bulk effect. This observation justifies our ignoring grain-boundary effects in the following computations.

In what follows, we will be looking to find a match between computational and experimental activation and migration energies, wherever possible. As a result, we have a route to uncover the dominant defect(s) and defect pathways that are present. With this information in hand, we hope to better inform device synthesis and offer a different bulk-defect passivation strategy to improve overall MHP performance.

2 Results and discussion

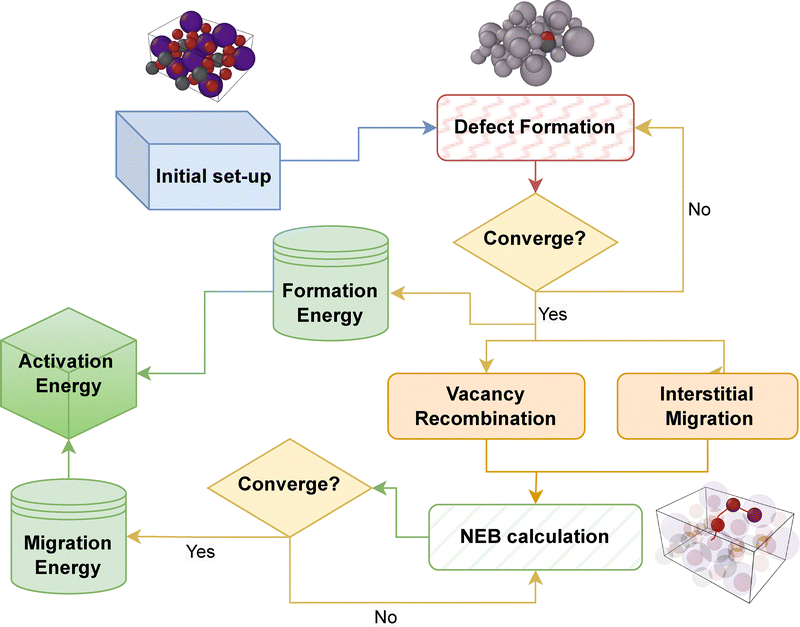
As a preliminary check on the validity of the ab initio calculations, we predicted an X-ray diffraction (XRD) pattern generated from our simulated pristine supercell using the VESTA software.⁴⁵ The comparison, found in the ESI,† shows that the DFT-simulated peaks line up, essentially perfectly, with the experimental results. The relaxed cell parameters for the pristine CsPbBr₃ supercell (3 × 3 × 2) (with Pnma spacegroup) were found to be 8.267, 8.177 and 11.768 Å. These values correspond very favorably to experimentally reported ones:⁴⁶ 8.23, 8.18 and 11.73 Å. The workflow for such calculations is shown in Fig. 1.

Fig. 1 Flowchart of defect studies in CsPbBr₃. This begins with an initial lattice set-up (top left; blue box). Then a defect is created, whether a vacancy or an interstitial (top right; pink box). Converged calculations yield a formation energy (middle; green cylinder). Additional calculations using NEB produce the migration energy (bottom right; green rectangle) for a set of considered pathways (middle; orange boxes). Converged NEB calculations produce E_m (botton left; green cylinder). Then the activation energy can be calculated (middle left; dark green cube).

A summary of formation and migration energies (neutral and charged) and the ensuing activation energy for all the results described below are collected together in Table 1. The defect formation energy (DFE) for positive charged defects is reported at the conduction band minimum (CBM), while the negative charged ones are reported at the valence band maximum (VBM). Comparison to prior work is also reported, where available.

2.1 Defect formation energies

First, we examined defect formation energy values in CsPbBr₃, focusing on the consideration of various kinds of off-lattice interstitial sites and on-lattice anti-site situations.

After introducing a defect atom into a pristine supercell, the defect formation energy (DFE) was computed based on the total energies of the defective and pristine relaxed structures, using the following equation:⁴⁷

where E^f(D^q) represents the defect formation energy of a defect D in charge state q and E_bulk the total energy of the pristine bulk supercell. Eqn (3) incorporates changes in the number of atoms (Δn_i) and chemical potentials (μ_i). The Fermi level (ε_F) of a semiconductor is treated as an independent variable that can assume any value within the band gap with respect to the valence band maximum of the pristine bulk material (E_VBM). The correction term (E_corr) accounts for the effects of finite size and periodic boundary conditions, which is calculated using Freysoldts correction scheme.⁴⁸ This correction is important to include when introducing charged defects into the system. We discuss the relevant mathematical expression, calculation methodology, and impact on the DFE of our specific systems in detail in the ESI.†

2.1.1 Halide interstitial defects. The halide interstitial is widely thought to be particularly important in defect studies of MHPs. In that regard, a Br_i atom was placed in a chosen interstitial position (off-lattice) and allowed to relax within the crystal. No matter where the defective atom was initiated, following a relax calculation to locate its preferred structure, both neutral and charged Br_i adopted a pentagonal bipyramidal coordination polyhedral structure surrounding a Pb atom (a PbBr₇ complex).

Pb polyhedral distortion has been documented within CsPbBr₃ systems due to stereochemical expression of the 6s² lone pair on the Pb₂⁺ atom.⁴⁹ The stereochemically active 6s² lone pair can push Pb₂⁺ off-center within a non-defective PbBr₆ octahedra, resulting in an asymmetric coordination environment and leading to Jahn–Teller type distortions, or rarely, a heptacoordinated PbBr₇. The interstitially induced pentagonal bipyramidal geometry observed within this work represents another route to PbBr₇ complex formation.

Some 2D lead bromide perovskites, particularly those with large lattice distortions, do – in fact – exhibit a large broadband emission Stokes shift at room temperature. As the structural origins of this shift are still under debate, the interstitial-induced formation of PbBr₇ pentagonal bipyramidal coordination shown in this work may help to explain this phenomenon.

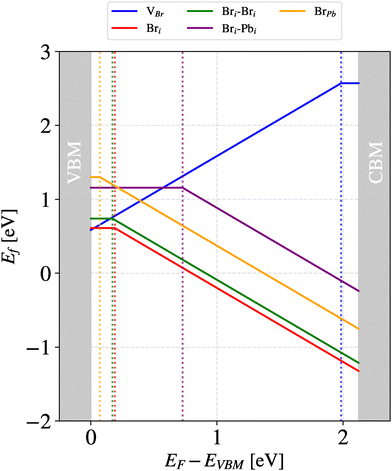
We observed defect formation energies for Br_i ranging from 0.60–0.71 eV and 0.59–0.63 eV for neutral Br_i 2 × 2 × 2 and 3 × 2 × 2 systems, respectively, and between 0.74–1.00 eV and 0.66–0.88 eV for 2 × 2 × 2 and 3 × 2 × 2 systems, respectively. Hence system size did not affect the defect formation energy values. However, choosing to model Br_i in a −1 charge state, rather than being neutral, resulted in a range of values from 0.03 to 0.25 eV for a larger system size at the VBM. A difference of 0.03 is insignificant, but a 0.25 eV difference is potentially significant. Fig. 2 provides a summary of the formation energies of all the defect types that we studied as we vary the Fermi energy level with respect to the VBM. This figure indicates that, at almost all the Fermi levels between the CBM and VBM a negatively charged Br interstitial has a lower formation energy than a neutral Br. The effect of charge to migrate the Br interstitial is discussed below (see Fig. 5).

Fig. 2 Formation energies of intrinsic point defects and anti-site defects in CsPbBr₃ as a function of the Fermi energy level, calculated with respect to the valence band maximum. Vertical dashed lines indicate defect charge-state transition points.

Fig. 3 Reaction energy profile (below) and ball-and-stick visualizations (above) depict the migration process of a Br–Pb split interstitial using a “domino strategy.” The local structures for the “reagent” (R), transition state (TS), and “product” (P) are derived from a 2 × 2 × 2 supercell NEB calculation. Each visualized state is annotated on the energy profile plot, indicating their respective positions within the migration process. Color coding: Cs – green, Pb – grey, Br – brown, with the interstitial and its first neighbor highlighted in orange.

2.1.2 Split interstitials. Split interstitials are known to exist in defective crystal lattices (see Fig. S2.2, ESI†), and this configuration can often be energetically preferred.⁵⁰ In a split interstitial configuration, two atoms share a single substitutional lattice site, resulting in a distinct local geometry compared to a conventional interstitial. This structural difference is illustrated in Fig. S2.2 (ESI†), which contrasts the split interstitial with a typical Br interstitial.

To our knowledge, the importance of split interstitials has not been considered in defective MHP systems. We consider two split interstitial cases: (1) two Br atoms sharing one Br lattice site and (2) one Pb interstitial (Pb_i) and one Br interstitial (Br_i) sharing a Pb lattice site.

We found that the defect formation energy (DFE) for the Br_i–Pb_i split interstitial configuration varies depending on the axis along which the Br–Pb pair is aligned. As depicted in Fig. S2.2 of the ESI,† the DFE is found to be around 0.83 eV when the pair is aligned along the z-axis. In contrast, the DFE value increases to 1.14 eV when the split interstitial is aligned along the y-axis. This energy difference of approximately 0.4 eV between the two orientations is significant and consistent, indicating a pronounced and anisotropic phenomenon in defect formation. We do not see this anisotropic effect for Br_i–Br_i split interstitials, but we do see polyhedral formation for Br_i interstitials, as explained later.

2.1.3 Pb_Br and Br_Pb anti-site defects. An anti-site defect exists when the occupant of a lattice site differs from what is expected in an ideal MHP lattice. We consider the energy it takes to form a lead atom on a bromine lattice site, and vice versa to determine the defect formation energy. Both neutral defects and charged anti-site defects were investigated. Our neutral calculations resulted in large formation energies of 6.1 eV and 1.3 eV for Pb_Br and Br_Pb anti-site defects, respectively. These values are in close agreement with values of 6.28 eV and 1.4 eV obtained by Kang et al.,⁵ who studied neutral defects. Pb_Br shows a particularly high DFE due to the introduction of a larger Pb atom in place of a smaller Br, causing a considerable strain on neighboring atomic positions. Our charged Pb_Br calculations show larger deviations from values for neutral Pb_Br formation energies. A neutral Pb_Br is calculated to have a formation energy of 6.18 eV. 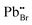The charged Pb_Br equivalent shows an increasing trend in DFE values: unsurprisingly, has the highest DFE (7.46 eV), followed by 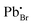(6.31 eV) at CBM.

Our investigation concludes that it is energetically unfavorable for a Pb_Br to form, regardless of the oxidation of Pb to a Pb²⁺ or a Pb⁺¹. This is to be expected since the geometric nature of the Pb-centered halide octahedra are less “soft” than the rest of the lattice. In contrast, the substitution of a smaller Br atom at a Pb site appears to be more energetically favorable. The defect formation energy (DFE) for a neutral Br_Pb is calculated to be 1.30 eV, close to the value of 1.27 eV for the negatively charged state at VBM. While these values are close, they are consistent with other reported computational values, see Table 1.^5,51

Table 1 reports DFE values for all the defects mentioned in this section, including comparison to prior work, as available.

2.2 Defect migration energies and mechanisms

We studied nudged elastic band (NEB) calculations of the movement of interstitial sites occurring via two distinct mechanisms: the first involved the assistance of vacancies in the lattice, while the second relied on a coordinated movement of the interstitials themselves without the presence of a paired vacancy. In this section, we concentrate on the mechanisms for migration of various defects. Values for the migration energies are shown in Table 1.

2.2.1 Vacancy-assisted mechanism. The first migration mechanism involved the introduction of a lattice site vacancy in addition to the presence of a Br_i interstitial. This approach allowed us to quantify the activation energies necessary. For an interstitial atom to migrate towards, and subsequently recombine with, the vacancy (resulting in a “healed,” perfect crystal).

In the context of vacancy-assisted migration, our investigations unveiled what we have termed a “domino effect” strategy that can assist the translocation of an interstitial across the lattice, a phenomenon particularly pronounced in interactions involving second and third nearest neighbors. Rather than migrating directly into the vacancy site, the interstitial atom induces successive movement of one or two adjacent atoms along the pathway, effectively achieving the final state through a series of intermediate steps. This phenomenon is clearly demonstrated in Fig. 4, which illustrates how the NEB-generated activation energy can be “flattened” (and lowered) by this domino effect, providing an easier migration pathway for the atoms. We are unaware of any other references to this newly discovered low-energy pathway in the literature.

Fig. 4 Migration energy of a Br_i–Pb_i split interstitial following two distinctly different pathways and its effect on the first, second and third nearest neighbors of the moving Br atom (first three columns, respectively). ((a), top) Energy barrier for the migration of a Br_i−Pb_i split interstitial via a direct jump to a neighboring vacancy site. Energy profiles for the first, second, and third nearest neighbors are grouped based on distance to the Br interstitial site. Each line stands for a different migration pathway which is color-coded by their activation rank order (shown as a bar on the far right). ((b), bottom) Energy barrier associated with a “domino effect” strategy for inter-lattice diffusion. Note the difference in the y-scale for the third neighbor jump. (c) Maps the correlation between activation energy and mean squared displacement (MSD) for the direct jump mechanism. Color-coded dots, based on activation energy, are rank-ordered with shaded areas indicating confidence intervals for the regression curve. This shows that E_a increases with MSD, as expected. (d) Displays a similar correlation to (c), except that this relates to the “domino effect” diffusion mechanism. Here, unlike in (c), the activation energy is pretty flat regardless of the MSD value.

We calculated the average mean square displacement (MSD) of each atom from its lattice site. This was computed for each pathway at the saddle point of diffusion moves that involve recombination of defects. Looking at the MSD in Fig. 4(a) and (c), we observe that it follows a linear regime in the direct jump scenario: the activation energy increases with increasing MSD, as might be expected. In contrast, in the domino effect strategy, Fig. 4(b) and (d), the activation energy tapered off for sufficiently large MSD values of the interstitials. This shows that, for any migration more than a second or a third neighbor distance away, a “domino” movement is far more probable than a direct jump.

A summary of the NEB findings will ultimately be found in Fig. 8, offering insights into the energetics of the vacancy-assisted migration process.

We examined one of the recombination pathways that involved a third neighbor jump. Here, we started from the direct jump and sequentially added one atom at a time to see how the number of intermediate atoms affects the final migration energy. As depicted in Fig. 4, the direct jump has two local energy peaks in the migration process, indicating two relatively high energy barriers that migration will need to overcome. When an intermediate atom is introduced, only one peak remains in the migration pathway and the migration energy is reduced. We posit that the involvement of an intermediate atom assisted in helping the original interstitial atom bypass one of the barriers, although one barrier still remains. Introduction of yet another intermediate atom flattens the leftmost barrier and the resulting migration energy is effectively reduced to near zero. This suggests that, even if the defect is relatively distant from the vacancy site, it can still migrate and recombine simultaneously. This suggests that interstitial defects can self-heal if the “domino effect” strategy can be engaged.

2.2.2 Interstitial migration mechanism. In addition to the previously described vacancy-assisted migration, our investigations have revealed that Br interstitials are quite capable of migrating to alternate interstitial sites without a paired vacancy nearby. E_m for both charged and neutral Br_i, as derived by NEB calculations, is presented in Fig. 5. The starred points represent the starting and ending relaxed images which, when summed together, constitute one continuous pathway: reaction coordinate number 10 (found on the x-axis of Fig. 5, for example, is both the ending image of the previous sub-path and the beginning image for the subsequent sub-path). The intermediary data points are interpolated structures along the NEB pathway with the highest point representing the transition structure along the reaction coordinate.

Fig. 5 Total energy for a neutral (black lines) and charged bromine interstitial (Br_i) (red lines), to move through a 2 × 2 × 2 CsPbBr₃ supercell containing 160 atoms. Calculations determined by nudged elastic band DFT runs without the presence of a paired vacancy. The corresponding energies for defect migration between these polyhedral configurations are provided as insets within the figure. Key: Pb = gray, Br = bronze, Br_i = red or black for the charged or neutral states, respectively. The polyhedral structures we observed during this traversal of the simulation cell have been oriented to best show the coordination type, not to preserve a global xyz orientation. For a spatially accurate depiction of the Br_i migration, see Fig. S2.11 (ESI†). Looking at the NEB results, the coordination polyhedra observed for neutral and charged selected (starred) points both followed this pattern: formation of a monocapped trigonal prism (image 1), pentagonal bipyramid (image 10), monocapped trigonal prism (image 19), pentagonal bipyramid (image 28), pentagonal bipyramid (image 37). As expected by the Kepert model,⁵² the energetically preferred coordination polyhedron for a PbBr₇ is a pentagonal bipyramid, with edge-sharing between neighboring polyhedra.

The coordination polyhedra shown in Fig. 5, and referenced by the reaction coordinate on the x-axis, depicts the local environment surrounding Br_i as it traverses the supercell. The polyhedra are not oriented with respect to a consistent xyz view but rather to best show the coordination type. For a spatially sensitive depiction of the migration of Br_i see the ESI,† Fig. S2.12.

For both the charged and neutral pathways, the coordination polyhedra for the starred points adopt the following structures: monocapped trigonal prism (coordinate 1), pentagonal bipyramid (coordinate 10), monocapped trigonal prism (coordinate 19), pentagonal bipyramid (coordinate 28), pentagonal bipyramid (coordinate 37). In agreement with the Kepert model,⁵² the energetically preferred, i.e., lowest energy, heptacoordination type is the pentagonal bipyramid. The monocapped trigonal prism and monocapped octahedron polyhedra are still “accessible” but non-preferred, and depending on the specific ligand environment, they may arise to minimize total ligand–ligand repulsion. The transition structures, shown as triangular points in Fig. 5, either assume a monocapped trigonal prism, or adopt a pentagonal bipyramid without shared edge wherein the Br_i is “cartwheeling” towards a perfect PbBr₆ octahedral structure. This restricts the strain induced by the presence of Br_i to just one polyhedron, rather than distributing it between multiple arrangements and, thus, is a less energetically preferred state. Polyhedral edge-sharing is an experimentally observed phenomenon for lead bromide perovskites; see ref. 49.

2.2.3 Anti-site recombination mechanism. The mechanism for recombination of a pair of anti-sites, Br_Pb + Pb_Br, to a null (perfect) crystal, follows a concerted-exchange pathway. This restoration of a perfect lattice involves a coupled mechanism of vacancy and interstitial migration. Both Br_Pb and Pb_Br undergo slight displacements from their anti-site positions, effectively generating vacancies at their original sites. These displacements simultaneously give rise to interstitial configurations (Br_i and Pb_i), marking an intermediate stage of the process. In the final step, the interstitial atoms traverse past one another and settle into their correct lattice positions, thus restoring the perfect crystal structure. This dynamic and cooperative motion, where the atoms rotate and exchange positions in a synchronized fashion, can be aptly described as a brief yet elegant atomic dance that restores lattice order. This recombination mechanism is quite energetically affordable for the crystal, with a E_a value of 0.335 eV. A visual representation of this exchange can be seen in Fig. 8(a).

2.3 Defect activation energies

The experimentally accessible activation energy is defined as:^53,54

E_a = E_f + E_m, (4)

For vacancy-assisted diffusion, the vacancy has to form first, followed by another atom migrating to the vacancy. Depending on the experiment, other defects may capture the activation energy or the migration energy.

When the vacancy is not the closest neighbor to the interstitial, the “domino effect” strategy appears to facilitate this migration as well. Fig. 6 accurately captures this lowering of the activation energy through the “domino effect.” We see that, for an interstitial to migrate, having one more intermediate atom involved reduced the migration barrier. Adding a second intermediate atom reduced this barrier almost to zero. This shows that for any defect traveling beyond the nearest neighbor, the migration barrier can be reduced by a “domino effect” of atoms moving in a concerted exchange for metal halide perovskites.

Fig. 6 Migration energy differences for a neutral Br_i migration with one (red line) or two (orange line) intermediate Br atoms participating in the motion compared to zero atoms in the defect transition (purple line). The migration energies become lower as one, and then two, intervening atoms are involved, representative of the “domino effect” strategy.

Considering the activation energies of halide interstitials, we note from the above discussion that the charged system pathway sits at a very slightly more energetically preferred position relative to the neutral pathway for E_m. This follows the trend found for E_f, the defect formation energy, for charged and neutral Br_i, resulting in charged interstitials being very slightly preferred; see Section 2.1.1. As a result, when E_f and E_m are summed to determine the activation energy, E_a values for charged and neutral Br interstitials are very similar; see Table 1. This is corroborated by the result in Section 2.2.2 and shown in Fig. 5 that the polyhedral motifs adopted in the migration mechanism are the same in both charge states. It is worth noting that the energy differences between neutral and charged Br interstitials is well within the uncertainty of the DFT calculations themselves. However, referring back to Fig. 2, it should be noted that the formation energy of the charged interstitial is preferred and depends strongly on the Fermi energy level. Hence the Br anion is often a favored species.

Results of the NEB calculations, in the form of migration energy barriers and a visualization of the pathway mechanism, are summarized in Fig. 7. The results are shown as initial, transition, and final states of the system. This figure offers a compact overview and associated insight into the energetics and mechanisms of the defect migration process. These results clearly indicate that the most favorable migration pathway amongst the ones we studied features a collective and concerted movement of several atoms, consistent with the interstitial “domino effect” in vacancy-assisted migration.

Fig. 7 Summary of defect migration energies for four selected defects: from top to bottom, a neutral Br vacancy, a positively charged Br vacancy, a Br interstitial and a Br_i−Pb_i splitting interstitial. Left column: The NEB-generated energy barrier. The right three columns show visualizations of the initial state (I), transition state (TS), and final state (P), corresponding to the points marked I, TS, and P on the left. Atoms involved in the pathway are shown with enhanced saturation and labeled accordingly. Key: brown = Br; orange = interstitial Br; grey = Pb; cyan = Cs. In all images, dashed arrows indicate the paths taken by atoms during migration.

Fig. 8 Summary of recombination energies for five defects: from top to bottom, a Br–Pb anti-site, a Br–Br split interstitial, and three Br–Pb split-interstitials that are aligned in the x-, y- and z-directions, respectively, in the lattice. Left column: The NEB-generated energy barrier. The right three columns show visualizations of the initial state (I), transition state (TS), and final state (P), corresponding to the points marked I, TS, and P on the left. Atoms involved in the pathway are shown with enhanced saturation and labeled accordingly. Key: brown = Br; orange = interstitial Br; grey = Pb; cyan = Cs. In all images, dashed arrows indicate the paths taken by atoms during migration.

A summary of the NEB-derived formation energies, migration energies and activation energies investigated in this work can be found in Table 1.

3 Methodology

This work reports computational values of both the formation energy and migration energy for a variety of defects in CsPbBr₃, the energy required to create and move the defect from point A to point B in the supercell. Both these energy barriers, E_f and E_m, contribute to the overall activation energy for CsPbBr₃, as explained in the Introduction.

We used a 3 × 3 × 2 supercell of CsPbBr₃ containing a total of 360 atoms for the calculation of defect formation energies. This large system is close to the practical limit of system size for a reasonably accessible computational resource effort. Perdew–Burke–Ernzerhof (PBE) calculations were performed using ultrasoft pseudopotentials⁵⁸ with a plane wave cut-off of 40 Ryd (400 Ryd on the charge density). These pseudopotentials were chosen because they accurately represent defects in these kinds of systems.³² The well-known electronic structure code, quantum ESPRESSO,^59–61 was used for all density functional theory (DFT) calculations reported below.

The migration energies and pathways for recombination of these defects were estimated using nudged elastic band DFT (NEB-DFT). NEB-DFT is a well-established methodology for finding the minimum energy pathway connecting one arrangement of atoms (the initial state) to a different arrangement (the final state).^62–65 The potential energy along the minimum energy pathway needed to affect the transition from the initial to final state is assumed to be the energy barrier, in this case, the migration energy for a defect to move from location A in the supercell to location B. Due to the high computational cost of running nudged elastic band simulations, we used a smaller 2 × 2 × 2 supercell containing 160 atoms to estimate the migration energy and the activation barrier for recombination. Details of all the parameters used to set up the quantum ESPRESSO calculations, as well as sample scripts, are provided in the ESI.†

Based on Kang et al.'s work and that of others, we selected point defects that are thought to be particularly prevalent in lead halide perovskites. Some were chosen for their low defect formation energies.⁵ While much of our focus involved looking at simple point defects (V, I), we also explored the migration and recombination of additional ones not considered previously, including “split interstitial” defects in which two atoms share a lattice site, as well as more concerted pathways.

In the ab initio calculations of defect energetics, we introduced a specific defect into a perfect lattice, fixed the cell parameters, and then allowed the atoms to relax.

The defect formation energy formulation is defined in Section 2.1 above. For the NEB calculations of the migration energy, we began by choosing initial and final configurations of a defective lattice and allowed them to relax. We created ten images between the initial and final states for each NEB-derived energy barrier to investigate a manually selected recombination or migration defect pathway.

As well as studies of simple vacancies and interstitials and anti-site defects, we also considered some more exotic, concerted defect pathways. A particularly interesting example involves a defect that moves in a concerted manner involving multiple atoms. It moves such that the interstitial atom you start with is not the same one that eventually moves across the lattice—a “domino effect.” as in Fig. 3. As we showed in the Results section, having other bromine interstitial atoms participate in the migration mechanism drastically reduces the associated activation barrier. A more comprehensive explanation of the “domino effect” in CsPbBr₃ can be found in the ESI.† We identified the intermediate atoms along the “domino effect” pathway in the NEB calculation and compared the migration energy with that of a direct jump, as well as a second neighbor jump (involving two Br atoms) and a third neighbor jump (involving three Br atoms). These comparisons allowed us to examine the contribution of each additional atom to the change in migration energy.

We now describe the creation of a set of defective systems studied in this paper.

3.1 Br vacancies

Halide point defects, especially vacancies, are expected to be one of the most, if not the most, readily movable defect in MHPs.^29,66 As there is a single unique site for bromine atoms, a vacancy can be formed by removing a bromine atom from the simulation cell and letting the system relax. We looked at the migration of both a charged and a neutral vacancy. The migration of a vacancy to its nearest neighbor site and the resulting activation energy associated with the creation and migration of these vacancies are given in Table 1.

3.2 Br interstitials

A Br_i is an additional Br atom in any off-lattice position. Following relax calculations of various Br_i initial placements, all Br_i assumed a PbBr₇ complex in a pentagontal bipyramidal coordination geometry, see Section 2.1.1. E_m values were determined via NEB-DFT for the migration between these relaxed structures, see Section 2.2.3.

3.3 Split interstitials

A split interstitial consists of two atoms sharing a single lattice site. These are some of the most common interstitials found in semiconductor materials,⁶⁷ especially amongst the halide defects.⁶⁸ However, they have not been considered in earlier publications of perovskite defects. We explored the defect migration energies of split interstitials involving two bromine atoms sharing one Br site (Br–Br) and a bromine and lead atom sharing a Pb site (Br–Pb).

3.4 Anti-sites

An anti-site refers to the presence of a “foreign” (unexpected) atom on a lattice site. Here, we explore two types of anti-sites: the first involves a lead atom that occupies a bromine site Pb_Br, the second involves a bromine atom occupying a lead site, Br_Pb. Both anti-sites were modeled with and without their respective charges. Pb_Br is charged +1 and Br_Pb is charged −1. The defect formation energies were calculated for a single anti-site defect and tabulated in Table 1. A nudged-elastic-band simulation of the recombination of a pair of anti-sites Br_Pb–Pb_Br into the null (perfect) crystal system was used to report the migration energy. The pair of anti-sites were treated as a neutral system, since there is no additional atomic species that would charge the system. To simulate the recombination of a pair of anti-sites into the bulk crystal, the two displaced atoms had to be introduced within a first nearest neighbor distance. 20 such candidate sites were identified. Among these, the lowest-energy system was selected to further investigate the recombination of a pair of anti-sites into the perfect crystal.

4 Conclusions

We have studied a broad range of neutral and charged interstitial and vacancy defects in the CsPbBr₃ metal halide perovskite. This included calculating the defect formation energies (E_f) and migration energies (E_m) using accurate ab initio nudged elastic band calculations. E_m values, in particular, will be a helpful addition to the literature. The formation energies reported here reproduce those of Kang and Wang.⁵

Unlike other studies, the ability to calculate both E_f and E_m allows us to calculate the activation energy of the various defects, which provides a direct comparison to experiment. Unfortunately, very few experimental values exist for the activation energy for this metal halide perovskite, or indeed perovskites in general. Above, we highlighted Tirmzi et al.'s experiment, which measured the slow, activated recovery of light-induced conductivity in CsPbBr₃. We find that the calculated range of migration energies, E_m for Br_i, lie between 0.20 and 0.54 eV, in good agreement with the lone value of a 0.53 eV activation energy for relaxation of light-induced conductivity in CsPbBr₃ observed by Tirmzi and co-workers.³⁹

Beyond more well-studied intrinsic defects, bromine vacancy and interstitial defects, we have included additional defects, like the split interstitials (Br–Br and Br–Pb) as well as anti-site defects. The family of split interstitials has not been considered for metal halide perovskites in the past, despite the fact that they are commonly found in more traditional inorganic semiconductors, such as silicon for which they are typically low-energy defects.⁶⁹ Finally, we have identified a formerly unexplored diffusion pathway, which we have labeled the “domino effect” strategy, involving the coordinated diffusion of multiple proximal Br interstitials. The merits of this latter pathway are described below.

The low activation energies that we observed for some of the recombination mechanisms can help explain the self-regulation process seen in perovskites.⁷⁰ Defects like vacancies, interstitials and anti-sites help the perovskite “heal” by adjusting the concentration of charge carriers. The pathways that the unusually extensive, 10-window, NEB calculations allowed us to explore give us accurate energy barriers as well as insight into the different mechanisms of self-regulation that metal halide perovskites can undergo. The domino effect of recombination aided by other nearby bromine atoms lowered the activation threshold, a phenomenon we saw across most of the pathways we studied.

Experimentally measured activation energies do not have the ability to identify the nature of the pathway with the atomic-level precision of DFT-NEB calculations; their values will, of necessity, be an ensemble average over a number of pathways, and must surely include many of the ones we have uncovered here. It is encouraging that the one experimental migration energy that exists for CsPbBr₃ (0.53 eV) lies well within the range that we found for the movement of common halide defects.

In addition to vacancy-assisted migration, Br interstitials (Br_i) can migrate independently between interstitial sites. The preferred coordination environment for both charged and neutral Br_i is a pentagonal bipyramidal PbBr₇, while higher-energy, non-preferred geometries like the monocapped trigonal prism arise to minimize ligand repulsion. The higher defect formation energies for charged versus neutral Br_i are supported by the larger ionic radii for Br⁻versus Br; however, the migration energies are largely unaffected by charge, perhaps due to the flexibility of the CsPbBr₃ lattice as the interstitial defect migrates through it.

Calculations of defect pathways, in addition to the values of E_f, E_m, and E_a provided in this paper, serve as a curated database that can be used to help design better inorganic perovskite materials and, ultimately, devices. Our findings can help guide experimental design: first, the links we provide between structure and their corresponding formation energies can be used to design experiments that would be sensitive to small concentrations of structural defects such as Raman, optical emission, or X-ray spectroscopy. While challenging, it could be possible to use this paper's data to uncover the type and concentration of defects that correspond to a particular choice of processing conditions. The conjunction of this paper's data and the XRD patterns could be used to guide the design of processing protocols to improve defect management, which is a key design feature for the future for perovskites.

Second, this paper suggested that there are low-energy pathways that can self-heal defects. How can we exploit this observation? We hypothesize that proximal (NN to 3rd NN) defects generated by illumination will readily heal. It is uncertain what will transpire in more defective systems, putting a premium on starting with more perfect crystals. This is a testable hypothesis, experimentally and computationally.

Literature suggests that one mechanism of permanent degradation of the halide perovskites involves the motion of halide atoms to the surface and/or interface where they have access to proton reactions (e.g., H₂O); these reactions can, for example, form a halide acid, which is very volatile, resulting in the permanent removal of the halide species from the material. The current report shows that different migration mechanisms have measurably different activation energies. Therefore, measuring the activation energy of defect movement in processed films can elucidate the type of defect and its primary mechanism for migration.

Here is one example how this hypothesis might be implemented experimentally. As a first step, we could experimentally determine the activation energy of defect migration using techniques such as broadband dielectric spectroscopy³⁹ starting with very good quality single crystals and moving to polycrystalline thin films. As the initial concentration of defects increases, the activation energy should decrease as those defects gain access to the “domino effect” described in our work. We could then correlate the initial defect concentration derived from higher-throughput experiments, such as impedance spectroscopy or deep-level transient spectroscopy (DLTS), to the activation energy and hence back out likely mechanisms by which defects would move. With that information, processed materials could be screened for potential material stability using the initial defect concentrations. That is, if the initial defect concentrations suggested that defects could migrate via the domino effect, they would be less likely to remain stable over long periods of time. For other materials within the larger class of halide perovskites, similar experimental approaches to the one described above could be taken provided there are measurable differences in activation energy for different defects and/or different mechanisms of defect motion.

Author contributions

Kumar Miskin: conceptualization, methodology, data curation, visualization and writing. Yi Cao, Madaline Marland, Farhan Shaikh: data curation, visualization and writing. David Moore: expertise on MHPs, funding acquisition, writing. John Marohn: conceptualization, funding acquisition, and writing. Paulette Clancy: conceptualization, funding acquisition, project administration, resources, supervision, and writing.

Conflicts of interest

There are no conflicts to declare.

Data availability

All scripts as detailed in ESI† can be found on the github link: https://github.com/pclancy-lab/perovskite_defect_study/.

Acknowledgements

The authors acknowledge support from the U.S. Department of Energy (DOE) Basic Energy Sciences award DE-SC0022305. Miskin thanks Johns Hopkins University for their support in AY 22-23. Kumar gratefully acknowledges support from the Kai Pan and Li Wang Fellowship, Donald S. Rodbell Memorial Graduate Fellowship, Robert B. Pond Sr. Fellowship, and the Edwin D. and Rachel Lowthian Endowed Fellowship. Computational resource support was provided by the petascale Hopkins facility, Advanced Research Computing at Hopkins (ARCH) (rockfish.jhu.edu), supported by National Science Foundation award OAC 1920103. Partial funding for ARCHs infrastructure was originally provided by the State of Maryland.

Notes and references

1. J. S. Manser, J. A. Christians and P. V. Kamat, Chem. Rev., 2016, 116(21), 12956–13008.
2. Y. Yuan and J. Huang, Acc. Chem. Res., 2016, 49, 286–293.
3. W.-J. Yin, T. Shi and Y. Yan, Appl. Phys. Lett., 2014, 104, 063903.
4. A. Walsh, D. O. Scanlon, S. Chen, X. G. Gong and S.-H. Wei, Angew. Chem., Int. Ed., 2015, 54, 1791–1794.
5. J. Kang and L. W. Wang, J. Phys. Chem. Lett., 2017, 8, 489–493.
6. W. Nie, J. C. Blancon, A. J. Neukirch, K. Appavoo, H. Tsai, M. Chhowalla, M. A. Alam, M. Y. Sfeir, C. Katan, J. Even, S. Tretiak, J. J. Crochet, G. Gupta and A. D. Mohite, Nat. Commun., 2016, 7, 11574.
7. F. Lang, N. H. Nickel, J. Bundesmann, S. Seidel, A. Denker, S. Albrecht, V. V. Brus, J. Rappich, B. Rech, G. Landi and H. C. Neitzert, Adv. Mater., 2016, 28, 8726–8731.
8. R. E. Brandt, J. R. Poindexter, P. Gorai, R. C. Kurchin, R. L. Hoye, L. Nienhaus, M. W. Wilson, J. A. Polizzotti, R. Sereika, R. Žaltauskas, L. C. Lee, J. L. Macmanus-Driscoll, M. Bawendi, V. Stevanović and T. Buonassisi, Chem. Mater., 2017, 29, 4667–4674.
9. D. Cahen, L. Kronik and G. Hodes, ACS Energy Lett., 2021, 6, 4108–4114.
10. F. Ambrosio, D. Meggiolaro, T. M. Almutairi and F. De Angelis, ACS Energy Lett., 2021, 6, 969–976.
11. R. I. Biega and L. Leppert, J. Phys. Energy, 2021, 3, 034017.
12. D. Meggiolaro, E. Mosconi and F. De Angelis, ACS Energy Lett., 2019, 4, 779–785.
13. S. Ten Brinck, F. Zaccaria and I. Infante, ACS Energy Lett., 2019, 4, 2739–2747.
14. H. Jin, E. Debroye, M. Keshavarz, I. G. Scheblykin, M. B. Roeffaers, J. Hofkens and J. A. Steele, Mater. Horiz., 2020, 7(2), 397–410.
15. D. Meggiolaro, F. Ambrosio, E. Mosconi, A. Mahata and F. De Angelis, Adv. Energy Mater., 2020, 10(13), 1902748.
16. T. Etienne, E. Mosconi and F. De Angelis, J. Phys. Chem. Lett., 2016, 7, 1638–1645.
17. L. M. Pazos-Outón, M. Szumilo, R. Lamboll, J. M. Richter, M. Crespo-Quesada, M. Abdi-Jalebi, H. J. Beeson, M. Vrućinić, M. Alsari, H. J. Snaith, B. Ehrler, R. H. Friend and F. Deschler, Science, 2016, 351, 1430–1433.
18. C. Cho, B. Zhao, G. D. Tainter, J.-Y. Lee, R. H. Friend, D. Di, F. Deschler and N. C. Greenham, Nat. Commun., 2020, 11, 611.
19. C. Eames, J. M. Frost, P. R. F. Barnes, B. C. ORegan, A. Walsh and M. S. Islam, Nat. Commun., 2015, 6, 7497.
20. J. Wiktor, F. Ambrosio and A. Pasquarello, J. Mater. Chem. A, 2018, 6, 16863–16867.
21. C. Tantardini, S. Kokott, X. Gonze, S. V. Levchenko and W. A. Saidi, Appl. Mater. Today, 2022, 26, 101380.
22. B. Kang and K. Biswas, J. Phys. Chem. Lett., 2018, 9, 830–836.
23. N. Österbacka, P. Erhart, S. Falletta, A. Pasquarello and J. Wiktor, Chem. Mater., 2020, 32, 8393–8400.
24. M. Puppin, S. Polishchuk, N. Colonna, A. Crepaldi, D. N. Dirin, O. Nazarenko, R. De Gennaro, G. Gatti and S. Roth, Phys. Rev. Lett., 2020, 124, 206402.
25. M. Sajedi, M. Krivenkov, D. Marchenko, J. Sánchez-Barriga, A. K. Chandran, A. Varykhalov, E. D. Rienks, I. Aguilera, S. Blügel and O. Rader, Phys. Rev. Lett., 2022, 128, 043016.
26. D. R. Ceratti, Y. Rakita, L. Cremonesi, R. Tenne, V. Kalchenko, M. Elbaum, D. Oron, M. A. C. Potenza, G. Hodes and D. Cahen, Adv. Mater., 2018, 30, 1706273.
27. K. Frohna, T. Deshpande, J. Harter, W. Peng, B. A. Barker, J. B. Neaton, S. G. Louie, O. M. Bakr, D. Hsieh and M. Bernardi, Nat. Commun., 2018, 9, 1829.
28. M. Sajedi, M. Krivenkov, D. Marchenko, A. Varykhalov, J. Sánchez-Barriga, E. D. Rienks and O. Rader, Phys. Rev. B, 2020, 102(8), 081116.
29. J. M. Azpiroz, E. Mosconi, J. Bisquert and F. D. Angelis, Energy Environ. Sci., 2015, 8, 2118–2127.
30. J. L. Minns, P. Zajdel, D. Chernyshov, W. van Beek and M. A. Green, Nat. Commun., 2017, 8, 15152.
31. H. Xue, G. Brocks and S. Tao, Phys. Rev. Mater., 2021, 5, 125408.
32. D. Meggiolaro and F. De Angelis, ACS Energy Lett., 2018, 3, 2206–2222.
33. A. Oranskaia, J. Yin, O. M. Bakr, J. L. Brédas and O. F. Mohammed, J. Phys. Chem. Lett., 2018, 9, 5474–5480.
34. R. A. Evarestov, E. A. Kotomin, A. Senocrate, R. K. Kremer and J. Maier, Phys. Chem. Chem. Phys., 2020, 22, 3914–3920.
35. H. Xue, J. M. Vicent-Luna, S. Tao and G. Brocks, J. Phys. Chem. C, 2023, 127, 1189–1197.
36. S. R. G. Balestra, J. M. Vicent-Luna, S. Calero, S. Tao and J. A. Anta, J. Mater. Chem. A, 2020, 8, 11824–11836.
37. M. Pazoki, M. J. Wolf, T. Edvinsson and J. Kullgren, Nano Energy, 2017, 38, 537–543.
38. J. Hafner and G. Kresse, Properties of Complex Inorganic Solids, Springer, 1997, pp. 69–82.
39. A. M. Tirmzi, R. P. Dwyer, T. Hanrath and J. A. Marohn, ACS Energy Lett., 2017, 2, 488–496.
40. A. M. Tirmzi, J. A. Christians, R. P. Dwyer, D. T. Moore and J. A. Marohn, J. Phys. Chem. C, 2019, 123, 3402–3415.
41. I. Poli, F. Ambrosio, A. Treglia, F. J. Berger, M. Prato, M. D. Albaqami, F. De Angelis and A. Petrozza, Adv. Sci., 2022, 9, 2202795.
42. E. Mosconi, D. Meggiolaro, H. J. Snaith, S. D. Stranks and F. D. Angelis, Energy Environ. Sci., 2016, 9, 3180–3187.
43. T. Lv, Y. Liang, F. Zeng, F. Li, X. Yang, J. Huang and R. Zheng, J. Phys. Chem. Lett., 2024, 15, 2929–2935.
44. G. Y. Kim, A. Senocrate, T.-Y. Yang, G. Gregori, M. Grätzel and J. Maier, Nat. Mater., 2018, 17, 445–449.
45. K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276.
46. C. A. López, C. Abia, M. C. Alvarez-Galván, B. K. Hong, M. V. Martínez-Huerta, F. Serrano-Sánchez, F. Carrascoso, A. Castellanos-Gómez, M. T. Fernández-Díaz and J. A. Alonso, ACS Omega, 2020, 5, 5931–5938.
47. J. Wang, B. Lukose, M. O. Thompson and P. Clancy, J. Appl. Phys., 2017, 121, 045106.
48. C. Freysoldt, J. Neugebauer and C. G. Van de Walle, Phys. Rev. Lett., 2009, 102, 016402.
49. X. Jiang, Y. Tao, J. Gu, L. Jin, C. Li, W. Zhang and Y. Fu, Dalton Trans., 2023, 52, 15489–15495.
50. S. G. Motti, D. Meggiolaro, S. Martani, R. Sorrentino, A. J. Barker, F. De Angelis and A. Petrozza, Adv. Mater., 2019, 31, 1901183.
51. M. Sebastian, J. A. Peters, C. C. Stoumpos, J. Im, S. S. Kostina, Z. Liu, M. G. Kanatzidis, A. J. Freeman and B. W. Wessels, Phys. Rev. B:Condens. Matter Mater. Phys., 2015, 92, 235210.
52. D. Kepert, Prog. Inorg. Chem., 1979, 41–144.
53. R. Car, P. J. Kelly, A. Oshiyama and S. T. Pantelides, Phys. Rev. Lett., 1985, 54, 360–363.
54. A. Kyrtsos, M. Matsubara and E. Bellotti, Phys. Rev. B, 2016, 93, 245201.
55. M. Pols, V. Brouwers, S. Calero and S. Tao, Chem. Commun., 2023, 59, 4660–4663.
56. A. A. Cheenady and K. Rajan, J. Appl. Phys., 2023, 133, 205105.
57. S. Meloni, T. Moehl, W. Tress, M. Franckevic̆ius, M. Saliba, Y. H. Lee, P. Gao, M. K. Nazeeruddin, S. M. Zakeeruddin, U. Rothlisberger and M. Graetzel, Nat. Commun., 2016, 7, 10334.
58. D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 7892–7895.
59. P. Giannozzi, et al. , J. Phys.: Condens. Matter, 2009, 21, 395502.
60. P. Giannozzi, et al. , J. Phys.: Condens. Matter, 2017, 29, 465901.
61. P. Giannozzi, O. Baseggio, P. Bonfà, D. Brunato, R. Car, I. Carnimeo, C. Cavazzoni, S. de Gironcoli, P. Delugas, F. Ruffino, A. Ferretti, N. Marzari, I. Timrov, A. Urru and S. Baroni, J. Chem. Phys., 2020, 152, 154105.
62. G. Mills and H. Jónsson, Phys. Rev. Lett., 1994, 72(7), 1124.
63. B. J. Berne; G. Ciccotti and D. F. Coker, Classical and Quantum Dynamics in Condensed Phase Simulations Euroconference on “Technical advances in Particie-based Computational Material Sciences”. Coordinator: M. Mareschal, LERICI, Villa Marigola Yfe, World Scientific, 1998.
64. G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904.
65. G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978–9985.
66. W. Kaiser, K. Hussain, A. Singh, A. A. Alothman, D. Meggiolaro, A. Gagliardi, E. Mosconi and F. De Angelis, J. Mater. Chem. A, 2022, 10, 24854–24865.
67. P. Masri, A. H. Harker and A. M. Stoneham, J. Phys. C-Solid State Phys., 1983, 16, L613–L616.
68. J.-S. Park, J. Calbo, Y.-K. Jung, L. D. Whalley and A. Walsh, ACS Energy Lett., 2019, 4, 1321–1327.
69. B. W. Roberts, W. Luo, K. A. Johnson and P. Clancy, Chem. Eng. J., 1999, 74, 67–75.
70. Z. Yao, Z. Xu, W. Zhao, J. Zhang, H. Bian, Y. Fang, Y. Yang and S. Liu, Adv. Energy Mater., 2021, 11, 2100403.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp01641j

---