Entropy-stabilized ZrHfCoNiSnSb half-Heusler alloy for thermoelectric applications: a theoretical prediction†
Received
27th April 2025
, Accepted 3rd July 2025
First published on 7th July 2025
Abstract
Half-Heusler (HH) alloys are potential thermoelectric materials for use at elevated temperatures due to their high Seebeck coefficient and superior mechanical and thermal stability. However, their enhanced lattice thermal conductivity is detrimental to thermoelectric applications. One way to circumvent this problem is to introduce mass disorder at lattice sites by mixing the components of two or more alloys. Such systems are typically stabilized by the entropy of mixing. In this work, using computational tools, we propose a mixed HH, namely, ZrHfCoNiSnSb, which can be formed by the elemental compositions of the parent half-Heuslers ZrNiSn/HfNiSn and HfCoSb/ZrCoSb. We propose that this new compound can be synthesized at elevated temperatures, as its Gibbs free energy is reduced due to higher configurational entropy, making it more thermodynamically stable than the parent compounds under such conditions. Our calculations indicate that it is a dynamically stable semiconductor with a band gap of 0.61 eV. Its lattice thermal conductivity at room temperature is 5.40 W m−1 K−1, which is significantly lower than those of the parent compounds. The peak value of this alloy's figure of merit (ZT) is 1.00 for the n-type carriers at 1100 K, which is 27% more than the best figure of merit obtained for the parent compounds.
1 Introduction
An enormous amount of waste heat is generated in automotive exhaust, home heating, and industrial processes. One of the ways of utilizing this wasted heat is to convert it to electricity by using the phenomenon of thermoelectricity. The efficiency of a thermoelectric material is determined by its figure of merit (ZT), which is a function of Seebeck coefficient (α), electrical conductivity (σ), thermal conductivity (kt), and temperature (T). This figure of merit is given by the relation:1| |  | (1) |
Thermal conductivity (kt) has contributions from both electrons (ke) and phonons (kL). To achieve a high value of ZT, which is required for being a good thermoelectric material, a high Seebeck coefficient, a high electrical conductivity, and a low thermal conductivity are required.
Half-Heusler alloys are one class of intermetallic compounds that exhibit great promise as thermoelectric materials suitable for high-temperature applications owing to their remarkable attributes, including a high Seebeck coefficient, exceptional mechanical strength, and thermal stability. On the contrary, the increased lattice thermal conductivity of these materials poses a disadvantage for thermoelectric applications. These compounds, having a composition of XYZ where X (Wyckoff position 4b (0.5, 0.5, 0.5)) and Y (Wyckoff position 4c (0.25, 0.25, 0.25)) are transition metals and Z (Wyckoff position 4a (0, 0, 0)) is a p-block element, comprise of three interlocking face-centred cubic sublattices and an additional vacant sublattice in the same cubic structure. The semiconducting properties and stability of half-Heusler compounds can be understood using the Zintl concept,2 according to which the most electropositive element, X, acts as a cation and donates all of its valence electrons to the tetrahedrally bonded YZ sublattice, effectively forming the anionic part of the structure. Based on this concept, a half-Heusler compound with a valence electron count (VEC) of 18 may be a stable semiconductor with potential for thermoelectric applications. TiNiSn,3,4 ZrNiSn,3,4 HfNiSn,3,5 TiCoSb,6,7 ZrCoSb6,7 and HfCoSb6,7 are some of the well-studied VEC 18 half-Heuslers for thermoelectric applications. The crystal structure of half-Heusler alloy XYZ is shown in Fig. 1.
 |
| | Fig. 1 Crystal structure of half-Heusler alloy XYZ. | |
To overcome the issue of lattice thermal conductivity, a potential solution involves inducing mass disorder at lattice sites by blending the elemental compositions of two or more half-Heusler (HH) alloys, thereby forming a high-entropy alloy. The concept of high entropy has been applied to various classes of materials, including chalcogenides8,9 and oxides.10,11 In these systems, a high configurational entropy favors the formation of a single-phase structure by contributing significantly to the Gibbs free energy.12 Compared to conventional solid solutions with low levels of elemental additions, the high-entropy effect can overcome limitations in solubility. This was demonstrated by the successful synthesis of a single-phase (MgCoNiCuZn)O compound with a rock-salt structure,11 which can be viewed as an equimolar mixture of MgO, CoO, NiO, CuO, and ZnO. In this system, the typical solubility limits of binary combinations such as MgO–ZnO and CuO–NiO were surpassed due to entropic stabilization. Among half-Heusler compounds, the high-entropy concept has also been successfully applied in the synthesis of a single-phase (TiZrHfVNbTa)Fe0.5Co0.5Sb,13 which is based on six VEC 18 half-Heuslers: TiCoSb, ZrCoSb, HfCoSb, VFeSb, NbFeSb, and TaFeSb. Similarly, stabilization of the VEC 17.5 half-Heusler compound ZrTiNiFeSnSb14 is achieved through the high-entropy effect, despite the individual instability of its VEC 17 and VEC 19 parent phases. Another notable example, though not a high-entropy alloy, is the synthesis of Ti2NiCoSnSb,15 which can be regarded as an equimolar mixture of the parent HHs TiNiSn and TiCoSb. This alloy has a lattice thermal conductivity of 7 W m−1 K−1 as compared to 24 W m−1 K−1 for TiCoSb7 and 13 W m−1 K−1 for TiNiSn3 at room temperature. However, its power factor is significantly reduced as compared to parent compounds, leading to the low value of the figure of merit. Intriguingly, the question arises as to whether it is feasible to synthesize a material by combining the compositions of two half-Heusler compounds with reduced lattice thermal conductivity while retaining the power factor of the original parent compounds. The investigation also seeks to ascertain the stability of this mixed compound in comparison to its parent compounds. Additionally, it will be interesting to understand how the blending process influences the electronic transport properties of this composite material.
ZrHfCoNiSnSb, which can be seen as a mixture of ZrNiSn/HfNiSn and HfCoSb/ZrNiSn, is dynamically stable and predicted to be synthesized at high temperatures. The lattice thermal conductivity of this compound is found to be 5.40 W m−1 K−1 at 300 K, which is much lower than the parent compounds. Additionally, for the n-type case, its power factor lies midway between the power factors of the constituent parent compounds, resulting in a ZT value of 1.00 at a temperature of 1100 K.
2 Computational details
The calculations were carried out using plane-wave density functional theory (DFT) based calculations as implemented in the Quantum ESPRESSO16,17 software. The electron–ion interactions were described using ultrasoft pseudopotentials. For the wavefunction (charge density), we have used a basis set whose size corresponds to a kinetic energy cutoff of 60 (480) Ry. The electron–electron exchange and correlation effects were treated using the Perdew–Burke–Ernzerhof (PBE)18 parametrization of the generalized gradient approximation (GGA). For electronic calculations, the Brillouin zone (BZ) was sampled with a shifted 10 × 10 × 10 and 6 × 6 × 6 Monkhorst–pack k-mesh for the conventional unit cell of the parent compounds and ZrHfCoNiSnSb, respectively. To compute the density of states (DOS) and the electronic transport properties we have used 20 × 20 × 20 k-mesh grid for the parent compounds and 18 × 18 × 18 k-mesh grid for ZrHfCoNiSnSb. Since spin–orbit interaction has a negligible effect in the HEA (as evident from the band structure shown in Fig. S3 of the ESI†), it was not included in the DFT calculations.
To study the dynamical stability, vibrational properties, and lattice thermal conductivity, the phonons were computed using density functional perturbation theory.19 The calculations were performed on a 6 × 6 × 6 q-mesh for the primitive unit cell of the parent compounds and a 3 × 3 × 3 q-mesh for ZrHfCoNiSnSb.
Electronic transport properties were calculated by using the semi-classical Boltzmann transport theory within the constant relaxation time and rigid band approximations as implemented in the BoltzTraP2 code.20 Under these approximations the (ij)th component of projected conductivity tensor per unit relaxation time 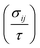 was calculated as
was calculated as
| | 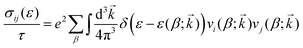 | (2) |
Here
e is the charge of the electron and
τ is the constant relaxation time.

is the group velocity of the electron occupying the
βth band at the
kth
k-point of the BZ and
ε(
β;
![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif)
) is the energy eigenvalue corresponding to that electronic state. The (
ij)th component of electrical conductivity per unit relaxation time

Seebeck coefficient (
αij(
T;
μ)) and electronic thermal conductivity per unit relaxation time
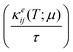
were calculated from
eqn (2) as:
| |  | (3) |
| |  | (4) |
and
| | 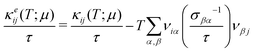 | (5) |
where
| | 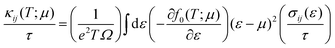 | (6a) |
and
| |  | (6b) |
In these equations
f0(
T;
μ) is the equilibrium Fermi–Dirac distribution at temperature
T and chemical potential
μ and
Ω is the unit cell volume. The values of
τ for electrons and holes, appearing in the above equations, were computed using deformation potential theory
21 as described in Sections 3.4 and 3.5.
3 Results and discussions
3.1 Structure, thermodynamic stability and bonding
To model the most disordered configuration of ZrHfCoNiSnSb, we employed the Monte Carlo Special Quasirandom Structure (McSQS) method, as implemented in the ATAT software.22 The quasirandom structures were generated with the constraint that the Zr and Hf atoms occupy the Wyckoff site 4b (0.5, 0.5, 0.5), Ni and Co atoms occupy the site 4c (0.25, 0.25, 0.25) and Sn and Sb atoms occupy the site 4a (0, 0, 0). We constructed four different quasirandom structures within this constraint. Three of these structures are the 12-atom structure in the conventional cubic HH supercell (Type I), the 24-atom quasirandom structure with the conventional cubic cell doubled along the c-direction (Type II), and the 24-atom quasirandom structure with a 2 × 2 × 2 primitive fcc supercell (Type III). Additionally, we also generated a 24-atom SQS with no constraints on the particular choice of crystal structure (Type IV). The initial structures of these unit cells are shown in Fig. S1 of the ESI,† while the optimized structures are shown in Fig. 2. The corresponding McSQSc transformation matrices for all the generated structures are provided in eqn (S2)–(S5) of ESI.†
 |
| | Fig. 2 Crystal structure of the optimized SQSs (a) conventional unit cell (b) 2 × 2 × 2 supercell (c) double conventional unit cell (d) unconstrained SQS with 24 atoms. | |
On optimizing the lattice parameters and the atomic positions of the above-mentioned unit cells, we find that the Type I structure is the lowest in energy. The relative energies per formula unit of the other structures with respect to that of Type I (ΔE) and the lattice parameters of all the structures are reported in Table 1. It is interesting to note that post-geometry optimization, the lattice parameters and the angles between the lattice vectors deviate from those observed in the supercells of fcc lattice. For example, in the lowest-energy Type I structure, all three lattice vectors are equal, and the interaxial angles are 90.000° prior to geometry optimization. After optimization, the structure relaxes into a monoclinic phase characterized by the C2 point group which includes only the identity and a 180° rotation about the Z-axis as its symmetry operations, due to slight variations in the lattice parameters and a deviation of the angle γ from 90.000°. Since Type I is the lowest energy structure amongst the ones considered in this study, all subsequent calculations for ZrHfCoNiSnSb were performed using this unit cell. To assess whether the Type I structure accurately captures the extensive disorder, a convergence analysis was performed by comparing the Type I McSQS with truly disordered 96-atom McSQSs (constructed as a 2 × 2 × 2 supercell of the conventional unit cell). The results of this analysis are presented in Section S10 of ESI.† As shown in Fig. S10 of the ESI,† the bond lengths and bond orders—which indicate how charge is distributed between atoms and thus partially characterize the local chemical environment—exhibit excellent agreement between the 12-atom and 96-atom SQS structures. This demonstrates that the 12-atom SQS effectively captures the key features of the extensive configurational disorder present in the larger 96-atom system.
Table 1 Computed relative energy per formula unit (ΔE), lattice parameters and angle between the lattice parameters for the different SQS structures considered in this study
| Structure |
Type-I |
Type-II |
Type-III |
Type-IV |
| ΔE (in eV) |
0.000 |
0.028 |
0.014 |
0.026 |
|
|
| Lattice parameters (in Å) |
a = 6.109, b = 6.107, c = 6.115 |
a = 6.101, b = 6.108, c = 12.199 |
a = 8.623, b = 8.628, c = 8.626 |
a = 4.318, b = 8.626, c = 12.204 |
|
|
| Angles |
α = β = 90.000°, γ = 90.004° |
α = 90.006°, β = 90.001°, γ = 89.979° |
α = 60.084°, β = 60.065°, γ = 60.075° |
α = 90.044°, β = 90.000°, γ = 90.000° |
These alloys are typically synthesized experimentally via arc melting of the elemental precursors. Hence, to check the stability of the HEA against segregation into the individual bulk components, we have computed their average formation energy (Ef),23 which is given as:
| | 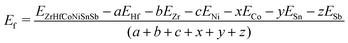 | (7) |
where
EZrHfCoNiSnSb is the total energy of the HEA and
Ei,
i = Hf, Zr, Ni, Co, Sn and Sb, are the energy per atom of the
ith element in its bulk.
a,
b,
c,
x,
y and
z are the number of atoms of Hf, Zr, Ni, Co, Sn and Sb, respectively, in the HEA. The conditions used for calculating
Ef in the above equation—including the elemental standard states, crystal structures, and temperature—are provided in Section S9 of the ESI.
† We find that our proposed HEA has a formation energy of −0.75 eV per atom, suggesting that this is highly stable with respect to the segregation into individual atomic phases.
Additionally, the proposed HEA might also be thought of as a mixture of two stable HHs, namely, HfNiSn and ZrCoSb HHs or ZrNiSn and HfCoSb HHs. Hence, it is also imperative to study the stability of the HEA with respect to phase segregation into these HHs. To do so, we considered the following chemical reactions:
| | | ZrHfCoNiSnSb → HfNiSn + ZrCoSb | (8) |
| | | ZrHfCoNiSnSb → ZrNiSn + HfCoSb | (9) |
and computed the enthalpy of formation (Δ
He), which is given by:
| | | ΔHe = EHfNiSn/ZrNiSn + EZrCoSb/HfCoSb − EZrHfCoNiSnSb | (10) |
where the first, second and third terms on the right-hand side of
eqn (10) are the total energies of the HHs into which they can phase segregate and HEA, respectively. For
reactions (8) and (9), we obtain Δ
He to be −70 meV and −86 meV per formula unit. While the negative values of Δ
He might initially suggest that ZrHfCoNiSnSb will phase segregate to either HfNiSn and ZrCoSb or ZrniSn and HfCoSb, the role of configurational entropy (Δ
Sconfig) at elevated synthesis temperatures become crucial in reducing the Gibbs free energy and contributing to the overall thermodynamic stability
12 of ZrHfCoNiSnSb over HfNiSn/ZrNiSn and ZrCoSb/HfCoSb. This configurational entropy is given by:
13| |  | (11) |
In
eqn (11),
kB is the Boltzmann constant. The summation over
x runs over all the sublattices (here it is 3) and
fxi is the fraction of element
i in the sublattice
x. For the case of ZrHfCoNiSnSb, in Type-I, each of Hf/Zr, Ni/Co, and Sn/Sb forms fcc sublattice. Using
eqn (11), Δ
Sconfig for the Type-I structure of the HEA comes out to be 2.079
kb. The temperature above which this system can be synthesized will be the one at which the change in the Gibbs free energy (Δ
G) is positive. This Gibbs free energy difference, Δ
G, is expressed as:
where the contributions of electronic energy and configurational entropy to the Gibbs free energy, Δ
Ge, are given by
| | | ΔGe = ΔHe − TΔSconfig | (13) |
and Δ
Gp represents the phonon contribution to the Gibbs free energy, defined as:
Here, Hp and Sp denote the phonon energy (or vibrational energy) and phonon entropy (or vibrational entropy) of the respective structures, given by:
| |  | (15) |
and
| |  | (16) |
In these expressions, g(ω) represents the phonon density of states corresponding to the frequency ω, and ωmax is the maximum phonon frequency.
Fig. 3 illustrates the variation of ΔG with temperature for the cases described in eqn (8) and (9).
 |
| | Fig. 3 (a) Individual components of ΔG as a function of temperature. (b) Total Gibbs free energy as a function of temperature. | |
As can be seen from the Fig. 3, ΔG is positive when T is greater than 367 K and 436 K for reactions (8) and (9), respectively. We note that these temperatures are only 67 K and 136 K above room temperature, and are much lower than the synthesis temperatures of half-Heusler systems. Thus, our analysis suggests that these materials will be stable towards segregation into the HHs. A more detailed discussion on segregation kinetics and the potential formation of secondary phases is provided in Section S11 of the ESI.†
At this point, it would be interesting to compare the local geometry of this HEA with those of conventional HHs. A conventional HH can be thought of as a combination of two zinc blende structures formed by the YZ elements and the XY elements. In each of the zinc blende structures, the Y element is at the centre of the tetrahedra formed either by the X or the Z element. Moreover, these are perfect tetrahedra, i.e., in each tetrahedra, the four Y–Z or Y–X bonds have the same bond lengths. In contrast, for the HEA, the introduction of the disorder at each of the atomic sites distorts these tetrahedra because two of the vertices are occupied by Hf (Sb) while the other two by Zr (Sn). In ZrNiSn and HfNiSn, the Ni–Sn bond lengths are 2.665 Å and 2.647 Å, respectively, while in the HEA we find the bond length to be 2.656 Å. Similarly, the Co–Sb bond length in HEA is 2.625 Å which is slightly shorter (similar) than (to) that of 2.642 Å (2.624 Å) in ZrCoSb (HfCoSb). Moreover, we also observe formation of new Ni–Sb and Co–Sn bonds with bond lengths of 2.625 Å and 2.662 Å, respectively. In the X–Y sublattice of the HEA, the Zr–Ni (Zr–Co) bonds are elongated (shortened) compared to those observed in ZrNiSn and ZrCoSb (dZr–Ni = 2.688 Å in HEA vs. 2.665 Å in ZrNiSn; dZr–Co = 2.609 Å in HEA vs. 2.642 Å in ZrCoSb). In contrast, both the Hf–Ni and Hf–Co bonds in HEA are shortened compared to those observed in the parent HHs. However, the Zr–Ni (Zr–Co) bond is elongated (shortened) than that observed in ZrNiSn (ZrCoSb). These asymmetries in the local geometry result in deviation from the cubic symmetry. Further, such a wide variation of bond lengths suggests that there is significant heterogeneity in terms of bonding and bond strength in the HEA, the implications of which on the thermoelectric properties are discussed later.
In order to understand the nature of the bonding between the different elements in the HEA, we have computed the difference between the charge density distribution and superposition of the atomic densities (Δρ) for the HEA and the parent compounds. Δρ provides information as to how the atomic charge densities are rearranged when the different elements interact to form a compound. Fig. 4 shows the Δρ for the HEA, while those for the parent compounds are shown in Fig. S5 of the ESI.† In the Co-containing parent compounds, namely ZrCoSb and HfCoSb, we observe that there is charge depletion from the Co atom (Turquoise isosurfaces in Fig. S5(b) and (d) of ESI†). Further, both charge depletion and accumulation can be observed around the Hf/Zr atoms, with the former dominating. Charge depletion is also observed around Sb. Importantly, we observe charge accumulation in between the Zr/Hf and Co bonds, suggesting a covalent nature of bonding between them. No such charge accumulation is observed between the Co–Sb bonds. Similarly, in the Ni-containing compounds, i.e., in ZrNiSn and HfNiSn, we primarily observe charge depletion around Zr/Hf and Sn. However, in contrast with Co, we observe both accumulation and depletion of charges from Ni, with the former dominating. Additionally, charge accumulation is also observed along the Ni–Zr/Hf bonds. The charge cloud, in this case, is more directional compared to the Co-containing HH and is localized closer to the Ni atom. Thus, in the Ni(Co) containing parent compounds, the X–Y bond is ionic (covalent) in nature. Interestingly, in the HEA, the electron rearrangement around the Ni and Co atoms remains similar to the parent compounds with slight deviations due to local distortion in its structure. This shows the presence of a bonding hierarchy in the HEA.
 |
| | Fig. 4 Isosurfaces of charge density difference (Δρ) between the electron density of the HEA and that obtained from the superposition of the atomic densities. Yellow (Turquoise) isosurfaces denote accumulation (depletion) of charge density. The isosurfaces correspond to an isovalue of 0.009 e bohr−3. | |
3.2 Phonon dispersion and lattice thermal conductivity
In order to assess the dynamical stability of the HEA, we have computed its phonon spectrum, which is shown in Fig. 5. Further, in order to understand how the lattice vibrations are altered in the HEA in comparison with the parent HHs, we have also computed the phonon spectra of the latter (Fig. S2 of the ESI†). Since both the parent compounds and the HEA lack a center of inversion, LO–TO splitting corrections were included in all phonon calculations. The absence of any imaginary modes in the HEA vibrational spectrum throughout the BZ suggests that the HEA is dynamically stable. A LO–TO splitting of approximately 25 cm−1 was observed in ZrNiSn and HfNiSn, around 50 cm−1 in HfCoSb and ZrCoSb, and about 21 cm−1 in the HEA ZrHfCoNiSnSb, as shown in Fig. S12 of the ESI.† Additionally, the Born effective charges—which determine the strength of the coupling between phonons and the macroscopic electric field (the main origin of LO-TO splitting)—were computed and compared with previously reported values3,6 in Tables S10 and S11 of the ESI.† Our results for the high-frequency dielectric tensor and Born effective charges of the parent HHs are in excellent agreement with previously reported values, as shown in Table S10 of the ESI.† Compared to the parent HHs, where there is either nil or negligible mixing of the acoustic and optical phonons, the HEA spectrum shows a significant overlap of these phonon modes. This enhanced mixing can be attributed to the softening of the low-frequency optical modes. Usually, this mixing between the heat-carrying acoustic modes with the optical ones results in scattering of the former, thereby reducing the lattice thermal conductivity. Moreover, in the HHs, the high-frequency optical phonon bands are flat, giving rise to sharp peaks in the phonon density of states (PhDOS). In contrast, in the HEA, the optical phonon bands become more dispersive, giving rise to the broader peaks in PhDOS. The atom projected PhDOS show that for the modes that have frequencies less than 125 cm−1, the major contribution is from the heaviest element Hf. The other heavy elements like Sb, Sn and Zr also have reasonable contributions in lower frequency modes. The Sb and Sn atoms have a dominant contribution to the phonon modes lying between 125 cm−1 and 175 cm−1. For 175 < ω < 200 cm−1, the lattice vibrations are dominated by the vibrations of the Zr atoms, while those having frequency beyond 200 cm−1, the major contributions are from the displacements of the lightest Ni and Co atoms.
 |
| | Fig. 5 (a) Irreducible Brillouin zone showing the path marked in green for the HEA (b) phonon dispersion, inverse participation ratio (IPR) of the phonon modes and phonon density of states of the HEA. | |
In order to understand whether the nature of localization of the phonon modes in the HEA changes compared to the HH, we have computed the inverse participation ratio for each mode (IPR). This IPR is computed as:24
| |  | (17) |
Here
εiα,n represents the eigenvector component along the
α-direction for mode
n.
IPR = 1 (IPR ≃ 1/N, N being the number of atoms in the unit cell) implies a completely localized (delocalized) phonon mode. Fig. 5 shows the IPR for the HEA, while those of the HHs are shown in Fig. S2 of ESI.† While for the HHs, all the phonon modes till about 130 cm−1 are completely delocalized, in HEA the phonon modes with frequency greater than 50 cm−1 tends to localize. However, relative to the HHs where we observe that the high-frequency phonon modes are highly localized (IPR = 1 for some modes), the overall degree of delocalization of the modes is relatively lower in the HEA suggesting that the modes are more diffusive in nature.
The effect of hierarchical bonding, discussed in the previous section, is reflected in the computed the mode resolved Gruneisan parameter (γki), which for the phonon of the ith branch with wave vector k is given by:
| |  | (18) |
where
V0 is the equilibrium volume of the unit cell and
ωki is the frequency corresponding to the phonon of the
ith branch with wave vector
k. The derivative in
eqn (18) is evaluated numerically by using the central difference method. To achieve this, we computed the phonon spectra by applying strain, varying the lattice parameters by ±1%. The
γki of the parent HH and the HEA are plotted in
Fig. 6. While for the HH
γki typically lies between 0 and 2.5, in the HEA, it varies from −1.4 to 7.4,
i.e. an overall spread of 8. Moreover, this enhancement in the spread of
γki is primarily restricted to the heat-carrying acoustic phonons. This suggests that the HEA lattice becomes significantly more anharmonic compared to that of the parent HHs.
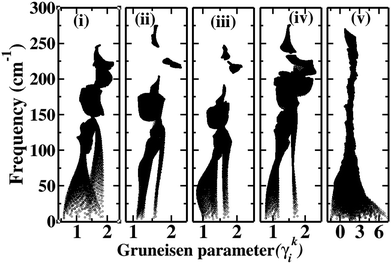 |
| | Fig. 6 Mode resolved Gruneisen parameters for the parent HHs (a) ZrNiSn (b) HfCoSb (c) HfNiSn (d) ZrCoSb and (e) ZrHfCoNiSnSb. | |
The effect of the changes in bonding of the HEA lattice and thereby their vibrational properties also affect thermal transport in these materials. We have computed the lattice thermal conductivity (kL) for all the systems using the Debye–Callaway model.25–27 According to this model, kL is the sum over the contribution to lattice thermal conductivity from one longitudinal acoustic (kLA) and two transverse acoustic branches (kTA and kTA′). For the ith phonon branch (where i = LA, TA, or TA′), the contribution to lattice thermal conductivity (ki) is given by
| |  | (19) |
where
ħ is the Planck constant,
kB is the Boltzmann constant,
vi is the long wavelength velocity of the
ith mode, and
τi−1c,
τi−1N and
τi−1R are the scattering rates for the
ith mode related to the total, normal and dissipative scattering processes.
x in
eqn (19) is given as

where
T represents temperature and
ω the phonon frequency. Further, in
eqn (19),
ΘiD is the Debye temperature corresponding to the
ith mode. This
ΘiD is given by:
28–30| | 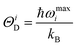 | (20) |
where
ωmaxi is the maximum phonon frequency for the
ith mode.
The τc, τN and τR in eqn (19) are related as:
For normal phonon scattering, the corresponding relaxation time for the longitudinal (
τLAN) and transverse acoustic

modes:
| |  | (22) |
| |  | (23) |
where
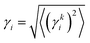
is the mode averaged Gruneissan parameter,
Ma is the average atomic mass per unit cell and
Va is the volume per atom.
In most crystalline solids, the dissipative scattering is primarily due to Umklapp processes and the corresponding relaxation time (τiU) for the ith mode is given by:
| |  | (24) |
Hence, for the parent HHs, for
ith mode, the total phonon scattering rate

depends on the scattering rates associated with the normal (N) and the Umklapp (U) processes and is given by:
| | 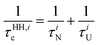 | (25) |
However, in the case of ZrHfCoNiSnSb HEA, significant mass fluctuation (MF) occurs at the Wyckoff position 4b (0.5, 0.5, 0.5), which can now be occupied either by Hf or Zr, the latter having a mass half of that of Hf. Further, the 4a (0, 0, 0) position, which is now occupied by either Sb or Sn will also exhibit mass fluctuations due to their different atomic masses. Hence, we expect that the propagating phonons will be scattered also by these mass defects in HEA caused by these mass fluctuations plays a crucial role in phonon scattering. Hence, to compute the scattering rates for dissipative processes in the HEA, we have also incorporated the effect of mass fluctuation scattering. Using Klemens
31 formalism, the relaxation time for mass fluctuation scattering (
τiM) is given by:
| |  | (26) |
where the disordered scattering parameter
ΓM is given by:
| |  | (27) |
where
cj represents the relative site degeneracy,
fj denotes the fractional occupation,
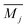
is the average mass at the site
j, and

is the average atomic mass of the compound. We note that these corrections have been successfully applied to double HHs previously.
29,32 Consequently, the total relaxation time for the
ith mode of ZrHfCoNiSnSb is given by:
| |  | (28) |
The values of the different parameters used to compute kL in eqn (19) are given in Table 2.
Table 2 Mode resolved Debye temperature (ΘiD), long wavelength phonon velocity (vi) and Gruneisen parameter (γi) for the parent systems and the HEA. The values given in square brackets are from (ref. 30)
| Property |
ZrNiSn |
HfCoSb |
HfNiSn |
ZrCoSb |
ZrHfCoNiSnSb |
|
Θ
LAD (K) |
217 [214] |
210 |
201 [196] |
238 |
153 |
|
Θ
TAD (K) |
170 [166] |
161 |
147 [145] |
185 |
146 |

|
186 [184] |
171 |
160 [160] |
200 |
148 |
|
v
LA (m s−1) |
5338 [5323] |
5115 |
4830 [4746] |
5746 |
5224 |
|
v
TA (m s−1) |
3080 [2852] |
2843 |
2540 [2508] |
3115 |
2499 |
|
v
TA′ (m s−1) |
3080 [3600] |
2843 |
2540 [3120] |
3115 |
2683 |
|
γ
LA
|
1.46 [1.69] |
1.62 |
1.53 [1.55] |
1.54 |
1.41 |
|
γ
TA
|
1.22 [1.30] |
1.36 |
1.28 [1.35] |
1.23 |
1.45 |
|
γ
TA′
|
1.27 [1.36] |
1.43 |
1.41 [1.38] |
1.25 |
1.58 |
|
γ
|
1.61 [1.71] |
1.64 |
1.59 [1.59] |
1.59 |
1.70 |
Fig. 7 shows the lattice thermal conductivity of the HHs and the HEA. Since the lattice thermal conductivity is primarily governed by acoustic phonon modes—while optical modes contribute minimally due to their low group velocities—the parameter reported in Table 2 is largely influenced by the acoustic modes. Consequently, as the Debye–Callaway model accounts only for acoustic contributions, the LO–TO splitting corrections have a negligible effect on the lattice thermal conductivity, as illustrated in Fig. S13 of the ESI.† We observe that at 300 K the kL of the HHs lie between 20.37 and 28.65 W m−1 K−1 with HfNiSn (ZrCoSb) having the lowest (highest) value. We note that our computed values of kL is in reasonably good agreement with those reported in the literature using the solutions of the semiclassical Boltzmann transport equations for phonons that are more computationally demanding but accurate.3,6,33 For all the systems, the lattice thermal conductivity is reduced with an increase in temperature. For the HEA, when we compute the lattice thermal conductivity by including only the Umklapp scattering, we obtain a value of 11.03 W m−1 K−1 at 300 K. We note that this is less than half of the values observed in the HHs. This drastic reduction in lattice thermal conductivity can be attributed to the different types of chemical bonding observed in the HEA lattice that resulted in enhanced anharmonicity. On incorporation of the scattering effects due to mass fluctuations, the lattice thermal conductivity is further reduced to 5.40 W m−1 K−1 at 300 K. Thus, our results suggest that the synergistic effect of the changes in bonding in the HEA lattice and the mass fluctuations can drastically reduce kL. At room temperature, the kL of the HEA is reduced by a factor of three compared to the parent HHs Hf/ZrNiSn, and by a factor of five compared to Zr/HfCoSb. Interestingly, in line with the findings reported by Anand et al.34 for double Heusler alloys, the HEA ZrHfCoNiSnSb exhibits lattice thermal conductivity values that are comparable to those of double Heusler compounds with the lowest KL. In fact, its lattice thermal conductivity is lower than that of most double Heusler systems discussed in the same reference.
 |
| | Fig. 7 Lattice thermal conductivity as a function of temperature. N, U and MF represent Normal, Umklapp and Mass fluctuation scattering processes. | |
3.3 Electronic properties
Fig. 8 shows the band structure of ZrHfCoNiSnSb, along with the contributions from the d-states of the transition metals and the p-states of the p-block elements. Those for the parent HHs are shown in Fig. S4 of the ESI.† In accordance with the literature report, we observe that all the HHs are semiconducting in nature, with HfCoSb having the largest band gap of 1.12 eV,6 followed by 1.05 eV for ZrCoSb,6 0.51 eV for ZrNiSn3 and 0.40 eV for HfNiSn.3 The conventional unit cell of these HHs have the conduction band minima (CBM) at the Γ point of the BZ. However, their valence band maxima (VBM) occurs at different points of the BZ. Similar to the CBM, the VBM of ZrNiSn and HfNiSn is at the Γ point of the BZ, making these two HHs as a direct band gap semiconductor. In contrast, ZrCoSb has VBM at the R point of the BZ making it an indirect band gap semiconductor. In the case of HfCoSb, there are two degenerate VBMs, namely at Γ and the R point of the BZ. Additionally, the VB and CB edges of Zr/HfNiSn are closer to the Fermi energy than those of Zr/HfCoSb. The band structure characteristics of the corresponding primitive unit cell, obtained using the unfolding technique,35 are presented in Section S13 of the ESI.†
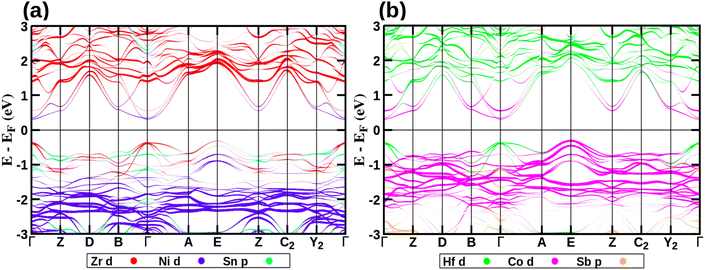 |
| | Fig. 8 Band structure of HEA showing contributions from (a) Zr-d (red), Ni-d (blue), and Sn-p (turquoise) orbitals (b) Hf-d (green), Co-d (pink), and Sb-p (orange) orbitals. | |
Similar to the HHs, the CBM of the HEA is at the Γ point of the BZ while the VBM is at E-point (Fig. 8). Since the lattice parameters of this monoclinic lattice are very close and the deviation of the γ from 90° is negligibly small, the E point of the BZ of this monoclinic lattice is the same as that of the R-point of the BZ of the cubic lattice. The HEA is an indirect semiconductor with a band gap of 0.61 eV, which is less than that of the Zr/HfCoSb and more than that of Zr/HfNiSn. Additionally, the maxima of the valence band at the Γ-point is only 60 meV below the VBM, suggesting that at high temperatures, p-type carriers belonging to this hole pocket will also contribute to the transport properties. We note that these features of the valence band are very similar to those observed in ZrCoSb (Fig. S4(e) of ESI†) and HfCoSb (Fig. S4(c) of ESI†). Furthermore, the conduction band of the HEA have additional electron pockets at the B and Z points of the BZ. These are about 280 and 250 meV higher in energy compared to the CBM. These high symmetry points of the BZ of the HEA are analogous to the X-point of the cubic BZ of the HHs. While the VBM at E-point have contributions from Co-d states, the hole pocket at the Γ point has a contribution from Zr and Hf-d states (Fig. 8 and Fig. S4(a) of ESI†). The Ni-d states lie deep inside the valence band. This is in contrast to that observed in Hf/ZrNiSn, where Ni-d orbitals contributed to hole pockets at the R-point of the cubic BZ. The CBM at Γ and the electron pockets at B and Z-points in the BZ of the HEA have contributions from the d-orbitals of all the transition metal elements.
3.4 Conductivity and density of states effective masses
Effective masses (m*) of charge carriers, which is a key component of transport properties like conductivity, mobility, Seebeck coefficient, etc., had been computed at the different valence and conduction band extrema. Within the parabolic band approximation m* is given by:| |  | (29) |
Near the extrema, the isosurfaces of energy are ellipsoids, and hence the effective mass is different along the longitudinal or transverse directions. The conductivity effective mass, which affects relaxation time and electrical conductivity, 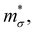 is given by the harmonic mean of the longitudinal effective mass
is given by the harmonic mean of the longitudinal effective mass  and the two transverse effective masses
and the two transverse effective masses  as:
as:| | 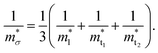 | (30) |
Similarly, the density of states (DOS) effective mass  is given by the geometric mean of the three masses weighted by the
is given by the geometric mean of the three masses weighted by the  power of the valley degeneracy (Nv) as:
power of the valley degeneracy (Nv) as:| |  | (31) |
The conductivity and DOS effective masses at the different extrema of the BZ are listed in Tables S1–S6 of ESI,† for the normal HHs and the HEA.
3.5 Carrier relaxation times
The relaxation times (τ) of the charge carriers in these materials were calculated using the deformation potential theory,21 which takes into account of their scattering by the acoustic phonons only. The relaxation time of carriers in a band b having dos effective mass  is given by:36
is given by:36| |  | (32) |
In the above equation, the elastic constant C and deformation potential Ξ are computed as:| |  | (33) |
Here E is the total energy of the system obtained from DFT calculation, a0 is the optimized lattice constant, Δa = a − a0 is the lattice distortion from its equilibrium value, V0 is the equilibrium volume of the unit cell, and Eedge is the energy of VB or CB extrema. The carrier mobility corresponding to this band μb is expressed as:| |  | (34) |
When there are many bands that are either degenerate or near degenerate to valence band (VB) or conduction band (CB), average carrier mobility μav and average conductivity effective mass 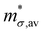 are given by:37
are given by:37| |  | (35) |
In the above equations, nb is the number of charge carriers in the valley of the band b and 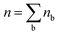 is the total number of the charge carriers. The fraction of the charge carriers carried by the valley of the band b and VB/CB is given by
is the total number of the charge carriers. The fraction of the charge carriers carried by the valley of the band b and VB/CB is given by| |  | (36) |
where ΔE is the difference in energy between the valley extrema and VBM/CBM. Finally, the average relaxation time, which considers the contributions from all the valley extrema is given by:37| |  | (37) |
The average relaxation time (τav) was calculated by including all electronic bands located within 150 meV above CBM (for electrons) and 150 meV below the VBM (for holes). The quantities required to compute τav using the above equations and the values of τav and μav for electrons and holes at 300 K for all the compounds are given in Tables 3 and 4, respectively. It is observed that all the parent HHs, except HfCoSb, the average conductivity effective mass of electrons is greater than that of holes. In contrast, for the HEA HHs  of electrons are smaller than that of holes. Further, we observe that the magnitude of the deformation potential of electrons and holes, which is a measure of the coupling between the charge carriers and acoustic phonons are similar. However, we find that |Ξ| of electrons for all the compounds are larger than that observed in holes. This suggests that in these materials, the electron–acoustic phonon coupling is larger than that between holes and acoustic phonons.
of electrons are smaller than that of holes. Further, we observe that the magnitude of the deformation potential of electrons and holes, which is a measure of the coupling between the charge carriers and acoustic phonons are similar. However, we find that |Ξ| of electrons for all the compounds are larger than that observed in holes. This suggests that in these materials, the electron–acoustic phonon coupling is larger than that between holes and acoustic phonons.
Table 3 Average conductivity effective mass  , deformation potentials (|Ξ|), elastic constants (C), average mobility (μav) and average relaxation time (τav) for electrons in the different materials. The values of μav and τav reported in the table had been computed at 300 K
, deformation potentials (|Ξ|), elastic constants (C), average mobility (μav) and average relaxation time (τav) for electrons in the different materials. The values of μav and τav reported in the table had been computed at 300 K
| Property |
ZrNiSn |
HfCoSb |
HfNiSn |
ZrCoSb |
ZrHfCoNiSnSb |

|
2.13 |
4.37 |
2.10 |
3.46 |
0.92 |
| |Ξ| (eV) |
16.12 |
15.51 |
16.20 |
15.42 |
15.75 |
|
C (GPa) |
233 |
275 |
242 |
264 |
247 |
|
μ
av (cm2 V−1 s−1) |
42.8 |
6.65 |
48.17 |
7.47 |
60.02 |
|
τ
av (fs) |
51.73 |
16.52 |
57.61 |
14.72 |
31.45 |
Table 4 Average conductivity effective mass  , deformation potentials (|Ξ|), elastic constants (C), average mobility (μav) and average relaxation time (τav) for holes in the different materials. The values of μav and τav reported in the table had been computed at 300 K
, deformation potentials (|Ξ|), elastic constants (C), average mobility (μav) and average relaxation time (τav) for holes in the different materials. The values of μav and τav reported in the table had been computed at 300 K
| Properties |
ZrNiSn |
HfCoSb |
HfNiSn |
ZrCoSb |
ZrHfCoNiSnSb |

|
0.75 |
5.74 |
0.61 |
1.54 |
1.27 |
| |Ξ| (eV) |
15.51 |
14.82 |
15.70 |
14.84 |
15.17 |
|
C (GPa) |
233 |
275 |
242 |
264 |
247 |
|
μ
av (cm2 V−1 s−1) |
153.3 |
8.33 |
241.68 |
3.91 |
5.30 |
|
τ
av (fs) |
65.23 |
27.20 |
83.61 |
3.41 |
3.83 |
Fig. 9 shows the variation of τav as a function of temperature. We find that τav of electrons in the HEA is smaller (larger) than that in ZrNiSn and HfNiSn (ZrCoSb and HfCoSb). For the holes, we find that while τav of the HEA is larger than that observed in ZrCoSb, it is smaller than that observed in the other parent HHs, namely ZrNiSn, HfCoSb and HfNiSn.
 |
| | Fig. 9 Average relaxation time (τav) of (a) electrons and (b) holes in the parent HHs and the HEA. | |
3.6 Electronic transport calculation
Full electronic transport calculations were performed by combining the Boltzmann transport equation with a constant relaxation time approximation and a relaxation time derived from the deformation potential theory. Fig. 10(a)–(d) illustrates the variation in the electronic transport properties of ZrHfCoNiSnSb with carrier concentration, ranging from 1019 to 1022 cm−3, at different temperatures. The Seebeck coefficient exhibits an initial increase followed by a decrease at elevated temperatures as the carrier concentration increases. With increasing temperature, the peak position shifts towards higher carrier concentrations while the peak magnitude decreases. At 900 K, the maximum Seebeck coefficient reaches 372 μV K−1 for n-type carriers and 413 μV K−1 for p-type carriers, occurring at carrier concentrations of 3.19 × 1019 cm−3 and 5.29 × 1019 cm−3, respectively. These concentrations correspond to chemical potentials of 0.16 eV below the conduction band minimum (CBM) for n-type carriers and 0.22 eV above the valence band maximum (VBM) for p-type carriers.
 |
| | Fig. 10 (a) Seebeck coefficient, (b) electrical conductivity, (c) electronic thermal conductivity, (d) power factor and (e) figure of merit as a function of carrier concentration at different temperatures for ZrHfCoNiSnSb. | |
Fig. 10(b) presents the electrical conductivity (σ) as a function of carrier concentration at different temperatures for both n-type and p-type carriers. The plot reveals that σ for n-type carriers is higher than that for p-type carriers. This is evident from the fact that the average effective conductive mass of electrons is smaller than that of holes, as indicated in Tables 3 and 4. The electrical conductivity for both types of carriers remains low up to a carrier concentration of approximately 1020 cm−3. This behavior arises because the chemical potential remains within the bandgap in this carrier concentration range, leading to a negligible value of the projected conductivity tensor σij(ε), as defined by eqn (2), at the peak of the selection function ϕ = −∂f0(T;μ)/∂ε. Consequently, only the tail of the selection function contributes to the electrical conductivity, resulting in extremely low values of σ. Beyond a carrier concentration of approximately 1020 cm−3, the electrical conductivity increases with increasing carrier concentration. This suggests that the chemical potential has shifted into the conduction or valence bands, where σij(ε) makes a significant contribution to the overall electrical conductivity σij(T;μ) at the peak of the selection function. According to the Wiedemann–Franz law, the electronic contribution to the thermal conductivity (ke) follows a similar trend as σ, as depicted in Fig. 10(c).
The performance of a thermoelectric device is characterized by the power factor (S2σ), which directly influences its efficiency. As shown in Fig. 10(a), the Seebeck coefficient generally decreases with increasing carrier concentration across most of the concentration range. Meanwhile, Fig. 10(b) indicates that electrical conductivity increases consistently throughout the entire carrier concentration range. Consequently, the power factor exhibits an optimal value, as observed in Fig. 10(d). With increasing temperature, the peak position of the power factor shifts toward higher carrier concentrations. From Fig. 10(d), it is evident that for both n-type and p-type carriers, the peak power factor initially increases and then decreases with rising temperature. For the n-type case, ZrHfCoNiSnSb achieves a maximum power factor of 3.32 (3.88) mW K−2 m−1 at a carrier concentration of 1.26 × 1021 (1.54 × 1021) cm−3 at 300 (900) K, for the chemical potential is located 0.24 (0.23) eV above the conduction band minimum (CBM). In contrast, for the p-type case, the maximum power factor reaches 1.16 (1.06) mW K−2 m−1 at a carrier concentration of 1.37 × 1021 (2.08 × 1021) cm−3 at 300 (900) K, corresponding to a chemical potential of 0.13 (0.09) eV below the valence band maximum (VBM). For comparison, the transport properties of different systems were plotted against the carrier concentration at 900 K in the ESI.† As shown in Fig. S7(a) (ESI†), which depicts electrical conductivity, HfNiSn exhibits the highest electrical conductivity across all carrier concentrations for the n-type case, followed by ZrNiSn, ZrHfCoNiSnSb, HfCoSb, and ZrCoSb. Similarly, for the p-type case, HfNiSn again shows the highest electrical conductivity, followed by ZrNiSn, HfCoSb, ZrHfCoNiSnSb, and ZrCoSb. Fig. S8(a) (ESI†) illustrates the variation of the Seebeck coefficient as a function of carrier concentration at 900 K for different structures. For the n-type case, ZrCoSb exhibits the highest Seebeck coefficient, followed by HfCoSb, ZrHfCoNiSnSb, ZrNiSn, and HfNiSn. In the p-type case, HfCoSb has the highest Seebeck coefficient, followed by ZrCoSb, ZrHfCoNiSnSb, ZrNiSn, and HfNiSn. These trends in electrical conductivity and the Seebeck coefficient are explained using the projected conductivity tensor σii(ε), the selection function ϕ = −∂f0(T;μ)/∂ε, and the projected Seebeck tensor αii(ε) (as defined in eqn (S1) of the ESI†). Fig. S9(a) in the ESI,† presents the variation of the electronic component of thermal conductivity as a function of carrier concentration for different structures at 900 K. In accordance with the Wiedemann–Franz law, this electronic contribution to thermal conductivity follows a similar trend to that of σ, with the structural hierarchy remaining consistent. Fig. S9(b) (ESI†) illustrates the variation of the power factor as a function of carrier concentration for different structures. As observed in the plot, HfNiSn and ZrNiSn exhibit the highest power factor for the n-type case, primarily due to their high electrical conductivity, followed by ZrHfCoNiSnSb, HfCoSb, and ZrCoSb. Similarly, for the p-type case, HfNiSn and ZrNiSn again demonstrate the highest power factor, followed by HfCoSb. However, for the p-type case, ZrHfCoNiSnSb and ZrCoSb show a power factor approximately an order of magnitude lower than the other systems, predominantly due to their lower electrical conductivity.
3.7 Figure of merit
The electronic transport properties, in combination with the lattice thermal conductivity, were used to compute the figure of merit (ZT) as a function of carrier concentration for different temperatures, as shown in Fig. 10(e). With increasing temperature, the ZT peak shifts toward higher carrier concentrations for both n-type and p-type carriers. At all temperatures, the ZT value for n-type carriers remains higher than that for p-type carriers. A comparison of ZT as a function of carrier concentration at 900 K among different structures is provided in the ESI.† As depicted in Fig. S9(c) (ESI†), for n-type carriers, ZrHfCoNiSnSb exhibits the highest ZT value up to a carrier concentration of 4 × 1021 cm−3, followed by ZrNiSn and HfNiSn, which display nearly identical ZT values across all carrier concentrations. Despite their high Seebeck coefficients, HfCoSb and ZrCoSb exhibit relatively low ZT values for n-type carriers due to their lower electrical conductivity and higher lattice thermal conductivity, as seen in Fig. S9(c) of ESI.† For p-type carriers, up to a concentration of 1 × 1021 cm−3, ZrNiSn and HfNiSn attain the highest and nearly identical ZT values, followed by HfCoSb. However, ZrHfCoNiSnSb and ZrCoSb display comparatively lower ZT values across all carrier concentrations, primarily due to their lower electrical conductivity. Fig. 11 presents a comparison of the peak ZT values for all structures at different temperatures. As observed, for n-type carriers, ZrHfCoNiSnSb consistently exhibits the highest peak ZT value across all temperatures, followed by HfNiSn and ZrNiSn. In contrast, HfCoSb and ZrCoSb show comparatively lower peak ZT values due to their lower electrical conductivity and higher lattice thermal conductivity. For p-type carriers, HfNiSn attains the highest peak ZT value, followed by HfCoSb and ZrNiSn, whereas ZrHfCoNiSnSb and ZrCoSb maintain lower peak ZT values across all temperatures due to their lower electrical conductivity. The peak ZT value of ZrHfCoNiSnSb for n-type carriers reaches 1.00 at 1100 K, which is 27, 104, 32, and 170% higher than that of ZrNiSn, HfCoSb, HfNiSn, and ZrCoSb, respectively. The optimized carrier concentration corresponding to this maximum ZT value at 300 K and 900 K is provided in Tables S7 and S8 in the ESI.†
 |
| | Fig. 11 (a) Peak value of figure of merit for electrons, (b) peak value of figure of merit for holes. | |
4 Conclusions
ZrHfCoNiSnSb exhibits greater stability at high temperatures compared to its parent compounds, largely due to the entropic contribution to the Gibbs free energy at elevated temperatures. The absence of imaginary modes in the phonon dispersion curve also confirms its dynamical stability. Additionally, based on both mode-resolved and average Gruneisen parameters, it is suggested that ZrHfCoNiSnSb possesses stronger anharmonicity and higher lattice thermal resistance than its parent compounds. The Seebeck coefficient and the other electronic transport properties of ZrHfCoNiSnSb exhibit comparability to the half-Heusler compounds from which it is composed (i.e., ZrNiSn/HfNiSn and HfCoSb/ZrCoSb). Notably, the lattice thermal conductivity of ZrHfCoNiSnSb is approximately one-third of ZrNiSn/HfNiSn and one-fifth of HfCoSb/ZrCoSb at room temperature, and it has significantly reduced lattice thermal conductivity compared to the parent half-Heusler compounds across all temperatures. For the case when the charge carriers are electrons, at 1100 K, the ZT value of ZrHfCoNiSnSb is 1.00, surpassing the values of all of the parent compounds.
Conflicts of interest
There are no conflicts to declare.
Data availability
The authors declare that the relevant data supporting the findings of this study are available within the article and the ESI.† The codes used in this work and other data will be made available from the author upon reasonable request.
Acknowledgements
The author gratefully acknowledges Dr Prasenjit Ghosh for his valuable guidance in structuring the results and the manuscript, as well as for providing access to computational resources. The author also thanks the National Supercomputing Mission (NSM) for providing computing facilities on the “Param Brahma” supercomputer at IISER Pune. The author further acknowledges Dr Gautam Sharma from Khalifa University for many insightful and fruitful discussions and IISER Pune for fellowship.
Notes and references
- G. J. Snyder and E. S. Toberer, Nat. Mater., 2008, 7, 105–114 CrossRef CAS PubMed.
- W. G. Zeier, J. Schmitt, G. Hautier, U. Aydemir, Z. M. Gibbs, C. Felser and G. J. Snyder, Nat. Rev. Mater., 2016, 1, 1–10 Search PubMed.
- A. N. Gandi and U. Schwingenschlögl, Phys. Chem. Chem. Phys., 2016, 18, 14017–14022 RSC.
- H. Muta, T. Kanemitsu, K. Kurosaki and S. Yamanaka, J. Alloys Compd., 2009, 469, 50–55 CrossRef CAS.
- D. Zou, S. Xie, Y. Liu, J. Lin and J. Li, J. Appl. Phys., 2013, 113, 8888–8896 Search PubMed.
- A. N. Gandi and U. Schwingenschlögl, Phys. Status Solidi B, 2017, 254, 1700419 CrossRef.
-
T. Sekimoto, K. Kurosaki, H. Muta and S. Yamasaka, ICT 2005. 24th International Conference on Thermoelectrics, 2005, 2005, pp. 347–350.
- R. Liu, H. Chen, K. Zhao, Y. Qin, B. Jiang, T. Zhang, G. Sha, X. Shi, C. Uher and W. Zhang,
et al.
, Adv. Mater., 2017, 29, 1702712 CrossRef PubMed.
- R.-Z. Zhang, F. Gucci, H. Zhu, K. Chen and M. J. Reece, Inorg. Chem., 2018, 57, 13027–13033 CrossRef CAS PubMed.
- S. Jiang, T. Hu, J. Gild, N. Zhou, J. Nie, M. Qin, T. Harrington, K. Vecchio and J. Luo, Scr. Mater., 2018, 142, 116–120 CrossRef CAS.
- C. M. Rost, E. Sachet, T. Borman, A. Moballegh, E. C. Dickey, D. Hou, J. L. Jones, S. Curtarolo and J.-P. Maria, Nat. Commun., 2015, 6, 8485 CrossRef CAS PubMed.
- R.-Z. Zhang and M. J. Reece, J. Mater. Chem. A, 2019, 7, 22148–22162 RSC.
- K. Chen, R. Zhang, J.-W. G. Bos and M. J. Reece, J. Alloys Compd., 2022, 892, 162045 CrossRef CAS.
- C. G. Adamo, A. Srivastava, S. S. Legese, Y. Kawamura, A. T. Serbesa, S. Punathil Raman, F. E. Olu, C. S. Tiwary, A. K. Singh and K. Chattopadhyay, Energy Technol., 2024, 12, 2301119 CrossRef CAS.
- A. Karati, M. Nagini, S. Ghosh, R. Shabadi, K. Pradeep, R. C. Mallik, B. Murty and U. Varadaraju, Sci. Rep., 2019, 9, 5331 CrossRef PubMed.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni and I. Dabo,
et al.
, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. B. Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. D. Corso, S. de Gironcoli, P. Delugas, R. A. DiStasio, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H.-Y. Ko, A. Kokalj, E. Küçükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H.-V. Nguyen, A. O. de-la Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.: Condens. Matter, 2017, 29, 465901 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- S. Baroni, S. De Gironcoli, A. Dal Corso and P. Giannozzi, Rev. Mod. Phys., 2001, 73, 515 CrossRef CAS.
- G. K. Madsen, J. Carrete and M. J. Verstraete, Comput. Phys. Commun., 2018, 231, 140–145 CrossRef CAS.
- J. Bardeen and W. Shockley, Phys. Rev., 1950, 80, 72 CrossRef CAS.
- A. Van de Walle, P. Tiwary, M. De Jong, D. Olmsted, M. Asta, A. Dick, D. Shin, Y. Wang, L.-Q. Chen and Z.-K. Liu, CALPHAD, 2013, 42, 13–18 CrossRef CAS.
- F. Aguilera-Granja, R. H. Aguilera-del Toro and J. L. Morán-López, Mater. Res. Express, 2019, 6, 106118 CrossRef CAS.
- A. Giri, B. F. Donovan and P. E. Hopkins, Phys. Rev. Mater., 2018, 2, 056002 CrossRef CAS.
- Y. Zhang, E. Skoug, J. Cain, V. Ozolinš, D. Morelli and C. Wolverton, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 054306 CrossRef.
- D. Morelli, J. Heremans and G. Slack, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 195304 CrossRef.
- M. Asen-Palmer, K. Bartkowski, E. Gmelin, M. Cardona, A. Zhernov, A. Inyushkin, A. Taldenkov, V. Ozhogin, K. M. Itoh and E. Haller, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 9431 CrossRef CAS.
- Y. Zhang, J. Materiomics, 2016, 2, 237–247 CrossRef.
- T. Fan and A. R. Oganov, Comput. Phys. Commun., 2020, 251, 107074 CrossRef CAS.
-
B. Sahni and A. Alam, arXiv, 2023, preprint, arXiv:2301.00598 DOI:10.48550/arXiv.2301.00598.
- P. Klemens, Phys. Rev., 1960, 119, 507 CrossRef CAS.
- A. Petersen, S. Bhattacharya, T. Tritt and S. Poon, J. Appl. Phys., 2015, 117, 035706 CrossRef.
- J. Carrete, W. Li, N. Mingo, S. Wang and S. Curtarolo, Phys. Rev. X, 2014, 4, 011019 CAS.
- S. Anand, M. Wood, Y. Xia, C. Wolverton and G. J. Snyder, Joule, 2019, 3, 1226–1238 CrossRef CAS.
- V. Popescu and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 085201 CrossRef.
- C. Zhang, N. Yan, C. Zhao and B. Wei, J. Appl. Phys., 2025, 137, 1234 Search PubMed.
- J. Liu, Q.-Y. Jiang, S.-D. Zhang and H. Zhang, Phys. Lett. A, 2019, 383, 125990 CrossRef CAS.
|
| This journal is © the Owner Societies 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article

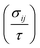 was calculated as
was calculated as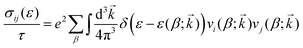
 is the group velocity of the electron occupying the βth band at the kth k-point of the BZ and ε(β;
is the group velocity of the electron occupying the βth band at the kth k-point of the BZ and ε(β;![[k with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006b_20d1.gif) ) is the energy eigenvalue corresponding to that electronic state. The (ij)th component of electrical conductivity per unit relaxation time
) is the energy eigenvalue corresponding to that electronic state. The (ij)th component of electrical conductivity per unit relaxation time  Seebeck coefficient (αij(T;μ)) and electronic thermal conductivity per unit relaxation time
Seebeck coefficient (αij(T;μ)) and electronic thermal conductivity per unit relaxation time 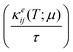 were calculated from eqn (2) as:
were calculated from eqn (2) as:

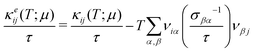
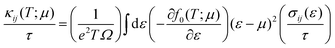


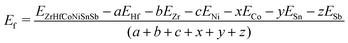








 where T represents temperature and ω the phonon frequency. Further, in eqn (19), ΘiD is the Debye temperature corresponding to the ith mode. This ΘiD is given by:28–30
where T represents temperature and ω the phonon frequency. Further, in eqn (19), ΘiD is the Debye temperature corresponding to the ith mode. This ΘiD is given by:28–30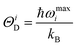
 modes:
modes:

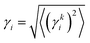 is the mode averaged Gruneissan parameter, Ma is the average atomic mass per unit cell and Va is the volume per atom.
is the mode averaged Gruneissan parameter, Ma is the average atomic mass per unit cell and Va is the volume per atom.

 depends on the scattering rates associated with the normal (N) and the Umklapp (U) processes and is given by:
depends on the scattering rates associated with the normal (N) and the Umklapp (U) processes and is given by: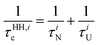


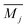 is the average mass at the site j, and
is the average mass at the site j, and  is the average atomic mass of the compound. We note that these corrections have been successfully applied to double HHs previously.29,32 Consequently, the total relaxation time for the ith mode of ZrHfCoNiSnSb is given by:
is the average atomic mass of the compound. We note that these corrections have been successfully applied to double HHs previously.29,32 Consequently, the total relaxation time for the ith mode of ZrHfCoNiSnSb is given by:



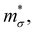 is given by the harmonic mean of the longitudinal effective mass
is given by the harmonic mean of the longitudinal effective mass  and the two transverse effective masses
and the two transverse effective masses  as:
as: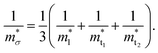
 is given by the geometric mean of the three masses weighted by the
is given by the geometric mean of the three masses weighted by the  power of the valley degeneracy (Nv) as:
power of the valley degeneracy (Nv) as:
 is given by:36
is given by:36


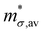 are given by:37
are given by:37
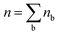 is the total number of the charge carriers. The fraction of the charge carriers carried by the valley of the band b and VB/CB is given by
is the total number of the charge carriers. The fraction of the charge carriers carried by the valley of the band b and VB/CB is given by

 of electrons are smaller than that of holes. Further, we observe that the magnitude of the deformation potential of electrons and holes, which is a measure of the coupling between the charge carriers and acoustic phonons are similar. However, we find that |Ξ| of electrons for all the compounds are larger than that observed in holes. This suggests that in these materials, the electron–acoustic phonon coupling is larger than that between holes and acoustic phonons.
of electrons are smaller than that of holes. Further, we observe that the magnitude of the deformation potential of electrons and holes, which is a measure of the coupling between the charge carriers and acoustic phonons are similar. However, we find that |Ξ| of electrons for all the compounds are larger than that observed in holes. This suggests that in these materials, the electron–acoustic phonon coupling is larger than that between holes and acoustic phonons.
 , deformation potentials (|Ξ|), elastic constants (C), average mobility (μav) and average relaxation time (τav) for electrons in the different materials. The values of μav and τav reported in the table had been computed at 300 K
, deformation potentials (|Ξ|), elastic constants (C), average mobility (μav) and average relaxation time (τav) for electrons in the different materials. The values of μav and τav reported in the table had been computed at 300 K
 , deformation potentials (|Ξ|), elastic constants (C), average mobility (μav) and average relaxation time (τav) for holes in the different materials. The values of μav and τav reported in the table had been computed at 300 K
, deformation potentials (|Ξ|), elastic constants (C), average mobility (μav) and average relaxation time (τav) for holes in the different materials. The values of μav and τav reported in the table had been computed at 300 K









