Nuclear quantum effects of metal surface-mediated C–H activation

Abstract

The nuclear quantum effects of surface-mediated C–H activation of surface CH₃ are considered for the pristine Pt(111) and Au(111) surfaces at 300 K. The kinetic barriers without nuclear quantum effects are calculated using both static density functional theory calculations and ab initio molecular dynamics. Static calculations are performed using the harmonic approximation while the free energy pathway is calculated using enhanced sampling molecular dynamics. Machine learning potentials are trained using generated datasets and validated against the ab initio molecular dynamics generated free energy pathways. The machine learning potentials are used to perform centroid molecular dynamics to consider the nuclear quantum effects of C–H activation. Nuclear quantum effects are found to have a very significant effect on the free energy pathway, with reduced importance at higher temperatures and in the CD₃ case.

---

Introduction

C–H bonds are ubiquitous across various branches of chemistry, including organic, inorganic, biochemistry, astrochemistry, and pharmaceutical chemistry.^1–4 Due to their non-polar nature, C–H bonds are often chemically inert,⁵ making them less reactive than other functional groups, such as C–O, C–C, or C–B bonds, which hold greater chemical and economic value.⁶ Ideally, C–H bonds would be functionalized into these more chemically active C–X bonds,⁵ or activated in processes such as dehydrogenation, which are crucial for applications like olefin production, combustion, and hydrogen storage.^7–9 Understanding C–H bond activation is essential for improving these processes.

C–H activation can proceed via several mechanisms, including oxidative addition, metathesis, or hydrogen atom transfer.¹⁰ For heterogeneous reactions on metal surfaces, surface-mediated activation is the dominant pathway, where the C–H bond breaks to form H–M and C–M surface bound species. The kinetics and thermodynamics of this elementary step govern the reaction rate, pathways, selectivity, and potential catalyst deactivation in any process involving C–H activation. Accurately modelling this step is therefore crucial for predicting these properties, requiring careful approaches to capture all factors that influence the reaction energetics.

Ab initio methods offer atomic-level insight into chemical processes on the femtosecond timescale.¹¹ Density functional theory (DFT) has been widely applied to condensed matter problems and is particularly useful in modelling heterogeneous catalytic systems. It has demonstrated its ability to predict catalyst reactivity, elucidate reaction mechanisms, and guide catalyst development in the condensed phase.¹² To reduce the computational cost, static calculations are often performed to predict initial, transition, and final states of elementary reaction steps. Free energy corrections are then applied to account for finite-temperature effects.¹³ Typically, surface species' free energy changes are estimated within the harmonic approximation, assuming limited movement on the surface, where only bond vibrations and molecular oscillations around the adsorption site contribute to the partition function. Whilst more accurate free energy profiles can be obtained through molecular dynamics (MD) methods, such as free energy perturbation, metadynamics, and umbrella sampling, these approaches are computationally demanding and challenging to implement with ab initio methods.¹⁴

Another challenge in predicting the kinetics of C–H bond activation is the presence of hydrogen atoms. Due to the light mass of hydrogen, nuclear quantum effects (NQEs) can play a significant role.^15–18 Experimentally, this is observed through kinetic isotope effects.¹⁹ Theoretically, NQEs have been shown to influence the dynamics of chemical processes such as hydrogen diffusion and dissociation on metal surfaces, proton transfer, and water splitting.^20–22

Nuclear quantum effects can be incorporated into atomistic simulations using the path integral formulation, where each atom is replicated into a “ring polymer”, with neighboring replicas connected by harmonic springs.^23,24 These extended systems are then evolved over time using classical MD, providing a fully quantum mechanical description of the system's properties. The number of replicas (or beads) required to accurately capture the quantum nature depends on both the process under study and the temperature. Typically, systems with stronger NQEs require more beads, thereby increasing the computational cost. This makes simulating condensed matter systems with NQEs particularly resource-intensive compared to classical simulations. Centroid molecular dynamics, like all path integral calculations, captures quantum mechanical information through the mapping of quantum nuclei onto a ring-polymer, which is evolved classically through time with the additional influence from the neighbouring replicas (beads) of the system. Centroid molecular dynamics uses the centroid (the average position of the polymer for each nucleus) as an approximation to propagate the dynamics of the system.

While ab initio methods are powerful tools to understand chemical systems, the computational cost limits the amount of sampling that is feasible. Machine learning interatomic potentials (MLIPs) can achieve chemical accuracy comparable to the ab initio methods used to train them,²⁵ while offering significantly faster computational performance due to their favourable scaling with system size. MLIPs have been successfully applied to catalytic systems, including hydrogen coupling, CO₂ reduction, and CO oxidation.^26–28 This makes MLIPs a promising approach for investigating NQEs, where ab initio methods are prohibitively expensive.

In this work, we explore the role of NQEs in C–H activation, focusing on the conversion of CH₃ to CH₂ on Pt(111) and Au(111) surfaces. Both the reactant and the products strongly interact with the metal surfaces, removing desorption as a reaction pathway. This system serves as an ideal model due to the degeneracy of the three hydrogen atoms and the ease of experimentally generating surface methyl groups from CH₃I.²⁹ Pt is selected for its higher reactivity in C–H activation, while Au is chosen for its lower reactivity. The (111) surface is chosen for both metals, as it is the most stable and prevalent facet.³⁰ Free energy profiles at 300 K are obtained using density functional theory (DFT) via static harmonic calculations and umbrella sampling combined with ab initio molecular dynamics (AIMD). The resulting AIMD trajectories are used to train equivariant MLIPs, which are validated by comparing the free energy profiles generated by the MLIPs with those from the reference method. We then perform biased centroid molecular dynamics using the MLIPs to assess the NQEs in the reaction. Additionally, we examine the systems at 400 K and where hydrogen is replaced by deuterium.

Computational methods

Density functional theory (DFT) calculations were performed with the Perdew–Burke–Ernzerhof (PBE)³¹ functional, as implemented in the Vienna ab initio simulation package (VASP).^32–34 The core-valence electron interactions were treated using the projector-augmented wave (PAW) method.^35,36 Dispersion forces were included using the D3 (with Becke–Johnson damping) vdW correction.³⁷ For the metal surfaces, a plane-wave cutoff energy of 400 eV was used. The Brillouin zone was sampled with a 2 × 2 × 1 k-point mesh using the Monkhorst–Pack scheme.³⁸ All calculations employed a p(3 × 4) orthogonal slab for the (111) FCC surfaces with a vacuum layer of 18 Å between slabs to prevent interactions between periodic images. The positions of atoms in the bottom two layers of the four layer slab were fixed during the calculations.

For static calculations, the structures were optimized until the forces on all atoms were less than 0.05 eV Å⁻¹. Transition states were identified using the climbing image-nudged elastic band (CI-NEB) method and verified by confirming the presence of a single imaginary vibrational frequency.³⁹ For static free energy corrections, the adsorbed surface species were assumed to have restricted translational and rotational entropy, with only vibrational entropy contributions considered in the harmonic approximation using the atomic simulation environment package.^40,41

All MD simulations were performed in the NVT ensemble with the Nosé–Hoover thermostat.⁴² A time step of 1 fs was used for DFT-based and validation MLIP simulations. In all other MD simulations, a smaller time step of 0.25 fs was employed to accurately capture the dynamics in the centroid molecular dynamics (CMD) calculations, which were performed in LAMMPS.^43,44 Unless stated otherwise, CMD simulations utilized 8 beads, with which the potential of mean force is converged. The free energy pathway for C–H activation of surface methyl groups was determined using umbrella sampling. A series of Gaussian bias constraints were applied to sample the reaction coordinate. The free energy profiles were derived from the simulations using the weighted histogram analysis method (WHAM), where all beads are integrated over for the CMD calculations.⁴⁵ The chosen collective variable for this process was the C–H bond distance, with bias windows spaced at most 0.1 Å apart. Each window was sampled for a minimum of 10 ps during the DFT calculations and the comparison made with ground truth MLIP results. For the MLIP calculations, each window was sampled for at least 100 ps.

To generate a dataset for MLIP training, initial configurations were selected from the biased DFT molecular dynamics calculations. A total of 2500 snapshots were chosen for both the Pt and Au surfaces. Gaussian smearing, with a standard deviation of 0.3 Å, was then applied to the relaxed atomic positions of these snapshots to enhance sampling beyond the Boltzmann distribution. Additional snapshots were also included around the transition state structure, where sampling was limited. Single-point energies were calculated using DFT for these initial configurations on both Pt(111) and Au(111). Snapshots with force components exceeding 15.0 eV Å⁻¹, due to close contacts from the Gaussian smearing on atomic positions, were excluded from the dataset. As a result, 6325 structures remained in the Au dataset, whilst the Pt dataset contained 6096 structures for training.

The MLIPs were trained using the Allegro package⁴⁶ and implemented within LAMMPS.⁴⁷ The neural network is trained on the local atomic environments that are input as irreducible representations of the O(3) symmetry group. The atomic environments were defined with a cutoff of 4.5 Å and 8 Bessel functions with a polynomial envelope function of p = 5. 16 features of even and odd parity were included, with a maximum rotation order truncation of l_max = 2. The network architecture comprised two interaction layers, with the two-body latent MLIP containing 2 hidden layers of 64 nodes each, while the latent MLIP had 4 hidden layers, also with 64 nodes per layer. The final edge energy layer of the latent MLIP consisted of 64 nodes, resulting in a total network of 69 312 weights. For training, 95% of the datasets were used for training (6009 for Au and 5791 for Pt), with the remaining 5% were reserved for validation (316 for Au and 305 for Pt). A batch size of 1 was used, and an initial learning rate of 0.001 was set, using a cost function ratio of 1 : 1 for force elements and total energies.

Results and discussion

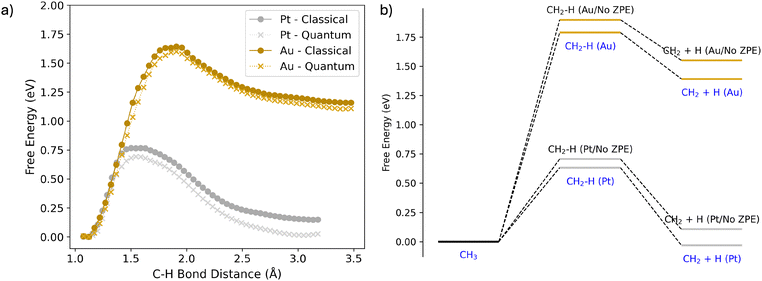
Umbrella sampling is performed to investigate the Helmholtz free energy of C–H dissociation (Fig. 1) and to provide a ground truth for the development of the MLIP. The free energy surface is standardised for both metals, where the CH₃ initial state is set as the reference. On first inspection, both reactions are endergonic, with a ΔF of 0.08 eV for Pt(111) and 1.18 eV for Au(111). Additionally, we find that Pt(111) exhibits a smaller activation barrier of 0.72 eV compared to 1.62 eV for Au(111). The location of the transition state also occurs at smaller distances for the Pt(111) (1.54 Å) surface than for Au(111) (1.91 Å). These findings show that Pt(111) is more reactive than Au(111) for C–H activation, due to the smaller activation barrier. Other computational studies have found the C–H activation of CH₄ to be much lower for Pt(111) over Au(111).^10,48 These results also correlate to experimental findings for methane oxidation, where Pt is a good catalyst compared to Au, noted by our result where C–H activation occurs more readily on platinum, with dehydrogenation of the alkane being both thermodynamically and kinetically more favoured.⁴⁹ Our results suggest that CH₃ can be stabilised on the Au(111) surface while it would be activated on Pt(111). We would expect that CH3 would also be stable on Au(111), as is observed for single-atom alloys.²⁹

Fig. 1 Free energy pathway of C–H activation for surface methyl to surface methylene and hydrogen for Pt(111) (grey) and Au(111) (gold). The free energy landscape is derived from umbrella sampling where the collective variable is a specific C–H bond length. The surface methyl state is standardised to 0 eV. The free energy pathway is generated with both AIMD (dark with circle points) and MLIP molecular dynamics (light with cross points) calculations. The timestep is 1 fs and the temperature is 300 K. Each window is sampled for 10 ps.

Two equivariant MLIPs, one for each metal, are trained using the Allegro package⁴⁶ from a modified dataset derived from the AIMD trajectories. These potentials are generated to provide the computational speedup required to include NQEs using CMD simulations. The training mean absolute errors for the force elements and energies for these potentials are: 0.0394 eV Å⁻¹ and 0.565 meV per atom, respectively, for Pt; and 0.0237 eV Å⁻¹ and 0.463 meV per atom, respectively, for Au (Fig. S1–S5, ESI†). As shown in Fig. 1, these potentials are then benchmarked to the DFT ground truth, successfully reproducing the potential energy surfaces produced by the AIMD. The error of the MLIP with respect to the ground truth is much smaller compared to other potential sources of error, such as the choice of exchange–correlation functional, with the PBE functional being known to underestimate energy barriers.⁵⁰

The MLIP-generated potentials closely reproduce the potential energy surfaces obtained from DFT-based simulations for both Pt and Au. Small differences of up to 0.03 eV are found across the potential energy surface. This can be attributed to the innate error of calculating the potential of mean force with restricted sampling time. With this considered, both potentials quantitatively describe the chosen DFT level of theory for the C–H activation of surface CH₃, with significant computational speedup. For perspective, for Fig. 1, each window required ∼29 h of computer time to calculate at the DFT level whilst it only required ∼4 min with the MLIPs.

We note that the sampling time and timestep used in Fig. 1 are not optimal. A longer sampling time is needed to more precisely capture the potential energy surface, while a smaller timestep would better model the high vibrational frequencies of the C–H bonds. The speedup from the MLIP allows longer sampling times (100 ps per window), and a shorter timestep (0.25 fs), which is computationally accessible with MLIPs. Making a comparison when the timestep and sampling time is changed, the PES changes slightly for both metals (Fig. 2). For Pt(111), the barrier increases by 0.02 eV, which falls within the error margin of the potential of mean force (PMF), while the free energy change becomes less exergonic by 0.05 eV. In the case of Au(111), the barrier also rises by 0.05 eV, with the free energy change remaining roughly equivalent, showing a slight increase in endergonicity of 0.01 eV. Nevertheless, the overall trend remains consistent for both surfaces, regardless of the timestep and sampling time adjustments.

Fig. 2 Classical and quantum free energy pathways for Pt(111) and Au(111). (a) Free energy pathway of C–H activation for Pt(111) (grey) and Au(111) (gold). The free energy landscape is derived from umbrella sampling. The free energy pathway is generated with both classical molecular dynamics (dark with circle points) and centroid molecular dynamics (light with cross points) calculations to consider the classical and quantum pathway, respectively. The timestep is 0.25 fs and the temperature is 300 K. Each window is sampled for 100 ps. (b) Free energy pathway from static DFT calculations. Entropy is calculated in the harmonic approximation. The pathways are shown with and without zero-point energy to show the effect of one aspect of NQEs.

Enhanced sampling centroid molecular dynamics calculations are performed to incorporate NQEs. The free energy pathway is generated through umbrella sampling, similar to the approach used in Fig. 1. Bead convergence is evaluated for the Pt(111) surface by considering 4, 8, and 16 beads (Fig. S6, ESI†). Convergence is achieved at 8 beads, as only a negligible difference (less than 0.02 eV) was observed across the free energy surface when comparing 8 and 16 beads. The inclusion of NQEs has important effects on the free energy pathway. For both surfaces, the barrier decreases and the free energy change of the reaction of C–H activation becomes more negative. More specifically, for Pt(111), the barrier decreases by 0.08 eV to 0.69 eV. The reaction rate is not explicitly computed, but assuming classical kinetics and the transmission coefficient being the same for both the classical and quantum path,⁵¹ the rate of C–H activation would be accelerated by a factor of ∼20. Additionally, the ΔF of the reaction decreases by 0.14 eV to 0.01 eV. For Au(111), the changes are less pronounced; in particular, the barrier decreases by 0.04 eV to 1.60 eV and the ΔF of the reaction decreases by 0.05 eV to 1.11 eV.

The primary factor contributing to the influence of NQEs on the free energy pathway is the zero-point energy that stems from the vibrational partition function. To quantify this, static calculations are performed, approximating the free energy in the harmonic limit. This allows us to remove the zero-point energy contribution from the free energy pathway (Fig. 2b).⁵² For Pt(111), the zero-point energy contribution within the harmonic approximation is −0.08 eV for the barrier and 0.14 eV for ΔF. The barrier values are reasonably close to both classical and quantum paths, differing by −0.05 eV and −0.06 eV, respectively. A similar trend is observed for ΔF, with differences of −0.04 eV and −0.04 eV, respectively. Notably, the harmonic approximation accurately describes the C–H activation process for Pt(111). In contrast, this is not the case for Au(111), where the harmonic approximation fails to satisfactorily capture the C–H activation dynamics for the classical system. This causes the NQEs to be less determined by zero-point energy, as there is coupling between the translational and vibrational partition functions. In this scenario, explicit consideration of the NQEs is required to capture them. This is the case both with and without zero-point energy contributions. Specifically, the static barrier differs significantly between the classical and quantum paths, with differences of 0.26 eV and 0.19 eV, respectively. This trend is mirrored for ΔF, with differences of 0.39 eV and 0.28 eV, respectively. These discrepancies may be attributed to the stronger versus weaker surface–adsorbate interactions in platinum and gold, with adsorbates being able to diffuse more readily across the surface rather than merely oscillating within surface sites. This result emphasises the importance of including NQEs when explicitly sampling the potential energy surface. This would notably apply when considering the free energy change in a solvated environment.

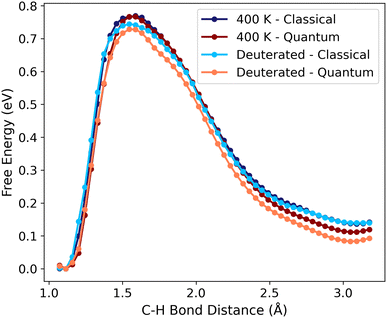
To further investigate the influence of NQEs on C–H activation, two additional scenarios are examined for Pt(111): one in which the elementary step occurs at a higher temperature of 400 K; and another where all hydrogen atoms are replaced by deuterium (Fig. 3). Both cases are anticipated to result in reduced NQEs. The Pt(111) system is chosen due to the more pronounced NQEs we have observed. For activation of CD₃, the difference of the barrier for the classical and the quantum path is reduced to 0.01 eV, while the free energy change difference is 0.06 eV, highlighting the impact of the heavier atomic nuclei. At the elevated temperature of 400 K, the barrier becomes nearly identical for both paths, with the free energy change differing by only 0.03 eV. While these results qualitatively align with the expected differences for both scenarios, the discrepancies approach the expected precision of the potential of mean force sampling. These results suggest that, under these conditions, the use of the path integral formalism for free energy sampling is unnecessary.

Fig. 3 Free energy pathway of C–H activation for Pt(111). The free energy landscape is derived from umbrella sampling. The free energy pathway is generated with both classical molecular dynamics (purple and blue) and centroid molecular dynamics (maroon and orange) calculations to consider the classical and quantum pathway, respectively. The system is considered at the higher temperature of 400 K (purple and maroon) and for deuterated surface methyl (CD₃) at 300 K (blue and orange). The timestep is 0.25 fs. Each window is sampled for 100 ps.

Conclusions

We employed machine learning interatomic potentials and centroid molecular dynamics simulations to explore the impact of nuclear quantum effects on C–H activation on Pt(111) and Au(111). Our findings indicate that incorporating NQEs leads to significant changes to reaction barriers and, consequently, reaction rates under room temperature-like conditions. We stress that NQEs should not exclusively be applied to low temperature conditions. The inclusion of zero-point energy corrections effectively captures NQEs for C–H activation, provided the harmonic approximation is valid; however, when this approximation fails, so does the ability to accurately describe the NQEs. Nonetheless, the qualitative accuracy of the description is maintained, reinforcing the good practice of their usage. There are still limitations in this work, especially with the Born–Oppenheimer approximation being used, hydrogen and hydride free radicals could be present as transient species.⁵³ Consideration of the lifetime of these species is beyond the scope of this work. There are also limitations with the MLIP used, where only short ranged interactions are considered. We hope future work can look at the C–H activation process whilst considering these important effects. Whilst our focus is on C–H activation at pristine solid–gas interfaces, we anticipate that explicitly modelling the NQEs of C–H activation using path integral formulation will be essential in solvated environments to accurately describe free energy pathways. In such cases, static calculations are problematic, making it impossible to account for zero-point energy using the harmonic limit. For these systems, the use of machine learning interatomic potentials presents a promising strategy to address the computational challenges.

Conflicts of interest

There are no conflicts to declare.

Data availability

Data and datasets will be made available pending review and release.

Acknowledgements

This work was performed under the auspices of the US Department of Energy by Lawrence Livermore National Laboratory under contract no. DE-AC52-07NA27344. Financial support is from the HydroGEN Advanced Water Splitting Materials Consortium, established as part of the Energy Materials Network under the US Department of Energy, Office of Energy Efficiency and Renewable Energy, Hydrogen and Fuel Cell Technologies Office. Additional support is from the LLNL Laboratory Directed Research and Development (LDRD) program (22-FS-036). Computational resources are supported by the LLNL Computing Grand Challenge Program.

Notes and references

1. T. Dalton, T. Faber and F. Glorius, ACS Cent. Sci., 2021, 7, 245–261.
2. Z. Zhuang, T. Sheng, J. X. Qiao, K.-S. Yeung and J.-Q. Yu, J. Am. Chem. Soc., 2024, 146, 17311–17317.
3. H. Sandström and M. Rahm, ACS Earth Space Chem., 2021, 5, 2152–2159.
4. J. Rittle and M. T. Green, Science, 2010, 330, 933–937.
5. N. J. Gunsalus, A. Koppaka, S. H. Park, S. M. Bischof, B. G. Hashiguchi and R. A. Periana, Chem. Rev., 2017, 117, 8521–8573.
6. J. He, M. Wasa, K. S. L. Chan, Q. Shao and J.-Q. Yu, Chem. Rev., 2017, 117, 8754–8786.
7. P. Preuster, C. Papp and P. Wasserscheid, Acc. Chem. Res., 2017, 50, 74–85.
8. R. J. Bunting, P. S. Rice, Z. Yao, J. Thompson and P. Hu, Chem. Commun., 2022, 58, 9622–9625.
9. R. J. Bunting, F. Wodaczek, T. Torabi and B. Cheng, J. Am. Chem. Soc., 2023, 145, 14894–14902.
10. A. A. Latimer, H. Aljama, A. Kakekhani, J. S. Yoo, A. Kulkarni, C. Tsai, M. Garcia-Melchor, F. Abild-Pedersen and J. K. Nørskov, Phys. Chem. Chem. Phys., 2017, 19, 3575–3581.
11. B. Hammer and J. Nørskov, Impact of Surface Science on Catalysis, Academic Press, 2000, vol. 45, pp. 71–129.
12. M. Busch, M. D. Wodrich and C. Corminboeuf, Chem. Sci., 2015, 6, 6754–6761.
13. M. Jørgensen and H. Grönbeck, J. Phys. Chem. C, 2017, 121, 7199–7207.
14. A. Laio and F. L. Gervasio, Rep. Prog. Phys., 2008, 71, 126601.
15. A. Wallqvist and B. J. Berne, J. Phys. Chem., 1993, 97, 13841–13851.
16. Y. Litman and M. Rossi, Phys. Rev. Lett., 2020, 125, 216001.
17. P. K. J. Kurapothula, S. Shepherd and D. M. Wilkins, J. Chem. Phys., 2022, 156, 084702.
18. A. C. Thakur and R. C. Remsing, J. Chem. Phys., 2024, 160, 024502.
19. A. Sattler, ACS Catal., 2018, 8, 2296–2312.
20. M. Ceriotti, W. Fang, P. G. Kusalik, R. H. McKenzie, A. Michaelides, M. A. Morales and T. E. Markland, Chem. Rev., 2016, 116, 7529–7550.
21. G. Kyriakou, E. R. M. Davidson, G. Peng, L. T. Roling, S. Singh, M. B. Boucher, M. D. Marcinkowski, M. Mavrikakis, A. Michaelides and E. C. H. Sykes, ACS Nano, 2014, 8, 4827–4835.
22. D. M. Wilkins, D. E. Manolopoulos, S. Pipolo, D. Laage and J. T. Hynes, J. Phys. Chem. Lett., 2017, 8, 2602–2607.
23. M. Parrinello and A. Rahman, J. Chem. Phys., 1984, 80, 860–867.
24. D. Chandler and P. G. Wolynes, J. Chem. Phys., 1981, 74, 4078–4095.
25. J. A. Keith, V. Vassilev-Galindo, B. Cheng, S. Chmiela, M. Gastegger, K.-R. Müller and A. Tkatchenko, Chem. Rev., 2021, 121, 9816–9872.
26. P. S. Rice, Z.-P. Liu and P. Hu, J. Phys. Chem. Lett., 2021, 12, 10637–10645.
27. Y. Chen, Y. Huang, T. Cheng and W. A. I. Goddard, J. Am. Chem. Soc., 2019, 141, 11651–11657.
28. L.-H. Luo, S.-D. Huang, C. Shang and Z.-P. Liu, ACS Catal., 2022, 12, 6265–6275.
29. M. D. Marcinkowski, M. T. Darby, J. Liu, J. M. Wimble, F. R. Lucci, S. Lee, A. Michaelides, M. Flytzani-Stephanopoulos, M. Stamatakis and E. C. H. Sykes, Nat. Chem., 2018, 10, 325–332.
30. R. Tran, Z. Xu, B. Radhakrishnan, D. Winston, W. Sun, K. A. Persson and S. P. Ong, Sci. Data, 2016, 3, 1–13.
31. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396.
32. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
33. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
34. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
35. P. E. Blöchl, O. Jepsen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 16223–16233.
36. A. Alavi, P. Hu, T. Deutsch, P. L. Silvestrelli and J. Hutter, Phys. Rev. Lett., 1998, 80, 3650–3653.
37. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
38. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192.
39. G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978–9985.
40. A. Hjorth Larsen, J. Jørgen Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Duak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. Bjerre Jensen, J. Kermode, J. R. Kitchin, E. Leonhard Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. Bergmann Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, J. Phys.: Condens. Matter., 2017, 29, 273002.
41. L. H. Sprowl, C. T. Campbell and L. Árnadóttir, J. Phys. Chem. C, 2016, 120, 9719–9731.
42. W. G. Hoover, Phys. Rev. A, 1985, 31, 1695–1697.
43. J. Cao and B. J. Berne, J. Chem. Phys., 1993, 99, 2902–2916.
44. J. Cao and G. A. Voth, J. Chem. Phys., 1994, 100, 5106–5117.
45. S. Kumar, J. M. Rosenberg, D. Bouzida, R. H. Swendsen and P. A. Kollman, J. Comput. Chem., 1992, 13, 1011–1021.
46. A. Musaelian, S. Batzner, A. Johansson, L. Sun, C. J. Owen, M. Kornbluth and B. Kozinsky, Nat. Commun., 2023, 14, 579.
47. A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. In’t Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171.
48. A. Trinchero, A. Hellman and H. Grönbeck, Surf. Sci., 2013, 616, 206–213.
49. R. Burch and P. Loader, Appl. Catal., B, 1994, 5, 149–164.
50. J. K. Nørskov, F. Abild-Pedersen, F. Studt and T. Bligaard, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 937–943.
51. D. M. Wilkins, D. E. Manolopoulos and L. X. Dang, J. Chem. Phys., 2015, 142, 064509.
52. A. Gross and M. Scheffler, J. Vac. Sci. Technol., A, 1997, 15, 1624–1629.
53. G. Piccini and J. Sauer, J. Chem. Theory Comput., 2014, 10, 2479–2487.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp01527h

---