Periodic precipitation banding of metal hydroxides in agarose gels via cyclic-voltage-driven reaction–transport–reaction process

Abstract

This study investigated how cyclic switching between high and low voltages can generate Liesegang-like (but not conforming to the scaling laws) periodic precipitation bands of metal hydroxides in agarose gel columns, aiming to uncover the generality and underlying mechanism of this reaction–transport–reaction process. The process is generalizable to various combinations of metal anodes and cathodes, with the number of bands typically increasing with cycle number. The spatiotemporal evolution of the bands exhibits considerable anode-element dependence, but is less dependent on the cathode element, as well as the dimensions of the gel column, demonstrating the generality of this banding phenomenon. Analyses of the time-dependence of the electric current and the morphology and composition of the anode-derived deposits indicate that OH⁻ ions react with the anode surface after their transport from the cathode. Numerical simulations based on extended Nernst–Planck equations suggest that periodic banding is possible if (i) the generation of reactant ions is periodically suppressed, (ii) the diffusion coefficients of the reactant ions differ considerably, and (iii) a quantitative imbalance exists between the produced and precipitated ions. A qualitative mechanism for the observed banding phenomenon is proposed, in which the tunneling effect of OH⁻ ions, owing to the Grotthuss mechanism, is suggested as a possible cause of this quantitative imbalance. These findings offer new insights into electrochemically induced pattern formation and highlight the potential of reaction–transport–reaction systems for advancing our understanding of coupled reaction–transport phenomena.

---

Introduction

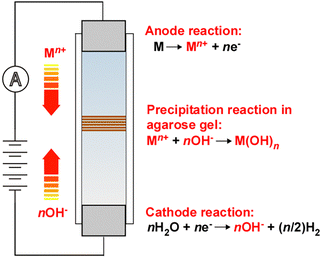
The interplay between chemical transformations and mass transport is a crucial topic in physical chemistry and chemical physics, particularly in electrochemistry and precipitation patterning, owing to its influence on the type and extent of the reactions that occur. The field of electrochemistry is based on the inherent coupling between reactions at electrodes and the migration, diffusion, and convection of ions in solution. In the field of precipitation patterning, the interaction between precipitation reactions and ionic diffusion in porous media (typically hydrogels) is attracting considerable interest for the generation of self-organized precipitation patterns,¹ the most famous of which is periodic Liesegang banding.² Despite the common importance of reaction–transport processes, few cross-disciplinary studies between electrochemistry and precipitation patterning have been conducted.^3–8

Recently, we discovered a new class of periodic banding system in which metal hydroxides precipitate in a gel column upon cyclic switching between a higher voltage (E_H) and a lower one (E_L) for times T_H and T_L, respectively (Fig. 1).⁹ Electrochemical reactions at the anode (M → Mⁿ⁺ + ne⁻, where M is a metal) and cathode (nH₂O + ne⁻ → nOH⁻ + (n/2)H₂) produce ions that move toward the opposite electrode; these ions then react (Mⁿ⁺ + nOH⁻ → M(OH)_n) to form precipitates in the gel. Because this system involves two types of reaction (electrochemical and precipitation) coupled with ion transport, we termed it a reaction–transport–reaction (RTR) process.¹⁰ The RTR mechanism operates based on the principle that more reactant ions are produced at higher voltages (i.e., at E_H), while the electric field simultaneously exerts a stronger ion-transport effect, whereas fewer ions are generated and the effect of the electric field is weaker at lower voltages (i.e., at E_L).

Fig. 1 Schematic of the basic RTR system with agarose gel inserted between two metal rods in a plastic tube. The applied voltage is switched between high voltage E_H and low voltage E_L for times T_H and T_L, respectively, for N_C cycles. The arrows indicate the direction of the movement of the reactant ions in the electric field.

When using an Fe anode, this RTR mechanism produces clear periodic banding of gelatinous Fe(OH)₃ precipitates, where the number of periodic bands (N_B) is given by N_C − N_C1 + 1 (where N_C and N_C1 are the number of cycles and the cycle number at which the first band emerges, respectively).⁹ This empirical relationship means that after the emergence of the first band, the number of periodic bands (N_B) increases by one from one cycle to the next. The N_C1 and N_B values decrease and increase, respectively, with increases in E_H, E_L, T_H, and T_L, as well as with decreases in gel column length (L).⁹

RTR systems have been overlooked throughout the history of periodic banding.^11–13 These systems differ from other periodic patterning systems in several respects. First, although similar systems, such as Liesegang banding under electric fields, have been examined,^3,5–8 conventional Liesegang systems operate without an applied voltage. In contrast, RTR systems are similar to typical electrochemical cells, in that reactant ions are generated by electrochemical reactions at the electrodes. Meanwhile, considerably fewer reactant ions are produced in RTR systems than in typical electrochemical cells, because RTR systems have considerably less (or no) supporting electrolyte. The low amount of supporting electrolyte also makes migration more dominant than diffusion in the transport of reactant ions, unlike in most electrochemical cells and conventional Liesegang banding systems, where diffusion is considered the main mechanism of ion transport. Additionally, because RTR systems use a gel medium, the speed of ion transport is expected to be considerably lower than that in conventional electrochemical cells, which employ electrolyte solutions. The mechanism of precipitation in RTR systems is similar to that in Liesegang banding systems, in which the reactant ions precipitate when their concentrations exceed the solubility product constant (K_sp). However, precipitation patterning in RTR systems requires an applied voltage, which is absent in conventional Liesegang banding systems. Thus, RTR systems have an interdisciplinary nature that enriches physical chemistry, specifically bridging the gap between electrochemistry and precipitation patterning.

Moreover, the RTR process has several notable features that render it suitable for controlling and engineering precipitation patterns. For example, the number and spacing of precipitation bands can be easily controlled by modifying the duration of voltage application.⁹ Furthermore, unlike most Liesegang banding systems, RTR systems do not have a continuous precipitation zone associated with the periodic bands. Additionally, the metal compound(s) in the precipitation patterns can be tailored by using an alloy anode and/or by replacing the anode with a different one during voltage application. These features are useful for expanding the applications of precipitation patterning, such as for the preparation of multi-component precipitation structures.¹⁴

The mechanism of periodic banding in RTR systems remains unknown.^9,10 To incorporate RTR systems in the science and engineering of precipitation patterning, this study aims to explore the periodic banding of diverse metal hydroxides through the RTR process, demonstrating that it is not specific to gelatinous Fe(OH)₃ systems,⁹ as well as to examine the experimental factors related to periodic banding and elucidate a possible banding mechanism. This was achieved with the aid of numerical simulations based on extended Nernst–Planck equations.

Extended Nernst–Planck equation model

To elucidate the mechanism of periodic banding in RTR systems, we simulated the concentrations of metal (Mⁿ⁺) and hydroxide (OH⁻) ions (C_M(x,t) and C_OH(x,t), respectively) contained between planes x and x + Δx of a gel-filled cylindrical tube at time t. The tube had a cross-sectional area A and length L, and the gel was assumed to be in contact with the anode and cathode surfaces at x = 0 and x = L, respectively. The density ρ(x,t) of the precipitated metal hydroxide (M(OH)_n) between x and x + Δx at time t was also considered. The following partial differential equations were used:

∂C_M/∂t = D_M(∂²C_M/∂x²) − (nFD_MX/RT)(∂C_M/∂x) − kΘ(C_MCⁿ_OH − K_sp), (1)

∂C_OH/∂t = D_OH(∂²C_OH/∂x²) + (FD_OHX/RT)(∂C_OH/∂x) − nkΘ(C_MCⁿ_OH − K_sp), (2)

∂ρ/∂t = M_WkΘ(C_MCⁿ_OH − K_sp) (3)

where D_M and D_OH are the diffusion coefficients of Mⁿ⁺ and OH⁻ ions, respectively; F is the Faraday constant (96 487 C mol⁻¹); R is the universal gas constant (8.314 J K⁻¹ mol⁻¹); X is the constant potential gradient in the gel; T is the temperature in Kelvin; n is the valence number of the Mⁿ⁺ ions; k is the rate of precipitation in each cylindrical section at time t; K_sp is the solubility product constant of M(OH)_n; Θ(r) is the Heaviside step function (Θ(r) = 0 for r ≤ 0 and Θ(r) = 1 for r > 0); and M_W is the molar mass of M(OH)_n. These partial differential equations are similar to those employed for analyzing the formation of Liesegang bands under an applied electric field.^5,8

In eqn (1) and (2), the first term after the equals sign describes the diffusion of Mⁿ⁺ and OH⁻ ions, respectively; the second term describes the migration of these ions under a constant potential gradient X; and the third term represents the disappearance of these ions from the gel by the formation of M(OH)_n precipitates, as described by eqn (3). In RTR systems, the value of X must be smaller than the applied voltage divided by the tube length ((E_H or E_L)/L) because of the formation of electric double layers at the electrodes.^15,16 Furthermore, eqn (3) assumes that M(OH)_n precipitates form rapidly when the product of the ion concentrations (C_M × Cⁿ_OH) exceeds the solubility product constant K_sp. For simplicity, we neglected the possible formation of intermediates, which do not immediately precipitate but are instead free to diffuse until their local concentration reaches some saturation threshold.¹⁷

When no precipitation occurs (i.e., when k = 0), eqn (1) and (2) represent the Nernst–Planck equation^15,16 for Mⁿ⁺ and OH⁻ ions, respectively, under no convection and a constant potential gradient. When no potential gradient exists (i.e., when X = 0), eqn (1)–(3) correspond to the equations provided by Grzybowski¹⁷ for Liesegang banding during ionic reactions (which are fundamentally based on the Keller–Rubinow theory¹⁸).

When the applied voltage exceeds a threshold E_thre, Mⁿ⁺ ions with a concentration C⁰_M are assumed to be constantly generated at the anode surface (x = 0), giving C_M(0,t) = C⁰_M and ∂C_M(0,t)/∂t = 0. Below this threshold, no Mⁿ⁺ ions are generated (i.e., C_M(0,t) = 0). Here, E_thre is the sum of the theoretical decomposition voltage (approximately the difference in standard electrode potential (E_STE) between the anode and cathode) and the overvoltage (typically ∼0.5 V).

Similarly, if the applied voltage exceeds a threshold E_thre, OH⁻ ions with a concentration nf_iC⁰_M are assumed to be constantly generated at the cathode surface (x = L), giving C_OH(L,t) = nf_iC⁰_M and ∂C_OH(L,t)/∂t = 0. Here, f_i (0 < f_i < 1) is a factor that considers the quantitative imbalance between the produced and precipitated ions, which is discussed further below. Below this threshold, no OH⁻ ions are generated (i.e., C_OH(L,t) = 0).

Thus, cyclic voltage switching between E_H > E_thre and E_L < E_thre results in continuous Mⁿ⁺ and OH⁻ ion production (with concentrations C⁰_M and nf_iC⁰_M, respectively) during E_H application, and no ion production during E_L application. The value of C⁰_M is dependent on E_H. We calculated C⁰_M using the Tafel equation (as a trial function): C⁰_M = β·exp(nαF|E_H − E_thre|/(RT)), where α and β were treated as fitting parameters.

If Mⁿ⁺ ions reach the cathode, they are assumed to disappear by forming M(OH)_n and/or M at the cathode surface, giving C_M(L,t) = 0. Similarly, if OH⁻ ions reach the anode, they are assumed to disappear by forming M(OH)_n at the anode surface, giving C_OH(0,t) = 0. The formation of M(OH)_n at the electrode surface may decrease the effective area of the electrode; however, this effect was ignored for simplicity.

The factor f_i was introduced to deal with the concept of quantitative imbalance between the produced and precipitated ions. Considering charge balance within the tube, we can assume the cathode produces OH⁻ ions with concentration nC⁰_M. If there is a quantitative imbalance between the produced and precipitated ions (i.e., if f_i < 1), some of the produced OH⁻ ions (concentration n(1 − f_i)C⁰_M) do not contribute to M(OH)_n precipitation and are instead consumed at the anode surface. By contrast, if there is no quantitative imbalance (i.e., if f_i = 1), all OH⁻ ions (concentration nC⁰_M) are free to contribute to M(OH)_n precipitation. The necessity of factor f_i and the possible cause for its decrease are discussed later.

Based on the aforementioned theoretical model, numerical simulations were conducted by applying the standard explicit method using a computer code written in MATLAB. The first derivatives with respect to x in eqn (1) and (2) were approximated using the upwind difference scheme. In all computations, the time difference Δt was set to 1.76 s, and the one-dimensional space ranging from 0 to L was divided into 1600 segments.

Materials and methods

Materials

Round bars of Al (99.99%), Ti (99.5%), Fe (99.5%), Co (99.98%), Ni (≥99%), Cu (99.9%), Zn (99.99%), Mo (99.95%), Ag (99.99%), In (99.99%), Sn (99.9%), and W (99.95%) were obtained from Nilaco Corporation (Tokyo, Japan) for use as electrodes. Analytical reagent-grade NaNO₃ and agarose (gel strength: 1800–2300 g cm⁻²) were purchased from Fujifilm Wako Pure Chemical Corporation (Osaka, Japan) and Kanto Chemical Co., Inc. (Tokyo, Japan). All chemicals were used without further purification. All aqueous solutions were prepared using deionized water, which was obtained by purifying tap water using a cartridge water purifier (G-10, Organo, Tokyo, Japan).

Gel column preparation

Plastic tubes were filled with agarose gel containing NaNO₃ as a supporting electrolyte. First, NaNO₃ powder was dissolved in deionized water at 298 K to form NaNO₃ solutions (30 mL) with concentrations (C_se) ranging from 0 to 40 mM. Next, 2.0 wt% agarose was added, and the mixture was stirred vigorously at 373 K for 45 s to produce a uniform NaNO₃–agarose sol. Using a Pasteur pipette, the prepared sol was transferred to a sample tube (plastic straws with inner diameters of 2, 4, or 6 mm and lengths of 55, 65, and 75 mm), the bottom end of which was plugged with a metal rod (4 mm diameter × 20 mm length) for use as the cathode. The hot sol in each sample tube was left to cool to 298 K to form a solidified gel. After solidification, another metal rod (3 mm diameter × 22 mm length) was placed in the top end of the tube to form the anode. To ensure reproducibility, each experiment was conducted using four samples that were prepared under the same conditions.

RTR patterning

To achieve RTR patterning, voltage was applied between the anode and cathode using a programmable power supply (PPS303, AS ONE, Osaka, Japan). The voltage was switched between E_H for time T_H and E_L for time T_L for N_C cycles. Tests were conducted with the following parameters: E_H = 3 V, E_L = 1–2 V, T_H = 1 h, T_L = 2 h, and N_C = 8–16. To investigate the generality of the RTR process, tests were conducted using several combinations of anodes (Al, Fe, Co, Ni, Cu, Zn, In, and Sn), cathodes (Ti, Ni, Cu, Mo, Ag, and W), NaNO₃ concentrations (C_se = 0–40 mM), and gel column dimensions (length L = 40–60 mm, diameter ϕ = 2–6 mm). All patterning processes were conducted at 298 K.

During the patterning process, the electric current within the sample tube and the precipitation patterns formed therein were monitored using a digital multimeter (BDM521, AS ONE) and digital camera (TG-7, OM Digital Solutions, Tokyo, Japan), respectively.

Once voltage application was discontinued, the sample tubes were photographed for further analysis. Depending on the color of the precipitation bands, the tubes were laid either on black paper (for the Al, Ni, Zn, In, and Sn anode samples) or on backlit white paper using an LED flashlight (for the Fe, Co, and Cu anode samples). A ruler with 1 mm increments was included in the photographs for scale reference. The photographs were then analyzed using graphic software (Canvas X, Canvas GFX, Inc., Boston, MA, USA) to measure the distances between adjacent bands (d), the widths of the precipitation bands (w), and the position of the first band (x_1st) with an uncertainty of ±0.01 mm.

Microscopy

After RTR patterning, some gel columns and metal electrodes (rods) were cut into ∼1 mm thick sections. The sections were mounted on an aluminum stub using double-sided adhesive carbon tape and observed using scanning electron microscopy (SEM; SU8220, Hitachi, Tokyo, Japan). The gel sections were allowed to dry for one week in a calm laboratory environment at 298 K prior to SEM analysis. SEM–energy dispersive X-ray spectroscopy (EDS) measurements were conducted at 15 kV with a working distance of 14.9 mm using an EMAX X-Max silicon drift detector (Oxford Instruments, Tokyo, Japan) in combination with analysis software (AZtec Live, Oxford Instruments).

Results and discussion

Generality of periodic banding of M(OH)_n precipitates through the RTR process

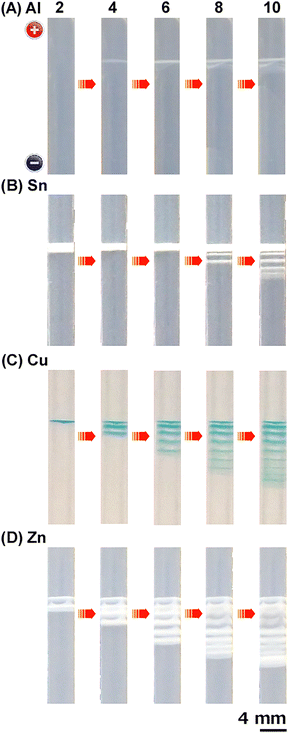
Fig. 2 shows examples of the periodic banding of M(OH)_n (M = Al, Fe, Co, Ni, Cu, Zn, In, and Sn) precipitates through the RTR process at 298 K for gels with NaNO₃ concentrations (C_se) of 10 mM (2 mM for Fe) under the following voltage conditions: E_H = 3 V, E_L = 1 V (2 V for Ni), T_H = 1 h, T_L = 2 h, and N_C = 10–16. For systems with Fe and Ni anodes, C_se = 10 mM and E_L = 1 V were too high and too low, respectively, to generate distinct periodic bands; therefore, these conditions were adjusted to C_se = 2 mM and E_L = 2 V, respectively. These systems are diverse in terms of the standard electrode potentials¹⁹ (E_STE) required to generate ions, the diffusion coefficients of these ions in infinitely dilute aqueous solutions²⁰ (D⁰), and the K_sp values of M(OH)_n precipitates²¹ (Table 1); however, (sub)millimeter-scale periodic precipitation banding was observed in each case (Fig. 2 and Table 2). This finding demonstrates the generality of the periodic banding phenomenon of M(OH)_n precipitates through the RTR process under voltage cycling. Gel distortion, which is widely observed in gelatinous Fe(OH)₃ systems during RTR patterning, particularly on the Fe anode side,⁹ was not noticeable in the examples in Fig. 2. This suggests that the influence of gel distortion on periodic banding, as discussed in a previous study,⁹ was negligible.

Fig. 2 Examples of periodic banding of M(OH)_n (M = Al, Fe, Co, Ni, Cu, Zn, In, and Sn) precipitates in gel columns (L = 50 mm, ϕ = 4 mm C_se = 10 mM (2 mM for Fe)) using M anodes through RTR processes at 298 K under the following voltage conditions: E_H = 3 V, E_L = 1 V (2 V for Ni), T_H = 1 h, T_L = 2 h, and N_C = 10–16. Each system had a Cu cathode. The sides of the anode (+) and cathode (−) are shown on the left of the image.

Table 1 Characteristic parameters for RTR processes with different metal ions

Ion	ESTE^a (V)	D^0^b (× 10^9 m^2 s^−1)	Ksp^c
a ESTE: standard electrode potential^19 for the ions forming the periodic bands in Fig. 2.b D^0: diffusion coefficient of these ions in infinitely dilute aqueous solutions.^20c Ksp: solubility product constant of M(OH)n precipitates.^21
OH^−	0.40	5.273	—
Al^3+	−1.66	0.541	1.3 × 10^−33
Fe^2+	−0.45	0.719	8.0 × 10^−16
Fe^3+	0.77	0.604	4 × 10^−38
Co^2+	−0.28	0.732	1.6 × 10^−15
Ni^2+	−0.26	0.661	2.0 × 10^−15
Cu^2+	0.34	0.714	2.2 × 10^−20
Zn^2+	−0.76	0.703	1.2 × 10^−17
In^3+	−0.34	—	6.3 × 10^−34
Sn^2+	−0.14	—	1.4 × 10^−28

---

Table 2 Banding parameters for the periodic bands shown in Fig. 2

Anode	dave^a (mm)	wave^b (mm)	x1st^c (mm)
a dave: average interband distance.b wave: average bandwidth.c x1st: average distance between the anode surface and the first precipitation band to emerge.
Al	0.41 ± 0.34	0.14 ± 0.10	15.9 ± 0.6
Fe	2.00 ± 0.30	0.45 ± 0.08	16.6 ± 0.7
Co	1.67 ± 0.72	0.41 ± 0.16	15.6 ± 1.8
Ni	1.38 ± 0.76	0.44 ± 0.24	14.3 ± 1.3
Cu	1.20 ± 0.40	0.33 ± 0.17	13.8 ± 0.7
Zn	1.35 ± 0.47	0.51 ± 0.16	13.6 ± 0.7
In	1.34 ± 0.56	0.54 ± 0.28	13.7 ± 1.6
Sn	0.90 ± 0.24	0.52 ± 0.40	16.8 ± 0.6

---

Conventional Liesegang bands typically adhere to several empirical scaling laws, including spacing and width laws, irrespective of the electrolyte pair and system geometry.^12,13,17 The spacing law describes the spatial ordering of Liesegang bands as x_i+1/x_i = 1 + p, where x_i is the position of the i-th band and p > 0 for most systems.^12,13 The width law describes the widths of the Liesegang band as w_i+1/w_i = (1 + p)^k, where w_i is the width of the i-th band and k ≈ 0.9.¹⁷ These laws mean that conventional Liesegang bands typically become wider and more distanced from each other as i increases.

By contrast, both the interband distances and widths of the periodic bands obtained through the RTR process remained approximately constant (with a broad dispersion), as shown in Fig. 2. As such, they did not conform to the empirical scaling laws of Liesegang banding. This is not entirely unexpected, because the mechanism of periodic banding in RTR systems is fundamentally different to that in conventional Liesegang banding systems, as shown later.

Table 2 shows the average interband distance (d_ave) and average width (w_ave) of the precipitation bands in Fig. 2. The average distance between the anode surface and the first precipitation band that emerged (x_1st) is also shown. Note that the first band that emerged was typically the band closest to the anode (i.e., the top bands in the RTR systems in Fig. 2). Interestingly, in the RTR systems showing clear periodic banding (Fe, Co, Ni, Cu, Zn, In, and Sn anode systems), these quantities were similar (d_ave ≈ 1.5 mm, w_ave ≈ 0.5 mm, and x_1st ≈ 15 mm) and lacked clear correlations with E_STE, D⁰, or pK_sp (= −log₁₀ K_sp) beyond statistical uncertainty (Fig. S1–S9, ESI†). This finding confirms that slight differences in E_STE, D⁰, and K_sp do not significantly affect the periodic banding of M(OH)_n precipitates in RTR systems, supporting the generality of the RTR process.

As suggested by the cathode reaction shown in Fig. 1 (water electrolysis), periodic banding through the RTR process is generalizable to different cathode materials. As an example, Fig. 3 shows the banding patterns of Cu(OH)₂ precipitates formed through RTR processes using different cathodes (Ti, Ni, Cu, Mo, Ag, and W) under the following voltage conditions: E_H = 3 V, E_L = 1 V, T_H = 1 h, T_L = 2 h, and N_C = 8. Although the obtained patterns differed, the formation of periodic bands was evident for all cathode materials in Fig. 3. The banding parameters are listed in Table S1 (ESI†).

Fig. 3 Banding patterns of Cu(OH)₂ precipitates in gel columns (L = 50 mm, ϕ = 4 mm, C_se = 10 mM) through RTR processes using Ti, Ni, Cu, Mo, Ag, and W cathodes at 298 K under the following voltage conditions: E_H = 3 V, E_L = 1 V, T_H = 1 h, T_L = 2 h, and N_C = 8. Each system had a Cu anode.

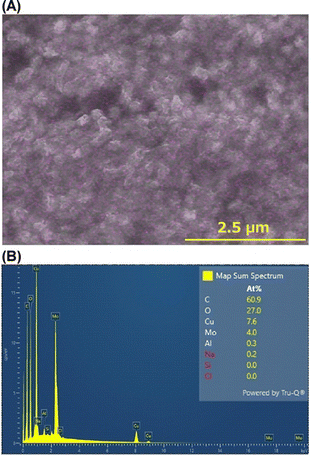
Fig. 3 indicates that the system with the Mo cathode produced fewer periodic bands than the systems with the other cathodes. Interestingly, SEM-EDS analysis of the system with the Mo cathode revealed that Mo atoms were uniformly dispersed within the micron-sized precipitates in the precipitation bands, along with C, O, and Cu (Fig. 4(A) and (B)). This suggests that Mo atoms emitted from the Mo cathode (possibly as MoO₄²⁻ ions) led to the formation of gelatinous CuMoO₄ as a byproduct in the agarose gel (notably, CuMoO₄ Liesegang band formation in agar gel has already been reported²²). This may have reduced the number of precipitation bands generated. Overall, Fig. 3 and 4 confirm that the cathode material has little influence on the formation of periodic bands via RTR processes, unless considerable cathode side reactions occur.

Fig. 4 (A) Scanning electron microscopy (SEM) image of the blue-green band formed in a gel column (L = 50 mm, ϕ = 4 mm, C_se = 10 mM) with a Mo cathode and Cu anode at 298 K under the following voltage conditions: E_H = 3 V, E_L = 1 V, T_H = 1 h, T_L = 2 h, and N_C = 8. The SEM image is overlaid with the Mo Lα intensity map (pink dots). (B) Energy dispersive X-ray spectroscopy (EDS) profile, where the measured intensities were averaged over the area of the SEM image. Inset: Estimated elemental concentration (wt%) of the studied area.

Periodic banding through the RTR process is also generalizable to different gel column lengths and diameters. As an example, Fig. 5 shows the banding patterns of Cu(OH)₂ precipitates formed in gel columns with various lengths (L = 40–60 mm) using a Cu anode and Cu cathode under the following voltage conditions: E_H = 3 V, E_L = 1 V, T_H = 1 h, T_L = 2 h, and N_C = 15. Periodic banding was evident in each case (the banding parameters are listed in Table S2, ESI†). With an increase in L (particularly from 40 to 50 mm), the position of the first band (x_1st) shifted slightly toward the cathode (Table S2 and Fig. S10, ESI†), the banding region broadened, and the bands lost some of their color. Similar discoloration was observed previously for the Fe(OH)₃ system.⁹ Such L dependence suggests that the potential gradient in the sample tube (X in eqn (1) and (2)) significantly influences the RTR process.

Fig. 5 Banding patterns of Cu(OH)₂ precipitates in gel columns with different lengths (L = 40, 50, and 60 mm, ϕ = 4 mm, C_se = 10 mM) through RTR processes at 298 K under the following voltage conditions: E_H = 3 V, E_L = 1 V, T_H = 1 h, T_L = 2 h, and N_C = 15. Each system had a Cu anode and Cu cathode.

Fig. 6 shows the banding patterns of Cu(OH)₂ precipitates formed in gel columns with various diameters (ϕ = 2–6 mm) through RTR processes using a Cu anode and Cu cathode under the following voltage conditions: E_H = 3 V, E_L = 1 V, T_H = 1 h, T_L = 2 h, and N_C = 16. The banding parameters are listed in Table S3 (ESI†). Periodic banding was evident for all ϕ values, suggesting that the diameter of the gel column is not a critical factor in the RTR process; however, as ϕ increased, the bands tended to be more distorted.

Fig. 6 Banding patterns of Cu(OH)₂ precipitates formed in gel columns with different diameters (L = 50 mm, ϕ = 2, 4, and 6 mm, C_se = 10 mM) through RTR processes at 298 K under the following voltage conditions: E_H = 3 V, E_L = 1 V, T_H = 1 h, T_L = 2 h, and N_C = 16. Each system had a Cu anode and Cu cathode.

Fig. 2, 3, 5, and 6 confirm the generality of periodic banding of M(OH)_n precipitates through RTR processes to different anodes, cathodes, and gel column dimensions. In each case, a small amount of supporting electrolyte (10 mM NaNO₃) was added to the gel to facilitate the RTR process. Fig. 7 shows the dependence of the periodic banding of Cu(OH)₂ precipitates on the NaNO₃ concentration (C_se); the banding parameters are listed in Table S4 (ESI†). At C_se = 0 mM, only a single faint blue band was observed near the cathode (red dashed box in Fig. 7). This contrasts significantly with the previously reported Fe(OH)₃ system, in which clear periodic banding was observed even without supporting electrolyte.⁹ At C_se = 5 mM, the Cu(OH)₂ system exhibited thin periodic bands at the anode side. At C_se = 10 mM, the color of the bands deepened, and the spacing between them narrowed. This color deepening and band-space narrowing became more pronounced as C_se increased further, accompanied by slight band distortion and a slight shift of the first band toward the anode (Fig. S11, ESI†). At C_se = 40 mM, only two relatively thick and virtually continuous bands were observed near the anode. Similar trends were observed for the other anode materials.

Fig. 7 Banding patterns of Cu(OH)₂ precipitates in gel columns with different NaNO₃ concentrations (L = 50 mm, ϕ = 4 mm, C_se = 0, 5, 10, 20, 30, and 40 mM) through RTR processes at 298 K under the following voltage conditions: E_H = 3 V, E_L = 1 V, T_H = 1 h, T_L = 2 h, and N_C = 16. All systems had a Cu anode (+) and Cu cathode (−), the sides of which are shown on the left of the image. The red broken square encloses the area where a faint precipitation band formed at C_se = 0 mM.

Thus, a NaNO₃ concentration of C_se ≈ 10 mM is suitable for the formation of periodic bands by RTR processes in systems with various anode materials, except for Fe, which requires a lower C_se (below approximately 2 mM) for periodic banding. The supporting electrolyte is expected to enhance reactions on the electrodes via the formation of an electric double layer.^16,23 The deepening color of the bands with increasing C_se is consistent with this hypothesis. Because of the very small K_sp value of gelatinous Fe(OH)₃ precipitates (Table 1), the Fe(OH)₃ system may require fewer reactant ions to achieve periodic banding and, consequently, less supporting electrolyte than other M(OH)_n systems.

In conventional Liesegang banding, adding a supporting electrolyte yields clear, well-resolved bands with a larger spacing coefficient.²⁴ According to the Derjaguin–Landau–Verwey–Overbeek theory, this effect is attributed to shielding of the electrostatic repulsion among the reaction products.²⁴ In the RTR systems, a similar shielding effect may also be achieved by increasing C_se; however, an increase in C_se is inevitably coupled with an increase in the concentration of the reactant ions, promoting their precipitation. Such a large increase in precipitation, as shown in Fig. 7, may have masked any increase in clarity of the precipitation bands owing to the shielding effect.

Anode-metal-dependence of periodic banding of M(OH)_n precipitates through the RTR process

The features of the periodic band patterns of M(OH)_n precipitates in RTR systems depend strongly on the anode material (M), although periodic banding itself occurs for many anode materials, as discussed above. To explore this further, the spatiotemporal evolution of periodic bands was analyzed in gel columns with Al, Co, Ni, Cu, Zn, In, and Sn anodes under the following voltage conditions: E_H = 3 V, E_L = 1 V, T_H = 1 h, T_L = 2 h, and N_C = 10. All systems had Cu cathodes and were operated at 298 K. Representative results for systems with Al, Sn, Cu, and Zn anodes are shown in Fig. 8(A)–(D), respectively; their banding parameters are listed in Table 2.

Fig. 8 Spatiotemporal evolution of typical periodic bands formed in gel columns (L = 50 mm, ϕ = 4 mm, C_se = 10 mM) using (A) Al, (B) Sn, (C) Cu, and (D) Zn anodes at 298 K under the following voltage conditions: E_H = 3 V, E_L = 1 V, T_H = 1 h, and T_L = 2 h. Each system had a Cu cathode. The cycle numbers (N_C) in which the images were captured are indicated at the top of the image: N_C = 2, 4, 6, 8, and 10. The sides of the anode (+) and cathode (−) are shown to the left of (A).

When using Al anodes (Fig. 8(A)), discrete precipitation bands were generated in a highly stochastic manner; that is, although they were prepared and tested under identical conditions, the band shapes, the timing of their appearance, and consequently the N_B values during N_C cycles varied considerably among the sample tubes (Fig. S12, ESI†). A single discrete band was observed until the end of the fifth cycle (15 h), whereas additional bands were generated on the cathode side of this band in subsequent cycles. These bands were generally thin and fragmented, suggesting that there was little Al(OH)₃ precipitate in the band. Similar results were observed for the Ni anode system (E_L = 1 V).

When using Sn anodes (Fig. 8(B) and Fig. S13, ESI†), a relatively broad white band emerged during the second cycle (∼5 h). This band gradually thickened until the end of the sixth cycle, suggesting accumulation of the precipitates (which would be hydrated oxides rather than Sn(OH)₂^25,26). After the sixth cycle, further discrete bands were successively generated at the cathode side with increasing N_C. For cycle N_C, the number of periodic bands followed the relationship N_B = N_C − N_start + 1, where N_start is the number of the cycle immediately before successive discrete precipitation bands started to form with N_C. The thickness of each successive band decreased slightly. The successive formation of periodic precipitation bands was similar to that observed for the Fe(OH)₃ system previously.⁹ However, these systems differ significantly in that N_start = N_C1 for the Fe anode system,⁹ whereas N_start = 6 and N_C1 = 2 for the Sn anode system. A similar discrepancy between N_start and N_C1 was observed for Ni (E_L = 2 V, N_start = 4 and N_C1 = 3) and In anode systems (N_start = 5 and N_C1 = 2).

The spatiotemporal evolution of the periodic bands formed in systems with Cu anodes (Fig. 8(C) and Fig. S14, ESI†) was similar to that in systems with Fe anodes;⁹ the periodic bands were successively generated at the cathode side, following the relation N_B = N_C − N_C1 + 1 (N_start = N_C1 = 2). As for the Sn anode systems, the band thickness decreased slightly with successive band formation up to 10 cycles (beyond 10 cycles, the band thickness occasionally deepened owing to overlapping of the newly formed bands, as observed in Fig. 5–7). Similar results were obtained for Co anode systems (N_start = N_C1 = 1).

The successive formation of periodic bands with N_C was also observed in systems with Zn anodes (Fig. 8(D) and Fig. S15, ESI†). Notably, in these systems, two discrete bands formed simultaneously during the first cycle, resulting in the relationship N_B = N_C − N_C1 + 2 (N_start = N_C1 = 1). This feature, as well as the considerable broadness and thickness of each band, suggests that Zn(OH)₂ easily precipitates under the current experimental conditions.

In summary, unless the amount of precipitation is very low (such as for systems with Al anodes), periodic bands successively form toward the cathode with increasing N_C during voltage cycling. The anode material influences the banding pattern owing to differences in the cycle in which the first band emerges (N_C1 = 1–5), the number of bands that form in cycle N_C1 (N_B1 = 1 or 2), and the cycle immediately before successive band formation starts (N_start = 1–6). Additionally, the anode material influences the band thickness and spacing (compare, for example, the results of Al and Zn anode systems in Fig. 8(A) and (D)). The anode dependence of the precipitation patterns is presumably due to coupling between the voltage-dependent rate of the anode reaction and the pH-dependent rate (related to the K_sp values) of the precipitation reaction. Although the details remain unclear, preliminary considerations are provided later.

Electrochemical reactions at electrodes

Fig. 9 shows the time-dependence of the electric currents in gel columns with Al, Sn, Cu, and Zn anodes, corresponding to the precipitation patterns shown in Fig. 8. Until the end of the second cycle (∼6 h), the time-dependence of the electric current varied considerably, corresponding to the diversity in the formation of the first band(s) during this period. This diversity typically decreased over time and the patterns stabilized after a certain number of cycles (second cycle (6 h) for the Sn and Cu anodes and seventh cycle (21 h) for the Al and Zn anodes). For a clearer view of the stabilized patterns, the inset in Fig. 9 shows an enlarged view of the electric current for the Cu anode system. For each anode, during this stabilized period, the electric current changed in the following pattern with high periodicity: (i) a sharp rise upon shifting to the high voltage (E_H = 3 V), (ii) a gradual decrease during its application (T_H = 1 h), (iii) a sharp decay upon shifting to the low voltage (E_L = 1 V), and (iv) a gradual increase during its application (T_L = 2 h).

Fig. 9 Time-dependence of electric current in gel columns (L = 50 mm, ϕ = 4 mm, C_se = 10 mM) using Al, Sn, Cu, and Zn anodes at 298 K under the following voltage conditions: E_H = 3 V, E_L = 1 V, T_H = 1 h, T_L = 2 h, and N_C = 10. Each system had a Cu cathode. Inset: Enlarged plot for system using Cu anode.

Although the time-dependence of the electric current is not yet fully understood, the following points are notable. First, even at the low voltage (E_L = 1 V), non-zero electric currents flowed for all the systems studied, indicating that ion transport and thus precipitate formation likely occurred during E_L application. This finding suggests that the periodic bands may thicken and deepen in color during the low voltage period. Notably, this agrees with the current and previous⁹ experimental results.

Second, the sharp rise followed by a gradual decrease in electric current upon switching to the higher voltage (E_H = 3 V) is widely observed in potential-step experiments of conventional electrochemical systems, where the rate-limiting step of the electrode reactions is the mass transport of reactants in solution via thermal diffusion.^15,16,23 The corresponding current is often referred to as diffusion-limited. In the RTR systems, the reactants of the expected electrochemical reactions (M (anode) and H₂O (solvent); see Fig. 1) are abundant and are hence likely to generate a time-independent current rather than a diffusion-limited one. Thus, the observed current, which resembles a diffusion-limited one, suggests that side reactions involving relatively small amounts of reactant ions occur significantly at the electrodes, and the observed current consists of a time-independent component (due to the main reactions) and a diffusion-limited component (due to the side reaction). In addition, because the electric current had a similar intensity in each cycle (inset of Fig. 9) during the stage in which precipitation bands were successively generated, the concentration distributions of the reactant ions of the side reactions probably reverted around the electrodes every cycle during the corresponding stages.

The occurrence of side reactions was investigated by studying the surfaces of the spent electrodes in the Cu anode/Cu cathode RTR system (Fig. 10). Fig. 10(A) shows a photograph of the spent anode and cathode; the anode surface in contact with the agarose gel was stained dark, whereas the cathode surface was not. Fig. 10(B) shows an SEM image of the contact surface of the anode, where numerous deposits were observed. Fig. 10(C) and (D) show Cu L and O Kα intensity maps, respectively, of the image area. These maps indicate that the deposits contain Cu and O, suggesting that they comprise CuO.

Fig. 10 (A) Anode and cathode used in the Cu anode/Cu cathode RTR system. The broken circles indicate the surfaces in contact with the gel. (B) SEM image of black deposits adhering to the anode. Intensity maps of the (C) Cu L and (D) O Kα emission lines. The positions where Cu L and O Kα emissions were observed are shown as orange and green dots, respectively.

Thus, Fig. 10 suggests that a side reaction, Cu + 2OH⁻ → 2e⁻ + Cu(OH)₂ (blue-white) → CuO (black) + H₂O, occurs at the anode surface. The decrease in electric current after the second cycle (6 h) in Fig. 9 may be related to coverage of the anode surface by CuO deposits. Because OH⁻ ions are generated at the cathode, they must move to the anode to participate in this side reaction. OH⁻ ions are also consumed to generate Cu(OH)₂ precipitates in the gel. Hence, the number of OH⁻ ions at the anode surface is small enough to generate a diffusion-limited current. Systems with other anode materials showed similar results regarding deposit accumulation on the anode surface and a considerable decrease in current during E_H application after N_C = 2 (compare, for example, the corresponding currents of the Sn and Zn anode systems between N_C = 1 (from 0 to 1 h) and N_C = 4 (from 9 to 10 h) in Fig. 9). Thus, similar anode side reactions (M + nOH⁻ → M(OH)_n + ne⁻) are suggested to occur widely on various anodes.

Simulation results

The following parameters were chosen for numerical simulations using eqn (1)–(3): D_M = 7.0 × 10⁻¹⁰ m² s⁻¹; D_OH = 9.8 × 10⁻¹⁰, 1.26 × 10⁻⁹, 1.54 × 10⁻⁹, 1.82 × 10⁻⁹, and 2.10 × 10⁻⁹ m² s⁻¹; T = 300 K; X = 9.42 × (E_H or E_L) V m⁻¹; k = 50 mol m⁻³ s⁻¹; M_W = 97.56 g mol⁻¹ (the M_W value for Cu(OH)₂); n = 2; K_sp = 2.2 × 10⁻²⁰ (the K_sp value for Cu(OH)₂, see Table 1); α = 0.0083; β = 0.010; E_thre = 1.5 V; f_i = 0.8, 0.9, and 1.0; E_H = 3 V; E_L = 1 V; T_H = 1 h; T_L = 2 h; and L = 50 mm. The obtained results are plotted in Fig. 11–13, where the horizontal axis indicates the distance from the anode surface (x) and the vertical axis represents the density of precipitates or the concentration of reactant ions.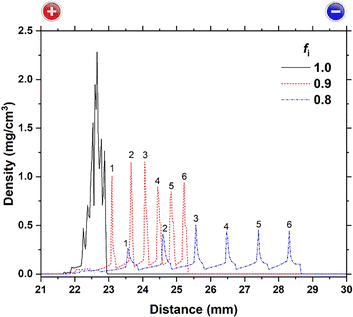

Fig. 11 Calculated D_OH/D_M dependence of the precipitate density distributions at t = 24 h (N_C = 8) for f_i = 1.0. For the data of D_OH/D_M = 1.8 and 2.6, the precipitation bands are numbered according to the order in which they are generated. The sides of the anode (+) and cathode (−), which exist at distances of 0 and 50 mm, respectively, are indicated at the top of the image.

Fig. 12 Imbalance parameter (f_i)-dependence of precipitate density distributions for D_OH/D_M = 2.2 at t = 24 h (N_C = 8). For the data of f_i = 0.8 and 0.9, the precipitation bands are numbered according to the order in which they are generated. The data for f_i = 1.0 is the same as that for D_OH/D_M = 2.2 in Fig. 11, but widened due to the larger scale. The sides of the anode (+) and cathode (−), which exist at distances of 0 and 50 mm, respectively, are indicated at the top of the image.

Fig. 13 Spatial density distributions of M(OH)₂ precipitates for D_OH/D_M = 2.2 and f_i = 0.8 at t = (A) 9 h, (B) 10 h, (C) 11 h, and (D) 12 h. The concentration distributions of M²⁺ (red) and OH⁻ (green) ions are also plotted, multiplied by 0.5 for clarity. For each time point, the location at which the two ion flows meet is indicated by a red arrow; these arrows are connected by orange dotted lines as a visual guide to demonstrate their temporal changes. The depletion regions of reactant ions near the electrodes are colored violet. The sides of the anode (+) and cathode (−), which exist at distances of 0 and 50 mm, respectively, are indicated at the top of the image.

A key condition for periodic banding in this theoretical model is the suppression of ion production at the electrodes during E_L application (i.e., C_M(0,t) = C_OH(L,t) = 0). Periodic bands are always generated in this model as long as this condition is satisfied, even if other parameters vary (although the banding properties strongly depend on the parameters used, as discussed below). Conversely, if a constant voltage is applied (E_H = E_L; no suppression of ion production), continuous banding occurs (Fig. S16, ESI†), which is consistent with the current (Fig. S17, ESI†) and previous⁹ experimental results. This finding suggests that the periodic suppression of ion production at the electrodes is fundamentally important for periodic banding in this model.

Fig. 11 shows the D_OH/D_M dependence of the density distributions of precipitates (ρ(x,t)) at t = 24 h (N_C = 8) in the simulation. Note that the distance x ranges from 0 mm at the anode surface to 50 mm at the cathode surface. The D_OH/D_M ratios reflect the difference in the transport velocities of the reactant ions due to both diffusion and migration (eqn (1) and (2)).

The simulation results indicate that periodic precipitation banding occurs over a wide range of D_OH/D_M ratios, although D_OH must be larger than D_M (D_OH ≈ 2D_M) to achieve effective periodic banding near the center of the gel (in contrast, when D_M > D_OH, precipitation occurs only in the immediate vicinity of the cathode). The simulated interband distances and band widths were approximately the same for each D_OH/D_M ratio, in agreement with the experimental results (Table 2, Tables S1–S4, ESI,† and Fig. 2, 3 and 5–8). Interestingly, the precipitate density distributions changed significantly with the D_OH/D_M ratio. For example, when D_OH/D_M = 2.2, only one precipitate density peak (which actually consists of several sub-peaks; see Fig. 12) emerged at x ≈ 22.5 mm (slightly toward the anode side). In contrast, six to eight bands were generated at the cathode (x ≥ 25 mm) and anode side (x ≤ 20 mm) for D_OH/D_M < 2.2 and D_OH/D_M > 2.2, respectively. Moreover, these bands successively formed toward the cathode and anode, respectively. The larger the deviation of D_OH/D_M from 2.2, the wider the band spacing.

Unfortunately, these interesting simulation results do not match the experimental results of the current RTR systems. As shown in Fig. 7 and by the x_1st values in Table 2 and Tables S1–S4 (ESI†), the periodic bands in the current RTR systems generally all formed at the anode side, which, according to the simulation results in Fig. 11, means that D_OH/D_M > 2.2. However, when D_OH/D_M > 2.2, the model showed successive band formation toward the anode, whereas the experimental results (Fig. 8 and Fig. S12–S15, ESI†) generally indicated successive formation toward the cathode. Furthermore, although this successive band formation toward the cathode was reproduced by the model when D_OH/D_M < 2.2, the precipitation bands first appeared on the cathode side, as opposed to the anode side in the experimental results (Table 2 and Tables S1–S4, ESI†). The model also suggests that the precipitate density is low in the first band and steadily increases up to the fourth band. These features are again inconsistent with the experimental results shown in Fig. 8 (particularly Fig. 8(B)) and Fig. S13 (ESI†), where the band thickness tended to decrease (slightly) with successive banding. It should also be noted that the D⁰ values for OH⁻ and Mⁿ⁺ ions (Table 1) have ratios of 7–10, which are considerably larger than the D_OH/D_M value of 2.2. These discrepancies suggest that factors other than D_OH > D_M are involved in the formation of periodic banding in the current RTR systems.

We next considered the influence of the quantitative imbalance between the produced and precipitated ions, represented by factor f_i (0 < f_i < 1). Fig. 12 shows the f_i dependence of the density distributions of precipitates obtained at D_OH/D_M = 2.2 and t = 24 h (N_C = 8). This figure indicates that quantitative imbalance (f_i < 1) can contribute to periodic banding. The profile for f_i = 1 (where reactant ions are produced and consumed at equal rates) is the same as that for D_OH/D_M = 2.2 in Fig. 11. Owing to the enlarged horizontal scale of Fig. 12, the single broad precipitate density peak (∼1 mm width) under these conditions can be more clearly observed to comprise several overlapping sub-peaks.

At f_i = 0.9 and 0.8 (i.e., where the ion consumption rate is 10% and 20% lower, respectively, than the production rate), six periodic bands were generated near the center of the gel (22 ≤ x < 29 mm). Notably, these bands developed toward the cathode with time (or N_C), holding the relation N_B = N_C − N_start + 1 (N_start = 3). The bands have relatively constant spacings (approximately 0.5 mm at f_i = 0.9 and 1.0 mm at f_i = 0.8) and their densities do not vary considerably. These features, obtained at a constant D_OH/D_M = 2.2, partially resolve the discrepancies between the model and experimental observations for D_OH/D_M < 2.2. Consequently, periodic precipitation banding in the current RTR systems, where bands develop successively toward the cathode, is suggested to involve a quantitative imbalance between the produced and precipitated ions (e.g., f_i < 0.9).

Fig. 13 shows the temporal evolution of the spatial density distribution of M(OH)₂ precipitates (ρ(x,t)) and the spatial concentration distributions of M²⁺ and OH⁻ ions (C_M(x,t) and C_OH(x,t)) for D_OH/D_M = 2.2 and f_i = 0.8. In general, the concentrations of M²⁺ and OH⁻ ions are higher on the anode and cathode sides, respectively, with the flows meeting toward the middle (the “meeting point” is indicated by a red arrow); this point also corresponds to the position of M(OH)₂ precipitation, as indicated by the growing M(OH)₂ density peak. The violet regions indicate depletion zones of reactant ions near the electrodes.

Fig. 13(A) shows the results at the end of the E_L period of N_C = 3 (t = 9 h). No reactant ions are generated at the electrodes during E_L application (7–9 h); therefore, the concentrations of these ions are suppressed in the regions around the electrodes (violet regions in Fig. 13(A)).

Fig. 13(B) shows the results at the end of the subsequent E_H period of N_C = 4 (t = 10 h). During E_H application, the ion depletion regions move toward the center of the gel, while ion production at the electrodes significantly increases the ion concentrations in the neighboring gel. The number of ions around the meeting point is relatively low at the beginning of E_H application (Fig. 13(A)); therefore, the amount of M(OH)₂ precipitation is also low. However, as the reactant ions are replenished by ion-transport from the electrodes, the amount of precipitation gradually increases over time (Fig. 13(B)). The quantitative imbalance factor in this simulation is below one (f_i = 0.8); therefore, more M²⁺ ions remain after M(OH)₂ precipitation than OH⁻ ions. This shifts the meeting point toward the cathode. A comparison between the results at 9 and 10 h (Fig. 13(A) and (B), respectively) shows a slight but definite increase in the M(OH)₂ density and movement of the meeting point toward the cathode with time.

Fig. 13(C) shows the results after 1 h of the subsequent E_L application of N_C = 4 (t = 11 h). Because reactant ions are not supplied from the electrodes during E_L application, depletion zones again form around the electrodes. Nevertheless, because of the relatively large influence of thermal diffusion (owing to the low E_L value), the concentration slopes of the reactant ions are smooth and broad. This ion diffusion means that a relatively large number of reactant ions, which were generated during the previous E_H period, gradually reach the meeting point to promote precipitation. Thus, during this period, the M(OH)₂ density increases sharply at the meeting point, with almost no change in its position. This favors the formation of a precipitation band.

Fig. 13(D) shows the results at the end of the E_L period of N_C = 4 (t = 12 h). During the second hour of E_L application, reactant ions are still not supplied from the electrodes. Thus, the total number of reactant ions in the gel continues to decrease, along with expansion of the depletion zones near the electrodes. Consequently, M(OH)₂ precipitation does not occur, except in the vicinity of the meeting point.

These processes are repeated in the following cycles to generate the periodic precipitation banding shown in Fig. 12. The above simulation results provide important information regarding the mechanism of periodic banding under quantitative imbalance conditions.

Mechanism of periodic banding of M(OH)_n precipitates through the RTR process

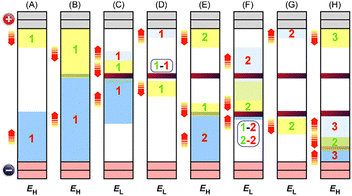
Based on the abovementioned experimental and simulation results, we propose a qualitative model for the periodic banding of M(OH)_n precipitates through RTR processes. Here, we focus on the successive periodic band formation with N_C, which is one of the most characteristic features of RTR periodic banding.⁹

To generate a precipitation band, the ion concentrations at the meeting point (i.e., where the two ion flows meet) must exceed the inherent K_sp value to precipitate M(OH)_n. If not, the two ion flows would pass each other, and the reactant ions would disperse over the gel column. Therefore, M(OH)_n precipitation banding only occurs once sufficient reactant ions have accumulated in the column. This leads to variation in the numbers of cycles required for the first band to emerge (N_C1) and for discrete precipitation bands to begin forming successively toward the cathode (N_start). N_C1 and N_start are particularly dependent on the anode material, because the Mⁿ⁺ ion production rates on different anodes, and the K_sp values of different M(OH)_n precipitates, differ considerably. This expectation is consistent with the experimental results shown in Fig. 8 and Fig. S12–S15 (ESI†).

A schematic of the periodic banding mechanism from N_start is shown in Fig. 14. Here, the reactant ions produced before N_start are assumed to be (i) uniformly distributed over the gel column and (ii) sufficiently accumulated to successively generate precipitation bands immediately after N_start. Furthermore, for simplicity, we only consider the case where N_start = N_C1.

Fig. 14 Schematic of periodic banding mechanism of M(OH)_n precipitates in agarose gel through the RTR process. (A)–(H) are respective steps of E_H and E_L application over three cycles (“1,” “2,” and “3”) from N_start (N_start = N_C1 = “1”). Yellow and blue regions represent flows of Mⁿ⁺ and OH⁻ ions, respectively, and the numbers within them represent the cycle number in which these ions were generated. Dark red lines are M(OH)_n precipitation bands; the numbers correspond to the numbers of the ion flows that formed them.

In Fig. 14(A), the yellow and blue regions represent the continuous flows of Mⁿ⁺ and OH⁻ ions from the anode and cathode, respectively, during E_H application. The number “1” in the flows indicates that these ion flows were generated during cycle N_C1 (= N_start). In aqueous solutions and hydrogels, the diffusion coefficient D (or the mobility given as nFD/(RT)^16,23) of OH⁻ ions is generally expected to be higher than that of metal ions (Table 1) because of the Grotthuss mechanism.^16,23,27 This expected difference is favorable for the formation of periodic bands, as shown in Fig. 11. In Fig. 14(A), it is reflected in the difference in the lengths of the flows; the blue (OH⁻) region is significantly longer than the yellow (Mⁿ⁺) region.

Fig. 14(B) shows the point at which the two ion flows meet to generate M(OH)_n precipitates during the E_H period of cycle N_C1. The generated precipitation bands are expressed as dark red lines. Because the precipitation band is often not clearly visible to the naked eye during this period, the precipitation band in the figure is shown in lighter coloring.

Fig. 14(C) shows the ion distribution during the E_L period of cycle N_C1. Here, Mⁿ⁺ and OH⁻ ions are transported under the E_L voltage and consumed by M(OH)_n precipitation. The color of the precipitation band gradually darkens, in accordance with the experimental results reported previously⁹ and the simulation results in Fig. 13. Few reactant ions are generated at the electrodes because the E_L value is generally set below the E_thre value of the electrochemical reactions in Fig. 1. Consequently, depletion regions of Mⁿ⁺ and OH⁻ ions are generated around the anode and cathode, respectively (see Fig. 13).

The transport of OH⁻ ions in aqueous systems obeys the Grotthuss mechanism, which involves the rearrangement of bonds through a long chain of H₂O molecules; that is, the rupture of an O–H bond in one H₂O molecule and the rapid formation of a new O–H bond with a neighboring molecule.^16,23,27 When the Mⁿ⁺ and OH⁻ flows intersect in the RTR system, the rapid hopping of OH⁻ ions via the Grotthuss mechanism may allow them to move through the Mⁿ⁺ front, thereby suppressing M(OH)_n precipitation.

Owing to this hopping (or “tunneling”) mechanism, not all reactant ions precipitate in the first precipitation band; the Mⁿ⁺ and OH⁻ ion flows continue to move toward the opposite electrode beyond the precipitation band during E_L application (Fig. 14(C) and (D)). Because no new ions are generated at the electrodes under E_L application, their concentrations are too low to precipitate M(OH)_n beyond the precipitation band. Therefore, no further precipitation bands form during a given cycle. Instead, because the mobility of OH⁻ ions is relatively high owing to the Grotthuss mechanism, these ions may reach the anode and possibly react with its surface to form M(OH)_n deposits (Fig. 10). However, the relatively low electric current during the E_L period (Fig. 9) suggests that the rate of this side reaction is significantly low at this stage, resulting in the accumulation of OH⁻ ions around the anode. This situation is illustrated in Fig. 14(D).

During the E_H period of the subsequent cycle (N_C1 + 1), the rate of the side reaction between OH⁻ ions and the anode surface increases owing to the increased voltage. This causes the accumulated OH⁻ ions to be consumed rapidly, contributing to the generation of a diffusion-limited-like current during this period. The E_H application during this period also restarts the emission of Mⁿ⁺ and OH⁻ ions (labeled “2”) from the anode and cathode, respectively, as shown in Fig. 14(E). The electric current generated by these main reactions is expected to be time-independent owing to the abundance of reactants (M and H₂O). Consequently, the electric current observed during this period (as well as in subsequent E_H periods) may be the sum of a time-independent current (due to the main reactions) and a diffusion-limited current (due to the side reaction), which is consistent with the experimental results shown in the inset of Fig. 9.

Owing to their high mobility, most OH⁻ ions generated in cycle N_C1 will have reached the anode and been consumed by the end of the E_H period of cycle N_C1 + 1. In contrast, owing to their low mobility, the Mⁿ⁺ ions generated in cycle N_C1 may still be moving through the gel column. These Mⁿ⁺ ions (“1”) react with the newly generated OH⁻ ions (“2”) to generate a new band of M(OH)_n precipitates on the cathode side (Fig. 14(E)).

During the subsequent E_L period of cycle N_C1 + 1, Mⁿ⁺ ion flows “1” and “2” and OH⁻ ion flow “2” are transported to the newly formed band, forming precipitates and causing the color of the precipitation band to gradually darken (Fig. 14(F)). This precipitation band is therefore formed by three ion flows (Mⁿ⁺ “1” and “2” and OH⁻ “2”). It is this consumption of Mⁿ⁺ ion flow “1” that causes the quantitative imbalance between the produced and precipitated ions (f_i < 1), through which periodic banding toward the cathode is shown to be promoted in Fig. 12 and 13.

Owing to the tunneling mechanism, not all reactant ions precipitate in the second precipitation band. The Mⁿ⁺ and OH⁻ ion flows continue to move toward the opposite electrode beyond the precipitation band(s), resulting in the accumulation of OH⁻ ions around the anode, during this E_L application (Fig. 14(G)).

During the E_H period of the subsequent cycle (N_C1 + 2), Mⁿ⁺ and OH⁻ ions (labeled “3”) are released again from the anode and cathode, respectively (Fig. 14(H)). Mⁿ⁺ ions “2” react with OH⁻ ions “3” to generate a further precipitation band on the cathode side. The accumulated OH⁻ ions “2” around the anode are consumed rapidly, again contributing to the generation of a diffusion-limited-like current.

Similar processes are repeated during subsequent cycles to generate periodic M(OH)_n precipitation bands. However, because periodic banding through these processes is based on the delicate coupling between ion production at the electrodes, ion transportation, and ion consumption by precipitation, it can be easily disturbed, particularly after many cycles, when the distribution of reactant ions in the gel column is expected to be considerably complex.

In summary, our qualitative model explains the development of periodic precipitation bands, forming successively toward the cathode, through the following two factors: (i) the suppression of reactant ion generation during the E_L application periods, and (ii) the Grotthuss mechanism, which leads to differences in the mobility between Mⁿ⁺ and OH⁻ ions and a possible tunneling effect for M(OH)_n precipitation. These two factors are independent of the anode and cathode materials and are not critically influenced by the length or diameter of the gel column, leading to the observed generality of M(OH)_n periodic banding in RTR systems.

Future issues

This study provides an overview of the periodic banding of metal hydroxides through the cyclic-voltage-driven RTR process. Cyclic voltages are a form of temporal oscillation, which can sometimes mediate the formation of spatially patterned structures, such as periodic banding.¹⁷ Therefore, at first glance, periodic banding in this system might seem like a common phenomenon. However, this study raises an intriguing question: why do systems with precipitation bands that first appear on the anode side generate new bands successively toward the cathode? The rudimentary simulations used in this study were unable to completely solve this problem (Fig. 11 and 12). Therefore, we hypothesized that tunneling occurs via the Grotthuss mechanism (Fig. 14). This hypothesis currently lacks experimental and theoretical evidence. However, if confirmed, the tunneling mechanism would have profound effects on a wide range of research fields, because the Grotthuss mechanism is a fundamental concept in physical chemistry, particularly in electrochemistry, where it was originally proposed to explain the high mobility of H⁺ and OH⁻ ions.^16,23

In addition to the tunneling effect via the Grotthuss mechanism, RTR systems present several experimental and theoretical challenges that must be addressed. For instance, whereas this study focuses on the common features and fundamental aspects of RTR systems, detailed analyses of specific features in individual RTR systems, including the characterization of the generated precipitates in the gels (Fig. 4) and on the electrodes (Fig. 10), are left for future research. Indeed, many phenomena seem to be considerably dependent on the anode elements, as suggested by Fig. 8 and Fig. S12–S15 (ESI†), which should be investigated in more detail. In addition, to further verify the proposed qualitative model, spatiotemporal variations in the reactant ions should be experimentally monitored. For such monitoring, in situ pH measurements and time-resolved X-ray fluorescence measurements over the gel column during voltage cycling are of interest. The experimental setups for conducting these measurements are currently under consideration. Furthermore, sophisticated and quantitative simulation models that incorporate the suggested tunneling effect should be developed. Finally, the solvability of the extended Nernst–Planck model and the accuracy of the simulations should be confirmed mathematically. Theoretical efforts are currently underway.

Conclusions

Periodic pattern formation in RTR systems offers new insights into physical chemistry (particularly electrochemistry and pattern-forming phenomena) and is expected to provide new clues in the science and engineering of gels.¹⁷ Moreover, M(OH)_n precipitation systems are attracting new scientific interest as oscillating reaction (periodic reaction in time) systems.²⁸ Hence, this new class of periodic patterning systems, as well as related phenomena,^10,29 warrants further investigation.

Author contributions

HH conceptualized the study, conducted experiments, analyzed results, wrote the manuscript, and prepared the figures. RA, KY, and MN conducted experiments and analyzed results under the guidance of HH. TA developed software to simulate precipitation bands and conducted simulations. KO conducted simulations under the guidance of TA.

Conflicts of interest

There are no conflicts of interest to declare.

Data availability

The data supporting this article have been included as part of the ESI;† further inquiries can be directed to the corresponding author.

Acknowledgements

This research was funded by JSPS KAKENHI (grant number JP25K08563). The authors would like to thank R. Akita, K. Unayama, M. Okami, M. Takeuchi, and S. Tanaka for their help with the preparation of the gel samples. SEM-EDS was conducted by Dr T. Takagi of the Laboratory of Electron Microscopy, Japan Women's University.

References

1. E. Nakouzi and O. Steinbock, Sci. Adv., 2016, 2, e1601144.
2. R. E. Liesegang, Naturwiss. Wochenschr., 1896, 11, 353.
3. I. Das, A. Pushkarna and S. Chand, J. Colloid Interface Sci., 1992, 150, 178.
4. K. Krischer, in Modern Aspects of Electrochemistry, Number 32, ed. B. E. Conway, J. O’M. Bockris and R. E. White, Kluwer Academic, Plenum Publishers, New York, 1999, pp. 1–142.
5. I. Lagzi, Phys. Chem. Chem. Phys., 2002, 4, 1268.
6. I. Bena, M. Droz, I. Lagzi, K. Martens, Z. Rácz and A. Volford, Phys. Rev. Lett., 2008, 101, 075701.
7. T. Karam and R. Sultan, Chem. Phys., 2013, 412, 7.
8. V. Kireev, B. Shalabayeva, N. Jaichibekov, A. Nizamova and Z. Kozhabay, J. Phys.: Conf. Ser., 2019, 1391, 012120.
9. H. Hayashi, Front. Phys., 2023, 11, 1114106.
10. H. Hayashi and K. Yamada, Front. Phys., 2024, 12, 1365863.
11. H. K. Henisch, Crystals in Gels and Liesegang Rings, Cambridge University Press, Cambridge, 1988.
12. H. Nabika, Curr. Phys. Chem., 2015, 5, 5.
13. H. Nabika, M. Itatani and I. Lagzi, Langmuir, 2020, 36, 481.
14. T. Karam, H. El-Rassy, F. Zaknoun, Z. Moussa and R. Sultan, Chem. Phys. Lett., 2012, 525–526, 54.
15. J. Wang, Analytical Electrochemistry, John Wiley & Sons, Hoboken, New Jersey, 3rd edn, 2009.
16. K. B. Oldham, J. C. Myland and A. M. Bond, Electrochemical Science and Technology Fundamentals and Applications, John Wiley & Sons, Chichester, UK, 2012.
17. B. A. Grzybowski, Chemistry in Motion: Reaction−Diffusion Systems for Micro- and Nanotechnology, John Wiley & Sons, Chichester, UK, 2009.
18. J. B. Keller and S. I. Rubinow, J. Chem. Phys., 1981, 74, 5000.
19. P. Vanýsek, in CRC Handbook of Chemistry and Physics, ed. W. M. Haynes, CRC Press, Boca Raton, USA, 95th edn, 2014, pp. 8–20.
20. P. Vanýsek, in CRC Handbook of Chemistry and Physics, ed. W. M. Haynes, CRC Press, Boca Raton, USA, 95th edn, 2014, pp. 5–75.
21. P. Patnaik, Dean's Analytical Chemistry Handbook, McGraw-Hill, New York, 2nd edn, 2004.
22. N. Rajurkar and B. Ambekar, J. Mol. Liq., 2013, 180, 70.
23. C. M. A. Brett and A. M. O. Brett, Electrochemistry Principles, Methods, and Applications, Oxford University Press, New York, 1993.
24. M. Matsue, M. Itatani, Q. Fang, Y. Shimizu, K. Unoura and H. Nabika, Langmuir, 2018, 34, 11188.
25. W. D. Honnick and J. J. Zuckerman, Inorg. Chem., 1976, 15, 3034.
26. F. A. Cotton, G. Wilkinson, C. A. Murillo and M. Bochmann, Advanced Inorganic Chemistry, John Wiley & Sons, Chichester, UK, 6th edn, 1999.
27. N. Agmon, H. J. Bakker, R. K. Campen, R. H. Henchman, P. Pohl, S. Roke, M. Thämer and A. Hassanali, Chem. Rev., 2016, 116, 7642.
28. N. Német, H. S. Lawson, M. Itatani, F. Rossi, N. J. Suematsu, H. Kitahata and I. Lagzi, Molecules, 2025, 30, 1323.
29. H. Hayashi, Front. Phys., 2022, 10, 828444.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp01515d

---