 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Understanding electrochemical reactions using density functional theory: the bridging theoretical scheme of squares and experimental cyclic voltammetry†
Amir
Mahdian
,
Arsalan
Hashemi
 and
Kari
Laasonen
and
Kari
Laasonen
 *
*
Department of Chemistry and Material Science, School of Chemical Engineering, Aalto University, 02150 Espoo, Finland. E-mail: kari.laasonen@aalto.fi
First published on 9th June 2025
Abstract
Mechanistic redox and acid–base reactions play pivotal roles in numerous applications in both chemistry and biology. Bridging the gap between computational insights and experimental observations is crucial to illuminate the mechanisms underlying these redox processes. In this study, we investigate electrochemical reactions by using the scheme of squares framework for a set of tens of molecules that have been examined for redox flow batteries. Furthermore, we focused on developing our computational models by calibrating the calculated redox potentials against experimental data, thereby enhancing the predictive accuracy of our approach. These findings are relevant across a wide range of applications from energy storage to medicine and synthetic chemistry.
1. Introduction
The study of electron and proton transfer and its role in chemical reactions is fundamental to the functionality of various electrochemical devices including batteries, fuel cells, and electrolysis systems.1–6 To enhance the performance of these applications, a thorough understanding of the energy pathways within the reaction mechanism is required. Accordingly, both kinetics and thermodynamics analyses are essential for assessing electrochemical reactions.7,8In flow batteries,9,10 reversible electrochemical reactions are essential for facilitating successful charging and discharging. Full reversibility occurs when electrons move back and force between an electrode and a redox-active molecule in a potential cycle. This means that any additional reactions consuming electrons11 must be minimal. An acid–base reaction,12 disproportionation,13 electrode passivation,14 and molecule decomposition15 are examples of chemical reactions, which add complexity to the mechanism of electron transfer and potentially introducing irreversibility into the desired redox reaction. Of these reactions, the acid–base reaction is a relatively simple reaction where an acid donates a proton (H+) to a base, forming a conjugate base and a conjugate acid. When this reaction takes place alongside the redox reactions, it will alter the overall process.16 The acid–base reaction is rather easy to model and should be added to the redox potential modelling whereas the other reactions are more difficult to model.
Cyclic voltammetry (CV) is one of the most widely used techniques for characterizing redox-active systems.17–20 This involves applying a potential to an electrode relative to a fixed reference potential, such as the standard hydrogen electrode (SHE).21 The potential varies linearly over time within the electrochemical potential window of the electrolyte. As an indicator of the number of electrons transferred, the current is measured simultaneously. Therefore, it is possible to determine the number of oxidation states and their stability, reaction rates, and redox potentials.22 With common experimental methods, it is challenging to obtain atomic-level details. Consequently, computational analyses are very useful for gaining a deeper understanding of electrochemical properties and redox mechanisms.
Through electrochemical reaction analyses, kinetics assessments, however, require very time consuming computations or model simplification.23–25 The thermodynamic data are easily evaluated by determining the changes in the Gibbs free energy (ΔG) of the reactants and products which are equivalent to the experimental redox potential obtained from the CV analysis. Therefore, the key is to computationally examine various reaction pathways to determine whether the process involves a decoupled electron transfer (ET) and proton transfer (PT) or a coupled (simultaneous) proton–electron transfer (PET).26,27 These pathways can be systematically diagrammed along the sides and diagonal of a square, forming a representation known as an electrochemical scheme of squares.28–30
The density functional theory (DFT) approach31,32 in combination with implicit solvation models33 and a computational standard hydrogen electrode (SHE)34 are frequently used to simulate electrochemical environments. Despite their widespread use, these methods face challenges, including the accurate modeling of charged systems and addressing deficiencies in exchange–correlation (XC) functionals.35 These limitations can lead to discrepancies, for example, in the Gibbs free energy, compared to the experimental values.36
To address this issue, one can scale the DFT results to the corresponding experimental results. This adjustment should eliminate discrepancies and indirectly incorporate the experimental effects into the calculated values. Generally, the validity and diversity of the collected data are crucial. For instance, our group,37 along with others,38–40 scaled theoretical pKa values to match experimental values in various solvents for organic molecules. ET redox potential has also been calibrated to align with experimental values with accuracy as good as about 0.1 V.41–44 For example, Hamza et al.42 adjusted the redox potential for pyridinium derivatives. These studies focus only on ET whereas we will also include the PET reactions.
In what follows, we explain how the electrochemical scheme of squares can be employed to interpret and predict the experiments. We also scale the redox potentials for both the ET and PET reactions to align with experimental data. To this end, a systematic effort was made to establish a relationship that reconciles the discrepancies between theoretical predictions and experimental measurements. This approach not only deepens our understanding of redox behavior but also establishes a foundational framework for accurately predicting the electrochemical properties of new molecular systems in other related fields of research.
2. Criteria for electrochemical reversibility
2.1. Redox potential
The CV technique measures the relationship between the potential and the current resulting from electrochemical reactions occurring at the working electrode surface. These reactions can be exemplified by the following reduction process:| [electrode]n + Xm → [electrode]n−ne + Xm+ne | (1) |
In this reaction, n and m represent the numbers of electrons in the electrode and molecule X, respectively. Additionally, ne represents the number of electrons transferred from the electrode to X during the reduction reaction. A reverse reaction, known as oxidation, can also be considered. During the redox (reduction–oxidation) process, each species may also undergo proton (H+) transfer reactions:
| Xm + npH+ → [XHnp]m−np. | (2) |
When the electrode potential is applied, the current peaks as a function of the ratio of the activities of the oxidized (ox) and reduced (red) species at the potential E:
 | (3) |
This equation is referred to as the Nernst equation.45 Here, E0ox/red is defined as the standard potential, which is equal for both the reduction and oxidation reactions. The parameter ai, which denotes the activity of species i, is defined as follows:
Now, let us examine how different reactions impact E:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio for the ET reactions (the oxidized and reduced species have the same activity) allows us to disregard the second term of eqn (3), simplifying it to E = E0ox/red (because ln
1 ratio for the ET reactions (the oxidized and reduced species have the same activity) allows us to disregard the second term of eqn (3), simplifying it to E = E0ox/red (because ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 = 0). E0ox/red can also be computed with quantum chemistry using the following equation:
1 = 0). E0ox/red can also be computed with quantum chemistry using the following equation: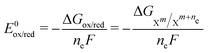 | (4) |
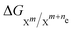 denotes the change in the Gibbs free energy associated with the different charge states of the molecule. Gibbs free energy of each molecule was computed using quantum chemistry software (Gaussian 16), employing the SMD solvation model to account for solvation effects.
denotes the change in the Gibbs free energy associated with the different charge states of the molecule. Gibbs free energy of each molecule was computed using quantum chemistry software (Gaussian 16), employing the SMD solvation model to account for solvation effects.
| [electrode]n + Xm + npH+ → [electrode]n−ne + [XHne]m+ne−np. | (5) |
In such a reaction, the activity of H+ is conventionally set to 1 (pH of 0) to determine E0ox/red. Eqn (4) is used again, but in this instance, with 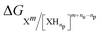 . The activity of the H+ species can be adjusted by the pH of the solution, as described by the following equation:
. The activity of the H+ species can be adjusted by the pH of the solution, as described by the following equation:
| pH = −log(aH+) | (6) |
Consequently, the activity aH+ is determined as follows:
| aH+ = 10−pH | (7) |
In reactions where there are np protons involved (as outlined in eqn (5)), the activity ratio can be expressed as follows:
 | (8) |
Integrating eqn (3), (7) and (8), the Nernst equation can be reformulated for our specific system as follows:
 | (9) |
At room temperature, the value of RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(10)/F is approximately 0.059 eV.
ln(10)/F is approximately 0.059 eV.
2.2. Reversible electrochemical reactions using the scheme of squares
The electrochemical reaction will be regarded reversible when oxidation and reduction reactions mirror each other near the E0ox/red. The E0ox/red is the average of voltage of the anodic and cathodic current peaks. In such cases, the characteristic duck-shaped voltammogram also indicates an absence of degradation reactions during measurements. There can be some electrochemical reactions within the potential scanning window with different E0,nox/red. They will be analysed in a similar manner as a single reaction. If all reactions are reversible, the total potential cycle is reversible. The applied potential has to be limited within the solvent electrochemical potential window (Ew). This is needed to exclude the reactions of the solvent molecules. For aqueous solutions, the Ew value is between −1.5 and +1.5 VSHE.46The irreversibility can be caused by the PT (or PET) reaction. The pKa 's of a molecule depend strongly on the charge state of it and we can assume that the pH is constant during the potential cycle. At certain voltage, a molecule can get to a protonation state which it cannot return to the earlier state via ET or PET, as demonstrated in examples presented later in this manuscript. As we study only a single molecule without changing its backbone connectivity, we cannot address irreversibility by molecule breaking, dimerization or other more complex reactions.
3. Computational frameworks
All DFT calculations were conducted using Gaussian 16 software.47 Molecular geometry optimizations were conducted using two separate sets of calculations: (i) the 6-31G(d) basis set48 combined with the M06-2X functional48 and (ii) the PM7 semiempirical method,49 both of which incorporate the SMD solvation model.50 Numerous studies have demonstrated the reliability of M06-2X in accurately predicting the reaction energies of organic transformations.51–58 The SMD solvation model has been widely used, and it is the best solvation model available in Gaussian. The frequency data were subsequently calculated at the same level of analysis. For total energy, the Def2-TZVP basis set,59 coupled with the M06-2X functional, was utilized to perform single-point energy calculations. We will refer to these two sets of calculations as 6-31G(d)-Def2TZVP and PM7-Def2TZVP. All numerical values in the manuscript and ESI† are computed with the 6-31G(d)-Def2TZVP method. Generally, the reactions can be represented by the following equation:| XHn ⇌ [XHn−np]ne + npH+ + nee− | (10) |
As previously discussed, the required H+ is sourced from an aqueous solution, while e− is derived from an electrode.
To assess the thermodynamics of the reaction, it is essential to determine the Gibbs free energy of each state involved in the process. The Gibbs free energies of the XHn and [XHn−np]ne species can be readily analyzed, while the energetics of H+ and e− prove to be more complex. To address this issue, two following reactions are essential:
(i) The standard potential of the hydrogen electrode, as the reference electrode, is 0 V for the reaction written as
 | (11) |
(ii) An experimental pKa, as a reference, is employed to capture the H+(aq) Gibbs free energy. Herein, the formic acid (HCOOH) dissociation reaction with a pKref.a of 3.77 is employed:60
| HCOOH → HCOO− + H+. | (12) |
The logarithm of an acidity constant (Ka), represented by the pKa value, is defined as follows:
 | (13) |
Therefore, the reference Gibbs free energy change for reaction (12), denoted as ΔGref.PT, is calculated to be 0.224 eV.
The calculation of the Gibbs free energies for HCOOH and HCOO− can be easily performed. We determined that the Gibbs free energy of the solvated proton, denoted as GH+(aq), is −11.798 eV. Referring back to eqn (11), we can compute that Ge− = −4.115 eV. This value is based on computations defined above and it differs a bit from the IUPAC recommendation of −4.44 eV.
Subsequently, the obtained pKa values need to be adjusted to address limitations inherent in the implicit solvation model used in our study,37 as described below:
| pKscaleda = 0.49 × pKa + 3.2 | (14) |
As previously noted, no scaling formula has been established for the redox potentials of the ET and PET reactions that fit our computational setup. In the present study, we delineated these relationships.
4. Results and discussion
4.1. Scheme of square usage
To enhance the understanding of the calculations performed in this study, three distinct molecules were selected from various literature sources to evaluate the scheme of squares method, with comparisons made to experimental cyclic voltammetry (CV) data. In the first case, a single molecule was tested across a broad pH range experimentally, and the scheme of square calculations were performed at pH 7, pH 3, and pH 6, with results at pH 3 and pH 6 presented in the ESI.† In the second example, it was demonstrated that for molecules possessing a common backbone but varying positions of functional groups, some of the resulting compounds exhibited reversible behavior, while others did not. The third example highlighted that by modifying the applied potential, certain molecules could display reversible or irreversible characteristics. | ||
| Fig. 2 (a) OTDFL participates in the ET and PET reactions during the reduction process. The oxygen atom in the ketone group is protonated. (b) Experimental cyclic voltammetry of OTDFL at different pH values from 3 to 7, taken from ref. 61. (c) The electrochemical scheme of the squares of OTDFL at pH 7. Vertical, horizontal, and diagonal arrows indicate the PT, ET, and PET reactions, respectively. PT is gauged by pKa, whereas ET and PET are assessed by redox potentials in V, with PET potentials adjusted for the corresponding pH. The redox potential was referenced to the SHE. X represents the OTDFL compound. | ||
CV experiments were conducted using 1 mM OTDFL at various pH values. The redox potential for the initial redox process remained untouched at 0.16 V. In contrast, the redox potential for the subsequent redox process exhibited a downward shift from 0.12 V to −0.09 V as the pH increased from 3 to 7. This pH-dependent variation in the second redox process demonstrated a slope of 0.059 V per pH unit, indicative of a PET reaction (Fig. 2(b)). Consequently, a single peak with a slight shoulder evolves into a two-peak diagram, where the higher-potential-positioned peak is always fixed. All reactions were reversible.
Our scheme of squares (Fig. 2(c)) elucidates the following aspects of the redox reactions: (i) at all studied pH levels, OTDFL is first reduced through the ET reaction; (ii) the second electron transfer proceeds via a PET reaction, influencing the redox potential downshifts in response to the pH increases; (iii) the pathway X-to-X−-to-XH− remains consistent throughout the redox processes; (iv) at pH values less than 3 or greater than 9.3, redox reactions should not be reversible, terminating at XH2 under acidic conditions or X2− under alkaline conditions; (v) a minor discrepancy between experimental and computational redox potentials. This will be discussed in the Scaling redox potential section. Overall, we found good agreement between our calculations and the experimental results. The scheme of squares for pH values of 3 and 6 is found in Fig. S1 of the ESI.†
 | ||
| Fig. 3 (a) Graphical representation of 9-fluorenone (FL) with numbered functionalization sites. (b) Experimental cyclic voltammetry measurements were conducted on 10 mM solutions of carboxylic acid-functionalized FL compounds in 1 M KOH. The scan rate was set at 100 mV s−1, as reported by Rodriguez et al.62 The compounds are named FL-1CA, FL-2CA, and FL-4CA. (c)–(f) Electrochemical scheme of squares of 9-fluorenone derivatives (FL-nCA) including FL-1CA, FL-2CA, FL-3CA, and FL-4CA, at a pH of 14. Vertical, horizontal, and diagonal arrows indicate PT, ET, and PET reactions, respectively. PT is evaluated by pKa, while ET and PET are assessed by redox potentials in VSHE, with PET potentials adjusted for a pH of 14. XH+ represents the initial compound before equilibration (with COOH). | ||
The electrochemical tests of FL-1CA, FL-2CA, and FL-4CA isomers are shown in Fig. 3(b). The FL-1CA compound underwent an irreversible reaction, whereas both FL-2CA and FL-4CA showed reversiblity. FL-1CA was reduced at a lower potential (≈−0.812 V), indicating that it is more difficult to add an electron to it compared to FL-2CA and FL-4CA, which both had a similar reduction potential of approximately −0.69 V. In experiments, a wider range of electrode potentials was used in the CV analysis of FL-1CA.
Adding the CA functional group not only increases the solubility of the compounds but also makes them more likely to undergo PT reactions during the stabilization process before starting CV measurements. FL-nCA derivatives can release H+ depending on the pH of the environment. If the compound is more acidic than its surroundings, it acts as a proton donor, releasing hydrogen ions and transforming –COOH into –COO−.
The calculated pKa values for FL-1CA, FL-2CA, FL-3CA, and FL-4CA are 5.8, 4.4, 5.9, and 4.8, respectively, as shown in Fig. 3(c)–(f). The initial compound in each scheme is denoted as XH+. Our calculated values indicate that these compounds are acidic and can immediately lose a proton under alkaline conditions. XH+ is converted into X.
It is important to note that when –COOH is positioned next to the ketone group (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O), it can form an internal hydrogen bond, significantly altering the electrochemical properties of the compound. As illustrated in Fig S2 (ESI†), the FL-1CA-H radical (XH form) is more stable than the other isomers due to the close proximity of the COOH hydrogen to the ketone oxygen. This increased stability reduces its acidic nature; compare the pKa values of different isomers in their XH form. FL-1CA-H has a pKa value of above 10, and the others are around 6.5. So it is less likely to be deprotonated. Overall, a planar structure is more favorable for all species in their XH radical form.
O), it can form an internal hydrogen bond, significantly altering the electrochemical properties of the compound. As illustrated in Fig S2 (ESI†), the FL-1CA-H radical (XH form) is more stable than the other isomers due to the close proximity of the COOH hydrogen to the ketone oxygen. This increased stability reduces its acidic nature; compare the pKa values of different isomers in their XH form. FL-1CA-H has a pKa value of above 10, and the others are around 6.5. So it is less likely to be deprotonated. Overall, a planar structure is more favorable for all species in their XH radical form.
To analyze the CV diagrams, one should begin with the deprotonated form X. The redox reaction of FL-1CA is irreversible, exhibiting only one peak at a pH of 14. This indicates that it can be reduced but cannot be fully oxidized back to its original state. Fig. 3(c) shows that X participates in two distinct reactions at similar redox potentials: ET and PET. For example, if X undergoes a PET reaction and forms an XH radical, it can evolve into either XH−, XH2, or X−. The first two pathways involve reduction, while the third pathway involves a deprotonation reaction. Conversely, if X forms X− radicals via an ET reaction, the subsequent step is a PET reaction, in which XH− equilibrates with XH2. The predominant pathway is determined by the reaction kinetics. However, the presence of multiple reactive species in the solution not only reduces the oxidation rate but may also increase the likelihood of side reactions.
The placement of the –COOH group at sites 2, 3, and 4 completely changed the reaction mechanism. Only one reaction can occur: the formation of X− from X. The X-to-XH pathway is blocked because at a pH of 14 it is hard to source H+. Applying more potential could push the PET reaction to occur in the range of −1.062 to −1.071 V. In the experiment, the applied potential was increased to −0.9 V; therefore, only one peak is expected.
 | ||
| Fig. 4 BenPy participates in the ET and PET reactions during the reduction process when a potential of up to −1 V is applied. (b) Experimental cyclic voltammetry of BenPy at different applied potentials of −0.73 and −1 V versus the SHE, taken from ref. 63. (c) The electrochemical scheme of the squares of BenPy at pH 7. Vertical, horizontal, and diagonal arrows indicate the PT, ET, and PET reactions, respectively. PT is gauged by pKa, whereas ET and PET are assessed by redox potentials in V, with PET potentials adjusted for the corresponding pH. The redox potential was referenced to the SHE. X represents the BenPy. | ||
The CV analysis exhibited two peaks at −0.63 and −0.73 V, with poor reversibility (Fig. 4(b), green symbols). Nonetheless, adhering to a conservative CV sweep limit of −0.73 V prevented adverse second reduction, revealing a reversible diagram (Fig. 4(b), blue symbols). Furthermore, during the bulk electrolysis experiments, the dissolution of compound X− in 1 M KOH (pH ≈ 14) at room temperature without the application of any potential demonstrated no reactivity. Conversely, dissolving in a 0.1 M HCl (pH ≈ 1) aqueous solution resulted in nearly instantaneous bleaching of the purple color of the radical.
Using the electrochemical scheme (Fig. 4(c)), starting with species X at a pH of 7, a potential of −0.331 V is required to initiate the first ET reaction. Subsequently, the second electron is transferred at −0.492 V through a PET mechanism, converting X− to XH−. Because this reaction is influenced by the pH, the redox potential becomes more negative as the pH increases. Eventually, compound XH−, which displays stronger basic characteristics than the medium, can be protonated, forming species XH2. The deprotonation reaction is no longer favored, and the system remains trapped in this state, unless the applied potential facilitates its reversibility through a PET reaction.
Given that the PET oxidation reaction (XH2 to XH path) is thermodynamically unfavorable, a much higher positive electrode potential is required. A comparison of the reduction and oxidation potentials highlights a significant overpotential, indicating that the reaction proceeds sluggishly and ultimately irreversibly.
Similar to the experiment, our calculations revealed a gap between the redox potentials of the ET (from X to X−) and PET (from X− to XH−) reactions. However, similar to the previous example, the calculated potentials were overestimated compared to the experimental values. Thus, calibration of the calculated values against the experimental data becomes useful.
Additionally, the bulk electrolysis results are supported by a pKa value of 3 for the XH-to-X− deprotonation reaction. This indicates that at a pH of >3, X− will remain stable in the solution, while at lower pH values, it will accept a proton and will be converted into XH. This explains the observed color change of the solution.
4.2. Scaling redox potentials
In addition to the three examples above, we have investigated 60 additional molecules and compared them to experimental CV analysis collecting data from the aqueous organic redox flow battery64–66 literature. For each case, we examined the reaction pathway and collected the corresponding redox potential quantities. The scheme of squares sheds light on which the ET or PET reaction corresponds to the observed current peak (further details are provided in Sections V and VI of the ESI†). The molecules considered for this purpose include quinones,67 phthalazines,68 phenazines,69 benzidines,70 TEMPO,71 and viologens.72 To our knowledge, this is the broadest comparison of the computational and experimental scheme of squares results.For the PET reactions, the redox potentials were adjusted to a pH of 0 using the Nernst equation (eqn (9)). All experiments were performed at room temperature. In total, 60 and 36 samples were used to establish linear scaling relationships for ET and PET, respectively.
To calculate the scheme of squares, we considered two computational setups. First, a more precise M062X-Def2TZVP setup was used which is suitable for the single-case studies, due to its high computational cost. Second, a PM7-Def2TZVP combination was employed, which is crucial for large database generation, as we did previously.30
As shown in Fig. 5, our computational setup demonstrated notable accuracy, particularly in the realm of ET reactions. Here, we report a R2 value of 0.98 and a scaling relationship of 0.91E0dft − 0.12. Our PET model has a small intercept value of 0.04 V. With a slope of 0.85, the calculations slightly overestimates the redox potential. The R2 value of 0.89 indicates a good level of reliability. Comparing to the fast calculations (see Fig. S3, ESI†), where a different method was used for geometry optimization (DFT vs. semiempirical method), we observed only slight variations in the coefficients of the linear model. This outcome is consistent with the findings reported in ref. 37 regarding pKa. The values reported earlier in this paper are unscaled but applying fitting relationships for the potentials, we generally find closer agreement with the experiments.
We see that the good scaling relationship is strong proof that our simple computational approach has good predictive power. The experimental systems are complex, with real electrodes, done in various pH values, possible concentrations and transport effects, whereas we model only one molecule with the continuum solvation model, and still the agreement is good on a large set of molecules. More detailed models for electrochemical reactions can be used23,73 but they are very time consuming and unsuitable for molecular screening. The current scaling results are very encouraging but if this computational approach is used for quite different molecules than studied here, careful comparisons to experimental results are needed.
The molecules presented in the ESI† provide a lot of details of the ET, PT and PET reactions of a rather broad range of molecules. With compounds 1–36, the agreement with experiments is good. Compounds A–F are more challenging and some results are not in good agreement. This is partly due to the complexity of the molecules and there can be other reactions, than the proton reactions we studied here, which affect the measured redox potentials.
5. Conclusions
Separating the PET reaction into distinct ET and PT reactions is experimentally possible but rather time consuming whereas it is computationally easy. With the computational setup in this work, the virtual screening of redox potentials of a large set of organic molecules is feasible. We can perform the electrochemical scheme of square computations and predict the experimental redox potentials at given pH values. The observed good scaling relationships with a quite large amount of molecules demonstrate that the computational procedure is reliable. These computations will also provide information on the reaction type (ET, PT, or PET). The computational approach can explain, in some cases, the irreversibility observed in cyclic voltammetry. Our approach is limited to irreversibility caused by the protonation states. Overall, the computations will provide a lot of information on electrochemical ET, PT, and PET-type reactions. This is useful when searching molecules with desired redox potentials at certain pH. These findings can be applied to redox reactions and acid–base reactions across a wide range of scientific fields, including energy storage, medicine, and synthetic chemistry.Author contributions
Amir Mahdian: investigation, software, methodology, formal analysis, data collection and writing. Arsalan Hashemi: conceptualization, software, data curation, and writing – review and editing. Kari Laasonen: conceptualization, resources, funding acquisition, project administration, supervision, and writing – review and editing.Conflicts of interest
There are no conflicts to declare.Data availability
Detailed molecular structures and computational inputs are available for download from the Zenodo database (https://zenodo.org/records/12736686).Acknowledgements
This project has received funding from the European Union – NextGenerationEU instrument via Research Council Finland under grant number 348327. We thank the CSC – IT Center for Science for computational resources.References
- X. Chen, X. Xie, P. Ruan, S. Liang, W.-Y. Wong and G. Fang, ACS Energy Lett., 2024, 9, 2037–2056 CrossRef CAS.
- R. Feng, Y. Chen, X. Zhang, B. J. Rousseau, P. Gao, P. Chen, S. T. Mergelsberg, L. Zhong, A. Hollas, Y. Liang, V. Murugesan, Q. Huang, E. Walter, S. Hammes-Schiffer, Y. Shao and W. Wang, Joule, 2023, 7, 1609–1622 CrossRef CAS.
- T. V. Sawant, C. S. Yim, T. J. Henry, D. M. Miller and J. R. McKone, Joule, 2021, 5, 360–378 CrossRef CAS.
- S. Srinivasan, Fuel Cells: From Fundamentals to Applications, Springer Science & Business Media, 2006 Search PubMed.
- W. Mook, M. Aroua and G. Issabayeva, Renewable Sustainable Energy Rev., 2014, 38, 36–46 CrossRef CAS.
- S. Grigoriev, V. Fateev, D. Bessarabov and P. Millet, Int. J. Hydrogen Energy, 2020, 45, 26036–26058 CrossRef CAS.
- M. Seralathan and S. Rangarajan, J. Electroanal. Chem., 1985, 191, 209–228 CrossRef CAS.
- C. Wiberg, M. Busch, L. Evenäs and E. Ahlberg, Electrochim. Acta, 2021, 367, 137480 CrossRef CAS.
- Q. Xu and T. S. Zhao, Prog. Energy Combust. Sci., 2015, 49, 40–58 CrossRef.
- G. L. Soloveichik, Chem. Rev., 2015, 115, 11533–11558 CrossRef CAS PubMed.
- A. Orita, M. Verde, M. Sakai and Y. Meng, J. Power Sources, 2016, 321, 126–134 CrossRef CAS.
- M. M. Cooper, H. Kouyoumdjian and S. M. Underwood, J. Chem. Educ., 2016, 93, 1703–1712 CrossRef CAS.
- T. Ree, J. Chem. Educ., 1971, 48, 467 CrossRef CAS.
- M. Ingelsson, N. Yasri and E. P. L. Roberts, Water Res., 2020, 187, 116433 CrossRef CAS PubMed.
- O. Nolte, P. Rohland, N. Ueberschaar, M. D. Hager and U. S. Schubert, J. Power Sources, 2022, 525, 230996 CrossRef CAS.
- M. Pourbaix, Corrosion, 1950, 6, 395–404 CrossRef CAS.
- G. A. Mabbott, J. Chem. Educ., 1983, 60, 697 CrossRef CAS.
- N. Elgrishi, K. J. Rountree, B. D. McCarthy, E. S. Rountree, T. T. Eisenhart and J. L. Dempsey, J. Chem. Educ., 2018, 95, 197–206 CrossRef CAS.
- P. Chooto, Voltammetry, IntechOpen, 2019, p. 1 Search PubMed.
- N. Navashree and P. Parthasarathy, Mater. Today: Proc., 2023 DOI:10.1016/j.matpr.2023.05.175.
- G. Korotcenkov, S. D. Han and J. R. Stetter, Chem. Rev., 2009, 109, 1402–1433 CrossRef CAS PubMed.
- J. J. Van Benschoten, J. Y. Lewis, W. R. Heineman, D. A. Roston and P. T. Kissinger, J. Chem. Educ., 1983, 60, 772 CrossRef CAS.
- A. Hashemi, P. Peljo and K. Laasonen, J. Phys. Chem. C, 2023, 127, 3398–3407 CrossRef CAS PubMed.
- J. Kim and H. Park, Renewable Energy, 2019, 138, 284–291 CrossRef CAS.
- V. Muralidharan, S. Jayasubramaniyan and H.-W. Lee, EES Catal., 2024, 2, 522–544 RSC.
- E. L. Lebeau, R. A. Binstead and T. J. Meyer, J. Am. Chem. Soc., 2001, 123, 10535–10544 CrossRef CAS PubMed.
- S. Hammes-Schiffer, Chem. Rev., 2010, 110, 6937–6938 CrossRef CAS PubMed.
- E. Laviron and L. Roullier, J. Electroanal. Chem., 1985, 186, 1–15 CrossRef CAS.
- M. Okubo, K. Kawai, Z. Ma and A. Yamada, Acc. Mater. Res., 2022, 3, 33–41 CrossRef CAS.
- A. Hashemi, R. Khakpour, A. Mahdian, M. Busch, P. Peljo and K. Laasonen, Digital Discovery, 2023, 2, 1565–1576 RSC.
- K. Burke, J. Chem. Phys., 2012, 136, 150901 CrossRef PubMed.
- F. Giustino, Materials Modelling Using Density Functional Theory: Properties and Predictions, Oxford University Press, 2014 Search PubMed.
- K. Mathew, R. Sundararaman, K. Letchworth-Weaver, T. Arias and R. G. Hennig, J. Chem. Phys., 2014, 140, 084106 CrossRef PubMed.
- J. Rossmeisl, Z.-W. Qu, H. Zhu, G.-J. Kroes and J. Nørskov, J. Electroanal. Chem., 2007, 607, 83–89 CrossRef CAS.
- M. Bursch, J.-M. Mewes, A. Hansen and S. Grimme, Angew. Chem., Int. Ed., 2022, 61, e202205735 CrossRef CAS PubMed.
- R. P. Fornari and P. de Silva, Molecules, 2021, 26, 3978 CrossRef CAS PubMed.
- M. Busch, E. Ahlberg, E. Ahlberg and K. Laasonen, ACS Omega, 2022, 7, 17369–17383 CrossRef CAS PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- A. Klamt, F. Eckert, M. Diedenhofen and M. E. Beck, J. Phys. Chem. A, 2003, 107, 9380–9386 CrossRef CAS PubMed.
- T. N. Brown and N. Mora-Diez, J. Phys. Chem. B, 2006, 110, 9270–9279 CrossRef CAS PubMed.
- L. Tomaník, L. Rulíšek and P. Slavíček, J. Chem. Theory Comput., 2023, 19, 1014–1022 CrossRef PubMed.
- A. Hamza, F. B. Nemeth, d Madarasz, A. Nechaev, P. M. Pihko, P. Peljo and I. Papai, Chem. – Eur. J., 2023, 29, e202300996 CrossRef CAS PubMed.
- A. R. McNeill, S. E. Bodman, A. M. Burney, C. D. Hughes and D. L. Crittenden, J. Phys. Chem. C, 2020, 124, 24105–24114 CrossRef CAS.
- M. Namazian, C. Y. Lin and M. L. Coote, J. Chem. Theory Comput., 2010, 6, 2721–2725 CrossRef CAS PubMed.
- A. J. Bard, L. R. Faulkner and H. S. White, Electrochemical Methods: Fundamentals and Applications, John Wiley & Sons, 2022 Search PubMed.
- D. Pavlov, Lead-Acid Batteries: Science and Technology: A Handbook of Lead-Acid Battery Technology and Its Influence on the Product, Elsevier Science Limited, 2011 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. J. Montgomery, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision C.01, 2016, Gaussian Inc., Wallingford CT Search PubMed.
- P. Hariharan and J. Pople, Theor. Chim. Acta, 1973, 28, 213–222 CrossRef CAS.
- J. J. Stewart, J. Mol. Model., 2013, 19, 1–32 CrossRef CAS PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- K. Farshadfar and K. Laasonen, ACS Catal., 2024, 14, 14486–14496 CrossRef CAS PubMed.
- T. Zheng, J. Ma, H. Chen, H. Jiang, S. Lu, Z. Shi, F. Liu, K. N. Houk and Y. Liang, J. Am. Chem. Soc., 2024, 146, 25058–25066 CrossRef CAS PubMed.
- C. R. Travis, R. G. Dumais, J. W. Treacy, K. M. Kean, K. N. Houk and M. L. Waters, J. Am. Chem. Soc., 2024, 146, 20678–20684 CrossRef CAS PubMed.
- P. Ma, D. Svatunek, Z. Zhu, D. L. Boger, X.-H. Duan and K. N. Houk, J. Am. Chem. Soc., 2024, 146, 18706–18713 CrossRef CAS PubMed.
- R. J. Monsky, Y. Li, K. N. Houk and W. R. Dichtel, J. Am. Chem. Soc., 2024, 146, 17150–17157 CrossRef CAS PubMed.
- M. Duan, Q. Shao, Q. Zhou, P. S. Baran and K. N. Houk, Nat. Commun., 2024, 15, 4630 CrossRef CAS PubMed.
- H. Tian, W. Lee, Y. Li, M. J. Dweck, A. Mendoza, P. G. Harran and K. N. Houk, J. Am. Chem. Soc., 2024, 146, 5375–5382 CrossRef CAS PubMed.
- S. Dutta, Y.-L. Lu, J. E. Erchinger, H. Shao, E. Studer, F. Schäfer, H. Wang, D. Rana, C. G. Daniliuc and K. N. Houk, et al. , J. Am. Chem. Soc., 2024, 146, 5232–5241 CrossRef CAS PubMed.
- F. Weigend, F. Furche and R. Ahlrichs, J. Chem. Phys., 2003, 119, 12753–12762 CrossRef CAS.
- J. Ho and M. L. Coote, Theor. Chem. Acc., 2009, 125, 3 Search PubMed.
- W. Li, J. Li, X. Yuan, Z. Xiang, Z. Liang and Z. Fu, J. Mater. Chem. A, 2023, 11, 19308–19311 RSC.
- J. Rodriguez, C. Niemet and L. D. Pozzo, ECS Trans., 2019, 89, 49 CrossRef CAS.
- C. S. Sevov, K. H. Hendriks and M. S. Sanford, J. Phys. Chem. C, 2017, 121, 24376–24380 CrossRef CAS.
- R. Chen, ChemElectroChem, 2019, 6, 603–612 CrossRef CAS.
- S. Gentil, D. Reynard and H. H. Girault, Curr. Opin. Electrochem., 2020, 21, 7–13 CrossRef CAS.
- C. Flox, C. Zhang and Y. Li, Curr. Opin. Chem. Eng., 2023, 39, 100880 CrossRef.
- R. H. R. H. Thomson, Naturally Occurring Quinones, Elsevier, 2012 Search PubMed.
- N. R. Patel, Phthalazines, John Wiley & Sons, Ltd, 1973, ch. II, pp. 323–760 Search PubMed.
- J. B. Laursen and J. Nielsen, Chem. Rev., 2004, 104, 1663–1686 CrossRef CAS PubMed.
- T. J. Haley, Clin. Toxicol., 1975, 8, 13–42 CrossRef CAS PubMed.
- T. Vogler and A. Studer, Synthesis, 2008, 1979–1993 CAS.
- C. L. Bird and A. T. Kuhn, Chem. Soc. Rev., 1981, 10, 49–82 RSC.
- R. Kronberg and K. Laasonen, ACS Catal., 2021, 22, 8062–8078 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp01464f |
| This journal is © the Owner Societies 2025 |



