Inhibition of oscillatory motion of a camphor float due to dissolution

Abstract

To elucidate significance of nonequilibrium at an air/aqueous interface during self-propulsion of a camphor object, oscillatory motion of a self-propelled object composed of a smaller camphor disk and larger plastic disk floating on an aqueous Na₂SO₄ phase was investigated. Both the frequency and maximum speed of the oscillatory motion decreased with an increase in the concentration of Na₂SO₄ in the aqueous phase, C_i. The decrease in the frequency of the oscillatory motion is attributed to the dissolution rate of camphor in the aqueous phase as a function of C_i. The frequency of the oscillatory motion was numerically calculated as a function of the dissolution rate constant, k, and the saturated concentration of camphor in the aqueous salt solution, C₀. The decrease in the maximum speed of the oscillatory motion as a function of C_i was reproduced by the difference in the surface tension (Δγ) as the driving force of motion and the friction coefficient of motion (μ) which corresponds to the viscosity of the aqueous phase. This study proposes that the nature of self-propulsion can be controlled by the dissolution into the bulk water phase as the 3D space and the nonequilibrium adsorption of energy source molecules on the interface as the 2D space.

---

Introduction

Living organisms move self-sustainably and autonomously under non-equilibrium conditions. Inanimate self-propelled objects with self-sustainability under nonequilibrium conditions are attracting attention for the development of life-like autonomous robots.^1–4 Symmetric and asymmetric self-propelled objects composed of camphor, referred to as camphor floats and camphor boats, respectively, have been investigated as models of active matter.^5,6 The characteristic self-propulsion of a single camphor object, including translational, rotational, reciprocating, and oscillatory motions, as well as the collective motions of camphor objects, such as synchronized self-propulsion, chain oscillation, and compressive wave motion, have been reported.^7–12 Notably, the physical or chemical environments induce characteristic information, i.e., the amplitude and the frequency in oscillatory motion of a self-propelled camphor float.^9,13,14

The nonequilibrium in a self-propelled camphor object placed on the surface of water is due to surface cleaning caused by the desorption of camphor molecules adsorbed on the water surface. Many theoretical models of self-propelled systems have been reported, in which camphor molecules are supplied from a source to the water surface.^15–18 Whether the desorption of camphor molecules from the surface of water into the bulk phase is attributable to sublimation into the air or dissolution into the water phase remains unclear. Because theoretical studies reported in 2021 indicated that dissolution is more effective than sublimation for camphor desorption from the surface,¹⁹ models of a self-propelled camphor object that consider dissolution and sublimation as mechanisms for the desorption of camphor from the surface have been reported.^20–23 The effect of both dissolution and sublimation of the camphor molecules on the self-propulsion has also been experimentally evaluated. For example, the oscillatory motion and bifurcation of the motion mode are affected by the desorption of camphor from the surface of the aqueous medium into the bulk aqueous phase owing to changes in the sublimation and dissolution rates with temperature²⁴ or the formation of complexes with amphiphilic molecules.^10,25–27 Although the existing account of the desorption of camphor molecules from the surface into the solution has begun to attract attention, the effect of camphor dissolution on desorption has not been experimentally distinguished from that of sublimation.

In this study, the effect of the dissolution of camphor molecules in water is demonstrated by the oscillatory motion of self-propelled camphor float on an aqueous Na₂SO₄ solution. Na₂SO₄ is used to control the dissolution rate of the camphor molecules, where the effect of Na₂SO₄ on the surface tension and viscosity is considered. The frequency and maximum speed of the oscillatory motion decrease as the concentration of Na₂SO₄ in the aqueous phase increases. The decrease in the frequency of the oscillatory motion is numerically calculated using the diffusion equation by applying the experimentally obtained dissolution rate constant and saturated concentration of camphor in aqueous Na₂SO₄ solution. The decrease in the maximum speed of the object is attributed to the surface tension as the self-propulsion force and the viscosity of the aqueous Na₂SO₄ solution. We propose that nonequilibrium in the self-propelled camphor system is triggered by the dissolution of camphor in the bulk phase.

Materials and methods

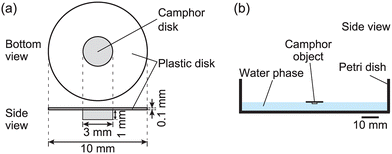
Na₂SO₄ was purchased from NACALAI TESQUE, Inc. (Kyoto, Japan). (+)-Camphor was purchased from FUJIFILM Wako Pure Chemical Corporation (Osaka, Japan). A camphor disk with a diameter of 3.0 mm, thickness of 1.0 mm, and mass of 5 mg was prepared according to the processes described in the previous work.¹³Fig. 1 shows a schematic of the self-propelled object composed of a solid camphor disk and a plastic polyester disk (diameter: 10 mm, thickness: 0.1 mm). This object is called a camphor float. The camphor float was placed in an aqueous Na₂SO₄ solution (volume: 30 mL, depth: 5 mm) in a Petri dish (inner diameter: 86 mm). Water was purified by filtration through active carbon, ion-exchange resin, a water distillation apparatus (RFD24ONC, ADVANTEC Co., Ltd, Tokyo, Japan), and Millipore Milli-Q filtering system (Merck Direct-Q 3UV, Germany; resistance: 18 MΩ cm). The experiments were performed at least three times under each experimental condition to confirm the reproducibility of the results. The motion of the camphor disk was monitored using a digital video camera (HDR-CX485, SONY, Tokyo, Japan; minimum time resolution: 1/30 s) in an air-conditioned room at 298 ± 2 K. The motion of the camphor float was analyzed using ImageJ software (National Institutes of Health, Bethesda, MD, USA). The surface tension at the air/aqueous interface was measured using a surface tensiometer (DY-300, Kyowa Interface Science Co., Ltd, Saitama, Japan). To evaluate the dissolution rate of camphor in aqueous Na₂SO₄ solution, six camphor disks were floated in the aqueous phase with different concentrations of Na₂SO₄ (0.5, 1.0, 1.5, and 1.7 M), and the mass of the disks was measured at different times after removing the moisture from the camphor disks, according to the processes described in the previous study.²⁸

Fig. 1 Schematic of (a) camphor float and (b) experimental system (side-view).

Results

The self-propulsion of camphor floats in aqueous solutions with different concentrations of Na₂SO₄ (C_i) was examined, as shown in Fig. 2. The oscillatory motion between rest and motion was maintained for at least 20 min without Na₂SO₄ (Fig. 2a). Both the frequency and amplitude of the oscillatory motion decreased with an increase in C_i (Fig. 2b and c). Here, 1.7 M is close to the saturated concentration of Na₂SO₄ in water. The trajectories of the oscillation were produced by random motion in 0, 1.0, and 1.7 M Na₂SO₄.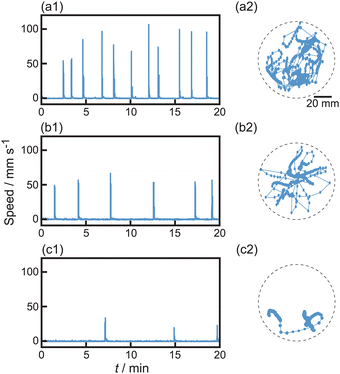

Fig. 2 Oscillatory motion of camphor float with variation of Na₂SO₄ concentration, C_i = (a) 0, (b) 1.0, and (c) 1.7 M. (1) Time-variation of the speed of motion for camphor float and (2) trajectories on the center position of camphor float on the surface of aqueous phase (top-view) at t = 0–20 min. The time interval of motion was 1/3 s. The dotted circles in (2) correspond to the Petri dish. Movies showing the motion in (a), (b), and (c) are provided in the ESI† as Movies S1, S2, and S3, respectively. The speed and motile length of the individual pulse-like motion were analyzed and shown in Fig. S1 (ESI†).

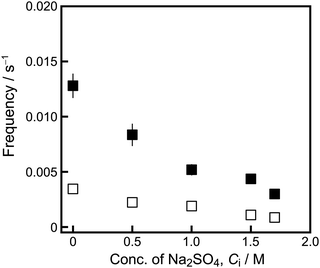
Fig. 3 shows the frequency and maximum speed of the oscillatory motion of the camphor float as a function of C_i. Both the frequency and the maximum speed of the oscillatory motion decreased with increasing C_i.

Fig. 3 (a) Frequency and (b) maximum speed of oscillatory motion depending on the concentration of Na₂SO₄, C_i. Error bars represent standard deviation.

The saturated concentration of camphor, C₀, and the amount of camphor dissolved in the aqueous Na₂SO₄ solution were measured as a function of time. The measured C₀ decreased with increasing C_i, as shown in Fig. 4a. Measurement of camphor dissolution in the aqueous Na₂SO₄ solution is described in the ESI† (see Fig. S2 and S3). The camphor concentration, C, increased linearly with time, as shown in Fig. S2 (ESI†). The dissolution rate constant of camphor, k, in the aqueous phase as a function of C_i was estimated using the values of C₀ and C, where ln(1 − C/C₀) = −kt; the surface area of the camphor disk was constant.²⁹ The value of k increased as a function of C_i (Fig. 4b).

Fig. 4 (a) C₀ as a function of C_i. Error bars represent the standard deviation of three experiments. (b) Dissolution rate constant of camphor, k, as a function of C_i obtained from Fig. S2 (ESI†).

The surface tension, γ, and the viscosity, η, were individually measured to elucidate the relationship between the maximum speed of oscillatory motion and C_i in the aqueous phase, as shown in Fig. 5. γ for the aqueous Na₂SO₄ solution with camphor was lower than that of the solution without camphor at the examined Na₂SO₄ concentration (Fig. 5a). With increasing C_i, γ increased for both the aqueous Na₂SO₄ solution with camphor and that without camphor. The difference in γ for the aqueous Na₂SO₄ solutions with and without camphor also decreased. η increased with increasing C_i, as shown in Fig. 5b.

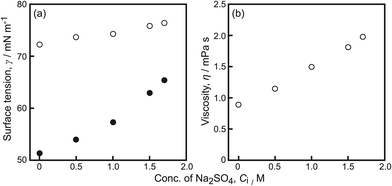Fig. 5 (a) Surface tension, γ, and (b) viscosity, η, of aqueous solution with camphor (filled circles) at C₀ and without (empty circles) camphor depending on C_i.

Discussion

Based on the experimental results and pertinent papers,^9,13,24,27 the dynamics of camphor floats are numerically calculated to explain the mechanism of the decrease in the frequency and maximum speed of oscillatory motion in the aqueous Na₂SO₄ solution. We found that pulse-like motility in Fig. 2 is due to the accumulation of camphor molecules at the basement of the plastic disk and spilling out of camphor molecules to the water surface.^13,30 As reported in our previous papers, the frequency of oscillation depends on the diffusion length of camphor at the bottom of the plastic plate and the threshold concentration of the aqueous camphor solution were required to accelerate from the resting state.^9,24,27

First, the maximum speed of the oscillatory motion is described as a function of C_i (Fig. 2 and 3b). The equation of motion is given by:

mdv/dt = Δγl − μv, (1)

where m is the mass of the camphor float, v is the speed of motion, and Δγ is the difference in the surface tension at both edges of the camphor float, i.e., Δγ = γ_a − γ_c. Here, γ_a is the surface tension of the aqueous Na₂SO₄ solution without camphor (empty circles in Fig. 5a) and γ_c is the surface tension of the aqueous Na₂SO₄ solution with saturated camphor (filled circles in Fig. 5a); l is the contact length of the camphor float on the aqueous phase and μ is the friction coefficient of motion. μ may be proportional to η, i.e., μ = aη, where a is a positive constant.^24,31 It is assumed that the speed of motion reaches its maximum value, V_max, when the system reaches a steady state, that is, dv/dt = 0. At the steady state, eqn (1) can be rewritten as:

V_max = (l/a) × (Δγ/η). (2)

Eqn (2) suggests that V_max is determined by Δγ/η in the present system. There is a correlation between V_max and Δγ/η, as shown in Fig. 6.

Fig. 6 Relationship between V_max and Δγ/η.

The frequency of the oscillatory motion as a function of C_i was numerically calculated (Fig. 2 and 3a). The diffusion of camphor molecules supplied from the camphor disk is expressed by the one-dimensional coordinate x (m):¹¹

where C(x, t) is the camphor concentration at x and t (s), and D (m² s⁻¹) is the camphor diffusion coefficient. The origin of the coordinate system is set at the edge of the camphor disk. For the boundary conditions on one side of the 1D coordinate system, the concentration of camphor at the edge of the camphor disk is described by C(0, t). The effect of the camphor dissolution rate was evaluated as a function of C_i, where the surface area of the camphor disk was constant (Fig. S2, ESI†). The dynamics of camphor dissolution from the disk are given by:

dC(0, t)/dt = k(C₀ − C). (4)

For the boundary condition on the other side, it was assumed that the concentration of camphor in the bulk near the air/water interface, C(0.0035, t), should be zero far from the camphor float because the distributed camphor molecules in the aqueous phase sublimate into the air phase and dissolve in the aqueous phase. Additionally, the initial value of C(x, 0) was set to zero.

Fig. 7 shows the numerical results for the frequency of the oscillatory motion depending on C_i based on eqn (3) and (4). In the numerical calculation, the time required for the concentration at the edge of the plastic plate (x = 0.0035) to reach a threshold value (C_thr), t_c, is regarded as the period of the oscillatory motion, assuming that this threshold concentration could provide a surface tension difference as a driving force. Here, C_thr was experimentally obtained. Actually, camphor solutions with different concentrations were dropped near the edge of a plastic disk floating on the water surface. When the concentration of the camphor solution was 0.4 mM, the plastic disk started to move drastically. Thus, we used this value as C_thr. In other words, 1/t_c is regarded as the frequency of the oscillatory motion. The experimentally determined frequency of the oscillatory motion was qualitatively reproduced by the numerical calculations (Fig. 7). In other words, the frequency of the oscillatory motion is determined by the dissolution rate of the camphor molecules, which depends on C_i. The camphor dissolution rate is represented by k and C₀, as indicated in eqn (4). C₀ decreased with increasing C_i (Fig. 4a), resulting in decreased dissolution rate. In contrast, k increased with increasing C_i (Fig. 4b). k must be influenced by physical properties such as the viscosity of the aqueous phase and the shape of the camphor float because of advection in the aqueous phase which was significantly affected by the Marangoni flow or sublimation.

Fig. 7 Frequency of oscillatory motion obtained from numerical calculation (empty squares) and experiments (filled squares). Error bars in the experimental results represent the standard deviation.

The relationship between dC(0, t)/dt and kC₀ was evaluated. From Fig. S2 (ESI†), it is reasonable to set t ≪ 1/k; thus, eqn (4) is transformed into:

dC(0, t)/dt = kC₀. (5)

The frequency of the oscillatory motion was found to be proportional to kC₀ (Fig. S4, ESI†). This is consistent with the assumption that the frequency of the oscillatory motion is determined by kC₀ in the camphor float system.

Conclusions

By varying the concentration of Na₂SO₄ salt, the dissolution dynamics of camphor in solution was manipulated, resulting in changes in the surface tension, dissolution rate, and viscosity of the solution. As a plausible mechanism, the self-propulsion of camphor floats is driven by dissolution of the camphor molecules in the aqueous phase. The frequency and maximum speed of the oscillatory motion decrease with increasing concentration of Na₂SO₄ in the aqueous phase. Using the experimentally obtained values for the surface tension at various Na₂SO₄ concentrations with or without camphor, dynamic analysis based on the equation of motion showed that the maximum speed of the oscillatory motion depending on the concentration of Na₂SO₄ is determined by the surface tension difference, as a self-propulsion force. In addition, the viscosity of the aqueous Na₂SO₄ solution contributed to the resistance to the motion of the camphor disk. The frequency of the oscillatory motion depending on the concentration of Na₂SO₄ was explained by a diffusion equation, indicating that the self-propulsive nature of the camphor float was determined by the dissolution rate constant, k, and the saturated concentration of camphor in the aqueous salt solution, C₀. This study experimentally and theoretically pioneers dissolution-based regulation and provides novel frontiers for self-organized camphor systems.

Author contributions

Conceptualization: MM, SN; data curation: MT; formal analysis: MT, MM; funding acquisition: MM, SN; investigation: MT; methodology: MM, SN; supervision: SN; validation: MK, YH, MM, SN; visualization: MK, MM, SN; writing original draft: MK, MM, SN; writing review and editing: MT, MK, YH, MM, SN.

Conflicts of interest

There are no conflicts to declare.

Data availability

The data supporting this article have been included as part of the ESI.†

Acknowledgements

This study was supported by JSPS KAKENHI (grant no. JP22K14657); the Ministry of Education, Culture, Sports, Science, and Technology Leading Initiative for Excellent Young Researchers grant (no. JPMXS0320230007) to M. M.; JSPS KAKENHI (grant no. JP20H02712, JP24K22324, and JP21H00996); Iketani Science and Technology Foundation (0351181-A); and Cooperative Research Program of the “Network Joint Research Center for Materials and Devices” (no. 20241009).

References

1. A. T. Liu, M. Hempel, J. F. Yang, A. M. Brooks, A. Pervan, V. B. Koman, G. Zhang, D. Kozawa, S. Yang, D. I. Goldman, M. Z. Miskin, A. W. Richa, D. Randall, T. D. Murphey, T. Palacios and M. S. Strano, Colloidal robotics, Nat. Mater., 2023, 22, 1453–1462.
2. R. Tiwari, M. Kolli, S. Chauhan and M. M. Yallapu, Tabletized nanomedicine: From the current scenario to developing future medicine, ACS Nano, 2024, 18, 11503–11524.
3. W. Zhu, P. Knoll and O. Steinbock, Exploring the synthesis of self-organization and active motion, J. Phys. Chem. Lett., 2024, 15, 5476–5487.
4. O. E. Shklyaev and A. C. Balazs, Interlinking spatial dimensions and kinetic processes in dissipative materials to create synthetic systems with lifelike functionality, Nat. Nanotechnol., 2024, 19, 146–159.
5. R. J. G. Löffler, T. Roliński, H. Kitahata, Y. Koyano and J. Górecki, New types of complex motion of a simple camphor boat, Phys. Chem. Chem. Phys., 2023, 25, 7794–7804.
6. M. Kuze, N. Kawai, M. Matsuo, I. Lagzi, N. J. Suematsu and S. Nakata, Oscillatory motion of a self-propelled object determined by the mass transport path, Phys. Chem. Chem. Phys., 2025, 27, 6640–6645.
7. S. Nakata, Y. Iguchi, S. Ose, M. Kuboyama, T. Ishii and K. Yoshikawa, Self-rotation of a camphor scraping on water: New insight into the old problem, Langmuir, 1997, 13, 4454–4458.
8. S. W. Song, S. Lee, J. K. Choe, A. C. Lee, K. Shin, J. Kang, G. Kim, H. Yeom, Y. Choi, S. Kwon and J. Kim, Pen-drawn Marangoni swimmer, Nat. Commun., 2023, 14, 3597.
9. Y. Xu, J. Kang, M. Sun, J. Shan, W. Guo and Q. Zhang, Insights into characteristic motions and negative chemotaxis of the inanimate motor sensitive to sodium chloride, J. Colloid Interface Sci., 2024, 660, 953–960.
10. E. Hua, J. Gao, Y. Xu, M. Matsuo and S. Nakata, Self-propelled motion controlled by ionic liquids, Phys. Chem. Chem. Phys., 2024, 26, 8488–8493.
11. S. Soh, M. Branicki and B. A. Grzybowski, Swarming in shallow waters, J. Phys. Chem. Lett., 2011, 2, 770–774.
12. C. Zhou, X. Tang, R. Shi, C. Liu, P. Zhu and L. Wang, All-aqueous soft milli-swimmers, ACS Appl. Mater. Interfaces, 2024, 16, 41450–41460.
13. R. Fujita, N. Takayama, M. Matsuo, M. Iima and S. Nakata, Height-dependent oscillatory motion of a plastic cup with a camphor disk floated on water, Phys. Chem. Chem. Phys., 2023, 25, 14546–14551.
14. R. Fujita, M. Matsuo and S. Nakata, Self-propelled object that generates a boundary with amphiphiles at an air/aqueous interface, J. Colloid Interface Sci., 2024, 663, 329–335.
15. M. Nagayama, S. Nakata, Y. Doi and Y. Hayashima, A theoretical and experimental study on the unidirectional motion of a camphor disk, Phys. D, 2004, 194, 151–165.
16. H. Kitahata and Y. Koyano, Mathematical modeling for the synchronization of two interacting active rotors, Phys. Rev. E, 2023, 107, 064607.
17. H. Ishikawa, Y. Koyano, H. Kitahata and Y. Sumino, Erratum: Pairing-induced motion of source and inert particles driven by surface tension [Phys. Rev. E 106, 024604 (2022)], Phys. Rev. E, 2024, 109, 029901.
18. R. J. G. Löffler and J. Gorecki, Dynamics of aggregation in systems of self-propelled rods, Entropy, 2024, 26, 980.
19. C. Gouiller, F. Raynal, L. Maquet, M. Bourgoin, C. Cottin-Bizonne, R. Volk and C. Ybert, Mixing and unmixing induced by active camphor particles, Phys. Rev. Fluids, 2021, 6, 014501.
20. S. Chen, Z. Zhang, Y. Zhang and Y. Sha, A three-dimensional multiphase numerical model for the influence of Marangoni convection on Marangoni self-driven object, Phys. Fluids, 2022, 34, 043308.
21. Y. Yasugahira and M. Nagayama, On a numerical bifurcation analysis of a particle reaction-diffusion model for a motion of two self-propelled disks, Jpn. J. Ind. Appl. Math., 2022, 39, 631–652.
22. M. Nagayama, H. Monobe, K. Sakakibara, K. Nakamura, Y. Kobayashi and H. Kitahata, On the reaction–diffusion type modelling of the self-propelled object motion, Sci. Rep., 2023, 13, 12633.
23. T. Roliński, H. Kitahata, Y. Koyano and J. Górecki, Quantitative analysis of the complex time evolution of a camphor boat, Appl. Sci., 2024, 14, 959.
24. R. Tenno, Y. Gunjima, M. Yoshii, H. Kitahata, J. Gorecki, N. J. Suematsu and S. Nakata, Period of oscillatory motion of a camphor boat determined by the dissolution and diffusion of camphor molecules, J. Phys. Chem. B, 2018, 122, 2610–2615.
25. S. Nakata and M. Murakami, Self-motion of a camphor disk on an aqueous phase depending on the alkyl chain length of sulfate surfactants, Langmuir, 2010, 26, 2414–2417.
26. Y. Karasawa, T. Nomoto, L. Chiari, T. Toyota and M. Fujinami, Motion modes of two self-propelled camphor boats on the surface of a surfactant-containing solution, J. Colloid Interface Sci., 2018, 511, 184–192.
27. Y. Xu, N. Takayama, Y. Komasu, N. Takahara, H. Kitahata, M. Iima and S. Nakata, Self-propelled camphor disk dependent on the depth of the sodium dodecyl sulfate aqueous phase, Colloids Surf., A, 2022, 635, 128087.
28. M. Matsuo, K. Ejima and S. Nakata, Recursively positive and negative chemotaxis coupling with reaction kinetics in self-organized inanimate motion, J. Colloid Interface Sci., 2023, 639, 324–332.
29. A. A. Noyes and W. R. Whitney, The rate of solution of solid substances in their own solutions, J. Am. Chem. Soc., 1897, 19, 930–934.
30. N. J. Suematsu, Y. Ikura, M. Nagayama, H. Kitahata, N. Kawagishi, M. Murakami and S. Nakata, Mode-switching of the self-motion of a camphor boat depending on the diffusion distance of camphor molecules, J. Phys. Chem. C, 2010, 114, 9876–9882.
31. N. J. Suematsu, T. Sasaki, S. Nakata and H. Kitahata, Quantitative estimation of the parameters for self-motion driven by difference in surface tension, Langmuir, 2014, 30, 8101–8108.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp01298h

---