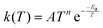Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Rapid unimolecular reactions of acyl peroxy radicals: extending the structure–activity relationships†
Lauri
Franzon
 *a,
Anni
Savolainen
*a,
Anni
Savolainen
 b,
Siddharth
Iyer
b,
Siddharth
Iyer
 b,
Matti
Rissanen
b,
Matti
Rissanen
 ab and
Theo
Kurtén
*a
ab and
Theo
Kurtén
*a
aDepartment of Chemistry, University of Helsinki, P.O. Box 55 (A.I. Virtasen aukio 1), 00014 Helsinki, Finland. E-mail: lauri.franzon@helsinki.fi; theo.kurten@helsinki.fi
bAerosol Physics Laboratory, Physics Unit, Tampere University, 33720 Tampere, Finland
First published on 3rd June 2025
Abstract
Acyl peroxy radicals are especially efficient at forming organic accretion products in the troposphere, but they also have short lifetimes due to rapid unimolecular reactions. For this reason, we find it important to accurately represent the reactions of these species in structure–activity relationships estimating the unimolecular reactivity of atmospheric peroxy radicals. To address this, we performed multi-conformer transition state theory calculations to determine H-shift and ring closure reaction rates for aldehyde-substituted and unsaturated acyl peroxy radicals over a wide temperature range. Similar calculations were performed for enol-substituted peroxy radicals, which are also underrepresented in SAR models. As a results, we found that H-shifts from aldehyde groups are highly competitive, that ring closures are overwhelmingly the major atmospheric fate of unsaturated acyl peroxy radicals, and that H-shifts from Z-enols outcompete all other unimolecular and bimolecular reactions whenever they are possible. In conclusion, in extending the SAR models we have gained valuable insight on some of the most rapid reactions for any peroxy radicals in the atmosphere.
1 Introduction
Organic peroxy radicals (RO2) are all-important for the atmospheric oxidation of volatile organic compounds (VOC) for two reasons: firstly, they form in abundance in all atmospheric environments where organic vapours are present, due to O2 molecules adding to carbon-centred radicals. Secondly, the competition among the various reactions of RO2 are an important branching point for the subsequent chemistry, with important implications for the environmental impact. In polluted conditions, reactions between RO2 and NO and NO3 radicals largely form alkoxy radicals (RO) and nitrogen dioxide (NO2), which typically leads to fragmentation into smaller organic molecules for the former and photolysis for the latter, contributing to ozone (O3) pollution.1 In clean and remote environments, however, the impact of RO2 chemistry is dependent on the competition between two reactions. RO2 either forms closed-shell hydroperoxides (ROOH) through reactions with hydroperoxy radicals (HO2), or reacts with other RO2 in peroxy radical recombination (RO2 + RO2) reactions. The latter is a complex reaction with multiple channels which has received increasing attention in recent years due to being a major source of low-volatility organic accretion products which may condense on aerosol particle surfaces.2 Tropospheric daytime concentrations of HO2 are roughly equal to those of total RO2 on average,3 and as such the former is generally viewed to be the dominant reaction channel due to the latters high variability in reaction rates.4 It is however uncertain whether this is the case in all pristine environments, since we lack accurate estimates of the relative abundance of rapidly and slowly recombining RO2.3 The key to determining the relative importance of RO2 + RO2 reactions in clean environments is then to quantify the concentrations of RO2 species with systematically rapid RO2 + RO2 rates.The most notable RO2 species with systematically rapid bimolecular reaction rates are acyl peroxy radicals (RC(O)O2), which form from O2 addition to acyl radicals (RCO).5 While their rate coefficients for reactions with NOx and HO2 are also higher than for non-acyl RO2, their collision-limited RO2 + RO2 reactions are especially notable, as this allows them to undergo rapid cross reactions with RO2 species for which both self-reactions and other RO2 + RO2 cross reactions are systematically slow.4,6,7 Unlike typical RO2, RC(O)O2 also have non-negligible reaction rates for bimolecular addition to alkenes,8 and this has recently been demonstrated to form stable accretion products in laboratory conditions.9 Both of these observations underline the importance of constraining the distribution of ambient RC(O)O2 species for the study of gas-phase formation of organic accretion products. The most common RC(O)O2 compound, the acetyl peroxy radical (CH3C(O)O2), has been shown to readily partake in a variety of RO2 + RO2 reactions,6 but similar data is scarcer for more complex RC(O)O2 compounds. A main reason for this is that these more complex RC(O)O2 are known to have rapid unimolecular hydrogen shift (H-shift) reactions resulting in either carbon-centered radicals or isomeric RO2, in case the H-shift occurred from a hydroperoxide group. In the former case the reaction is often immediately followed by O2 addition to the carbon-centered radical, in which case the process is known as autoxidation.10–12 The latter type of H-shift is better known as H-scrambling, which is considered rapid and reversible for all RO2 except RC(O)O2.13 A recent computational study by Seal et al.14 evaluated H-shift reaction rates for larger RC(O)O2, but only for linear, unsubstituted RC(O)O2. The highly systematic structure–activity relationship (SAR) for H-shift reactions of general RO2 by Vereecken & Nozière (from now on H-SAR)15 suggest that the fastest autoxidation reactions occur in unsaturated and aldehydic RO2, but the model lacks detailed data on RC(O)O2 with these substituents. Individual computational rate coefficients collected from a variety of sources5,16–18 disagree with the H-SAR predictions mainly within a factor of 5, though with two significant outliers: it overestimates both the aldehydic H-shift rates calculated by da Silva16 and Møller et al.18 by two orders of magnitude (see Section S1 of the ESI†). Unsaturated RO2 may also undergo ring closure reactions, which also leads to autoxidation,19,20 for which another structure–activity relationship (from now on R-SAR) has been developed by Vereecken et al.,21 but here the data on RC(O)O2 is even more scarce. Computational ring closure rates with both the inner and outer C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C carbons for a single RC(O)O2 radical are provided by Vereecken et al.,21 who note that the former reaction is 20 times faster than the reaction for the corresponding alkyl RO2, whereas the latter is only sped up by a factor of 3. We have no way to know how systematic these differences are without further data. Thus, we conclude that the systematic computations initiated by Seal et al.14 for H-shift reactions of aliphatic RC(O)O2 ought to be extended to unsaturated and aldehydic RC(O)O2, with similarly systematic calculations performed on ring closure rates for the unsaturated RC(O)O2. The predictions from these calculations would then be used to update both SAR models to represent the decisive role of acyl peroxy radicals more accurately.
C carbons for a single RC(O)O2 radical are provided by Vereecken et al.,21 who note that the former reaction is 20 times faster than the reaction for the corresponding alkyl RO2, whereas the latter is only sped up by a factor of 3. We have no way to know how systematic these differences are without further data. Thus, we conclude that the systematic computations initiated by Seal et al.14 for H-shift reactions of aliphatic RC(O)O2 ought to be extended to unsaturated and aldehydic RC(O)O2, with similarly systematic calculations performed on ring closure rates for the unsaturated RC(O)O2. The predictions from these calculations would then be used to update both SAR models to represent the decisive role of acyl peroxy radicals more accurately.
In addition to RC(O)O2, there is another class of RO2 currently not represented in the SAR models but known to autoxidize rapidly: enol-substituted RO2. Peeters & Nguyen discovered an exceptionally rapid H-shift for an isoprene-derived non-acyl RO2 for the Z-isomer but not the E-isomer of the enol C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond.22 The necessity to include this reaction in atmospheric modelling was acknowledged not only by Vereecken & Nozière,15 but also by Jenkin et al. in their review of the most important RO2 reactions to include in automatic mechanism generation.4 Despite this, we have very little data on how rapidly other enol-substituted RO2 autoxidize. As with the unsaturated and aldehyde-substituted RC(O)O2, our GECKO-A-based large exploration of potential RO2 + RO2 reactions23 tentatively indicated that other enol-substituted RO2 structures do form downstream from OH addition to organics with multiple C
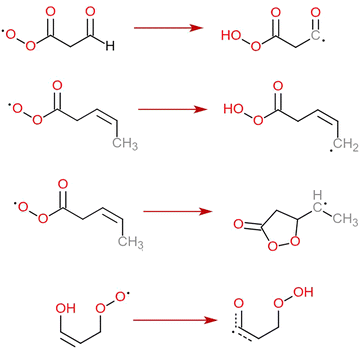
C bond.22 The necessity to include this reaction in atmospheric modelling was acknowledged not only by Vereecken & Nozière,15 but also by Jenkin et al. in their review of the most important RO2 reactions to include in automatic mechanism generation.4 Despite this, we have very little data on how rapidly other enol-substituted RO2 autoxidize. As with the unsaturated and aldehyde-substituted RC(O)O2, our GECKO-A-based large exploration of potential RO2 + RO2 reactions23 tentatively indicated that other enol-substituted RO2 structures do form downstream from OH addition to organics with multiple C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds (see Section S1 in the ESI†). Thus, we also performed a set of calculations on enol-substituted RO2 to extend the H-SAR further. All four reaction types discussed in this work are presented in Fig. 1.
C bonds (see Section S1 in the ESI†). Thus, we also performed a set of calculations on enol-substituted RO2 to extend the H-SAR further. All four reaction types discussed in this work are presented in Fig. 1.
2 Methods
In order to extend the aforementioned SAR models, we calculated multi-conformer transition state theory24,25 (MCTST) reaction rates in the temperature interval 200–400 K for a total of 78 reactions: 8 H-shifts from aldehyde groups, 14 H-shifts from allylic carbons, 40 ring closures in unsaturated RC(O)O2, and 16 H-shifts from enol groups. In our selection of reactions, we have considered all the most impactful functionalities in the existing SAR models, and selected one simple RC(O)O2 to represent all other RC(O)O2 with the same functionality. No additional calculations were performed to validate our extended SAR models with, but considering the general scarcity of literature data on functionalized RC(O)O2, we consider this the most economical usage of computational resources. Our procedure for calculating these MCTST rates largely follows the cost-efficient workflow developed by Møller et al.24 with minor modifications to further increase the cost-efficiency. The MCTST rates are calculated using the equation: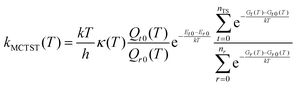 | (1) |
(1) Metadynamics-based conformer search with the CREST software,33 using the GFN1-xTB method34 and an energy cutoff of 41.84 kJ mol−1 for filtering.
(2) Optimization of all conformers found by CREST with B3LYP-D3/ma-def2-SVP35–38 followed by uniqueness filtering using the energy and dipole moment cutoffs 1.5 × 10−5 Ha and 1.5 × 10−2 D. Conformers more than 10 kJ mol−1 above the minimum E conformer in electronic energy were also filtered out after this step, as they have a negligible contribution to the quotient of Boltzmann sums in eqn (1) at atmospheric temperatures. The choice of duplicate filtering thresholds and conformer energy cutoff are both based on the work of Møller et al.24
(3) The remaining conformers are re-optimized with the ωB97X-D3/jun-cc-pVTZ level of theory,39,40 after which a frequency analysis is performed. Another uniqueness filtering is performed, this time by visually inspecting all conformer pairs with E or μ values close to the previously mentioned cutoffs.
(4) A DLPNO-CCSD(T)/aug-cc-pVTZ41–47 single point energy calculation is performed for the global minimum conformer, with aug-cc-pVQZ auxiliary basis.
(5) For a single representative reaction of each type, the reoptimization done at step 3 and the single-point calculation at step 4 are redone at the ωB97X-D3/aug-cc-pVTZ, and RI-CCSD(T)-F12/cc-pVDZ-F1248,49 levels of theory, respectively. For the latter calculation aug-cc-pVDZ was used as auxiliary basis and cc-pVDZ-F12-CABS as complementary auxiliary basis for the F12 calculation. The observed differences in single point energies ΔEF12-DLPNO and vibrational zero-point energies ΔZPEaug-jun are used to scale energies calculated using the cheaper DLPNO and jun-cc-pVTZ up or down when calculating MCTST rates. We call these reactions ‘anchor reactions’.
For determining transition state (TS) energies, largely the same steps were followed, with a few modifications:
(1) First, a ‘TS guess geometry’ was built. A constrained optimization with the B3LYP/def2-SVP level of theory was performed with the interatomic distances most relevant for the reaction (as well as the RO2 O–O bond length for additional stability) frozen. This was followed by a saddle point search and frequency analysis, also using B3LYP/def2-SVP, after which it was confirmed that the imaginary normal mode corresponded to the intended reaction.
(2) CREST was again used for conformer search with the B3LYP/def2-SVP saddle point used as starting geometry. Constraints were placed on relevant bond lengths, as well as C–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–C dihedral angles for molecules with Z/E-isomerism, as unwanted interconversions were occasionally observed in the CREST-generated ensembles for these radicals.
C–C dihedral angles for molecules with Z/E-isomerism, as unwanted interconversions were occasionally observed in the CREST-generated ensembles for these radicals.
(3) With the initial conformer ensemble generated, a constrained optimization followed by saddle point search and frequency analysis was performed for all conformers using B3LYP-D3/ma-def2-SVP. Uniqueness filtering was performed similarly as for the reactant conformers.
(4) All unique conformers with E or G (T = 298 K) values within 10 kJ mol−1 of the global minimum TS were re-optimized at the ωB97X-D3/jun-cc-pVTZ level of theory, followed by another frequency analysis and another round of uniqueness filtering.
(5) Again, a DLPNO-CCSD(T)/aug-cc-pVTZ single point calculation with aug-cc-pVQZ auxiliary basis was performed for the global minimum conformer.
(6) For anchor reactions, ωB97X-D3/aug-cc-pVTZ reoptimization of the final set of TS conformers and a RI-CCSD(T)-F12/cc-pVDZ-F12 single point energy calculation with aug-cc-pVDZ auxiliary basis and cc-pVDZ-F12-CABS complementary auxiliary basis for the global minimum TS.
For brevity, we will be referring to the RI-CCSD(T)-F12/cc-pVDZ-F12//ωB97X-D3/aug-cc-pVTZ and DLPNO-CCSD(T)/aug-cc-pVTZ//ωB97X-D3/jun-cc-pVTZ levels of quantum theory as F12//aug and DLPNO//jun, respectively. The level-of-theory-based CCSD(T) single point and ZPE corrections for the reactants and TS may be combined into a single ‘TS energy shift’:
| ΔEts = ΔEts0,F12-DLPNO + ΔZPEts0,aug-jun − ΔEr0,F12-DLPNO − ΔZPEr0,aug-jun | (2) |
All saddle point searches were initialized with a Hessian calculation for improved geometry convergence. The tunneling coefficient κ(T) was calculated using the Eckart approach50,51 for the reaction coordinate of the lowest G (298 K) transition state. As H-shift reaction rates are especially sensitive to tunneling, a few additional calculations were performed to accurately represent the energetics of the reaction coordinate. An intrinsic reaction coordinate52 (IRC) calculation was performed, using the B3LYP-D3/ma-def2-SVP level of theory starting from the geometry and Hessian obtained from the saddle point optimization at that level of theory. The reactant and product geometries obtained from the IRC were then reoptimized with ωB97X-D3/jun-cc-pVTZ followed by a DLPNO single point energy calculation (for anchor reactions F12//aug energies were also calculated). These zero-point corrected electronic energies, along with the TS imaginary frequency, were used as parameters for the Eckart κ(T) calculation.
All thermodynamic partition functions were calculated using the rigid-rotor harmonic oscillator (RRHO) approximation for the vibrational frequencies. Being aware of this model's limitations, we experimented with Grimme's quasi-harmonic oscillator approach, in which the vibrational entropy of each normal mode is calculated with an interpolation function that treats high frequency vibrations as harmonic oscillators and low-frequency vibrations as free rotors.53 However, as detailed in Sections S2 and S3 of the ESI,† this approach did not improve our rate calculations’ accuracy. Furthermore, we found that naively applying Grimme's correction only to the vibrational entropy but not the enthalpy (as suggested in the original source) leads to unphysical errors, which at certain frequency ranges could outweight the inaccuracies of the RRHO approximation. Nevertheless, rigorous benchmarking of the accuracy of various approaches to calculating Q is beyond the scope of this work.
In order to benchmark our ability to make accurate rate predictions with this computational workflow, we performed test calculations for three RO2 H-shift reactions whose rates have already been experimentally constrained. These were the aldehydic H-shift in HOCH2C(CH3)(CHO)O2 measured by Crounse et al.,54 the allylic H-shift in Z-HOCH2C(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHCH2O2 measured by Teng et al.,55 and the H-shift from the α-OH carbon in CH3CH(OH)CH2CH(C2H5)O2 measured by Praske et al.56 These were selected due to the relative similarity to the RC(O)O2 reactions considered in this work. In Section S2 of the ESI† we compare our MCTST calculations to these experimental rates. We found that while reaction rates calculated using the DLPNO//jun energies agree with the experiments within a factor of 4, the rates using the more expensive F12//aug methods reach an agreement within a factor of 2. This observation resulted in workflow described above, in which DLPNO//jun energies were calculated for all reactions, with F12//aug energies calculated for a few anchor reactions. We also find that our usage of B3LYP-D3/ma-def2-SVP rather than B3LYP/6-31+G* (used by Møller et al.24) improves the accuracy of the low-cost conformer filtering step of the workflow.
CHCH2O2 measured by Teng et al.,55 and the H-shift from the α-OH carbon in CH3CH(OH)CH2CH(C2H5)O2 measured by Praske et al.56 These were selected due to the relative similarity to the RC(O)O2 reactions considered in this work. In Section S2 of the ESI† we compare our MCTST calculations to these experimental rates. We found that while reaction rates calculated using the DLPNO//jun energies agree with the experiments within a factor of 4, the rates using the more expensive F12//aug methods reach an agreement within a factor of 2. This observation resulted in workflow described above, in which DLPNO//jun energies were calculated for all reactions, with F12//aug energies calculated for a few anchor reactions. We also find that our usage of B3LYP-D3/ma-def2-SVP rather than B3LYP/6-31+G* (used by Møller et al.24) improves the accuracy of the low-cost conformer filtering step of the workflow.
2.1 Additional notes on conformer sampling
In previous works from our research group involving conformer sampling,7,57–59 we have typically used the molecular mechanics force field in the commercial Spartan software for initial conformer ensemble generation. In this work, we opted for the open source software CREST in order to experiment with sampling methods that do not rely on explicit treatment of covalent bonds. As all the reactions treated in this work are unimolecular isomerizations, they provide a suitable model system where it is relatively easy to tell if crucial bond rotations are missed by the sampling algorithm. As CREST is only compatible with the GFN family of semi-empirical methods, we opted to use the GFN1-xTB method for conformer sampling, as GFN2-xTB has been observed to perform poorly for H-bonded acid–base clusters,60 despite reportedly outperforming GFN1-xTB in established benchmark datasets for non-covalent interactions.61 We see this as evidence that GFN1-xTB is more robust than GFN2-xTB, and thus more reliable for sampling H-bonding interactions in system well outside the GFN reference molecules, ‘predominantly of closed-shell character and covering common bonding situations.’34 In some initial test calculations for RC(O)O2 we observed a conspicuous lack of C–O bond rotations in the acyl peroxy functional group, and opted therefore to perform a relaxed surface scan of the O–O–C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O dihedral angle in CH3C(O)O2 with both GFN methods and DFT methods (Fig. 2) to access the thermal accessibility of these rotations. We found that the torsional barrier was around 25 kJ mol−1 according to both B3LYP-D3/ma-def2-SVP and ωB97X-D3/jun-cc-pVTZ, indicating that these rotations should indeed be included in the conformer ensemble. Both XTB methods overestimate the barrier by around 5 kJ mol−1, and it appears that this prevents the CREST conformer sampling runs from accessing these rotations when the default energy filter of around 25 kJ mol−1 is used. Fig. 2 also shows that GFN1-xTB gets the relative energy difference of the two conformers wrong by 6 kJ mol−1, which is roughly in line with the mean average error of 7–16 kJ mol−1 for relative conformer energies observed in our benchmarking (see Section S2 in the ESI†). Due to this, we increased CREST's energy cutoff to 41.84 kJ mol−1 (‘–ewin 10’ in the input) to ensure that all thermally relevant conformers are found.
O dihedral angle in CH3C(O)O2 with both GFN methods and DFT methods (Fig. 2) to access the thermal accessibility of these rotations. We found that the torsional barrier was around 25 kJ mol−1 according to both B3LYP-D3/ma-def2-SVP and ωB97X-D3/jun-cc-pVTZ, indicating that these rotations should indeed be included in the conformer ensemble. Both XTB methods overestimate the barrier by around 5 kJ mol−1, and it appears that this prevents the CREST conformer sampling runs from accessing these rotations when the default energy filter of around 25 kJ mol−1 is used. Fig. 2 also shows that GFN1-xTB gets the relative energy difference of the two conformers wrong by 6 kJ mol−1, which is roughly in line with the mean average error of 7–16 kJ mol−1 for relative conformer energies observed in our benchmarking (see Section S2 in the ESI†). Due to this, we increased CREST's energy cutoff to 41.84 kJ mol−1 (‘–ewin 10’ in the input) to ensure that all thermally relevant conformers are found.
 | ||
| Fig. 2 Relaxed surface scan of the acetyl peroxy radical dihedral angle with GFN1-xTB, GFN2-xTB, B3LYP-D3/ma-def2-SVP, and ωB97X-D3/jun-cc-pVTZ. | ||
A few of the systems studied in this work turned out to be so unstable on the GFN1-xTB PES that the optimization preceding the metadynamics simulation always resulted in an unwanted reaction. In some cases this could be solved by rotating the input geometry into an unreactive conformer, but this occasionally led to crucial reactive conformers (such as the IRC reactant) missing from the final conformer ensemble. The systems for which this was the case were CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)CH2C(O)O2, CH2
C(CH3)CH2C(O)O2, CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(C2H5)CH2C(O)O2, CH2
C(C2H5)CH2C(O)O2, CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(i-C3H7)CH2C(O)O2, and all Z-enol-RO2. In these cases, we attempted to perform the conformer sampling with the GFN-FF forcefield62 as recommended by the CREST output, as it disallows changes to bond topology. However, this approach often led to physical inconsistencies in the reactive energetics, such as the IRC reactant having a lower energy than the lowest-energy reactant conformer found after the DFT re-optimizations were performed on top of the GFN-FF conformer ensemble. We interpreted this as a sign that many of the potential wells on the DFT PES do not exist on the GFN-FF PES, leading to systematic errors when trying to use the latter for conformer sampling. This observation is consistent with a recent performance comparison of low-cost conformer sampling methods,63 in which GFN-FF on average failed to find a third of the potential wells on higher-level PES of model radical systems. For the set of problematic radicals listed above, an additional conformer search was performed using ORCA 6.0's new Global Optimizer GOAT,64 again using GFN1-xTB. This approach proved much more consistent at generating full conformer ensembles for these radicals, despite utilizing the same level of theory as CREST. This is likely due to differences in the conformer search algorithm: CREST's atomistic metadynamics simulations coupled with automatic filtering of reacted structures likely leads it to miss conformers with especially low reactive barriers on the utilized level of theory. GOAT, on the other hand, freezes all covalent bond lengths and dihedral angles of strong sp2 bonds during the conformer search to prevent these unwanted reactions from occurring altogether.64 These experiences have led us to believe that the latter approach is more suited to atmospheric organic radicals and other systems with low-barrier reactions, especially if they are not well represented by the benchmark sets used to parametrize the GFN methods.34
C(i-C3H7)CH2C(O)O2, and all Z-enol-RO2. In these cases, we attempted to perform the conformer sampling with the GFN-FF forcefield62 as recommended by the CREST output, as it disallows changes to bond topology. However, this approach often led to physical inconsistencies in the reactive energetics, such as the IRC reactant having a lower energy than the lowest-energy reactant conformer found after the DFT re-optimizations were performed on top of the GFN-FF conformer ensemble. We interpreted this as a sign that many of the potential wells on the DFT PES do not exist on the GFN-FF PES, leading to systematic errors when trying to use the latter for conformer sampling. This observation is consistent with a recent performance comparison of low-cost conformer sampling methods,63 in which GFN-FF on average failed to find a third of the potential wells on higher-level PES of model radical systems. For the set of problematic radicals listed above, an additional conformer search was performed using ORCA 6.0's new Global Optimizer GOAT,64 again using GFN1-xTB. This approach proved much more consistent at generating full conformer ensembles for these radicals, despite utilizing the same level of theory as CREST. This is likely due to differences in the conformer search algorithm: CREST's atomistic metadynamics simulations coupled with automatic filtering of reacted structures likely leads it to miss conformers with especially low reactive barriers on the utilized level of theory. GOAT, on the other hand, freezes all covalent bond lengths and dihedral angles of strong sp2 bonds during the conformer search to prevent these unwanted reactions from occurring altogether.64 These experiences have led us to believe that the latter approach is more suited to atmospheric organic radicals and other systems with low-barrier reactions, especially if they are not well represented by the benchmark sets used to parametrize the GFN methods.34
The conformer ensembles generated with GOAT were optimized using B3LYP-D3/ma-def2-SVP, after which uniqueness filtering was performed to determine which conformers in the GOAT conformer ensemble included structures not present in the CREST/GFN-FF ensemble after B3LYP-D3/ma-def2-SVP optimization. After this, our normal conformer filtering workflow was resumed from step 3 for reactant conformers and step 4 for TS conformers. For clarity, conformers located using GOAT but not CREST are respectively labelled ‘ReacG’ or ‘TSG’ in our ESI.†
3 Computational results
3.1 Aldehydic H-shifts
Our MCTST results for aldehydic H-shifts are presented in Table 1. The simplest possible RC(O)O2 in which an aldehydic H-shift is possible is the 2-formyl acyl peroxy radical, CHOC(O)O2, for which G. Silva has previously calculated a H-shift rate using a higher level of quantum theory than ours: G3SX//B3LYP/6-31G(2df,p)16 fitting master equation results over a temperature range from 150 K to 400 K, he obtained an Arrhenius expression of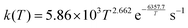 . Silva's results are likely more accurate than our MCTST calculation for the same radical in terms of energetics and fall-off effects, but his calculations do not consider multi-conformer effects. Therefore, uniquely for this reaction we derive the SAR expression by applying a T-dependent multi-conformer correction to Silva's rate expression:
. Silva's results are likely more accurate than our MCTST calculation for the same radical in terms of energetics and fall-off effects, but his calculations do not consider multi-conformer effects. Therefore, uniquely for this reaction we derive the SAR expression by applying a T-dependent multi-conformer correction to Silva's rate expression: | (3) |
![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) = −1143.56 cm−1, determined from B3LYP/6-31G(2df,p) frequency analysis on top of Silva's TS geometry.
= −1143.56 cm−1, determined from B3LYP/6-31G(2df,p) frequency analysis on top of Silva's TS geometry.  includes only multi-conformer effects from the reactant side as there is only one TS conformer. Our MCTST correction resulted in a slightly lower rate coefficient, scaling Silva's rates down by a factor between 0.65 at 200 K and 0.42 at 400 K. Slightly different Arrhenius parameters (see Table 8) and a 298 K rate coefficient of 6.20 s−1 were obtained as a result.
includes only multi-conformer effects from the reactant side as there is only one TS conformer. Our MCTST correction resulted in a slightly lower rate coefficient, scaling Silva's rates down by a factor between 0.65 at 200 K and 0.42 at 400 K. Slightly different Arrhenius parameters (see Table 8) and a 298 K rate coefficient of 6.20 s−1 were obtained as a result.
| Radical | Structure | E ts − Er0 | G ts − Gr0 |
![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) (cm−1) (cm−1) |
E ts − Erirc | E ts − Epirc | κ | k MCTST (s−1) |
|---|---|---|---|---|---|---|---|---|
| a Determined by calculating the B3LYP/6-31G(2df,p) Hessian at Silva's published TS geometry.16 b Rate calculated using eqn (3). | ||||||||
| CHOC(O)O2(Silva)16 | 1,4-CHO | 65.27 | 70.64 | −1143.56a | 6.20b | |||
| CHOC(O)O2(F12) | 1,4-CHO | 69.91 | 70.60 | −1153.33 | 67.33 | 90.92 | 5.25 | 7.01 |
| CHOC(O)O2(DLPNO) | 1,4-CHO | 77.39 | 79.97 | −1164.78 | 74.42 | 97.54 | 5.59 | 2.52 × 10−1 |
| CHOCH2C(O)O2(F12) | 1,5-CHO | 69.64 | 74.97 | −1641.45 | 66.51 | 74.97 | 51.08 | 8.93 |
| CHOCH2C(O)O2(DLPNO) | 1,5-CHO | 72.21 | 77.61 | −1642.82 | 70.58 | 80.08 | 57.70 | 3.19 |
| CHOC2H4C(O)O2 | 1,6-CHO | 69.14 | 76.32 | −1530.55 | 60.35 | 65.24 | 22.91 | 9.12 |
| CHOC3H6C(O)O2 | 1,7-CHO | 66.48 | 71.80 | −1473.13 | 48.13 | 60.66 | 14.89 | 2.40 × 101 |
| CHOC4H8C(O)O2 | 1,8-CHO | 66.14 | 74.79 | −1516.29 | 60.17 | 71.84 | 22.32 | 1.76 × 101 |
| CHOC4H8CH2O2(F12) | 1,8-CHO | 70.63 | 80.06 | −1981.53 | 57.34 | 48.17 | 143.08 | 1.01 |
| CHOC4H8CH2O2(DLPNO) | 1,8-CHO | 72.86 | 82.15 | −1985.27 | 59.76 | 51.96 | 176.58 | 4.82 × 10−1 |
| CHOC4H8CH(CH3)O2 | 1,8-CHO | 75.15 | 84.16 | −2000.03 | 61.06 | 49.97 | 155.78 | 7.22 × 10−1 |
| CHOC4H8C(CH3)2O2 | 1,8-CHO | 74.85 | 83.52 | −2015.01 | 60.20 | 47.97 | 149.52 | 6.01 × 10−1 |
For the same reaction, there was a significant discrepancy between our F12//aug and DLPNO//jun results, stemming from a combination of CCSD(T) single points, relative conformer energies and vibrational partition functions. As we already obtained an accurate SAR rate for the 1,4-CHO H-shift from the comparison with Silva's results, we opted to instead use the 1,5-CHO H-shift in CHOCH2C(O)O2 as an anchor reaction. Here we obtained much better agreement between the F12//aug and DLPNO//jun results. Thus, the ΔEts correction obtained from this reaction was used for the aldehydic H-shifts of span 6, 7 and 8. Since the H-SAR lacked rate expressions for aldehydic H-shifts of span 8, we also calculated reference rates for primary, secondary and tertiary alkyl RO2, with the first of these used as an anchor reaction.
When comparing our results to those already in the H-SAR,15 we note first that our 1,8-CHO rate for CHOC4H8CH2O2 calculated using the F12//aug energetics is approximately half that of Vereecken's recommended 1,7-CHO rate for Prim-RO2, based on his MCTST calculation using CBS-QB3//B3LYP/6-31G(d,p) energetics on CHOC3H6CH2O2. Notably, this is the only 1,7-CHO rate in the H-SAR reference data, with the recommended rates for sec-RO2 and tert-RO2 being based on linear extrapolations of relative rates. This makes it all the more significant that our directly calculated 1,8-CHO rates for sec-RO2 and tert-RO2 (0.722 and 0.601 s−1 at 298 K, respectively) exceed the H-SAR for the corresponding 1,7-CHO reactions (0.171 and 0.032, respectively), implying that the true reaction rates for the latter may in fact be higher than the current SAR predictions. By comparison, our calculations for CHO-substituted RC(O)O2 are slower than the previous H-SAR predictions, and show a different span dependence, peaking at 7 rather than 5 (using the H-SAR's generic RC(O)O2 factor of  ) or 4 (using Seal's span-dependent correction factors14). Taken as a whole, the data in Table 1 demonstrate a delicate balance between energetic, entropic, and tunneling contributions to the reaction rate, all of which have a span dependence of their own.
) or 4 (using Seal's span-dependent correction factors14). Taken as a whole, the data in Table 1 demonstrate a delicate balance between energetic, entropic, and tunneling contributions to the reaction rate, all of which have a span dependence of their own.
3.2 Allylic H-shifts
Our MCTST results for allylic H-shifts are presented in Table 2. The combination of the H-SAR parameters for allylic H-shifts15 and the span-dependent RC(O)O2 parameters from Seal et al.14 predict 298 K rates on the order of 102 to 103 s−1, with the most extreme rate prediction being 1.16 × 106 s−1 for 1,7-CH shifts with endocyclic C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds. Taken at face value, this rate would imply that certain allylic H-shifts in unsaturated RC(O)O2 may even outcompete H-shifts from –OOH groups, which are conventionally viewed to outcompete all other RO2 reactions.65 By comparison, our MCTST rates are much more modest, most fitting within the ‘competitive but not immediate’ range between 10−3 and 102 s−1. These results seem to imply that the parameters of Seal et al. are only applicable to RC(O)O2 with flexible carbon backbones.
C bonds. Taken at face value, this rate would imply that certain allylic H-shifts in unsaturated RC(O)O2 may even outcompete H-shifts from –OOH groups, which are conventionally viewed to outcompete all other RO2 reactions.65 By comparison, our MCTST rates are much more modest, most fitting within the ‘competitive but not immediate’ range between 10−3 and 102 s−1. These results seem to imply that the parameters of Seal et al. are only applicable to RC(O)O2 with flexible carbon backbones.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C H-shifts, the ΔEts shift 2.02 kJ mol−1 for endo-C
C H-shifts, the ΔEts shift 2.02 kJ mol−1 for endo-C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C H-shifts, and the ΔEts shift 1.30 kJ mol−1 for exo-C
C H-shifts, and the ΔEts shift 1.30 kJ mol−1 for exo-C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C H-shifts
C H-shifts
| Radical | Structure | E ts − Er0 | G ts − Gr0 |
![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) (cm−1) (cm−1) |
E ts − Erirc | E ts − Epirc | κ | k MCTST (s−1) |
|---|---|---|---|---|---|---|---|---|
CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)C(O)O2(F12) C(CH3)C(O)O2(F12) |
1,5-CH3-gem | 104.92 | 109.42 | −1987.73 | 90.75 | 90.99 | 1229.60 | 4.02 × 10−4 |
CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)C(O)O2(DLPNO) C(CH3)C(O)O2(DLPNO) |
1,5-CH3-gem | 103.17 | 107.31 | −1997.63 | 89.49 | 93.77 | 1375.90 | 9.13 × 10−4 |
CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(C2H5)C(O)O2 C(C2H5)C(O)O2 |
1,5-CH2-gem | 89.71 | 95.59 | −1903.95 | 75.16 | 91.16 | 445.30 | 4.05 × 10−2 |
CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(i-C3H7)C(O)O2 C(i-C3H7)C(O)O2 |
1,5-CH-gem | 77.08 | 81.03 | −1740.96 | 64.95 | 91.91 | 108.23 | 1.07 |
CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)CH2C(O)O2 C(CH3)CH2C(O)O2 |
1,6-CH3-gem | 84.49 | 90.32 | −2052.14 | 79.59 | 91.69 | 1566.13 | 2.03 × 10−1 |
CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(C2H5)CH2C(O)O2 C(C2H5)CH2C(O)O2 |
1,6-CH2-gem | 70.73 | 75.65 | −1944.43 | 67.88 | 90.47 | 445.10 | 2.26 × 101 |
CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(i-C3H7)CH2C(O)O2 C(i-C3H7)CH2C(O)O2 |
1,6-CH-gem | 62.11 | 68.37 | −1785.52 | 56.64 | 85.34 | 104.64 | 1.14 × 102 |
Z-CH3CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHC(O)O2(F12) CHC(O)O2(F12) |
1,6-CH3-endo | 97.33 | 107.21 | −2126.48 | 82.12 | 93.13 | 2791.38 | 2.80 × 10−3 |
Z-CH3CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHC(O)O2(DLPNO) CHC(O)O2(DLPNO) |
1,6-CH3-endo | 95.31 | 105.15 | −2136.59 | 80.82 | 95.24 | 2968.05 | 4.91 × 10−3 |
Z-C2H5CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHC(O)O2 CHC(O)O2 |
1,6-CH2-endo | 82.30 | 91.40 | −2022.18 | 68.42 | 97.52 | 834.68 | 2.29 × 10−1 |
Z-i-C3H7CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHC(O)O2 CHC(O)O2 |
1,6-CH-endo | 74.52 | 84.10 | −1874.81 | 61.21 | 90.41 | 219.44 | 8.45 × 10−1 |
Z-CH3CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHCH2C(O)O2 CHCH2C(O)O2 |
1,7-CH3-endo | 80.47 | 90.15 | −2042.67 | 75.36 | 96.02 | 1328.76 | 2.56 × 10−1 |
Z-C2H5CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHCH2C(O)O2 CHCH2C(O)O2 |
1,7-CH2-endo | 68.39 | 76.64 | −1911.6 | 67.25 | 98.37 | 378.32 | 1.67 × 101 |
Z-i-C3H7CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHCH2C(O)O2 CHCH2C(O)O2 |
1,7-CH-endo | 62.10 | 69.87 | −1752.06 | 63.57 | 87.64 | 109.53 | 1.08 × 102 |
CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHCH2C3H6C(O)O2(F12) CHCH2C3H6C(O)O2(F12) |
1,7-CH2-exo | 65.49 | 79.32 | −1811.99 | 57.26 | 87.93 | 116.96 | 1.17 × 101 |
CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHCH2C3H6C(O)O2(DLPNO) CHCH2C3H6C(O)O2(DLPNO) |
1,7-CH2-exo | 64.33 | 74.36 | −1810.71 | 56.78 | 91.32 | 115.78 | 2.23 × 101 |
CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHCH(CH3)C3H6C(O)O2 CHCH(CH3)C3H6C(O)O2 |
1,7-CH-exo | 59.76 | 70.61 | −1682.08 | 46.40 | 82.52 | 42.25 | 7.41 × 101 |
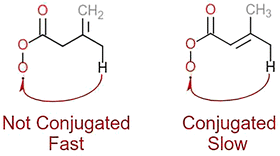
Another notable detail in our results is the significant difference between the 1,6-CHn H-shifts with endocyclic C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds and those with geminal C
C bonds and those with geminal C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds (i.e., with one sp2 carbon inside the TS ring and the second outside). The H-SAR treats these two structures as equivalent, but from these results it is evident that the π-orbital conjugation of the C
C bonds (i.e., with one sp2 carbon inside the TS ring and the second outside). The H-SAR treats these two structures as equivalent, but from these results it is evident that the π-orbital conjugation of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond and the RC(O)O2 group plays a role for these systems (see Fig. 3). This finding is partially in line with Vereecken & Nozière's speculation on the impact of conjugated double-bonds rendering allylic H-shifts energetically unfavourable but entropically favourable.15 At least for these conjugated RC(O)O2 radicals we observe the former but not the latter effect.
C bond and the RC(O)O2 group plays a role for these systems (see Fig. 3). This finding is partially in line with Vereecken & Nozière's speculation on the impact of conjugated double-bonds rendering allylic H-shifts energetically unfavourable but entropically favourable.15 At least for these conjugated RC(O)O2 radicals we observe the former but not the latter effect.
Another detail of note regarding allylic H-shifts is that Nozière and Vereecken have recently performed an experimental validation study of both the H-SAR and R-SAR for unsaturated RO2, in which the predicted allylic H-shift rates were often found to be too high.66 In the article they discuss updating these allylic H-shift parameters in a companion paper, which is unpublished at the time of writing. A proper comparison of our allylic H-shifts trends in RC(O)O2 with those in non-acyl RO2 may thus have to wait.
3.3 Enolic H-shifts
For these reactions we performed an extra set of benchmarking calculations for the three radicals treated by Peeters & Nguyen, in which our F12//aug and DLPNO//jun results are compared against their CBS-QB3//UB3LYP/6-31+G** results.22 This comparison is found in Table 3, whereas our MCTST calculations for a set of monosubstituted enol-RO2 are presented in Table 4.| Radical | E ts − Er0 | G ts − Gr0 |
![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) (cm−1) (cm−1) |
E ts − Erirc | E ts − Epirc | κ | k MCTST (s−1) |
|---|---|---|---|---|---|---|---|
Z-HOCH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHCH2O2(Peeters) CHCH2O2(Peeters) |
48.91 | −1614.01 | 53.09 | 56.78 | |||
Z-HOCH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHCH2O2(F12) CHCH2O2(F12) |
57.37 | 60.20 | −2270.52 | 57.37 | 57.91 | 810.72 | 1.33 × 105 |
Z-HOC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)CH(CH2OH)O2(Peeters) C(CH3)CH(CH2OH)O2(Peeters) |
42.59 | −1543.33 | 33.81 | 65.27 | 15.38 | 2.00 × 106 | |
Z-HOC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)CH(CH2OH)O2(F12) C(CH3)CH(CH2OH)O2(F12) |
47.85 | 49.87 | −2326.02 | 39.99 | 64.78 | 346.70 | 7.57 × 106 |
Z-HOC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)CH(CH2OH)O2(DLPNO) C(CH3)CH(CH2OH)O2(DLPNO) |
53.85 | 55.87 | −2326.02 | 44.98 | 71.88 | 565.75 | 1.10 × 106 |
Z-HOC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHC(CH3)(CH2OH)O2(Peeters) CHC(CH3)(CH2OH)O2(Peeters) |
51.17 | −1632.21 | 51.17 | 20.77 | 6.23 × 104 | ||
Z-HOC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHC(CH3)(CH2OH)O2(F12) CHC(CH3)(CH2OH)O2(F12) |
61.71 | 64.22 | −2328.58 | 52.14 | 60.06 | 859.08 | 3.07 × 104 |
Z-HOC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHC(CH3)(CH2OH)O2(DLPNO) CHC(CH3)(CH2OH)O2(DLPNO) |
66.38 | 68.74 | −2330.25 | 56.42 | 66.62 | 1322.16 | 7.30 × 103 |
| Radical | Structure | E ts − Er0 | G ts − Gr0 |
![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) (cm−1) (cm−1) |
E ts − Erirc | E ts − Epirc | κ | k MCTST (s−1) |
|---|---|---|---|---|---|---|---|---|
Z-HOCH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHCH2O2(F12) CHCH2O2(F12) |
1,6-Prim | 57.37 | 60.20 | −2270.52 | 57.37 | 57.91 | 810.72 | 1.33 × 105 |
Z-HOCH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHCH2O2 (DLPNO) CHCH2O2 (DLPNO) |
1,6-Prim | 61.18 | 64.09 | −2272.21 | 61.18 | 64.04 | 1203.13 | 4.12 × 104 |
Z-HOCH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHCH(CH3)O2 CHCH(CH3)O2 |
1,6-sec | 58.46 | 61.35 | −2203.1 | 58.32 | 58.45 | 470.13 | 2.20 × 105 |
Z-HOCH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHC(CH3)2O2 CHC(CH3)2O2 |
1,6-tert | 57.61 | 60.50 | −2234.65 | 57.61 | 61.80 | 587.20 | 4.20 × 105 |
Z-HOCH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)CH2O2 C(CH3)CH2O2 |
1,6-Prim (Subst) | 53.80 | 56.47 | −2356.43 | 53.79 | 71.53 | 947.02 | 2.76 × 106 |
Z-HOCH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)CH(CH3)O2 C(CH3)CH(CH3)O2 |
1,6-sec (Subst) | 50.83 | 53.38 | −2273.04 | 50.83 | 60.27 | 455.72 | 4.21 × 106 |
Z-HOCH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)C(CH3)2O2 C(CH3)C(CH3)2O2 |
1,6-tert (Subst) | 47.00 | 49.64 | −2351.62 | 47.00 | 69.75 | 511.18 | 1.99 × 107 |
Z-HOCH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHCH2CH2O2 CHCH2CH2O2 |
1,7-Prim | 61.15 | 67.75 | −2839.02 | 61.14 | 86.27 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 152 152 |
1.78 × 105 |
E-HOCH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHCH2CH2O2 CHCH2CH2O2 |
1,7-Prim (E) | 134.32 | 141.47 | −1569.89 | 131.97 | 142.57 | 103.44 | 1.48 × 10−10 |
Z-HOCH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHCH2CH(CH3)O2 CHCH2CH(CH3)O2 |
1,7-sec | 61.20 | 66.84 | −2842.91 | 60.69 | 82.89 | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 848 848 |
4.12 × 105 |
Z-HOCH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHCH2C(CH3)2O2 CHCH2C(CH3)2O2 |
1,7-tert | 64.41 | 67.49 | −2880.57 | 61.56 | 82.26 | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 206 206 |
8.68 × 105 |
Z-HOCH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHC2H4CH2O2 CHC2H4CH2O2 |
1,8-Prim | 60.40 | 63.77 | −2119.7 | 41.73 | 69.01 | 143.94 | 1.96 × 104 |
E-HOCH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHC2H4CH2O2 CHC2H4CH2O2 |
1,8-Prim (E) | 76.16 | 86.48 | −2032.88 | 69.58 | 85.56 | 580.74 | 2.45 |
Z-HOCH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHC2H4CH(CH3)O2 CHC2H4CH(CH3)O2 |
1,8-sec | 49.49 | 57.91 | −2118.65 | 39.42 | 67.77 | 119.38 | 1.16 × 105 |
Z-HOCH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHC2H4C(CH3)2O2 CHC2H4C(CH3)2O2 |
1,8-tert | 51.40 | 58.02 | −2178.14 | 38.93 | 65.22 | 137.78 | 2.65 × 105 |
The most notable difference between our results and those reported by Peeters & Nguyen are that our barrier heights and imaginary frequencies are higher, especially the latter. We suspect the latter difference is due to Peeters's use of B3LYP for frequency analysis. As shown in Table 1 of Peeters and Nguyen,22 UB3LYP/6-31+G** on its own underestimates the barrier height for Z-HOCH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHCH2O2 by about half compared to CBS-QB3//UB3LYP/6-31+G** (26.99 vs. 48.91 kJ mol−1). The barrier being that much lower on the B3LYP PES implies that it is also less steep, resulting in an underestimation of the imaginary frequency. By comparison, the ωB97X-D3/aug-cc-pVTZ barrier for the same molecule is 52.56 kJ mol−1, which is much closer to the values calculated with more accurate levels of theory. Thus we assume that our imaginary frequencies are more accurate. As seen in Table 3, these frequencies lead to significantly higher tunneling corrections, which to some extent compensate for our slightly higher barriers. On the whole however, both ours and Peeters's reaction rates are sufficiently high to outcompete all other irreversible RO2 reactions, the fastest being the HO2 elimination from RO2 with gemini-OH substituents, which has a thermal rate on the order of 103 s−1 at 298 K.67 Thus, the small observed differences in rates may be seen as insignificant in terms of atmospheric relevance.
CHCH2O2 by about half compared to CBS-QB3//UB3LYP/6-31+G** (26.99 vs. 48.91 kJ mol−1). The barrier being that much lower on the B3LYP PES implies that it is also less steep, resulting in an underestimation of the imaginary frequency. By comparison, the ωB97X-D3/aug-cc-pVTZ barrier for the same molecule is 52.56 kJ mol−1, which is much closer to the values calculated with more accurate levels of theory. Thus we assume that our imaginary frequencies are more accurate. As seen in Table 3, these frequencies lead to significantly higher tunneling corrections, which to some extent compensate for our slightly higher barriers. On the whole however, both ours and Peeters's reaction rates are sufficiently high to outcompete all other irreversible RO2 reactions, the fastest being the HO2 elimination from RO2 with gemini-OH substituents, which has a thermal rate on the order of 103 s−1 at 298 K.67 Thus, the small observed differences in rates may be seen as insignificant in terms of atmospheric relevance.
Our selection was aimed first to test both the impact of the methyl group in E position relative to the enol and the impact of the β-OH group outside the TS cycle present in both of the OH + isoprene-derived RO2 studied by Peeters & Nguyen. As expected, the former speeds up the reaction by a factor of 10. The impact of the latter seems less straightforward, as the OH-substituted secondary RO2 in Table 3 has an energy barrier 3 kJ mol−1 higher than its unsubstituted equivalent, whereas the tertiary RO2 has a barrier 9 kJ mol−1 above. A second objective was to calculate rates for enol H-shifts at longer spans in order to observe the decay of the reaction rates, and estimate at which spans the mechanism stops mattering. This expected reduction in the H-shift rates is however not present in our results, with the slowest 1,8-Z-enol H-shift having a rate of 1.96 × 104 s−1 at 298 K and a rate of 2.37 × 103 s−1 at 250 K. We conclude that these Z-enol H-shift reactions are effectively immediate under all ambient atmospheric conditions, at least in the absence of severe steric hindrance in the molecular structure.
In order to test the impact of this steric hindrance, we also calculated two MCTST rates for the E isomers of the Prim-RO2 with TS ring spans 7 and 8. Surprisingly, the latter of these turned out to be rapid enough to occur in tropospheric conditions, implying that even E-enol H-shifts ought to be considered for RO2 where the enol oxygen is attached to the ε-carbon (e.g. in HOCH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHC2H4CH2O2) or further. However, we suspect that additional functional groups might provide additional constraints, and thus render these reactions uncompetitive.
CHC2H4CH2O2) or further. However, we suspect that additional functional groups might provide additional constraints, and thus render these reactions uncompetitive.
3.4 Ring closures in β-unsaturated RC(O)O2
In the computational reference data for the R-SAR, Vereecken et al. calculated 4- and 5-membered ring closure rates for CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHCH2O2, and noted that both rates were far too low to have atmospheric relevance.21 Thus, the R-SAR includes no parameters for ring closure rates in β-unsaturated RO2. However, in our recent work on the atmospheric oxidation of aromatics we discovered a surprisingly rapid 4-membered ring closure reaction in CH3C(O)CH(OH)CH(OOH)C(CH3)
CHCH2O2, and noted that both rates were far too low to have atmospheric relevance.21 Thus, the R-SAR includes no parameters for ring closure rates in β-unsaturated RO2. However, in our recent work on the atmospheric oxidation of aromatics we discovered a surprisingly rapid 4-membered ring closure reaction in CH3C(O)CH(OH)CH(OOH)C(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHC(O)O2, which forms downstream from OH oxidation of para-xylene.68 This implies that 4-membered ring closures may in fact have atmospheric relevance in β-unsaturated RC(O)O2, if not in the corresponding non-acyl RO2.
CHC(O)O2, which forms downstream from OH oxidation of para-xylene.68 This implies that 4-membered ring closures may in fact have atmospheric relevance in β-unsaturated RC(O)O2, if not in the corresponding non-acyl RO2.
In our calculations, we first calculated the 4- and 5-membered ring closure rates for the acryl peroxy radical (CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHC(O)O2), and used the former as an anchor reaction. This radical has been found to form in isoprene ozonolysis,69 and may thus be one of the most abundant RC(O)O2 in the troposphere. The 4-membered ring closure was found to be the more competitive reaction, in line with our previous findings.68 However, neither of these reactions are rapid enough to compete under atmospheric conditions, implying that ring closures for β-unsaturated systems only become important with the correct substituents. We calculated 4-membered ring closure rates for β-unsaturated RC(O)O2 with a similar set of carbon substituents as for the γ and δ-unsaturated RC(O)O2 discussed below, in addition to a few other substituted structures that may activate the reaction. Unsurprisingly, we found that the fully substituted (CH3)2C
CHC(O)O2), and used the former as an anchor reaction. This radical has been found to form in isoprene ozonolysis,69 and may thus be one of the most abundant RC(O)O2 in the troposphere. The 4-membered ring closure was found to be the more competitive reaction, in line with our previous findings.68 However, neither of these reactions are rapid enough to compete under atmospheric conditions, implying that ring closures for β-unsaturated systems only become important with the correct substituents. We calculated 4-membered ring closure rates for β-unsaturated RC(O)O2 with a similar set of carbon substituents as for the γ and δ-unsaturated RC(O)O2 discussed below, in addition to a few other substituted structures that may activate the reaction. Unsurprisingly, we found that the fully substituted (CH3)2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)C(O)O2 has the highest reaction rate, along with, somewhat more surprisingly, Z-C2H5CH
C(CH3)C(O)O2 has the highest reaction rate, along with, somewhat more surprisingly, Z-C2H5CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(i-C3H7)C(O)O2 (see Table 5). We suspect that the high amount of branching in the molecular structure of the latter adds steric hindrance to the reactant side that is not equally present in the TS. Generally, it seems that having a carbon substituent on both sides of the C
C(i-C3H7)C(O)O2 (see Table 5). We suspect that the high amount of branching in the molecular structure of the latter adds steric hindrance to the reactant side that is not equally present in the TS. Generally, it seems that having a carbon substituent on both sides of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond is enough to bring the room temperature reaction rates above 10−2 s−1, allowing them to outcompete the lowest known bimolecular RO2 decay rates in ambient tropospheric conditions, determined from the rate of RO2 + HO2 reactions in low NOx regimes.3
C bond is enough to bring the room temperature reaction rates above 10−2 s−1, allowing them to outcompete the lowest known bimolecular RO2 decay rates in ambient tropospheric conditions, determined from the rate of RO2 + HO2 reactions in low NOx regimes.3
| Radical | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond, ring size C bond, ring size |
E ts − Er0 | G ts − Gr0 |
![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) (cm−1) (cm−1) |
E ts − Erirc | E ts − Epirc | κ | k MCTST (s−1) |
|---|---|---|---|---|---|---|---|---|
CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHC(O)O2(F12) CHC(O)O2(F12) |
β-CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2, 4 CH2, 4 |
95.88 | 99.26 | −586.65 | 94.95 | 60.18 | 1.44 | 2.00 × 10−5 |
CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHC(O)O2(DLPNO) CHC(O)O2(DLPNO) |
β-CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2, 4 CH2, 4 |
94.77 | 97.87 | −588.02 | 94.28 | 61.94 | 1.44 | 3.33 × 10−5 |
CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHC(O)O2(F12) CHC(O)O2(F12) |
β-CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2, 5 CH2, 5 |
100.41 | 99.26 | −735.73 | 85.98 | 122.29 | 1.80 | 2.79 × 10−6 |
CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHC(O)O2(DLPNO) CHC(O)O2(DLPNO) |
β-CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2, 5 CH2, 5 |
98.58 | 102.93 | −740.09 | 85.25 | 122.33 | 1.82 | 1.31 × 10−6 |
C2H5CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHC(O)O2 CHC(O)O2 |
β-CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH(CH3) CH(CH3) |
91.83 | 93.34 | −471.65 | 82.23 | 58.16 | 1.26 | 1.31 × 10−4 |
C3H7C(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHC(O)O2 CHC(O)O2 |
β-CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)2 C(CH3)2 |
83.22 | 84.56 | −392.45 | 81.90 | 54.86 | 1.17 | 7.51 × 10−3 |
CH3C(O)CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHC(O)O2 CHC(O)O2 |
β-CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHCO CHCO |
85.11 | 88.45 | −749.42 | 85.11 | 78.48 | 1.85 | 1.40 × 10−3 |
i-C3H7C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2)C(O)O2 CH2)C(O)O2 |
β-C(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2 CH2 |
81.64 | 84.58 | −508.87 | 69.99 | 62.67 | 1.31 | 9.53 × 10−3 |
Z-C2H5CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)C(O)O2 C(CH3)C(O)O2 |
β-C(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH(CH3) CH(CH3) |
74.88 | 79.98 | −427.5 | 62.17 | 59.36 | 1.21 | 7.08 × 10−2 |
Z-C2H5CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(i-C3H7)C(O)O2 C(i-C3H7)C(O)O2 |
β-C(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH(CH3) CH(CH3) |
64.06 | 66.76 | −356.73 | 61.13 | 59.00 | 1.14 | 3.37 |
(CH3)2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)C(O)O2 C(CH3)C(O)O2 |
β-C(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)2, 4 C(CH3)2, 4 |
63.03 | 69.06 | −369.01 | 62.22 | 59.45 | 1.15 | 2.98 |
(CH3)2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)C(O)O2 C(CH3)C(O)O2 |
β-C(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)2, 5 C(CH3)2, 5 |
70.90 | 80.58 | −320.90 | 68.98 | 139.67 | 1.11 | 2.06 × 10−2 |
CH3CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(OH)C(O)O2 C(OH)C(O)O2 |
β-C(OH)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH(CH3) CH(CH3) |
84.54 | 86.81 | −311.00 | 69.85 | 60.26 | 1.10 | 2.66 × 10−3 |
C2H5CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH2OH)C(O)O2 C(CH2OH)C(O)O2 |
β-CC(OH)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH(CH3) CH(CH3) |
74.15 | 79.32 | −404.76 | 62.52 | 61.38 | 1.18 | 9.52 × 10−2 |
C2H5CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CHO)C(O)O2 C(CHO)C(O)O2 |
β-C(CHO)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH(CH3) CH(CH3) |
82.43 | 85.50 | −404.25 | 78.26 | 50.86 | 1.18 | 5.47 × 10−3 |
CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHCH CHCH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHC(O)O2 CHC(O)O2 |
β-CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHCH CHCH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2 CH2 |
88.02 | 90.10 | −748.4 | 80.83 | 89.58 | 1.84 | 1.18 × 10−3 |
Regarding the fate of the highly strained cyclic peresters formed from these reactions, we suspect that the ring closure is eventually followed by a CO2 elimination either before or after O2 adds to the radical carbon, leaving behind a carbonyl at the carbon where the ring closure occurred. Unfortunately, we were neither able to confirm nor eliminate these suspicions, as the TS proved highly multi-configurational. Nevertheless, we have documented our attempts in Section S5 of the ESI.†
3.5 Ring closures in γ and δ-unsaturated RC(O)O2
The R-SAR already covers ring closure reactions for γ, δ, and ε-unsaturated non-acyl RO2. We performed calculations of all of the equivalent γ- and δ-unsaturated RC(O)O2, except for CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHCH2C(O)O2, the radical already treated by Vereecken et al.21 These MCTST rates are found in Tables 6 and 7.
CHCH2C(O)O2, the radical already treated by Vereecken et al.21 These MCTST rates are found in Tables 6 and 7.
| Radical | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond, ring size C bond, ring size |
E ts − Er0 | G ts − Gr0 |
![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) (cm−1) (cm−1) |
E ts − Erirc | E ts − Epirc | κ | k MCTST (s−1) |
|---|---|---|---|---|---|---|---|---|
| a From Vereecken et al.21 | ||||||||
CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHCH2C(O)O2a CHCH2C(O)O2a |
γ-CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2, 5 CH2, 5 |
54.63 | 1.33 × 102 | |||||
CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHCH2C(O)O2a CHCH2C(O)O2a |
γ-CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2, 6 CH2, 6 |
72.62 | 1.08 × 10−1 | |||||
CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)CH2C(O)O2(F12) C(CH3)CH2C(O)O2(F12) |
γ-C(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2, 5 CH2, 5 |
43.90 | 48.98 | −479.92 | 39.95 | 67.27 | 1.27 | 6.43 × 103 |
CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)CH2C(O)O2(DLPNO) C(CH3)CH2C(O)O2(DLPNO) |
γ-C(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2, 5 CH2, 5 |
44.31 | 49.13 | −480.59 | 41.05 | 71.81 | 1.27 | 5.07 × 103 |
CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)CH2C(O)O2(F12) C(CH3)CH2C(O)O2(F12) |
γ-C(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2, 6 CH2, 6 |
69.10 | 72.43 | −468.98 | 65.15 | 87.82 | 1.26 | 5.31 × 10−1 |
CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)CH2C(O)O2(DLPNO) C(CH3)CH2C(O)O2(DLPNO) |
γ-C(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2, 6 CH2, 6 |
68.66 | 72.23 | −470.55 | 65.61 | 90.16 | 1.26 | 4.95 × 10−1 |
Z-CH(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHCH2C(O)O2 CHCH2C(O)O2 |
γ-CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH(CH3), 5 CH(CH3), 5 |
37.98 | 45.33 | −446.55 | 36.54 | 64.73 | 1.23 | 7.51 × 104 |
Z-CH(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHCH2C(O)O2 CHCH2C(O)O2 |
γ-CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH(CH3), 6 CH(CH3), 6 |
66.83 | 74.80 | −468.94 | 65.39 | 97.28 | 1.26 | 1.98 × 10−1 |
E-CH(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHCH2C(O)O2 CHCH2C(O)O2 |
γ-CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH(CH3), 6 CH(CH3), 6 |
65.24 | 70.87 | −412.64 | 63.02 | 93.13 | 1.19 | 2.08 |
Z-CH(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)CH2C(O)O2 C(CH3)CH2C(O)O2 |
γ-C(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH(CH3), 5 CH(CH3), 5 |
30.82 | 37.21 | −398.15 | 26.85 | 66.52 | 1.18 | 1.01 × 106 |
Z-CH(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)CH2C(O)O2 C(CH3)CH2C(O)O2 |
γ-C(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH(CH3), 6 CH(CH3), 6 |
59.67 | 65.58 | −451.06 | 55.71 | 92.90 | 1.23 | 8.35 |
E-CH(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)CH2C(O)O2 C(CH3)CH2C(O)O2 |
γ-C(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH(CH3), 6 CH(CH3), 6 |
58.66 | 62.59 | −350.75 | 54.55 | 92.93 | 1.13 | 2.42 × 101 |
C(CH3)2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHCH2C(O)O2 CHCH2C(O)O2 |
γ-CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)2, 5 C(CH3)2, 5 |
31.32 | 40.14 | −383.60 | 32.79 | 62.25 | 1.16 | 2.99 × 105 |
C(CH3)2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHCH2C(O)O2 CHCH2C(O)O2 |
γ-CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)2, 6 C(CH3)2, 6 |
55.65 | 66.56 | −406.87 | 56.95 | 93.89 | 1.19 | 9.09 |
C(CH3)2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)CH2C(O)O2 C(CH3)CH2C(O)O2 |
γ-C(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)2, 5 C(CH3)2, 5 |
26.78 | 34.31 | −324.89 | 23.31 | 68.93 | 1.11 | 2.79 × 106 |
C(CH3)2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)CH2C(O)O2 C(CH3)CH2C(O)O2 |
γ-C(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)2, 6 C(CH3)2, 6 |
46.97 | 56.55 | −342.14 | 43.53 | 96.66 | 1.13 | 2.98 × 102 |
| Radical | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond, ring size C bond, ring size |
E ts − Er0 | G ts − Gr0 |
![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) (cm−1) (cm−1) |
E ts − Erirc | E ts − Epirc | κ | k MCTST (s−1) |
|---|---|---|---|---|---|---|---|---|
CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHC2H4C(O)O2(F12) CHC2H4C(O)O2(F12) |
δ-CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2, 6 CH2, 6 |
47.82 | 55.29 | −552.11 | 41.70 | 59.35 | 1.38 | 4.99 × 102 |
CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHC2H4C(O)O2(DLPNO) CHC2H4C(O)O2(DLPNO) |
δ-CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2, 6 CH2, 6 |
46.52 | 53.98 | −552.26 | 40.94 | 61.85 | 1.38 | 8.99 × 102 |
CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHC2H4C(O)O2(F12) CHC2H4C(O)O2(F12) |
δ-CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2, 7 CH2, 7 |
59.81 | 67.89 | −522.12 | 53.69 | 71.34 | 1.33 | 3.11 |
CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHC2H4C(O)O2(DLPNO) CHC2H4C(O)O2(DLPNO) |
δ-CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2, 7 CH2, 7 |
58.28 | 66.35 | −522.88 | 52.51 | 73.20 | 1.33 | 6.13 |
CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)C2H4C(O)O2 C(CH3)C2H4C(O)O2 |
δ-C(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2, 6 CH2, 6 |
40.74 | 49.06 | −493.49 | 35.75 | 61.90 | 1.29 | 2.93 × 103 |
CH2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)C2H4C(O)O2 C(CH3)C2H4C(O)O2 |
δ-C(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2, 7 CH2, 7 |
52.16 | 59.59 | −482.05 | 47.44 | 70.23 | 1.27 | 4.22 × 101 |
Z-CH(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHC2H4C(O)O2 CHC2H4C(O)O2 |
δ-CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH(CH3), 6 CH(CH3), 6 |
38.42 | 46.09 | −478.70 | 34.16 | 59.24 | 1.27 | 1.43 × 104 |
Z-CH(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHC2H4C(O)O2 CHC2H4C(O)O2 |
δ-CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH(CH3), 7 CH(CH3), 7 |
50.19 | 61.63 | −497.33 | 46.20 | 77.97 | 1.29 | 2.75 × 101 |
E-CH(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHC2H4C(O)O2 CHC2H4C(O)O2 |
δ-CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH(CH3), 7 CH(CH3), 7 |
49.53 | 57.36 | −468.61 | 45.61 | 71.54 | 1.26 | 1.66 × 102 |
Z-CH(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)C2H4C(O)O2 C(CH3)C2H4C(O)O2 |
δ-C(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH(CH3), 6 CH(CH3), 6 |
29.16 | 36.59 | −432.19 | 27.72 | 59.47 | 1.21 | 4.72 × 105 |
Z-CH(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)C2H4C(O)O2 C(CH3)C2H4C(O)O2 |
δ-C(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH(CH3), 7 CH(CH3), 7 |
41.22 | 50.23 | −452.65 | 39.66 | 69.92 | 1.24 | 2.23 × 103 |
E-CH(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)C2H4C(O)O2 C(CH3)C2H4C(O)O2 |
δ-C(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH(CH3), 7 CH(CH3), 7 |
41.90 | 51.74 | −404.85 | 39.85 | 64.19 | 1.19 | 2.17 × 103 |
C(CH3)2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHC2H4C(O)O2 CHC2H4C(O)O2 |
δ-CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)2, 6 C(CH3)2, 6 |
33.49 | 39.75 | −430.54 | 29.83 | 55.87 | 1.21 | 1.42 × 105 |
C(CH3)2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CHC2H4C(O)O2 CHC2H4C(O)O2 |
δ-CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)2, 7 C(CH3)2, 7 |
43.42 | 53.98 | −452.96 | 39.77 | 75.81 | 1.24 | 3.94 × 102 |
C(CH3)2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)C2H4C(O)O2 C(CH3)C2H4C(O)O2 |
δ-C(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)2, 6 C(CH3)2, 6 |
22.29 | 35.49 | −348.90 | 20.21 | 57.34 | 1.13 | 1.71 × 106 |
C(CH3)2![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)C2H4C(O)O2 C(CH3)C2H4C(O)O2 |
δ-C(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)2, 7 C(CH3)2, 7 |
33.08 | 49.00 | −374.14 | 31.18 | 62.13 | 1.16 | 8.75 × 103 |
In short, our main conclusion is that unsaturated RC(O)O2 indeed systematically prefer forming a ring with the inner sp2-carbon, regardless of the substitution around the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond. Also notably, the 5-membered ring closure reactions in the more substituted γ-unsaturated RC(O)O2 are sped up by two or three orders of magnitude relative to their respective non-acyl RO2. The 6-membered ring closure reactions in δ-unsaturated RC(O)O2 are even more rapid relative to their respective non-acyl RO2 reactions, usually reaching within an order of magnitude of the corresponding γ-RC(O)O2 reactions. Furthermore, the 7-membered ring closure rates in δ-unsaturated RC(O)O2 are also significantly sped up relative to their respective non-acyl RO2 reactions, while still being essentially uncompetitive compared to the 6-membered ring closures. In short, we observe a similar shift in ring size trends as with the allylic and aldehydic H-shifts, with the peak of the ‘rate as a function of ring size’ curve being shifted to larger ring sizes for RC(O)O2 relative to other RO2. This is likely a consequence of the C
C bond. Also notably, the 5-membered ring closure reactions in the more substituted γ-unsaturated RC(O)O2 are sped up by two or three orders of magnitude relative to their respective non-acyl RO2. The 6-membered ring closure reactions in δ-unsaturated RC(O)O2 are even more rapid relative to their respective non-acyl RO2 reactions, usually reaching within an order of magnitude of the corresponding γ-RC(O)O2 reactions. Furthermore, the 7-membered ring closure rates in δ-unsaturated RC(O)O2 are also significantly sped up relative to their respective non-acyl RO2 reactions, while still being essentially uncompetitive compared to the 6-membered ring closures. In short, we observe a similar shift in ring size trends as with the allylic and aldehydic H-shifts, with the peak of the ‘rate as a function of ring size’ curve being shifted to larger ring sizes for RC(O)O2 relative to other RO2. This is likely a consequence of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group adding additional strain to the smaller rings.
O group adding additional strain to the smaller rings.
One especially notable detail about these ring closure reactions is that the fastest rates reach the same order of magnitude as the irreversible hydroperoxide H-shift reactions. Unlike the case with the allylic H-shift mentioned above, these rates are directly computed rather than SAR-predicted, giving more credence to the suggestion that these reactions could outcompete the H-shift. To investigate this, we calculated 5-membered ring closure and –OOH H-shift rates for two hypothetical RC(O)O2 containing both a γ-C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond and a hydroperoxide on either side of the C
C bond and a hydroperoxide on either side of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond. The full results for this are presented in Section S4 of the ESI,† but in short our results suggest that the presence of the C
C bond. The full results for this are presented in Section S4 of the ESI,† but in short our results suggest that the presence of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond slows down the H-shifts from the OOH groups. Based on these results, we conclude that ring closures in γ and δ-unsaturated RC(O)O2 presumably always outcompete the –OOH H-shift.
C bond slows down the H-shifts from the OOH groups. Based on these results, we conclude that ring closures in γ and δ-unsaturated RC(O)O2 presumably always outcompete the –OOH H-shift.
4 Extension of structure–activity relationships
Our MCTST results for aldehydic and allylic H-shifts as well as the ring closures were used to derive the T-dependent SAR parameters, using the same modified Arrhenius expression as in the original H-SAR and R-SAR articles15,21 (eqn (4)). The results are found in Tables 8 and 9. In addition, we estimate rate coefficients and T-dependent SAR parameters for ε-unsaturated RC(O)O2 using the relative rate coefficients of δ- and ε-unsaturated RO2 from the R-SAR along with our rates for δ-unsaturated RC(O)O2 (eqn (5)). | (4) |
 | (5) |
| RO2 | Span & H | A (s−1) | n | E a (K) | RO2 | Span & H | A (s−1) | n | E a (K) |
|---|---|---|---|---|---|---|---|---|---|
| RC(O)O2 | 1,4-CHO | 2.16 × 106 | 1.60 | 6517 | RCH2O2 | 1,8-CHO | 1.92 × 10−35 | 14.26 | 381 |
| RC(O)O2 | 1,5-CHO | 6.67 × 10−60 | 23.03 | −2160 | RCH(R)O2 | 1,8-CHO | 1.80 × 10−33 | 13.63 | 765 |
| RC(O)O2 | 1,6-CHO | 2.12 × 10−45 | 18.24 | −340 | RC(R)2O2 | 1,8-CHO | 1.82 × 10−31 | 2.98 | 1095 |
| RC(O)O2 | 1,7-CHO | 2.87 × 10−30 | 13.25 | 1277 | RC(O)O2 | 1,8-CHO | 4.21 × 10−47 | 18.82 | −720 |
| RC(O)O2 | 1,5-CH3-gem | 1.11 × 10−77 | 28.53 | −2047 | RC(O)O2 | 1,6-CH3-endo | 3.17 × 10−65 | 23.92 | −1896 |
| RC(O)O2 | 1,5-CH2-gem | 7.68 × 10−71 | 26.56 | −2074 | RC(O)O2 | 1,6-CH2-endo | 1.60 × 10−58 | 21.94 | −1819 |
| RC(O)O2 | 1,5-CH-gem | 1.41 × 10−63 | 24.31 | −1867 | RC(O)O2 | 1,6-CH-endo | 2.76 × 10−56 | 21.49 | −1587 |
| RC(O)O2 | 1,6-CH3-gem | 1.26 × 10−69 | 25.38 | −3805 | RC(O)O2 | 1,7-CH3-endo | 1.20 × 10−64 | 23.64 | −3332 |
| RC(O)O2 | 1,6-CH2-gem | 9.75 × 10−61 | 22.82 | −3360 | RC(O)O2 | 1,7-CH2-endo | 2.61 × 10−65 | 24.44 | −3669 |
| RC(O)O2 | 1,6-CH-gem | 5.93 × 10−51 | 19.79 | −2280 | RC(O)O2 | 1,7-CH-endo | 8.97 × 10−64 | 24.29 | −3421 |
| RC(O)O2 | 1,7-CH2-exo | 1.11 × 10−49 | 19.11 | −1876 | RC(O)O2 | 1,7-CH-exo | 4.49 × 10−38 | 15.61 | −402 |
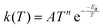
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond, ring size C bond, ring size |
A (s−1) | n | E a (K) | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond, ring size C bond, ring size |
A (s−1) | n | E a (K) |
|---|---|---|---|---|---|---|---|
| a From Vereecken et al.21 | |||||||
β-CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2, 4 CH2, 4 |
8.80 × 107 | 1.32 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 921 921 |
β-CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2, 5 CH2, 5 |
4.75 × 103 | 2.61 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 770 770 |
β-C(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2, 4 CH2, 4 |
2.84 × 109 | 0.98 | 9543 | β-CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH(CH3), 4 CH(CH3), 4 |
2.40 × 1010 | 0.67 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 917 917 |
β-CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)2, 4 C(CH3)2, 4 |
1.01 × 1011 | 0.61 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 041 041 |
β-C(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH(CH3), 4 CH(CH3), 4 |
6.57 × 106 | 1.93 | 8742 |
β-C(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)2, 4 C(CH3)2, 4 |
9.40 × 1010 | 0.25 | 7621 | β-C(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)2, 5 C(CH3)2, 5 |
1.24 × 1011 | −0.10 | 8598 |
γ-CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2, 5a CH2, 5a |
8.05 × 108 | 0.65 | 5757 | γ-CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2, 6a CH2, 6a |
3.05 × 1011 | −0.16 | 8271 |
γ-C(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2, 5 CH2, 5 |
7.68 × 1010 | −0.03 | 4808 | γ-C(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2, 6 CH2, 6 |
5.89 × 1011 | −0.20 | 7920 |
γ-CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH(CH3), 5 CH(CH3), 5 |
8.97 × 1010 | 0.02 | 4205 |
Z-γ-CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH(CH3), 6 CH(CH3), 6 |
4.02 × 1010 | −0.08 | 7626 |
E-γ-CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH(CH3), 6 CH(CH3), 6 |
2.54 × 1010 | 0.40 | 7599 | ||||
γ-C(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH(CH3), 5 CH(CH3), 5 |
3.53 × 1010 | 0.12 | 3315 |
Z-γ-C(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH(CH3), 6 CH(CH3), 6 |
1.23 × 1010 | 0.30 | 6805 |
E-γ-C(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH(CH3), 6 CH(CH3), 6 |
1.68 × 1013 | −0.70 | 6941 | ||||
γ-CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)2, 5 C(CH3)2, 5 |
1.62 × 1010 | 0.07 | 3362 | γ-CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)2, 6 C(CH3)2, 6 |
2.88 × 109 | 0.25 | 6259 |
γ-C(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)2, 5 C(CH3)2, 5 |
1.04 × 1011 | −0.14 | 2894 | γ-C(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)2, 6 C(CH3)2, 6 |
6.74 × 109 | 0.14 | 5288 |
δ-CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2, 6 CH2, 6 |
1.16 × 109 | 0.47 | 5169 | δ-CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2, 7 CH2, 7 |
3.94 × 108 | 0.61 | 6604 |
δ-C(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2, 6 CH2, 6 |
2.32 × 109 | 0.25 | 4470 | δ-C(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2, 7 CH2, 7 |
6.39 × 109 | 0.20 | 5952 |
δ-CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH(CH3), 6 CH(CH3), 6 |
1.77 × 1010 | 0.13 | 4394 |
Z-δ-CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH(CH3), 7 CH(CH3), 7 |
1.09 × 108 | 0.64 | 5615 |
E-δ-CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH(CH3), 7 CH(CH3), 7 |
1.14 × 109 | 0.56 | 5634 | ||||
δ-C(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH(CH3), 6 CH(CH3), 6 |
2.52 × 1010 | 0.05 | 3322 |
Z-δ-C(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH(CH3), 7 CH(CH3), 7 |
3.60 × 109 | 0.33 | 4920 |
E-δ-C(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH(CH3), 7 CH(CH3), 7 |
3.89 × 109 | 0.32 | 4841 | ||||
δ-CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)2, 6 C(CH3)2, 6 |
1.20 × 106 | 1.65 | 3432 | δ-CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)2, 7 C(CH3)2, 7 |
5.17 × 108 | 0.34 | 4781 |
δ-C(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)2, 6 C(CH3)2, 6 |
4.47 × 109 | 0.03 | 2397 | δ-C(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)2, 7 C(CH3)2, 7 |
1.65 × 108 | 0.39 | 3603 |
ε-CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2, 7 CH2, 7 |
2.51 × 1010 | −0.07 | 6324 | ε-CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2, 8 CH2, 8 |
2.05 × 104 | 1.75 | 5358 |
ε-C(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2, 7 CH2, 7 |
1.07 × 1011 | −0.39 | 5571 | ε-C(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2, 8 CH2, 8 |
3.79 × 105 | 1.30 | 4719 |
ε-CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH(CH3), 7 CH(CH3), 7 |
9.35 × 109 | 0.14 | 5330 |
Z-ε-CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH(CH3), 8 CH(CH3), 8 |
1.33 × 103 | 2.00 | 4346 |
E-ε-CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH(CH3), 8 CH(CH3), 8 |
1.66 × 103 | 2.20 | 4029 | ||||
ε-C(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH(CH3), 7 CH(CH3), 7 |
5.76 × 109 | 0.17 | 4071 |
Z-ε-C(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH(CH3), 8 CH(CH3), 8 |
1.27 × 104 | 1.92 | 3714 |
E-ε-C(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH(CH3), 8 CH(CH3), 8 |
4.28 × 105 | 1.42 | 3418 | ||||
ε-CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)2, 7 C(CH3)2, 7 |
4.51 × 105 | 1.72 | 4503 | ε-CH![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)2, 8 C(CH3)2, 8 |
1.89 × 103 | 1.90 | 3528 |
ε-C(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)2, 7 C(CH3)2, 7 |
2.84 × 108 | 0.30 | 3020 | ε-C(CH3)![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C(CH3)2, 8 C(CH3)2, 8 |
2.68 × 103 | 1.63 | 1955 |
Similarly, we note that Carter et al.70 have used the reference data of Vereecken & Nozière along with the computed reaction rates of Møller et al.18 to extrapolate the reaction rates predicted by the H-SAR up to arbitrarily high H-shift spans. Something similar may be done to estimate rates for RC(O)O2 H-shifts with higher spans than those calculated here, but our view is that such an estimation ought to also include not only our results, but also the computational results of Seal et al.14 and the forthcoming extended H-SAR by Vereecken & Nozière66 as reference data. Thus, we will perform this extrapolation in a future paper, in which we introduce both extended SAR models into the automatic mechanism generator GECKO-A.71
We opted not to derive SAR parameters for the Z-enol H-shifts, as our recommendation for these reactions is to simply assume that they are always instantaneous, as all of our computed reaction rates are well above those of any competing RO2 reactions. As noted in Section 3.3, E-enol H-shifts may also prove important for larger molecules with long and flexible carbon backbones between the RO2 and enol groups. We have not derived SAR parameters for these either, as we are unsure to which extent our linear, monofunctional model radicals represent true atmospheric radicals, as these are likely to have multiple substituents. We may revisit the subject when such data is available.
In terms of atmospheric significance of our results, we expect the aldehydic H-shift parameters to be an especially crucial refinement of the H-SAR, as aldehydes occur commonly in highly oxidized RO2 structures.23 Additionally, as we already noted in Section 3.1, our computational results are in some ways more complete than the reference data that informed the original SAR, which only included sec- and tert-RO2 with short H-shift spans. We find that a re-parametrization of the aldehydic H-shifts may also be in order for non-acyl RO2. For unsaturated RC(O)O2 with at least one carbon between the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and C
O and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond, our findings suggest that ring closure reactions, especially with the inner sp2 carbon, are overwhelmingly the major fate in atmospheric conditions. For β-unsubstituted RC(O)O2, on the other hand, allylic H-shifts and 4-membered ring closure reactions may both be competitive depending on the molecular structure. Nevertheless, the allylic H-shifts are also a valuable addition to the H-SAR for completion purposes, despite the fact that they seem to be outcompeted by the ring closures in most cases.
C bond, our findings suggest that ring closure reactions, especially with the inner sp2 carbon, are overwhelmingly the major fate in atmospheric conditions. For β-unsubstituted RC(O)O2, on the other hand, allylic H-shifts and 4-membered ring closure reactions may both be competitive depending on the molecular structure. Nevertheless, the allylic H-shifts are also a valuable addition to the H-SAR for completion purposes, despite the fact that they seem to be outcompeted by the ring closures in most cases.
Due to the scarcity of literature rates of unimolecular reactions in functionalized acyl peroxy radicals (let alone experimentally constrained literature rates, which do not exist to our knowledge), we do not have much data to validate our SAR extensions with. This is especially true for ring closure reactions, for which the sole unsaturated RC(O)O2 system studied by Vereecken et al.21 is already incorporated into our R-SAR extension. For H-shifts, however, we may use the computational literature rates in Table S1 (ESI†) to tentatively estimate the applicability of the extended H-SAR for arbitrary RC(O)O2 with the correct substituents. For the sole aldehydic H-shift rate calculated by Møller et al.,18 which the original H-SAR overestimates by a factor of 124 at 298 K, our extended H-SAR predicts a rate of 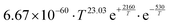 , where the second exponential function is the β-OH factor from Vereecken and Nozière.15 This results in a rate of 1.51 s−1 at 298 K, which overestimates Møller's directly calculated rate by a factor of 5.8. While not ideal, this disagreement is largely in line with the others in Table S1 (ESI†), for which the maximum is 7.69 and the geometric mean is 2.59. We thus assume that the extended SAR models predict rates for arbitrary RC(O)O2 within an order of magnitude at atmospheric temperatures.
, where the second exponential function is the β-OH factor from Vereecken and Nozière.15 This results in a rate of 1.51 s−1 at 298 K, which overestimates Møller's directly calculated rate by a factor of 5.8. While not ideal, this disagreement is largely in line with the others in Table S1 (ESI†), for which the maximum is 7.69 and the geometric mean is 2.59. We thus assume that the extended SAR models predict rates for arbitrary RC(O)O2 within an order of magnitude at atmospheric temperatures.
5 Conclusions
In this work, we have extended the structure–activity relationships for unimolecular reactions of RO2 developed by Vereecken and coworkers to several classes of rapid reactions that were previously only rudimentarily included in the SAR: H-shifts in CHO-substituted RC(O)O2, allylic H-shifts and ring closures in unsaturated RC(O)O2, and H-shifts in enol-substituted RO2. These groups of radicals are among the shortest-lived of all RO2 in the atmosphere, and we therefore find it crucial that their fates are accurately represented by the SAR. While deriving this SAR extension, we have also gained new mechanistic insight on the reactivity trends of substituted acyl peroxy radicals.In the process of calculating the reactions kinetics for all these unimolecular reactions, we have also further improved the cost-effective conformer sampling workflow of Møller et al.24 Based on our experiences, we recommend using ORCA's new global optimizer code GOAT for generation of an initial conformer ensemble, and performing low-level filtering optimizations with B3LYP-D3 rather than B3LYP. Furthermore, ωB97X-D(3)/aug-cc-pVTZ optimizations may be swapped out for ωB97X-D(3)/jun-cc-pVTZ optimizations, and CCSD(T)-F12 single-points for DLPNO-CCSD(T) single points, but both of these changes come with a minor decrease in accuracy.
Author contributions
LF performed the quantum chemistry calculations, MCTST rate calculations, derived the SAR parameters, and drafted the manuscript. AS performed the quantum chemistry calculations on the 4-membered ring closures. SI, MR & TK provided consultation and useful discussions. The manuscript was reviewed and revised by all authors.Data availability
Multi-conformer transition state theory reaction rates from 200 K to 400 K, ORCA output files for all published results, as well as our bash-wrapped python script for calculating the former from the latter, are freely available in a F.A.I.R Zenodo repository: https://zenodo.org/records/15089952.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Research Council of Finland through the Virtual Laboratory for Molecular Level Atmospheric Transformations Centre of Excellence (VILMA, grant numbers 346369 and 346373) and Academy Research Fellow grant 355966, as well as the Jane ja Aatos Erkon Säätiö Foundation (grant number 200038). This project has received funding from the European Research Council under the European Unions Horizon 2020 research and innovation programme under Grant No. 101002728. Computational resources for the quantum chemical scans were provided by the Finnish Centre for Scientific Computing (CSC). LF acknowledges Thomas Golin-Almeida, Christopher Daub, Aliisa Ojala and Benjamin Frandsen for useful discussions.References
- J. J. Orlando and G. S. Tyndall, Chem. Soc. Rev., 2012, 41, 6294–6317 RSC.
- M. Ehn, J. A. Thornton, E. Kleist, M. Sipilä, H. Junninen, I. Pullinen, M. Springer, F. Rubach, R. Tillmann, B. Lee, F. Lopez-Hilfiker, S. Andres, I.-H. Acir, M. Rissanen, T. Jokinen, S. Schobesberger, J. Kangasluoma, J. Kontkanen, T. Nieminen, T. Kurtén, L. B. Nielsen, S. Jørgensen, H. G. Kjaergaard, M. Canagaratna, M. Dal Maso, T. Berndt, T. Petäjä, A. Wahner, V.-M. Kerminen, M. Kulmala, D. R. Worsnop, J. Wildt and T. F. Mentel, Nature, 2014, 506, 476–479 CrossRef CAS PubMed.
- H. S. Kenagy, C. L. Heald, N. Tahsini, M. B. Goss and J. H. Kroll, Sci. Adv., 2024, 10, eado1482 CrossRef CAS PubMed.
- M. E. Jenkin, R. Valorso, B. Aumont and A. R. Rickard, Atmos. Chem. Phys., 2019, 19, 7691–7717 CrossRef CAS.
- S. Barua, S. Iyer, A. Kumar, P. Seal and M. Rissanen, Atmos. Chem. Phys., 2023, 23, 10517–10532 CrossRef CAS.
- E. Villenave, R. Lesclaux, S. Seefeld and W. R. Stockwell, J. Geophys. Res.: Atmos., 1998, 103, 25273–25285 Search PubMed.
- V.-T. Salo, R. Valiev, S. Lehtola and T. Kurtén, J. Phys. Chem. A, 2022, 126, 4046–4056 CrossRef CAS PubMed.
- B. Nozière and F. Fache, Chem. Sci., 2021, 12, 11676–11683 RSC.
- B. N. Frandsen, L. Franzon, M. Meder, D. Pasik, E. Ahongshangbam, N. Vinkvist, N. Myllys, S. Iyer, M. P. Rissanen, M. Ehn and T. Kurtén, Detailed Investigation of 2,3-Dimethyl-2-butene Ozonolysis-Derived Hydroxyl, Peroxy, and Alkoxy Radical Chemistry, ACS Earth Space Chem., 2025 DOI:10.1021/acsearthspacechem.4c00355.
- J. J. Orlando, Phys. Chem. Chem. Phys., 2007, 9, 4189–4199 RSC.
- J. D. Crounse, L. B. Nielsen, S. Jørgensen, H. G. Kjaergaard and P. O. Wennberg, J. Phys. Chem. Lett., 2013, 4, 3513–3520 CrossRef CAS.
- J. Peeters, T. L. Nguyen and L. Vereecken, Phys. Chem. Chem. Phys., 2009, 11, 5935–5939 RSC.
- H. C. Knap and S. Jørgensen, J. Phys. Chem. A, 2017, 121, 1470–1479 Search PubMed.
- P. Seal, S. Barua, S. Iyer, A. Kumar and M. Rissanen, Phys. Chem. Chem. Phys., 2023, 25, 28205–28212 Search PubMed.
- L. Vereecken and B. Nozière, Atmos. Chem. Phys., 2020, 20, 7429–7458 CrossRef CAS.
- G. da Silva, Phys. Chem. Chem. Phys., 2010, 12, 6698–6705 RSC.
- M. P. Rissanen, T. Kurtén, M. Sipilä, J. A. Thornton, J. Kangasluoma, N. Sarnela, H. Junninen, S. Jørgensen, S. Schallhart, M. K. Kajos, R. Taipale, M. Springer, T. F. Mentel, T. Ruuskanen, T. Petäjä, D. R. Worsnop, H. G. Kjaergaard and M. Ehn, J. Am. Chem. Soc., 2014, 136, 15596–15606 CrossRef CAS PubMed.
- K. H. Møller, K. H. Bates and H. G. Kjaergaard, J. Phys. Chem. A, 2019, 123, 920–932 Search PubMed.
- L. Vereecken and J. Peeters, J. Phys. Chem. A, 2004, 108, 5197–5204 CrossRef CAS.
- K. H. Møller, R. V. Otkjær, J. Chen and H. G. Kjaergaard, J. Phys. Chem. A, 2020, 124, 2885–2896 CrossRef PubMed.
- L. Vereecken, G. Vu, A. Wahner, A. Kiendler-Scharr and H. Nguyen, Phys. Chem. Chem. Phys., 2021, 23, 16564–16576 RSC.
- J. Peeters and T. L. Nguyen, J. Phys. Chem. A, 2012, 116, 6134–6141 CrossRef CAS PubMed.
- L. Franzon, M. Camredon, R. Valorso, B. Aumont and T. Kurtén, Atmos. Chem. Phys., 2024, 24, 11679–11699 CrossRef CAS.
- K. H. Møller, R. V. Otkjær, N. Hyttinen, T. Kurtén and H. G. Kjaergaard, J. Phys. Chem. A, 2016, 120, 10072–10087 CrossRef PubMed.
- L. Vereecken and J. Peeters, J. Chem. Phys., 2003, 119, 5159–5170 CrossRef CAS.
- F. Neese, Wiley Interdiscip. Rev.:Comput. Mol. Sci., 2022, 12, e1606 Search PubMed.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, L224108 CrossRef PubMed.
- F. Neese, J. Comput. Chem., 2003, 24, 1740–1747 CrossRef CAS.
- F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98–109 Search PubMed.
- D. Bykov, T. Petrenko, R. Izsak, S. Kossmann, U. Becker, E. Valeev and F. Neese, Mol. Phys., 2015, 113, 1961–1977 CrossRef CAS.
- B. Helmich-Paris, B. de Souza, F. Neese and R. Izsák, J. Chem. Phys., 2021, 155, 104109 Search PubMed.
- F. Neese, J. Comput. Chem., 2022, 1–16 Search PubMed.
- P. Pracht, S. Grimme, C. Bannwarth, F. Bohle, S. Ehlert, G. Feldmann, J. Gorges, M. Müller, T. Neudecker and C. Plett, et al. , J. Chem. Phys., 2024, 160, 114110 CrossRef CAS PubMed.
- S. Grimme, C. Bannwarth and P. Shushkov, J. Chem. Theory Comput., 2017, 13, 1989–2009 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B:Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef.
- J. Zheng, X. Xu and D. G. Truhlar, Theor. Chem. Acc., 2011, 128, 295–305 Search PubMed.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- E. Papajak, J. Zheng, X. Xu, H. R. Leverentz and D. G. Truhlar, J. Chem. Theory Comput., 2011, 7, 3027–3034 CrossRef CAS PubMed.
- F. Neese, A. Hansen and D. Liakos, J. Chem. Phys., 2009, 131, 064103 CrossRef PubMed.
- F. Neese, F. Wennmohs and A. Hansen, J. Chem. Phys., 2009, 130, 114108 CrossRef.
- C. Riplinger and F. Neese, J. Chem. Phys., 2013, 138, 034106 CrossRef PubMed.
- C. Riplinger, B. Sandhoefer, A. Hansen and F. Neese, J. Chem. Phys., 2013, 139, 134101 CrossRef PubMed.
- C. Riplinger, P. Pinski, U. Becker, E. Valeev and F. Neese, J. Chem. Phys., 2016, 144, 024109 CrossRef PubMed.
- G. Bistoni, C. Riplinger, Y. Minenkov, L. Cavallo, A. Auer and F. Neese, J. Theor. Comput. Chem., 2017, 13, 3220–3227 CrossRef CAS PubMed.
- M. Saitow, U. Becker, C. Riplinger, E. Valeev and F. Neese, J. Chem. Phys., 2017, 146, 164105 CrossRef PubMed.
- G. Knizia, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2009, 130, 054104 CrossRef PubMed.
- F. Pavosevic, F. Neese and E. Valeev, J. Chem. Phys., 2014, 141, 054106 CrossRef PubMed.
- C. Eckart, Phys. Rev., 1930, 35, 1303 CrossRef CAS.
- H. S. Johnston and J. Heicklen, J. Phys. Chem., 1962, 66, 532–533 CrossRef.
- K. Ishida, K. Morokuma and A. Komornicki, J. Chem. Phys., 1977, 66, 2153–2156 CrossRef CAS.
- S. Grimme, Chem. – Eur. J., 2012, 18, 9955–9964 CrossRef CAS PubMed.
- J. D. Crounse, H. C. Knap, K. B. Ørnsø, S. Jørgensen, F. Paulot, H. G. Kjaergaard and P. O. Wennberg, J. Phys. Chem. A, 2012, 116, 5756–5762 CrossRef CAS PubMed.
- A. P. Teng, J. D. Crounse and P. O. Wennberg, J. Am. Chem. Soc., 2017, 139, 5367–5377 CrossRef CAS PubMed.
- E. Praske, R. V. Otkjær, J. D. Crounse, J. C. Hethcox, B. M. Stoltz, H. G. Kjaergaard and P. O. Wennberg, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 64–69 CrossRef CAS PubMed.
- S. Iyer, H. Reiman, K. H. Møller, M. P. Rissanen, H. G. Kjaergaard and T. Kurtén, J. Phys. Chem. A, 2018, 122, 9542–9552 CrossRef CAS PubMed.
- T. G. Almeida and T. Kurtén, ACS Earth Space Chem., 2022, 6, 2453–2464 CrossRef CAS.
- L. Franzon, J. Peltola, R. Valiev, N. Vuorio, T. Kurtén and A. Eskola, J. Phys. Chem. A, 2023, 127, 477–488 CrossRef CAS PubMed.
- A. B. Jensen, J. Kubecka, G. Schmitz, O. Christiansen and J. Elm, J. Chem. Theory Comput., 2022, 18, 7373–7383 Search PubMed.
- C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671 CrossRef CAS PubMed.
- S. Spicher and S. Grimme, Angew. Chem., Int. Ed., 2020, 59, 15665–15673 Search PubMed.
- H. Mun, W. Lorpaiboon and J. Ho, J. Phys. Chem. A, 2024, 128, 4391–4400 CrossRef CAS PubMed.
- B. de Souza, Angew. Chem., Int. Ed., 2025, e202500393 CAS.
- S. Jørgensen, H. C. Knap, R. V. Otkjær, A. M. Jensen, M. L. Kjeldsen, P. O. Wennberg and H. G. Kjaergaard, J. Phys. Chem. A, 2016, 120, 266–275 CrossRef PubMed.
- B. Nozière and L. Vereecken, Phys. Chem. Chem. Phys., 2024, 26, 25373–25384 RSC.
- I. Hermans, J.-F. Müller, T. L. Nguyen, P. A. Jacobs and J. Peeters, J. Phys. Chem. A, 2005, 109, 4303–4311 CrossRef CAS PubMed.
- S. Iyer, A. Kumar, J. Zhao, S. Barua, A. Savolainen, A. Ojala, L. Pichelstorfer, P. Seal, M. Boy, M. Ehn, P. Roldin and M. P. Rissanen, Manuscript in Preparation Search PubMed.
- T. B. Nguyen, G. S. Tyndall, J. D. Crounse, A. P. Teng, K. H. Bates, R. H. Schwantes, M. M. Coggon, L. Zhang, P. Feiner, D. O. Milller, K. M. Skog, J. C. Rivera-Rios, M. Dorris, K. F. Olson, A. Koss, R. J. Wild, S. S. Brown, A. H. Goldstein, J. A. de Gouw, W. H. Brune, F. N. Keutsch, J. H. Seinfeld and P. O. Wennberg, Phys. Chem. Chem. Phys., 2016, 18, 10241–10254 RSC.
- W. P. Carter, J. Jiang, J. J. Orlando and K. C. Barsanti, Atmos. Chem. Phys., 2025, 25, 199–242 CrossRef CAS.
- B. Aumont, S. Szopa and S. Madronich, Atmos. Chem. Phys., 2005, 5, 2497–2517 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Comparison of SAR predictions with literature, a thorough benchmarking of the accuracy of our computational methods, and discussion of the competition between hydroperoxide H-shifts & ring closure as well as CO2 elimination following ring closure, are found in the ESI document. ORCA output files and MCTST codes are found in a Zenodo archive. See DOI: https://doi.org/10.1039/d5cp01175b |
| This journal is © the Owner Societies 2025 |