Observation of the hemibond formation in (H₂O–Ar_n)⁺ radical cation clusters by electronic spectroscopy and ion imaging technique

Abstract

The hemibond is a non-classical covalent bond formed by the overlap of non-bonding orbitals of a radical (cation) and a closed-shell molecule. For (H₂O–Ar_n)⁺ radical cation clusters, competition between the hemibonded type and hydrogen-bonded (H-bonded) type isomers has been discussed on the basis of infrared spectroscopy and theoretical computations. It has been commonly recognized that the H-bonded type is predominant, while the coexistence of the hemibonded type remains a topic of debate. Hemibonded species are known to exhibit very strong electronic transitions in the ultraviolet and/or visible (UV-vis) region, which are marker bands for hemibond formation. In this study, we performed electronic spectroscopy and photofragment ion imaging experiments on (H₂O–Ar_n)⁺ to observe the hemibond formation between H₂O⁺ and Ar. The observed spectra of (H₂O–Ar_n)⁺ (n = 1–3) exhibit absorption in the UV and visible regions. A comparison with quantum chemical calculations suggests the coexistence of the hemibonded type in (H₂O–Ar_n)⁺ (n = 1 and 2). In addition, the photofragment ion imaging experiment on (H₂O–Ar)⁺ showed an angular distribution attributed to the absorption of the hemibonded type, providing firm experimental evidence of the coexistence of the hemibonded type.

---

1. Introduction

The hemibond is a non-classical covalent bond formed by the overlap of a non-bonding orbital of a radical cation and a closed-shell molecule.^1–3 The hemibond has attracted attention mainly in systems containing third-period elements such as sulfur.^1–23 In recent years, the hemibond formation by the water radical cation H₂O⁺ has been demonstrated by mass spectrometry^24–26 and infrared (IR) spectroscopy^27–30 in the gas phase, and its contribution to the initial ionization process in aqueous environments is of interest.^31–34 The (H₂O–X)⁺ cluster formed between H₂O⁺ and another molecule X can form two structural motifs: hydrogen-bonded (H-bonded) and hemibonded type isomers. The H-bonded type has a H-bond between the OH group of H₂O⁺ and the molecule X (HOH⋯X), while the hemibonded type has a hemibond formed between the oxygen atom of H₂O⁺ and X (H₂O⋯X). The hemibonded type can be more stable than the H-bonded type, depending on the proton affinity and ionization potential of the molecule X, and the hemibonded type has been observed as the predominant structure for X = N₂O, Kr, and CO by IR spectroscopy.^27–29 In addition, the energetically unfavorable hemibonded (H₂O)₂⁺ has been observed in helium droplets, where the initial structure following ionization is preserved due to rapid cooling.³⁰ However, in most cases, the H-bonded type is energetically more stable and predominant in (H₂O–X)⁺ due to the high acidity of H₂O⁺. Therefore, the H-bonded type is primarily observed for various molecules X (X = He, Ne, Ar, CO₂, N₂, and H₂O).^29,35–43 When the H-bonded type is more stable than the hemibonded type, only the abundant H-bonded type is generally observed in IR spectroscopy. This is because there is no significant difference in IR absorption intensity between H-bonded and hemibonded types. Furthermore, the H-bonded type tends to exhibit a greater IR absorption intensity of OH stretching vibration due to H-bond formation, making the H-bonded type more readily detected in IR spectroscopy. Consequently, in IR spectroscopy, it is difficult to obtain experimental evidence of the coexistence of hemibonded (H₂O–X)⁺, which exists in a small amount.

To address this, we focused on ultraviolet-visible (UV-vis) spectroscopy. It is well known that hemibonded species exhibit characteristic transitions in the (near-) UV and visible regions, which are marker bands for hemibond formation. These transitions have been observed in numerous cases in the condensed phase, primarily in S∴S hemibonds.^4–12,44,45 In addition, in gas-phase spectroscopy, it has been studied as “charge resonance bands” in various cation species such as (CO₂)₂⁺ and benzene dimer cations.^46–49 These transitions originate from the σ–σ* transition of the hemibond formed by the overlap of the lone pair orbitals. It should be noted that the absorption intensity of hemibonded species is expected to be several tens of times greater than that of the H-bonded type, whose transition arises from its radical site in (H₂O–X)⁺. Therefore, if the hemibonded type exists at even a few percent relative to the H-bonded type in (H₂O–X)⁺, it is expected to be detectable by UV-vis spectroscopy.

Here, we investigate the (H₂O–Ar_n)⁺ radical cation cluster, in which the competition between H-bonded and hemibonded types has been the subject of long-standing discussions. For n = 1 and 2, IR spectroscopy and quantum chemical calculations have firmly established that the H-bonded type is energetically more stable and dominant in the isomer distribution than the hemibonded type.^40–42 At n = 2, however, the measured IR spectra show weak bands attributed to the hemibonded type, suggesting the partial coexistence of the hemibonded type.⁴¹ On the other hand, the anharmonic calculations have indicated that the observed band at n = 2 can be reproduced by combination bands attributed to the H-bonded type.⁴² Thus, debate remains as to whether the hemibonded type coexists in (H₂O–Ar_n)⁺.

In this study, UV-vis spectroscopy and photofragment ion imaging experiments are performed on (H₂O–Ar_n)⁺ to observe the hemibond formation between H₂O⁺ and Ar. Observing the characteristic transitions of the hemibonded type by electronic spectroscopy of (H₂O–Ar_n)⁺ (n = 1–3) is expected to provide evidence for its coexistence. Furthermore, photofragment ion imaging experiments allow us to investigate the nature of the transition in (H₂O–Ar)⁺, thereby providing more definitive experimental evidence for the hemibond formation.

2. Methods

2.1 UV-vis spectroscopy

Details of the experimental apparatus have been described elsewhere.⁵⁰ The (H₂O–Ar_n)⁺ (n = 1–3) radical cation clusters were generated by electron impact ionization in a supersonic jet of water vapor seeded in Ar gas, which was expanded through a high-pressure pulsed valve (Even–Lavie valve⁵¹). The produced (H₂O–Ar_n)⁺ were mass-selected at the first stage of the quadrupole mass spectrometer and then irradiated with UV and visible light in the octupole ion guide. When the UV-vis light frequency resonates with the electronic transition of the (H₂O–Ar_n)⁺, fragment ions such as H₂O⁺ or Ar⁺ ions are produced. No (H₂O–Ar_n′)⁺ fragments were observed, indicating the evaporation of all solvent molecules upon photoexcitation. By monitoring the intensity of mass-selected fragment ions at the second stage of the quadrupole mass spectrometer, UV-vis PD spectra of the (H₂O–Ar_n)⁺ were recorded. It should be noted that for the mass selection of parent ions, the mass resolution was set to Δm/z ≤ 1 to remove the corresponding protonated cluster (H₃O–Ar_n)⁺, while for the detection of the fragment ions, the mass resolution was intentionally reduced to enhance signal intensity. Consequently, Ar⁺ and H⁺Ar were detected without being distinguished when detecting the Ar⁺ channel. The UV-vis light source used was an OPO (NT342, EKSPLA). Although the linewidth of the UV-vis light output from the OPO is less than 5 cm⁻¹, the observed spectra are expected to lack fine structure; therefore, measurements were performed using a step scan with 5 nm increments.

2.2 Photofragment ion imaging experiments

The experimental setup has been described previously.⁵² Briefly, (H₂O–Ar)⁺ ions were generated by electron impact ionization in a supersonic expansion of water and Ar gas mixture at a stagnation pressure of 5 atm. The produced (H₂O–Ar)⁺ ions were introduced into a time-of-flight mass spectrometer equipped with a double linear reflectron. After mass selection by the first reflectron, (H₂O–Ar)⁺ ions were irradiated with a linearly polarized laser at 532 nm (the second harmonic of a Nd:YAG laser, Spectra Physics, LAB-150). The resultant H₂O⁺ photofragment ions were mass-selected by the second reflectron and subsequently detected by a position-sensitive detector. The observed two-dimensional projection images of photofragment ions were reconstructed into three-dimensional distributions using the pBASEX method,⁵³ from which the translational energy and angular distributions of the photofragments were obtained.

2.3 Computational methods

Quantum chemical computations of (H₂O–Ar_n)⁺ were performed using the Gaussian 16 program package.⁵⁴ Energy-optimized structure searches were performed at the CCSD/aug-cc-pVTZ level. Additionally, excited-state calculations were conducted at the EOM-CCSD/aug-cc-pVTZ level to determine the vertical excitation energies and oscillator strengths of (H₂O–Ar_n)⁺. In addition, for (H₂O–Ar)⁺, potential energy curves (PECs) and potential energy surfaces (PESs) for the electronic ground state and the electronically excited state were calculated at the same level of theory.

3. Results and discussion

3.1 Observed and simulated UV-vis spectra of (H₂O–Ar_n)⁺ (n = 1–3)

Fig. 1 shows the observed and simulated UV-vis spectra of (H₂O–Ar)⁺. The observed spectrum in Fig. 1 represents the sum of H₂O⁺ and Ar⁺ fragment ion intensities. Fig. S1 in ESI,† shows the UV-vis spectra obtained by detecting H₂O⁺ and Ar⁺ (or H⁺Ar) fragments, respectively. Notably, in the visible region, H₂O⁺ fragments were predominantly detected. This is likely due to the excess energy of photo-excited (H₂O–Ar)⁺. Fig. S2 (ESI†) shows the energy diagram of (H₂O–Ar)⁺. This diagram indicates that the dissociation channel leading to the H₂O⁺ fragment is energetically accessible in the visible region, whereas the dissociation channels leading to Ar⁺ or H⁺Ar are energetically unfavorable. For the calculated isomers, we obtained the H-bonded type (isomer H), in which Ar is H-bonded to one of the OH groups of H₂O⁺, and the hemibonded type (isomer h), in which a hemibond is formed between the O and Ar atoms, as in the previous studies.^40–42 Note the labels H and h represent the H-bond and hemibond formation between H₂O⁺ and Ar, respectively. The H-bonded type is more energetically stable and predominant. Wagner et al. reported that the isomerization barrier from isomer h to isomer H was calculated to be 10.6 kJ mol⁻¹ at the CCSD(T)/cc-pVTZ level.⁴²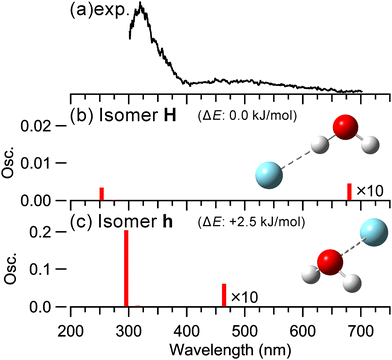

Fig. 1 (a) Observed and (b) and (c) calculated spectra of (H₂O–Ar)⁺ at the EOM-CCSD/aug-cc-pVTZ. Note that the scales of the plots in (b) and (c) differ. The energies shown in the figure represent the ZPE-corrected relative energies. The electronic energy was calculated at the CCSD(T)/CBS, and the ZPE was obtained from an anharmonic calculation at the CCSD(T)/cc-pVTZ level.⁴²

In the observed spectrum, a strong band at ∼320 nm and a weak and broad band at ∼500 nm were observed. In the calculated spectrum for isomer H, two main absorptions are predicted: one in the UV region and one in the visible region. Fig. S3 (ESI†) shows the molecular orbitals corresponding to these electronic transitions. As shown in Fig. S3 (ESI†), these transitions are attributed to charge transfer between H₂O⁺ and Ar and local excitation in the H₂O⁺ subunit from one lone pair orbital to another. In the calculated spectrum for isomer h, two main absorptions are also predicted: one in the UV region and one in the visible region. These transitions are attributed to a σ–σ* transition of the hemibond formed by the overlap of the lone pair orbitals of H₂O⁺ and Ar and a transition from the lone pair orbital of H₂O⁺ to the σ* orbital of the hemibond, respectively, as shown in Fig. S3 (ESI†). Notably, the oscillator strength of isomer h is several tens of times greater than that of isomer H. That is, as expected, the absorption of the hemibonded type is significantly stronger than that of the H-bonded type, suggesting that the hemibonded type can be observed even if it is energetically less favorable.

Here, we compare the observed and calculated spectra. Since the predicted absorption bands of both isomer H and isomer h appear at similar positions, it is difficult to assign the observed spectrum unambiguously. However, the predicted absorption bands of isomer h in the UV and visible regions exhibit greater consistency with the experimentally observed peak positions. Therefore, a comparison of the experimental and calculated spectra suggests the contribution of the hemibonded type. Note that a contribution from the H-bond type cannot be ruled out in the observed spectrum as its population is predominant though its absorption intensity is much lower.

Thus, the results of UV-vis spectroscopy suggest the coexistence of the hemibonded type. However, since the absorption bands of both the H-bonded and hemibonded types are calculated to be at similar positions, it remains challenging to definitively confirm the presence of the hemibonded type based solely on the comparison between the experimental and calculated spectra. First, the results of the excited-state calculations may depend on the computational level. Additionally, regarding absorption in the visible region, it is known that bare H₂O⁺ exhibits a very broad absorption in this region, which is attributed to vibronic transitions caused by the excitation of the bending vibration of H₂O⁺.^55–61 Since the absorption of the H-bonded type in the visible region is localized in the H₂O⁺ subunit, it may also exhibit broad absorption in the visible region, similar to bare H₂O⁺. Therefore, the spectroscopic results obtained in this study alone do not provide conclusive evidence for the presence of the hemibonded type. To obtain more definitive experimental evidence for the coexistence of the hemibonded type, further verification for n = 1 was conducted using photofragment ion imaging experiments, as described in Section 3.3.

Fig. 2 shows the observed UV-vis photodissociation spectrum for n = 2, along with the calculated spectra of the stable isomers. Similar to the previous studies,^40–42 the calculated isomers include isomer H–H, in which Ar atoms are H-bonded to both OH groups of H₂O⁺, and isomer h–H, in which one Ar forms a hemibond while the other Ar forms a H-bond. The experimental and calculated spectra for n = 2 are almost identical to those for n = 1. In other words, for n = 2, the calculated spectrum of the hemibonded type (isomer h–H) agrees well with the observed spectrum, suggesting that the hemibonded type coexists with the H-bonded type (isomer H–H), which is the most stable isomer. Here, the broad band of the observed spectrum in the visible region is red-shifted compared to that for n = 1. The calculated spectrum also exhibits a red-shift in the visible absorption of the hemibonded type, indicating good agreement between the experimental and the calculated results. However, the H-bonded type also exhibits a red-shift in its visible absorption, which should be taken into account when interpreting the results.

Fig. 2 (a) Observed and (b) and (c) calculated spectra of (H₂O–Ar₂)⁺ at the EOM-CCSD/aug-cc-pVTZ. Note that the scales of the plots in (b) and (c) differ. The energies shown in the figure represent the ZPE-corrected relative energies. The electronic energy was calculated at the CCSD(T)/CBS, and the ZPE was obtained from an anharmonic calculation at the CCSD(T)/cc-pVTZ level.⁴²

Finally, Fig. 3 shows the observed electronic spectrum for n = 3, along with the calculated spectrum. The calculated isomer structure is consistent with those reported in the previous studies.^40–42 The most stable structure, isomer h–H–H, was found to exhibit a fully solvated configuration, where two Ar atoms are H-bonded to both OH groups of H₂O⁺, while the third Ar atom forms a hemibond with the O atom of H₂O⁺. Notably, the first solvation shell of H₂O⁺ is closed in this structure. The experimental and calculated spectral profiles are similar to those for n = 1 and 2, and the experimental spectrum exhibits good agreement with the calculated spectrum. It should be noted that, for n = 3, the most stable structure (isomer h–H–H) features a hemibond between Ar and H₂O⁺, leading to strong absorption. In contrast, for n = 1 and 2, the H-bonded type is the most stable and predominantly present, resulting in weaker absorption. Consequently, the fragment ion intensities for n = 3 were significantly greater in the experiment. In the following section, we provide a detailed discussion on the relative intensities of the photodissociation spectra in the UV region for n = 1–3.

Fig. 3 (a) Observed and (b) calculated spectra of (H₂O–Ar₃)⁺ at the EOM-CCSD/aug-cc-pVTZ.

3.2 Comparison among the observed UV-vis spectra of (H₂O–Ar_n)⁺ (n = 1–3)

Fig. 4 shows the observed UV-vis spectra of (H₂O–Ar_n)⁺ (n = 1–3). Each spectrum represents the sum of the H₂O⁺ and Ar⁺ fragment ion intensities, normalized by the laser power and parent ion intensities. Thus, the relative intensities of the spectra can be compared across different cluster sizes (n). As mentioned above, in the observed spectra for n = 1–3, a strong absorption appears at approximately 320 nm in the UV region, while a broad and weak absorption is observed around 500 nm in the visible region. The most notable feature in this comparison of the observed spectra is that the fragment ion intensity for n = 3 is two ∼ three times higher than that for n = 1 and 2. For n = 1 and 2, the H-bonded type is predominantly formed, resulting in weak absorption intensity, as shown in Fig. 1 and 2. Additionally, the population of the hemibonded type, which contributes efficiently to the spectrum, is relatively minor. In contrast, for n = 3, as shown in Fig. 3, a hemibond is formed between H₂O⁺ and Ar, and the other Ar atoms are H-bonded, resulting in a fully solvated structure (isomer h–H–H), which is the most stable. Therefore, for n = 3, structures containing a hemibond predominantly exist, and the observed spectral intensity is significantly stronger, due to the σ–σ* transition of the hemibond. Consequently, the UV-vis spectroscopy experiment demonstrated that H₂O⁺ and Ar form a hemibond for n = 3.

Fig. 4 Comparison among the observed UV-vis spectra of (H₂O–Ar_n)⁺ (n = 1–3). These spectra are normalized by the laser power and parent ion intensities.

Here, we discuss the intensity ratio of the observed spectra in Fig. 4 in more detail. Fig. 4 shows that the observed intensity ratio in the UV region differs by a factor of two ∼ three between n = 1, 2 and n = 3. On the other hand, as shown in Fig. 1–3, the oscillator strength in the UV region calculated at the EOM-CCSD/aug-cc-pVTZ level is almost same among the hemibonded isomers of n = 1–3, but that of the H-bonded type of n = 1 and 2 is weaker by an order of magnitude than the hemibonded type. Therefore, the intensity ratio obtained from the experiment does not quantitatively match that obtained from the calculations when we suppose a single isomer for n = 1 and 2. This discrepancy can be explained by the coexistence of a minor fraction of the hemibonded type in the observed spectra for n = 1 and 2. Assuming the hemibonded type coexists for n = 1 and 2, the absorption intensity of the system would be largely enhanced from that of a population consisting solely of the H-bonded type. As a result, the absorption intensity for n = 3 is two ∼ three times greater than that for n = 1 and 2, as seen in Fig. 4.

To further investigate this, we quantitatively estimated the fraction of the hemibonded type in n = 1, 2 based on the integrated peak area from the experiment and the calculated oscillator strength in the UV region. This estimation suggests that if approximately 30% of the (H₂O–Ar_n)⁺ for n = 1 and 2 are the hemibonded type, the observed intensity ratio in the experimental spectra can be explained. However, this estimated fraction of ∼30% appears to be somewhat overestimated. In fact, according to a previous study,⁴² the relative energy between the H-bonded and hemibonded types calculated at the CCSD(T)/CBS level with zero-point energy (ZPE) corrections from an anharmonic calculation at the CCSD(T)/cc-pVTZ level is 2.5 kJ mol⁻¹ for n = 1 and 3.3 kJ mol⁻¹ for n = 2. Based on these values, the estimated population of the hemibonded type is approximately 5% at 100 K and ∼20% at 250 K. This discrepancy may arise from experimental conditions due to mass-dependent effects, such as variations in detection efficiency caused by the mass spectrometer transmission rate.

Therefore, to summarize this section, the intensity ratio of the observed spectra for n = 1, 2 and n = 3 can be explained by the coexistence of the hemibonded type in n = 1, 2, providing experimental evidence supporting the hemibond formation between H₂O⁺ and Ar. However, precisely quantifying its population remains challenging due to limitations in controlling experimental conditions. Nevertheless, by comparing the experimental spectra with the calculational results and analyzing the relative intensity ratio of the observed spectra, we have obtained experimental evidence supporting the coexistence of the hemibonded type in (H₂O–Ar_n)⁺ for n = 1 and 2. The following section presents the results of photofragment ion imaging experiments to obtain more definitive experimental evidence for the presence of the hemibonded type in (H₂O–Ar)⁺.

3.3 Photofragment ion imaging: translational energy and angular distributions

This section describes the results of the photofragment ion imaging experiments on (H₂O–Ar)⁺. Fig. 5 shows the transition dipole moments (μ) of the H-bonded and hemibonded types of (H₂O–Ar)⁺ in the visible region calculated at the EOM-CCSD/aug-cc-pVTZ level. For the H-bonded type, the orientation of μ is nearly perpendicular to the dissociation axis of H₂O and Ar, whereas for the hemibonded type, it is nearly parallel. Therefore, we can distinguish whether the visible absorption originates from the H-bonded or hemibonded type through the photofragment ion imaging experiments using a linearly polarized laser and analyzing the angular distribution of the fragment ions, as discussed later. This approach is expected to provide definitive evidence for the hemibond formation in (H₂O–Ar)⁺. It should be noted that for the stronger transitions in the UV region, unfortunately, both isomers are predicted to have μ aligned parallel to the dissociation axis. As a result, no significant difference in the angular distribution between the two isomers is expected upon UV excitation. Therefore, in this study, photofragment ion imaging experiments were performed using visible light excitation (532 nm). Notably, the absorption of the hemibonded type in the visible region is attributed to a transition from the lone pair orbital of H₂O⁺ to the σ* orbital of the hemibond. Thus, this electronic excited state differs from the σ–σ* transition observed in the UV region.

Fig. 5 Transition dipole moments μ of (H₂O–Ar)⁺ in the visible region calculated at the EOM-CCSD/aug-cc-pVTZ level.

Fig. 6(a) shows the observed image of the H₂O⁺ photofragment ions, produced by excitation of (H₂O–Ar)⁺ with 532 nm dissociation light. First, we focus on the angular distribution relative to the polarization direction (E) of the dissociation laser light. The angular distribution of the photofragment ions produced by single-photon dissociation is given by the equation: I(θ) = (1/4π)[1 + βP₂(cos θ)],⁶² where θ is the angle between the light polarization direction and the recoil direction of the photofragment ions, and P₂(x) is the second-order Legendre polynomial, given by: P₂(x) = (3x² − 1)/2. Additionally, β is the anisotropy parameter, which ranges from −1 to +2 and characterizes the angular distribution. For a single-photon dissociation process, the anisotropy parameter β can be theoretically expressed as: β = 2P₂(cos χ)P₂(cos a)g(ωτ),^63,64 where χ is the angle between μ and the dissociation axis, and a is the rotation angle of the dissociation axis induced by the rotational excitation of the photofragments. Furthermore, g(ωτ) represents the deviation in anisotropy due to the dissociation lifetime, given by: g(ωτ) = (1 + (ωτ)²)/(1 + 4(ωτ)²). Here, ω and τ denote the rotational angular velocity of the parent ion and the dissociation lifetime, respectively. When the dissociation lifetime is short compared to the rotational period (τ ∼ 0), this term approaches 1, meaning its effect is negligible. Conversely, when the dissociation lifetime is long compared to the rotational period, this term cannot be ignored and takes a minimum value of 1/4. Here, under the axial recoil approximation, where the dissociation lifetime is sufficiently short and the rotation of the dissociation axis can be neglected (P₂(cos a)g(ωτ) ∼ 1), the β value is determined solely by the angle χ between μ and the dissociation axis. From the angles between μ and the dissociation axis of (H₂O–Ar)⁺ shown in Fig. 5, the expected β values are −1.00 for the H-bonded type and +1.98 for the hemibonded type. Thus, the β value obtained from the experiment should allow us to distinguish whether the visible absorption originates from the H-bonded or the hemibonded type, thereby providing evidence for the hemibond formation in (H₂O–Ar)⁺.

Fig. 6 (a) Ion images of H₂O⁺ photofragment ions at 532 nm excitation. The left half is the observed image, and the right half is the sliced image of the three-dimensional distribution reconstructed using the pBASEX method. E indicates the polarization direction of the dissociation laser light. (b) The corresponding translational energy distribution. Shaded regions represent the statistical error from three independent measurements. E_avl(A) represents the available energy for the dissociation channel leading to the H₂O⁺(A) fragment (see text for details.).

In Fig. 6(a), the observed images exhibited a nearly isotropic angular distribution but were clearly elongated along the E direction. In more detail, the image analysis yielded a β value of 0.46 ± 0.04. The β value was determined from the peak position of the velocity distribution of the H₂O⁺ photofragment ions. Therefore, under the visible-light (532 nm) excitation of (H₂O–Ar)⁺, the orientation of μ is nearly parallel to the dissociation axis. That is, based on the present experimental results and the direction of μ in the two isomers shown in Fig. 5, it is concluded that the visible absorption originates from the hemibonded type, providing direct evidence for the hemibond formation in (H₂O–Ar)⁺. Here, the β value predicted from the axial recoil approximation for the visible-light excitation of the hemibonded type is 1.98, whereas the experimentally obtained β value is much smaller than this prediction. This discrepancy can be attributed to either the long dissociation lifetime of the excited (H₂O–Ar)⁺ compared to its rotational period or the contribution of the H-bonded type, which is expected to have a negative β value in the observed image.

Next, we discuss the translational energy distribution of the photofragments obtained from the analysis of the observed images. In the following discussion, we primarily focus on the photodissociation processes of the hemibonded type, as the positive β value indicates a major contribution from the hemibonded type. Fig. 6(b) shows the translational energy distribution (E_t distribution) of the photofragments derived from the velocity distribution of the H₂O⁺ photofragment ions using the momentum conservation principle. The available energy (E_avl) for the photodissociation reaction is also shown. E_avl is defined as follows: for the electronic ground state H₂O⁺(X) channel, E_avl(X) = hν − D₀, and for the electronically excited state H₂O⁺(A) channel, E_avl(A) = hν − D₀ – E_elec(H₂O⁺(A)). Here, D₀ represents the dissociation energy of the hemibonded (H₂O–Ar)⁺, and E_elec(H₂O⁺(A)) denotes the excitation energy to the electronic excited A state of H₂O⁺ (for details, see the energy diagram in Fig. S2, ESI†). The E_avl was calculated using well-known literature data.^65,66 Additionally, the binding energy of the hemibonded (H₂O–Ar)⁺ was calculated using the experimental binding energy of the H-bonded (H₂O–Ar)⁺ and the relative energy between the hemibonded and H-bonded types.^41,42,67E_avl(X) and E_avl(A) represent the available energy that can be distributed among the translational, vibrational, and rotational energy of the photofragments in each electronic state of H₂O⁺. According to Fig. 6(b), the E_t distribution appears at lower energy relative to E_avl(A), indicating that most of the excess energy is distributed to the internal energy of the H₂O⁺ fragment ions. This suggests that the potential energy surface of the excited state of hemibonded (H₂O–Ar)⁺ is not repulsive, which may be related to the long dissociation lifetime of (H₂O–Ar)⁺. It is well known that in the electronically excited A state, H₂O⁺ exhibits a linear structure.^55–61 Therefore, upon electronic excitation in (H₂O–Ar)⁺, the bending vibration of the H₂O⁺ subunit is expected to be significantly excited. As a result, a large portion of the available energy is distributed to the vibrational energy of the H₂O⁺ fragment ions, leading to a smaller fraction distributed to translational energy. In the next section, we calculate the potential energy curves and surfaces of (H₂O–Ar)⁺ to investigate the visible-light dissociation processes of the hemibonded type.

3.4 Potential energy curves and surfaces of (H₂O–Ar)⁺

Fig. 7(a) shows the potential energy curves (PECs) of the electronic ground state and the first electronically excited state of the hemibonded (H₂O–Ar)⁺, calculated at the EOM-CCSD/aug-cc-pVTZ level. The vertical axis represents the electronic energy, while the horizontal axis corresponds to the O–Ar distance R, as defined in Fig. 7 (top panel). All other structural parameters were fixed at the equilibrium values obtained from the geometry optimization during the calculations.

Fig. 7 (a) Potential energy curves and (b) surfaces of hemibonded (H₂O–Ar)⁺ calculated at the EOM-CCSD/aug-cc-pVTZ. R and θ are defined as shown in the structure of (H₂O–Ar)⁺ in the figure. The structural parameters other than R and θ were fixed at the equilibrium values obtained from the geometry optimization in the electronic ground state during the calculations.

In Fig. 7(a), the PEC of the first electronically excited state exhibits a slightly repulsive nature in the Franck–Condon region; however, it remains nearly flat overall with a shallow potential well. This nearly flat PEC shape can be explained by the orbitals involved in the visible-light excitation of the hemibonded type. As shown in Fig. S3 (ESI†), the visible-light absorption of the hemibonded type corresponds to a transition from the lone pair orbital of H₂O⁺ to the σ* orbital of the hemibond. Here, the hemibond is formed when two electrons occupy the intermolecular σ orbital and one electron occupies the σ* orbital. Upon visible-light excitation of hemibonded (H₂O–Ar)⁺, both the σ and σ* orbitals become doubly occupied, leading to bond cleavage (effectively reducing the bond order to zero), without introducing the significant repulsive force between H₂O⁺ and Ar. Therefore, the first electronically excited state PEC does not become strongly repulsive but remains nearly flat. This characteristic is consistent with the experimentally observed low fraction of energy distributed to translational motion. Similarly, this nearly flat PEC shape suggests that the dissociation lifetime of the visible-light-excited (H₂O–Ar)⁺ may be long, which could also explain the experimentally observed smaller β value than the prediction based on the axial recoil approximation. However, PEC calculations alone do not provide information on the dissociation lifetime, making it difficult to determine whether the smaller β value originates from the dissociation lifetime or the contribution of the H-bonded type. Fig. S4 (ESI†) shows the PECs of the H-bonded type. For the H-bonded type as well, the first electronically excited state PEC, which corresponds to visible-light excitation, is not repulsive. Therefore, when the H-bonded type is excited, it is also unlikely that a significant fraction of energy would be distributed to translational degrees of freedom.

To investigate the photodissociation process of hemibonded (H₂O–Ar)⁺ in more detail, with a particular focus on the distribution of excess energy, we performed potential energy surface (PES) calculations. Fig. 7(b) shows the potential energy surfaces (PESs) of the electronic ground state and the first electronically excited state of the hemibonded (H₂O–Ar)⁺. The horizontal axis represents the O–Ar distance (R) and the vertical axis corresponds to the HOH bond angle (θ) as defined in Fig. 7 (top panel). Upon 532 nm photoexcitation of the hemibonded (H₂O–Ar)⁺, the HOH bond angle changes significantly, while the OH distance remains relatively constant. Therefore, the HOH bending mode is the dominant Franck–Condon active mode. Consequently, we chose θ to the second coordinate in the PES. The dashed lines on the PESs represent the equilibrium values of R and θ for the hemibonded (H₂O–Ar)⁺ in the electronic ground state. The PESs suggest the following dissociation process for the visible-light-excited hemibonded (H₂O–Ar)⁺: (1) upon excitation to the first electronically excited state, the system undergoes elongation of R and increases in θ. (2) As it approaches the region where θ ≈ 180°, the energy gap between the electronic ground and excited states narrows, facilitating a nonadiabatic transition to the electronic ground state. (3) In the electronic ground state PES, the system further elongates R while θ undergoes large oscillations. Thus, these PES calculations indicate that highly vibrationally excited H₂O⁺ is produced. Consequently, most of the excess energy is distributed to the bending vibration of H₂O⁺, leaving little for the translational energy of the photofragments. This dissociation process in the PESs rationalizes the observed translational energy distribution. Fig. S4 (ESI†) shows the PESs of the H-bonded type, suggesting that vibrationally excited H₂O⁺ fragment ions are also likely to be produced.

4. Conclusion

To observe the formation of a hemibond between H₂O⁺ and Ar, we performed UV-vis photodissociation spectroscopy experiments on (H₂O–Ar_n)⁺ (n = 1–3) and photofragment ion imaging experiments on (H₂O–Ar)⁺. The experimentally obtained UV-vis spectra exhibited absorption in both the UV and visible regions for all cluster sizes (n = 1–3). For n = 1 and 2, a comparison between the observed UV-vis photodissociation spectra and quantum chemical calculations suggested the coexistence of the hemibonded type. Additionally, in the photodissociation spectra, the observed relative intensity for each cluster size differed by approximately a few times between n = 1, 2 and n = 3 in the UV region. This intensity difference in n = 1, 2 and n = 3 was explained by the fully solvated structure containing a hemibond at n = 3 and the partial coexistence of the hemibonded type at n = 1 and 2. Therefore, by comparing the experimentally observed absorption wavelengths with theoretical calculations and analyzing the intensity ratios of the observed spectra, we obtained experimental evidence for the coexistence of the hemibonded type in (H₂O–Ar_n)⁺.

Additionally, the results of the photofragment ion imaging experiment on (H₂O–Ar)⁺ exhibited a small recoil velocity and a positive anisotropy parameter. The obtained positive anisotropy parameter indicates that the visible absorption of (H₂O–Ar)⁺ originates from the hemibonded type, providing definitive experimental evidence for the existence of the hemibonded type. Furthermore, PEC and PES calculations revealed that most of the excess energy is distributed to the bending vibration of the H₂O⁺ fragment ions. Consequently, a smaller fraction of the excess energy is transferred to the translational energy of the photofragments.

Based on these results, we conclude that electronic spectroscopy and photofragment ion imaging experiments enabled the observation of the hemibonded type, which is energetically less stable and has a lower population. In the future, applying these methods to other systems is expected to provide experimental evidence for hemibond formation in a broader range of molecular systems.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This study is supported by a Grant-in-Aid for Scientific Research (Project No. 21H04671) from JSPS. M. K. was supported by JST SPRING, Grant Number JPMJSP2114. A part of the computation was performed at the Research Center for Computational Science, Okazaki, Japan. We thank Mr Tatsuki Hosoda for his help in preparation of the TOC figure.

References

1. T. Clark, J. Am. Chem. Soc., 1988, 110, 1672–1678.
2. P. C. Hiberty, S. Humbel and P. Archirel, J. Phys. Chem., 1994, 98, 11697–11704.
3. T. Clark, ChemPhysChem, 2017, 18, 2766–2771.
4. D. Bahnemann and K.-D. Asmus, J. Chem. Soc., Chem. Commun., 1975, 238–239.
5. K. D. Asmus, Acc. Chem. Res., 1979, 12, 436–442.
6. M. Bonifačić and K.-D. Asmus, J. Chem. Soc., Perkin Trans. 2, 1980, 758–762.
7. S. A. Chaudhri and K.-D. Asmus, Angew. Chem., Int. Ed. Engl., 1981, 20, 672–673.
8. M. Goebl, M. Bonifacic and K. D. Asmus, J. Am. Chem. Soc., 1984, 106, 5984–5988.
9. K.-D. Asmus, M. Göbl, K.-O. Hiller, S. Mahling and J. Mönig, J. Chem. Soc., Perkin Trans. 2, 1985, 641–646.
10. T. Drewello, C. B. Lebrilla, H. Schwarz, L. J. de Koning, R. H. Fokkens, N. M. M. Nibbering, E. Anklam and K.-D. Asmus, J. Chem. Soc., Chem. Commun., 1987, 1381–1383.
11. K.-D. Asmus, Sulfur-Centered Reactive Intermediates in Chemistry and Biology, NATO-ASI Series, Series A: Life Sciences, Springer, 1990, pp. 155–172.
12. H. Hungerbühler, S. N. Guha and K.-D. Asmus, J. Chem. Soc., Chem. Commun., 1991, 999–1001.
13. C. Schöneich, D. Pogocki, G. L. Hug and K. Bobrowski, J. Am. Chem. Soc., 2003, 125, 13700–13713.
14. A. Adhikary, A. Kumar, B. J. Palmer, A. D. Todd and M. D. Sevilla, J. Am. Chem. Soc., 2013, 135, 12827–12838.
15. C. H. Hendon, D. R. Carbery and A. Walsh, Chem. Sci., 2014, 5, 1390–1395.
16. J. Jie, Y. Xia, C.-H. Huang, H. Zhao, C. Yang, K. Liu, D. Song, B.-Z. Zhu and H. Su, Nucleic Acids Res., 2019, 47, 11514–11526.
17. D. Wang and A. Fujii, Chem. Sci., 2017, 8, 2667–2670.
18. M. Xie, Z. Shen, D. Wang, A. Fujii and Y.-P. Lee, J. Phys. Chem. Lett., 2018, 9, 3725–3730.
19. D. Wang, K. Hattori and A. Fujii, Chem. Sci., 2019, 10, 7260–7268.
20. K. Hattori, D. Wang and A. Fujii, Phys. Chem. Chem. Phys., 2019, 21, 16064–16074.
21. M. Xie, H.-R. Tsai, A. Fujii and Y.-P. Lee, Phys. Chem. Chem. Phys., 2019, 21, 16055–16063.
22. X. Sun, M. Xie, W. Qiu, C. Wei, X. Chen and Y. Hu, Phys. Chem. Chem. Phys., 2022, 24, 19354–19361.
23. T. Kato and A. Fujii, J. Phys. Chem. A, 2023, 127, 742–750.
24. S. Yamaguchi, S. Kudoh, Y. Kawai, Y. Okada, T. Orii and K. Takeuchi, Chem. Phys. Lett., 2003, 377, 37–42.
25. M. Wang, X.-F. Gao, R. Su, P. He, Y.-Y. Cheng, K. Li, D. Mi, X. Zhang, X. Zhang, H. Chen and G. R. Cooks, CCS Chem., 2022, 4, 1224–1231.
26. X. Zhang, Y. Zhang, X. Zhou, J. Xu and D. Mi, Heliyon, 2023, 9, e17763.
27. R. Matsushima, T. Ebata and Y. Inokuchi, J. Phys. Chem. A, 2010, 114, 11037–11042.
28. J.-M. Liu, T. Nishigori, T. Maeyama, Q.-R. Huang, M. Katada, J.-L. Kuo and A. Fujii, J. Phys. Chem. Lett., 2021, 12, 7997–8002.
29. M. Kominato and A. Fujii, Phys. Chem. Chem. Phys., 2023, 25, 14726–14735.
30. A. Iguchi, A. Singh, S. Bergmeister, A. A. Azhagesan, K. Mizuse, A. Fujii, H. Tanuma, T. Azuma, P. Scheier, S. Kuma and A. F. Vilesov, J. Phys. Chem. Lett., 2023, 14, 8199–8204.
31. J. Ma, F. Wang and M. Mostafavi, Molecules, 2018, 23, 244.
32. J. Ma, S. A. Denisov, A. Adhikary and M. Mostafavi, Int. J. Mol. Sci., 2019, 20, 4963.
33. D. Mi and K. Chingin, Molecules, 2020, 25, 3490.
34. L. Qiu and R. G. Cooks, Angew. Chem., Int. Ed., 2024, 63, e202400118.
35. G. H. Gardenier, M. A. Johnson and A. B. McCoy, J. Phys. Chem. A, 2009, 113, 4772–4779.
36. K. Mizuse, J.-L. Kuo and A. Fujii, Chem. Sci., 2011, 2, 868–876.
37. K. Mizuse and A. Fujii, J. Phys. Chem. A, 2013, 117, 929–938.
38. D. Roth, O. Dopfer and J. P. Maier, Phys. Chem. Chem. Phys., 2001, 3, 2400–2410.
39. O. Dopfer, D. Roth and J. P. Maier, J. Chem. Phys., 2001, 114, 7081–7093.
40. O. Dopfer, J. Phys. Chem. A, 2000, 104, 11693–11701.
41. O. Dopfer, D. Roth and J. P. Maier, J. Phys. Chem. A, 2000, 104, 11702–11713.
42. J. P. Wagner, D. C. McDonald II and M. A. Duncan, J. Chem. Phys., 2017, 147, 104302.
43. Y. Inokuchi, Y. Kobayashi, A. Muraoka, T. Nagata and T. Ebata, J. Chem. Phys., 2009, 130, 154304.
44. R. W. Alder, M. Bonifačić and K.-D. Asmus, J. Chem. Soc., Perkin Trans. 2, 1986, 277–284.
45. H. Mohan and K. D. Asmus, J. Am. Chem. Soc., 1987, 109, 4745–4746.
46. M. A. Johnson, M. L. Alexander and W. C. Lineberger, Chem. Phys. Lett., 1984, 112, 285–290.
47. Y. Inokuchi and N. Nishi, J. Chem. Phys., 2001, 114, 7059–7065.
48. K. Ohashi and N. Nishi, J. Phys. Chem., 1992, 96, 2931–2932.
49. M. Koyama, S. Muramatsu, Y. Hirokawa, J. Iriguchi, A. Matsuyama and Y. Inokuchi, J. Phys. Chem. Lett., 2024, 15, 1493–1499.
50. K. Mizuse and A. Fujii, Phys. Chem. Chem. Phys., 2011, 13, 7129–7135.
51. U. Even, J. Jortner, D. Noy, N. Lavie and C. Cossart-Magos, J. Chem. Phys., 2000, 112, 8068–8071.
52. K. Okutsu, Y. Nakashima, K. Yamazaki, K. Fujimoto, M. Nakano, K. Ohshimo and F. Misaizu, Rev. Sci. Instrum., 2017, 88, 053105.
53. G. A. Garcia, L. Nahon and I. Powis, Rev. Sci. Instrum., 2004, 75, 4989–4996.
54. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Rev. C.01, Gaussian, Inc., Wallingford CT, 2016.
55. H. Lew and I. Heiber, J. Chem. Phys., 1973, 58, 1246–1247.
56. H. Lew, Can. J. Phys., 1976, 54, 2028–2049.
57. B. Das and J. W. Farley, J. Chem. Phys., 1991, 95, 8809–8815.
58. R. A. Dressler and S. T. Arnold, J. Chem. Phys., 1995, 102, 3481–3482.
59. T. R. Huet, I. Hadj Bachir, J.-L. Destombes and M. Vervloet, J. Chem. Phys., 1997, 107, 5645–5651.
60. S. Wu, X. Yang, Y. Guo, H. Zhuang, Y. Liu and Y. Chen, J. Mol. Spectrosc., 2003, 219, 258–262.
61. Y. Gan, X. Yang, Y. Guo, S. Wu, W. Li, L. Yuyan and Y. Chen, Mol. Phys., 2004, 102, 611–621.
62. R. N. Zare, Mol. Photochem., 1972, 4, 1–37.
63. C. Jonah, J. Chem. Phys., 1971, 55, 1915–1922.
64. S.-C. Yang and R. Bersohn, J. Chem. Phys., 1974, 61, 4400–4407.
65. in CRC handbook of chemistry and physics, ed. D. R. Lide, CRC Press, Boca Raton, FL, 90th edn, 2009.
66. S. G. Lias, J. E. Bartmess, J. F. Liebman, J. L. Holmes, R. D. Levin and W. G. Mollard, J. Phys. Chem. Ref. Data, 1988, 17(suppl. 1), 1–861.
67. Y. Nakashima, Y. Ito, M. Kominato, K. Ohshimo and F. Misaizu, J. Chem. Phys., 2021, 154, 174301.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp01001b

---