Study of proximity-coupled magnetic anisotropy in V-doped SnTe using spin resonance and magnetic measurements†
Subhadip
Ghosh
 *a and
Sanjeev Kumar
Srivastava
*a and
Sanjeev Kumar
Srivastava
 b
b
aSchool of Nano Science and Technology, Indian Institute of Technology, Kharagpur 721302, West Bengal, India. E-mail: subhadipjrc@gmail.com
bDepartment of Physics, Indian Institute of Technology, Kharagpur, West Bengal 721302, India. E-mail: sanjeev@phy.iitkgp.ac.in
First published on 21st May 2025
Abstract
SnTe is a topological crystalline insulator with topological surface states (TSSs) protected by crystal symmetries. This, along with an associated Berry-phase π, results in a positive quantum correction in electrical conductivity, known as weak antilocalization (WAL). The applied magnetic field breaks down the TSS protection, resulting in a cusp-like negative magnetoconductance (MC). SnTe has a large amount (1021 cm−3) of Sn vacancies, leading to considerable bulk conductivity with a parabolic background over the WAL MC. In this work, we observe an enhancement of the WAL signal in V-doped SnTe using electron spin resonance (ESR) measurements by substituting Sn vacancies with V atoms and charge-transfer-induced and temperature-dependent localization of itinerant carriers, called bound magnetic polarons (BMPs), which increases the effective mass of both electrons and holes and reduces bulk conductivity, as a consequence of magnetic anisotropy. Additionally, spin–orbit-coupling (SOC) induced spin canting, BMPs, interstitial, and substitutional occupation of V-impurities lead to competing ferromagnetic and antiferromagnetic proximity-coupled itinerant carrier-mediated Ruderman–Kittel–Kasuya–Yosida interaction in bare and V-doped SnTe, as evidenced by normal and parallel components of internal magnetic fields, observed in low-temperature ESR absorption spectral and temperature-dependent DC magnetization measurements. This proximity-coupled magnetic anisotropy makes V-doped SnTe a potential candidate for catalysis, thermoelectric, and spintronic applications. Density functional theory computations support SOC-induced spin canting, proximity-coupled magnetic order, and the charge transfer between V, Sn, and Sn vacancies.
1 Introduction
Topological materials have emerged as one of the most influential, interdisciplinary and rapidly expanding research fields of the last two decades, with the invention of numerous topological materials, including topological insulators (TI),1 topological crystalline insulators (TCI),2–4 Dirac semimetals,5 Weyl semimetals,6 topological superconductors3 and others. TCIs have prospective applications in optoelectronics, spintronics,3 quantum computing,3,4 energy conversion,7,8 catalysis9 and quantum transport. The proximity-coupled order10,11 of magnetic topological insulators12–14 facilitates the room-temperature application of magnetic topological phases due to the interaction between the topological electronic states and the magnetic degrees of freedom.10,15–17Topological crystalline insulators (TCIs) like SnTe, with a rock salt structure, exhibit four Dirac cones, with one on each of the (001) and(110) surfaces and two on the (111) surface centered at the Γ and M points,2,18 while trivial topological insulators (TIs) such as Bi2Te3 and Bi2Se319,20 have only one Dirac cone. Angle-resolved photoemission spectroscopy (ARPES)11,21–23 and scanning tunneling microscopy (STM)24,25 confirm the presence of topological surface states (TSSs). Theoretical and experimental studies have shown that the formation energy of Sn vacancies is significantly lower than that of Te vacancies.26–28 As a result, SnTe exhibits a high concentration of Sn vacancies (1021 cm−3), which contributes to its semimetallic behavior. However, for SnTe, bulk conductivity, influenced by intrinsic p-type defects (1021 cm−3),2,3,29 contributes to negative magnetoconductance (NMC). Enhancing TSS conductance involves nanostructuring and doping strategies. Thin film growth techniques (MBE and CVD)2,4,30 and chemical reduction methods (hydrothermal and solvothermal)20,31 are widely used for the synthesis of nanostructured TCIs. Pb doping in SnTe reduces hole carrier density, while Fe,19 Co,20 Dy, Cu,19 V,14,32 Cr,16,19,33 Eu,18 and Mn23,34,35 doping in TIs and TCIs enhances TSS conductance and induces magnetic ordering. Incorporating magnetic impurity in SnTe of the order of Sn vacancy concentration has reduced the contribution of hole conductivity by substitution or charge transfer-induced hole localization,2,36–38 leading to topological quantum interference. Magnetic dopants introduce anisotropic interactions,34,39,40 resulting in canted ferromagnetic (FM) and antiferromagnetic (AFM) states,14,32 often explained by percolation theory33,36–38,41,42 and RKKY interactions.13,14,43 Electron spin resonance (ESR)44–47 helps to distinguish bulk and surface characteristics, detecting signatures of magnetic interactions. At low temperatures, TCIs exhibit weak antilocalization (WAL) or weak localization (WL) effects,47,48 which can be reversed by an external magnetic field,47,48 affecting ESR spectra and revealing cyclotron resonance and SdH oscillations.45,46
In this paper, we have synthesized bare and V-doped (0 < x < 0.08) SnTe nanoparticles (NPs) using the chemical reflux method with a co-precipitation reaction mechanism. The present work is focused on studying the carrier-mediated magnetism, photoluminescence (PL), and weak antilocalization (WAL) effects in highly disordered SnTe and V-doped SnTe using SQUID, PL spectroscopy, and electron spin resonance (ESR) spectroscopy. To support ESR and SQUID results, other measurements such as X-ray diffraction (XRD), X-ray photoelectron spectroscopy, Raman scattering, and density functional theory (DFT) computation have been carried out.2–4,45 Our computational investigation evaluates the role of Sn vacancies in the charge transfer, density of states (DOS), and band structure modulation of the simulated structures of SnTe and V-doped SnTe, including and excluding SOC.
2 Experimental section
2.1 Materials synthesis
VxSn1−xTe (x = 0, 0.03, 0.05, and 0.08) nano-alloys are prepared by a simultaneous reaction using the chemical reflux method with a co-precipitation49 reaction mechanism. SnCl2·2H2O (99.99%), VCl3·6H2O, Te powder, glycine amino acid (as a surfactant reactant) and NaBH4 (as a reducing agent) are used as precursors. At first, 1 mmol SnCl2·2H2O solution is prepared in a round bottom flask, and 5 mmol glycine is added. The solution is heated at 80 °C for 45 minutes with magnetic starring, and a grey-color colloidal Sn+2 solution is observed. At the same time, 1 mmol Te powder is taken in 20 mL of water, and 10 mmol NaBH4 is added to the Te solution and left for 45 min with magnetic stirring to reduce Te into Te−2.| 2Te + 4NaBH4 + 7H2O → 2NaHTe + Na2B4O7 + 14H2O | (1) |
Then Te−2 colloidal solutions are mixed with the Sn+2 solution, and the condenser is connected to the mouth of the round bottom flask and left for 5 to 6 hours at 100 °C with magnetic starring. Finally, the obtained black precipitate is separated from the solution by centrifugation and cleaned with distilled water and 99.99% ethanol (several times) to remove unwanted impurities. After that, the black precipitate is dried in a vacuum hot air oven for 24 h to avoid unnecessary oxidation in the presence of air. In addition to pristine SnTe, V-doped SnTe with different concentrations is prepared with VCl3 as a source of V+2 ion. 0.03, 0.05, and 0.08 mmol VCl3·6H2O salt is added to 0.97, 0.95, 0.92 mmol SnCl2·2H2O solution for the preparation of 3%, 5% and 8% V doped SnTe. The same amounts of Te powder, glycine amino acid, and NaBH4 are used as precursors. The resultant solution is processed via a similar procedure49,50 and left for 6 hours at 100 °C with magnetic stirring. The obtained black precipitates are separated and collected using the above-mentioned procedure.
2.2 Characterization technique
The crystal structure and phase composition of the nano alloys are investigated by powder X-ray diffraction using a Bruker D2 phase 2nd generation X-ray diffractometer and Cu Kα = 1.5406 Å. The diffraction data are collected at room temperature with a step size of 4.67° per minute, over (10° < θ < 80°). The morphology of the synthesized nanoalloys is explored using a Zeiss Supra 40 field-emission scanning electron microscope (accelerating voltage 200 kV) and JEM ARM 300 F2 high-resolution transmission electron microscope (accelerating voltage 300 kV) equipped with energy-dispersive X-ray spectroscopy (EDX) detectors. The ethanol pre-sonicated colloidal NP droplets are placed on a small thin glass wafer to perform field-emission-gun scanning electron microscopy (FEGSEM). Further stoichiometric verification is done by X-ray photoelectron spectroscopy using a PHI5000 Versa probe system equipped with an Al Kα (hν = 1486.6 eV) source. The binding energies are charge referenced to C 1s at 284.6 eV. High-resolution XPS spectra are taken at 58.7 eV analyzer pass energy in a step size of 0.125 eV. XPS valence band spectra are taken at 23.5 eV analyzer pass energy in a step size of 0.125 eV. DC magnetization measurements are carried out using a quantum design MPMS SQUID VSM, attached with liquid He 3 cryostats. The symmetric vibration states of the nano-compounds are investigated by Raman spectroscopy using a T64000 (JY, France) micro-Raman spectrometer with an excitation wavelength of 532 nm. The complementary anti-symmetric vibrational states are investigated using the NICOLET 6700 FTIR spectrometer. The room temperature photo-luminance (PL) spectra are collected to investigate the modulation of charge transfer and band structure in the presence of defects and magnetic impurities. The room temperature and the low-temperature X band ESR spectra are recorded using a Bruker ELEXYS E-580 spectrometer for the investigation of magnetic interaction,45–47 hyperfine Zeeman splitting45,51 and topological quantum interference46,52 of the observed compounds.2.3 Computational details
We investigate the charge transfer effects, electronic structure, density of states, and magnetic properties of bare and impurity-doped topological insulators with Sn vacancies. All simulations are carried out using the plain wave DFT method implemented in the quantum espresso code.53 The Purdue–Burke–Ernzerhof54,55 scheme of the generalized gradient approximation (GGA) is used for the exchange–correlation potential.54,55 The experimentally reported lattice constant with a = 6.32 Å in FCC structure having the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group is used as the initial parameter29 and the CIF file is taken from the Materials Project Crystallographic database. We have taken a 2 × 2 × 2 supercell structure of bare SnTe to further confirm the theoretical results. All cell atoms are relaxed using the Broyden–Fletcher–Goldfarb–Shannon (BFGS) quasi-Newton algorithm until the Hellmann–Feynman force reached 1 mRy per a.u. with the optimization energy of 10−9 Ry per a.u. A Sn atom has been removed from the SnTe unit cell and 2 × 2 × 2 supercell to create Sn vacancies. All structures containing Sn vacancies were modeled with a total charge of +2 and adjusted using Makov–Payne electrostatic corrections to account for finite-size effects in charged supercells. Subsequently, we replaced one Sn atom with a V atom to investigate the magnetic proximity3,11,17 in modulating the DOS, band structure, LDOS, and charge transfer effects of all of the above-simulated compounds. All structures containing a V atom but without Sn vacancies were also adjusted using Makov–Payne electrostatic corrections to account for electrostatic interactions in charged supercells. Optimization is performed for SOC and non-SOC calculations until inter-atomic force and stress become less than 10−5 eV Å−1. We used the full relativistic pseudopotential for the noncollinear SOC calculation. The crystal structures are optimized with a kinetic-energy cut-off of 89 Ry and a charge-density cut-off of 810 Ry with 20 × 20 × 20 K-mesh.
m space group is used as the initial parameter29 and the CIF file is taken from the Materials Project Crystallographic database. We have taken a 2 × 2 × 2 supercell structure of bare SnTe to further confirm the theoretical results. All cell atoms are relaxed using the Broyden–Fletcher–Goldfarb–Shannon (BFGS) quasi-Newton algorithm until the Hellmann–Feynman force reached 1 mRy per a.u. with the optimization energy of 10−9 Ry per a.u. A Sn atom has been removed from the SnTe unit cell and 2 × 2 × 2 supercell to create Sn vacancies. All structures containing Sn vacancies were modeled with a total charge of +2 and adjusted using Makov–Payne electrostatic corrections to account for finite-size effects in charged supercells. Subsequently, we replaced one Sn atom with a V atom to investigate the magnetic proximity3,11,17 in modulating the DOS, band structure, LDOS, and charge transfer effects of all of the above-simulated compounds. All structures containing a V atom but without Sn vacancies were also adjusted using Makov–Payne electrostatic corrections to account for electrostatic interactions in charged supercells. Optimization is performed for SOC and non-SOC calculations until inter-atomic force and stress become less than 10−5 eV Å−1. We used the full relativistic pseudopotential for the noncollinear SOC calculation. The crystal structures are optimized with a kinetic-energy cut-off of 89 Ry and a charge-density cut-off of 810 Ry with 20 × 20 × 20 K-mesh.
3 Results and discussion
3.1 X-Ray diffraction
Fig. 1(a) shows the XRD patterns of the as-synthesized VxSn1−xTe samples. The prominent reflection peaks are observed at 2θ values of 28.30°, 40.45°, 50.10°, 58.46°, 66.20°, and 73.40°, aligning with the (200), (220), (222), (400), (420), and (422) planes of the FCC crystallographic structure of SnTe, characterized by octahedral symmetry, as confirmed through comparison with the joint committee on powder diffraction standard data.8,29,56,57Fig. 1(b) illustrates that the most intense (200) peak of V0.03Sn0.97Te has shifted towards a higher diffraction angle, whereas V0.05Sn0.95Te and V0.08Sn0.92Te have shifted towards lower diffraction angles compared to bare SnTe. The radii of V+2 ions are less than those of Sn+2 ions. The observation indicates that at a lower doping concentration (3%), the substitutional occupation of vanadium is preferred, while at higher doping concentrations (5% and 8%), the interstitial occupation becomes more favorable. The observation of Te, TeO2, and SnO2 as impurity phases in bare SnTe, V0.05Sn0.95Te, and V0.08Sn0.92Te indicates the presence of unreacted Te and surface oxidation of NPs. The minimal peak intensity of TeO2 and SnO2 compared to the SnTe characteristic (200) peak suggests a clear indication of surface oxidation of the NPs. Consequently, nearly phase-pure SnTe and VxSn1−xTe samples are produced without the segregation of the impurity phase.| Sample name | Atomic% of Sn | Atomic% of Te | Atomic% of V |
|---|---|---|---|
| SnTe | 52.12 | 47.88 | 0 |
| SnTeTEM | 52.10 | 47.90 | 0 |
| V0.03Sn0.97Te | 56.33 | 42.23 | 1.444 |
| V0.03Sn0.97TeTEM | 53.65 | 42.65 | 3.69 |
| V0.05Sn0.95Te | 57.01 | 38.14 | 4.85 |
| V0.08Sn0.92Te | 48.24 | 44.52 | 7.24 |
The HRTEM images and SAED patterns of bare and 3% V-doped SnTe were recorded to examine nanoplates, defect states, and crystallinity. Fig. S1(a) and (b) (ESI†) display HRTEM images and EDX spectra, confirming a deformed circular disc-like morphology with radii of 5–50 nm. The formation of larger nanoparticles occurs as a result of coalescence-induced elongation driven by magnetic forces and van der Waals interactions. The weight percentages obtained from HRTEM EDX are consistent with the SEM EDX results, as shown in the insets of Fig. S1(a) and (b) (ESI†) and Table 1. Elemental mapping (Fig. 1(c) and (f)) reveals a consistent distribution of Sn, Te, and V, indicating the high quality of the sample.7,56Fig. 1(c) shows the bare SnTe nanograins and grain boundaries, where the smaller grains (5–10 nm) exhibit fewer defects and single crystallinity,57,58 while the larger grains (10–50 nm) display more defects and polycrystalline structures.59 The enlarged HRTEM image of a larger grain (Fig. 1(d)) reveals multiple defects. The interplanar spacings of the (200) and (220) planes in bare SnTe are 0.32 nm and 0.222 nm, consistent with the reported values.7,56,57 The accumulated defects in approximately 10 nm grains suggest a lower crystallinity. The enlarged view of the red square marked region of Fig. 1(d), on a 1 nm scale, depicted the dislocation of the atoms, vacancies, and defects, shown in Fig. 1(e). The SAED pattern of bare SnTe (Fig. S1(c), ESI†) displays faint7 and bright diffraction spots, which confirms its crystallinity. Certain diffraction spots (Fig. S1(c), ESI†) show deviations from the expected circular ring pattern, attributed to incomplete layers and defects.59 Multiple orientations of planes further confirm polycrystallinity in larger grains. For V0.03Sn0.97Te, the enlarged HRTEM image (Fig. S1(b), ESI†) of a 47.32 nm grain shows twin boundaries,58,59 dense stacking faults,7,58 atomic dislocations,58 and vacancies (Fig. 1(f)–(h)).58 The (200) and (220) interplanar spacings of V0.03Sn0.97Te are 0.318 and 0.222 nm, consistent with the literature.7,56 The inset of Fig. 1(h) shows a clear visual of dense stacking faults, accumulation of vacancies, and interstitial occupation of atoms. The SAED pattern (Fig. 1(i)) displays a square diffraction spot arrangement, indicating improved crystallinity, consistent with fewer defect states in larger grains. The manifestation of the square SAED pattern in V0.03Sn0.97Te reveals that the zone axis of the diffraction is [001].57 The presence of split diffraction spots in the SAED pattern of V0.03Sn0.97Te is the consequence of the increase or decrease of interplanar spacing due to the presence of internal and external stocking faults.58,59 Consequently, HRTEM, SAED, elemental mapping, and EDX validate the crystallinity, defect states, and superior quality of the sample.
3.2 X-Ray photoelectron spectroscopy
XPS analysis was performed to confirm impurity phases and oxidation states, with all spectra charge-referenced to the C 1s peak at 285.6 eV.20Fig. 2(a)–(d) show high-resolution XPS spectra of the Sn 3d, Te 3d, V 3p, and O 1s regions, with survey spectra (Fig. S2(a), ESI†) validating the presence of Sn and Te. The Sn 3d5/2 and Sn 3d3/2 peaks of pristine SnTe at 485.85 eV and 494.3 eV8,56,60,61 shift positively (0.05–0.15 eV) in VxSn1−xTe (x = 0.03, 0.05, 0.08) due to charge transfer from Sn+2 ions to Sn vacancies. Surface degradation results in a Sn0 state in V0.03Sn0.97Te, shifting negatively due to charge transfer from V.60 Increased V doping creates additional Sn vacancies via interstitial V+4 occupation, further altering charge distribution. Surface oxidation produces Sn+4 peaks at 486.64 and 495 eV,62 which shift slightly (0.06–0.4 eV) in V-doped samples. O 1s spectra at 530.2 eV and 529 eV for V0.05Sn0.95Te and V0.08Sn0.92Te confirm SnOx8,61,62 and TeOx,61,63 which reveal the surface oxidation of the mentioned compounds.8,61 Peaks at 530.6 eV and 531.8 eV for all samples arise from hydroxyl (–OH) and carbonyl (C–O–C) groups due to ethanol adsorption during cleaning. Te 3d5/2 and 3d3/2 peaks in SnTe appear at 571.8 eV and 582.22 eV (Te−2) and 576.13 eV and 586.59 eV (Te+4).8,60,61,64 In VxSn1−xTe, Te−2 states shift by 0.2–0.25 eV due to charge transfer to Sn vacancies and V–Te bond formation, indicating a stronger V–Te bond than Sn–Te.32 Te+4 binding energy decreases at higher V doping due to partial oxidation (TeOx) and increased Sn vacancies.9 The intensity of the V 3p peak increases with V doping, which confirms the presence and increase of V with V doping. For V0.03Sn0.97Te, peaks at 39.11 eV, 40.55 eV, 43.69 eV, and 44.7 eV indicate substitutional (+2, +3) and interstitial (+4, +5) states. For V0.05Sn0.95Te and V0.08Sn0.92Te, V+2 and V+3 peaks shift positively (0.9 eV, 0.76 eV) due to charge transfer from V ions to Sn vacancies.64 At x = 0.03, V primarily substitutes Sn in the +2 and +3 states, while at x = 0.05 and 0.08, the interstitial V+4 and V+5 dominate. XPS valence band spectra reveal Fermi level shifts with V doping, described in the ESI† section of this paper.3.3 RAMAN and FTIR
Raman spectroscopy explores the symmetric vibrational modes of SnTe and V-doped SnTe NPs. In pure SnTe, octahedral symmetry (Oh) cancels the net dipole moment, deactivating the first-order Raman modes. Vacancies induce polarizability, activating frozen Raman modes, while doping disrupts FCC symmetry, restoring Raman activity.29,57,65 SnTe exhibits A1 and ETO phonon modes at 118.62 cm−1 and 138.10 cm−1 (Fig. S3(a), ESI†). In V-doped SnTe, both peaks shift towards the higher wave number side due to charge transfer from the V to SnTe matrix, increasing the force constant and bulk modulus.8,65 At higher doping concentrations, the shift remains constant as V occupies both substitutional and interstitial sites, causing opposing vibrational shifts.29,65 Again, the lighter V atoms reduce the V–Te bond mass and shift Raman peaks towards higher wave numbers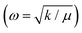 . The lower intensity in V0.03Sn0.97Te suggests reduced Sn vacancies due to V+2 substitution.57,65 The presence of the A1 and ETO modes in all samples confirms the high quality of the sample.
. The lower intensity in V0.03Sn0.97Te suggests reduced Sn vacancies due to V+2 substitution.57,65 The presence of the A1 and ETO modes in all samples confirms the high quality of the sample.
FTIR spectroscopy50 complements Raman spectroscopy by detecting asymmetric molecular vibrations. Fig. S3(b) (ESI†) shows the FTIR spectra of bare and V-doped SnTe, where doping reduces peak intensity and shifts peaks to higher wavenumbers due to stress in NPs and charge transfer,66 respectively. The peaks observed at 492.89 cm−1 and 636.85 cm−1 are associated with the vibrations of Te–Sn–Te and Sn–Te–Sn,50 respectively. The Te–Sn–Te vibration appears first, attributed to its lower reduced mass. A new peak at 796.82 cm−1 is observed, resulting from Te–V–Te vibrations. The presence of common H–O stretching, H–O–H bending, and C–O, C–O–H stretching shows that the surface of NPs is associated with dangling H2O, –COOH, and CO2 molecules.50,66 These results confirm charge-transfer effects, phase formation, and surface carboxyl (–O–C–O) and hydroxyl (–OH) groups, supporting the observed XPS O 1s spectra.
The presence of Urbach's tail in UV-VIS-NIR spectra is attributed to defects found in bare, doped, and surface-modified nanoparticles, leading to inaccuracies in the estimation of the band gap due to interband states.67 FTIR transmittance, facilitated by a Michelson interferometer and Fourier transform, is more effective in identifying sub-bandgap states and actual band gaps.67 Bulk SnTe exhibits a band gap of 0.18 eV,60,61 and the UV-vis-NIR spectra (performed but not presented) span from 1.23 to 4.13 eV, resulting in broadband absorption with Urbach's tail.50,66 FTIR, with a range of 0.045–0.495 eV, is better suited for narrow-band semiconductors. Fig. S3(c) (ESI†) presents the Tauc plot of SnTe and VxSn1−xTe (x = 0.03, 0.05, 0.08), showing band gaps of 0.31 eV, 0.3 eV, 0.372 eV, and 0.41 eV, respectively. The widening of the band gap results from nanostructuring and the presence of cationic defect states. The sample with 3% V doping exhibits the lowest band gap, attributed to the presence of minimal vacancies and the role of V as a donor impurity. Increased doping levels (x = 0.05, 0.08) lead to a widening of the band gap due to the introduction of additional Sn vacancies by interstitial V+4 ions. These findings are consistent with XPS and DFT computations.
3.4 Photoluminescence spectroscopy
Symmetric ideal SnTe does not exhibit PL spectra; however, the presence of intrinsic Sn vacancies and defect states leads to observable PL emission. Photoluminescence spectroscopy elucidates these defects and impurity states. The PL spectra (Fig. S3(d), ESI†) of bare SnTe at 769.40 nm, 786.82 nm, 868.39 nm, and 955.01 nm are attributed to intraband transitions associated with defects, anti-sites, and cationic/anionic vacancies,11,68 as corroborated by DFT simulations. The incorporation of V modifies defect states, resulting in the emergence of new PL peaks.50,66 The 769.40 nm peak disappears with V doping, while a new 852.83 nm peak emerges due to V impurity states. Peaks at 786.82 nm, 955.94 nm, and 926.32 nm show a redshift, indicating denser defect states with V doping. In contrast, the 870.21 nm peak exhibits blue shifts. The red and blue shifts of the PL peaks after the incorporation of the V impurity corroborate the modulation of the band structure of V-doped SnTe. PL quenching in V0.03Sn0.97Te corresponds to reduced Sn vacancies due to V+2 substitution, which is consistent with the minimum Raman intensity of this composition. The enhanced PL intensity in V0.05Sn0.95Te and V0.08Sn0.92Te indicates elevated defect concentrations due to interstitial V atoms, which is also reflected in the elevated Raman intensity of these compositions.3.5 DFT computations
DFT computations reveal charge transfer-induced hole localization and magnetism in bulk and V-doped SnTe with an FCC structure (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group). The role of Sn vacancies with V doping was analyzed using the PBE exchange–correlation scheme in Quantum Espresso.54,55 Charge transfer and magnetic proximity effects were established via V substitution or interstitial incorporation with Sn vacancies. Theoretical and experimental studies have shown that SnTe has a high concentration of Sn vacancies due to lower formation energy of Sn vacancies than that of Te vacancies.26–28 Fig. S4(a)–(f) and S10(a)–(f) (ESI†) illustrate the FCC structure with the Fm
m space group). The role of Sn vacancies with V doping was analyzed using the PBE exchange–correlation scheme in Quantum Espresso.54,55 Charge transfer and magnetic proximity effects were established via V substitution or interstitial incorporation with Sn vacancies. Theoretical and experimental studies have shown that SnTe has a high concentration of Sn vacancies due to lower formation energy of Sn vacancies than that of Te vacancies.26–28 Fig. S4(a)–(f) and S10(a)–(f) (ESI†) illustrate the FCC structure with the Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group of SnTe, SnTe with Sn vacancies (SnVTe), V-doped SnTe (VSnTe), V-doped SnTe with Sn vacancies (VSnVTe), SnTe with interstitial V (vSnTe), and SnTe with Sn vacancies and interstitial V (vSnvTe), in the unit-cell and 2 × 2 × 2 supercell, respectively. Sn vacancy and V impurity formation energy in the 2 × 2 × 2 supercell is 3.46 eV and 2.56 eV, respectively. The obtained formation energy values are consistent with the literature.26–28 Fig. S5(a)–(f) and S6(a)–(f) (ESI†) depict DOS and band structures using GGA and GGA+SOC of six simulated unit cell structures mentioned above. Fig. 3 shows the DOS of six simulated 2 × 2 × 2 supercell structures mentioned above. Non-collinear GGA+SOC calculations reveal SOC-induced magnetic anisotropy34,35,39,40 from spin flipping. The computed band gaps for SnTe are 0.06 eV (GGA) and 0.228 eV (GGA+SOC),1,29 which are consistent with the experimental value of 0.31 eV. The DOS of SnVTe indicates a shift of the Fermi level towards the valence band, confirming the Sn vacancies as acceptors in p-type SnTe. Non-collinear GGA+SOC calculations yield a magnetic moment of 0.01 and 0.05μB per cell in the unit cell and supercell structures, respectively, attributed to SOC-induced spin flipping near Sn vacancies. Both VSnTe and vSnTe defects shift the Fermi level toward the conduction band, exhibiting magnetic moments of 3.01 and 1.29μB per cell in the unit cell and 3.47 and 1.64μB per cell in the supercell, respectively; when V substitutes Sn+2 as V+2, its localized 3d orbital contains three unpaired electrons, leading to a magnetic moment close to 3μB per cell. The size of the octahedral hole in SnTe is 93 pm, and V can occupy an interstitial site in the V+4 state, with an ionic radius of 86 pm. In this oxidation state, the V atom has one unpaired 3d electron, contributing a magnetic moment close to 1μB per cell. These considerations suggest that V can substitute Sn+2 as V+2 ions or occupy an interstitial site as V+4, acting as a donor impurity. For VSnVTe and vSnvTe the magnetic moments are reduced to 2.17 and 1.06μB per cell for the unit cell and 3.05 and 1.19μB per cell for the supercell. This reduction in the moment is attributed to charge transfer from V to Sn vacancies, which introduces localized states.37,69 The observed decrease in magnetic moment implies the presence of antiferromagnetic interactions among localized charge.20,36,37,70
m space group of SnTe, SnTe with Sn vacancies (SnVTe), V-doped SnTe (VSnTe), V-doped SnTe with Sn vacancies (VSnVTe), SnTe with interstitial V (vSnTe), and SnTe with Sn vacancies and interstitial V (vSnvTe), in the unit-cell and 2 × 2 × 2 supercell, respectively. Sn vacancy and V impurity formation energy in the 2 × 2 × 2 supercell is 3.46 eV and 2.56 eV, respectively. The obtained formation energy values are consistent with the literature.26–28 Fig. S5(a)–(f) and S6(a)–(f) (ESI†) depict DOS and band structures using GGA and GGA+SOC of six simulated unit cell structures mentioned above. Fig. 3 shows the DOS of six simulated 2 × 2 × 2 supercell structures mentioned above. Non-collinear GGA+SOC calculations reveal SOC-induced magnetic anisotropy34,35,39,40 from spin flipping. The computed band gaps for SnTe are 0.06 eV (GGA) and 0.228 eV (GGA+SOC),1,29 which are consistent with the experimental value of 0.31 eV. The DOS of SnVTe indicates a shift of the Fermi level towards the valence band, confirming the Sn vacancies as acceptors in p-type SnTe. Non-collinear GGA+SOC calculations yield a magnetic moment of 0.01 and 0.05μB per cell in the unit cell and supercell structures, respectively, attributed to SOC-induced spin flipping near Sn vacancies. Both VSnTe and vSnTe defects shift the Fermi level toward the conduction band, exhibiting magnetic moments of 3.01 and 1.29μB per cell in the unit cell and 3.47 and 1.64μB per cell in the supercell, respectively; when V substitutes Sn+2 as V+2, its localized 3d orbital contains three unpaired electrons, leading to a magnetic moment close to 3μB per cell. The size of the octahedral hole in SnTe is 93 pm, and V can occupy an interstitial site in the V+4 state, with an ionic radius of 86 pm. In this oxidation state, the V atom has one unpaired 3d electron, contributing a magnetic moment close to 1μB per cell. These considerations suggest that V can substitute Sn+2 as V+2 ions or occupy an interstitial site as V+4, acting as a donor impurity. For VSnVTe and vSnvTe the magnetic moments are reduced to 2.17 and 1.06μB per cell for the unit cell and 3.05 and 1.19μB per cell for the supercell. This reduction in the moment is attributed to charge transfer from V to Sn vacancies, which introduces localized states.37,69 The observed decrease in magnetic moment implies the presence of antiferromagnetic interactions among localized charge.20,36,37,70
 | ||
| Fig. 3 DOS with GGA and GGA+SOC of SnTe, SnVTe, VSnTe, VSnVTe, vSnTe, and vSnvTe in the 2 × 2 × 2 supercell structure. | ||
According to Z. Ma et al., the work function of bulk SnTe61,71 is 4.68 eV, while that of vanadium72 is 4.3 eV. Nanostructuring increases71,72 the work function of both SnTe and vanadium, revealing strong charge transfer from V to Sn atoms. To quantify charge transfer efficiency, we compare unpolarized Lowdin charge densities of (100) planes for SnTe, SnVTe, VSnTe, and VSnVTe, depicted in Fig. S8(a)–(d) for the unit cell and S11(a)–(f) (ESI†) for the 2 × 2 × 2 supercell, respectively. The increase in contour radii in the 2D charge density plot indicates charge transfer to the Sn vacancy. Fig. S9(a) and S12(a) (ESI†) compare the local density of states (LDOS) of the Sn 3d orbitals in the unit cell and supercell, respectively. The average localized integrated valence band charge of the Sn atom in SnTe is 0.0078 a.u. (0.00558 a.u. for the unit cell), reducing to 0.00417 (0.00428 a.u. for the unit cell) in SnVTe, confirming 0.00363 a.u. (0.00141 a.u. for the unit cell) charge transfer to the Sn vacancy. The charge content of the Sn 3d orbitals increases in VSnTe and VSnVTe due to the charge transfer from V, shown in Table SI for the unit cell and SIII (ESI†) for the supercell, respectively. The interstitial V of vSnTe and vSnVTe enables van der Waals bonding, easing the additional charge transfer to SnTe,32 as shown in Table SI for the unit cell and SIII (ESI†) for the supercell, respectively. The reduced localized charge of V in V-doped SnTe with Sn vacancies further supports this charge transfer (Tables SII and SIV, Fig. S6(b), ESI†). Incorporating SOC with noncollinear interactions induces hybridization3,17 with higher atomic orbitals, resulting in proximity coupling10 in the Sn 4d and V 5d orbitals.
3.6 Magnetization
Magnetically, SnTe is diamagnetic, while V is paramagnetic. The field-cooled (FC) and zero-field-cooled (ZFC) M–T curves at 500 Oe for SnTe (Fig. 4(a)) show bifurcation near room temperature. Non-collinear DFT computations indicate that the SOC-induced magnetic moment cancels out in the ideal SnTe, making it diamagnetic. However, Sn vacancies introduce small ferromagnetic interactions due to SOC-induced spin flipping, forming BMPs.29,68 An appreciable amount of charge transfer from the SnTe matrix to the Sn vacancy position is confirmed by the charge density contour plots and valence band charge of the Sn 3d and V 4d orbitals. XPS confirms charge transfer from Sn to Sn vacancies in VxSn1−xTe (x = 0.03, 0.05, 0.08). This carrier-mediated semi-localization increases the electron and hole effective mass,36–38 generating semi-magnetic order or localized moments. The vacancy in the SnTe matrix produces magnetocrystalline anisotropy,68 indicating appreciable thermomagnetic irreversibility in the ZFC–FC curves of bare and V-doped compounds.39,40,73 The ZFC curve of bare SnTe drops slowly and sharply beyond 289.6 K and 60 K, indicating competing FM and AFM23,74 interaction due to the freezing of spins (spin-glass) and RKKY type itinerant carrier-mediated double exchange interaction among BMPs,10,37,38,68,73 respectively. The M–H curve of SnTe (Fig. 5(a)) has a negative slope, confirming diamagnetism, with an upward shift suggesting weak ferromagnetism. SOC is the key determining factor for a material to be topological. V+2 or V+4 ions in substitutional or interstitial positions13 experience crystal field splitting,73 leading to hybridization and s–d/p–d exchange.32,43 This induces spin canting and magnetic proximity effects.10,11,39,40 In the dilute magnetic regime, the individual induced moments of the impurity-ligand dimer interact through the itinerant carrier-mediated RKKY double exchange interaction.10,13,43,73 | ||
| Fig. 4 M–T ZFC and FC curves at 500 Oe from 10 K–300 K for (a) SnTe, (b) V0.03Sn0.97Te, (c) V0.05Sn0.95, and (d) V0.08Sn0.92. | ||
 | ||
| Fig. 5 M–H curves of (a) bare SnTe, (b) V0.03Sn0.97Te, (c) V0.05Sn0.95Te, and (d) V0.08Sn0.92Te at 10 K. | ||
V0.03Sn0.97Te exhibits reduced hole concentration due to the Sn vacancies replaced by V.32 DFT calculations give magnetic moments of 3.01 and 1.29μB per cell, indicating V+2 substitution and V+4 interstitial occupation, as described in the DFT results. The FC–ZFC M–T@500 Oe (Fig. 4(b)) curve bifurcates at 267.08 K and beyond 267.08 K (Tirr), a gradual upturn in the FC and ZFC curve indicates competing FM–AFM interactions.74 FM arises from RKKY interactions among BMP and V–Te proximity-coupled induced magnetic moments for substitutional doping of V+2 ions and V–Te-induced moments,3,10,13,17,43,73 while interstitial V+4 ions induce Sn vacancies, breaking crystal symmetry and opening the band gap.43 This introduces an Ising term, leading to BR-type AFM RKKY interactions,43 which is shown in the schematic S6 (ESI†). The M–H curve (Fig. 5(b) and its inset) shows hysteresis with remanent magnetization (7.15 × 10−4 emu per g), coercivity (127.67 Oe), and saturation magnetization (0.04815 emu per g), confirming FM dominance. For V0.05Sn0.95Te (Fig. 4(c)), FC–ZFC curves show a broad blocking temperature range, indicating anisotropic FM–AFM competition.74 This is probably due to the possible BR-correlated AFM interaction13 overcome or comparable to the above-mentioned FM interaction due to the minimal substitutional V+2 or V+3 ions, confirmed by the XPS result. Below 70.65 K and 24 K, upturns in FC–ZFC curves reflect localization of the itinerant carrier with decreasing temperature, which increases the corresponding Fermi wavelength (λF) and makes the RKKY interaction ferromagnetic.13M–H (Fig. 5(c)) curves indicate superparamagnetic/paramagnetic surface components, with coercivity (65.55 Oe) and retentivity (5.14 × 10−4 emu per g) at the lowest observable temperature (10 K), shown in the inset of Fig. 5(c). Removing paramagnetic contributions reveals a saturation magnetization of 0.06574 emu per g. The nonsaturating superparamagnetic/paramagnetic surface components44 of the M–H curve at the higher magnetic field regime originate from non-interacting or weakly interacting spins within BMPs and surface anisotropy.3,44 The M–T and M–H curves of V0.08Sn0.92Te are depicted in Fig. 4(d) and 5(d), respectively. The continuous increasing and decreasing trend of the ZFC curve is the signature of competing FM–AFM interactions74 due to the comparable substitutional and interstitial occupation of the V impurity and the itinerant carrier-dependent oscillating RKKY interaction with temperature.13,43 The broad ZFC and FC curves reveal a wide distribution of the blocking temperature (TB), approximately close to 277 K. The FC and ZFC curves bifurcate at 276.2 K. The sudden upturn of the FC curve and the increasing separation between the FC and ZFC curves at 230.2 K and 81.07 K are the consequences of magnetic anisotropy34,35,39,40 along the magnetic hard and easy axes, respectively. Subtracting the paramagnetic contribution from the M–H curve reveals a saturation magnetization of 0.0958 emu per g, with a coercivity of 110.676 Oe and a retentivity of 0.000455 emu per g. The sudden sharp increase in ZFC and FC curves below 20 K for all V-doped compounds is a consequence of surface-state-assisted enhancement of magnetic order10 at the interface because, at this temperature, the chiral carriers of the surface of TCI are activated.10 The above results conclude that intrinsic Sn vacancies and substitutional and interstitial occupation of the V+2 and V+4 ions lead to a competing FM and AFM correlation,74 as temperature-dependent localization of the itinerant carrier results in an oscillating RKKY interaction.10,13,36,37,43,73
3.7 Electron spin resonance
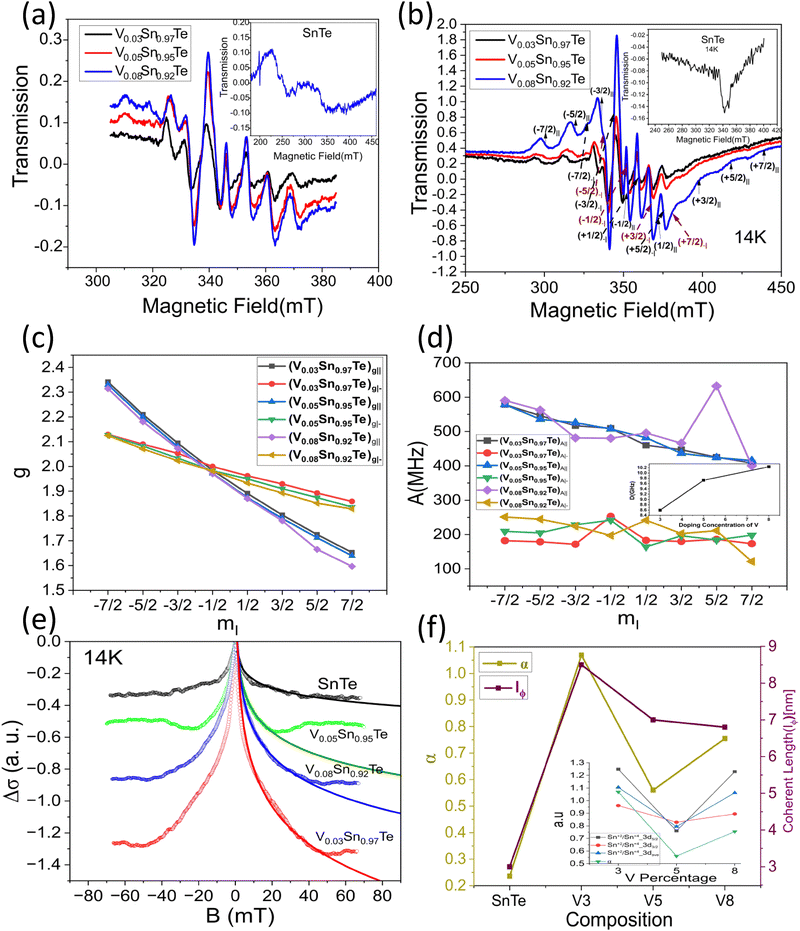
To investigate the anisotropic anomalous behavior of chiral and impurity electrons under SOC, defects, and impurities, electron spin resonance (ESR) has been studied.34,35 ESR spectroscopy12,15,46–48,75 probes exchange interactions in transition metals and paramagnetic systems. In weakly coupled magnetic systems, single-crystal spectra result from the superposition of non-equivalent spins, while strong exchange interactions lead to exchange narrowing and collapsed spectra.46–48,75 Hyperfine interactions provide additional anisotropy34,35,39,40 insight. Besides the tuned magnetic field of the TE102 cavity, unpaired electrons are sensitive to their local environment.45–48Fig. 6(a) and (b) show room-temperature and low-temperature (14 K) ESR spectra of bare SnTe and V-doped SnTe. Bare SnTe exhibits a dip-like signal (inset of Fig. 6(b)) at g = 2.052, likely due to trapped electrons at Sn vacancies.76,77 V has a nuclear moment I = 7/2 and hyperfine Zeeman splitting51,74,78 into eight components76,77 appears in both low- and room-temperature spectra. Even at low impurity concentrations (x = 0.03), splitting is observed at room temperature, with intensity reduced nearly sevenfold from low temperature. The Landé g factor at the microwave absorption peak reveals normal and parallel internal magnetic field components, leading to sixteen ESR absorption components,77,78 confirming magnetic anisotropy in nano-compounds.39,40,75,76Fig. 6(c) shows the variation of normal and parallel Landé g factors with the nuclear magnetic quantum number (mI), reinforcing magnetic anisotropy.34,35,39,40,44,75,76 The slope of the parallel component is 2.5 times larger than the normal component, while the normal component's intensity is 1.76 times higher, indicating an easy axis along the normal direction and a hard axis along the parallel direction, consistent with non-collinear DFT results.44,75 The Landé g factor for both components decreases with increased doping concentration, suggesting weaker electron interactions at 3% V doping due to reduced vacancies and increased separation between V impurities. Higher doping increases Sn vacancies and enhances itinerant carrier-mediated RKKY interaction45,75 and the g value. The g⊥ values of VxSn1−xTe (x = 0.03, 0.05, 0.08) are 2.0217, 2.0237, and 2.02482, indicating stronger V interactions at higher doping levels. Fig. 6(d) shows the variation of the hyperfine splitting parameter (A)34,35,51,74 with mI. The A⊥ component remains nearly constant, while A‖ exhibits a slight decaying trend, illustrating nanocompound anisotropy.34,35,40,51,74 The inset of Fig. 6(d) displays the variation of the large axial zero-field splitting parameter (D) (Kramers doublets)45–47 with V concentration. At 14 K, D values for VxSn1−xTe (x = 0.03, 0.05, 0.08) are 8.5967, 9.728, and 10.236 GHz × h, respectively. Increased V doping enhances defect concentration and RKKY interaction, strengthening the axial field75 and increasing D. The D parameter depends on anion covalency, with Te > Se > S due to decreasing electronegativity.45 This results in Te exhibiting a larger D parameter. Some studies attribute D increment to anisotropic Korringa relaxation34,35,40,74via Bloch–Wangsness–Redfield theory,34,35,51 which is linked to strong spin–orbit coupling in heavy elements.74The ESR spectral intensity is proportional to the first derivative of the microwave-cavity quality factor (Q) to the magnetic field (dQ/dB), as revealed by magnetic field modulation within the lock-in-detection approach.48,53 The cavity Q factor determines sample conductivity and energy absorption in a tuned magnetic field, making the ESR signal strength linearly related to conductivity variations. Unlike contact measurements such as PPMS, ESR provides highly accurate differential conductivity.46–48,53 ESR spectroscopy measures WL and WAL15,48,52,79 with high accuracy, independent of impurity phases like SnO2 and TeO2.48 Electrons following diffusive random walks exhibit magnetoconductance in topological insulators.48 Spin-momentum locking minimizes backscattering, reducing resistance and increasing conductivity, leading to WAL effects.46,47 A magnetic field disrupts the Berry phase, decreasing conductivity and enhancing backscattering, causing weak localization (WL). The applied magnetic field reverses the phase of scattering electrons,48 generating positive (WL) or negative (WAL) magnetoconductance.79 X-band (9.7 GHz) CW-ESR at 14 K in the zero-field regime provides differential magnetoconductivity of the TCI system. Fig. S2(b) (ESI†) and Fig. 6(e) compare the differential and integrated magnetoconducting behavior of SnTe and VxSn1−xTe (x = 0.03, 0.05, 0.08). V0.03Sn0.97Te exhibits maximum intensity due to minimal defect-induced anisotropy via Sn vacancy occupation by V+2 ions and prominent reduction of surface degradation, which is shown in the inset of Fig. 6(f). The negative magnetoconductivity of V0.05Sn0.95Te is smaller than V0.08Sn0.92Te, as V+4 interstitial occupation creates additional Sn vacancies, which enhance surface degradation and increase bulk conductivity. This indicates that hole localization or reduction via Sn vacancy substitution enhances topological conductivity of chiral electrons mediated through an even number of Dirac cones of topological crystalline insulators (SnTe).2–4,7,30 The cusp-like negative magnetoconductivity variation is due to the WAL effect in topological surface states (TSSs). Fitting the MC curve with the HLN (Hikami–Larkin–Nagaoka) equation2,20 will further confirm WAL effects.
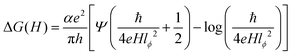 | (2) |
| Sample name | l ϕ (nm) | α |
|---|---|---|
| SnTe | 3 ± 2 | 0.2358 ∓ 0.08 |
| V0.03Sn0.97Te | 8.5 ± 1.5 | 1.06918 ∓ 0.12 |
| V0.05Sn0.95Te | 7 ± 1.8 | 0.566037 ∓ 0.1 |
| V0.08Sn0.92Te | 6.8 ± 1.5 | 0.7547 ∓ 0.12 |
Theoretically, one transport channel is fitted with one Dirac cone for typical topological insulators like Bi2Te3, Bi2Se3, etc., with α = 0.5. The top and bottom surface states influence two surface transport channels with α = 1. SnTe has four Dirac cones on its topological surface. The presence of both the upper and lower surfaces gives eight transport channels with α = 4.2,30 The value of α at 14 K of SnTe is 0.2358 ∓ 0.08, which is reasonable and shows that the contribution of the TSS transport channel is small due to surface degradation and intrinsic hole conductivity. The increase in α values for VxSn1−xTe (x = 0.03, 0.05, 0.08) V-doped compounds reveals the reduction in surface degradation, hole conductivity by substituting Sn vacancies and charge transfer-induced localization of itinerant carriers, which enhances the conductivity of TSSs. This anisotropic behavior of magnetoresistance is evidence of magnetic anisotropy within the NPs.
4. Conclusions
VxSn1−xTe NPs are synthesized by the chemical reflux method using glycine amino acid as a surfactant reactant and sodium borohydride as a reducing agent. The synthesized NPs are characterized by XRD, HRTEM, FEGSEM, XPS, Raman, and FTIR spectroscopy. HRTEM and FEGSEM showed that the average particle size of bare NPs is 5–50 nm, with different types of defect states. The charge transfer effects and the modification of the optical, magnetic, and magnetoconducting properties of NPs are experimentally validated by XPS, PL, magnetization, and magnetoconductance measurements, respectively. The DFT computations suggest that vanadium acts as a donor impurity, Sn vacancies make SnTe a p-type semiconductor, and SOC-induced spin canting and incorporating V bring magnetic ordering in bare and V-doped SnTe. The DC magnetization results showed a competing FM and AFM order due to the itinerant carrier-mediated RKKY interaction among interstitial and substitutional V ions and charge-transfer-induced BMPs. The linear variation of the M–H curve at high field regimes is the signature of the superparamagnetic or paramagnetic surface contribution of the V-doped NPs. The intrinsic carrier localization in the BMP and reduction of hole concentration and surface degradation by substituting Sn vacancies with vanadium (V) atoms diminished the intrinsic carrier conductance and intensified the weak TSS conductance. The improved TSS conductance in the SnTe and V-doped compounds concurrently raises the WAL existing temperature, the fraction of an independent transport channel in the TSS, and the phase-coherent length. This indicates that the localization of intrinsic carriers (holes) by suitable charge transfer from the SnTe matrix and dopant (V) atoms to Sn vacancy positions and the minimizing hole concentration and surface degradation by substituting Sn vacancies are optimum strategies to suppress bulk transport and promote the TSS conductance in the TCI SnTe system. This anomalous behavior of magnetoresistance reveals magnetic anisotropy within the NPs. This proximity-coupled magnetic anisotropy makes V-doped SnTe a potential candidate for catalysis, thermoelectric, and spintronic applications.Author contributions
Subhadip Ghosh: conceptualization, formal analysis, methodology, investigation, writing – original draft preparation and Sanjeev K. Srivastava: conceptualization, formal analysis, methodology, supervision, resources, writing – reviewing and editing.Data availability
The data supporting this study are included in this article and as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to acknowledge CSIR-HRDG and DST India, Ministry of Science and Technology, Govt. of India, Grant/Award Number: 09/081(1368)/2019-EMR-I, the XPS facility, Department of Physics, and Central Research Facility (CRF) IIT Kharagpur for providing the infrastructural support for the characterization of samples, the National Supercomputing Mission (NSM) for providing the computational facility of “PARAM Shakti” at IIT Kharagpur, supported by the Ministry of Electronics and Information Technology and DST, Govt. of India, and the Sophisticated Analytical Technical Help Institute (SATHI) IIT Kharagpur for HRTEM measurement. S. Ghosh would like to thank CSIR-HRDG and DST India for the financial assistance to carry out the research.Notes and references
- A. Phutela, P. Bhumla, M. Jain and S. Bhattacharya, Sci. Rep., 2022, 12, 21970 CrossRef CAS PubMed.
- C. Yan, F. Wei, Y. Bai, F. Wang, A. Zhang, S. Ma, W. Liu and Z. Zhang, J. Mater. Sci. Technol., 2020, 44, 223–228 CrossRef CAS.
- R. Mozumder, J. Wasmer, D. Antognini Silva, S. Blügel and P. Rüßmann, Phys. Rev. Mater., 2024, 8, 104201 CrossRef CAS.
- C.-W. Liu, Z. Wang, R. L. Qiu and X. P. Gao, Nanotechnology, 2020, 31, 192001 CrossRef CAS PubMed.
- F. Le Mardelé, J. Wyzula, I. Mohelsky, S. Nasrallah, M. Loh, S. Ben David, O. Toledano, D. Tolj, M. Novak and G. Eguchi, et al. , Phys. Rev. B, 2023, 107, L241101 CrossRef.
- B. Lv, H. Weng, B. Fu, X. P. Wang, H. Miao, J. Ma, P. Richard, X. Huang, L. Zhao and G. Chen, et al. , Phys. Rev. X, 2015, 5, 031013 Search PubMed.
- B.-Z. Tian, J. Chen, X.-P. Jiang, J. Tang, D.-L. Zhou, Q. Sun, L. Yang and Z.-G. Chen, ACS Appl. Mater. Interfaces, 2021, 13, 50057–50064 CrossRef CAS.
- Z. Li, E. Xu, Y. Losovyj, N. Li, A. Chen, B. Swartzentruber, N. Sinitsyn, J. Yoo, Q. Jia and S. Zhang, Nanoscale, 2017, 9, 13014–13024 RSC.
- Q. Qu, B. Liu, H. Liu, J. Liang, J. Wang, D. Pan and I. K. Sou, Nanoscale, 2021, 13, 18160–18172 RSC.
- S. Bhattacharyya, G. Akhgar, M. Gebert, J. Karel, M. T. Edmonds and M. S. Fuhrer, Adv. Mater., 2021, 33, 2007795 CrossRef CAS.
- R. Vidal, H. Bentmann, J. Facio, T. Heider, P. Kagerer, C. Fornari, T. Peixoto, T. Figgemeier, S. Jung and C. Cacho, et al. , Phys. Rev. Lett., 2021, 126, 176403 CrossRef CAS.
- R. C. Vidal, A. Zeugner, J. I. Facio, R. Ray, M. H. Haghighi, A. U. Wolter, L. T. C. Bohorquez, F. Caglieris, S. Moser and T. Figgemeier, et al. , Phys. Rev. X, 2019, 9, 041065 CAS.
- Q. Liu, C.-X. Liu, C. Xu, X.-L. Qi and S.-C. Zhang, Phys. Rev. Lett., 2009, 102, 156603 CrossRef PubMed.
- M. Li, C.-Z. Chang, L. Wu, J. Tao, W. Zhao, M. H. Chan, J. S. Moodera, J. Li and Y. Zhu, Phys. Rev. Lett., 2015, 114, 146802 CrossRef.
- A. Alfonsov, K. Mehlawat, A. Zeugner, A. Isaeva, B. Büchner and V. Kataev, Phys. Rev. B, 2021, 104, 195139 CrossRef CAS.
- X. Kou, W. Jiang, M. Lang, F. Xiu, L. He, Y. Wang, X. Yu, A. Fedorov, P. Zhang and K. Wang, J. Appl. Phys., 2012, 112, 063912 CrossRef.
- A. Grutter and Q. He, Phys. Rev. Mater., 2021, 5, 090301 CrossRef CAS.
- I. Costa, U. Mengui, E. Abramof, P. Rappl, D. Soares, S. de Castro and M. Peres, Phys. Rev. B, 2021, 104, 125203 CrossRef CAS.
- Y. Choi, N. Jo, K. Lee, J. Yoon, C. You and M. Jung, J. Appl. Phys., 2011, 109, 07E312 CrossRef.
- A. Gupta, A. Hillier, M. Telling and S. Srivastava, Nanotechnology, 2022, 33, 215701 CrossRef CAS.
- J. Zhang, C.-Z. Chang, P. Tang, Z. Zhang, X. Feng, K. Li, L.-L. Wang, X. Chen, C. Liu and W. Duan, et al. , Science, 2013, 339, 1582–1586 CrossRef CAS PubMed.
- D. Zhang, A. Richardella, D. W. Rench, S.-Y. Xu, A. Kandala, T. C. Flanagan, H. Beidenkopf, A. L. Yeats, B. B. Buckley and P. V. Klimov, et al. , Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 205127 CrossRef.
- M. M. Otrokov, I. I. Klimovskikh, H. Bentmann, D. Estyunin, A. Zeugner, Z. S. Aliev, S. Gaß, A. Wolter, A. Koroleva and A. M. Shikin, et al. , Nature, 2019, 576, 416–422 CrossRef CAS PubMed.
- A. M. Shikin, D. Estyunin, I. I. Klimovskikh, S. Filnov, E. Schwier, S. Kumar, K. Miyamoto, T. Okuda, A. Kimura and K. Kuroda, et al. , Sci. Rep., 2020, 10, 13226 CrossRef CAS PubMed.
- S. Harrison, L. J. Collins-McIntyre, P. Schönherr, A. Vailionis, V. Srot, P. A. van Aken, A. Kellock, A. Pushp, S. S. Parkin and J. Harris, et al. , Sci. Rep., 2015, 5, 15767 CrossRef CAS.
- T. Zhang, W. Pan, S. Ning, N. Qi, Z. Chen, X. Su and X. Tang, Adv. Funct. Mater., 2023, 33, 2213761 CrossRef CAS.
- N. Wang, D. West, J. Liu, J. Li, Q. Yan, B.-L. Gu, S. Zhang and W. Duan, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 045142 CrossRef.
- N. Mishra and G. Makov, J. Alloys Compd., 2024, 986, 174157 CrossRef CAS.
- S. Acharya, J. Pandey and A. Soni, Appl. Phys. Lett., 2016, 109, 133904 CrossRef.
- S. Singh, H. Afzal, V. Kaushik, S. Kumar, P. Behera and R. Venkatesh, Langmuir, 2022, 38, 3122–3128 CrossRef CAS.
- D. Feng, Z.-H. Ge, Y.-X. Chen, J. Li and J. He, Nanotechnology, 2017, 28, 455707 CrossRef.
- J. S. Dyck, P. Hájek, P. Lošt’ák and C. Uher, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 115212 CrossRef.
- J. Dyck, Č. Drašar, P. Lošt’ák and C. Uher, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 115214 CrossRef.
- A. Alfonsov, J. Facio, K. Mehlawat, A. Moghaddam, R. Ray, A. Zeugner, M. Richter, J. van den Brink, A. Isaeva and B. Büchner, et al. , Phys. Rev. B, 2021, 103, L180403 CrossRef CAS.
- A. Alfonsov, K. Mehlawat, A. Zeugner, A. Isaeva, B. Büchner and V. Kataev, Phys. Rev. B, 2021, 104, 195139 CrossRef CAS.
- A. Kaminski and S. D. Sarma, Phys. Rev. Lett., 2002, 88, 247202 CrossRef CAS PubMed.
- S. D. Sarma, E. Hwang and A. Kaminski, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 155201 CrossRef.
- P. Wolff, R. Bhatt and A. Durst, J. Appl. Phys., 1996, 79, 5196–5198 CrossRef CAS.
- M. Heming and G. Lehmann, Z. Naturforsch., A, 1983, 38, 149–153 Search PubMed.
- D. Vaknin, D. Davidov, V. Zevin and H. Selig, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 35, 6423–6431 CrossRef CAS PubMed.
- J. König, H.-H. Lin and A. H. MacDonald, Phys. Rev. Lett., 2000, 84, 5628 CrossRef.
- M. Berciu and R. Bhatt, Phys. Rev. Lett., 2001, 87, 107203 CrossRef CAS PubMed.
- J.-J. Zhu, D.-X. Yao, S.-C. Zhang and K. Chang, Phys. Rev. Lett., 2011, 106, 097201 CrossRef PubMed.
- G. C. Papaefthymiou, Nano Today, 2009, 4, 438–447 CrossRef CAS.
- A. Wolos, A. Drabinska, J. Borysiuk, K. Sobczak, M. Kaminska, A. Hruban, S. G. Strzelecka, A. Materna, M. Piersa and M. Romaniec, et al. , J. Magn. Magn. Mater., 2016, 419, 301–308 CrossRef CAS.
- A. Wolos, S. Szyszko, A. Drabinska, M. Kaminska, S. Strzelecka, A. Hruban, A. Materna and M. Piersa, Phys. Rev. Lett., 2012, 109, 247604 CrossRef CAS PubMed.
- H. Steinberg, J.-B. Laloë, V. Fatemi, J. S. Moodera and P. Jarillo-Herrero, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 233101 CrossRef.
- A. Drabińska, M. Kamińska, A. Wołoś, W. Strupinski, A. Wysmołek, W. Bardyszewski, R. Bożek and J. M. Baranowski, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 165413 CrossRef.
- V. L. Nguyen, D. C. Nguyen, H. Hirata, M. Ohtaki, T. Hayakawa and M. Nogami, Adv. Nat. Sci.: Nanosci. Nanotechnol., 2010, 1, 035012 Search PubMed.
- S. K. Cgandomani, B. Khoshnevisan and R. Yousefi, J. Lumin., 2018, 203, 481–485 CrossRef.
- R. Walstedt and A. Narath, Phys. Rev. B, 1972, 6, 4118 CrossRef CAS.
- H.-T. He, G. Wang, T. Zhang, I.-K. Sou, G. K. Wong, J.-N. Wang, H.-Z. Lu, S.-Q. Shen and F.-C. Zhang, Phys. Rev. Lett., 2011, 106, 166805 CrossRef PubMed.
- A. Wolos and A. Drabinska, J. Cryst. Grow., 2014, 401, 314–318 CrossRef CAS.
- M. Sharma, D. Mishra and J. Kumar, Phys. Rev. B, 2019, 100, 045151 CrossRef CAS.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni and I. Dabo, et al. , J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- Y. Xie, Q. He, J. Guo, X. Li, J. Wei, Y. Zhang, C. Gu, P. Lu and X. Shen, Adv. Opt. Mater., 2024, 12, 2400632 CrossRef CAS.
- Y. Su, C. Ding, Y. Yao, R. Fu, M. Xue, X. Liu, J. Lin, F. Wang, X. Zhan and Z. Wang, Nanotechnology, 2023, 34, 505206 CrossRef CAS PubMed.
- D. Hull and D. J. Bacon, Introduction to dislocations, Elsevier, 2011, vol. 37 Search PubMed.
- V. Varadaraajan, PhD thesis, The University of Michigan, 2015.
- S. Ahmad, A. Singh, S. Bhattacharya, M. Navaneethan, R. Basu, R. Bhatt, P. Sarkar, K. Meshram, A. Debnath and K. Muthe, et al. , ACS Appl. Energy Mater., 2020, 3, 8882–8891 CrossRef CAS.
- H.-S. Yoon, J. Lee, J. Park, J.-W. Oh and Y.-C. Kang, Phys. Status Solidi A, 2022, 219, 2200059 CrossRef CAS.
- M. A. Stranick and A. Moskwa, Surf. Sci. Spectra, 1993, 2, 50–54 CrossRef CAS.
- A. Saini, K. Dhanwant, K. Dewangan, R. Thirumoorthi, A. Jaiswal, I. Bahadur, F. Mohammad and A. A. Soleiman, Results Mater., 2023, 18, 100397 CrossRef CAS.
- R. Zimmermann, R. Claessen, F. Reinert, P. Steiner and S. Hüfner, J. Phys.: Condens. Matter, 1998, 10, 5697 CrossRef CAS.
- S. Sugai, K. Murase and H. Kawamura, Solid State Commun., 1977, 23, 127–129 CrossRef CAS.
- S. Khosravi Ghandomani, B. Khoshnevisan and R. Yousefi, J. Mater. Sci.: Mater. Electron., 2018, 29, 18989–18996 CrossRef CAS.
- P. Makuła, M. Pacia and W. Macyk, How to correctly determine the band gap energy of modified semiconductor photocatalysts based on UV-Vis spectra, 2018 Search PubMed.
- D. Mosca, J. Varalda and C. Dartora, Phys. Rev. B, 2023, 108, 134410 CrossRef CAS.
- M. Schlaak and A. Weiss, Z. Naturforsch., A, 1972, 27, 1624–1633 CAS.
- V. Fernandes, R. Mossanek, P. Schio, J. Klein, A. De Oliveira, W. Ortiz, N. Mattoso, J. Varalda, W. Schreiner and M. Abbate, et al. , Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 035202 CrossRef.
- Z. Ma, C. Wang, Y. Chen, L. Li, S. Li, J. Wang and H. Zhao, Mater. Today Phys., 2021, 17, 100350 CrossRef CAS.
- C. Ko, Z. Yang and S. Ramanathan, ACS Appl. Mater. Interfaces, 2011, 3, 3396–3401 CrossRef CAS.
- D. I. Khomskii, Transition metal compounds, Cambridge University Press, 2014 Search PubMed.
- J. Vithayathil, D. MacLaughlin, E. Koster, D. L. Williams and E. Bucher, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 4705 CrossRef CAS.
- J. Kreissl, W. Gehlhoff, P. Omling and P. Emanuelsson, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 42, 1731 CrossRef CAS PubMed.
- V. Ivanshin, V. Yushankhai, J. Sichelschmidt, D. Zakharov, E. Kaul and C. Geibel, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 064404 CrossRef.
- A. Nakajima, Talanta, 2002, 57, 537–544 CrossRef CAS PubMed.
- A. Nakajima, Talanta, 2002, 57, 537–544 CrossRef CAS PubMed.
- H.-Z. Lu, J. Shi and S.-Q. Shen, Phys. Rev. Lett., 2011, 107, 076801 CrossRef PubMed.
- N. Berchenko, R. Vitchev, M. Trzyna, R. Wojnarowska-Nowak, A. Szczerbakow, A. Badyla, J. Cebulski and T. Story, Appl. Surf. Sci., 2018, 452, 134–140 CrossRef CAS.
- P. Ngabonziza, R. Heimbuch, N. De Jong, R. Klaassen, M. Stehno, M. Snelder, A. Solmaz, S. Ramankutty, E. Frantzeskakis and E. Van Heumen, et al. , Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 035405 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp00962f |
| This journal is © the Owner Societies 2025 |