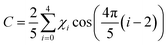The challenging conformer assignment of proline methyl ester from rotational spectroscopy

Abstract

The conformational structures of proline methyl ester (PrOMe) were modeled using CREST and further optimized using ωB97XD and MP2 methods with the 6-311++G(d,p) and aug-cc-pVDZ basis sets. Among the seven lowest energy conformers, two unique conformers, C^γ-exo/C^δ-endo and C^γ-endo, were found to be very close to the minimum energy. A rotational spectrum consisting of 51 rotational transitions was recorded for PrOMe using a cavity-based Fourier-transform microwave spectrometer in the range 9–20 GHz. The rotational transitions, split into resolved ¹⁴N-nuclear quadrupole hyperfine components for the A- and E-methyl-internal-rotation tunneling states, were fit using XIAM: A = 3678.4360(7) MHz, B = 1037.5616(3) MHz, and C = 944.2045(3) MHz, and the barrier to methyl torsion was found to be 393.54(9) cm⁻¹. Comparison of model and spectroscopic moments of inertia is insufficient to conclusively assign the conformational structure. Analysis of second moments of inertia, dipole moment projections, and nuclear quadrupole hyperfine constants provides sufficient additional evidence to determine that the rotational spectrum is from a structure with an intramolecular hydrogen bond from the imino hydrogen to the carbonyl oxygen and with C^γendo.

---

Introduction

The conformational behavior of amino acids and their derivatives is important to better understand the role of structure in polypeptide and protein function. Rotational spectroscopic investigations of the structures of amino acids have been reported previously.^1–9 Conformational analysis of the amino acid glycine – the smallest amino acid – found two energetically different structures.^1–6 The higher energy conformer, assigned from the rotational spectrum first because of its larger dipole moment, has a trans-COOH arrangement with an intramolecular hydrogen bond from the carboxylic acid to the amino nitrogen.^1,2 The lowest energy conformation – observed later – has a cis-COOH arrangement with bifurcated intramolecular hydrogen bonds from the amine to the carbonyl oxygen.³

Laser-ablation Fourier-transform microwave spectroscopy has been employed for investigations of larger amino acids including proline^7,8 and valine.⁹ Rotational spectra of the two lowest energy conformers of proline were reported first.⁷ The two lowest energy conformers of proline have the trans-COOH configuration with an intramolecular hydrogen bond to the imino nitrogen. The conformers are distinguished by different ring puckering: C^γ-endo (lowest energy) and C^γ-exo (+3.2 kJ mol⁻¹). Endo refers to puckering toward the same side of the ring as the carboxylic acid. Proline conformers with the cis-COOH arrangement and an intramolecular hydrogen bond from the imino hydrogen to the carbonyl oxygen were calculated to be higher in energy (8.9 kJ mol⁻¹ and 9.4 kJ mol⁻¹); spectra from these conformers were found and reported later.⁸ The higher-energy conformers have C^γ-exo and C^γ-endo ring puckering, respectively. Two conformations of neutral valine were identified from rotational spectra. Both conformers have the same orientation of the isopropyl group (χ₁ = H^β–C^β–C^α–H^α ≈ −60°; χ₁ is standard notation for the first torsional angle of an amino acid side chain) for each of the two backbone conformations observed for glycine.⁹

Derivatization of the amino acid backbone structure affects the intramolecular hydrogen bonding networks and may also influence the relative energies for side chain orientations and conformational preferences. The carboxylic acid of the amino acid is replaced by an amide in prolinamide and valinamide, and only a single conformer, stabilized by an intramolecular hydrogen bond from the amide to the amino nitrogen, was observed in the rotational spectrum of each species.^10,11 The isopropyl side group is oriented with χ₁ = −62° in valinamide.¹¹ However, we recently reported the rotational spectra of two conformers of valine methyl ester.¹² Both conformers are stabilized by a network of bifurcated hydrogen bonds from the amine to the carbonyl oxygen, similar to the lowest energy conformation of glycine, with two different orientations of the isopropyl side chain: χ₁ = −64.0° and χ₁ = 173.6°. Interestingly, the conformer with χ₁ = 173.6° had not been previously detected in the rotational spectra of neutral valine or valinamide.

In the present investigation we report the rotational spectra and conformational structures of proline methyl ester (PrOMe); the structure of PrOMe is compared to neutral proline and prolinamide in Fig. 1. The pyrrolidine ring adds significant complexity to the possible conformational structures. To relieve torsional strain, the five-membered ring adopts envelope or twist (half-chair) structures, with the puckers either endo or exo at different ring positions. While the ester blocks acid-to-imino-nitrogen hydrogen bonding, PrOMe conformers may be stabilized by hydrogen bonds from the imino hydrogen to the carbonyl or ester oxygens. The intramolecular hydrogen bonding in PrOMe may also influence the pyrrolidine ring puckering conformations compared to prolinamide and neutral proline.

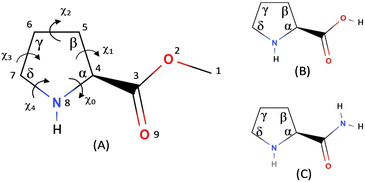Fig. 1 Numbering scheme for (A) PrOMe and comparison to the structures of (B) neutral proline and (C) prolinamide.

Computational and experimental methods

Theoretical modeling of PrOMe structures was initiated using CREST¹³ for a comprehensive exploration of conformational minima. The GFN2-xTB semi-empirical method was used with the tight-binding criterion¹⁴ to generate starting structures for subsequent DFT and ab initio optimizations. The fourteen lowest energy semi-empirical (<15 kJ mol⁻¹) structures were then optimized using both ωB97XD¹⁵ and MP2¹⁶ methods with the 6-311++G(d,p) basis set¹⁷ in GAUSSIAN 16¹⁸ on the Owens cluster at the Ohio Supercomputer Center. Each set of optimizations converged to seven unique conformational structures, which were further optimized using the aug-cc-pVDZ basis set¹⁹ for each method. Frequency calculations were used to ensure optimization to minima.

L-Proline methyl ester hydrochloride (98% pure) was purchased from Sigma-Aldrich. Free L-proline methyl ester was isolated following a previously reported procedure.²⁰ In an oven-dried 100 mL round bottom flask, L-proline methyl ester hydrogen chloride salt (10.0 g, 60.6 mmol, 1 eq.) was mixed with chloroform (45 mL) under argon gas. A solution of triethylamine (8.44 mL, 60.6 mmol, 1 eq.) in chloroform was added dropwise. The reaction mixture was stirred for 4 hours at room temperature and then heated to reflux for an hour. The mixture was then cooled to room temperature and concentrated to obtain a white solid. The obtained crude was diluted with diethyl ether, filtered, and washed with diethyl ether. The filtrate was concentrated to obtain L-proline methyl ester as a free amino ester (7.05 g, 90%, yellow oil). ¹H NMR (400 MHz, CDCl₃) δ 3.74 (dd, J = 8.7, 5.7 Hz, 1H), 3.69 (s, 3H), 3.04 (dt, J = 10.2, 6.7 Hz, 1H), 2.93–2.82 (m, 1H), 2.45 (s, 1H), 2.17–2.03 (m, 1H), 1.86–1.68 (m, 3H). Characterization data are consistent with the reported literature.²¹

A high-resolution mini cavity-based Fourier-transform microwave spectrometer was used to record the rotational spectrum of proline methyl ester in the 9–19 GHz frequency range. The detailed description of the instrument has been provided elsewhere.²² Approximately 0.5 mL of free PrOMe was placed in the reservoir nozzle,²³ heated to 85 °C using a Watlow band heater and an Omega CN8201 temperature controller, and carried into the Fabry–Perot resonant cavity with Argon gas at 1 atm backing pressure. The coaxial expansion into the resonator cavity results in a ca. 60 kHz Doppler splitting of the observed transitions. The Nyquist digital frequency resolution of the spectrometer is 2.5 kHz, but experimental uncertainties depend on actual linewidths and line shapes, which may be distorted by overlapping transitions. We estimate that the experimental line uncertainties are 7–10 kHz, with some congested transitions having uncertainties approaching 20 kHz. A portion of the microwave spectrum of PrOMe, with resolved nuclear quadrupole hyperfine and tunneling splittings, is shown in Fig. 2.

Fig. 2 Portion of the microwave spectrum of PrOMe showing (A) and (E) tunneling state components and nuclear quadrupole hyperfine components of the 5₁₅–4₀₄ rotational transition with 25 free induction decays averaged.

Spectral fitting of rotational and nuclear quadrupole hyperfine transitions from both the A and E methyl internal rotation states was performed using XIAM.²⁴ This fitting program is based on the combined-axis method²⁵ and can be used to obtain the rotational constants, principal nuclear quadrupole coupling constants (χ_aa, χ_bb, and χ_cc), barrier to methyl internal rotation (V₃), and the angles between the internal rotation axis and the principal inertial axes. The rotor moment of inertia was fixed to 3.2 amu Ų.

Results

Density functional theory (ωB97XD) and ab initio (MP2) calculations each identified seven low-energy conformational structures from the fourteen starting structures. Three low-energy structures optimized at the ωB97XD/6-311++G(d,p) level are shown in Fig. 3. Principal results from each of the computational methods are summarized in Table 1 for conformers 1, 2, and 5. A more detailed comparison, including relative energies, rotational constants, dipole moment components, and the diagonal elements of the nuclear quadrupole coupling tensor, is given in the ESI† Tables S1–S4 for the seven lowest-energy conformers. Principal-axis atomic coordinates for each of the model conformers are also given in the ESI† (Tables S5–S30). The MP2/aug-cc-pVDZ calculation of conformer 3 and ωB97XD/aug-cc-pVDZ calculation for conformer 4 did not converge and are not included those tables.

Fig. 3 Optimized structures and relative energies of model conformers of PrOMe at the ωB97XD/6-311++G(d,p) level. The pseudorotational phase angle (P) and amplitude (χ_max) are described in the Discussion section.

Table 1 Summary of the principal results for three model conformers of proline methyl ester

	A/MHz	B/MHz	C/MHz	ΔIrms/amu Å^2	χ aa /MHz	χ bb /MHz	χ cc /MHz
Conformer 1 C^γexo/C^δendo
ωB97XD/6-311++G(d,p)	3761.186	1029.830	895.284	17.11	1.018	2.4856	−3.5036
MP2/6-311++G(d,p)	3685.038	1042.925	912.522	10.83	0.4395	2.2466	−2.6861
ωB97XD/aug-cc-pVDZ	3728.661	1031.110	895.682	16.87	0.8216	2.3305	−3.1521
MP2/aug-cc-pVDZ	3580.901	1048.502	918.755	9.30	0.0224	1.9374	−1.9598
Conformer 2 C^γendo
ωB97XD/6-311++G(d,p)	3672.991	1044.732	946.416	2.06	2.4440	1.9160	−4.3600
MP2/6-311++G(d,p)	3779.396	1018.287	937.272	6.17	2.6905	1.4068	−4.0973
ωB97XD/aug-cc-pVDZ	3731.363	1026.436	931.582	5.30	2.4846	1.5128	−3.9974
MP2/aug-cc-pVDZ	3711.213	1017.340	936.800	6.14	2.2799	1.3183	−3.5982
Conformer 5 C^γendo/C^δexo
ωB97XD/6-311++G(d,p)	3694.479	1036.012	920.162	8.09	0.9834	2.6446	−3.6280
MP2/6-311++G(d,p)	3682.824	1038.214	929.014	5.06	0.8920	2.3553	−3.2473
ωB97XD/aug-cc-pVDZ	3693.649	1030.293	907.976	12.49	1.0297	2.5152	−3.5448
MP2/aug-cc-pVDZ	3650.192	1029.363	920.318	8.35	0.7767	2.1055	−2.8822

---

A rotational spectrum consisting of 39 R-branch (16 a-type, 18 b-type, and 5 c-type) and 12 Q-branch transitions was assigned for PrOMe. Each rotational transition was split into A- and E-state tunneling components from internal rotation of the methyl group and further split into nuclear quadrupole hyperfine components. The hyperfine components of several rotational transitions could not be resolved as they overlap each other; these congested transitions were not included in the fit. The frequencies of all resolved hyperfine components for PrOMe are available in the ESI,† Table S31. 144 A-state hyperfine components and 149 E-state components were assigned and fit using XIAM. The fit has an RMS error of 7.4 kHz, and the best-fit values for the spectroscopic constants and tunneling parameters are given in Table 2.

Table 2 Experimentally determined spectroscopic parameters for PrOMe

Parameter	XIAM
a Polar-coordinate angles describing the orientation of the internal rotor axis. b Number of rotational transitions in the fit. c Root-mean-square deviation of the fit.
A/MHz	3678.4360(7)
B/MHz	1037.5616(3)
C/MHz	944.2045(3)
Δ J /kHz	0.423(15)
Δ JK /kHz	−2.889(7)
Δ k /kHz	11.41(6)
δ J /kHz	0.0367(8)
δ K /kHz	0.97(9)
P aa /amu Å^2	442.4684(3)
P bb /amu Å^2	92.7747(3)
P cc /amu Å^2	44.6149(3)
χ aa /MHz	2.302(6)
χ bb /MHz	1.593(5)
χ cc /MHz	−3.894(10)
V 3/cm^−1	393.54(9)
ε /°	299.6(11)
δ /°	28.40(10)
∠(i, a)/°	28.4(11)
∠(i, b)/°	76.4(5)
∠(i, c)/°	114.4(4)
N	51
RMS^c/kHz	7.4

---

Extensive searches for transitions arising from the ¹³C isotopologues were conducted, but no isotopologue spectra could be identified or assigned. A few very weak transitions were found in these searches, but these transitions were not consistent with the pattern expected for the six different ¹³C species. Instead these few remaining unassigned transitions likely arise from a high-energy (low population) conformer of the most abundant isotopic species.

Discussion

Proline methyl ester presents a challenging system for conformational identification from the rotational spectrum of a single isotopologue. The different intramolecular hydrogen bonding motifs and the many different orientations of ring puckering create numerous plausible conformer models. The CREST program identified 14 structures with relative energy < 15 kJ mol⁻¹; further optimization using ωB97XD and MP2 methods with the 6-311++G(d,p) and aug-cc-pVDZ basis sets converged to 7 unique conformational structures within 11 kJ mol⁻¹ of the lowest energy structure (Tables S1–S4, ESI†). Conformers 1 and 2 are consistently calculated to be very close in energy, and the MP2/aug-cc-pVDZ calculation finds that conformer 2 is 0.29 kJ mol⁻¹ lower in energy than conformer 1. These two structures have an intramolecular hydrogen bond from the imino nitrogen to the carbonyl oxygen, but with different ring puckering structures.

Nominal descriptions of puckering structure are given for each conformer in Table 1 and Tables S1–S4 (ESI†). Pseudorotational coordinates were developed by Kilpatrick et al.²⁶ to conveniently describe the structure of cyclopentane. The phase angle (P) and amplitude (χ_max) provide a useful description of puckering and can be determined from the endocyclic torsion angles (χ₀ − χ₄; Fig. 1A) of the five-membered ring. The pseudorotational concept has been applied to pyrrolidine rings such as found in proline.²⁷ The torsional angles and origin of the pseudorotational cycle for PrOMe were defined as described by Westhof and Sundaralingam.²⁸ The pseudorotational coordinates can be calculated using²⁹

where the constants C and S are calculated from the endocyclic torsion angles using
and
The pseudorotational coordinates are given in Tables S1–S4 (ESI†) for each model structure and level of theory. Note that the values of P reported in a comprehensive ab initio investigation of neutral proline conformers³⁰ are 72° larger than the P values reported here because of the choice for the origin of the pseudorotational cycle.

The pseudorotational coordinates show small variations in puckering for each model among the different computational approaches. These variations lead to ranges of up to 180 MHz for the A rotational constants of model conformers 1 and 2 among the different computational approaches (Table 1). The B and C rotational constants for these conformers are generally within a 25 MHz range. The root mean square difference between the model and experimental moments of inertia, (ΔI)_rms where ΔI = I_x(obs.) − I_x(model) and I_x is the moment of inertia about the a, b, and c axes, is often used to identify the structure that best reproduces the spectroscopically determined moments of inertia. The (ΔI)_rms values (Table 1) for conformer 2 show consistently better agreement with experiment than those for conformer 1. Given the variation in the calculated rotational constants for each conformer model, (ΔI)_rms values alone are insufficient for a conclusive assignment of the spectrum to conformer 2. Moreover, the (ΔI)_rms values for conformer 5 are also small, indicating that that this higher energy conformer may also be consistent with the spectroscopic rotational constants.

The second moments of inertia, P_aa, P_bb, and P_cc often provide a more definitive assignment of the structure to the spectrum. The second moment along the a-axis was calculated from the model structures using

where the m_i are the atomic masses, a_i are the atomic coordinates along the a-inertial axis, and I_a, I_b, and I_c are the principal moments of inertia. There are similar expressions for P_bb and P_cc.³¹ The values of the second moments for the different computational models of each structure are given in Tables S1–S4 (ESI†), and the experimental values, calculated using the second equality, are given in Table 2. For ease of comparison, root mean squares (RMS) of the differences between model and experimental second moments were calculated; these are given in Table S32 (ESI†) for all conformers. These RMS differences range from 8.9–14.8 amu Ų for conformer 1, from 1.6–5.5 amu Ų for conformer 2, and from 4.5–10.4 amu Ų for conformer 5. Comparison of the P_bb and P_cc second moment components reveals substantial differences among the models. The experimentally determined value for P_bb is 92.7747(3) amu Ų. The ranges of P_bb values calculated from theoretical model structures are 103.2–104.8 amu Ų for conformer 1, 88.3–93.9 amu Ų for conformer 2, and 97.2–101.5 amu Ų for conformer 5. Likewise, the experimental value of P_cc is 44.6149(3) amu Ų, and the ranges of P_cc values calculated from theoretical model structures are 30.3–36.5 amu Ų for conformer 1, 42.7–46.7 amu Ų for conformer 2, and 35.4–40.1 amu Ų for conformer 5. Model conformer 2 again matches the experimental constants best, and model 5 remains in plausible agreement. Conformer models 1, 3, 4, 6, and 7 are inconsistent with the second moment data.

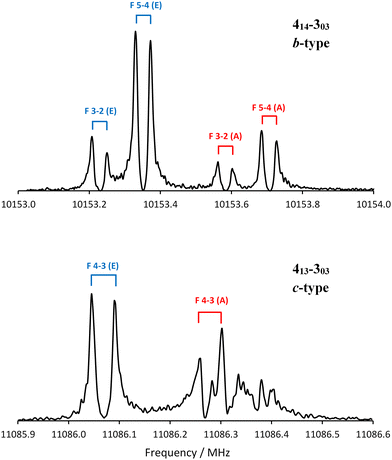
The electronic properties of the models may also help identify the conformer detected spectroscopically. All models of conformer 2 have a large projection of the dipole moment onto the b-inertial axis (μ_b), with μ_b > μ_a > μ_c (Tables S1–S4, ESI†). Models of conformer 5 predict that μ_b and μ_c will be almost equally large. The relative intensity of two different types of rotational transitions originating from the same rotational state depends in large part on the ratio of the projections of the dipole moments, so the b-type transitions associated with conformer 2 should be much more intense than the c-type transitions. For conformer 5, the b- and c-type transitions should have similar intensities. Fig. 4 compares a portion of the b-type transition 4₁₄–3₀₃ acquired by averaging 120 free induction decays to a portion of the c-type transition 4₁₃–3₀₃ acquired by averaging 13 000 free induction decays. Fig. 4 demonstrates that the b-type transitions are approximately 10 times more intense than the c-type transitions, consistent with conformer 2.

Fig. 4 Portions of the microwave spectrum of PrOMe showing a b-type transition (120 free induction decays averaged) and a c-type transition (13 000) free induction decays averaged. The weak features near 11 086.35 MHz remain unassigned.

Alonso et al.⁸ demonstrated that the experimental nuclear quadrupole coupling constants, obtained by fitting resolved nuclear quadrupole hyperfine components of rotational transitions, may be useful for conformational assignments. The calculated values of the quadrupole coupling constants for the different conformer models are given in Table 1 and Tables S1–S4 (ESI†), and the spectroscopically determined values are given in Table 2. Table S33 (ESI†) gives the root mean squares of the differences between model and experimental nuclear quadrupole coupling constants for each of the PrOMe conformers. The RMS differences range from 0.93–1.74 MHz for conformer 1, from 0.13–0.34 MHz for conformer 2, and from 0.93–1.1 MHz for conformer 5. The value of the χ_aa nuclear quadrupole coupling constants provides the clearest differentiation among the model conformers. Experimentally, χ_aa = 2.302(6) MHz; the ranges of χ_aa calculated for the model structures are 0.02–1.02 MHz for conformer 1, 2.28–2.69 MHz for conformer 2, and 0.78–1.03 MHz for conformer 5. The calculated dipole moment projections and nuclear quadrupole coupling constants conclusively identify the spectrum as arising from conformer 2.

Structural information may also be deduced from the rotor-axis angles calculated from fitting the methyl internal rotation splittings. The angles that the methyl rotor axis makes with the a-, b-, and c-inertial axes (∠(i, x) where x = a, b, or c) were calculated from the XIAM fitting and are given in Table 2. Rotor axis angles were also calculated for each of the model conformers, and these values are given in Tables S1–S4 (ESI†). The rotor-axis angles are very similar for most conformers, and the uncertainties of the rotor-axis angle values obtained from XIAM fitting are 0.5–1°. The comparison of model and experimental values is again made with root mean square differences, and these are given in Table S34 (ESI†) for each model conformer. The RMS differences are very small, 1–3 degrees, for most conformers, and the rotor axis angles do not provide any additional evidence supporting any of the conformer models for PrOMe.

The V₃ barrier to internal rotation of the ester methyl group was obtained from fitting the A- and E-state transitions using XIAM. The best fit value for the methyl V₃ in PrOMe is 393.54(9) cm⁻¹, which is very close to the experimentally determined barriers for related methyl ester systems. The rotational spectrum of glycine methyl ester was assigned to a single conformer,³² and the methyl V₃ barrier was found to be 411.66(10) cm⁻¹. The methyl ester barrier was found to be 401.64(19) and 409.74(16) cm⁻¹ for the two conformers of valine methyl ester.¹² The two different methyl groups in N-acetyl alanine methyl ester cause a complicated pattern of tunneling pairs (AA, AE, and EA); the barriers for the methoxy and acetyl methyl groups were found to be 396.46(7) cm⁻¹ and 64.96(4) cm⁻¹, respectively.³³

The lowest energy model (ωB97XD/6-311++G(d,p)) conformers of PrOMe, 1 and 2, are stabilized by similar intramolecular hydrogen bonds to the carbonyl oxygen. The imino NH⋯O⁹ distance is 2.37 Å in conformer 1 and 2.24 Å in conformer 2. Despite the close interaction distances, these hydrogen bonds are expected to be weak because the N⋯H⋯O⁹ angles are 105° and 112° respectively. There are additional close interactions to the ester oxygen (C^βH⋯O²) in both model conformers. For conformer 1 the C^βH⋯O² distances are 2.83 and 3.19 Å, but for conformer 2 there is only one 2.67-Å interaction. Model conformers with intramolecular hydrogen bonds to the ester oxygen (NH⋯O²) were all significantly higher in energy, as was also found by Braga et al.³⁴ both computationally (ωB97XD and MP2 with aug-cc-pVTZ) and by analysis of ³J_HH NMR coupling constants in solvents of varying polarity. The relative energies of the conformers are expected to depend on the aggregate of all H-bonding and other weak interactions.

The theoretical methods vary significantly in their predictions of spectroscopic parameters. The ωB97XD/6-311++G(d,p) model is in best agreement with the experimental moments of inertia and second moments, but the ωB97XD/aug-cc-pVDZ method modeled the nuclear quadrupole coupling constants better. Three theoretical methods predict conformer 1 to be slightly more stable, but we only observed one rotational spectrum that could be assigned to a single conformation: conformer 2. We hypothesize that conformer 2 is in fact slightly lower energy than 1, consistent with the MP2/aug-cc-pVDZ model, and that the argon expansion significantly relaxes population from higher energy conformations through interconversion barriers less than 5 kJ mol⁻¹.^35,36 The barriers to interconvert puckering conformations of pyrrolidine were calculated to be 2–4 kJ mol⁻¹.^37–39 Experiments conducted using neon are likely to exhibit less conformational relaxation.

The C^γ-endo structure of PrOMe (ωB97XD/6-311++G(d,p): P = 192°; χ_max = 39°), conformer 2, that we report here compares well with puckering conformations in similar systems. Czinki et al.³⁰ reported a C^γ-endo structure of neutral proline as the lowest energy using several high-level computational methods; this structure has P = 198° (reported as P = −90° with their coordinate origin) and χ_max = 39°. The C^γ-exo (P = 16°) conformer of neutral proline was calculated to be 1–3 kJ mol⁻¹ higher in energy. The initial report of the rotational spectra of neutral proline in neon characterized two conformers – C^γ-endo and C^γ-exo, both with the carboxylic acid donating a hydrogen bond to the imino nitrogen; the C^γ-endo conformer was associated with stronger transitions.⁷ Likewise, the rotational spectra of 3 isotopologues of prolinamide in argon were best described by a C^β-exo/C^γ-endo pyrrolidine ring structure with P = 185° and χ_max = 33°.¹⁰ While the energy ordering of the puckering conformers may depend on second-order effects such as interactions with the backbone moieties, the spectral assignments for these species indicate a gas-phase ring puckering preference near P = 190° and χ_max = 35–40° for prolyl systems.

Conclusions

Fifty-one rotational transitions have been recorded and assigned for PrOMe. The nuclear quadrupole hyperfine and A/E methyl-internal-rotation state splittings were resolved and fit with a 7.4 kHz RMS error. Density functional and ab initio computational methods were used to model the low energy conformational structures of PrOMe. Conformer models 2 and 5 were most consistent with the experimentally determined moments of inertia, but the conformer 2 models have much better agreement with the observed nuclear quadrupole coupling constants and second moments of inertia. Moreover, conformer 2 is consistent with the observation of a strong b-type rotational spectrum with weaker a- and c-type transitions. Conformer 2 is characterized by an intramolecular hydrogen bond from the imino hydrogen to the carbonyl oxygen and C^γ-endo pyrrolidine ring puckering. This ring structure has pseudorotational coordinates P = 192° and χ_max = 39° and is similar to ring puckering structures found for neutral proline and prolinamide.

Author contributions

Dinesh Marasinghe: investigation, data curation, formal analysis, writing – original draft. Michael J. Carrillo: investigation, data curation, formal analysis. Dakota Z. Smallridge: investigation. Kaitlyn E. Butts: investigation. Bijaya Bagale: investigation. Michael J. Tubergen: conceptualization, formal analysis, supervision, writing – review & editing.

Data availability

The data supporting this article have been included in the ESI.†

Conflicts of interest

The authors have no conflicts to declare.

Acknowledgements

Kaitlyn E. Butts gratefully acknowledges support from the NSF-REU program under Grant No. 2050873. The Ohio Supercomputer Center⁴⁰ is acknowledged for a grant of resources.

Notes and references

1. R. D. Brown, P. D. Godfrey, J. W. V. Storey and M. P. Bassez, J. Chem. Soc., Chem. Commun., 1978, 547–548,  10.1039/C39780000547.
2. R. D. Suenram and F. J. Lovas, J. Mol. Spectrosc., 1978, 72, 372–382,  DOI:10.1016/0022-2852(78)90137-6.
3. R. D. Suenram and F. J. Lovas, J. Am. Chem. Soc., 1980, 102, 7180–7184,  DOI:10.1021/ja00544a002.
4. P. D. Godfrey and R. D. Brown, J. Am. Chem. Soc., 1995, 117, 2019–2023,  DOI:10.1021/ja00112a015.
5. S. J. McGlone, P. S. Elmes, R. D. Brown and P. D. Godfrey, J. Mol. Struct., 1999, 485–486, 225–238,  DOI:10.1016/S0022-2860(99)00181-7.
6. F. J. Lovas, Y. Kawashima, J.-U. Grabow, R. D. Suenram, G. T. Fraser and E. Hirota, Astrophys. J., 1995, 455, 201–204,  DOI:10.1086/309844.
7. A. Lesarri, S. Mata, E. J. Cocinero, S. Blanco, J. C. López and J. L. Alonso, Angew. Chem., Int. Ed., 2002, 41, 4673–4676,  DOI:10.1002/anie.200290012.
8. S. Mata, V. Vaquero, C. Cabezas, I. Peña, C. Pérez, J. C. López and J. L. Alonso, Phys. Chem. Chem. Phys., 2009, 11, 4141–4144,  10.1039/B904633J.
9. A. Lesarri, E. J. Cocinero, J. C. López and J. L. Alonso, Angew. Chem., Int. Ed., 2004, 43, 605–610,  DOI:10.1002/anie.200352543.
10. K. A. Kuhls, C. A. Centrone and M. J. Tubergen, J. Am. Chem. Soc., 1998, 120, 10194–10198,  DOI:10.1021/ja981775z.
11. R. J. Lavrich, C. R. Torok and M. J. Tubergen, J. Phys. Chem. A, 2002, 106, 8013–8018,  DOI:10.1021/jp020663y.
12. D. Marasinghe, R. M. Gurusinghe and M. J. Tubergen, J. Phys. Chem. A, 2024, 128, 3266–3272,  DOI:10.1021/acs.jpca.4c00388.
13. P. Pracht, F. Bohle and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192,  10.1039/C9CP06869D.
14. S. Grimme, C. Bannwarth and P. Shushkov, J. Chem. Theory Comput., 2017, 13, 1989–2009,  DOI:10.1021/acs.jctc.7b00118.
15. J. D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620,  10.1039/B810189B.
16. C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622,  DOI:10.1103/PhysRev.46.618.
17. R. Ditchfield, W. J. Hehre and J. A. Pople, J. Chem. Phys., 1971, 52, 724–728,  DOI:10.1063/1.1674902.
18. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson and H. Nakatsuji, et al.,Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016.
19. T. H. Dunning Jr., J. Chem. Phys., 1989, 90, 1007–1023,  DOI:10.1063/1.456153.
20. J. D. McKerrow, J. M. A. Al-Rawi and P. Brooks, Synth. Commun., 2010, 40, 1161–1179,  DOI:10.1080/00397910903051259.
21. K. Omata, S. Aoyagi and K. Kabuto, Tetrahedron: Asymmetry, 2004, 15, 2351–2356,  DOI:10.1016/j.tetasy.2004.06.021.
22. A. R. Conrad, N. H. Teumelsan, P. E. Wang and M. J. Tubergen, J. Phys. Chem. A, 2010, 114, 336–342,  DOI:10.1021/jp908351u.
23. F. J. Lovas, R. D. Suenram, G. T. Fraser, C. W. Gillies and J. Zozom, J. Chem. Phys., 1988, 88, 722–729,  DOI:10.1063/1.454151.
24. H. Hartwig and H. Dreizler, Z. Naturforsch., A, 1996, 51, 923–932,  DOI:10.1515/zna-1996-0807.
25. R. C. Woods, J. Mol. Spectrosc., 1966, 21, 4–24,  DOI:10.1016/0022-2852(66)90117-2.
26. J. E. Kilpatrick, K. S. Pitzer and R. Spitzer, J. Am. Chem. Soc., 1947, 69, 2483–2488,  DOI:10.1021/ja01202a069.
27. D. F. DeTar and N. P. Luthra, J. Am. Chem. Soc., 1977, 99, 1232–1244,  DOI:10.1021/ja00446a040.
28. E. Westhof and M. Sundaralingam, J. Am. Chem. Soc., 1983, 105, 970–976,  DOI:10.1021/ja00342a054.
29. J. M. Schmidt, R. Brüschweiler, R. R. Ernst, R. L. Dunbrack Jr., D. Joseph and M. Karplus, J. Am. Chem. Soc., 1993, 115, 8747–8756,  DOI:10.1021/ja00072a030.
30. E. Czinki and A. G. Császár, Chem. – Eur. J., 2003, 9, 1008–1019,  DOI:10.1002/chem.200390103.
31. W. Gordy and R. L. Cook, Microwave Molecular Spectra, John Wiley and Sons, Inc., New York, 3rd edn, 1984.
32. W. Caminati and R. Cervellati, J. Am. Chem. Soc., 1982, 104, 4748–4752,  DOI:10.1021/ja00382a002.
33. D. F. Plusquellic, I. Kleiner, J. Demaison, R. D. Suenram, R. J. Lavrich, F. J. Lovas, G. T. Fraser and V. V. Ilyushin, J. Chem. Phys., 2006, 125, 104312,  DOI:10.1063/1.2348871.
34. C. B. Braga, L. C. Ducati, C. F. Tormena and R. Rittner, J. Phys. Chem. A, 2014, 118, 1748–1758,  DOI:10.1021/jp5007632.
35. R. S. Ruoff, T. D. Klots, T. Emilsson and H. S. Gutowsky, J. Chem. Phys., 1990, 93, 3142–3150,  DOI:10.1063/1.458848.
36. C. Cabezas, J.-C. Guillemin and Y. Endo, J. Chem. Phys., 2018, 149, 084309,  DOI:10.1063/1.5045768.
37. G. Pfafferott, H. Oberhammer, J. E. Boggs and W. Caminati, J. Am. Chem. Soc., 1985, 107, 2305–2309,  DOI:10.1021/ja00294a017.
38. L. Carballeira and I. Pérez-Juste, J. Chem. Soc., Perkin Trans. 2, 1998, 1339–1346,  10.1039/A801249K.
39. S. J. Han and Y. K. Kang, J. Mol. Struct.:THEOCHEM, 1996, 369, 157–165,  DOI:10.1016/S0166-1280(96)04594-0.
40. Ohio Supercomputer Center. Ohio Supercomputer Center; Ohio Supercomputer Center: Columbus, OH. https://osc.edu/ark:/19495/f5s1ph73/ (accessed Mar. 5, 2025).

---

Footnote

† Electronic supplementary information (ESI) available: Principal-axis atomic coordinates of the optimized model conformers, summaries of the principal results of the model conformers, and frequencies of the assigned rotational transitions. See DOI: https://doi.org/10.1039/d5cp00898k

---