Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Generalized quadratic model for charge transfer†
Angel
Albavera-Mata‡
 a,
José Luis
Gázquez
a,
José Luis
Gázquez
 b and
Alberto
Vela
b and
Alberto
Vela
 *c
*c
aDepartment of Physics, University of Florida, Gainesville, Florida 32611, USA
bDepartamento de Química, Centro de Investigación y de Estudios Avanzados, Av. Instituto Politécnico Nacional 2508, 07360 CDMX, Mexico
cDepartamento de Química, Universidad Autónoma Metropolitana-Iztapalapa, Av. San Rafael Atlixco 186, 09340 CDMX, Mexico. E-mail: avela@cinvestav.mx
First published on 13th May 2025
Abstract
We present a two-parabola interpolation model that reproduces the observed behavior for the total energy as a function of fractional occupation for known density functional approximations to the Kohn–Sham exchange–correlation energy. The model is based on the second-order Taylor series expansion of the energy as a function of the electron number for a reference chemical species, and it correctly reduces to a linear regime for density functionals satisfying the ionization theorems. The use of this generalized quadratic model results in revised definitions of electrodonating and electroaccepting powers that correctly diverge for the exact functional. Further application to charge transfer processes using two hydration reaction sets shows that this quadratic generalization unequivocally distinguishes between electrophilic and nucleophilic reaction mechanisms. This distinction was unattainable with previous approximations based on one- and two-parabolas.
1 Introduction
Chemical reactivity theory within the density functional formalism is known for its remarkable success in describing chemical events and charge transfer in particular.1–6 It often is denoted in the literature by the acronym CDFT that stands for conceptual density functional theory. Its main purpose is to reproduce trends observed in chemical reactivity studies and provide an explanation for them in terms of reactivity indexes defined within the context of density functional theory.7–9 The fundamentals of CDFT rely on a perturbation-based approach by means of the functional Taylor series expansion of the energy for a many-electron system, where the energy has a function-like dependence on the number of electrons N and a functional-like dependence on the external potential ν(r). The expansion is centered on a reference system with N0 electrons, and in the external potential ν0(r).It is undeniable that much has been learned by assuming that the energy is a continuous function of N, for processes or events occurring at fixed ν(r),10–12 where explicit inclusion of high-order terms13,14 from the series expansion has been used to assess reactivity trends for molecule families.15 These are the so called charge transfer models in CDFT,16–18 with extensions to account for the effects of finite temperature,19–25 or the presence of solvents and external fields.26,27 The literature discussing the basics and applications of CDFT, and the fundamentals for the entirety of chemical descriptors is too rich to survey here. Instead, we refer the reader to ref. 6, 28, and 29.
These chemical reactivity studies evidently depend not only upon the underlying nature of the approximation to the exchange–correlation energy,30–32 but also on the fundamentals for the charge transfer model at hand. Therefore, clear distinction between the exact properties for each, and their relationships, is pivotal. For completeness, one can mention that among the exact constraints32 known for the exchange–correlation functional are the homogeneous and non-homogeneous scaling relationships,33,34 self-interaction35–40 and many-electron self-interaction,41,42 the Lieb–Oxford bound43–46 and its strongly tightened counterpart for single-orbital systems,47 in addition to decaying48–52 and cusp53,54 conditions for the exchange and correlation potential, respectively. We refer the reader to ref. 32 and 53 for complete references and detailed discussions. Some of the prominent constraints used in CDFT include Janak's theorem55 and the ionization theorems,49,56–60 related to the frontier orbital energies, as well as the ensemble theorem61–63 that provides the basis for the assumption that the energy is a continuous function of N. The derivative discontinuity for the exchange–correlation energy,64,65 on the other hand, also has been studied extensively64–73 both for density functional design and in the context of CDFT for the calculation of fundamental gaps74–78 and the energy curvatures for E(N) using fractional charges79–84 under the assumption that the total energy, and its derivatives, are differentiable.
In the late 70s and early 80s, R. G. Parr realized the fact of the continuity for E(N) and introduced a quadratic model E(N), allowing the formalization of important concepts in chemistry. More specifically, the electronegativity was identified with (∂E/∂N)ν(r),85,86 and the chemical hardness with (∂2E/∂N2)ν(r).87 This one-parabola model further inspired and justified principles such as Sandersons electronegativity equalization,88 Pearsons hard–soft acid–base principle,89 and also new concepts like electrophilicity,90,91 and hyperhardness.92 A drawback of this one-parabola model (1PM), however, is its failure to satisfy the ensemble theorem.61–63 This is a rigorous restriction for an open quantum system in a grand-canonical ensemble at 0 K. For these conditions, the theorem establishes that the energy for a fermionic system is comprised by a set of straight lines connected at the integers N, resulting in a linear piecewise continuous function with first derivatives that are constant for any fractional number of electrons, and with derivative discontinuities at every positive integer number of electrons.61–63
Thus, restoration of the piecewise linearity is the evident and necessary next step. In 2007, the two-parabola model (2PM) was introduced to account for the missing derivative discontinuities93 but keeping Parr's original quadratic model proposal. The 2PM succeeded in capturing the fundamental fact that chemical species respond differently to the direction of charge transfer processes. Here, in the context of chemical reactivity, the directionality of charge transfer means addition or removal of charge density. Similar to the 1PM, this revised model generalized the electrophilicity concept by defining the electrodonating and electroaccepting powers in global and local versions. Later works proved the importance of distinguishing the direction of electron transfer for the understanding of some chemical reactions.7,94–103 Two of the authors of this work showed the utility of the 2PM in defining nucleophilic and electrophilic channels to determine the electron transfer process prevailing in electron-donor reactions.104–106
From the mathematical point of view, the 2PM assumes that E(N) can be expressed as
 | (1) |
 | (2) |
From the perspective of practical Kohn–Sham implementations for the evaluation of the basic ingredients for these chemical models, the inexorable role played by the choice of density functional approximation to the exchange–correlation energy cannot be overlooked. In the context of the dependence of the energy on fractional occupation numbers, it is well known that common exchange–correlation approximations deviate from the exact linear behavior dictated by the ensemble theorem at 0 K,75,76,82,110–121 regardless the use of single-determinant exchange in hybrid functionals. As defined in the so-called Jacob's Ladder classification.122 The nature of this deviation, whether associated with the delocalization error,112–115 or the many-electron self-interaction error,41,42 makes possible the existence of a non-zero chemical hardness in the one- and two-parabolas models. For the exact density functional, however, η = 0 for any fractional number of electrons, and it is undefined at every integer number of electrons. The consequence of these exact requirement is that, by construction, neither of the quadratic models discussed so far satisfy this condition. Imposing this exact constraint to the different chemical descriptors within the framework of CDFT remained missing.
Therefore, the present work aims to address this omitted aspect in CDFT by developing a model for ΔE(ΔN) that imposes restoration of the piecewise linear condition to (1), for any density functional approximation that is many-electron self-interaction free. For this purpose, we start by analyzing the dependence of the energy on the number of electrons for the molecular systems in the G3/99 set.123 We provide support to propose a generalized quadratic model for ΔE(ΔN), and show that incorporation of the frontier orbital energies leads to distinction between the left and right hardness. We apply the resulting generalized quadratic model to obtain expressions for the global hardness and improve upon the well-known electrodonating and electroaccepting powers. Finally, we evaluate the performance of our generalized quadratic model on the description of charge transfer processes for the nucleophilic and electrophilic channels for a series of hydration reactions of aldehydes, ketones and alkenes.
2 Methods
We now proceed to detailing the technicalities for all calculations in our study. The NWChem code124 was chosen for the single-point energy calculations used to asses the influence of different mixtures of the single-determinant exchange contribution for PBE,125 PBE0,126 PBEh,126,127 LC-PBE,128 and the CAM-PBE0128 exchange–correlation density functionals. These calculations were done with the def2-TZVPP spherical basis set,129 and for the NH molecule that is part of the G3/99 set.123We considered the aug-cc-pVQZ spherical basis set130–133 to compare the quadratic models for BeH and NOCl with the PBE density functional approximation. Likewise, these molecules are part of the G3/99 set and were calculated with NWChem. We further note that the choice of a larger basis set was made to improve the description of the anionic interval for both molecules.
All calculations for the NH, BeH, and NOCl molecules were done with the convergence thresholds for the total energy, density and orbital gradient fixed to 10−6, 10−5, and 10−4 atomic units, respectively.
Regarding the additional charge transfer computations, we chose two sets for hydration reactions to asses the three different quadratic models; the first is constituted by eleven protonated aldehydes and ketones taken from ref. 104, and the second includes twelve alkenes taken from ref. 106. Computations were done with NWChem and the widely used PBE+D3125 with the Becke–Johnson damping function for the dispersion correction134 and using the Ahlrich's VTZ spherical basis set.135 We emphasize that we report all values for the optimized equilibrium geometry for each chemical species in these sets, and asserted no imaginary frequencies for the final structures. For these geometry relaxations we used a threshold of 10−4 for the maximum and root mean squared gradient, and for the maximum and root mean squared of the Cartesian step as the optimization criteria. We tightened the convergence threshold for the total energy, density and orbital gradient to 10−8, 10−7, and 10−6 atomic units, respectively.
The numerical integrations for all previous calculations with NWChem were done with 70 shells using an Euler–MacLaurin scheme for the radial components, and 302 shells with a Lebedev scheme for the angular components. We disabled the level shifting for the unoccupied diagonal elements of the Fock matrix. Moreover, the Schwarz screening tolerance for the Coulomb integrals was set to 10−12, as well as for the electron density.
The single-point energies with fractional number of electrons used to compare the different approximations to the chemical hardness, η, and η± were done with a local version of the deMon2k electronic structure code.136 For this analysis, a series of single-point calculations in an unrestricted spin formalism were done for every molecule in the G3/99 set123 for the interval −1 ≤ ΔN ≤ +1 with a step ΔN = 1/10. Here, we considered the VWN137 local density approximation; the PBE,125 RPBE,138 CAP,72 and lsRPBE139 generalized gradient approximations; the TPSS,140 SCAN,141 and M06-L142meta-generalized gradient approximations; and the PBE0,126 lsRPBE0,143 M06,144 B3LYP,145,146 and M06-2X144 global hybrids that, overall, sample the first four rungs of Jacob's ladder.
For these calculations with deMon2k we chose the def2-TZVPP spherical basis set129 and the GEN-A2* Hermite auxiliary function set. The threshold tolerance for the self-consistent field, screening, and single value decompositions were set to 10−6, 1.25−11, and 10−7, respectively, using an adaptive grid with 70 shells for a Gauss–Chebyshev radial quadrature, 590 shells for the angular quadrature, and a grid tolerance of 10−5. Same as for NWChem, we disabled the level shifting option for all calculations with deMon2k. Detailed data for all 223 species and density functional approximations is included as ESI.†
3 Discussion
We begin our discussion by first addressing the basis of our approach, namely, the deviation of the linearity constraint in (1). Since this artifact has been used to fit parameters in density functional approximations,147 we remind the reader that our work is not focused on developing density functionals nor re-parameterizing existing ones. As already stated, the ensemble theorem establishes that at T = 0 K, E(N) is a series of straight lines with different slopes connected at integer N, hence having a discontinuity in the first derivatives. Common approximations to the exchange–correlation functional, however, are well known for exhibiting the prototypical behaviors depicted in Fig. 1. Different density functionals show different behaviors. Most of them are convex in both the electron-deficient and electron-rich intervals, and some like CAM-PBE0 are concave for the NH molecule shown in Fig. 1. The role of the single-determinant exchange contribution becomes evident while climbing Jacobs ladder. The main message from Fig. 1 is that by improving the exchange and correlation description, the E(N) curves get closer to a linear behavior with respect to N.Quantifying the deviation from this exact linear behavior, for non-degenerate ground state reference species with N electrons, is important for at least three reasons,
• First, the ionization theorems state that for a Kohn–Sham potential that decays asymptotically to zero, said species satisfy the condition εHOMO = −I.49,56–60
• Second, the extent to which the previous identity is not fully satisfied defines the magnitude of the many-electron self-interaction error.41,42
• Lastly, a quadratic model that recovers linearity for the exact functional must then satisfy εHOMO = −I for η = 0.
The relationship between the many-electron self-interaction and the chemical hardness thus becomes evident, namely, that density functional approximations with η > 0 will inevitably result in εHOMO + I > 0.77,148
3.1 Chemical hardness
An alternative to gaining deeper insight into this relationship, in the context of CDFT, is to focus attention on the behavior of η for different choices of density functionals. For that purpose, we calculated the curves for the energy as a function of fractional occupation numbers, ΔE(ΔN), for the 223 molecules comprising the G3/99 set, using a selection of different density functionals to sample different rungs of the Jacobs ladder categorization. For the sake of additional context, we also note that there are three different alternatives to calculate the chemical hardness. This is a consequence of the different considerations that define the 1PM and 2PM. First, as already stated, Parr and Pearson87 defined η = I – A, where I and A are the vertical first ionization potential and the vertical electron affinity, respectively.86,87,89,149 These are calculated by finite energy differences between the total energies for the cation, neutral, and anion for the corresponding species with N number of electrons. Second, the reference η extracted from the second-order coefficient using a quadratic fit for self-consistent calculations with fractional occupations for the interval −1 ≤ ΔN ≤ +1. Third, the analogous reference η− using a quadratic fit but for −1 ≤ ΔN ≤ 0 that is related to the electron-deficient interval in eqn (1), and the reference η+ for 0 ≤ ΔN ≤ +1 that instead is related to the electron rich interval in eqn (1).In an effort to summarize the large number of results for all 223 molecules, we selected a representative subset of density functional approximations, and depicted in Fig. 2 are the average values for η = I − A, the reference η, and η±. Individual results are available in the ESI.†
We first note that the difference between the reference η and I − A is relatively small, differing by no more than 1 eV. This indicates that use of a single quadratic function to fit the interval −1 ≤ ΔN ≤ +1 essentially results in magnitudes for the chemical potential and global hardness comparable to those using finite energy differences. Evidently, using three points, as originally suggested by Parr, is the most computationally efficient approach.
The second message from Fig. 2 is that the magnitudes for η and I − A always are larger than both η− and η+. This difference becomes more evident for higher rungs in Jacobs ladder, and more noticeable the larger the mixing of single-determinant exchange. The averages for η− and η+ roughly resemble half the average for η, especially for local, VWN; generalized gradient, PBE, RPBE, CAP, lsRPBE; and meta-generalized gradient approximations, TPSS, SCAN, M06-L. This trend, of course, is not general and cannot be extrapolated to the hybrid approximations PBE0, lsRPBE0, M06, B3LYP, and M06-2X. It serves nonetheless to provide numerical support for the assumption that η− = η+ = μ+ − μ− = (I − A)/2, at the core of the 2PM.
A final noticeable observation in Fig. 2 is that we confirm the previous finding108,109 for eqn (2) that, on average, η+ < η−, indicating that the curvature for the electron-deficient interval tends to be larger than that for the electron-rich interval.
3.2 Alternative expression for the energy as a function of the number of electrons
An enticing aspect of the one- and two-parabola models relates to the coefficients μ and η for ΔE(ΔN). These only depend upon knowledge of I and A, that are obtained from the energies for the neutral species, its cation, and its anion. In order to improve the description for ΔE(ΔN), it is necessary to extend the quadratic model. In this vein, we appeal to the following considerations. According to Janaks theorem,55 the chemical potentials μ− and μ+ may be approximated by μ− = εHOMO and μ+ = εLUMO. Since this information already is available for the reference system, we can include the orbital energies for the frontier molecular orbitals without any increase in computing demand. Preserving the spirit of the 2PM, we additionally distinguish the direction of electron transfer. For a charge removal process, (−), where the reference system loses an electron,| ΔE−(ΔN)|ΔN=0 = 0, | (3) |
| ΔE−(ΔN)|ΔN=−1 = E(N0 − 1) − E(N0) = I, | (4) |
| μ− = εHOMO(N0). | (5) |
| ΔE+(ΔN)|ΔN=0 = 0, | (6) |
| ΔE+(ΔN)|ΔN=1 = E(N0) − E(N0 + 1) = A, | (7) |
| μ+ = εLUMO(N0). | (8) |
Substituting eqn (3)–(8) in the corresponding (−) and (+) expressions in eqn (1), leads to the following expressions,
 | (9) |
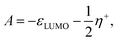 | (10) |
 and
and  are the shifts added to the frontier orbitals εHOMO and εLUMO, to attain the exact values for I and A, respectively.
are the shifts added to the frontier orbitals εHOMO and εLUMO, to attain the exact values for I and A, respectively.
In order to obtain the correct energy values at the endpoints when N = N0 − 1 or N = N0 + 1, and considering the perspective of the parabolic nature for the density functional shown in Fig. 1, we can state that the quadratic term, as constructed in the present approach, corrects for the incorrect slope given by εHOMO and εLUMO, around N = N0. In other words, eqn (5) and (8) fix the values for the first-order coefficient μ− and μ+, while from eqn (9) and (10) one finds that η− and η+ can be determined through the expressions
η− = 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (I + εHOMO), (I + εHOMO), | (11) |
η+ = −2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (A + εLUMO), (A + εLUMO), | (12) |
Notice that eqn (11) relates the chemical hardness and the many-electron self-interaction error. In fact, eqn (11) establishes that η− is twice the many-electron self-interaction error as defined in ref. 41 and 42.
With all three quadratic models properly defined, and their different parameters collected in Table 1, we now proceed to scrutinize the prototypical behavior for charge transfer processes, depicted in Fig. 3(a) for the BeH molecule and in Fig. 3(b) for the NOCl molecule. It is evident in Fig. 3 that neither the 1PM nor the 2PM reproduce the self-consistent calculations using fractional occupation numbers, depicted with the filled circles, that are the reference (exact) values for PBE. Moreover, the 1PM overestimates the maximum energy deviation ΔE±max, whereas the 2PM underestimates this maximum deviation. The GQM, on the other hand, resembles closely the self-consistent reference points for both molecules, regardless whether these curvatures are asymmetric, as for the BeH molecule in Fig. 3(a), or symmetric as for NOCl in Fig. 3(b).
| 1PM | 2PM | GQM |
|---|---|---|
| μ = −(I + A)/2 | μ − = −(3I + A)/4 | μ − = εHOMO |
| μ + = −(I+ 3A)/4 | μ + = εLUMO | |
| η = I − A | η − = (I − A)/2 | η − = 2(I + εHOMO) |
| η + = (I − A)/2 | η + = −2(A + εLUMO) | |
Furthermore, any quadratic model based on the energies for the species with N0 − 1, N0 and N0 + 1 electrons has an extremum at these rotated representations exactly at the middle of each branch, i.e., 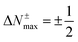 . The energy values at these extrema are ΔE±max(ΔN±max) = −η±/8. Clearly, when both (+) and (−) are equal, the extrema in both branches have the same value. This result implies that for the 1PM the energy value at these extrema is −(I − A)/8, a quantity that always is negative, provided that I > A. On the other hand, the corresponding values at the extrema for the 2PM are −(I − A)/16. The relation between the two is a factor 1/2, hence establishing that the 2PM minima are half that for the 1PM, as observed for both panels in Fig. 3.
. The energy values at these extrema are ΔE±max(ΔN±max) = −η±/8. Clearly, when both (+) and (−) are equal, the extrema in both branches have the same value. This result implies that for the 1PM the energy value at these extrema is −(I − A)/8, a quantity that always is negative, provided that I > A. On the other hand, the corresponding values at the extrema for the 2PM are −(I − A)/16. The relation between the two is a factor 1/2, hence establishing that the 2PM minima are half that for the 1PM, as observed for both panels in Fig. 3.
Another interesting aspect worth analyzing with the GQM are the electrodonating and electroaccepting powers. Gázquez, Cedillo, and Vela93 showed that these quantities are associated to the maximum number of electrons that a system can exchange with an electron bath. These are given by
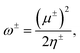 | (13) |
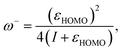 | (14) |
 | (15) |
A first feature worth noting is that the GQM electrodonating and electroaccepting powers depend solely on quantities associated with the same charge transfer branch. This contrasts the 1PM and 2PM expressions that depend both on the ionization potential and the electron affinity. Another distinctive aspect of eqn(14) and (15) relates to the exact exchange–correlation functional. For the exact functional, the Kohn–Sham frontier orbital energies satisfy εHOMO = −I and εLUMO ≅ −A, implying that ω− diverges, whereas ω+ has a large non-diverging absolute value. Certainly, this is the expected behavior for the exact functional where the energy as a function of the number of electrons follows a strict linear behavior. Thus, one can conclude that one characteristic of the exact Kohn–Sham functional is that it must have an infinite electrodonating power and a large but finite electroacepting power.
4 Application to chemical reactions
One of the interests of this work is to benchmark the GQM against the 1PM and 2PM in discerning charge transfer trends for donor–acceptor reactions. For this purpose, and for reproducibility as well, we made the same assumptions used for the 1PM and 2PM. More specifically, the space of chemical reactions comprises those with early transition states where the geometries for the reacting fragments in the transition state can be considered the same as those for the isolated fragments. Granted that reactant A is donating charge while reactant B accepts it, then, the interaction energy can be expressed as| ΔEAB ≅ ΔE−A + ΔE+B. | (16) |
Substituting eqn (1) for each (+) and (−) interval in eqn (16) and imposing charge conservation, namely, ΔN+B = −ΔN−A, leads to
 | (17) |
Minimizing this last expression with respect to ΔN−A results in the well-known expression stating that the number of electrons transferred from A to B is given by
 | (18) |
The analogous procedure but for the opposite situation where A is accepting the electrons donated by reactant B leads to
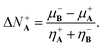 | (19) |
Eqn (18) and (19) are the generalized charge transfer expressions. Note that (18) and (19) reduce to the 2PM expressions when η−A = η+A = ηA and η−B = η+B = ηB without need to assume equality for the nucleophilic and electrophilic hardnesses.
Substituting eqn (9)–(12) in eqn (18) and (19) lead to the following expressions for the amount of transferred charge:
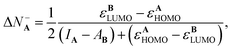 | (20) |
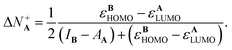 | (21) |
It is appealing that both expressions depend explicitly on the frontier orbital energies for the donor and the acceptor. Note that if εAHOMO > εBLUMO and IA > AB, which are reasonable and expected conditions for a reaction where A is a donor and B an acceptor, then eqn (20) correctly implies that ΔN−A < 0. Eqn (21) also predicts the correct sign for the reverse situation.
For in-depth analysis of eqn (20) and (21), we chose two hydration reactions studied previously to assess the validity of the chemical trends observed for the GQM, and compare the tendencies provided by the three quadratic charge transfer models. The general chemical reaction for the set of eleven aldehydes and ketones from ref. 104 is R1C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O–H)+R2 + H2O ⇌ R1C(OH)2R2 + H+, and in analogy for the set of twelve alkenes from ref. 106, R1R2C
O–H)+R2 + H2O ⇌ R1C(OH)2R2 + H+, and in analogy for the set of twelve alkenes from ref. 106, R1R2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CR3R4 + H3O+ ⇌ R1R2C(H)−C(OH)R3R4 + H+, where R1, R2, R3, and R4 label different substituent groups.
CR3R4 + H3O+ ⇌ R1R2C(H)−C(OH)R3R4 + H+, where R1, R2, R3, and R4 label different substituent groups.
As stated in the Introduction, recall that charge transfer models are meant to determine the direction of electron transfer between two reactants. For that we need an appropriate protocol. First, we will denote by A any R1(COH)+R2 or R1R2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CR3R4, and by B the target reagent, i.e., H2O for R1(COH)+R2, and H3O+ for R1R2C
CR3R4, and by B the target reagent, i.e., H2O for R1(COH)+R2, and H3O+ for R1R2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CR3R4. Then, the protocol is as follows:
CR3R4. Then, the protocol is as follows:
1. Directionality must remain consistent for the 2PM and GQM with built-in information for the direction of charge transfer. If species A is the electron donor and B is the acceptor, then the associated chemical potentials must satisfy μ−A > μ+B. Distinction of charge transfer (±) with the 1PM is not possible, by construction, and the condition at hand is μA > μB.
2. If the previous ordering of chemical potentials is not satisfied, then the reaction conditions ought to be analyzed in more detail. Use the reaction mechanism to identify the interacting chemical species that satisfy the preceding step.
3. Provided a reaction with an early transition state, such that rearrangement of nuclear positions for the interacting species is negligible, consider the following ansatz: a property P that measures the extent of a chemical reaction may be linearly related to the amount of charge transfer ΔN±A, to wit
P(ΔN±A) = m![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ΔN±A + b, ΔN±A + b, | (22) |
Following ref. 104, we considered that hydration of aldehydes and ketones is done under mild acidic conditions and, therefore, these reactants are protonated. For the hydration of alkenes, the acidic conditions are stronger, therefore, water is considered to be protonated, as it was done in ref. 106. The global chemical reactivity indexes for the three quadratic models calculated using the expressions in Table 1 are reported in Table 2 for both reactions.
| I | A | 1PM | 2PM | GQM | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| μ | η | μ − | μ + | η | μ − | μ + | η − | η + | |||
| Aldehydes and ketones | |||||||||||
| CH3(COH)+CH3 | 18.55 | 5.74 | −12.15 | 12.80 | −15.35 | −8.94 | 6.40 | −14.90 | −9.27 | 7.30 | 7.05 |
| ClCH2(COH)+CH3 | 16.18 | 6.21 | −11.19 | 9.96 | −13.69 | −8.70 | 4.98 | −12.18 | −9.60 | 7.98 | 6.78 |
| CH3CH2CH2(CHOH)+ | 16.18 | 6.03 | −11.10 | 10.15 | −13.64 | −8.57 | 5.07 | −12.81 | −9.45 | 6.74 | 6.84 |
| CH3CH2(CHOH)+ | 17.33 | 6.07 | −11.70 | 11.25 | −14.52 | −8.89 | 5.63 | −13.67 | −9.75 | 7.33 | 7.34 |
| CH3(CHOH)+ | 19.43 | 6.31 | −12.87 | 13.12 | −16.15 | −9.59 | 6.56 | −15.51 | −10.15 | 7.84 | 7.67 |
| Cl2CH(COH)+CH3 | 15.68 | 6.73 | −11.20 | 8.95 | −13.44 | −8.97 | 4.47 | −12.43 | −9.89 | 6.49 | 6.33 |
| ClCH2(COH)+CH2Cl | 15.18 | 6.48 | −10.83 | 8.71 | −13.01 | −8.65 | 4.35 | −11.94 | −9.79 | 6.49 | 6.63 |
| CH3CH2ClCH(CHOH)+ | 15.79 | 6.35 | −11.07 | 9.45 | −13.43 | −8.71 | 4.72 | −12.78 | −9.63 | 6.03 | 6.57 |
| ClCH2(CHOH)+ | 17.20 | 6.72 | −11.96 | 10.48 | −14.58 | −9.34 | 5.24 | −13.11 | −10.46 | 8.19 | 7.49 |
| CH2(OH)+ | 21.41 | 7.29 | −14.35 | 14.12 | −17.88 | −10.82 | 7.06 | −16.61 | −11.63 | 9.61 | 8.69 |
| Cl3C(CHOH)+ | 16.02 | 7.43 | −11.72 | 8.59 | −13.87 | −9.58 | 4.30 | −12.96 | −10.73 | 6.12 | 6.61 |
| H2O | 12.55 | −2.58 | −4.99 | 15.13 | −8.77 | −1.20 | 7.57 | −6.82 | −0.28 | 11.47 | 5.71 |
| Alkenes | |||||||||||
| CH2CH2 | 10.67 | −2.40 | −4.14 | 13.07 | −7.40 | −0.87 | 6.53 | −6.71 | −0.91 | 7.92 | 6.62 |
| (Me)CHCH2 | 9.74 | −2.55 | −3.60 | 12.28 | −6.67 | −0.53 | 6.14 | −6.19 | −0.57 | 7.09 | 6.24 |
| (Et)CHCH2 | 9.54 | −2.43 | −3.55 | 11.98 | −6.55 | −0.56 | 5.99 | −6.16 | −0.50 | 6.77 | 5.87 |
| (n-But)CHCH2 | 9.47 | −2.24 | −3.61 | 11.71 | −6.54 | −0.69 | 5.85 | −6.15 | −0.51 | 6.62 | 5.50 |
| E-(Me)CHCH(Me) | 9.01 | −2.68 | −3.16 | 11.69 | −6.09 | −0.24 | 5.85 | −5.74 | −0.27 | 6.53 | 5.91 |
| Z-(Me)CHCH(Me) | 9.02 | −2.55 | −3.24 | 11.57 | −6.13 | −0.35 | 5.78 | −5.74 | −0.23 | 6.57 | 5.55 |
| Z-(Et)CHCH(Et) | 8.81 | −1.97 | −3.42 | 10.78 | −6.12 | −0.73 | 5.39 | −5.78 | −0.39 | 6.07 | 4.72 |
| E-(Et)CHCH(Et) | 8.80 | −2.02 | −3.39 | 10.82 | −6.10 | −0.69 | 5.41 | −5.79 | −0.40 | 6.03 | 4.84 |
| (Me)2CCH(Me) | 9.19 | −2.36 | −3.42 | 11.55 | −6.30 | −0.53 | 5.77 | −5.89 | −0.44 | 6.61 | 5.61 |
| (c-Pr)CHCH2 | 9.01 | −2.10 | −3.46 | 11.11 | −6.23 | −0.68 | 5.56 | −5.95 | −0.70 | 6.13 | 5.61 |
| (MeO)CHCH2 | 8.96 | −2.60 | −3.18 | 11.56 | −6.07 | −0.29 | 5.78 | −5.51 | −0.27 | 6.90 | 5.74 |
| (EtO)CHCH2 | 8.81 | −2.45 | −3.18 | 11.26 | −5.99 | −0.36 | 5.63 | −5.46 | −0.22 | 6.71 | 5.34 |
| H3O+ | 24.06 | 5.10 | −14.58 | 18.96 | −19.32 | −9.84 | 9.48 | −17.86 | −8.18 | 12.41 | 6.15 |
Now, we apply the protocol presented above. For aldehydes and ketones, the chemical potentials for the 1PM result in μA < μB for the hydration of R1(COH)+R2. Recall that A is reserved for R1(COH)+R2 and B for H2O. This indicates that H2O donates electrons to any aldehyde or ketone in the set. Put simple, aldehydes and ketones (A) are electrophiles and H2O (B) is the nucleophile. Keep in mind that for the 1PM, there exists no electrophilic nor nucleophilic distinction for the species.
Moving forward to the 2PM, the protocol states that if H2O is the electron donor, then the chemical potentials must satisfy  . This inequality states that the electrons donated through the nucleophilic (−) branch for H2O are accepted through the electrophilic (+) branch for R1(COH)+R2. The data reported in Table 2 shows that this condition is not satisfied for all species. Compare, for instance,
. This inequality states that the electrons donated through the nucleophilic (−) branch for H2O are accepted through the electrophilic (+) branch for R1(COH)+R2. The data reported in Table 2 shows that this condition is not satisfied for all species. Compare, for instance,  with μ+A for ClCH2(COH)+CH3, CH3CH2CH2(CHOH)+, ClCH2(COH)+CH2Cl, and CH3CH2ClCH(CHOH)+.
with μ+A for ClCH2(COH)+CH3, CH3CH2CH2(CHOH)+, ClCH2(COH)+CH2Cl, and CH3CH2ClCH(CHOH)+.
Turning to the GQM, we see that the model itself complies with the ordering for the chemical potential. Here,  , while the chemical potentials
, while the chemical potentials  are in the range −11.63 ≤ μ+A ≤ −9.27 eV. Thus, the GQM leads to concluding that water plays the nucleophile role during the hydration of aldehydes and ketones that act as electrophiles.
are in the range −11.63 ≤ μ+A ≤ −9.27 eV. Thus, the GQM leads to concluding that water plays the nucleophile role during the hydration of aldehydes and ketones that act as electrophiles.
For the hydration of alkenes in a strong acidic medium, the chemical potentials reported in Table 2 for the 1PM establish that  , indicating that all alkenes donate electrons to the H3O+ moiety. For this reaction, the 2PM and GQM coincide with the prediction provided by 1PM. The reason is that the chemical potentials satisfy the inequality
, indicating that all alkenes donate electrons to the H3O+ moiety. For this reaction, the 2PM and GQM coincide with the prediction provided by 1PM. The reason is that the chemical potentials satisfy the inequality 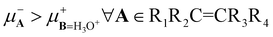 . We thus conclude that these three charge transfer models predict that alkenes are nucleophiles whereas H3O+ is an electrophile.
. We thus conclude that these three charge transfer models predict that alkenes are nucleophiles whereas H3O+ is an electrophile.
Regarding the charge transfer analysis, Table 3 reports detailed data for ΔN±A. Table 3 also highlights the columns corresponding to the correct electrophile, ΔN+A, or nucleophile, ΔN−A, behavior for each set to facilitate identification. Here, species A is reported as both an electrophile and nucleophile for comparison purposes despite setting the conditions for having a preference in the electron transfer direction. This means that we should expect unphysical results whenever considering the opposite (incorrect) electron transference direction. We verify this last statement in the following paragraphs.
| 1PM | 2PM | GQM | pKhyd | ||||
|---|---|---|---|---|---|---|---|
| ΔN−A | ΔN+A | ΔN−A | ΔN+A | ΔN−A | ΔN+A | ||
| Aldehydes and ketones | |||||||
| CH3(COH)+CH3 | −0.122 | 0.378 | 1.013 | 0.013 | 1.124 | 0.132 | 2.70 |
| ClCH2(COH)+CH3 | −0.126 | 0.374 | 0.995 | −0.005 | 0.870 | 0.153 | 1.00 |
| CH3CH2CH2(CHOH)+ | −0.129 | 0.371 | 0.984 | −0.016 | 1.006 | 0.144 | 0.30 |
| CH3CH2(CHOH)+ | −0.123 | 0.377 | 1.009 | 0.009 | 1.027 | 0.156 | 0.20 |
| CH3(CHOH)+ | −0.111 | 0.389 | 1.058 | 0.058 | 1.124 | 0.174 | −0.10 |
| Cl2CH(COH)+CH3 | −0.121 | 0.379 | 1.016 | 0.016 | 0.996 | 0.173 | −0.50 |
| ClCH2(COH)+CH2Cl | −0.127 | 0.373 | 0.990 | −0.010 | 0.956 | 0.164 | −1.00 |
| CH3CH2ClCH(CHOH)+ | −0.126 | 0.374 | 0.995 | −0.005 | 1.065 | 0.156 | −1.20 |
| ClCH2(CHOH)+ | −0.114 | 0.386 | 1.045 | 0.045 | 0.923 | 0.192 | −1.60 |
| CH2(OH)+ | −0.090 | 0.410 | 1.140 | 0.140 | 1.066 | 0.239 | −3.30 |
| Cl3C(CHOH)+ | −0.108 | 0.392 | 1.068 | 0.068 | 1.072 | 0.217 | −4.50 |
| Alkenes | log[k] | ||||||
| CH2CH2 | −0.413 | 0.087 | −0.152 | −1.152 | −0.104 | −0.890 | −14.80 |
| (Me)CHCH2 | −0.426 | 0.074 | −0.203 | −1.203 | −0.150 | −0.927 | −8.60 |
| (Et)CHCH2 | −0.428 | 0.072 | −0.213 | −1.213 | −0.156 | −0.949 | −8.60 |
| (n-But)CHCH2 | −0.429 | 0.071 | −0.215 | −1.215 | −0.158 | −0.968 | −8.40 |
| E-(Me)CHCH(Me) | −0.436 | 0.064 | −0.245 | −1.245 | −0.192 | −0.960 | −7.80 |
| Z-(Me)CHCH(Me) | −0.436 | 0.064 | −0.243 | −1.243 | −0.192 | −0.982 | −7.40 |
| Z-(Et)CHCH(Et) | −0.438 | 0.062 | −0.250 | −1.250 | −0.196 | −1.020 | −7.10 |
| E-(Et)CHCH(Et) | −0.438 | 0.062 | −0.252 | −1.252 | −0.196 | −1.012 | −7.00 |
| (Me)2CCH(Me) | −0.433 | 0.067 | −0.232 | −1.232 | −0.180 | −0.966 | −3.70 |
| (c-Pr)CHCH2 | −0.435 | 0.065 | −0.240 | −1.240 | −0.181 | −0.952 | −3.60 |
| (MeO)CHCH2 | −0.437 | 0.063 | −0.247 | −1.247 | −0.204 | −0.969 | −0.10 |
| (EtO)CHCH2 | −0.439 | 0.061 | −0.255 | −1.255 | −0.212 | −0.993 | 0.20 |
For the first set of reactions R1(COH)+R2, Table 3 shows ΔN−A > 0 for magnitudes that should be negative, in addition to showing some magnitudes larger than one. Both are unphysical situations, provided that the maximum number of electrons either donated or accepted strictly is sensibly bounded to one for all these quadratic models. An analogous situation prevails for the set R1R2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CR3R4 in Table 3. The 2PM and GQM result in ΔN+A < 0 for magnitudes that should be positive, and the absolute values for several species also are larger than unity. As an aside, we note that for charge transfer processes where |ΔN±| > 1, proper incorporation of more energy intervals seems mandatory.
CR3R4 in Table 3. The 2PM and GQM result in ΔN+A < 0 for magnitudes that should be positive, and the absolute values for several species also are larger than unity. As an aside, we note that for charge transfer processes where |ΔN±| > 1, proper incorporation of more energy intervals seems mandatory.
The 1PM, however, shows no ambiguities in Table 3. Charge partitioning results in correct signs and reasonable magnitudes for both the R1(COH)+R2 and R1R2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CR3R4 sets. Its limitation, nonetheless, is that unlike the 2PM and GQM, the 1PM provides no means for discarding charge directionality on the basis of identifying incorrect signs for ΔN± or |ΔN±| > 1. Therefore, the propositions discussed previously for determining the prevailing direction of charge transfer are useful for the 2PM or GQM, but otherwise for the 1PM.
CR3R4 sets. Its limitation, nonetheless, is that unlike the 2PM and GQM, the 1PM provides no means for discarding charge directionality on the basis of identifying incorrect signs for ΔN± or |ΔN±| > 1. Therefore, the propositions discussed previously for determining the prevailing direction of charge transfer are useful for the 2PM or GQM, but otherwise for the 1PM.
In the interest of a simpler pictorial perspective, we can use eqn (22) as supplement to the foregoing discussion. We start with Fig. 4 depicting the results from Table 3 for the R1(COH)+R2 set, where eqn (22) is used to correlate pKhyd and ΔN±A. We stated already that these species are electrophiles and that charge transfer takes place through ΔN+A. Notice that the 1PM and 2PM result in practically identical R2 for the nucleophilic and electrophilic channels in Fig. 4. This means that the 1PM and 2PM cannot differentiate between an increasing Khyd as |ΔN−A| increases in Fig. 4(a), from an increasing Khyd as |ΔN+A| increases in Fig. 4(b). We remind the reader that pKhyd = −log[Khyd], meaning that Khyd is larger for a negative pKhyd than for its positive counterpart. A different picture arises for the GQM. Fig. 4(a) shows a nearly zero R2 for the nucleophilic channel, which means that the GQM results in no correlation between an increasing Khyd with an increasing |ΔN−A|. On the contrary, the R2 = 0.79 in Fig. 4(b) for the GQM distinguishes successfully the electrophilic channel for which Khyd increases with |ΔN+A|.
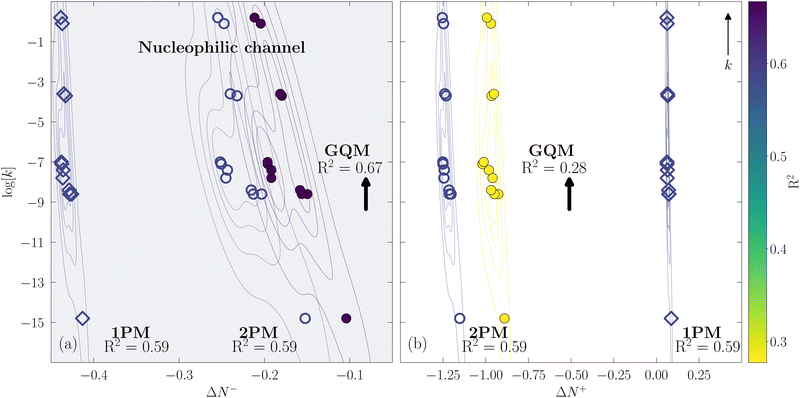
The analogous comparison holds for the R1R2C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CR3R4 set shown in Fig. 5, where we again use eqn (20) but now for the correlation between log[k] and ΔN±A. We stated previously that these molecules are nucleophiles and that charge transfer occurs through ΔN−A. Same as before, the 1PM and 2PM flounder differentiating between the nucleophilic and electrophilic channels. Both models result in essentially the same R2 that suggests a failed distinction between an increasing k as |ΔN−A| increases in Fig. 5(a), from an increasing k as |ΔN+A| increases in Fig. 5(b). Notice that the plot shows log[k] and not k. Once again the GQM offers a distinct picture. Fig. 5(a) shows an R2 = 0.67 and Fig. 5(b) an R2 = 0.28 for the nucleophilic and electrophilic channels, respectively, evidencing the correct preference towards an increasing k for an also increasing |ΔN−A| in Fig. 5(a).
CR3R4 set shown in Fig. 5, where we again use eqn (20) but now for the correlation between log[k] and ΔN±A. We stated previously that these molecules are nucleophiles and that charge transfer occurs through ΔN−A. Same as before, the 1PM and 2PM flounder differentiating between the nucleophilic and electrophilic channels. Both models result in essentially the same R2 that suggests a failed distinction between an increasing k as |ΔN−A| increases in Fig. 5(a), from an increasing k as |ΔN+A| increases in Fig. 5(b). Notice that the plot shows log[k] and not k. Once again the GQM offers a distinct picture. Fig. 5(a) shows an R2 = 0.67 and Fig. 5(b) an R2 = 0.28 for the nucleophilic and electrophilic channels, respectively, evidencing the correct preference towards an increasing k for an also increasing |ΔN−A| in Fig. 5(a).
It also is possible to state that the GQM results in tendencies slightly different than those observed for the other two models. These subtle changes in ΔN±A can be attributed to the finer information in the GQM due to its dependence on the frontier orbital energies. See eqn (20) and (21). Finally, regarding the chemical behavior for the reactants participating in these reactions, all three models agree in determining that the protonated (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O–H)+ group in aldehydes and ketones acts as an electrophile in the presence of H2O and that the C
O–H)+ group in aldehydes and ketones acts as an electrophile in the presence of H2O and that the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C group in alkenes acts as a nucleophile when these chemical species are in the presence of H3O+.
C group in alkenes acts as a nucleophile when these chemical species are in the presence of H3O+.
5 Conclusions
A generalized quadratic model was proposed by incorporating the frontier orbital energies through an ansatz based on the ionization theorems and Janaks theorem. The analysis of the delocalization error for the family of quadratic charge models provides an explanation for several results observed previously and strengthens the considerations used in the two-parabola model proposed by Gázquez, Cedillo, and Vela. By construction, the proposed generalized quadratic model correctly recovers the linear behavior of the energy as a function of the fractional occupation for the exact exchange–correlation energy functional in the Kohn–Sham formalism. The model clearly shows that the chemical hardness may be associated with a measure of the delocalization error prevailing in density functional approximations. The expressions derived for the electrodonating and electroaccepting powers show that, for the exact functional, the electrodonating power diverges, and the electroacepting power is large but finite. We further evidenced that this generalized quadratic model successfully distinguishes between electrophilic and nucleophilic species for two sets of hydration reactions. Previous quadratic models failed to provide an unequivocal distinction between these two charge transfer processes. We finally showed that including frontier orbital energies in charge transfer evaluations improves correlations with experimental equilibrium and rate constants, and that the amount of charge transfer remains within physical bounds. The local version for this generalized quadratic model will be reported elsewhere.Author contributions
All authors contributed equally to this work.Conflicts of interest
The authors declare no conflicts of interest, nor competing financial or non-financial interests.Acknowledgements
AAM and AV gratefully acknowledge support from Conacyt through Project Fronteras 867; JLG and AV thank Conahcyt for grant Sinergia 1561802.Notes and references
- R. G. Pearson, Chemical Hardness: Applications from Molecules to Solids, Wiley-VCH, Oxford, 1997 Search PubMed.
- W. Koch and M. C. Holthausen, A Chemist's Guide to Density Functional Theory, Wiley-VCH, New York, 2000 Search PubMed.
- H. Chermette, J. Comput. Chem., 1999, 20, 129–154 CrossRef CAS.
- P. Geerlings, F. De Proft and W. Langenaeker, Chem. Rev., 2003, 103, 1793–1873 CrossRef CAS PubMed.
- P. K. Chattaraj, U. Sarkar and D. R. Roy, Chem. Rev., 2006, 106, 2065–2091 CrossRef CAS PubMed.
- S. Liu, Conceptual Density Functional Theory: Towards a New Chemical Reactivity Theory, Wiley-VCH, GmbH, 2022 Search PubMed.
- P. W. Ayers, J. S. M. Anderson and L. J. Bartolotti, Int. J. Quantum Chem., 2005, 101, 520–534 CrossRef CAS.
- J. L. Gázquez, J. Mex. Chem. Soc., 2008, 52, 3–10 Search PubMed.
- P. Geerlings, E. Chamorro, P. K. Chattaraj, F. D. Proft1, J. L. Gázquez, S. Liu, C. Morell, A. Toro-Labbé, A. Vela and P. W. Ayers, Theor. Chem. Acc., 2020, 139, 36 Search PubMed.
- D. J. Tozer and F. De Proft, J. Phys. Chem. A, 2005, 109, 8923–8929 CrossRef CAS PubMed.
- E. R. Johnson, A. Otero-de-la Roza and S. G. Dale, J. Chem. Phys., 2013, 139, 184116 CrossRef PubMed.
- R. Pal, A. Poddar and P. K. Chattaraj, J. Phys. Chem. A, 2022, 126, 6801–6813 CrossRef CAS PubMed.
- A. Malek and R. Balawender, J. Chem. Phys., 2015, 142, 054104 CrossRef PubMed.
- M. Franco-Pérez, J. L. Gázquez, P. W. Ayers and A. Vela, J. Chem. Theory Comput., 2018, 14, 597–606 CrossRef PubMed.
- C. Morell, A. Grand, A. Toro-Labbé and H. Chermette, J. Mol. Model., 2013, 19, 2893–2900 CrossRef CAS PubMed.
- B. G. Baekelandt, A. Cedillo and R. G. Parr, J. Chem. Phys., 1995, 103, 8548–8556 CrossRef CAS.
- W. Kohn, A. D. Becke and R. G. Parr, J. Phys. Chem., 1996, 100, 12974–12980 CrossRef CAS.
- R. Pal and P. K. Chattaraj, J. Indian Chem. Soc., 2021, 98, 100008 CrossRef CAS.
- M. Franco-Pérez, J. L. Gázquez and A. Vela, J. Chem. Phys., 2015, 143, 024112 CrossRef PubMed.
- M. Franco-Pérez, P. W. Ayers, J. L. Gázquez and A. Vela, J. Chem. Phys., 2015, 143, 154103 CrossRef PubMed.
- R. A. Miranda-Quintana and P. W. Ayers, Phys. Chem. Chem. Phys., 2016, 18, 15070–15080 RSC.
- M. Franco-Pérez, P. W. Ayers, J. L. Gázquez and A. Vela, J. Chem. Phys., 2017, 147, 094105 CrossRef PubMed.
- R. A. Miranda-Quintana, P. K. Chattaraj and P. W. Ayers, J. Chem. Phys., 2017, 147, 124103 CrossRef PubMed.
- J. L. Gázquez, M. Franco-Pérez, P. W. Ayers and A. Vela, Int. J. Quantum Chem., 2018, e25797, 1–21 Search PubMed.
- R. A. Miranda-Quintana, F. Franco-Pérez, J. L. Gázquez and A. Vela, J. Chem. Phys., 2018, 149, 124110 CrossRef PubMed.
- D. Chakraborty and P. K. Chattaraj, Chem. Sci., 2021, 12, 6264–6279 RSC.
- M. Franco-Perez, F. Heidar-Zadeh, P. W. Ayers, F. De Proft, A. Vela, J. L. Gázquez and P. Geerlings, Chem. Sci., 2024, 15, 20090–20121 RSC.
- S. Liu, Exploring Chemical Concepts Through Theory and Computation, Wiley-VCH, GmbH, 2024 Search PubMed.
- S. Ghosh and P. K. Chattaraj, Concepts and Methods in Modern Theoretical Chemistry, CRC Press, Boca Raton, 2016 Search PubMed.
- J. P. Perdew and A. Ruzsinszky, Int. J. Quantum Chem., 2010, 110, 2801–2807 CrossRef CAS.
- J. P. Perdew, J. Sun, R. M. Martin and B. Delley, Int. J. Quantum Chem., 2016, 116, 847–851 CrossRef CAS.
- A. D. Kaplan, M. Levy and J. P. Perdew, Annu. Rev. Phys. Chem., 2023, 74, 193–218 CrossRef CAS PubMed.
- G. L. Oliver and J. P. Perdew, Phys. Rev. A: At., Mol., Opt. Phys., 1979, 20, 397–403 CrossRef CAS.
- M. Levy and J. P. Perdew, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 32, 2010–2021 CrossRef CAS PubMed.
- E. Fermi and E. Amaldi, Mem. Accad. d’Italia, 1934, 6, 119–149 CAS.
- J. C. Slater, Quantum Theory of Molecules and Solids, The Self-Consistent Field for Molecules and Solids, McGraw-Hill, New York, 1974, vol. 4 Search PubMed.
- J. P. Perdew and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 5048–5079 CrossRef CAS.
- J. P. Perdew, Self-Interaction Correction, Local Density Approximations in Quantum Chemistry and Solid State Physics, 1984, pp. 173–205.
- J. P. Perdew, Driving out the Self-Interaction Error, en Electronic Density Functional Theory: Recent Progress and New Directions, 1998, pp. 31–41 Search PubMed.
- S. Kümel and J. P. Perdew, Mol. Phys., 2003, 101, 1363–1368 CrossRef.
- A. Ruzsinszky, J. P. Perdew, G. I. Csonka, O. A. Vydrov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 194112 CrossRef PubMed.
- A. Ruzsinszky, J. P. Perdew, G. I. Csonka, O. A. Vydrov and G. E. Scuseria, J. Chem. Phys., 2007, 126, 104102 CrossRef PubMed.
- J. P. Perdew, Electronic Structure of Solids ‘91, Berlin, 1991, pp. 11–20 Search PubMed.
- M. M. Odashima and K. Capelle, J. Chem. Phys., 2007, 127, 054106 CrossRef PubMed.
- E. H. Lieb and S. Oxford, Int. J. Quantum Chem., 1981, 19, 427–439 CrossRef CAS.
- G. K. L. Chan and N. C. Handy, Phys. Rev. A: At., Mol., Opt. Phys., 1999, 59, 3075–3077 CrossRef.
- J. P. Perdew, A. Ruzsinszky, J. Sun and K. Burke, J. Chem. Phys., 2014, 140, 18A533 CrossRef PubMed.
- L. J. Sham, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 32, 3876–3882 CrossRef CAS PubMed.
- C.-O. Almbladh and U. von Barth, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31, 3231 CrossRef CAS PubMed.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS PubMed.
- M. K. Harbola and V. Sahni, Phys. Rev. Lett., 1989, 62, 489–492 CrossRef CAS PubMed.
- E. Engel, J. A. Chevary, L. D. Macdonald and S. H. Vosko, Z. Phys. D, 1992, 23, 7–14 CrossRef CAS.
- V. N. Staroverov, G. E. Scuseria, J. Tao and J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 075102 CrossRef.
- V. N. Staroverov, G. E. Scuseria, J. Tao and J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 239907 CrossRef.
- J. F. Janak, Phys. Rev. B: Condens. Matter Mater. Phys., 1978, 18, 7165–7168 CrossRef CAS.
- M. Levy, J. P. Perdew and V. Sahni, Phys. Rev. A: At., Mol., Opt. Phys., 1984, 30, 2745 CrossRef.
- L. Kleinman, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 12042 CrossRef CAS.
- J. P. Perdew and M. Levy, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 16021 CrossRef CAS.
- L. Kleinman, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 16029 CrossRef CAS.
- M. K. Harbola, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 4545 CrossRef CAS.
- J. P. Perdew, R. G. Parr, M. Levy and J. L. Baldúz, Phys. Rev. Lett., 1982, 49, 1691–1694 CrossRef CAS.
- W. T. Yang, Y. K. Zhang and P. W. Ayers, Phys. Rev. Lett., 2000, 84, 5172–5175 CrossRef CAS PubMed.
- P. W. Ayers, J. Math. Chem., 2008, 43, 285–303 CrossRef CAS.
- J. P. Perdew and M. Levy, Phys. Rev. Lett., 1983, 51, 1884–1887 CrossRef CAS.
- L. J. Sham and M. Schlüter, Phys. Rev. Lett., 1983, 51, 1888–1891 CrossRef.
- W. Kohn, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 4331–4333 CrossRef PubMed.
- M. K. Harbola, Phys. Rev. A: At., Mol., Opt. Phys., 1998, 57, 4253–4256 CrossRef CAS.
- E. Sagvolden and J. P. Perdew, Phys. Rev. A: At., Mol., Opt. Phys., 2008, 77, 012517 CrossRef.
- P. Mori-Sánchez, A. J. Cohen and W. Yang, Phys. Rev. Lett., 2009, 102, 066403 CrossRef PubMed.
- A. J. Cohen, P. Mori-Sánchez and W. Yang, J. Chem. Theory Comput., 2009, 5, 786–792 CrossRef CAS PubMed.
- P. Mori-Sánchez and A. J. Cohen, Phys. Chem. Chem. Phys., 2014, 16, 14378–14387 RSC.
- J. Carmona-Espíndola, J. L. Gázquez, A. Vela and S. B. Trickey, J. Chem. Phys., 2015, 142, 054105 CrossRef PubMed.
- J. Carmona-Espíndola, J. L. Gázquez, A. Vela and S. B. Trickey, J. Chem. Theory Comput., 2018, 15, 303–310 CrossRef PubMed.
- T. J. Stein, J. Autschbach, N. Govind, L. Kronik and R. Baer, J. Phys. Chem. Lett., 2012, 3, 3740–3744 CrossRef CAS PubMed.
- E. Kraisler and L. Kronik, Phys. Rev. Lett., 2013, 110, 126403 CrossRef PubMed.
- E. Kraisler and L. Kronik, J. Chem. Phys., 2014, 140, 18A540 CrossRef PubMed.
- E. Kraisler, T. Schmidt, S. Kümmel and L. Kronik, J. Chem. Phys., 2015, 143, 104105 CrossRef PubMed.
- Z.-H. Yang, H. Peng, J. Sun and J. P. Perdew, Phys. Rev. B, 2016, 93, 205205 CrossRef.
- Y. Zhang and W. Yang, J. Chem. Phys., 1998, 109, 2604–2608 CrossRef CAS.
- Y. Zhang and W. Yang, Theor. Chem. Acc., 2000, 103, 346–348 Search PubMed.
- A. J. Cohen, P. Mori-Sánchez and W. Yang, Chem. Rev., 2012, 112, 289–320 CrossRef CAS PubMed.
- E. Kraisler and L. Kronik, Phys. Rev. A: At., Mol., Opt. Phys., 2015, 91, 032504 CrossRef.
- V. Vlček, R. E. Eisenberg, G. Steinle-Neumann, L. Kronik and B. Roi, J. Chem. Phys., 2015, 142, 034107 CrossRef PubMed.
- C. Li and W. Yang, J. Chem. Phys., 2017, 146, 074107 CrossRef PubMed.
- L. Pauling, J. Am. Chem. Soc., 1932, 54, 3570–3582 CrossRef CAS.
- R. G. Parr, R. A. Donnelly, M. Levy and W. E. Palke, J. Chem. Phys., 1978, 68, 3801–3807 CrossRef CAS.
- R. G. Parr and R. G. Pearson, J. Am. Chem. Soc., 1983, 105, 7512–7516 CrossRef CAS.
- R. T. Sanderson, J. Am. Chem. Soc., 1983, 105, 2259–2261 CrossRef CAS.
- R. G. Pearson, J. Am. Chem. Soc., 1963, 85, 3533–3539 CrossRef CAS.
- R. G. Parr, L. v Szentpály and S. Liu, J. Am. Chem. Soc., 1999, 121, 1922–1924 CrossRef CAS.
- R. Pal and P. K. Chattaraj, J. Comput. Chem., 2023, 44, 278–297 CrossRef CAS PubMed.
- P. Geerlings and F. De Proft, Phys. Chem. Chem. Phys., 2008, 10, 3028–3042 RSC.
- J. L. Gázquez, A. Cedillo and A. Vela, J. Phys. Chem. A, 2007, 111, 1966–1970 CrossRef PubMed.
- P. K. Chattaraj, S. Duleya and L. R. Domingo, Org. Biomol. Chem., 2012, 10, 2855–2861 RSC.
- K. Gupta, S. Giri and P. K. Chattaraj, J. Phys. Org. Chem., 2013, 26, 187–193 CrossRef CAS.
- U. Orozco-Valencia, J. L. Gázquez and A. Vela, Acta Phys.-Chim. Sin., 2018, 34, 692–698 CAS.
- U. Orozco-Valencia, J. L. Gázquez and A. Vela, J. Mol. Model., 2018, 24, 250 CrossRef PubMed.
- J.-Z. Ramírez-Ramírez, R. Vargas, J. Garza and J. L. Gázquez, J. Phys. Chem. A, 2010, 114, 7945–7951 CrossRef PubMed.
- A. Morales-Bayuelo, J. Sánchez-Márquez, G. Jana and P. K. Chattaraj, Struct. Chem., 2020, 31, 1745–1756 CrossRef CAS.
- R. A. Miranda-Quintana, P. W. Ayers and F. Heidar-Zadeh, ChemistrySelect, 2021, 6, 96–100 CrossRef CAS.
- N. Redjem, S. Lakehal, A. Lakehal, C. Morell, L. Merzoud and H. Chermette, Inorg. Chem., 2022, 61, 4673–4680 CrossRef CAS PubMed.
- S. G. Patra, R. Jha, H. Mondal and P. K. Chattaraj, J. Phys. Org. Chem., 2022, 36, e4337 CrossRef.
- J. Sánchez-Márquez, H. Mondal, S. G. Patra, A. Morales-Bayuelo and P. K. Chattaraj, Int. J. Quantum. Chem., 2023, 123, e27129 CrossRef.
- A. U. Orozco-Valencia, J. L. Gázquez and A. Vela, J. Phys. Chem. A, 2017, 121, 4019–4029 CrossRef CAS PubMed.
- U. Orozco-Valencia, J. L. Gázquez and A. Vela, J. Mol. Model., 2017, 23, 207 CrossRef PubMed.
- U. Orozco-Valencia, J. L. Gázquez and A. Vela, J. Phys. Chem. A, 2018, 122, 1796–1806 CrossRef CAS PubMed.
- W. Yang, R. Parr and R. Pucci, J. Chem. Phys., 1984, 81, 2862–2863 CrossRef CAS.
- J. L. Gázquez, J. Garza, F. D. Hinojosa and A. Vela, J. Chem. Phys., 2007, 126, 214105 CrossRef PubMed.
- J. L. Gázquez, B. Gómez, F. D. Hinojosa and A. Vela, Indian J. Chem., 2014, 53A, 949–957 Search PubMed.
- M. Lundberg and P. E. M. Siegbahn, J. Chem. Phys., 2005, 122, 224103 CrossRef PubMed.
- O. A. Vydrov and G. E. Scuseria, J. Chem. Phys., 2007, 126, 154109 CrossRef PubMed.
- P. Mori-Sánchez, A. J. Cohen and W. Yang, Phys. Rev. Lett., 2008, 100, 146401 CrossRef PubMed.
- E. R. Johnson, P. Mori-Sánchez, A. J. Cohen and W. Yang, J. Chem. Phys., 2008, 129, 204112 CrossRef PubMed.
- A. J. Cohen, P. Mori-Sánchez and W. Yang, Science, 2008, 321, 792–794 CrossRef CAS PubMed.
- A. J. Cohen, P. Mori-Sánchez and W. Yang, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 115123 CrossRef.
- A. J. Cohen, P. Mori-Sánchez and W. Yang, J. Chem. Phys., 2012, 136, 204111 CrossRef PubMed.
- C. Li, X. Zheng, A. J. Cohen, P. Mori-Sánchez and W. Yang, Phys. Rev. Lett., 2015, 114, 053001 CrossRef CAS PubMed.
- B. Mussard and J. Toulouse, Mol. Phys., 2017, 115, 161–173 CrossRef CAS.
- B. G. Janesko, Phys. Chem. Chem. Phys., 2017, 19, 4793–4801 RSC.
- E. Kraisler, J. Chem. Theory Comput., 2024, 21, 155–169 CrossRef PubMed.
- Y. Goshen and E. Kraisler, J. Phys. Chem. Lett., 2024, 15, 2337–2343 CrossRef CAS PubMed.
- J. P. Perdew and K. Schmidt, AIP Conf. Proc., 2001, 577, 1–20 CrossRef CAS.
- L. A. Curtiss, K. Raghavachari, P. C. Redfern and J. A. Pople, J. Chem. Phys., 2000, 112, 7374 CrossRef CAS.
- M. Valiev, E. J. Bylaska, N. Govind, K. Kowalski, T. P. Straatsma, H. J. J. van Dam, D. Wang, J. Nieplocha, E. Apra, T. L. Windus and W. A. de Jong, Comput. Phys. Commun., 2010, 181, 1477 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158 CrossRef CAS.
- P. Cortona, J. Chem. Phys., 2012, 136, 086101 CrossRef PubMed.
- M. A. Rohrdanz and J. M. Herbert, J. Chem. Phys., 2008, 129, 034107 CrossRef PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- D. E. Woon and T. H. Dunning, J. Chem. Phys., 1993, 98, 1358–1371 CrossRef CAS.
- B. P. Prascher, D. E. Woon, K. A. Peterson, T. H. Dunning and A. K. Wilson, Theor. Chem. Acc., 2011, 128, 69–82 Search PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- A. Schafer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571 CrossRef.
- G. Geudtner, P. Calaminici, J. Carmona-Espíndola, J. M. del Campo, V. D. Domínguez-Soria, R. F. Moreno, G. U. Gamboa, A. Goursot, A. M. Köster, J. U. Reveles, T. Mineva, J. M. Vásquez-Pérez, A. Vela, B. Zúñinga-Gutierrez and D. R. Salahub, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 548–555 CAS.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS.
- B. Hammer, L. B. Hansen and J. K. Nørskov, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 7413–7421 CrossRef.
- J. C. Pacheco-Kato, J. M. del Campo, J. L. Gázquez, S. B. Trickey and A. Vela, Chem. Phys. Lett., 2016, 651, 268–273 CrossRef CAS.
- J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401 CrossRef PubMed.
- J. Sun, A. Ruzsinszky and J. P. Perdew, Phys. Rev. Lett., 2015, 115, 036402 CrossRef PubMed.
- Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101 CrossRef PubMed.
- A. Albavera-Mata, C. Zicovich-Wilson, J. Gázquez, S. Trickey and A. Vela, Theor. Chem. Acc., 2018, 137, 26 Search PubMed.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- L. O. Hemmingsen, O. A. J. H. Hervir and S. G. Dale, J. Chem. Phys., 2022, 156, 014106 CrossRef CAS PubMed.
- S. Lavie, Y. Goshen and E. Kraisler, J. Chem. Phys., 2023, 158, 154111 CrossRef CAS PubMed.
- R. S. Mulliken, J. Chem. Phys., 1934, 2, 782–793 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Detailed computed chemical hardness for the G3/99 set, sorted by species and choice of density functional approximation. See DOI: https://doi.org/10.1039/d5cp00866b |
| ‡ Previous address: Departamento de Química, Centro de Investigación y de Estudios Avanzados, Av. Instituto Politécnico Nacional 2508, 07360 CDMX, Mexico. |
| This journal is © the Owner Societies 2025 |