Electron impact single and double ionization and dissociation: revisiting CF₄ and CHF₃ with an improved experimental method

Abstract

The absolute total and partial ionization cross sections resulting from electron collisions with fluorinated molecules CF₄ and CHF₃ were obtained by recoil-ion momentum spectroscopy with full acceptance for energetic ionic fragments. For absolute normalization the relative-flow technique was applied. The cross sections for single and double ionization as well as for dissociation were measured for electron energies from 20 eV to 1 keV. The data are compared with previous experiments and model calculations. The dissociation channel specific differences between CF₄ and CHF₃ are discussed. The present data are relevant for the evaluation of the electron interaction on these potent greenhouse gases with a high global warming potential in the Earth biosphere and in plasma and other industrial applications.

---

1 Introduction

Laboratory experiments for halocarbons, such as tetrafluoromethane (CFC-14, CF₄) and fluoroform (HFC-23, CHF₃), are relevant in atmospheric physics and chemistry, astrochemistry and in industrial applications. For these molecules, we report data for electron impact ionization and subsequent dissociation with the production of reactive ions and neutrals. The total and partial ionization cross sections determine the survival probability of the molecules and govern the production of smaller radicals. Accurate measurements of these cross sections for electron collisions are needed to understand and model the impact of these processes on the environment.^1,2

Satellite observations, balloons, and ground-based collection stations are providing information on extraterrestrial particles and radiation (solar wind and cosmic rays) that impinge on the atmosphere of the Earth,³ as well as on the composition of the atmosphere that includes trace gases as a function of altitude.^4,5 The upper troposphere and the mid to lower stratosphere comprise greenhouse and ozone damaging molecules. The impact of highly fluorinated molecules on climate change is a concern primarily determined by stratospheric loss processes and their strong absorption in the infrared region.⁶

In the last 16 years, the concentration arising from the natural and anthropogenic emissions of the CHF₃ was increasing from 23 ppm to 36 ppm and that of CF₄ from 74 to 90 ppm in the lower troposhere.⁷ CF₄ and CHF₃ molecules concentrate at altitudes of 10 km up to 50 km.^8–11 Measurements show that the troposphere is warming up, whereas the stratosphere is cooling down in response to stronger absorption by greenhouse gases and in response to the depletion of ozone in the lower stratosphere.^4,6,8,12

The global lifetime of CHF₃ in the atmosphere is 250 years, much shorter in comparison to that of CF₄ of 50.000 years, but its stratospheric lifetime is 2347 years.^5,13 The large difference in lifetimes is due to the presence of a hydrogen atom in CHF₃, which reacts in the troposphere by oxidation with hydroxyl (OH) radicals and in the lower stratosphere by reactions with free OH and atomic oxygen, as well as by UV photolysis.¹⁴ The degradation of hydrofluorocarbons (HFCs) results in carbon dioxide (CO₂) and hydrogen fluoride (HF) as stable breakdown products.^15,16

CHF₃ was first recognized as a hydrofluorocarbon (HFC) with zero ozone depletion potential and, therefore, these compounds are being used as an alternative to ozone-depleting substances such as chlorofluorocarbons (CFC) and hydrochlorofluorocarbons (HCFC).¹⁷ However, their high global warming potentials and atmospheric residence times pose challenges. The metrics of the global warming potentials (GWP) of CHF₃ and CF₄ are rather high with a GWP of 11 700 and 5200 fold the one of CO₂.⁴ Therefore, the Kigali amendment to the Montreal Protocol and the European Union Regulation 2024/573¹⁸ have established rules and outlined a roadmap for the phased reduction of fluorinated greenhouse gases.

Halogen compounds are of interest not only in aeronomy but are of importance in organic, inorganic, biochemical, and material chemistry.¹⁹ They are used as products and are emitted as by-products of industrial processes. Understanding its electron impact-induced dissociation is required in reactive-ion etching in micro/nanoelectronics fabrication. HFCs are increasingly being used in heat-pump technology for air and water heating, clothing drying, fire extinguishing agents, and cooling devices,²⁰ and are large-volume by-products in the manufacture of Teflon and foams. Their large-scale use may lead to continued emissions if there is no transition to alternatives with low global-warming potential.

CF₄ was widely used as the primary feed gas for plasma processing discharges because the parent molecule is relatively non-reactive and in a discharge dissociates readily into chemically reactive ionic and neutral species, owing to the fact that the electronically excited states of CF₄ and CF₄⁺ are unstable. CF₄ is weakly electronegative and the cross section for dissociative electron attachment is extremely small.²¹ Here electronegativity is used as defined by Christophorou²² describing the ability of a gas to form long-lived negative ions.

CHF₃ is part of several homologous chemical series, such as the CH_nF_4−n and the CXF₃ (where X is a hydrogen or halogen atom) series and other series with combinations of hydrogen and halogen atoms. Therefore, CHF₃ is a keystone in the study of the effects of atomic substitution on the chemical and physical molecular properties. The physico-chemical properties and radiation impact cross-section data are closely related to the halogen molecular structure.²³

Experimental absolute cross sections are required to test theoretical models, predict and mitigate the molecular interactions, such as in the biosphere,²⁴ and correctly model and control its action in industrial applications.^25–32 In this respect, there is particular interest in plasmas sustained in CHF₃.³³

Theoretical methods of the total ionization cross sections (ICS) for molecules such as CF₄ and CHF₃ have been the subject of extensive research. The most widely accepted models in this context include the binary encounter-Bethe (BEB) and binary encounter-dipole (BED) methods,^34,35 the Deutsch and Mark (DM) formalism,³⁶ and the modified additive rule (MAR).³⁷ Each of these models has its strengths and specific applications when dealing with molecules containing fluorine and chlorine, where the inclusion of electron correlations and empirical corrections are often necessary.

The BEB and BED models combine classical collision theory with quantum-mechanical principles to predict ICSs. The DM formalism was particularly modified for molecules containing fluorine. The MAR formalism adjusts the additivity rule for cross sections to account for the presence of heavy atoms and other effects for complex molecules. In addition, there is the empirical and semi-empirical Harland and Vallance (HV) method.³⁸ The agreement between the different theoretical models and the experimental data varies, with some models aligning closely with specific experimental results, while others deviate, highlighting the complexity of accurately modeling these interactions. Systematic studies on the fluorinated molecules revealed that the energy positions of the experimental cross-section maxima depend on the binding energy depths of the valence and inner-valence orbitals. However, the magnitude of the cross section is related to the polarizability of molecular dipoles.³⁹

Given the challenges in performing accurate experiments on the absolute scale as well as accurate calculations for CF₄^21,40–48 and CHF₃^{1,21,29,43,49–55} molecules, there is still a need for methodologies capable of obtaining reliable electron impact cross section data. The purpose of this work is to provide accurate absolute cross sections for single- and double-ionization and dissociation. Therefore, we employ an ion imaging spectrometer with full solid-angle acceptance for fragment ions produced even with large kinetic energies in combination with the relative-flow technique to bring the data to an absolute scale.

2 Experimental setup

The experimental setup closely followed the methodology used in a previous study, and the absolute cross section measurement technique was described in detail before.⁵⁶ A brief description of the experimental setup will be given here. The measurements used a recoil-ion momentum spectrometer (RIMS) and a target gas mixing setup, as depicted in Fig. 1. A pulsed electron beam, emitted from a home-built electron gun, was crossed with a target gas beam. The electron pulses had a repetition frequency of 15.75 kHz and a pulse duration of 20 ns, with the electron beam's diameter collimated to approximately 1 mm at the interaction region.

Fig. 1 Schematic diagram of the experimental setup with electron gun, recoil ion momentum spectrometer (RIMS) and a gas-mixing setup.

The generated ions were extracted towards a position-sensitive detector (PSD) by applying a pulsed electric field of 50 V cm⁻¹ in the target region. As a result, the ions are collected for emission over the full solid angle. The extraction field is high enough to guarantee the collection of fragment ions with appreciable kinetic energies and preserve a sufficient mass resolution.

A mixture of the selected halomethane and a reference gas was introduced into the chamber through a small tube (inner diameter of 1.0 mm), placed between the ion extraction electrodes. The gas flow was controlled by a precision leak valve. The background vacuum of the reaction chamber was maintained at better than 3 × 10⁻⁹ mbar, while the working pressure was kept at approximately 1.5 × 10⁻⁷ mbar to ensure a high signal-to-noise ratio. The partial pressures of the reference and target gases were measured in a small reservoir with a capacitance manometer at an accuracy of 1% before mixing them in a large reservoir.

Partial ionization cross sections were measured and converted to absolute values by applying the relative-flow technique.⁵⁶ In the present experiments, the reference gas was krypton, selected for its proximity in mass to the fluoromethane fragments. This minimizes the mass effects in the target gas density, the extraction, flight, and detection processes and still allows for the discrimination of the charged atomic ions from the molecular fragments.

Combining the RIMS technique and the reference and target gas-mixing technique, the overall uncertainty of the absolute cross sections obtained is estimated to be ∼10%.

3 Results and discussion

The vertical ionization potentials and the appearance energies of the fragment ions for both molecules are listed in ref. 43. From these tables, it is expected that the dissociation cross sections into an ion and a neutral will be dissimilar for both molecules considering that the ionization energies of the molecular orbitals differ by ∼1 eV. The bond lengths in CH₄ and CF₄ are 1.0864 Å and 1.3122 Å, respectively, and in CHF₃ the C–H and C–F bond lengths are 1.0849 Å and 1.3267 Å, respectively.^57,58 The displacement of the halogen atoms results in a larger delocalization of the charge fluxes (long-range electronic charge transfers). This probably leads to relationships between halogen charge fluxes and bond character descriptors. The dissociation energy of the bond (BDE) is C–H (4.27 eV) in the CH₄ and the C–F bonds in CF₄ (5.34 eV) resulting in a difference in the BDE of 1.1 eV between CH₄ and CF₄, while between CH₄ and CF₃–H (BDE = 4.49 eV) of only 0.22 eV.^59,60

A series of experimental works from different groups have undergone successive remeasurements and reanalysis, as discussed in the articles by Christophorou et al.^44,45,49 Uncertainties in previous absolute cross-section measurements arise partly from experimental difficulties such as detector efficiencies, grid transmissions, signal processing, reduced extraction efficiencies for energetic fragments and inclusion of false events. Fragments can be lost during collection and transport or not detected. In cases of ion–ion pair production, if one of the ions is not detected, it can introduce double-ionization events into the single-ionization spectrum. Such factors may have systematically led to an overestimation in the total and partial ionization cross sections in earlier work.

First, we present the experimental data set of tetrafluoromethane and then fluoroform. In the following, to get more insight into the break-up processes and subsequent ion- and ion-pair formation, dissimilar features are highlighted by comparing the dissociative single- and double-ionization cross sections of these fluorine-based methane molecules.

3.1 Tetrafluoromethane (CF₄) single and double ionization cross sections

The TOF spectrum of CF₄ with and without the reference gas Kr is shown in Fig. 2. All fragments of CF₄ are clearly separated from the krypton ions. The absence of the parent ion CF₄⁺ in the spectrum is expected, as its ionic states are inherently unstable and dissociate within femtoseconds after formation.

Fig. 2 TOF spectrum for CF₄ (red line) and mixed CF₄ + Kr gases (black line) at 200 eV impact energy. Both spectra were normalized for the CF₃⁺ ion peak. The krypton lines are split since there are six stable isotopes with significant abundance.

If the ion intensity is plotted both as a function of time-of-flight (TOF) and the position of the ions on the detector, it can be seen in Fig. 3 that essentially all fragment ions are collected over their full momentum spread. The projection of the 2D-map on the horizontal TOF axis corresponds to the single ionization TOF spectrum, which allows for the extraction of the intensities of the single-ion channels.

Fig. 3 (left) 2D map of Y-position on the detector and time-of-flight (TOF) spectrum for CF₄ at 200 eV. (right) Projection onto the Y-axis of the 2D spectrum.

As discussed in detail in ref. 56 the ion signal from double ionization needs to be subtracted from the measured ionization yield for the precise determination of the total and partial dissociative single ionization cross sections. Therefore, the double ionization contributions were derived from the ion–ion coincidence signal. Table 1 shows the percentage corrections of the single ionization cross section values for the contributions of ion–ion pairs⁵⁶ for the different electron impact energies. The contribution of double ionization events is higher for the fluorine ion F⁺ than for CF_n=0–3⁺. Due to its large kinetic energy, this ion additionally has a higher probability of escaping detection or being lost in the collection process. In contrast, the lowest contribution is noted for the heavier CF₃⁺ ion. The ion–ion pair correction reaches at most 3% for the total single ionization cross section (TSICS), while for the fluorine atomic ion channel it amounts to almost 15% at 200 eV, respectively.

Table 1 Correction of the partial single ionization cross sections for CF₄ due to the subtraction of the ion-pair contribution from the measured ion yield (in percent, %). Also given is the resulting correction of the total single ionization cross section (TSICS)

E (eV)	CF3^+	CF2^+	CF^+	F^+	C^+	TSICS
30	0.00	0.00	0.00	0.00	0.00	0.00
40	0.00	0.00	0.00	0.00	0.00	0.00
70	0.21	2.14	2.27	10.61	2.28	0.76
100	0.48	3.71	5.76	13.61	2.28	1.99
200	0.54	4.25	11.11	14.48	4.78	3.01
400	0.45	3.96	9.79	14.19	5.41	2.71
600	0.36	2.82	8.65	12.72	3.72	2.01
800	0.45	3.41	8.89	15.08	4.36	2.30
1000	0.37	3.07	7.44	13.83	3.73	1.95

---

CF₄ has been extensively studied in terms of absolute total single ionization cross sections (TSICS). Fig. 4 presents the current TSICS data along with several sets of reported single-ionization measurements^{33,41,42,46,61–67} and calculations.^{33,38,55,64,67–72} For the total absolute single-ionization cross section of CF₄, both experimental and theoretical data show a broad range of peak cross sections and positions for the maxima. Across all experimental data, the highest cross section is reached at ∼120 eV with a maximum of 6.0 × 10⁻²⁰ m².⁶⁵ The cross section of ref. 73 gives a maximum of 3.6 × 10⁻²⁰ m², while the present work obtains 4.1 × 10⁻²⁰ m² which is free of double ionization contributions as discussed above and also of the meta-stable ions CF₃²⁺, CF₂²⁺. The series of BEB calculations, which included different effects, to describe the improved cross sections, show a varying range of amplitudes and the position of the maxima.⁵⁶

Fig. 4 Absolute total cross-section for single-ionization (TSICS) of CF₄. Present work (in black solid squares) compared to previous (a) experimental data^{33,41,42,46,61–67} and (b) theoretical calculations^{33,38,55,64,67–72} as a function of the electron energy.

In the case of CF₄, all primary ionization events lead to fragmentation of the molecule. The absolute partial single-ionization cross sections (PSICS) for CF₃⁺, CF₂⁺, CF⁺, F⁺, C⁺ are displayed in Fig. 5 and the double ionization cross sections resulting in CF₃²⁺, CF₂²⁺ ions are shown in Fig. 6. The numerical values are listed in Table 2.

Fig. 5 Absolute partial single ionization cross sections (PSICS) for CF₄. Present work (in black solid squares) compared to previous data^{41–43,46,61,62,65,66} available in the literature as a function of the electron energy. (a) Present data for all fragments for CF₄, (b) CF₃⁺, (c) CF₂⁺, (d) CF⁺, (e) F⁺ and (f) C⁺.

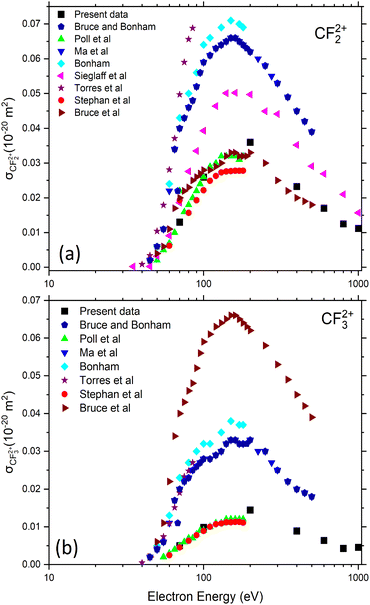Fig. 6 Absolute partial cross-section for double-ionization of CF₄ yielding (a) CF₂²⁺ and (b) CF₃²⁺. Present work (black solid squares) compared to previous data^{41–43,46,61,62,65,66} available in the literature as a function of the electron energy.

Table 2 TSICS, PSICS and MDICSs for CF₄ (in 10⁻²⁰ m²) as function of electron impact energies in eV

E (eV)	CF3^+	CF2^+	CF^+	F^+	C^+	TSICS	CF3^2+	CF2^2+
30	1.294	0.059	—	—	—	1.353	—	—
40	2.047	0.126	0.037	—	0.007	2.217	—	—
70	3.257	0.225	0.181	0.115	0.115	3.893	0.005	0.013
100	3.219	0.254	0.254	0.249	0.160	4.136	0.010	0.026
200	2.804	0.245	0.202	0.336	0.173	3.759	0.014	0.036
400	2.153	0.168	0.155	0.233	0.116	2.824	0.009	0.023
600	1.808	0.148	0.106	0.158	0.090	2.311	0.006	0.017
800	1.519	0.116	0.094	0.123	0.070	1.922	0.004	0.012
1000	1.338	0.103	0.084	0.101	0.062	1.688	0.005	0.011

---

Despite the previous experimental studies on CF₄, uncertainties remain about the precision of much of the work. Various studies have attempted to measure partial and total cross sections, with revisions and corrections made over time. Bonham⁶¹ provided corrected ICSs that account for multiple ionization and detector efficiency, based on earlier work by Ma et al.⁴² and Bruce and Bonham.⁶² In the work of Torres and Martinez,⁴³ the detection losses have been assumed to correspond to the escape of ions on their path to the detector. However, only a few studies have assigned uncertainties to their data, making comparisons challenging. All present PSICSs for dissociation into an ionized fragment plus a neutral are shown in Fig. 5a. The CF₃⁺ channel is predominant at all electron energies reaching a maximum of 3.2 × 10⁻²⁰ m² around 100 eV, while the other fragment channels are on average twelve to twenty times smaller and their maxima are at ∼200 eV. In Fig. 5 the current data for CF₃⁺ (b), CF₂⁺ (c), CF⁺ (d), F⁺ (e) and C⁺ (f) are compared with experimental data available in the literature. Especially F⁺ in Fig. 5e shows some inconsistencies in the course of the data and the magnitudes of the reported cross sections. For completeness we give the appearance energies for formation of the ion-neutral channels which for CF₃⁺, CF₂⁺, CF⁺, C⁺, and F⁺ are (15–16) eV, (20–22) eV, (27–29) eV, (34–35) eV, and (34–35) eV, respectively. The given intervals correspond to the spreading of the different works.^43,53,63,74

Absolute metastable double ionization cross sections (MDICS) were measured for production of two different ions, as seen in Fig. 6(a) CF₂²⁺ and (b) CF₃²⁺. They are relatively small and the previous results are strongly scattering. Generally few measurements have been made for the double ionization cross sections of CF₄.^41,46,61,75 In a recent work, five dissociative channels were observed by Wolff et al.⁵⁶ Here double ionization cross sections resulting in two charged fragments were extracted from ion–ion coincidence events. The fragmentation channel (CF₃⁺ + F⁺) is identified as a pure Coulomb explosion, whereas other channels, which produce neutral species, are classified as incomplete Coulomb explosion channels. The predominant channels for the formation of ion pairs include the fluorine ion in coincidence with 4 possible ion radicals, such as CF₂⁺ + F⁺ + F, CF⁺ + F⁺ + 2F, C⁺ + F⁺ + 3F, and F⁺ + F⁺ + CF₂. Interestingly, the pair of C⁺ + F⁺ atomic ions, the ion pair with by far the highest KER, and the pair of F⁺ + F⁺ have quite similar cross sections in agreement with a previous measurement.⁷⁵ The total and partial ion pair double ionization cross sections (TDICS and PDICS, respectively) are shown in Fig. 7 and listed in Table 3 for the TDICS (Fig. 7a) and for the production of CF₃⁺ + F⁺ (AE = 37.6 eV) (Fig. 7b), CF₂⁺ + F⁺ + F (AE = 42.4 eV) (Fig. 7c), CF⁺ + F⁺ + 2F (AE = 47.5 eV) (Fig. 7d), C⁺ + F⁺ + 3F (AE = 62.0 eV) (Fig. 7e) and F⁺ + F⁺ + CF₂ (Fig. 7e). The appearance energies (AE) are given in parentheses for completeness.^41,44,76

Fig. 7 Absolute total and partial cross-sections for double-ionization (TDICS and PDICS, respectively) of CF₄. Present work (in black solid squares) compared to previous data^41,46,61 available in the literature as a function of the electron energy. (a) Present TDICS, (b) CF₃⁺ + F⁺, (c) CF₂⁺ + F⁺ + F, (d) CF⁺ + F⁺ + 2F, (e) C⁺ + F⁺ + 3F and (f) F⁺ + F⁺ + CF₂ for the CF₄ molecule.

Table 3 TDICS and PDICS for CF₄ (in 10⁻²⁰ m²) as function of electron impact energies in eV

E (eV)	CF3^+ + F^+	CF2^+ + F^+	CF^+ + F^+	F^+ + F^+	C^+ + F^+	TDICS
70	0.01324	0.00960	0.00820	0.00066	0.00063	0.03233
100	0.03024	0.01913	0.03026	0.00772	0.00729	0.09464
200	0.02972	0.02123	0.04923	0.01798	0.01698	0.1352
400	0.01892	0.01352	0.03279	0.01371	0.01295	0.09188
600	0.01273	0.00838	0.01966	0.00720	0.00680	0.05478
800	0.01340	0.00798	0.01795	0.00656	0.00620	0.05209
1000	0.00972	0.00636	0.01321	0.00496	0.00469	0.03894

---

The present PDICS shown in Fig. 7b–e for each ion–ion pair are smaller than any measured PDICS. The double ionization cross sections of the ion–ion pairs follow the trend that σ(CF⁺ + F⁺) > σ(CF₂⁺ + F⁺) ∼ σ(CF₃⁺ + F⁺) in ref. 41,46,61. These experiments measured maxima ∼0.2 (CF⁺ + F⁺), 0.06 (CF₂⁺ + F⁺) and 0.06 × 10⁻²⁰ m² (CF₃⁺ + F⁺) and disagree with the current measurements reaching at maximum 0.049, 0.021 and 0.030 × 10⁻²⁰ m² at 200 eV respectively.

In ion–ion coincidence experiments^41,61 the ratios of TSICS and TDICS for CF₄ were found to be 13 and 11, values which are close to 13 for CH₄ evaluated from ref. 77–79. However, it should be realized that the smaller ratio compared to CH₄ of the pr esent work is not surprising. The high electronegativity and ionization energy of fluorine makes the formation of two positive ions less favourable in CF₄ than in CH₄. Also it is interesting to see that for single ionization the F⁺ production is a minor dissociation channel while all ion pair channels inevitably produce F⁺. As result the ratio of TDICS for all pairs of (ions + F⁺) and PSICS for (F⁺ + neutral) amounts ∼40% at impact energies of 100 eV and higher (see Tables 2 and 3).

3.2 Fluoroform (CHF₃)

Due to its highly polar nature, CHF₃ differs from unpolar CF₄. Its dipole moment leads to a strong rotational spectrum and significant static polarizability. On the other hand, it is similar to CH₄ in terms of cross sections of vibrational excitation.

Electron impact ionization of CHF₃ was reported in both the high-energy and threshold regions.^27–29,80 However, similar to CH₄, the published experimental data for TICS and PICS vary, with disagreements and inconsistencies between the different studies.²⁷

Fig. 9 shows the ion TOF spectrum for CHF₃ and the reference gas krypton. All ions from CHF₃ are clearly separated from the krypton ions. A very small amount of CHF₃⁺ ions is found with a reflectron TOF spectrometer (see Fig. 11 and discussion below) which is in contrast to the CF₄⁺ ion, which is not stable and was not found in our measurements with an estimated detection limit of 10⁻²³ m². It should be noted that the CHF₃⁺ cation was never unambiguously observed in photoionization experiments.^58,81

Using the present RIMS setup, it was not possible to separate ions with and without the bound hydrogen atom; therefore, the product ions with and without the hydrogen atom were analyzed together, a procedure adopted in most previous studies.^29,32,67,74 According to high mass resolution measurements (see below) the three fragments CF₃⁺, CHF₂⁺ and CF⁺ show higher intensity while the fragments CHF₃⁺, CF₂⁺ and CHF⁺, respectively, have lower intensity and are observed as shoulders on the peaks of the former species.

The 2D map in Fig. 8 showing ion intensity as function of y-coordinate on the detector and ion TOF confirms that the ions are spread out across the detector and along the TOF coordinate due to their kinetic energies but, nevertheless, they are collected with high efficiency. From this 2D map conclusions on the momenta and the kinetic energies (KE) of the fragments can be drawn: light ions, such as (H)F⁺ and (H)C⁺ have much higher kinetic energy than heavier ions, such as C(H)F₃⁺, C(H)F₂⁺ and C(H)F⁺ ions.

Fig. 8 (Left panel) 2D map of Y position on the detector and time of flight (TOF) spectrum for CHF₃ at 200 eV. (Right panel) Projection onto the Y-axis of the 2D spectrum.

Fig. 9 TOF spectrum for CHF₃ (red line) and mixed CHF₃ + Kr (black line) gases at 200 eV. Both spectra were normalized by the CF₃⁺ ion peak.

In CHF₃ carbon is slightly more electronegative than hydrogen pulling electrons toward itself, while fluorine is more electronegative than carbon. In neutral CHF₃, the lengths of carbon hydrogen bonds are ∼1.09 Å, while those of carbon fluorine are typically 1.34 Å.⁵⁸ However, recent calculations determine that the length of the C–H bond is significantly elongated to 1.321 Å in the cation, while the C–F bond shrinks slightly to 1.284 Å.⁵⁸ The lengths of the bonds may suggest competition between the cleavage of the C–H bond and the C–F bond. In the case of the cationic CHF₃⁺ formation, it shows a low dissociation barrier of the C–H bond and a likely dissociation resulting in a very low yield of the parent ion.

Without overinterpreting the bond parameters, the first fragment ion, CF₃⁺, is a significant dissociation pathway but the predominant fragment ions are CHF₂⁺ (maximum of 1.9 × 10⁻²⁰ m² at 100 eV) with a relatively large release of kinetic energy during the cleavage of the C–F bond, implying a repulsive bond character. The intensity of the CF⁺ ion channel with the emission of one or more neutral fragments increases rapidly for energies greater than 40 eV and becomes the ion with the second highest yield. The single atomic ions (with H-linked or H-loss) are less abundant in single-ionization events and reveal themselves as competing pathways. All these observations are qualitatively in agreement with previous measurements for photoionization, with calculations and arguments based on molecular selective states.^58,81

Fig. 10 presents for the different break-up channels the ratio CHF_n⁺/CF_n⁺ as a function of the impact energy. These data are taken from literature^29,43 and from present experiments with a high-resolution reflectron mass spectrometer (RTOF)^56,82 for which only two channels CHF⁺ and CHF₃⁺ are included which have lower ion kinetic energies and, thus, good ion collection efficiency. For the other ones the reflectron spectrometer lacks full ion collection efficiency due to the higher ion kinetic energies. This is demonstrated in Fig. 11 where reflectron TOF spectra are shown for an electron energy of 150 eV. For break-up into CHF₂⁺, CH⁺, F⁺ and HF⁺, where double or triple peaks are found. This indicates that ions which are emitted perpendicular to the spectrometer axis are not reaching the detector pointing to a high transmission loss of part of the momentum distribution. Simulations of the ion trajectories might enable reconstructing the whole distribution. The use of a high-resolution time-of-flight spectrometer combined with good collection efficiency for high kinetic energies of the ions would warrant extracting precise cross sections, but this experimental condition is not available in most setups as well as in the present reflectron spectrometer.

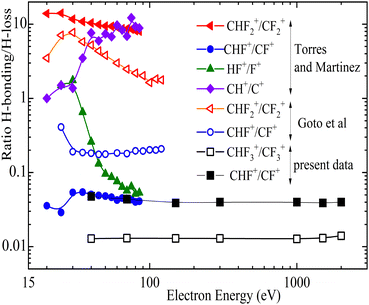Fig. 10 Ratios of hydrogen loss or attachment to radicals. Full symbols data extracted from ref. 43, open symbols from ref. 29 and present work, closed and open black square symbols (the measurements were done with a high resolution reflectron mass spectrometer).

Fig. 11 Representative reflectron time-of-flight spectra of the non-dissociative and dissociative ionization channels of CHF₃ collected at 150 eV electron impact. Insets were included to point out the detection of the CHF₃⁺ and CHF⁺ ions.

In Fig. 10 the cross section ratios of CHF₂⁺/CF₂⁺ and HF⁺/F⁺ reach a maximum around 30 eV impact energy. This is also the case for the ratio CHF⁺/CF⁺ of Torres and Martinez⁴³ which agrees with the present results while the respective data by Goto et al.²⁹ are a factor of four higher. The ratio CH⁺/C⁺ by Torres and Martinez⁴³ is rising until the high energy end of the measurement range at 100 eV. Also the published data for the CHF₂⁺/CF₂⁺ ratios are not in agreement which each other^29,43 concerning the magnitude and also the course as function of energy.

A particularly interesting behavior is found for the ratios of CH⁺/C⁺ and HF⁺/F⁺ measured by Torres and Martinez. For increasing impact energy, the C–H⁺ ion gets more favored, while the more convoluted formation of hydrogen bonded to a fluorine (HF⁺) is relatively declining. Finally, in the case of CHF⁺ and CF⁺ channels, the hydrogen loss resulting in CF⁺ strongly exceeds the CHF⁺ formation, probably due to the tight C–F bond.

These RTOF measurements in Fig. 11 have additionally enabled qualitative evaluation of the CHF₃⁺ parent ion intensity, which is indeed very weak, two orders of magnitude lower (1.3%) than the CF₃⁺ signal (98.7%). This suggests that in CHF₃⁺ there is only a small barrier along the C–H coordinate. In contrast, in the formation of the CHF₂⁺ species, the parent ion is repulsive along the C–F coordinate. The negligible formation of CHF⁺ and that of the favored CF⁺, follows probably some preferential decaying states as suggested in ref. 81.

Most doubly charged ions CHF₃²⁺ ions are unstable and dissociate into ion–ion pairs. From the 2D time-of-flight coincidence map, eight ion–ion pairs were predominantly observed: C(H)F₂⁺ + F⁺, C(H)F⁺ + F⁺ + F, (H)C⁺ + F⁺ + CF and (H)F⁺ + F⁺ + CF. In the Coulombic charge separation process of CHF₃²⁺, mostly a single atomic fluorine ion is ejected with charged carbon bonded to fluorines. Atomization with ejection of atomic ions (F⁺ + F⁺ or C⁺ + F⁺) is not a dominant channel.

The detection of the metastable dication CF₂²⁺ with m/z = 25 a.u. is interesting (see Fig. 8 at TOF 4700 ns). The small widths in the y-position on the detector and the TOF show reduced kinetic energy compared to the other heavier fragments. This species was collected by the recoil ion-momentum setup as well as by the reflectron time-of-flight spectrometer at electron energies ranging from threshold to 2000 eV. The reaction pathway of its formation is intriguing and further theoretical work describing its thermodynamics and structure is called for. In addition, CF₄ forms two metastable double charged species, CF₂²⁺ and CF₃²⁺, but the latter was not observed in the fluoroform case. The absolute metastable double ionization cross sections of CF₂²⁺ for CHF₃ at 200, 400, and 600 eV were measured as 0.011, 0.151, and 0.04 (× 10⁻²² m²), respectively.

Table 4 shows the percentage change (%) of the total and partial single-ionization cross section values if the ion contribution from ion-pair formation is subtracted. It is seen that the ion-pair contribution is rather low, less than 2% for the total single ionization cross section of CHF₃, but for the fluorine atomic ion the partial single ionization cross section decreases by almost 20% at 200 eV. In Table 5 we report TSICS and PSICS for the production of various ions, including (CF₃⁺ + CHF₃⁺), (CF₂⁺ + CHF₂⁺), (CF⁺ + CHF⁺), (F⁺ + HF⁺), (C⁺ + HC⁺), in the energy range from threshold to 1 keV.

Table 4 Ion–ion pair contribution in single ionization for CHF₃. Percentage of false ion–ion pairs in the single ionization cross sections (see text for definition) as function of electron impact energies in eV

E (eV)	C(H)F2^+	C(H)F^+	(H)F^+	(H)C^+	TSICS
70	0.26	0.56	9.00	0.51	0.54
100	0.48	1.25	13.92	1.91	1.21
200	0.62	1.93	19.44	4.04	1.93
400	0.60	1.94	15.12	4.42	1.85
600	0.51	1.62	13.47	3.83	1.54
800	0.44	1.48	12.98	3.39	1.38
1000	0.46	1.40	15.20	3.38	1.34

---

Table 5 TSICS and PSICS for CHF₃ (in 10⁻²⁰ m²) as function of electron impact energies in eV

E (eV)	C(H)F3^+	C(H)F2^+	C(H)F^+	(H)F^+	(H)C^+	TSICS
20	0.177	0.201	—	—	—	0.378
30	0.401	0.798	0.207	—	—	1.405
40	0.544	1.220	0.407	—	0.036	2.206
70	0.654	1.713	0.693	0.090	0.150	3.300
100	0.664	1.852	0.794	0.134	0.196	3.639
200	0.551	1.660	0.731	0.132	0.177	3.251
400	0.422	1.162	0.472	0.122	0.112	2.290
600	0.348	0.977	0.388	0.095	0.084	1.891
800	0.287	0.851	0.335	0.075	0.071	1.620
1000	0.253	0.756	0.293	0.053	0.059	1.414

---

The results presented in Fig. 12 show the combined cross-section data for CHF₃ and its fragments ((a) TSICS, (b) CF₃⁺ + CHF₃⁺, (c) CF₂⁺ + CHF₂⁺, (d) CF⁺ + CHF⁺, (e) F⁺ + HF⁺, (f) C⁺ + HC⁺). The present data are compared with existing experimental data from the literature. In some of the previous experiments, the ions formed as a result of multiple ionization could not be separated, and extra corrections were made. This is one reason, why the ionization cross sections were higher than the present values.

Fig. 12 Absolute total and partial cross-section for single-ionization (TSICS and PSICS) of CHF₃. Present work (in black solid squares) compared to previous data^{29,43,51–55} as a function of the electron energy. (a) TSICS (b) (CF₃⁺ + CHF₃⁺), (c) (CF₂⁺ + CHF₂⁺), (d) (CF⁺ + CHF⁺), (e) (F⁺ + HF⁺), (f) (C⁺ + HC⁺).

The earlier measurements by Goto et al.^27,29 and Poll et al.⁵³ within the 0–125 eV electron impact energy range are notably inconsistent with each other. Iga et al.⁵¹ discussed these discrepancies in detail, providing a reasoning for such differences. When comparing their cross-section results with the present study, it is found that the values of Iga et al. are closest but still larger than the current measurements. The energies of the cross section maxima are similar for all measured data, including the present one.

Results from four theoretical approaches are available for comparison to our data^33,67 and shown in Fig. 13. The position of the experimental cross section maximum is reproduced by the calculations within a few eV except the HV model by Torres et al.⁶⁷ where the deviation is almost 20 eV. The MAR results show the best agreement with the present TSICS in the shape and position of the maximum.

Fig. 13 Absolute total cross-sections for single-ionization of CHF₃ as function of the electron energy in eV. Present experimental work (black solid line and squares) compared to theoretical results for BEB and DM calculations of ref. 33 and MAR and HV calculations of ref. 67.

Earlier studies often underestimated the intensitiy of light ions as a result of insufficient detection efficiency for energetic fragments, leading to reliance on simulation programs. Additionally, fragment ions from double-ionization channels contributed to the single event counts. Double-ionization cross sections of CHF₃ have not been measured in the past, to the best of our knowledge. The double ionization cross sections are shown in Fig. 14 and are listed in Table 6 (TDICS and PDICS, respectively) for the production of the ion pairs CF₃⁺ + H⁺, C(H)F₂⁺ + F⁺, C(H)F⁺ + F⁺ + F, C(H)⁺ + F⁺ + 2F and (H)F⁺ + F⁺ + CF. The cross sections show maxima at ∼200 eV and decrease continuously for higher energies. The total double ionization cross section of CHF₃ is about two orders of magnitude lower than the single ionization cross section, which is comparable to the respective ratio for the CF₄ molecule.

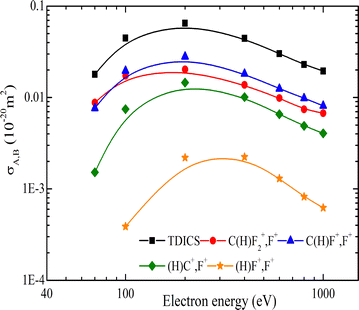Fig. 14 TDICS and PDICS for CHF₃ as function of the electron impact energy in eV. The lines are to guide the eye.

Table 6 TDICS and PDICS for CHF₃ (in 10⁻²⁰ m²) as function of electron impact energies in eV

E (eV)	C(H)F2^+ + F^+	C(H)F^+ + F^+	(H)F^+ + F^+	(H)C^+ + F^+	TDICS
70	0.00879	0.00762	0.00000	0.00152	0.01793
100	0.01731	0.01963	0.00039	0.00746	0.04479
200	0.02033	0.02801	0.0022	0.0146	0.06513
400	0.01378	0.01826	0.00224	0.01011	0.0444
600	0.00985	0.01248	0.0013	0.00656	0.03018
800	0.00741	0.00984	0.00082	0.0049	0.02297
1000	0.00674	0.00811	0.00062	0.00405	0.01953

---

By addressing the double-ionization issue, the current study provides more accurate counts of light ions coming from single-ionization discriminated from ion pair events. Therefore, previous studies reported higher numbers for the cross sections of light ions, while current values for heavier ions are more consistent with the measurements reported by Iga et al.⁵¹ and Torres et al.⁴³ This condition indicates a greater impact on single light-ion cross sections, while the heavier ones are less affected by the lack of pathway discrimination in earlier setups. The current methodology corrects this, leading to lower but more accurate values.

3.3 Comparison of the cross-sections of CF₄ and CHF₃ molecules

In Fig. 15, the TOF spectra of CF₄ and CHF₃ molecules are compared. As shown in Fig. 16f, the cross sections for the C⁺ ion in both molecules are comparable to each other. Based on this evidence, the TOF spectra were normalized for the C⁺ ion fragment. As shown in Fig. 15, the amount of C⁺ and F⁺ ions are similar for both molecules. On the other hand, CF⁺ and CF₂⁺ ions are more intense for CHF₃, while CF₃⁺ ions are more likely produced from the CF₄ molecule.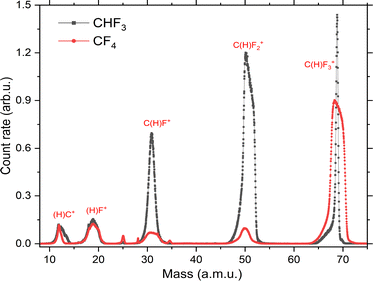

Fig. 15 Comparison of TOF spectra of CF₄ and CHF₃ molecules. Both spectra were normalized at the C⁺ ion peak.

Fig. 16 Total and partial cross-section for single-ionization of CF₄ and CHF₃. (a) TSICS (b) (CF₃⁺ + CHF₃⁺), (c) (CF₂⁺ + CHF₂⁺), (d) (CF⁺ + CHF⁺), (e) (F⁺ + HF⁺), (f) (C⁺ + HC⁺).

In Fig. 16, the absolute values of the single ionization cross section for the CF₄ and CHF₃ molecules are compared for each fragment ion, as well as the total ionization cross section. The cross sections are similar in trend and shape to each other as seen in Fig. 16a, but for the CF₄ molecule the absolute TICS is slightly higher. In the fluorcarbon series the cross section maximum increases with the molecular dipole polarizability α and the number of valence electrons Z of the molecule^39,83 according to 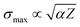. The energy position of σ_max should also increase, but this cannot be confirmed with the present data which are too sparse around the cross section maximum.

Comparing the charged fragment cross sections relative to the total single ionization cross section (see Fig. 17) following conclusions can be drawn: the channel with the ejection of one fluorine atom is strongly favored in the break up process for both molecules. In CF₄, the remaining channels have similar weak intensities. In CHF₃ the ejection of two fluorine atoms and the hydrogen emision are the next strongest channels. Rather unlikely channels are the production of C⁺ with a complete break-up of the molecules with the ejection of several neutral species.

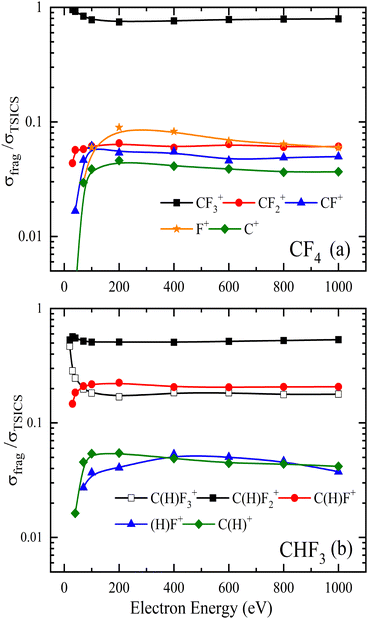Fig. 17 Ratio of the partial single ionization cross-section relative to the total single ionization of (a) CF₄ and (b) CHF₃.

The same analysis has been performed for the double ionization channels of both molecules (see Fig. 18). At the lowest impact energies the Coulombic channels CF₃⁺ + F⁺, CF₂⁺ + F⁺ and C(H)F₂⁺ + F⁺ dominate. At higher energies where all double dissociate channels are open, these channels decrease and the breakdown with the ejection of CF⁺ + F⁺ prevails.

Fig. 18 Ratio of the partial double ionization cross-section relative to the total double ionization of (a) CF₄ and (b) CHF₃.

4 Conclusion

This study of the electron impact ionization of CF₄ and CHF₃ obtained consistent and reliable data for the production of various ions, providing a comprehensive description of the single and double dissociative ionization processes.

The experimental RIMS setup used in this study can efficiently detect ions with fairly large kinetic energies over the full solid angle, ensuring a comprehensive data collection. The ion–ion coincidence technique allows for the identification of ions resulting from doubly ionized states and their discrimination from ions produced in single-ionization events. This distinction is crucial for obtaining accurate cross section data. In an earlier work, dissociative double ionization cross sections of CHF₃ were not measured, and only a few respective works are available for CF₄. The benefit of improved detection resulted in smaller cross sections compared to previous studies.

Refinements in experimental techniques and theoretical models, along with comprehensive data sets, are essential to advance the understanding and application of these relevant molecular processes. All theoretical models and experimental results represent significant efforts to improve the predictive capabilities of total and partial single- and double-ionization cross sections. The data are crucial for describing the environmental impact of these greenhouse gases in the atmosphere and application in plasma physics.

Data availability

The cross section data are given in tabular form in the article. All raw data are available upon request made to the corresponding author.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The project 21GRD02 BIOSPHERE has received funding from the European Partnership on Metrology, co-financed by the Horizon Europe Research and Innovation Program of the European Union and the participating States. Funder ID: 10.13039/100019599. Grant number: 21GRD02 BIOSPHERE. Open Access funding provided by the Max Planck Society.

Notes and references

1. W. Han, Y. Li, H. Tang and H. Liu, J. Fluorine Chem., 2012, 140, 7–16.
2. I. Mironova, M. Sinnhuber and E. Rozanov, XI International Conference “Solar-Terrestrial Relations and Physics of Earthquake Precursors”: Paratunka, Kamchatka region, Russia, September 22-25, 2020. Ed. A. Dmitriev, 2020, pp. Art.-Nr.: 01005.
3. I. Mironova, G. Bazilevskaya, G. Kovaltsov, A. Artamonov, E. Rozanov, A. Mishev, V. Makhmutov, A. Karagodin and K. Golubenko, Sci. Total Environ., 2019, 693, 133242.
4. P. M. Förster, V. Ramaswamy, P. Artaxo, T. K. Berntsen, R. A. Betts, D. W. Fahey, J. M. Haywood, J. L. Lean, D. Lowe, G. Myhre, J. Nganga, R. G. Prinn, G. B. Raga, M. Schulz and R. van Dorland, Changes in Atmospheric Constituents and in Radiative Forcing, https://api.semanticscholar.org/CorpusID:92599513/, 2007, ch. 2, Accessed: 2024.
5. V. Naik, A. K. Jain, K. O. Patten and D. J. Wuebbles, J. Geophys. Res.:Atmos., 2000, 105, 6903–6914.
6. F. Ladstädter, A. K. Steiner and H. Gleisner, Sci. Rep., 2023, 13, 1306.
7. R. Zander, S. Solomon, E. Mahieu, A. Goldman, C. P. Rinsland, M. R. Gunson, M. C. Abrams, A. Y. Chang, R. J. Salawitch, H. A. Michelsen, M. J. Newchurch and G. P. Stiller, Geophys. Res. Lett., 1996, 23, 2353–2356.
8. D. Gupta and B. Antony, J. Electron Spectrosc. Relat. Phenom., 2013, 186, 25–29.
9. A. M. Fernando, P. F. Bernath and C. D. Boone, J. Quant. Spectrosc. Radiat. Transfer, 2019, 238, 106540.
10. D. E. Oram, W. T. Sturges, S. A. Penkett, A. McCulloch and P. J. Fraser, Geophys. Res. Lett., 1998, 25, 35–38.
11. P. Fabian and D. Gömer, Fresenius' Z. Anal. Chem., 1984, 319, 890–897.
12. A. K. Steiner, F. Ladstädter, W. J. Randel, A. C. Maycock, Q. Fu, C. Claud, H. Gleisner, L. Haimberger, S.-P. Ho, P. Keckhut, T. Leblanc, C. Mears, L. M. Polvani, B. D. Santer, T. Schmidt, V. Sofieva, R. Wing and C.-Z. Zou, J. Clim., 2020, 33, 8165–8194.
13. M. Baasandorj, B. D. Hall and J. B. Burkholder, Atmos. Chem. Phys., 2012, 12, 11753–11764.
14. G. Jarvis, C. Mayhew, L. Singleton and S. Spyrou, Int. J. Mass Spectrom. Ion Processes, 1997, 164, 207–223.
15. A. R. Ravishankara and E. R. Lovejoy, J. Chem. Soc., Faraday Trans., 1994, 90, 2159–2169.
16. K. K. Irikura, M. A. Ali and Y. K. Kim, Int. J. Mass Spectrom., 2003, 222, 189–200.
17. J. A. P. David, W. Fahey, P. A. Newman and B. Safari, World Meteorological Organization (WMO). Scientific Assessment of Ozone Depletion, World Meteorological Organization, 2022.
18. Regulation (EU) 2024/573 of the European Parliament and of the Council of 7February 2024 on fluorinated greenhouse gases, amending Directive (EU)2019/1937 and repealing Regulation (EU) No 517/2014, 2024, Accessed: 2024.
19. R. Gopi, N. Ramanathan and K. Sundararajan, Spectrochim. Acta, Part A, 2017, 181, 137–147.
20. R. Motkuri, H. Annapureddy, M. Vijaykumar, H. Schaef, P. Martin, B. McGrail, L. Dang, R. Krishna and P. Thallapally, Nat. Commun., 2014, 5, 1–6.
21. L. G. Christophorou and J. K. Olthoff, Fundamental Electron Interactions with Plasma Processing Gases, Springer, 2004.
22. L. G. Christophorou, in Electronegative Gases, ed. E. E. Kunhardt and L. H. Luessen, Springer US, Boston, MA, 1983, pp. 133–176.
23. D. Gupta and B. Antony, Mol. Phys., 2014, 112, 1816–1823.
24. J. M. Wissing and M.-B. Kallenrode, J. Geophys. Res.:Space Phys., 2009, 114, A06104.
25. D. G. Voloshin, T. V. Rakhimova, K. S. Klopovskiy and Y. A. Mankelevich, J. Phys.:Conf. Ser., 2006, 44, 121.
26. G. Ko, E. Kim, D. Lee and Y. Seo, Korean J. Chem. Eng., 2023, 40, 1725–1730.
27. M. J. Kushner and D. Zhang, J. Appl. Phys., 2000, 88, 3231–3234.
28. S. Motlagh and J. H. Moore, in Radicals from Electron Impact on Fluorocarbons, ed. L. G. Christophorou and J. K. Olthoff, Springer US, New York, 1998, pp. 15–21.
29. M. Goto, K. Nakamura, H. Toyoda and H. Sugai, Jpn. J. Appl. Phys., 1994, 33, 3602.
30. B. K. Antony, K. N. Joshipura and N. J. Mason, J. Phys. B: At., Mol. Opt. Phys., 2005, 38, 189.
31. S. Tinck and A. Bogaerts, J. Phys. D: Appl. Phys., 2016, 49, 195203.
32. Q. Fu, Y. Qin and D. Zhang, Microporous Mesoporous Mater., 2020, 306, 110395.
33. M. Bart, P. W. Harland, J. E. Hudson and C. Vallance, Phys. Chem. Chem. Phys., 2001, 3, 800–806.
34. Y.-K. Kim and M. E. Rudd, Phys. Rev. A:At., Mol., Opt. Phys., 1994, 50, 3954–3967.
35. W. Hwang, Y. Kim and M. E. Rudd, J. Chem. Phys., 1996, 104, 2956–2966.
36. H. Deutsch, K. Becker, S. Matt and T. Märk, Int. J. Mass Spectrom., 2000, 197, 37–69.
37. H. Deutsch, K. Becker, R. Basner, M. Schmidt and T. D. Märk, J. Phys. Chem. A, 1998, 102, 8819–8826.
38. P. W. Harland and C. Vallance, Int. J. Mass Spectrom. Ion Processes, 1997, 171, 173–181.
39. G. P. Karwasz, P. Możejko and M.-Y. Song, Int. J. Mass Spectrom., 2014, 365–366, 232–237.
40. L. Mi and R. A. Bonham, J. Chem. Phys., 1998, 108, 1910–1914.
41. M. Bruce, C. Ma and R. Bonham, Chem. Phys. Lett., 1992, 190, 285–290.
42. C. Ma, M. R. Bruce and R. A. Bonham, Phys. Rev. A:At., Mol., Opt. Phys., 1991, 44, 2921–2934.
43. I. Torres and R. Martinez, J. Phys. B: At., Mol. Opt. Phys., 2002, 35, 2423.
44. L. G. Christophorou, J. K. Olthoff and M. V. V. S. Rao, J. Phys. Chem. Ref. Data, 1996, 28, 967.
45. L. G. Christophorou and J. K. Olthoff, J. Phys. Chem. Ref. Data, 1999, 25, 1341.
46. D. R. Sieglaff, R. Rejoub, B. G. Lindsay and R. F. Stebbings, J. Phys. B: At., Mol. Opt. Phys., 2001, 34, 799.
47. R. Martinez, B. Sierra, C. Redondo and M. N. S. Rayo, J. Chem. Phys., 2004, 121, 11653–11660.
48. L. Chen, E. Wang, X. Shan, Z. Shen, X. Zhao and X. Chen, Phys. Rev. A, 2021, 104, 032814.
49. L. G. Christophorou, J. K. Olthoff and M. V. V. S. Rao, J. Phys. Chem. Ref. Data, 1997, 26, 1–15.
50. J. L. Hernández-Ávila, E. Basurto and J. de Urquijo, J. Phys. D: Appl. Phys., 2004, 37, 3088.
51. I. Iga, I. P. Sanches, S. Srivastava and M. Mangan, Int. J. Mass Spectrom., 2001, 208, 159–167.
52. J. A. Beran and L. Kevan, J. Phys. Chem., 1969, 73, 3866–3876.
53. H. U. Poll and J. Meichsner, Beitr. Plasmaphys., 1987, 27, 359–372.
54. C. Jiao, R. Nagpal and P. Haaland, Chem. Phys. Lett., 1997, 269, 117–121.
55. Y. K. Kim, W. Hwang, M. A. Ali and M. E. Rudd, APS Annual Gaseous Electronics Meeting Abstracts, 1996, p. MPC.01.
56. W. Wolff, M. Dogan, H. Luna, L. H. Coutinho, D. Mootheril, W. Baek, T. Pfeifer and A. Dorn, Rev. Sci. Instrum., 2024, 95, 095103.
57. T. Q. Teodoro and R. L. Andrade Haiduke, RSC Adv., 2014, 4, 39853–39859.
58. Y. Chen, T. Yu, X. Wu, X. Zhou, S. Liu, F. Liu and X. Dai, Phys. Chem. Chem. Phys., 2020, 22, 13808–13817.
59. G. O. Pritchard and R. L. Thommarson, J. Phys. Chem., 1964, 68, 568–571.
60. L. A. Gribov, I. A. Novakov, A. I. Pavlyuchko and O. Y. Shumovskii, J. Struct. Chem., 2007, 48, 400–406.
61. R. A. Bonham, Jpn. J. Appl. Phys., 1994, 33, 4157.
62. M. Bruce and R. Bonham, Int. J. Mass Spectrom. Ion Processes, 1993, 123, 97–100.
63. C. Ma, M. R. Bruce and R. A. Bonham, Phys. Rev. A:At., Mol., Opt. Phys., 1992, 45, 6932.
64. H. Nishimura, W. M. Huo, M. A. Ali and Y.-K. Kim, J. Chem. Phys., 1999, 110, 3811–3822.
65. H. Poll, C. Winkler, D. Margreiter, V. Grill and T. Märk, Int. J. Mass Spectrom. Ion Processes, 1992, 112, 1–17.
66. K. Stephan, H. Deutsch and T. D. Märk, J. Chem. Phys., 1985, 83, 5712–5720.
67. I. Torres, R. Martinez and M. N. Sanchez Rayo, J. Chem. Phys., 2001, 115, 4041–4050.
68. M. Gryzinski, Phys. Rev., 1965, 138, A305–A321.
69. W. M. Huo, Phys. Rev. A:At., Mol., Opt. Phys., 2001, 64, 042719.
70. V. Graves, B. Cooper and J. Tennyson, J. Chem. Phys., 2021, 154, 114104.
71. D. Margreiter, H. Deutsch, M. Schmidt and T. Märk, Int. J. Mass Spectrom. Ion Processes, 1990, 100, 157–176.
72. W. Huo, V. Tarnovsky and K. Becker, Chem. Phys. Lett., 2002, 358, 328–336.
73. K. Stephan, H. Helm and T. D. Märk, J. Chem. Phys., 1980, 73, 3763–3778.
74. T. Fiegele, G. Hanel, I. Torres, M. Lezius and T. D. Märk, J. Phys. B: At., Mol. Opt. Phys., 2000, 33, 4263.
75. M. R. Bruce, L. Mi, C. R. Sporleder and R. A. Bonham, J. Phys. B: At., Mol. Opt. Phys., 1994, 27, 5773.
76. S. Tinck and A. Bogaerts, J. Phys. D: Appl. Phys., 2016, 49, 195203.
77. M. D. Ward, S. J. King and S. D. Price, J. Chem. Phys., 2011, 134, 024308.
78. P. Wang and C. Vidal, Chem. Phys., 2002, 280, 309–329.
79. B. G. Lindsay, R. Rejoub and R. F. Stebbings, J. Chem. Phys., 2001, 114, 10225–10226.
80. J. E. Baio, H. Yu, D. W. Flaherty, H. F. Winters and D. B. Graves, J. Phys. D: Appl. Phys., 2007, 40, 6969.
81. M. A. Parkes, R. Y. L. Chim, C. A. Mayhew, V. A. Mikhailov and R. P. Tuckett, Mol. Phys., 2006, 104, 263–272.
82. W. Wolff, A. Perlin, R. R. Oliveira, F. Fantuzzi, L. H. Coutinho, F. de A Ribeiro and G. Hilgers, J. Phys. Chem. A, 2020, 124, 9261–9271.
83. H. Nishimura, W. M. Huo, M. A. Ali and Y.-K. Kim, J. Chem. Phys., 1999, 110, 3811–3822.

---