Magnetic transition and work function modulation of Ti₂C MXene via porphine adsorption

Abstract

In this study, the adsorption of free-base and metal (Cu, Ag, Au) doped porphine molecules onto Ti₂C monolayer were simulated using DFT methods to study the structural and electronic properties of these hybrids. Results reveal that these structures may have interesting electronic properties that may vary depending on the type of the metal atom and the adsorption configuration of the molecule. In all structures, molecule adsorption triggered a magnetic transition from a semiconductor AFM state to a metallic FM state, demonstrating the potential of these hybrids in spin-dependent molecular electronics design. It is also shown that porphine adsorption can significantly reduce the work function of the Ti₂C monolayer, and this change, contrary to expectations, depends not only on the direction of charge transfer but also on the polarization of the total charge on the molecule. Additionally, no structural deformation was observed in any of the MD calculations performed at 300 K and 600 K for the porphine + Ti₂C hybrids.

---

1 Introduction

In recent years, a new era has begun in materials science with the discovery of graphene.^1,2 The unique technological properties of this monolayer have led researchers to search for new two dimensional (2D) materials with different properties.^3–6 Since 2D materials are only one or a few atoms thick, small chemical and physical manipulations can cause important changes in their observed properties.^1,3 The tunability of these changes has significantly increased the research potential of 2D structures, as it is useful in developing specifically designed materials for advanced technological applications.^7–9 It is possible to obtain monolayer structures not only from a single type of element but also from the combination of several different elements by using mechanical and chemical exfoliation or deposition methods.^3,5 Therefore, 2D materials research is carried out in a wide range. For example, in addition to single-element monolayers such as silicene,¹⁰ germanene,¹¹ and phosphorene,¹² 2D structures such as h-BN,^6,13 MoS₂, WSe₂,^14,15 and AsP^16,17 have also been studied experimentally and theoretically.

One of the interesting classes of 2D materials is MXenes which are obtained by etching away the layer-A from bulk MAX phases.^18–20 They are generally formulated as M_n+1X_nT_x (M = transition metals; X = C, N; n = 1–3 and T_x = surface termination, e.g., –OH, –F, –O). MXenes are chemically stable, have good electrical conductivity and high elastic moduli.²¹ Since they are hydrophilic and have highly active functional sites on their surfaces, they can serve as an effective substrate for the adsorption of many molecules or ions.^22,23 This feature makes MXenes to be tailored for many applications such as adsorptive remediation of pollutants,²³ energy storage/conversion,²⁴ sensor applications,^25,26 biomedical applications,^27–29 catalysts,^30,31 and supercapacitors.³² Ti₂C, one of the interesting members of the MXene family, has also been reported to have potential in lithium-ion batteries,^19,33,34 hydrogen adsorption and diffusion,³⁵ spin-based applications,^36,37 and sensing technologies.^38,39 It is also shown that the electronic and magnetic properties of this 2D structure can be modified by electric field, strain, and molecule adsorption.^37,40,41 The reaction of organic molecules with 2D materials is a topic that is being investigated for many purposes. In addition to determining the effects of the presence of these molecules on the fabrication process, how the surface can be specifically decorated with these molecules to design sensitive nanodevices is also the main focus of these research.^37,42–45 Thus, 2D surfaces can be further functionalized for many applications from biomedical to electronics.^23,46–48

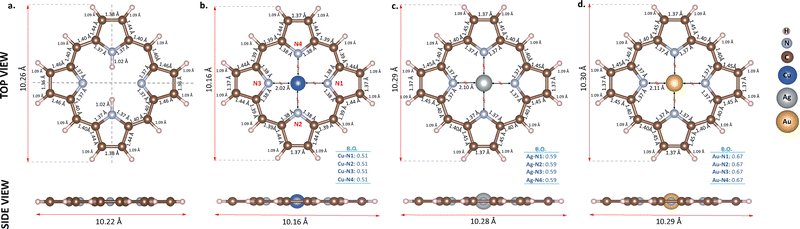
Porphine (2H-P) is a planar, aromatic macrocyclic molecule with the formula C₂₀H₁₄N₄, in which four pyrrole-like rings are connected to each other by a methine bridge, and is the most basic structure of porphyrins.^49–51 It can also be attributed as the main skeleton of the porphyrin family.⁵² Different atoms placed in the center of the porphine cycle lead the molecule to gain new and tuneable properties. If these atoms are metals (Cu, Ag, Co, Au, Sn etc.) they are called metalloporphines.^53–56 Their structural versatility, planarity and high conjugation make them quite remarkable for molecular-scale device design. There are interesting studies in the literature on hybrid structures formed by porphine-based molecules with other materials such as graphene,^7,57–59 Ag(111),^60–62 ZnO,⁶³ Cu(111),^53,64 carbon nanotube (CNT)⁶⁵ and Ag(100).⁶⁶

With this motivation, porphine adsorption onto Ti₂C surface was investigated in this study. Along with free-base porphine, which can be obtained naturally and synthetically; Cu, Ag and Au-doped metalloporphines were also taken into account due to their significant effects on anticancer, antitumor and antimicroorganisms.^67–72 Structural, electronic and magnetic properties of the considered hybrid structures were investigated by using ab initio DFT methods in order to provide information about their potential in molecular-based applications.

2 Method

In this study, spin polarized density functional theory (DFT)⁷³ calculations were performed by using the Vienna ab initio Simulation Package (VASP)^74,75 program to obtain the geometric, electronic and magnetic properties of considered structures. Projector-augmented wave (PAW)^76,77 potentials with a cut-off value of 550 eV were used for electron–ion interactions, while Perdew–Burke–Ernzerhof (PBE)⁷⁸ functionals with generalized gradient approximation (GGA) at the DFT-D3^79,80 level were adopted for electron–electron interactions. Brillouin zone was integrated according to the Monkhorst–Pack method⁸¹ with a (18 × 18 × 18) mesh for the unit cell, and a (3 × 3 × 1) mesh for molecule adsorbed ones. A (7 × 7) Ti₂C monolayer was used as the substrate. A vacuum distance of 25 Å was given between the two supercell layers to avoid interactions between the periodic images. All atomic positions and lattice constants were relaxed using the conjugate gradient algorithm.⁸² The total energy and the Hellman–Feynman force convergence limits between two self-consistent electronic steps were set to be 10⁻⁵ eV and 0.01 eV Å⁻¹, respectively. Gaussian smearing was used with a smear width of 0.01 eV. Optimization of isolated molecules was also performed in the simulation box with the same dimensions as the substrate. For the adsorption studies, molecules were placed on the optimized clean surface, keeping the dimensions of the simulation box constant, and relaxed with the same convergence criteria. In order to better include the electronic correlations of metal atoms, Hubbard + U method with Dudarev's approach⁸³ was considered and the effective Coulomb interaction parameters (U_eff) for metal atoms were calculated by using the linear response approach of Cococcioni and De Gironcoli.⁸⁴ The calculated U_eff parameters are Ti: 3.53 eV, Cu: 7.38 eV, Ag: 3.17 eV, and Au: 4.64 eV. Atomic structures were created with the VESTA⁸⁵ program. The adsorption energies were calculated according to the eqn (1).

E_Ads = E_{molecule+substrate} − (E_molecule + E_substrate) (1)

where E_{subsrate+molecule}, E_subsrate, E_molecule are the total energy values (per cell) of molecule adsorbed substrate, bare substrate, and isolated molecules, respectively. Net charges on atoms were calculated by using both of the Bader analysis⁸⁶ and density derived electrostatic and chemical charge analysis (DDEC) methods,^87,88 and the total charge transfer distribution of the resulting structures was calculated with eqn (2).

Δρ = ρ_{subsrate+molecule} − (ρ_subsrate + ρ_molecule) (2)

Work function ϕ is defined as the difference between the vacuum potential E_vac and the Fermi energy E_F as given in eqn (3).

ϕ = E_vac − E_F (3)

In order to determine the thermal stability of the corresponding hybrid structures, molecular dynamics (MD) simulations were performed in the NVT ensemble with the Nosé–Hoover thermostat at 300 K and 600 K.

3 Results

3.1 Properties of metalloporphine molecules and the clean Ti₂C surface

In the first stage of the study, porphine molecules and clean Ti₂C surface were modeled individually to determine their structural and electronic properties before the adsorption process. Fig. 1 shows the optimized geometries of the free-based porphine (2H-P) and functionalized ones with Cu, Ag, and Au atoms. In order to obtain metalloporphines, H atoms in the middle of the 2H-P cycle were replaced by metal atoms as shown in Fig. 1(b)–(d). All molecules kept their square planar geometry after optimization. Calculated molecular bond lengths of the free-based molecule are in full agreement with the previously given values.⁵⁰ Additionally, metal–N distances in doped molecules are also in compatible with the literature.^68,89,90 These organometallic bond lengths around 2 Å indicate direct binding. The total (TDOS) and partial (PDOS) density of states of all molecules are plotted in Fig. 2. According to this figure, the HOMO–LUMO (highest occupied molecular orbital–lowest unoccupied molecular orbital) gap of the 2H-P is 1.94 eV, and the spin up/down states are symmetric. However, the symmetry of the spin states is broken in all metal-functionalized molecules. This asymmetry is more pronounced near Fermi level for Ag and Au, while it is observed at lower energy levels for Cu. The total magnetic moments of these molecules were calculated as 1μ_B for Ag and Au while it is −1μ_B for Cu. Furthermore, the Fermi level (E_F) of each molecule is written inside the corresponding DOS plots in Fig. 2. While the Fermi level of 2H-P is −4.76 eV, the Fermi level of the Ag- and Au-doped molecules are −4.06 eV and −3.30 eV, respectively. The states around the Fermi level are dominated by the hybridization of the d-orbitals of the metal with the p-orbitals of the N atoms in the majority channel for Ag and Au. However, the situation is different for Cu-P. The contribution from Cu atom is almost negligible near the Fermi level (see Fig. 2b), which is why the Fermi energy of this structure (−4.80 eV) is almost the same as the free-based one. On the other hand, Au and Ag doping significantly decreased the HOMO–LUMO gap of the molecule, while Cu doping slightly increased it. As a result, it is clear that the electronic properties of the porphine molecule can be modified depending on the type of metal placed at the center.

Fig. 1 Top and side views of the optimized structures. (a) Free-based (2H-P) (b) Cu doped (Cu-P) (c) Ag doped (Ag-P) and (d) Au doped (Au-P). Bond order (BO) values of the metal atoms are given as insets.

Fig. 2 Total and partial DOS plots of molecules. (a) Free-based (2H-P) (b) Cu doped (Cu-P) (c) Ag doped (Ag-P) and (d) Au doped (Au-P). Fermi level is shown by the dotted vertical lines set to 0 eV.

The structural representation of Ti₂C is given in Fig. 3(a). This surface has a three-fold heterostructure formed with a C atom between two Ti atoms. While the bond length between Ti and C atoms in the hexagonal unitcell was 2.15 Å, the bond length between consecutive Ti–Ti and C–C atoms was calculated as 3.06 Å. These unit cell parameters are in good agreement with those in the literature.^{34,37,40,91–93} For the adsorption calculations, Ti₂C unitcell was enlarged to a (7 × 7) supercell due to the large size of the porphine molecules. According to the DOS plots shown in Fig. 3(b), p- and d-orbitals of Ti and the p-orbitals of C are continuous throughout the entire energy range considered. Ti₂C is a semiconductor with a band gap of 0.054 eV, where Fermi level lies at −2.31 eV. Band gap is also calculated as 0.17 eV without U parameter. This small band gap is seen to be indirect in the band structure plot given in Fig. 3(c). This surface also exhibits an AFM character with a magnetic moment of 1.22μ_B for Ti atoms and 0μ_B for C atoms. Magnetic moment values were calculated as μ_Ti = 0.77μ_B and μ_C = 0μ_B without including the U parameter. These above-mentioned results are consistent with many studies in the literature,^34,37,41 contrary to the ones that say Ti₂C is a magnetic metal.^40,93,94 On the other hand, the work function (ϕ) of Ti₂C, which is the minimum energy required for an electron to move from the surface to a vacuum point, was calculated as 4.08 eV (see Table 1). This result is also within the range of 3.98–4.67 eV values given in previous studies.^95–98 The differences between the calculated values are due to the use of different parameters and methods in the simulations.

Fig. 3 (a) Top and side view of Ti₂C surface and AFM Ti₂C unitcell. (b) Total and partial DOS graph Ti₂C (7 × 7) supercell. (c) Band diagram of Ti₂C supercell.

Table 1 Calculated parameters for free-based/doped porphine adsorption on Ti₂C surface. Adsorption energy (E_ads); the shortest distance (d_Ads), values in the parenthesis are the distances from the metal atom to the nearest Ti atom; Fermi energy (E_F); magnetic moment (μ); total charge transfer on the molecule (Δρ), the values in parentheses are the changes in the charges of the metal atoms in the adsorbed state compared to their charges in the isolated state, negative Δρ values correspond to the increase of e; work function of upper side with molecule (ϕ_upper); work function of lower side without molecule (ϕ_lower)

Structure	Eads (eV)	dAds (Å)	EF (eV)	μ (μB)	Δρ DDEC/Bader (e)	ϕlower (eV)	ϕupper (eV)
2H-P + Ti2C-I	−8.72	1.84	−1.88	−12.00	−3.17/−5.26	4.01	3.60
Cu-P + Ti2C-I	−9.23	1.89 (2.42)	−1.84	−9.75	−2.93/−4.80 (−0.39/−0.48)	3.98	3.57
Ag-P + Ti2C-I	−10.82	1.84 (2.77)	−1.86	−9.03	−3.13/−5.09 (−0.12/−0.32)	4.01	3.59
Au-P + Ti2C-I	−9.46	1.82 (2.67)	−1.83	−9.68	−2.94/−4.78 (−0.19/−0.45)	3.98	3.58
2H-P + Ti2C-II	−9.09	1.68	−1.85	−11.88	−3.28/−5.43	3.98	3.58
Cu-P + Ti2C-II	−9.66	1.86 (2.31)	−1.84	−6.80	−2.80/−4.48 (−0.48/−0.54)	3.98	3.62
Ag-P + Ti2C-II	−10.53	1.82 (2.94)	−1.81	−6.89	−2.86/−4.50 (−0.13/−0.32)	3.98	3.57
Au-P + Ti2C-II	−9.64	1.79 (2.70)	−1.83	−6.93	−2.85/−4.54 (−0.22/−0.47)	3.98	3.62
Bare Ti2C	—	—	−2.31	AFM	—	4.08	4.08

---

3.2 Adsorption of porphine molecules on Ti₂C surface

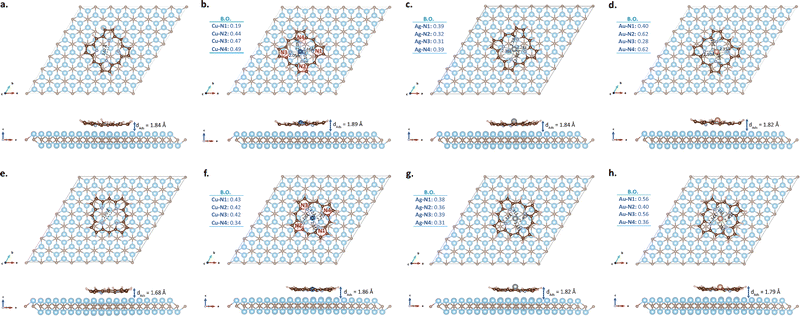
When modeling heterostructures, investigating the possible adsorption configurations of the molecule or another second 2D layer on the substrate is important for accurate modeling of the reactions occurring on the surface.^43,99,100 In some previous studies examining the adsorption of porphine onto Cu(111), Ag(111) and Au(111), it was stated that the first layer molecule adsorbs on the surface in a flat pattern rather than edgewise.^64,101–103 Based on this, to simulate the adsorption process of porphine molecules on the Ti₂C surface, the molecules were placed in two different orientations parallel to the surface. The initial images of these two models before optimization are given in Fig. S1 (ESI†). The molecules in these two starting models are rotated by 45° compared to each other. In order to estimate the appropriate initial distance between the surface and the molecule for structural optimization, firstly single point energy calculations were performed for 3.5 Å, 3 Å and 2.6 Å with the centers of the molecules directly above the upper Ti atoms. According to the total energy values in Table S1 (ESI†), molecules were found to be more stable at 2.6 Å above the surface.

In the next step, structural optimization was performed by dropping molecules onto the substrate from 2.6 Å with their centers (a) directly above the top Ti atoms and (b) above the hole region between the top Ti atoms. After optimization, the molecular centers of all metalloporphines initially located on the Ti atom shifted towards the hole region due to the repulsive interaction between the metal and Ti. The optimized configurations are presented in Fig. 4 (a–d for model-I; e–h for model-II), and related parameters are given in Table 1. The first structural situation that stands out for all molecules in Fig. 4 is that all the H atoms in the pyrrole rings are pushed upwards from the surface, and the outermost C atoms tend to bend slightly. Furthermore, the metal atoms of Ag-P and Au-P in both models are pushed significantly upwards from the plane of the molecule, while the core regions of 2H-P and Cu-P remain relatively planar. The orientation of the molecules in model-I after optimization has not changed significantly compared to the initial states given in Fig. S1 (ESI†), only a small rotation in Ag-P is noticeable. On the other hand, while metalloporphines in model-II largely maintain their initial orientation after optimization, a very obvious rotation is observed in 2H-P. When the metal–N distances in Fig. 4 are compared with those given in Fig. 1, it is seen that the D_4h symmetry of the molecules at the center is disrupted due to adsorption. According to Fig. 4, symmetry breaking also depends on the different orientation of the same molecule on the surface, because the position of the atoms in the molecule with respect to the substrate is effective in the reaction at the interface. Since the distances of the N and metal atoms of metalloporphines to the surface in model-I and model-II are not the same, both the bond lengths and bond orders between M–N are different. Therefore, the orientation of the molecule on the Ti₂C surface is a notable parameter in terms of structural and electronic characterization.

Fig. 4 Adsorption of bare/doped porphine molecules on Ti₂C surface. (a)–(d) 2H-P, Cu-P, Ag-P, and Au-P for model-I, respectively. (e)–(h) 2H-P, Cu-P, Ag-P, and Au-P for model-II, respectively. Bond order (BO) values of the metal atoms are given as insets.

The shortest adsorption distance (d_Ads) in Table 1 is defined as the vertical height difference between the bottom atom of the molecule (which is one of the N atoms in all molecules) and the nearest Ti atom. This value does not show any significant difference between the two different adsorption models of each metalloporphine, but still the ones in model-I are slightly larger than those in model-II. When looking at 2H-P, the d_Ads value was measured significantly larger (∼9.5%) in model-I than in model-II. In general, d_Ads of the metalloporphines is seen to increase inversely proportional to the atomic radius of the included metal in both models. However, the similar trend shown by d_Ads depending on the type of metal was not observed at the distances of the metals from the surface due to the symmetry breaking of the molecular nuclei and the downward migration of the substrate Ti atom after adsorption (see the d_Ads values in the parenthesis in Table 1). In both models, the shortest metal–surface distance was measured for Cu and the longest for Ag.

Table 1 also shows the adsorption energies (E_ads) calculated for all molecules. E_ads is an indicator of how strong the interaction between the molecule and the substrate is, and can therefore be used to compare the relative stability of systems. According to Table 1, the E_ads of 2H-P + Ti₂C is −8.72 eV for model-I and −9.09 eV for model-II. The adsorption energy of 2H-P on Cu(110) and Cu(111) is given as −3.47 eV and −4.03 eV in the literature, respectively.^102,104 As for the E_ads value of Cu-P, it is −9.23 eV for model-I and −9.66 eV for model-II, which is given as −4.26 eV for Cu-P/Cu(111).¹⁰² In other words, it can be said that 2H-P and Cu-P adhere more tightly to Ti₂C than Cu(110) and Cu(111). When the E_ads values of metal-doped porphines are compared with the undoped ones, it is seen that they are larger than the 2H-P in both adsorption models. Among them, the largest one belongs to Ag-P; −10.82 eV for model-I and −10.53 eV for model-II. Accordingly, it can be stated that Ag-P adheres more strongly to the Ti₂C surface than the others. The adsorption energies of all hybrid structures are negative, indicating that the process is exothermic and can occur spontaneously. These large E_ads values also indicate that the molecules chemisorbed to the Ti₂C surface. This interaction is also seen in the charge transfer data (Δρ) in Table 1 and charge transfer isosurfaces plotted in Fig. 5. Although the Δρ results obtained from Bader⁸⁶ and DDEC^87,88 methodologies are quantitatively different, both indicate that a significant charge transfer from the substrate to the molecule occurred in all configurations. The largest charge transfer per molecule was calculated for 2H-P in both models. Among the metallized ones, while the Δρ of Ag-P is clearly larger than the others in model-I, there is no such clear distinction for model-II. The values in model-II are so close to each other that the Δρ ordering of the DDEC and Bader results are different. In addition, the differences in the calculated Δρ values for each molecule for model-I and model-II indicate that the adsorption configurations have a significant effect on the charge transfer values. After adsorption, all metal atoms gained |e| compared to the isolated molecule states (see the Δρ values in parentheses in Table 1). As seen from the isosurfaces in Fig. 5, the charge exchange between the surface and the molecule occurs in almost every region of the molecule rather than in a limited region. This situation also supports quite large E_ads values.

Fig. 5 PDOS plots and charge transfer isosurfaces of free-based/doped porphine molecules adsorbed on Ti₂C. (a)–(d) 2H-P, Cu-P, Ag-P, and Au-P for model-I, respectively. (e)–(h) 2H-P, Cu-P, Ag-P, and Au-P for model-II, respectively. The red (blue) color in isosurfaces represents charge accumulation (depletion). The isosurface value is ±0.002 e Å⁻³.

The adsorption process affected the electronic state of the molecules and the substrate, causing the Fermi levels of the molecule + Ti₂C systems to increase compared to the pre-adsorption states (see the E_F values given in Table 1 for bare substrate and molecule + Ti₂C systems, and in Fig. 2 for isolated molecules). This molecule–substrate interaction can be clearly seen in the DOS and charge transfer plots in Fig. 5. The accumulation and depletion regions of the charge transfer isosurfaces are given separately and zoomed in on the molecule region for a clearer visibility. The superimposed images from a wider perspective can also be seen in Fig. S3 (ESI†). According to Fig. S3 (ESI†), molecules mainly interact with the top layer Ti atoms of the Ti₂C matrix, while the contribution from the other two bottom layers is quite small. During adsorption, large charge depletion regions appear on both the substrate and the molecules. The depletion regions on the substrate are the upper and lower edges of the top Ti atoms. In molecules, charges are depleted from C–C and some C–H bonds, as well as from the upper and lower edges of the metal atoms. On the other hand, in the Fermi neighborhood of the PDOS plots, the hybridization between the p- and d-orbitals of Ti atoms and the p-orbitals of molecules is more prominent. Similarly, charge accumulation regions mostly arise from the vertical overlap of C p_z-orbitals with Ti d_z²-orbitals. There is also charge accumulation on the side surfaces of the metals at the center of the molecules (see d_x²−y²-like orbitals in the top views in Fig. S3, ESI†), but this is not clearly visible in the PDOS plots due to the relatively large number of substrate atoms. Moreover, the comparison of the DOS plots in Fig. 5 (and Fig. S2, ESI†) with those in Fig. 2 also reveals that the discrete states of the isolated molecules are extended along the energy axis by hybridizing with the substrate during adsorption. The general electronic character for all molecules is metallic. The unsymmetrical DOS plots of the spin up and down states for each molecule in Fig. 5 and the total magnetic moment (μ) values given in Table 1 indicate that these structures gain FM character upon adsorption. When the magnetic moment values obtained for different adsorption models in Table 1 were compared, no significant difference was observed for 2H-P. However, the μ values of all metal-doped model-II configurations were found to be smaller than those in model-I. The μ values in Table 1 reveal that the magnetic moment of Ti₂C can vary depending on the adsorption orientation of the metalloporphines, but do not present a clear trend regarding the dependence of this change on the type of metal atom.

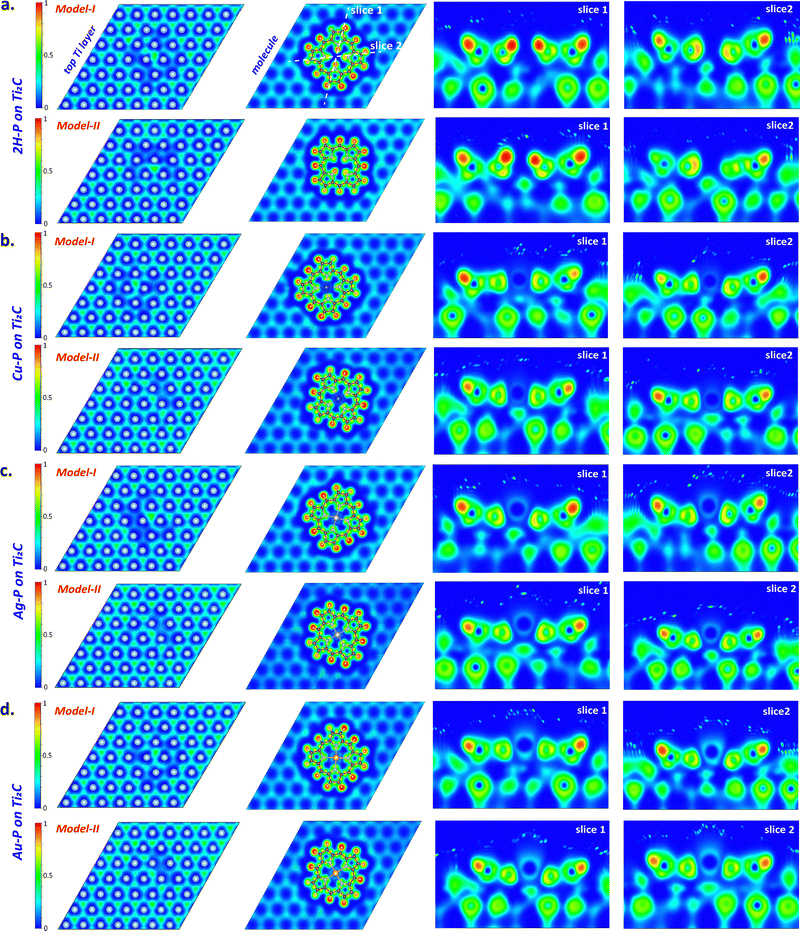
To further understand the nature of interaction between the molecule and the surface, the computed electron localization function (ELF) maps for different slices of the structures are given in Fig. 6. The electron distribution of the top Ti layer of all structures seen in the first column of Fig. 6 shows electron-gas-like continuity in the hole region between the metals with an ELF value of ∼0.5. Here, the homogeneity of the region at the bottom of the molecule is also disrupted, which is consistent with the charge transfer from the substrate to the molecule given in Table 1. On the molecular plane (second column in Fig. 6), strong covalent-type electron localization is found in the C and H networks. However, since there is no localization between N and metal atoms, metals are incorporated into porphine networks in ionic form. On the other hand, slice-1 and slice-2 in Fig. 6 cut the molecule center in two different orientations along the surface normal. In these slices, partial electron sharing is observed in the region between the C atoms of the molecule and the top layer Ti atoms, which is indicative of a weak covalent-like character. This is also consistent with the DOS overlap of C and Ti atoms and the charge transfer plots in Fig. 5. The electron sharing between C–Ti in 2H-P model-II is more pronounced, which is consistent with the Δρ value of this model being larger than model-I in Table 1. On the other hand, the electron distribution in the region between model-I metalloporphines and the substrate appears larger, in agreement with the Δρ values in Table 1.

Fig. 6 Computed electron localization function (ELF) plots for both models of (a) 2H-P, (b) Cu-P, (c) Ag-P, (d) Au-P. The first two columns are images of the top Ti layer and the molecule from planes parallel to the surface, respectively. The last two columns are images of slices cutting the structure along the surface normal, as shown by the dashed lines in (a). ELF values are normalized to the range of 0–1 in the color bars, where ELF = 1 represents the complete localization of electrons. ELF values around 0.5 (greenish colors) express that the electron localization in that area is comparable to that of a uniform electron gas, indicating a condition of moderate electron localization.

Work function (ϕ), and tunability of work function of technologically important materials by surface modification is an important parameter to determine the potential of these materials in various electronic applications.^{95,96,98,105,106} In addition to traditional explanations, factors affecting the ϕ characteristics of nanosurfaces are also discussed from new perspectives such as space groups or atomic-scale properties of the composition.¹⁰⁷ At this stage of our study, the effect of porphine/metalloporphine adsorption on the work function of Ti₂C was investigated. The work function of the bare Ti₂C was calculated as 4.08 eV for both upper and lower sides of the monolayer. This value is within the range given in the literature.^96–98,108 The new ϕ values of both sides of the monolayer after molecule adsorption can be seen in Table 1. It is clear that, porphine adsorption caused a significant decrease about ∼0.5 eV in the work function of the upper side. However, the closeness of the calculated values for model-I and model-II indicates that ϕ does not depend significantly on the adsorption orientation of the porphine molecule on the surface. The variation of the electrostatic potential in these structures along the z-axis can also be seen in Fig. S4 of the ESI.† At first glance, it would be expected that an inward dipole would form due to the charge transfer from the surface to the molecule, thus increasing the work function. However, the H atoms at the edges of the adsorbed molecules are curved upwards from the plane of the molecule, and although the total charge flow occurs from the surface to the molecule, the partial charge on the H atoms is positive. The total charge depletion values on the H atoms of each molecule after (model-I/model-II) adsorption are 2H-P = +2.02e/+2.01e, Cu-P = +1.35e/+1.32e, Ag-P = +1.40e/+1.32e and Au-P = +1.33e/+1.32e. On the other hand, negative charges are mostly collected on the lower edge of the molecule, which is close to the monolayer surface. Due to these charge depletion and accumulation regions within the molecule in the z-axis, a dipole is formed that reduces the dipole caused by total electron transfer. Thus, a decrease in the work function of the upper surface of the monolayer is observed. A similar situation is explained in detail in ref. 109. Moreover, it is clearly seen from the results in ref. 110 that the change in ϕ does not only depend on the charge transfer direction but is also strongly related to the molecule polarization. This adsorption induced work function change can also be used as a kind of detection and surface modification mechanism.¹¹¹ Furthermore, organic molecule-modified monolayer interfaces, due to their environmental friendliness, could be key materials in applications requiring low-work-function materials, such as electron microscopes, X-ray types of imaging, and medical equipment.³⁷ Therefore, based on our findings, porphines can be considered as good candidates for the work function modulation of the Ti₂C monolayer. In addition, although the differences between the ϕ values of the porphine + Ti₂C structures in Table 1 are small, this can be considered as an indication of the usability of different metal types for further fine tuning.

To test the stability of these hybrid structures, MD simulation for each molecule on Ti₂C surface were carried out for 4.5 ps at 300 K and 600 K with 1 fs intervals. The final structural models obtained after MD simulations and the time-dependent changes of energy and temperature during these simulations are shown in Fig. 7. The fact that no structural deformation is observed and the fluctuations in temperature and energy are quite small indicates that these structures are thermodynamically stable around 300 K and 600 K.

Fig. 7 Ab initio molecular dynamics (AIMD) simulation results at 300 K and 600 K. (a)–(d) 2H-P, Cu-P, Ag-P, and Au-P for model-I, respectively. (e)–(h) 2H-P, Cu-P, Ag-P, and Au-P for model-II, respectively.

4. Conclusions

This study examined the adsorption properties of free-based, Cu, Ag, and Au doped porphine molecules on Ti₂C monolayer. For all molecules the adsorption energy is negative, indicating the exothermic nature of the reactions. Besides, metal doping appears to increase the E_ads values compared to free-based porphine. All adsorption configurations are thermodynamically stable at 300 K and 600 K. Additionally, it can be said that the Ti₂C surface is a suitable substrate for porphine polymerization since all molecules maintain their structural integrity at these temperatures. Furthermore, adsorption of porphines shifted the Ti₂C surface from a semiconductor AFM state to a metallic FM state. Although the Cu/Ag/Au-doping seems to reduce the total magnetic moment of the molecule + Ti₂C systems compared to the free-based molecule, it can still be said that the functionalization of Ti₂C surface with these porphines has a high potential for spin-dependent applications. On the other hand, all molecules were found to act as a charge acceptor. The redistribution of charge via adsorption caused a resultant dipole to form between the molecular and nonmolecular sides of the substrate, changing the work function of these two faces. ϕ values decreased significantly on the molecule-located side of the monolayer. Small differences in the amount of decrease were observed depending on whether the molecule was doped or not and even on the type of dopant atom. It was observed that the change in the work function depends not only on the direction of the total charge transfer but also on the polarization of the molecule itself after adsorption. The results indicate that porphines are good candidates for the work function modulation of the Ti₂C monolayer.

Author contributions

P. Kaya: formal analysis, investigation, methodology, validation, visualization. Ç. Kaderoğlu: conceptualization, investigation, methodology, writing – original draft, supervision. E. Aktürk: conceptualization, investigation, methodology, resources, supervision. H. Arkın: conceptualization, investigation, methodology, resources, supervision, project administration.

Conflicts of interest

There are no conflicts to declare.

Data availability

The data supporting this article have been included as part of the ESI.†

Acknowledgements

Computing resources used in this work were provided by the TÜBİTAK (The Scientific and Technological Research Council of Türkiye) ULAKBIM, High Performance and Grid Computing Center (TR-Grid e-Infrastructure). ÇK also acknowledges the scientific collaboration with the Turkish Accelerator and Radiation Laboratory (TARLA). HA and EA acknowledge support from Alexander von Humboldt Foundation (Germany).

References

1. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669.
2. P. Suvarnaphaet and S. Pechprasarn, Sensors, 2017, 17(10), 2161.
3. A. K. Geim and K. S. Novoselov, Nat. Mater., 2007, 6, 183–191.
4. R. Mas-Balleste, C. Gomez-Navarro, J. Gomez-Herrero and F. Zamora, Nanoscale, 2011, 3(1), 20–30.
5. H. Zhang, Chem. Rev., 2018, 118(13), 6089–6090.
6. J. Zhou, Q. Wang, Q. Sun and P. Jena, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81(8), 085442.
7. Y. He, M. Garnica, F. Bischoff, J. Ducke, M. L. Bocquet, M. Batzill and J. V. Barth, Nat. Chem., 2017, 9(1), 33–38.
8. Y. L. Liu, Y. Shi, H. Yin and C. L. Yang, Appl. Phys. Lett., 2020, 117, 6.
9. J. Jalilian, G. Rezaei, B. Vaseghi, E. Zare, F. Kanjouri and F. Taghizadeh, Phys. Lett. A, 2024, 506, 129459.
10. J. Zhao, H. Liu, Z. Yu, R. Quhe, S. Zhou, Y. Wang and K. Wu, Prog. Mater. Sci., 2016, 83, 24–151.
11. M. E. Dávila, L. Xian, S. Cahangirov, A. Rubio and G. L. Lay, New J. Phys., 2014, 16(9), 095002.
12. H. Liu, A. T. Neal, Z. Zhu, Z. Luo, X. Xu, D. Tománek and P. D. Ye, ACS Nano, 2014, 8(4), 4033–4041.
13. B. Roondhe and P. K. Jha, ACS Appl. Nano Mater., 2019, 2(3), 1552–1561.
14. S. Manzeli, D. Ovchinnikov, D. Pasquier, O. V. Yazyev and A. Kis, Nat. Rev. Mater., 2017, 2(8), 1–15.
15. J. R. Schaibley, H. Yu and G. Clark, et al., Nat. Rev. Mater., 2016, 1(11), 1–15.
16. W. Yu, C. Y. Niu, Z. Zhu, X. Wang and W. B. Zhang, J. Mater. Chem. C, 2016, 4(27), 6581–6587.
17. T. Hu, B. Xu and J. Hong, Curr. Appl. Phys., 2017, 17(2), 186–191.
18. M. Naguib, M. Kurtoglu, V. Presser, J. Lu, J. Niu, M. Heon, L. Hultman, Y. Gogotsi and M. W. Barsoum, Adv. Mater., 2011, 23, 4248–4253.
19. S. Das, S. U. D. Shamim, Md. K. Hossain, F. Ahmed, Md. A. Hossain and M. O. Rahman, Appl. Surf. Sci., 2022, 600, 154173.
20. M. Faraji, A. Bafekry, M. M. Fadlallah, F. Molaei, N. N. Hieu, P. Qian and D. Gogova, Phys. Chem. Chem. Phys., 2021, 23(28), 15319–15328.
21. M. Kurtoglu, M. Naguib, Y. Gogotsi and M. W. Barsoum, MRS Commun., 2012, 2, 133.
22. M. Naguib, V. N. Mochalin, M. W. Barsoum and Y. Gogotsi, Adv. Mater., 2014, 26, 992–1005.
23. Y. Zhang, L. Wang, N. Zhang and Z. Zhou, RSC Adv., 2018, 8(36), 19895–19905.
24. X. Zhang, Z. Zhang and Z. Zhou, J. Energy Chem., 2018, 27(1), 73–85.
25. A. Shahzad, K. Rasool, W. Miran, M. Nawaz, J. Jang, K. A. Mahmoud and D. S. Lee, ACS Sustainable Chem. Eng., 2017, 5(12), 11481–11488.
26. R. Bhardwaj and A. Hazra, J. Mater. Chem. C, 2021, 9(44), 15735–15754.
27. K. Huang, Z. Li, J. Lin, G. Han and P. Huang, Chem. Soc. Rev., 2018, 47(14), 5109–5124.
28. K. Rasool, M. Helal, A. Ali, C. E. Ren, Y. Gogotsi and K. A. Mahmoud, ACS Nano, 2016, 10(3), 3674–3684.
29. A. Parihar, A. Singhal, N. Kumar, R. Khan, M. A. Khan and A. K. Srivastava, Nano-Micro Lett., 2022, 14(1), 100.
30. Y. Lan, L. Li, L. T. Zhang, Y. Jin, L. X. Xia, G. F. Huang and W. Q. Huang, Appl. Surf. Sci., 2022, 602, 154313.
31. N. Ma, N. Li, T. Wang, X. Ma and J. Fan, J. Mater. Chem. A, 2022, 10(3), 1390–1401.
32. W. Zhao, J. Peng, W. Wang, B. Jin, T. Chen, S. Liu and W. Huang, Small, 2019, 15(18), 1901351.
33. M. Naguib, J. Come, B. Dyatkin, V. Presser, P. L. Taberna, P. Simon, M. W. Barsoum and Y. Gogotsi, Electrochem. Commun., 2012, 16, 61–64.
34. Q. Wan, S. Li and J. Liu, ACS Appl. Mater. Interfaces, 2018, 10, 6369–6377.
35. S. Wang, Y. Du, W. Liao and Z. Sun, Int. J. Hydrogen Energy, 2017, 42, 27214–27219.
36. N. García-Romeral, Á. Morales-García, F. Viñes, I. P. R. Moreira and F. Illas, J. Phys. Chem. C, 2023, 127(7), 3706–3714.
37. T. Gorkan, H. Arkin and E. Aktürk, Phys. Chem. Chem. Phys., 2022, 24(4), 2465–2475.
38. T. Yang, X. Jiang, W. Yi, X. Cheng and T. Cheng, Appl. Surf. Sci., 2021, 544, 148925.
39. G. Jiang, R. Yang, J. Liu, H. Liu, L. Liu, Y. Wu and A. Youmei, Sens. Actuators, B, 2022, 350, 130859.
40. S. Zhao, W. Kang and J. Xue, Appl. Phys. Lett., 2014, 104(13), 133106.
41. P. Lv, Y. L. Li and J. F. Wang, Phys. Chem. Chem. Phys., 2020, 22, 11266.
42. A. N. Enyashin and A. L. Ivanovskii, J. Phys. Chem. C, 2013, 117, 13637–13643.
43. P. Kaya, O. Tercan, Ç. Kaderoğlu, E. Aktürk and H. Arkın, Surf. Interfaces, 2024, 46, 104087.
44. M. Boota, C. Chen, L. Yang, A. I. Kolesnikov, N. C. Osti, W. Porzio, L. Barba and J. Jiang, Chem. Mater., 2020, 32, 7884–7894.
45. J. D. Gouveia, G. Novell-Leruth, P. M. Reis, F. Viñes, F. Illas and J. R. Gomes, ACS Appl. Bio Mater., 2020, 3(9), 5913–5921.
46. Y. Zhong, S. Huang, Z. Feng, Y. Fu and A. Mo, J. Biomed. Mater. Res., Part A, 2022, 110, 1840–1859.
47. M. Mozafari and M. Soroush, Mater. Adv., 2021, 2, 7277–7307.
48. Z. Yen, D. G. Bradley, Y. Wang, J. V. Hanna and Y. M. Lam, ACS Appl. Nano Mater., 2024, 7(7), 7430–7441.
49. P. Rothemund, J. Am. Chem. Soc., 1936, 58(4), 625–627.
50. L. E. Webb and E. B. Fleischer, J. Chem. Phys., 1965, 43(9), 3100–3111.
51. H. C. Longuet-Higgins, C. W. Rector and J. R. Platt, J. Chem. Phys., 1950, 18(9), 1174–1181.
52. M. O. Senge and M. Davis, J. Porphyrins Phthalocyanines, 2010, 14(07), 557–567.
53. M. Schwarz and M. Garnica, et al., J. Phys. Chem. C, 2018, 122(10), 5452–5461.
54. F. Bischoff, K. Seufert, W. Auwarter, A. P. Seitsonen, D. Heim and J. V. Barth, J. Phys. Chem. C, 2018, 122(9), 5083–5092.
55. O. Albeydani, Phys. Scr., 2023, 98, 085403.
56. A. Mahmood, J. Y. Hu, B. Xiao, A. Tang, X. Wang and E. Zhou, J. Mater. Chem. A, 2018, 6(35), 16769–16797.
57. J. Zeng, K. Q. Chen and Y. X. Tong, Carbon, 2018, 127, 611–617.
58. V. A. Karachevtsev, S. G. Stepanian, M. V. Karachevtsev and L. Adamowicz, Comput. Theor. Chem., 2018, 1133, 1–6.
59. Y. H. Zhou, Y. Li, X. Zheng and K. Chen, Phys. E, 2021, 134, 114867.
60. P. Knecht, P. T. Ryan, D. A. Duncan, L. Jiang, J. Reichert, P. S. Deimel and A. C. Papageorgiou, J. Phys. Chem. C, 2021, 125(5), 3215–3224.
61. P. Knecht, B. Zhang, J. Reichert, D. A. Duncan, M. Schwarz, F. Haag and A. C. Papageorgiou, J. Am. Chem. Soc., 2021, 143(11), 4433–4439.
62. F. Bischoff, K. Seufert, W. Auwarter, S. Joshi, S. Vijayaraghavan, D. Ecija and J. V. Barth, ACS Nano, 2013, 7(4), 3139–3149.
63. M. Ekrami, G. Magna, Z. Emam-Djomeh, M. Saeed Yarmand, R. Paolesse and C. Di Natale, Sensors, 2018, 18(7), 2279.
64. M. Müller, K. Diller, R. J. Maurer and K. Reuter, J. Chem. Phys., 2016, 144(2), 024701.
65. J. D. Correa and W. Orellana, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86(12), 125417.
66. M. Uphoff, G. S. Michelitsch, R. Hellwig, K. Reuter, H. Brune, F. Klappenberger and J. V. Barth, ACS Nano, 2018, 12(11), 11552–11560.
67. D. Han, J. Niu, Y. Yang, C. Huang, W. Tan and X. Zhang, Chemosphere, 2024, 346, 140665.
68. W. J. Fu, W. L. Li, Y. X. Zhang, J. X. Zhang and J. Li, Comput. Theor. Chem., 2022, 1211, 113685.
69. T. Rundstadler, E. Mothes, S. Amrane, J. L. Stigliani, P. Verhaeghe and G. Pratviel, J. Inorg. Biochem., 2021, 223, 111551.
70. J. Zhang, L. Chang, R. Hao, G. Zhang, T. Liu, Z. Li and L. Zeng, Chem. Eng. J., 2023, 474, 145485.
71. M. Kielmann, C. Prior and M. O. Senge, New J. Chem., 2018, 42(10), 7529–7550.
72. G. V. Gyulkhandanyan, R. K. Ghazaryan, M. H. Paronyan, G. I. Ulikhanyan, A. G. Gyulkhandanyan and L. A. Sahakyan, Mechanisms for Low-Light Therapy VII, SPIE, 2012.
73. W. Kohn and L. J. Sham, Phys. Rev., 1965, 140(4A), A1133.
74. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(16), 11169.
75. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6(1), 15–50.
76. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50(24), 17953.
77. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59(3), 1758.
78. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77(18), 3865.
79. S. Grimme, J. Antony, S. Ehrlich and S. Krieg, J. Chem. Phys., 2010, 132, 154104.
80. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456.
81. H. J. Monkhorst and J. D. Pack, Phys. Rev. B, 1976, 13(12), 5188.
82. C. G. Broyden, IMA J. Appl. Math., 1970, 6(1), 76–90.
83. S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505.
84. M. Cococcioni and S. De Gironcoli, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035105.
85. K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44(6), 1272–1276.
86. G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360.
87. T. A. Manz and N. G. Limas, RSC Adv., 2016, 6, 47771–47801.
88. T. A. Manz, RSC Adv., 2017, 7, 45552–45581.
89. H. Y. Ammar and H. M. Badran, Heliyon, 2019, 5, 10.
90. M. J. Białek, K. Hurej, H. Furuta and L. Latos-Grażyński, Chem. Soc. Rev., 2023, 52(6), 2082–2144.
91. Z. Huang, Y. Wang and M. Zhang, Int. J. Hydrogen Energy, 2021, 46(66), 33176–33185.
92. D. Wang, Y. Gao, Y. Liu, Y. Gogotsi, X. Meng, G. Chen and Y. Wei, J. Mater. Chem. A, 2017, 5(47), 24720–24727.
93. X. Si, Q. Xu, J. Lin and G. Yang, Appl. Surf. Sci., 2023, 618, 156586.
94. G. Gao, G. Ding, J. Li, K. Yao, M. Wu and M. Qian, Nanoscale, 2016, 8, 8986.
95. S. Thomas and M. Asle Zaeem, Adv. Theory Simul., 2021, 4(3), 2000250.
96. S. Ozcan and B. Biel, RSC Adv., 2023, 13, 17222–17229.
97. L. Y. Gan, Y. J. Zhao, D. Huang and U. Schwingenschlögl, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 245307.
98. M. Khazaei, M. Arai, T. Sasaki, A. Ranjbar, Y. Liang and S. Yunoki, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92(7), 075411.
99. G. Zhang, J. Peng and Y. Zhang, Mater. Sci. Semicond. Process., 2024, 184, 108811.
100. J. Peng, G. Zhang, X. Guo and Y. Zhang, Surf. Interfaces, 2025, 57, 105774.
101. K. Leung, S. B. Rempe, P. A. Schultz, E. M. Sproviero, V. S. Batista, M. E. Chandross and C. J. Medforth, J. Appl. Chem. Sci., 2006, 128, 3472–3848.
102. D. A. Duncan, P. Casado Aguilar and M. Paszkiewicz, et al., J. Chem. Phys., 2019, 150(9), 094702.
103. K. Diller, F. Klappenberger and F. Allegretti, et al., J. Chem. Phys., 2014, 141(14), 144703.
104. M. S. Dyer, A. Robin, S. Haq, R. Raval, M. Persson and J. Klimes, ACS Nano, 2011, 5(3), 1831–1838.
105. K. Yusupov, J. Björk and J. Rosen, Nanoscale Adv., 2023, 5, 3976.
106. I. Ozdemir, H. Arkin, M. V. Milošević, J. V. Barth and E. Aktürk, Surf. Interfaces, 2024, 46, 104169.
107. L. Cui, Q. Li, Y. Zhang, J. Zhang, Z. Wang, J. Chena and B. Zheng, Chem. Sci., 2024, 15, 19375–19389.
108. S. Gohri, J. Madan and R. Pandey, Phys. Status Solidi A, 2024, 221, 2300650.
109. T. C. Leung, C. L. Kao and W. S. Su, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 195408.
110. P. Panigrahi, H. Vovusha, Y. Pal, H. Bae, H. Lee, T. Kaewmaraya, S. Nazir, M. J. A. Shiddiky and T. Hussain, ACS Appl. Nano Mater., 2023, 6, 22117–22127.
111. Y. Yong, R. Gao, X. Wang, X. Yuan, S. Hu and Z. Zhao, et al., Results Phys., 2022, 33, 105208.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp00622h

---