Identifying efficiency-loss pathways in triplet–triplet annihilation upconversion systems

Abstract

Triplet–triplet annihilation upconversion (TTA-UC) systems have been studied extensively recently, and have been proposed for use in a wide range of applications. Identification of the dominant mechanisms of upconversion-efficiency loss (UEL) will assist in the development of efficient TTA-UC systems. In this work, we combine experiments and kinetic analysis to study UEL. We identify exciplex formation and reverse triplet energy transfer (TET) as the two most important UEL mechanisms in the model TTA-UC system of platinum octaethylporphyrin (PtOEP) and 9,10-diphenylanthracene (DPA). Based on spectral analysis and time-resolved photoluminescence experiments, we show that exciplex formation is a potent UEL pathway in the PtOEP–DPA system. We demonstrate that prolonged sensitizer phosphorescence arises from reverse TET from annihilator triplet states, and that the reverse TET is likely facilitated by thermal population of low-frequency vibrational states in the sensitizer and the annihilator. Additionally, we demonstrate how the rate constants for reverse TET and exciplex formation can be estimated based on knowledge of a few key parameters and the experimental value of the optimum sensitizer concentration.

---

Introduction

Triplet–triplet annihilation upconversion (TTA-UC) is a process in which two annihilator triplet states that were created via triplet energy transfer (TET) from photogenerated sensitizer triplet states undergo disproportionation to produce an annihilator in a fluorescent singlet state and an annihilator in the ground electronic state. TTA-UC does not require high excitation powers to achieve frequency upconversion,^1–3 and can even be driven by an incoherent light source, such as a light-emitting diode (LED).^4–7 TTA-UC is being pursued for a variety of applications, such as bioimaging,^3,8–10 solar-cell performance enhancement,^11–15 and organic LEDs.^16–19 A kinetic analysis of the TTA-UC process indicates that the intensity of the upconverted light depends quadratically on irradiance under conditions in which unimolecular annihilator triplet-decay processes are favored over the bimolecular TTA process.^20–22 In the converse situation, the intensity of the upconverted light depends linearly on the irradiance. The irradiance at which the quadratic and linear regimes meet is commonly referred to as the threshold irradiance (I_th).²³ A higher sensitizer concentration increases the concentration of photogenerated sensitizer triplet states, thereby decreasing I_th. A smaller I_th is generally desirable, and is indicative of a TTA-UC system that performs efficiently at low irradiances. However, increasing the concentration of sensitizers has been observed to be deleterious to both the upconverted fluorescence intensity and the upconversion quantum yield.^24,25 Sensitizer TTA, which results in the net loss of one sensitizer triplet for every two that are photogenerated, is one suspected culprit in the decrease of the upconversion quantum yield with increasing sensitizer concentration.^26,27 However, for ideal TTA-UC systems, sensitizer TTA is often outcompeted by TET to the annihilator, and so sensitizer TTA may not be the sole driver behind the upconversion efficiency loss (UEL) that arises at high sensitizer concentrations. Back energy transfer from the emissive annihilator singlet states to the sensitizer, via long-range energy-transfer mechanisms such as Förster resonance energy transfer (FRET), has also been identified as a UEL mechanism that has the potential to become more important at high sensitizer concentrations.^28,29

Isokuortii et al. studied the effects of reverse TET, i.e., from the annihilator triplet state to the sensitizer, in cases in which the annihilator triplet energy was lower than, or slightly higher than, the sensitizer triplet energy.³⁰ These authors found that for an endothermic system in which the triplet energy of the annihilator was ∼0.08 eV lower than the triplet energy of the sensitizer, the rate constant for reverse TET from the annihilator to the sensitizer was twenty times larger than that for forward TET to the annihilator. A key finding of Isokuortii et al. is that even for a system in which the difference between the sensitizer triplet energy and the annihilator triplet energy is several times larger than the thermal energy, reverse TET can be the dominant annihilator triplet decay pathway at low irradiances. As discussed below, we believe that low-frequency vibrational modes are a key consideration in this phenomenon.

Efforts to reduce efficiency losses in the TTA-UC process, for example by minimizing the energy difference between the singlet and triplet states of the sensitizer,^31–33 or by minimizing the energy difference between the annihilator and sensitizer triplet states,^34,35 may inadvertently lead to UEL due to increased rate of reverse intersystem crossing (RISC) in the sensitizer in the first case, and of reverse TET in the second case. There have been numerous studies on photochemical upconversion systems in which the effect of reverse TET is manifested in the form of long-lived sensitizer emission.^36–38 Meroni et al. note, in a study of a TTA-UC system comprising Pd(II) meso-tetraphenyl tetrabenzoporphine and perylene,³⁸ that the lifetimes of the annihilator triplets and of the delayed phosphorescence that arises due to reverse TET must be equal. These authors concluded that an increase in the concentration of annihilators suppresses the effects of reverse TET, and increases the lifetime of upconverted emission. Although Meroni et al. did not study the effects of an increase in the sensitizer concentration, presumably such an increase would induce the opposite effect, i.e., enhancing the effects of reverse TET and reducing the lifetime of the upconverted emission.

Gholizadeh et al. reported the sensitizer-concentration-dependent quenching of annihilator triplets, a process they termed “dynamic quenching.”²⁴ These authors discovered that for a TTA-UC system consisting of platinum octaethylporphyrin (PtOEP) and diphenylanthracene (DPA), the dynamic quenching rate constant was 4.6 × 10⁶ M⁻¹ s⁻¹, roughly four orders of magnitude larger than the rate of intrinsic annihilator decay. Spin–orbit coupling (SOC) induced in the annihilator by the heavy central atoms common in photosensitizers, which is known as the heavy-atom effect,^39,40 is one possible origin of dynamic quenching. However, Gholizadeh et al. showed that the addition of a bromine-containing compound to a solution containing PtOEP and DPA did not affect the upconverted fluorescence intensity significantly. These authors also reported an increase in the empirically determined rate of dynamic quenching upon the replacement of the platinum in PtOEP with zinc, a lighter element. An important distinction between ZnOEP and PtOEP is that the triplet energy of the former (1.78 eV) is closer to that of the annihilator, DPA (1.77 eV), than is the triplet energy of the former.⁴¹ Therefore, reverse TET may also affect the apparent rate of dynamic quenching when ZnOEP is the sensitizer. The work of Gholizadeh et al. demonstrates that the heavy-atom effect cannot be the sole origin of dynamic quenching.

Although a large body of work has been dedicated to exploring UEL mechanisms on an individual basis, we are not aware of any concerted effort to analyze the potentially important UEL mechanisms with a mass-conserving kinetic model. A mass-conserving TTA-UC model accounts accurately for the steady-state concentration of ground-state molecules that can participate in various UEL processes.⁴² Therefore, it would be beneficial to use such a model to analyze UEL mechanisms that are driven by interactions between ground-state and excited molecules at high irradiances. Here we perform such an analysis of mechanisms whereby an increase in the concentration of sensitizers hinders the upconversion ability of a TTA-UC system. Using PtOEP and DPA as a benchmark TTA-UC system, we also performed steady-state and time-resolved TTA-UC measurements. Based on the results of these experiments, we explore a range of UEL pathways, and use our kinetic model to determine which of these UEL mechanisms are the most influential. We employ the ratio of the sensitizer phosphorescence intensity to the upconverted fluorescence intensity, a quantity that we term the emission ratio, to identify UEL mechanisms that reduce the upconverted fluorescence intensity at steady state, while either not affecting, or even enhancing, the amount of sensitizer phosphorescence. We also use our kinetic model to analyze the effects of reverse TET on the upconversion quantum yield, the sensitizer emission decay, and the annihilator triplet lifetime. We demonstrate how reverse TET can affect the rate of dynamic quenching, as determined from the dependence of the rate of annihilator triplet decay on the sensitizer concentration. We show how the balance between enhanced upconverted emission due to an increase in sensitizer triplet concentration on the one hand, and enhanced rates of reverse TET and dynamic quenching due to a high concentration of sensitizers on the other hand, is affected by the rate constants for the latter two processes. Finally, we demonstrate how the rates of reverse TET and dynamic quenching can be ascertained independently based on determination of the sensitizer concentration that leads to the maximum upconversion quantum yield and of the experimentally-determined overall rate of sensitizer-dependent annihilator triplet decay.

Methods

Experimental

PtOEP, DPA, 1,3-diphenylisobenzofuran (DPBF), and dimethyl sulfide (DMS) were purchased from Sigma Aldrich and used as received. TTA-UC samples were prepared by mixing stock solutions of PtOEP and DPA in toluene. DMS (0.5 M) was added to each sample to scavenge the singlet oxygen that forms during photoexcitation. For optical measurements, TTA-UC samples were prepared in a 1 cm × 1 cm quartz cuvette (FireflySci). To ensure effective removal of oxygen, the TTA-UC samples were sealed with rubber septa and then purged with N₂ gas for 10 min. To ensure that the DMS had removed the majority of any remaining oxygen, we only recorded data after the steady-state upconverted fluorescence intensity had stabilized. The phosphorescence lifetime of DPA in our samples (vide infra) is well in line with literature values for freeze/pump/thawed samples.^43,44 Taken together, these observations suggest that the oxygen removal in our samples was sufficient.

Upconversion data were collected at room temperature using a custom-designed setup that is shown schematically in Fig. S1 (ESI†). A 532-nm, continuous-wave (CW) laser (Coherent, Verdi V12) served as the excitation source. For time-resolved emission experiments, TTA-UC samples were excited by a train of square pulses that was generated by an acousto-optic modulator. A function generator (WaveTek, Model 29) and a radio-frequency generator (IntraAction, Model ME) were used to control the repetition rate, amplitude, and duty cycle of the pulse train. Emission from the TTA-UC samples was projected onto a forward-biased Si photodiode (NewFocus, 2001-FS) after passing through a 532-nm notch filter and a bandpass filter designed to isolate either the phosphorescence from PtOEP or the upconverted fluorescence from DPA. The time-resolved emission decay was detected by the Si photodiode and collected by a digital oscilloscope (LeCroy 9400A).

For steady-state TTA-UC measurements, samples were excited by a spatially-filtered, 532-nm CW beam. The excitation power was controlled with a half-wave plate and a polarizing beam cube. The half-wave plate was mounted in a computer-controlled rotation stage (Aerotech, Ensemble Epaq). The excitation power was measured by directing a portion of the spatially-filtered excitation beam through a mechanical chopper (Maxxon DC Motors) and onto a calibrated Si photodiode (Thorlabs, DET36A2). Steady-state emission from the TTA-UC sample was collected and projected through a mechanical chopper (Maxxon DC Motors) onto a matched Si photodiode. Upconverted light was isolated with a ±20 nm bandpass filter with its passband centered at 435 nm. Two digital lock-in amplifiers (Stanford Research Systems, DSP-SR810) were used to amplify the photodiode signals and to reject noise. Steady-state fluorescence measurements at various excitation powers were acquired in an automated fashion using a LabView program that rotated the half-wave plate by a 0.5° increment following each 2-s fluorescence-measurement interval. An entire set of upconverted fluorescence data typically consisted of data points collected at 32 different irradiances over a period of less than 70 s. Where needed, additional measurement intervals were added and a longer signal averaging time was used, resulting in an extended data-acquisition period of 135 s.

For spectral measurements, emission from the TTA-UC sample was coupled into a fiber-optic cable that was connected to a photospectrometer (Ocean Optics USB2000). A 532-nm notch filter was used to reject scattered excitation light. Emission ratios were calculated using the ratio of the “area under the curve” (AUC) of the emission spectra between 600 nm and 700 nm and the AUC of the emission spectra between 380 nm and 530 nm. These calculations were performed with MATLAB. To obtain emission ratio measurements at different excitation powers, a LabView program was used to rotate the half-wave plate by a 0.5° increment following each 4-s spectral measurement interval.

Kinetic modeling

The time-dependent concentrations of sensitizers in the lowest triplet state ([³S*]), annihilators in the emissive excited singlet state ([¹A*]), annihilators in the lowest triplet state ([³A*]), and annihilators in a higher triplet state ([³A**]) were computed numerically using MATLAB. A simulation covering dynamics over a period of 400 μs was performed with a fixed irradiation profile that consisted of a 200 μs, constant-amplitude, 2 W cm⁻² pulse, followed by a 200 μs “dark” period. [³S*]_t, [¹A*]_t, [³A*]_t, and [³A**]_t were computed with a time step of 1 ns. We note that the sensitizer singlet state was not modelled explicitly. Because ISC in most TTA-UC sensitizers, including PtOEP, takes place on a time scale that is far shorter than the time step of our simulations, the sensitizer triplet state was treated as being populated directly and losslessly via absorption of light from the ground state.

We now develop equations for [³S*]_t, [¹A*]_t, [³A*]_t, and [³A**]_t. A detailed derivation of these equations is given in the ESI.† For [³S*]_t, we find

where dt is the simulation time step. [S]₀ and [A]₀ represent the initial concentrations of sensitizers and annihilators in the TTA-UC system, respectively, and k_ex, k_FRET, k^S_T, k_ph, and k^S_q are the rate constants for excitation of ground-state sensitizers, FRET, intrinsic sensitizer triplet decay, sensitizer phosphorescence decay, and sensitizer triplet self-quenching, respectively. Additionally, k^S_TTA is the rate constant for TTA between two sensitizers, and k^F_sens and k^R_sens are the rate constants for triplet energy transfer from the sensitizer to the annihilator and from the annihilator to the sensitizer, respectively. For [³A*]_t we findwhere k^A_TTA is the rate constant for TTA between two annihilators, k^A_T is the rate constant for intrinsic annihilator triplet quenching, k_IC is the rate constant for internal conversion from the T_n state to the T₁ state of the annihilator, and k^A_q is the rate constant for dynamic quenching. For [¹A*]_t we findwhere k_fl and k^A_NR are the rate constants for the radiative and non-radiative decay of annihilator singlets, respectively, and k_RISC is the rate constant for reverse ISC from the T_n state to the excited singlet state of the annihilator. For [³A**]_t we find

[³A**]_t ≈ [³A**]_t−dt + dt(0.75k^A_TTA[³A*]_t−dt² − (k_IC + k_RISC)[³A**]_t−dt). (4)

Finally, the upconverted fluorescence rate, Fl(t), and the sensitizer phosphorescence rate, Ph(t), were calculated using

Fl(t) = k_fl[¹A*]_t (5)

and

Ph(t) = k_ph[³S*]_t, (6)

respectively. The initial conditions [³S*]₀, [³A*]₀, [¹A*]₀, [³A**]₀ = 0 were used when solving these equations. The smaller the time step dt, the more accurate the results for [³S*]_t, [³A*]_t, [¹A*]_t, [³A**]_t. A time step of 1 ns was chosen as a compromise between accuracy and efficiency.

The effective sensitizer and annihilator triplet lifetimes were calculated from the slopes of logarithms of the phosphorescence and fluorescence decays immediately after the excitation ceased,

andrespectively. The factor of ½ in eqn (8) arises from the fact that upconverted fluorescence depends quadratically on the population of annihilator triplets.

To model the formation and decay of radiative excimers and exciplexes explicitly, the concentrations of two additional species were introduced. The time evolution of the concentration of sensitizer excimers ([S*S]_t) is given as

[S*S]_t ≈ [S*S]_t−dt + dt(k^S_q([S]₀ − [³S*]_t−dt)[³S*]_t−dt − k^excimer_ph·[S*S]_t−dt), (9)

where k^excimer_ph is the rate constant for the radiative decay of sensitizer excimers. No non-radiative pathway was considered for the decay of sensitizer excimers. The rate of sensitizer excimer phosphorescence is then given by

Ph_excimer(t) = k^excimer_ph[S*S]_t. (10)

The time evolution of the concentration of exciplexes ([A*S]_t) is given as

[A*S]_t ≈ [A*S]_t−dt + dt(δ·k^A_q([S]₀ − [³S*]_t−dt)[³A*]_t−dt − k^ex_ph[A*S]_t−dt), (11)

where δ is the fraction of dynamic quenching events that result in the formation of sensitizer–annihilator exciplexes and k^ex_ph is the rate constant for the radiative decay of sensitizer–annihilator exciplexes. No non-radiative pathway was considered for the decay of sensitizer–annihilator exciplexes.

The steady-state phosphorescence and upconverted fluorescence rates were calculated by starting with the kinetic equations

andeqn (12)–(15) are solved under steady-state conditions to obtain the steady-state concentration of sensitizer triplets ([³S*]_SS), annihilator triplets ([³A*]_SS), annihilator singlets ([¹A*]_SS), and higher annihilator triplet states ([³A**]_SS). The rates of phosphorescence and upconverted fluorescence at steady state are given by

Fl_SS = k_fl[¹A*]_SS (16)

and

Ph_SS = k_ph[³S*]_SS, (17)

respectively. The emission ratio at steady state is given byThe quantum yield of delayed phosphorescence from reverse TET (Φ^R_ph) is given by[³A*]_t, [³S*]_t, [S]_t, and [A]_t were calculated numerically. Simulated irradiation of the TTA-UC sample occurred during the first 0.2 ms. Therefore, the total number of photons consumed as a result of photoexcitation is given by

Density–functional–theory calculations

Density–functional–theory (DFT) calculations on DPA and DPBF in their lowest triplet states were performed using (u)B3LYP-d3/def2SVP, i.e., the unrestricted B3LYP functional using Grimme's empirical dispersion correction⁴⁵ (d3) and the basis set of Weigend and Ahlrichs⁴⁶ (def2SVP). The vibrational frequencies obtained from the calculations on DPA were used to calculate the average energy in each mode via the equipartition theorem, which dictates that, for each mode,

〈E_vib〉 = ħω(1/(exp(ħω/k_BT) − 1)). (21)

Because the goal of these calculations was to determine the order of magnitude of the thermal vibrational energy, we did not include an anharmonic correction to the mode frequencies (which would increase the thermal vibrational energy) or attempt to use a more accurate method for treating the triplet state.

Results and discussion

A summary of the kinetic processes that constitute our basic mass-conserving TTA-UC model is shown in Fig. 1. The basic model does not consider any UEL mechanisms other than the intrinsic decays of sensitizer and annihilator triplets and the non-radiative decay of annihilator singlets. The rate equations for [³S*]_t, [³A*]_t, [¹A*]_t, and [³A**]_t were presented previously.⁴² Although our mass-conserving TTA-UC model provides valuable mechanistic insights into the TTA-UC process, the model does not predict that UEL is correlated with the sensitizer concentration.

Fig. 1 A schematic illustrating the processes that are considered in the basic TTA-UC model.

Fig. 2a and b show that the experimental upconverted fluorescence intensity at any given value of the irradiance increases when the sensitizer concentration goes from 2.5 μM to 10 μM. However, at higher sensitizer concentrations, the upconverted fluorescence intensity at any given value of the irradiance decreases with increasing [S]₀. A high concentration of sensitizers therefore appears to limit the upconversion yield, presumably through mechanisms such as quenching of annihilator triplets, expenditure of sensitizer triplets through sensitizer TTA, parasitic absorption of upconverted emission, and FRET.

Fig. 2 Experimental TTA-UC data for PtOEP–DPA samples. (a) The dependence of the upconverted fluorescence intensity on irradiance. The data (squares) were fit with the basic mass-conserving TTA-UC model. (b) The dependence of the upconverted fluorescence intensity at specific excitation powers on the sensitizer concentration. (c) The dependence of the emission ratio on the irradiance. (d) Emission spectra of PtOEP-DPA samples normalized to the emission intensity at 445 nm. The peaks that originate from upconverted fluorescence are indicated by *, and the peaks that originate from sensitizer phosphorescence are indicated by #. The arrow indicates scattered excitation light and sample emission around 532 nm, which were blocked using a notch filter. The concentration of the annihilator was 1 mM.

The emission ratio, eqn (18), allows us to differentiate between loss mechanisms that affect the yields of both sensitizer triplets and annihilator singlets upon photoexcitation on the one hand, and loss mechanisms that only impact the yield of annihilator singlets on the other. In the basic TTA-UC model, the expression for the emission ratio can be expanded as

In the low-irradiance regime, [³S*]_SS is small, so the dominant term within the radicand in eqn (20) is k^A_T. It is also the case when [³S*]_SS is small thatUnder these conditions eqn (22) can be simplified to

Therefore, at low irradiances, the emission ratio decreases as [³S*]_SS increases. Because [³S*]_SS is proportional to I, the emission ratio is inversely proportional to I at low irradiances. As I increases, [¹A*]_SS becomes proportional to I until, at high enough irradiance, [¹A*]_SS ceases to increase. When [¹A*]_SS and [³S*]_SS are both proportional to I, the emission ratio is independent of I. This trend in decreasing emission ratios with increasing I is consistent with the experimental TTA-UC data in Fig. 2c, which show that emission ratios decrease monotonically with I for all samples. Moreover, the rate of this decrease, i.e., the slope in Fig. 2c, becomes smaller with increasing I until the emission ratios are almost independent of I. An increase in [S]₀ will result in an increase in [³S*]_SS, all other things being equal. Therefore, according to eqn (24), we can expect that samples with higher sensitizer concentrations should exhibit lower emission ratios. This expectation is not consistent with the data in Fig. 2c. Our experiments show that when [S]₀ is within two orders of magnitude of [A]₀, the emission ratio increases with increasing [S]₀. We posit that this behavior is indicative of the existence of UEL mechanisms that quench excited annihilator molecules selectively while leaving the excited sensitizer population unaffected. Another possibility is that these UEL mechanisms enhance the yield of sensitizer triplets at the expense of excited annihilator molecules.

Fig. 2d shows emission spectra of TTA-UC samples with varying sensitizer concentrations. The spectra are normalized to the emission intensity at 445 nm. With increasing sensitizer concentration, the phosphorescence intensity increases relative to the intensity of the upconverted emission at 445 nm. Furthermore, an additional emission feature appears in the near-infrared (NIR) between 750 nm and 800 nm at higher sensitizer concentrations. This feature is not observed in the absence of the annihilator (Fig. S2a, ESI†). Therefore, we can rule out sensitizer-excimer emission and aggregation-induced emission as the cause of this NIR emission band. Radiative decay of exciplexes is a more likely explanation for the appearance of this feature. Indeed, we find that the integrated intensity of the NIR emission band has a dynamic dependence on excitation power, which is akin to the relationship between the upconverted fluorescence intensity and the excitation power (Fig. S2b, ESI†). Because the relationship between the integrated intensity of the NIR emission band and the excitation power is linear, rather than quadratic, at low excitation powers, we conclude that the concentration of the NIR-emissive species is directly proportional to the concentration of annihilator triplets. The data in Fig. S2a (ESI†) also reveal the presence of a secondary sensitizer emission peak at 680 nm that is suppressed upon the addition of the annihilator. Upon close inspection (Fig. S2c, ESI†), it is apparent that in the absence of the annihilator, the intensity of this secondary sensitizer-emission peak increases with increasing sensitizer concentration. We therefore believe that the sensitizer-concentration dependence of the emission peak at 680 nm is likely indicative of the formation of PtOEP triplet excimers, which have a broader, and slightly red-shifted, emission profile as compared to that of the monomer (at ∼650 nm).

Based on the above, we identify sensitizer-triplet excimer formation and quenching of annihilator triplets by ground-state sensitizer molecules to form exciplexes as two key UEL mechanisms in the PtOEP–DPA system. Additionally, because sensitizer phosphorescence is enhanced at the expense of upconverted fluorescence, we also consider the possibilities that FRET between the annihilator singlet state and the sensitizer singlet state and/or reverse TET are important UEL mechanisms. We additionally assess the effects of sensitizer TTA, a UEL mechanism that could be influential under circumstances in which the ratio between the concentrations of sensitizers and annihilators is high.

Fig. 3 shows a version of the Jablonski diagram from Fig. 1 in which the above-mentioned additional UEL mechanisms are included. Because the emissive annihilator singlet excited state is typically substantially higher in energy than the lowest sensitizer singlet excited state, FRET is assumed to be a unidirectional process from the annihilator to the sensitizer. Sensitizer TTA refers to the disproportionation of two sensitizer triplets, a process that ultimately results in the loss of one triplet, assuming a lossless ISC process should the annihilation generate an excited singlet state. Sensitizer self-quenching refers to the sensitizer-triplet excimer-formation process. The rate and quantum yield of the radiative decay of sensitizer triplet excimers may differ from those of an isolated sensitizer in the triplet state. Reverse TET refers to the Dexter energy-transfer process from the annihilator triplet to the sensitizer triplet. Finally, dynamic quenching is a catch-all term for processes in which annihilator triplets are quenched by sensitizer molecules, including the formation of an exciplex between an annihilator triplet and a sensitizer molecule and SOC induced by heavy-metal-based sensitizer compounds. The list of UEL mechanisms that we consider here is not exhaustive. For example, the reabsorption of upconverted light by the sensitizer may lead to outcoupling losses in TTA-UC systems,⁴⁷ and a concomitant reduction in overall upconversion efficiency.⁷ Functionally, this UEL pathway is similar to FRET, in that a sensitizer singlet state is generated in conjunction with the loss of an annihilator singlet state. The total rate at which upconverted light is extracted from the TTA-UC system can be expressed as β_extk_fl[¹A*]_SS. β_ext is a branching ratio that determines the proportion of upconverted light that can be extracted from a TTA-UC system, and is given by where k_ext is the rate constant for the external extraction of upconverted photons from the TTA-UC system and is the rate constant for the reabsorption of upconverted light by the sensitizer. When is large and k_ext is small, β_ext becomes small and the reabsorption of upconverted light can emerge as a highly influential UEL mechanism. In reality, k_ext depends on a variety of factors, including the geometry of system, and therefore it is non-trivial to obtain a definitive estimate for β_ext. For those reasons, here we have opted to not study the impact of the reabsorption of upconverted light by the sensitizer on emission ratios or upconversion quantum yields. However, we do offer further insights into this parasitic reabsorption process in the ESI.† Other potential UEL mechanisms, such as absorption of the upconverted light or of the excitation light by annihilators in the T₁ state and annihilator triplet-excimer formation, are not considered here, because the magnitudes of these mechanisms do not depend on the concentration of sensitizers.

Fig. 3 A schematic illustrating the processes that are considered in the enhanced TTA-UC model, with the UEL pathways depicted as red arrows.

Analytical, steady-state modelling was conducted to determine which of the aforementioned UEL mechanisms could replicate an upward trend in the emission ratio with increasing sensitizer concentration. The emission ratio at steady state was calculated from eqn (18). Fig. 4a shows that when k_FRET, k^S_TTA, k^S_q, k^R_sens, and k^A_q are all set to 0, the emission ratio at irradiances below 100 mW cm⁻² is inversely proportional to [S]₀. A similar trend in the emission ratio is observed when k_FRET = 2 × 10⁹ M⁻¹ s⁻¹ and k^S_TTA, k^S_q, k^R_sens, and k^A_q are zero (Fig. 4b). It is apparent that if FRET is to be competitive with the radiative annihilator singlet-decay pathway, it must be the case that k_FRET[S] ≈ k_FRET[S]₀ > k_fl. Typically, [S]₀ is orders of magnitude smaller than 1 M. Therefore, k_FRET must be several orders of magnitude larger than k_fl, which is usually on the order of 10⁸ s⁻¹, for FRET to become an influential loss pathway. An inverse relationship between the emission ratio and [S]₀ persists at moderate-to-low irradiances in instances in which sensitizer TTA or sensitizer self-quenching are the only UEL loss pathways, barring intrinsic quenching effects (Fig. 4c and d, respectively). This result is not surprising, because both sensitizer TTA and sensitizer self-quenching decrease the upconversion efficiency by reducing the availability of sensitizer triplets.

Fig. 4 Plots, based on kinetic modeling, of the dependence of the emission ratio on the irradiance for TTA-UC systems with UEL mechanisms including: (a) intrinsic quenching effects only; (b) FRET and intrinsic quenching effects only; (c) sensitizer TTA and intrinsic quenching effects only; (d) sensitizer self-quenching and intrinsic quenching effects only; (e) reverse TET and intrinsic quenching effects only; and (f) dynamic and intrinsic quenching effects only.

Reverse TET is an interesting case. Fig. 4e demonstrates that when k^R_sens = 2 × 10⁹ M⁻¹ s⁻¹ and k^S_TTA, k^S_q, k_FRET and k^A_q are 0, the emission ratio decreases with an increase in [S]₀ from 10 μM to 100 μM. However, a further increase in [S]₀ from 100 μM to 1 mM results in an increase in the emission ratio. There are two reasons why reverse TET is more likely to enhance the rate of sensitizer phosphorescence at the expense of upconverted fluorescence in TTA-UC systems than is FRET. First, reverse TET is a competitive pathway for the depletion of annihilator triplets, as long as k^R_sens[S] > k^A_T and k^R_sens[S] > k^A_TTA[³A*]. The rate constant k^A_T for annihilators such as DPA has been shown to be as low as 200 s⁻¹. Therefore, at low irradiances reverse TET can easily outcompete intrinsic annihilator triplet-quenching effects and TTA. At high irradiances, reverse TET can continue to outpace TTA, as long as the value of k^R_sens is on par with that of k^A_TTA and [³A*] does not exceed [S]. Second, the upconverted fluorescence rate depends quadratically on [³A*]. Therefore, mechanisms that reduce the population of annihilator triplet states will have a stronger impact on emission ratios than do mechanisms that reduce the population of annihilator singlet states, such as FRET.

Finally, as seen in Fig. 4f, dynamic quenching on its own, when k^A_q = 2 × 10⁹ M⁻¹ s⁻¹ and k^S_TTA, k^S_q, k_FRET and k^R_sens are 0, can reverse the decreasing trend in emission ratios with increasing [S]₀. An increase in [S]₀ from 100 μM to 1 mM elicits a larger increase in the emission ratio than does an increase from 10 μM to 100 μM. In a similar vein to reverse TET, dynamic quenching becomes a dominant depletion mechanism for annihilator triplets when k^A_q[S] > k^A_T and k^A_q[S] > k^A_TTA[³A*]. Unlike reverse TET, however, dynamic quenching does not generate an excited molecule that can participate in the upconversion process or can phosphoresce. Therefore, when compared to reverse TET, dynamic quenching has a stronger effect on suppressing the rate of upconverted fluorescence, but does not enhance sensitizer phosphorescence. Of the five UEL mechanisms discussed here, only reverse TET and dynamic quenching are consistent with the experimentally observed trends in emission ratios with increasing [S]₀.

We first consider the behavior when only reverse TET is added to the basic model. In this situation, the effective annihilator-triplet lifetime, which is half the value of the slope of the log–log plots of normalized upconverted emission at time scales longer than ∼50 μs, decreases with increasing sensitizer concentration (Fig. 5a). On the other hand, under the influence of reverse TET alone, the phosphorescence lifetime is initially dominated by the rapid forward TET process, and only on time scales longer than ∼50 μs does the radiative decay of sensitizer triplets that have been repopulated via reverse TET appear as a second exponential component (Fig. 5b). The form of the slow decay component in Fig. 5b mimics the form of the upconverted-emission decays in Fig. 5a.

Fig. 5 Transient decays derived from kinetic models including: (a) upconverted fluorescence in the presence of reverse TET only; (b) phosphorescence in the presence of reverse TET only; (c) upconverted fluorescence in the presence of dynamic quenching only; (d) phosphorescence in the presence of dynamic quenching only; (e) upconverted fluorescence in the presence of both reverse TET and dynamic quenching; and (f) phosphorescence in the presence of both reverse TET and dynamic quenching.

Fig. 5c and d show the results of kinetic modeling of the sensitizer phosphorescence and upconverted emission for systems in which dynamic quenching is the only UEL mechanism. Due to the dominance of dynamic quenching over TTA, no bimolecular decay component is visible in the upconverted-emission decays. However, the effective lifetime of annihilator triplets decreases rapidly with increasing sensitizer concentration. On the other hand, there is no change in the sensitizer-phosphorescence decays with increasing sensitizer concentration.

Fig. 5e demonstrates that when the effects of reverse TET and dynamic quenching are combined, the upconverted-emission decay at long times is dominated by the effects of dynamic quenching. The sensitizer-phosphorescence decays under the influence of both reverse TET and dynamic quenching resemble biexponential decays at all three sensitizer concentrations studied here (Fig. 5f). The form of the slow decay component in this case mimics that of the upconverted-emission decay curves in Fig. 5e.

The effects of reverse TET and dynamic quenching on the effective lifetime of the annihilator are most prominent when k^A_T < k^R_sens[S] < k^F_sens[A] or k^A_T < k^A_q[S] < k^F_sens[A]. Fig. S3a (ESI†) shows the dependence of the effective annihilator triplet lifetime on log(k^R_sens). This function has an inverse sigmoid shape. With increasing k^R_sens, the repopulation of annihilator triplets via forward TET becomes the rate-limiting step in the quenching of annihilator triplets via reverse TET, as shown in Fig. S3b (ESI†). Therefore, the upper asymptote in Fig. S3a and b (ESI†) is limited by the rate of intrinsic annihilator-triplet decay, and the lower asymptote is limited by the rate of forward TET. A similar relationship exists between both the effective sensitizer and annihilator triplet lifetimes and log([S]₀) (Fig. S3c and d, ESI†). Note that because the slow decay of the phosphorescence is a direct result of reverse TET, the effective lifetime of the sensitizer triplets is identical to that of annihilator triplets (i.e., τ_A = τ_S). Experimentally, a straightforward method of establishing the influence of reverse TET and dynamic quenching is to determine the dependence of τ_A⁻¹ on [S]₀. Fig. S4a (ESI†) illustrates the dependence of τ_A⁻¹ on [S]₀ under different UEL mechanisms. When dynamic quenching is the sole UEL mechanism, τ_A⁻¹ is linearly dependent on [S]₀, and the rate constant for dynamic quenching can be determined from the slope of the curve. However, with the inclusion of reverse TET, τ_A⁻¹ tapers off with increasing [S]₀. Fig. S4b (ESI†) shows that when reverse TET is the only UEL mechanism, this tapering-off effect of τ_A⁻¹ is more prominent for smaller values of [A]₀. With increasing [A]₀/[S]₀, the rate of forward TET is enhanced, thus decreasing τ_A⁻¹ and diminishing the overall impact of reverse TET, in agreement with the experimental results of Meroni et al.³⁸ Meroni et al. also found that the improvement in the overall efficiency of triplet sensitization with an increased annihilator concentration reaches a plateau. However, our results indicate that the critical parameter is not [S]₀, but rather [A]₀/[S]₀. Indeed, for a given set of rate parameters, we find that a near universal relationship exists between τ_A⁻¹ and log([A]₀/[S]₀), indicating that the effects of reverse TET on τ_A⁻¹ are negated once [A]₀/[S]₀ exceeds a certain value. Fig. S5a and b (ESI†) show that in a TTA-UC system that possesses identical k^R_sens and k^F_sens of 2 × 10⁹ M⁻¹ s⁻¹, the effects of reverse TET on τ_S⁻¹ and τ_A⁻¹ are largely negated when the annihilator concentration is roughly two orders of magnitude larger than the sensitizer concentration.

We next compare the dependence of τ_A on log([S]₀) when reverse TET is the only UEL mechanism and when both reverse TET and dynamic quenching are present (Fig. S6a and b, respectively, ESI†). These figures also show the dependence of Φ^R_ph, the quantum yield for delayed phosphorescence from reverse TET measured over a 400-μs period, on log([S]₀). Φ^R_ph is the difference in the quantum yield for phosphorescence (i.e., the number of emissive sensitizer triplets divided by the number of absorbed photons) with and without reverse TET. Fig. S6a (ESI†) shows that the growth in Φ^R_ph with increasing [S]₀ begins to accelerate when [S]₀ > 10⁻⁶ M. The growth in Φ^R_ph becomes linear with respect to log([S]₀) when log([S]₀) is ∼10⁻⁵ M. With a further increase in [S]₀, Φ^R_ph reaches an asymptote. On the other hand, the decrease in τ_A with increasing [S]₀ accelerates when k^R_sens[S]₀ ≫ k^A_T, a region in which the growth in Φ^R_ph with log([S]₀) has already begun to saturate. Fig. S6b (ESI†) demonstrates that dynamic quenching causes τ_A to begin to decrease at approximately the value of [S]₀ at which Φ^R_ph begins to increase, and that the behaviors of these two quantities roughly mirror one another. Once again, we find that dynamic quenching has a stronger effect on τ_A than does reverse TET. Moreover, dynamic quenching noticeably reduces Φ^R_ph. When k^R_sens = 2 × 10⁹ M⁻¹ s⁻¹, k^A_q = 0 M⁻¹ s⁻¹, and [S]₀ = 1 mM, Φ^R_ph is almost 90%, indicating that the vast majority of sensitizer phosphorescence originates from resensitized triplet states. The total phosphorescence quantum yield in this case is ∼19.0%. On the other hand, when k^R_sens and [S]₀ are maintained at their original values but k^A_q is increased to 2 × 10⁹ M⁻¹ s⁻¹, Φ^R_ph drops to just below 50%, indicating that a smaller proportion of the sensitizer phosphorescence can be attributed to reverse TET in this case.

Now that we have established that an increase in the sensitizer concentration can lead to an increase in τ_A, and thereby limit the upconverted fluorescence yield and the upconversion quantum efficiency, we turn to the dependence of the upconverted quantum yield, Φ_UC, on the sensitizer concentration. Φ_UC is calculated under the steady-state approximation for a specific value of I, and is defined as

In Fig. 6a–c, we demonstrate that Φ_UC possesses a Gaussian-like distribution as a function of log([S]₀). When [S]₀ is small, Φ_UC increases with increasing [S]₀, because a larger value of [S]₀ leads to larger values of [³S*]_SS and [³A*]_SS. A higher value of [³A*]_SS implies that the bimolecular TTA process is favored over all other annihilator-triplet-depletion mechanisms, thereby increasing Φ_UC. However, with further increases in [S]₀, the effects of an increase in [³A*]_SS are outweighed by an increase in the rates at which annihilator triplets undergo dynamic quenching and reverse TET. For pure dynamic quenching, an increase in [S]₀ is detrimental to Φ_UC when k^A_q[S]₀ > k^A_T.

Fig. 6 Dependence of Φ_UC on log([S]₀) for TTA-UC systems with UEL mechanisms including: (a) dynamic quenching effects only, varying k^A_q; (b) reverse TET only, varying k^R_sens; and (c) both dynamic quenching and reverse TET, varying k^A_q. (d) [S]_0,ideal for TTA-UC systems with both dynamic quenching and reverse TET, varying k^A_q and k^R_sens. Ascending numeric labels for k^A_q from 1 through 7 indicate increasing values, by one order of magnitude each, from 2 × 10³ M⁻¹ s⁻¹ to 2 × 10⁹ M⁻¹ s⁻¹, and the ascending numeric labels for k^R_sens from 1 through 4 indicate increasing values, by one order of magnitude each, from 2 × 10⁴ M⁻¹ s⁻¹ to 2 × 10⁷ M⁻¹ s⁻¹. The dashed lines in (a)–(c) represent the concentrations at which the maximum value for Φ_UC is found.

When a TTA-UC system possesses a large enough pool of ground-state annihilator molecules that annihilator mass conservation can be ignored, d[³A*]/dt can be expressed as

When the unimolecular decay terms are dominant, we can approximate thatAt steady state, [³A*]_SS can then be expressed asand the rate of fluorescence becomesWhen the bimolecular decay term is dominant, we can approximate that[³A*]_SS can then be expressed asand the rate of fluorescence isSetting eqn (29) equal to eqn (32), we find thatΦ_UC for any TTA-UC system is higher when the bimolecular TTA process dominates over unimolecular annihilator triplet-decay processes. Therefore, a system with a lower I_th exhibits a higher Φ_UC. According to eqn (33), the critical condition for an increase in [S]₀ to be detrimental to Φ_UC is that . The value of [S]₀ that leads to the largest Φ_UC, for a TTA-UC system that is affected by dynamic quenching, which we denote [S]_0,ideal, isThe ideal concentration of ground-state sensitizers can therefore be estimated from the value of k^A_T/k^A_q. Fig. 6c shows that with increasing k^A_q, the peak of a plot of Φ_UC as a function of [S]₀ (dashed lines) shifts towards smaller values of [S]₀. The magnitude of the peak value of Φ_UC also decreases with increasing k^A_q.

In the case of reverse TET, determining the value of [S]_0,ideal becomes more complicated. Once again ignoring the effects of annihilator mass conservation, d[³A*]/dt can be expressed as

Under the steady-state approximation, eqn (35) yields a quadratic expression for [³A*] in the low-irradiance regime (in which the unimolecular decay term dominates), and a cubic expression for [³A*] in the high-irradiance regime (in which the bimolecular decay term dominates). Although I_th can be obtained analytically from eqn (35), no analytical solution exists for [S]_0,ideal. Fig. 6b demonstrates that when k^R_sens is below 2 × 10⁹ M⁻¹ s⁻¹ and [A]₀ = 1 mM, Φ_UC continues to increase with increasing [S]₀, even as [A]₀/[S]₀ reaches unity. When k^R_sens = 2 × 10⁹ M⁻¹ s⁻¹ and [A]₀ remains unchanged, a peak value of Φ_UC is reached when [S]₀ ∼ 3.1 × 10³ M. When k^R_sens is increased further to 2 × 10⁹ M⁻¹ s⁻¹ and [A]₀ remains unchanged, [S]_0,ideal is near 3.2 × 10⁻⁴ M. Fig. 6c and d illustrate the combination of the effects of reverse TET and dynamic quenching on [S]_0,ideal. In Fig. 6c, k^R_sens was fixed at 2 × 10⁹ M⁻¹ s⁻¹ and k^A_q was varied from 2 × 10⁷ M⁻¹ s⁻¹ to 2 × 10¹⁰ M⁻¹ s⁻¹. Dynamic quenching has its strongest effect on [S]_0,ideal when k^R_q is on the same order of magnitude as k^A_q.

The intrinsic annihilator triplet-quenching rate has a prominent effect on Φ_UC and [S]_0,ideal. In the case of dynamic quenching, [S]_0,ideal is given roughly by k^A_T/k^A_q. Fig. S7a (ESI†) shows that when k^A_T is set at 2 × 10² s⁻¹ and k^A_q is fixed at 2 × 10⁹ M⁻¹ s⁻¹, [S]_0,ideal is precisely 10⁻⁷ M. When k^A_T is increased by an order of magnitude, [S]_0,ideal becomes 10⁻⁶ M. In contrast, with increasing k^A_T, Φ_UC decreases even as [S]_0,ideal increases. In the case of reverse TET, [S]_0,ideal increases proportionally with k^A_T, Φ_UC increases with increasing k^A_T, and there is a change in the shape of the distribution of Φ_UC. When k^A_T is small, the distribution in Φ_UC is broader than when k^A_T is large. Fig. S7b (ESI†) shows that when k^A_T is set at 2 × 10² s⁻¹ and k^R_sens is fixed at 2 × 10⁹ M⁻¹ s⁻¹, there is a less than a 1% drop in Φ_UC as [S]₀ increases by one order of magnitude from [S]_0,ideal. On the other hand, when k^A_T is set at 2 × 10³ s⁻¹, there is a nearly 2% drop in Φ_UC as [S]₀ increases by an order of magnitude from [S]_0,ideal. The implication of this finding is that for systems that possess smaller values of k^A_T, the impact on Φ_UC due to deviations from [S]_0,ideal is greatly reduced compared to what happens in systems with larger values of k^A_T. Φ_UC increases with increasing irradiance. However, [S]_0,ideal is largely independent of I. Fig. S7c (ESI†) demonstrates that even under varying conditions, [S]_0,ideal is independent of I.

Spin statistics dictate that for every excited singlet state that is populated via TTA, a higher triplet state and a quintuplet state should be populated as well. Typically, the quintuplet states are energetically inaccessible to the TTA pair. However, reverse ISC from a higher triplet state to the excited singlet state is possible. The effects of RISC can be captured by a branching ratio, β_RISC, which is given by

Here, the rate constant k_RISC governs the rate at which RISC occurs between the higher triplet state and the emissive excited singlet state.

The maximum theoretical value for Φ_UC, Φ_UC,max, is dependent on β_RISCvia

We investigated whether delayed upconverted emission via reverse ISC from higher triplet states could alter our analysis of [S]_0,ideal. Because RISC between higher triplet states and excited singlet states in the annihilator affects only the total yield of singlets following a TTA event, β_RISC would not affect the impact of reverse TET or dynamic quenching on τ_A, F_SS, or Φ_UC. Indeed, in our analysis of the effects of reverse TET and dynamic quenching, we find that β_RISC affects the magnitude of Φ_UC, but does not affect [S]_0,ideal (Fig. S7d, ESI†).

To assess the impacts of dynamic quenching and reverse TET on the model PtOEP–DPA upconversion system, we conducted transient photoluminescence experiments. The upconverted fluorescence decay of the PtOEP/DPA system in deaerated toluene is shown in Fig. 7a. Annihilator-singlet decay occurs on a time scale of several ns, and does not limit the rate of the fluorescence decay. Therefore, the data in Fig. 7a must reflect the normalized logarithmic decay of [³A*]². A function of the form

was used to fit the fluorescence decays. In eqn (38), α is a proportionality constant and β is a constant that describes the fraction of annihilator triplets that decay through bimolecular channels. Eqn (38) was adapted from Edhborg et al., whose β′ is identical to β.⁴⁸ However, to obtain the best fit to our data, β′ must be slightly larger than β. We believe that the need for using a different value in the denominator arises from the fact that in the approximation used by Edhborg et al., no new annihilator triplet states are generated after irradiation ceases, i.e. their kinetic equation contains only loss terms for annihilator triplet states. However, there remain excited sensitizers when irradiation ceases that can generate additional annihilator triplet states via TET. The full kinetic expression does not have an analytical solution, but we find that the partially ad hoceqn (38) provides better fits to our data than does the expression of Edhborg et al.

Fig. 7 Transient photoluminescence data. (a) Normalized upconverted fluorescence decay for TTA-UC samples with varying sensitizer concentrations. The data were fit to eqn (38). (b) Values of τ_A⁻¹ extracted from the data in (a). The solid line is the best linear fit to the data. (c) Normalized phosphorescence decays fit to eqn (39). (d) Values of τ_S⁻¹ extracted from the data in (c). The solid line is the best linear fit to the data. (e) Normalized phosphorescence decays fit to eqn (40). (f) Values of τ_A⁻¹ extracted from (a) and (e). The concentration of the annihilator was 1 mM.

The most important fitting parameter in eqn (38) is τ_A. Unsurprisingly, we find the bimolecular component of the upconverted-fluorescence decay to be dominant when the initial concentration of the sensitizer is high. More interestingly, we find that an increase in the initial concentration of PtOEP from 2.5 μM to 273 μM is accompanied by a steady decrease in τ_A⁻¹. When the experimentally-extracted values of τ_A⁻¹ are plotted as a function of [S]₀ (Fig. 7b), a linear relationship between τ_A⁻¹ and [S]₀ is apparent. The slope of the best linear fit in Fig. 7b is 3.6 × 10⁷ M⁻¹ s⁻¹, and the y-intercept is 312 s⁻¹. From the slope of the linear fit in Fig. 7b, we can estimate that k^R_sens + k^A_q = 3.6 × 10⁷ M⁻¹ s⁻¹, and from the y-intercept of the best linear fit in Fig. 7b, we estimate that k^A_T = 312 s⁻¹. The experimentally determined value of k^A_T is likely an underestimate, given that τ_A⁻¹ in the limit [S]₀ → 0 is smaller than k^A_T according to our simulations. Our result for k^R_sens + k^A_q is roughly an order of magnitude larger than the rate constant for dynamic quenching that was obtained by the Schmidt group.²⁴

To determine whether reverse TET takes place in the PtOEP–DPA system, we measured the sensitizer-phosphorescence decay of the samples for which the upconversion data are shown in Fig. 7a. It is evident that the phosphorescence decays in Fig. 7c are biphasic. There is a rapid decay of sensitizer phosphorescence that we ascribe to forward TET, as well as a slower, non-exponential decay component. The decay curves in Fig. 7a and c bear a strong degree of similarity. We fit the phosphorescence decays to

where k₁ is a rate constant corresponding to sensitizer triplet decay, which arises primarily from forward TET. The inverse lifetime of the long-lived component of phosphorescence decay, which we denote τ_P⁻¹, depends linearly on [S]₀, in analogy with the relationship between τ_A⁻¹ and [S]₀. However, the values of τ_A⁻¹ extracted from the experimental data are nearly twice as large as the corresponding values of τ_P⁻¹. When the phosphorescence-decay curves are fit instead with an equation of the formthe experimentally extracted values of τ_P⁻¹ are substantially closer to those of τ_A⁻¹ (Fig. 7e and f). Therefore, the slow component in the phosphorescence decays must represent a static portion of the population of the annihilator triplet states, rather than the population of the annihilator singlet states. Accordingly, FRET can be ruled out as the origin of the slow decay component in the sensitizer-phosphorescence decays. Hence, reverse TET is the most probable source of this slow decay, because the rate at which reverse TET occurs must depend linearly on the population of annihilator triplets. Furthermore, the rate of forward TET is typically expected to be higher than the rate at which the sensitizer triplet manifold is repopulated via reverse TET. Therefore, the rate-limiting step in prolonged sensitizer emission should be the lifetime of the annihilator triplets, in agreement with our experimental observations.

It is natural to question why reverse TET from DPA to PtOEP might occur in the first place, given that it is generally accepted that an energy difference of ∼0.14 eV exists between the energies of the triplet states of the two molecules (∼1.91 eV and ∼1.77 eV for PtOEP and DPA, respectively).^41,49–51 The triplet energy of PtOEP is commonly determined from a phosphorescence peak at ∼650 nm.^18,51–53 The triplet energy of DPA that is cited most often was determined from direct singlet–triplet absorption experiments in chloroform.⁴⁹ Given the uncertainty inherent in these measurements, it is certainly possible that the energy difference between the triplet states of PtOEP and DPA is smaller than the commonly accepted value.

The use of pure electronic energies, as opposed to vibronic energies, to determine the likelihood of triplet-energy transfer can be misleading. For instance, it has been shown that triplet sensitization with a large energy gap can lead to vibrational excitation in the triplet state of the acceptor molecule.⁵⁴ Detailed balance implies that the opposite process can also occur, i.e., a vibrationally excited “acceptor” molecule may be more likely to undergo reverse TET to a “donor” molecule. To assess this possibility, we performed DFT calculations on the lowest triplet state of DPA to determine the frequencies of its vibrational modes. Accordingly, we can estimate the average amount of vibrational energy at room temperature. Given the relatively large size of DPA, it is not surprising that this average energy comes out to be 0.46 eV, which is more than three times the gap between the triplet energies of PtOEP and DPA. PtOEP is also a large molecule that has floppy pendant groups, and so should have an even larger average thermal vibrational energy than does DPA. This factor also works in favor of reverse TET, in that vibrations that are populated in the electronic ground state of PtOEP need not be populated following reverse TET, effectively lowering the energy gap between the singlet and triplet states in this molecule. The rate of Dexter transfer between two species is related to the integral of the product of the normalized singlet–triplet absorption spectrum of the acceptor (PtOEP for reverse TET in our case) and the phosphorescence spectrum of the donor (DPA for reverse TET in our case),⁵⁵ so we can think of the thermally-populated vibrations as creating hot bands in these spectra. Therefore, only thermally-populated, Franck–Condon-active modes of the donor and acceptor will help to promote reverse TET. Although it is not possible to make a quantitative estimate of the rate of reverse TET based on these arguments, it is clear that even if a small fraction of the thermally-populated vibrations in PtOEP and DPA are involved in a reverse TET transition, the 0.14 eV “barrier” can easily be overcome.

Changes in the conformation of the sensitizer or the annihilator that result from thermal fluctuations can also alter the driving force for TET substantially.^56,57 For TTA-UC systems in which the triplet energy gap between the sensitizer and annihilator is small, endothermic reverse TET can be facilitated by small conformational changes that decrease the S₀–T₁ energy gap. Computational work by Zapata et al. showed that in-plane and out-of-plane distortions in the geometry of porphyrin molecules can alter the S₀–T₁ gap by as much as 0.15 eV at room temperature.⁵⁸ Moreover, Gray et al. showed that at room temperature, the S₀–T₁ gap of DPA can fluctuate by ±1k_BT as the orientations of the molecules’ two phenyl rings change.⁴¹ In our case, such conformational changes may induce small changes in the S₀–T₁ gaps of DPA and PtOEP molecules, thereby reducing the energy barrier to reverse TET by several k_BT and subsequently increasing the rate constant for reverse TET by an order of magnitude or more.

Finally, it is important to understand that even when the rate constant for reverse TET is several orders of magnitude smaller than the diffusion-limited value of ∼10⁹ M⁻¹ s⁻¹, Φ^R_ph may be large enough for the effects of reverse TET to be observed in the form of a slow decay component in sensitizer phosphorescence-decay curves. Critically, Φ^R_ph values increase exponentially as the magnitude of the product k^R_sens[S] begins to exceed the rate constant for intrinsic annihilator triplet decay. We highlight this behavior in Fig. S6a (ESI†), in which Φ^R_ph remains close to 0 when k^R_sens[S] ≪ k^T_A, but rises exponentially with increases in [S]. As [S] rises to 10⁻⁶ M, Φ^R_ph grows to a value of 0.1, indicating that more than 10% of total sensitizer phosphorescence now arises from the decay of triplet states that are populated via reverse TET. In Fig. S6 (ESI†), k^R_sens is ∼10⁹ M⁻¹ s⁻¹, and k^T_A is ∼10⁴ s⁻¹. In a more experimentally relevant scenario, k^T_A values may be as small as ∼10² s⁻¹. Therefore, Φ^R_ph values well in excess of 10% can easily be achieved even when reverse TET is energetically unfavorable and k^R_sens is ∼10⁷ M⁻¹ s⁻¹. When the effects of dynamic quenching are factored in, Φ^R_ph is smaller, yet remains above 10% for sensitizer concentrations in excess of 10⁻⁶ M (Fig. S6b, ESI†). In our case, we find that even if reverse TET only accounts for a fraction of the value of k^R_sens + k^A_q (3.6 × 10⁷ M⁻¹ s⁻¹) that we obtained from transient photoluminescence studies, Φ^R_ph should be large enough to lead to the observation of delayed sensitizer phosphorescence.

We also consider the possibility that the slow component in the sensitizer phosphorescence-decay curves arises from exciplex emission. The rate of formation of sensitizer–annihilator exciplexes, a process that falls under the umbrella of dynamic quenching, is linearly dependent on the concentration of annihilator triplets. In a scenario in which the overall rate constant for the radiative and nonradiative decay of the sensitizer–annihilator exciplexes exceeds the rate at which the exciplexes are formed, the combined decay of sensitizer phosphorescence and exciplex emission would be similar to the decay we observe experimentally. In Fig. S8a (ESI†), decays for the sum of sensitizer phosphorescence and exciplex emission were calculated for a variety of rate constants for the radiative decay of sensitizer–annihilator exciplexes (k^ex_ph). Reverse TET was not included in the model, and the emission quantum yield of sensitizer–annihilator exciplexes (Φ_ex) was assumed to be unity. When k^ex_ph is 200 s⁻¹, a strong accumulation in the population of exciplexes is observed at long times, as evidenced by the growth in total emission even 0.2 ms after the excitation ceases. Only when the value of k^ex_ph is sufficiently large do the total emission decays resemble the phosphorescence decays observed experimentally.

A second experimentally relevant scenario is that Φ_ex < 1, but the sum of the radiative and nonradiative sensitizer–annihilator exciplex decay processes is sufficiently large to avoid an accumulation of exciplexes on the sub-ms time scale. However, a small Φ_ex would decrease the contribution of exciplex emission. Exciplex emission from DPA–PtOEP samples, as characterized by emission peaks in the 750 nm to 800 nm range, was suppressed completely by the addition of DPBF (Fig. S8b, ESI†). DFT calculations revealed that the energy of the T₁ state of DPBF lies in the vicinity of 1.43 eV, which is well below the energy of DPA's T₁ state. Therefore, it is not surprising that the addition of DPBF to a sample containing DPA and PtOEP rapidly quenches the triplet states of DPA, thereby suppressing exciplex formation and subsequent emission. However, a slow bimolecular component in the sensitizer–phosphorescence decay is still observed for a TTA-UC sample containing DPBF, DPA, and PtOEP, despite the complete absence of exciplex emission from this sample (Fig. S8c, ESI†). For reference, no slow component could be identified in the sensitizer-phosphorescence decay for a TTA-UC sample containing only DPBF and PtOEP. Therefore, from Fig. S8b and c (ESI†) it is evident that the slow component that we observe in the phosphorescence decays in Fig. 7 cannot be attributed solely to exciplex emission, and must instead arise in large part from reverse TET.

We can conceive of only one scenario involving excimers in which the radiative decay of sensitizer triplet excimers results in the nonexponential decay of sensitizer emission. In the presence of the annihilator, the rate of forward TET would need to exceed the rate of sensitizer-excimer formation, and of all other sensitizer triplet-depletion mechanisms. Therefore, a biexponential decay of sensitizer emission, without any bimolecular decay features, would result when the rate of excimer decay, including all radiative and nonradiative pathways, is less than the rate of forward TET (Fig. S8d, ESI†). However, in this scenario, the lifetime of the delayed excimer emission would be independent of the concentration of sensitizer molecules. Therefore, we conclude that sensitizer excimer emission cannot be the origin of the slow component observed in the phosphorescence decays.

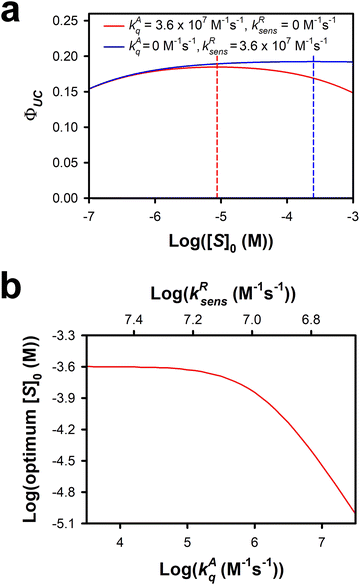
Having determined the sum of the rate constants for the sensitizer-dependent quenching processes from the slope of the linear fit to Fig. 7b, we now turn to determining the rate constants for reverse TET and dynamic quenching. We demonstrate that with knowledge of [S]_0,ideal and k^R_sens + k^A_q, we can estimate k^R_sens and k^A_q. Fig. 8a shows the expected value of Φ_UC as a function of [S]₀ for two cases, one in which k^A_q is equal to the slope of the linear fit to Fig. 7b (3.6 × 10⁷ M⁻¹ s⁻¹) and k^R_sens is zero, and another in which k^A_q is zero and k^R_sens is equal to the slope of the linear fit to Fig. 7b (3.6 × 10⁷ M⁻¹ s⁻¹). In the first case, we find that [S]_0,ideal ∼ 10⁻⁵ M, which is close to the lower limit of [S]_0,ideal that is given by k^A_T/k^A_q = 8.64 × 10⁻⁶ M. In the second case, [S]_0,ideal is roughly 3.1 × 10⁻⁴ M. Therefore, for the given set of system parameters, including the experimentally obtained values of k^A_T and k^A_q + k^R_sens, we find that 8.64 × 10⁻⁶ M < [S]_0,ideal < 3.1 × 10⁻⁴ M. Fig. 8b shows [S]_0,ideal for different combinations of k^R_sens and k^A_q, with the constraint that k^A_q + k^R_sens = 3.6 × 10⁷ M⁻¹ s⁻¹. Experimentally, [S]_0,ideal can be estimated from the dependence of Φ_UC on [S]₀. Here, Φ_UC can be obtained experimentally at any value of the irradiance, as long as the irradiance at which Φ_UC is measured is unchanged for all samples with different [S]₀. As an example, if [S]_0,ideal were to be estimated as 1 × 10⁻⁵ M, k^A_q ∼ 2.5 × 10⁷ M⁻¹ s⁻¹, which would mean that k^R_sens ∼ 1.1 × 10⁷ M⁻¹ s⁻¹. With k^R_sens = 1.1 × 10⁷ M⁻¹ s⁻¹, k^A_q = 2.5 × 10⁷ M⁻¹ s⁻¹ and k^A_T = 312 s⁻¹, we calculate Φ^R_ph to be 0.67% when [S]₀ = 10⁻⁵ M. When [S]₀ = 10⁻⁴ M, Φ^R_ph increases to 1.92%. Finally, when [S]₀ is increased to be on par with [A]₀, 1 mM, Φ^R_ph increases to 5.15%.

Fig. 8 Determining the rate constants for reverse TET and dynamic quenching. (a) Dependence of Φ_UC on log([S]₀) for TTA-UC systems with different values of k^R_sens and k^A_q. (b) Dependence of [S]_0,ideal on k^A_q; k^A_q + k^R_sens was constrained to be 3.6 × 10⁷ M⁻¹ s⁻¹ and k^A_T was set to the experimentally-determined value of 312 s⁻¹.

Conclusions

We have used new experimental approaches for the rapid collection of steady-state and time-resolved TTA-UC data to explore several possible mechanisms whereby an increased concentration of sensitizers might lead to UEL. The observation of an enhancement in sensitizer phosphorescence with increasing concentration of sensitizers, at the expense of upconverted fluorescence, led to the identification of reverse TET and dynamic quenching as the two most influential UEL mechanisms.

Spectral measurements on PtOEP–DPA samples revealed the emergence of a new NIR emission peak with increasing concentration of sensitizers; this peak was absent when no annihilator was present. Unlike the intensity of the principal phosphorescence peak centered at ∼650 nm, the intensity of the NIR emission peak is not proportional to the excitation power. Therefore, we believe that the NIR emission results from exciplex formation between annihilator triplets and sensitizers. These exciplexes constitute a potential source of dynamic quenching.

Transient photoluminescence measurements of PtOEP–DPA samples in toluene indicated that the effective lifetime of annihilator triplets decreases with increasing concentration of sensitizers, with an overall sensitizer-dependent-quenching rate constant of 3.6 × 10⁷ M⁻¹ s⁻¹. Reverse TET was identified as the probable cause of the majority of the prolonged sensitizer emission, which had an effective lifetime on par with that of the annihilator triplets. Although at first glance reverse TET might appear unlikely to be an efficient UEL mechanism in the PtOEP–DPA system, we believe that thermal vibrational excitation in DPA and PtOEP, and conformation-dependent S₀–T₁ energy gaps make the reverse TET process considerably more likely than is implied by the energies of the triplet-state origins in the equilibrium geometries of the molecules. The same phenomenon can occur in any TTA-UC system in which one or more of the components has a substantial number of low-frequency vibrational modes, and so we believe that reverse TET is likely to be an important UEL mechanism in many TTA-UC systems.

We also demonstrated that the rate constants for reverse TET and dynamic quenching can be determined given knowledge of [S]_0,ideal, k^R_sens + k^A_q, and k^A_T. We showed that [S]_0,ideal can be determined from plots of the upconversion quantum yield as a function of the sensitizer concentration at constant irradiance, and that k^R_sens + k^A_q and k^A_T can be determined from transient TTA-UC measurements performed at different sensitizer concentrations. This methodology should be applicable to a wide range of TTA-UC systems.

It will be of great interest to perform further experiments that can assess the role that thermal vibrational excitation plays in reverse TET in TTA-UC systems. One obvious approach is to perform temperature-dependent experiments in which the role of reverse TET can be assessed. However, a potentially confounding factor is such experiments is that other experimental parameters that are relevant to TTA-UC, such as the diffusion rate, are also sensitive to temperature.

Data availability

The data sets generated and/or analyzed in this study are available from the first/corresponding author on reasonable request.

Conflicts of interest

There are no conficts of interest to declare.

Acknowledgements

This work was supported by the National Science Foundation, grant CHE-1800491 (J. T. F. and A. K.). A. K. would also like to thank the University of Maryland's Graduate School and the Department of Materials Science and Engineering for supporting this research through a Summer Graduate Research Fellowship.

References

1. Y. C. Simon and C. Weder, J. Mater. Chem., 2012, 22, 20817–20830.
2. Y. C. Simon, S. Bai, M. K. Sing, H. Dietsch, M. Achermann and C. Weder, Macromol. Rapid Commun., 2012, 33, 498–502.
3. Q. Dou, L. Jiang, D. Kai, C. Owh and X. J. Loh, Drug Discovery Today, 2017, 22, 1400–1411.
4. R. W. MacQueen, Y. Y. Cheng, A. N. Danos, K. Lips and T. W. Schmidt, RSC Adv., 2014, 4, 52749–52756.
5. X. Yu, X. Cao, X. Chen, N. Ayres and P. Zhang, Chem. Commun., 2015, 51, 588–591.
6. D. K. Limberg, J.-H. Kang and R. C. Hayward, J. Am. Chem. Soc., 2022, 144, 5226–5232.
7. L. Zeng, L. Huang, J. Han and G. Han, Acc. Chem. Res., 2022, 55, 2604–2615.
8. C. Wohnhaas, V. Mailänder, M. Dröge, M. A. Filatov, D. Busko, Y. Avlasevich, S. Baluschev, T. Miteva, K. Landfester and A. Turshatov, Macromol. Biosci., 2013, 13, 1422–1430.
9. Q. Liu, M. Xu, T. Yang, B. Tian, X. Zhang and F. Li, ACS Appl. Mater. Interfaces, 2018, 10, 9883–9888.
10. W. Lin, J. Li, H. Feng, F. Qi and L. Huang, J. Anal. Test., 2023, 7, 327–344.
11. Y. Y. Cheng, A. Nattestad, T. F. Schulze, R. W. MacQueen, B. Fückel, K. Lips, G. G. Wallace, T. Khoury, M. J. Crossley and T. W. Schmidt, Chem. Sci., 2016, 7, 559–568.
12. T. Dilbeck and K. Hanson, J. Phys. Chem. Lett., 2018, 9, 5810–5821.
13. M. Kinoshita, Y. Sasaki, S. Amemori, N. Harada, Z. Hu, Z. Liu, L. K. Ono, Y. Qi, N. Yanai and N. Kimizuka, ChemPhotoChem, 2020, 4, 5271–5278.
14. T. F. Schulze, J. Czolk, Y.-Y. Cheng, B. Fückel, R. W. MacQueen, T. Khoury, M. J. Crossley, B. Stannowski, K. Lips, U. Lemmer, A. Colsmann and T. W. Schmidt, J. Phys. Chem. C, 2012, 116, 22794–22801.
15. W. Sheng, J. Yang, X. Li, G. Liu, Z. Lin, J. Long, S. Xiao, L. Tan and Y. Chen, Energy Environ. Sci., 2021, 14, 3532–3541.
16. C.-H. Chen, Y.-S. Li, S.-C. Fang, B.-Y. Lin, C.-Y. Li, Y.-C. Liao, D.-G. Chen, Y.-R. Chen, Y.-C. Kung, C.-C. Wu, Y. Lin, W.-Y. Hung, T.-L. Chiu, C.-F. Lin, E. Y. Li, T.-F. Guo, J.-H. Lee, K.-T. Wong and P.-T. Chou, Adv. Photonics Res., 2023, 4, 2200204.
17. D. Di, L. Yang, J. M. Richter, L. Meraldi, R. M. Altamimi, A. Y. Alyamani, D. Credgington, K. P. Musselman, J. L. MacManus-Driscoll and R. H. Friend, Adv. Mater., 2017, 29, 1605987.
18. L. Xing, Z.-L. Zhu, J. He, Z. Qiu, Z. Yang, D. Lin, W.-C. Chen, Q. Yang, S. Ji, Y. Huo and C.-S. Lee, Chem. Eng. J., 2021, 421, 127748.
19. L. Yang, X. W. Chua, Z. Yang, X. Ding, Y. Yu, A. Suwardi, M. Zhao, K. L. Ke, B. Ehrler and D. Di, Nanoscale Adv., 2022, 4, 1318–1323.
20. Y. Murakami and K. Kamada, Phys. Chem. Chem. Phys., 2021, 23, 18268–18282.
21. A. Monguzzi, R. Tubino, S. Hoseinkhani, M. Campione and F. Meinardi, Phys. Chem. Chem. Phys., 2012, 14, 4322–4332.
22. E. A. Josie, C. Yuen Yap, K. Tony, G. C. R. C. Raphaël, N. J. Ekins-Daukes, J. C. Maxwell and W. S. Timothy, J. Phys.: Conf. Ser., 2009, 185, 012002.
23. A. Monguzzi, J. Mezyk, F. Scotognella, R. Tubino and F. Meinardi, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 195112.
24. E. M. Gholizadeh, L. Frazer, R. W. MacQueen, J. K. Gallaher and T. W. Schmidt, Phys. Chem. Chem. Phys., 2018, 20, 19500–19506.
25. T. Kashino, R. Haruki, M. Uji, N. Harada, M. Hosoyamada, N. Yanai and N. Kimizuka, ACS Appl. Mater. Interfaces, 2022, 14, 22771–22780.
26. S. P. Hill, T. Dilbeck, E. Baduell and K. Hanson, ACS Energy Lett., 2016, 1, 3–8.
27. A. Nattestad, Y. Y. Cheng, R. W. MacQueen, G. G. Wallace and T. W. Schmidt, J. Visualized Exp., 2014, e52028.
28. D. Beery, T. W. Schmidt and K. Hanson, ACS Appl. Mater. Interfaces, 2021, 13, 32601–32605.
29. V. Gray, K. Moth-Poulsen, B. Albinsson and M. Abrahamsson, Coord. Chem. Rev., 2018, 362, 54–71.
30. J. Isokuortti, S. R. Allu, A. Efimov, E. Vuorimaa-Laukkanen, N. V. Tkachenko, S. A. Vinogradov, T. Laaksonen and N. A. Durandin, J. Phys. Chem. Lett., 2020, 11, 318–324.
31. J. Peng, X. Guo, X. Jiang, D. Zhao and Y. Ma, Chem. Sci., 2016, 7, 1233–1237.
32. M. Yang, S. Sheykhi, Y. Zhang, C. Milsmann and F. N. Castellano, Chem. Sci., 2021, 12, 9069–9077.
33. Y. Zhao, Y. Wu, W. Chen, R. Zhang, G. Hong, J. Tian, H. Wang, D. Zheng, C. Wu, X. Jiang, X. Huo, L. Sun, W. Deng, K. Han and F. Song, Adv. Opt. Mater., 2022, 10, 2102275.
34. N. Yanai, M. Kozue, S. Amemori, R. Kabe, C. Adachi and N. Kimizuka, J. Mater. Chem. C, 2016, 4, 6447–6451.
35. N. Nishimura, V. Gray, J. R. Allardice, Z. Zhang, A. Pershin, D. Beljonne and A. Rao, ACS Mater. Lett., 2019, 1, 660–664.
36. C. Wang, F. Reichenauer, W. R. Kitzmann, C. Kerzig, K. Heinze and U. Resch-Genger, Angew. Chem., Int. Ed., 2022, 61, e202202238.
37. X. Qiao, H. Liu, S. Xiao, P. Yuan, J. Yao, Y. Chen, P. Lu and D. Ma, Adv. Opt. Mater., 2022, 10, 2200074.
38. D. Meroni, A. Monguzzi and F. Meinardi, J. Chem. Phys., 2020, 153, 114302.
39. S. P. McGlynn, R. Sunseri and N. Christodouleas, J. Chem. Phys., 2004, 37, 1818–1824.
40. M. N. Berberan Santos, Phys. Chem. Commun., 2000, 3, 18–23.
41. V. Gray, A. Dreos, P. Erhart, B. Albinsson, K. Moth-Poulsen and M. Abrahamsson, Phys. Chem. Chem. Phys., 2017, 19, 10931–10939.
42. A. Kalpattu, T. Dilbeck, K. Hanson and J. T. Fourkas, Phys. Chem. Chem. Phys., 2022, 24, 28174–28190.
43. A. Olesund, V. Gray, J. Mårtensson and B. Albinsson, J. Am. Chem. Soc., 2021, 143, 5745–5754.
44. P. Baronas, J. Lekavičius, M. Majdecki, J. L. Elholm, K. Kazlauskas, P. Gaweł and K. Moth-Poulsen, ACS Cent. Sci., 2025, 11, 413–421.
45. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
46. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
47. T. F. Schulze and T. W. Schmidt, Energy Environ. Sci., 2015, 8, 103–125.
48. F. Edhborg, A. Olesund and B. Albinsson, Photochem. Photobiol. Sci., 2022, 21, 1143–1158.
49. J. S. Brinen and J. G. Koren, Chem. Phys. Lett., 1968, 2, 671–672.
50. Y. V. Aulin, M. van Sebille, M. Moes and F. C. Grozema, RSC Adv., 2015, 5, 107896–107903.
51. X. Cao, B. Hu and P. Zhang, J. Phys. Chem. Lett., 2013, 4, 2334–2338.
52. F. Laquai, C. Im, A. Kadashchuk and H. Bässler, Chem. Phys. Lett., 2003, 375, 286–291.
53. K. Guo, C. Lin, Y. Wu, S. Xiao, X. Qiao, D. Yang, Y. Dai, Q. Sun, J. Chen, D. Hu, L. Ying, Y. Ma and D. Ma, Adv. Opt. Mater., 2023, 11, 2202988.
54. K.-Y. Kuan and D. A. Singleton, J. Am. Chem. Soc., 2020, 142, 19885–19888.
55. C. B. Murphy, Y. Zhang, T. Troxler, V. Ferry, J. J. Martin and W. E. Jones, J. Phys. Chem. B, 2004, 108, 1537–1543.
56. F. Zapata, M. Marazzi, O. Castaño, A. U. Acuña and L. M. Frutos, J. Chem. Phys., 2014, 140, 034102.
57. J. Saltiel, J. L. Charlton and W. B. Mueller, J. Am. Chem. Soc., 1979, 101, 1347–1348.
58. F. Zapata, M. Nucci, O. Castaño, M. Marazzi and L. M. Frutos, J. Chem. Theory Comput., 2021, 17, 5429–5439.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp00578g

---