Rotational and vibrational spectroscopy of a weakly bound hexafluoroisopropanol⋯dinitrogen complex: ¹⁴N hyperfine splittings, molecular geometry, and experimental benchmarks

Abstract

The rotational spectrum of a weakly bound binary complex of hexafluoroisopropanol (HFIP) with molecular nitrogen was measured using chirped-pulse and cavity-based Fourier transform microwave spectrometers. In addition, its infrared spectrum was measured in the OH stretching region. An extensive conformational search identified multiple binding sites on HFIP, with the global minimum structure featuring a trans-HFIP conformation and nitrogen weakly bound at the acidic proton (H_tN_H). Good agreement between the experimentally determined rotational constants and the relative intensity patterns of a-, b-, and c-type transitions with theoretical predictions conclusively identified the H_tN_H conformer. This assignment is further corroborated by an analysis of the ¹⁴N nuclear quadrupole hyperfine structure. The non-equivalence of the two ¹⁴N nuclei in H_tN_H is confirmed through a detailed molecular symmetry group analysis, as well as the ¹⁴N nuclear quadrupole hyperfine analysis. Examination of the experimental nuclear quadrupole coupling constants offers additional insights into the orientation and large-amplitude vibrational motions of the N₂ subunit. Furthermore, the experimentally derived rotational constants and the OH stretching band position of the complex, compared with previously known values for the isolated monomer, serve as complementary benchmarks for evaluating the systematic quality of predictions from electronic structure calculations across several levels of theory. This combined examination of vibrational energy levels and structural parameters aids in distinguishing fortuitously accurate predictions of individual properties.

---

1. Introduction

Per- and polyfluoroalkyl substances (PFAS), also known as forever chemicals, are synthetic molecules containing stable perfluoroalkyl moieties.¹ These molecules have many desirable physical and chemical properties, such as high thermal resistance and oil and water repellence, and have found wide application in consumer products and industrial processes since the 1940s.² The same properties that have made these molecules very useful have also contributed to their ability to accumulate in human bodies and the environment, leading to an increased interest in studying the health and environmental impacts of these molecules.¹ Concerns related to PFAS include their resistance to biodegradation and the tendency of neutral PFAS to be found in the atmosphere due to their high volatility.¹

1,1,1,3,3,3-Hexafluoro-2-propanol or hexafluoroisopropanol (HFIP) is a low boiling point (59 °C)³ fluorinated alcohol belonging to the family of PFAS. HFIP has been shown to be a “magic solvent” for a variety of synthetic reactions, thanks to its hydrogen bond donating ability and cation stabilization capacity.⁴ For example, the rate of epoxidation of olefins by H₂O₂ was raised 10⁵ times in HFIP compared to in conventional solvents.⁵ Despite its valuable properties, HFIP is a potent greenhouse gas with a global warming potential (GWP) of about 200,⁶ making it ∼200 times more harmful to the atmosphere than CO₂, which has a GWP of 1 by definition. Although HFIP has not yet been observed in the atmosphere, its carbon–fluorine bonds can absorb radiation in the atmospheric window, contributing to positive radiative forcing and global warming.⁶ To appreciate the behaviour of this molecule, research has been performed to characterize its structure^7–9 and intermolecular interactions with itself^10,11 and other relevant molecules in the atmosphere.¹² The investigation of the intermolecular interactions at the level of small binary complexes with HFIP is vital for developing a thorough understanding of the fascinating macroscopic properties of HFIP and its potential behaviour in the atmosphere.

The HFIP monomer has one important dihedral angle, HOCH, which can adopt values near 180, 60 and −60 degrees, corresponding to trans (t), gauche+ (g+), and gauche− (g−) conformations, respectively. Here, g+ and g− are non-superposable mirror images of each other and HFIP possesses transient chirality. For simplicity, we name the trans and gauche conformations of HFIP as H_t and H_g, respectively (see Fig. 1). Although one expects the localized ground state wavefunctions of the g± forms to overlap and give rise to symmetric and antisymmetric eigenstates, no associated tunneling splittings have been reported so far for H_g or its complexes. For convenience, they are given the same label in this study. Based on the previous infrared (IR) vibrational spectroscopic studies,^7,8 free HFIP exists in two conformations, where H_g is 4.0(1.6) kJ mol⁻¹ less stable than H_t. In two previous rotational spectroscopic studies,^9,12 only the H_t monomer and its complex with water were observed experimentally. Later, the H_g⋯water complex (with “⋯” indicating a non-covalent interaction) was also experimentally identified in a chirped pulse-Fourier transform microwave (CP-FTMW) spectroscopic study,¹³ confirming that hydrogen bonding with water preferentially stabilizes the gauche form. Interestingly, while both hydrogen-bonded HFIP dimers, H_tH_t and H_gH_t, were detected experimentally, the only observed HFIP trimer contains three metastable chiral monomer units, H_gH_gH_g, underscoring how the conformational preference of HFIP evolves upon self-aggregation.^10,11 On the other hand, only the trans form of HFIP was detected in the more recent jet-cooled rotational spectroscopic investigations of HFIP⋯Ne,Ar¹⁴ and HFIP⋯1,4-dioxane¹⁵ complexes. All these observations indicate that the conformational conversion through the internal torsion of the OH group can happen efficiently in a jet expansion. However, the associated conversion barrier may be significantly modified by non-covalent interactions.

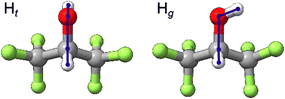Fig. 1 Two conformers of the HFIP monomer. The HOCH dihedral angle for H_t is ∼180° while conformers with dihedral angles of ∼±60° are labelled with H_g.

In the current study, we probe structural and dynamical properties of a non-covalently bonded complex consisting of HFIP and molecular nitrogen, N₂, a significant ingredient in the atmosphere, using CP-FTMW and cavity-based FTMW spectroscopy in combination with computational chemistry calculations. Additionally, we complement the study with FTIR measurements in the OH stretching region. In prior studies on binary complexes with HFIP, the chosen binding partners were strong hydrogen bond donors (e.g., H₂O, HFIP), hydrogen bond acceptors (e.g., 1,4-dioxane, HFIP), or weak van der Waals partners (e.g., Ne, Ar). Replacing these with molecular N₂, which has a large molecular electric quadrupole moment, could provide intermediate intermolecular interaction strength, leading to weak hydrogen bonding interactions and moderate OH stretching frequency shifts. Importantly, we analyse the nuclear quadrupole hyperfine structures of the ¹⁴N nuclei to extract information about the orientation of the N₂ subunit and the nuclear large-amplitude motions within the complex. This may include nuclear quantum tunnelling, as seen in H₂O⋯N₂¹⁶ and CO⋯N₂.^17,18 Additionally, these experimentally determined complex properties provide an opportunity to establish restrictive experimental benchmarks¹⁹ for standard harmonic quantum chemical calculations once anharmonic vibrational effects can be properly estimated.

2. Methods

2.1 Experimental methods

The broadband rotational spectrum of the HFIP⋯N₂ complex was recorded using a 2–6 GHz chirped-pulse Fourier-transform microwave (CP-FTMW) spectrometer^20,21 which was designed based on a similar instrument by Pate and co-workers.²² We note that transitions in the 6–7 GHz range could also be detected using this instrument.²³ The detection in the 6–7 GHz range is made possible because of the near-Nyquist aliasing of the CP in the arbitrary waveform generator (12 GS per s sampling rate), although the sensitivity achieved is generally less than in the 2–6 GHz region. A mixture of 0.1% HFIP (Sigma Aldrich, 99.9%), 0.4% nitrogen (Praxair, 99.995%), and 6 bar of helium (Praxair, 99.995%) was prepared for the CP-FTMW measurements. All chemicals were used without further purification. Briefly, a 1 μs chirped MW pulse was produced using a 12 GS/s arbitrary waveform generator, amplified using a 400 W, 2.5 to 7.5 GHz travelling wave tube amplifier, and then broadcasted perpendicularly to the molecular supersonic expansion to excite the molecular targets. A total of 665 000 free induction decays (FIDs) were collected, averaged, and underwent an FT to obtain the spectrum in the frequency domain. A typical full width at half maximum of ∼120 kHz and a frequency uncertainty of ∼10 kHz was estimated for a well-isolated transition.

Additionally, a 4–18 GHz cavity-based FTMW spectrometer,²⁴ based on the Balle–Flygare instrument,²⁵ was used to obtain rotational transitions in the 4–12 GHz range. For the cavity FTMW experiments, a mixture of 0.1% HFIP, 5% N₂, and 6 bar of neon (Praxair, 99.999%) was prepared and injected into the cavity chamber parallel to the MW radiation direction. As a result, each transition was observed as a pair of Doppler components. Experimental parameters, such as the mirror separation distance, the molecular and microwave pulse widths, and the delay between them, needed to be optimized for each rotational transition in order to achieve the desired level of signal-to-noise ratio and resolution. A typical full width at half maximum is ∼10–12 kHz, and the frequency uncertainty is ∼1–2 kHz.

The related infrared spectra were obtained using an FTIR spectrometer (Bruker IFS 66v/S) with a sample mixture consisting of 0.1% HFIP (99%, FluoroChem) with helium (99.996%, Linde) and optionally 0.4% nitrogen (99.999%, Air Liquide). The sample was expanded from a 67 L Teflon-coated reservoir through a 600 × 0.2 mm² slit nozzle²⁶ with a backing pressure of 0.75 bar into an FTIR-synchronized 147 ms gas pulse. Typically, the final FTIR spectra were obtained by co-adding 325 gas pulses.

2.2 Computational methods

To investigate the conformational landscape of the HFIP⋯N₂ complex, we applied the conformer-rotamer ensemble sampling tool (CREST) developed by Grimme and co-workers.^27,28 CREST performs metadynamics simulations at the (semi)empirical GFN2-xTB²⁹ level, providing systematic and efficient conformational searches.²⁷ Several HFIP⋯N₂ geometries were used as inputs in the CREST simulations to ensure adequate sampling of the conformational space. Additionally, the NCI mode was used where an ellipsoid potential is placed around the complex to prevent dissociation.²⁸ To effectively identify the low-energy conformers, a multi-step screening procedure was developed^30,31 and adopted in the current search. Using CREGEN, the built-in sorting and screening tool, together with an RMSD threshold of 0.125 and an energy window of 30 kJ mol⁻¹, the redundant and high-energy CREST candidates were removed. The remaining candidates were then optimized at the B3LYP^32,33-D4³⁴/def2-TZVP(-f)^35,36 level using the ORCA³⁷ software package and the default integration grid. In this ORCA step, the RI-JK approximation³⁸ and the def2/JK³⁹ auxiliary basis set were used to reduce computational cost. Next, the newly optimized structures were screened in CREGEN using the same parameters, optimized again in ORCA with a large integration grid and the larger def2-TZVPP basis set, and screened for a final time with CREGEN. Unreasonable structures, having the two subunits separated by more than 6.00 Å, were removed manually. The final geometry optimization, harmonic and anharmonic frequency calculations of the remaining structures were performed with Gaussian09⁴⁰ and 16,⁴¹ using the B3LYP hybrid functional in combination with Grimme's dispersion correction (D3),⁴² Becke–Johnson damping (BJ)⁴³ and the def2-QZVP basis set. Lastly, the counterpoise correction scheme was used for the basis set superposition error (BSSE) correction.⁴⁴

For benchmarking purposes, geometry optimizations and harmonic frequency calculations of the most stable conformer identified experimentally were carried out at various levels of theory. These include the M06-2X/aVTZ, PBE0-D3(BJ)/aVTZ and ωB97-XD/aVTZ calculations using Gaussian16, and the PBEh-3c,⁴⁵ B97-3c, MP2, SCS-MP2 and B2PLYP-D3(BJ) calculations with the ORCA⁴⁶ (Version 4.0.1) program package. Calculations using the MP2, SCS-MP2, and B2PLYP-D3(BJ) methods were performed with each of the following basis sets: VTZ, aug-cc-pVTZ (aVTZ), VQZ, and aug-cc-pVQZ (aVQZ). Geometries of all HFIP⋯N₂ complexes are visualized by using both Avogadro⁴⁷ and Chimera⁴⁸ programs.

3. Results and discussion

3.1 Conformational search results

The initial CREST search outputted 738 candidates, and further screening steps produced 115 geometries. The final DFT geometry optimizations and harmonic frequency calculations resulted in 11 stable conformers within an energy window of 15 kJ mol⁻¹. Their optimized geometries are shown in Fig. 2, while the corresponding spectroscopic parameters are summarised in Table S1, ESI.† The Cartesian coordinates of the 11 conformers are listed in Table S2, ESI.† The complexes are abbreviated as HN, where the subscript at the H indicates the trans (H_t) or gauche (H_g) conformation of the HFIP subunit, and the subscript at the N denotes the specific HFIP site used to bind to the N₂ molecule. As seen in Fig. 2, six different HFIP binding sites were identified, including the acidic hydroxyl proton (H), the CH proton (C), the alcohol oxygen (O), the face formed by the two F atoms in each CF₃ group furthest from the CH proton (F), and each face formed by the three F atoms of a CF₃ group (F′ and F′′). In the case of H_tN_F′ and H_tN_F′′, these two structures are mirror images of each other and are labelled as H_tN_F′ for simplicity. The ΔE_e and ΔE₀ rankings (Table S1, ESI†) indicate the same global minimum geometry: H_tN_H. For H_tN_H, the calculated intermolecular distance, i.e., the centre-of-mass separation of the two subunits, is 4.231 Å, and the binding energy after zero-point energy and BSSE correction is 7.4 kJ mol⁻¹.

Fig. 2 Geometries of the 11 lowest energy conformers of the HFIP⋯N₂ complex at the B3LYP-D3(BJ)/def2-QZVP level of theory. Conformers in the top row contain the trans-HFIP subunit, H_t, while those in the bottom row contain the gauche HFIP subunit, H_g. The HFIP subunit in all conformers is oriented with one CF₃ group pointing towards the front and the other, which is mostly blocked from view, to the back. The size of the N₂ molecule indicates its nearness to the viewer, with larger sizes indicating a positioning above the plane of the page. ΔE₀ values (in kJ mol⁻¹) are shown in brackets.

In the HFIP⋯N₂ complex, clusters containing the less stable H_g subunit are predicted to be at a significant energy disadvantage of 4.5 kJ mol⁻¹ or more relative to the lowest energy H_tN_H structure at the B3LYP-D3(BJ)/def2-QZVP level of theory. This energy gap between the H_g- and H_t-containing complexes is similar to the separation (about 4.1 kJ mol⁻¹) between the monomeric conformer, H_g, and the global minimum, H_t (Table S1, ESI†). A similar observation was reported for the weakly bound complexes of HFIP with rare gas atoms (Ne and Ar), where the corresponding energy gap is about 4.0 kJ mol⁻¹.¹⁴ For the complex of HFIP with H₂O, although the preference for the H_t-containing binary conformers remains, the energy gap is reduced to about 2.1 kJ mol⁻¹. As a result, both H_g- and H_t-containing water complexes were observed experimentally.^12,13 For these reasons, it is natural to divide conformers of the HFIP⋯N₂ complex into two groups based on the conformations of the HFIP subunit.

For both groups of the HFIP⋯N₂ conformers, the lowest energy conformer features the quadrupolar nitrogen molecule participating in a weak hydrogen bond with the acidic OH proton. This preference has also been reported for binary complexes of N₂ with aliphatic alcohols (methanol, ethanol, and tert-butyl)⁴⁹ and in the complex of N₂ with the lowest energy HFIP dimer,¹⁰ which each feature this same O–H⋯N–N motif. While other HFIP binding sites correspond to less stable conformers by more than 3 kJ mol⁻¹, it is interesting to note that their preferred ordering within a group is the same as in the cases of HFIP with Ne and Ar.¹⁴ Additionally, the energy windows for the binding sites within a group are smallest for the rare gas complexes (1.0 kJ mol⁻¹ for Ne and 2.5 kJ mol⁻¹ for Ar),¹⁴ followed by the N₂ complex (6.2 kJ mol⁻¹) and finally the H₂O complex (around 26 kJ mol⁻¹).¹³

3.2 Rotational spectroscopic assignments

The recorded broadband spectrum is dominated by strong transitions of the known trans-HFIP monomer.⁹ The spectrum also features transitions associated with the two monosubstituted ¹³C isotopologues of the trans-HFIP monomer,⁹ the achiral H_tH_t and chiral H_gH_t HFIP dimers,¹¹ and the lowest energy monohydrate^12,13 (see Fig. S1, ESI†). After removing these known transitions, a much weaker spectrum remains, displaying mainly transitions of partially resolved ¹⁴N nuclear hyperfine structures. This partially resolved spectral pattern helps discriminate against lines which do not belong to N₂-containing complexes. A set of rotational transitions was assigned, guided by the simulated spectra of the low-energy HFIP⋯N₂ conformers. By using the estimated unsplit central frequencies, an initial fit to Watson's A-reduction Hamiltonian in the I^r representation⁵⁰ was performed with the PGOPHER program.⁵¹ Based on a comparison of the calculated and experimental rotational constants alone, H_tN_H, H_tN_C, and H_gN_C are all potential carriers of the observed set of transitions. However, the absence of b-type transitions, along with the intensity ratio of a- to c-type transitions, clearly indicates that H_tN_H, the predicted most stable conformer, is the only suitable carrier. Efforts to identify transitions of the other low-energy HFIP⋯N₂ conformers were unsuccessful. Below, we explain the challenges in the fitting process.

Before the analysis, it was uncertain whether the two ¹⁴N nuclei are equivalent, as in H₂O⋯N₂¹⁶ and CO⋯N₂,^17,18 or inequivalent, as in ICF₃⋯N₂⁵² and ICl⋯N₂.⁵³ In all four previous N₂-containing complexes, the intermolecular bonding axis aligns with the a-principal moment of inertia axis, and the associated rotational fits required only the B rotational constant and two centrifugal distortion constants. However, in the HFIP⋯ N₂ complex, the orientation of the N₂ subunit does not align with any of the principal moment of inertia axes, complicating analysis of the nuclear quadrupole hyperfine patterns.

Our attempt to fit the ¹⁴N nuclear quadrupole constants with the broadband data was not successful since the ¹⁴N (nitrogen nuclear spin = 1) hyperfine components were generally not well resolved in the 2–6 GHz region. This is seen, for example, in the hyperfine pattern of the J_KaKc = 4₂₃ ← 3₂₂ transition (Fig. 3). Trial fits were then performed using either the estimated central frequencies or the strongest hyperfine components while fixing the ¹⁴N nuclear quadrupole coupling constants to the calculated values. As a result, the standard deviations of these trial fits were in the range of about 100 kHz, considerably larger than the experimental uncertainty. Significant effort was then dedicated to optimizing the performance of the cavity-based FTMW spectrometer in the 5–11 GHz range to resolve the narrowly split ¹⁴N hyperfine structures. Fig. 3 shows an example of a transition, 5₁₄ ← 4₁₃, with well-resolved hyperfine components.

Fig. 3 An example CP-FTMW rotational transition (top left) with partially resolved ¹⁴N nuclear quadrupole splittings, and an example cavity-based FTMW rotational transition (top right) with well-resolved ¹⁴N nuclear quadrupole splittings. The experimental cavity spectrum is composed of five different measurements, centred at 6297.37, 6297.50, 6297.65, 6297.80, and 6297.95 MHz. Simulations of the rotational spectrum, shown in the middle row, were performed using experimentally obtained nuclear quadrupole coupling constants and experimental Doppler splitting.⁵⁴ Lorentzian linewidths of 80 and 5 kHz were used for the CP-FTMW and cavity-based FTMW simulations, respectively. The hypothetical unsplit central frequencies are indicated by vertical lines. See the main text for further details.

A similar challenge in achieving an assignment of the ¹⁴N hyperfine structure was encountered in a complex of ICF₃⋯N₂. There, the problem was addressed with a multi-step fitting procedure.⁵¹ First, the better-resolved ¹⁴N hyperfine components obtained with the cavity-based FTMW spectrometer were fitted separately. The resulting ¹⁴N nuclear quadrupole coupling constants were held fixed in a subsequent overall fit that included all lines measured in the broadband spectrum. For HFIP⋯N₂, to achieve definite rotational and ¹⁴N hyperfine component assignments, we applied a slightly different iterative process to combine the lower-resolution chirped-pulse and higher-resolution cavity-based FTMW data in the same fit.

First, a general rotational assignment was achieved using only the lower-resolution chirped-pulse data while holding the ¹⁴N nuclear quadrupole coupling constants at their calculated values. Here, the experimental frequencies for the strongest predicted hyperfine components were used in the fit. Second, since the ¹⁴N nuclear hyperfine structure patterns only minorly depend on the rotational constants, one can directly compare the simulated hyperfine structure patterns with the cavity-based measurements of selected rotational transitions with well-separated hyperfine components, i.e., lower J transitions. A new fit was conducted exclusively with these well-resolved transitions to improve the ¹⁴N coupling constants. The fitted rotational constants were not as well determined because of the limited number of rotational transitions used in the assignment. Third, the hyperfine features of each rotational transition were simulated using the improved ¹⁴N coupling constants and the rotational constants from the broadband data. The experimental Lorentzian linewidths and Doppler splittings were included for cavity-based and broadband measurements. Then, we used the offset key in PGOPHER to align predicted patterns with the corresponding experimental features in the cavity- or CP-FTMW spectra. Example mappings for both CP-FTMW and cavity-based transitions are shown in Fig. 3. Once a match was deemed satisfactory, the ¹⁴N coupling constants were set to zero to extract the hypothetical unsplit central frequency. Fourth, the obtained central frequencies from both the cavity- and CP-FTMW measurements were used in a fit to further refine the rotational and centrifugal distortion constants. The hypothetical unsplit central frequencies extracted from the cavity-based measurements were given a relative uncertainty of 1, whereas a value of 2 was used for those obtained from the broadband measurements. Steps 2–4 were repeated to ensure the convergence of the fitted spectroscopic constants, i.e., no further changes within the error bar (or uncertainty). Using this approach, hypothetical unsplit central frequencies can be extracted from the CP-FTMW data, minimizing the large uncertainty caused by the broad, overlapped features in the recorded spectrum.

The resulting experimental spectroscopic constants are summarized in Table 1, along with the theoretical values calculated at the equilibrium geometry. The fit standard deviation is about 1.6 kHz, consistent with the ∼1–2 kHz uncertainty of the cavity-based data. The hypothetical unsplit central frequencies and ¹⁴N hyperfine components used in the fits are listed in Tables S3 and S4, ESI,† respectively. The nuclear coupling scheme used is: I_Ni + I_No = I_N; I_N + J = F. A comparison of the experimental and theoretical χ values will be discussed in Section 3.4 Structure and dynamics, while that of rotational and centrifugal distortion constants will be presented in Section 3.6 Benchmarking quantum chemical calculations.

Table 1 Theoretical and experimental spectroscopic parameters of the most stable HFIP⋯N₂ conformer, H_tN_H

Parameters	Theo.	Exp. fit I^f	Exp. fit II^f
a Ni (No) indicates the ^14N nucleus closer to (further away from) the HFIP subunit. Refer to Section 3.4 Structure and dynamics for the identification of the inner and outer ^14N nuclei. b Number of distinct frequencies included in the fit. c Standard deviation of the fit. d The listed theoretical rotational and nuclear quadrupole coupling constants were calculated at the equilibrium geometry. e The calculated harmonic/anharmonic quartic centrifugal distortion constants which are obtained using the τ values from the Gaussian output files and the conversion formulas from τ to quartic distortion constants.^55 f Exp. fit I parameters are obtained by fitting the hypothetical unsplit central rotational frequencies, while exp. fit II parameters are obtained by fitting the well-resolved ^14N nuclear quadrupole hyperfine components from the cavity-based measurements using an iterative procedure. See text for further discussion.
A/MHz	958.2^d	968.11413(69)	968.11413
B/MHz	743.0^d	734.35194(23)	734.35194
C/MHz	535.7^d	533.26427(12)	533.26427
Δ J /kHz	0.4441/0.4755^e	0.5227(29)	0.5227
Δ JK /kHz	1.7294/0.0542^e	2.791(14)	2.791
Δ K /kHz	−1.9849/−0.4094^e	−3.002(56)	−3.002
δ J /kHz	0.1313/0.1056^e	0.1184(14)	0.1184
δ k /kHz	−0.0037/0.4661^e	1.8455(73)	1.8455
χ aa (Ni)/MHz^a	−3.040^d	—	−2.490(18)
χ bb − χcc(Ni)/MHz	2.733^d	—	2.174(39)
χ aa (No)/MHz^a	−3.222^d	—	−2.621(17)
χ bb − χcc(No)/MHz	2.916^d	—	2.281(37)
N	—	40	78
σ/kHz^c	—	1.6	1.6

---

3.3 Molecular symmetry group and spin statistics

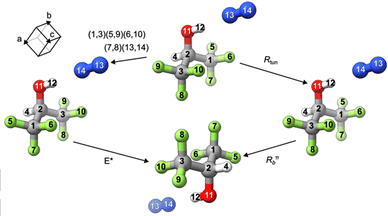
During the initial assignment based on the CP-FTMW data, there was much confusion about whether the two ¹⁴N nuclei are equivalent or not because of the large uncertainty associated with the assignment of ¹⁴N nuclear quadrupole hyperfine structures. Furthermore, it is desirable to verify whether the N₂ subunit undergoes internal tunnelling motions, similar to those in H₂O⋯N₂¹⁶ and CO⋯N₂,^17,18 making the two ¹⁴N nuclei equivalent. Nuclear spin statistics can offer insights into the equilibrium structure of a molecule and the nature of tunnelling motions since equivalent nuclei often lead to unique relative intensity patterns for the associated transitions.⁵⁶ A molecular symmetry (MS) group analysis based on nuclear permutation inversion group theory and the concept of feasible operations was performed, following the example of Ne⋯cyclopropane.⁵⁷ We start by assuming that the N₂ subunit undergoes free internal rotation, i.e., the two ¹⁴N nuclei are equivalent, and determine the corresponding MS group to be C_2V (MS), as shown in Table 2. The corresponding equivalent rotation labels are also included, where R₀ corresponds to the identity operation, R_tun describes the exchange of the two N nuclei, i.e., the internal tunnelling motion of the N₂ subunit, R^π_b means rotating 180° about the principal b-axis, and R^π_bR_tun is the direct product of the R^π_b and R_tun operations. In Fig. 4, the operation (1,3)(5,9)(6,10)(7,8)(13,14)* and the corresponding equivalent rotation are visualized.

Table 2 Character table of the C_2V molecular symmetry group with the equivalent rotation labels

C 2V	E	(13,14)	(1,3)(5,9)(6,10)(7,8)(13,14)*	(1,3)(5,9)(6,10)(7,8)*
Equi. rot.	R 0	R tun	R ^π b R tun	R ^π b
A 1	1	1	1	1
A 2	1	1	−1	−1
B 1	1	−1	−1	1
B 2	1	−1	1	−1

---

Fig. 4 Visualization of the operation (1,3)(5,9)(6,10)(7,8)(13,14)* and the associated equivalent rotation R^π_bR_tun. Note that the a- and c-axes are in the symmetry plane of the complex, and the b-axis is perpendicular to it.

Since the total wavefunction must be symmetric with respect to the permutation of bosons (spin I_N = 1 for the nitrogen nuclei and I_C = 0 for the carbon nuclei) and even permutation of fermions (spin I_F and I_H equal ½), and antisymmetric with respect to the odd permutation of fermions (spin I_F and I_H equal ½), it transforms as A₁ or A₂, taking into account the ± parity under the E* operation. Finally, the total number of spin functions is Π(2I_i + 1) = (2I_N + 1)² (2I_F + 1)⁶ (2I_C + 1)² (2I_H + 1) (2I_H + 1) (2I_C + 1) (2I_O + 1) = 3² × 2⁶ × 2² = 2304. The last four terms are related to the H, C and O nuclei in the symmetry plane, which do not undergo permutation. The reducible representation can be decomposed into 864A₁ + 672A₂ + 432B₁ + 336B₂. Next, we consider the symmetry labels of the rotational, tunnelling, vibrational and electronic states. To assign the symmetry of the rotational wavefunction, the rotational four-group V is used. Since the equivalent rotation of the HFIP⋯N₂ complex is R^π_b, the symmetry labels for the rotational levels K_aK_c = ee and oo are A₁ and for eo and oe are A₂. The ground (first excited) tunnelling state wavefunction transforms as A₁ (B₁), while the ground vibrational and electronic states are of A₁ symmetry. It is clear that in the ground tunnelling state, the rotational levels can only be combined with A₁ and A₂ spin functions, resulting in a total spin weight of 1536, whereas in the first excited tunnelling state, the rotational levels can only be combined with B₁ and B₂ spin functions, leading to a total spin weight of 768. As a result, the spin weight ratio is 2 : 1 for the ground versus the excited tunnelling state, where the former is associated only with ortho nitrogen (spin quantum numbers 0 and 2) and the latter with para nitrogen (spin quantum number 1).

As a result, if the two ¹⁴N nuclei are equivalent, the nuclear hyperfine structure patterns would be greatly simplified. For example, in the ground tunnelling state, the rotational transition 4₁₃ ← 3₁₂ (see Fig. 5) would exhibit only the nuclear hyperfine structure components (blue) corresponding to spin quantum numbers 0 and 2. Similarly, in the first excited tunnelling state, the same 4₁₃ ← 3₁₂ transition would display hyperfine structure components (red) corresponding to spin quantum number 1. These red components would appear elsewhere in the spectrum due to the different rotational constants in the excited tunnelling state. Clearly, the above prediction does not agree with the experimental observations. Rather, the experimental hyperfine structures align with those generated for spin quantum numbers 0, 1, and 2, without the spin statistics constraint predicted for two equivalent nitrogen nuclei. Therefore, based on the MS group theory analysis, one can confidently conclude that the two ¹⁴N nuclei in HFIP⋯N₂ are not equivalent, even though the difference in their nuclear quadrupole coupling constants are very small, only slightly larger than the uncertainties obtained (see Table 1).

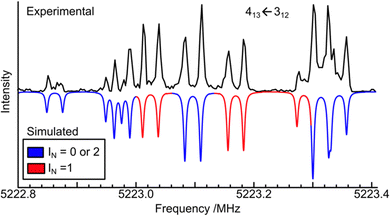Fig. 5 Experimental and simulated ¹⁴N nuclear quadrupole hyperfine components of the 4₁₃–3₁₂ rotational transition. The nuclear quadrupole coupling scheme used is: I_Ni + I_No = I_N; I_N + J = F. If the two nitrogen nuclei were equivalent, only the blue components with I_N = 0 and 2 would be present in the ground tunnelling state, whereas only the red components with I_N = 1 would be present in the first excited state and would appear in a different frequency region. See text for discussions. The experimental cavity-based FTMW spectrum is a composite of eight measurements centred at 5222.83, 5222.87, 5222.90, 5223.0, 5223.10, 5223.25, 5223.32, and 5223.37 MHz. Each hyperfine component is split into a pair of Doppler components.⁵³ The component centred at 5223.3 MHz contains a strong blue and a weak red component.

3.4 Structure and dynamics

The experimental nuclear quadrupole coupling constants of the two ¹⁴N nuclei (Table 1) differ slightly, consistent with the conclusion of their non-equivalency derived in the previous section. To determine which set of χ values belongs to the inner or outer ¹⁴N nucleus, we turned to the theoretical ¹⁴N coupling constants of H_tN_H and of the free N₂ molecule at the B3LYP-D3(BJ)/def2-QZVP and B3PW91/6-311+G(df,pd) levels. A previous theoretical benchmark study showed that the latter level of theory provides good predictions for nuclear quadrupole coupling constants.⁵⁸ The resulting theoretical χ values are summarized in Table 3, together with the corresponding experimental values. Since the experimental χ value of the free N₂ molecule is not available, we estimated this quantity from the corresponding ¹⁴N χ_cc values of the rare gas (Kr,⁵⁹ Ar,⁶⁰ Ne⁶¹)⋯N₂ complexes. It is important to point out that χ(N₂) is estimated from −2χ_cc of the complexes, which is independent of the large-amplitude vibrational motions common in these weakly bound complexes. Furthermore, the χ(N₂) value derived from all three complexes agrees within mutual error limits. Therefore, the average of all available data, χ(N₂) = −5.372(2) MHz is used here. The B3PW91/6-311+G(df,pd) χ(N₂) value agrees reasonably well with the experimental value, with a percentage error of 4.7%, whereas the B3LYP-D3(BJ)/def2-QZVP value shows a noticeably larger error of 13.2%.

Table 3 Comparison of theoretical and experimental ¹⁴N nuclear quadrupole coupling constants for H_tN_H and free N₂

Parameters	B3LYP-D3(BJ)/def2-QZVP	B3PW91/6-311+G(df,pd)	Experimental
a Diff is defined as (χbb − χy)/χy in percent. All corresponding values are bolded for easy recognition. b The values are taken directly from or derived from the values listed in Table 1 using the relationship χaa + χbb + χcc = 0. c For the free N2 molecule, χx= χy = −1/2χz = −1/2χ(N2) by symmetry.
HFIP⋯N2 HtNH conformer
χ aa (Ni)/MHz	−3.0396	−2.8965	−2.490(18)^b
χ bb (Ni)/MHz	2.8864	2.6784	2.332(21)
Diff^a	−5.1%	−4.8%	−13.2%
χ cc (Ni)/MHz	0.1533	0.21809	0.158(21)^b
χ aa (No)/MHz	−3.2220	−3.0885	−2.621(17)^b
χ bb (No)/MHz	3.0688	2.8580	2.451(20)
Diff^a	+0.9%	+1.6%	−8.7%
χ cc (No)/MHz	0.1532	0.2304	0.170(20)^b
Free N2 molecule
χ x /MHz	3.0400	2.8136	2.686(1)^c
χ y /MHz	3.0400	2.8136	2.686(1)
χ z /MHz	−6.0801	−5.6271	−5.372(2)^c

---

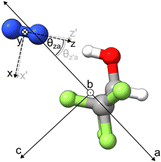
The comparison between the experimental and theoretical χ values of the weakly bound complex is more nuanced. Assuming that at equilibrium, the N₂ subunit lies in the symmetry plane of H_tN_H as predicted theoretically, the b-axis of H_tN_H (see Fig. 6) is expected to be parallel with one of the principal axes of the ¹⁴N nuclear quadrupole coupling tensor (the axis labelled as y), which is perpendicular to the N–N axis (labelled as z). Ignoring any charge redistribution upon complexation at the ¹⁴N nuclei of N₂ and effects of the out-of-plane (i.e., the symmetry plane) N₂ vibrational motions, the χ_bb and χ_y values would be identical. Therefore, the difference between the theoretical χ_bb of H_tN_H and χ_y of N₂ values directly reflects the effect of the hydrogen bonding interaction since no large-amplitude vibrational contributions are considered. While χ_bb(N_o) of the complex is 1.6% larger than χ_y of N₂, the corresponding χ_bb(N_i) is 4.8% smaller at the B3PW91 level, indicating a more noticeable change of the electric field gradient at the inner versus outer ¹⁴N nucleus upon complexation. The same trend with +0.9% and −5.1% is predicted at the B3LYP level. Based on this common theoretical trend, we can confidently associate the sets of the experimental χ values with the inner and outer ¹⁴N, as shown in Tables 1 and 3. It is important to note that the corresponding experimental changes in χ_bb(N_i) and χ_bb(N_o) from the χ_y value are −13.2% and −8.7%, respectively, both of which are much larger than the theoretical changes shown above. This discrepancy can be attributed to the out-of-plane vibrational motions of the N₂ subunit in the complex, which are expected to further reduce both χ_bb(N_i) and χ_bb(N_o) by a similar percentage. This point will be discussed in more detail below.

Fig. 6 Orientation of the N₂ subunit in the most stable conformer of the HFIP⋯N₂ complex, H_tN_H. The optimized geometry at the B3LYP-D3(BJ)/def2-QZVP level yields θ_za, θ_zb, and θ_zc values of 34.2°, 90.0°, and 55.8°, respectively. These can be compared with the corresponding angles of 35.8°, 80.2°, and 56.0° derived from the outer ¹⁴N nuclear quadrupole coupling constants; see the main text for details. The symmetry plane of HFIP⋯N₂ coincides with the paper plane, where only the front CF₃ group is visible, while the other CF₃ group is nearly completely obscured.

As demonstrated in Table 3, complexation has only a very minor effect on the electric field gradient at the outer ¹⁴N nucleus. Therefore, the χ(N_o) constants are used to extract the orientation of the N₂ subunit in the complex, ignoring the vibrational effects. Under the above conditions, the χ_aa, χ_bb, and χ_cc values are projections of the free N₂ nuclear quadrupole coupling tensor onto the principal inertial axes of the complex. Using the equation χ_aa = χ_zP₂(cos θ_za) = ½χ_z (3cos² θ_za − 1),⁵³ we obtained a θ_za value of 35.8°, as well as θ_zb and θ_zc values of 80.2° and 56.0°, respectively, using the analogous formulas. It is well known that in weakly bound complexes, large amplitude vibration motions can have considerable effects on the resulting χ values. However, it is often difficult to separate the effects from vibrational motions and orientation.

For θ_zb, the equilibrium value is 90°, as established by the DFT calculation and verified experimentally through the absence of b-type transitions. The derived value of 80.2° can be seen as an indication of the noticeable out-of-plane vibrational amplitude. For θ_za and θ_zc, their equilibrium values are 34.2° and 55.8°, respectively, which are very similar to the values of 35.8° and 56.0° derived from the experimental χ(N_o). This suggests that the effects of in-plane vibrations are much smaller than those of out-of-plane vibrations.

3.5 Infrared spectra

The experimental OH stretching infrared spectra obtained with only HFIP and with a mixture of HFIP and N₂ in jet expansions are shown in Fig. 7. The uncertainties for unresolved band centre positions are conservatively estimated to be ±2 cm⁻¹, consistent with the observed width, the employed resolution, and minor asymmetries.⁶² Upon nitrogen addition, a new vibrational band (see ref. 10 where a tentative assignment with wavenumber was already given) appears at 3605 ± 2 cm⁻¹, downshifted from the isolated H_t monomer vibration by 18 ± 4 cm⁻¹. This new band can be unambiguously assigned to the hydrogen-bonded binary complex H_tN_H since this is the only H_t structure (among those listed in Table S1, ESI†) with a significant OH stretching downshift predicted. The magnitude of the nitrogen-induced spectral shift is very similar to the one found for binary aggregates of nitrogen with small carboxylic acids⁶⁰ like formic acid (17 ± 4 cm⁻¹) and acetic acid (13 ± 6 cm⁻¹), but significantly smaller than the ≥34 cm⁻¹ for the corresponding vibration in the ternary complexes of N₂ with the most stable HFIP dimer and the metastable dimer.¹⁰ The cooperative effects in the HFIP dimers greatly enhance their capacity as a hydrogen bond donor and, therefore, lead to such large downshifts, even by a weak hydrogen bond acceptor like nitrogen.

Fig. 7 The OH-stretching FTIR spectra of HFIP/He expansions with (top trace c) and without (bottom trace a) addition of dinitrogen. A monomer-corrected difference spectrum (trace b) is included. Wavenumbers and labels for the proposed assignments (monomer H_t, binary complex H_tN_H) are provided.

3.6 Benchmarking quantum chemical calculations

The popular double harmonic approximation applied in most quantum chemical calculations poses a major obstacle for direct comparisons of theoretical predictions with experimental findings for both rotational^63,64 and vibrational data.⁶⁰ Therefore, a careful assessment of experimental errors and deviations introduced by neglecting anharmonic vibrational effects on rotational constants and vibrational band centre positions is necessary. This assessment allows us to define error bounds for predictions from harmonic theory that can be considered compatible with experimental findings.

Before discussing the rotational constants and OH vibrational band positions, we first compare the experimental and theoretical quartic centrifugal distortion constants (see Table 1). The signs for Δ_J, Δ_JK, Δ_K and δ_J were correctly predicted, and the calculated magnitudes agree reasonably well with the experimental values, showing deviations similar to those recently reported for several monomeric species.⁶⁵ However, the predicted sign and magnitude for δ_k deviate significantly. This discrepancy is unsurprising, given that HFIP⋯N₂ is a weakly bound complex with pronounced large-amplitude motions, as discussed in the previous section. The anharmonic calculation produced correct signs for all distortion constants, although the agreement in magnitudes improved in some cases and worsened in others. A recent study has noted that even for small linear molecules, anharmonic effects can contribute substantially, though the reasons for such large contributions in certain cases remain unclear.⁶⁶ For these reasons, quartic centrifugal distortion constants are excluded from the following benchmark discussions.

Typically, theoretical rotational constants are derived from equilibrium structures, neglecting both harmonic and anharmonic vibrational effects.⁶² This leads to deviations between theoretical and experimental rotational constants. To include only harmonic effects would be counterproductive, as they typically have the opposite sign and a smaller magnitude when compared with anharmonic effects, as seen easily for diatomic molecules.⁶⁷ On average, vibrational effects contribute about 0.2% to 1.6% in terms of rotational constants for most small molecules.⁶¹ We have adopted these values as the lower and upper bounds of the anharmonic contribution to rotational constants for the HFIP monomer, H_t. For (very) weakly bound binary complexes, the centre of mass separation between the two subunits in the ground vibrational state is noticeably larger than at equilibrium. For instance, in He⋯N₂O, the equilibrium distance at the CCSD(T)/aug-cc-pVTZ level is 2.979 Å, whereas the experimental ground-state separation is 3.3915 Å.⁶⁸ Consequently, equilibrium rotational constants tend to be larger than their ground-state counterparts, and vibrational effects on rotational constants can thus exceed 10%. For less weakly bound complexes, a range of −2% to +4% was previously proposed.⁶⁹ Here, we choose a more moderate extension of the small molecule range from 0 to 1.8% for anharmonic effects in A, B, and C of the weakly bound H_tN_H complex, though future work may refine these bounds.

While a full list of all theoretical rotational constants (i.e., A_e, B_e, and C_e) of H_t and H_tN_H can be found in Table S5, ESI,† the relative deviations—defined as (A_e − A_exp)/A_e, (B_e − B_exp)/B_e, and (C_e − C_exp)/C_e—are depicted for H_t and H_tN_H at multiple levels of theory in Fig. S2–S4, ESI.† From the plots, one can see that, in general, relative deviations of theory from experiment are lowest for A and substantially larger for B and C. While the MP2, PBE0-D3 and M06-2X methods predict A for both the monomer and dimer within the constraint percentages for nuclear motion effects, none of the methods successfully predict B and C for either structure within the constraint percentages. SCS-MP2 generally predicts dimer rotational constants that are too low, while B2PLYP-D3 predicts monomer constants that are too low in most cases and dimer constants that are somewhat too high.

With regard to the OH vibrational wavenumbers, the experimental anharmonic trans monomer OH stretching band centre of 3623 ± 2 cm⁻¹ needs to be converted to an estimated experimental harmonic value to allow for comparison with theoretical values predicted within the double harmonic approximation.⁶⁰ This was done using the experimental overtone band position²⁶ of 7078 cm⁻¹ and the resulting diagonal anharmonicity of 84 ± 2 cm⁻¹. 10% of the diagonal anharmonicity is added to the error bar due to an unknown sum of off-diagonal contributions, resulting in an estimated harmonic monomer band centre of (3791 ± 23) cm⁻¹.¹⁰ For the H_tN_H complex, neither the overtone band nor any combination bands are known. For this reason, a large error bar of 50% of the entire anharmonic downshift of 18 ± 4 cm⁻¹ was added to the experimental uncertainty when comparing the experimental downshift to the harmonic predictions.^10,60 Therefore, predicted OH stretching downshifts of (18 ± 13) cm⁻¹ will be regarded as being compatible with experiment.⁶⁷

The predicted harmonic (ω_OH) OH stretching wavenumber, hydrogen bond induced downshift (Δω_OH), lowest predicted wavenumber (ω₁, typically CF₃ torsion in H_t and intermolecular torsion in H_tN_H), and IR intensity (S_OH) at multiple levels of theory are summarized in Table S5, ESI.† In Fig. 8, the ω_OH values at multiple levels of theory are plotted against the Δω_OH values. The corresponding plots for complexes of N₂ with formic acid and acetic acid exhibit very similar distribution patterns with respect to different levels of theory.⁶⁰ The methods that correctly predict the downshift and the monomer band position are SCS-MP2/aVTZ and B2PLYP-D3/VTZ. The fact that the predicted rotational constants at these levels of quantum chemical approximation do not match the experimental ones very well after allowing for typical vibrational effects and that the agreement with the vibrational experiment gets worse with increasing basis set size hints at substantial error cancellation. The MP2 and B3LYP-D3 methods, as well as the B2PLYP-D3 method with the three other basis sets, accurately predict the monomer OH stretching wavenumbers but overestimate the downshifts induced by the OH⋯N₂ interaction.

Fig. 8 Theoretically predicted harmonic O–H stretching band position of H_t (ω_OH(H_t)) plotted against the harmonic downshift (Δω_OH) from H_t to H_tN_H for different computational methods. Each method is represented by a symbol. For MP2, SCS-MP2, and B2PLYP-D3, four basis sets (VTZ, aVTZ, VQZ, and aVQZ) were used. Increasing basis set size from VTZ to aVQZ is indicated by progressively larger symbols, which are connected by dashed lines for each method. The experimental harmonic monomer band position was approximately derived from the fundamental and first overtone transitions.^10,26 Experimental wavenumber downshifts are anharmonic. Harmonic values are assumed to deviate from them by up to ±50% due to anharmonic effects for hydrogen-bond-induced shifts.^10,60 The estimated zone of incompatibility with the experiment is dark grey, and predictions within the white area are compatible with experiment for both properties.

Of the tested electronic structure methods, which are routinely used for systems such as HFIP⋯N₂ and even those of smaller size, none are able to predict accurate structures and vibrational energy levels simultaneously. Overall, depending on the employed basis set, SCS-MP2 may come closest. It appears that an inexpensive level of computation, which is applicable to such a model system of weak hydrogen bonding and provides consistent agreement with experiments in the field of rotational and vibrational spectroscopy within rather generous error bars, is yet to be found. One may choose composite methods, like structure optimization and harmonic frequency calculation at a less expensive level followed by accurate single point energy calculations to correct the electronic energy error, but such approaches hide and mix the limits of each component calculation. For systems of this size and complexity, experiment currently remains the only reliable source for vibrational shifts induced by weak hydrogen bonds, and their harmonic contribution remains quite uncertain. It is somewhat unsatisfactory that weak perturbations of stable molecules by inert binding partners like nitrogen are still so poorly understood at a modest quantitative level.

4. Conclusions

The combined analysis of the experimental rotational spectrum and the ¹⁴N nuclear quadrupole hyperfine splittings, supported by theoretical calculations, unambiguously determines the global minimum energy structure of the weakly bound HFIP⋯N₂ complex, H_tN_H. This conformer, featuring a trans-HFIP conformation with N₂ weakly bound at the acidic proton, is considerably favoured over other binding topologies predicted theoretically. The identification of the inner and outer ¹⁴N nuclei was achieved by comparing experimental and theoretical ¹⁴N χ values in H_tN_H and free N₂, while their non-equivalency was confirmed through a detailed molecular symmetry group analysis. Further examination of the ¹⁴N nuclear quadrupole coupling constants revealed large-amplitude vibrational motions of the N₂ subunit in the out-of-plane direction (approximately 10°), with in-plane motions being much more restricted.

Although N₂ forms a weak yet directional hydrogen bond with the alcohol OH proton, this interaction induces a noticeable downshift in the OH stretching vibrational frequency. Both the rotational constants and the infrared downshift provide critical benchmarks for quantum chemical calculations. The results reveal that none of the tested electronic structure methods accurately predicts both structures and vibrational energy levels simultaneously, suggesting substantial error cancellation in cases of selectively accurate predictions. The findings underscore the vital role of experimental data in identifying such error cancellation and refining theoretical models.

Author contributions

Conceptualization, SEB and YX; formal analysis, SEB, SO, NAS, and BW; investigation, SEB, SO, NAS, and BW; data curation, SEB, NAS, BW, WJ; writing – original draft preparation, SEB (main), SO and YX; writing – review and editing, SEB, WJ, MS, NAS and YX; visualization, SEB and SO; supervision, YX, WJ and MS; funding acquisition and resources, YX and WJ. All authors have read and agreed to the published version of the manuscript.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was funded by the Natural Sciences and Engineering Research Council (NSERC) of Canada and the University of Alberta. We gratefully acknowledge access to the computing facilities by the Shared Hierarchical Academic Research Computing Network (SHARCNET), the Western Canada Research Grid (Westgrid), and Digital Research Alliance of Canada. SEB acknowledges an NSERC undergraduate summer research award. We thank CD Carlson for discussions about centrifugal distortion constants. SO thanks the Fonds der Chemischen Industrie for financial support. BW acknowledges the support of a H. E. Gunning Research Fellowship. YX is a Tier 1 Canada Research Chair in Chirality and Chirality Recognition.

References

1. Draft state of per- and polyfluoroalkyl substances (PFAS) report, https://www.canada.ca/en/environment-climate-change/services/evaluating-existing-substances/draft-state-per-polyfluoroalkyl-substances-report.html, (accessed April 1, 2024).
2. Our Current Understanding of the Human Health and Environmental Risks of PFAS, https://www.epa.gov/pfas/our-current-understanding-human-health-and-environmental-risks-pfas, (accessed April 1, 2024).
3. L. Eberson, M. P. Hartshorn and O. Persson, J. Chem. Soc., Perkin Trans. 2, 1995, 1735–1744.
4. I. Colomer, A. E. R. Chamberlain, M. B. Haughey and T. J. Donohoe, Nat. Rev. Chem., 2017, 1, 0088.
5. A. Berkessel and J. A. Adrio, Adv. Synth. Catal., 2004, 346, 275–280.
6. P. J. Godin, K. Le Bris and K. Strong, J. Quant. Spectrosc. Radiat. Transfer, 2017, 203, 522–529.
7. A. J. Barnes and J. Murto, J. Chem. Soc., Faraday Trans. 2, 1972, 68, 1642–1651.
8. J. R. Durig, R. A. Larsen, F. O. Cox and B. J. van der Veken, J. Mol. Struct., 1988, 172, 183–201.
9. A. Shahi and E. Arunan, J. Phys. Chem. A, 2015, 119, 5650–5657.
10. S. Oswald and M. A. Suhm, Angew. Chem., Int. Ed., 2017, 56, 12672–12676.
11. S. Oswald, N. A. Seifert, F. Bohle, M. Gawrilow, S. Grimme, W. Jäger, Y. Xu and M. A. Suhm, Angew. Chem., Int. Ed., 2019, 58, 5080–5084.
12. A. Shahi and E. Arunan, Phys. Chem. Chem. Phys., 2015, 17, 24774–24782.
13. B. Wu, A. S. Hazrah, N. A. Seifert, S. Oswald, W. Jäger and Y. Xu, J. Phys. Chem. A, 2021, 125, 10401–10409.
14. B. Wu, N. A. Seifert, S. Oswald, W. Jäger and Y. Xu, J. Phys. Chem. A, 2021, 125, 5355–5364.
15. Q. Yang, F. Xie, T. Lu, N. Bui, W. Jäger and Y. Xu, J. Mol. Spectrosc., 2021, 376, 111408.
16. H. O. Leung, M. D. Marshall, R. D. Suenram and F. J. Lovas, J. Chem. Phys., 1989, 90, 700–712.
17. Y. Xu, W. Jäger, L. A. Surin, I. Pak, L. A. Panfilov and G. Winnewisser, J. Chem. Phys., 1999, 111, 10476–10483.
18. Y. Xu and W. Jäger, J. Chem. Phys., 2000, 113, 514–524.
19. R. A. Mata and M. A. Suhm, Angew. Chem., Int. Ed., 2017, 56, 11011–11018.
20. N. A. Seifert, J. Thomas, W. Jäger and Y. Xu, Phys. Chem. Chem. Phys., 2018, 20, 27630–27637.
21. F. Xie, N. A. Seifert, W. Jäger and Y. Xu, Angew. Chem., Int. Ed., 2020, 59, 15703–15710.
22. C. Pérez, S. Lobsiger, N. A. Seifert, D. P. Zaleski, B. Temelso, G. C. Shields, Z. Kisiel and B. H. Pate, Chem. Phys. Lett., 2013, 571, 1–15.
23. A. Insausti, J. Ma, Q. Yang, F. Xie and Y. Xu, ChemPhysChem, 2022, 23, e202200176.
24. Y. Xu and W. Jäger, J. Chem. Phys., 1997, 107, 4788–4796.
25. T. J. Balle and W. H. Flygare, Rev. Sci. Instrum., 1981, 52, 33–45.
26. M. A. Suhm and F. Kollipost, Phys. Chem. Chem. Phys., 2013, 15, 10702–10721.
27. S. Grimme, J. Chem. Theory Comput., 2019, 15, 2847–2862.
28. P. Pracht, S. Grimme, C. Bannwarth, F. Bohle, S. Ehlert, G. Feldmann, J. Gorges, M. Müller, T. Neudecker, C. Plett, S. Spicher, P. Steinbach, P. A. Wesołowski and F. Zeller, J. Chem. Phys., 2024, 160, 114110.
29. C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671.
30. A. N. Mort, F. Xie, A. S. Hazrah and Y. Xu, Phys. Chem. Chem. Phys., 2023, 25, 16264–16272.
31. C. D. Carlson, J. Ma, M. H. Al-Jabiri, A. Insausti and Y. Xu, Phys. Chem. Chem. Phys., 2024, 26, 18067–18075.
32. A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377.
33. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
34. E. Caldeweyher, S. Ehlert, A. Hansen, H. Neugebauer, S. Spicher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2019, 150, 154122.
35. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
36. A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829–5835.
37. F. Neese, Wiley Interdiscip. Rev.:Comput. Mol. Sci., 2022, 12, e1606.
38. F. Weigend, Phys. Chem. Chem. Phys., 2002, 4, 4285–4291.
39. F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065.
40. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Peterssonet al., Gaussian 09 Revision E.01, Gaussian, Inc., Wallingford CT, 2009.
41. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, et al., Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016.
42. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
43. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
44. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566.
45. S. Grimme, J. G. Brandenburg, C. Bannwarth and A. Hansen, J. Chem. Phys., 2015, 143, 054107.
46. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
47. M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminf., 2012, 4, 1–17.
48. E. F. Pettersen, T. D. Goddard, C. C. Huang, G. S. Couch, D. M. Greenblatt, E. C. Meng and T. E. Ferrin, J. Comput. Chem., 2004, 25, 1605–1612.
49. S. Oswald, M. Wallrabe and M. A. Suhm, J. Phys. Chem. A, 2017, 121, 3411–3422.
50. J. K. G. Watson, Vibrational Spectra and Structure: A Series of Advances, Elsevier, New York, 1977, vol. 6.
51. C. M. Western, J. Quant. Spectrosc. Radiat. Transfer, 2017, 186, 221–242.
52. J. P. Anable, D. E. Hird, S. L. Stephens, D. P. Zaleski, N. R. Walker and A. C. Legon, Chem. Phys. Lett., 2015, 625, 179–185.
53. J. B. Davey, A. C. Legon and E. R. Waclawik, J. Mol. Struct.:THEOCHEM, 2000, 500, 403–411.
54. J.-U. Grabow and W. Stahl, Z. Naturforsch., A:Phys. Sci., 1990, 45, 1043–1044.
55. W. Gordy and R. L. Cook, Microwave molecular spectra, John Wiley & Sons, Inc., 2nd edn, 1984.
56. P. R. Bunker and P. Jensen, Molecular Symmetry and Spectroscopy, NRC Research Press, Ottawa, 2nd edn, 2006.
57. Y. Xu and W. Jäger, J. Chem. Phys., 1997, 106, 7968–7980.
58. W. C. Bailey, Chem. Phys., 2000, 252, 57–66.
59. W. Jäger, Y. Xu, N. Heineking and M. C. L. Gerry, J. Chem. Phys., 1993, 99, 7510–7520.
60. W. Jäger, M. C. L. Gerry, C. Bissonnette and F. R. W. McCourt, Faraday Discuss., 1994, 97, 105–118.
61. W. Jäger, Y. Xu, G. Armstrong, M. C. L. Gerry, F. Y. Naumkin, F. Wang and F. R. W. McCourt, J. Chem. Phys., 1998, 109, 5420–5432.
62. S. Oswald, E. Meyer and M. A. Suhm, J. Phys. Chem. A, 2018, 122, 2933–2946.
63. T. Risthaus, M. Steinmetz and S. Grimme, J. Comput. Chem., 2014, 35, 1509–1516.
64. S. Grimme and M. Steinmetz, Phys. Chem. Chem. Phys., 2013, 15, 16031.
65. B. Hartwig, M. Schnell, M. A. Suhm and D. A. Obenchain, Phys. Chem. Chem. Phys., 2024, 26, 9432–9452.
66. P. R. Franke and J. F. Stanton, J. Chem. Phys., 2024, 160, 014102.
67. G. Herzberg, Molecular Spectra and Molecular Structure. I. Spectra of Diatomic Molecules, Van Nostrand, New York, 2nd edn, 1950.
68. X. Song, Y. Xu, P. N. Roy and W. Jäger, J. Chem. Phys., 2004, 121, 12308–12314.
69. S. Oswald and M. A. Suhm, Phys. Chem. Chem. Phys., 2019, 21, 18799–18810.

---

Footnote

† Electronic supplementary information (ESI) available: Cartesian coordinates of 11 conformers, experimental CP-FTMW spectrum, lists of transition frequencies including ¹⁴N nuclear quadrupole hyperfine components, plots of relative deviation of predicted rotational constants from the experimental ones, theoretical predictions of ω_OH, Δω_OH, ω₁, and other properties at multiple levels of theory. See DOI: https://doi.org/10.1039/d5cp00478k

---